Evaluation of HFE-73DE/Ethyl Acetate Mixtures for Use in Minichannel Heat Exchangers

Abstract

Binary mixtures of HFE-73DE and ethyl acetate are investigated as dielectric working fluids for laminar minichannel cooling. Thermophysical properties of the pure components and four mixtures (10/90, 25/75, 50/50 and 75/25 mass % HFE-73DE/ethyl acetate) were measured over the relevant temperature range. Single-phase convective heat transfer tests were then carried out in a heated 1 × 4 × 180 mm minichannel test section under constant heat-flux conditions for pure HFE-73DE. A three-dimensional conjugate CFD model with temperature-dependent liquid properties was developed in Simcenter STAR-CCM+ and validated against these measurements; the average relative temperature difference between CFD and experiment remained below 0.5%, while a grid-convergence study based on the Grid Convergence Index (GCI) confirmed that the numerical uncertainty is comparable to the experimental one. The validated model was subsequently used to predict the axial evolution of wall temperature, fluid-core temperature, velocity and heat transfer coefficient for the four mixtures under identical conditions. The mean Nusselt numbers obtained from CFD were further compared with the classical Shah and London fully developed laminar solution for rectangular ducts, revealing that the present configuration yields values about 35–42% higher than the theoretical prediction owing to asymmetric heating and conjugate heat transfer. The results show that increasing the HFE-73DE mass fraction strengthens convective heat transfer and reduces fluid-temperature rise, while intermediate compositions (50/50 and 75/25) provide a favourable compromise between enhanced heat transfer performance and moderate pressure drop. The study provides guidance for composition selection and the design of dielectric minichannel heat exchangers operating with HFE-73DE/ethyl acetate mixtures.

1. Introduction

Heat exchangers are fundamental components in thermal systems, from refrigeration and air conditioning through high power electronics, to cryogenic systems, photovoltaics, and industrial installations. Their efficiency depends to a large extent on the selection of the working medium, whose thermophysical properties must be matched to the requirements of a given application: temperature range, operating pressures, flow character (laminar, turbulent), as well as chemical compatibility and operational safety. Among modern refrigerants, fluorinated compounds are gaining widespread use, including fluids from the HFE (hydrofluoroethers), PFPE (perfluoropolyethers) and FC (fluorinerts) groups. They are characterised by low electrical conductivity, high chemical and thermal stability, and wide normal-pressure boiling ranges (from about 300 K to over 500 K), which makes them particularly useful in cooling electronic and optoelectronic components. Despite these advantages, such fluids have limited thermal conductivity and are often expensive, which motivates the search for mixtures that enable the working fluid properties to be tuned to specific process needs. Binary mixtures of fluorinated liquids with organic solvents or other fluorinated fluids are being intensively studied as potential alternatives to ionic liquids and nanofluids. They enable the design of media with specified boiling temperature, density, viscosity, and specific heat while maintaining compatibility with existing construction materials and pumping systems.

Muñoz-Rujas et al. [1] investigated the thermophysical properties of binary HFE-7200 + 2-propanol mixtures over a wide pressure range (0.1–140 MPa) and several temperatures (293.15–393.15 K). The density data were correlated using a Tait-type equation, derivative properties were evaluated, and sound speeds were measured at 0.1 MPa. In a related study [2], the authors reported sound speed and density data for HFE-7500 + diisopropyl ether mixtures up to 100 MPa. Aminian et al. [3] modelled the ideal-gas heat capacity and critical properties of hydrofluoroethers from the HFE-7000–7500 series using ab initio methods combined with Peng–Robinson equations of state. Urata et al. [4] proposed an artificial-neural-network model to predict vapour–liquid equilibria in HFE-containing systems. Xu et al. [5] demonstrated that zeotropic, partially immiscible mixtures in pulsating heat pipes can form emulsions enhancing heat transfer. Ogawa et al. [6] analysed the thermodynamic properties of hydrofluoroether mixtures with selected organic solvents and reported positive excess molar volumes and composition-dependent excess enthalpies. HFE-73DE has been identified as an attractive base component because it is non-flammable, electrically non-conductive, and exhibits a relatively low normal-boiling temperature (≈314.35 K), making it favourable for low-temperature, two-phase cooling. Ethyl acetate (EA), on the other hand, shows moderate polarity, low viscosity, relatively high specific heat, and complete miscibility with many organic and fluorinated liquids. Combining HFE-73DE with EA provides a simple and practical way to tune key thermophysical properties without resorting to complex or costly working media such as ionic liquids or nanofluids. However, the mixture behaviour is rarely ideal: excess volumes and enthalpies, zeotropic effects, as well as sequential boiling and entrainment, can shift the apparent boiling temperature and alter heat- and mass-transfer characteristics. These phenomena remain insufficiently characterised for HFE-based binary systems within the composition range relevant to compact heat exchangers.

Other researchers have also examined different aspects of binary mixtures, focussing not only on thermophysical and transport properties but also on molecular interactions, phase behaviour, and interfacial phenomena.

Eissa et al. [7] developed a generalised non-equilibrium heat transfer model for predicting flow condensation of binary zeotropic mixtures, integrating vapour-phase mass diffusion and interfacial temperature coupling. Their framework, validated against 871 experimental data points, demonstrated excellent agreement with the measurements (92% within ±30%), providing a robust tool for designing compact heat exchangers. Wu et al. [8] proposed a machine learning-based group contribution model for estimating critical temperatures of binary refrigerant mixtures from molecular structure. Using 275 data points for 61 systems, the MLP algorithm achieved R² > 0.99 and accurately captured nonlinear composition effects, supporting the design of low GWP refrigerant blends. Verma et al. [9] investigated the thermophysical properties of binary mixtures containing diethyl ether and hydrocarbons (cyclohexane, benzene, toluene). From density, ultrasonic velocity, and refractive index data, they revealed strong donor–acceptor interactions between ether oxygen and aromatic π-electrons, especially in the ether + toluene system, highlighting structure-dependent molecular association. Tsai et al. [10] performed molecular dynamics simulations to evaluate the transport properties of alcohol/water mixtures, testing 25 force field combinations. The TIP4P/2005 + OPLS-AA pairing yielded the best overall accuracy for predicting diffusion and density, providing a benchmark for simulating mass-transfer processes in aqueous organic systems. Soria-Lopez et al. [11] compared classical viscosity mixing rules with ML algorithms for 67 binary alkane mixtures at 298 K. The Redlich–Kister correlation and the SVM model achieved the highest accuracy, demonstrating that machine learning can effectively capture nonlinear composition–viscosity relationships, offering a modern alternative to empirical correlations.

In addition to property-oriented studies of liquid mixtures, numerous numerical investigations of flow boiling in mini- and microchannel geometries have been reported. Recent work increasingly employs diffuse-interface and phase-field formulations to resolve bubble-scale dynamics. Using a Cahn–Hilliard phase-field model implemented in COMSOL Multiphysics^TM, the authors in [12] simulated subcooled water boiling from a single artificial cavity in a square microchannel. Their model resolved bubble nucleation, growth, departure and subsequent slug-flow development. The results showed that cavity-induced boiling can locally enhance the wall heat transfer coefficient by more than an order of magnitude compared with single-phase convection, although this enhancement decays as the flow becomes thermally developed in the streamwise direction. The local heat flux and heat transfer coefficient exhibit pronounced temporal oscillations, with higher average values at larger mass fluxes, while the peak heat transfer coefficient gradually decreases as mass flux is increased. In [13], 2D numerical simulations of flow boiling using the Cahn–Hilliard phase-field method were performed for a 200 µm wide microchannel with single and multiple cavities in COMSOL Multiphysics^TM (v5.3). It was demonstrated that bubble nucleation and thin-film evaporation dominate the heat-transfer mechanism. Increasing the number of active cavities from two to five significantly intensified bubble interaction and coalescence, yielding an approximate 30% increase in overall heat-transfer performance compared with the single-cavity configuration. In [14], stratified flow boiling in rectangular mini-channels was analysed using a coupled volume-of-fluid and level-set (VOSET) method. The simulations showed that, compared with fully filled channels, stratified configurations can promote bubble detachment, reduce dry-patch formation and lower wall superheat by up to about 28%, owing to favourable free-surface fluctuations and bubble-merging processes. At higher heat fluxes, fragmentation of the thin liquid film near the channel outlet increases the area of local dry patches and locally deteriorates heat transfer, although the net effect of fluctuation and merging can still yield a modest overall enhancement (on the order of 9–12% for selected conditions). For even higher heat fluxes and thicker liquid films, lifting of the liquid layer by vapour can induce film boiling and a marked degradation of heat-transfer performance, highlighting the need to control the liquid-film height to avoid detrimental fragmentation and lifting effects.

Despite the growing interest in fluorinated dielectric liquids and their mixtures, and the progress in high-fidelity flow boiling simulations discussed above, systematic data on the thermophysical properties and convective heat-transfer performance of HFE-type binary systems in minichannel configurations remain limited. In particular, there is a lack of combined experimental and numerical studies that quantify how the composition of HFE-based mixtures influences local heat transfer coefficients, fluid temperature and velocity distributions under well-controlled single-phase conditions in compact geometries. This gap constrains the rational selection and optimisation of such mixtures for minichannel heat exchangers and electronics-cooling applications, where electrical insulation, environmental acceptability and thermal efficiency must be balanced.

The present work addresses this gap by:

• experimentally characterising the key thermophysical properties of HFE-73DE/ethyl acetate mixtures over a composition range relevant for thermal-engineering applications;
• analysing single-phase laminar heat transfer in a heated minichannel module for a selected base fluid (pure HFE-73DE) under representative operating conditions;
• developing and validating a three-dimensional CFD model that reproduces the experimentally observed thermal and hydraulic behaviours, including conjugate heat transfer and temperature-dependent liquid properties.

In addition, the predicted mean Nusselt numbers are benchmarked against the classical fully developed laminar solution of Shah and London for a rectangular duct with all walls uniformly heated, which allows the enhancement due to asymmetric heating and conjugate heat conduction to be quantified. The validated model is then used to analyse the influence of mixture composition on the axial distributions of heat transfer coefficient, velocity and fluid-core temperature. The overall objective is to provide quantitative guidance for the design and optimisation of minichannel heat exchangers employing HFE-73DE/ethyl acetate mixtures as tunable dielectric working fluids.

The paper is organised as follows. Section 2 introduces the investigated HFE-73DE/ethyl acetate mixtures and summarises their experimentally determined thermophysical properties. Section 3 describes the experimental setup, measurement techniques and data-reduction procedures. Section 4 presents the three-dimensional CFD model and its numerical implementation. Section 5 discusses the experimental and numerical results, Section 6 presents validation and verification of the numerical model, while Section 7 summarises the main conclusions and outlines directions for future work.

2. Selected Binary Mixtures and Property Analysis

Two completely miscible liquids with different physicochemical properties were selected for the study: the fluorinated ether HFE-73DE and the organic ester ethyl acetate. Both components exhibit favourable features for use in thermal systems, while their combination allows a mixture with intermediate properties and adjustable working fluid parameters. Binary mixtures were investigated for selected mass fractions, determining the boiling temperature, thermal conductivity, density, and specific heat.

3M^TM Novec^TM 73DE [15] is a specialised fluorinated ether from the family of engineered fluids, originally designed for vapour phase degreasing and precision cleaning in immersion baths. It features high solvating power, low surface tension, non-flammability, and excellent physicochemical stability. From a thermal engineering perspective, 73DE offers a low boiling temperature at normal pressure (~314.35 K), high density (~1520 kg/m³), low kinematic viscosity (~0.4 × 10⁻⁶ m²/s), low thermal conductivity (~0.075 W/(m·K)), and moderate specific heat (~1020 J/(kg·K)). It is electrically nonconducting, chemically inert and compatible with a broad range of construction materials.

Ethyl acetate [16] is a widely used solvent of moderate polarity. Its physical properties, including a relatively low viscosity and a high specific heat, make it applicable in many technological processes. It mixes well with many organic compounds, including fluoroethers. For heat exchanger applications, its thermal conductivity and boiling temperature serve as reference values that can be modified by adding more volatile components.

Table 1. Selected physical properties of ethyl acetate [16] and HFE-73DE [15].

Physical Property	Ethyl Acetate	HFE-73DE
Density, kg/m3	894	1520
Kinematic viscosity, mm2/s	0.463	0.403
Thermal conductivity, W/(m·K)	0.149	0.075
Specific heat, J/(kg·K)	2020	1020
Boiling temperature, K	350.25	314.35

presents the selected parameters of the base fluids.

Four binary mixtures were selected, containing 10%, 25%, 50% and 75% mass fractions of HFE-73DE, the remainder being ethyl acetate. For each mixture, density, kinematic viscosity, thermal conductivity and specific heat were measured at room temperature (20–23 °C) and atmospheric pressure (~101.3 kPa). The boiling temperature was determined at atmospheric pressure (~101.3 kPa) using the ASTM D86 distillation procedure.

Table 2. Binary mixtures: components, mass fractions, and selected physical properties (measured in the present study).

Mixture (Mass Fractions)	Density (kg/m3)	Kinematic Viscosity (mm2/s)	Thermal Conductivity (W/(m·K))	Specific Heat (J/(kg·K))	Boiling Temperature Tsat (K) Tsat,theor/Tsat,exp
73DE 10%/EA 90%	931.0	0.5081	0.165	503.8	314.35/348.15
73DE 25%/EA 75%	969.0	0.5033	0.189	313.3	314.35/342.15
73DE 50%/EA 50%	1035.0	0.4676	0.207	444.6	314.35/341.15
73DE 75%/EA 25%	1169.0	0.4218	0.344	971.5	314.35/333.15

summarises the determined properties of the binary mixtures.

Physicochemical parameters were determined at the Faculty of Civil Engineering, Mechanics and Petrochemistry of the Warsaw University of Technology in Płock (Poland). The density of the liquid samples was determined using a Mettler Toledo Densito densimeter according to the ASTM D1250 standard [17]. Kinematic viscosity at various temperatures was determined using an Ubbelohd capillary with appropriately selected constants, thermostated in water baths according to the EN-ISO 3104 standard [18]. The initial boiling point was determined according to the ASTM D86 standard in a glass atmospheric distillation setup with a water-cooled condenser [19]. The thermal properties were measured using the DSC method in a Netzsch Maia 200 F3 calorimeter. An empty crucible was used as a reference sample in the tests. The mass of the research samples placed in the DSC crucibles was in the range of 60–70 mg [20,21].

Specific heat of simple liquid mixtures is often treated as an additive quantity; therefore, taking into account the pure components and their mass fractions, a theoretically expected value of this parameter can be calculated [22]. In contrast, thermal conductivity is generally non-additive and is frequently estimated using the Maxwell model, which accounts for spherical inclusions dispersed in a continuous matrix [23,24]. In the present case, the situation is further complicated by the fact that HFE-73DE is itself not a single compound, but an azeotropic blend of a hydrofluoroether and trans-1,2-dichloroethylene, as reported by the manufacturer. When ethyl acetate is added, the working fluid becomes an effectively ternary liquid system. Under such conditions, the formation of microdomains enriched in individual components cannot be excluded, leading to local contrasts in thermal conductivity that are not fully captured by simple effective-medium approaches such as the Maxwell model. This model assumes the absence of strong specific intermolecular interactions, such as hydrogen bonding or the presence of associated structures, which may not be fully satisfied in the present mixtures. In this study, the theoretical expectations for specific heat and thermal conductivity were calculated and compared with the values obtained from DSC measurements. The elevated thermal-conductivity values, especially at ethyl acetate contents above approximately 19%, are therefore qualitatively consistent with a percolation-like microstructural mechanism, in which more conductive domains form partially connected pathways within the multicomponent liquid. However, this does not explain the markedly lower specific-heat values observed for some compositions. We attribute these discrepancies primarily to the volatility of the tested samples and the resulting change in sample mass during the measurement, as well as to vapour condensation on the measuring sensors. An additional contributing factor may be the presence of trace amounts of stabilisers (often polymeric) in the commercially available components. These findings indicate that, for such systems, simple mixing rules and semi-theoretical models are insufficient, and that directly measured temperature-dependent specific-heat and thermal-conductivity data [25] should be used whenever possible.

When analysing the results shown in Table 2, it is apparent that within the investigated composition range the physicochemical properties exhibit a distinctly nonlinear character, indicating excess effects and possible molecular interactions between the components. The density increases almost monotonically with increasing HFE-73DE content, whereas the kinematic viscosity decreases; both trends directly influence the flow conditions in heat exchangers. The thermal conductivity rises nonlinearly, more than doubling between the 10/90 and 75/25 mixtures. The specific heat displays a non-monotonic profile, with a minimum at 25/75 and the highest value at 75/25, clearly evidencing deviations from ideal mixing.

In multicomponent mixtures, particularly those containing components with significantly different boiling points, the observed boiling temperature of the system may deviate from the thermodynamic boiling points of the pure substances. This deviation results from the dynamic nature of the process: the more volatile component evaporates first, but the presence of less volatile species and intermolecular interactions can shift the measured boiling point. Under conditions of vigorous boiling and flow, an additional entrainment effect may occur, in which droplets of the less volatile liquid are mechanically carried by the vapour of the more volatile component, producing a vapour composition that differs from the equilibrium composition. This phenomenon masks the sequential character of the phase change and makes the process observed experimentally appear as quasi single-stage boiling. In fluorinated organic systems (e.g., HFE + acetates, HFE + alcohols), this effect can be intensified due to the low surface tension and non-ideal behaviour of the mixtures. For the HFE-73DE + ethyl acetate system, where the boiling points differ substantially (~314.35 K vs. ~350.25 K), the initial evaporation stage is dominated by HFE-73DE, while traces of ethyl acetate appear in the vapour phase not due to its own evaporation but as a result of mechanical entrainment. This explains the absence of a distinct boiling boundary and the observation of a smooth, continuous process. In Table 2, these temperatures are listed as experimental boiling temperature T_sat,exp, whereas the theoretical boiling temperature T_sat,theor corresponds to the boiling point of the more volatile component (HFE-73DE).

3. Experimental Setup

3.1. Experimental Setup Overview

The investigations were carried out using the experimental setup shown in Figure 1, which includes a schematic diagram (Figure 1a) and a photographic view (Figure 1b). In the main circulation loop, the working fluid flowed through the minichannel module under controlled volumetric flow rate, inlet temperature, and pressure. The measurements were performed under steady-state conditions for different levels of electric power supplied to the heater, which resulted in varying heat fluxes transferred to the fluid.

The experiment focused on single-phase convection as the dominant heat transfer mechanism between the flowing fluid and the heated wall. The temperature of the working fluid at the inlet and outlet of the test section, the inlet pressure, the pressure drop along the minichannel, the mass flow rate, and the electrical power supplied to the heater were continuously monitored. In addition, the temperature distribution on the surface of the insulating foil separating the heater from the surroundings was measured.

The pump delivered the fluid to the pressure control system, which also acted as an expansion vessel. The working fluid occupied one side of the vessel, while compressed air on the opposite side maintained the desired system pressure. From the pressure control unit, the fluid was directed to the preheater, where it was heated to a temperature close to the saturation point. A detailed description of the experimental facility can be found in [26].

3.2. Minichannel Module

The essential component of the experimental setup was the horizontal minichannel module, whose schematic diagram is shown in Figure 2a,b: the longitudinal section (Figure 2a) and the cross-section (Figure 2b). The minichannel, 1 mm deep, 4 mm wide and 180 mm long, was formed by three transparent glass plates mounted and bonded to a cuboidal copper block. The copper block was heated by four resistive heaters placed on the opposite wall of the block (hereafter referred to as the “heater”). The heater was powered by a programmable high-current DC supply manufactured by TDK-Lambda. Type-K thermocouples with a diameter of 0.5 mm and pressure sensors (range 0–2.5 bar) were used for temperature and pressure measurements, respectively. A detailed description of the minichannel module is provided in [27].

3.3. Experimental Methodology

From the complete set of experiments, the single-phase convection regime was selected for detailed analysis, as it represents the fundamental mode of heat transfer. The temperatures of the working fluid at the inlet and outlet of the minichannel module, the inlet gauge pressure, the pressure drop between the inlet and outlet, the mass flow rate, and the electrical parameters used to determine the heat flux were recorded, along with the temperatures at selected points on the surface of the insulating foil. All measurements were taken using a data acquisition system integrated with the experimental setup.

3.4. Measurement Uncertainty

The uncertainties of the measured quantities and of the derived heat-transfer parameters were evaluated using standard error-propagation procedures. The main sources of experimental uncertainty are associated with the measurement of temperature, pressure, mass flow rate and electrical power supplied to the heater.

Fluid and wall temperatures were measured using type K thermocouples with a diameter of 0.5 mm, with an accuracy of ±0.2 K after calibration. The pressure drop across the minichannel was obtained from a differential pressure transducer (range 0–1500 Pa) with an accuracy of ±0.25% of full scale. The liquid mass flow rate was determined from the volumetric flow rate measured by the Coriolis mass flow meter with an accuracy of ±0.2%. Electrical power was calculated from voltage and current measurements with an estimated accuracy of ±(3.6–9.0)%, according to [28].

The combined standard uncertainties of the derived quantities, such as the heat flux and the local heat transfer coefficient, were estimated by applying the law of propagation of uncertainty to the defining equations. Assuming uncorrelated input quantities, the resulting relative uncertainties do not exceed about ±(4.4–9.4)% for the heat flux and ±8% for the local heat transfer coefficient under typical operating conditions. These values are used as a reference when assessing the agreement between experimental data and numerical predictions in the Results and Discussion section.

3.5. Selected Experimental Series

The main operating parameters of the selected experimental series used in the subsequent calculations are summarised in

Table 3. Basic operating parameters of the selected experimental series.

Experimental Parameter	Set #1	Set #2	Set #3
Volumetric flow rate (m3/s)	5.75 × 10−8	5.45 × 10−8	5.18 × 10−8
Inlet fluid temperature (K)	302.74	304.62	305.76
Outlet fluid temperature (K)	307.65	316.50	322.68
Heater section temperature (K)	312.28; 312.41; 312.35	323.44; 323.61; 323.55	326.94; 327.04; 326.92
Pressure drop (Pa)	419.62	395.97	827.58
Inlet gauge pressure (Pa)	14,585.0	15,660.9	15,198.0
Heating power (W)	3.62	15	23

. These are steady-state measurements corresponding to three operating settings (Sets #1–#3) within a single experimental series. Each set represents a different level of electrical heating power applied to the minichannel module. The experimental data set corresponding to set #1 was selected for illustrative purposes.

4. Numerical Calculations

4.1. General Information

To assess the suitability of the selected mixtures for potential applications in minichannel heat exchangers, numerical simulations were carried out for four HFE-73DE/ethyl acetate compositions, as well as for the pure components HFE-73DE and ethyl acetate for comparison. Ethyl acetate was used as a reference fluid to evaluate the influence of adding HFE-73DE. Although it is not a typical refrigerant, its low viscosity, moderate thermal conductivity, and relatively high thermal expansivity make it a useful baseline for interpreting the results. The purpose of the numerical analysis was to determine how far fluorinated liquid mixtures can be considered as working fluids with properties adaptable to the operating conditions of compact minichannel heat exchangers.

4.2. CAD Model of the Test Module

Numerical modelling was performed to analyse the behaviour of the working fluid flowing through the minichannel module described in the previous section. A three-dimensional CAD model of the test module, used for numerical simulations, was created in SolidWorks (SOLIDWORKS programme 2023 SP3). The geometry of the module is shown in Figure 3, including the cross-section (Figure 3a) and a fragment of the longitudinal section (Figure 3b). The computational mesh used in the numerical analysis is also indicated in the figure. To improve the accuracy of the results, mesh optimisation was performed. A polyhedral mesh with a base cell size of 8 mm was used, with local refinements introduced in the region of the minichannel (1 mm deep, 4 mm wide, and 180 mm long), where two dimensions are significantly smaller than the base size. These local refinements, clearly visible in Figure 3a,b, allowed accurate representation of the channel geometry and local flow characteristics, particularly near the fluid–heater interface. In the fluid domain of the minichannel, eight prism layers were generated near the walls, with a total thickness corresponding to approximately 15% of the base cell size. The thickness of successive layers gradually increased towards the flow core, ensuring proper resolution of near-wall gradients within the liquid region. The individual components of the test module were divided into a finite number of control volumes corresponding to the cells of the computational mesh.

4.3. Simcenter STAR-CCM+ Software

Numerical simulations were performed in Simcenter STAR-CCM+, a professional CAE environment capable of modelling complex physical phenomena. The software provides a comprehensive set of models for computational fluid dynamics, heat conduction, and multiphase flows. The minichannel module was represented within a three-dimensional computational domain, with simplifications applied to geometrically non-essential regions such as the inlet and outlet plenums. For the calculations, Simcenter STAR-CCM+ version 2020.2.1 (Build 15.04.010) was used. The computing system was equipped with an Intel Core i9 processor (24 cores, 3.50 GHz) and 256 GB RAM. The simulations were based on selected experimental data combined with defined boundary conditions. Detailed information on the computational methodology implemented in the Simcenter STAR-CCM+ environment is available in [26,29,30].

4.4. Governing Equations and Material Properties

Numerical modelling was performed to analyse the behaviour of the selected HFE-73DE/ethyl acetate mixtures in the minichannel test module described in Section 3.2 and shown in Figure 2. The computational domain comprised both the liquid flowing in the minichannel and the surrounding solid regions, which allowed for conjugate heat transfer between the working fluid and the copper/glass walls. The domain was discretised into control volumes corresponding to the cells of the computational mesh, and the governing equations were solved using the numerical schemes implemented in the Simcenter STAR-CCM+ environment.

Given the low Reynolds numbers obtained in the experiments, the liquid was treated as a steady-state, laminar, incompressible Newtonian fluid. For each control volume, the discrete forms of the governing continuity, momentum, and energy equations were applied. The steady-state forms of these equations, describing the fluid flow in the minichannel ${\mathsf{\Omega }}_f$, are given by Equations (1)–(3) [31].

$$\nabla ·\left(\rho \mathit{v}\right)=0$$

(1)

$$\nabla ·\left(\rho \mathit{v}\otimes \mathit{v}\right)=\nabla ·\left(\mathit{T}-p\mathit{I}\right)+{\mathit{f}}_b$$

(2)

$$\nabla ·\left(\rho E\mathit{v}\right)={\mathit{f}}_b\mathit{v}+\nabla ·\left(\mathit{v}\left(\mathit{T}-p\mathit{I}\right)\right)-\nabla ·{\mathit{q}}_f+S_E$$

(3)

where $\rho$ is the density, $\mathit{v}$ is the velocity vector, $\otimes$ denotes the outer product, ${\mathit{f}}_b$ is the body force per unit volume, $p$ is the pressure, I is the identity tensor, $\mathit{T}$ denotes the shear stress tensor, $E$ is the total energy per unit mass, ${\mathit{q}}_f$ is the heat flux vector in the fluid, $S_E$ is the energy source term (per unit volume), and ∇ denotes the nabla operator.

In the solid domains (denoted by the subscript s), which include the heater ${\mathsf{\Omega }}_H$, copper block ${\mathsf{\Omega }}_{Cu}$, and glass ${\mathsf{\Omega }}_g$, the steady-state heat-conduction equation, like in [32], is written as

$$-\nabla ·{\mathit{q}}_s+S_E=0,\mathrm{with}{\mathit{q}}_s=-k_s\nabla T_s,S_E={\displaystyle \frac{P}{V_H}}\mathrm{in}{\mathsf{\Omega }}_H,\mathrm{and}{S}_E=0\mathrm{in}{\mathsf{\Omega }}_{Cu}\bigcup {\mathsf{\Omega }}_g$$

(4)

where ${\mathit{q}}_s$ is the heat flux vector in the solid, $P$ is the heating power, $k_s$ is the thermal conductivity of the solid, $T_s$ is the solid temperature, and $V_H$ is the heater volume.

The thermophysical properties of the solid materials of the minichannel module used in the simulations are listed in

Table 4. Material properties of the solid materials.

Element of the Minichannel Module
Material parameter	Copper block [33]	Heater [34]	Glass [35]
Density [kg/m3]	8940.0	7832.0	2500
Specific heat [J/(kg·K)]	386.0	434.0	840
Thermal conductivity [W/(m·K)]	398.0	63.9	1.4

.

The thermophysical parameters for the fluids are presented in Table 1 and Table 2.

The following modelling assumptions were adopted:

• the fluid flow in the minichannel is incompressible, with a constant mass flow rate;
• temperature-dependent thermophysical properties of the working fluid are applied based on the experimental data obtained in Section 2;
• the material properties of the solid parts of the test module (copper block, glass cover, insulation) are independent of temperature;
• heat losses from the test module to the surroundings are taken into account through an effective convective boundary condition at the external surfaces.

4.5. Boundary Conditions

Based on the governing Equations (1)–(4), the conjugate heat transfer problem is closed by the following boundary conditions:

$$\mathit{v}·\mathit{n}={\displaystyle \frac{\dot{V}}{A_c}},T_f=T_{in}\mathrm{at}\mathrm{the}\mathrm{minichannel}\mathrm{inlet}{\Gamma }_{f,in}$$

(5)

$$p=p_{out}\mathrm{at}\mathrm{the}\mathrm{minichannel}\mathrm{outlet}{\Gamma }_{f,out}$$

(6)

$$\mathit{v}=\mathbf{0},T_f=T_s,-{\mathit{q}}_f·\mathit{n}=-{\mathit{q}}_s·\mathit{n}\mathrm{at}\mathrm{the}\mathrm{fluid}\text{–}\mathrm{solid}\mathrm{interface}{\Gamma }_{f-s}$$

(7)

$$T_H=T_{Cu},-{\mathit{q}}_H·\mathit{n}=-{\mathit{q}}_{Cu}·\mathit{n}\mathrm{at}\mathrm{the}\mathrm{heater}\text{–}\mathrm{copper}\mathrm{block}\mathrm{interface}{\Gamma }_{H-Cu}$$

(8)

$$-{\mathit{q}}_s·\mathit{n}=h_{ext}(T_s-T_{\infty })\mathrm{at}\mathrm{the}\mathrm{external}\mathrm{surfaces}{\Gamma }_{ext}$$

(9)

where $\dot{V}$ denotes the volumetric flow rate, $A_c$ is the channel cross-sectional area, $T_f$ is the fluid temperature, $T_H$ is the heater temperature, $T_{Cu}$ is the copper block temperature, $h_{ext}$ is the external heat transfer coefficient, $T_{\infty }$ is the ambient temperature, and $\mathit{n}$ is the unit outward normal vector.

For each HFE-73DE/ethyl acetate composition, the density ρ(T), dynamic viscosity μ(T), thermal conductivity k(T) and specific heat capacity c_p(T) of the liquid were implemented as temperature-dependent functions obtained from the measurements reported in Section 2. The thermophysical properties of the solid materials were taken from manufacturers’ data and previous work by the authors on similar minichannel modules.

The same set of boundary conditions, for the inlet, outlet, walls, and external surfaces, was applied in all validation cases (pure HFE-73DE, sets #1–#3) and in the subsequent simulations of the four HFE-73DE/ethyl acetate mixtures, in order to investigate the effect of mixture composition on the flow and heat transfer.

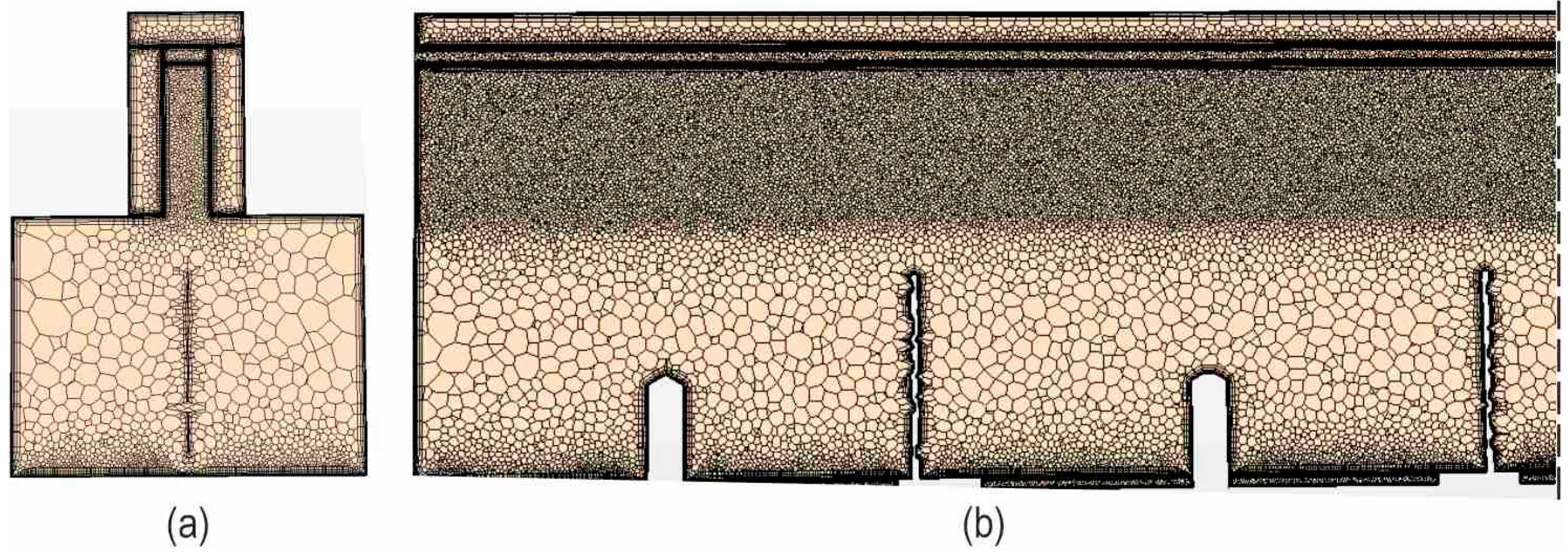
4.6. Mesh Independence Study

To evaluate the influence of mesh density on the numerical results and to ensure the grid independence of the CFD simulations, the Grid Convergence Index (GCI) method was applied according to the recommendations of the ASME Verification and Validation Committee [36]. This approach enables a quantitative estimation of the discretisation error using the Richardson extrapolation procedure [37]. The calculations were carried out analogously to the methodology presented in our previous work published in [26].

The analysis employed three systematically refined grids of 7,573,690, 2,837,607, and 1,251,945 cells, corresponding to base cell sizes of 5 mm (fine), 8 mm (medium), and 12 mm (coarse), respectively. The fine grid (5 mm) served as the reference, while the medium grid (8 mm) was used for the final simulations reported in this paper.

The GCI value was determined for the temperature at the copper block–minichannel interface according to the ASME-recommended formula [36]:

$${GCI}_{ij}={\displaystyle \frac{1.25e_{ij}}{{r_{ij}}^s-1}}$$

(10)

where $e_{ij}$ denotes the relative error between the temperature values obtained using two successive grids, $r_{ij}$ is the grid refinement factor, and s is the observed order of accuracy.

For the fine–medium pair:

• $r_{21}$ = 1.39,
• average observed order s = 0.425,
• average relative error $e_{21}=4.54\times {10}^{-4}$,
• average ${GCI}_{21}=3.93\times {10}^{-3}$.

For the medium–coarse pair:

• $r_{32}$ = 1.31,
• average observed order s is the same as for the fine–medium pair,
• average relative error $e_{32}=3.29\times {10}^{-4}$,
• average ${GCI}_{32}=3.46\times {10}^{-3}$.

In the Roache approach proposed in [36], the grid convergence consistency is verified by comparing the normalised errors for consecutive grid pairs using the GCI consistency ratio, defined as

$$R_{GCI}={\displaystyle \frac{{GCI}_{32}}{{r_{21}}^s{GCI}_{21}}}$$

(11)

When $R_{GCI}$ approaches unity, the solution is considered to be within the asymptotic range of grid convergence [36,37]. In the present study, R_GCI = 0.77, which confirms monotonic grid convergence and indicates that the results suggests close to the asymptotic range.

4.7. Simulation Procedure

The simulation procedure consisted of several key stages. First, the three-dimensional CAD model of the test module (Figure 3) was imported into Simcenter STAR-CCM+ and the liquid and solid regions were defined. The computational mesh was then generated according to the strategy described in Section 4.6, and the material properties of the liquid mixtures and solid components were assigned as functions of temperature, as outlined in Section 4.4. Subsequently, the boundary conditions described in Section 4.5 were applied to the inlet, outlet, heater surface, internal walls and external surfaces of the test module and insulation panel.

For each simulated case, the steady-state governing Equations (1)–(3) were discretised for all control volumes and solved using an iterative segregated solver. In this approach [38], the energy equation for the liquid phase is solved separately from the momentum and continuity equations. This means that the temperature field is calculated after the velocity and pressure fields have been iteratively updated, instead of solving the entire system of Navier–Stokes and energy equations in a fully coupled manner.

The finite volume method (FVM) [39] was employed to discretise the governing equations. The sought variable was determined iteratively at each mesh node. Each iteration involved solving the momentum and pressure equations (also using the FVM), then solving the energy equation (again using the FVM) with a fixed velocity field, and finally updating the solution fields until convergence was achieved.

The continuity, momentum and energy equations in the liquid domain were coupled with the heat-conduction equation in the solid regions through the common liquid–solid interfaces.

The model was first validated against the experimental data for pure HFE-73DE (sets #1–#3 in Section 6) by using the same mass flow rates and heating powers as in the measurements. Once satisfactory agreement between computed and measured wall temperatures and heat transfer coefficients had been obtained, the validated numerical setup was used to simulate the four HFE-73DE/ethyl acetate mixtures under identical operating conditions. For each composition, the axial distributions of the local heat transfer coefficient, fluid temperature and velocity were extracted along the minichannel, providing a detailed picture of how changes in thermophysical properties with mixture composition influence laminar convective heat transfer in the studied geometry.

5. Results and Analysis

5.1. General Information

Section 5.2 and Section 5.3 present and interpret the results of numerical simulations performed for four HFE-73DE/ethyl acetate mixtures (10/90, 25/75, 50/50 and 75/25 by mass). The discussion focuses on the heat transfer coefficient (HTC), the velocity and the fluid-core temperature at mid-depth, and the observed trends are analysed in relation to the thermophysical properties established in Section 2. Section 5.4 presents the HTC distributions and the corresponding mean Nusselt numbers for pure HFE-73DE for three operating sets (#1–#3) that correspond to the selected experimental runs. Section 5.5 presents the associated velocity and mid-depth fluid-core temperature distributions for pure HFE-73DE obtained from the validation simulations. These results for pure HFE-73DE form the basis for the validation and verification analyses discussed in Section 6.

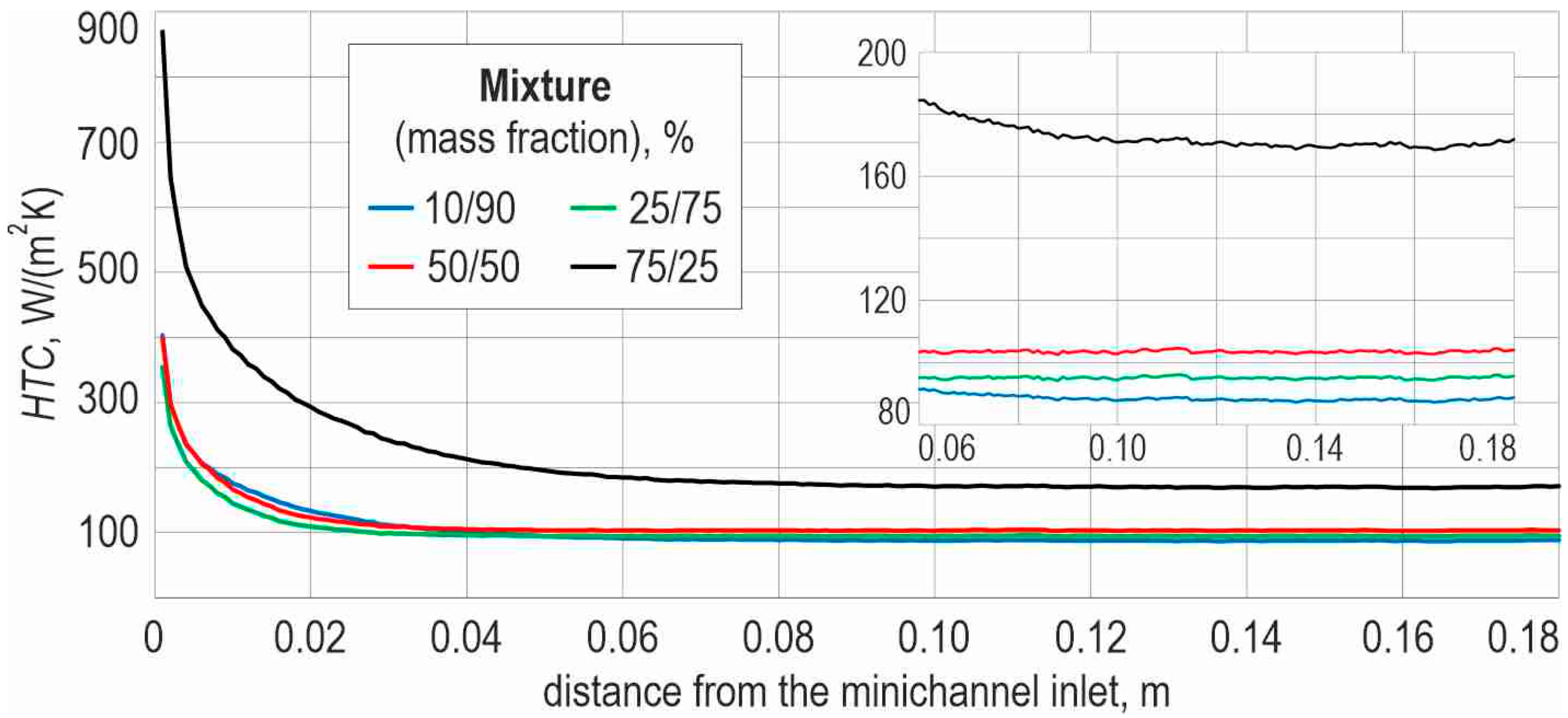
5.2. Heat Transfer Coefficient Distributions for HFE-73DE/Ethyl Acetate Mixtures

Figure 4 illustrates the local heat transfer coefficient as a function of the distance from the minichannel inlet for the mixtures investigated. All profiles exhibit a gradual decrease in the heat transfer coefficient (HTC) with distance from the minichannel inlet. This behaviour is consistent with laminar single-phase flow under constant wall heat flux when temperature-dependent liquid properties and conjugate heat transfer in the solid are taken into account. The decrease results primarily from the progressive increase in bulk fluid temperature and the corresponding reduction in the wall-to-bulk temperature difference, together with the development of the thermal boundary layer in the developing region. The magnitude of the local heat transfer coefficients obtained in this study, ranging from a few hundred up to about 1 kW/(m²·K) under the considered laminar single-phase conditions, is consistent with values reported for flow in minichannels [14,26,30]. Typical discrepancies of up to ±30% can be attributed to differences in channel geometry, surface roughness and the exact thermophysical properties of the working fluids. At the same time, to the best of the authors’ knowledge, no prior minichannel heat-transfer data are available for HFE-73DE/ethyl acetate mixtures themselves, so quantitative one-to-one comparisons for the same fluid system are not yet possible.

A clear composition dependence is observed. Increasing the proportion of HFE-73DE raises the overall HTC level: the 75/25 mixture exhibits the highest values, while the 10/90 mixture yields the lowest. This trend corresponds to the experimentally measured nonlinear variation in thermal conductivity and specific heat with composition, which affects thermal boundary layer development. The 75/25 mixture shows approximately twice the HTC of the 10/90 case, confirming that a higher HFE-73DE fraction enhances heat transfer intensity through improved thermal conduction and convective dispersion.

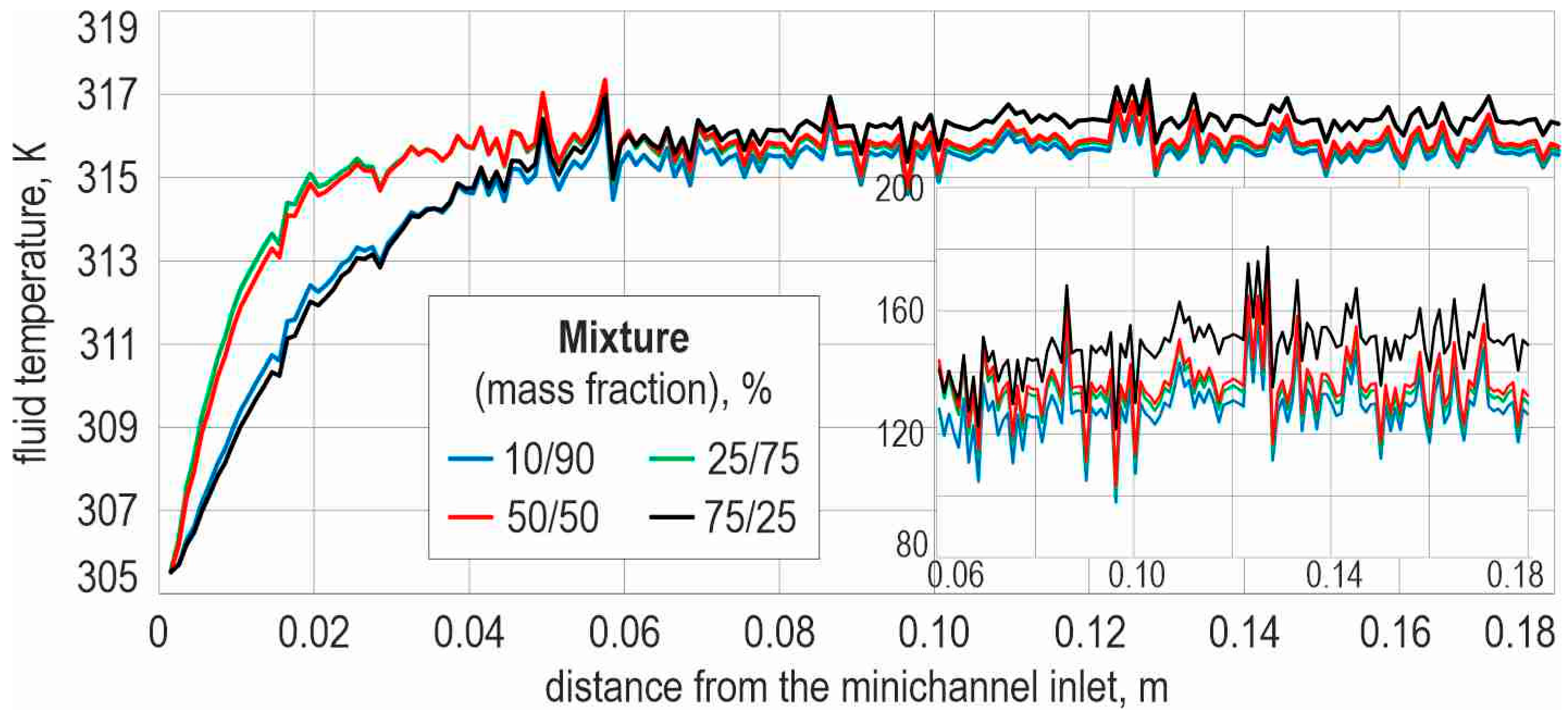
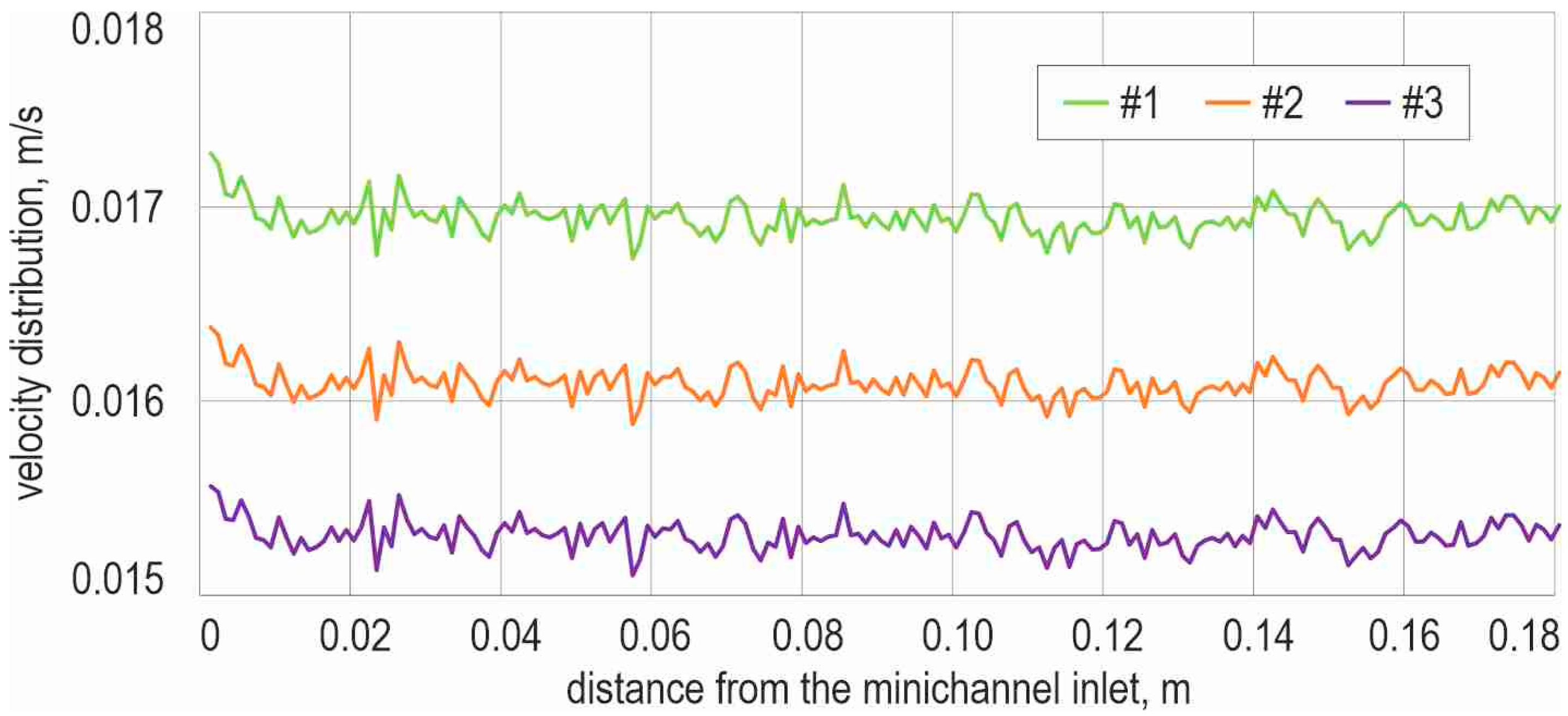
5.3. Flow Velocity and Fluid-Core Temperature at Mid-Depth for HFE-73DE/Ethyl Acetate Mixtures

Figure 5 shows the streamwise velocity distribution along the centreline of the minichannel.

When analysing the data presented in Figure 5, it can be observed that for all mixtures the centreline velocity increases near the inlet section but remains nearly constant along the channel, with only minor variations arising from temperature-dependent changes in density and viscosity. These variations are small compared with the mean flow velocity and do not alter the overall laminar character of the flow. Mixtures with a larger proportion of ethyl acetate show slightly stronger axial variations than those rich in HFE-73DE, which is consistent with their lower density and higher thermal expansivity. Overall, the results confirm that mixture composition has a measurable, though moderate, influence on the hydraulic behaviour and pressure-drop characteristics.

Figure 6 presents the distribution of the fluid-core temperature as a function of the distance from the minichannel inlet for all mixtures. The measurement was taken at mid-depth of the minichannel, along the flow axis.

According to the data presented in Figure 6, the fluid temperature changes along the minichannel length, increasing steadily from the inlet to the outlet for all mixtures. The smallest temperature rise is observed for the 75/25 and 50/50 compositions, which indicates higher cooling efficiency, whereas the 10/90 mixture exhibits the largest increase. The trend is consistent with the distributions of the heat transfer coefficient and wall temperature, confirming a coherent dependence of the entire thermal field on mixture composition. This behaviour can be explained by the nonlinear variation in mixture properties discussed in Section 2: the combined influence of thermal conductivity, viscosity, and heat capacity governs the observed differences in the bulk heating rate.

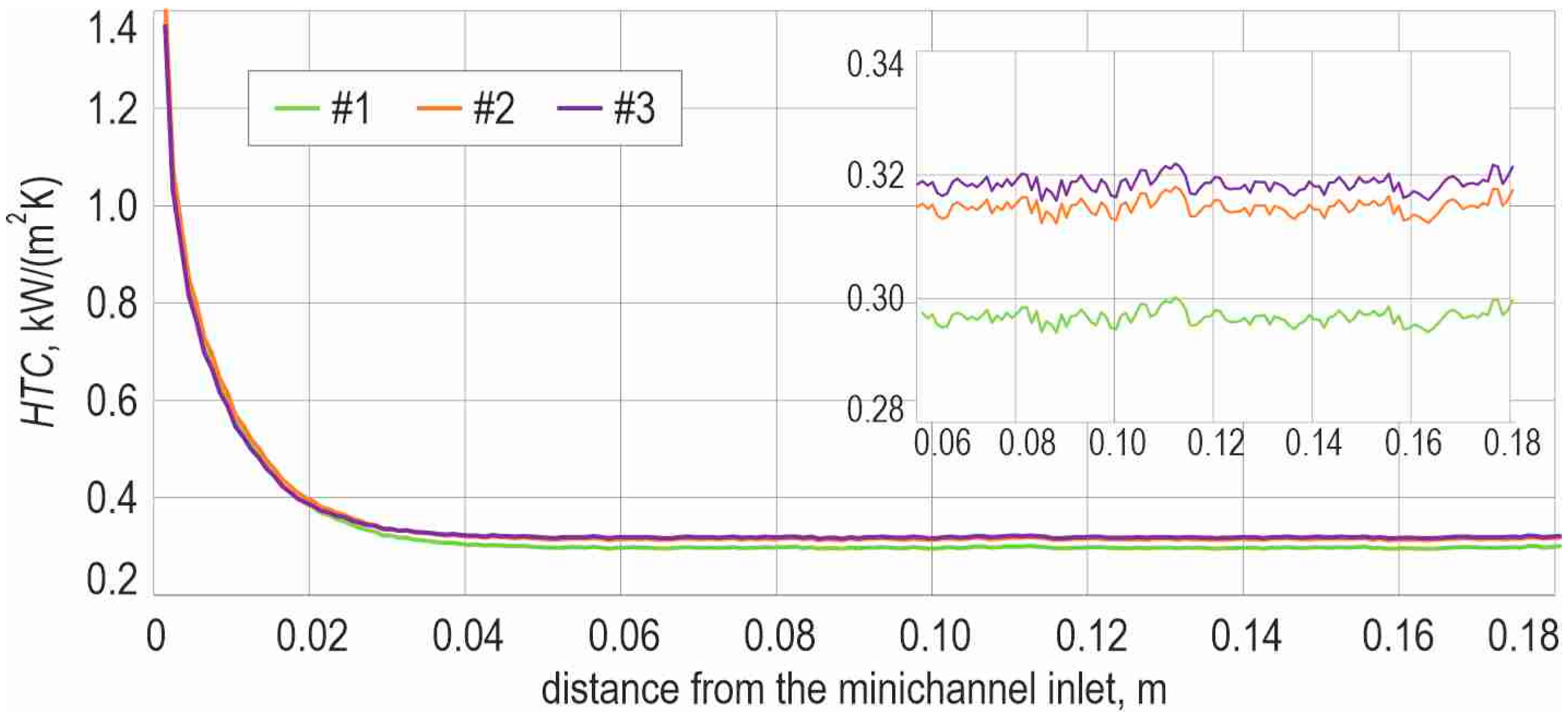
5.4. Heat Transfer Coefficient Distributions for HFE-73DE

Figure 7 shows the distributions of the heat transfer coefficient obtained from numerical calculations, corresponding to the selected experimental runs (#1, #2, and #3) with pure HFE-73DE. The inset presents an enlarged section of the same data to highlight the subtle differences between the cases.

When analysing the results shown in Figure 7, it was observed that in each set the simulations reproduced the expected axial decrease in the heat transfer coefficient and maintained the correct order corresponding to changes in inlet temperature, mass flow rate, and heating power. The numerical results are consistent with the experimental data and remain within the uncertainty range of the wall temperature measurements. This consistency confirms that the modelling assumptions adopted in the study, namely laminar incompressible flow and temperature-independent solid properties, are appropriate for the present single-phase regime. The results also indicate that Simcenter STAR-CCM+ can be reliably used for further analyses involving different mixture compositions and for future two-phase flow studies.

To provide a compact quantitative measure of the numerically predicted heat transfer performance, the local HTC distributions shown in Figure 7 were post-processed to obtain average heat transfer coefficients over the heated minichannel length L = 0.18 m for each operating condition. The resulting mean HTCs for pure HFE-73DE, together with the corresponding mean Nusselt numbers based on the hydraulic diameter D_h = 0.0016 m, are summarised in

Table 5. Reynolds and Prandtl numbers, average heat transfer coefficients and corresponding Nusselt numbers, HFE-73DE (results from Simcenter STAR-CCM+, based on the experimental data).

Set	Re	Pr	${\mathit{H}\mathit{T}\mathit{C}}_{\mathit{C}\mathit{F}\mathit{D}}$ (W/(m2·K))	${\mathit{N}\mathit{u}}_{\mathit{C}\mathit{F}\mathit{D}}$ (-)
#1	57.0	8.34	337.33	7.20
#2	54.1	8.34	354.76	7.57
#3	51.4	8.34	354.64	7.57

. The average HTC lies in a relatively narrow range between approximately 337 and 355 W/(m²·K), which translates into mean Nusselt numbers of about 7.2–7.6. These values are higher than those expected from classical laminar duct theory for the same geometry, indicating that the combination of conjugate heat transfer in the copper block and the asymmetric heating configuration enhances the effective convective heat transfer relative to idealised models. A more detailed comparison with a selected literature correlation is presented in Section 6.3.

5.5. Flow Velocity and Fluid-Core Temperature at Mid-Depth for HFE-73DE

For completeness, Figure 8 shows the velocity, while Figure 9 presents the fluid-core temperature at mid-channel depth as a function of the distance from the minichannel inlet. Both quantities were obtained during the validation runs.

The distributions shown in Figure 8 and Figure 9 exhibit consistent and physically meaningful trends. The velocity increases only near the inlet section, remains approximately constant along the channel, with only small axial variations that reflect the modest changes in fluid properties with temperature under the present operating conditions. The wall and mid-channel temperatures remain in the expected relative order, reflecting stable thermal stratification within the flow. The agreement between results obtained for three selected experimental runs (#1, #2 and #3) confirms the reproducibility of the numerical procedure and its accurate calibration to the experimentally measured boundary conditions.

6. Validation and Verification of the Results

6.1. General Remarks

In this section, the reliability of the numerical model developed in Simcenter STAR-CCM+ is assessed on two complementary levels. First, the CFD predictions are directly validated against the experimental data for three selected operating conditions with pure HFE-73DE (Section 6.2). This step focuses on a point-wise comparison of temperatures along the heated section of the minichannel module and quantifies the average relative difference between CFD and measurements. Second, the CFD-based mean Nusselt numbers are compared with an established analytical solution for laminar forced convection in rectangular ducts (Section 6.3). This verification step positions the present configuration with asymmetric heating and conjugate heat transfer against an idealised, fully developed laminar-flow model. Together, these two levels of analysis provide a consistent basis for judging both the accuracy of the numerical simulations and the physical plausibility of the obtained heat transfer characteristics.

6.2. Validation of the Numerical Simulations

The validation was carried out using three operating conditions corresponding to three selected experimental runs with the working fluid being pure HFE-73DE (Sets #1–#3). The comparison between the numerical simulations performed in Simcenter STAR-CCM+ and the experimental data was conducted for the measured temperatures by thermocouples, along the heated section of the minichannel module.

The average relative difference ${\delta }_T$ was calculated according to the following expression:

$${\delta }_T={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\left|{\displaystyle \frac{T_{CFD,i}-T_{exp,i}}{T_{exp,i}}}\right|\times 100\%$$

(12)

where $T_{CFD,i}$ and $T_{exp,i}$ denote CFD-predicted and experimental temperatures at the i-th measurement location, respectively, and N is the total number of compared temperature points.

Table 6. Average relative differences between the results obtained from numerical simulations in Simcenter STAR-CCM+ and the experimental data.

Number of Set	#1	#2	#3
Average relative differences δT [%]	0.4	0.48	0.46

presents the average relative differences δ_T obtained for the three validation sets.

When analysing the results shown in Table 6, it can be concluded that the obtained average relative differences are very small, below 0.5%, which confirms the high consistency between the numerical and experimental results. This finding shows that the numerical model accurately reproduces the thermal and hydraulic behaviour of the tested minichannel module and can be confidently used for further parametric and predictive analyses.

6.3. Verification of the Results with a Selected Correlation from the Literature

To further assess the plausibility of the numerical results and to quantify how the present configuration differs from idealised laminar-flow models, the mean Nusselt numbers obtained from CFD (Table 5) were compared with a widely used correlation for single-phase laminar convection in internal flows. This correlation is the fully developed solution of Shah and London for rectangular channels with all walls subject to a uniform heat flux. Although this boundary condition does not exactly match the present configuration with one wall directly heated and conjugate conduction in the copper block, it provides a useful reference for quantifying the enhancement of convective heat transfer due to asymmetric heating and conjugate effects.

For the fully developed laminar regime in a rectangular duct, the Nusselt numbers can be calculated using the empirical formula developed by Shah and London [40]:

$${Nu}_{theor}=8.235\left[1-2.0421\alpha +3.0853{\alpha }^2-2.4765{\alpha }^3+1.0578{\alpha }^4-0.1861{\alpha }^5\right]$$

(13)

where α = a/b is the aspect ratio defined as the ratio of the smaller side a to the larger side b of the rectangular cross-section. For the present 1 × 4 mm minichannel, this expression yields a constant value ${Nu}_{theor}$ ≈ 5.33, independent of Reynolds number and Prandtl number in the laminar regime.

Table 7. Nusselt numbers as numerical results from Simcenter STAR-CCM+ based on experimental data with HFE-73DE and comparison with the theoretical value from the Shah and London correlation.

Set	${\mathit{N}\mathit{u}}_{\mathit{C}\mathit{F}\mathit{D}}$	${\mathit{N}\mathit{u}}_{\mathit{t}\mathit{h}\mathit{e}\mathit{o}\mathit{r}}$	${\mathit{\delta }}_{\mathit{N}\mathit{u}}$ [%]
#1	7.20	5.33	35
#2	7.57	5.33	42
#3	7.57	5.33	42

summarises the comparison between the CFD-based mean Nusselt numbers (${Nu}_{CFD}$) and the theoretical Nusselt number from the Shah and London correlation (${Nu}_{theor}$) for the three validation sets. The relative difference ${\delta }_{Nu}$ is defined as

$${\delta }_{Nu}=\left|{\displaystyle \frac{{Nu}_{CFD}-{Nu}_{theor}}{{Nu}_{theor}}}\right|\times 100\%$$

(14)

The results in Table 7 show that the fully developed Shah and London correlation for a 1 × 4 mm rectangular duct with all four walls uniformly heated underpredicts the CFD-based Nusselt numbers by about 35–42% for the three operating sets. These systematic deviations confirm that classical laminar correlations for idealised ducts do not fully capture the enhanced convective heat transfer arising from the combined effects of asymmetric heating, conjugate heat conduction in the copper block, and the actual three-dimensional temperature field in the minichannel module. At the same time, the good agreement between the numerical predictions and experimental data for pure HFE-73DE (Section 6.2) indicates that the higher Nusselt numbers obtained from the CFD model are physically meaningful and representative of the real thermal performance of the system, rather than an artefact of numerical modelling.

7. Conclusions

This study investigated single-phase laminar heat transfer of HFE-73DE/ethyl acetate mixtures flowing through a heated minichannel by combining experimental measurements with three-dimensional CFD simulations. The main conclusions are as follows:

• The thermophysical properties of HFE-73DE/ethyl acetate mixtures exhibit a strongly nonlinear dependence on composition. Density increases almost monotonically and kinematic viscosity decreases with increasing HFE-73DE content, whereas thermal conductivity increases by more than a factor of two between the 10/90 and 75/25 mixtures. The specific heat shows a non-monotonic variation, with a minimum near 25/75 and the highest value for the 75/25 mixture, indicating deviations from ideal mixing. These trends directly affect both the hydraulic and thermal performance of the mixtures in minichannel flow and confirm that, for such non-ideal systems, directly measured temperature-dependent c_p(T) and k(T) data are needed instead of simple mixing rules.
• Under constant heat-flux conditions, the local heat transfer coefficient in the heated minichannel decreases gradually with distance from the inlet, reflecting the development of the thermal boundary layer and the evolving wall-to-bulk temperature difference. Mixture composition has a pronounced influence on the magnitude of the heat transfer coefficient and on the axial temperature rise in the fluid, with HFE-richer mixtures providing higher heat transfer coefficients and lower fluid-temperature increases.
• A three-dimensional CFD model developed in Simcenter STAR-CCM+, incorporating conjugate heat transfer in the solid parts and temperature-dependent liquid properties, reproduces the experimentally observed behaviour with good accuracy. A mesh-independence study based on the Grid Convergence Index (GCI) confirmed that discretisation errors are small, and comparisons with representative experimental cases show that the predicted temperatures differ from the measurements by less than 0.5% on average. Additional verification against the fully developed laminar Shah and London solution for a 1 × 4 mm rectangular duct demonstrates that the CFD-based mean Nusselt numbers are about 35–42% higher than the theoretical value, highlighting the impact of asymmetric heating and conjugate heat conduction on the effective single-phase heat transfer coefficient.
• Intermediate mixtures with 50/50 and 75/25 mass % HFE-73DE/ethyl acetate provide a favourable compromise between heat-transfer performance and pressure drop. Under the conditions studied, these mixtures yield significantly higher local heat transfer coefficients and smaller fluid-temperature increases along the minichannel than the 10/90 mixture, while avoiding the very low viscosities that could occur in even more HFE-rich compositions.
• The validated CFD framework offers a reliable tool for analysing and optimising minichannel heat exchangers operating with HFE-73DE/ethyl acetate mixtures and, more broadly, other HFE-based binary systems. It can be used to evaluate alternative channel geometries, operating conditions and mixture compositions, and thereby support the tailored design of dielectric cooling systems for power electronics and other compact thermal-management applications.

Future work will focus on extending the present approach to two-phase flow and flow boiling of HFE-73DE/ethyl acetate mixtures in minichannels and on integrating the CFD model with advanced thermodynamic and data-driven property-prediction methods. This will further enhance the capability to design compact, high-performance heat exchangers employing dielectric binary mixtures as tunable working fluids.