Abstract
The integration of renewable energy sources (RESs), such as wind and solar, introduces significant uncertainties into power system operations, complicating Available Transfer Capability (ATC) assessment. A key factor in ATC determination, the Transmission Reliability Margin (TRM), accounts for uncertainties like load variations, generation fluctuations, and network dynamics. The traditional deterministic TRM methods often fail to capture the stochastic nature of modern grids, leading to inaccurate estimations. This paper reviews the TRM assessment methodologies, emphasizing probabilistic approaches that enhance accuracy in high-RES environments. It explores adaptive statistical techniques, such as rolling window analysis, for dynamic TRM computation. Key challenges, emerging trends, and potential solutions are discussed to support the development of robust ATC modeling frameworks for secure and efficient renewable energy integration.
1. Introduction
In modern power systems, the Available Transfer Capability (ATC) and Transmission Reliability Margin (TRM) are crucial for ensuring secure and efficient grid operations. The ATC represents the maximum power that can be reliably transferred across the network while maintaining system security, whereas the TRM acts as a safety buffer to account for uncertainties in the power system conditions [1,2].
The traditional ATC and TRM assessment methods rely on deterministic approaches, assuming stable and predictable grid conditions. However, with the increasing integration of renewable energy sources (RESs), such as wind and solar, these static methodologies face significant limitations [3,4,5]. Figure 1 illustrates the ATC calculation process in an RES-integrated system, highlighting how renewable energy source variability influences the transfer capacity and TRM allocation.
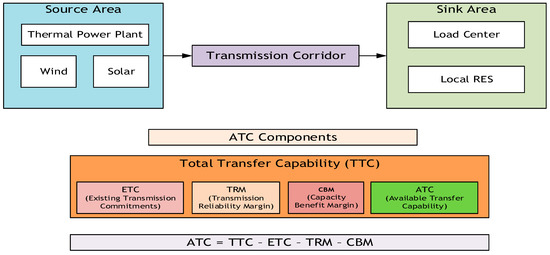
Figure 1.
Transmission system flow and ATC components in an RES-penetrated grid.
Conventional ATC assessments typically employ standardized load flow analysis with predefined margins, while TRM calculations use static confidence factors. These methods fail to capture the dynamic nature of modern grids, where fluctuating renewable generation and rapid system condition changes introduce uncertainties.
As a result, TRM and ATC estimates may be either overestimated, leading to potential security risks, or underestimated, causing the inefficient utilization of the transmission capacity.
To address these challenges, dynamic, real-time approaches are needed to optimize both the ATC and TRM while accounting for RES-induced variability. This review focuses on the TRM as a key factor in ATC assessment. While deterministic TRM methods have been widely used, they fail to reflect the stochastic nature of modern grids, leading to inaccurate ATC estimations. This paper conducts a comprehensive investigation of the existing techniques in the literature that address TRM assessment. It provides a critical analysis of the various methodologies used to estimate the TRM, highlighting their underlying principles, strengths, and limitations in modern power systems, particularly those with high-RES penetration.
Recent studies have proposed probabilistic and data-driven methods to improve the accuracy of ATC and TRM assessments. In [6], the authors introduced a multi-time-step ATC evaluation method based on typical scenario sets of the renewable power output and load demand, using conditional generative adversarial networks (CGANs) to generate and screen stochastic scenarios. Similarly, ref. [7] proposed a combined approach leveraging load-side price-based demand response and grid-side Thyristor-Controlled Series Compensation (TCSC) measures to enhance the ATC, effectively mitigating wind power generation uncertainties. Their method employs Latin Hypercube Sampling (LHS) and an improved particle swarm optimization (PSO) algorithm to solve the source–grid load cooperative optimization problem. Additionally, ref. [8] presented a streamlined iterative method for the power system ATC and security analysis, demonstrating improved computational efficiency and reliability. Another study [9] proposed a data-driven sparse polynomial chaos expansion (DDSPCE) method to estimate the probabilistic characteristics of the total transfer capability in renewable-energy-source-integrated power systems.
Furthermore, the paper identifies key challenges associated with TRM estimation, including uncertainty modeling, real-time adaptability, and integration with ATC assessments. These challenges arise due to the increasing variability in generation and demand patterns, the evolving complexity of power grids, and the limitations of traditional deterministic approaches [10]. In addition, this study explores emerging research opportunities to enhance the TRM estimation accuracy and reliability. It discusses advanced techniques such as probabilistic modeling, data-driven methods, and adaptive statistical approaches that can improve the grid resilience and operational efficiency. The review also examines the potential for machine learning, artificial intelligence, and real-time forecasting models to optimize TRM calculations in dynamic power system environments.
This review offers a comprehensive analysis of the TRM estimation methods, emphasizing the challenges posed by high renewable energy integration and system uncertainties. By identifying the gaps in the dynamic modeling approaches and exploring the integration of data-driven techniques, the paper aims to provide actionable insights for developing adaptive and resilient TRM assessment strategies suited to modern power grid environments.
2. ATC Terminologies and Concepts
The ATC is determined by several key parameters that define a power system’s operational limits and reliability margins. These include the total transfer capability (TTC), TRM, Existing Transmission Commitments (ETCs), and Capacity Benefit Margin (CBM).
Figure 2 provides a graphical representation of how these parameters interact, illustrating how the TTC values fluctuate in response to system constraints such as the stability, voltage, and thermal limits, and also highlighting the relationships between the ATC, TRM, and CBM. It emphasizes their critical roles in ensuring secure and efficient power transfer under varying system conditions.

Figure 2.
ATC limitations and related parameters.
The ATC is then determined by subtracting the key parameters—the TRM, ETC, and CBM—from the TTC, as expressed in Equation (1) [1]:
The calculation of the power transfer capability typically relies on offline computer simulations of the power system network under projected operational conditions. Each load flow analysis represents a specific operating state of the interconnected network, incorporating key factors such as the system configuration, the load demand, the generation dispatch, contingencies, and base case scheduled transfers [11,12].
The TTC is determined through load flow analysis while accounting for critical system constraints, including stability limits, voltage limits, and thermal ratings, as depicted in Figure 2. The TTC calculation involves incrementally increasing the power transfer until any of these limits is reached. The final TTC value corresponds to the most restrictive limit among the three, represented by the blue dashed line in Figure 2 [12].
The analysis employs the Continuation Power Flow (CPF) method to solve load flow equations under both equality and inequality constraints, yielding TTC values that reflect the system limitations. For clarity, the three limits considered in this study are defined as follows:
- ▪
- The thermal limit:The thermal limit is the maximum power transfer constrained by the steady-state MVA ratings of transmission lines or transformers. Exceeding this limit risks equipment overheating and potential damage;
- ▪
- The stability limit (Voltage Stability Boundary):The stability limit is the maximum power transfer point identified by the CPF method (i.e., the ‘nose point’ or saddle-node bifurcation) before voltage collapse occurs under quasi-steady-state conditions. This limit is associated with the singularity of the power flow Jacobian matrix and is distinct from the following:
- o
- The small-signal stability (oscillation damping, evaluated via modal analysis);
- o
- The transient stability (synchronism loss following large disturbances);
- o
- The frequency stability [13,14,15].
Note: these were not assessed in this study, as standard CPF focuses solely on the voltage stability; - ▪
- The voltage limit:The voltage limit is the violation of the operational steady-state voltage magnitude constraints, where bus voltages fall outside the permissible range of 0.95–1.05 p.u., as mandated by industry standards for system reliability and equipment protection [16,17].
2.1. Total Transfer Capability (TTC)
The TTC is a crucial metric in power systems, representing the maximum power transfer between two areas while ensuring the system’s reliability and stability. It is determined by considering the operational limits, such as the voltage, thermal, and stability constraints, to maintain the grid integrity during transfers. The integration of RESs has underscored the need for more adaptive TTC assessment methods, as the traditional static approaches often fail to capture the variability inherent in modern grids. To address these limitations, various methodologies have been explored for TTC assessment, including deterministic techniques to advanced computational approaches. The following subsections outline the key methods and their contributions to improving the TTC evaluation in modern power systems.
2.1.1. Methods for TTC Assessment
Various methodologies have been developed to calculate or predict the total transfer capability (TTC), ranging from traditional deterministic approaches to advanced computational techniques. These methods aim to ensure reliable power transfer across interconnected power systems while maintaining stability and adhering to the operational constraints:
- A. Deterministic Methods
Traditional TTC calculations rely on fixed load and generation scenarios [18]. Early studies, such as [19], provided reliable estimates under steady-state conditions but required conservative margins to account for operational uncertainties. However, these methods lack flexibility in addressing dynamic conditions introduced by renewable energy sources (RESs);
- B. Interconnected Systems
To address the complexities of multi-area power grids, ref. [20] proposed a multi-area TTC framework, which incorporates dynamic adjustments based on inter-regional constraints. This approach emphasizes the need to account for the renewable energy variability in interconnected systems [21,22];
- C. Optimization-Based Techniques
Advanced optimization methods, such as mathematical programming and sequential quadratic programming (SQP), have been employed to enhance the TTC accuracy [21]. These techniques integrate reactive power flows, voltage constraints, and other system limits to maximize the transfer capability while ensuring operational feasibility;
- D. Probabilistic and Data-Driven Approaches
With increasing RES penetration, probabilistic methods—such as Monte Carlo simulations and data-driven sparse polynomial chaos expansion (DDSPCE)—have become essential for robust TTC assessment [9]. These approaches quantify the uncertainties in the renewable generation, load variations, and system dynamics, providing probabilistic TTC distributions that reflect real-world variability;
- E. Machine Learning Techniques
Recent advancements leverage AI and deep learning to improve the TTC prediction efficiency and accuracy [23,24]. These methods include the following:
- Surrogate models that emulate complex power flow relationships;
- Hybrid approaches combining multiple techniques for enhanced robustness.
By analyzing real-time and historical data, machine learning models capture the nonlinear dependencies among key variables, such as the following:
- ✓
- Bus voltages;
- ✓
- Line power flows;
- ✓
- The system frequency;
- ✓
- The generation variability;
- ✓
- Load fluctuations;
- ✓
- Transmission capacity changes;
- ✓
- The network topology.
This adaptability makes them particularly effective at managing the stochastic nature of RESs, reducing the computational burden while maintaining accuracy.
2.1.2. TTC Enhancement Techniques
In addition to the assessment methodologies, significant research and industry efforts focus on advanced technologies to actively enhance the usable transfer capability of existing transmission infrastructures. The key techniques include the following:
- A. Power Flow Control Devices
Unified Power Flow Controllers (UPFCs) optimize the TTC in renewable-rich grids by dynamically balancing the load and generation [25,26,27]. These FACTS devices simultaneously control multiple parameters—the active/reactive power flow, voltage magnitude, and phase angle—enabling real-time adjustments to mitigate rapid generation/load fluctuations while improving the grid security and TTC [28,29];
- B. Other FACTS Devices
- Thyristor-Controlled Series Compensators (TCSCs) adjust the line impedance to optimize the power flow, reduce congestion, and enhance the TTC [30];
- Static VAR Compensators (SVCs) and STATCOMs provide reactive power support to improve the voltage stability margins [25];
- C. Dynamic Line Rating (DLR)
DLR systems leverage real-time ambient temperature monitoring to increase the line capacity by 10–30% compared to static ratings, enabling the higher utilization of the existing infrastructure [31];
- D. Synchronized Phasor Measurement Units (PMUs)
Integrated into Wide-Area Monitoring Systems (WAMSs), PMUs deliver synchronized, high-resolution grid measurements. This enhances situational awareness, enabling operators to implement stability-focused control strategies [32,33];
- E. High-Temperature Low-Sag (HTLS) Conductors
HTLS conductors operate at temperatures up to 180 °C with minimal sag, using advanced cores (e.g., carbon/glass fiber composites). They increase the transfer capacity without tower modifications, offering a cost-effective solution for grid upgrades [34,35];
- F. Demand Response (DR) Programs
DR programs incentivize load adjustments to align with grid conditions, alleviating congestion and enhancing the TTC. The key studies demonstrate the following:
- A two-stage ATC framework incorporating the DR can optimize the transfer capacity by matching the demand to the supply [36];
- The IEA identifies the DR as critical for managing the renewable energy source variability and growing demand [37].
The TTC measures the maximum amount of electric power that can be reliably transferred over the interconnected transmission network under specified system conditions. To model the TTC, the CPF method is employed, introducing a scalar parameter, λ (the load scaling factor), which proportionally scales the system loads and generations [15]. The objective is to determine the maximum value of the at which the system remains stable [38,39,40,41].
To integrate the load scaling factor (λ) into the system, the power generation and load values need to be adjusted, as expressed in Equations (2)–(4):
where , , and represent the base case initial power generation and load values, while , , and denote the incremental changes in the power generation and load associated with the transfer scenario under consideration.
By systematically raising the and solving the power flow equations at each step, the system’s loadability curve can be traced and the maximum load scaling factor () that the transmission corridor can accommodate without violating operational constraints can be identified. The evaluation of the TTC for the power transfer is shown in Equation (5):
Note that the modification of the active power generation and loads using the scalar parameter (λ) plays a vital role in maintaining a stable and efficient power grid, allowing operators to adjust the power flow when necessary, ensuring a reliable electricity supply for consumers.
2.2. Existing Transmission Commitment (ETC)
The ETC represents a real-time measure of the power transfer capability between interconnected areas within a power system, accounting for the current operational conditions. Unlike the TTC, which estimates the maximum transferable power under ideal conditions, the ETC provides a dynamic, real-time assessment of the available capacity based on ongoing load, generation, and transmission constraints. This adaptability is essential in modern power grids with high renewable energy integration, where the variability in the wind and solar generation requires the continuous recalibration of the available capacity.
The ETC offers an operational snapshot that helps grid operators efficiently manage power flows. However, traditional ETC calculations, which assume steady-state conditions, often fall short in renewable-dominated grids. The unpredictability of RESs, such as wind and solar, introduces variability that the traditional methods cannot adequately capture. The ETC is highlighted as a critical parameter in [6,42] for real-time grid operations, emphasizing the need for advanced techniques to enhance the ETC in renewable-rich networks, as expressed in Equation (6):
where is the power reserved on transmission line for firm commitments.
2.3. Capacity Benefit Margin (CBM)
The CBM is a reserved portion of the transmission capacity set aside to meet emergency power needs during unforeseen events, such as generator outages or unexpected demand surges. The CBM allows utilities to access external generation resources through interconnected transmission networks, ensuring system reliability and preventing power supply shortages. When emergencies do not occur, the reserved CBM is considered surplus [43].
A precise assessment of the CBM is essential for accurate calculations of the ATC. Overestimation can result in underutilized transmission resources, while underestimation may lead to insufficient reserves and unexpected generation shortages [44,45]. Despite its importance, limited research has been conducted on CBM assessment [46].
CBM Calculation Method
CBM evaluation in the transmission network can be performed using two methods: deterministic and probabilistic methods. Deterministic methods, which estimate the CBM as a fixed percentage of the TTC or are based on the failure of the largest generating units, are less accurate and cannot account for system state variations [47]. Probabilistic methods, particularly using the reliability metric the Loss of Load Expectation (LOLE), estimate the average duration of time that the load exceeds the available generation over a defined period. The LOLE is also known as the Loss of Load Probability (LOLP), with a threshold of one day per ten years (or 2.4 h per year) set as the standard for acceptable reliability [12,20]. Notably, transmission line faults are not included in CBM evaluations; they are addressed within the TRM, which covers transmission uncertainties, while the CBM reserves capacity for accessing external generation resources during emergencies, such as demand surges or generation shortages.
The mathematical formulation of the LOLE is given as Equation (7) [48]:
where the LOLE is usually measured in hours/year. is the total number of time intervals per year (e.g., h in a standard year, or 8736 for a leap year). is the probability that the available generation capacity () is less than the load demand () at the time interval, with as the actual time interval considered within the year (e.g., ).
2.4. Transmission Reliability Margin (TRM)
The TRM reserves the transmission capacity to handle uncertainties like load variability, generation outages, and the intermittent nature of RESs, ensuring system reliability and preventing instability during unanticipated events [42]. While the traditional methods use deterministic approaches, modern power systems increasingly rely on probabilistic methods [49,50,51]. The TRM is calculated as a fixed fraction or percentage of the TTC, based on engineering judgment or historical data, assuming static system conditions and predefined margins for uncertainties [52]. This is represented by Equation (8):
where is the factor or fixed percentage derived from historical data.
The deterministic method is simple and efficient but limited in terms of accounting for the dynamic variability from RESs, often leading to over-conservative or underutilized margins and inefficient transmission network use.
3. Challenges and Impacts of RES Integration on ATC
The integration of RESs, particularly wind and solar, presents both opportunities and challenges for power systems. While RESs offer significant environmental benefits, their inherent variability and uncertainty can substantially impact the ATCs of transmission networks [6]. This section examines the key challenges and impacts of RES integration on the ATC, supported by case studies and advanced assessment methodologies. Figure 3 illustrates these impacts, emphasizing the need for probabilistic approaches.
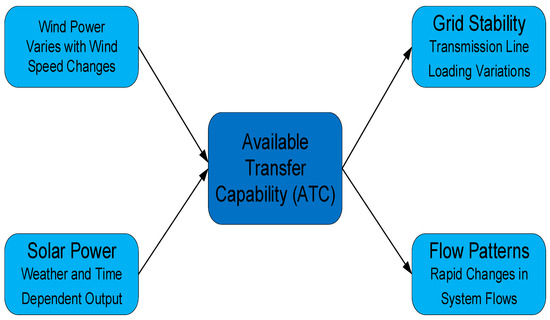
Figure 3.
Impact mechanisms of RESs on ATC.
3.1. Variability and Uncertainty of RESs
Wind and solar generation are inherently intermittent and unpredictable [53,54], posing challenges for ATC evaluation. The traditional deterministic methods often fail to account for rapid fluctuations in the RES output, such as the following:
- Wind power variability due to changing weather conditions;
- Solar power fluctuations caused by cloud cover and diurnal cycles.
These dynamics can push transmission lines closer to their operational limits, reducing power transfer margins and complicating ATC calculations [55,56,57]. To address this, probabilistic methods have been developed to incorporate RES uncertainties into ATC assessments, providing a more realistic evaluation of the transmission capacity under variable generation.
3.2. Transmission Infrastructure Constraints
Many existing transmission systems were not designed for high-RES penetration, which is often concentrated in remote areas far from load centers [58]. This geographical mismatch necessitates the following:
- Grid expansion (e.g., the UK’s upgrades for offshore wind integration);
- Reinforcement projects (e.g., the U.S. SunZia transmission line for wind power delivery) [59,60].
Without adequate infrastructure, RES integration can lead to the following:
- ✓
- The congestion and curtailment of the renewable generation;
- ✓
- A reduced ATC due to constrained power flows.
Strategic investments in transmission are thus critical to unlocking the RES potential.
3.3. Advanced ATC Assessment Methods
To address the limitations of the deterministic approaches, the following advanced methods have emerged:
- A. Probabilistic Methods
Probabilistic methods model the RES variability using probability distributions of the generation, load, and system parameters, for example, canonical low-rank approximation for efficient ATC evaluation in wind-rich systems [61];
- B. Interval-Based Methods
Interval-based methods define the ATC ranges via interval optimization, avoiding probability assumptions, and are applied in hybrid energy systems to bound the wind power uncertainty [62,63,64].
These methods enhance the ATC assessment accuracy and reliability in high-RES grids, although dynamic TRM calculations remain essential for operational robustness (see Section 5).
3.4. Case Studies on RES Impacts
Empirical evidence underscores RESs’ real-world effects on the ATC:
- Israel: distributed RES generation risks overloading key transmission corridors due to power flow volatility [65];
- Korea: high-RES penetration increases congestion, reducing the system flexibility and ATC [66].
Interconnected Systems: the Net Transfer Capacity (NTC) declines with RES integration, exacerbating ramping shortages in conventional generation [67].
Figure 3 synthesizes these impacts, showing how wind/solar variability alters the power flows and grid stability.
4. Stochastic Approaches in Power System Analysis
Stochastic methods have become crucial in power system analysis for handling uncertainties [68]. In [69], a stochastic security model for systems with high wind power penetration demonstrated the effectiveness of these approaches in managing wind variability. A stochastic programming approach for determining the operational reserve requirements under significant wind power, presented in [70], accounted for uncertainties in both load and wind forecasts. Monte Carlo simulations, discussed in [71], generate numerous scenarios for power generation, the load demand, and system outages, helping grid operators assess the likelihood of different outcomes. In ATC evaluations, Monte Carlo simulations model the stochastic behavior of renewable energy sources, providing a more accurate assessment of the grid capabilities and risks associated with renewable energy penetration.
However, while MCS provides a highly detailed probabilistic analysis, it is computationally intensive, requiring many simulations to achieve convergence and statistically reliable results. This is particularly problematic for real-time ATC assessments, where computational efficiency is crucial. Studies such as [72,73] have highlighted that the standard MCS methods often suffer from slow convergence and high computational demands, especially when applied to large-scale power systems with high renewable penetration.
To overcome these challenges, Latin Hypercube Sampling (LHS) is incorporated as an alternative stochastic approach for ATC evaluation. LHS provides a well-distributed and stratified sampling method, ensuring that the entire range of possible uncertainties (e.g., variations in the renewable generation and load demand) is covered more efficiently compared to the random sampling in traditional MCS. Unlike simple random sampling, which may cluster samples unevenly, LHS ensures a more uniform distribution of the input variables, leading to faster convergence and a reduced computational burden while maintaining high accuracy [74]. Table 1 presents the summary of the comparison of stochastic approaches for uncertainty modeling.

Table 1.
Comparison of stochastic approaches or uncertainty modeling.
5. Probabilistic Methods for TRM Assessment
Probabilistic methods for the TRM and ATC address the limitations of deterministic approaches by modeling uncertainties in RESs [61,80,81]. These methods, using statistical techniques and scenario-based simulations, enable dynamic assessments of the TRM and ATC under fluctuating grid conditions, essential for renewable-dominated systems. Studies show that probabilistic evaluations improve the ATC accuracy and grid stability, with methods like Monte Carlo simulations (MCSs) and Bayesian Networks (BNs) accounting for renewable variability and uncertainties in power generation [82,83,84]. MCS estimates ATC probability distributions, while Latin Hypercube Sampling (LHS) enhances efficiency by reducing the scenarios needed [79]. Bayesian Networks provide adaptive updates based on real-time data, supporting dynamic ATC management [85]. Other approaches, such as Stochastic Activity Networks (SANs) and Markov Chains, model renewable variability and outages, improving the resilience in renewable-rich grids [86]. However, these methods face challenges, including high computational demands and the need for accurate input data.
In summary, dynamic approaches like MCS, LHS, and BNs improve the ATC/TRM accuracy by accounting for the RES variability and enabling real-time adjustments. These probabilistic methods offer more realistic estimates than deterministic models but face scalability issues and require significant computational resources. Statistical techniques, such as time series rolling window analysis, further enhance adaptability. The literature highlights the shift towards dynamic, adaptive methodologies for the TRM and ATC, crucial for ensuring the system security in renewable-rich power systems, as presented in Table 2.

Table 2.
Summary of existing TRM assessment approaches.
5.1. Probabilistic Models for TRM Calculation
Recognizing the limitations of deterministic methods, probabilistic approaches incorporate statistical tools to model uncertainties dynamically. The TRM is calculated as a multiple of the standard deviation of uncertainty and is expressed as Equation (9):
where K is the confidence factor, which is determined by the desired confidence level using the cumulative distribution function (CDF) of a normal distribution.
In probability theory, the CDF of a normal distribution represents the probability that a random variable () takes a value less than or equal to a specific threshold.
Mathematically, the CDF of a normally distributed random variable () with the mean (μ) and standard deviation (σ) is given by Equation (10):
where μ is the mean of the normal distribution; σ is the standard deviation of the normal distribution; is the point at which the CDF is evaluated.
The integral represents the area under the normal distribution curve from negative infinity to . For TRM calculations, the confidence factor () is chosen based on a pre-defined probability threshold from the normal distribution. For a 95% confidence level, 95% of the possible uncertainty values lie within ±1.645 standard deviations of the mean. Using the CDF, we determine the so that a specific proportion of the uncertainty values are accounted for in the TRM calculations, ensuring that the estimated margins are neither too conservative nor underestimated.
The probabilistic method uses sensitivity analysis to quantify the impact of uncertain parameters on the transfer capability and is expressed as Equation (11) [42]:
where A represents the transfer capability of the transmission corridor, which is a function of the uncertain parameters () such that the load variation, generation variability, and transmission line capacity change. is the transfer capability calculated using the mean values of these parameters, representing the baseline or expected value.
The variance in the uncertainty is written as Equation (12):
and the standard deviation of the uncertainty is expressed as Equation (13):
From Equation (14), the conventional mathematical model for the probabilistic assessment of power grids is expressed as the product of the sensitivity factor, the standard deviation of the uncertainties, and the confidence factor (K), as given in Equation (14):
where is the number of uncertain parameters (); are the system variables that impact the transfer capability; is the sensitivity of the transfer capability (A) to parameter (i.e., showing how sensitive the transfer capability (A) is to changes in parameter); is the standard deviation (uncertainty) of the parameter .
The increasing penetration of RESs presents significant challenges in determining the appropriate TRM and ATC, primarily due to the static nature of the current TRM methods. The traditional approaches use fixed parameters that fail to adapt to the dynamic system conditions, resulting in overly conservative or insufficient security margins [19,90,91]. This is particularly problematic in grids with high renewable penetration, where the generation and load patterns fluctuate unpredictably. The inability to dynamically adjust the security margins leads to inefficient transmission capacity use and increased grid instability risks. The complex interactions of system uncertainties call for a more adaptive approach to ensure grid security and operational efficiency.
5.2. Limitations of the Traditional Methods
The conventional TRM calculation method has several drawbacks:
- I. Static Confidence Factors
Fixed confidence factors may lead to overly conservative or insufficient TRM estimates based on real-time conditions;
- II. Limited Adaptability
It does not dynamically adjust to uncertainties like rapid loads or renewable generation changes;
- III. Fixed Time Intervals
The TRM is recalculated periodically rather than continuously updated to reflect the real-time system changes.
These limitations highlight the need for a dynamic approach to TRM calculation that better accommodates the modern power system variability, as presented in Table 3.

Table 3.
Comparison of existing probabilistic/statistical TRM estimation methods.
6. Challenges of the Existing TRM Assessment Methods
Accurate and adaptive TRM estimation is crucial for the reliable ATC assessment of modern power grids [94]. However, the existing TRM assessment methods face several challenges, some of which are as follows:
- ▪
- Fixed-margin TRM: Many methods use fixed margins (e.g., a percentage of the TTC) that fail to account for real-time system variations, such as load fluctuations, topology changes, and renewable generation [95,96]. Modern power systems require dynamic TRM assessments to account for uncertainties in weather-dependent resources and evolving grid configurations;
- ▪
- Computational complexity: Probabilistic methods, like Monte Carlo simulations, require significant computational resources, making them unsuitable for real-time applications in large-scale power systems, especially as grids integrate more variable RESs [49]. This is due to the extensive number of simulations needed to capture the system uncertainties, which results in longer processing times and computational costs [5,73];
- ▪
- Limited real-world validation: Most TRM models are validated through simulations, not real-world power grids, limiting their effectiveness in dynamic conditions. This reliance on simulated data, often devoid of real-world noise and variability, can lead to models that perform well in environments but falter under actual operating conditions [10,97,98];
- ▪
- Static confidence factors: Many statistical models rely on fixed confidence factors (K-Factors), which may lead to the over- or underestimation of the TRM values under varying conditions. This approach assumes a constant level of uncertainty, failing to account for the dynamic nature of power systems wherein uncertainties can significantly fluctuate [91,99];
- ▪
- Climate change impacts: Changing weather patterns and extreme weather events affect the transmission line ratings and system reliability, necessitating more dynamic TRM assessment methods. As climate change leads to more frequent, extreme weather events, various natural disasters pose risks to the operation of transmission lines. Transmission line failures caused by natural disasters are unpredictable and add extra maintenance costs [100,101,102];
- ▪
- Data quality and availability: Accurate TRM estimation depends on high-quality data, which may not always be readily available or reliable, especially in regions with less advanced monitoring infrastructures. Inadequate data quality can lead to suboptimal asset management decisions, affecting the reliability and efficiency of power systems [103].
7. Conclusions and Future Work
7.1. Conclusions
This study presents significant advancements in the evaluation of the TRM for power systems with high levels of renewable energy integration. The primary finding of the investigation is the development of a dynamic TRM calculation framework, which holds substantial potential for overcoming the limitations of the traditional static methods. The traditional TRM calculation methods typically rely on fixed margins or predetermined safety factors, which do not adapt to the rapidly fluctuating conditions inherent in modern renewable-rich grids. As a result, these static approaches can lead to the overestimation of the required capacity, reserving an unnecessary transmission margin that could otherwise be utilized for power transfer, or its underestimation, risking grid instability during periods of high variability.
The dynamic TRM framework introduced in this study is designed to update continuously based on real-time system data, allowing it to adjust to changes in the generation, load, and transmission conditions. This real-time adaptability ensures that the margin is neither too excessive, leading to the underutilization of the available transmission capacity, nor too tight, which could compromise the system security. By accurately reflecting the current state of the power grid, this dynamic approach ensures that the transmission margin is optimized for efficiency while safeguarding against potential reliability risks.
From a practical standpoint, the dynamic TRM approach allows for more accurate ATC values. These improved ATC values are critical for grid operators, as they provide a more realistic assessment of the system’s ability to transfer power without exceeding safe limits. With the dynamic TRM framework, operators are better equipped to accommodate higher levels of renewable generation—such as wind and solar—without sacrificing system reliability or efficiency. This capability is essential, as renewable energy sources are known for their variability, which has traditionally posed challenges for grid stability and operational efficiency.
Furthermore, the dynamic TRM method helps to ensure that renewable energy integration does not lead to underutilized transmission assets or an overreliance on conservative margin estimates. By continuously adapting to real-time conditions, this approach enhances the grid stability, reduces operational costs, and ensures that transmission resources are used to their fullest potential. Overall, the findings underscore the critical role of dynamic TRM approaches in enhancing the resilience and operational efficiency of power systems with increasing renewable energy penetration. This methodology not only helps maintain grid stability but also supports the continued transition to more sustainable energy sources by optimizing the transmission network performance amidst rising uncertainty.
7.2. Future Work
Despite the progress, there are several areas for future research to fully realize the benefits of dynamic TRM:
- Methodological improvements: Future work should enhance uncertainty modeling, particularly for correlated renewable and load fluctuations, using more sophisticated probability distributions. Improving the real-time optimization of algorithms for TRM/ATC calculations, such as through faster techniques (importance sampling, surrogate models, parallel computing), will reduce the computational burden and enable more timely updates;
- Real-world implementation: The dynamic TRM frameworks should be validated through pilot projects and field tests using live grid data to confirm their efficacy and identify challenges like communication delays and measurement errors. Research on the computational feasibility in control centers, the compatibility with existing grid management systems, and user-friendly interfaces for operators is crucial for successful integration;
- Emerging research areas: AI and machine learning can improve TRM estimation by learning complex patterns and making data-driven predictions. Hybrid deterministic–probabilistic approaches can combine the reliability of deterministic criteria with the flexibility of probabilistic assessments. Additionally, research on decentralized TRM management for future smart grids, including multi-area coordination and self-healing capabilities, will be valuable to support grid resilience.
By addressing these gaps, dynamic TRM can evolve into a key component of secure and efficient grid operations in renewable-rich power systems.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- North American Electric Reliability Council. Available Transfer Capability Definitions and Determination; North American Electric Reliability Council: Atlanta, GA, USA, 1996. [Google Scholar]
- Murugesan, K.; Jeyanthy, P.A.; Durairaj, D.; Velusamy, A.I.S. Probabilistic day ahead dynamic available transfer capability estimation in solar integrated deregulated power system. Int. Trans. Electr. Energy Syst. 2021, 31, e13081. [Google Scholar] [CrossRef]
- Mastoi, M.S.; Zhuang, S.; Haris, M.; Hassan, M.; Ali, A. Large-scale wind power grid integration challenges and their solution: A detailed review. Environ. Sci. Pollut. Res. 2023, 30, 103424–103462. [Google Scholar] [CrossRef] [PubMed]
- Pupo-Roncallo, O.; Campillo, J.; Ingham, D.; Hughes, K.; Pourkashanian, M. Large scale integration of renewable energy sources (RES) in the future Colombian energy system. Energy 2019, 186, 115805. [Google Scholar] [CrossRef]
- Abud, T.P.; Augusto, A.A.; Fortes, M.Z.; Maciel, R.S.; Borba, B.S.M.C. State of the Art Monte Carlo Method Applied to Power System Analysis with Distributed Generation. Energies 2023, 16, 394. Available online: https://www.mdpi.com/1996-1073/16/1/394 (accessed on 22 April 2025). [CrossRef]
- Meng, X.; Zhang, L.; Tian, X.; Chu, H.; Wang, Y.; Shi, Q. Available Transfer Capability Assessment of Multiarea Power Systems with Conditional Generative Adversarial Network. Int. Trans. Electr. Energy Syst. 2024, 2024, 5225784. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, T.; Yang, X.; Wang, J. Calculation and optimization of inter-regional available transfer capability considering wind power uncertainty and system improvement measures. Front. Energy Res. 2023, 11, 1177754. [Google Scholar] [CrossRef]
- Chauhan, R.; Naresh, R.; Kenedy, M.; Aharwar, A. A streamlined and enhanced iterative method for analysing power system available transfer capability and security. Electr. Power Syst. Res. 2023, 223, 109528. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Sheng, H.; Lin, X. A data-driven sparse polynomial chaos expansion method to assess probabilistic total transfer capability for power systems with renewables. IEEE Trans. Power Syst. 2020, 36, 2573–2583. [Google Scholar] [CrossRef]
- Nadia, A.; Hossain, S.; Hasan, M.; Afrin, S.; Shafiullah; Hossain, B.; Islam, K.Z. Determination of transmission reliability margin for brownout. AIMS Energy 2021, 9, 1009–1026. [Google Scholar] [CrossRef]
- NERC. A Reference Document for Calculating and Reporting the Electric Power Transfer Capability of Interconnected Electric Systems; North American Electric Reliability Council: Atlanta, GA, USA, 1995. [Google Scholar]
- Mohammed, O.O.; Mustafa, M.W.; Mohammed, D.S.S.; Otuoze, A.O. Available transfer capability calculation methods: A comprehensive review. Int. Trans. Electr. Energy Syst. 2019, 29, e2846. [Google Scholar] [CrossRef]
- Kumar, G.N.; Kalavathi, M.S.; Reddy, B.R. Eigen Value Techniques for Small Signal Stability Analysis in Power System Stability. J. Theor. Appl. Inf. Technol. 2009, 6, 182–188. [Google Scholar]
- Nirbhavane, P.S.; Corson, L.; Rizvi, S.M.H.; Srivastava, A.K. TPCPF: Three-phase continuation power flow tool for voltage stability assessment of distribution networks with distributed energy resources. IEEE Trans. Ind. Appl. 2021, 57, 5425–5436. [Google Scholar] [CrossRef]
- Wang, G. Voltage-Stability-Based ATC and Congestion Management for Simultaneous Multi-Area Transactions. Doctoral Dissertation, Iowa State University, Ames, IA, USA, 1998. [Google Scholar]
- Nassar, I.; Seif, M.; ElAttar, M. Improving the voltage quality of Abu Hummus network in Egypt. Int. J. Electr. Comput. Eng. 2020, 10, 4458–4468. [Google Scholar] [CrossRef]
- Tatikayala, V.K.; Dixit, S. Multi-stage voltage control in high photovoltaic based distributed generation penetrated distribution system considering smart inverter reactive power capability. Ain Shams Eng. J. 2024, 15, 102265. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, B.; Wu, W. Total transfer capability calculation method for power system operation and decision. Autom. Electr. Power Syst. 2008, 32, 12–17. [Google Scholar]
- Ou, Y.; Singh, C. Assessment of available transfer capability and margins. IEEE Trans. Power Syst. 2002, 17, 463–468. [Google Scholar] [CrossRef]
- Ford, A.; Harm, W. Market based adequacy: Reliability and CBM/ATC calculations. An independent system operator’s perspective. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 02CH37309), New York, NY, USA, 27–31 January 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 18–23. [Google Scholar]
- Shaaban, M.; Li, W.; Yan, Z.; Ni, Y.; Wu, F.F. Calculation of total transfer capability incorporating the effect of reactive power. Electr. Power Syst. Res. 2003, 64, 181–188. [Google Scholar] [CrossRef]
- Xu, S.; Miao, S. Calculation of TTC for multi-area power systems based on improved Ward-PV equivalents. IET Gener. Transm. Distrib. 2017, 11, 987–994. [Google Scholar] [CrossRef]
- Jamshidzadeh, Z.; Latif, S.D.; Ehteram, M.; Khozani, Z.S.; Ahmed, A.N.; Sherif, M.; El-Shafie, A. An advanced hybrid deep learning model for predicting total dissolved solids and electrical conductivity (EC) in coastal aquifers. Environ. Sci. Eur. 2024, 36, 20. [Google Scholar] [CrossRef]
- Yan, J.; Li, C.; Liu, Y. Deep learning based total transfer capability calculation model. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 952–957. [Google Scholar]
- Alajrash, B.H.; Salem, M.; Swadi, M.; Senjyu, T.; Kamarol, M.; Motahhir, S. A comprehensive review of FACTS devices in modern power systems: Addressing power quality, optimal placement, and stability with renewable energy penetration. Energy Rep. 2024, 11, 5350–5371. [Google Scholar] [CrossRef]
- Ravindra, S.; Suresh, C.V.; Sivanagaraju, S.; Reddy, V.C.V. Power system security enhancement with unified power flow controller under multi-event contingency conditions. Ain Shams Eng. J. 2017, 8, 9–28. [Google Scholar] [CrossRef]
- Rajabi-Ghahnavieh, A.; Fotuhi-Firuzabad, M.; Othman, M. Optimal unified power flow controller application to enhance total transfer capability. IET Gener. Transm. Distrib. 2015, 9, 358–368. [Google Scholar] [CrossRef]
- Gandotra, R.; Pal, K. FACTS Technology: A Comprehensive Review on FACTS Optimal Placement and Application in Power System. Iran. J. Electr. Electron. Eng. 2022, 18, 95–109. Available online: https://ijeee.iust.ac.ir/article-1-2390-en.html (accessed on 25 April 2025).
- Kumar, C.K.; Kumar, M.S.; SriramBabu, V.; Nagulmeera, S. A comparative analysis of UPFC as a Power Flow controller with applications. IOSR J. Electr. Electron. Eng. 2013, 4, 28–36. [Google Scholar] [CrossRef]
- Gautam, A.; Ibraheem; Sharma, G.; Bokoro, P.N.; Ahmer, M.F. Available Transfer Capability Enhancement in Deregulated Power System Through TLBO Optimised TCSC. Energies 2022, 15, 4448. Available online: https://www.mdpi.com/1996-1073/15/12/4448 (accessed on 22 April 2025). [CrossRef]
- Bhattarai, B.P.; Gentle, J.P.; McJunkin, T.; Hill, P.J.; Myers, K.S.; Abboud, A.W.; Renwick, R.; Hengst, D. Improvement of transmission line ampacity utilization by weather-based dynamic line rating. IEEE Trans. Power Deliv. 2018, 33, 1853–1863. [Google Scholar] [CrossRef]
- Ortiz, G.; Rehtanz, C.; Colomé, G. Monitoring of power system dynamics under incomplete PMU observability condition. IET Gener. Transm. Distrib. 2021, 15, 1435–1450. [Google Scholar] [CrossRef]
- Chintakindi, R.; Mitra, A. WAMS challenges and limitations in load modeling, voltage stability improvement, and controlled island protection—A review. Energy Rep. 2022, 8, 699–709. [Google Scholar] [CrossRef]
- Riba, J.-R.; Bogarra, S.; Gómez-Pau, Á.; Moreno-Eguilaz, M. Uprating of transmission lines by means of HTLS conductors for a sustainable growth: Challenges, opportunities, and research needs. Renew. Sustain. Energy Rev. 2020, 134, 110334. [Google Scholar] [CrossRef]
- Kgoete, F.M.; Uyor, U.O.; Popoola, A.P.; Popoola, O. Insight on the recent materials advances for manufacturing of high-voltage transmission conductors. Int. J. Adv. Manuf. Technol. 2024, 130, 4123–4136. [Google Scholar] [CrossRef]
- Hou, L.; Li, W.; Zhou, K.; Jiang, Q. Integrating flexible demand response toward available transfer capability enhancement. Appl. Energy 2019, 251, 113370. [Google Scholar] [CrossRef]
- IEA. “Demand Response”. International Energy Agency. Available online: https://www.iea.org/energy-system/energy-efficiency-and-demand/demand-response? (accessed on 21 April 2025).
- Ajjarapu, V. (Ed.) Continuation Power Flow. In Computational Techniques for Voltage Stability Assessment and Control; Springer: Boston, MA, USA, 2007; pp. 49–116. [Google Scholar]
- Keskin, M.B. Continuation Power Flow and Voltage Stability in Power Systems. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2007. [Google Scholar]
- Ajjarapu, V.; Christy, C. The continuation power flow: A tool for steady state voltage stability analysis. IEEE Trans. Power Syst. 1992, 7, 416–423. [Google Scholar] [CrossRef]
- Bislimi, A. Comprehensive analysis of power system: Exploring load factor, power balance, active load variation, and increment factors with iterative implications. Int. J. Electr. Comput. Eng. Syst. 2024, 15, 105–112. [Google Scholar] [CrossRef]
- Dobson, I.; Greene, S.; Rajaraman, R.; DeMarco, C.L.; Alvarado, F.L.; Glavic, M.; Zhang, J.; Zimmerman, R. Electric Power Transfer Capability: Concepts, Applications, Sensitivity and Uncertainty; PSerc Publication: Austin, TX, USA, 2001. [Google Scholar]
- Kuraishi, H.; Yokoyama, A. Optimal CBM of tie lines between control areas in a deregulated environment. Electr. Eng. Jpn. 2009, 167, 35–48. [Google Scholar] [CrossRef]
- Savulescu, S.C. A metric for quantifying the risk of blackout. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 1661–1664. [Google Scholar]
- Bouwmans, I.; Weijnen, M.P.; Gheorghe, A. Infrastructures at risk. In Critical Infrastructures at Risk: Securing the European Electric Power System; Springer: Berlin/Heidelberg, Germany, 2006; pp. 19–36. [Google Scholar]
- Ramezani, M.; Falaghi, H.; Singh, C. Capacity Benefit Margin Evaluation in Multi-area Power Systems Including Wind Power Generation Using Particle Swarm Optimization. In Wind Power Systems: Applications of Computational Intelligence; Wang, L., Singh, C., Kusiak, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 105–123. [Google Scholar]
- Rajathy, R.; Gnanadass, R.; Manivannan, K.; Kumar, H. Computation of capacity benefit margin using differential evolution. Int. J. Comput. Sci. Math. 2010, 3, 275–287. [Google Scholar] [CrossRef]
- Voorspools, K.R.; D’haeseleer, W.D. Are deterministic methods suitable for short term reserve planning? Energy Convers. Manag. 2005, 46, 2042–2052. [Google Scholar] [CrossRef]
- Zhang, J.; Dobson, I.; Alvarado, F.L. Quantifying transmission reliability margin. Int. J. Electr. Power Energy Syst. 2004, 26, 697–702. [Google Scholar] [CrossRef]
- Zaini, R.; Othman, M.B.; Musirin, I.; Mohamed, A.; Hussain, A. Determination of transmission reliability margin considering uncertainties of system operating condition and transmission line outage. Eur. Trans. Electr. Power 2011, 21, 380–397. [Google Scholar] [CrossRef]
- Nadia, A.; Chowdhury, A.; Mahfuj, E.; Hossain, M.; Islam, K.; Rahman, M. Determination of transmission reliability margin using AC load flow. AIMS Energy 2020, 8, 701–720. [Google Scholar] [CrossRef]
- European Commission and Transport. Identification of Appropriate Generation and System Adequacy Standards for the Internal Electricity Market; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- Batalla-Bejerano, J.; Trujillo-Baute, E. Impacts of intermittent renewable generation on electricity system costs. Energy Policy 2016, 94, 411–420. [Google Scholar] [CrossRef]
- Asiaban, S.; Kayedpour, N.; Samani, A.E.; Bozalakov, D.; De Kooning, J.D.M.; Crevecoeur, G.; Vandevelde, L. Wind and Solar Intermittency and the Associated Integration Challenges: A Comprehensive Review Including the Status in the Belgian Power System. Energies 2021, 14, 2630. Available online: https://www.mdpi.com/1996-1073/14/9/2630 (accessed on 25 April 2025). [CrossRef]
- Huangpu, X.-L. Available Transfer Capability Calculation for Wind-Integrated Power Systems Considering Wind Speed Spatiotemporal Correlation and Primal-Dual Interior Point Method. arXiv 2024, arXiv:2409.14093. [Google Scholar]
- Chen, H.; Fang, X.; Zhang, R.; Jiang, T.; Li, G.; Li, F. Available transfer capability evaluation in a deregulated electricity market considering correlated wind power. IET Gener. Transm. Distrib. 2018, 12, 53–61. [Google Scholar] [CrossRef]
- Luo, G.; Chen, J.; Cai, D.; Shi, D.; Duan, X. Probabilistic assessment of available transfer capability considering spatial correlation in wind power integrated system. IET Gener. Transm. Distrib. 2013, 7, 1527–1535. [Google Scholar] [CrossRef]
- Nielsen, S.; Østergaard, P.A.; Sperling, K. Renewable energy transition, transmission system impacts and regional development–a mismatch between national planning and local development. Energy 2023, 278, 127925. [Google Scholar] [CrossRef]
- Zhou, D.; Feng, S.; Zhu, Y.; Ding, Y.; Sang, M.; Guo, L.; Bao, M.; Wu, X.; Wang, Z. Application analysis and key issues of available transfer capability (ATC) adapted to electricity market environment in China. Power Syst. Technol. 2021, 45, 3357–3366. [Google Scholar]
- Technology, P. “SunZia Transmission Project, US.” Power Technology. Available online: https://www.power-technology.com/projects/sunzia-transmission-project-us/?cf-view&cf-closed (accessed on 19 April 2025).
- Sun, X.; Tian, Z.; Rao, Y.; Li, Z.; Tricoli, P. Probabilistic available transfer capability assessment in power systems with wind power integration. IET Renew. Power Gener. 2020, 14, 1912–1920. [Google Scholar] [CrossRef]
- Khosravifard, M.; Shaaban, M. Risk-based available transfer capability assessment including nondispatchable wind generation. Int. Trans. Electr. Energy Syst. 2015, 25, 3169–3183. [Google Scholar] [CrossRef]
- Kou, X.; Li, F. Interval optimization for available transfer capability evaluation considering wind power uncertainty. IEEE Trans. Sustain. Energy 2018, 11, 250–259. [Google Scholar] [CrossRef]
- Jiang, T.; Li, X.; Kou, X.; Zhang, R.; Tian, G.; Li, F. Available transfer capability evaluation in electricity-dominated integrated hybrid energy systems with uncertain wind power: An interval optimization solution. Appl. Energy 2022, 314, 119001. [Google Scholar] [CrossRef]
- Navon, A.; Kulbekov, P.; Dolev, S.; Yehuda, G.; Levron, Y. Integration of distributed renewable energy sources in Israel: Transmission congestion challenges and policy recommendations. Energy Policy 2020, 140, 111412. [Google Scholar] [CrossRef]
- Sajadi, A.; Strezoski, L.; Kolacinski, R.; Loparo, K. Transmission System Planning for Integration of Renewable Electricity Generation Units. arXiv 2020, arXiv:2001.03449. [Google Scholar]
- Min, C. Impact Analysis of Transmission Congestion on Power System Flexibility in Korea. Energies 2020, 13, 2191. Available online: https://www.mdpi.com/1996-1073/13/9/2191 (accessed on 25 April 2025). [CrossRef]
- Zhou, Z.; Liu, C.; Botterud, A. Stochastic Methods Applied to Power System Operations with Renewable Energy: A Review; Argonne National Laboratory: Lemont, IL, USA, 2016. [Google Scholar]
- Bouffard, F.; Galiana, F.D. Stochastic security for operations planning with significant wind power generation. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–11. [Google Scholar]
- Morales, J.M.; Conejo, A.J.; Pérez-Ruiz, J. Economic valuation of reserves in power systems with high penetration of wind power. IEEE Trans. Power Syst. 2009, 24, 900–910. [Google Scholar] [CrossRef]
- Rollett, A.D.; Manohar, P. The monte carlo method. In Continuum Scale Simulation of Engineering Materials: Fundamentals–Microstructures–Process Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 77–114. [Google Scholar]
- Keramat, M.; Kielbasa, R. Modified Latin hypercube sampling Monte Carlo (MLHSMC) estimation for average quality index. Analog. Integr. Circuits Signal Process. 1999, 19, 87–98. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, J.; Chen, X.; Liu, F.; Songy, Y. Fast Monte Carlo Simulation of Dynamic Power Systems Under Continuous Random Disturbances. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Shu, Z.; Jirutitijaroen, P. Latin hypercube sampling techniques for power systems reliability analysis with renewable energy sources. IEEE Trans. Power Syst. 2011, 26, 2066–2073. [Google Scholar]
- Afzali, P.; Hosseini, S.A.; Peyghami, S. A Comprehensive Review on Uncertainty and Risk Modeling Techniques and Their Applications in Power Systems. Appl. Sci. 2024, 14, 12042. [Google Scholar] [CrossRef]
- Yin, W.; Hou, Y. Models and applications of stochastic programming with decision-dependent uncertainty in power systems: A review. IET Renew. Power Gener. 2024, 18, 2819–2834. [Google Scholar] [CrossRef]
- Chib, S. Markov chain Monte Carlo methods: Computation and inference. Handb. Econom. 2001, 5, 3569–3649. [Google Scholar]
- Yang, C.; Sun, W.; Han, D.; Yin, X. Research on power system flexibility considering uncertainties. Front. Energy Res. 2022, 10, 967220. [Google Scholar] [CrossRef]
- Avila, N.F.; Chu, C.-C. Distributed probabilistic ATC assessment by optimality conditions decomposition and LHS considering intermittent wind power generation. IEEE Trans. Sustain. Energy 2018, 10, 375–385. [Google Scholar] [CrossRef]
- Hakami, A.M.; Hasan, K.N.; Alzubaidi, M.; Datta, M. A Review of Uncertainty Modelling Techniques for Probabilistic Stability Analysis of Renewable-Rich Power Systems. Energies 2023, 16, 112. Available online: https://www.mdpi.com/1996-1073/16/1/112 (accessed on 25 April 2025).
- Audomvongseree, K.; Yokoyama, A.; Verma, S.C.; Nakachi, Y. A novel TRM calculation method by probabilistic concept. IEEJ Trans. Power Energy 2004, 124, 1400–1407. [Google Scholar] [CrossRef][Green Version]
- Zio, E. Monte carlo simulation: The method. In The Monte Carlo Simulation Method for System Reliability and Risk Analysis; Springer: Berlin/Heidelberg, Germany, 2012; pp. 19–58. [Google Scholar]
- Landau, D.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Koski, T.; Noble, J.; Wiley, J. Bayesian Networks: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Adedipe, T.; Shafiee, M.; Zio, E. Bayesian network modelling for the wind energy industry: An overview. Reliab. Eng. Syst. Saf. 2020, 202, 107053. [Google Scholar] [CrossRef]
- Sedaghatbaf, A.; Azgomi, M.A. Attack modelling and security evaluation based on stochastic activity networks. Secur. Commun. Netw. 2014, 7, 714–737. [Google Scholar] [CrossRef]
- Madadi, S.; Mohammadi-Ivatloo, B.; Tohidi, S. Probabilistic available transfer capability evaluation considering dynamic line rating based on a sequential game-theoretic approach. IEEE Syst. J. 2021, 16, 891–901. [Google Scholar] [CrossRef]
- Reyad, H.W.; Elfar, M.; El-Araby, E. Probabilistic Assessment of Available Transfer Capability Incorporating Load and Wind Power Uncertainties. IEEE Access 2023, 11, 39048–39065. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, A. ATC determination with heuristic techniques and comparison with sensitivity based methods and GAMS. Procedia Comput. Sci. 2018, 125, 389–397. [Google Scholar] [CrossRef]
- Pandiyan, M.K.; Idhayaselvi, V.A.; Danalakshmi, D.; Sheela, A. Online estimation of control parameters of FACTS devices for ATC enhancement using artificial neural network. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1055, 012146. [Google Scholar] [CrossRef]
- Othman, M.M.B.; Mohamed, A.; Hussain, A. Determination of transmission reliability margin using parametric bootstrap technique. IEEE Trans. Power Syst. 2008, 23, 1689–1700. [Google Scholar] [CrossRef]
- Nadia, A.; Chowdhury, A.H. Correlation between Transmission Reliability Margin and Standard Deviation of Uncertainty. In Proceedings of the 2019 5th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 26–28 September 2019; pp. 251–254. [Google Scholar] [CrossRef]
- Karuppasamypandiyan, M.; Jeyanthy, P.A.; Devaraj, D.; Selvi, V.A.I. Day ahead dynamic available transfer capability evaluation incorporating probabilistic transmission capacity margins in presence of wind generators. Int. Trans. Electr. Energy Syst. 2021, 31, e12693. [Google Scholar] [CrossRef]
- Nadia, A.; Hossain, M.S.; Rahman, M.I.; Shafiullah, M. Transmission Reliability Margin Determination for DC and DCQ Load Flow Method. Authorea Prepr. 2023. [Google Scholar] [CrossRef]
- Sauer, P.W. Alternatives for calculating transmission reliability margin (TRM) in available transfer capability (ATC). In Proceedings of the Thirty-First Hawaii International Conference on System Sciences, Kohala Coast, HI, USA, 6–9 January 1998; Volume 3, p. 89. [Google Scholar] [CrossRef]
- Salim, N.A.; Othman, M.M.; Musirin, I.; Serwan, M.S. Evaluation of Transfer Capability Considering Uncertainties of System Operating Condition and System Cascading Collapse. Int. J. Energy Power Eng. 2014, 8, 241–246. [Google Scholar]
- Birchfield, A.B.; Schweitzer, E.; Athari, M.H.; Xu, T.; Overbye, T.J.; Scaglione, A.; Wang, Z. A Metric-Based Validation Process to Assess the Realism of Synthetic Power Grids. Energies 2017, 10, 1233. Available online: https://www.mdpi.com/1996-1073/10/8/1233 (accessed on 25 April 2025). [CrossRef]
- Linearization Technology. Why Current Power Flow Models May Not Work in Real-World Scenarios. The HackerNoon Newsletter. 17 February 2025. Available online: https://hackernoon.com/why-current-power-flow-models-may-not-work-in-real-world-scenarios? (accessed on 17 February 2025).
- Khatavkar, V.; Swathi, D.; Mayadeo, H.; Dharme, A. Short-Term Estimation of Transmission Reliability Margin Using Artificial Neural Networks. In International Proceedings on Advances in Soft Computing, Intelligent Systems and Applications; Reddy, M.S., Viswanath, K., Eds.; Springer: Singapore, 2018; pp. 17–27. [Google Scholar]
- Fan, R.; Zeng, W.; Ming, Z.; Zhang, W.; Huang, R.; Liu, J. Risk Reliability Assessment of Transmission Lines under Multiple Natural Disasters in Modern Power Systems. Energies 2023, 16, 6548. [Google Scholar] [CrossRef]
- Sergio, M.-S.; Andrea, M. Assessment of the influence of climate change on power grid transmission capacity. Sustain. Energy Grids Netw. 2025, 42, 101695. [Google Scholar] [CrossRef]
- Peters, G.; DiGioia, J.A.M.; Hendrickson, C.; Apt, J. Transmission Line Reliability: Climate Change and Extreme Weather. In Electrical Transmission Line and Substation Structures; ASCE: Reston, VA, USA, 2012; pp. 12–26. [Google Scholar]
- Naim, W. On the Role of Data Quality and Availability in Power System Asset Management. Comprehensive Summary, TRITA-EECS-AVL. Licentiate Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2021. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-295696 (accessed on 25 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).