Drainage Characteristics and Heat Transfer Performance of Fin Surfaces in Desert Greenhouse Environments
Abstract
1. Introduction
2. Experimental Tests
2.1. Experimental Setup
2.2. Experimental Operation Flow
2.3. Experimental Error and Uncertainty
2.4. Selecting the Experimental Conditions
2.5. Experimental Data Processing
- (1)
- Heat transfer:
- (2)
- Sensible heat transfer:
- (3)
- Latent heat transfer:
- (4)
- Air-side heat transfer coefficient:
- (5)
- Nusselt number:
- (6)
- Reynolds number
- (7)
- Fin surface condensation generation rate:
- (8)
- Fin surface condensation removal rate:
3. Results and Discussion
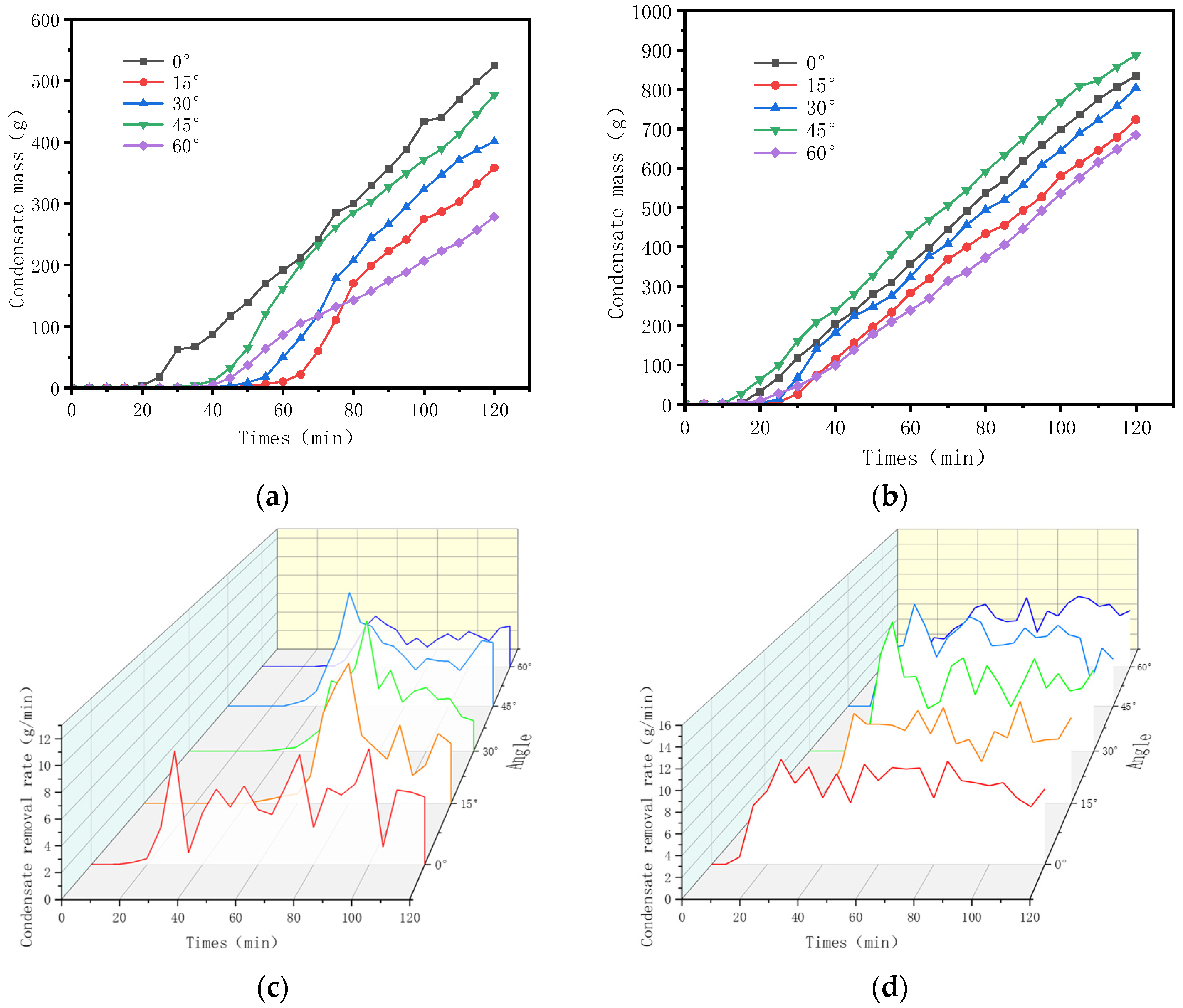
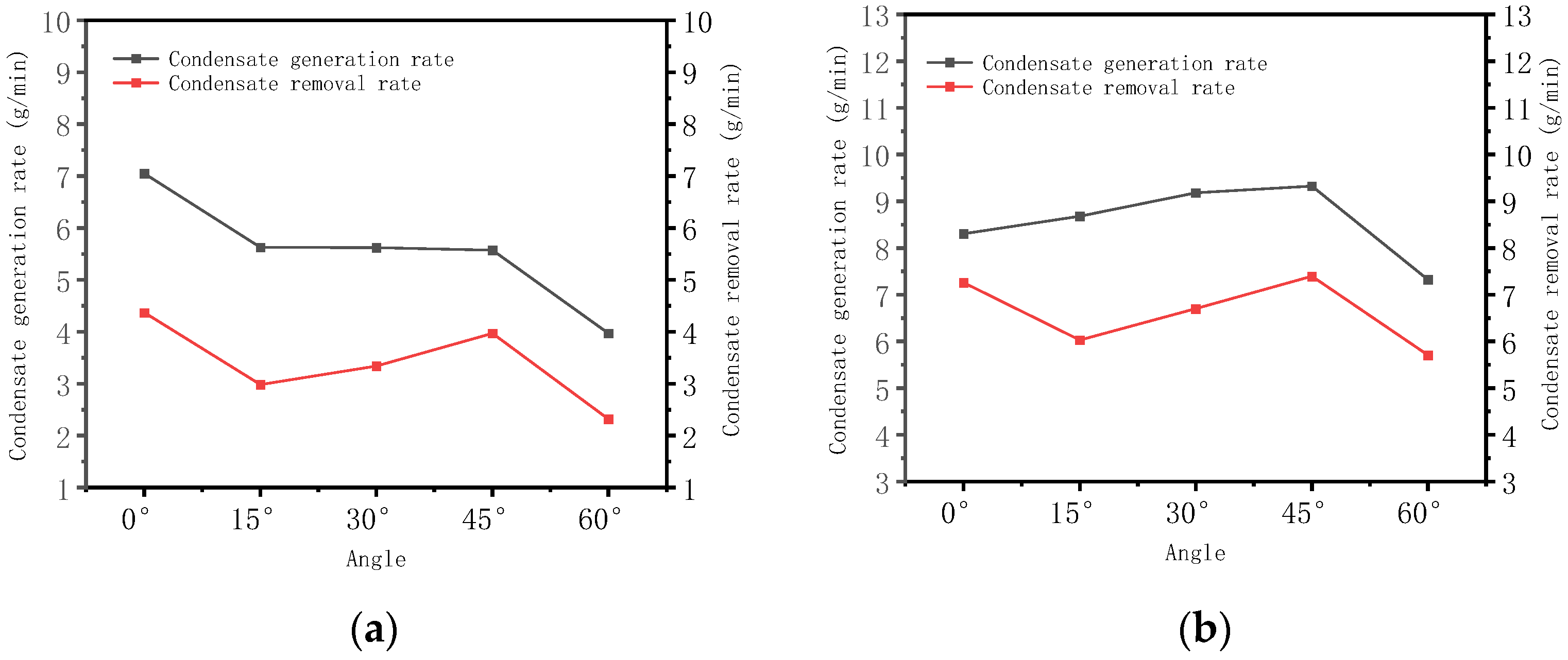
3.1. Effect of Fin Angle on Surface Drainage Characteristics
The Effect of Fin Inclination Angle on Condensate Mass and Condensation Rate
3.2. The Effect of Flow Velocity on the Fin Surface Drainage Characteristics and Heat Transfer Performance
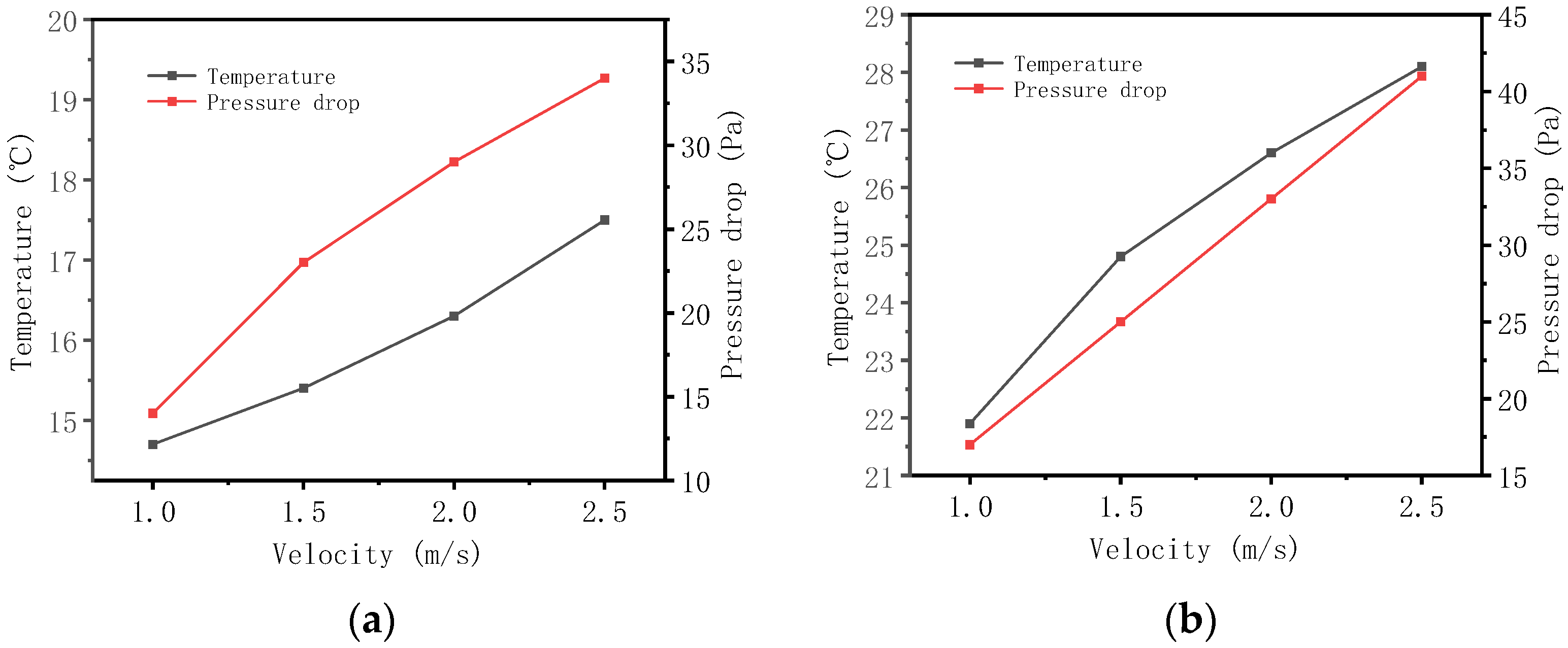
3.2.1. The Effect of Air Velocity on the Outlet Air Temperature and Pressure Drop
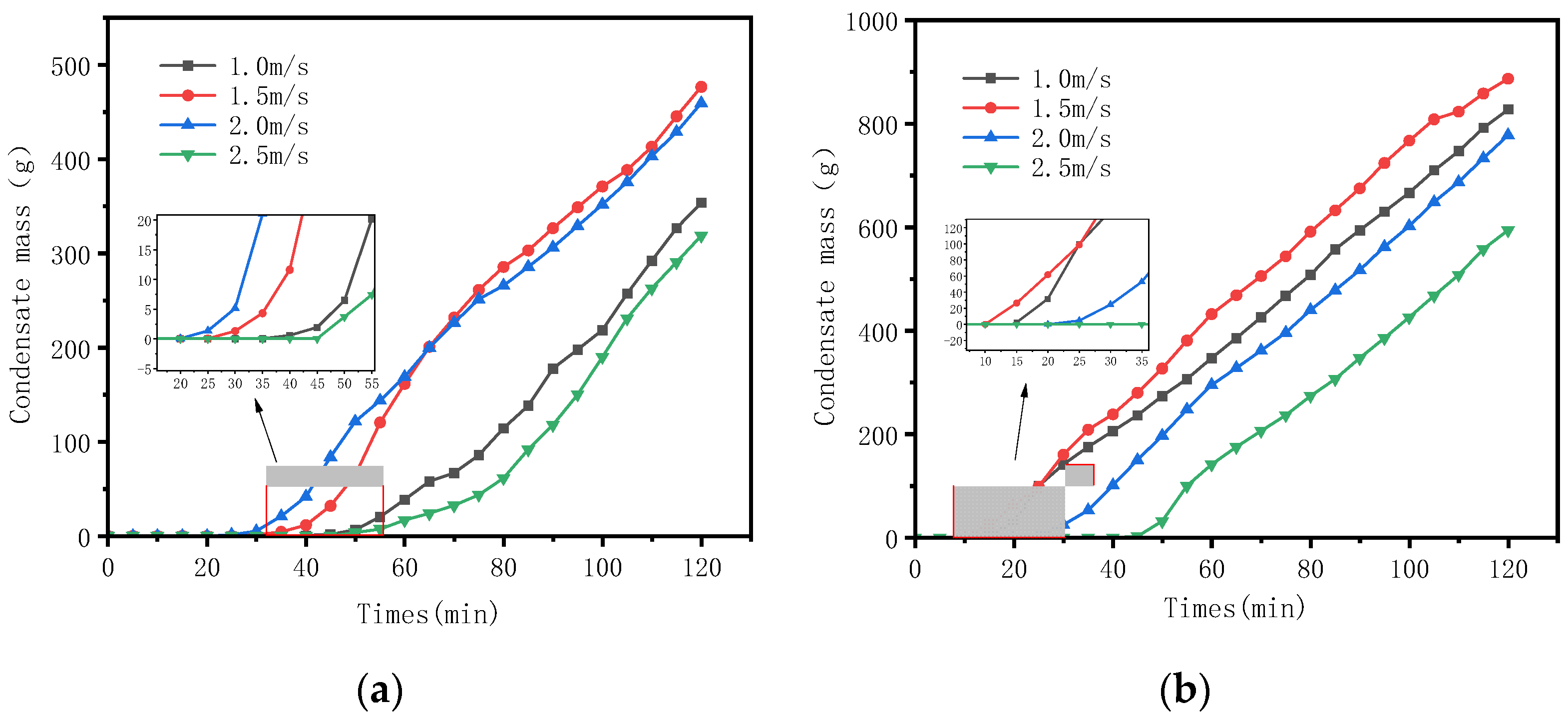
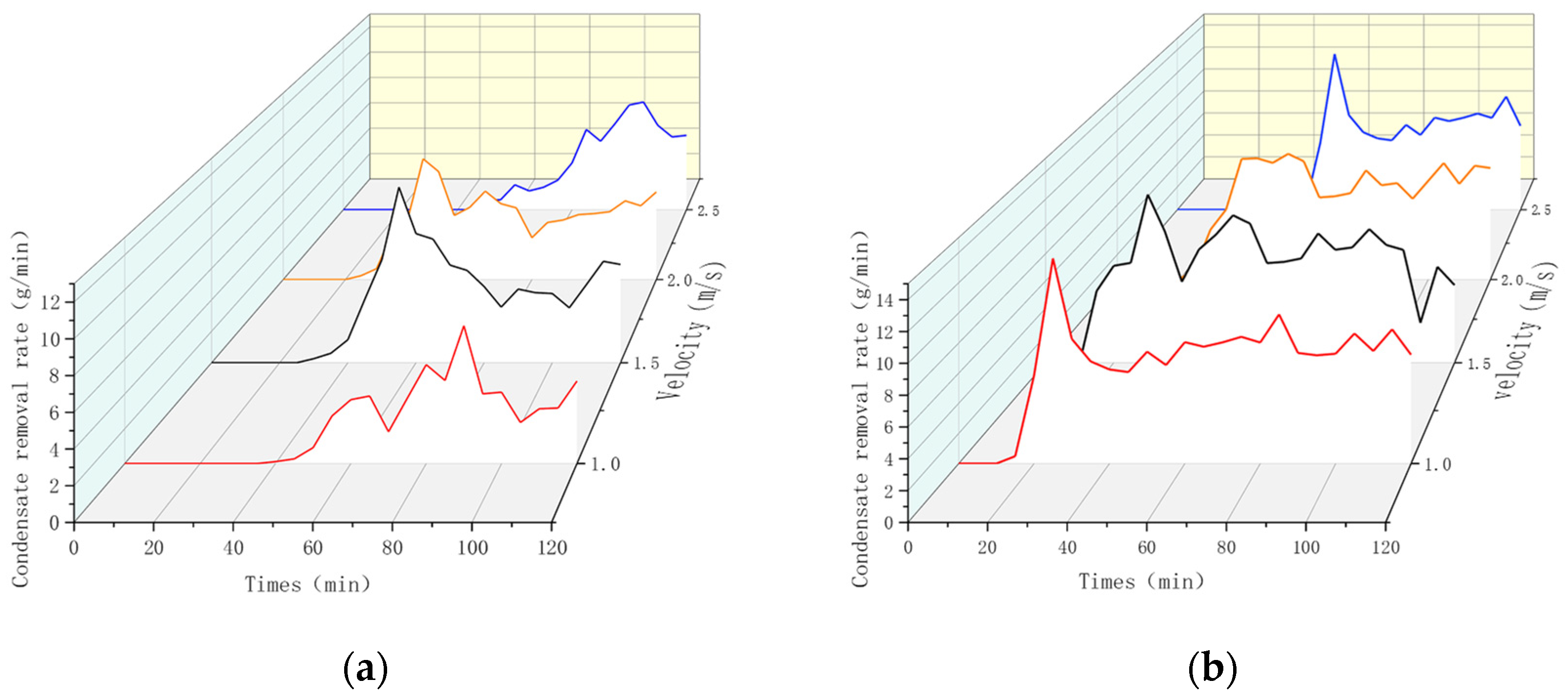
3.2.2. The Influence of Air Velocity on the Amount and Rate of Condensate Water
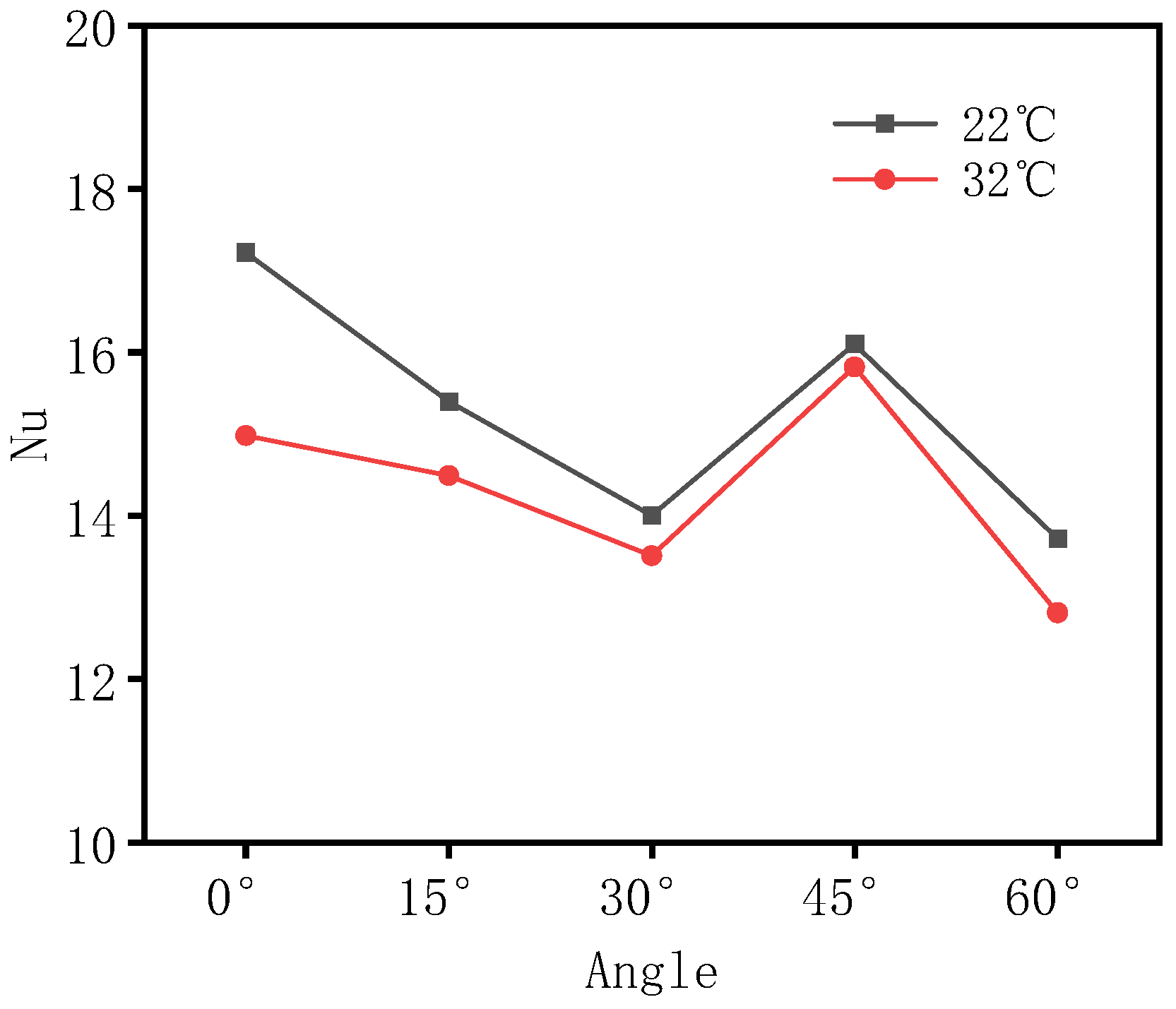
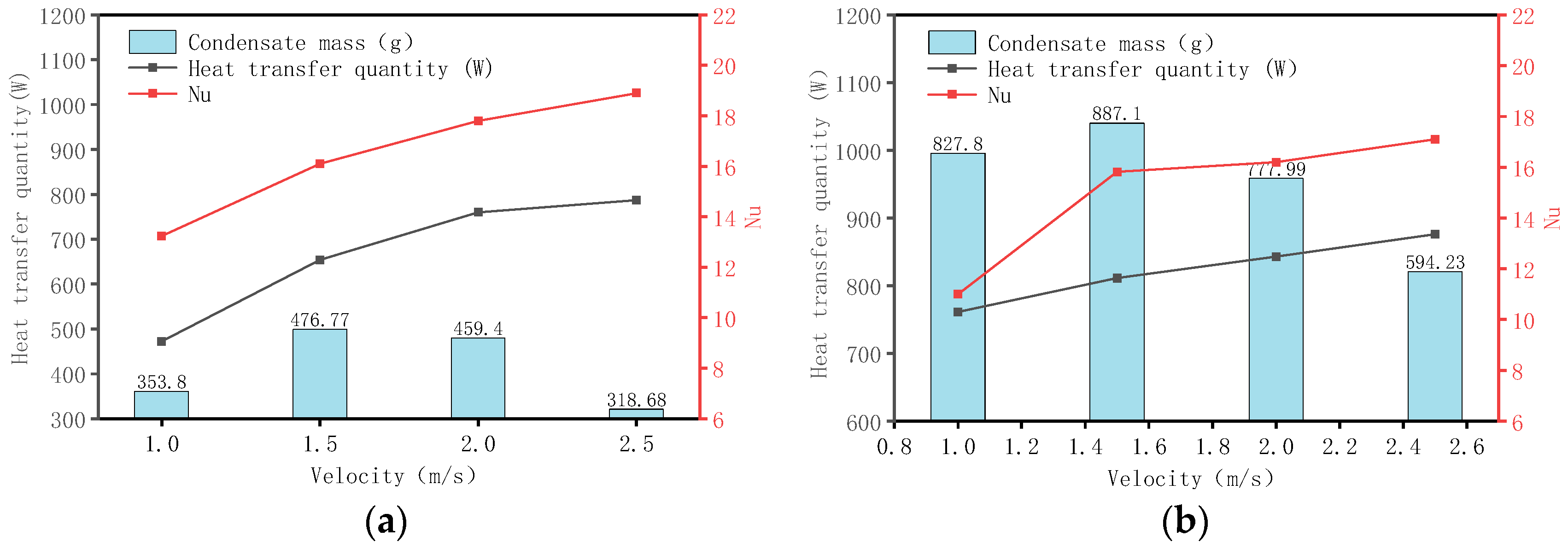
3.2.3. The Influence of Air Velocity on the Heat Transfer Efficiency of Fins
4. Conclusions
- At 22 °C with 85% relative humidity, the vertical fins (0° inclination) performed best, achieving a condensate amount of 524.2 g within 120 min. Gravity-driven droplet movement facilitated rapid sliding, minimizing the liquid film retention time and maximizing heat exchange. As the inclination increased, the liquid film coverage decreased, and flow separation effects became significant, leading to a reduced heat exchange efficiency and a decrease in the condensate amount to approximately 278.3 g.
- At 32 °C with 85% relative humidity, a 45° inclination yielded the best performance, with a condensate amount of 887.1 g in 120 min. At this moderate inclination, a balance between turbulent disturbance and liquid film stability was achieved, extending the air residence time and enhancing latent heat release. In contrast, at 0° under high temperatures, the reduced viscosity of the liquid film and insufficient shear force resulted in a condensate amount approximately 5.8% lower than that at a 45° inclination.
- When the wind speed increased from 1.0 m/s to 2.5 m/s, both the outlet air temperature and air-side pressure drop rose. The rate of condensation exhibited a unimodal characteristic, peaking at a wind speed of 1.5 m/s. Within the 1.0–1.5 m/s range, enhanced turbulence promoted convective heat exchange, and the condensation rate increased with wind speed; however, beyond 1.5 m/s, the reduced air residence time led to insufficient latent heat release, resulting in a lower condensation rate.
- For desert greenhouses, a dynamic strategy for adjusting wind speed and fin heat exchanger angle is recommended. In low-temperature environments (22 °C and 85% humidity), vertical fins (0° inclination) combined with a wind speed of 2.0 m/s should be used to promote droplet sliding through gravity, avoiding flow separation induced by inclinations greater than 30°. In high-temperature environments (32 °C), switching to a 45° inclination and a wind speed of 1.5 m/s balances turbulent disturbance with liquid film stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | total surface heat transfer area [m2] | ∆Tlm | logarithmic mean temperature difference |
| Amin | minimum cross-sectional area for flow in the flow channel [m2] | Tin | inlet air temperature [°C] |
| Ao | total interfacial area between the air-side fluid and the solid [m2] | Tout | outlet air temperature [°C] |
| d1 | humidity of inlet air [g/kg] | Twall | wall temperature [°C] |
| d2 | humidity of outlet air [g/kg] | um | minimum flow surface air velocity [m/s] |
| e | relative error | V1 | condensate formation rate [g/min] |
| G | air mass flow [kg/s] | V2 | condensate removal rate [g/min] |
| h | air-side heat transfer coefficient [kJ/kg] | V3 | condensate aggregation rate [g/min] |
| ha | air-side convective heat transfer coefficient [W/(m K)] | n | absolute error |
| hn | air enthalpy | x | independent variable |
| Lx | length of the heat transfer channel [m] | y | dependent variable |
| ∆m | condensate water weight change value [g] | air thermal conductivity [W/(m K)] | |
| Nu | Nusselt number | σ | standard deviations |
| Q | sensible heat transfer [kg/s] | air kinematic viscosity [m2/s] | |
| ∆t | condensation time [min] |
References
- Özçelep, Y.; Bekdaş, G.; Apak, S. Meeting the Electricity Demand for the Heating of Greenhouses with Hydrogen: Solar Photovoltaic-Hydrogen-Heat Pump System Application in Turkey. Int. J. Hydrogen Energy 2023, 48, 2510–2517. [Google Scholar] [CrossRef]
- Villagran, E.; Bojacá, C.; Akrami, M. Contribution to the Sustainability of Agricultural Production in Greenhouses Built on Slope Soils: A Numerical Study of the Microclimatic Behavior of a Typical Colombian Structure. Sustainability 2021, 13, 4748. [Google Scholar] [CrossRef]
- Miller, A.; Langenhoven, P.; Nemali, K. Maximizing Productivity of Greenhouse-Grown Hydroponic Lettuce during Winter. HortScience 2020, 55, 1963–1969. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, N.; Chang, C.; Hu, X.; Liu, Y.; Liu, L.; Wang, J. Comparative Analysis of the Filling Mass of Vertical Heat Exchanger Tubes on the Thermal Environment of Arched Greenhouses. Energies 2023, 16, 5118. [Google Scholar] [CrossRef]
- Davies, P.A.; Zaragoza, G. Ideal Performance of a Self-Cooling Greenhouse. Appl. Therm. Eng. 2019, 149, 502–511. [Google Scholar] [CrossRef]
- Fatnassi, H.; Poncet, C.; Bazzano, M.M.; Brun, R.; Bertin, N. A Numerical Simulation of the Photovoltaic Greenhouse Microclimate. Sol. Energy 2015, 120, 575–584. [Google Scholar] [CrossRef]
- Albornoz, F.; Del Río, C.; Carter, V.; Escobar, R.; Vásquez, L. Fog Water Collection for Local Greenhouse Vegetable Production in the Atacama Desert. Sustainability 2023, 15, 15720. [Google Scholar] [CrossRef]
- Piscia, D. Analysis of Night-Time Climate in Plastic-Covered Greenhouses. Ph.D. Thesis, Universitat Politecnica de Catalunya, Barcelona, Spain, 2012. [Google Scholar]
- Maslak, K.; Nimmermark, S. Thermal Energy Use for Dehumidification of a Tomato Greenhouse by Natural Ventilation and a System with an Air-to-Air Heat Exchanger. Agric. Food Sci. 2017, 26, 56–66. [Google Scholar] [CrossRef]
- Hu, W.-L.; Ma, A.-J.; Guan, Y.; Cui, Z.-J.; Zhang, Y.-B.; Wang, J. Experimental Study of the Air Side Performance of Fin-and-Tube Heat Exchanger with Different Fin Material in Dehumidifying Conditions. Energies 2021, 14, 7030. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Wang, C.-C. Superhydrophobic Fins with Inclined Arrangement for Enhancing Energy Saving of Air-Cooled Wet Heat Exchangers. Int. J. Heat Mass Transf. 2021, 178, 121636. [Google Scholar] [CrossRef]
- Kim, M.-H.; Youn, B.; Bullard, C.W. Effect of Inclination on the Air-Side Performance of a Brazed Aluminum Heat Exchanger under Dry and Wet Conditions. Int. J. Heat Mass Transf. 2001, 44, 4613–4623. [Google Scholar] [CrossRef]
- Kim, M.-H.; Song, S.; Bullard, C.W. Effect of Inlet Humidity Condition on the Air-Side Performance of an Inclined Brazed Aluminum Evaporator. Int. J. Refrig. 2002, 25, 611–620. [Google Scholar] [CrossRef]
- Kim, N.-H.; Kim, D.-Y.; Hwang, J.-H. Wet Surface Heat Transfer and Pressure Drop of Aluminum Parallel Flow Heat Exchangers at Different Inclination Angles. J. Mech. Sci. Technol. 2008, 22, 2498–2508. [Google Scholar] [CrossRef]
- Wang, X.; Xu, W.; Chen, Z.; Xu, B. Dropwise Condensation Heat Transfer on Nanostructured Superhydrophobic Surfaces with Different Inclinations and Surface Subcoolings. Int. J. Heat Mass Transf. 2021, 181, 121898. [Google Scholar] [CrossRef]
- Gungor, S. Analytical investigation on the condensation performance of vertical, tilted and horizontal surfaces for passive water harvesting. Mugla J. Sci. Technol. 2023, 9, 63–73. [Google Scholar] [CrossRef]
- Li, G.; Cao, B.; Zhou, S.; Bian, H.; Ding, M. Effects of Inclination and Flow Velocity on Steam Condensation Consisting of Air on Tube Bundle External Surfaces. Prog. Nucl. Energy 2021, 136, 103722. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Tam, L.; Zeng, M.; Wang, Q. Impact of Inclination Angle on Flow Boiling Heat Transfer of Refrigerants in Elliptical Mini-Channel with Micro Fins. Appl. Therm. Eng. 2025, 269, 126184. [Google Scholar] [CrossRef]
- Havlík, J.; Dlouhý, T. Effect of Flow Velocity on the Process of Air-Steam Condensation in a Vertical Tube Condenser. EPJ Web Conf. 2018, 180, 02033. [Google Scholar] [CrossRef]
- Babaei, M.; Etemad, S.G.; Haghshenasfard, M.; Kruczek, B.; Morante, E.J.; Thibault, J. Water Extraction from Air via Passive Plate Condensation: Potential and Limitations. JFFHMT 2020, 7, 12–26. [Google Scholar] [CrossRef]
- Tarigan, B.V.; Gere, Y.V.; Jafri, M.; Riwu, D.B.N.; Adoe, D.G.H. Analisis pengaruh kecepatan udara masuk PAWG terhadap volume kondensat, kinerja sistem, Psys dan COP. Armatur 2023, 4, 87–95. [Google Scholar] [CrossRef]
- Wirangga, R.; Mugisidi, D.; Sayuti, A.T.; Heriyani, O. The Impact of Wind Speed on the Rate of Water Evaporation in a Desalination Chamber. ARFMTS 2023, 106, 39–50. [Google Scholar] [CrossRef]
- Chávez-Modena, M.; Broatch, A.; García-Tíscar, J.; Felgueroso, A.; González, L.M.; Valero, E. Numerical and Experimental Analysis of Rounded Fins for High Speed Air-Cooled Heat Exchangers. SSRN J. 2022, 1–34. [Google Scholar] [CrossRef]
- Vu, T.X.; Dhir, V.K. Enhancement of air-side heat transfer in air-cooled heat exchangers using dimpled fins. J. Enhanc. Heat Transf. 2021, 28, 63–84. [Google Scholar] [CrossRef]
- Yao, J.; Wang, X.; Zhu, J.; Wang, B.; Niu, J. Experimental Investigation of a Novel Extracting Water System from Air by Soil Cold Source. Math. Probl. Eng. 2021, 2021, 2740081. [Google Scholar] [CrossRef]
- Kline, S.; McClintock, F. Describing Uncertainties in Single-Sample Experiments. Am. Soc. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Appolloni, E.; Paucek, I.; Pennisi, G.; Manfrini, L.; Gabarrell, X.; Gianquinto, G.; Orsini, F. Winter Greenhouse Tomato Cultivation: Matching Leaf Pruning and Supplementary Lighting for Improved Yield and Precocity. Agronomy 2023, 13, 671. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Zhang, L.; Xu, X. Effect of Environmental Pressure on Heat and Mass Transfer Characteristics for Fin-and-Tube Heat Exchangers under Non-Unit Lewis Factor. Appl. Therm. Eng. 2017, 116, 784–791. [Google Scholar] [CrossRef]
- Roge, N.H.; Krishnan, S.; Prabhu, S.V. Local Heat Transfer Distribution in Channel Flow through a Periodic Octet Foam with Separation of Fin and Wall Heat Transfer. Appl. Therm. Eng. 2025, 260, 124945. [Google Scholar] [CrossRef]
- Bouzennada, T.; Mechighel, F.; Ismail, T.; Kolsi, L.; Ghachem, K. Heat Transfer and Fluid Flow in a PCM-Filled Enclosure: Effect of Inclination Angle and Mid-Separation Fin. Int. Commun. Heat Mass Transf. 2021, 124, 105280. [Google Scholar] [CrossRef]
- Bi, X.; Ma, Q.; Wang, X.; Zhang, X. Application of Phase Change Material on Solar-Greenhouse Back Wall and Its Effects on Indoor Thermal Environment and Cucumber Production in Winter. J. Build. Eng. 2024, 93, 109883. [Google Scholar] [CrossRef]
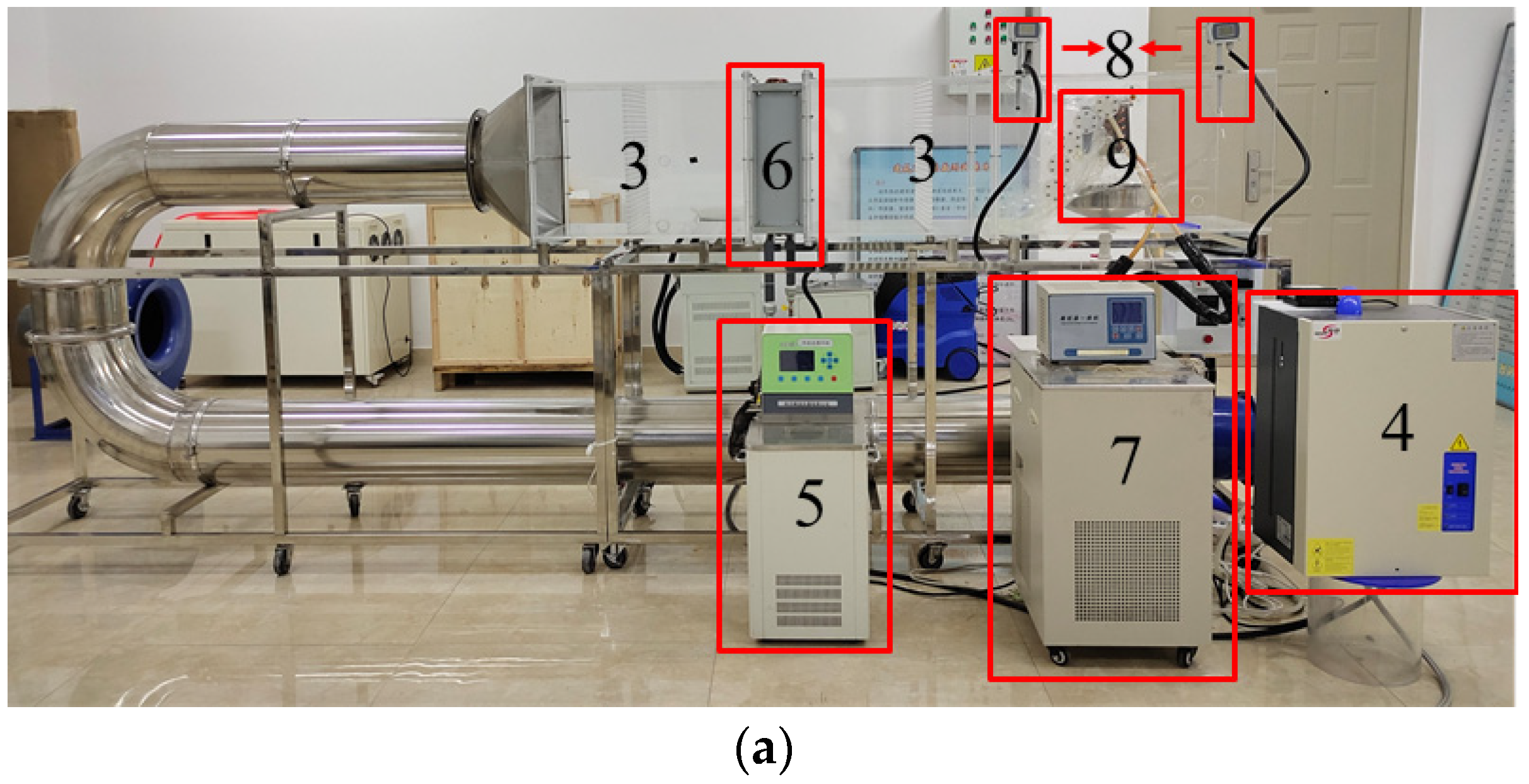
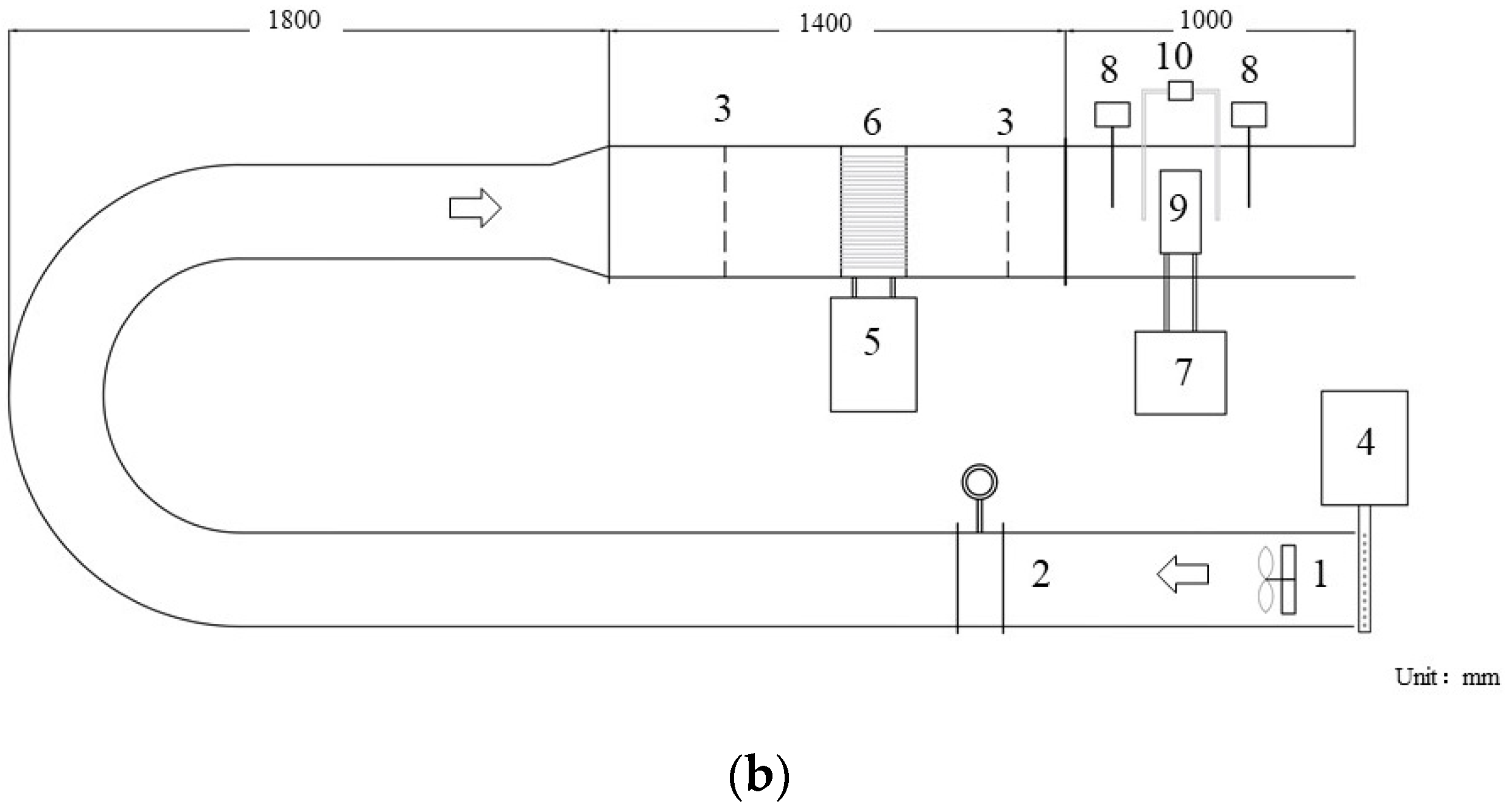

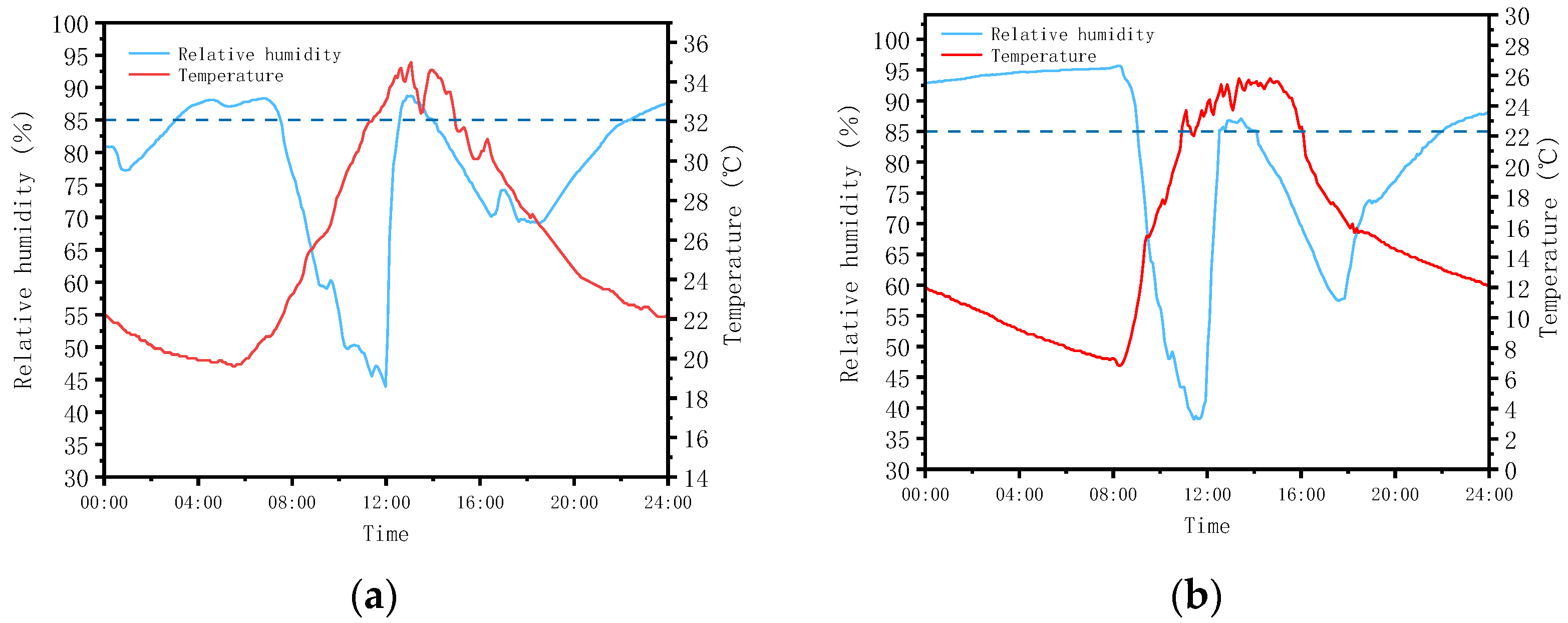
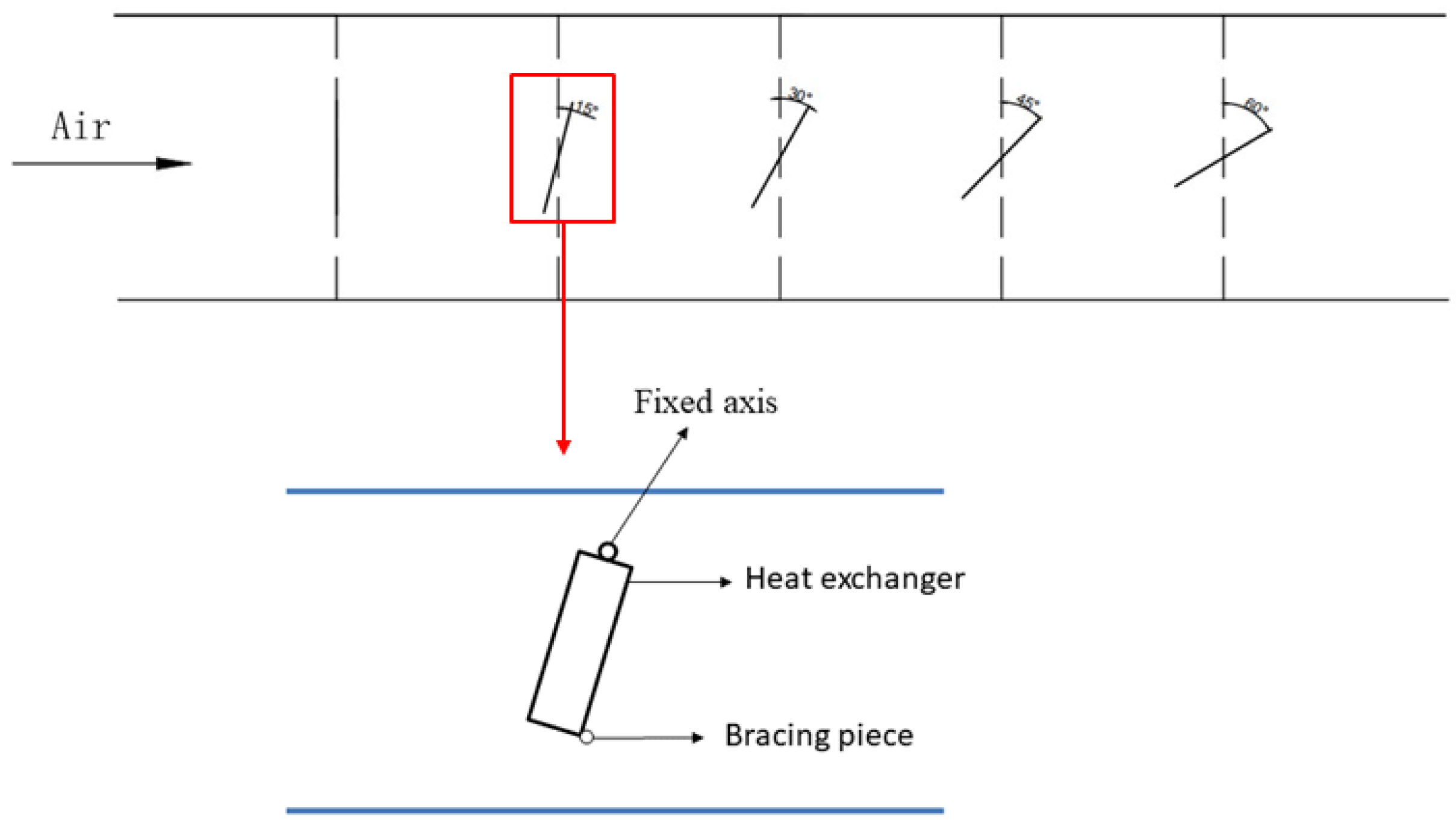

| Equipment | Measuring Range | Accuracy/Error Limit |
|---|---|---|
| T-type thermocouple | −50.0–200.0 °C | ±0.5 °C |
| Temperature and humidity meter | −40–125 °C 0–100% RH | ±0.3 °C ±2% RH |
| Vortex flowmeter | 0.1–7 m/s | ≤±0.75% |
| Differential pressure meter | 0–100 hpa | ±0.25% FS |
| Anemometer | 0.3–45 m/s | ±3% + 0.1 dgt |
| Frequency converter | 0–60 Hz | 0.01 Hz |
| Temperature | Relative Humidity | Velocity | Angle |
|---|---|---|---|
| 22 °C | 85% | 1.5 m/s | 0° |
| 15° | |||
| 30° | |||
| 45° | |||
| 60° | |||
| 32 °C | 85% | 1.5 m/s | 0° |
| 15° | |||
| 30° | |||
| 45° | |||
| 60° | |||
| 22 °C | 85% | 1.0 m/s | 45° |
| 1.5 m/s | |||
| 2.0 m/s | |||
| 2.5 m/s | |||
| 32 °C | 85% | 1.0 m/s | 45° |
| 1.5 m/s | |||
| 2.0 m/s | |||
| 2.5 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Bai, F.; Yu, R.; Liu, Y.; Ma, Y.; Liu, Y.; Rasakhodzhaev, B. Drainage Characteristics and Heat Transfer Performance of Fin Surfaces in Desert Greenhouse Environments. Energies 2025, 18, 2061. https://doi.org/10.3390/en18082061
Zhao M, Bai F, Yu R, Liu Y, Ma Y, Liu Y, Rasakhodzhaev B. Drainage Characteristics and Heat Transfer Performance of Fin Surfaces in Desert Greenhouse Environments. Energies. 2025; 18(8):2061. https://doi.org/10.3390/en18082061
Chicago/Turabian StyleZhao, Mingzhi, Feng Bai, Rong Yu, Yuru Liu, Yixuan Ma, Yingjie Liu, and Bakhramzhan Rasakhodzhaev. 2025. "Drainage Characteristics and Heat Transfer Performance of Fin Surfaces in Desert Greenhouse Environments" Energies 18, no. 8: 2061. https://doi.org/10.3390/en18082061
APA StyleZhao, M., Bai, F., Yu, R., Liu, Y., Ma, Y., Liu, Y., & Rasakhodzhaev, B. (2025). Drainage Characteristics and Heat Transfer Performance of Fin Surfaces in Desert Greenhouse Environments. Energies, 18(8), 2061. https://doi.org/10.3390/en18082061






