Towards Nonlinear Magnetic Rotating Pendula for Low-Frequency Weak Vibration Energy Harvesting
Abstract
1. Introduction
2. Magnetic Pendulum Vibration Energy Harvester
2.1. Pendulum VEH Limitations
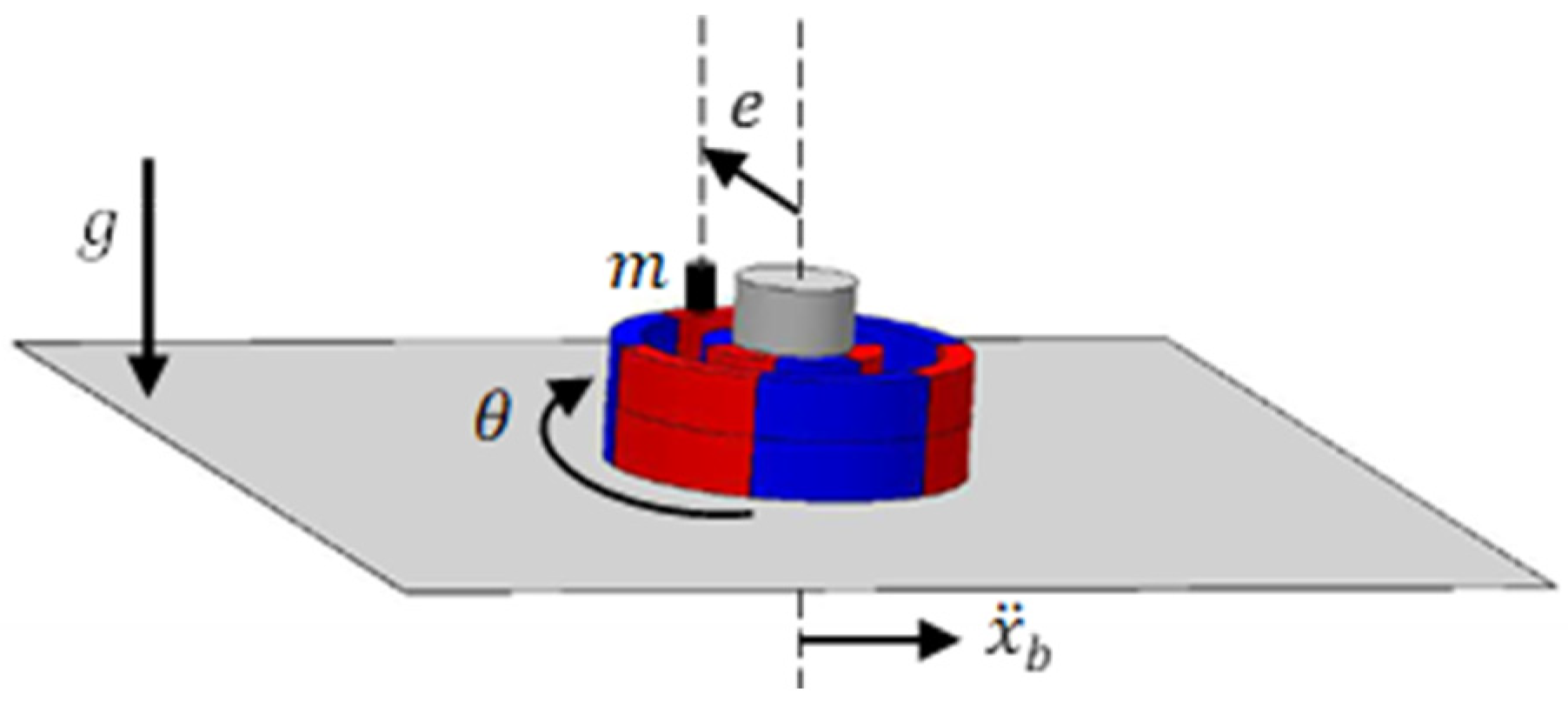
2.2. The Proposed Concept
2.3. Mathematical Model
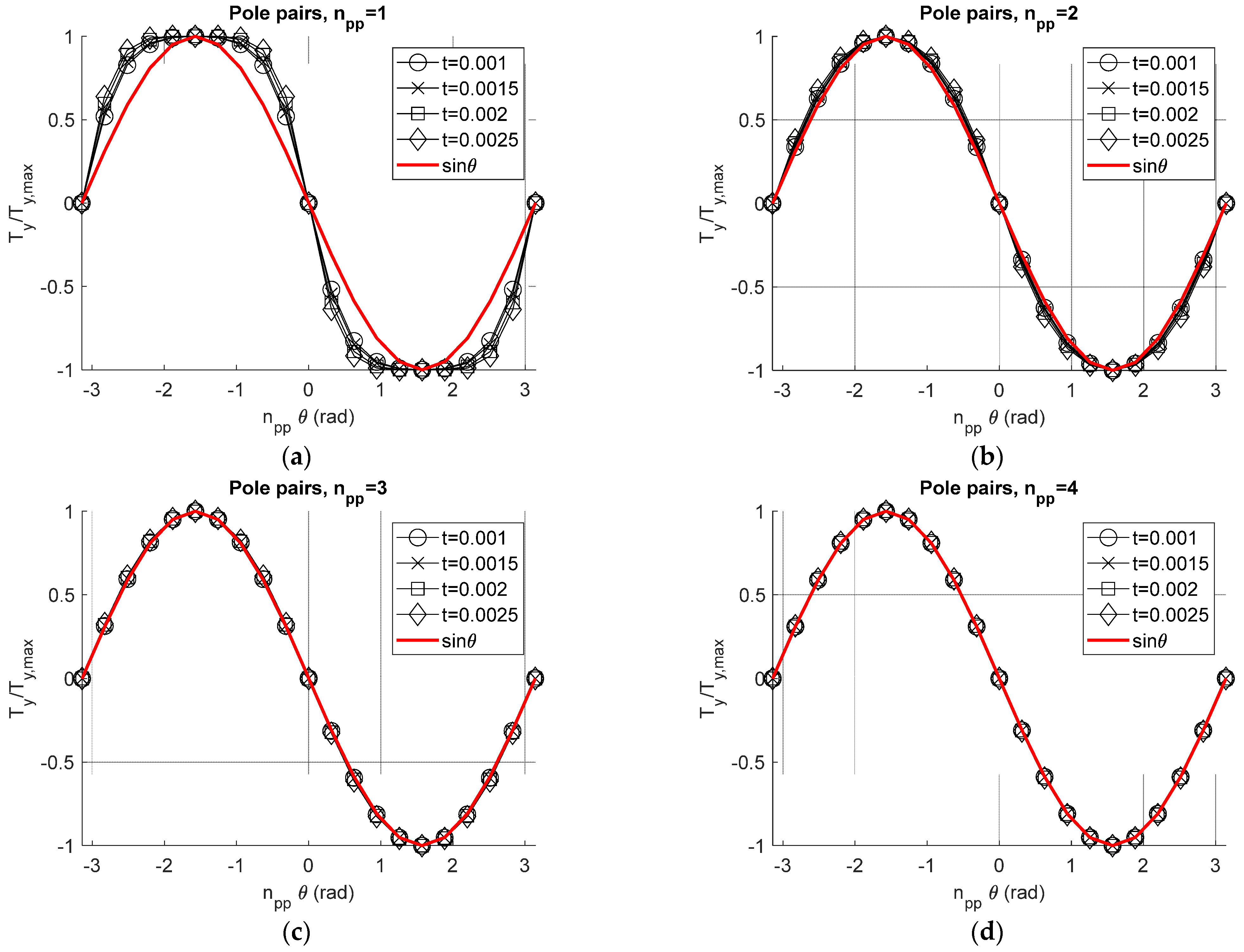
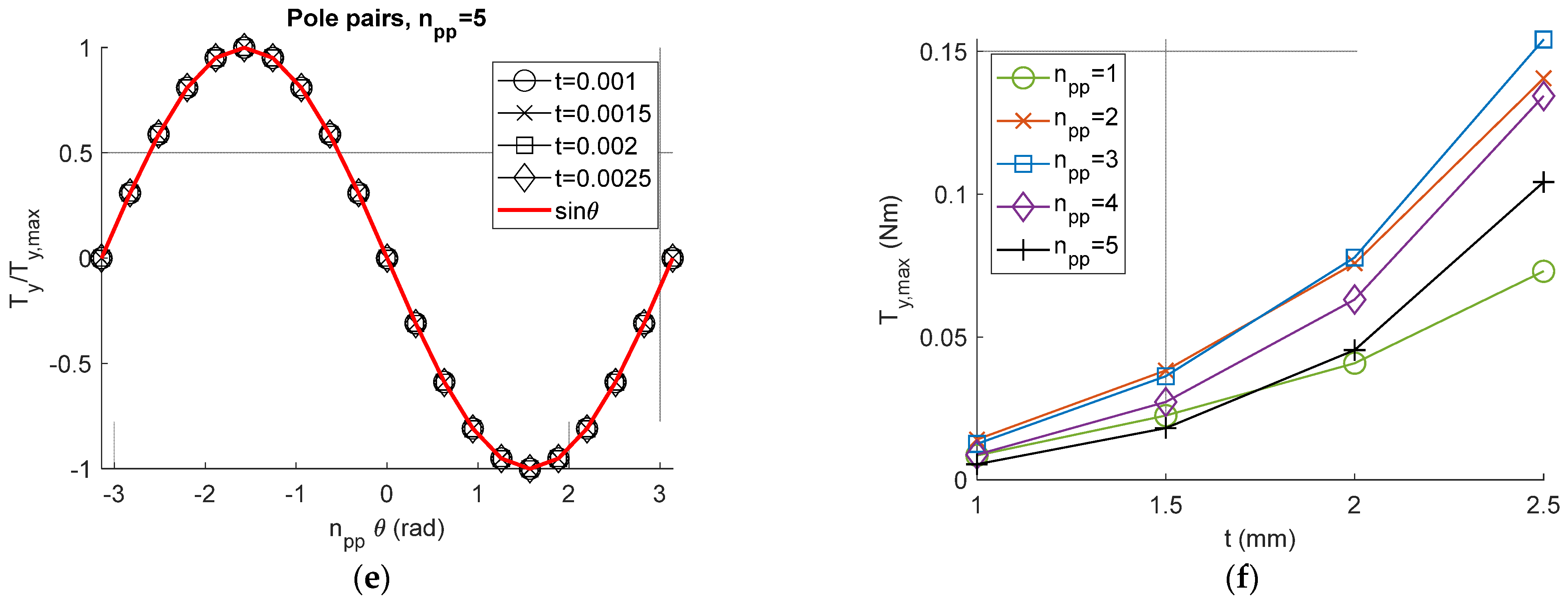
2.3.1. Restoring Magnetic Torque
2.3.2. Equation of Motion
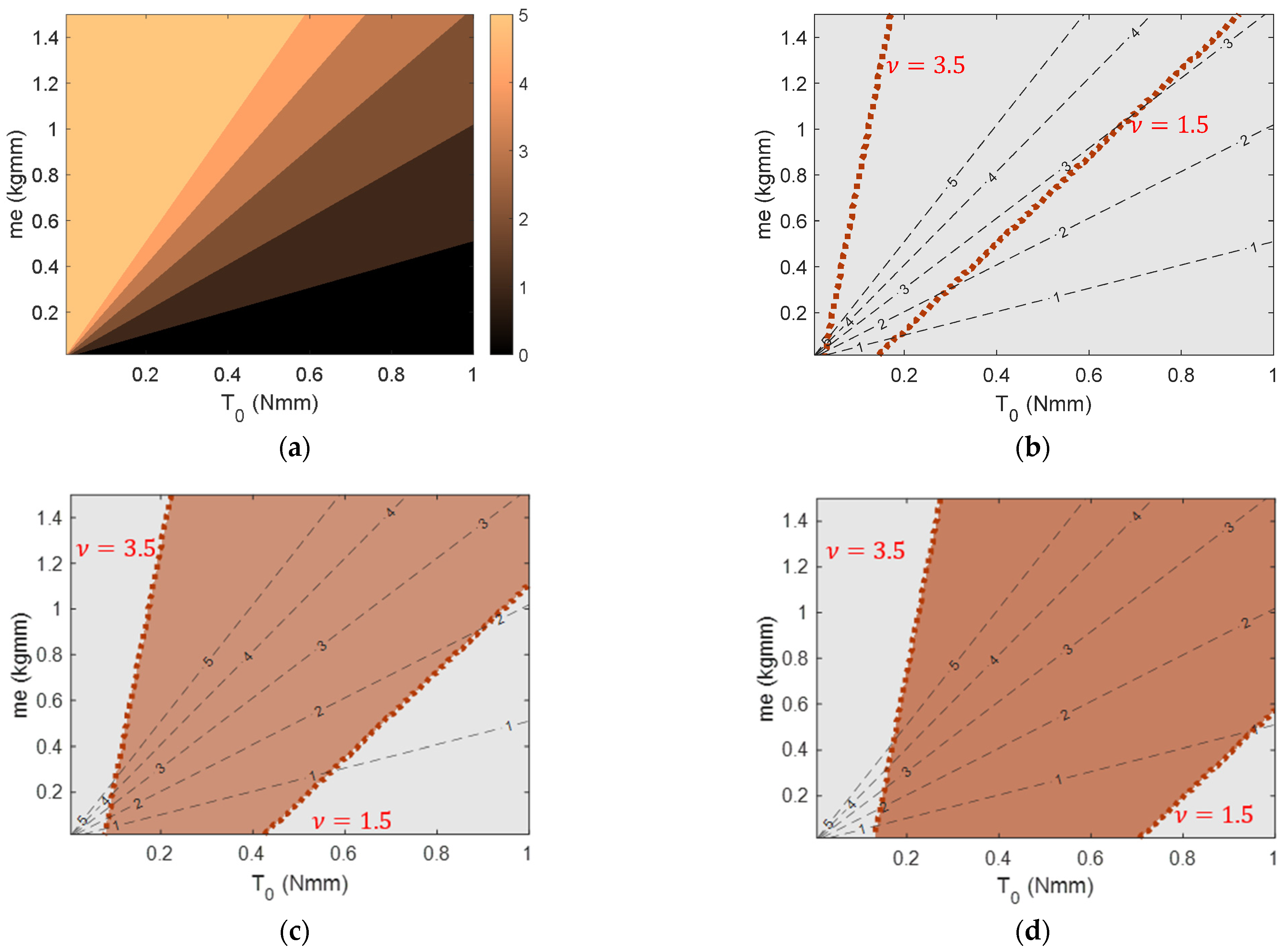
3. Numerical Results
3.1. Parameter Space Plots
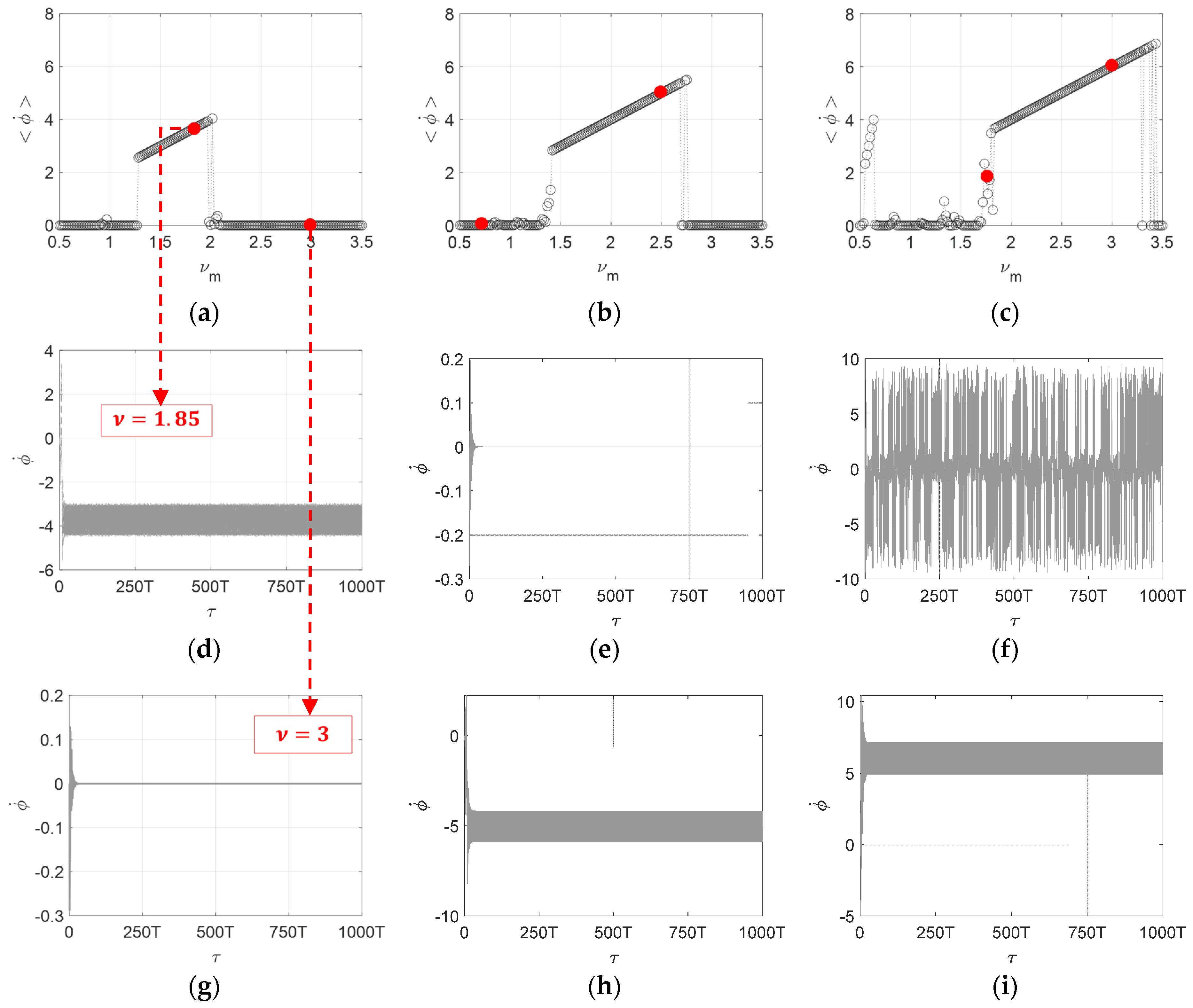
3.2. Frequency and Amplitude Response Curves
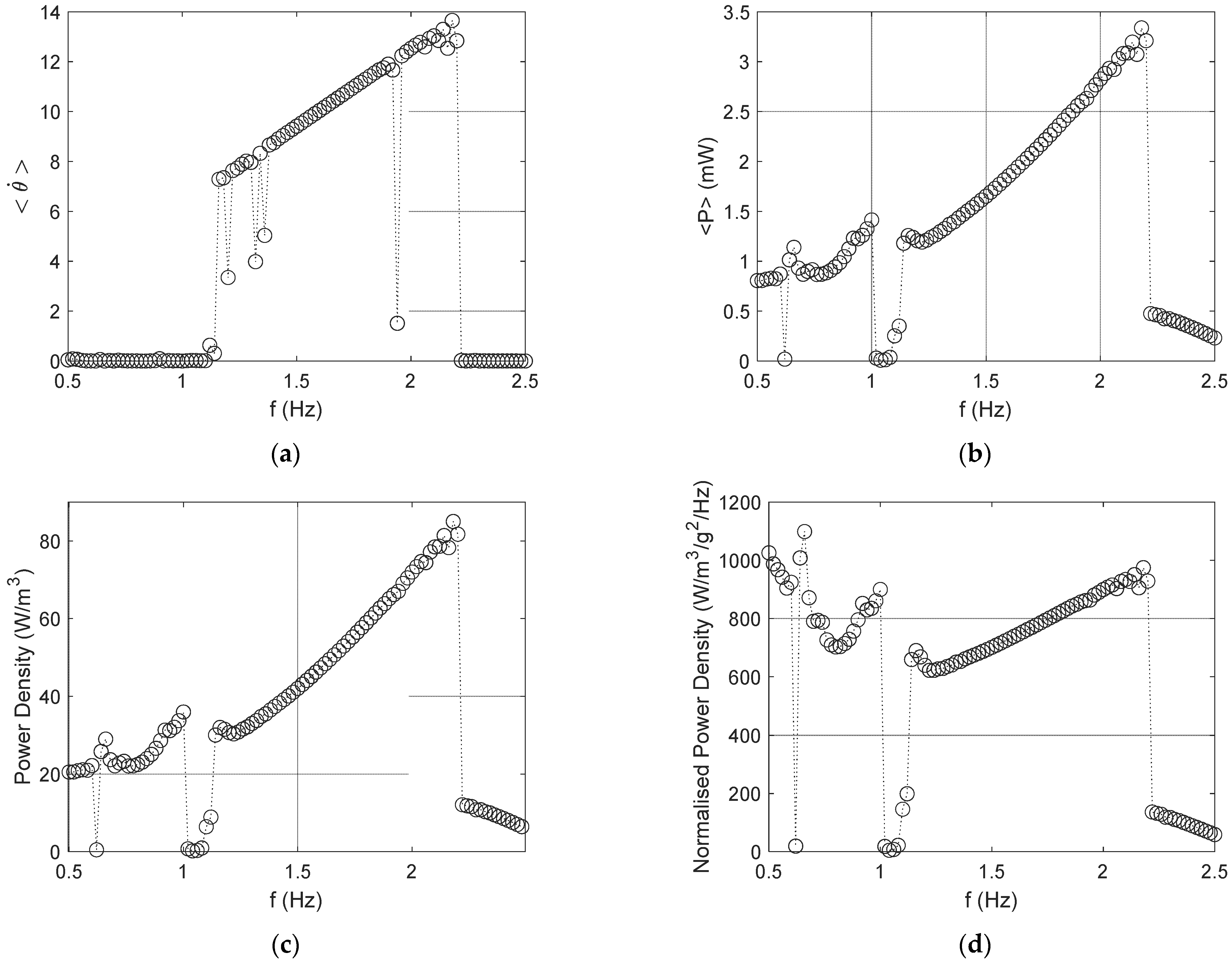
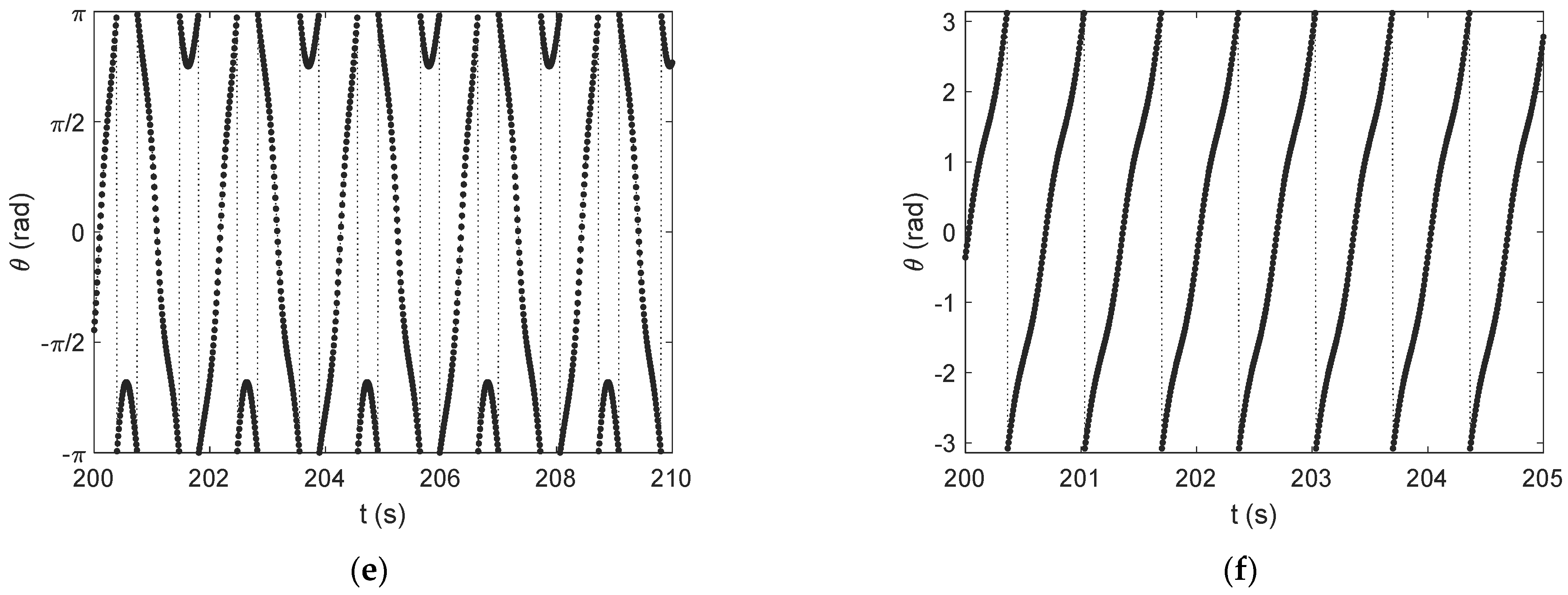
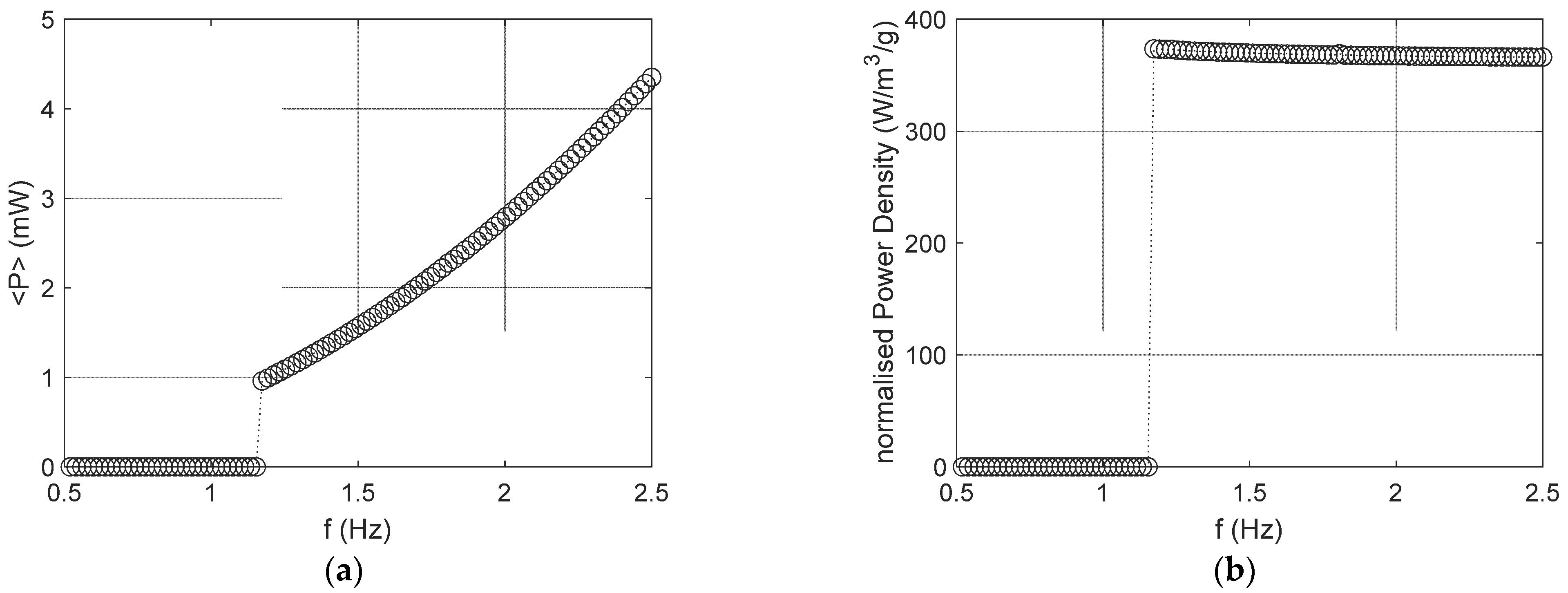
3.3. Case Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ells, D.A.; Mechefske, C.; Lai, Y. Innovative electromagnetic vibration energy harvester with free-rotating mass for passive resonant frequency tuning. Appl. Energy 2025, 377, 124622. [Google Scholar] [CrossRef]
- Muscat, A.; Bhattacharya, S.; Zhu, Y. Electromagnetic Vibrational Energy Harvesters: A Review. Sensors 2022, 22, 5555. [Google Scholar] [CrossRef] [PubMed]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: Boston, MA, USA, 2009. [Google Scholar] [CrossRef]
- Ylli, K.; Hoffmann, D.; Willmann, A.; Folkmer, B.; Manoli, Y. Human motion energy harvesting: Numerical analysis of electromagnetic swing-excited structures. Smart Mater. Struct. 2016, 25, 095014. [Google Scholar] [CrossRef]
- Iqbal, M.; Nauman, M.M.; Khan, F.U.; Abas, P.E.; Cheok, Q.; Iqbal, A.; Aissa, B. Vibration-based piezoelectric, electromagnetic, and hybrid energy harvesters for microsystems applications: A contributed review. Int. J. Energy Res. 2020, 45, 65–102. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Huang, M.; Sun, L.; Liu, H.; Lee, C. Self-Sustained Artificial Internet of Things Based on Vibration Energy Harvesting Technology: Toward the Future Eco-Society. Adv. Energy Sustain. Res. 2024, 5, 2400116. [Google Scholar] [CrossRef]
- Barton, D.A.W.; Burrow, S.G.; Clare, L.R. Energy Harvesting from Vibrations with a Nonlinear Oscillator. J. Vib. Acoust. 2010, 132, 021009. [Google Scholar] [CrossRef]
- Boisseau, S.; Despesse, G.; Seddik, B.A. Nonlinear H-Shaped Springs to Improve Efficiency of Vibration Energy Harvesters. J. Appl. Mech. 2013, 80, 061013. [Google Scholar] [CrossRef]
- Mann, B.; Sims, N. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear Energy Harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed]
- Alevras, P.; Theodossiades, S.; Rahnejat, H. On the dynamics of a nonlinear energy harvester with multiple resonant zones. Nonlinear Dyn. 2018, 92, 1271–1286. [Google Scholar] [CrossRef]
- Sommermann, P.; Cartmell, M.P. The dynamics of an omnidirectional pendulum harvester. Nonlinear Dyn. 2021, 104, 1889–1900. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Morel, A.; Badel, A.; Gasnier, P.; Gibus, D.; Pillonnet, G. Short Circuit Synchronized Electric Charge Extraction (SC-SECE): A tunable interface for wideband vibration energy harvesting. arXiv 2018, arXiv:1808.04461. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-low frequency vibration energy harvesting: Mechanisms, enhancement techniques, and scaling laws. Energy Convers. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Castagnetti, D. A simply tunable electromagnetic pendulum energy harvester. Meccanica 2019, 54, 749–760. [Google Scholar] [CrossRef]
- Wang, T. Pendulum-based vibration energy harvesting: Mechanisms, transducer integration, and applications. Energy Convers. Manag. 2023, 276, 116469. [Google Scholar] [CrossRef]
- Ma, T.-W.; Zhang, H.; Xu, N.-S. A novel parametrically excited non-linear energy harvester. Mech. Syst. Signal Process. 2012, 28, 323–332. [Google Scholar] [CrossRef]
- Alevras, P.; Theodossiades, S.; Rahnejat, H. Broadband energy harvesting from parametric vibrations of a class of nonlinear Mathieu systems. Appl. Phys. Lett. 2017, 110, 233901. [Google Scholar] [CrossRef]
- Lee, B.; Chung, G. Design and analysis of a pendulum-based electromagnetic energy harvester using anti-phase motion. IET Renew. Power Gener. 2016, 10, 1625–1630. [Google Scholar] [CrossRef]
- Yakubu, G.; Olejnik, P.; Adisa, A.B. Variable-Length Pendulum-Based Mechatronic Systems for Energy Harvesting: A Review of Dynamic Models. Energies 2024, 17, 3469. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Fang, S.; Qiao, Z.; Yurchenko, D.; Lai, Z. A pendulum-based absorber-harvester with an embedded hybrid vibro-impact electromagnetic-dielectric generator. Nano Energy 2023, 107, 108126. [Google Scholar] [CrossRef]
- Marszal, M.; Witkowski, B.; Jankowski, K.; Perlikowski, P.; Kapitaniak, T. Energy harvesting from pendulum oscillations. Int. J. Non-Linear Mech. 2017, 94, 251–256. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, S.; Ali, S.F. Energy harvesting from chaos in base excited double pendulum. Mech. Syst. Signal Process. 2019, 124, 49–64. [Google Scholar] [CrossRef]
- Shi, G.; Chen, J.; Peng, Y.; Shi, M.; Xia, H.; Wang, X.; Ye, Y.; Xia, Y. A Piezo-Electromagnetic Coupling Multi-Directional Vibration Energy Harvester Based on Frequency Up-Conversion Technique. Micromachines 2020, 11, 80. [Google Scholar] [CrossRef] [PubMed]
- Yurchenko, D.; Naess, A.; Alevras, P. Pendulum’s rotational motion governed by a stochastic Mathieu equation. Probabilistic Eng. Mech. 2013, 31, 12–18. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P. Parametric pendulum based wave energy converter. Mech. Syst. Signal Process. 2018, 99, 504–515. [Google Scholar] [CrossRef]
- Alevras, P.; Brown, I.; Yurchenko, D. Experimental investigation of a rotating parametric pendulum. Nonlinear Dyn. 2015, 81, 201–213. [Google Scholar] [CrossRef]
- Graves, J.; Kuang, Y.; Zhu, M. Scalable pendulum energy harvester for unmanned surface vehicles. Sens. Actuators Phys. 2020, 315, 112356. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P. Dynamics of the N-pendulum and its application to a wave energy converter concept. Int. J. Dyn. Control 2013, 1, 290–299. [Google Scholar] [CrossRef]
- Ylli, K.; Hoffmann, D.; Willmann, A.; Folkmer, B.; Manoli, Y. Investigation of Pendulum Structures for Rotational Energy Harvesting from Human Motion. In Proceedings of the 15th International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS 2015), Boston, MA, USA, 1–4 December 2015; Volume 660, p. 012053. [Google Scholar] [CrossRef]
- Dai, X. An vibration energy harvester with broadband and frequency-doubling characteristics based on rotary pendulums. Sens. Actuators A Phys. 2016, 241, 161–168. [Google Scholar] [CrossRef]
- Kuang, Y.; Hide, R.; Zhu, M. Broadband energy harvesting by nonlinear magnetic rolling pendulum with subharmonic resonance. Appl. Energy 2019, 255, 113822. [Google Scholar] [CrossRef]
- Hou, C.; Chen, T.; Li, Y.; Huang, M.; Shi, Q.; Liu, H.; Sun, L.; Lee, C. A rotational pendulum based electromagnetic/triboelectric hybrid-generator for ultra-low-frequency vibrations aiming at human motion and blue energy applications. Nano Energy 2019, 63, 103871. [Google Scholar] [CrossRef]
- Li, M.; Deng, H.; Zhang, Y.; Li, K.; Huang, S.; Liu, X. Ultra-Low Frequency Eccentric Pendulum-Based Electromagnetic Vibrational Energy Harvester. Micromachines 2020, 11, 1009. [Google Scholar] [CrossRef]
- Masabi, S.N.; Fu, H.; Flint, J.A.; Theodossiades, S. A pendulum-based rotational energy harvester for self-powered monitoring of rotating systems in the era of industrial digitization. Appl. Energy 2024, 365, 123200. [Google Scholar] [CrossRef]
- Litak, G.; Kondratiuk, M.; Wolszczak, P.; Ambrożkiewicz, B.; Giri, A.M. Energy Harvester Based on a Rotational Pendulum Supported with FEM. Appl. Sci. 2024, 14, 3265. [Google Scholar] [CrossRef]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Masabi, S.N.; Fu, H.; Flint, J.; Theodossiades, S. A multi-stable rotational energy harvester for arbitrary bi-directional horizontal excitation at ultra-low frequencies for self-powered sensing. Smart Mater. Struct. 2024, 33, 095017. [Google Scholar] [CrossRef]


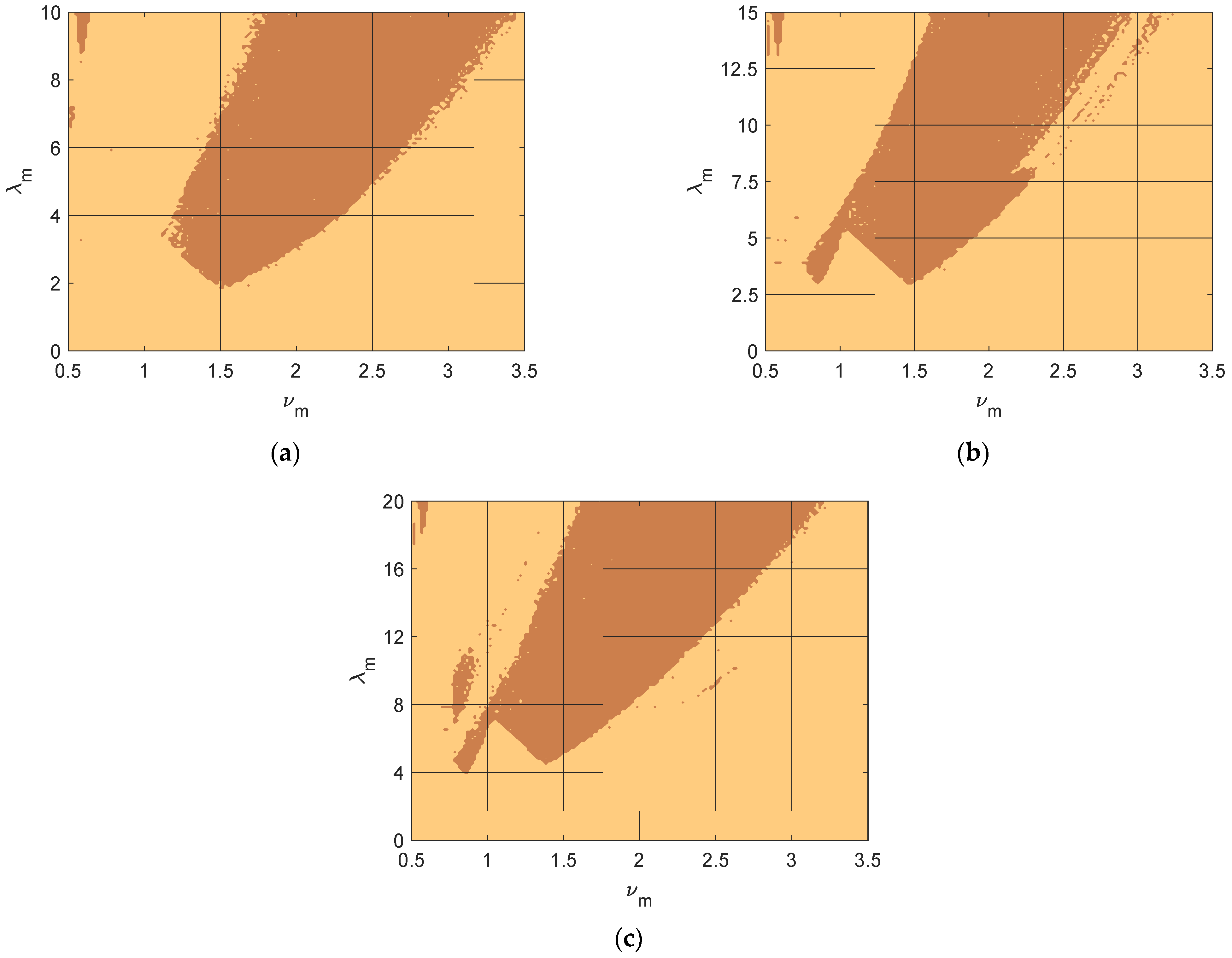


| Parameter | Value |
|---|---|
| (Nmm) | 0.5 |
| 2 | |
| m (grams) | 60 |
| e (mm) | 20 |
| (mm) | 25 |
| (kgmm2) | 31.2 |
| (rad/s) | 5.66 |
| () (Nms/rad) | 1.77 × 10−5 |
| (T) | 1.315 |
| (T) | 0.23 |
| (mm) | 10 |
| (mm) | 50 |
| (mm) | 1 |
| (mm) | 5 |
| (mm) | 5 |
| (N/A) | 0.47 |
| (Ohms) | 3 |
| 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trandafir, M.I.; Alevras, P. Towards Nonlinear Magnetic Rotating Pendula for Low-Frequency Weak Vibration Energy Harvesting. Energies 2025, 18, 2058. https://doi.org/10.3390/en18082058
Trandafir MI, Alevras P. Towards Nonlinear Magnetic Rotating Pendula for Low-Frequency Weak Vibration Energy Harvesting. Energies. 2025; 18(8):2058. https://doi.org/10.3390/en18082058
Chicago/Turabian StyleTrandafir, Mihai Ionut, and Panagiotis Alevras. 2025. "Towards Nonlinear Magnetic Rotating Pendula for Low-Frequency Weak Vibration Energy Harvesting" Energies 18, no. 8: 2058. https://doi.org/10.3390/en18082058
APA StyleTrandafir, M. I., & Alevras, P. (2025). Towards Nonlinear Magnetic Rotating Pendula for Low-Frequency Weak Vibration Energy Harvesting. Energies, 18(8), 2058. https://doi.org/10.3390/en18082058







