Energy-Efficient Near-Field Beamforming: A Review on Practical Channel Models
Abstract
1. Introduction
1.1. Background
1.2. Related Reviews for Energy-Efficient Techniques on Near-Field Communication
| Title | Year | Main Achievements | Limitations |
|---|---|---|---|
| [4] | 2024 | Reviewed resource allocation problems and highlighted the potential of massive MIMO systems in improving spectrum and energy efficiency. | Lack of focus on channel models and optimization techniques in complex near-field environments. |
| [36] | 2024 | Focused on reviewing “Spot Beamforming” in near-field applications. The review does not detail energy-efficient techniques or optimization algorithms. | The review does not detail the energy-efficient techniques or the optimization algorithms |
| [15] | 2024 | Summarized energy efficiency, localization, channel estimation, and multiuser access techniques in near-field driven 6G networks. | A review of insufficient channel modeling or optimization techniques in high frequency bands is not provided. |
| [22] | 2024 | Highlighted the potential in enhancing spatial multiplexing gain and positioning accuracy. | Lack of focus on channel models and channel estimation in diverse communication environment. |
| [34] | 2024 | Focused on reviewing the new channel characteristics of near-field communications. | |
| [37] | 2024 | Introduced the performance degradation caused by traditional far-field beamforming designs in near-field environments and integrated sensing and communication (ISAC) systems. | The review does not detail the channel modeling techniques or the energy-efficient techniques. |
| [32] | 2024 | Detailed explanations of the fundamental principles, channel modeling, and performance metrics. | Insufficient hybrid-field channel modeling and lack of focus on integrating near-field models. |
| [33] | 2023 | Reviewed the fundamental near-field channel models and the focus on the near-field spherical wave propagation designs | No emphasis on the practical hardware costs and insufficient energy-efficient techniques provided. |
1.3. Motivation and Contribution
- (a)
- We examine current energy-efficient techniques for near-field communication, focusing on their characteristics, advantages, and limitations. In addition, we clarify the capabilities of advanced channel models and optimization algorithms within near-field environments.
- (b)
- We explore and highlight the characteristics, strengths, weaknesses, and potential of energy-efficient techniques documented in the existing literature. Additionally, we identify several unresolved fundamental research challenges in this rapidly evolving field to advance energy-efficient techniques and propose future research directions.
- (1)
- We offer comprehensive reviews of energy-efficient techniques in near-field communication, analyzing their characteristics, strengths, and potential.
- (2)
- We pinpoint the capabilities of advanced signal and channel models, including their roles in improving energy efficiency and reducing hardware requirements. We explain the reasons for leveraging these techniques in near-field communication and provide energy consumption models tailored to various scenarios within near-field communication.
- (3)
- We highlight existing energy-efficient techniques in near-field communication and discuss their applications in diverse communication environments.
- (4)
- We emphasize the challenges in near-field communication, such as the development of accurate channel models and the use of energy-efficient techniques.
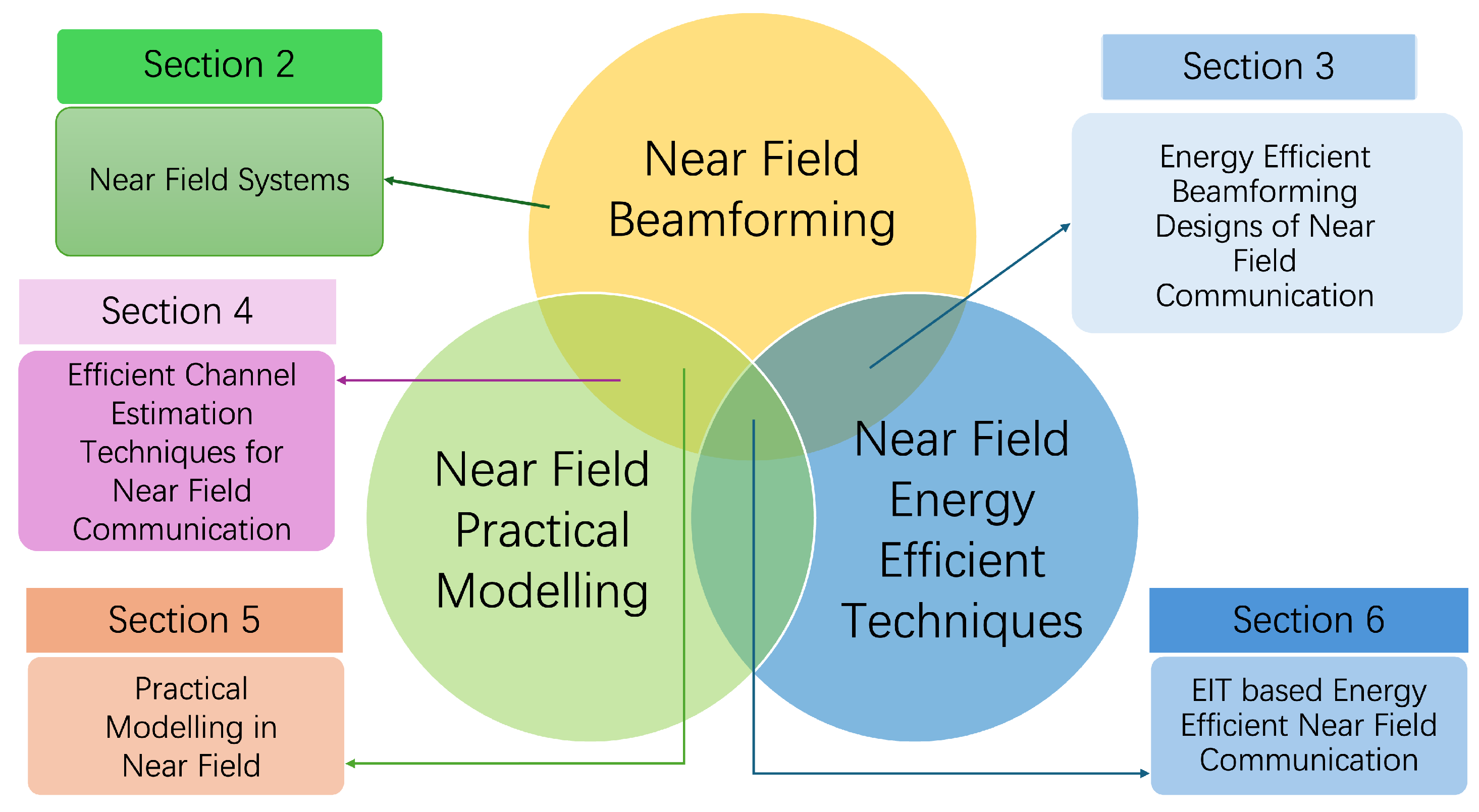
1.4. Paper Organization
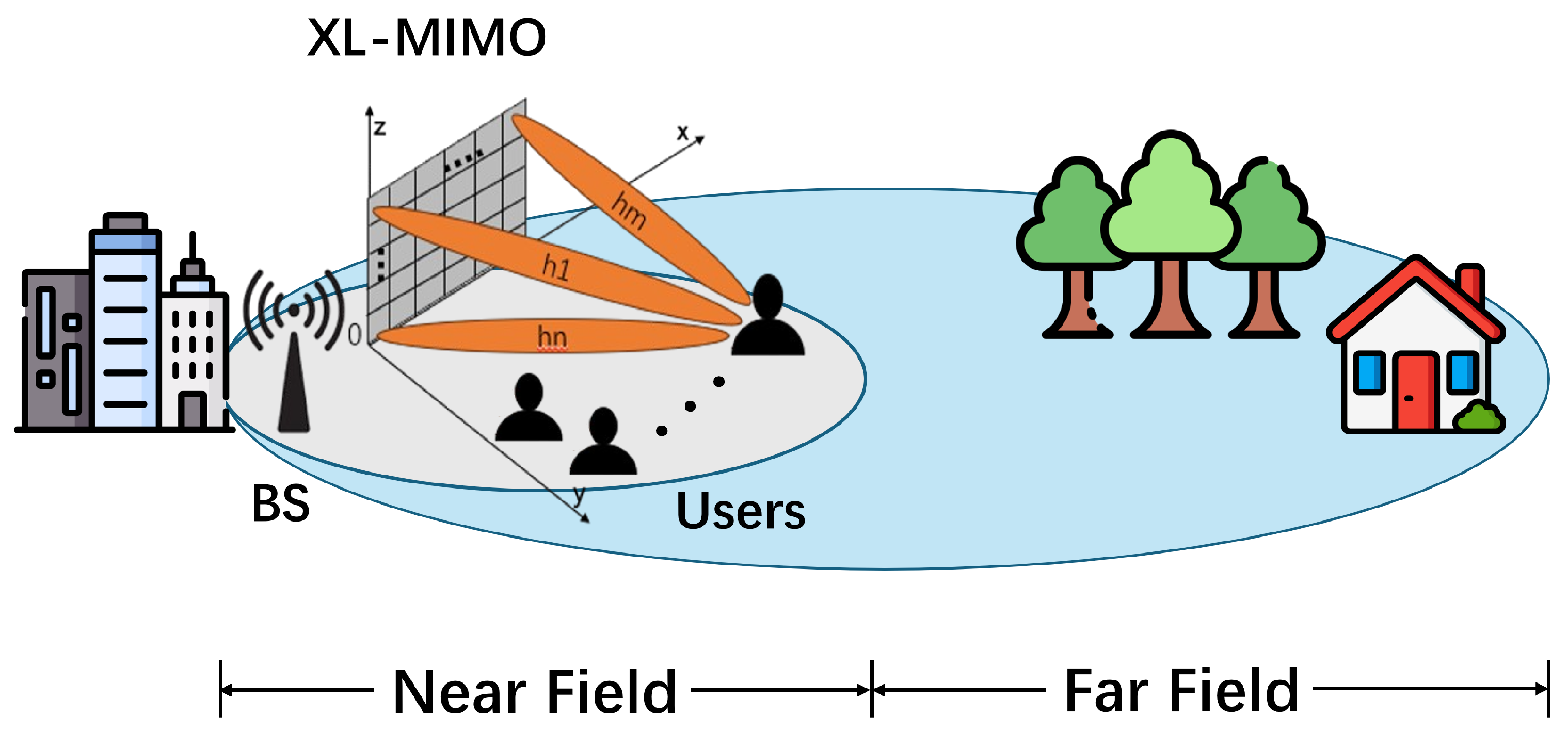
2. Near-Field Beamforming
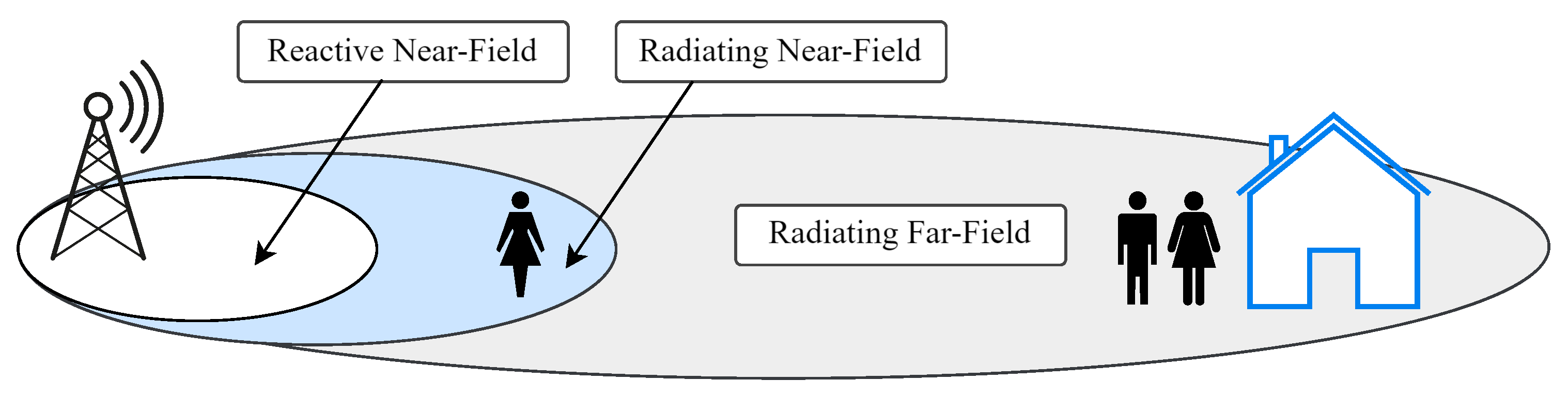
2.1. Wave Propagation Regions
2.1.1. Reactive Near-Field Region
- Energy: The energy is non-radiating and experiences rapid decay in field strength [42].
- Frequency: A higher frequency of operation extends the reactive near-field of the system [14].
- Wavefronts: Wavefronts are not entirely formed in this region and, therefore, cannot be approximated as planar waves.
- Power: The reactive near-field region has non-uniform power distribution with respect to spatial dimensions.
- Phase: The phase shifts in this region are non-linear and not approximated using simple linear equations.
2.1.2. Radiating Near-Field
- Energy: The energy is partially radiating.
- Power: The radiating near-field region has uniform power distribution as the electromagnetic waves are not reactive.
- Phase: The phase shifts in this region are non-linear in relation to the antenna aperture [14].
2.1.3. Far Field
- Energy: The energy is fully radiating, enabling the modeling of antenna radiation patterns.
- Frequency: A lower frequency of operation shortens the near-field region and, therefore, begins the far-field approximation closer to the antenna source.
- Wavefronts: Wavefronts are fully formed and can be approximated as planar waves [44].
- Power: The radiating near-field region has uniform power distribution as the electromagnetic waves are not reactive.
- Phase: The phase shifts in this region are linear with respect to the antenna aperture. This enables efficient beamforming.
2.2. Challenges of Near-Field Systems
2.2.1. Near-Field Channel Modeling and Channel Estimation
2.2.2. Beamforming and Beamtraining
2.2.3. Mutual Coupling Effects
2.2.4. Interference
2.2.5. Hardware Implementation
2.3. Opportunities in Near-Field Systems
2.3.1. High Spatial Multiplexing
2.3.2. Beamfocusing
2.3.3. High-Precision Sensing
3. Energy-Efficient Beamforming in Near-Field Systems
3.1. Energy-Efficient Techniques in Near-Field MIMO
3.1.1. Codebook Design and Beamtraining
3.1.2. Beamfocusing
3.2. Challenges of Energy Efficiency in Near-Field MIMO
3.2.1. System Scalability
3.2.2. Dynamic Beamforming
3.2.3. Processing Overhead
4. Efficient Channel Estimation Techniques for Near-Field Communication
4.1. Near-Field Channel Estimation
4.2. Hybrid-Field Channel Estimation
4.3. LoS/NLoS Channel Estimation
4.4. XL-MIMO Channel Estimation
4.5. THz and mmWave Channel Estimation
5. Practical Modeling for Energy-Efficient Near-Field Communications
5.1. Signal Models
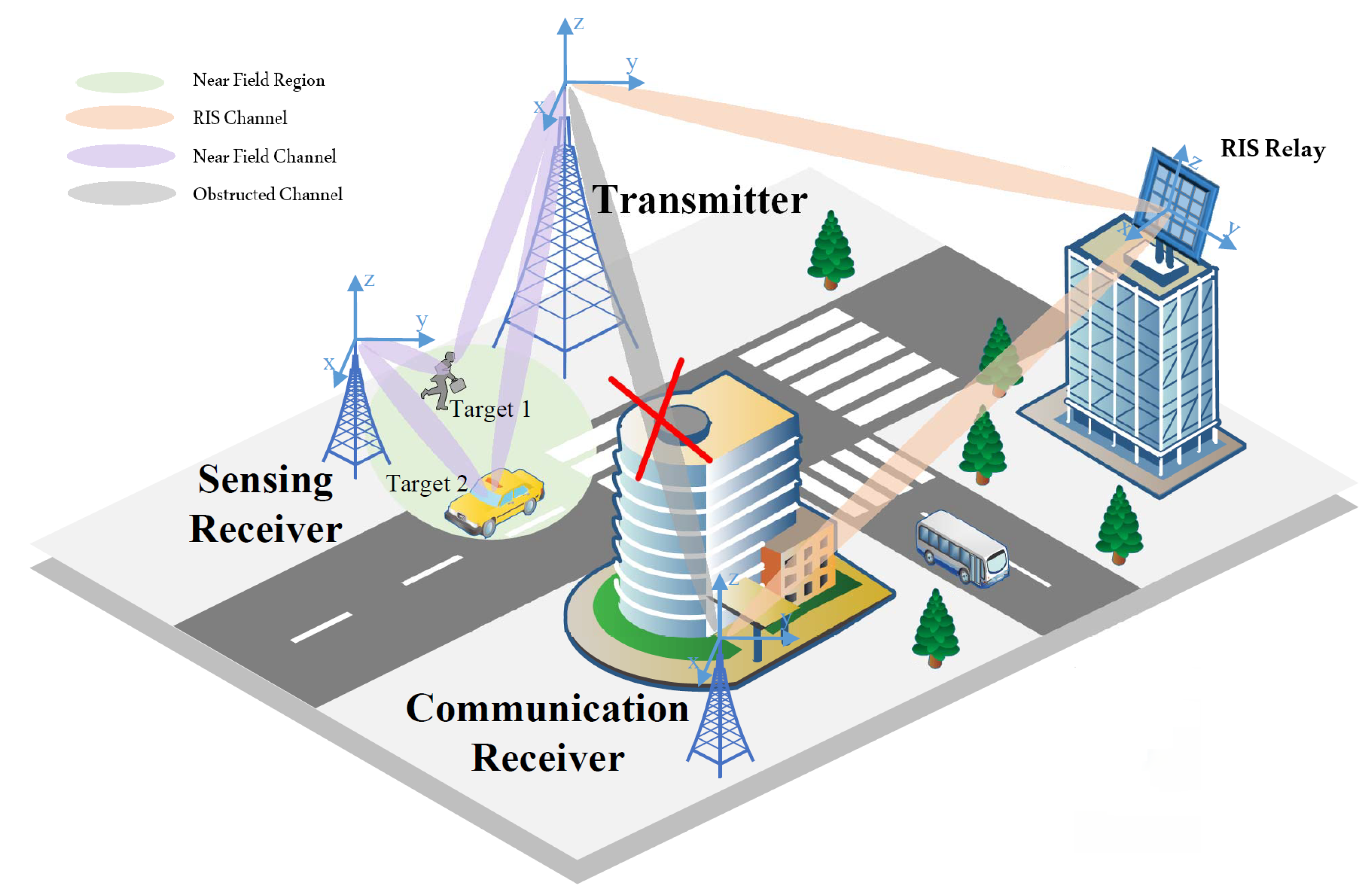
5.1.1. RIS
5.1.2. Holographic MIMO
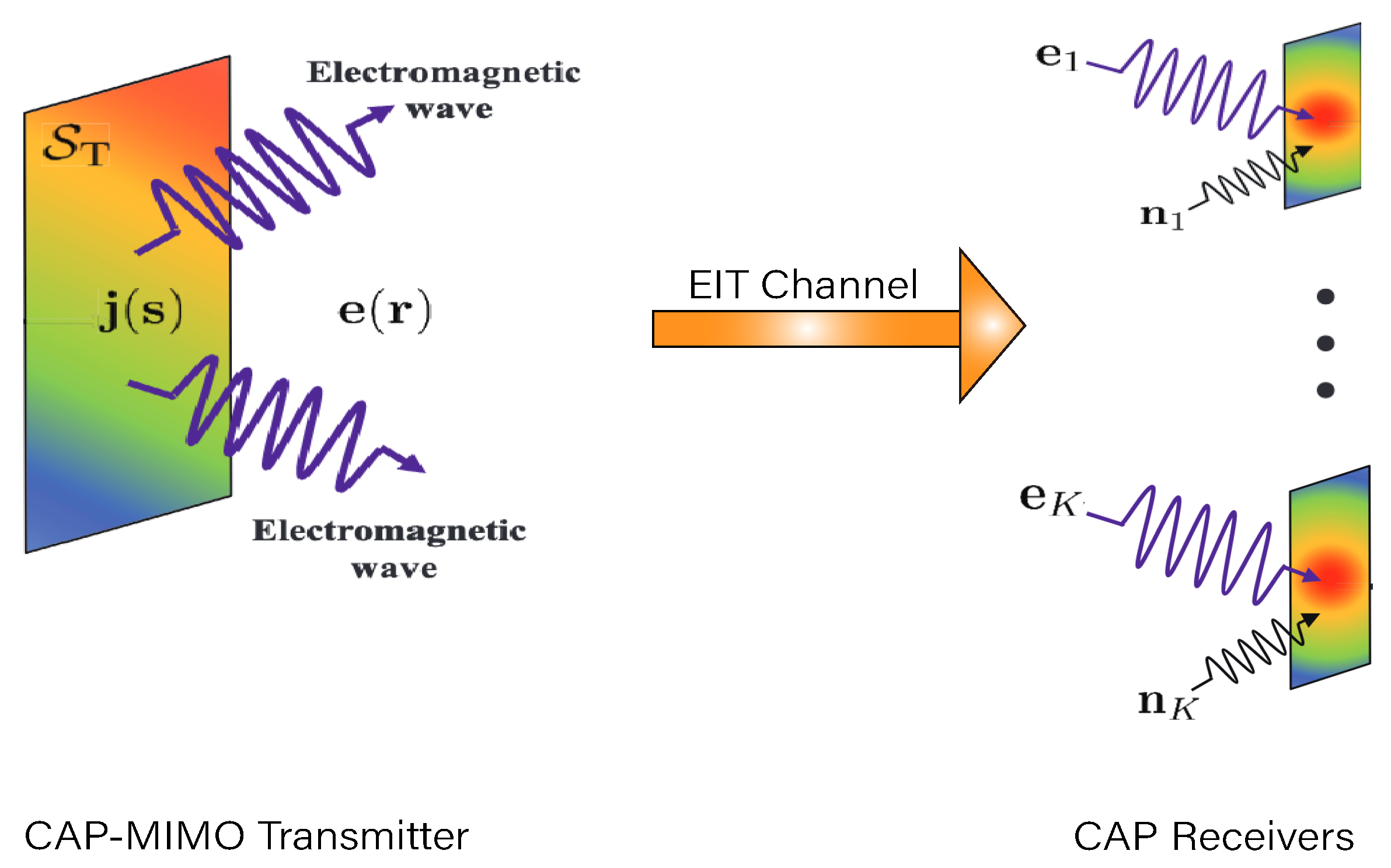
5.1.3. CAP MIMO
5.2. Limitations of Existing Signal Models
6. Electromagnetic Information Theory Based Energy-Efficient Near-Field Communication
6.1. Basic Principle
6.2. Energy Sustainability
6.3. EIT-Motivated Channel Modeling and Channel Estimation
6.4. Limitations
7. Conclusions
- Comprehensive Energy-Efficient Techniques: The paper reviews energy-efficient strategies in near-field communication, examining their characteristics, advantages, and potential future.
- Advanced Signal and Channel Models: This paper identifies the capabilities of sophisticated signal and channel models, explaining their role in enhancing energy efficiency and minimizing hardware requirements. The paper also introduces energy consumption models suited for various near-field communication scenarios.
- Diverse Applications of Existing Techniques: The research highlights existing energy-efficient techniques and discusses their applicability across different communication environments.
- Open Research Challenges: The paper outlines the open research challenges in near-field communication, such as developing accurate channel models and energy-efficient techniques.
Funding
Informed Consent Statement
Conflicts of Interest
References
- Banafaa, M.; Shayea, I.; Din, J.; Azmi, M.H.; Alashbi, A.; Daradkeh, Y.I.; Alhammadi, A. 6G mobile communication technology: Requirements, targets, applications, challenges, advantages, and opportunities. Alex. Eng. J. 2023, 64, 245–274. [Google Scholar] [CrossRef]
- Research, V.B.C.M. The Global Beamformer Market Size Will Be USD 201451.2 Million in 2024; Cognitive Market Research: Chicago, IL, USA, 2024. [Google Scholar]
- Ning, B.; Tian, Z.; Mei, W.; Chen, Z.; Han, C.; Li, S.; Yuan, J.; Zhang, R. Beamforming technologies for ultra-massive MIMO in terahertz communications. IEEE Open J. Commun. Soc. 2023, 4, 614–658. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Du, H.; Wang, Z.; Liu, Y.; Niyato, D.; Ai, B.; Letaief, K.B. Resource allocation for near-field communications: Fundamentals, tools, and outlooks. IEEE Wirel. Commun. 2024, 31, 42–50. [Google Scholar] [CrossRef]
- Cui, T.; You, X.; Eldar, Y.; Dai, L.; Zhang, J.; Yuan, Y.; Zheng, B.; Ai, B.; Wang, B.; Xu, B.; et al. 6G Near-Field Technologies White Paper. [CrossRef]
- Devi, P.; Bharti, M.R.; Gautam, D. A Survey on Physical Layer Security for 5G/6G Communications over Different Fading Channels: Approaches, Challenges, and Future Directions. Veh. Commun. 2025, 53, 100891. [Google Scholar] [CrossRef]
- Elzanaty, A.; Liu, J.; Guerra, A.; Guidi, F.; Ma, Y.; Tafazolli, R. Near and far field model mismatch: Implications on 6G communications, localization, and sensing. IEEE Internet Things Mag. 2024, 7, 120–126. [Google Scholar] [CrossRef]
- Zhang, H.; Shlezinger, N.; Guidi, F.; Dardari, D.; Imani, M.F.; Eldar, Y.C. Beam focusing for near-field multiuser MIMO communications. IEEE Trans. Wirel. Commun. 2022, 21, 7476–7490. [Google Scholar] [CrossRef]
- Azarbahram, A.; López, O.L.; Latva-Aho, M. Waveform optimization and beam focusing for near-field wireless power transfer with dynamic metasurface antennas and non-linear energy harvesters. IEEE Trans. Wirel. Commun. 2024, 24, 1031–1045. [Google Scholar] [CrossRef]
- Cg, B.; Ponnusamy, S. Adaptive Beamforming and Energy-Efficient Resource Allocation for Sustainable 6G THz Networks. IETE J. Res. 2025, 1–15. [Google Scholar] [CrossRef]
- Shlezinger, N.; Dicker, O.; Eldar, Y.C.; Yoo, I.; Imani, M.F.; Smith, D.R. Dynamic metasurface antennas for uplink massive MIMO systems. IEEE Trans. Commun. 2019, 67, 6829–6843. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, Z.; Lyu, Y.; Zhang, J.; Pedersen, G.; Borrill, J.; Zhang, F. Near-Field Channel Characterization for Mid-band ELAA Systems: Sounding, Parameter Estimation, and Modeling. arXiv 2024, arXiv:2405.06159. [Google Scholar]
- Hasan, S.R.; Sabuj, S.R.; Hamamura, M.; Hossain, M.A. A comprehensive review on reconfigurable intelligent surface for 6G communications: Overview, deployment, control mechanism, application, challenges, and opportunities. Wirel. Pers. Commun. 2024, 139, 375–429. [Google Scholar] [CrossRef]
- Cui, M.; Wu, Z.; Lu, Y.; Wei, X.; Dai, L. Near-field MIMO communications for 6G: Fundamentals, challenges, potentials, and future directions. IEEE Commun. Mag. 2023, 61, 40–46. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Tseng, F.S.; Singh, K.; Singh, S.K.; Dev, K.; Pan, C. A Tutorial on Near-Field Driven 6G Networks. Authorea Prepr. 2024. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, X.; You, C. Fast near-field beam training for extremely large-scale array. IEEE Wirel. Commun. Lett. 2022, 11, 2625–2629. [Google Scholar] [CrossRef]
- Wei, X.; Dai, L.; Zhao, Y.; Yu, G.; Duan, X. Codebook design and beam training for extremely large-scale RIS: Far-field or near-field? China Commun. 2022, 19, 193–204. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Zhang, J.; Li, C.; Huang, Y.; Yang, L. Codebook design for extremely large-scale MIMO systems: Near-field and far-field. IEEE Trans. Commun. 2024, 72, 1191–1206. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Wang, R.; Wu, J. A Near Field Low Time Complexity Beam Training Scheme Based on Spatial Orthogonal Decomposition. arXiv 2023, arXiv:2312.09659. [Google Scholar]
- Droulias, S.; Stratidakis, G.; Alexiou, A. Near-field orthogonality and cosine beams for near-field space division multiple access in 6G communications and beyond. arXiv 2024, arXiv:2408.13190. [Google Scholar]
- Yang, S.; Lyu, W.; Zhang, Z.; Yuen, C. Enhancing near-field sensing and communications with sparse arrays: Potentials, challenges, and emerging trends. arXiv 2023, arXiv:2309.08681. [Google Scholar]
- An, J.; Yuen, C.; Dai, L.; Di Renzo, M.; Debbah, M.; Hanzo, L. Near-field communications: Research advances, potential, and challenges. IEEE Wirel. Commun. 2024, 31, 100–107. [Google Scholar] [CrossRef]
- Cui, M.; Dai, L. Near-field wideband beamforming for extremely large antenna arrays. IEEE Trans. Wirel. Commun. 2024, 23, 13110–13124. [Google Scholar] [CrossRef]
- You, L.; Xu, J.; Alexandropoulos, G.C.; Wang, J.; Wang, W.; Gao, X. Dynamic metasurface antennas for energy efficient massive mimo uplink communications. arXiv 2021, arXiv:2106.09442. [Google Scholar]
- Li, X.; Wang, X.; Hou, X.; Chen, L.; Suyama, S. Two-step beamforming scheme for large-dimension reconfigurable intelligent surface. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Wang, F.; Wang, X.; Li, X.; Hou, X.; Chen, L.; Suyama, S.; Asai, T. Near-Field Beam Management with Ring-type Codebook. In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Jian, M.; Tang, A.; Chen, Y.; Zhao, Y. Fractional Fourier Transformation Based XL-MIMO Near-Field Channel Analysis. In Proceedings of the 2024 IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 10–13 September 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 221–225. [Google Scholar]
- Nie, J.; Cui, Y.; Yang, Z.; Yuan, W.; Jing, X. Near-field Beam Training for Extremely Large-scale MIMO Based on Deep Learning. IEEE Trans. Mob. Comput. 2025, 24, 352–362. [Google Scholar] [CrossRef]
- Han, S.; Chih-Lin, I.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, C.; Peng, W.; Debbah, M.; Hanzo, L.; Yuen, C. Achievable rate optimization of the RIS-aided near-field wideband uplink. IEEE Trans. Wirel. Commun. 2023, 23, 2296–2311. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, H.; Shi, Z.; Ge, Y.; Fu, Y. On Sum-Rate Maximization for Cooperative STAR-RIS-Assisted Near-Field NOMA Network. In Proceedings of the 2024 IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 7–9 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 271–276. [Google Scholar]
- Liu, Y.; Ouyang, C.; Wang, Z.; Xu, J.; Mu, X.; Swindlehurst, A.L. Near-field communications: A comprehensive survey. IEEE Commun. Surv. Tutor. 2024. [CrossRef]
- Liu, Y.; Wang, Z.; Xu, J.; Ouyang, C.; Mu, X.; Schober, R. Near-field communications: A tutorial review. IEEE Open J. Commun. Soc. 2023, 4, 1999–2049. [Google Scholar] [CrossRef]
- Lu, H.; Zeng, Y.; You, C.; Han, Y.; Zhang, J.; Wang, Z.; Dong, Z.; Jin, S.; Wang, C.X.; Jiang, T.; et al. A tutorial on near-field XL-MIMO communications towards 6G. IEEE Commun. Surv. Tutor. 2024, 26, 2213–2257. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, X.; Liu, Y. Beamfocusing optimization for near-field wideband multi-user communications. IEEE Trans. Commun. 2024, 73, 555–572. [Google Scholar] [CrossRef]
- Monemi, M.; Fallah, M.A.; Rasti, M.; Latva-Aho, M.; Debbah, M. Towards near-field 3d spot beamfocusing: Possibilities, challenges, and use-cases. arXiv 2023, arXiv:2401.08651. [Google Scholar]
- Qu, K.; Guo, S.; Saeed, N.; Ye, J. Near-field integrated sensing and communication: Performance analysis and beamforming design. IEEE Open J. Commun. Soc. 2024, 5, 6353–6366. [Google Scholar] [CrossRef]
- Dibner, B. James Clerk Maxwell. IEEE Spectr. 1964, 1, 50–56. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Salazar-Palma, M.; Sengupta, D.L. Who Was James Clerk Maxwell and What Was and Is His Electromagnetic Theory? IEEE Antennas Propag. Mag. 2009, 51, 97–116. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Heyman, E. Wave propagation in media having negative permittivity and permeability. Phys. Rev. E 2001, 64, 056625. [Google Scholar] [CrossRef]
- Gennarelli, C.; Capozzoli, A.; Foged, L.J.; Fordham, J.; Van Rensburg, D.J. Recent Advances in Near-Field to Far-Field Transformation Techniques. Int. J. Antennas Propag. 2012, 2012, 1–3. [Google Scholar] [CrossRef]
- Ouyang, C.; Wang, Z.; Zhao, B.; Zhang, X.; Liu, Y. On the Impact of Reactive Region on the Near-Field Channel Gain. arXiv 2024, arXiv:2404.08343. [Google Scholar] [CrossRef]
- Xie, J.; Tao, H.; Rao, X.; Su, J. Localization of mixed far-field and near-field sources under unknown mutual coupling. Digit. Signal Process. 2016, 50, 229–239. [Google Scholar] [CrossRef]
- Cui, M.; Dai, L. Channel Estimation for Extremely Large-Scale MIMO: Far-Field or Near-Field? IEEE Trans. Commun. 2022, 70, 2663–2677. [Google Scholar] [CrossRef]
- Pizzo, A.; Sanguinetti, L.; Marzetta, T.L. Spatial characterization of electromagnetic random channels. IEEE Open J. Commun. Soc. 2022, 3, 847–866. [Google Scholar] [CrossRef]
- Marzetta, T.L. Plane-Wave Analysis of Near-Field Communications. In Proceedings of the 2024 58th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 27–30 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 158–162. [Google Scholar]
- Zhang, X.; Wang, Z.; Zhang, H.; Yang, L. Near-Field Channel Estimation for Extremely Large-Scale Array Communications: A Model-Based Deep Learning Approach. IEEE Commun. Lett. 2023, 27, 1155–1159. [Google Scholar] [CrossRef]
- Wei, X.; Dai, L. Channel Estimation for Extremely Large-Scale Massive MIMO: Far-Field, Near-Field, or Hybrid-Field? IEEE Commun. Lett. 2022, 26, 177–181. [Google Scholar] [CrossRef]
- Liang, P.; Wu, Q. Characteristic Mode Analysis of Antenna Mutual Coupling in the Near Field. IEEE Trans. Antennas Propag. 2018, 66, 3757–3762. [Google Scholar] [CrossRef]
- Frid, H.; Holter, H.; Jonsson, B.L.G. An Approximate Method for Calculating the Near-Field Mutual Coupling Between Line-of-Sight Antennas on Vehicles. IEEE Trans. Antennas Propag. 2015, 63, 4132–4138. [Google Scholar] [CrossRef]
- Dong, B.; Yan, Z.; Zhang, Y.; Han, T.; Zhou, H.; Wang, Y. Analysis of near field mutual coupling in wideband magnetoelectric antennas array. J. Appl. Phys. 2023, 134, 114103. [Google Scholar] [CrossRef]
- Ahmed, I.; Khammari, H.; Shahid, A.; Musa, A.; Kim, K.S.; De Poorter, E.; Moerman, I. A Survey on Hybrid Beamforming Techniques in 5G: Architecture and System Model Perspectives. IEEE Commun. Surv. Tutor. 2018, 20, 3060–3097. [Google Scholar] [CrossRef]
- Biral, A.; Centenaro, M.; Zanella, A.; Vangelista, L.; Zorzi, M. The challenges of M2M massive access in wireless cellular networks. Digit. Commun. Netw. 2015, 1, 1–19. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Chen, C.; Cai, W.; Cheng, X.; Yang, L.; Jin, Y. Low Complexity Beamforming and User Selection Schemes for 5G MIMO-NOMA Systems. IEEE J. Sel. Areas Commun. 2017, 35, 2708–2722. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X.G. 3-D Beamforming for Flexible Coverage in Millimeter-Wave UAV Communications. IEEE Wirel. Commun. Lett. 2019, 8, 837–840. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, Y.; Jing, Y.; Yang, L. Energy Efficient Beamforming for Massive MIMO Public Channel. IEEE Trans. Veh. Technol. 2017, 66, 10595–10600. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Xu, W. 5G Cellular User Equipment: From Theory to Practical Hardware Design. IEEE Access 2017, 5, 13992–14010. [Google Scholar] [CrossRef]
- Rihan, M.; Abed Soliman, T.; Xu, C.; Huang, L.; Dessouky, M.I. Taxonomy and Performance Evaluation of Hybrid Beamforming for 5G and Beyond Systems. IEEE Access 2020, 8, 74605–74626. [Google Scholar] [CrossRef]
- Liu, S.; Yu, X.; Gao, Z.; Ng, D.W.K. DPSS-Based Codebook Design for Near-Field XL-MIMO Channel Estimation. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 3864–3870. [Google Scholar] [CrossRef]
- Wang, F.; Hou, X.; Li, X.; Chen, L. Plane Wave Expansion-based Codebook Design for 6G Near-field MIMO. In Proceedings of the 2024 IEEE 29th Asia Pacific Conference on Communications (APCC), Bali, Indonesia, 5–7 November 2024; pp. 536–541. [Google Scholar] [CrossRef]
- Huang, W.; Li, C.; Zeng, Y.; Kai, C.; He, S. Near-Field Full Dimensional Beam Codebook Design for XL-MIMO Communications. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 4902–4908. [Google Scholar] [CrossRef]
- Zheng, F.; Yu, H.; Wang, C.; Sun, L.; Wu, Q.; Chen, Y. Extremely Large-scale Array Systems: Near-Field Codebook Design and Performance Analysis. IEEE Trans. Commun. 2025. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Zhang, H.; Xu, Y.; Zheng, F.C. Near-Field Codebook Design for Extremely Large Cylindrical Antenna Array Systems. IEEE Trans. Commun. 2024, 72, 5380–5395. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Li, D.; Jiang, R.; Xu, Y. Codebook Design for Beamforming in Near-Field Cylindrical Antenna Array Systems. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 2348–2353. [Google Scholar] [CrossRef]
- Wu, X.; You, C.; Li, J.; Zhang, Y.; Chen, L.; Han, K. Near-Field Beam Training with DFT Codebook. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, C.; You, C.; Zhou, J.; Shi, S. Near-field Beam Training with Sparse DFT Codebook. IEEE Trans. Commun. 2024. [Google Scholar] [CrossRef]
- Chen, Y.; Han, C.; Björnson, E. Can Far-Field Beam Training Be Deployed for Cross-Field Beam Alignment in Terahertz UM-MIMO Communications? IEEE Trans. Wirel. Commun. 2024, 23, 14972–14987. [Google Scholar] [CrossRef]
- Liu, W.; Pan, C.; Ren, H.; Wang, J.; Schober, R. Near-Field Multiuser Beam-Training for Extremely Large-Scale MIMO Systems. IEEE Trans. Commun. 2024, 73, 2663–2679. [Google Scholar] [CrossRef]
- Jiang, G.; Qi, C. Near-Field Beam Training Based on Deep Learning for Extremely Large-Scale MIMO. IEEE Commun. Lett. 2023, 27, 2063–2067. [Google Scholar] [CrossRef]
- Huang, W.; Huang, X.; Zhang, H.; Sun, K.; Kai, C.; He, S. Vision Image Aided Near-Field Beam Training for Internet of Vehicle Systems. In Proceedings of the 2024 IEEE International Conference on Communications Workshops (ICC Workshops), Denver, CO, USA, 9–13 June 2024; pp. 390–395. [Google Scholar] [CrossRef]
- Luo, J.; Fan, J.; Xie, K.; Shi, X. Efficient Hybrid Near- and Far-Field Beam Training for XL-MIMO Communications. IEEE Trans. Veh. Technol. 2024, 73, 19785–19790. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Z.; Dai, L. Hierarchical Beam Training for Extremely Large-Scale MIMO: From Far-Field to Near-Field. IEEE Trans. Commun. 2024, 72, 2247–2259. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Z.; Dai, L. Near-Field 2D Hierarchical Beam Training for Extremely Large-Scale MIMO. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 7176–7181. [Google Scholar] [CrossRef]
- Weng, C.; Guo, X.; Wang, Y. Near-Field Beam Training With Hierarchical Codebook: Two-Stage Learning-Based Approach. IEEE Trans. Veh. Technol. 2024, 73, 14003–14008. [Google Scholar] [CrossRef]
- Wu, X.; You, C.; Li, J.; Zhang, Y. Near-Field Beam Training: Joint Angle and Range Estimation with DFT Codebook. IEEE Trans. Wirel. Commun. 2024, 23, 11890–11903. [Google Scholar] [CrossRef]
- Chen, J.; Gao, F.; Jian, M.; Yuan, W. Hierarchical Codebook Design for Near-Field mmWave MIMO Communications Systems. IEEE Wirel. Commun. Lett. 2023, 12, 1926–1930. [Google Scholar] [CrossRef]
- Liu, W.; Ren, H.; Pan, C.; Wang, J. Deep Learning Based Beam Training for Extremely Large-Scale Massive MIMO in Near-Field Domain. IEEE Commun. Lett. 2023, 27, 170–174. [Google Scholar] [CrossRef]
- Liu, W.; Pan, C.; Ren, H.; Wang, C.X.; Wang, J.; You, X. NMBEnet: Efficient Near-field mmWave Beam Training for Multiuser OFDM Systems Using Sub-6 GHz Pilots. IEEE Trans. Commun. 2024, 73, 3119–3135. [Google Scholar] [CrossRef]
- Cui, M.; Dai, L.; Wang, Z.; Zhou, S.; Ge, N. Near-Field Rainbow: Wideband Beam Training for XL-MIMO. IEEE Trans. Wirel. Commun. 2023, 22, 3899–3912. [Google Scholar] [CrossRef]
- Zheng, T.; Cui, M.; Wu, Z.; Dai, L. Near-Field Wideband Beam Training Based on Distance-Dependent Beam Split. IEEE Trans. Wirel. Commun. 2025, 24, 1278–1292. [Google Scholar] [CrossRef]
- Xie, Y.; Ning, B.; Li, L.; Chen, Z. Near-Field Beam Training in THz Communications: The Merits of Uniform Circular Array. IEEE Wirel. Commun. Lett. 2023, 12, 575–579. [Google Scholar] [CrossRef]
- Shin, S.; Moon, J.; Kim, S.; Shim, B. Subarray-Based Near-Field Beam Training for 6G Terahertz Communications. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 3189–3194. [Google Scholar] [CrossRef]
- Xu, Y.; Li, W.; Huang, C.; Zhu, C.; Yang, Z.; Yang, J.; He, J.; Zhang, Z.; Debbah, M. Hashing Beam Training for Near-Field Communications. In Proceedings of the 2024 IEEE International Conference on Communications Workshops (ICC Workshops), Denver, CO, USA, 9–13 June 2024; pp. 732–737. [Google Scholar] [CrossRef]
- Wang, H.; Fang, J.; Duan, H.; Li, H. Fast Hybrid Far/Near-Field Beam Training for Extremely Large-Scale Millimeter Wave/Terahertz Systems. IEEE Trans. Commun. 2024. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Z.; Liu, Y. Sense-Then-Train: An Active-Sensing-Based Beam Training Design for Near-Field MIMO Systems. IEEE Trans. Wirel. Commun. 2024, 23, 15525–15539. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, W.; Li, M.; Zhao, M.J. Position-Aware Beam Training for Near-Field Milimeter-Wave XL-MIMO Communications. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Anjum, M.; Mishra, D.; Seneviratne, A. Power-Efficient Transceiver Design for Full-Duplex Dual-Function Radar Communication Systems. In Proceedings of the 2024 IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 10–13 September 2024; pp. 11–15. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, X.; Liu, Y. Near-Field Velocity Sensing and Predictive Beamforming. IEEE Trans. Veh. Technol. 2025, 74, 1806–1810. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, X.; Liu, Y. Near-Field Integrated Sensing and Communications. IEEE Commun. Lett. 2023, 27, 2048–2052. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, X.; Liu, Y. Rethinking Integrated Sensing and Communication: When Near Field Meets Wideband. IEEE Commun. Mag. 2024, 62, 44–50. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Wang, X.; Amin, M.G.; Cai, K. Wideband Near-Field Integrated Sensing and Communication with Sparse Transceiver Design. IEEE J. Sel. Top. Signal Process. 2024, 18, 662–677. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. NOMA-Based Coexistence of Near-Field and Far-Field Massive MIMO Communications. IEEE Wirel. Commun. Lett. 2023, 12, 1429–1433. [Google Scholar] [CrossRef]
- Li, Y.; Gong, S.; Liu, H.; Xing, C.; Zhao, N.; Wang, X. Near-Field Beamforming Optimization for Holographic XL-MIMO Multiuser Systems. IEEE Trans. Commun. 2024, 72, 2309–2323. [Google Scholar] [CrossRef]
- Myers, N.J.; Heath, R.W. InFocus: A Spatial Coding Technique to Mitigate Misfocus in Near-Field LoS Beamforming. IEEE Trans. Wirel. Commun. 2022, 21, 2193–2209. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, J.; Zou, Y.; Xie, W.; Liu, Y. Wideband Beamforming for RIS Assisted Near-Field Communications. IEEE Trans. Wirel. Commun. 2024, 23, 16836–16851. [Google Scholar] [CrossRef]
- Zhang, Y.; Alkhateeb, A. Deep Learning of Near Field Beam Focusing in Terahertz Wideband Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2023, 12, 535–539. [Google Scholar] [CrossRef]
- Ferreira, J.; Guerreiro, J.; Dinis, R. Physical Layer Security with Near-Field Beamforming. IEEE Access 2024, 12, 4801–4811. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Wang, Z.; Mu, X.; Chen, J. Physical Layer Security in Near-Field Communications. IEEE Trans. Veh. Technol. 2024, 73, 10761–10766. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, Y.; Liu, K.; Zhong, Y.; Lei, X.; Xiao, M. Physical Layer Security for Near-Field Communications via Directional Modulation. IEEE Trans. Veh. Technol. 2024, 73, 12242–12246. [Google Scholar] [CrossRef]
- Anjum, M.; Mishra, D.; Matthaiou, M.; Seneviratne, A. QoS-Aware Power Minimization for Fluid Antennas Assisted Integrated Sensing and Communication. In Proceedings of the Proceeding IEEE ICC, Penang, Malaysia, 27–29 June 2025; pp. 1–6. [Google Scholar]
- Anjum, M.; Mishra, D.; Seneviratne, A. Green Transceiver Design for Integrated Sensing and Backscatter Communication with QoS Demands. In Proceedings of the Proceeding IEEE ICC, Penang, Malaysia, 27–29 June 2025; pp. 1–6. [Google Scholar]
- Eslami, S.; Gouda, B.; Tölli, A. Near-Field MIMO Channel Reconstruction Via Limited Geometry Feedback. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 9256–9260. [Google Scholar] [CrossRef]
- Cao, R.; Yu, W.; He, H.; Yu, X.; Song, S.; Zhang, J.; Gong, Y.; Letaief, K.B. Newtonized Near-Field Channel Estimation for Ultra-Massive MIMO Systems. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Kosasih, A.; Demir, Ö.T.; Björnson, E. Parametric Near-Field Channel Estimation for Extremely Large Aperture Arrays. In Proceedings of the 2023 57th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2023; pp. 162–166. [Google Scholar] [CrossRef]
- Yu, W.; He, H.; Yu, X.; Song, S.; Zhang, J.; Murch, R.; Letaief, K.B. Bayes-Optimal Unsupervised Learning for Channel Estimation in Near-Field Holographic MIMO. IEEE J. Sel. Top. Signal Process. 2024, 18, 714–729. [Google Scholar] [CrossRef]
- Yue, S.; Zeng, S.; Liu, L.; Eldar, Y.C.; Di, B. Hybrid Near-Far Field Channel Estimation for Holographic MIMO Communications. IEEE Trans. Wirel. Commun. 2024, 23, 15798–15813. [Google Scholar] [CrossRef]
- Jang, S.; Lee, C. Neural Network-Aided Near-Field Channel Estimation for Hybrid Beamforming Systems. IEEE Trans. Commun. 2024, 72, 6768–6782. [Google Scholar] [CrossRef]
- Jiang, H.; Xiong, B.; Zhang, H.; Basar, E. Hybrid Far- and Near-Field Modeling for Reconfigurable Intelligent Surface Assisted V2V Channels: A Sub-Array Partition Based Approach. IEEE Trans. Wirel. Commun. 2023, 22, 8290–8303. [Google Scholar] [CrossRef]
- Lu, Y.; Dai, L. Near-Field Channel Estimation in Mixed LoS/NLoS Environments for Extremely Large-Scale MIMO Systems. IEEE Trans. Commun. 2023, 71, 3694–3707. [Google Scholar] [CrossRef]
- Lee, J.; Hong, S. Near-Field LoS/NLoS Channel Estimation for RIS-Aided MU-MIMO Systems: Piece-Wise Low-Rank Approximation Approach. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- Lu, Y.; Dai, L. Mixed LoS/NLoS Near-Field Channel Estimation for Extremely Large-Scale MIMO Systems. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 1506–1511. [Google Scholar] [CrossRef]
- Xiang, M.; Chang, Y.; Zeng, T. Channel estimation for 3D MIMO system based on LOS/NLOS identification. IET Commun. 2019, 13, 898–904. [Google Scholar] [CrossRef]
- Huang, C.; Xu, J.; Xu, W.; You, X.; Yuen, C.; Chen, Y. Low-Complexity Channel Estimation for Extremely Large-Scale MIMO in Near Field. IEEE Wirel. Commun. Lett. 2024, 13, 671–675. [Google Scholar] [CrossRef]
- Cui, M.; Dai, L. Near-Field Channel Estimation for Extremely Large-scale MIMO with Hybrid Precoding. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, W.; Li, M.; Liu, Q. A Practical Channel Estimation Strategy for XL-MIMO Communication Systems. IEEE Commun. Lett. 2023, 27, 1580–1583. [Google Scholar] [CrossRef]
- Wu, J.; Kim, S.; Shim, B. Near-Field Channel Estimation for RIS-Assisted Wideband Terahertz Systems. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 3893–3898. [Google Scholar] [CrossRef]
- Lee, A.; Ju, H.; Kim, S.; Shim, B. Intelligent Near-Field Channel Estimation for Terahertz Ultra-Massive MIMO Systems. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 5390–5395. [Google Scholar] [CrossRef]
- Yu, X.; Shen, W.; Zhang, R.; Xing, C.; Quek, T.Q.S. Channel Estimation for XL-RIS-Aided Millimeter-Wave Systems. IEEE Trans. Commun. 2023, 71, 5519–5533. [Google Scholar] [CrossRef]
- Pan, Y.; Pan, C.; Jin, S.; Wang, J. RIS-Aided Near-Field Localization and Channel Estimation for the Terahertz System. IEEE J. Sel. Top. Signal Process. 2023, 17, 878–892. [Google Scholar] [CrossRef]
- Elbir, A.M.; Shi, W.; Papazafeiropoulos, A.K.; Kourtessis, P.; Chatzinotas, S. Near-Field Terahertz Communications: Model-Based and Model-Free Channel Estimation. IEEE Access 2023, 11, 36409–36420. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Ahmed, M.; Raza, S.; Soofi, A.A.; Khan, F.; Khan, W.U.; Abideen, S.Z.U.; Xu, F.; Han, Z. Active reconfigurable intelligent surfaces: Expanding the frontiers of wireless communication-a survey. IEEE Commun. Surv. Tutor. 2024, 27, 839–869. [Google Scholar] [CrossRef]
- Besser, K.L.; Jorswieck, E.A. Reconfigurable intelligent surface phase hopping for ultra-reliable communications. IEEE Trans. Wirel. Commun. 2022, 21, 9082–9095. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Wang, M.; Yang, X.; Tan, J.; Bi, S.; Xu, S.; Yang, F.; Chen, Z.; Di Renzo, M.; et al. Reconfigurable intelligent surface-based wireless communications: Antenna design, prototyping, and experimental results. IEEE Access 2020, 8, 45913–45923. [Google Scholar] [CrossRef]
- Rihan, M.; Zappone, A.; Buzzi, S.; Fodor, G.; Debbah, M. Passive versus active reconfigurable intelligent surfaces for integrated sensing and communication: Challenges and opportunities. IEEE Netw. 2023, 38, 218–226. [Google Scholar] [CrossRef]
- Al-Nahhal, I.; Dobre, O.A.; Basar, E.; Ngatched, T.M.; Ikki, S. Reconfigurable intelligent surface optimization for uplink sparse code multiple access. IEEE Commun. Lett. 2021, 26, 133–137. [Google Scholar] [CrossRef]
- Soleymani, M.; Santamaria, I.; Jorswieck, E.; Schober, R.; Hanzo, L. Optimization of the downlink spectral-and energy-efficiency of RIS-aided multi-user URLLC MIMO systems. IEEE Trans. Commun. 2024, 73, 3497–3513. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Wang, Z.; Chen, J.; Kim, D.I. Near field communications for DMA-NOMA networks. IEEE Internet Things J. 2024, 11, 28021–28035. [Google Scholar] [CrossRef]
- Zhao, Y. RIS constructing 6G near-field networks: Opportunities and challenges. arXiv 2024, arXiv:2403.15390. [Google Scholar]
- Anjum, M.; Khan, M.A.; Basharat, S.; Hassan, S.A.; Jung, H. Dedicated versus Shared Element-Allotment in IRS-aided Wireless Systems: When to Use What? In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, M.A.; Anjum, M.; Hassan, S.A.; Jung, H. Machine Learning-Based Resource Allocation for IRS-Aided UAV Networks. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 3051–3057. [Google Scholar] [CrossRef]
- Yan, H.; Chen, H.; Liu, W.; Yang, S.; Wang, G.; Yuen, C. RIS-enabled joint near-field 3D localization and synchronization in SISO multipath environments. IEEE Trans. Green Commun. Netw. 2024, 9, 367–379. [Google Scholar] [CrossRef]
- Chen, R.; Liu, M.; Hui, Y.; Cheng, N.; Li, J. Reconfigurable intelligent surfaces for 6G IoT wireless positioning: A contemporary survey. IEEE Internet Things J. 2022, 9, 23570–23582. [Google Scholar] [CrossRef]
- de Souza, J.H.I.; Marinello Filho, J.C.; Abrão, T.; Panazio, C. Reconfigurable intelligent surfaces to enable energy-efficient IoT networks. In Proceedings of the 2022 Symposium on Internet of Things (SIoT), Sao Paulo, Brazil, 24–28 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Kisseleff, S.; Martins, W.A.; Al-Hraishawi, H.; Chatzinotas, S.; Ottersten, B. Reconfigurable intelligent surfaces for smart cities: Research challenges and opportunities. IEEE Open J. Commun. Soc. 2020, 1, 1781–1797. [Google Scholar] [CrossRef]
- Rihan, M.; Zappone, A.; Buzzi, S.; Wübben, D.; Dekorsy, A. Energy efficiency maximization for active RIS-aided integrated sensing and communication. EURASIP J. Wirel. Commun. Netw. 2024, 2024, 20. [Google Scholar] [CrossRef]
- Ahmed, M.; Wahid, A.; Khan, W.U.; Khan, F.; Ihsan, A.; Ali, Z.; Rabie, K.; Shongwe, T.; Han, Z. A survey on RIS advances in terahertz communications: Emerging paradigms and research frontiers. IEEE Access 2024, 12, 173867–173901. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, L.; Chen, X.; Liu, C.; Yang, F.; Schober, R.; Poor, H.V. Active RIS vs. passive RIS: Which will prevail in 6G? IEEE Trans. Commun. 2022, 71, 1707–1725. [Google Scholar] [CrossRef]
- Rahmani, H.; Shetty, D.; Wagih, M.; Ghasempour, Y.; Palazzi, V.; Carvalho, N.B.; Correia, R.; Costanzo, A.; Vital, D.; Alimenti, F.; et al. Next-generation IoT devices: Sustainable eco-friendly manufacturing, energy harvesting, and wireless connectivity. IEEE J. Microw. 2023, 3, 237–255. [Google Scholar] [CrossRef]
- Du, L.; Zhang, W.; Ma, J.; Tang, Y. Reconfigurable intelligent surfaces for energy efficiency in multicast transmissions. IEEE Trans. Veh. Technol. 2021, 70, 6266–6271. [Google Scholar] [CrossRef]
- Hua, S.; Zhou, Y.; Yang, K.; Shi, Y.; Wang, K. Reconfigurable intelligent surface for green edge inference. IEEE Trans. Green Commun. Netw. 2021, 5, 964–979. [Google Scholar] [CrossRef]
- Lv, S.; Liu, Y.; Xu, X.; Nallanathan, A.; Swindlehurst, A.L. RIS-Aided Near-Field MIMO Communications: Codebook and Beam Training Design. IEEE Trans. Wirel. Commun. 2024, 23, 12531–12546. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Di, B. Large-Scale Intelligent Surfaces Enabled Unified Near-Field and Far-Field Communications: Codebook Design and Beam Training. IEEE Netw. 2025, 39, 90–96. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Di, B. Near-Far Field Codebook Design for IOS-Aided Multi-User Communications. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 2888–2893. [Google Scholar] [CrossRef]
- Nor, A.M.; Fratu, O.; Halunga, S.; An, J.; Zaharis, Z.; Velanas, P. Position based Near-Field Codebook Design and Beam Training for Extremely Large-Scale ARIS. In Proceedings of the 2024 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Madrid, Spain, 8–11 July 2024; pp. 215–220. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, W. IRS-aided Indoor Millimeter-wave System: Near-field Codebook Design. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1489–1494. [Google Scholar] [CrossRef]
- Hibi, R.; Hashida, H.; Kawamoto, Y.; Kato, N. 3D Codebook Construction Strategy based on Control Accuracy Index for Intelligent Reflecting Surface in Near-field. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 7–10 October 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Li, X.; Hou, X.; Chen, L.; Suyama, S.; Asai, T. Ring-type Codebook Design for Reconfigurable Intelligent Surface Near-field Beamforming. In Proceedings of the 2022 IEEE 33rd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Kyoto, Japan, 12–15 September 2022; pp. 391–396. [Google Scholar] [CrossRef]
- Tian, X.; Gonzalez-Prelcic, N.; Heath, R.W. Variable Beamwidth Near Field Codebook Design for Communications Aided by A Large Scale RIS. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 2021–2026. [Google Scholar] [CrossRef]
- Wang, T.; Lv, J.; Tong, H.; You, C.; Yin, C. Near-Field Beam Training for Extremely Large-Scale IRS. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, W.; Pan, C.; Ren, H.; Shu, F.; Jin, S.; Wang, J. Low-Overhead Beam Training Scheme for Extremely Large-Scale RIS in Near Field. IEEE Trans. Commun. 2023, 71, 4924–4940. [Google Scholar] [CrossRef]
- Jiang, Y.; Gao, F.; Jian, M.; Zhang, S.; Zhang, W. Reconfigurable Intelligent Surface for Near Field Communications: Beamforming and Sensing. IEEE Trans. Wirel. Commun. 2023, 22, 3447–3459. [Google Scholar] [CrossRef]
- Björnson, E.; Demir, Ö.T.; Sanguinetti, L. A Primer on Near-Field Beamforming for Arrays and Reconfigurable Intelligent Surfaces. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 105–112. [Google Scholar] [CrossRef]
- Palmucci, S.; Guerra, A.; Abrardo, A.; Dardari, D. Two-Timescale Joint Precoding Design and RIS Optimization for User Tracking in Near-Field MIMO Systems. IEEE Trans. Signal Process. 2023, 71, 3067–3082. [Google Scholar] [CrossRef]
- Hu, S.; Wang, H.; Ilter, M.C. Design of Near-Field Beamforming for Large Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2024, 23, 762–774. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Kourtessis, P.; Chatzinotas, S.; Kaklamani, D.I.; Venieris, I.S. Near-Field Beamforming for Stacked Intelligent Metasurfaces-Assisted MIMO Networks. IEEE Wirel. Commun. Lett. 2024, 13, 3035–3039. [Google Scholar] [CrossRef]
- Gong, T.; Gavriilidis, P.; Ji, R.; Huang, C.; Alexandropoulos, G.C.; Wei, L.; Zhang, Z.; Debbah, M.; Poor, H.V.; Yuen, C. Holographic MIMO communications: Theoretical foundations, enabling technologies, and future directions. IEEE Commun. Surv. Tutor. 2023, 26, 196–257. [Google Scholar] [CrossRef]
- Iacovelli, G.; Sheemar, C.K.; Khan, W.U.; Mahmood, A.; Alexandropoulos, G.C.; Querol, J.; Chatzinotas, S. Holographic MIMO for Next Generation Non-Terrestrial Networks: Motivation, Opportunities, and Challenges. arXiv 2024, arXiv:2411.10014. [Google Scholar]
- Omam, Z.R.; Taghvaee, H.; Araghi, A.; Garcia-Fernandez, M.; Alvarez-Narciandi, G.; Alexandropoulos, G.C.; Yurduseven, O.; Khalily, M. Holographic Metasurfaces Enabling Wave Computing for 6G: Status Overview, Challenges, and Future Research Trends. arXiv 2025, arXiv:2501.05173. [Google Scholar]
- Deng, R.; Di, B.; Zhang, H.; Tan, Y.; Song, L. Reconfigurable holographic surface: Holographic beamforming for metasurface-aided wireless communications. IEEE Trans. Veh. Technol. 2021, 70, 6255–6259. [Google Scholar] [CrossRef]
- Deng, R.; Zhang, Y.; Zhang, H.; Di, B.; Zhang, H.; Poor, H.V.; Song, L. Reconfigurable holographic surfaces for ultra-massive MIMO in 6G: Practical design, optimization and implementation. IEEE J. Sel. Areas Commun. 2023, 41, 2367–2379. [Google Scholar] [CrossRef]
- Adhikary, A.; Raha, A.D.; Qiao, Y.; Saad, W.; Han, Z.; Hong, C.S. Holographic MIMO with integrated sensing and communication for energy-efficient cell-free 6G networks. IEEE Internet Things J. 2024, 11, 30617–30635. [Google Scholar] [CrossRef]
- Pizzo, A.; Marzetta, T.L.; Sanguinetti, L. Spatially-stationary model for holographic MIMO small-scale fading. IEEE J. Sel. Areas Commun. 2020, 38, 1964–1979. [Google Scholar] [CrossRef]
- Xu, J.; You, L.; Alexandropoulos, G.C.; Yi, X.; Wang, W.; Gao, X. Near-field wideband extremely large-scale MIMO transmissions with holographic metasurface-based antenna arrays. IEEE Trans. Wirel. Commun. 2024, 23, 12054–12067. [Google Scholar] [CrossRef]
- Ji, R.; Huang, C.; Chen, X.; Wei, E.; Dai, L.; He, J.; Zhang, Z.; Yuen, C.; Debbah, M. Electromagnetic hybrid beamforming for holographic MIMO communications. IEEE Trans. Wirel. Commun. 2024, 23, 15973–15986. [Google Scholar] [CrossRef]
- Gong, T.; Wei, L.; Huang, C.; Yang, Z.; He, J.; Debbah, M.; Yuen, C. Holographic MIMO communications with arbitrary surface placements: Near-field LoS channel model and capacity limit. IEEE J. Sel. Areas Commun. 2024, 42, 1549–1566. [Google Scholar] [CrossRef]
- He, J.; Huang, C.; Wei, L.; Xu, Y.; Al Hammadi, A.; Debbah, M. Technological evolution from RIS to holographic MIMO. In MIMO Communications-Fundamental Theory, Propagation Channels, and Antenna Systems; IntechOpen: London, UK, 2023. [Google Scholar]
- Zeng, S.; Zhang, H.; Di, B.; Qin, H.; Su, X.; Song, L. Reconfigurable refractive surfaces: An energy-efficient way to holographic MIMO. IEEE Commun. Lett. 2022, 26, 2490–2494. [Google Scholar] [CrossRef]
- Gong, T.; Wei, L.; Huang, C.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Near-field channel modeling for holographic MIMO communications. IEEE Wirel. Commun. 2024, 31, 108–116. [Google Scholar] [CrossRef]
- Ji, R.; Chen, S.; Huang, C.; Yang, J.; Wei, E.; Zhang, Z.; Yuen, C.; Debbah, M. Extra DoF of near-field holographic MIMO communications leveraging evanescent waves. IEEE Wirel. Commun. Lett. 2023, 12, 580–584. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Zhang, Y.; Yao, Y.; Liu, G. Capacity analysis of holographic MIMO channels with practical constraints. IEEE Wirel. Commun. Lett. 2023, 12, 1101–1105. [Google Scholar] [CrossRef]
- Wan, Z.; Zhu, J.; Dai, L. Can continuous aperture MIMO obtain more mutual information than discrete MIMO? IEEE Commun. Lett. 2023, 27, 3185–3189. [Google Scholar] [CrossRef]
- Wan, Z.; Zhu, J.; Dai, L. Can continuous aperture MIMO achieve much better performance than discrete MIMO? arXiv 2023, arXiv:2301.08411. [Google Scholar]
- Sayeed, A.; Behdad, N. Continuous aperture phased MIMO: Basic theory and applications. In Proceedings of the 2010 48th annual allerton conference on communication, control, and computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1196–1203. [Google Scholar]
- Ouyang, C.; Wang, Z.; Zhang, X.; Liu, Y. Performance of linear receive beamforming for continuous aperture arrays (CAPAs). arXiv 2024, arXiv:2411.06620. [Google Scholar]
- Sun, M.; Ouyang, C.; Wang, Z.; Wu, S.; Liu, Y. Secure Beamforming for Continuous Aperture Array (CAPA) Systems. arXiv 2025, arXiv:2501.04924. [Google Scholar]
- Zhao, B.; Ouyang, C.; Zhang, X.; Liu, Y. Physical Layer Security for Continuous-Aperture Array (CAPA) Systems. arXiv 2024, arXiv:2412.13748. [Google Scholar]
- Guo, J.; Liu, Y.; Shin, H.; Nallanathan, A. Deep learning for beamforming in multi-user continuous aperture array (CAPA) systems. arXiv 2024, arXiv:2411.09104. [Google Scholar]
- Taigbenu, A.E.; Onyejekwe, O.O. Green’s function-based integral approaches to nonlinear transient boundary-value problems (II). Appl. Math. Model. 1999, 23, 241–253. [Google Scholar] [CrossRef]
- Wang, T.; Kang, Z.; Li, T.; Chen, Z.; Wang, S.; Lin, Y.; Wang, Y.; Yu, Y. Electromagnetic Information Theory: Fundamentals, Paradigm Shifts, and Applications. arXiv 2025, arXiv:2503.06651. [Google Scholar]
- Gebremedhin, R.G.; Marzetta, T.L. Thermal conduction as a wireless communication channel. In Proceedings of the GLOBECOM 2022-2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1085–1090. [Google Scholar]
- Frank, R.; Lubatsch, A.; Kroha, J. Theory of strong localization effects of light in disordered loss or gain media. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 245107. [Google Scholar] [CrossRef]
- Wei, L.; Gong, T.; Huang, C.; Zhang, Z.; Sha, W.E.; Chen, Z.N.; Dai, L.; Debbah, M.; Yuen, C. Electromagnetic information theory for holographic MIMO communications. arXiv 2024, arXiv:2405.10496. [Google Scholar]
- Bidabadi, S.; Ouameur, M.; Bagaa, M.; Massicotte, D.; Figueiredo, F.; Chaaban, A. Physically-consistent EM models-aware RIS-aided communication—A survey. Comput. Netw. 2025, 257, 110963. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, L. Pattern-division multiplexing for continuous-aperture MIMO. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 3287–3292. [Google Scholar]
- Di Renzo, M.; Migliore, M.D. Electromagnetic signal and information theory. IEEE BITS Inf. Theory Mag. 2024. [Google Scholar] [CrossRef]
- Li, R.; Li, D.; Ma, J.; Feng, Z.; Zhang, L.; Tan, S.; Sha, W.E.; Chen, H.; Li, E.P. An electromagnetic information theory based model for efficient characterization of MIMO systems in complex space. IEEE Trans. Antennas Propag. 2023, 71, 3497–3508. [Google Scholar] [CrossRef]
- Lyu, R.; Cheng, W.; Du, Q.; Quek, T.Q. Capacity Analysis on OAM-Based Wireless Communications: An Electromagnetic Information Theory Perspective. arXiv 2024, arXiv:2412.11524. [Google Scholar]
- Wan, Z.; Zhu, J.; Dai, L. Near-field channel modeling for electromagnetic information theory. IEEE Trans. Wirel. Commun. 2024, 23, 18004–18018. [Google Scholar] [CrossRef]
- Wan, Z.; Zhu, J.; Dai, L. Electromagnetic Information Theory Motivated Near-Field Channel Model. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 7–12 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1800–1805. [Google Scholar]
- Wan, Z.; Zhu, J.; Zhang, Z.; Dai, L. Capacity for electromagnetic information theory. arXiv 2021, arXiv:2111.00496. [Google Scholar]
- Zhu, J.; Tan, V.Y.; Dai, L. MIMO capacity analysis and channel estimation for electromagnetic information theory. arXiv 2024, arXiv:2406.04881. [Google Scholar]
- Zhu, J.; Su, X.; Wan, Z.; Dai, L.; Cui, T.J. The benefits of electromagnetic information theory for channel estimation. In Proceedings of the ICC 2024-IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 4869–4874. [Google Scholar]
- Zhu, J.; Wan, Z.; Dai, L.; Cui, T.J. Electromagnetic Information Theory-Based Statistical Channel Model for Improved Channel Estimation. IEEE Trans. Inf. Theory 2025, 71, 1777–1793. [Google Scholar] [CrossRef]

| Abbr. | Full Form | Abbr. | Full Form |
|---|---|---|---|
| 3GPP | 3rd Generation Partnership Project | ADC | Analog-to-Digital Converter |
| AoAs | Angles of Arrival | BA | Beam Alignment |
| BER | Bit Error Rate | BS | Base Station |
| CAP | Continuous Aperture Phased | CAGR | Compound Annual Growth Rate |
| CAP-RISs | Continuous Aperture RISs | CLA | Cylindrical Antenna Array |
| CNN | Convolutional Neural Network | CRB | Cramér–Rao Bound |
| CS | Compressed Sensing | CSI | Channel State Information |
| D-NFCE | Deep-Learning-based Near-field Channel Estimation | DAC | Digital-to-Analog Converters |
| DFT | Discrete Fourier Transform | DMAs | Dynamic Metasurface Antennas |
| DoF | Degrees of Freedom | DPP | Delay Phase Precoding |
| EIT | Electromagnetic Information Theory | FSBL | Fast Sparse Bayesian Learning |
| FUs | Far-Field Users | GNN | Graph Neural Network |
| GS | Gerchberg–Saxton | HMA | Holographic Metasurface Antennas |
| HMIMO | Holographic MIMO | IOSs | Intelligent Omnisurfaces |
| ISAC | Integrated Sensing and Communication | LISs | Large Intelligent Surfaces |
| LISTA | Learning Iterative Shrinkage and a Thresholding Algorithm | LoS | Line of Sight |
| LS | Least Squares | MIMO | Multiple-input Multiple-output |
| MSE | Mean Square Error | MUSIC | Multiple Signal Classification |
| MVs | Mobile Vehicles | NB | Near-Field Beamsquint |
| NF | Near Field | NF-JCEL | Near-Field Channel Estimation and Localization |
| NOMA | Non-Orthogonal Multiple Access | NUs | Near-Field Users |
| OMP | Orthogonal Matching Pursuit | OFDM | Orthogonal Frequency Division Multiplexing |
| PD | Power Diffusion | PD-OMP | Power Diffusion aware Orthogonal Matching Pursuit |
| Phase Delay Focusing | PF-RCE | Polar-domain Frequency-dependent RIS-assisted Channel Estimation | |
| P-SOMP | Polar-domain Simultaneous Orthogonal Matching Pursuit | PWE | Plane Wave Expansion |
| QoS | Quality of Service | RCRB | Root of Cramér–Rao Bound |
| RF | Radio Frequency | RIS | Reconfigurable Intelligent Surface |
| R-LS | Regularized Least Squares | SA-RIS | Subarray-based RIS |
| SIMs | Stacked Intelligent Metasurfaces | SINR | Signal-to-Interference-plus-Noise Ratio |
| SNR | Signal-to-Noise Ratio | STT | Sense-then-Train |
| THz | Terahertz | TPBE | Two-phase Angle and Distance Beam Estimator |
| ToI | Targets of Interest | TTD-RIS | True Time Delay RIS |
| UE | User Equipment | ULA | Uniform Linear Array |
| ULAAs | Ultra-large-scale Antenna Arrays | UPA | Uniform Planar Array |
| UPW | Uniform Plane Wave | V2V | Vehicle-to-Vehicle |
| VR | Visual Region | XL | Extremely Large-scale |
| XL-IRS | Extremely Large-scale Intelligent Reflecting Surface | XLARIS | Extremely Large-scale Aerial RIS |
| Aspect | Challenges | Opportunities |
|---|---|---|
| Channel Modeling and Estimation | Spherical wave models complicate channel modeling and estimation. Distance-dependent channel variations increase and computational complexity increases. | Higher channel rank and distance-dependent channel variations enable higher multiplexing gains. |
| Beamforming and Beamtraining | Beamtraining is hard because the codebook size increases owing to the dual angular and distance sampling. The expanded codebook search space increases training overhead and computational complexity. | The dual angular and distance sampling creates beamfocusing opportunities that realize precise energy focusing in 3D spaces. This enables higher channel and system capacity. |
| Mutual Coupling Effects | Densely positioned antenna elements distort radiation patterns and reduce spatial multiplexing. | Advanced antenna isolation techniques can mitigate coupling and enhance system efficiency. |
| Interference Management | Complex interference patterns owing to the spherical wave model which require both angular and distance separation for interference mitigation. | Enhanced spatial DoF provide fine-grained control of interference and improve spectral efficiency. |
| Hardware Implementation | Higher computational complexity, which increases power consumption and requires high-precision RF chain components with extreme synchronization across large antenna arrays. | Energy-efficient hardware can enable feasible near-field signal processing and improve system performance. |
| Type | Work | Methodology | Motivation |
|---|---|---|---|
| Codebook Design | [60,61,62,63,64,65,66,67] | NF Wavefront Modeling, DFT-Based Beam Optimization, and Beam Gain and Correlation Control | Conventional codebook designs are not valid in near-field systems as the spherical wavefront is not negligible, and the computational overhead is infeasible. |
| Beamtraining designs | [68,69,70,71] | Hybrid-field Training, Learning-Driven Codeword Optimization, and Vision-Aided Multimodal Sensing | Conventional beamtraining algorithms do not consider the range domain, and exhaustive search algorithms have high pilot overheads. |
| Hierarchical designs | [18,72,73,74,75,76,77] | Hierarchical Spatial Partitioning, DFT Off-Grid Hybridization, and Modular Leakage-Aware Optimization | Practical environments cannot have exhaustive angle and range designs. These domains should be resolved independently to enable feasible overheads. |
| Deep learning | [28,78,79] | Neural-Driven Training, Cross-Signal Codeword Estimation, and Hybrid Architecture Optimization | Conventional beamtraining and codebook designs can have high processing and pilot overheads. Data-driven and reinforcement-learning-based designs can mitigate these challenges. |
| Wideband, THz, and mmWave designs | [80,81,82,83,84,85] | Beamsplit Exploitation, Sparse Codebook Design, and Hybrid Domain Training | THz, mmWave, and wideband systems have non-negligible near-field effects. Conventional beamtraining and codebook designs are not feasible for these systems. |
| Sensing-based designs | [86,87] | Position-Aware Bayesian Adaptation and Active Sensing Optimization | The range information of near-field systems can assist in codebook design and beamtraining. |
| Type | Work | Methodology | Motivation |
|---|---|---|---|
| Designs for sensing and communication | [37,88,89,90,91,92] | CRB-Driven Sensing-Comms Integration, Sparse Transceiver Architectures, Multidimensional Near-Field Differentiation, SINR-QoS Co-optimization Frameworks, Hybrid Antenna Optimization, and Predictive Beamforming | Integrated sensing and communication systems experience higher levels of interference and demand precise beamforming for successful dual functioning. |
| Near-field precoding | [93,94] | NOMA-Based Hybrid Field Coexistence, HMA Array Design and Precoder-Weighting Optimization, and Iterative Algorithms for HMA Optimization | Precise beamfocusing is challenging in near-field systems owing to the joint angle-range dependence of the channel, which results in high computational complexity. |
| Wideband, THz, and mmWave designs | [3,23,95,96,97] | Wideband Phase-Delay Correction, Frequency-Adaptive RIS Architectures, THz UM-MIMO System Design, and Decomposed Optimization Frameworks | Designing beams for mmWave and THz systems is challenging owing to the wide bandwidth of these systems. The wideband links may have optimized beams at the center frequency but have poor performance at frequencies that are further from the central frequency. |
| Physical layer security | [98,99,100] | Near-Field Security Parameter Analysis, Hybrid Beamforming for Secure Transmission, Distance-Domain Security Exploitation, and Eavesdropper Antenna Impact Mitigation | The high spatial multiplexing gains of near-field systems can enable advanced security features such as increased eavesdropping protection and jamming using precise beamforming. |
| Type | Work | Methodology | Motivation |
|---|---|---|---|
| Near-field | [44,103,104,105,106] | Geometry-Aided Pilot Reduction, Unsupervised Bayesian Learning, Sparsity-Driven Polar-Domain Estimation, Parametric MUSIC Enhancement, and Optimized Codebook Algorithms | Accurate channel estimation is necessary to enable high spectral efficiency of near-field systems. |
| Hybrid-Field | [48,107,108,109] | PD Mitigation, Dynamic Subarray Modeling, Hybrid-Field Component Separation, and Neural Network Joint Optimization | Conventional near-field or far-field only channel estimation methods are not suitable for hybrid near–far field communications realized by large-scale antenna arrays where the users and scatterers are randomly situated in both near-field and far-field zones. |
| NLoS/LoS | [110,111,112,113] | LoS/NLoS Path Decoupling, Theoretical Performance Bounds, Low-Rank Collaborative Estimation, and Condition-Adaptive Algorithms | Practical environments are not only limited to LoS links. Accurate channel estimation of mixed LoS/NLoS near-field systems is required for feasible deployments. |
| XL-MIMO | [47,114,115,116] | Parameter Decoupling with 2D-DFT, Polar-Domain Sparsity Exploitation, and Compressed Sensing with Deep Learning | Effective beamforming requires accurate CSI estimation, which is challenging in XL-MIMO owing to the extremely high pilot overhead. |
| THz or mmWave | [117,118,119,120,121] | Polar-Domain and Wideband Sparsity Exploitation, Deep Learning-Driven Parameter Extraction, Sparse Bayesian Learning for Hybrid Models, Covariance Matrix Decoupling, and NB-aware OMP and Federated Learning | THz and mmWave systems undergo severe attenuation. Large arrays are required to form feasible directed beams, which require precise channel estimation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, H.; Anjum, M.; Mishra, D.; Seneviratne, A. Energy-Efficient Near-Field Beamforming: A Review on Practical Channel Models. Energies 2025, 18, 2966. https://doi.org/10.3390/en18112966
Ni H, Anjum M, Mishra D, Seneviratne A. Energy-Efficient Near-Field Beamforming: A Review on Practical Channel Models. Energies. 2025; 18(11):2966. https://doi.org/10.3390/en18112966
Chicago/Turabian StyleNi, Haoran, Mahnoor Anjum, Deepak Mishra, and Aruna Seneviratne. 2025. "Energy-Efficient Near-Field Beamforming: A Review on Practical Channel Models" Energies 18, no. 11: 2966. https://doi.org/10.3390/en18112966
APA StyleNi, H., Anjum, M., Mishra, D., & Seneviratne, A. (2025). Energy-Efficient Near-Field Beamforming: A Review on Practical Channel Models. Energies, 18(11), 2966. https://doi.org/10.3390/en18112966








