Study on Flow and Heat Transfer Characteristics of Battery Thermal Management System with Supercritical CO2 for Energy Storage Stations
Abstract
1. Introduction
2. Geometry and Numerical Methods
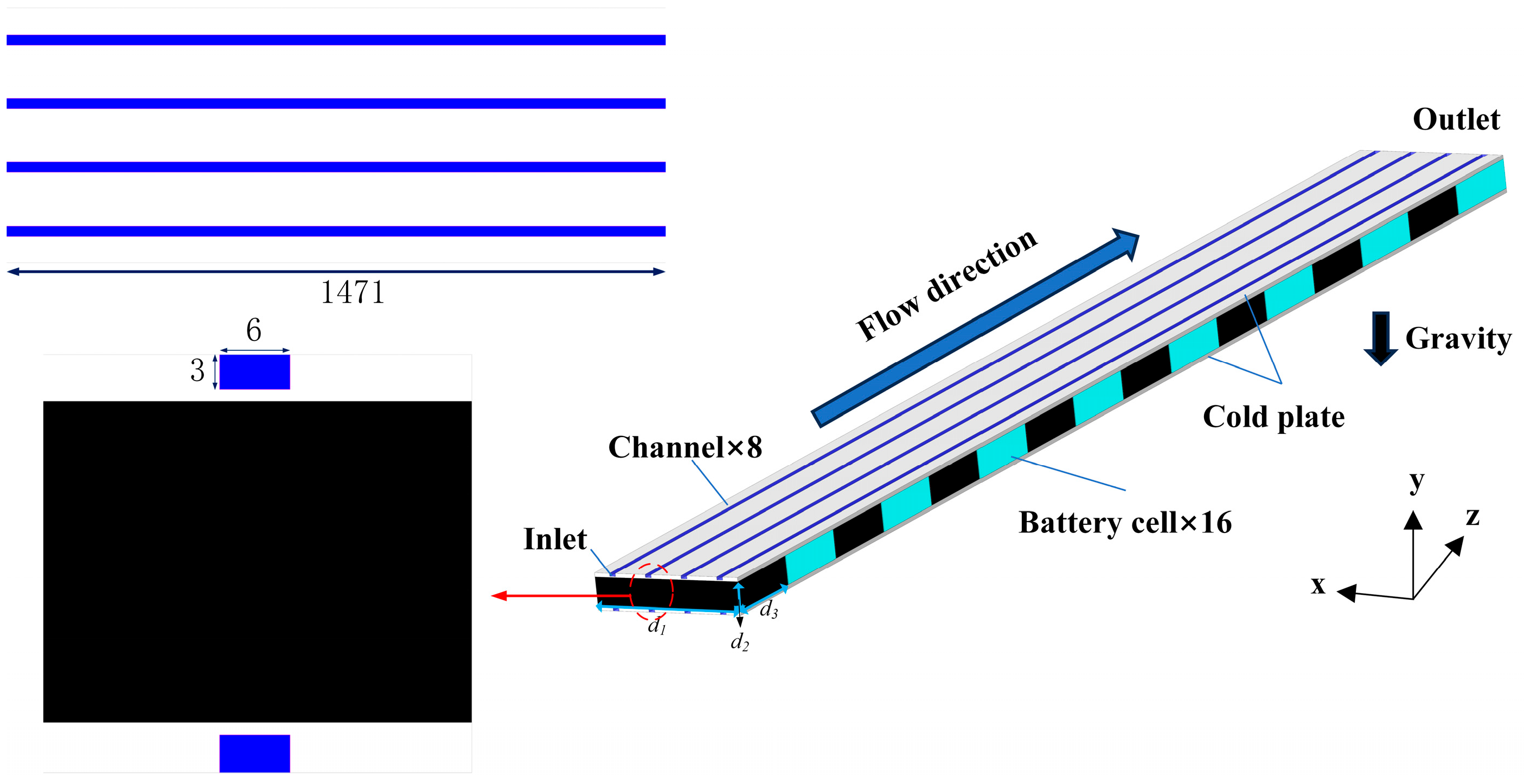
2.1. Geometrical Model
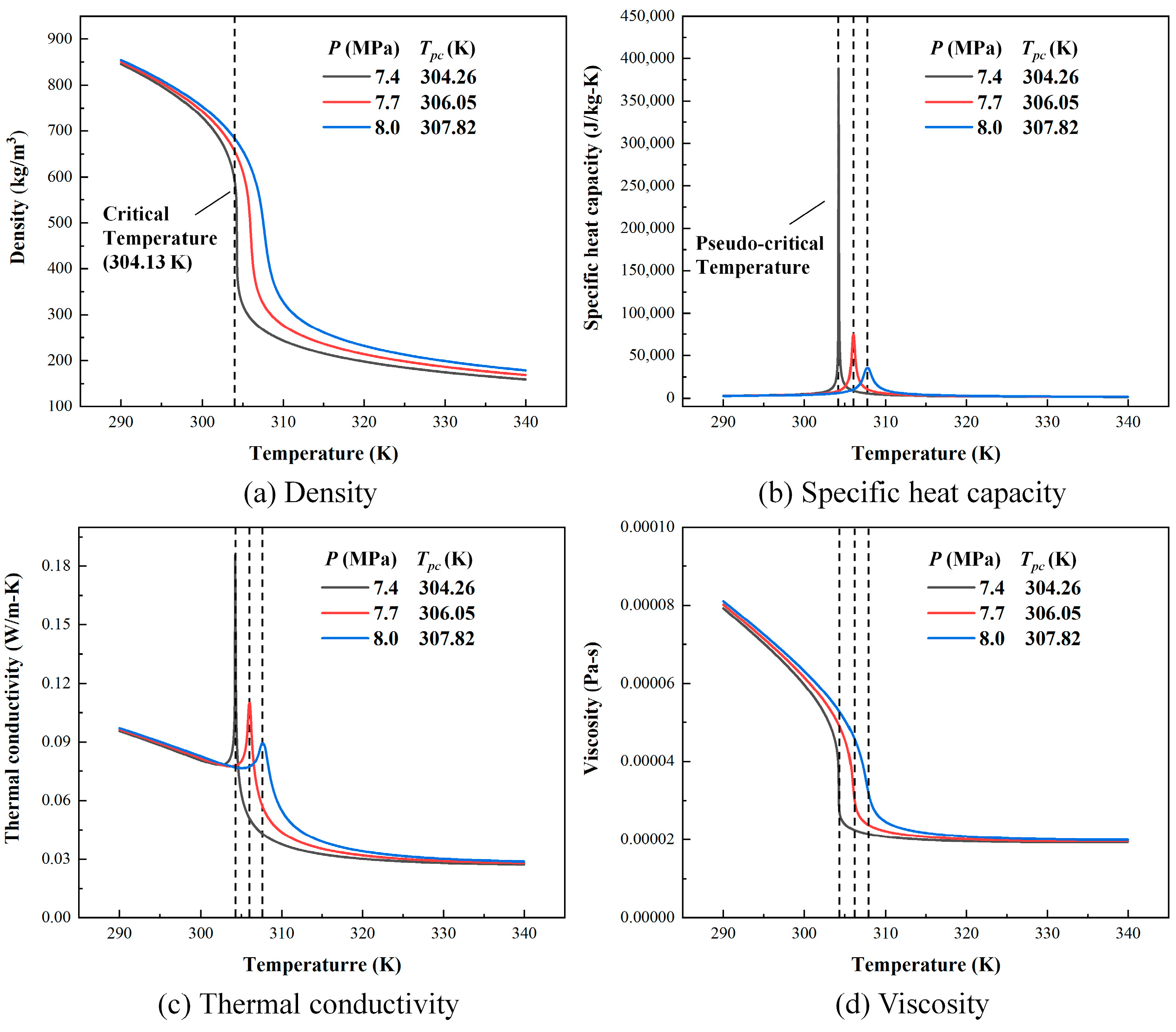
2.2. Governing Equations
2.3. Parameter Definition
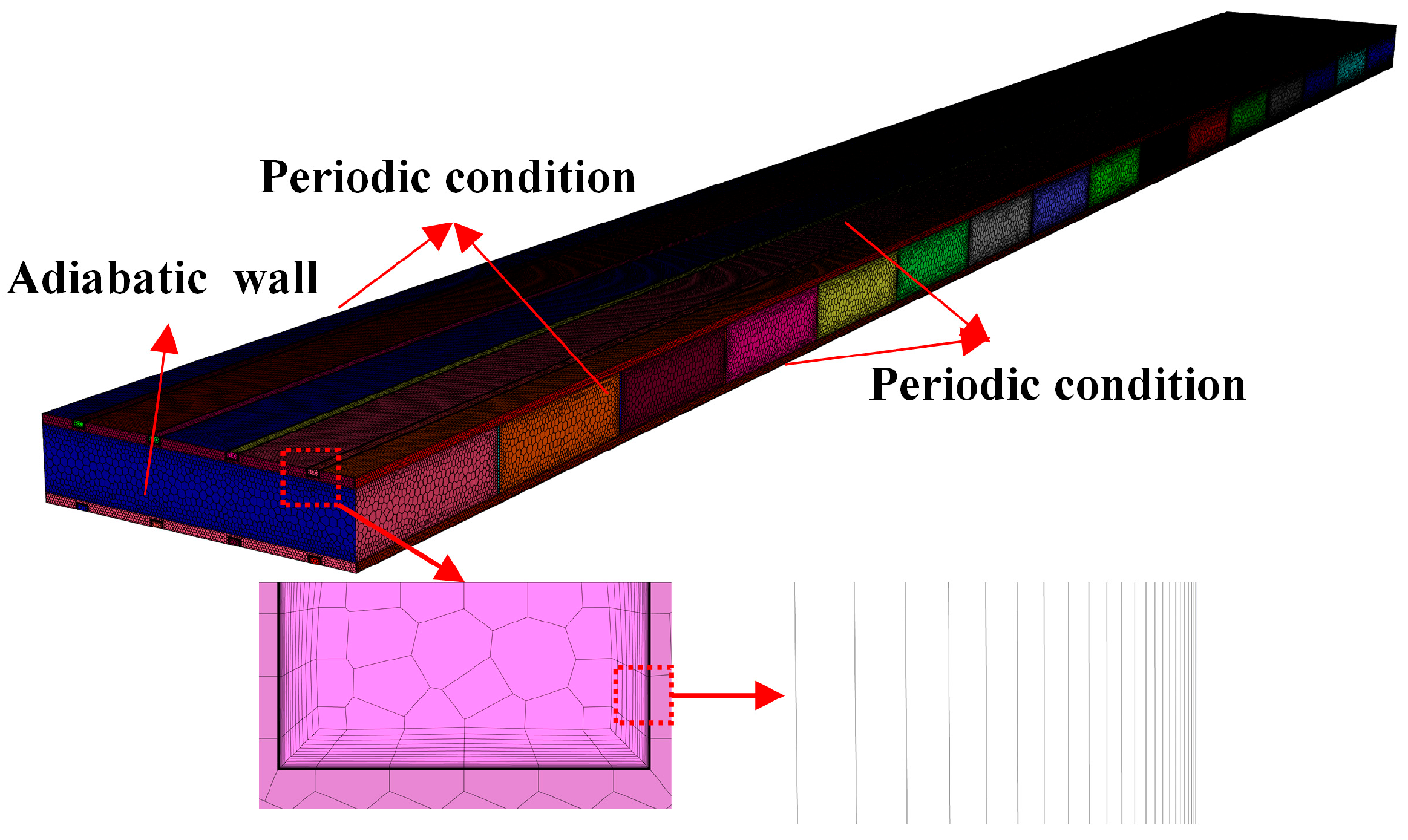
2.4. Boundary Conditions
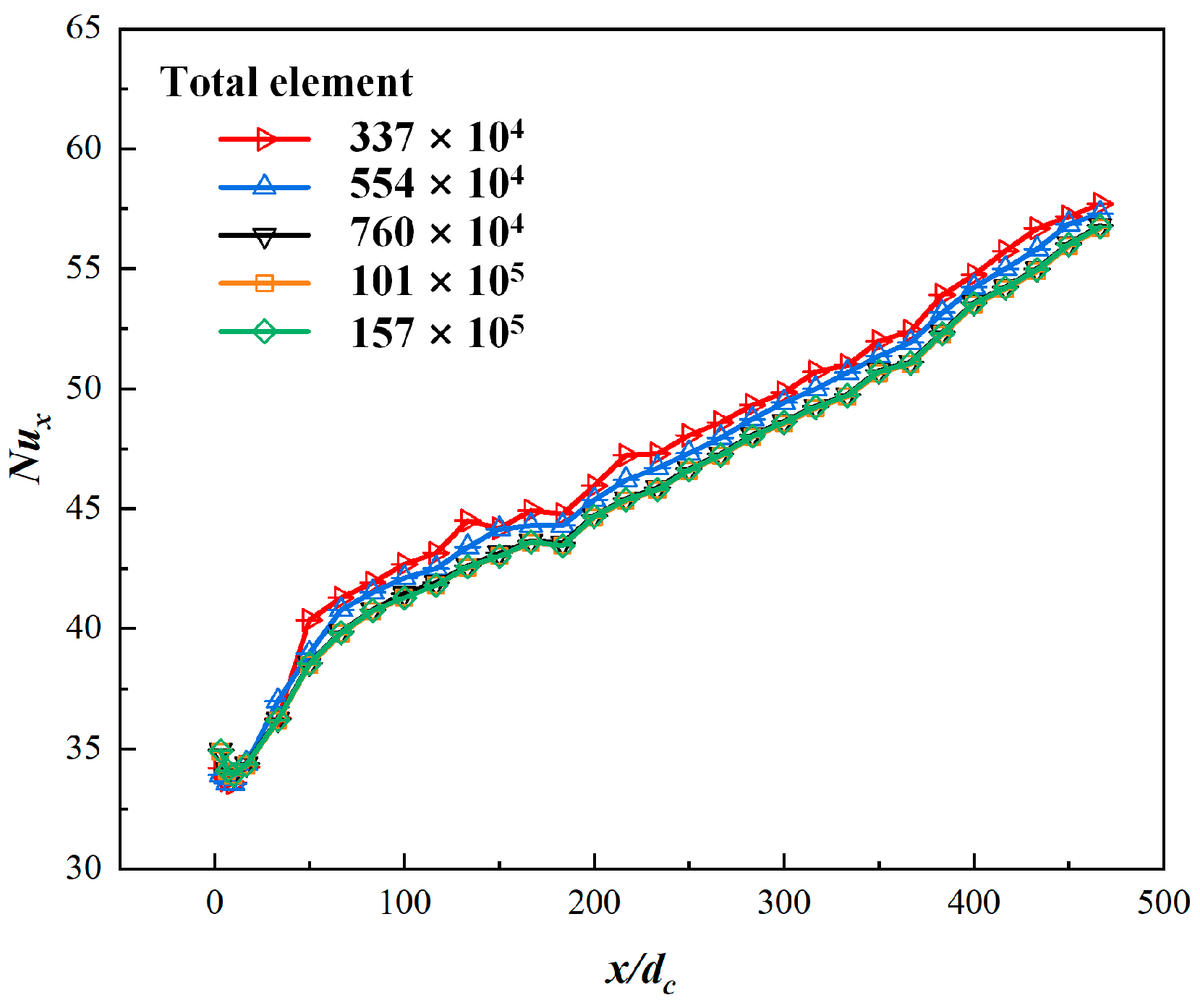
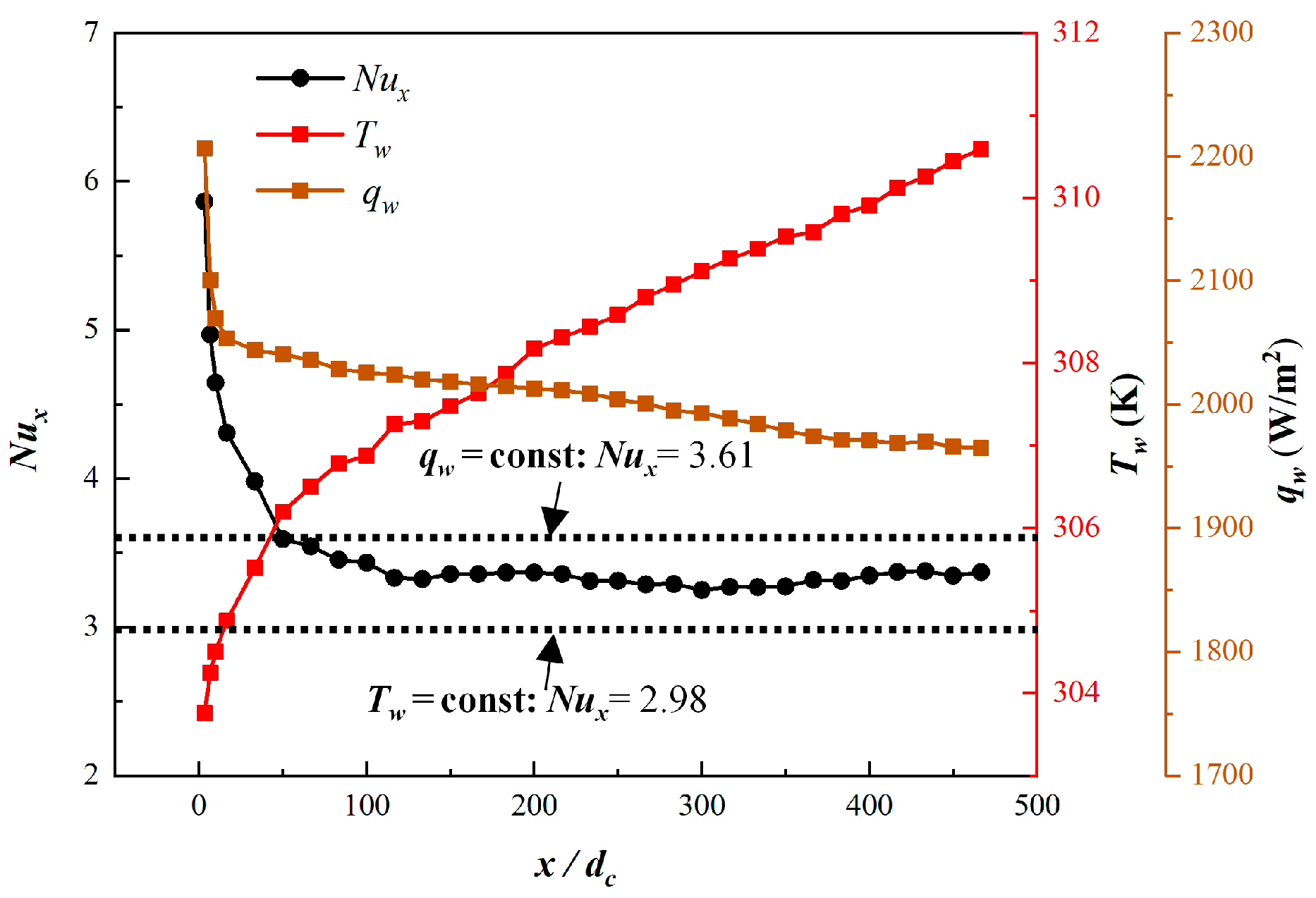
2.5. Grid Independence Tests and Validation
3. Results and Discussion
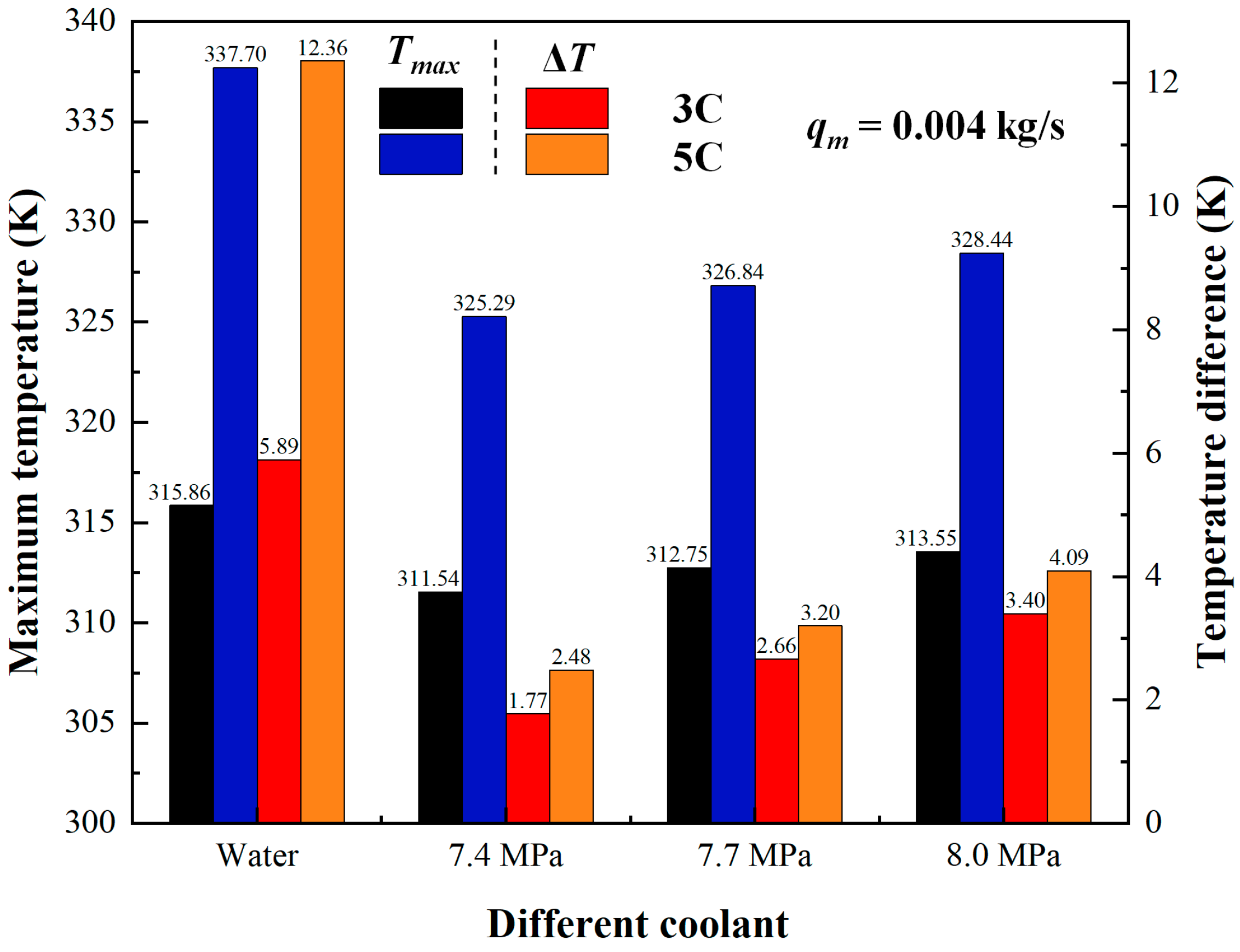
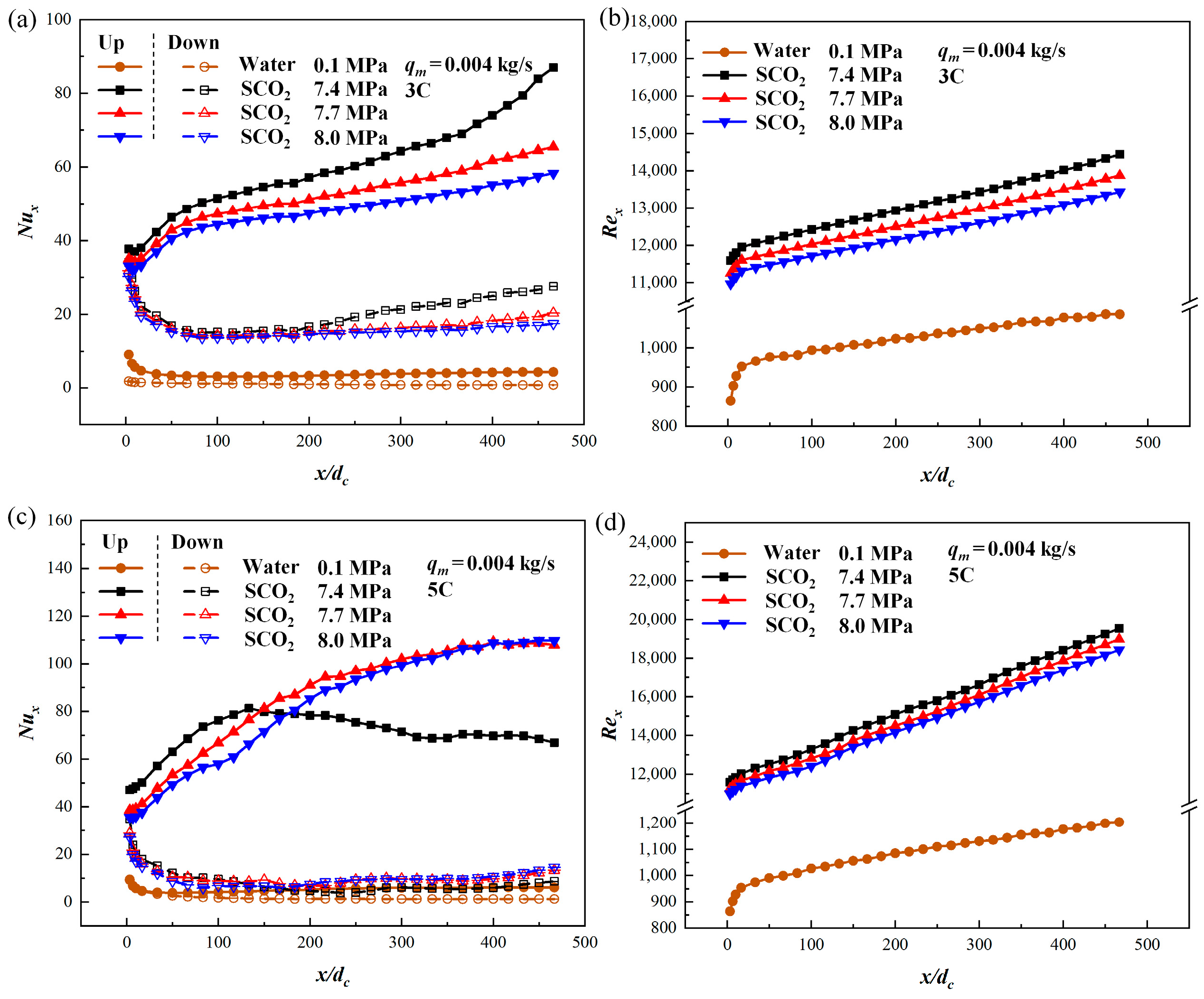
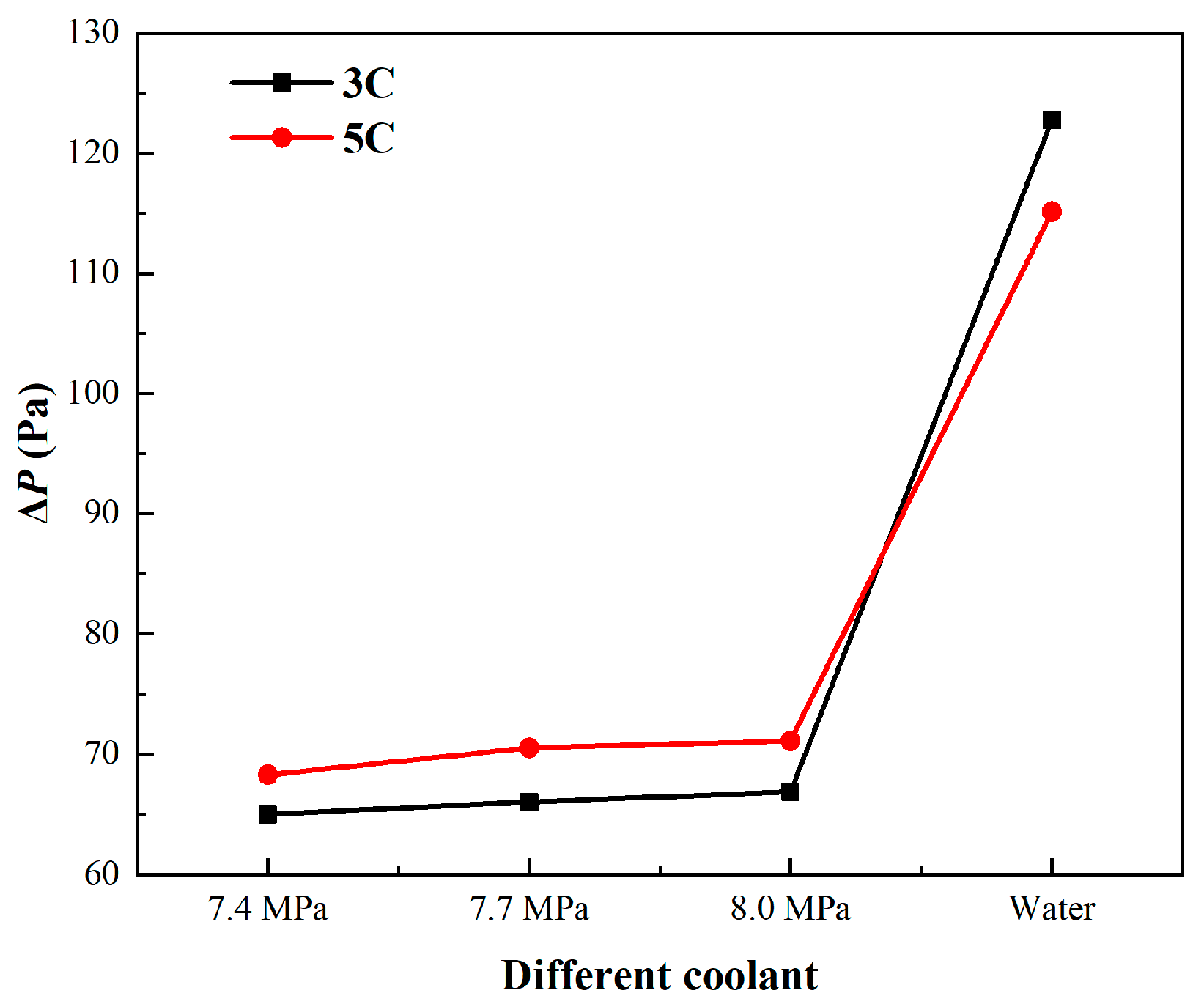
3.1. Comparison of SCO2 with Water
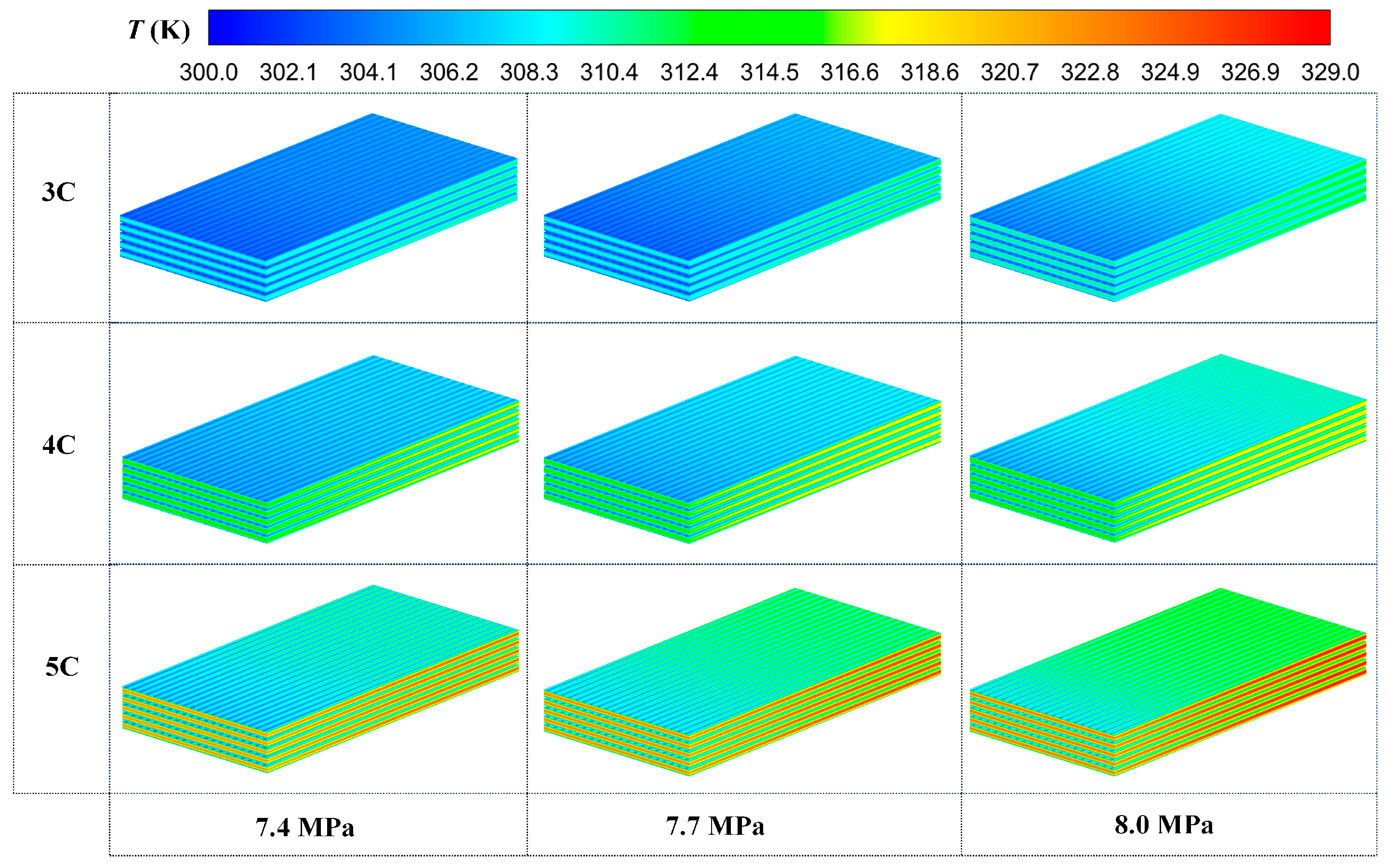
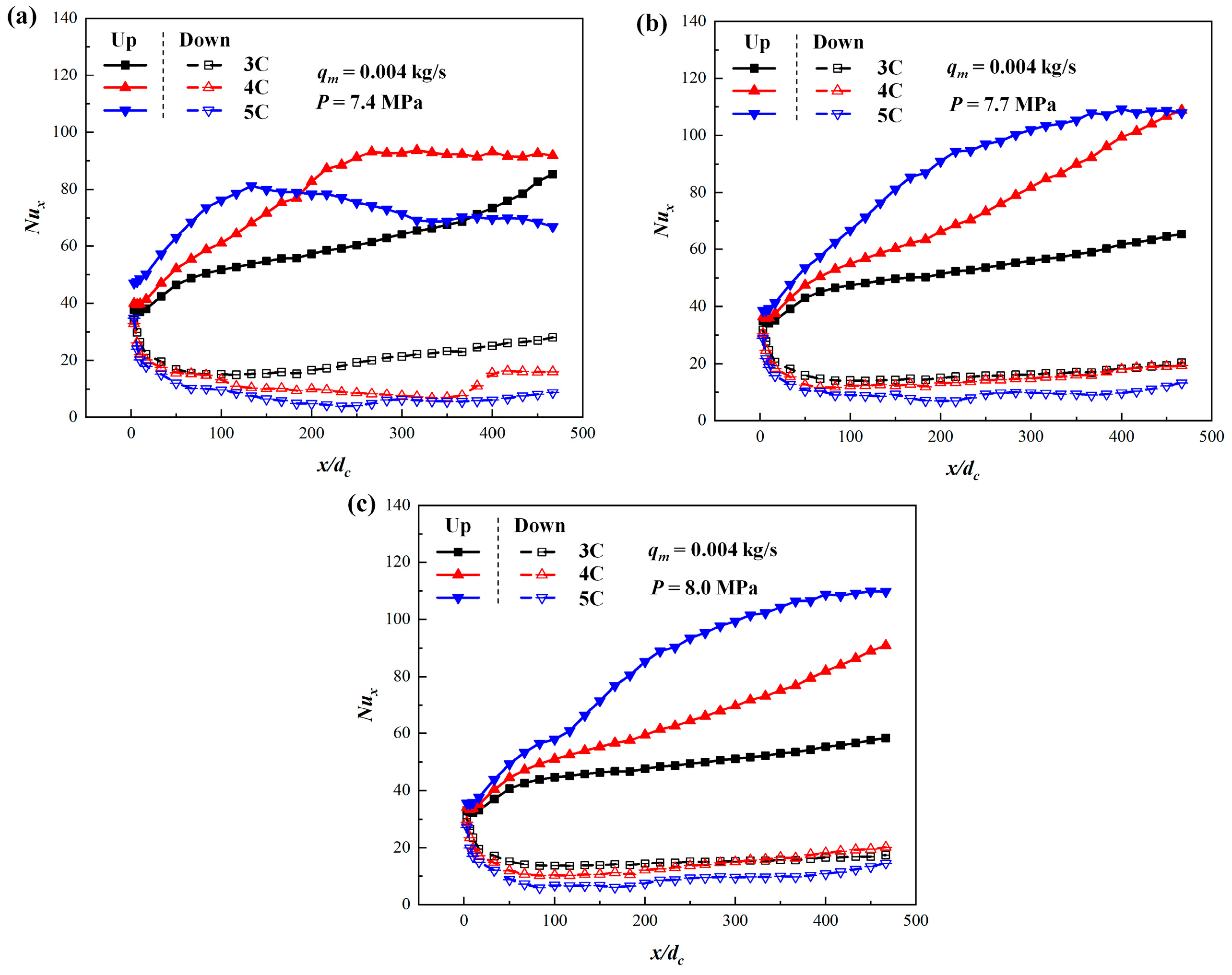
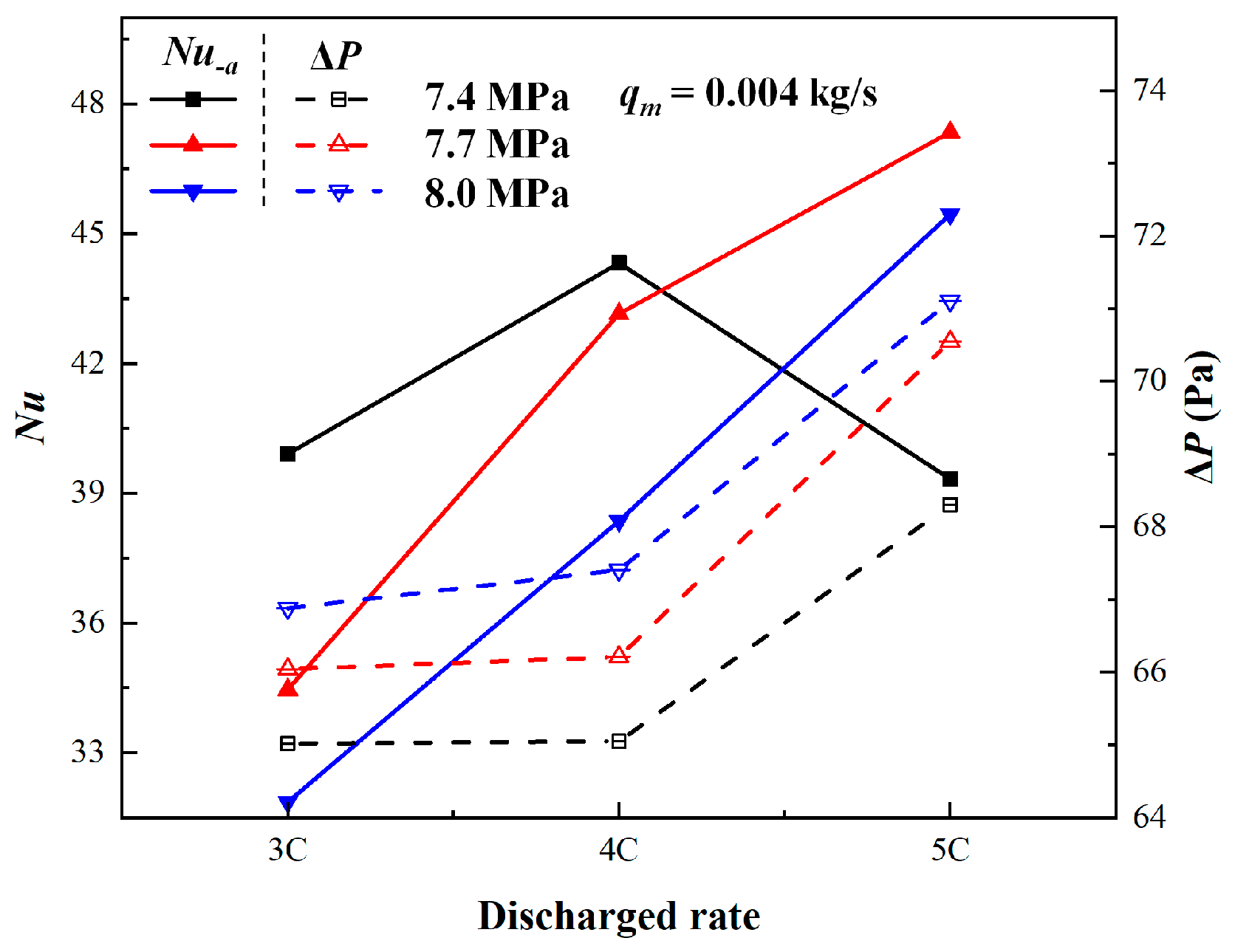
3.2. Comparison of Different Discharge Rates
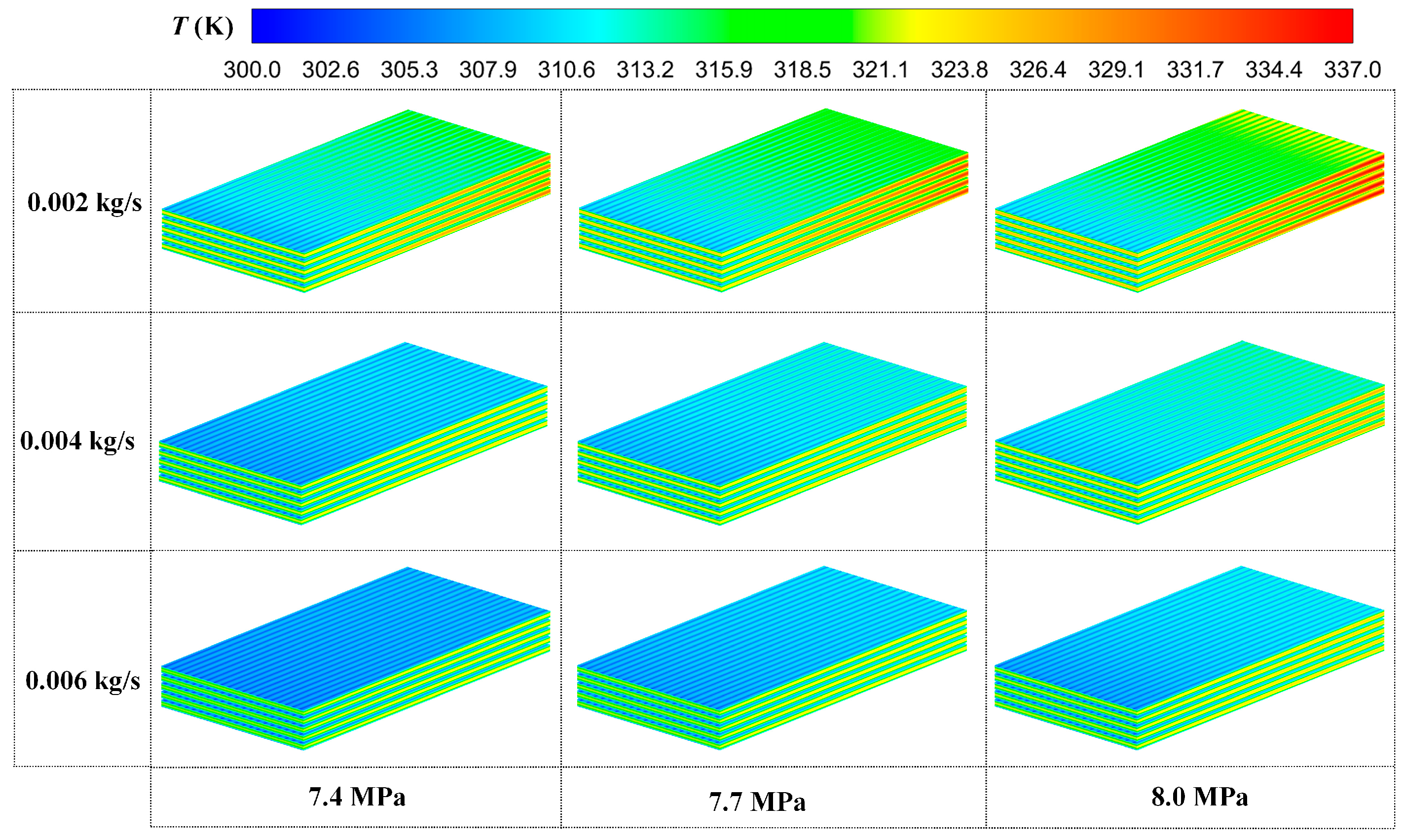
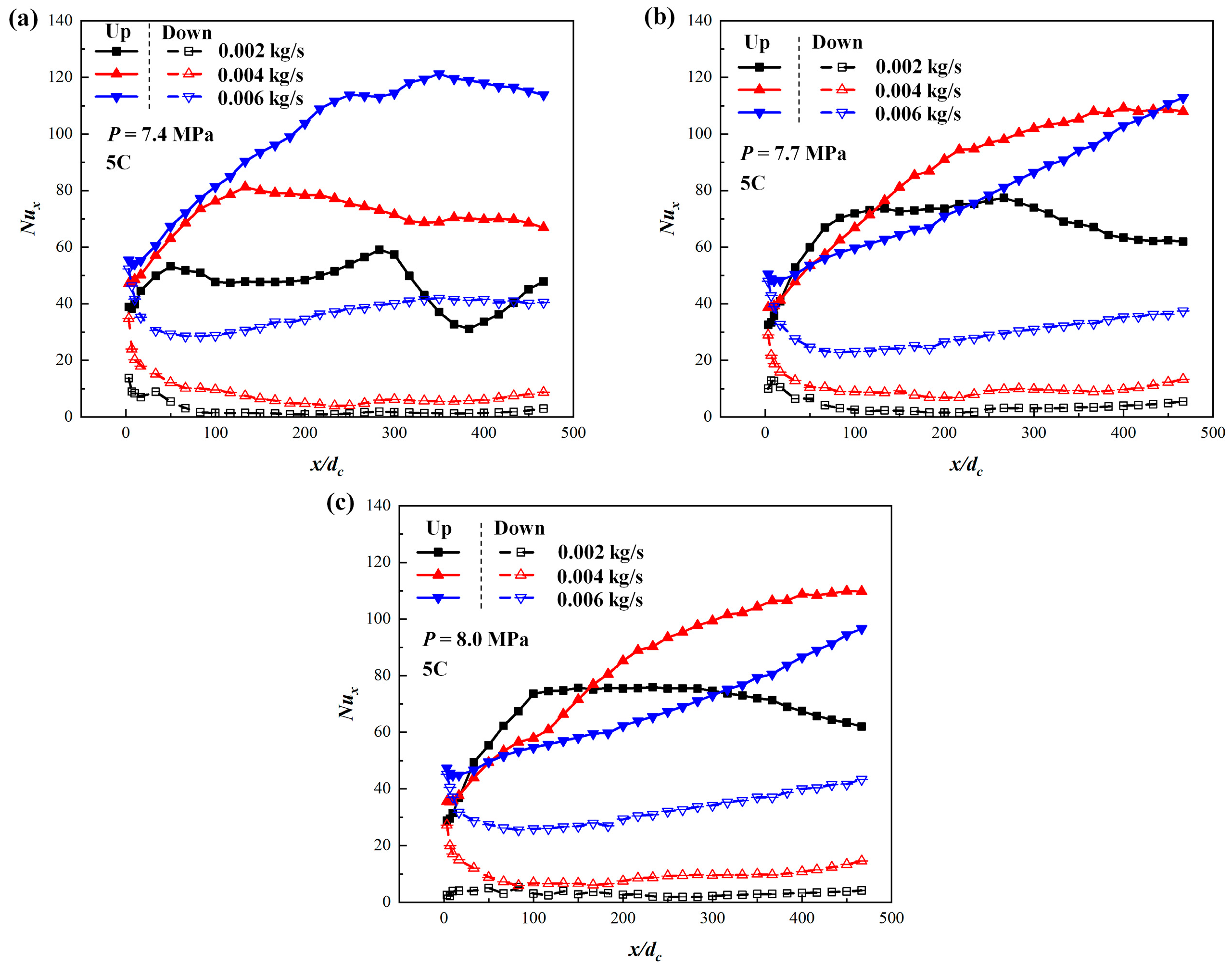
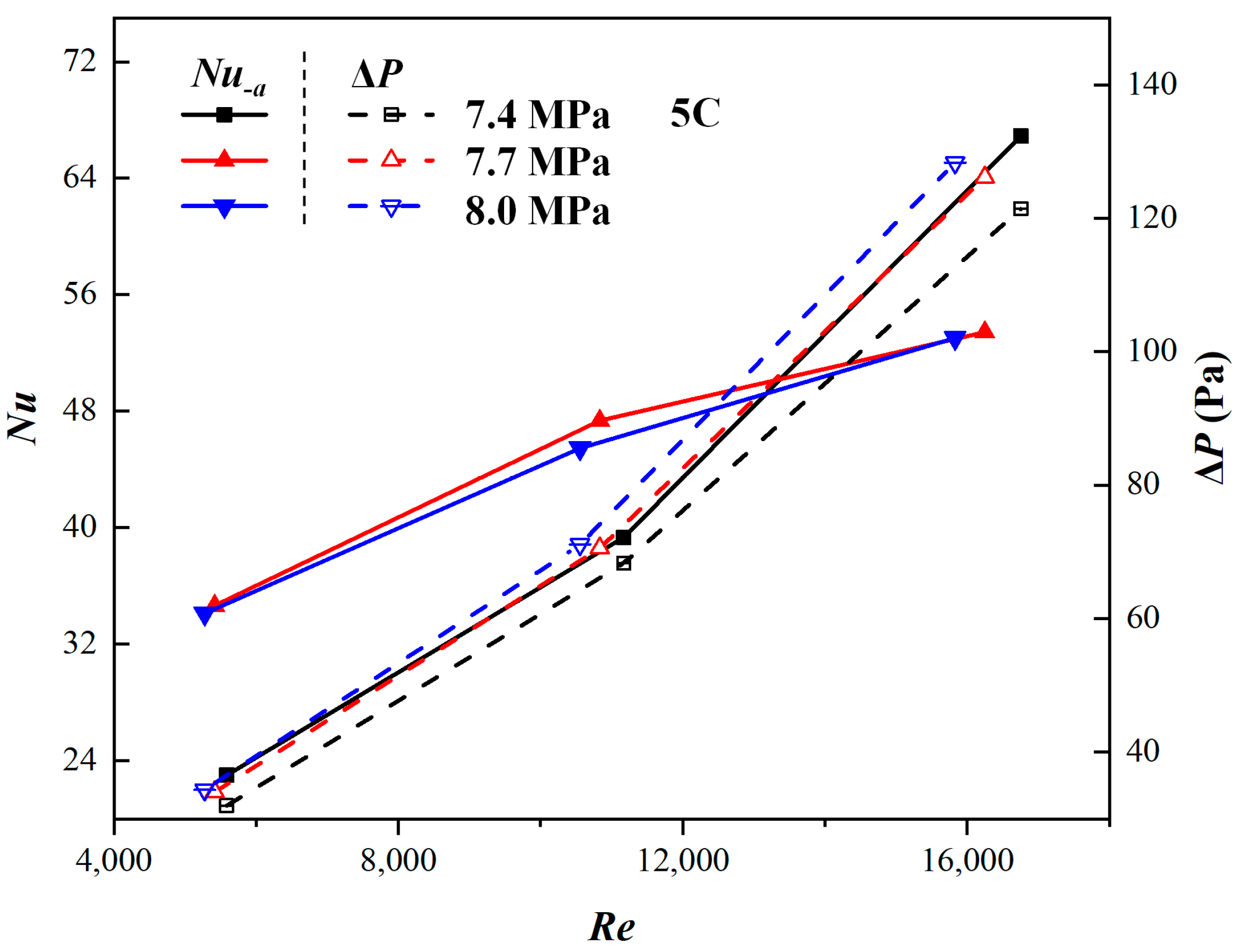
3.3. Comparison of Different Mass Flow Rates of Coolant
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BTMS | Battery thermal management system |
| ESS | Energy storage station |
| LCP | Liquid cold plate |
| SCO2 | Supercritical carbon dioxide |
References
- Darcovich, K.; MacNeil, D.D.; Recoskie, S.; Cadic, Q.; Ilinca, F. Comparison of Cooling Plate Configurations for Automotive Battery Pack Thermal Management. Appl. Therm. Eng. 2019, 155, 185–195. [Google Scholar] [CrossRef]
- Hannan, M.A.; Al-Shetwi, A.; Begum, R.A.; Young, S.E.; Hoque, M.M.; Ker, P.; Alzaareer, K. The Value of Thermal Management Control Strategies for Battery Energy Storage in Grid Decarbonization: Issues and Recommendations. J. Clean. Prod. 2020, 276, 124223. [Google Scholar] [CrossRef]
- Elaadouli, N.; Lajouad, R.; El Magri, A.; Mansouri, A.; Elmezdi, K. Adaptive Control Strategy for Energy Management in a Grid-Connected Battery Energy Storage System Using a Bidirectional Vienna Rectifier. J. Energy Storage 2024, 104, 114382. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Saleem, M.S.; Kalair, A.R.; Khan, N. Role of Energy Storage Systems in Energy Transition from Fossil Fuels to Renewables. Energy Storage 2021, 3, e135. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal Issues about Li-Ion Batteries and Recent Progress in Battery Thermal Management Systems: A Review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety Issues and Mechanisms of Lithium-Ion Battery Cell upon Mechanical Abusive Loading: A Review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Borah, R.; Hughson, F.R.; Johnston, J.; Nann, T. On Battery Materials and Methods. Mater. Today Adv. 2020, 6, 100046. [Google Scholar] [CrossRef]
- Shahjalal, M.; Shams, T.; Islam, M.E.; Alam, W.; Modak, M.; Hossain, S.B.; Iqbal, A. A Review of Thermal Management for Li-Ion Batteries: Prospects, Challenges, and Issues. J. Energy Storage 2021, 39, 102518. [Google Scholar] [CrossRef]
- Ahmed, D.; Ebeed, M.; Ali, A.; Alghamdi, A.S.; Kamel, S. Multi-Objective Energy Management of a Micro-Grid Considering Stochastic Nature of Load and Renewable Energy Resources. Electronics 2021, 10, 403. [Google Scholar] [CrossRef]
- Xie, J.; Ge, Z.; Zang, M.; Wang, S. Structural Optimization of Lithium-Ion Battery Pack with Forced Air Cooling System. Appl. Therm. Eng. 2017, 126, 583–593. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Khattari, Y.; Lamrani, B.; Maaroufi, M.; Zeraouli, Y.; Kousksou, T. Key Challenges for a Large-Scale Development of Battery Electric Vehicles: A Comprehensive Review. J. Energy Storage 2021, 44, 103273. [Google Scholar] [CrossRef]
- Li, Y.; Du, Y.; Xu, T.; Wu, H.; Zhou, X.; Ling, Z.; Zhang, Z. Optimization of Thermal Management System for Li-Ion Batteries Using Phase Change Material. Appl. Therm. Eng. 2018, 131, 766–778. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, F.; Fang, X.; Gao, X.; Zhang, Z. A Hybrid Thermal Management System for Lithium-Ion Batteries Combining Phase Change Materials with Forced-Air Cooling. Appl. Energy 2015, 148, 403–409. [Google Scholar] [CrossRef]
- Weragoda, D.M.; Tian, G.; Burkitbayev, A.; Lo, K.H.; Zhang, T. A Comprehensive Review on Heat Pipe Based Battery Thermal Management Systems. Appl. Therm. Eng. 2023, 224, 120070. [Google Scholar] [CrossRef]
- Mei, N.; Xu, X.; Li, R. Heat Dissipation Analysis on the Liquid Cooling System Coupled with a Flat Heat Pipe of a Lithium-Ion Battery. ACS Omega 2020, 5, 17431–17441. [Google Scholar] [CrossRef]
- Xia, G.; Cao, L.; Bi, G. A Review on Battery Thermal Management in Electric Vehicle Application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Tan, X.; Lyu, P.; Fan, Y.; Rao, J.; Ouyang, K. Numerical Investigation of the Direct Liquid Cooling of a Fast-Charging Lithium-Ion Battery Pack in Hydrofluoroether. Appl. Therm. Eng. 2021, 196, 117279. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, Q.; Wang, G.; Gu, Y.; Wang, Y.; Bao, W.; Zhang, D. Investigation on the Promotion of Temperature Uniformity for the Designed Battery Pack with Liquid Flow in Cooling Process. Appl. Therm. Eng. 2017, 116, 655–662. [Google Scholar] [CrossRef]
- Xu, J.; Guo, Z.; Xu, Z.; Zhou, X.; Mei, X. A Systematic Review and Comparison of Liquid-Based Cooling System for Lithium-Ion Batteries. eTransportation 2023, 17, 100242. [Google Scholar] [CrossRef]
- Hall, W.B. Heat Transfer near the Critical Point. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1971; Volume 7, pp. 1–86. [Google Scholar]
- Austin, B.T.; Sumathy, K. Transcritical Carbon Dioxide Heat Pump Systems: A Review. Renew. Sustain. Energy Rev. 2011, 15, 4013–4029. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J. Application of Supercritical Carbon Dioxide in Nuclear Reactor System. Nucl. Power Eng. 2012, 33, 21–27. [Google Scholar]
- Li, H.; Zhang, Y.; Zhang, L.; Yao, M.; Kruizenga, A.; Anderson, M. Based Modeling on the Turbulent Convection Heat Transfer of Supercritical CO2 in the Printed Circuit Heat Exchangers for the Supercritical CO2 Brayton Cycle. Int. J. Heat Mass Transf. 2016, 98, 204–218. [Google Scholar] [CrossRef]
- Khalesi, J.; Sarunac, N. Numerical Analysis of Flow and Conjugate Heat Transfer for Supercritical CO2 and Liquid Sodium in Square Microchannels. Int. J. Heat Mass Transf. 2019, 132, 1187–1199. [Google Scholar] [CrossRef]
- da Rosa, O.C.; Battisti, F.G.; Hobold, G.M.; da Silva, A.K. Enhancing Heat Rejection from Electronic Devices with a Supercritical Carbon Dioxide Minichannel Heat Exchanger. Int. J. Refrig. 2019, 106, 463–473. [Google Scholar] [CrossRef]
- Huang, H.; Zhai, Y.; Li, Z.; Wang, H. Thermo-Hydraulic Characteristics and Structural Optimization of Supercritical CO2-Cooled Microchannel Heat Sink. Int. Commun. Heat Mass Transf. 2024, 154, 107438. [Google Scholar] [CrossRef]
- Huang, H.; Zhai, Y.; Li, Z.; Li, Y.; Wang, H. Thermal Management for Microelectronic Chips under Non-Uniform Heat Flux with Supercritical CO2. Int. J. Heat Mass Transf. 2025, 236, 126271. [Google Scholar] [CrossRef]
- Khan, S.A.; Ahmad, S.; Lau, K.T.; Dong, K.; He, S.; Liu, H.; Zhao, J. A Novel Strategy of Thermal Management System for Battery Energy Storage System Based on Supercritical CO2. Energy Convers. Manag. 2023, 277, 116676. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Song, X.; Gu, Z. Thermal Management Performance of Lithium-Ion Battery Using Supercritical CO2 as Cooling Fluid. Heat Transf. Eng. 2023, 44, 1452–1465. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, Z.; Fu, T.; Wu, H. Numerical Investigation on Lithium-Ion Battery Thermal Management Utilizing a Novel Tree-Like Channel Liquid Cooling Plate Exchanger. Int. J. Heat Mass Transf. 2022, 183, 122143. [Google Scholar] [CrossRef]
- Li, B.; Wang, W.; Bei, S.; Quan, Z. Analysis of Heat Dissipation Performance of Battery Liquid Cooling Plate Based on Bionic Structure. Sustainability 2022, 14, 5541. [Google Scholar] [CrossRef]
- Ding, Y.; Ji, H.; Wei, M.; Liu, R. Effect of Liquid Cooling System Structure on Lithium-Ion Battery Pack Temperature Fields. Int. J. Heat Mass Transf. 2022, 183, 122178. [Google Scholar] [CrossRef]
- Deng, T.; Zhang, G.; Ran, Y.; Liu, P. Thermal Performance of Lithium-Ion Battery Pack by Using Cold Plate. Appl. Therm. Eng. 2019, 160, 114088. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Zakizadeh-Matak, T. Mechanism Analysis of Turbulent Convective Heat Transfer of Supercritical Carbon Dioxide in Serpentine Tubes. Appl. Therm. Eng. 2024, 257, 124490. [Google Scholar] [CrossRef]
- Fu, J.; Liu, H.Y.; Wang, Y. Numerical Analysis of Mechanism on Heat Transfer Deterioration of Hexamethyldisiloxane in a Vertical Upward Tube at Supercritical Pressures. J. Appl. Fluid Mech. 2024, 17, 1967–1980. [Google Scholar]
- Xu, X.; Tong, G.; Li, R. Numerical Study and Optimizing on Cold Plate Splitter for Lithium Battery Thermal Management System. Appl. Therm. Eng. 2020, 167, 114787. [Google Scholar] [CrossRef]
- Huang, D.; Li, W. A Brief Review on the Buoyancy Criteria for Supercritical Fluids. Appl. Therm. Eng. 2018, 131, 977–987. [Google Scholar] [CrossRef]
- Jackson, J.D. Models of Heat Transfer to Fluids at Supercritical Pressure with Influences of Buoyancy and Acceleration. Appl. Therm. Eng. 2017, 124, 1481–1491. [Google Scholar] [CrossRef]
- Kim, T.H.; Kwon, J.G.; Kim, M.H.; Park, H.S. Experimental Investigation on Validity of Buoyancy Parameters to Heat Transfer of CO2 at Supercritical Pressures in a Horizontal Tube. Exp. Therm. Fluid Sci. 2018, 92, 222–230. [Google Scholar] [CrossRef]



| Specifications | Details |
|---|---|
| Battery | |
| Material | LiFePO4 |
| Dimension | 148 × 27.5 × 91 mm |
| Nominal capacity | 40 Ah |
| Nominal voltage | 3.2 V |
| Density | 2160 kg/m3 |
| Specific heat | 1129 J/kg·K |
| Cold plate | |
| Density | 7980 kg/m3 |
| Specific heat | 500 J/kg·K |
| Thermal conductivity | 16.3 W/m·K |
| Discharge Rates (C) | Mass Flow Rates (kg/s) | Operational Pressure (MPa) |
|---|---|---|
| 3 | 0.002 | 7.4 |
| 4 | 0.004 | 7.7 |
| 5 | 0.006 | 8.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, F.; Cao, F.; Liang, S.; Fu, J. Study on Flow and Heat Transfer Characteristics of Battery Thermal Management System with Supercritical CO2 for Energy Storage Stations. Energies 2025, 18, 2030. https://doi.org/10.3390/en18082030
Wang Y, Li F, Cao F, Liang S, Fu J. Study on Flow and Heat Transfer Characteristics of Battery Thermal Management System with Supercritical CO2 for Energy Storage Stations. Energies. 2025; 18(8):2030. https://doi.org/10.3390/en18082030
Chicago/Turabian StyleWang, Ya, Fengbin Li, Feng Cao, Shaozhong Liang, and Jian Fu. 2025. "Study on Flow and Heat Transfer Characteristics of Battery Thermal Management System with Supercritical CO2 for Energy Storage Stations" Energies 18, no. 8: 2030. https://doi.org/10.3390/en18082030
APA StyleWang, Y., Li, F., Cao, F., Liang, S., & Fu, J. (2025). Study on Flow and Heat Transfer Characteristics of Battery Thermal Management System with Supercritical CO2 for Energy Storage Stations. Energies, 18(8), 2030. https://doi.org/10.3390/en18082030





