Non-Fault Detection Scheme Before Reclosing Using Parameter Identification for an Active Distribution Network
Abstract
1. Introduction
2. Fault Characterization
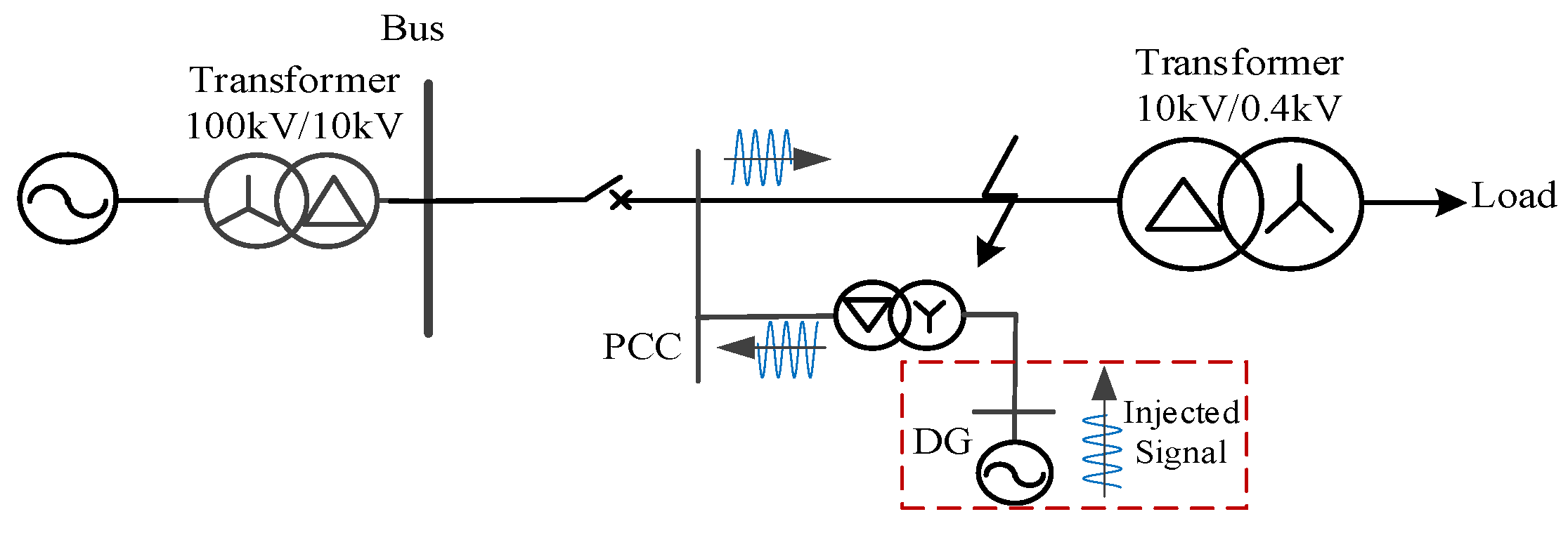
2.1. Fault Detection Scheme Using DG Injection
2.2. Fault Modeling
2.2.1. Transient Fault (i.e., Non-Fault)
2.2.2. Permanent Fault
3. Non-Fault Detection Principle and Criterion Based on R–L Parameter Identification
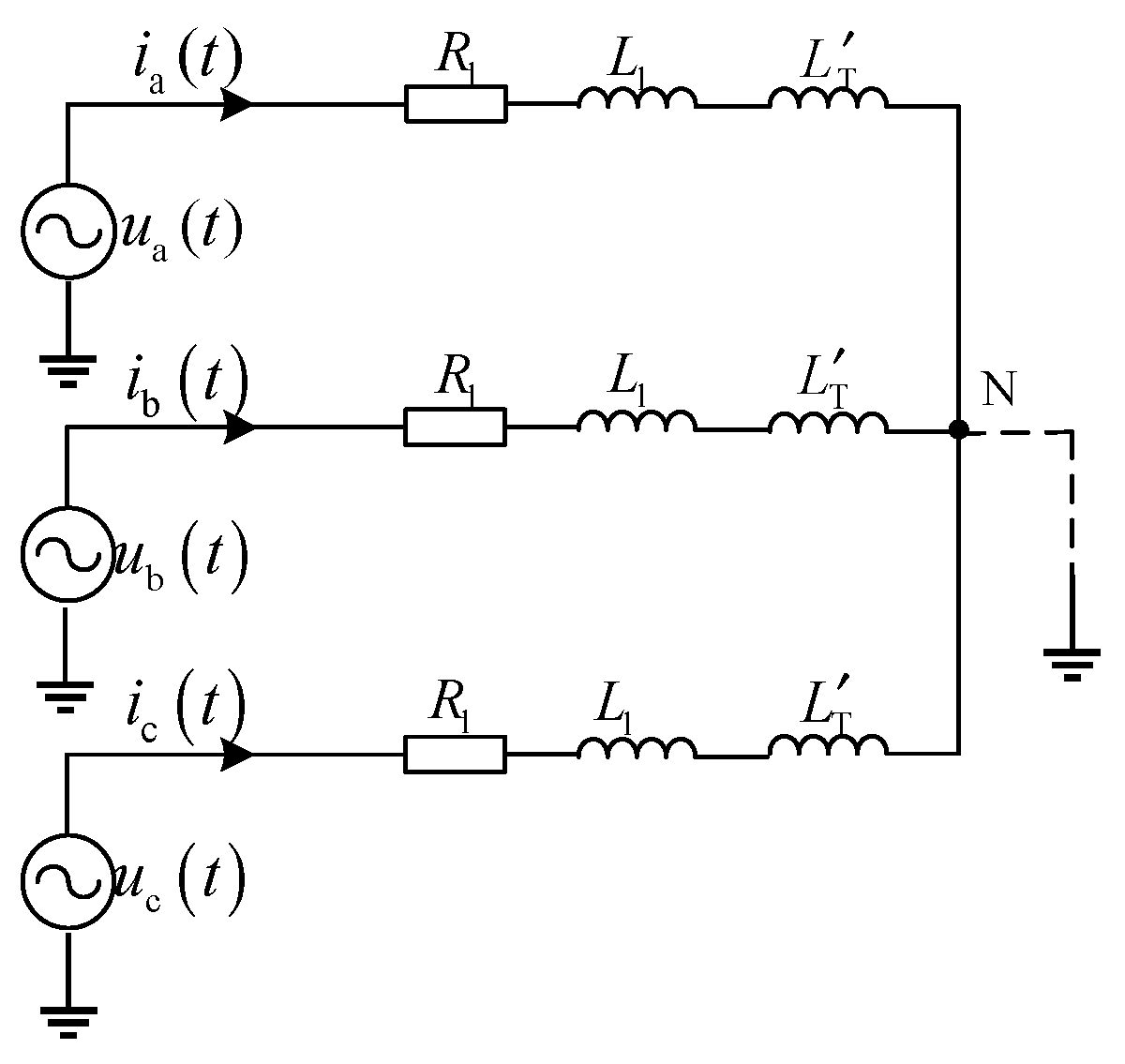
3.1. Fundamentals
3.2. Non-Fault Identification Criteria
3.3. Realizing Scheme
4. Simulation Experiment Based on PSCAD
4.1. Simulation Model
4.2. Simulation Calculations
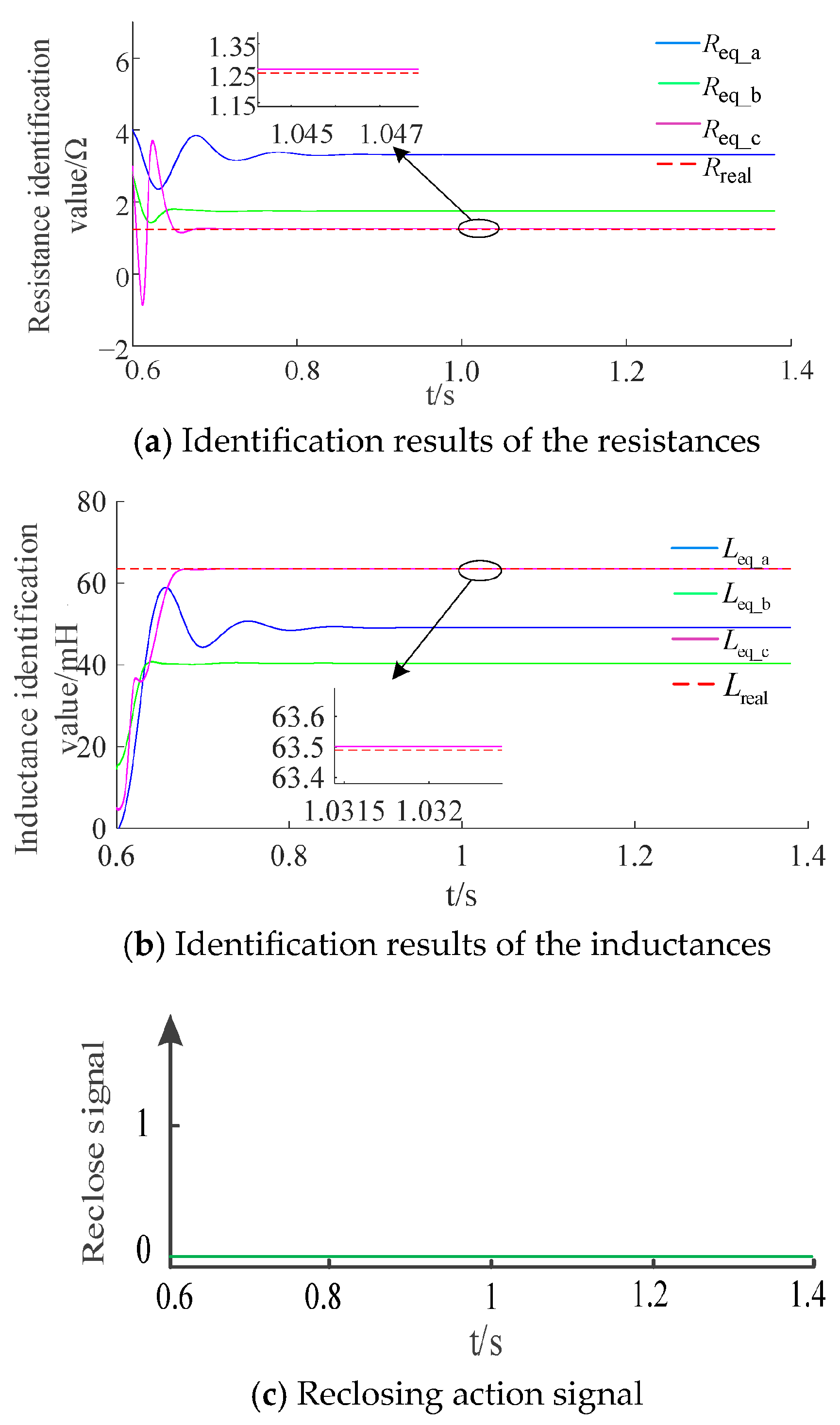
4.2.1. Identification Criterion Principles Verification
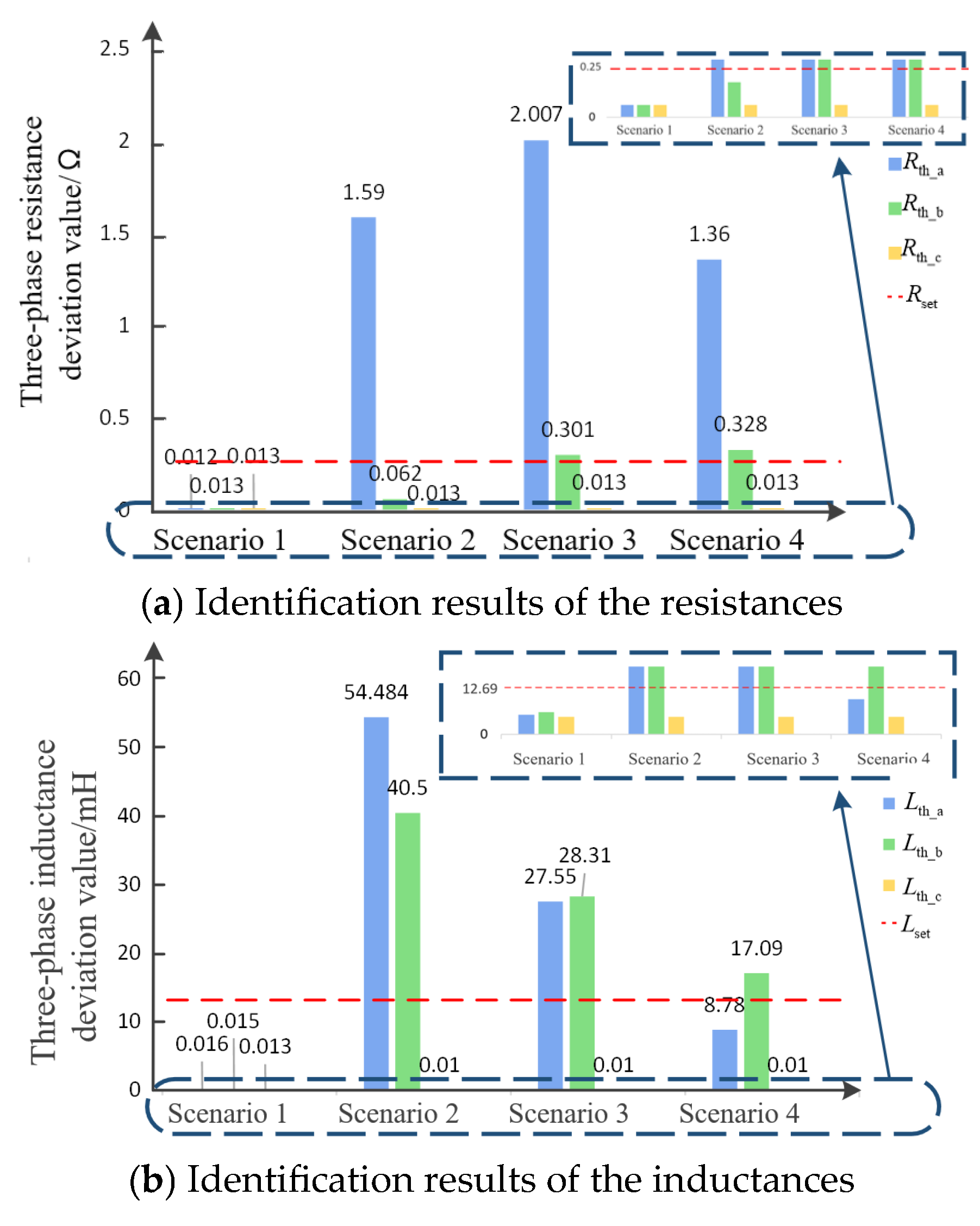
4.2.2. Performance Analysis Under Different Fault Conditions
- Scenario 1: Transient fault occurs with 1 Ω transition resistance.
- Scenario 2: Permanent fault occurs with 5 Ω transition resistance.
- Scenario 3: Permanent fault occurs with 10 Ω transition resistance.
- Scenario 4: Permanent fault occurs with 20 Ω transition resistance.
5. Comparison with Other Methods
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| voltage of each phase at the PCC | |
| current in each phase | |
| fault transition resistance | |
| self-resistance of each phase of the detected line | |
| equivalent inductance of the distribution transformer | |
| equivalent impedance from the fault point to the end of the line | |
| m | distance from the fault point to the head end of the line as a proportion of the total length of the line |
| calculated resistance of the detected line | |
| calculated inductance of the detected line | |
| the jth of the calculated resistance | |
| the jth of the calculated inductance | |
| and | margin coefficients |
| average deviation between the calculated value and the real value of the resistance | |
| average deviation between the calculated value and the real value of the inductance |
References
- Si, R.; Yan, X.; Liu, W.; Zhang, P.; Wang, M.; Li, F.; Yang, J.; Su, X. Hybrid optimization-based sequential placement of DES in unbalanced active distribution networks considering multi-scenario operation. Energies 2025, 18, 474. [Google Scholar] [CrossRef]
- Ma, X.; Zhen, W.; Ren, H.; Zhang, G.; Zhang, K.; Dong, H. A method for fault localization in distribution networks with high proportions of distributed generation based on graph convolutional networks. Energies 2024, 17, 5758. [Google Scholar] [CrossRef]
- Ayanlade, S.O.; Ariyo, F.K.; Jimoh, A.; Akindeji, K.T.; Adetunji, A.O.; Ogunwole, E.I.; Owolabi, D.E. Optimal Allocation of photovoltaic distributed geberation in radial distribution networks. Sustainability 2023, 15, 13933–13956. [Google Scholar]
- Gao, W.L.; Xi, M.D.; Wang, H. New method of small current grounding line selection based on feature fusion and extreme learning machine. Electron. Meas. Technol. 2023, 46, 176–184. [Google Scholar]
- Zhao, J.W.; Zhang, H.B.; Hu, Y.J. Adaptive distance protection for distributed generation distribution network with T-connected inverter interfaced distributed generation. Renew. Energy Resour. 2024, 42, 64–70. [Google Scholar]
- Sao, W.Q.; Liu, Y.; Zhang, Z.H. Non-Fault detection for three-phase reclosing in transmission lines based on calculated differential-currents. Power Syst. Clean Energy 2017, 33, 18–23. [Google Scholar]
- Cao, H.; Xia, Q.; Yu, B. Intelligent reclosing strategy for near area AC transmission lines connected with UHVDC. Power Syst. Prot. Control 2022, 50, 156–163. [Google Scholar]
- Shen, J.; Shu, Z.S.; Chen, J. Application of adaptive auto-reclosure in power system. Autom. Electr. Power Syst. 2018, 42, 152–156. [Google Scholar]
- Khan, W.A.; Tianshu, B.I.; Ke, J. A review of single phase adaptive auto-reclosing schemes for EHV transmission lines. Prot. Control Mod. Power Syst. 2019, 4, 205–214. [Google Scholar]
- Deb, S.; Lata, S.; Bhadoria, V.S. Improved Relay Algorithm for Detection and Classification of Transmission Line Faults in Monopolar HVDC Transmission System Using Signum Function of Transient Energy. IEEE Access 2024, 12, 15561–15571. [Google Scholar]
- Li, C.L.; Ma, C.; Wang, C.Y. Study on relay protection of distribution network containing distributed generation based on adaptive algorithm. Renew. Energy Resour. 2015, 33, 1329–1339. [Google Scholar]
- Zhang, Z.H.; Qiao, H.; Shao, W.Q. Non-fault detection in phase-to-phase faults before reclosing in distribution network. Grid Anal. Study 2018, 46, 66–71. [Google Scholar]
- Liao, H.Y.; Kang, X.N.; Yuan, Y.L. Adaptive three-phase reclosing device of distribution network based on injected signals. Power Syst. Technol. 2021, 45, 2623–2630. [Google Scholar]
- Song, M.M.; Liu, J.; Zhang, Z.H. Power quality analysis based on power consumption information acquisition data. Distrib. Util. 2020, 37, 51–57. [Google Scholar]
- Shao, W.Q.; Liu, Y.X.; Guan, X. An active detection scheme for permanent fault identification before phase-to-phase reclosing in a distribution network. Power Syst. Prot. Control 2021, 49, 96–103. [Google Scholar]
- Shao, W.Q.; He, Y.X.; Guan, X. Identification method for an interphase permanent fault in a distribution network using waveform characteristics of multiple disturbance currents. Power Syst. Prot. Control 2023, 51, 146–157. [Google Scholar]
- Zu, K.; Song, Y.T.; Xu, Y.G. An active adaptive reclosing scheme for distribution lines. Power System Technology 2017, 41, 993–999. [Google Scholar]
- Zhuo, J.; Shao, W.Q.; Guan, X. Permanent fault identification method of distribution network based on parameter identification. Distrib. Energy 2022, 7, 37–45. [Google Scholar]
- Zhang, Z.H.; Liu, J.; Ren, B.J. Permanent fault identification for distribution network based on characteristic frequency signal injection using power electronic technology. Front. Energy Res. 2022, 10, 967592. [Google Scholar] [CrossRef]
- Jiao, Z.B.; Ma, T.; Qu, Y.J. A novel excitation inductance-based power transformer protection scheme. Proc. CSEE 2014, 34, 1658–1666. [Google Scholar]
- Huang, Z.H.; Zou, J.Y.; Zou, Q.T. Research on controlled reclosing for solidly earthed neutral systems. Proc. CSEE 2016, 36, 4753–4762. [Google Scholar]
- Meng, H.D.C.F.; Zhao, L. Fault identification technology for distribution line based on distributed generation injection signal. High Volt. Appar. 2022, 58, 123–129+146. [Google Scholar]
- GB/T 12325-2008; Power Quality—Deviation of Supply Voltage. Standards Press of China: Beijing, China, 2008.
- Xu, R.D.; Chang, Z.X.; Song, G.B. Grounding fault identification method for DC distribution network based on detection signal injection. Power Syst. Technol. 2021, 45, 4269–4277. [Google Scholar]
- Lin, J.Y.; Chen, R.; Li, Y.L. Fault Location Method for Distribution Network Based on Parameter Identification. South. Power Syst. Technol. 2019, 13, 80–87. [Google Scholar]



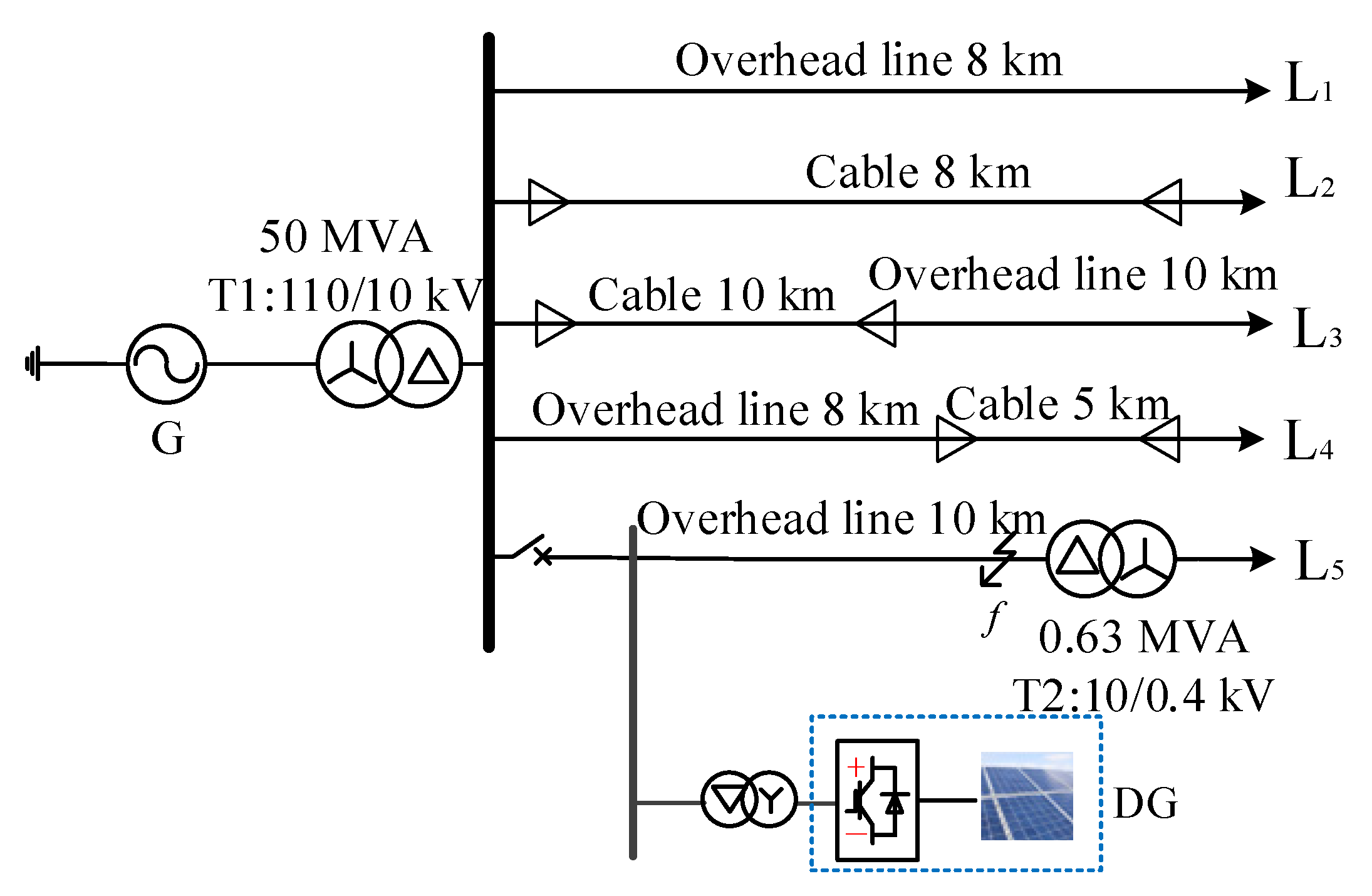



| Line Type | Phase Sequence | Resistance (Ω/km) | Inductance (mH/km) | Capacitance (μF/km) |
|---|---|---|---|---|
| overhead line | positive sequence | 0.125 | 1.299 | 0.040 |
| zero sequence | 0.275 | 4.586 | 0.012 | |
| cable line | positive sequence | 0.270 | 0.254 | 0.339 |
| zero sequence | 2.700 | 1.019 | 0.280 |
| Scenario | |||
|---|---|---|---|
| Scenario 1 | 0.0072 | 0.0003 | 0.0310 |
| Scenario 2 | 1.2720 | 0.6379 | 0.1930 |
| Scenario 3 | 1.6056 | 0.4339 | 0.1252 |
| Scenario 4 | 1.0880 | 0.26918 | 0.1184 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; A, S.; Sun, X.; Zhang, S.; Liu, D.; Shao, W. Non-Fault Detection Scheme Before Reclosing Using Parameter Identification for an Active Distribution Network. Energies 2025, 18, 1932. https://doi.org/10.3390/en18081932
Sun Z, A S, Sun X, Zhang S, Liu D, Shao W. Non-Fault Detection Scheme Before Reclosing Using Parameter Identification for an Active Distribution Network. Energies. 2025; 18(8):1932. https://doi.org/10.3390/en18081932
Chicago/Turabian StyleSun, Zhebin, Sileng A, Xia Sun, Shuang Zhang, Dinghua Liu, and Wenquan Shao. 2025. "Non-Fault Detection Scheme Before Reclosing Using Parameter Identification for an Active Distribution Network" Energies 18, no. 8: 1932. https://doi.org/10.3390/en18081932
APA StyleSun, Z., A, S., Sun, X., Zhang, S., Liu, D., & Shao, W. (2025). Non-Fault Detection Scheme Before Reclosing Using Parameter Identification for an Active Distribution Network. Energies, 18(8), 1932. https://doi.org/10.3390/en18081932






