Frequency-Adaptive Current Control of a Grid-Connected Inverter Based on Incomplete State Observation Under Severe Grid Conditions

Abstract

Grid-connected inverter (GCI) plays a crucial role in facilitating stable and efficient power delivery, especially under severe and complex grid conditions. Harmonic distortions and imbalance of the grid voltages may degrade the grid-injected current quality. Moreover, inductive-capacitance (LC) grid impedance and the grid frequency fluctuation also degrade the current control performance or stability. In order to overcome such an issue, this study presents a frequency-adaptive current control strategy of a GCI based on incomplete state observation under severe grid conditions. When LC grid impedance exists, it introduces additional states in a GCI system model. However, since the state for the grid inductance current is unmeasurable, it yields a limitation in the state feedback control design. To overcome such a limitation, this study adopts a state feedback control approach based on incomplete state observation by designing the controller only with the available states. The proposed control strategy incorporates feedback controllers with ten states, an integral controller, and resonant controllers for the robustness of the inverter operation. To reduce the reliance on additional sensing devices, a discrete-time full-state current observer is utilized. Particularly, with the aim of avoiding the grid frequency dependency of the system model, as well as the complex online discretization process, observer design is developed in the stationary reference frame. Additionally, a moving average filter (MAF)-based phase-locked loop (PLL) is incorporated for accurate frequency detection against distortions of grid voltages. For evaluating the performance of the designed control strategy, simulations and experiments are executed with severe grid conditions, including grid frequency changes, unbalanced grid voltage, harmonic distortion, and LC grid impedance.

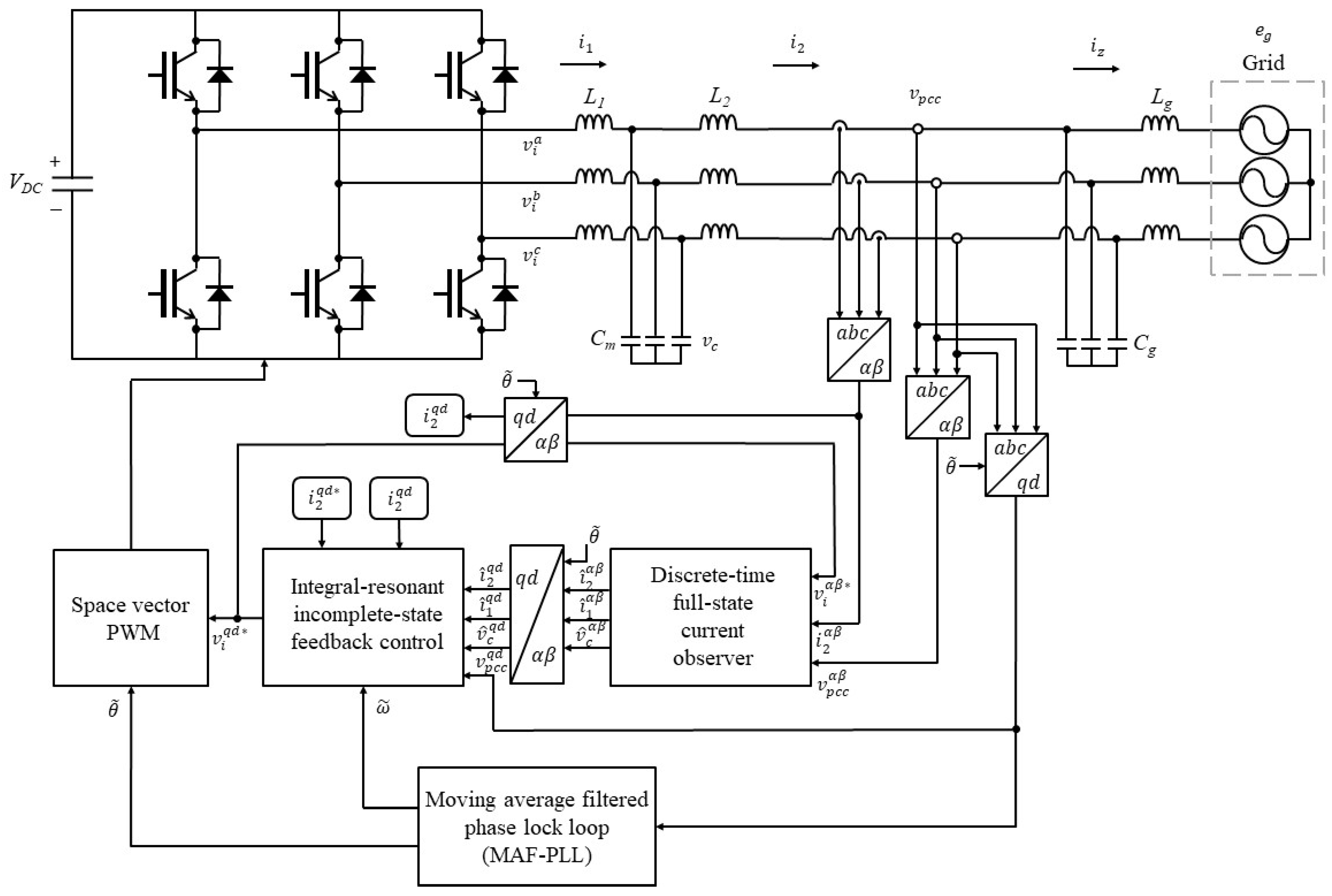
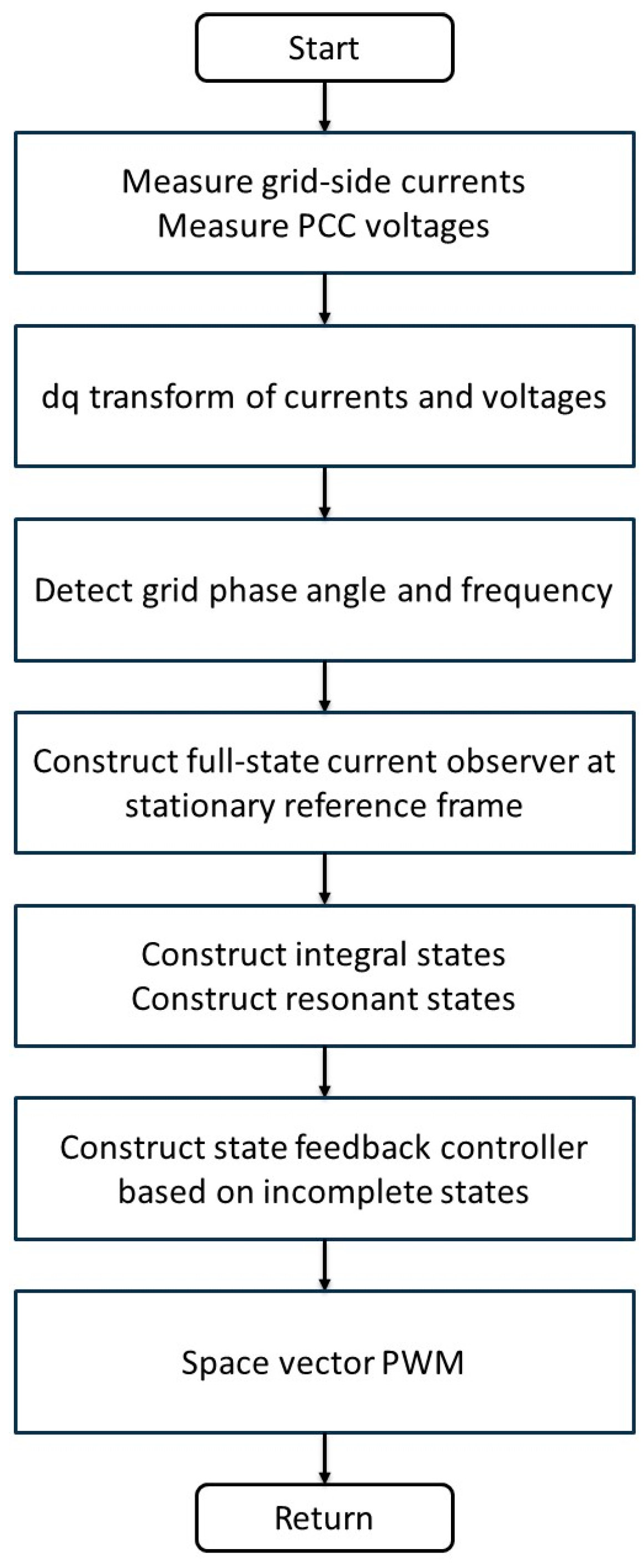
1. Introduction

In the past few years, renewable energy sources (RESs) and distributed generations (DGs) have gained significant attention as effective solutions to fulfill the expanding energy demands while alleviating environmental impacts [1]. The increasing adoption of renewable energy technologies has amplified the importance of grid-connected voltage source inverters (VSIs) in energy conversion systems. These inverters significantly contribute to facilitating the seamless integration of RESs into the utility grid while maintaining stable and reliable power delivery. A key challenge in grid-connected inverters (GCIs) is to maintain a robust control performance against adverse grid conditions, such as harmonic distortions and frequency deviations. Effective control strategies are essential to ensure that active power from distributed generation systems is injected into the grid with minimal distortion, meeting stringent power quality standards. Particularly, RESs are deployed as a main DG and serve as a fundamental component for modern energy networks [2]. As a result, DG systems based on RESs must comply with rigorous power quality standards, for instance, the IEEE standard 1547 [3], to ensure that the injected current meets grid code requirements and maintains the stability of the overall power system [4].

Typically, harmonic distortion, which degrades the current quality, commonly occurs in a pulse width modulation (PWM) switching control of GCIs. To address this issue, inductive (L) filters or inductive–capacitive–inductive (LCL) filters are used. Compared to L filters, LCL filters are more popular for connecting the GCI to the utility grid because of their superior ability to suppress the current harmonics [5]. The proportional–integral (PI) controller is often employed for controlling a GCI due to its simplicity of implementation. However, this control cannot guarantee stability in inverters equipped with LCL filters due to the LCL filter resonance peak. Several research studies in [6,7,8] propose a state-space control method, offering an efficient, uncomplicated, and straightforward approach for mitigating the resonance effect. Another approach introduced in [9] utilizes the optimal control by applying a linear quadratic regulator (LQR) method. This method determines the system’s optimal gains in state-space by minimizing a defined cost function for the purpose of avoiding the degradation of control performance caused by various distortion conditions.

Furthermore, grid voltage distortion can occur due to various external factors, such as nonlinear loads and the LC impedance characteristics of the power network. The LC impedance, in particular, may amplify harmonic distortions at specific resonant frequencies. Grid impedance arises primarily from the physical characteristics of the transmission system, including the inductive properties of long-distance power lines and the capacitive effects introduced by power factor correction devices [10]. These components are combined to form a complex impedance network that influences the system stability along with the dynamics of the GCI system. Variations in this impedance, often due to load changes or transmission line conditions, can exacerbate harmonic distortion and resonance, further complicating control system design. To address the issue of the grid impedance interactions, the study in [11] presents a stability enhancement method using a discrete derivative controller. However, this scheme does not consider severe grid conditions with unbalanced and distorted grid voltages. Moreover, such grid impedance and distorted grid voltages can negatively impact the current injected by the inverter, often resulting in increased levels of distortion in the injected current [4,12,13]. Therefore, the current control design must guarantee the grid-injected currents with good quality and maintain the system stability against the resonance phenomenon and grid distortion.

Besides the distortion resulting from the grid impedance, the grid frequency variation can also result in a significant degradation of control performance. Grid frequency variation is often caused by an imbalance between power generation and load demand, as sudden changes in either can disrupt the frequency stability [14]. Such frequency variation impacts the quality of the current delivered to the grid, as well as the operational stability of the system. In particular, frequency variations affect phase-locked loop (PLL) synchronization, leading to inaccuracies in frequency and phase estimation. Since the controller parameters are often designed for a specific frequency, the frequency deviation affects the current control performance. These effects contribute to increased harmonic distortion and degraded power quality. Therefore, adopting a systematic approach to frequency-adaptive control is essential to guarantee high-quality grid-injected currents and keep the system stable in the face of unexpected situations [15,16]. As introduced by the study [17], an enhanced repetitive control (RC) strategy utilizing a finite impulse response (FIR) filter is able to dynamically adapt the frequencies of resonant controllers to align the resonant controller frequency with the grid fundamental and harmonic components, ensuring better performance under varying grid frequencies. A selective harmonic control (SHC) method is proposed in the study [18] to deal with the harmonics induced by the grid distortion. Despite the advancements in frequency-adaptive control techniques and harmonic distortion mitigation methods, the existing approaches face limitations, such as slower dynamic response, higher computational complexity, or the need for high switching frequencies, limiting their practical applicability in real-time grid-connected systems.

The exact detection of the frequency and phase angle of grid voltage is a key element in designing a current controller of GCI systems. A synchronous reference frame PLL (SRF-PLL) is commonly used with the grid voltage measurement for this purpose. However, it encounters difficulties in determining the grid frequency and phase angle correctly under distorted or unbalanced grid voltages [19]. One way to enhance the robustness of the SRF-PLL under severely distorted grid conditions is to incorporate a moving average filter (MAF) into the system [19,20,21]. The standard MAF-PLL technique presented in [22] is utilized to estimate the grid frequency with robustness under the circumstance of harmonic distortions and noise. Under severe grid conditions, this method significantly improves not only the overall system performance but also the phase angle and frequency detection accuracy by mitigating the effects of grid harmonic distortion and noise. Moreover, the MAF characteristic of effectively filtering out high-frequency noise enhances both the stability and reliability of the PLL scheme during operation. A precise frequency and phase angle detection conducted by the MAF-PLL technique enables harmonic compensation in resonant controllers, thereby improving the power quality in DG systems. To enable more precise control of the system, a full-state current observer is implemented in this study, enhancing state estimation accuracy.

When designing a GCI system, observers are employed to reduce the reliance on multiple sensors while providing the availability of system state variables required for the implementation of advanced control strategies. Observers can effectively estimate the internal state variables, simplifying the hardware design and lowering implementation costs. Several research studies, such as [7,8,23], have presented full-state prediction observers for state estimation in a GCI system, whereas the research in [24] has proposed a reduced-order observer approach to further simplify the system. In addition, the current observer, which estimates the system states based on the current estimation error, provides precise state estimation and reduces the influence of noise from system output signals.

When LC grid impedance exists caused by the complex grid, it introduces additional state variables. Even with LC grid impedance, state variables caused by the LCL filter are effectively estimated by designing a state observer. In this case, the point of common coupling (PCC) voltages act as additional state variables. Meanwhile, the currents flowing into the grid inductance are not measurable or cannot be estimated. Consequently, due to the unavailability of a state for grid inductance current, full-state feedback for current control design is not feasible. In such a case, a state feedback current control needs to be designed with incomplete state observation. On the other hand, the existing full-state feedback control methods have several limitations under the unavailability of grid inductance current, as well as severe grid conditions such as grid frequency variations and unbalanced or distorted grid conditions.

The uncertainties of grid impedance and grid frequency variations become even worse in weak grid conditions, which further affects the system stability, as well as the current control performance. In this paper, to ensure superior current control performance under severe grid conditions, a frequency-adaptive current control of a GCI based on incomplete state observation is presented. The main contributions of this research are presented as follows:

(i)

A frequency-adaptive current control strategy is developed under the existence of LC grid impedance to enhance the stability and quality of current injected into the grid under varying grid frequency conditions. By integrating the MAF-PLL, the proposed control strategy enhances the accuracy of frequency detection and alleviates the negative impact of frequency fluctuations on control performance.

(ii)

When LC grid impedance exists, it introduces additional states in a GCI system model. However, since the state for the grid inductance current is unmeasurable, it yields a limitation in the state feedback control design. To address this issue, this study adopts a state feedback control approach based on an incomplete state observation, which designs a controller using only the available states. This approach simplifies the control design and implementation while ensuring a robust performance under uncertain grid conditions.

(iii)

With severe grid conditions, the performance of the designed system is assessed to confirm its robustness and effectiveness. Severe grid conditions in this study include unbalanced grid voltages, harmonic distortion of grid voltages, uncertainty caused by LC grid impedance, and grid frequency variation, which are common in practical power systems. Imbalance and harmonic distortion of grid voltages are compensated using resonant controllers. Grid impedance and frequency variation are handled by a frequency-adaptive current control strategy with incomplete observation to enhance the system stability and robustness under varying grid conditions.

To reduce steady-state errors in grid-injected currents, the integral controller is also incorporated into the state feedback controller. In particular, with the purpose of suppressing the influence induced by the unbalanced grid voltages and low-order grid harmonic distortions, the resonant controllers are deployed at the harmonic orders of second, sixth, and twelfth. A full-state current observer is introduced for accurate state estimation while minimizing the reliance on additional sensors. To ensure that the estimated states are unaffected by the grid frequency changes, the observer design is accomplished in the stationary reference frame. In addition, an LQR optimization technique is applied to determine the optimal gains for the state feedback controller and full-state observer. The usefulness and robustness of the designed current controller are verified through the simulation using Powersim (PSIM) software (v9.1, Powersim, Rockville, MD, USA). Furthermore, its effectiveness is verified through laboratory experiments utilizing a three-phase 2kVA prototype GCI under severe grid conditions.

2. System Representation of GCI with LCL Filter Under LC Grid Impedance

2.1. Description of State-Space Model

Figure 1 presents the depiction of a three-phase LCL-filtered GCI incorporating LC grid impedance. Severe grid conditions, such as the grid frequency variation and the unbalanced and distorted grid voltages, are considered. To attenuate the high frequency harmonic components, the GCI system is connected to the utility grid through LCL filters. The LCL filter parameters are denoted as $L_1$, $L_2$, and $C_m$. In addition to the disturbance caused by unbalanced and distorted voltages, the utility grid also has uncertainty due to the components of the grid inductance and capacitance. The LC grid impedance parameters are represented as $L_g$ and $C_g$, respectively. The inverter-side current and grid-side current are represented as $i_1\mathrm{a}\mathrm{n}\mathrm{d}{i}_2$, respectively. The capacitor voltage is represented as $v_c$. The PCC voltage, which is the connection point linking the grid inductance with LCL filter, is defined as $v_{pcc}$. The grid inductance current is represented as $i_z$, the grid voltage as $e_g$, the inverter output voltage as $v_i$, and the DC-link voltage as V_DC, respectively.

To implement the proposed control scheme, first, two currents and PCC voltages are measured. After the measurements, the acquired signals are transformed into the appropriate coordinate frames. To enhance the precision of frequency and phase detection under distorted grid environments, the PCC voltage information at the synchronous reference frame is provided to the MAF-PLL to obtain the grid phase angle $\tilde{\theta }$. The system input, grid-side currents, and PCC voltages are fed into the full-state current observer. The estimated states with the grid-side currents and PCC voltages are utilized to constitute an integral-resonant state feedback current controller. Finally, the inverter reference voltages obtained with the proposed control strategy are processed through the space vector PWM with $\tilde{\theta }$ to determine the switching states of the inverter. In this figure, the symbol “^” refers to an estimated value, and “*” indicates a reference value.

The state equations describing the GCI with LC grid impedance are formulated in the SRF as follows:

$${\displaystyle \frac{d}{dt}}{i}_2^q\left(t\right)=-\omega i_2^d\left(t\right)+{\displaystyle \frac{1}{L_2}}{v}_c^q(t)-{\displaystyle \frac{1}{L_2}}{v}_{pcc}^q(t)$$

(1)

$${\displaystyle \frac{d}{dt}}{i}_2^d(t)=\omega i_2^q(t)+{\displaystyle \frac{1}{L_2}}{v}_c^d(t)-{\displaystyle \frac{1}{L_2}}{v}_{pcc}^d(t)$$

(2)

$${\displaystyle \frac{d}{dt}}{i}_1^q(t)=-\omega i_1^d(t)-{\displaystyle \frac{1}{L_1}}{v}_c^q(t)+{\displaystyle \frac{1}{L_1}}{v}_i^q(t)$$

(3)

$${\displaystyle \frac{d}{dt}}{i}_1^d(t)=\omega i_1^q(t)-{\displaystyle \frac{1}{L_1}}{v}_c^d(t)+{\displaystyle \frac{1}{L_1}}{v}_i^d(t)$$

(4)

$${\displaystyle \frac{d}{dt}}{v}_c^q\left(t\right)=-{\displaystyle \frac{1}{C_m}}{i}_2^q\left(t\right)+{\displaystyle \frac{1}{C_m}}{i}_1^q(t)-\omega v_c^d(t)$$

(5)

$${\displaystyle \frac{d}{dt}}{v}_c^d\left(t\right)=-{\displaystyle \frac{1}{C_m}}{i}_2^d\left(t\right)+{\displaystyle \frac{1}{C_m}}{i}_1^d(t)+\omega v_c^q(t)$$

(6)

$${\displaystyle \frac{d}{dt}}{v}_{pcc}^q(t)={\displaystyle \frac{1}{C_g}}{i}_2^q(t)-\omega v_{pcc}^d(t)-{\displaystyle \frac{1}{C_g}}{i}_z^q(t)$$

(7)

$${\displaystyle \frac{d}{dt}}{v}_{pcc}^d(t)={\displaystyle \frac{1}{C_g}}{i}_2^d(t)+\omega v_{pcc}^q(t)-{\displaystyle \frac{1}{C_g}}{i}_z^d(t)$$

(8)

$${\displaystyle \frac{d}{dt}}{i}_z^q(t)={\displaystyle \frac{1}{L_g}}{v}_{pcc}^q(t)-\omega i_z^d(t)-{\displaystyle \frac{1}{L_g}}{e}_g^q(t)$$

(9)

$${\displaystyle \frac{d}{dt}}{i}_z^d\left(t\right)={\displaystyle \frac{1}{L_g}}{v}_{pcc}^d\left(t\right)+\omega i_z^q\left(t\right)-{\displaystyle \frac{1}{L_g}}{e}_g^d\left(t\right)$$

(10)

where the superscript “q” and “d” indicate the values in the SRF. The state equations in (1)–(6) represent the dynamic model of the LCL filter, which interconnects the GCI with the utility grid for the purpose of attenuating the inverter switching harmonics. On the other hand, the state equations in (7)–(10) represent the dynamic model caused by uncertain LC grid impedance, which is not a designed filter stage but an uncertain component in the utility grid. Moreover, $\omega$ represents the grid angular frequency. The system model described by Equations (1)–(10) can be represented as the state-space model in continuous time as follows:

$$\dot{\mathbf{x}}\left(t\right)=\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{B}\mathbf{u}\left(t\right)+\mathbf{E}\mathbf{e}\left(t\right)$$

(11)

$$\mathbf{y}\left(t\right)=\mathbf{C}\mathbf{x}\left(t\right)$$

(12)

where $\mathbf{x}={\left[i_2^q,i_2^d,i_1^q,i_1^d,v_c^q,v_c^d,v_{pcc}^q,v_{pcc}^d,i_z^q,i_z^d\right]}^T$ is the system state, $\mathbf{u}={\left[v_i^q,v_i^d\right]}^T$ is the system input, $\mathbf{e}={\left[e_g^q,e_g^d\right]}^T$ is the grid voltage, and $\mathbf{y}={\left[i_2^q,i_2^d\right]}^T$ is system output. The state-space matrices A, B, C, and E are represented as follows:

$$\mathbf{A}=\left[\begin{array}{cccccccccc}0& -\omega & 0& 0& 1/L_2& 0& -1/L_2& 0& 0& 0\\ \omega & 0& 0& 0& 0& 1/L_2& 0& -1/L_2& 0& 0\\ 0& 0& 0& -\omega & -1/L_1& 0& 0& 0& 0& 0\\ 0& 0& \omega & 0& 0& -1/L_1& 0& 0& 0& 0\\ -1/C_m& 0& 1/C_m& 0& 0& -\omega & 0& 0& 0& 0\\ 0& -1/C_m& 0& 1/C_m& \omega & 0& 0& 0& 0& 0\\ 1/C_g& 0& 0& 0& 0& 0& 0& -\omega & -1/C_g& 0\\ 0& 1/C_g& 0& 0& 0& 0& \omega & 0& 0& -1/C_g\\ 0& 0& 0& 0& 0& 0& 1/L_g& 0& 0& -\omega \\ 0& 0& 0& 0& 0& 0& 0& 1/L_g& \omega & 0\end{array}\right]$$

$$\mathbf{B}=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 1/L_1& 0\\ 0& 1/L_1\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right],\mathbf{E}=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ -1/L_g& 0\\ 0& -1/L_g\end{array}\right],\mathbf{C}=\left[\begin{array}{cccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].$$

2.2. Discretization of GCI System

Due to the digital implementation, the control signal $\mathbf{u}\left(k\right)$, which is computed at the current time step, cannot be directly applied to the system. Instead, it is processed through the space vector PWM in the subsequent time step to generate reference voltages. Consequently, the control input $\mathbf{u}\left(k-1\right)$, which is calculated in the prior time step, is applied to the system at time step $k$. This introduces a one-step time delay in the system dynamics, which can be effectively incorporated into the system model by $\mathbf{u}\left(k-1\right)$ as a time-delayed input [25]. Considering the time delay effect, the system model is expressed as follows [26,27]:

$$\mathbf{x}(k+1)={\mathbf{A}}_{\mathbf{k}}\mathbf{x}\left(k\right)+{\mathbf{B}}_{\mathbf{k}}{\mathbf{u}}_{\mathbf{d}}\left(k\right)+{\mathit{E}}_{\mathbf{k}}\mathbf{e}\left(k\right)$$

(13)

$${\mathbf{u}}_{\mathbf{d}}(k+1)=\mathbf{u}\left(k\right)$$

(14)

$$\mathbf{y}\left(k\right)={\mathbf{C}}_{\mathbf{k}}\mathbf{x}\left(k\right)$$

(15)

where ${\mathbf{A}}_{\mathbf{k}}$, ${\mathbf{B}}_{\mathbf{k}}$, ${\mathbf{C}}_{\mathbf{k}}$, and ${\mathbf{E}}_{\mathbf{k}}$ are the matrices for discretized forms of (11)–(12), and ${\mathbf{u}}_{\mathbf{d}}$ is the one-step delay system input vector.

Equations (13) and (14) are integrated in the matrix form to describe the complete system model as follows:

$$\left[\begin{array}{c}\mathbf{x}\left(k+1\right)\\ {\mathbf{u}}_{\mathbf{d}}\left(k+1\right)\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}}_{\mathbf{k}}& {\mathbf{B}}_{\mathbf{k}}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathbf{x}\left(k\right)\\ {\mathbf{u}}_{\mathbf{d}}\left(k\right)\end{array}\right]+\left[\begin{array}{c}\mathbf{0}\\ \mathbf{I}\end{array}\right]\mathbf{u}\left(k\right)+\left[\begin{array}{c}{\mathbf{E}}_{\mathbf{k}}\\ \mathbf{0}\end{array}\right]\mathbf{e}\left(k\right).$$

(16)

3. Proposed Frequency-Adaptive Control with Incomplete State Observation

This section presents a state feedback current control design utilizing incomplete state observation to stabilize a GCI operating in the presence of LC grid impedance conditions. The designed controller is constructed with the aim of meeting key goals such as accurate reference tracking and effective compensation of harmonic disturbance, along with ensuring robustness against grid frequency fluctuations. To mitigate the influence of grid angular frequency variations, the current observer is constructed at the stationary frame in which the system is not dependent on grid angular frequency. Furthermore, by applying MAF-PLL, the proposed control strategy maintains superior performance despite the grid frequency fluctuations caused by the harmonic distortion of grid voltages.

3.1. Frequency Detection in the Existence of Distorted and Unbalanced Grid Voltages

Figure 2 illustrates the method to extract the frequency and phase angle of grid voltages utilizing the MAF-PLL. The conventional PLL generates the signal $\overline{\omega }$, which is processed by the MAF to obtain $\tilde{\omega }$. The MAF-PLL output $\tilde{\omega }$ represents the fundamental grid frequency with reduced oscillations and fluctuations. Frequency deviations in grid voltage significantly affect the control performance of GCIs and severely degrade the power quality of DG systems, especially those employing resonant control for harmonic compensation. To resolve this problem, this study introduces a frequency-adaptive current control strategy based on MAF-PLL. The PLL extracts the frequency information from the distorted grid voltage, while the MAF additionally removes the fluctuations caused by harmonic distortions [16].

3.2. Current Control for GCI in Existence of LC Impedance and Distorted Grid

To reduce the steady-state error and attenuate harmonic components of the sixth and twelfth orders, the integral-resonant state feedback controller is developed by incorporating integral and resonant components into the system model. In addition, the mitigation of the second harmonic components is also considered to compensate for the impact of unbalanced grid voltages. Integral control, which eliminates the reference tracking error in the steady-state, is represented in the discrete domain as follows [28]:

$$\left[\begin{array}{c}{x}_i^q(k+1)\\ x_i^d(k+1)\end{array}\right]=\mathbf{I}\left[\begin{array}{c}{x}_i^q\left(k\right)\\ x_i^d\left(k\right)\end{array}\right]+H\mathbf{I}\left[\begin{array}{c}{\mathsf{\epsilon }}^q\left(k\right)\\ {\mathsf{\epsilon }}^d\left(k\right)\end{array}\right]$$

(17)

where $\mathsf{\epsilon }={\left[\begin{array}{cc}{\mathsf{\epsilon }}^q& {\mathsf{\epsilon }}^d\end{array}\right]}^T={\mathbf{I}}_2^{*}-{\mathbf{C}}_{\mathbf{d}}\mathbf{x}$ is the current error, ${\mathbf{I}}_2^{*}={\left[\begin{array}{cc}{i}_2^{q*}& i_2^{d*}\end{array}\right]}^T$ is the reference current, and $\mathbf{I}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ is the identity matrix.

Resonant control is designed in the discrete domain [29]. The transfer function of the resonant controller is represented below:

$$R_n\left(z\right)={\displaystyle \frac{z^2-\cos \left({\omega }_{n}H\right)}{z^2-2\cos \left({\omega }_{n}H\right)z+1}}$$

(18)

where ${\omega }_n$ represents the resonant angular frequency and H is the sampling time. By applying the cascade canonical form to (18), a discrete-time state-space representation is given as follows [30]:

$$\left[\begin{array}{c}{x}_{r1j}^q(k+1)\\ x_{r2j}^q(k+1)\\ x_{r1j}^d(k+1)\\ x_{r2j}^d(k+1)\end{array}\right]={\mathbf{A}}_{\mathbf{r}\mathbf{e}j}\left[\begin{array}{c}{x}_{r1j}^q\left(k\right)\\ x_{r2j}^q\left(k\right)\\ x_{r1j}^d\left(k\right)\\ x_{r2j}^d\left(k\right)\end{array}\right]+{\mathbf{B}}_{\mathbf{r}\mathbf{e}j}\left[\begin{array}{c}{\mathsf{\epsilon }}^q\left(k\right)\\ {\mathsf{\epsilon }}^d\left(k\right)\end{array}\right]\mathrm{f}\mathrm{o}\mathrm{r} j=2, 6,12$$

(19)

where

$${\mathbf{A}}_{\mathbf{r}\mathbf{e}j}=\left[\begin{array}{cc}\begin{array}{cc}2\cos \left({j\omega }_{n}H\right)& 1\\ -1& 0\end{array}& \begin{array}{cc}& \\ & \end{array}\\ \begin{array}{cc}& \\ & \end{array}& \begin{array}{cc}2\cos \left({j\omega }_{n}H\right)& 1\\ -1& 0\end{array}\end{array}\right],$$

$${\mathbf{B}}_{\mathbf{r}\mathbf{e}j}=\left[\begin{array}{c}\begin{array}{c}\cos \left({j\omega }_{n}H\right)\\ -1\end{array}\\ \begin{array}{c}\\ \end{array}\end{array}\begin{array}{c}\begin{array}{c}\\ \end{array}\\ \begin{array}{c}\cos \left({j\omega }_{n}H\right)\\ -1\end{array}\end{array}\right].$$

The sixth- and twelfth-order resonant controllers are specifically designed to reduce the effects of harmonic components in distorted grid voltages, while the second-order resonant controller is designed to attenuate the harmonic components that arise due to unbalanced grid voltages. The integral term (17) and resonant term (19) are reformulated as follows:

$${\mathbf{x}}_{\mathbf{I}\mathbf{R}}\left(\mathrm{k}+1\right)=\mathsf{\Phi }{\mathbf{x}}_{\mathbf{I}\mathbf{R}}\left(\mathrm{k}\right)+\mathsf{\Psi }\mathsf{\epsilon }\left(\mathrm{k}\right).$$

(20)

where ${\mathbf{x}}_{\mathbf{I}\mathbf{R}}={\left[\begin{array}{cccc}{\mathbf{x}}_{\mathrm{I}}^T& {\mathbf{x}}_{\mathrm{r}2}^T& {\mathbf{x}}_{\mathrm{r}6}^T& {\mathbf{x}}_{\mathrm{r}12}^T\end{array} \right]}^T$ represents the state variables for integral and resonant terms. The internal state ${\mathbf{x}}_{\mathrm{I}}={\left[\begin{array}{cc}{x}_i^q& x_i^d\end{array}\right]}^T$ is the integral state variables. The other states ${\mathbf{x}}_{\mathrm{r}2}={\left[\begin{array}{cccc}{x}_{r12}^q& x_{r22}^q& x_{r12}^d& x_{r22}^d\end{array}\right]}^T$, ${\mathbf{x}}_{\mathrm{r}6}={\left[\begin{array}{cccc}{x}_{r16}^q& x_{r26}^q& x_{r16}^d& x_{r26}^d\end{array}\right]}^T$, and ${\mathbf{x}}_{\mathrm{r}12}={\left[\begin{array}{cccc}{x}_{r112}^q& x_{r212}^q& x_{r112}^d& x_{r212}^d\end{array}\right]}^T$ are resonant state variables.

$$\mathsf{\Phi }=\left[\begin{array}{cccc}\mathbf{I}& & & \\ & {\mathbf{A}}_{\mathrm{r}\mathrm{e}2}& & \\ & & {\mathbf{A}}_{\mathrm{r}\mathrm{e}6}& \\ & & & {\mathbf{A}}_{\mathrm{r}\mathrm{e}12}\end{array}\right]\mathrm{a}\mathrm{n}\mathrm{d}\mathsf{\Psi }=\left[\begin{array}{c}H\mathbf{I}\\ {\mathbf{B}}_{\mathrm{r}\mathrm{e}2}\\ {\mathbf{B}}_{\mathrm{r}\mathrm{e}6}\\ {\mathbf{B}}_{\mathrm{r}\mathrm{e}12}\end{array}\right].$$

By augmenting (20) into (16), the overall system model for a GCI control is expressed below:

$$\left[\begin{array}{c}\mathbf{x}{\left(k+1\right)}^{10\times 1}\\ {\mathbf{u}}_{\mathbf{d}}{\left(k+1\right)}^{2\times 1}\\ {\mathbf{x}}_{\mathbf{I}\mathbf{R}}{\left(k+1\right)}^{14\times 1}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{A}}_{\mathrm{k}}^{10\times 10}& {\mathbf{B}}_{\mathbf{k}}^{10\times 2}& {\mathbf{0}}^{10\times 14}\\ {\mathbf{0}}^{2\times 10}& {\mathbf{0}}^{2\times 2}& {\mathbf{0}}^{2\times 14}\\ -{\left(\mathsf{\Psi }{\mathbf{C}}_{\mathbf{k}}\right)}^{14\times 10}& {\mathbf{0}}^{14\times 2}& {\mathsf{\Phi }}^{14\times 14}\end{array}\right]\left[\begin{array}{c}\mathbf{x}\left(k\right)\\ {\mathbf{u}}_{\mathbf{d}}\left(k\right)\\ {\mathbf{x}}_{\mathbf{I}\mathbf{R}}\left(k\right)\end{array}\right]+\left[\begin{array}{c}\mathbf{0}\\ \mathbf{I}\\ \mathbf{0}\end{array}\right]\mathbf{u}(k)+\left[\begin{array}{c}{\mathbf{E}}_{\mathbf{k}}\\ \mathbf{0}\\ \mathbf{0}\end{array}\right]\mathbf{e}(k)+\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ \mathsf{\Psi }\end{array}\right]{\mathbf{I}}_2^{*}(k)$$

(21)

where the states in system model (21) are mainly composed of three parts ,which are the states from LCL-filtered GCI and LC grid impedance, the states considering the time delay effect of the system input, and states from the integral and resonant control terms. Equation (21) is expressed in a simplified manner as follows:

$${\mathbf{x}}_{\mathbf{f}}(k+1)={\mathbf{A}}_{\mathbf{f}}{\mathbf{x}}_{\mathbf{f}}\left(k\right)+{\mathbf{B}}_{\mathbf{f}}\mathbf{u}\left(k\right)+{\mathbf{E}}_{\mathbf{f}}\mathbf{e}\left(k\right)+{\mathsf{\Psi }}_{\mathbf{f}}{\mathbf{I}}_2^{*}\left(k\right).$$

(22)

In (22), the entire system consists of twenty-six states, which include ten system states (six states for LCL filter and four states for LC impedance), two states for time delay, two states for integral control, and twelve states for resonant controls at the second, sixth, and twelfth orders. The feedback control is obtained as follows:

$$\mathbf{u}(k)=-\mathbf{K}{\mathbf{x}}_{\mathbf{f}}(k)=-\left[\begin{array}{ccc}{\mathbf{K}}_{\mathbf{x}} & {\mathbf{K}}_{\mathbf{u}}& {\mathbf{K}}_{\mathbf{I}\mathbf{R}}\end{array}\right]\left[\begin{array}{c}\mathbf{x}(\mathrm{k})\\ {\mathbf{u}}_{\mathbf{d}}(\mathrm{k})\\ {\mathbf{x}}_{\mathbf{I}\mathbf{R}}(\mathrm{k})\end{array}\right]={\mathbf{u}}_{\mathbf{x}}(k)+{\mathbf{u}}_{\mathbf{u}}(k)+{\mathbf{u}}_{\mathbf{I}\mathbf{R}}(k)$$

(23)

where ${\mathbf{u}}_{\mathbf{x}}\left(k\right)=-{\mathbf{K}}_{\mathbf{x}}\mathbf{x}\left(k\right),$ ${\mathbf{u}}_{\mathbf{u}}\left(k\right)=-{\mathbf{K}}_{\mathbf{u}}{\mathbf{u}}_{\mathbf{d}}\left(k\right),$ ${\mathbf{u}}_{\mathbf{I}\mathbf{R}}\left(k\right)=-{\mathbf{K}}_{\mathbf{I}\mathbf{R}}{\mathbf{x}}_{\mathbf{I}\mathbf{R}}\left(k\right)$, and $\mathbf{K}=\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{x}} & {\mathbf{K}}_{\mathrm{u}}& {\mathbf{K}}_{\mathrm{I}\mathrm{R}}\end{array}\right].$ In these matrices, ${\mathbf{K}}_{\mathbf{x}}$ is the gain associated with state feedback control, ${\mathbf{K}}_{\mathbf{u}}$ is the gain associated with feedback control for time delay component, and ${\mathbf{K}}_{\mathbf{I}\mathbf{R}}$ is the gain for the integral-resonant control terms.

The control gain matrix $\mathbf{K}$ in (23) is determined with the LQR method by minimizing a specified cost function defined as follows [31]:

$$\mathbf{J}={\displaystyle \frac{1}{2}}\sum _{k=0}^{\infty }{{\mathbf{x}}_{\mathrm{f}}}^T\left(k\right)\mathbf{Q}{\mathbf{x}}_{\mathrm{f}}\left(k\right)+{\mathbf{u}}^T\left(k\right)\mathbf{R}\mathbf{u}\left(k\right)$$

(24)

where $\mathbf{Q}$ is a positive semi-definite matrix, and $\mathbf{R}$ is the positive definite matrix. The matrices $\mathbf{Q}$ and $\mathbf{R}$ are determined in accordance with the relative importance of performance measures. To determine an optimal feedback gain matrix $\mathbf{K}$ systematically, the discrete Algebraic Riccati Equation (ARE) is solved. The matrices $\mathbf{Q}$ and $\mathbf{R}$ are chosen as follows:

$$\mathbf{Q}={\left[ \begin{array}{c} {\mathbf{I}}_{10\times 10}\\ {\mathbf{0}}_{2\times 10}\\ {\mathbf{0}}_{2\times 10}\\ { \mathbf{0}}_{12\times 10}\end{array} \begin{array}{c}{ \mathbf{0}}_{10\times 2}\\ {\mathbf{I}}_{2\times 2}\\ {\mathbf{0}}_{2\times 2}\\ {\mathbf{0}}_{12\times 2}\end{array} \begin{array}{c} {\mathbf{0}}_{10\times 2}\\ {\mathbf{0}}_{2\times 2}\\ 6.3·{10}^8·{\mathbf{I}}_{2\times 2}\\ {\mathbf{0}}_{12\times 2}\end{array} \begin{array}{c}{ \mathbf{0}}_{10\times 12}\\ {\mathbf{0}}_{2\times 12}\\ {\mathbf{0}}_{2\times 12}\\ {0.03·\mathbf{I}}_{12\times 12}\end{array} \right]}_{26\times 26}, \mathbf{R}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

where $\mathbf{0}$ represents the zero matrix with suitable dimension. The weighting for the integral control term is chosen at a high value to ensure accurate reference tracking. Meanwhile, the weighting for the resonant control terms is chosen at a lower value for effective harmonic suppression without excessive sensitivity to grid distortions. The MATLAB R2024a function “dlqr” is utilized to calculate the optimal feedback gains systematically with $\mathbf{Q}$ and $\mathbf{R}$. As mentioned earlier, the state equations for the GCI are expressed as (1)–(10) when LC grid impedance exists caused by the complex grid. A full-state feedback control is not available because it is not possible to measure or estimate the grid inductance current $i_z$. Instead, the state feedback control, except the states $i_z$, should be used. For this purpose, the state vector without the grid inductance current $i_z$ is defined as follows:

$${\mathbf{x}}_{\mathbf{e}\mathbf{x}\mathbf{c}}={\left[i_2^q,i_2^d,i_1^q,i_1^d,v_c^q,v_c^d,v_{pcc}^q,v_{pcc}^d,u_d^q,u_d^d,x_i^q, x_i^d,x_{r12}^q,x_{r22}^q,x_{r12}^d,x_{r22}^d,x_{r16}^q,x_{r26}^q,x_{r16}^d,x_{r26}^d,x_{r112}^q,x_{r212}^q,x_{r112}^d,x_{r212}^d \right]}^T={\mathbf{C}}_{\mathbf{f}}{\mathbf{x}}_{\mathbf{f}}\left(k\right)$$

(25)

where ${\mathbf{C}}_{\mathbf{f}}={\left[\begin{array}{ccc}{\mathbf{I}}_{8\times 8}& {\mathbf{0}}_{8\times 2}& {\mathbf{0}}_{8\times 16}\\ {\mathbf{0}}_{16\times 8}& {\mathbf{0}}_{16\times 2}& {\mathbf{I}}_{16\times 16}\end{array}\right]}_{24\times 26}$.

With (25), the incomplete state feedback control input can be expressed as follows:

$${\mathbf{u}}_{\mathbf{e}\mathbf{x}\mathbf{c}}\left(k\right)=-\mathbf{K}{\mathbf{C}}_{\mathbf{f}}^T{\mathbf{x}}_{\mathbf{e}\mathbf{x}\mathbf{c}}\left(k\right)=-\mathbf{K}{\mathbf{C}}_{\mathbf{f}}^T{\mathbf{C}}_{\mathbf{f}}{\mathbf{x}}_{\mathbf{f}}\left(k\right).$$

(26)

By substituting (26) into the entire system dynamic model (22), the closed-loop system is reformulated as follows:

$${\mathbf{x}}_{\mathrm{f}}\left(k+1\right)=\left({\mathbf{A}}_{\mathrm{f}}-{\mathbf{B}}_{\mathrm{f}}\mathbf{K}{{\mathbf{C}}_{\mathrm{f}}^T\mathbf{C}}_{\mathrm{f}}\right){\mathbf{x}}_{\mathrm{f}}\left(k\right)+{\mathbf{E}}_{\mathrm{f}}\mathbf{e}\left(k\right)+{\mathsf{\Psi }}_{\mathrm{f}}{\mathbf{I}}_2^{*}\left(k\right).$$

(27)

By excluding the state for the grid inductance current due to the uncertainty caused by grid impedance, (23) is rewritten in detail as follows:

$$\mathbf{u}\left(k\right)=-{\mathbf{K}}^{\mathrm{e}\mathrm{x}\mathrm{c}}{\mathbf{x}}_{\mathrm{f}}\left(k\right)=-\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}& {\mathbf{K}}_{\mathrm{u}}& {\mathbf{K}}_{\mathrm{I}\mathrm{R}}\end{array}\right]\left[\begin{array}{c}\mathbf{x}\left(k\right)\\ {\mathbf{u}}_{\mathrm{d}}\left(k\right)\\ {\mathbf{x}}_{\mathrm{I}\mathrm{R}}\left(k\right)\end{array}\right]={\mathbf{u}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}\left(k\right)+{\mathbf{u}}_{\mathrm{u}}\left(k\right)+{\mathbf{u}}_{\mathrm{I}\mathrm{R}}\left(k\right)$$

(28)

where ${\mathbf{K}}^{\mathrm{e}\mathrm{x}\mathrm{c}}=\mathbf{K}{\mathbf{C}}_{\mathbf{f}}^T{\mathbf{C}}_{\mathbf{f}}=\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{x}} & {\mathbf{K}}_{\mathrm{u}}& {\mathbf{K}}_{\mathrm{I}R}\end{array}\right]{\mathbf{C}}_{\mathrm{f}}^T{\mathbf{C}}_{\mathrm{f}}=\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}& {\mathbf{K}}_{\mathrm{u}}& {\mathbf{K}}_{\mathrm{I}\mathrm{R}}\end{array}\right]$ is the gain matrix designed to generate the control input utilizing the measurable and estimated states. This modification solves the limitation of the unavailable grid inductance current state. The control input ${\mathbf{u}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}\left(k\right)=-{\mathbf{K}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}\mathbf{x}\left(k\right)$ represents the term derived from the modified state feedback gain ${\mathbf{K}}_{\mathrm{x}}^{\mathrm{e}\mathrm{x}\mathrm{c}}$. Figure 3 shows the flowchart to clearly represent the methodology and execution of the entire control algorithm. After two grid-side currents and PCC voltages are measured, the proposed control scheme sequentially executes the MAF-PLL, construction of full-state current observer, construction of state feedback controller based on incomplete states, and implementation of the space vector PWM scheme.

3.3. Observer Implementation in Stationary Reference Frame

State equations in (1)–(10) describe the dynamic model of the GCI system at the SRF when the utility grid has uncertain LC grid impedance. Among them, while the equations in (1)–(6) represent the dynamic model of the LCL filter, the equations in (7)–(10) represent the dynamic model caused by uncertain LC grid impedance, which is not designed filter parameters but uncertain and unknown components in the utility grid. Instead of using a reduced-order state observer for (1)–(10) with uncertain and unknown parameters, a full-state current observer for (1)–(6) with known designed LCL parameters is employed in this paper. A full-state current observer is designed to minimize the dependency on extra sensing devices. The observer is developed at the stationary reference frame to avoid the need for varying frequency information. By implementing the observer in the stationary reference frame, the system model is unaffected by the grid frequency information. As a result, a complex online discretization process can be avoided. Otherwise, if the SRF is applied for observer design, online discretization is unavoidable because the system model includes the varying parameters of the grid frequency information. The continuous-time LCL-filtered GCI system model is given at the stationary reference frame as follows:

$${\displaystyle \frac{d}{dt}}{i}_2^{\alpha }(t)={\displaystyle \frac{1}{L_2}}{v}_c^{\alpha }(t)-{\displaystyle \frac{1}{L_2}}{v}_{pcc}^{\alpha }(t)$$

(29)

$${\displaystyle \frac{d}{dt}}{i}_2^{\beta }(t)={\displaystyle \frac{1}{L_2}}{v}_c^{\beta }(t)-{\displaystyle \frac{1}{L_2}}{v}_{pcc}^{\beta }(t)$$

(30)

$${\displaystyle \frac{d}{dt}}{i}_1^{\alpha }\left(t\right)=-{\displaystyle \frac{1}{L_1}}{v}_c^{\alpha }\left(t\right)+{\displaystyle \frac{1}{L_1}}{v}_i^{\alpha }(t)$$

(31)

$${\displaystyle \frac{d}{dt}}{i}_1^{\beta }\left(t\right)=-{\displaystyle \frac{1}{L_1}}{v}_c^{\beta }\left(t\right)+{\displaystyle \frac{1}{L_1}}{v}_i^{\beta }(t)$$

(32)

$${\displaystyle \frac{d}{dt}}{v}_c^{\alpha }\left(t\right)=-{\displaystyle \frac{1}{C_m}}{i}_2^{\alpha }\left(t\right)+{\displaystyle \frac{1}{C_m}}{i}_1^{\alpha }(t)$$

(33)

$${\displaystyle \frac{d}{dt}}{v}_c^{\beta }\left(t\right)=-{\displaystyle \frac{1}{C_m}}{i}_2^{\beta }\left(t\right)+{\displaystyle \frac{1}{C_m}}{i}_1^{\beta }\left(t\right)$$

(34)

where the superscripts $“\alpha$” and “$\beta ”$ represent the stationary reference frame. The above equations are formulated in the state-space model as follows:

$${\dot{\mathbf{x}}}_{\mathrm{e}}\left(t\right)={\mathbf{A}}_{\mathrm{e}}{\mathbf{x}}_{\mathrm{e}}\left(t\right)+{\mathbf{B}}_{\mathrm{e}}{\mathbf{u}}_{\mathrm{e}}\left(t\right)+{\mathbf{E}}_{\mathrm{e}}{\mathbf{v}}_{\mathrm{e}}\left(t\right)$$

(35)

$${\mathbf{y}}_{\mathrm{e}}\left(t\right)={\mathbf{C}}_{\mathrm{e}}{\mathbf{x}}_{\mathrm{e}}\left(t\right)$$

(36)

where ${\mathbf{x}}_{\mathrm{e}}={\left[i_2^{\alpha },i_2^{\beta },i_1^{\alpha },i_1^{\beta },v_c^{\alpha },v_c^{\beta }\right]}^T$ is the system state vector, ${\mathbf{u}}_{\mathrm{e}}={\left[v_i^{\alpha },v_i^{\beta }\right]}^T$ is the system input vector, ${\mathbf{v}}_{\mathrm{e}}={\left[v_{pcc}^{\alpha },v_{pcc}^{\beta }\right]}^T$ is the PCC voltage vector, and ${\mathbf{y}}_{\mathbf{e}}={\left[i_2^{\alpha },i_2^{\beta }\right]}^T$ is system output. The observer system matrices ${\mathbf{A}}_{\mathrm{e}}$, ${\mathbf{B}}_{\mathrm{e}}$, ${\mathbf{C}}_{\mathrm{e}},$ and ${\mathbf{E}}_{\mathrm{e}}$ are given as follows:

$${\mathbf{A}}_{\mathrm{e}}=\left[\begin{array}{cccccc}0& 0& 0& 0& 1/L_2& 0\\ 0& 0& 0& 0& 0& 1/L_2\\ 0& 0& 0& 0& -1/L_1& 0\\ 0& 0& 0& 0& 0& -1/L_1\\ -1/C_m& 0& 1/C_m& 0& 0& 0\\ 0& -1/C_m& 0& 1/C_m& 0& 0\end{array}\right]$$

$${\mathbf{B}}_{\mathrm{e}}=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 1/L_1& 0\\ 0& 1/L_1\\ 0& 0\\ 0& 0\end{array}\right], {\mathbf{E}}_{\mathrm{e}}=\left[\begin{array}{cc}-1/L_2& 0\\ 0& -1/L_2\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right],\mathrm{a}\mathrm{n}\mathrm{d}{\mathbf{C}}_{\mathrm{e}}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\end{array}\right].$$

Equations (35) and (36) are discretized using the ZOH method as follows:

$${\mathbf{x}}_{\mathrm{e}}(k+1)={\mathbf{A}}_{\mathrm{e}\mathrm{k}}{\mathbf{x}}_{\mathrm{e}}\left(k\right)+{\mathbf{B}}_{\mathrm{e}\mathrm{k}}{\mathbf{u}}_{\mathrm{e}}\left(k\right)+{\mathbf{E}}_{\mathrm{e}\mathrm{k}}{\mathbf{v}}_{\mathrm{e}}\left(k\right)$$

(37)

$${\mathbf{y}}_{\mathrm{e}}\left(k\right)={\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\mathbf{x}}_{\mathrm{e}}\left(k\right).$$

(38)

The matrices ${\mathbf{A}}_{\mathrm{e}\mathrm{k}}, {\mathbf{B}}_{\mathrm{e}\mathrm{k}}, {\mathbf{E}}_{\mathrm{e}\mathrm{k}}$, and ${\mathbf{C}}_{\mathrm{e}\mathrm{k}}$ are the discretized forms for the matrices ${\mathbf{A}}_{\mathrm{e}}, {\mathbf{B}}_{\mathrm{e}}, {\mathbf{E}}_{\mathrm{e}}$, and ${\mathbf{C}}_{\mathrm{e}}$. Because the systems of (37) and (38) are observable, the full state can be estimated by the observer [27]. In this study, the state variables of the above model are estimated by utilizing a current observer, which utilizes measurable current states for state estimation. In contrast to the prediction observer, which estimates the system states based on the measurement at time $\left(k-1\right)H$, the current observer estimates the states by using the measurement at time $kH$. By employing a current observer, it is possible to implement the feedback current control with accurate state variables. The discrete-time current observer is constructed as follows:

$${\overline{\mathbf{x}}}_{\mathrm{e}}(k+1)={\mathbf{A}}_{\mathrm{e}\mathrm{k}}{\widehat{\mathbf{x}}}_{\mathrm{e}}\left(k\right)+{\mathbf{B}}_{\mathrm{e}\mathrm{k}}\mathbf{u}\left(k\right)+{\mathbf{E}}_{\mathrm{e}\mathrm{k}}{\mathbf{v}}_{\mathrm{e}}\left(k\right)$$

(39)

$${\widehat{\mathbf{x}}}_{\mathrm{e}}\left(k+1\right)={\overline{\mathbf{x}}}_{\mathrm{e}}\left(k+1\right)+{\mathbf{K}}_{\mathrm{e}}\left({\mathbf{y}}_{\mathrm{e}}\left(k+1\right)-{\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\overline{\mathbf{x}}}_{\mathrm{e}}\left(k+1\right)\right)$$

(40)

where ${\mathbf{K}}_{\mathrm{e}}$ represents the observer gain matrix obtained by the “dlqr” function in MATLAB. The variable ${\overline{\mathbf{x}}}_{\mathrm{e}}(k+1)$ denotes the predicted state vector based on the system dynamics and input signal at the given sampling step $kH$, while the symbol “^” indicates the estimated value obtained from the predicted state. From (37), (38), and (40), the estimation error ${\mathsf{\epsilon }}_e\left(k\right)={\mathbf{x}}_{\mathrm{e}}\left(k\right)-{\widehat{\mathbf{x}}}_{\mathrm{e}}\left(k\right)$ is obtained as follows:

$${\mathsf{\epsilon }}_e\left(k+1\right)={(\mathbf{A}}_{\mathrm{e}\mathrm{k}}-{{\mathbf{K}}_{\mathrm{e}}\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\mathbf{A}}_{\mathrm{e}\mathrm{k}}){\mathsf{\epsilon }}_e\left(k\right).$$

(41)

The observer gain ${\mathbf{K}}_{\mathrm{e}}$ is determined to ensure that all eigenvalues of ${(\mathbf{A}}_{\mathrm{e}\mathrm{k}}-{{\mathbf{K}}_{\mathrm{e}}\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\mathbf{A}}_{\mathrm{e}\mathrm{k}})$ lie in the stable region.

Figure 4 represents the entire control block diagram based on incomplete state observation, which includes the state feedback controller, integral-resonant controller, and full-state current observer based on incomplete states.

3.4. Stability Analysis

This section provides a stability analysis for the proposed control scheme and full-state current observer for the GCI system when LC grid impedance exists. To guarantee robustness and stability, all eigenvalues of the matrix $\left({\mathbf{A}}_{\mathrm{f}}-{\mathbf{B}}_{\mathrm{f}}\mathbf{K}{{\mathbf{C}}_{\mathrm{f}}^T\mathbf{C}}_{\mathrm{f}}\right)$ in (27) must lie within the unit circle. Also, all eigenvalues of ${(\mathbf{A}}_{\mathrm{e}\mathrm{k}}-{{\mathbf{K}}_{\mathrm{e}}\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\mathbf{A}}_{\mathrm{e}\mathrm{k}})$ in (41) must exist within the unit circle to ensure stability of the designed full-state current observer. Figure 5a,b depicts the eigenvalues of the matrices $\left({\mathbf{A}}_{\mathrm{f}}-{\mathbf{B}}_{\mathrm{f}}\mathbf{K}{{\mathbf{C}}_{\mathrm{f}}^T\mathbf{C}}_{\mathrm{f}}\right)$ and ${(\mathbf{A}}_{\mathrm{e}\mathrm{k}}-{{\mathbf{K}}_{\mathrm{e}}\mathbf{C}}_{\mathrm{e}\mathrm{k}}{\mathbf{A}}_{\mathrm{e}\mathrm{k}})$, respectively, under LC grid impedance with $L_g$ of 3 mH and $C_g$ of 6 µF. As shown in these figures, all the eigenvalues lie within the unit circle. These analyses substantiate the stability of both the proposed control approach for the LCL-filtered GCI and full-state current observer.

4. Simulation Results

The performance of the designed current control strategy is assessed by conducting simulations for an LCL-filtered GCI with the PSIM software. Figure 6 represents the schematic for GCI implementation of PSIM. In this section, the monitored variables include the grid voltages, PCC voltages, inverter-side current, grid-side current, and capacitor voltages, which are essential for evaluating the control performance.

The control performance is evaluated under severe grid conditions, including the distorted grid voltages with imbalance at a-phase, grid frequency variations, and existence of LC grid impedance. Detailed system parameters for the GCI are represented in

Table 1. Parameters of a GCI system.

Parameters	Value	Units
DC-link voltage	420	V
Grid voltage (line-to-neutral)	180	V
Grid frequency	60/50/55	Hz
Grid capacitance	6	µF
Grid inductance	3	mH
Grid-side filter inductance	0.9	mH
Inverter-side filter inductance	1.7	mH
Filter capacitance	4.5	µF

.

Figure 7a shows the grid voltages with harmonic distortion and imbalance, and Figure 7b presents the fast Fourier transform (FFT) result obtained from a-phase grid voltage. These figures indicate a seriously distorted grid condition applied to the simulation. The magnitude of a-phase grid voltage is 10% lower than those of the other phase voltages. The grid voltages possess harmonic distortions of the fifth, seventh, eleventh, and thirteenth orders. The FFT result demonstrates significant harmonic components, resulting in a total harmonic distortion (THD) of 9.97%.

Figure 8a depicts the corresponding PCC voltages between the LC grid impedance and LCL filter. The PCC voltages are also contaminated with harmonic distortion like grid voltages. However, because of LC impedance, the harmonic characteristics of the PCC voltages deteriorated more from those of the grid voltages, exhibiting more distortion. Figure 8b represents the FFT result of a-phase PCC voltage in which the THD is increased to 10.32%. Such a severe distortion significantly influences the frequency detection accuracy and grid-injected current quality.

With the given grid conditions in Figure 7 and Figure 8, the robustness of the designed control strategy is evaluated. Figure 9a depicts the grid-side currents at steady-state along with the q-axis current. Phase currents maintain quite sinusoidal without the influence of harmonic distortion and imbalance of grid voltages. Figure 9b depicts the FFT result of a-phase grid-side current. All harmonic components are suppressed well with the THD of 1.24%, which indicates an effective harmonic suppression and stable operation of the proposed control strategy. Moreover, the grid-injected currents controlled by the designed control strategy satisfy the harmonic limits and power quality requirements specified in IEEE Standard 1547.

The simulation tests for the grid-side currents, inverter-side currents, and capacitor voltages are illustrated in Figure 10 with the step change in the q-axis current reference. Even during the step change moment, distortion remains minimal, which demonstrates the superior transient response of the proposed control strategy. The grid-side current accurately tracks the reference under step change conditions without a significant overshoot or oscillation.

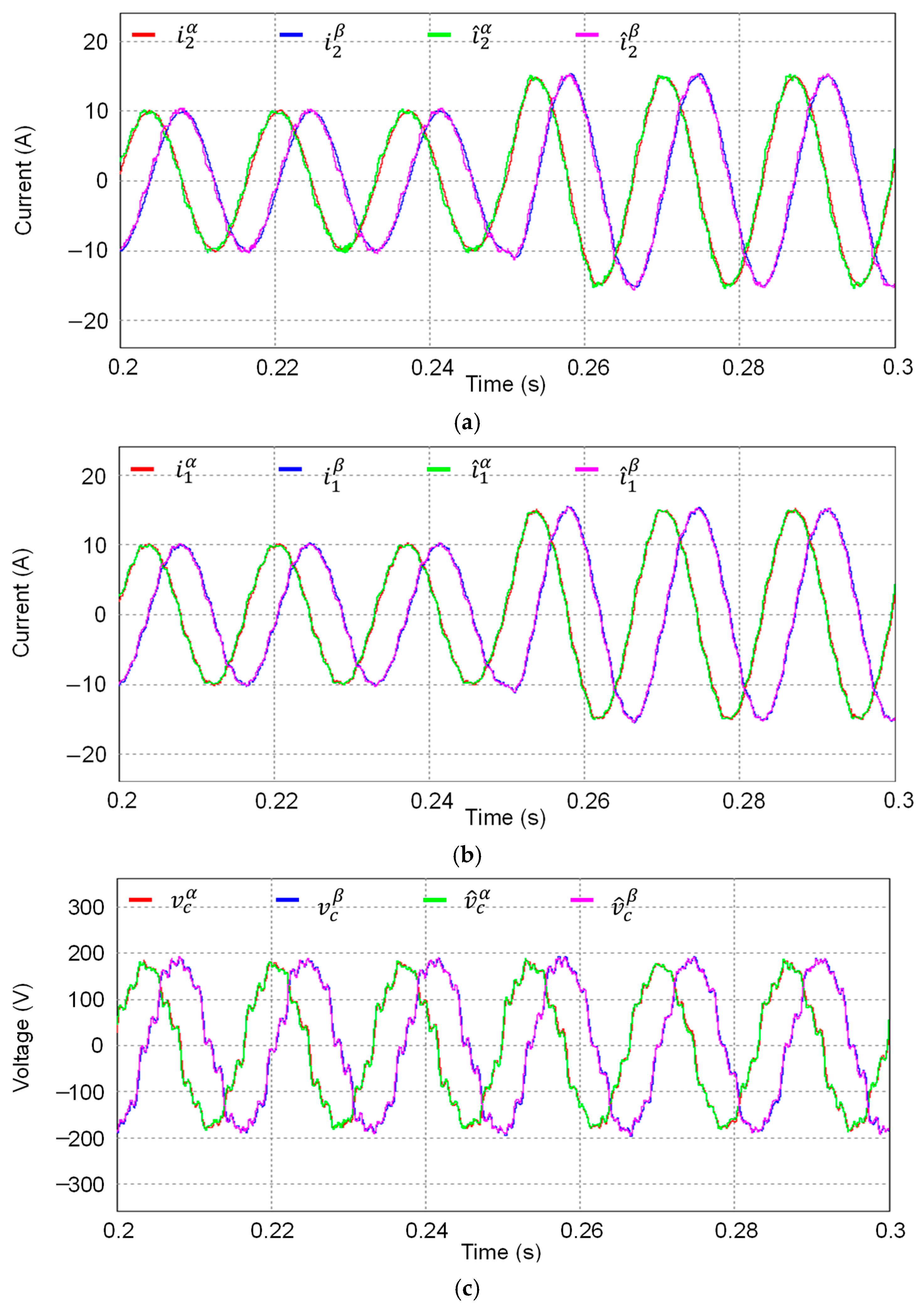
The simulation results of the full-state current observer designed at stationary frame are depicted in Figure 11. Figure 11a–c represents the waveforms of the grid-side currents, inverter-side currents, and capacitor voltages for sensed and estimated values respectively. It demonstrates that the states obtained by the observer accurately track the actual states even during transient conditions.

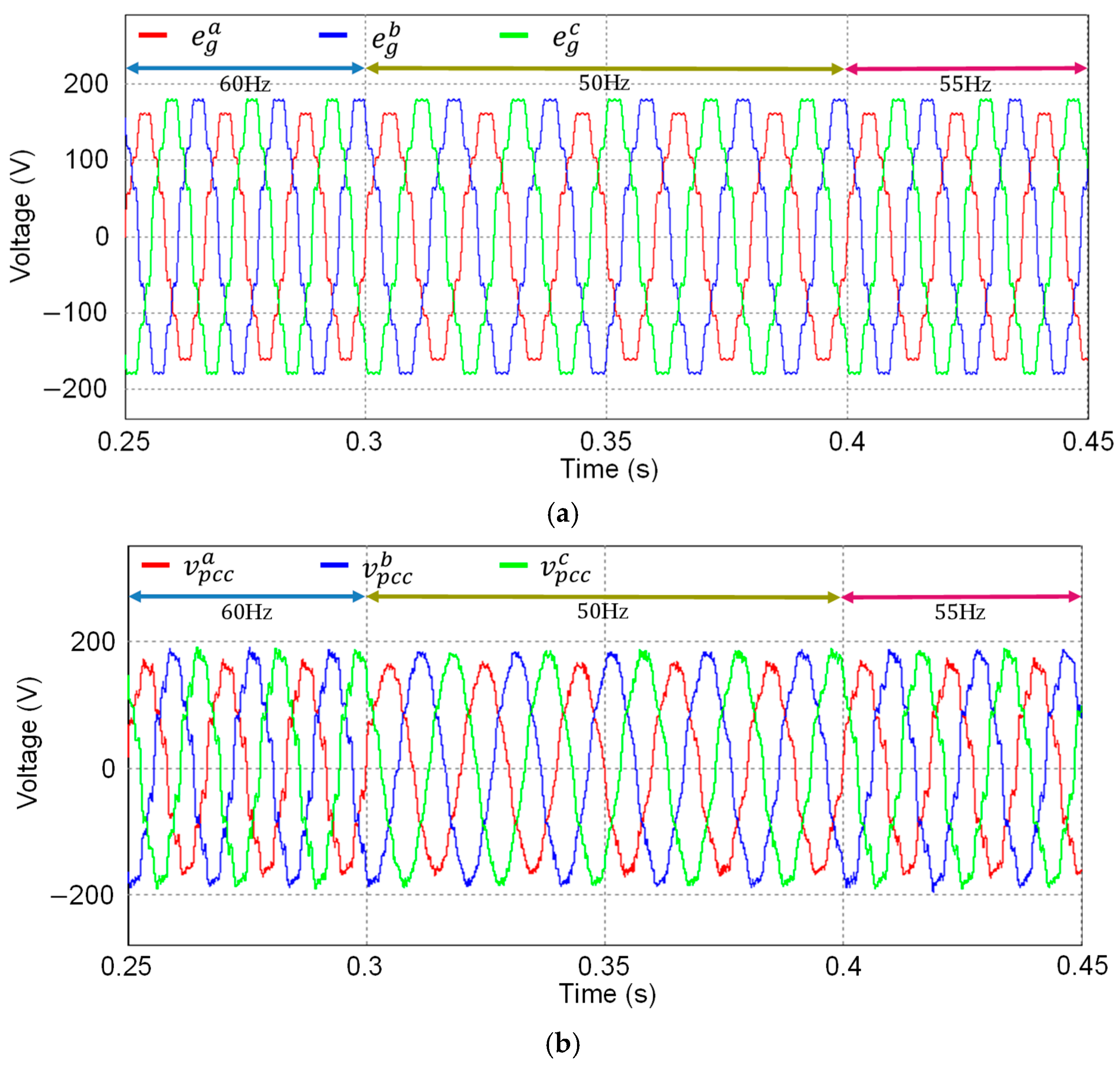
In addition to the validation of current control performance under severe grid conditions, the efficiency of the designed frequency-adaptive current control strategy is also evaluated with varying grid frequency conditions. Figure 12a,b show the grid voltages and PCC voltages with the grid frequency variation from 60 Hz to 50 Hz at 0.3 s and variation from 50 Hz to 55 Hz at 0.4 s. The grid voltages have the same distortion and imbalance as shown in Figure 7 and Figure 8. Even though such large frequency variation is not common in actual power grids, it is applied to assess the performance of the control strategy rigorously with severe grid conditions in simulation.

The simulation tests in Figure 13 represent the capability of the proposed control strategy to maintain stability by adapting effectively under dynamic grid frequency changes. Figure 13a shows the enhanced frequency detection performance achieved by the MAF-PLL. Compared with the conventional PLL, the MAF-PLL exhibits superior accuracy in detecting the grid frequency without severe fluctuation caused by the grid voltage distortion, which facilitates effective current control even under grid frequency variation conditions. Figure 13b–d illustrate the responses for the grid-side currents, inverter-side currents, and capacitor voltages under grid frequency changes. Figure 13e,f show the enlarged waveforms for the grid-side currents captured at the moments of frequency variation. Current waveforms are distorted at the grid frequency change instant. However, the current distortion and oscillation are rapidly recovered to sinusoidal waveform even under grid frequency variations, which confirms the stability and resilience of the designed frequency-adaptive current control.

Figure 14 shows the simulation results of the grid-side currents at the instant of frequency change when the scheme in [25] is used with the same grid conditions under grid frequency changes. Contrary to the proposed control scheme in Figure 13, since the scheme in [25] lacks frequency-adaptive capability, the current control performance is degraded under the grid frequency variation, yielding a poor quality of injected currents.

For comparison with the proposed control scheme under the same severe grid conditions, Figure 15 shows the simulation result of the conventional frequency-adaptive current controller in [22], which does not consider the uncertainty of LC grid impedance. Whereas Figure 15a shows the grid-side current responses without uncertain LC impedance, Figure 15b shows the responses with uncertain LC impedance. From these tests, the frequency-adaptive capability is well demonstrated when uncertain LC grid impedance is not present. However, since this control scheme does not consider the robustness under uncertain LC grid impedance, the current control performance is severely degraded under the presence of LC grid impedance.

Additionally, the estimation accuracy of the current observer is assessed under the grid frequency variations. Figure 16 depicts the simulation tests of the discrete-time current observer with identical grid frequency changes as in Figure 12. Figure 16a–c represents the sensed and estimated grid-side currents, inverter-side currents, and capacitor voltages, respectively. Even under grid frequency variations, the full-state current observer effectively estimates the state variables.

The comprehensive simulation results from Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 confirm the stable performance of the designed frequency-adaptive current control strategy and observer under very severe grid conditions. In the next section, the experimental tests are demonstrated to further confirm the proposed control strategy.

5. Experimental Results

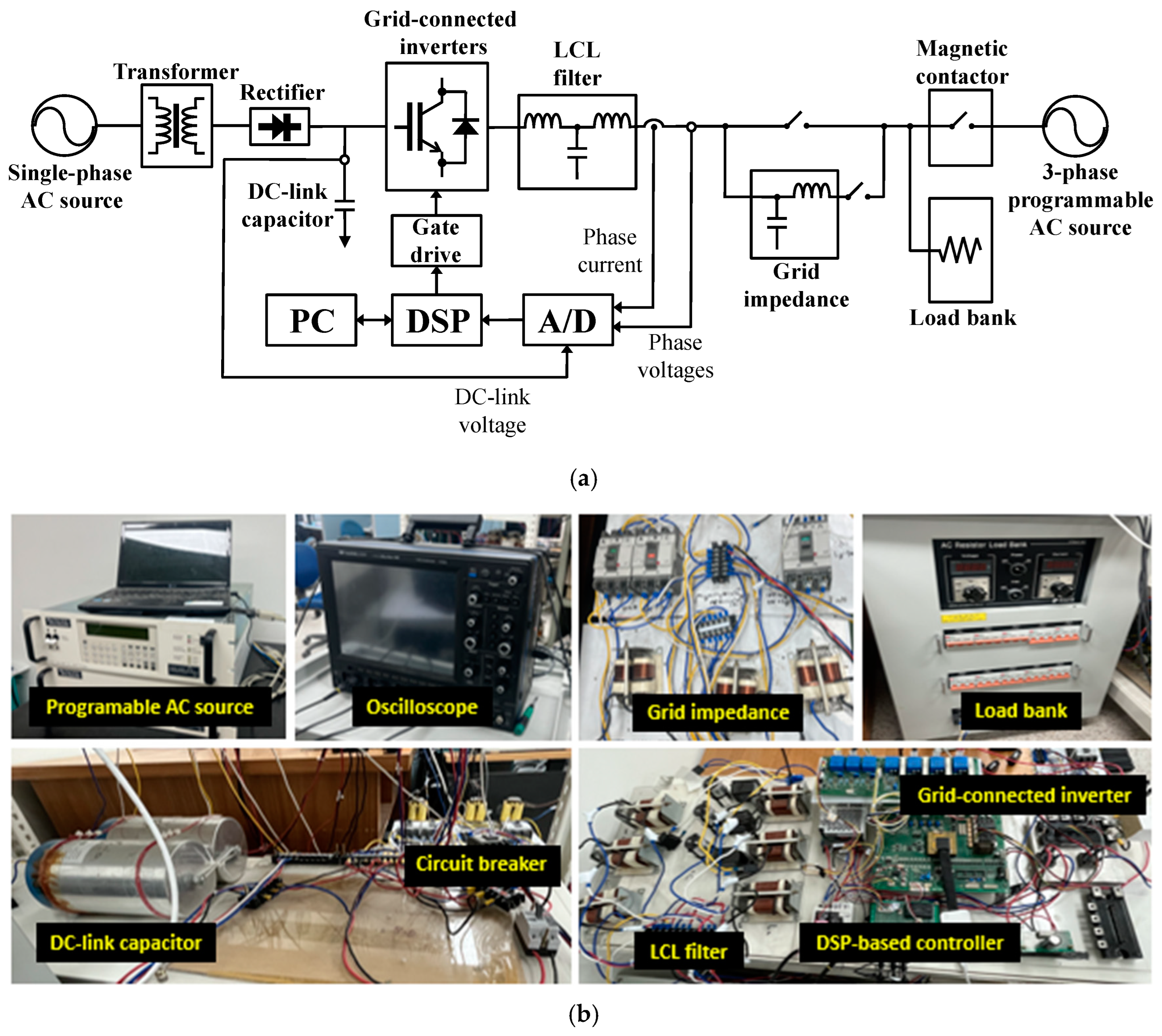
Figure 17a depicts the experimental setup utilized to substantiate the effectiveness of the designed current control strategy. The entire control algorithm for the GCI system is executed on 32-bit floating-point digital signal processor (DSP) TMS320F28335. The single-phase AC source is rectified to produce a DC source voltage for the GCI system. Through the LCL filter and magnetic contactor, the GCI system is linked to a three-phase programmable AC source, which is employed to generate several grid conditions, including the frequency variation, harmonic distortion, and imbalance of the grid voltages. In the experimental setup, several sensors are employed to measure the DC-link voltage, PCC voltages, and grid-side currents, which provide feedback signals to the controller. The measurement signals by sensors are sent to the DSP board utilizing an analog-to-digital (A/D) converter. The computed references in the DSP are used to generate the PWM signals through the space vector PWM method. Figure 17b represents the photograph of the experimental system.

Table 2. Execution time of the proposed control scheme.

Full algorithm	73 μs
Space vector modulation, PLL	50 μs
Data acquisition (three voltage sensors and two current sensors)	5 μs
Current-type full state observer	10 μs
Proposed current controller	8 μs

shows the execution time to implement the proposed control scheme in DSP. The execution of the overall control algorithm needs 73 µs. As a result, the proposed scheme can be effectively realized in a commercial DSP with a reasonable sampling time.

Figure 18a illustrates the grid voltages with harmonic distortion and imbalance, which are used in the experiment. Figure 18b depicts the PCC voltages measured between the LCL filter and LC grid impedance, and Figure 18c displays the FFT result of a-phase PCC voltage. The grid voltages and PCC voltages have the harmonic components of the fifth, seventh, eleventh, and thirteenth orders. Due to the detrimental effect of LC impedance, the PCC voltages are more distorted compared to the grid voltages. Moreover, Figure 18c demonstrates that high-order harmonic components are more affected by grid impedance compared to lower-order harmonics. In addition to harmonic distortions, grid voltages also have imbalances such that the magnitude of a-phase grid voltage is 90% of the other phase voltages.

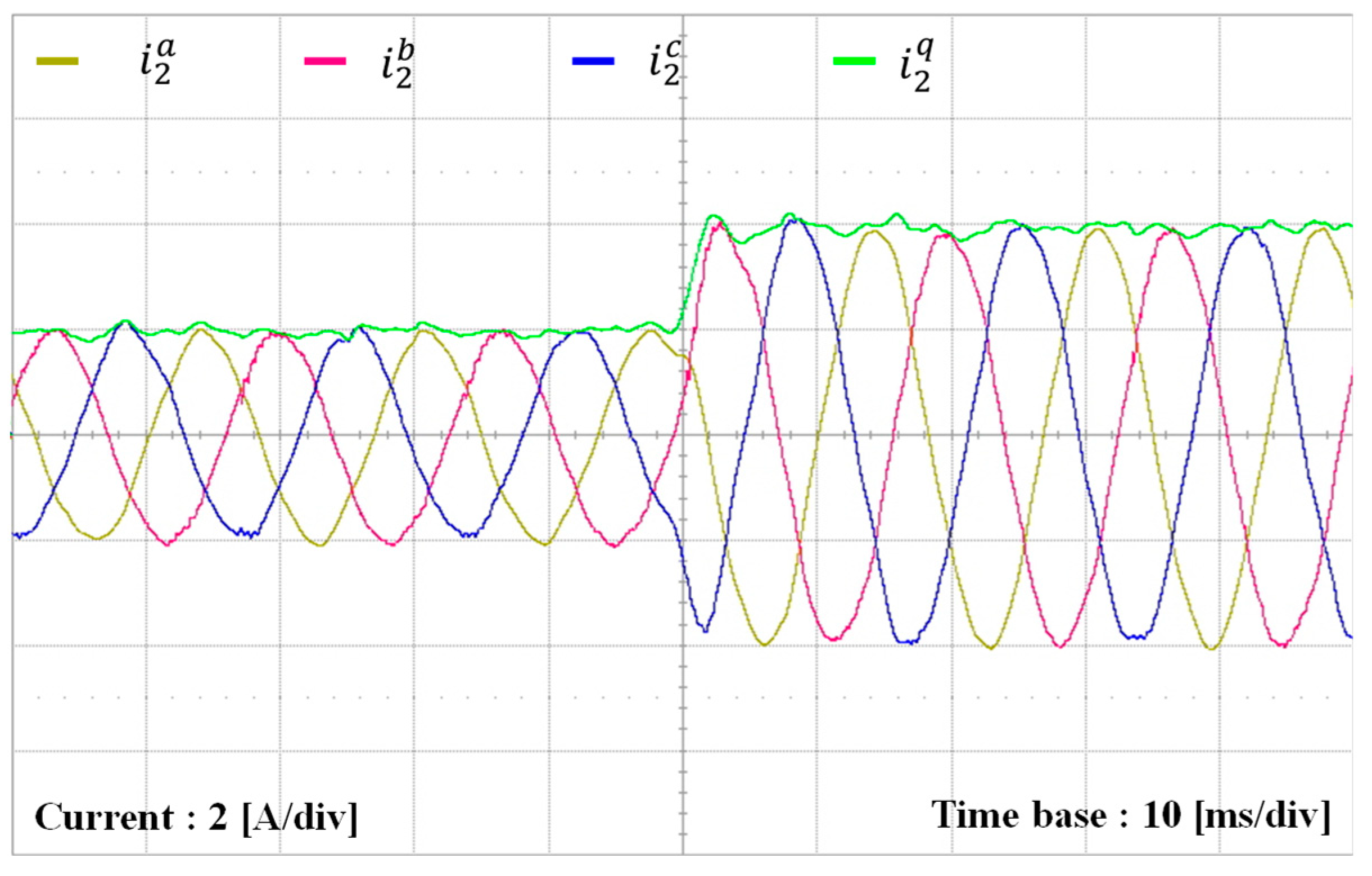
To validate the steady-state behavior of the proposed control strategy, Figure 19a depicts the grid-side phase currents and q-axis current waveforms, and Figure 19b depicts the FFT result of the a-phase current. Despite severe grid conditions, the phase currents maintain a sinusoidal waveform without significant harmonic distortion, similar to the simulation results. Also, the proposed strategy successfully reduces the harmonic distortions in the grid voltage and produces only minor harmonic components, as illustrated in the FFT of a-phase current.

To evaluate the transient response, Figure 20 depicts the experimental tests for the grid-side currents when a step change occurs in the q-axis current reference from 2 A to 4 A. The grid-side currents respond to updated current reference expeditiously, achieving a reasonable settling time only with a slight overshoot. Thus, the control strategy maintains the robust stability during transients, ensuring the reliable performance under dynamic conditions.

Furthermore, Figure 21 represents the experimental tests of the proposed observer performance with the step change of the current reference. Figure 21a–c presents the sensed and estimated values of the grid-side currents, inverter-side currents, and capacitor voltages for a-phase and b-phase, respectively. All figures distinctly indicate a precise tracking capability of the proposed current observer under the step change of the current reference.

Figure 22a,b depicts the grid and PCC voltages in the presence of the grid frequency change from 60 Hz to 50 Hz under the same harmonic distortion and imbalance, as shown in Figure 18. Both the grid and PCC voltages exhibit quite severe distortions, such as harmonic distortion, unbalanced a-phase voltage, grid frequency changes, and LC grid impedance. As in the previous case, the PCC voltages show more distortion compared to the grid voltages.

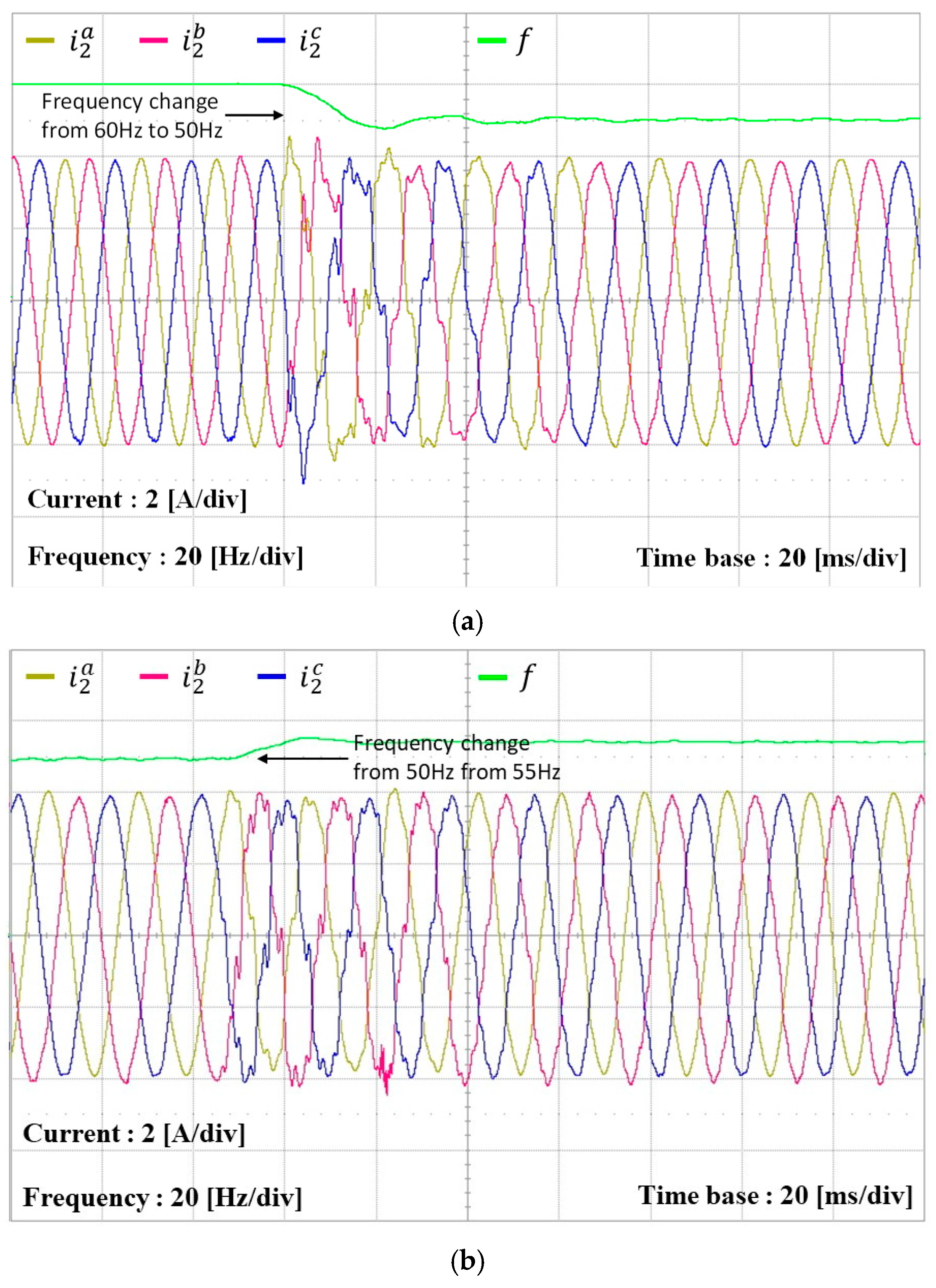
To assess the performance of the proposed control strategy with the grid frequency fluctuation, Figure 23 illustrates the transient behaviors of MAF-PLL-based frequency detection and grid-side currents during frequency changes. Figure 23a presents the responses for a frequency decrease from 60 Hz to 50 Hz, while Figure 23b presents the responses for a frequency increase from 50 Hz to 55 Hz. In both cases, although some oscillations occur at the moments of frequency change, the system quickly regains control stability and sinusoidal waveform in three to four fundamental cycles. The test results clearly confirm that the frequency-adaptive performance of the current control scheme is still maintained even with severe harmonic distortions and imbalance, as well as LC grid impedance.

The frequency-adaptive capability and robustness of the proposed current control scheme highly rely on the observer estimation capability. Figure 24 demonstrates the performance of the current observer introduced in Section 3.3 during the grid frequency transition from 60 Hz to 50 Hz. Figure 24a–c shows the sensed and estimated values for a-phases and b-phases of the grid-side currents, inverter-side currents, and capacitor voltages, respectively. Despite oscillations in currents and voltages, the observer precisely tracks system states under frequency variations.

Figure 25 depicts the experimental results for the current observer under the grid frequency variation from 50 Hz to 55 Hz. Similar to Figure 24, the estimated values closely match the sensed values, which confirms the usefulness of the designed current observer with grid frequency changes. Despite the design in the stationary frame, the observer demonstrates a robust estimation capability.

6. Conclusions

In this study, a frequency-adaptive current control of a GCI based on incomplete state observation is proposed under severe grid conditions. A control strategy for the GCI equipped with LCL filters is specifically designed to handle severe grid conditions characterized by the grid frequency variation, harmonic distortion and imbalance of the grid voltages, and the presence of LC grid impedance. When LC grid impedance exists, it introduces additional states in a GCI system model. However, since the state for the grid inductance current is unmeasurable, it yields a limitation in THE state feedback control design. To overcome such a limitation, this study adopts a state feedback control approach based on incomplete state observation by designing the controller only with the available states. This approach simplifies the control design and implementation while ensuring a robust performance under uncertain grid conditions. In addition, to ensure a stable and high-quality current injection into the grid with varying grid frequency conditions, the MAF-PLL is incorporated into the proposed control scheme. For the purpose of tracking the reference currents precisely and mitigating the harmonic disturbances effectively, the proposed method also integrates integral state feedback and resonant control schemes. In order to reduce the reliance on additional sensing devices, a discrete-time full-state current observer is utilized. In particular, to avoid the grid frequency dependency of the system model, as well as the complex online discretization process, the stationary reference frame observer design is developed in this study. The overall control algorithm is executed on 32-bit floating-point DSP TMS320F28335 and tested with a three-phase prototype GCI system under severe grid conditions. Simulation and experimental results confirm the robustness and effectiveness of the proposed control scheme in delivering stable and high-quality currents into the grid even in the presence of severe grid conditions, such as harmonic distortion, unbalanced grid voltage, grid frequency changes, and LC grid impedance.

Simulation and experimental test results demonstrate that the proposed control scheme provides quite sinusoidal high-quality current with very low THD levels, even under distorted and unbalanced grid voltages. The performance of the proposed control scheme is also compared with two conventional methods. Whereas the conventional methods fail to show a frequency-adaptive capability or stable currents under LC grid impedance, the proposed scheme maintains the frequency-adaptive capability under the grid frequency change, as well as the stability of current response under LC grid impedance.