Efficient Short-Term Wind Power Prediction Using a Novel Hybrid Machine Learning Model: LOFVT-OVMD-INGO-LSSVR
Abstract
1. Introduction
- (1)
- The LOF algorithm was employed to filter the wind power data features to preserve reasonable data for sudden changes in wind speed while eliminating outliers.
- (2)
- The VT algorithm was utilized to categorize wind power data according to seasonal types and weather conditions to develop a corresponding wind electricity forecasting model.
- (3)
- The optimized VMD algorithm was used to perform multimodal decomposition of the historical wind power data, which can enable analysis of the time-varying characteristics of wind power time series under different sub-signals to enhance the predictive performance of the model.
- (4)
- The NGO algorithm was enhanced by incorporating logical chaos initialization and chaotic adaptive inertia weights. The improved algorithm was employed to optimize the LSSVR model. The goal is to accelerate the convergence of the model training process and prevent the model from being trapped in a local optimum solution.
2. Methodology
2.1. Data Pre-Processing
2.1.1. Local Outlier Factor (LOF)
2.1.2. Savitzky–Golay Filter
2.1.3. Voting Tree Algorithm (VT)
2.1.4. L2 Normalization
2.2. Improved Northern Goshawk Optimization Algorithm (INGO)
2.2.1. Logical Chaos Initialization
2.2.2. Chaotic Adaptive Inertia Weights
| Algorithm 1. INGO Algorithm Process |
| Start INGO. 1. Input the parameters of the optimization problem. 2. Input the INGO population size (N) and the number of iterations (T). 3. Initialize the position of the northern eagle using the logistic chaos Equation (13). 4. For t = 1: T 5. Generate the position of the prey at random. 6. Phase 1: Identifying prey(exploration phase). 7. For j = 1: N 8. Calculate new status of the th dimension using Equation (9). 9. End. 10. Update the th population member using Equation (10). 11. Phase 2: Tracking prey(development phase). 12. For j = 1: N 13. Update the chaotic adaptive inertia weights using Equation (14). 14. Calculate new status of the th dimension using Equation (11). 15. End. 16. Update the th population member using Equation (12). 17. Update best candidate solution. 18. End. 19. Output best candidate solution obtained by INGO. End INGO. |
2.3. Variational Mode Decomposition (VMD)
2.4. Least Squares Support Vector Regression Model (LSSVR)
3. Composition of the Proposed Model
4. Case Study
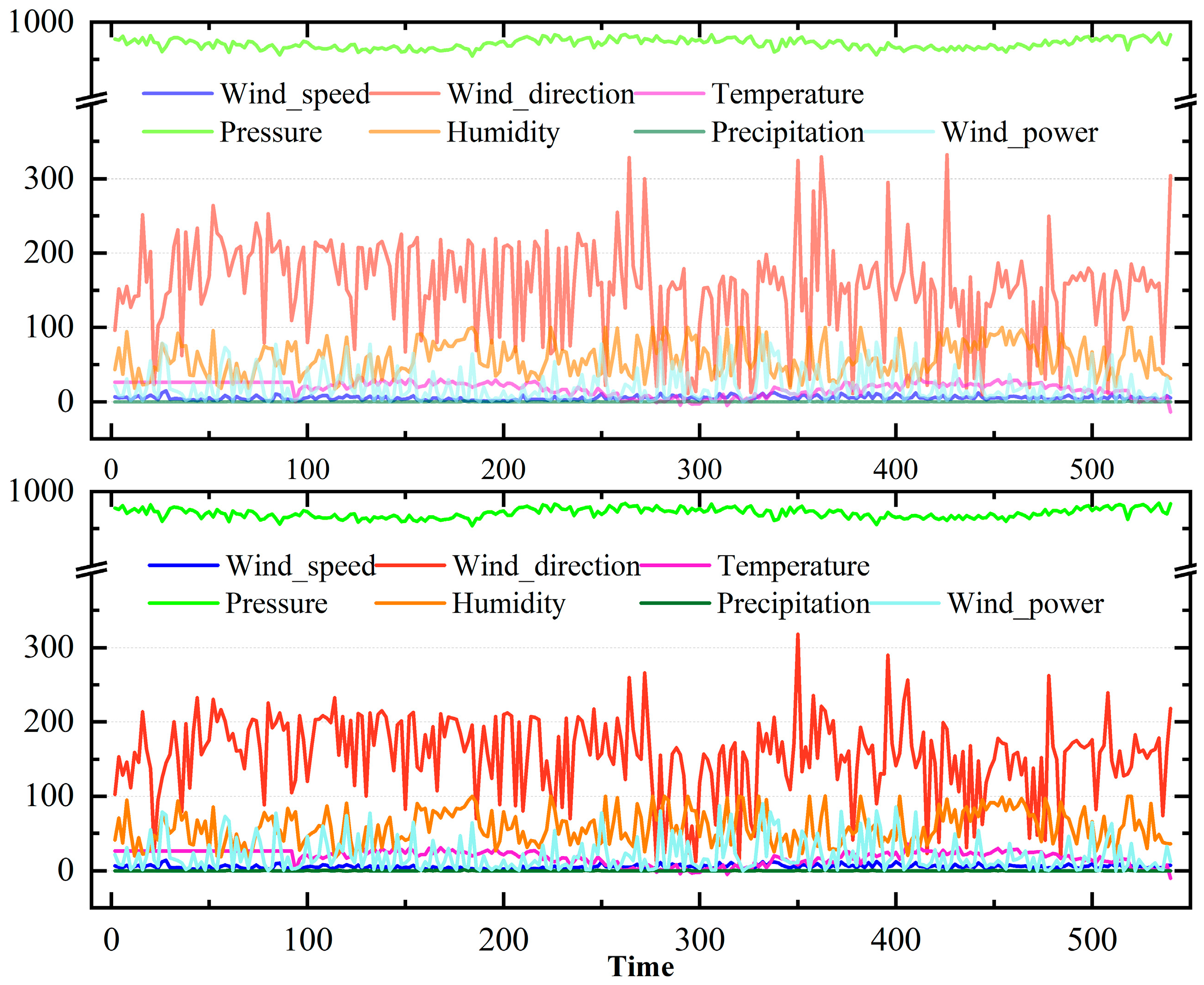
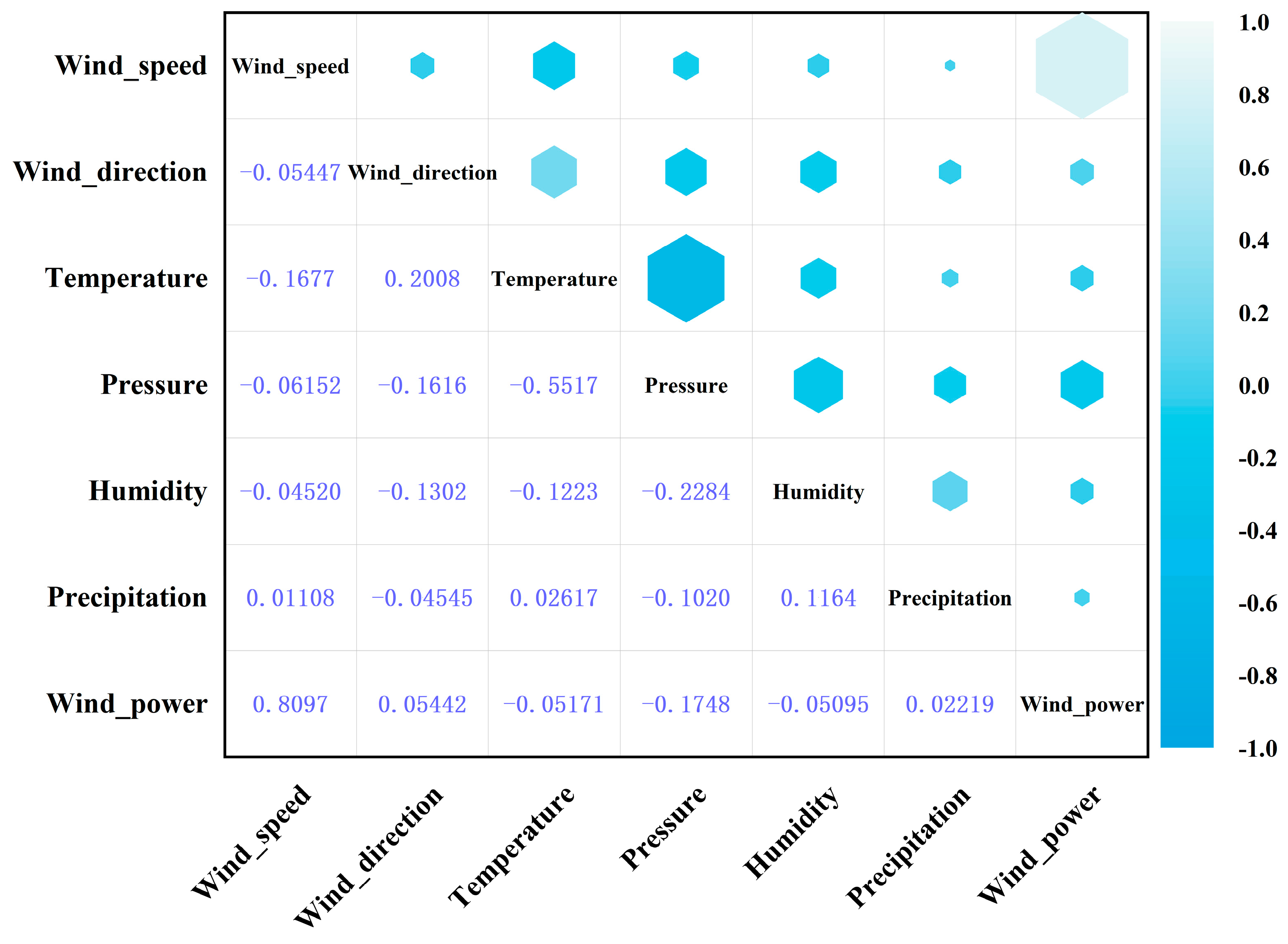
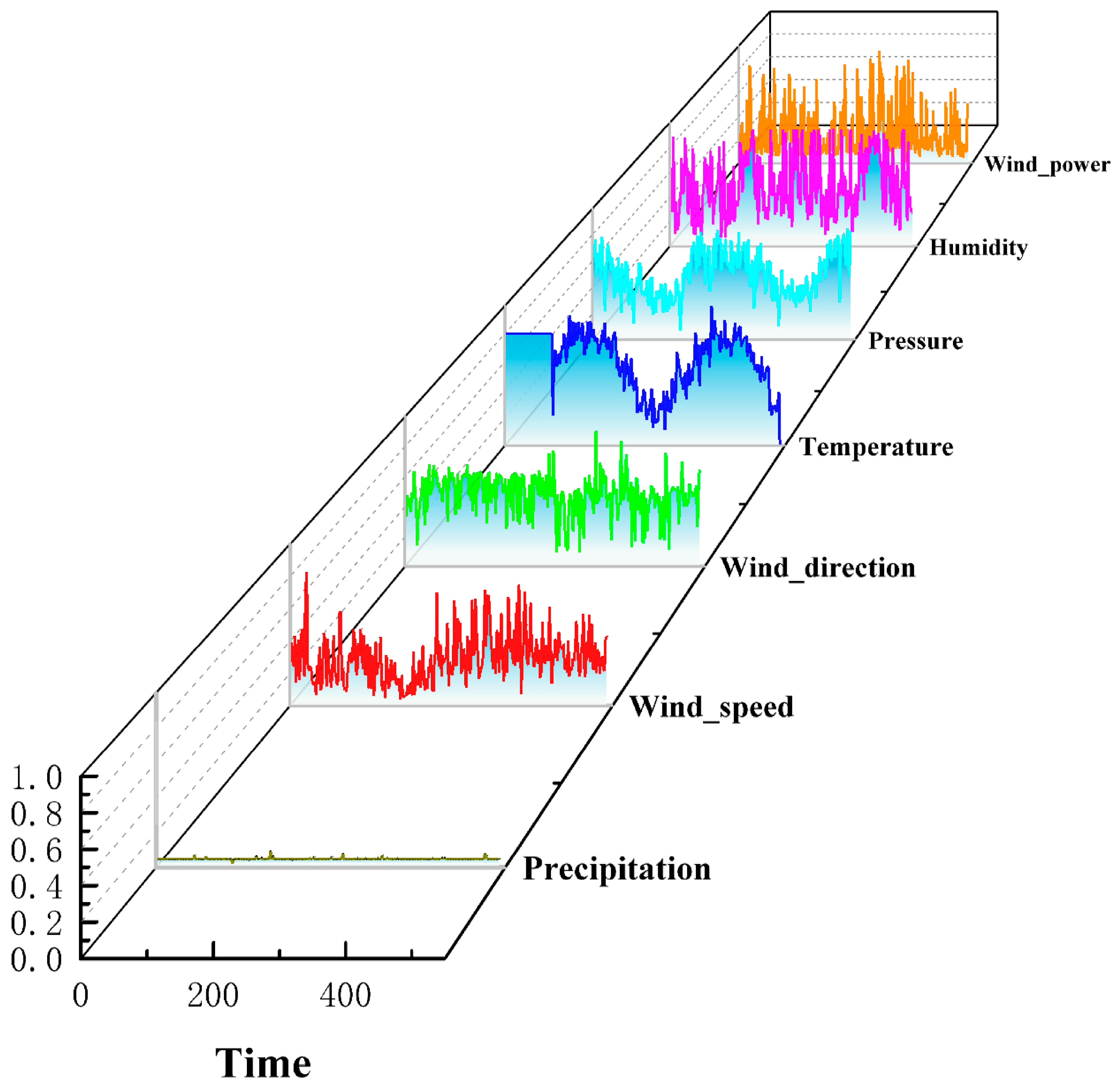
4.1. Data Description and Cleaning
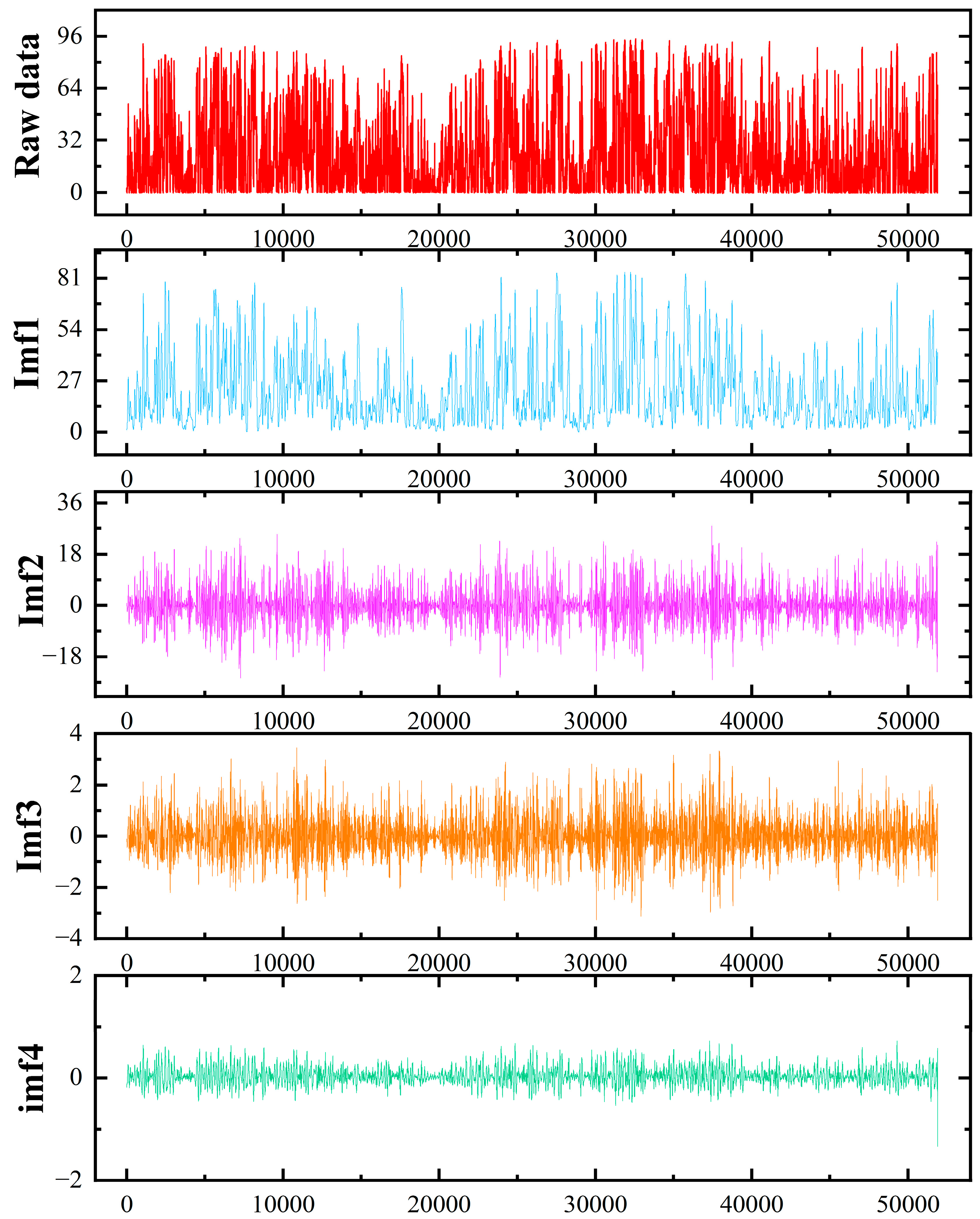
4.2. Experimental Results of Data Processing
4.3. Testing and Analysis of Model Performance
4.4. Analysis of the Effect of Time Duration
4.5. Comparative Analysis of the Performance of Different Models
5. Conclusions
- (1)
- The proposed model can accurately forecast the power production of large wind power plants up to 15 min in advance. The experimental results show that the proposed model has an average R2 of 0.9998.
- (2)
- The average MSE, average MAE, and average MAPE are as low as 0.0244, 0.1073, and 0.3587, which displayed the best results in ultra-short-term WPF. This model provided a reliable method for stable operation, planning, and maintenance of wind power plants, which offers robust support for the continued development of clean energy and energy distribution planning.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | data set area |
| R | weighting factor |
| A | amplitude |
| envelope entropy | |
| probability distribution series | |
| kernel function | |
| Greek letters | |
| weight | |
| phase | |
| gradient operator | |
| pulse signal | |
| Lagrange multiplier | |
| second-order penalty factor | |
| stopping threshold | |
| radial basis kernel function width | |
| penalty factor | |
| error variable | |
| mapping function | |
| covariance matrix | |
| Abbreviation | |
| dist | distance |
| norm | normalization |
| KNN | k-nearest neighbor |
| DT | decision tree |
| IDA | improved dragonfly algorithm |
| MSVM | multicategory support vector machines |
| GWO | grey wolf optimization |
| KHC | k-means–hierarchical clustering |
| SVD | singular value decomposition |
| WT | wavelet transform |
| MRMLE | multi-resolution multi-learner ensemble |
| AMS | adaptive model selection |
| WT | wavelet transform |
| ENN | Elman neural network |
| SSA | sparrow search algorithm |
| LSTM | long short-term memory |
| GRU | gate recurrent unit |
| BiGRU | bidirectional gated recurrent unit |
| WPCA | feature-weighted principal component analysis |
| PSO | particle swarm optimization |
| ED | encoder–decoder |
| FT-Attention | feature–temporal attention |
| MOBA | multi-objective bat algorithm |
| SSA | singular spectrum analysis |
| EMD | empirical mode decomposition |
| KRR | kernel ridge regression |
| PSR | phase space reconstruction |
| GAWNN | wavelet neural network optimized by genetic algorithm |
| VMD | variational mode decomposition |
| MIC | maximum information coefficients |
| MTL | multi-task learning |
| CEEMDAN | complete ensemble empirical mode decomposition with adaptive noise |
| ICS | improved cuckoo search |
| LSSVM | least squares support vector machine |
| LOF | local outlier factor |
| VT | voting tree |
| SVC | support vector classifier |
| LSSVR | least squares support vector regression |
| NGO | northern goshawk optimization |
| R2 | coefficient of determination |
| MSE | mean square error |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| BP | back propagation |
| BiLSTM | bidirectional long short-term memory |
| Subscripts | |
| k-distance(o) | distance of x points from point o |
| MinPts | nearest point of distance |
| min | minimum weight |
| max | maximum weight |
| best | best location |
| t | time |
References
- Wu, Z.; Zeng, S.; Jiang, R.; Zhang, H.; Yang, Z. Explainable temporal dependence in multi-step wind power forecast via decomposition based chain echo state networks. Energy 2023, 270, 126906. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Z.; He, Y.; Xiong, X.; Li, F. An algorithm for forecasting day-ahead wind power via novel long short-term memory and wind power ramp events. Energy 2023, 263, 125888. [Google Scholar] [CrossRef]
- Dai, X.; Liu, G.-P.; Hu, W. An online-learning-enabled self-attention-based model for ultra-short-term wind power forecasting. Energy 2023, 272, 127173. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z. A bilateral branch learning paradigm for short term wind power prediction with data of multiple sampling resolutions. J. Clean. Prod. 2022, 380, 134977. [Google Scholar] [CrossRef]
- Shi, J.; Wang, B.; Luo, K.; Wu, Y.; Zhou, M.; Watada, J. Ultra-short-term wind power interval prediction based on multi-task learning and generative critic networks. Energy 2023, 272, 127116. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, K.; Wu, C.; Tan, J.; He, R.; Ye, S.; Fan, J. Inter-farm cluster interaction of the operational and planned offshore wind power base. J. Clean. Prod. 2023, 396, 136529. [Google Scholar] [CrossRef]
- Marčiukaitis, M.; Žutautaitė, I.; Martišauskas, L.; Jokšas, B.; Gecevičius, G.; Sfetsos, A. Non-linear regression model for wind turbine power curve. Renew. Energy 2017, 113, 732–741. [Google Scholar] [CrossRef]
- Chen, H.; Birkelund, Y.; Zhang, Q. Data-augmented sequential deep learning for wind power forecasting. Energy Convers. Manag. 2021, 248, 114790. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Zhou, B.; Wu, Q.; Shen, X.; Liu, H.; Gong, Z. An adaptive time-resolution method for ultra-short-term wind power prediction. Int. J. Electr. Power Energy Syst. 2020, 118, 105814. [Google Scholar] [CrossRef]
- Wang, H.; Ye, J.; Huang, L.; Wang, Q.; Zhang, H. A multivariable hybrid prediction model of offshore wind power based on multi-stage optimization and reconstruction prediction. Energy 2023, 262, 125428. [Google Scholar] [CrossRef]
- Jin, H.; Li, Y.; Wang, B.; Yang, B.; Jin, H.; Cao, Y. Adaptive forecasting of wind power based on selective ensemble of offline global and online local learning. Energy Convers. Manag. 2022, 271, 116296. [Google Scholar] [CrossRef]
- Jørgensen, K.L.; Shaker, H.R. Wind Power Forecasting Using Machine Learning: State of the Art, Trends and Challenges. In Proceedings of the 2020 IEEE 8th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2020; pp. 44–50. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhong, W.; Qu, Y.; Zhai, B.; Tang, Y.; Zhao, Y. A novel spatio-temporal wind power forecasting framework based on multi-output support vector machine and optimization strategy. J. Clean. Prod. 2020, 254, 119993. [Google Scholar] [CrossRef]
- Wen, S.; Li, Y.; Su, Y. A new hybrid model for power forecasting of a wind farm using spatial–temporal correlations. Renew. Energy 2022, 198, 155–168. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H. Medium-term wind power forecasting based on multi-resolution multi-learner ensemble and adaptive model selection. Energy Convers. Manag. 2020, 206, 112492. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Ahmadian, S.; Khodayar, M.; Khosravi, A.; Shafie-khah, M.; Nahavandi, S.; Catalao, J.P. An advanced short-term wind power forecasting framework based on the optimized deep neural network models. Int. J. Electr. Power Energy Syst. 2022, 141, 108143. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Zhang, M. An improved Wavelet Transform using Singular Spectrum Analysis for wind speed forecasting based on Elman Neural Network. Energy Convers. Manag. 2017, 148, 895–904. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.; Zhang, Y.; Cheng, F.; Zhou, C. A novel prediction model for wind power based on improved long short-term memory neural network. Energy 2023, 265, 126283. [Google Scholar] [CrossRef]
- Xiao, Y.; Zou, C.; Chi, H.; Fang, R. Boosted GRU model for short-term forecasting of wind power with feature-weighted principal component analysis. Energy 2023, 267, 126503. [Google Scholar] [CrossRef]
- Wang, J.; Heng, J.; Xiao, L.; Wang, C. Research and application of a combined model based on multi-objective optimization for multi-step ahead wind speed forecasting. Energy 2017, 125, 591–613. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P.K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y. Multi-step ahead wind speed forecasting using an improved wavelet neural network combining variational mode decomposition and phase space reconstruction. Renew. Energy 2017, 113, 1345–1358. [Google Scholar] [CrossRef]
- Wei, J.; Wu, X.; Yang, T.; Jiao, R. Ultra-short-term forecasting of wind power based on multi-task learning and LSTM. Int. J. Electr. Power Energy Syst. 2023, 149, 109073. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Tang, Y.; Zhao, Y.; Zhong, W.; Qu, Y.; Zhai, B. Ultra-short-term combined prediction approach based on kernel function switch mechanism. Renew. Energy 2021, 164, 842–866. [Google Scholar] [CrossRef]
- Niu, D.; Sun, L.; Yu, M.; Wang, K. Point and interval forecasting of ultra-short-term wind power based on a data-driven method and hybrid deep learning model. Energy 2022, 254, 124384. [Google Scholar] [CrossRef]
- Yu, M.; Niu, D.; Gao, T.; Wang, K.; Sun, L.; Li, M.; Xu, X. A novel framework for ultra-short-term interval wind power prediction based on RF-WOA-VMD and BiGRU optimized by the attention mechanism. Energy 2023, 269, 126738. [Google Scholar] [CrossRef]
- Liu, L.; Liu, J.; Ye, Y.; Liu, H.; Chen, K.; Li, D.; Dong, X.; Sun, M. Ultra-short-term wind power forecasting based on deep Bayesian model with uncertainty. Renew. Energy 2023, 205, 598–607. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; ACM: New York, NY, USA, 2000; pp. 93–104. [Google Scholar] [CrossRef]
- Gorry, P.A. General least-squares smoothing and differentiation by the convolution (Savitzky-Golay) method. Anal. Chem. 1990, 62, 570–573. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern. Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B Methodol. 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Jiang, H.; Kwong, C.K.; Chen, Z.; Ysim, Y.C. Chaos particle swarm optimization and T–S fuzzy modeling approaches to constrained predictive control. Expert Syst. Appl. 2012, 39, 194–201. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar]
- Wu, X.; Ye, Q. Fault diagnosis and prognostic of solid oxide fuel cells. J. Power Sources 2016, 321, 47–56. [Google Scholar] [CrossRef]
- Ghaedi, M.; Rahimi M reza Ghaedi, A.M.; Tyagi, I.; Agarwal, S.; Gupta, V.K. Application of least squares support vector regression and linear multiple regression for modeling removal of methyl orange onto tin oxide nanoparticles loaded on activated carbon and activated carbon prepared from Pistacia atlantica wood. J. Colloid Interface Sci. 2016, 461, 425–434. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association Between Two Things; American Psychological Association (APA): Washington, DC, USA, 1961. [Google Scholar]
- Mohamed, M.; Gharib, M. PAM: Cultivate a Novel LSTM Predictive analysis Model for The Behavior of Cryptocurrencies. Sustain. Mach. Intell. J. 2024, 6, 1–10. [Google Scholar] [CrossRef]
- Zhao, Z.; Yun, S.; Jia, L.; Guo, J.; Meng, Y.; He, N.; Li, X.; Shi, J.; Yang, L. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features. Eng. Appl. Artif. Intell. 2023, 121, 105982. [Google Scholar] [CrossRef]
- Li, Z.; Luo, X.; Liu, M.; Cao, X.; Du, S.; Sun, H. Wind power prediction based on EEMD-Tent-SSA-LS-SVM. Energy Rep. 2022, 8, 3234–3243. [Google Scholar] [CrossRef]
- Abouhawwash, M.; Jameel, M.; Askar, S.S. Machine intelligence framework for predictive modeling of CO2 concentration: A path to sustainable environmental management. Sustain. Mach. Intell. J. 2023, 2, 1–8. [Google Scholar] [CrossRef]
- El-Shahat, D.; Tolba, A. A Hybridized CNN-LSTM-MLP-KNN Model for Short-Term Solar Irradiance Forecasting. Sustain. Mach. Intell. J. 2025, 10, 1–22. [Google Scholar] [CrossRef]
- Metwaly, A.A.; Elhenawy, I. Predictive Intelligence Technique for Short-Term Load Forecasting in Sustainable Energy Grids. Sustain. Mach. Intell. J. 2023, 5, 1–7. [Google Scholar] [CrossRef]
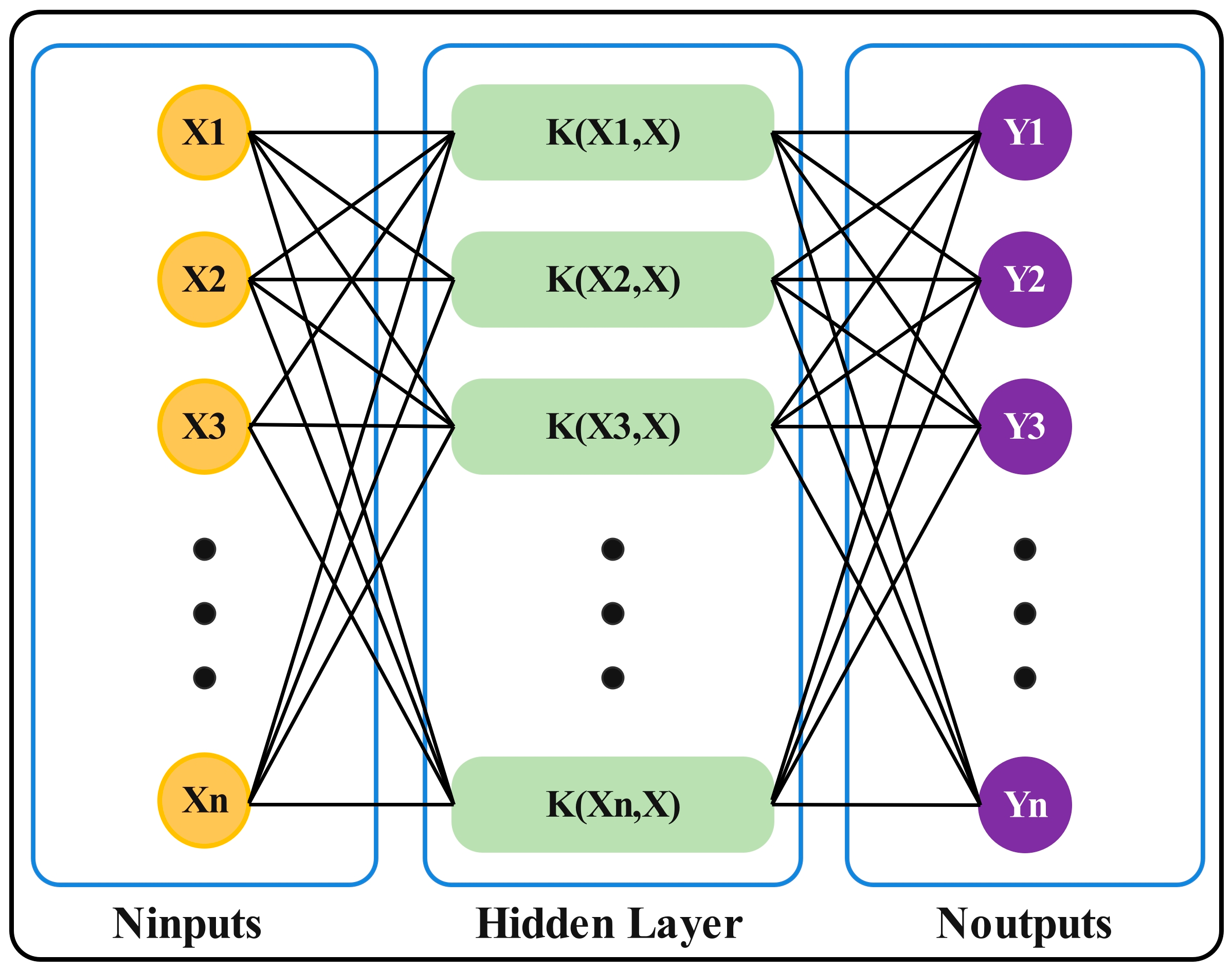
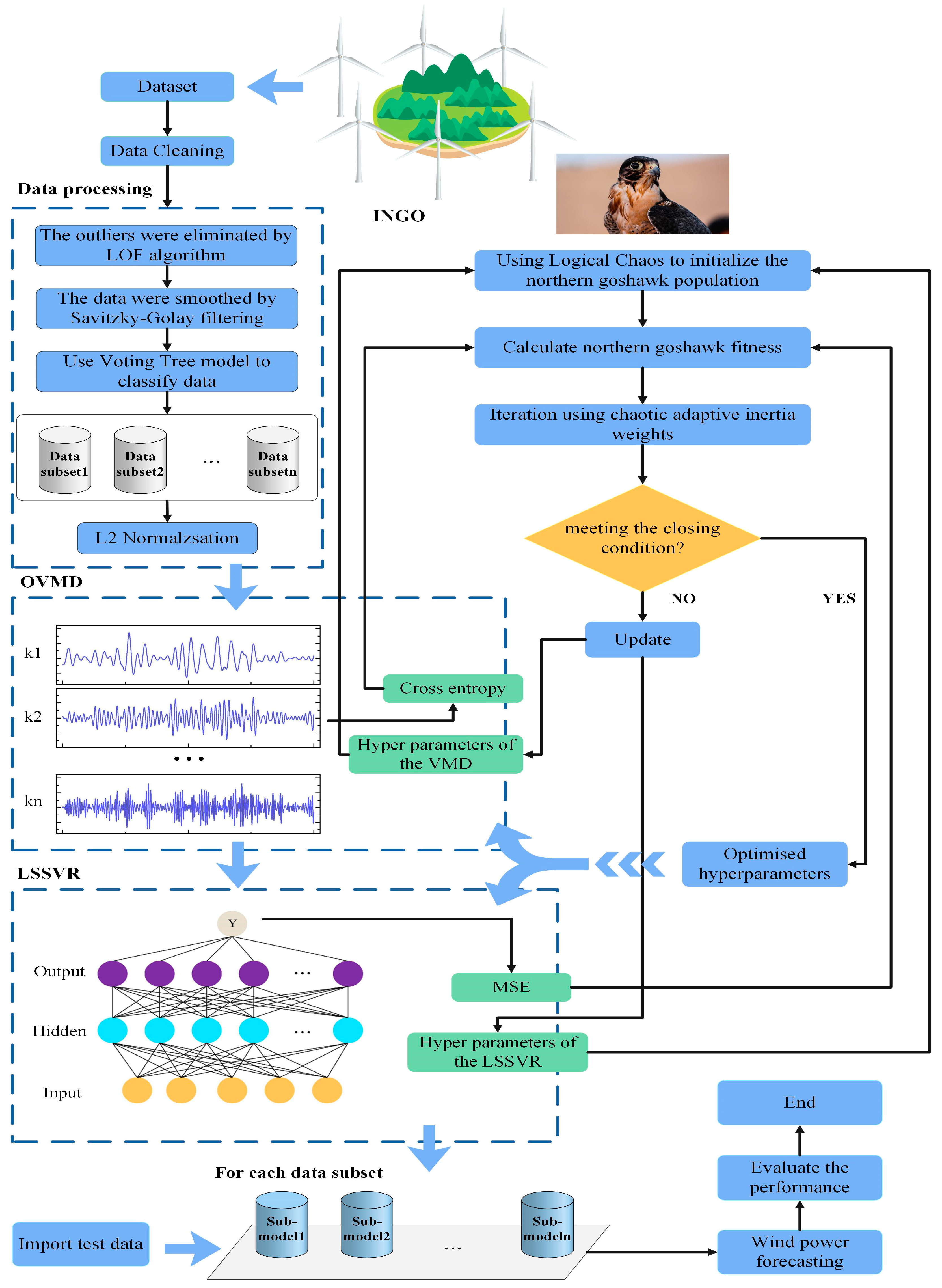
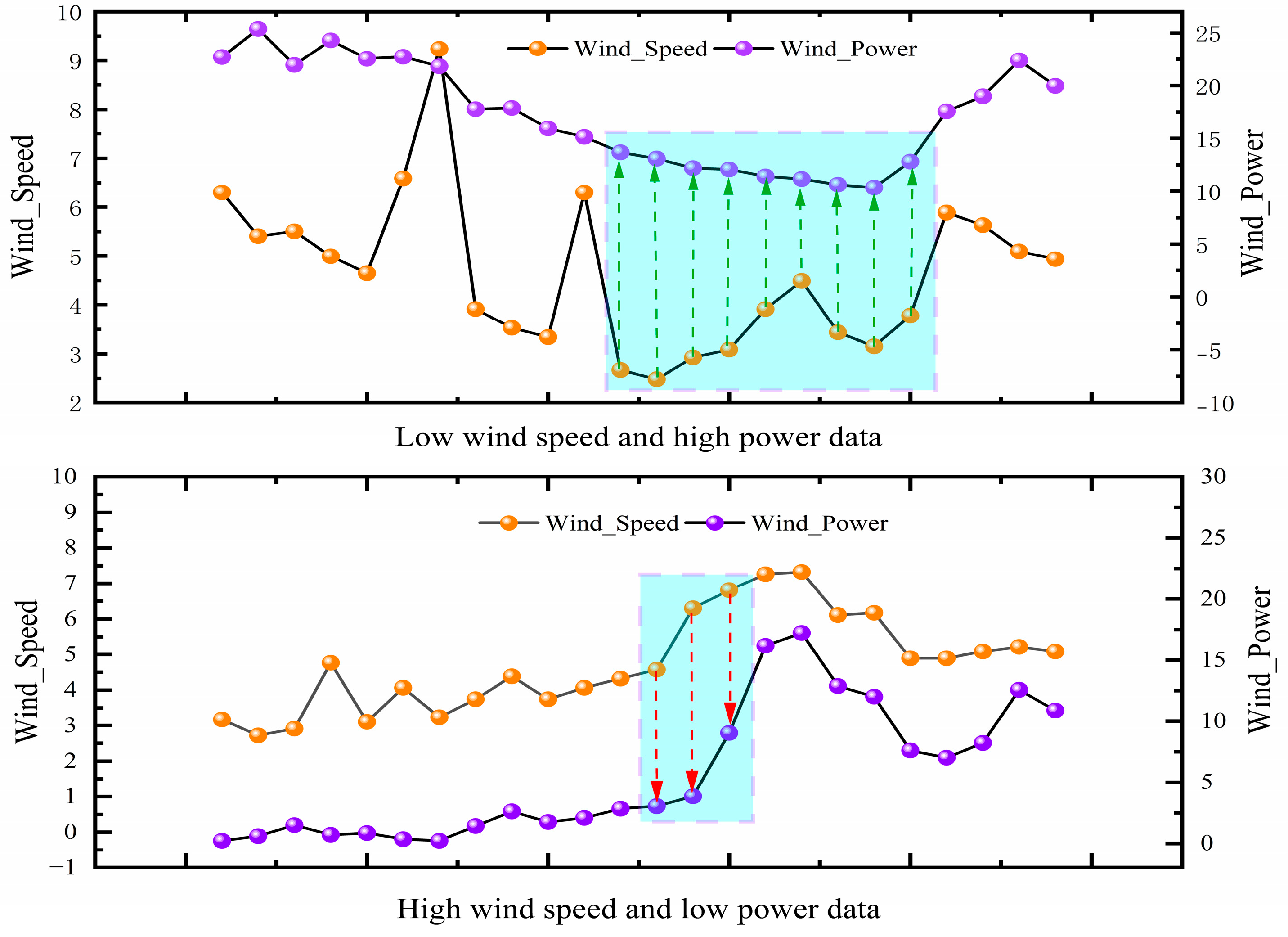
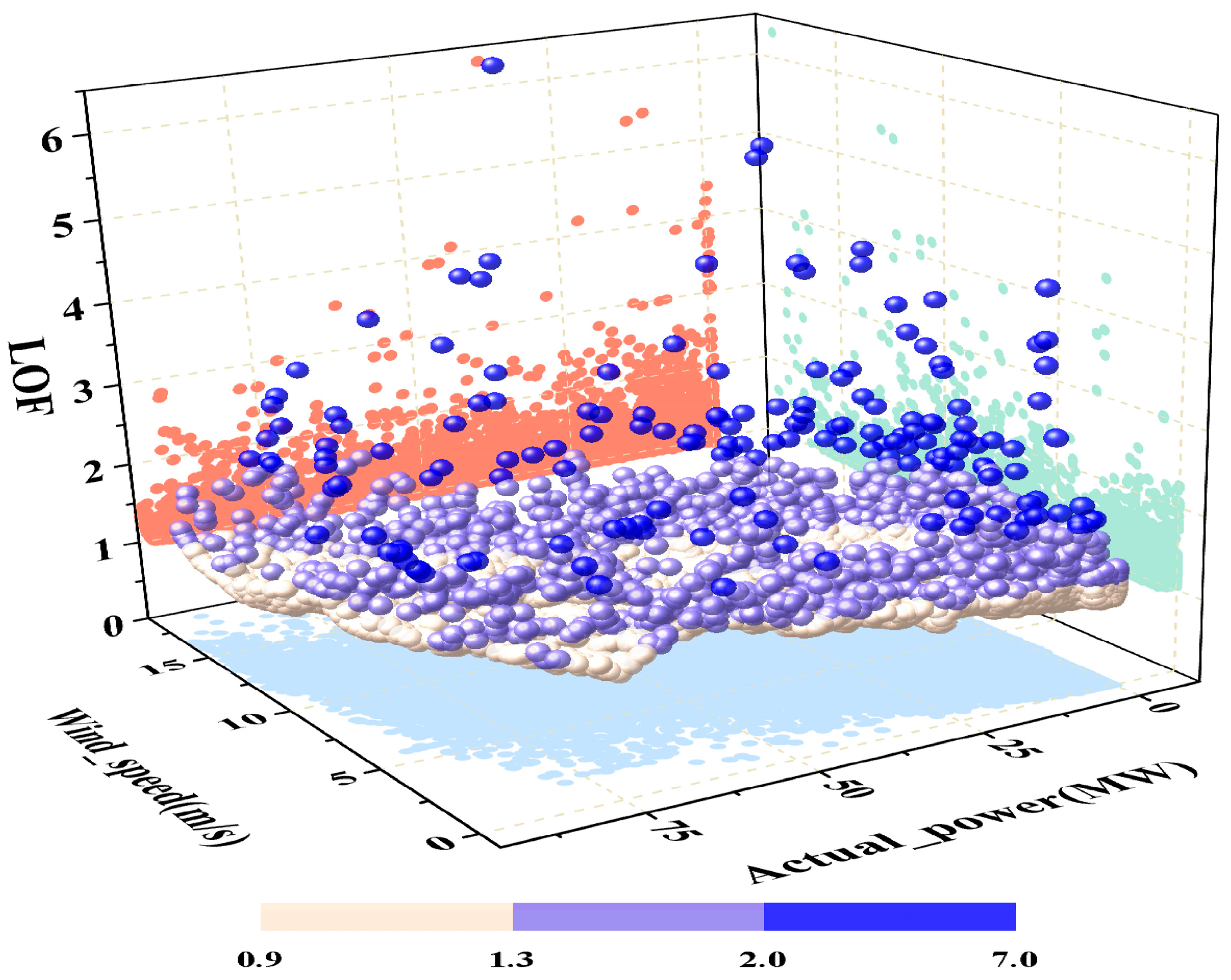
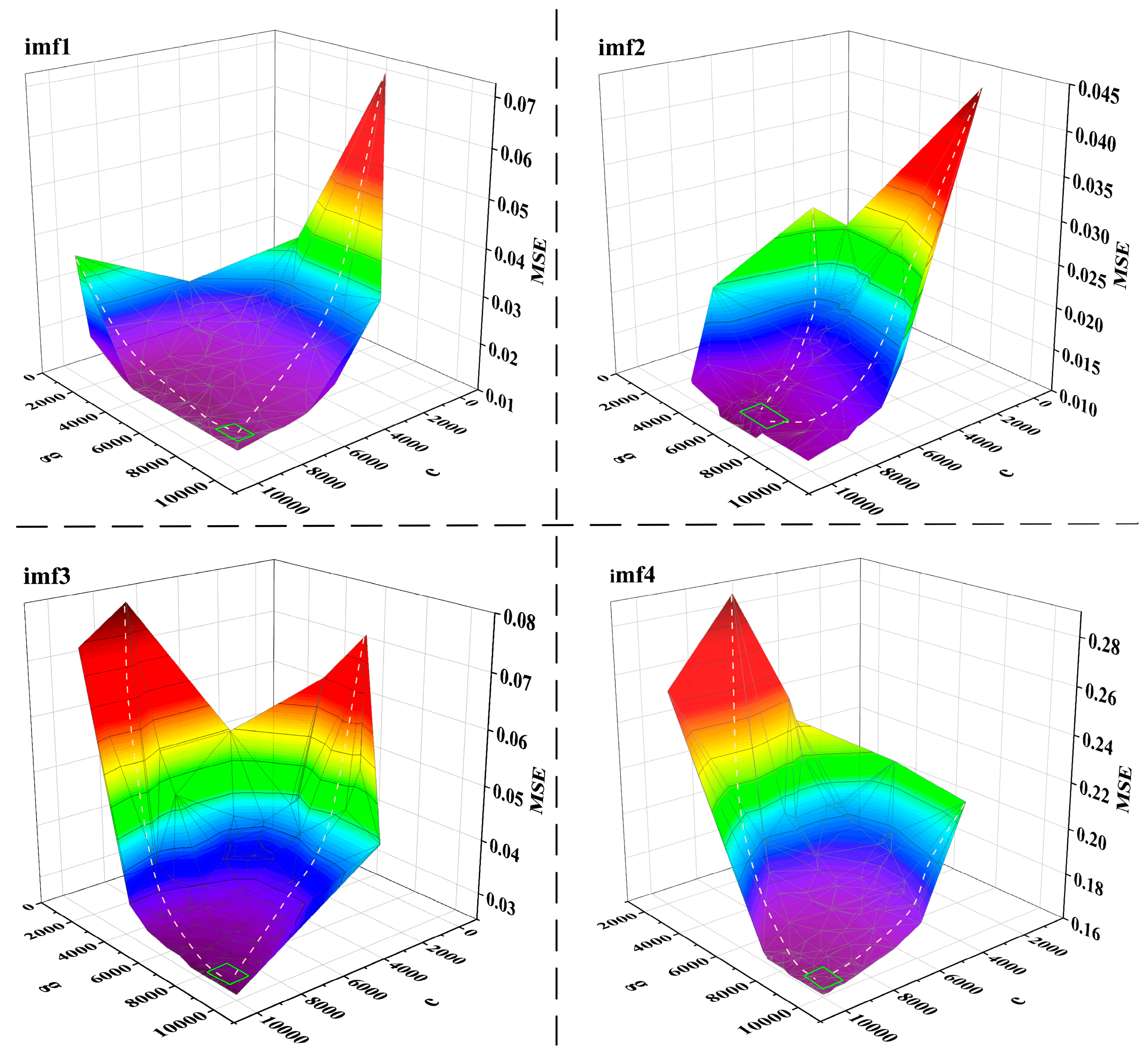
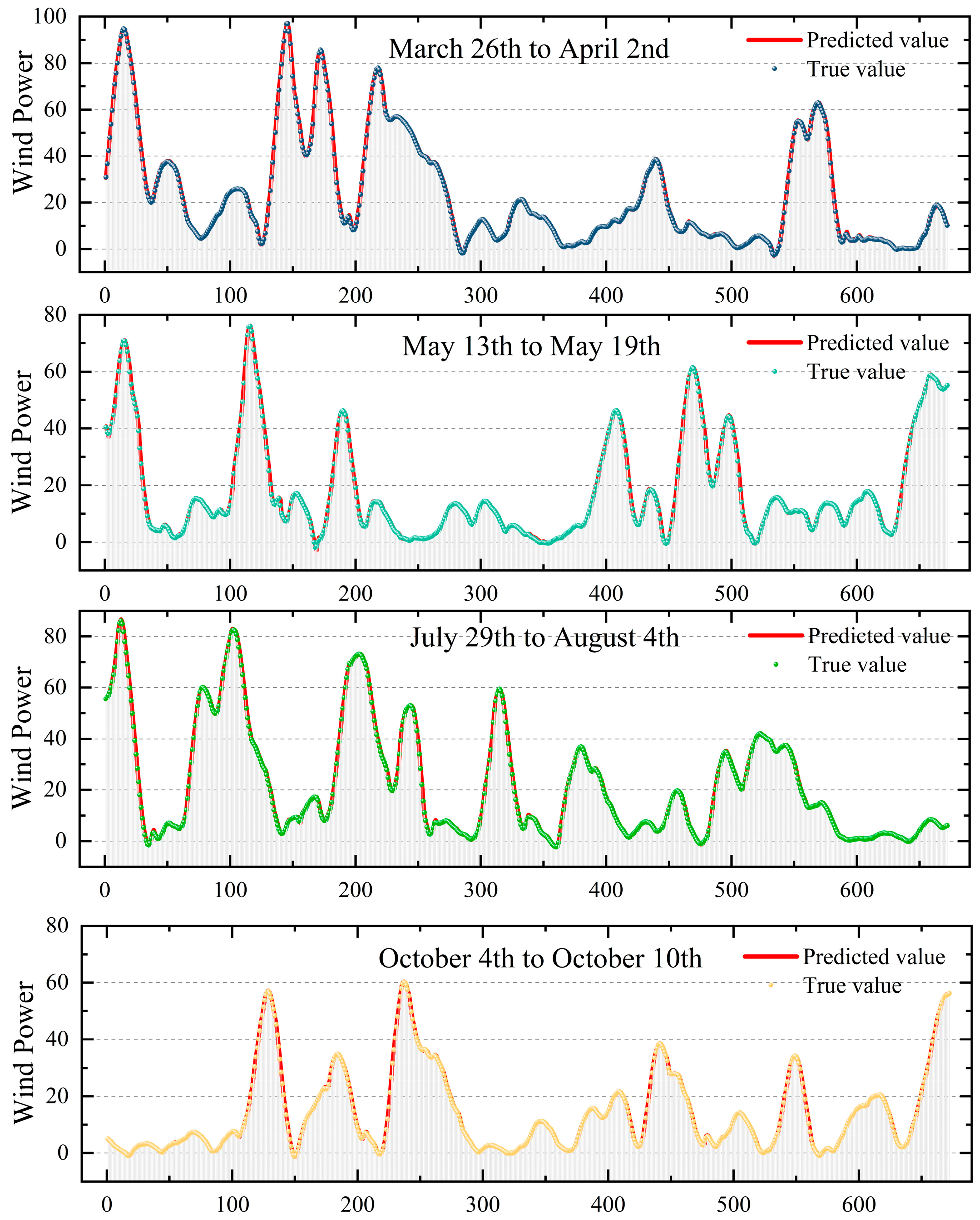
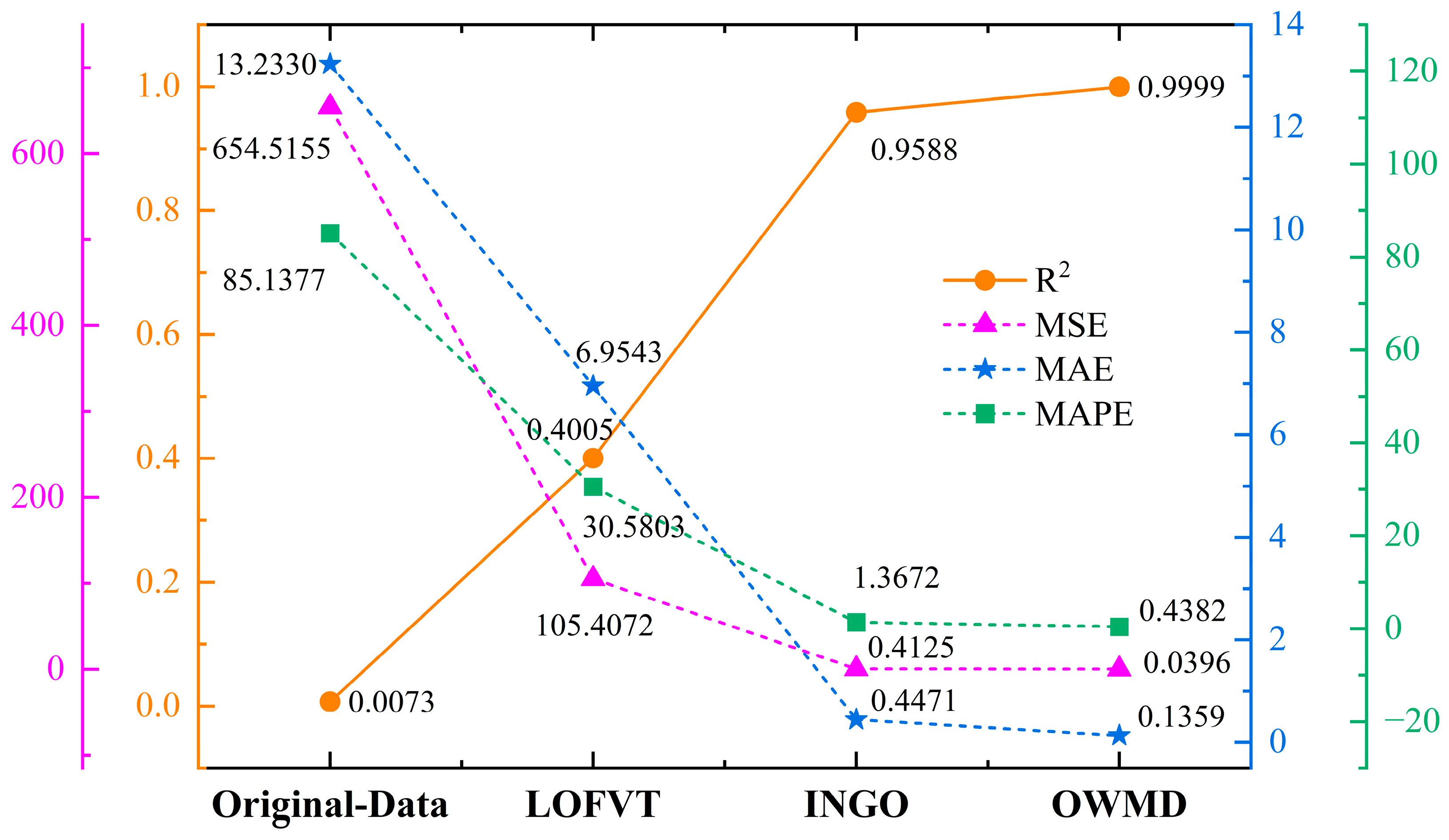

| Process | Input | Algorithm | Function | Output |
|---|---|---|---|---|
| 1 | Raw data | LOF | Remove outliers and retain reasonable wind power data | Normal data |
| 2 | Normal data | SG filter | Eliminate noise interference from the data | Denoised data |
| 3 | Denoised data | VT | Divide the data into multiple sub-datasets to reduce model computation | Classified data |
| 4 | Classified data | L2 normalization | Normalize multi-dimensional features to the same scale, aiding model learning | Normalized data |
| 5 (for each sub-dataset) | Normalized data | INGO-OVMD | Optimize VMD hyper-parameters using INGO to obtain the optimal decomposed frequency domain information | Decomposed data |
| 6 | Decomposed data | INGO-LSSVR | Optimize LSSVR hyper-parameters using INGO to enhance model performance | Predicted data |
| Season | Spring and Autumn | Summer | Winter | |||
|---|---|---|---|---|---|---|
| Weather | Cloudy and Rainy | Sunny | Cloudy and Rainy | Sunny | Cloudy and Rainy | Sunny |
| Amount | 2349 | 879 | 3346 | 1516 | 1677 | 582 |
| Logistic Regression | 1903 | 44 | 2862 | 413 | 1288 | 413 |
| Accuracy | 81.01% | 5.01% | 85.53% | 27.24% | 76.80% | 3.09% |
| SVC | 2314 | 0 | 3341 | 0 | 1653 | 0 |
| Accuracy | 98.51% | 0% | 99.85% | 0% | 98.57% | 0% |
| Random Forest | 2349 | 879 | 3346 | 1516 | 1677 | 582 |
| Accuracy | 100% | 100% | 100% | 100% | 100% | 100% |
| Predicted Moments | Cloudy–Rainy (Spring–Autumn) 1 | Sunny (Spring–Autumn) 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| 12 | 0.9998 | 0.0284 | 0.1213 | 0.3793 | 0.9997 | 0.0500 | 0.1665 | 0.4890 |
| 6 | 0.9998 | 0.0264 | 0.1158 | 0.3682 | 0.9998 | 0.0425 | 0.1515 | 0.4294 |
| 3 | 0.9998 | 0.0244 | 0.1073 | 0.3587 | 0.9998 | 0.0438 | 0.1505 | 0.4473 |
| 2 | 0.9998 | 0.0300 | 0.1197 | 0.3948 | 0.9997 | 0.0526 | 0.1673 | 0.4758 |
| Cloudy–Rainy (Summer) 3 | Sunny (Summer) 4 | |||||||
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| 12 | 0.9973 | 0.7069 | 0.2777 | 1.1421 | 0.9996 | 0.0424 | 0.1465 | 0.4928 |
| 6 | 0.9978 | 0.5700 | 0.2601 | 1.0407 | 0.9998 | 0.0434 | 0.1409 | 0.4796 |
| 3 | 0.9987 | 0.3287 | 0.2072 | 0.7508 | 0.9999 | 0.0395 | 0.1329 | 0.4579 |
| 2 | 0.9994 | 0.2225 | 0.1903 | 0.6034 | 0.9998 | 0.0505 | 0.1498 | 0.5185 |
| Cloudy–Rainy (Winter) 5 | Sunny (Winter) 6 | |||||||
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| 12 | 0.9997 | 0.0604 | 0.1617 | 0.4720 | 0.9998 | 0.0905 | 0.2203 | 0.5795 |
| 6 | 0.9997 | 0.0448 | 0.1469 | 0.4311 | 0.9998 | 0.0771 | 0.1922 | 0.5089 |
| 3 | 0.9997 | 0.0424 | 0.1379 | 0.4167 | 0.9999 | 0.0674 | 0.1746 | 0.5070 |
| 2 | 0.9997 | 0.0531 | 0.1548 | 0.4768 | 0.9998 | 0.0849 | 0.2005 | 0.5356 |
| Model | Cloudy–Rainy (Spring–Autumn) 1 | Sunny (Spring–Autumn) 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| RF | 0.9642 | 12.6803 | 2.3702 | 1.1204 | 0.9447 | 24.8045 | 3.3552 | 2.4979 |
| SVM | 0.9723 | 9.8112 | 2.0545 | 0.9328 | 0.9544 | 20.4520 | 2.9548 | 2.1315 |
| BP | 0.9737 | 9.3282 | 2.1182 | 1.4274 | 0.9567 | 19.3965 | 3.0852 | 3.5038 |
| LSTM | 0.9708 | 10.3681 | 2.1875 | 1.3118 | 0.9618 | 17.1685 | 2.7071 | 2.9555 |
| GRU | 0.9770 | 8.1756 | 2.0697 | 1.4930 | 0.9671 | 14.7880 | 2.6527 | 3.6855 |
| BiLSTM | 0.9733 | 9.4630 | 2.0714 | 1.2465 | 0.9651 | 15.6774 | 2.7597 | 4.1799 |
| VMD-CNN-GRU | 0.9839 | 5.7166 | 1.6152 | 0.8507 | 0.9859 | 6.3392 | 1.7496 | 0.8820 |
| EEMD-Tent-ISSA-LSSVM | 0.9947 | 1.8755 | 0.9311 | 0.7243 | 0.9917 | 3.7271 | 1.4983 | 1.1071 |
| This study | 0.9998 | 0.0244 | 0.1073 | 0.3587 | 0.9998 | 0.0425 | 0.1515 | 0.4294 |
| Cloudy–Rainy (Summer) 3 | Sunny (Summer) 4 | |||||||
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| RF | 0.9565 | 13.5186 | 2.3189 | 1.1105 | 0.9397 | 26.4657 | 3.2104 | 1.4290 |
| SVM | 0.9674 | 10.1306 | 2.0274 | 1.1489 | 0.9457 | 22.7681 | 2.9666 | 1.0941 |
| BP | 0.9695 | 9.4569 | 2.0355 | 0.9290 | 0.9539 | 19.3426 | 2.9034 | 1.3445 |
| LSTM | 0.9644 | 11.0549 | 2.2376 | 1.5858 | 0.9618 | 16.0321 | 2.6734 | 1.1414 |
| GRU | 0.9671 | 10.2121 | 2.1687 | 1.1958 | 0.9666 | 14.0147 | 2.4278 | 0.8392 |
| BiLSTM | 0.9649 | 10.8831 | 2.2691 | 1.4837 | 0.9626 | 15.6901 | 2.5952 | 0.9851 |
| VMD-CNN-GRU | 0.9914 | 2.6783 | 1.0699 | 0.6762 | 0.9698 | 12.6618 | 2.5256 | 1.3718 |
| EEMD-Tent-ISSA-LSSVM | 0.9952 | 1.4734 | 0.8747 | 0.6391 | 0.9939 | 2.5483 | 1.1099 | 0.6022 |
| This study | 0.9994 | 0.2225 | 0.1903 | 0.6034 | 0.9999 | 0.0395 | 0.1329 | 0.4579 |
| Cloudy–Rainy (Winter) 5 | Sunny (Winter) 6 | |||||||
| R2 | MSE | MAE | MAPE | R2 | MSE | MAE | MAPE | |
| RF | 0.9443 | 26.8113 | 3.0183 | 1.1126 | 0.9457 | 29.2208 | 3.4596 | 1.7838 |
| SVM | 0.9448 | 26.6055 | 2.9256 | 1.0871 | 0.9444 | 29.8866 | 3.4573 | 2.4774 |
| BP | 0.9605 | 19.0411 | 2.7824 | 1.8197 | 0.9494 | 27.1994 | 3.4152 | 2.9089 |
| LSTM | 0.9533 | 22.4837 | 2.8158 | 1.8817 | 0.9531 | 25.2925 | 3.3272 | 2.5044 |
| GRU | 0.9620 | 18.3114 | 2.4565 | 0.8655 | 0.9541 | 24.7380 | 2.3252 | 2.6394 |
| BiLSTM | 0.9505 | 23.8340 | 2.7814 | 1.0198 | 0.9568 | 23.2750 | 3.2884 | 2.6072 |
| VMD-CNN-GRU | 0.9809 | 9.1978 | 1.9237 | 0.7960 | 0.9846 | 8.3161 | 1.9797 | 1.4777 |
| EEMD-Tent-ISSA-LSSVM | 0.9930 | 3.3692 | 1.1673 | 1.2333 | 0.9927 | 3.9321 | 1.3815 | 1.4261 |
| This study | 0.9997 | 0.0424 | 0.1379 | 0.4167 | 0.9999 | 0.0674 | 0.1746 | 0.5070 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Zhao, D. Efficient Short-Term Wind Power Prediction Using a Novel Hybrid Machine Learning Model: LOFVT-OVMD-INGO-LSSVR. Energies 2025, 18, 1849. https://doi.org/10.3390/en18071849
Wei Z, Zhao D. Efficient Short-Term Wind Power Prediction Using a Novel Hybrid Machine Learning Model: LOFVT-OVMD-INGO-LSSVR. Energies. 2025; 18(7):1849. https://doi.org/10.3390/en18071849
Chicago/Turabian StyleWei, Zhouning, and Duo Zhao. 2025. "Efficient Short-Term Wind Power Prediction Using a Novel Hybrid Machine Learning Model: LOFVT-OVMD-INGO-LSSVR" Energies 18, no. 7: 1849. https://doi.org/10.3390/en18071849
APA StyleWei, Z., & Zhao, D. (2025). Efficient Short-Term Wind Power Prediction Using a Novel Hybrid Machine Learning Model: LOFVT-OVMD-INGO-LSSVR. Energies, 18(7), 1849. https://doi.org/10.3390/en18071849






