Abstract
Hybrid electric vehicles have received more and more attention owing to energy saving and environmental protection. Optimized energy-management strategies are critical to improve vehicle energy efficiency and reduce the emissions of hybrid electric vehicles. This study summarized the research status of energy-management strategies for hybrid electric vehicles and analyzed the energy allocation and modeling methods of hybrid power systems. The principles, advantages, and limitations of rule-based and optimized and learning-based energy-management strategies were compared. It is found that the optimized energy-management strategies can improve fuel economy by approximately 6% compared with the rule-based energy-management strategies. The learning-based energy-management strategies can reduce fuel consumption by about 5.2~17%. This study can provide a theoretical basis and practical guidance for the efficient design and optimization of hybrid electric vehicle energy-management systems, which can promote the development and application of related technologies.
1. Introduction
With the increase in global greenhouse gases emissions and the intensification of the energy crisis, environmental protection and sustainable development have become the focus of governments and society [1]. As one of the major hydrocarbon emission sources, transportation has an increasingly urgent need for energy conservation and emission reductions [2]. Against this backdrop, hybrid electric vehicles (HEVs) have emerged as a critical solution. HEVs are vehicles powered by multiple drive systems in combination, with the most common type being the gasoline–electric hybrid. They can leverage the high energy density of fossil fuels and the renewability of electricity [3], which are the key driver for green transportation.
Series, parallel, and series-parallel HEVs are the typically feature core architectures, which are defined by distinct mechanical configurations. The engine is mechanically decoupled from wheels in series HEVs to drive only a generator [4]. In parallel HEVs, the traction power can be supplied by the internal combustion engine alone, the electric motor alone, or both acting together [5]. Series–parallel HEVs integrate mechanical components to dynamically switch between series and parallel operation modes. Each architecture exhibits unique energy flow dynamics and loss patterns. In series HEVs, energy flows electrically (engine→generator→battery/motor) with losses from generator inefficiency and battery cycles. For parallel HEVs, energy flows mechanically from the engine, electrically from the motor, or both. Losses arise from engine operation outside its optimal efficiency zone or inefficient power splitting between sources. Series–parallel HEVs enable flexible energy paths but face complex losses from coordinating engine-motor operations and battery management. Each architecture’s energy dynamics demand tailored energy-management strategies (EMSs) to minimize waste and optimize performance.
The EMS optimizes the power allocation from multiple sources to meet the driving demands. The core objectives of EMSs include minimizing fuel consumption, reducing harmful emissions, and extending the battery lifespan by managing the state of charge (SOC). Balancing these objectives requires dynamic prioritization to optimize HEV performance, sustainability, and component longevity. Effectiveness is typically evaluated against baselines like traditional rule-based strategies with metrics of fuel economy, equivalent hydrogen consumption, and computational latency. These metrics are quantifiable. In the field of HEV EMSs, the rule-based, optimized, and learning-based strategies are the research hotspots [6]. Each strategy is grounded in distinct theoretical frameworks and practical requirements.
The rule-based strategies are characterized by a series of fixed rules extracted from experienced designers or optimized rules [7]. Deterministic rules play a crucial role due to their simplicity, reliability, and wide-spread acceptance. Although deterministic rule-based strategies dominate in this field, our study mainly focuses on the fuzzy rules. As an important branch of the rule-based strategy, the fuzzy rules innovatively introduce the concept of fuzzy logic, which allows the input variables and the output variables to have fuzziness and uncertainty. This characteristic makes the fuzzy rules more flexible in dealing with the complex conditions and dynamic changes.
The use of fuzzy rule-based strategies can effectively reduce fuel consumption and emissions. Yang et al. proposed a fuzzy logic rule-based EMS, which fully considered the real-time storage and release of the flywheel’s kinetic energy. The strategy effectively reduced the equivalent fuel consumption and exhaust emissions [8]. This demonstrated the direct benefits of fuzzy rules in optimizing energy-management systems. Building on this, some researchers have made improvements and expansions to fuzzy rules from different perspectives. Mazouzi et al. used the genetic algorithm (GA) to optimize the fuzzy logic parameters, which significantly improved the fitness function and highlighted the high sensitivity of fuzzy logic systems to optimize the parameters [9]. Bo et al. utilized an adaptive network-based fuzzy inference system (ANFIS) to construct the optimal control strategy and objective function. Online training on the fuzzy rules and the parameters was conducted via the Q-learning algorithm. The gradient descent methods were conducted, which significantly reduced the training time [10]. Luca et al. proposed a mutant fuzzy controller, which can output a membership function based on the degradation changes of the fuel cell to extend the fuel cell’s lifespan [11]. Vignesh et al. proposed an EMS based on the ANFIS, which integrated the intelligent control logic and used a combination of three standard driving cycles for training. It can significantly improve fuel efficiency [12].
The optimized strategies are based on mathematical models, which can achieve the optimal solution for energy distribution through the global or local optimization to improve the system efficiency. The dynamic programming (DP) methods and model predictive control (MPC) are widely applied [13].
DP is a method of global optimization. It obtains the theoretically global optimal solution by conducting an exhaustive search of all possible energy distribution paths. This characteristic makes DP a powerful tool for finding the best solutions in complex optimization problems. Using DP in vehicle control systems can effectively reduce fuel consumption by optimizing driving strategies. For instance, Xu et al. utilized the knowledge extracted from DP to effectively improve the control performance of the EMS based on the soft actor-critic (SAC) algorithm, which reduced energy consumption [14]. Tang et al. proposed an adaptive DP approach that utilized the heuristic DP and dual heuristic programming. The approach reduced fuel consumption and ensured the real-time planning speed, as well as good tracking performance [15]. Liu et al. introduced the reference information of DP during the training process of reinforcement learning (RL) and constructed a reward function related to the optimal trajectory to implement imitation learning, which significantly improved fuel economy [16]. Moreover, during the RL process, training the agent with the optimal solution of the DP can alleviate the cold start problem caused by random exploration [17].
In contrast to the global optimization nature of DP, MPC exhibits the characteristic of local optimization. It is based on the vehicle powertrain model, which predicts the vehicle’s driving conditions over a future period and optimizes the energy distribution strategy according to the prediction results. Zhou et al. proposed an EMS that fused the whale optimization algorithm, DP, sequential quadratic programming (SQP), and the back propagation neural network (BPNN). In the MPC controller of the EMS, the multi-collision method was used to discretize the control variables of the optimal control problem during the prediction period, which successfully reduced costs and improved the system performance [18]. Han et al. proposed a predictive EMS that took the electric motor (EM) thermal control into account. The study put forward an MPC framework based on the pontryagin’s minimum principle (PMP). This framework effectively improved the fuel economy and ensured that the EM temperature remained below the limit to feature high computational efficiency [19].
The optimized strategies apply some algorithms to enhance the scientific nature and the efficiency of energy distribution. The particle swarm optimization (PSO) algorithm abstracted the potential solutions to the problem as particles with each particle representing a solution, which conducted an iterative optimization in a multi-dimensional search space. The hierarchical EMS proposed by Tang et al. achieved an energy consumption reduction while ensuring the safe and efficient passage of vehicles in uncertain traffic scenarios through scenario-adaptive speed planning, offline optimization of the ANFIS, and the PSO algorithm [20]. The Lyapunov algorithm analyzed the change trend of the system state by constructing an appropriate Lyapunov function, which judged the stability of the system. Li et al. optimized the EMS with the Lyapunov algorithm, achieving better performance compared with the adaptive equivalent consumption minimization strategy (AECMS) [21]. The golden section search (GSS) can effectively find the optimal solution within a specific interval and perform optimization within the defined search interval. Yang et al. proposed a collaborative EMS based on the variable optimization domain, which adopted a sub-cycle division method based on the historical driving data and was optimized by the GSS algorithm, outperforming the conventional AECMS [22].
The learning-based strategies leverage artificial intelligence technologies to achieve adaptive control in a data-driven manner. The strategy can keenly sense and adapt to the complex and changeable operating environments. The cutting-edge technologies, such as RL and neural networks, are the research focus, which are applied to the strategy optimization under complex working conditions.
The learning-based strategies can effectively reduce fuel consumption, improve convergence speed, and mitigate battery degradation. Zou et al. applied the prioritized replay strategy in the deep Q-network (DQN), which adopted the normalized advantage function, priority rule, and the Markov chain working condition prediction method. The method conferred fast convergence speed and accurate working condition prediction to the model [23]. The EMS proposed by Chen et al. embedded the fuzzy logic control (FLC) as an expert demonstration into the learning process of the twin delayed deep deterministic policy gradient (TD3) [24]. It was a good balance between the operational efficiency improvement and maintenance of the SOC of the battery. The EMS proposed by Qi et al. used a hierarchical structure in deep Q-learning (DQL). Compared with non-hierarchical DQL, the training speed was significantly increased and the fuel consumption was remarkably reduced [25]. Lv et al. modified the reward function with the weight coefficients obtained through inverse RL, which fed the updated reward function into the forward RL task. The SOC change range was maintained in the region where the battery featured the high efficiency and low internal resistance [26]. Huang et al. utilized the TD3 algorithm and integrated the operating cost and energy source aging terms as the primary components into the multi-objective reward function. Compared with the EMS that ignores the energy aging factor, this approach led to significant improvements in reducing operating costs and the attenuation of the fuel cell under the suburbs city highway driving cycle (SCHDC), the urban dynamometer driving schedule (UDDS), and the new European driving cycle (NEDC) [27]. Hua et al. proposed a handshake strategy by introducing the correlation ratio in the multi-agent deep reinforcement learning (MADRL) framework. This allowed for two learning agents using the deep deterministic policy gradient (DDPG) algorithm to collaborate. Compared with traditional rule-based EMSs, this strategy significantly reduced energy consumption [28]. Qin et al. considered the thermal characteristics of the electric drive system and adjusted the weight coefficients with DDPG, which controlled the battery and the motor temperatures within a safe range and improved the overall performance of the vehicle [29]. In the neural network domain, Madhanakkumar et al. employed the hybrid waterwheel plant algorithm and dual stream spectrum deconvolution neural network, achieving notable fuel savings [30]. Chen et al. utilized the bidirectional recurrent neural network and the BPNN and trained the model with the optimal solution of DP, which can significantly improve fuel economy [31]. Nayak et al. utilized the three-layer back propagation artificial neural network, which effectively reduced the overall energy cost when the initial SOC level was 0.95 [32].
In addition, learning-based strategies have been improved from different perspectives, which demonstrated the stronger adaptability and the optimization capabilities under complex and changeable operating conditions. Huang et al. introduced deep reinforcement learning (DRL) into the MPC framework, which alleviated the inherent drawbacks of poor generalization and insufficient adaptability in DRL. The DRL significantly enhanced the robustness of economic driving decisions in unknown scenarios [33]. Chen et al. developed a multi-experience replay buffer with the improved TD3 to enhance the quality and efficiency of agent exploration [34]. The adaptive cruise control-EMS (ACC-EMS) based on the hierarchical RL proposed by Zhang et al. successfully solved the local optimum problem of the standard RL-based ACC-EMS through self-learning, which achieved an interaction to improve the training speed and stability [35]. Chen et al. adopted the improved SAC algorithm and replaced the Gaussian policy by the infinite support with the Beta policy with the finite support, which effectively reduced the cost [36]. The EMS proposed by Guo et al. was based on the FIS, which used the fuzzy baseline function to approximate the EMS strategy function and learned the strategy parameters through the policy gradient RL [37]. It had fast and stable convergence, which can adapt to environmental changes.
In HEVs, the optimized energy management can improve the vehicle’s energy efficiency and reduce fuel consumption and operating costs, which can decrease harmful gas emissions and contribute to environmental protection. Compared with previous studies, this study innovatively conducted a comparison of the energy-saving effects that different types of EMSs can achieve. It systematically examined the research status of EMSs for HEVs. Then, it conducted an in-depth comparative analysis of various strategies and provided a clear direction for future research. These efforts established a theoretical foundation for the optimization of energy management systems. They also offered practical guidance for the efficient design of HEV energy management systems. This study’s findings can directly support the development and application of related technologies. These contributions will help accelerate the widespread adoption of HEVs and advance the global goals of sustainable transportation.
2. Energy Configuration Methods of Hybrid Power Systems
Among the global energy transition, the configuration of hybrid power systems and the key components have emerged as the critical determinants.
2.1. Typical Hybrid Energy Configuration of the HEV
Hybrid power systems balance the power performance and the fuel economy via rational energy configuration and efficient use, which integrate the benefits of multiple energy sources. As illustrated in Figure 1, the three primary system architectures of the series, parallel, and series–parallel dominate the current landscape of the HEV [38]. Based on the distinct energy flow patterns and the efficiency characteristics, the designs are pivotal for developing effective EMSs to enhance the overall system performance.
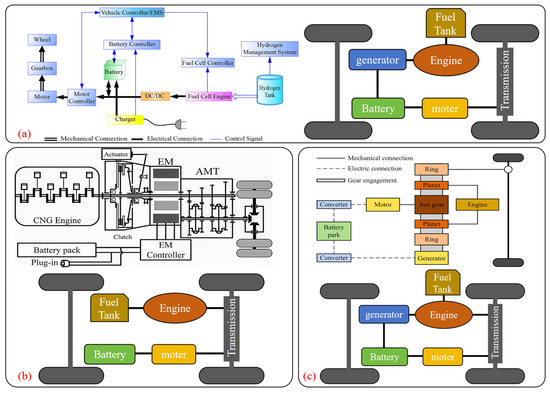
Figure 1.
Three main energy configuration methods of hybrid power systems: (a) series hybrid power system [39]; (b) parallel hybrid power system [40]; (c) series–parallel hybrid power system [41].
2.1.1. Series Hybrid Power System
In series power system design, the integrating fuel cells and electric energy enhance the vehicle power system flexibility and efficiency. As shown in Figure 1a, the vehicles utilize the fuel and the electricity as dual energy sources. Unlike conventional internal combustion engines (ICEs), the engine in series HEVs does not directly power the drive wheels. Instead, it converts the generated electricity via the DC/DC converter to the power system, which supplies the EM for propulsion [39]. The engine can adapt its operation to real-time power demands to ensure optimal efficiency, which lacks a direct mechanical link to the wheels. The proposed approach boosts the engine performance, which can minimize energy losses and improve the overall vehicle economy.
Despite the relatively mature architecture design of the series HEVs, there is still room for improvement. Under most operating conditions, the EM needs to generate 50% of the total power required to drive the vehicle, which means that series HEVs need to be equipped with capacious and expensive batteries [42]. Moreover, the inherent multiple energy conversion stages are coupled with battery voltage and current constraints, which diminish the overall system efficiency [43].
2.1.2. Parallel Hybrid Power System
In the parallel hybrid power system given in Figure 1b, the engine and EM share a common shaft to enable joint or independent propulsion. The power coupling of this system is achieved through the dry clutch, and the EM functions as either the motor or the generator based on the power demands. Depending on its different operating modes, parallel HEVs have multiple driving modes, including engine, EM, and hybrid driving modes. These modes can be flexibly switched according to the different situations to improve the vehicle’s fuel economy effectively. In addition, the six-speed automated mechanical transmission (AMT) can match the torque-to-speed ratios between the driveshaft and the wheels, which can ensure efficient power delivery [40].
The parallel power system does not require capacious batteries resulting in a limited pure-electric driving range and greater reliance on an engine for energy. However, the multi-component architecture increases the design complexity, manufacturing difficulty, and production costs. Due to complex power coupling and switching, coordinating engine EM operation across driving modes also presents challenges.
2.1.3. Series–Parallel Hybrid Power System
In the series–parallel hybrid power system of Figure 1c, the planetary gear set efficiently connects the ICE, traction motor, generator, and driveshaft. By virtue of its high reduction ratio and the linear arrangement of the input and output shafts [44], the planetary gear enables efficient power coupling and transmission among the system components [41]. This architecture allows the ICE and motor to drive the vehicle independently, which is similar to parallel hybrid power systems. The ICE also drives the generator to supply power for motor assistance, which is similar to the series hybrid power system. As a result, series–parallel HEVs combine the strengths of series and parallel configurations, which can balance the power output, fuel consumption, and driving smoothness.
The series–parallel system incurs efficiency losses during the energy conversion process. When the electrical energy is converted into mechanical energy, a certain amount of energy loss in each component of the system reduces the overall performance below ideal levels. In addition, the frequent mode switching further challenges the coordinated control to cause short-term efficiency drops. Consequently, the power conversion efficiency may be lower than that expected in real-world driving under the high load or the complex traffic environments, which affects the fuel economy and the environmental friendliness.
Table 1 is the respective advantages and limitations of the different hybrid power systems. The configurations critically inform the EMS design and guide the energy distribution and mode-switching control. To meet the current social demands for energy conservation and emission reductions, as well as the increasingly stringent requirements of users for vehicle performance, the research should address system inefficiencies, optimize energy utilization, and advance sustainable transportation.

Table 1.
The advantages and limitations of different hybrid power systems.
2.2. Key Components of the Power System
The power system components are essential for the energy flow analysis and the performance characteristics of hybrid power systems. As the core energy storage unit, the power battery needs to have a high energy density to support the pure-electric driving range and should meet the cycle-life requirements for frequent charging and discharging. The power battery performance directly affects the system energy efficiency. The drive motor serves as the energy conversion interface, which can efficiently transform the electricity into the mechanical power during the operation and recover the energy via regenerative braking. The coordinated operation of the power battery and the drive motor determines the dynamic response and overall energy consumption performance of the hybrid power system.
2.2.1. Power Battery Energy Expression of the HEV
Under the worldwide harmonized light vehicles test cycle (WLTC) conditions, the error between the results of the model in series–parallel HEVs and the vehicle experiment results was less than 0.02. The battery model can reflect the changing state of the battery with relatively high accuracy [45]. According to Kirchhoff’s laws, the power, current, and charge state of a power battery can be calculated using Equation (1) [29]:
where Pe is the power of the battery, W. Uoc is the open-circuit voltage, V. Ibat is the charging and discharging current of the battery, A. Rin is internal resistance of the battery, Ω.
The commonly used methods for SOC estimation are the Coulomb counting method and Kalman filter (KF) method, which are applicable to all battery systems. The Coulomb counting method calculates the SOC value by integrating the battery current over the usage time. The SOC can be calculated with Equation (2) [45] and Equation (3), respectively [46]:
where Ceq is equivalent capacitance, F.
where SOC(t0) is the initial SOC. I(t) is the current at time t, A. η is the Coulomb coefficient. QN is the rated capacity of the battery, As. t is the time, s.
The accuracy of this method mainly depends on the precise measurement of the battery current and the accurate estimation of the initial SOC. Therefore, if there are deviations in the current measurement or the initial SOC is inaccurate, errors will accumulate over time, which require additional SOC calibration [47].
The KF method is a dynamic estimation method that consists of two steps of prediction and measurement. Based on the state-space model, it integrates the real-time measured data, such as current and voltage, to estimate the SOC through the prediction-update iterative process. The state equation and measurement equation are given in Equation (4) and Equation (5), respectively [48]:
where Xk is the estimated SOC at time step k. f(·) is the system state function. ηbat is the charging and discharging efficiency of the battery. Ik is the battery current at the time step k, A. Δt is the sampling interval, s. vk−1 is the noise item, which is added to the state equation.
where Zk is the voltage at time step k, V. G(·) is the system measurement function. Tk is the battery temperature at time step k, °C. Vk−1 is the battery voltage at time step k−1, V. ωk−1 is the noise items, which is added to the measurement equation, V.
The KF first predicts the output of the SOC and the covariance error. Then, the Kalman gain and the state value are calculated, which corrects the covariance error and eliminates the influence of noise in the internal parameter estimation [49]. However, KF is the most suitable model for linear systems. The extended KF and the unscented KF were developed to estimate the SOC more accurately because many systems are nonlinear in nature.
2.2.2. Drive Motor Parameter of the HEV
The most used motor in HEVs is the permanent magnet synchronous motor (PMSM). The PMSM is a three-phase AC motor. Its electromagnetic torque is generated by the interaction between the stator current and the rotor magnetic field. The motor controls the power distribution of two power sources through the motor windings with the dual inverters, which can serve in the vehicle’s energy management [50]. The voltage, current, and torque can be calculated with Equation (6), Equation (7), and Equation (8), respectively [50]:
where ud and uq are the voltages of the d-axis and q-axis, respectively, V. id and iq are the currents of the d-axis and q-axis, respectively, A. Rs is the stator resistance of the motor, Ω. Ld and Lq are the inductances of the d-axis and q-axis, respectively, H. ωs is the electrical angular velocity of the motor, rad/s. ψf is the flux linkage of the permanent magnet, Wb.
where ivd is the effective component of id, A. ivq is the effective component of iq, A. Rc is the equivalent core loss resistance of the motor, Ω.
where Te is the electromagnetic torque, N·m. p is the number of pole pairs of the motor.
PMSMs have advantages of a high-power density, high torque density, compact structure, and high efficiency [51,52]. The models correct the variation of inductance and flux linkage by improving the parameters of the nonlinear function [53]. The advanced control strategies of the adaptive control [54] and robust control [55,56] are employed in terms of control algorithms to enable the motor control system to adapt to real-time changes in motor parameters, which can ensure that the motor always operates in an efficient and stable state.
Collectively, this comprehensive analysis of hybrid power system configurations and key components provides both a theoretical basis and practical guidance for the efficient design and optimization of HEV energy-management systems. It serves as a solid foundation for promoting the development and application of related technologies, ultimately contributing to more sustainable and efficient hybrid electric vehicle solutions.
3. Classification and Comparison of EMSs
In the actual operation of HEVs, the EMS is pivotal for maximizing the efficiency and minimizing the energy consumption. As shown in Figure 2, three primary EMS categories dominating this field are the rule-based strategies, optimized strategies, and learning-based strategies. Rooted in the fundamental theories of vehicle dynamics and energy conversion, the strategies integrate the multi-dimensional data, including real-time driving cycle information and the SOC, which can dynamically regulate and optimize the energy flow among power system components. This approach effectively curbs fuel usage, which can enhance the overall vehicle performance and promote efficient energy utilization. While the following sections review various EMSs and their reported performance, it is critical to contextualize these findings. The reliability of quantitative metrics is inherently tied to their validation platforms (SIL (Software-in-the-Loop), HIL (Hardware-in-the-Loop), processor-in-the-loop testing, testbench, or final vehicle), which are explicitly documented for each study in the subsequent analysis. This transparency aims to facilitate a nuanced understanding of each method’s applicability across different experimental contexts.
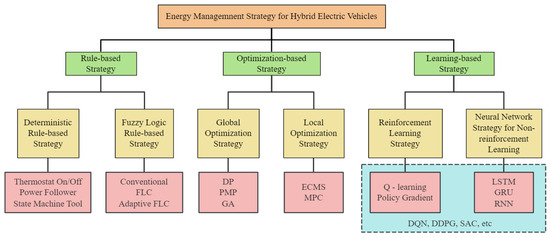
Figure 2.
Classification of EMSs in HEVs.
3.1. Rule-Based Strategy of EMSs
As simple and highly implementable EMSs, the rule-based strategies typically adopt the “if-then” structure, which is widely utilized in real-time energy management. This approach primarily comprises two subtypes of the deterministic rule-based and fuzzy logic rule-based strategies [57]. Deterministic rule-based strategies set thresholds based on the predefined conditions, such as the vehicle speed, torque, power demand, and battery state. The conditions determine the energy distribution and the operational modes across various driving conditions, which can improve the vehicle performance and optimize fuel efficiency. These strategies are further categorized into the thermostat, power follower, and state machine strategies. The thermostat (ON/OFF) strategy employs the generator and ICE to generate electricity, which can keep the battery SOC within preset limits [58]. The power follower strategy can dynamically adjust the power output of the ICE and generator according to the vehicle power demands, which can ensure the efficient system operation. The state machine strategy partitions the energy system into multiple distinct states, and each is linked to specific operating modes and control rules. For example, Li et al. leveraged this strategy to distribute the required power according to the state changes. As a result, the vehicle had safe operating conditions during idle periods to achieve better energy efficiency [59].
The traditional deterministic rule-based strategies face limitations in complex scenarios in practice. Takrouri et al. addressed this by introducing the improved power follower strategy with an exponential smoothing function with a single adjustable parameter [60]. Compared with the conventional power follower strategies, this strategy reduced the battery root-mean-square current by 19%, which can mitigate the fluctuations to extend the battery lifespan and enhance efficiency (HIL). Wang et al. extracted the control rules from the recognized optimal algorithms to optimize the control parameters offline and refine online, which achieved the near-optimal fuel economy and SOC balance [61]. FLC is the control algorithm based on the fuzzy set theory, the linguistic variables, and logic reasoning [57]. FLC can accurately transform the linguistic control built on the expert knowledge into the automated control as an advanced control strategy. The FLC operation process mainly comprises three stages. The first process is the fuzzification. The precise input values are converted into corresponding fuzzy sets via predefined membership functions. The second process is the rule application stage. The rules exacted from extensive expert knowledge are applied to determine the fuzzy output level. The final process is the defuzzification. The core task of this stage is to accurately convert the fuzzy output level determined in the previous stage into the precise value through the specific algorithm [62]. The FIS integrated the fuzzification interface, the rule base, the inference engine, and the defuzzification interface (Figure 3). FLC can efficiently and robustly handle the uncertainties and fuzziness in the system, which can significantly enhance the flexibility and efficiency of the control process.
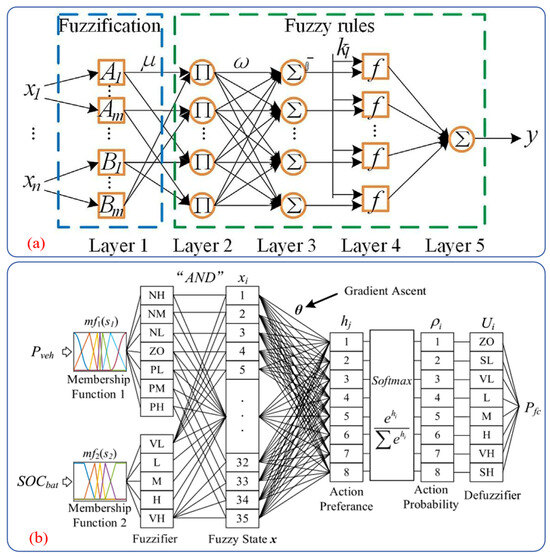
Figure 3.
The different structures of FIS: (a) classic FIS [10]; (b) FIS integrated with fuzzy REINFORCE algorithm [37].
Recent studies have advanced the FLC-based EMS applications. Yang et al. optimized strategy parameters with the adaptive fireworks algorithm and developed the rule-based shift strategy and the Takagi–Sugeno controller for torque distribution. Compared with the classical fuzzy torque distribution strategy, the approach improved HEV fuel economy by approximately 11% under the Chinese urban cycle with 14% in real-world driving (HIL) [40]. Deng et al. integrated FLC with the state machine, which leveraged the vehicle power demands, the SOC, and the battery power limit to control the fuel cell operations. Under the WLTC, hydrogen consumption was reduced by approximately 9.8% compared with the power follower control (PFC), and the SOC of the battery was effectively stabilized (SIL) [63]. Rezk et al. proposed EMS switching between fuzzy logic and proportional integral (PI) control strategies based on the thresholds, achieving approximately 3.4% and 9.1% performance boosts over PI and FLC alone, respectively (SIL) [64].
There are differences between the deterministic and fuzzy logic rule-based strategies, which both have the characteristics of high computational efficiency, simple control, and strong robustness [57]. The deterministic rules can quickly respond to changes in the vehicle state, making them suitable for the application scenarios with high real-time requirements. The fuzzy logic rules are more suitable for handling complex and nonlinear systems, which could make effective decisions under uncertain conditions and enhance the flexibility of control. The overall performance can be enhanced by combining the approaches. However, the traditional rule-based EMSs rely heavily on expert experience [65]. They cannot dynamically optimize energy distribution, which makes it difficult to achieve optimal performance [66]. Moreover, the fuzzy logic-based power distribution may additionally introduce the optimization parameters causing deviations from the global optimal solution [45]. Nowadays, research has introduced improvements, such as modified power follower strategies and integrations with fuzzy logic controllers, which have enhanced fuel economy and other performance metrics. Moving forward, efforts should focus on combining the strengths of rule-based EMSs with advanced optimization techniques to reduce dependence on expert knowledge and improve adaptability. This will drive the development of more efficient and intelligent rule-based EMSs for HEV technology and sustainable transportation.
3.2. Optimized Strategy of EMSs
Optimized EMSs aim to adjust the control variables based on the numerical calculation results by minimizing a predetermined cost function under feasible constraints [67]. The methods are mainly divided into two categories: global and the local optimization. Global-optimized EMSs apply the static data to optimize entire control sequences for specific operating conditions [68] with the DP, PMP, and GA. However, the reliance on prior global knowledge restricts the online implementation. Consequently, the local optimization often serves as a practical approximation to the global optima [68]. Local-optimized EMSs focus on the specifically regional or sub systemic searches, which solve the standalone subproblems or are integrated into the global frameworks. Common local methods include the Equivalent Consumption Minimization Strategy (ECMS) and MPC.
3.2.1. Global-Optimized EMSs
DP is grounded in Bellman’s optimality principle, which decomposes complex multi-stage problems into a series of simpler single-stage problems [69]. It identifies the global optimal solution by recursively solving subproblems. The EMSs optimized by the DP algorithm can significantly enhance fuel economy. The EMSs that combined DP and decision rules improved fuel economy by approximately 6% compared with the rule-based EMSs (SIL) [70]. Since DP can obtain the global optimal solution, it was often regarded as a benchmark for other EMSs [71,72], which was limited to offline use owing to the requirement for predefined speed profiles [6]. Moreover, the computational complexity of the DP algorithm increased sharply when it dealt with large-scale problems [73]. Additionally, the computation time of DP grew exponentially with the change in the problem dimension, which led to the low computational efficiency [74].
PMP transforms the global optimization problems into the instantaneous Hamiltonian optimization problems via the variational calculus of DP, which is an optimal control theory-based approach [58]. The EMS proposed by Sun et al. identified driving characteristics by collecting the output power of the motor, which used the suboptimal costate to implement the PMP algorithm in real-time during driving. It cut the hydrogen consumption by approximately 29% compared to rule-based EMSs, with an average online computation time of about 3.6 ms per step and sampling intervals of less than 1 s (SIL and final vehicle) [75]. The PMP strategies can outpace DP-based EMSs with a computation time reduction of up to 89%, which greatly reduced the computational complexity and made it suitable for real-time application scenarios (SILs) [76]. Quan et al. proposed the PMP-EMS to dynamically update costate variables according to the real-time driving conditions, which slashed the equivalent hydrogen consumption by approximately 14% and 9.2% compared with the traditional PFC strategies and static PMP-EMSs with fuel cell degradation rate reductions of 93% and 8.7% (SIL) [77]. The PMP combined with the real-time driving conditions can achieve optimal control with both instantaneous and global characteristics [78]. It should be noted that the PMP-based EMSs cannot guarantee the optimality of its solution in the absence of information about future driving conditions [79].
As a heuristic global optimization method, GA mimics the mechanisms of natural selection and genetics, which seeks the optimal solution through an iterative evolutionary process. The core process of GA involves initializing a population within the feasible solution space to generate the new populations with genetic operations, which includes the selection, the crossover, and the mutation to evaluate the termination criteria for population convergence [58]. Ma et al. used GA to adjust the weights and constraints of MPC strategies to achieve an optimal flexible power allocation process [80]. Wang et al. optimized the formulas of the fuzzy membership functions with GA to narrow the gap with a DP of 2.7%, which boosted the energy economy by 2.6%, 2.4%, and 3.3% at different temperatures (10 °C, 25 °C, 40 °C) (SIL) [65]. Nassar et al. used a variant of the GA algorithm, multi-objective GA, optimized EMS offline, and stored optimal maps to enable the EMS to provide a continuous improvement in fuel economy across multiple driving cycles [81]. Li et al. modified an Otto-cycle engine to an Atkinson-cycle engine, which was optimized with the non-dominated sorting GA-II. The cumulative fuel consumption was reduced by approximately 4.6% under the NEDC condition (Testbench and SIL) [82]. GA had a strong global search ability to effectively avoid getting trapped in local optimal solutions, which made it suitable for handling nonlinear, multi-objective, and high-dimensional optimization problems. However, GA had issues of high computational requirements [58], slow convergence speed, and sensitivity to parameter settings.
3.2.2. Local Optimized EMSs
ECMS is the local optimization method based on the PMP, which calculates the equivalent factor (EF) to equate the process of electrical energy consumption and fuel consumption. It achieves the optimal power distribution between the engine and motor in hybrid systems by optimizing the EF. The optimization effect of the ECMS depends on the accuracy of the EF. Hu et al. introduced a data-driven driving condition recognition model [83]. Sun et al. added the correction factor that can adjust the EF according to the motion characteristics of each driving segment [84]. Vignesh et al. combined ECMSs with intelligent technologies and proposed a robust EF correction method for the SOC under various uncertain driving conditions to realize the adaptive adjustment of the equivalent factor [85].
The innovative methods of the ECMS in reducing fuel consumption have been deeply explored. At present, ECMSs can effectively reduce fuel consumption to approximately 5.3 L per 100 km (SIL) [86]. Zhang et al. fused the advanced driver assistance system and maps, who proposed a data-driven predictive equivalent consumption minimization strategy (D-PECMS) with a multi-variable long short-term memory (LSTM) network. The method reduced the computational burden and slashed fuel consumption by approximately 13% versus rule-based control strategies (HIL) [87]. The energy management problem of HEV can be transformed into an optimal path search with the breadth-first search algorithm to achieve global optimization. Hao et al. took the breadth-first search results as the reference to propose an AECMS, which used the PSO algorithm to adjust the EF in real-time. Compared with the rule-based strategies, the fuel consumption can be reduced by approximately 10–15% and 8–10% under the federated test procedure (FTP75) and the worldwide harmonized light vehicles test procedure (WLTP) cycles (SIL) [88]. Gao et al. proposed the scenario-oriented AECMS that predicted the future speeds with a hybrid neural network model based on the Nanjing oriented driving cycle. It effectively restricted the SOC within a narrow fluctuation range of 0.12–0.33%. The equivalent hydrogen fuel consumption was reduced to approximately 7.1 g/km (SIL) [89]. Figure 4a,b are the framework diagrams of D-PECMS and AECMS, respectively. Despite the online viability and the low complexity [90,91], ECMS still has difficulty in maintaining the optimal performance of the charge in real-time applications [42] to balance the driving performance with computational efficiency [58].
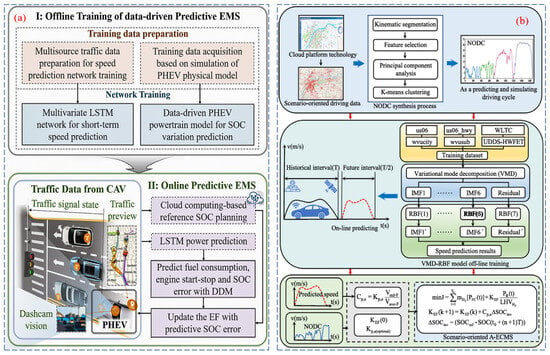
Figure 4.
The different frameworks of ECMS: (a) D-PECMS [87]; (b) A-ECMS [89].
The MPC targets efficient energy management and power distribution like the ECMS. MPC strategies forecast future driving with the system models and prediction algorithms, which leverage the forecasts to inform the power allocation and the control decisions. Xue et al. organically combined the MPC with ECMS by means of driving mode recognition technology, which retained the advantage of the MPC in obtaining optimization results through rolling optimization to update and predict control parameters in the next time domain [68]. The hybrid approach achieved fuel economy, adaptability, and near-global optimality with high computational efficiency [92]. Cui et al. proposed a multi-objective hierarchical EMS that merged resistance network-triggered DP for motion planning with MPC for the convex torque optimization. The framework demonstrated the excellent robustness against the random fluctuations of traffic flow by applying the alternating direction method of multipliers [93]. The strong robustness of the MPC made it suitable for the control of uncertain and nonlinear dynamic systems [94]. However, the performance highly depends on the accuracy of the prediction model. It may lead to unsatisfactory control effects if the prediction error is significant. The constant speed prediction method can mitigate the inaccuracies caused by the changes in traffic fluctuations or driving habits, which can significantly improve the prediction accuracy [68]. Nevertheless, the MPC has the high computational complexity and requires substantial computational resources.
In conclusion, optimized EMSs for HEVs have their respective merits and drawbacks. Global optimization methods are capable of achieving high-quality optimization. However, they face challenges such as high computational demands, reliance on prior knowledge, or a lack of optimality guarantees without future information. On the other hand, local optimization methods offer online viability and lower complexity to some extent. Nevertheless, these methods struggle with maintaining optimal performance or heavily depend on the prediction accuracy. These strategies have advanced HEV energy management, but continuous research is needed to address their limitations. Combining the strengths of global and local optimization approaches could lead to the development of more efficient, robust, and adaptable EMSs for the evolving needs of HEV technology.
3.3. Learning-Based Strategy
Learning-based strategies deeply integrate cutting-edge technologies, such as artificial intelligence and RL, which optimize energy management through iterative learning and experience accumulation driven by data. The intelligent approaches have shown remarkable effectiveness in controlling large nonlinear systems as given in Figure 5 [95]. As a transformative technology in planning and optimization, RL empowered agents to learn model-free and efficiently by interacting with their environment [58]. Rooted in the Markov decision process, RL conducted the learning and decision-making. The model of the Markov decision process involved the construction of state spaces, action spaces, and reward functions. This framework has significant advantages in solving sequential decision-making problems under uncertain conditions, which can ensure global optimality within the entire planning scope [96]. The main algorithms involved in RL are policy gradient and Q-learning. Policy gradient directly tuned policy parameters by estimating gradients and updating in the ascent direction to maximize cumulative rewards. Conversely, Q-learning was a model-free algorithm based on the value function. By iteratively updating the Q-value function with the Bellman equation, the agent learns in different states to obtain the maximum long-term cumulative reward to obtain the optimal policy. Figure 5a is the framework of the EMS based on Q-learning. Figure 5b–d are the framework of the EMSs based on DQN, DDPG, and SAC, respectively. The neural networks underpin energy system prediction, optimization, and control. Each neural network receives multiple input signals comprising the interconnected neurons, which are processed through weighted summation and nonlinear activation functions to generate an output signal. The networks capture complex input–output mappings, enabling energy system modeling and prediction by adjusting the connection weights between neurons.
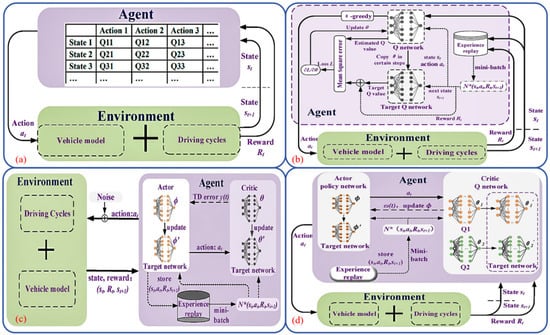
Figure 5.
The different frameworks of the learning-based strategies: (a) the EMS based on Q-learning; (b) the EMS based on DQN; (c) the EMS based on DDPG; (d) the EMS based on SAC [14]. (The notation “*” in N*(si, ai, Ri, si+1) indicates a target value. This value is calculated by the target network and serves as a reference for updating the main network (such as the Critic network) during the learning process of the agent in its interaction with the environment).
Non-RL neural networks mainly include the LSTM, the gated recurrent units (GRUs), and the recurrent neural networks (RNNs). Figure 6a–c are the structures of the LSTM, GRU, and RNN [97,98]. DRL combines RL with the neural networks to effectively handle the complex scenes with high-dimensional sensory inputs [58]. Key DRL algorithms include DQN, DDPG, and SAC. DQN integrates deep learning with Q-learning, which uses the Q-network to approximate Q-values and improve the training stability via experience replay and target networks. It is used to solve RL problems in discrete action spaces, and its neural network structure is listed in Figure 6d [99]. Wang et al. applied the parameterized DQN to reduce the lithium-ion battery aging by approximately 11% while achieving approximately 99.5% of DP global optimality (HIL) [100]. DDPG combines the deep neural networks with the deterministic policies, which is suitable for continuous action spaces. In DDPG, the actor network outputs deterministic actions and the critic network evaluates the action values. The neural network structure is given in Figure 6e [101]. SAC is grounded in the maximum entropy RL to maximize the cumulative reward, which performs well in continuous space. Studies confirmed the DRL-based EMSs’ superior fuel economy. Table 2, Table 3 and Table 4 show the fuel consumption, hydrogen consumption, and fuel economy across diverse learning-based strategies.
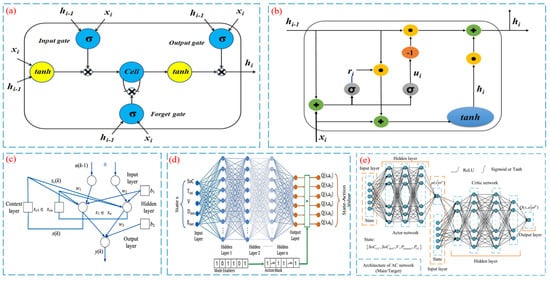
Figure 6.
The different structures of neural networks: (a) LSTM [97]; (b) GRU [97]; (c) RNN [98]; (d) DQN [99]; (e) DDPG [101].

Table 2.
The performance of different learning-based strategies based on fuel consumption.

Table 3.
The performance of different learning-based strategies based on hydrogen fuel consumption.

Table 4.
The performance of different learning-based strategies based on fuel economy.
The solutions have been actively explored to address the prolonged training time of DRL. Li et al. designed novel reward terms to prompt agents to autonomously identify the optimal SOC range by randomly combining diverse load curves for DQL model training. It achieved a 96.5% reduction in the training time with a 55.4% decrease in the computation time compared with the Q-learning-based strategies (SIL) [114]. Li et al. also proposed the EMS based on DDPG and designed a new reward function that considered the battery aging model to conduct the training within a vehicle-to-cloud framework. This approach reduced the number of training rounds by 98.5% and 20.0% relative to Q-learning and DQL-based strategies, respectively (processor-in-the-loop testing) [115]. Other researchers have targeted the convergence speed. Table 5 compares the convergence performance of various learning-based strategies. While the results demonstrated in Table 2, Table 3, Table 4 and Table 5 show performance improvements, it is essential to emphasize that the reliability of these metrics is closely linked to their respective validation platforms. All such platforms are explicitly denoted in the corresponding studies to ensure transparency. Nevertheless, hybrid algorithms often demand extensive data support [58]. Moreover, the complexity of RL-based EMSs has been continuously increasing as RL algorithms evolve and deep neural networks become more complex, which affect the computational workload and time consumption during the strategy application phase [96].

Table 5.
The performance of different learning-based strategies on convergence rate.
In conclusion, learning-based strategies have revolutionized HEV energy management by leveraging artificial intelligence and RL. These strategies excel in handling complex nonlinear systems and sequential decision-making under uncertainty, significantly enhancing fuel economy and system performance. While innovative solutions have been developed to mitigate long training times and slow convergence, challenges remain. The increasing complexity of hybrid algorithms and their high data requirements pose obstacles to practical implementation. Continued research should focus on simplifying algorithms, reducing data dependence, and improving the computational efficiency to fully realize the potential of learning-based strategies in HEV energy management.
Table 6 summarizes the advantages and limitations of rule-based, optimized, and learning-based EMSs for HEVs, revealing the characteristics of each type. Rule-based EMSs are known for their computational efficiency and robustness but lack dynamic optimization capabilities. In contrast, optimized EMS methods, such as DP, can achieve global optimality but require significant computational resources, while PMP strikes a balance between optimization and complexity. Learning-based EMS approaches, such as RL and DRL, offer the potential for model-free learning and improved fuel economy. However, they face challenges related to long training times and high algorithmic complexity. This detailed comparative study provides guidance for EMS strategy selection and improvement. The EMS analysis underpins the development of more efficient, intelligent EMSs, driving innovation in HEVs and related fields to meet the evolving energy and performance demands [118].

Table 6.
Advantages and limitations of different types of EMSs.
4. Future Development Trends
Traditional EMSs increasingly struggle to meet the requirements of efficient, intelligent, and eco-friendly development. In the future, EMSs will make significant strides towards the in-depth integration of intelligence and real-time optimization, as well as multi-objective optimization. Through multi-dimensional in-depth integration and continuous optimization, EMSs will drive the efficient and sustainable operation of energy systems.
Future EMSs will closely integrate learning-based algorithms with optimized models to achieve dynamic adaptive control. The learning-based algorithms extract complex patterns from vast datasets, while the optimized models provide precise decision-making frameworks, which can interplay to propel EMSs’ intelligence to new heights. Ma et al. combined MPC with TD3 and used an improved SQP algorithm to enhance the real-time performance, which can minimize battery degradation and boost efficiency [119]. Edge computing will further amplify system responsiveness by reducing data latency to underpin the intelligent real-time integration. Zhang et al. developed a mobile edge computing framework, which decentralized the traditional on-board control units into cloud-integrated hierarchical asynchronous controllers [120]. This enabled load balance across the local nodes and near-zero communication delays.
Multifaceted objectives like fuel economy, emissions control, and drivability will define future EMS design, presenting a significant challenge in balancing these goals within dynamic real-world scenarios. Li et al. proposed a multi-objective EMS, which considered fuel economy to maintain the SOC and reduce battery degradation [121]. It used a multi-agent DDPG algorithm and treated the engine and the battery as cooperative agents to optimize power distribution and outperform traditional methods in multi-objective tasks. Cheng et al. proposed an adaptive EMS that integrated the rule-based control with multi-objective optimization [122], which incorporated a point-line strategy optimized by PSO. This approach reduced operational costs, extended the fuel cell lifespan, and enhanced the operating efficiency.
Among these research efforts, the multi-objective evolutionary algorithm based on decomposition (MOEAD) stands out as a highly innovative and promising approach. The MOEAD decomposes the multi-objective optimization problem into multiple subproblems, which can search for Pareto optimal solutions in a large solution space to achieve global optimization. This unique feature endows MOEAD with the ability to handle complex multi-objective problems more effectively compared to many traditional methods. Cui et al. applied MOEAD within a cyber–physical interaction framework, achieving remarkable results. Not only did it increase the computational speed while maintaining energy efficiency, but it also outperformed synchronous and hierarchical methods by a significant margin [123]. In future research, in-depth exploration of MOEAD is essential. First, its parameter settings should be optimized to adapt to different vehicle models and driving conditions. Then, it should be combined with emerging control strategies to enhance the efficiency of EMSs. Additionally, analyzing the potential of MOEAD in dealing with new multi-objective problems that may arise in the development of HEVs will also be an important research topic.
The convergence of intelligence and real-time optimization of the EMSs along with the widespread application of multi-objective strategies will herald a paradigm shift in energy management. Through continuous innovation, future EMSs will be pivotal in driving efficient energy use, environmental protection, and sustainable growth to steer the society toward a greener, smarter future.
5. Conclusions
The principles, advantages, and disadvantages of the rule-based, optimized, and learning-based EMSs and energy configuration methods (series, parallel, and series–parallel) for HEVs were introduced. The EMSs have played a significant role in fuel consumption reduction to improve fuel economy and vehicle performance in practical effectiveness. Compared with the rule-based strategies, the learning-based strategies can reduce fuel consumption by approximately 5.2%~17% with hydrogen consumption reductions by up to 56% and fuel economy improvements by up to 10.5%.
With the continuous development of intelligent and information technologies, the in-depth integration of intelligent and real-time optimization and multi-objective optimization strategies have become a highly promising development direction. The results of this study not only conformed this development trend but also further enriched it. This study aligned with global efforts to reduce carbon emissions in the automotive sector. By systematically analyzing EMSs for HEVs, the findings established a theoretical framework for optimizing system efficiency. Significant fuel savings and emission reductions can be achieved. These insights can directly inform the development of next-generation energy-management systems. The widespread adoption of such technologies will advance sustainable mobility and support decarbonization targets. Future research should focus on developing algorithms with high adaptability and robustness, emphasizing cost scalability to overcome barriers in real-world implementation.
Author Contributions
Conceptualization, F.W. and X.Z.; methodology, F.W.; formal analysis, Y.H.; investigation, Y.H.; resources, F.W.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H. and X.Z.; supervision, F.W. and X.Z.; project administration, F.W.; funding acquisition, F.W. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the Young Scientists Fund of the National Natural Science Foundation of China] grant number [52106151] and [the Ministry of Education collaborates with industry and academia to promote collaborative education] grant number [230800287172939].
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
Thank you to the relevant personnel who provided suggestions for the writing of this article.
Conflicts of Interest
The authors declare that they have no conflicts of interests regarding the publication of this paper.
Abbreviations
| Abbreviation | |
| HEV | Hybrid electric vehicle |
| EMS | Energy management strategy |
| GA | Genetic algorithm |
| ANFIS | Adaptive network-based fuzzy inference system |
| PI | Proportional integral |
| PFC | Power follower control |
| MPC | Model predictive control |
| DP | Dynamic programming |
| SQP | Sequential quadratic programming |
| BPNN | Back propagation neural network |
| PMP | Pontryagin’s minimum principle |
| EM | Electric motor |
| SAC | Soft actor-critic |
| RL | Reinforcement learning |
| PSO | Particle swarm optimization |
| GSS | Golden section search |
| DQN | Deep Q-network |
| FLC | Fuzzy logic control |
| TD3 | Twin delayed deep deterministic policy gradient |
| SOC | State of charge |
| DQL | Deep Q-learning |
| SCHDC | Suburbs city highway driving cycle |
| UDDS | Urban dynamometer driving schedule |
| NEDC | New European driving cycle |
| WLTC | Worldwide harmonized light vehicles test cycle |
| DDPG | Deep deterministic policy gradient |
| DRL | Deep reinforcement learning |
| MADRL | Multi-agent DRL |
| ACC-EMS | Adaptive cruise control-EMS |
| ICE | Internal combustion engine |
| AMT | Automated mechanical transmission |
| KF | Kalman Filter |
| PMSM | Permanent magnet synchronous motor |
| HIL | Hardware-in-the-Loop |
| SIL | Software-in-the-Loop |
| ECMS | Equivalent consumption minimization strategy |
| AECMS | Adaptive ECMS |
| EF | Equivalent factor |
| LSTM | long short-term memory |
| D-PECMS | data-driven predictive ECMS |
| WLTP | Worldwide harmonized light vehicles test procedure |
| FTP75 | Federated test procedure |
| GRU | Gated recurrent units |
| RNN | Recurrent neural networks |
| MOEAD | Multi-objective evolutionary algorithm based on decomposition |
| RBFNN | Radial basis function neural network |
| PER | Prioritized experience replay |
| ERE | Emphasizing recent experience |
| CD/CS | Charge depleting/charge sustaining |
| Nomenclature | |
| Pe | the power of battery, W; |
| Uoc | the open-circuit voltage, V; |
| Ibat | the charging and discharging current of the battery, A; |
| Rin | the internal resistance of the battery, Ω; |
| Ceq | the equivalent capacitance, F; |
| SOC(t0) | the initial SOC; |
| I(t) | the current at time t, A; |
| η | the Coulomb coefficient; |
| QN | the rated capacity of the battery, As; |
| t | the time, s; |
| Xk | the estimated SOC at time step k; |
| Zk | the voltage at time step k, V; |
| ηbat | the charging and discharging efficiency of the battery; |
| Ik | the battery current at time step k, A; |
| Δt | the sampling interval, s; |
| f(·) | the system state function; |
| G(·) | the system measurement function; |
| Vk−1 | the battery voltage at time step k−1, V; |
| Tk | the battery temperature at time step k, °C; |
| vk−1 | the noise item, which is added to the state equation; |
| ωk−1 | the noise item, which is added to the measurement equation, V; |
| ud | the voltage of the d-axis, V; |
| uq | the voltage of the q-axis, V; |
| id | the current of the d-axis, A; |
| iq | the current of the q-axis, A; |
| ivd | the effective component of id, A; |
| ivq | the effective component of iq, A; |
| ψf | the flux linkage of the permanent magnet, Wb; |
| ωs | the electrical angular velocity of the motor, rad/s; |
| Rs | the stator resistance of the motor, Ω; |
| Rc | the equivalent core loss resistance of the motor, Ω; |
| Ld | the inductance of the d-axis, H; |
| Lq | the inductance of the q-axis, H; |
| Te | the electromagnetic torque, N·m; |
| p | the number of pole pairs of the motor |
References
- Zhou, S.; Tong, Q.; Pan, X.; Cao, M.; Wang, H.; Gao, J.; Ou, X. Research on low-carbon energy transformation of China necessary to achieve the Paris agreement goals: A global perspective. Energy Econ. 2021, 95, 105137. [Google Scholar] [CrossRef]
- Tran, D.-D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Mierlo, J.V.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, C.; Wu, D.; Huang, C.; Yan, F. A tolerant sequential correction predictive energy management strategy of hybrid electric vehicles with adaptive mesh discretization. Energy 2023, 274, 127314. [Google Scholar] [CrossRef]
- Sabri, M.F.M.; Danapalasingam, K.A.; Rahmat, M.F. A review on hybrid electric vehicles architecture and energy management strategies. Renew. Sustain. Energy Rev. 2016, 53, 1433–1442. [Google Scholar] [CrossRef]
- Tametang, M.I.M.; Tameze, P.L.L.; Tchaya, G.B.; Yemele, D. Improvement of fuel economy and efficiency in a modified parallel hybrid electric vehicle architecture with wind turbine device: Effect of the external energy source. Next Energy 2025, 7, 100301. [Google Scholar] [CrossRef]
- Ganesh, A.H.; Xu, B. A review of reinforcement learning based energy management systems for electrified powertrains: Progress, challenge, and potential solution. Renew. Sustain. Energy Rev. 2022, 154, 111833. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, L.; Liang, B.; Huangfu, Z. A route identification-based energy management strategy for plug-in fuel cell hybrid electric buses. J. Power Sources 2025, 638, 236576. [Google Scholar] [CrossRef]
- Yang, B.; Si, S.; Zhang, Z.; Gao, B.; Zhao, B.; Xu, H.; Zhang, T. Fuzzy energy management strategy of a flywheel hybrid electric vehicle based on particle swarm optimization. J. Energy Storage 2024, 101, 114003. [Google Scholar] [CrossRef]
- Mazouzi, A.; Hadroug, N.; Alayed, W.; Hafaifa, A.; Iratni, A.; Kouzou, A. Comprehensive optimization of fuzzy logic-based energy management system for fuel-cell hybrid electric vehicle using genetic algorithm. Int. J. Hydrog. Energy 2024, 81, 889–905. [Google Scholar] [CrossRef]
- Bo, L.; Han, L.; Xiang, C.; Liu, H.; Ma, T. A Q-learning fuzzy inference system based online energy management strategy for off-road hybrid electric vehicles. Energy 2022, 252, 123976. [Google Scholar] [CrossRef]
- Luca, R.; Whiteley, M.; Neville, T.; Shearing, P.R.; Brett, D.J.L. Comparative study of energy management systems for a hybrid fuel cell electric vehicle—A novel mutative fuzzy logic controller to prolong fuel cell lifetime. Int. J. Hydrog. Energy 2022, 57, 24042–24058. [Google Scholar] [CrossRef]
- Vignesh, R.; Ashok, B.; Kumar, M.S.; Szpica, D.; Harikrishnan, A.; Josh, H. Adaptive neuro fuzzy inference system-based energy management controller for optimal battery charge sustaining in biofuel powered non-plugin hybrid electric vehicle. Sustain. Energy Technol. Assess. 2023, 59, 103379. [Google Scholar] [CrossRef]
- Chen, J.; He, H.; Wang, Y.-X.; Quan, S.; Zhang, Z.; Wei, Z.; Han, R. Research on energy management strategy for fuel cell hybrid electric vehicles based on improved dynamic programming and air supply optimization. Energy 2024, 300, 131567. [Google Scholar] [CrossRef]
- Xu, D.; Cui, Y.; Ye, J.; Cha, S.W.; Li, A.; Zheng, C. A soft actor-critic-based energy management strategy for electric vehicles with hybrid energy storage systems. J. Power Sources 2022, 524, 231099. [Google Scholar] [CrossRef]
- Tang, W.; Wang, Y.; Jiao, X.; Ren, L. Hierarchical energy management strategy based on adaptive dynamic programming for hybrid electric vehicles in car-following scenarios. Energy 2023, 265, 126264. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Wang, X.; Li, L.; Zhang, Y.; Chen, Z. Energy management for hybrid electric vehicles based on imitation reinforcement learning. Energy 2023, 263, 125890. [Google Scholar] [CrossRef]
- Sun, W.; Zou, Y.; Zhang, X.; Guo, N.; Zhang, B.; Du, G. High robustness energy management strategy of hybrid electric vehicle based on improved soft actor-critic deep reinforcement learning. Energy 2022, 258, 124806. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, D.; Zeng, X.; Zhang, X.; Song, D. Multi-objective real-time energy management for series–parallel hybrid electric vehicles considering battery life. Energy Convers. Manag. 2023, 290, 117234. [Google Scholar] [CrossRef]
- Han, J.; Shu, H.; Tang, X.; Lin, X.; Liu, C.; Hu, X. Predictive energy management for plug-in hybrid electric vehicles considering electric motor thermal dynamics. Energy Convers. Manag. 2022, 251, 115022. [Google Scholar] [CrossRef]
- Tang, W.; Jiao, X.; Zhang, Y. Hierarchical energy management control for connected hybrid electric vehicles in uncertain traffic scenarios. Energy 2025, 315, 134291. [Google Scholar] [CrossRef]
- Li, Y.; Deng, X.; Liu, B.; Ma, J.; Yang, F.; Ouyang, M. Energy management of a parallel hybrid electric vehicle based on Lyapunov algorithm. eTransportation 2022, 13, 100184. [Google Scholar] [CrossRef]
- Yang, C.; Du, X.; Wang, W.; Yuan, L.; Yang, L. Variable optimization domain-based cooperative energy management strategy for connected plug-in hybrid electric vehicles. Energy 2024, 290, 130206. [Google Scholar] [CrossRef]
- Zou, R.; Fan, L.; Dong, Y.; Zheng, S.; Hu, C. DQL energy management: An online-updated algorithm and its application in fix-line hybrid electric vehicle. Energy 2021, 225, 120174. [Google Scholar] [CrossRef]
- Chen, F.; Wang, B.; Ni, M.; Gong, Z.; Jiao, K. Online energy management strategy for ammonia-hydrogen hybrid electric vehicles harnessing deep reinforcement learning. Energy 2024, 301, 131562. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Song, C.; Yan, G.; Xiao, F.; Wang, D.; Zhang, X.; Cao, J.; Song, S. Hierarchical reinforcement learning based energy management strategy for hybrid electric vehicle. Energy 2022, 238, 121703. [Google Scholar] [CrossRef]
- Lv, H.; Qi, C.; Song, C.; Song, S.; Zhang, R.; Xiao, F. Energy management of hybrid electric vehicles based on inverse reinforcement learning. Energy Rep. 2022, 8, 5215–5224. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, Z.; Mao, X.; Hu, H.; Tan, J.; Xuan, D. Deep reinforcement learning based energymanagement strategy considering running costs and energy source aging for fuel cell hybrid electric vehicle. Energy 2023, 283, 129177. [Google Scholar] [CrossRef]
- Hua, M.; Zhang, C.; Zhang, F.; Li, Z.; Yu, X.; Xu, H.; Zhou, Q. Energy management of multi-mode plug-in hybrid electric vehicle using multi-agent deep reinforcement learning. Appl. Energy 2023, 348, 121526. [Google Scholar] [CrossRef]
- Qin, J.; Huang, H.; Lu, H.; Li, Z. Energy management strategy for hybrid electric vehicles based on deep reinforcement learning with consideration of electric drive system thermal characteristics. Energy Convers. Manag. 2025, 332, 119697. [Google Scholar] [CrossRef]
- Madhanakkumar, N.; Vijayaragavan, M.; Anbarasan, P.; Reshmila, S. Smart energy management for plug-in hybrid electric vehicles: Integration of waterwheel plant algorithm and dual stream spectrum deconvolution neural network. J. Energy Storage 2024, 102, 113867. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Zhang, Y.; Lei, Z.; Chen, Z.; Li, G. A neural network-based ECMS for optimized energy management of plug-in hybrid electric vehicles. Energy 2022, 243, 122727. [Google Scholar] [CrossRef]
- Nayak, N.; Satpathy, A. An Adaptive Energy Management Strategy for Plug-in Hybrid Electric Vehicles (PHEVs) Utilizing Real-Time Speed Profiles and Optimized Battery Discharge Levels. Energy Storage Sav. 2025, in press. [CrossRef]
- Huang, X.; Zhang, J.; Ou, K.; Huang, Y.; Kang, Z.; Mao, X.; Zhou, Y.; Xuan, D. Deep reinforcement learning-based health-conscious energy management for fuel cell hybrid electric vehicles in model predictive control framework. Energy 2024, 304, 131769. [Google Scholar] [CrossRef]
- Chen, B.; Wang, M.; Hu, L.; Zhang, R.; Li, H.; Wen, X.; Gao, K. A hierarchical cooperative eco-driving and energy management strategy of hybrid electric vehicle based on improved TD3 with multi-experience. Energy Convers. Manag. 2025, 326, 119508. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, J.; Dong, H.; Tan, H.; Ding, F. Hierarchical reinforcement learning based energy management strategy of plug-in hybrid electric vehicle for ecological car-following process. Appl. Energy 2023, 333, 120599. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Chen, J.; Zhou, J.; Wei, Z.; Ma, C. Health-considered energy management strategy for fuel cell hybrid electric vehicle based on improved soft actor critic algorithm adopted with Beta policy. Energy Convers. Manag. 2023, 292, 117362. [Google Scholar] [CrossRef]
- Guo, L.; Li, Z.; Outbib, R.; Gao, F. Function approximation reinforcement learning of energy management with the fuzzy REINFORCE for fuel cell hybrid electric vehicles. Energy AI 2023, 13, 100246. [Google Scholar] [CrossRef]
- Yang, C.; Zha, M.; Wang, W.; Liu, K.; Xiang, C. Efficient energy management strategy for hybrid electric vehicles/plug-in hybrid electric vehicles: Review and recent advances under intelligent transportation system. IET Intell. Transp. Syst. 2020, 7, 702–711. [Google Scholar] [CrossRef]
- Song, K.; Ding, Y.; Hu, X.; Xu, H.; Wang, Y.; Cao, J. Degradation adaptive energy management strategy using fuel cell state-of-health for fuel economy improvement of hybrid electric vehicle. Appl. Energy 2021, 285, 116413. [Google Scholar] [CrossRef]
- Yang, C.; Liu, K.; Jiao, X.; Wang, W.; Chen, R.; You, S. An adaptive firework algorithm optimization-based intelligent energy management strategy for plug-in hybrid electric vehicles. Energy 2022, 239, 122120. [Google Scholar] [CrossRef]
- Zhang, D.; Li, J.; Guo, N.; Liu, Y.; Shen, S.; Wei, F.; Chen, Z.; Zheng, J. Adaptive deep reinforcement learning energy management for hybrid electric vehicles considering driving condition recognition. Energy 2024, 313, 134086. [Google Scholar] [CrossRef]
- Pan, M.; Cao, S.; Zhang, Z.; Ye, N.; Qin, H.; Li, L.; Guan, W. Recent progress on energy management strategies for hybrid electric vehicles. J. Energy Storage 2025, 116, 115936. [Google Scholar] [CrossRef]
- Kim, Y.; Salvi, A.; Siegel, J.B.; Filipi, Z.S.; Stefanopoulou, A.G.; Ersal, T. Hardware-in-the-loop validation of a power management strategy for hybrid powertrains. Control Eng. Pract. 2014, 29, 277–286. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Pan, W.; Wu, Y.; Tong, Y.; Li, J.; Liu, Y. Optimal rule extraction-based real-time energy management strategy for series-parallel hybrid electric vehicles. Energy Convers. Manag. 2023, 293, 117474. [Google Scholar] [CrossRef]
- Monirul, I.M.; Qiu, L.; Ruby, R.; Ullah, I.; Sharafian, A. Accurate SOC estimation in power lithium-ion batteries using adaptive extended Kalman filter with a high-order electrical equivalent circuit model. Measurement 2025, 249, 117081. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Xu, K.; He, T.; Yang, P.; Meng, X.; Zhu, C.; Jin, X. A new online SOC estimation method using broad learning system and adaptive unscented Kalman filter algorithm. Energy 2024, 309, 132920. [Google Scholar] [CrossRef]
- Rimsha; Murawwat, S.; Gulzar, M.M.; Alzahrani, A.; Hafeez, G.; Khan, F.A.; Abed, A.M. State of charge estimation and error analysis of lithium-ion batteries for electric vehicles using Kalman filter and deep neural network. J. Energy Storage 2023, 72, 108039. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, A.; Zhang, Q.; Xu, N. Power allocation-Oriented stator current optimization and dynamic control of a dual-inverter open-winding PMSM drive system for dual-power electric vehicles. Energy 2025, 322, 135587. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, J.; Chen, K.; Wen, X. A Static Current Error Elimination Algorithm for Predictive Current Control in PMSM for Electric Vehicles. Green Energy Intell. Transp. 2025, in press. [CrossRef]
- Guo, L.; Jin, X.; Wang, H. On winding reconstruction method for six-phase motor with single-phase winding open-circuit faults. J. Magn. Magn. Mater. 2023, 587, 171365. [Google Scholar] [CrossRef]
- Belkhier, Y.; Fredj, S.; Rashid, H.; Benbouzid, M. Robust nonlinear control of permanent magnet synchronous motor drives: An evolutionary algorithm optimized passivity-based control approach with a high-order sliding mode observer. Eng. Appl. Artif. Intell. 2025, 145, 110256. [Google Scholar] [CrossRef]
- Liu, W.; Sui, S.; Chen, C.L.P. Event-triggered predefined-time output feedback fuzzy adaptive control of permanent magnet synchronous motor systems. Eng. Appl. Artif. Intell. 2025, 142, 109882. [Google Scholar] [CrossRef]
- Kasri, A.; Ouari, K.; Belkhier, Y.; Oubelaid, A.; Bajaj, M.; Tuka, M.B. Real-time and hardware in the loop validation of electric vehicle performance: Robust nonlinear predictive speed and currents control based on space vector modulation for PMSM. Results Eng. 2024, 22, 102223. [Google Scholar] [CrossRef]
- Guo, Z.; Zhen, S.; Liu, X.; Zhong, H.; Yin, J.; Chen, Y.-H. Design and application of a novel approximate constraint tracking robust control for permanent magnet synchronous motor. Comput. Chem. Eng. 2023, 173, 108206. [Google Scholar] [CrossRef]
- Xiong, R.; Chen, H.; Wang, C.; Sun, F. Towards a smarter hybrid energy storage system based on battery and ultracapacitor—A critical review on topology and energy management. J. Clean. Prod. 2018, 202, 1228–1240. [Google Scholar] [CrossRef]
- Urooj, A.; Nasir, A. Review of intelligent energy management techniques for hybrid electric vehicles. J. Energy Storage 2024, 92, 112132. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A state machine strategy based on droop control for an energy management system of PEMFC-battery-supercapacitor hybrid tramway. Int. J. Hydrog. Energy 2016, 36, 16148–16159. [Google Scholar] [CrossRef]
- Al Takrouri, M.; Idris, N.R.N.; Aziz, M.J.A.; Ayop, R.; Low, W.Y. Refined power follower strategy for enhancing the performance of hybrid energy storage systems in electric vehicles. Results Eng. 2025, 25, 103960. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Wang, Q.; Zeng, X. Control rules extraction and parameters optimization of energy management for bus series-parallel AMT hybrid powertrain. J. Frankl. Inst. 2018, 5, 2283–2312. [Google Scholar] [CrossRef]
- Abdelhedi, F.; Jarraya, I.; Bawayan, H.; Abdelkeder, M.; Rizoug, N.; Koubaa, A. Optimizing Electric Vehicles efficiency with hybrid energy storage: Comparative analysis of rule-based and neural network power management systems. Energy 2024, 313, 133979. [Google Scholar] [CrossRef]
- Deng, L.; Radzi, M.A.M.; Shafie, S.; Hassan, M.K. Optimizing energy management in fuel cell hybrid electric vehicles using fuzzy logic control with state machine approach: Enhancing SOC stability and fuel economy. J. Eng. Res. 2025, in press. [CrossRef]
- Rezk, H.; Fathy, A. Combining proportional integral and fuzzy logic control strategies to improve performance of energy management of fuel cell electric vehicles. Int. J. Thermofluids 2025, 26, 101076. [Google Scholar] [CrossRef]
- Wang, C.; Liu, R.; Tang, A. Energy management strategy of hybrid energy storage system for electric vehicles based on genetic algorithm optimization and temperature effect. J. Energy Storage 2022, 51, 104314. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, J.; Qin, D.; Zhang, Y.; Lei, Z. Rule-corrected energy management strategy for hybrid electric vehicles based on operation-mode prediction. J. Clean. Prod. 2018, 188, 796–806. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Song, K.; Huang, X.; Cai, Z.; Huang, P.; Li, F. Research on energy management strategy of fuel-cell vehicles based on nonlinear model predictive control. Int. J. Hydrog. Energy 2024, 50, 1604–1621. [Google Scholar] [CrossRef]
- Bao, S.; Sun, P.; Zhu, J.; Ji, Q.; Liu, J. Improved multi-dimensional dynamic programming energy management strategy for a vehicle power-split hybrid powertrain. Energy 2022, 256, 124682. [Google Scholar] [CrossRef]
- Si, S.; Yang, B.; Gao, B.; Zhang, Z.; Zhao, B.; Zhang, T.; Xu, H. A real-time energy management strategy combining rule and optimization for minimizing energy consumption and emissions of flywheel hybrid electric vehicle (FHEV). Appl. Therm. Eng. 2024, 255, 124013. [Google Scholar] [CrossRef]
- Guo, L.; Liu, H.; Han, L.; Yang, N.; Liu, R.; Xiang, C. Predictive energy management strategy of dual-mode hybrid electric vehicles combining dynamic coordination control and simultaneous power distribution. Energy 2023, 263, 125598. [Google Scholar] [CrossRef]
- Huang, R.; He, H.; Su, Q.; Härtl, M.; Jaensch, M. Enabling cross-type full-knowledge transferable energy management for hybrid electric vehicles via deep transfer reinforcement learning. Energy 2024, 305, 132394. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef]
- Chen, S.; Hu, M.; Guo, S. Fast dynamic-programming algorithm for solving global optimization problems of hybrid electric vehicles. Energy 2023, 273, 127207. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, Y.; Huang, L.; Lian, J. A real-time PMP energy management strategy for fuel cell hybrid buses based on driving segment feature recognition. Int. J. Hydrog. Energy 2021, 80, 39983–40000. [Google Scholar] [CrossRef]
- Liu, X.; Du, J.; Ma, J.; Liu, G.; Xiong, Y. An adaptive co-state design method for PMP-based energy management of plug-in hybrid electric vehicles based on fuzzy logical control. J. Energy Storage 2024, 102, 114118. [Google Scholar] [CrossRef]
- Quan, R.; Guo, H.; Li, X.; Zhang, J.; Chang, Y. A real-time energy management strategy for fuel cell vehicle based on Pontryagin’s minimum principle. iScience 2024, 4, 109473. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Qi, B.; Wang, S.; Ma, Q.; Sui, Z.; Gao, J. Real-time energy management of fuel cell hybrid electric vehicle based on variable horizon velocity prediction considering power source durability. Energy 2025, 315, 134359. [Google Scholar] [CrossRef]
- Kim, N.; Jeong, J.; Zheng, C. Adaptive Energy Management Strategy for Plug-in Hybrid Electric Vehicles with Pontryagin’s Minimum Principle Based on Daily Driving Patterns. Int. J. Precis. Eng. Manuf.-Green. Technol. 2019, 6, 539–548. [Google Scholar] [CrossRef]
- Ma, B.; Li, P.-H. Optimal flexible power allocation energy management strategy for hybrid energy storage system with genetic algorithm based model predictive control. Energy 2025, 324, 135958. [Google Scholar] [CrossRef]
- Nassar, M.Y.; Shaltout, M.L.; Hegazi, H.A. Multi-objective optimum energy management strategies for parallel hybrid electric vehicles: A comparative study. Energy Convers. Manag. 2023, 277, 116683. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Duan, X.; Liu, S.; Liu, J.; Hu, S. Multi-objective energy management for Atkinson cycle engine and series hybrid electric vehicle based on evolutionary NSGA-II algorithm using digital twins. Energy Convers. Manag. 2021, 230, 113788. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, P.; Wu, Z.; Tian, J. A real-time multi-objective optimization method in energy efficiency for plug-in hybrid electric vehicles considering dynamic electrochemical characteristics of battery and driving conditions. J. Energy Storage 2024, 84, 110779. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Z.; Han, S.; Tian, X.; Jin, Z.; Cao, Y.; Xue, M. Adaptive real-time ECMS with equivalent factor optimization for plug-in hybrid electric buses. Energy 2024, 304, 132014. [Google Scholar] [CrossRef]
- Vignesh, R.; Ashok, B. Intelligent energy management through neuro-fuzzy based adaptive ECMS approach for an optimal battery utilization in plugin parallel hybrid electric vehicle. Energy Convers. Manag. 2023, 280, 116792. [Google Scholar] [CrossRef]
- Sun, W.; Liu, H.; Han, M.; Sun, K.; Bai, S.; Li, G. A Novel Method for the Application of the ECMS (Equivalent Consumption Minimization Strategy) to Reduce Hydrogen Consumption in Fuel Cell Hybrid Electric Vehicles. Fluid Dyn. Mater. Process. 2022, 4, 867–882. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, N.; Liu, S.; Fan, Q.; Wang, Z. Data-driven predictive energy consumption minimization strategy for connected plug-in hybrid electric vehicles. Energy 2023, 283, 128514. [Google Scholar] [CrossRef]
- Hao, L.; Wang, Y.; Bai, Y.; Zhou, Q. Energy management strategy on a parallel mild hybrid electric vehicle based on breadth first search algorithm. Energy Convers. Manag. 2021, 243, 114408. [Google Scholar] [CrossRef]
- Gao, S.; Zong, Y.; Ju, F.; Wang, Q.; Huo, W.; Wang, L.; Wang, T. Scenario-oriented adaptive ECMS using speed prediction for fuel cell vehicles in real-world driving. Energy 2024, 304, 132028. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, Y. Intelligent ECMS for Connected Plug-in Hybrid Electric Vehicles. IFAC-Pap. 2021, 10, 278–283. [Google Scholar] [CrossRef]
- Sahwal, C.P.; Sengupta, S.; Dinh, T.Q. Advanced Equivalent Consumption Minimization Strategy for Fuel Cell Hybrid Electric Vehicles. J. Clean. Prod. 2024, 437, 140366. [Google Scholar] [CrossRef]
- Xue, J.; Jiao, X.; Yu, D.; Zhang, Y. Predictive hierarchical eco-driving control involving speed planning and energy management for connected plug-in hybrid electric vehicles. Energy 2023, 283, 129058. [Google Scholar] [CrossRef]
- Cui, W.; Cui, N.; Li, T.; Cui, Z.; Du, Y.; Zhang, C. An efficient multi-objective hierarchical energy management strategy for plug-in hybrid electric vehicle in connected scenario. Energy 2022, 257, 124690. [Google Scholar] [CrossRef]
- Zhao, Z.; Xun, J.; Wan, X.; Yu, R. MPC Based Hybrid Electric Vehicles Energy Management Strategy. IFAC-PapersOnLine 2021, 10, 370–375. [Google Scholar] [CrossRef]
- Kamal, E.; Adouane, L. Intelligent Energy Management Strategy Based on Artificial Neural Fuzzy for Hybrid Vehicle. IEEE Trans. Intell. Veh. 2018, 1, 112–125. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Yang, Q.; Wang, T.; He, H.; Wang, H.; Sun, F. Reinforcement learning based energy management for fuel cell hybrid electric vehicles: A comprehensive review on decision process reformulation and strategy implementation. Renew. Sustain. Energy Rev. 2025, 213, 115450. [Google Scholar] [CrossRef]
- Das, T.; Guchhait, S. A hybrid GRU and LSTM-based deep learning approach for multiclass structural damage identification using dynamic acceleration data. Eng. Fail. Anal. 2025, 170, 109259. [Google Scholar] [CrossRef]
- Chen, Z.; Gu, H.; Shen, S.; Shen, J. Energy management strategy for power-split plug-in hybrid electric vehicle based on MPC and double Q-learning. Energy 2022, 245, 123182. [Google Scholar] [CrossRef]
- Mousa, A. Extended-deep Q-network: A functional reinforcement learning-based energy management strategy for plug-in hybrid electric vehicles. Eng. Sci. Technol. Int. J. 2023, 43, 101434. [Google Scholar] [CrossRef]
- Wang, H.; He, H.; Bai, Y.; Yue, H. Parameterized deep Q-network based energy management with balanced energy economy and battery life for hybrid electric vehicles. Appl. Energy 2022, 320, 119270. [Google Scholar] [CrossRef]
- Lu, H.; Tao, F.; Fu, Z.; Sun, H. Battery-degradation-involved energy management strategy based on deep reinforcement learning for fuel cell/battery/ultracapacitor hybrid electric vehicle. Electr. Power Syst. Res. 2023, 220, 109235. [Google Scholar] [CrossRef]
- Zare, A.; Boroushaki, M. A knowledge-assisted deep reinforcement learning approach for energy management in hybrid electric vehicles. Energy 2024, 313, 134113. [Google Scholar] [CrossRef]
- Wang, Z.; He, H.; Peng, J.; Chen, W.; Wu, C.; Fan, Y.; Zhou, J. A comparative study of deep reinforcement learning based energy management strategy for hybrid electric vehicle. Energy Convers. Manag. 2023, 293, 117442. [Google Scholar] [CrossRef]
- Wang, H.; Ye, Y.; Zhang, J.; Xu, B. A comparative study of 13 deep reinforcement learning based energy management methods for a hybrid electric vehicle. Energy 2023, 266, 126497. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Tang, Y.; Li, Q.; He, H. Cooperative energy management and eco-driving of plug-in hybrid electric vehicle via multi-agent reinforcement learning. Appl. Energy 2023, 332, 120563. [Google Scholar] [CrossRef]
- Shi, D.; Xu, H.; Wang, S.; Hu, J.; Chen, L.; Yin, C. Deep reinforcement learning based adaptive energy management for plug-in hybrid electric vehicle with double deep Q-network. Energy 2024, 305, 132402. [Google Scholar] [CrossRef]
- Qi, C.; Zhu, Y.; Song, C.; Cao, J.; Xiao, F.; Zhang, X.; Xu, Z.; Song, S. Self-supervised reinforcement learning-based energy management for a hybrid electric vehicle. J. Power Sources 2021, 514, 230584. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, W.; Zou, Y.; Zhang, X.; Zhang, Y. An improved soft actor-critic-based energy management strategy of heavy-duty hybrid electric vehicles with dual-engine system. Energy 2024, 308, 132938. [Google Scholar] [CrossRef]
- Kang, X.; Wang, Y.; Chen, Z. A reinforcement learning energy management strategy for fuel cell hybrid electric vehicles considering driving condition classification. Sustain. Energy Grids Netw. 2024, 38, 101298. [Google Scholar] [CrossRef]
- Ren, X.; Ye, J.; Xie, L.; Lin, X. Battery longevity-conscious energy management predictive control strategy optimized by using deep reinforcement learning algorithm for a fuel cell hybrid electric vehicle. Energy 2024, 286, 129344. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, H.; Tan, J.; Lu, C.; Xuan, D. Deep reinforcement learning based energy management strategy for range extend fuel cell hybrid electric vehicle. Energy Convers. Manag. 2023, 277, 116678. [Google Scholar] [CrossRef]
- Du, G.; Zou, Y.; Zhang, X.; Guo, L.; Guo, N. Energy management for a hybrid electric vehicle based on prioritized deep reinforcement learning framework. Energy 2022, 241, 122523. [Google Scholar] [CrossRef]
- Tao, F.; Fu, Z.; Gong, H.; Ji, B.; Zhou, Y. Twin delayed deep deterministic policy gradient based energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles considering predicted terrain information. Energy 2023, 283, 129173. [Google Scholar] [CrossRef]
- Li, W.; Cui, H.; Nemeth, T.; Jansen, J.; Ünlübayir, C.; Wei, Z.; Zhang, L.; Wang, Z.; Ruan, J.; Dai, H.; et al. Deep reinforcement learning-based energy management of hybrid battery systems in electric vehicles. J. Energy Storage 2021, 36, 102355. [Google Scholar] [CrossRef]
- Li, W.; Cui, H.; Nemeth, T.; Jansen, J.; Ünlübayir, C.; Wei, Z.; Feng, X.; Han, X.; Ouyang, M.; Dai, H.; et al. Cloud-based health-conscious energy management of hybrid battery systems in electric vehicles with deep reinforcement learning. Appl. Energy 2021, 293, 116977. [Google Scholar] [CrossRef]
- Ruan, J.; Wu, C.; Liang, Z.; Liu, K.; Li, B.; Li, W.; Li, T. The application of machine learning-based energy management strategy in a multi-mode plug-in hybrid electric vehicle, part II: Deep deterministic policy gradient algorithm design for electric mode. Energy 2023, 269, 126792. [Google Scholar] [CrossRef]
- Huo, W.; Zhao, T.; Yang, F.; Chen, Y. An improved soft actor-critic based energy management strategy of fuel cell hybrid electric vehicle. J. Energy Storage 2023, 72, 108243. [Google Scholar] [CrossRef]
- Hong, J.; Zhang, T.; Zhang, Z.; Zhang, H. Investigation of energy management strategy for a novel electric-hydraulic hybrid vehicle: Self-adaptive electric-hydraulic ratio. Energy 2023, 278, 127582. [Google Scholar] [CrossRef]
- Ma, X.; Liu, H.; Han, L.; Yang, N.; Li, M. An real-time intelligent energy management based on deep reinforcement learning and model predictive control for hybrid electric vehicles considering battery life. Energy 2025, 324, 135931. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, C.; Liu, Y.; Ding, F.; Chen, Z.; Hao, W. A novel strategy for power sources management in connected plug-in hybrid electric vehicles based on mobile edge computation framework. J. Power Sources 2020, 477, 228650. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Wei, C.; Gao, X.; Zhang, Y. Multi-objective optimization of hybrid electric vehicles energy management using multi-agent deep reinforcement learning framework. Energy AI 2025, 20, 100491. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, F.; Zhang, H.; Yang, A.; Xu, Y. Multi-objective adaptive energy management strategy for fuel cell hybrid electric vehicles considering fuel cell health state. Appl. Therm. Eng. 2024, 257, 124270. [Google Scholar] [CrossRef]
- Cui, W.; Cui, N.; Li, T.; Du, Y.; Zhang, C. Multi-objective hierarchical energy management for connected plug-in hybrid electric vehicle with cyber–physical interaction. Appl. Energy 2024, 360, 122816. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).