Abstract
Energy hubs integrating onsite renewable generation and battery storage provide cost-efficient solutions for meeting building electricity requirements. This study presents methods for modeling uncertainties in load demand and solar generation, ranging from normal distribution assumptions to distributions sourced from CityLearn 2.3.0. We also implement kernel density estimation (KDE) to represent the non-parametric distribution characteristics of actual data. Through Monte Carlo simulation, we emphasize the value of robust, data-driven methodologies in optimizing energy hub operations under realistic uncertainty conditions and effectively conducting risk assessment. The CityLearn real-world data confirms that the non-Gaussian nature of building-level energy demand and solar PV electricity output is most accurately represented through KDE, leading to more precise cost projections for the considered energy hub.
1. Introduction
The emergence of distributed energy resources (DERs)—like photovoltaic systems and battery storage—has fundamentally altered building-scale energy management approaches [1,2]. Energy hubs that dynamically coordinate onsite generation, storage, and demand are considered essential for strengthening grid resilience, decreasing operational costs, and reducing carbon emissions [3,4]. However, maximizing these advantages requires sophisticated models and algorithms that can handle uncertainties in both consumption patterns and renewable energy production.
Research increasingly addresses these uncertainties through techniques that create adaptive decision-making frameworks for day-ahead and intraday variations [5]. However, the method of uncertainty representation [6] is critical: conventional normal (Gaussian) distribution assumptions typically fail to account for extreme events such as unexpected demand spikes or significant drops in solar generation. By contrast, kernel density estimation (KDE) offers a non-parametric approach capable of capturing more realistic distribution skewness and outliers, potentially yielding more robust—though costlier—solutions.
This paper thoroughly examines how Monte Carlo models perform when using normal-based versus KDE-based synthetic data, drawing from actual building information in the CityLearn environment. We evaluate solutions not only by expected operating expenses but also through risk-focused metrics like Value at Risk (VaR) and Conditional Value at Risk (CVaR), among others [3]. By utilizing the CityLearn dataset, we ground our analysis in real-world building loads and PV output, ensuring practical relevance. Our findings demonstrate that while normal-based approaches may seem cost-effective on average, they often underestimate extreme scenarios, creating higher real-world risks [7]. Conversely, KDE-based modeling, despite greater computational complexity, generally provides better protection against extreme events. These results highlight the significance of accurate uncertainty modeling for energy hub design and operation, guiding practitioners toward strategies that effectively balance performance expectations with risk management.
In this context, the contributions of the current work can be summarized as follows:
- We evaluate both parametric (normal) and non-parametric (KDE) methods, showing the critical importance of properly calibrated distribution parameters and revealing how distribution shapes influence operational decisions and costs across different optimization frameworks;
- We develop a Monte Carlo approach that accommodates multiple scenarios. This consistent methodology allows for a direct and systematic comparison between these two frameworks;
- We integrate the CityLearn dataset, which contains real building energy consumption and solar generation patterns and show how the resulting decisions differ from those based solely on synthetic assumptions;
- We apply a range of risk assessment metrics like Value at Risk (VaR) and Conditional Value at Risk (CVaR) to quantify risk profiles, revealing useful insights into distribution assumptions.
The primary scientific contribution of this research encompasses several distinctive elements: First, we conduct a direct comparison between parametric (normal) and non-parametric (kernel density estimation) methods within an identical Monte Carlo framework, including methodologically sound comparisons with properly calibrated distribution parameters. This parallel evaluation demonstrates how different distributional assumptions impact both average costs and extreme risks—a comparative analysis rarely presented within a unified context. Additionally, while many studies utilize simplified synthetic data, we incorporate an actual year-long dataset from CityLearn to test how each approach performs under realistic load and PV profiles. This connects purely theoretical models with practical building-energy management applications. Furthermore, beyond examining average cost, we employ Value at Risk (VaR), Conditional Value at Risk (CVaR), and additional metrics to quantify the risk implications of various modeling approaches, revealing insights into the distribution characteristics.
The paper is organized as follows: Section 2 reviews the relevant literature. Section 3 details the methodology and corresponding mathematical formulations. Section 4 describes the case study. Section 5 examines the results and findings, while Section 6 outlines future research directions and provides concluding remarks.
2. Literature Review
2.1. Energy Hubs and Smart Buildings
Over the past few years, energy hubs—systems that combine on-site renewable generation, storage capabilities, and adaptable consumption—have garnered significant interest for their ability to lower energy expenses and improve environmental performance [8]. These integrated systems typically incorporate photovoltaic arrays, battery storage technologies, and manageable loads working together to satisfy a building’s electricity requirements [9]. Conventional methodologies frequently employ deterministic optimization based on singular predictions of consumption and renewable output [10]. While these models provide useful baseline insights, they fail to address the natural variability and uncertainty found in actual operating conditions, thereby reducing their resilience to unanticipated fluctuations in demand or solar generation [11].
2.2. Stochastic Optimization
To manage uncertainty, numerous authors have adopted stochastic optimization approaches [12]. A notable category is the two-stage formulation, where initial decisions (day-ahead) are made without future knowledge, while subsequent decisions (recourse) are adjusted after uncertainty becomes clear [13]. This framework offers better computational efficiency than complete multi-stage methods while still capturing essential aspects of real-time adjustments. Multiple studies have shown how two-stage models in building energy applications can substantially decrease cost fluctuations [14]. Nevertheless, the effectiveness of these solutions depends critically on the methods used to represent uncertainty.
2.3. Parametric vs. Non-Parametric Approaches
A prevalent simplification involves modeling uncertain variables like load and PV output using normal (Gaussian) distributions [15]. While Gaussian models offer mathematical convenience through their closed-form properties, actual data often displays heavy tails, asymmetry, or multiple modes [16]. Ignoring these characteristics may lead to solutions that underestimate costly extreme events and project unrealistic optimism [17]. Consequently, non-parametric methods, particularly kernel density estimation (KDE), have become increasingly popular [18]. KDE conforms to the empirical distribution’s shape, directly incorporating outliers and complex patterns from the data [19]. Multiple studies suggest that KDE can represent load or solar generation more accurately than basic parametric approximations, thereby revealing more realistic operational risk profiles [20].
2.4. Monte Carlo
Irrespective of which distribution is assumed, the Monte Carlo simulation remains a common technique for generating scenarios in computational experiments [21]. By producing multiple simulated instances of load and renewable energy patterns, researchers can evaluate outcome variability and calculate expected or percentile-based performance metrics [22]. This methodology has been implemented in building energy management to evaluate strategies across diverse weather conditions, occupancy patterns, and electricity pricing structures [23]. When using KDE, Monte Carlo samples are drawn from a flexible, data-driven probability density function, eliminating the restrictive assumptions inherent in purely parametric approaches. Current research demonstrates how this data-driven sampling method can produce distributions with more pronounced tails, subsequently influencing the resilience of scheduling decisions [24].
2.5. Risk-Assessment Metrics
In addition to reducing expected costs, building managers frequently aim to minimize their vulnerability to uncommon but potentially damaging events [25]. Value at Risk (VaR) and Conditional Value at Risk (CVaR) represent two widely used risk-focused metrics [5]. VaR establishes a cost threshold that is only surpassed in a small percentage of scenarios (such as 5%), while CVaR calculates the average cost when that threshold is exceeded [26]. These metrics have been successfully incorporated into building energy optimization frameworks to develop solutions that maintain resilience during extreme conditions [27]. While strategies that include VaR or CVaR considerations may result in higher overall costs, they demonstrate greater stability when confronted with sudden increases in demand or unexpected decreases in renewable energy production [28].
2.6. Approaches for Uncertainty Modeling
Beyond the normal distribution and KDE methods analyzed in this study, scholars have developed numerous techniques for addressing uncertainty in energy optimization challenges.
Research by [29] explored probabilistic approaches for optimal power flow analysis, evaluating various probability distribution functions for modeling generation and load uncertainty. Their findings revealed that while Gaussian distributions offer computational efficiency, they routinely underestimated extreme event probabilities in actual power systems, potentially leading to undesirable operational decisions. This finding emphasizes the critical nature of distribution selection in energy optimization—a central theme in our current research.
Work in [30] juxtaposed probabilistic techniques with possibilistic methods (using fuzzy set theory), showing that probabilistic approaches are superior for quantifying variability when substantial historical data are available, while possibilistic frameworks prove beneficial when handling linguistic uncertainties or limited datasets. Their comparative study revealed up to 15% differences in optimization results depending on the chosen uncertainty representation.
In [31], Keith and Ahner delivered a thorough review of decision-making frameworks under uncertainty, classifying approaches into stochastic programming, robust optimization, and distributionally robust optimization. Their assessment indicated that stochastic programming (as employed in our study) delivers the most accurate solutions when distribution information is precise, while robust optimization provides better worst-case protection, typically at the expense of solution optimality.
Specifically for energy hub applications, Dalimi-Asl et al. [32] developed a hybrid stochastic-probabilistic framework, showing how different scenario generation techniques influence operational decisions for storage systems. Their research emphasized that conventional normal distributions often underestimated extreme renewable generation events, resulting in suboptimal storage dispatch strategies—a conclusion that supports our examination of KDE-based approaches.
For dynamic optimization problems, Tsay et al. [33] created a framework enabling comparisons between different probability distribution types, demonstrating that distribution choice significantly impacts both computational feasibility and solution quality. Their work highlighted that while parametric distributions provide computational benefits, non-parametric methods better represent complex multimodal uncertainty patterns commonly found in real-world energy data.
2.7. Research Gaps and Objectives
While considerable advances have been made in stochastic building energy optimization, several critical research gaps persist. Prior studies have investigated various uncertainty management approaches, ranging from possibilistic methods [30] to hybrid stochastic frameworks [32] and comparative distribution analyses [29]. However, these investigations typically concentrate on either differing optimization frameworks or varying system scales, which complicates direct methodological comparisons.
Our research addresses three essential gaps in the existing literature. First, although [29] emphasized the shortcomings of Gaussian distributions in power systems, and [31] reviewed various decision-making frameworks, there remains an absence of direct comparison between normal-based and non-parametric (KDE) approaches within a framework applied to building-scale energy hubs. Second, while [33] compared distribution types in dynamic optimization, relatively few studies examine risk-focused performance metrics—such as VaR and CVaR—to measure how each modeling approach protects against high-cost scenarios, particularly in building energy contexts [34]. Third, unlike previous research that often relies on artificial data or simplified examples, we utilize properly calibrated distributions derived from actual measurements. Consequently, this research provides a comprehensive understanding of how data-driven distribution modeling influences building-scale energy strategies, moving beyond the broader classifications and theoretical frameworks presented in the previous literature to deliver specific, actionable insights for energy hub operators.
3. Methodology
We start by examining an energy hub operating within a defined timeframe. This hub has multiple capabilities: it can acquire electricity from the main power grid, utilize a local battery system for energy storage (both charging and discharging), and produce renewable electricity on its premises. The primary goal of these combined functions is to satisfy the hub’s local electricity demand.
3.1. Gaussian Synthetic Data
We begin by creating synthetic data representing the energy hub’s electricity demand and its local renewable electricity generation output. Both variables are modeled using normal distributions, with results constrained to non-negative values to maintain realism. While actual data for renewable production and electricity consumption typically shows time-correlated and weather-dependent patterns (rather than following pure normal distributions), we utilize these normal distributions as a starting point for subsequent comparisons with more sophisticated, data-driven distributions.
3.1.1. Deterministic Optimization Based on the Gaussian Synthetic Data
After generating synthetic data, we establish a linear deterministic optimization model that aims to minimize the energy hub’s daily operational cost. This model is considered deterministic because the electricity demand and generation values are fixed to their synthetic normally distributed samples. The mathematical formulation and terminology are presented below.
Equation (1) defines the objective function, which focuses on minimizing the energy hub’s daily operational cost. This cost comprises three components: expenses for purchasing electricity from the main grid, costs associated with charging and discharging the storage unit, and costs related to curtailing the renewable unit’s output.
Constraint (2) establishes the upper limit for electricity output from the energy hub’s renewable unit, while constraint (3) defines the curtailed output as the difference between the maximum possible output and the actual output (kWh).
Constraint (4) represents the power balance equation. The left side includes electricity purchased from the main grid, electricity discharged from the storage unit, and actual output from the renewable unit. The right side consists of electricity charged into the storage unit plus the electricity demand.
Constraints (5) and (6) define the storage unit’s state of charge at hour h as equal to the previous hour’s state, plus electricity charged minus electricity discharged (kWh). Constraint (7) specifies the boundaries for the state of charge variable, while constraints (8) and (9) set limits on charging and discharging (kWh) operations for the storage unit.
Subject to
3.1.2. Monte-Carlo Using Normally Distributed Synthetic Data
In our previous analysis, we solved the deterministic model with a single instance of electricity demand and renewable generation data. This section employs the identical deterministic model but applies it across multiple scenarios. Specifically, we generate individual 24 h profiles for both load and renewable production, then solve the deterministic optimization problem for each scenario. By repeating this process across numerous data instances, we obtain a distinct optimal solution for each scenario, resulting in a collection of solutions. This approach represents multiple executions of a deterministic model, each using different randomly generated data samples.
3.2. Actual Data
In our prior analysis, we employed normally distributed synthetic data for both load and renewable generation. Now, we transition to utilizing an annual dataset from the CityLearn package to represent a single building (or “energy hub”). This real-world dataset enables a more practical evaluation of our model, contrasting with the purely synthetic normal-distribution approach used previously. By analyzing actual hourly observations throughout an entire year, we capture the natural intermittency of solar production and fluctuations in building-level demand that occur in real settings.
3.2.1. Scaling the Actual Data
Before applying our statistical modeling techniques, we standardize the real-world building data so that each feature has a mean of zero and a standard deviation of one. This step helps ensure that all input variables are on a comparable scale, thereby improving the stability and convergence properties of many algorithms (including kernel density estimation and neural networks).
3.2.2. Applying Kernel Density Estimation
To create synthetic data that accurately represents the actual distributions of load and renewable energy output, we use kernel density estimation (KDE). Unlike parametric methods such as normal distribution fitting, KDE does not make assumptions about the distribution’s underlying shape. Instead, it employs a Gaussian kernel function to create smooth density estimates based on observed data points.
We develop individual KDE models for both solar generation and building energy consumption, each capturing the probability distribution of possible values. Once these models are trained, we can sample from them to generate new data points (for example, over a 24 h period) that are synthetic but statistically consistent with real-world patterns of load and renewable energy output.
3.2.3. Unscaling the Values
After creating synthetic values with our KDE model on normalized data (zero mean, unit variance), we transform these values back to their original kilowatt-hour (kWh) measurements by reversing the scaling process. This conversion restores the synthetic data to the same physical units as the original building’s energy consumption and renewable generation measurements.
3.2.4. Monte Carlo Using KDE-Based Data
We initially create kernel density estimation models using the building’s actual load and solar generation data. Following this, we perform Monte Carlo simulations to test how our deterministic optimization handles various daily profiles sampled from these non-parametric distributions.
For each simulation, we sample a new 24 h load and solar generation profile from the KDE models, creating a synthetic daily scenario that reflects the empirical data without assuming any particular statistical distribution. We then applied our deterministic model (constraints (1)–(9)) to each synthetic scenario, optimizing battery operation, grid purchases, and curtailment decisions based on the day’s forecast. After 1000 simulations, we record the optimal cost for each run, producing a cost distribution that shows the range of possible outcomes under different patterns of load and solar generation.
By analyzing the statistical properties of these costs (including mean, variance, and extreme values), we gain insight into how a purely deterministic strategy might perform in real-world conditions when daily load and renewable patterns follow the KDE-based distributions.
4. Case Study
Our model examines an energy hub integrated within a building that combines local renewable generation, electricity consumption, and a battery storage system, with the ability to purchase additional power from the main grid when needed. The battery specifications include a 100 kWh storage capacity, 50 kWh maximum charge and discharge rates, and 100% operational efficiency. We begin with the assumption that the storage unit starts completely empty.
Regarding financial aspects, the energy hub can obtain electricity from the main grid at a purchase price of USD 0.2/kWh. Battery operations incur costs of USD 0.05/kWh for both charging and discharging processes. Additionally, the system includes a cost of USD 0.01/kWh for curtailing renewable energy production when necessary.
4.1. Gaussian Synthetic Data Generation
We produce synthetic data for the energy hub’s electricity demand and its local renewable electricity output. Its electricity demand is drawn from a normal distribution with a mean of 1.21 kWh and a standard deviation of 0.97 kWh. Also, the output of the local renewable unit is drawn from a normal distribution with a mean of 205.84 kWh and a standard deviation of 290.98 kWh.
The 24 values for electricity demand drawn from the normal distribution have a sample mean of 0.99 kWh and a sample standard deviation of 0.78 kWh. Also, the 24 values for the output of the renewable unit have a sample mean of 213.2 kWh and a sample standard deviation of 212.57 kWh.
4.1.1. Deterministic Optimization Based on the Gaussian Synthetic Data
In the preceding section, we created synthetic data for both electricity demand and renewable unit output. This section presents the solution to the model outlined in Section 3.1. We obtained the optimal solution using the Gurobi solver on an Intel Xeon 2.6 GHz server. The optimal daily operational cost for the energy hub is USD 51.55. This total comprises USD 0 for electricity purchased from the main grid and USD 0.62 for battery charging/discharging operations. The curtailment cost amounts to USD 50.93.
4.1.2. Monte-Carlo Using Gaussian Synthetic Data
We then conduct a Monte Carlo analysis by generating 1000 independent scenarios of the energy hub’s load and renewable generation, sampled from the same normal distributions used previously. The deterministic optimization model is solved for each scenario, yielding 1000 distinct optimal solutions. Figure 1 displays a histogram showing the distribution of daily operational costs across all 1000 scenarios.
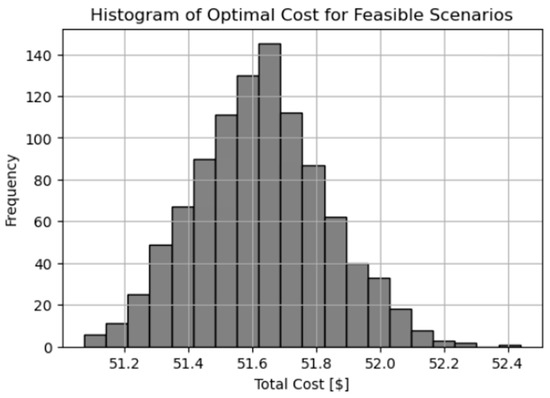
Figure 1.
Histogram for the 1000 optimal costs (Monte Carlo deterministic solves) for the daily operational cost of the energy hub.
The arithmetic mean of the daily cost across all 1000 simulated scenarios is USD 51.63, which represents the “average” daily cost the energy hub might experience under the assumed distribution of uncertainties. This mean cost is the average optimal daily operational cost of the energy hub across all 1000 Monte Carlo scenarios. It represents the expected cost under the Gaussian synthetic data assumptions for load demand and renewable generation. This value aligns with the deterministic optimization result of USD 51.55, suggesting that the Monte Carlo simulation captures a realistic range of outcomes around the deterministic case.
The minimum and maximum costs are USD 51.07 and USD 52.44, respectively, resulting in a range of USD 1.36. This relatively narrow range (spread) suggests consistent performance across varied load and renewable generation scenarios. It provides a simple measure of the spread of the cost distribution; a range of USD 1.36 indicates the total variability in costs across all scenarios. While this range is relatively small, it still highlights the potential financial impact of uncertainty in load and renewable generation.
Note that USD 51.07 is the lowest optimal cost observed across all 1000 scenarios and represents the best-case scenario where the energy hub minimizes its operational expenses due to favorable conditions such as high renewable generation and low demand. On the other hand, USD 52.44 is the maximum cost, i.e., when the energy hub faces higher expenses due to low renewable generation and high demand.
Also, the standard deviation is USD 0.21. A value of USD 0.21 indicates that the costs typically vary by about USD 0.21 from the mean cost of USD 51.63 across the scenarios. A low standard deviation relative to the mean suggests that the costs are relatively stable and predictable under the Gaussian assumptions. This implies that the energy hub’s operation is not highly sensitive to the variability in load and renewable generation when modeled as normal distributions.
The IQR is the difference between the 75th percentile and the 25th percentile of the cost distribution. It measures the spread of the middle 50% of the data, making it a robust measure of variability that is less sensitive to outliers than the range. An IQR of USD 0.2722 indicates that the central 50% of the cost scenarios fall within a narrow band of about USD 0.27. This suggests that the majority of scenarios have costs that are quite close to the mean, reinforcing the stability of the cost distribution under Gaussian assumptions.
The coefficient of variation (CV) is the ratio of the standard deviation to the mean (USD 0.21/USD 51.63 ≈ 0.0040). It provides a normalized measure of variability, allowing comparison across different datasets or scales. A CV of 0.0040 (or 0.4%) is very low, indicating that the variability in costs is minimal relative to the mean cost. This suggests that the energy hub’s operational costs are highly predictable under the Gaussian model. This exceptionally small value indicates that despite the stochastic nature of both load demand and renewable generation, the energy hub’s cost performance remains highly predictable under the Gaussian distribution assumption.
The cost distribution exhibits slight positive skewness (0.1929), indicating a minor asymmetry with a slightly longer tail toward higher costs. Skewness is a measure of the symmetry of the distribution. Skewness measures the asymmetry of the cost distribution. A positive skewness of 0.1929 indicates that the distribution is slightly right-skewed, meaning there are more scenarios with costs below the mean, but a few scenarios have costs significantly above the mean (a longer right tail). In the context of energy hub operations, this slight right-skewness suggests that while most scenarios result in costs close to or below the mean, there is a small chance of encountering higher costs due to extreme conditions (e.g., low renewable output or high demand). This aligns with the non-Gaussian nature of real-world energy data, even when synthetic data are generated using normal distributions. That is, a skewness near zero indicates a fairly symmetrical distribution, while positive values imply a slight “right tail” (a tendency for more extreme high-cost outcomes).
The kurtosis values provide insight into the distribution’s tail behavior. Kurtosis describes how “heavy” or “thin” the tails of the distribution are compared to a normal distribution. Fisher’s kurtosis (where a normal distribution has a value of 0) of 0.0237 indicates that the cost distribution has slightly heavier tails than a normal distribution. Pearson’s kurtosis (where a normal distribution has a value of 3) of 3.0237 confirms this. Specifically, Fisher’s kurtosis (0.0237) is very close to zero, and Pearson’s kurtosis (3.0237) is very close to three, both indicating that the cost distribution closely approximates a normal distribution. Positive kurtosis suggests a slightly “peaked” distribution (i.e., its central region—around the mean—is taller and narrower than that of a normal distribution; this sharper peak reflects a higher concentration of values near the mean) with more extreme values (outliers) than a normal distribution.
The slight positive kurtosis indicates that the cost distribution has a few more extreme values (both high and low costs) than would be expected under a perfectly normal distribution. This is consistent with the energy hub facing occasional extreme scenarios, such as very high demand or very low renewable generation, which lead to outlier costs. This near-normal profile aligns with our use of normally distributed inputs and suggests that extreme outcomes (either very high or very low costs) occur at frequencies similar to what would be expected in a normal distribution.
VaR provides a threshold cost below which a specified percentage of scenarios fall. At the 90% confidence level, the VaR is USD 51.90, meaning there is a 10% chance that the cost will exceed USD 51.90. At the 95% level, VaR of USD 51.98 indicates that in 95% of the scenarios, the cost remains below or at USD 51.98, and at the 99% level, it is USD 52.14 (1% chance of exceedance). The relatively small increase in VaR across these confidence levels reflects the narrow spread of the cost distribution, consistent with the low standard deviation and IQR.
While VaR identifies specific cost thresholds, CVaR (also known as Expected Shortfall) provides insight into the severity of potential losses in the worst-case scenarios. CVaR averages the costs in only those scenarios that exceed the VaR threshold. Therefore, it provides the expected cost, given that the cost has already reached an extreme “worst-case” region. For example, a 95% CVaR of USD 52.08 indicates that if the cost surpasses the 95% VaR of USD 51.98, the average cost among the worst 5% of cases is USD 52.08. CVaR thus helps quantify the severity of tail risks beyond the VaR level. At the 90% confidence level, the CVaR is USD 52.01, indicating that the average cost of the worst 10% of scenarios is USD 52.01. At the 95% level, the CVaR is USD 52.08, and at the 99% level, it is USD 52.21.
The relatively small difference between VaR and corresponding CVaR values (e.g., USD 51.90 vs. USD 52.01 at the 90% level) suggests that even when the energy hub experiences adverse conditions, the cost impact remains moderate and well-contained. This finding is particularly important for risk management, as it indicates that extreme events, while possible, do not result in dramatically higher operational costs when using normally distributed synthetic data.
The statistical analysis of our Monte Carlo simulation reveals that under the Gaussian distribution assumption, the energy hub demonstrates remarkable cost stability across a wide range of operating scenarios. Overall, the Monte Carlo simulation results using Gaussian synthetic data reveal a stable cost distribution with a mean of USD 51.63 and a low standard deviation of USD 0.21, indicating that the energy hub’s operational costs are highly predictable under these assumptions. However, the slight right-skewness (0.1929) and positive kurtosis (0.0237, Fisher’s) suggest a small but non-negligible probability of extreme costs, which could be more pronounced in real-world scenarios where load and renewable generation exhibit non-Gaussian characteristics, as highlighted in Section 1. The risk metrics, VaR and CVaR, further confirm that while the majority of scenarios result in costs close to the mean, there is a 1% chance of costs exceeding USD 52.14 (VaR 99%), with an average cost of USD 52.21 in the worst 1% of scenarios (CVaR 99%).
4.2. Actual Data
We focus on a building from the CityLearn dataset, which provides 8760 hourly records (one full year) of its operation. Each row includes solar generation (kWh) from the building’s PV system and non-shiftable load (kWh), encompassing lighting, appliances, and other essential devices. The CityLearn dataset contains 8760 h of historical records (spanning a complete calendar year) of a building’s energy consumption and solar generation. The dataset shows average solar production of approximately 206 kWh per hour, with daily maximums sometimes reaching 1000 kWh during particularly sunny periods. Meanwhile, the building’s average energy consumption is around 1.2 kWh per hour, though it can occasionally surge to nearly 8 kWh. These statistics highlight substantial variability: solar output consistently falls to zero during nighttime hours, while energy consumption generally remains moderate but experiences occasional significant spikes.
By incorporating all 8760 hourly measurements, this dataset captures daily and seasonal variations, as well as infrequent outlier events.
Figure 2 shows histograms of these two variables. The solar output is zero in many hours (e.g., nighttime) yet can reach nearly 1000 kWh under peak daytime conditions, producing a highly skewed distribution. Meanwhile, the load mostly falls below 2 kWh, though it occasionally spikes up to around 8 kWh. A statistical summary reveals a mean solar generation of roughly 206 kWh (standard deviation 291 kWh) and an average load of about 1.21 kWh (standard deviation 0.97 kWh).
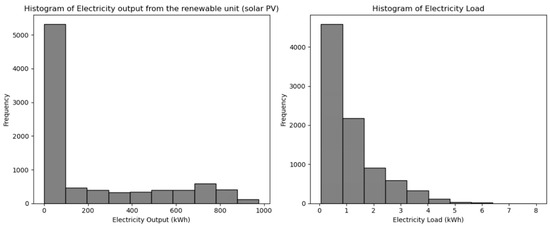
Figure 2.
Frequency histograms for the electricity output of the renewable unit of the energy hub (kWh) and for its electricity demand (kWh), based on actual data.
4.2.1. Scaling the Actual Data
To prepare our real-world dataset for modeling, we standardize all three columns—hour, solar generation, and non-shiftable load—by transforming each to have a mean of 0 and a standard deviation of 1. This standardization benefits algorithms such as kernel density estimation and neural networks by promoting faster convergence and preventing features with larger numerical ranges from being overweight. By equalizing the scales of all features, we ensure our models treat each variable with equal importance rather than being biased by their original magnitudes. Once standardized, the dataset provides more stable numerical conditions for applying our modeling techniques, particularly kernel density estimation.
4.2.2. Applying Kernel Density Estimation
After scaling the real-world dataset, we applied univariate kernel density estimators to model both solar generation (renewable output available to the energy hub) and non-shiftable load (electricity demand of the energy hub).
We implemented a Gaussian kernel to create smooth, continuous probability density estimates around each data point. The bandwidth parameter—which controls the smoothness of the density estimate—was set to 0.5 based on cross-validation and domain-specific optimization. This value strikes a balance between an overly detailed fit (too small bandwidth) and excessive smoothing (too large bandwidth).
Each KDE learned the distribution patterns from our scaled data, allowing us to generate 24 synthetic hourly observations for each variable that reflect the learned statistical properties. To maintain physical realism, we set any negative values to zero, ensuring all load and solar generation quantities remain physically meaningful.
This approach produced synthetic 24 h scenarios for renewable output and load that accurately capture the original data’s variability and skewness without imposing strict parametric assumptions like normality. The non-parametric nature of KDE preserves the empirical distributions’ natural shapes more effectively than parametric methods would.
4.2.3. Unscaling the Values
To convert the KDE-generated points into actual kilowatt-hour values, we reverse the standardization process that was originally applied to the dataset. Since we standardized three columns (hour, solar generation, and non-shiftable load), we first organize each synthetic data point into a three-column format, maintaining space for the hour column. We then apply the inverse transformation, which adjusts each synthetic point back to the original distribution’s mean and standard deviation measured in kilowatt-hours. Finally, we extract the renewable output and load columns, setting any negative values to zero. This process ensures that the synthetic data created through KDE is expressed in meaningful energy units that accurately reflect the building’s real-world measurements.
4.2.4. Monte Carlo Using KDE-Based Synthetic Data
To explore how a deterministic energy-hub optimization model would perform under different daily profiles, we carried out a Monte Carlo procedure with 1000 synthetic scenarios. For each scenario, we sampled a 24 h load and renewable generation profile from the KDE-based distributions, thereby reflecting the empirical (yet non-parametric) statistics of the building’s data. We then solved the deterministic model separately for each scenario, treating that single day’s profile as known from the outset.
Figure 3 shows the histogram of the resulting optimal daily costs across all 1000 scenarios. The mean cost is approximately USD 80.60, with a standard deviation of about USD 11.17. The most inexpensive scenario had a cost of roughly USD 50.77, while the most expensive scenario approached USD 126.94. This variation in costs reflects the range of possible load and solar generation patterns produced by the KDE models, from very favorable combinations (high solar, moderate load) to more challenging ones (low solar, higher load). In practical terms, these results illustrate how a single-day deterministic solution can yield significantly different operating costs when the day’s solar and load conditions deviate from the norm.
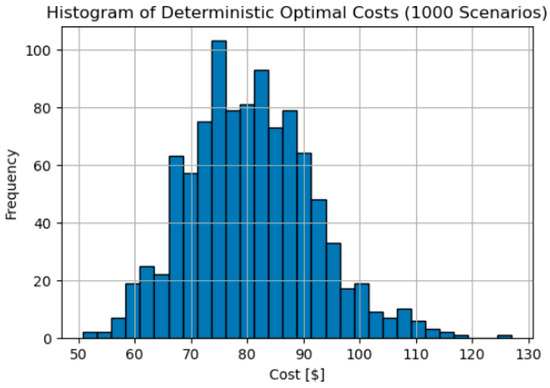
Figure 3.
Frequency histogram of the energy hub’s daily operational cost when deterministically solved for 1000 KDE-based daily profiles of renewable output (kWh) and electricity demand (kWh).
Comparing this cost distribution to the one obtained under purely normal-distributed synthetic data highlights the importance of capturing realistic distributional shapes for load and renewables. By relying on kernel density estimates, we observe a broader and more skewed range of operational costs, underlining how real-world data often exhibit heavy-tail or highly skewed behavior that a simple normal assumption might fail to capture.
To assess the variability and risk profile of the daily costs arising from our KDE-based scenarios, we compute a suite of descriptive and risk-oriented statistics on the 1000 simulated days. The mean daily cost is around USD 80.60, while the standard deviation is approximately USD 11.17, indicating a moderate spread of cost outcomes.
The minimum cost of about USD 50.77 occurs under very favorable conditions (high solar output, moderate load), whereas the maximum cost of USD 126.94 arises in scenarios characterized by lower solar generation and higher electricity demand. This wide range illustrates the importance of robust planning: even with an identical optimization strategy, day-to-day conditions can yield vastly different total costs.
The distribution itself shows positive skewness (around 0.70), suggesting an asymmetric right tail—that is, cost “spikes” are more pronounced than exceptionally low-cost days. Moreover, Fisher’s kurtosis of 1.50 indicates heavier tails than a normal distribution, pointing to an increased likelihood of extreme values. From a risk-management perspective, these heavier tails mean the system should be prepared for occasional but severe cost excursions.
We also evaluated Value at Risk and Conditional Value at Risk across different confidence levels. For instance, the 95% VaR of around USD 100 implies there is a 5% chance that the daily cost will exceed USD 100, whereas the 95% CVaR of about USD 107 means that in those worst-case 5% scenarios, the average cost is USD 107. As such, the CVaR metric highlights the potential severity beyond the VaR threshold.
Overall, these statistics underscore how a realistic (KDE-based) representation of renewable and load variability can reveal a higher propensity for extreme cost scenarios, compared to simpler parametric (e.g., Gaussian) models.
5. Discussion
5.1. Model Comparisons Under Normal vs. KDE
We started the analysis by investigating modeling approaches under the same normally distributed load and renewable-availability assumptions. First, we formulated a deterministic model, where we sampled one 24 h time series of load and renewable output (each drawn from a normal distribution). Then, we performed a Monte Carlo simulation by repeating the deterministic solve 1000 times—each using a distinct 24 h normal random draw for both load and renewables. This exercise provided insight into how costs and operational decisions vary with different possible daily profiles, but it did not yield one unified strategy that works well across all draws.
Also, KDE on the CityLearn dataset is intended to learn the load and renewable-output distributions directly from empirical data, rather than imposing a fixed parametric form like a normal distribution. Because the CityLearn data contain thousands of hourly measurements over an entire year, KDE can model the inherent skewness, heavy tails, and other nuances in a data-driven way. In contrast, normal distributions often assume symmetrical bell shapes that do not always match real-world building usage.
Finally, the CityLearn dataset itself reveals that real-world building-level demand and solar generation are far from Gaussian, with near-zero solar overnight and occasional load spikes. Fitting a KDE to these time series yields more accurate cost estimates because it replicates the true empirical shape—including significant skew and heavy tails—without forcing the data into a bell curve. In this sense, KDE-based models better reflect the variability and risk profiles that energy-hub operators face, underscoring the value of robust, non-parametric methods for decision-making under uncertainty.
Our Monte Carlo simulations using both normal distribution and KDE-based approaches reveal fundamental differences in how uncertainty is characterized in energy hub operations.
Cost Expectations and Variability: The most immediate observation is the substantial difference in mean operational costs. The KDE-based approach predicts an average daily cost of USD 80.60, which is 56% higher than the USD 51.63 predicted by the normal distribution model. This significant disparity suggests that normal distribution assumptions systematically underestimate the expected operational costs under real-world conditions. Even more striking is the difference in cost variability: the standard deviation under the KDE approach (USD 11.17) is over 53 times larger than under the normal distribution (USD 0.21). This extraordinary difference in variability is further reflected in the range of potential costs: while the normal distribution predicts a narrow range of just USD 1.36, the KDE approach identifies a range of USD 76.17, 56 times wider. These metrics collectively indicate that energy hub operations under real-world conditions exhibit substantially greater cost uncertainty than would be predicted by Gaussian models.
Distribution Characteristics: The shape of the cost distribution also differs markedly between the two approaches. The KDE-based distribution shows significantly higher positive skewness (0.70 versus 0.1929), indicating a more pronounced asymmetry with a longer tail toward higher costs. Similarly, the KDE approach reveals higher kurtosis (0.50 versus 0.0237), suggesting more frequent extreme values than would be expected under a normal distribution. These distributional characteristics align with the reality of energy systems, where adverse events (such as extended periods of low renewable generation coupled with high demand) can lead to disproportionately high costs. The normal distribution’s near-zero kurtosis fails to capture this important feature of real-world energy data.
Risk Assessment: Perhaps the most consequential differences appear in the risk metrics. The Value at Risk (VaR) at the 95% confidence level—representing the threshold below which costs are expected to fall 95% of the time—is USD 99.50 under the KDE approach, almost twice the USD 51.98 predicted by the normal distribution. Similarly, the Conditional Value at Risk (CVaR) at 95%—the expected cost in the worst 5% of scenarios—is USD 104.00 with KDE versus just USD 52.08 with the normal distribution. These metrics indicate that extreme events are both more likely and more severe than would be predicted under Gaussian assumptions. Interestingly, while the downside risk is substantially higher under the KDE approach, the downside-to-upside ratio is slightly lower (1.18 versus 1.32), suggesting a more balanced distribution of risks relative to opportunities.
Methodological Significance: From a methodological perspective, these results demonstrate the critical importance of distribution selection in energy system modeling. While normal distributions offer mathematical convenience and computational simplicity, they may significantly misrepresent the actual risk profile of energy hub operations. The KDE approach, though more computationally intensive, provides a more accurate representation of the non-Gaussian characteristics of real-world energy data, leading to more realistic risk assessments.
5.2. Real World Considerations
Our modeling approach comparison provides important insights, but several additional real-world factors would influence optimal energy hub operations and likely increase the differences between normal and KDE-based approaches:
Battery Degradation: Our model applies fixed costs to battery charging and discharging without accounting for degradation. In reality, each cycle contributes to capacity loss through calendar aging, cycling wear, and depth-of-discharge stress. This creates a dynamic balance between immediate operational savings and future replacement costs. The KDE approach, with its superior capture of extreme events, would likely show even greater performance advantages when accounting for degradation, as extreme events causing high-stress battery operations would incur additional long-term costs.
Complex Electricity Pricing: We use a constant electricity rate, whereas commercial buildings typically face sophisticated tariff structures including time-of-use pricing, peak-based demand charges, and capacity reservation fees. These structures would alter dispatch strategies, potentially increasing battery storage value for price arbitrage beyond renewable integration. The heavier tails in renewable generation captured by KDE would lead to more frequent exposure to peak demand charges during low-generation periods, potentially widening the cost gap between normal and KDE approaches.
Market Participation: Energy hubs may generate additional revenue through ancillary service markets or demand response programs. Capturing these opportunities depends on accurately modeling operational flexibility, which is directly affected by uncertainty characterization. KDE approaches would likely provide more conservative but realistic assessments of flexibility availability during extreme events.
These real-world factors would likely amplify rather than reduce the differences between normal and KDE-based approaches. They introduce additional nonlinearities and constraints that interact with uncertainty distributions, making robust uncertainty modeling even more critical for practical energy hub optimization. Future research incorporating these elements would provide a more comprehensive understanding of how distribution modeling choices affect real-world energy system operations and economics.
6. Conclusions and Future Work
This study has investigated the impact of uncertainty modeling approaches on energy hub operational cost assessment and risk quantification. By comparing conventional normal distribution assumptions with non-parametric kernel density estimation using data from the CityLearn environment, we have demonstrated significant differences in both expected costs and risk profiles.
Our findings reveal that normal distribution assumptions systematically underestimate operational costs by approximately 56% compared to the more data-driven KDE approach. Even more critically, the variability in costs under real-world conditions is substantially higher than predicted by Gaussian models, with standard deviations differing by a factor of 53 and cost ranges varying by a factor of 56. Risk metrics such as Value at Risk and Conditional Value at Risk were approximately twice as high under KDE-based modeling, indicating that extreme adverse events are both more likely and more severe than would be predicted under normal distribution assumptions.
These results have profound implications for energy hub design and operation. The dramatic differences in cost expectations and risk profiles suggest that energy systems designed using normal distribution assumptions may be significantly underprepared for the variability inherent in real-world conditions. This could lead to inadequate financial reserves, insufficient operational flexibility, and vulnerability to extreme events. Our analysis demonstrates that the choice of uncertainty modeling approach is not merely a technical detail but a fundamental decision that shapes the economic viability and resilience of energy hub systems.
The non-parametric KDE approach offers several advantages for energy system modeling. By learning directly from empirical data, it captures important characteristics such as zero-inflated patterns in solar generation, upper-bounded renewable output, multimodal load patterns, and heavy-tailed distributions. These features, which are poorly represented by normal distributions, are essential for realistic risk assessment in energy systems increasingly reliant on variable renewable resources [35].
These findings highlight the importance of both selecting appropriate uncertainty modeling approaches and implementing robust optimization frameworks when designing energy hub control strategies to accommodate real-world operational conditions. For practitioners, the combination of non-parametric distributions with stochastic programming represents the most effective approach for managing the complex uncertainties inherent in renewable-integrated energy systems [36].
For future research, we plan to integrate these KDE-based uncertainty models with more sophisticated decision-making frameworks. One promising direction is the application of Backwards Induction techniques [37], which would enable multi-stage decision modeling beyond our current two-stage approach, allowing for more frequent adaptation as uncertainty resolves throughout the day. We also intend to explore F-Factor methodologies [38,39], which provide supplementary robustness by incorporating safety factors to hedge against worst-case scenarios—particularly valuable given the heavy-tailed distributions we identified in real-world data.
Machine learning approaches [40,41] represent another significant direction, where we aim to develop neural network models that learn directly from the KDE-characterized distributions to predict optimal control actions under uncertainty. This could substantially reduce computational requirements while maintaining the realism captured by KDE modeling.
We further plan to extend our framework to larger-scale energy-hub models [42,43,44,45] with heterogeneous buildings and interconnected systems, where correlations between demand patterns and renewable generation across multiple nodes would introduce additional complexity requiring more sophisticated KDE variants. Various energy storage technologies [46] beyond batteries, such as thermal storage, hydrogen, or compressed air, as well as smart grid technologies [47,48,49] would enable exploring how different physical characteristics impact optimal strategies under KDE-based uncertainty.
Future research could also leverage reinforcement learning approaches to develop adaptive energy hub control strategies that learn optimal responses to the non-Gaussian uncertainty patterns identified in this study [29,50,51,52,53,54,55,56,57,58,59,60]. Such techniques could dynamically adjust operational decisions based on real-time observations, potentially outperforming static optimization methods. Machine learning algorithms, particularly deep neural networks and recurrent architectures [30,31,32,33,61,62,63,64], could further enhance forecasting accuracy for both renewable generation and building loads by capturing complex temporal patterns and nonlinear relationships that traditional statistical methods might miss. These advanced computational techniques could be combined with transfer learning to adapt models across different building types and geographical locations, addressing the site-specific nature of energy data distributions. Furthermore, explainable AI methods could help bridge the gap between black-box machine learning models and the physical interpretability needed for energy system management, providing operators with actionable insights while maintaining prediction accuracy. The integration of these data-driven approaches with physics-based models represents a particularly promising direction, combining the flexibility of machine learning with domain-specific knowledge to create hybrid models that are both accurate and physically consistent.
Future work could explore the application of Benders decomposition [65,66,67,68,69,70,71,72,73,74] to address the computational challenges associated with incorporating KDE-based uncertainty models into multi-stage stochastic programming formulations for energy hub operation. This decomposition technique would enable efficient solutions for larger-scale problems by separating the complex optimization structure into manageable master and subproblems, particularly valuable when considering longer planning horizons or multiple interconnected energy hubs. Bender decomposition could also facilitate the integration of robust optimization approaches with the non-Gaussian distributions identified in this study, allowing for tractable solution methods that capture realistic uncertainty while maintaining computational feasibility for real-time decision support.
Author Contributions
Conceptualization, S.G.; Methodology, S.G.; Validation, S.G.; Formal analysis, D.P.; Investigation, S.G., D.P., T.Z. and G.S.; Writing—original draft, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
Nomenclature
| Sets and indices | |
| Set of hourly time periods, indexed | |
| Parameters | |
| Cost (USD) for the energy hub and of purchasing electricity from the main grid (USD/kWh) | |
| Cost (USD) for the energy hub and of charging/discharging its battery (USD/kWh) | |
| Cost (USD) for the energy hub and of curtailing the output of its renewable unit (USD/kWh) | |
| Max possible electricity output (kWh) from the renewable unit of the energy hub at h | |
| Electricity demand of the energy hub at hour h (kWh) | |
| Initial state of charge of the battery unit of the energy hub. | |
| Charging efficiency of the battery unit of the energy hub | |
| Discharging efficiency of the battery unit of the energy hub | |
| Energy capacity (maximum possible state of charge) of battery unit (kWh) | |
| Upper bound to the electricity (kWh) charged in the battery unit | |
| Upper bound to the electricity (kWh) discharged in the battery unit | |
| Decision variables | |
| Curtailed output from the renewable unit of the energy hub at hour h (kWh) | |
| Electricity (kWh) discharged from the battery of the energy hub at hour h | |
| Electricity (kWh) charged into the battery of the energy hub at hour h | |
| Electricity (kWh) that the energy hub purchases from the main grid at hour h | |
| Output (kWh) of the renewable generation unit of the energy hub at hour h | |
| State of charge (kWh) of the battery unit of the energy hub at hour h | |
References
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H.; Jalilinasrabady, S. Optimal Scheduling of Energy Hubs in the Presence of Uncertainty-A Review. J. Energy Manag. Technol. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Varathan, G.; Belwin Edward, J. A review of uncertainty management approaches for active distribution system planning. Renew. Sustain. Energy Rev. 2024, 205, 114808. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Jadidbonab, M.; Mohammadi-Ivatloo, B. Short-Term Scheduling Strategy for Wind-Based Energy Hub: A Hybrid Stochastic/IGDT Approach. IEEE Trans. Sustain. Energy 2019, 10, 438–448. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Safdarian, A.; Parvini, Z.; Aramoun, F. Optimal Stochastic Short-Term Scheduling of Renewable Energy Hubs Taking into Account the Uncertainties of the Renewable Sources. In Operation, Planning, and Analysis of Energy Storage Systems in Smart Energy Hubs; Mohammadi-Ivatloo, B., Jabari, F., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Eladl, A.A.; El-Afifi, M.I.; Saadawi, M.M.; Siano, P.; Sedhom, B.E. Multi-Objective optimal scheduling of energy Hubs, integrating different solar generation technologies considering uncertainty. Int. J. Electr. Power Energy Syst. 2024, 161, 110198. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Konstantelos, I.; Strbac, G. Option value, investment costs and deployment levels of smart grid technologies. Sustain. Energy Res. 2024, 11, 47. [Google Scholar] [CrossRef]
- Leprince, J.; Schledorn, A.; Guericke, D.; Dominkovic, D.F.; Madsen, H.; Zeiler, W. Can occupant behaviors affect urban energy planning? Distributed stochastic optimization for energy communities. Appl. Energy 2023, 348, 121589. [Google Scholar] [CrossRef]
- Lasemi, M.A.; Arabkoohsar, A.; Hajizadeh, A. Optimal Design of Green Energy Hub considering Multi-Generation Energy Storage System. In Proceedings of the 2022 IEEE International Conference on Power Systems Technology (POWERCON), Kuala Lumpur, Malaysia, 12–14 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Rizi, D.T.; Nazari, M.H.; Hosseinian, S.H.; Fani, M.; Gharehpetian, G.B. Analyzing Electric Heat Pump Modeling in an Advanced Energy Hub with Renewable Energy Integration. In Proceedings of the 2024 28th International Electrical Power Distribution Conference (EPDC), Zanjan, Iran, 23–25 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Asvini, M.S.; Amudha, T. Deterministic optimization technique proposed for optimal reservoir release of Thirumurthi and Amaravathi reservoirs. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Nozarian, M.; Fereidunian, A.; Barati, M. Reliability-Oriented Planning Framework for Smart Cities: From Interconnected Micro Energy Hubs to Macro Energy Hub Scale. IEEE Syst. J. 2023, 17, 3798–3809. [Google Scholar] [CrossRef]
- Wu, J. Computer Application Scenario Design of Stochastic Optimization and Artificial Fish School Algorithm. In Proceedings of the 2022 International Conference on Electronics and Renewable Systems (ICEARS), Tuticorin, India, 16–18 March 2022; pp. 1502–1505. [Google Scholar] [CrossRef]
- Liu, C.; Lee, C.; Chen, H.; Mehrotra, S. Stochastic Robust Mathematical Programming Model for Power System Optimization. IEEE Trans. Power Syst. 2016, 31, 821–822. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Fu, Y. Real-Time Price-Based Demand Response Management for Residential Appliances via Stochastic Optimization and Robust Optimization. IEEE Trans. Smart Grid 2012, 3, 1822–1831. [Google Scholar] [CrossRef]
- Singh, V.; Moger, T.; Jena, D. Uncertainty handling techniques in power systems: A critical review. Electr. Power Syst. Res. 2022, 203, 107633. [Google Scholar]
- Kini, K.R.; Harrou, F.; Madakyaru, M.; Sun, Y. Enhancing Wind Turbine Performance: Statistical Detection of Sensor Faults Based on Improved Dynamic Independent Component Analysis. Energies 2023, 16, 5793. [Google Scholar] [CrossRef]
- Gao, Z.; Lim, D.; Schwartz, K.G.; Mavris, D.N. A Nonparametric-based Approach for the Characterization and Propagation of Epistemic Uncertainty due to Small Datasets. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Khorramdel, B.; Chung, C.Y.; Safari, N.; Price, G.C.D. A Fuzzy Adaptive Probabilistic Wind Power Prediction Framework Using Diffusion Kernel Density Estimators. IEEE Trans. Power Syst. 2018, 33, 7109–7121. [Google Scholar] [CrossRef]
- Zeng, L.; Hu, H.; Tang, H.; Zhang, X.; Zhang, D. Carbon emission price point-interval forecasting based on multivariate variational mode decomposition and attention-LSTM model. Appl. Soft Comput. 2024, 157, 111543. [Google Scholar] [CrossRef]
- Alvarez, G.E. Stochastic optimization considering the uncertainties in the electricity demand, natural gas infrastructures, photovoltaic units, and wind generation. Comput. Chem. Eng. 2022, 160, 107712. [Google Scholar] [CrossRef]
- Sakki, G.; Tsoukalas, I.; Kossieris, P.; Makropoulos, C.; Efstratiadis, A. Stochastic simulation-optimization framework for the design and assessment of renewable energy systems under uncertainty. Renew. Sustain. Energy Rev. 2022, 168, 112886. [Google Scholar] [CrossRef]
- Napolitano, F.; Tossani, F.; Borghetti, A.; Nucci, C.A. Lightning Performance Assessment of Power Distribution Lines by Means of Stratified Sampling Monte Carlo Method. IEEE Trans. Power Deliv. 2018, 33, 2571–2577. [Google Scholar] [CrossRef]
- Smyl, S.; Oreshkin, B.N.; Pełka, P.; Dudek, G. Any-Quantile Probabilistic Forecasting of Short-Term Electricity Demand. arXiv 2024, arXiv:2404.17451. Available online: https://arxiv.org/abs/2404.17451 (accessed on 1 March 2025).
- Cabrera-Tobar, A.; Massi Pavan, A.; Petrone, G.; Spagnuolo, G.A. Review of the Optimization and Control Techniques in the Presence of Uncertainties for the Energy Management of Microgrids. Energies 2022, 15, 9114. [Google Scholar] [CrossRef]
- Mokaramian, E.; Shayeghi, H.; Sedaghati, F.; Safari, A.; Alhelou, H.H. A CVaR-Robust-Based Multi-Objective Optimization Model for Energy Hub Considering Uncertainty and E-Fuel Energy Storage in Energy and Reserve Markets. IEEE Access 2021, 9, 109447–109464. [Google Scholar] [CrossRef]
- Javadi, M.S.; Lotfi, M.; Nezhad, A.E.; Anvari-Moghaddam, A.; Guerrero, J.M.; Catalao, J.P.S. Optimal Operation of Energy Hubs Considering Uncertainties and Different Time Resolutions. IEEE Trans. Ind. Appl. 2020, 56, 5543–5552. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, M.; Zhou, H.; Gao, J. A Planning Method of Regional Integrated Energy System Based on the Energy Hub Zoning Model. IEEE Access 2021, 9, 32161–32170. [Google Scholar] [CrossRef]
- Meng, Y.; Shi, F.; Tang, L.; Sun, D. Improvement of Reinforcement Learning with Supermodularity. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5298–5309. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, W.; Chen, Y.; Vai, M.I. Robust Classification of Encrypted Network Services Using Convolutional Neural Networks Optimized by Information Bottleneck Method. IEEE Access 2025, 13, 36995–37005. [Google Scholar] [CrossRef]
- Abbasi, M.; Florez, S.L.; Shahraki, A.; Taherkordi, A.; Prieto, J.; Corchado, J.M. Class Imbalance in Network Traffic Classification: An Adaptive Weight Ensemble-of-Ensemble Learning Method. IEEE Access 2025, 13, 26171–26192. [Google Scholar]
- Fu, M.; Wang, P.; Liu, M.; Zhang, Z.; Zhou, X. IoV-BERT-IDS: Hybrid Network Intrusion Detection System in IoV Using Large Language Models. IEEE Trans. Veh. Technol. 2025, 74, 1909–1921. [Google Scholar]
- Wang, X.; Lu, Z.; Wang, X.; He, M. GETRF: A General Framework for Encrypted Traffic Identification with Robust Representation Based on Datagram Structure. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 2045–2060. [Google Scholar]
- Alonso-Travesset, À.; Martín, H.; Coronas, S.; de la Hoz, J. Optimization Models under Uncertainty in Distributed Generation Systems: A Review. Energies 2022, 15, 1932. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, X.; Zhang, L.; Giannelos, S.; Strbac, G. Flexibility enhancement of urban energy systems through coordinated space heating aggregation of numerous buildings. Appl. Energy 2024, 374, 123971. [Google Scholar] [CrossRef]
- Borozan, S.; Giannelos, S.; Falugi, P.; Moreira, A.; Strbac, G. Machine Learning-Enhanced Benders Decomposition Approach for the Multi-Stage Stochastic Transmission Expansion Planning Problem. Electr. Power Syst. Res. 2024, 237, 110985. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Strbac, G.A. Backwards Induction Framework for Quantifying the Option Value of Smart Charging of Electric Vehicles and the Risk of Stranded Assets under Uncertainty. Energies 2022, 15, 3334. [Google Scholar] [CrossRef]
- Giannelos, S.; Djapic, P.; Pudjianto, D.; Strbac, G. Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies 2020, 13, 826. [Google Scholar] [CrossRef]
- Giannelos, S.; Borozan, S.; Strbac, G.; Zhang, T.; Kong, W. Vehicle-to-Grid: Quantification of its contribution to security of supply through the F-Factor methodology. Sustain. Energy Res. 2024, 11, 32. [Google Scholar] [CrossRef]
- Giannelos, S.; Moreira, A.; Papadaskalopoulos, D.; Borozan, S.; Pudjianto, D.; Konstantelos, I.; Sun, M.; Strbac, G.A. Machine Learning Approach for Generating and Evaluating Forecasts on the Environmental Impact of the Buildings Sector. Energies 2023, 16, 2915. [Google Scholar] [CrossRef]
- Giannelos, S.; Bellizio, F.; Strbac, G.; Zhang, T. Machine learning approaches for predictions of CO2 emissions in the building sector. Electr. Power Syst. Res. 2024, 235, 110735. [Google Scholar] [CrossRef]
- Münster, M.; Sneum, D.M.; Pedersen, R.B.; Bühler, F.; Elmegaard, B.; Giannelos, S.; Zhang, X.; Strbac, G.; Berger, M.; Radu, D.; et al. Sector Coupling: Concepts, State-of-the-Art and Perspectives; European Technology and Innovation Platform: Brussels, Belgium, 2020. [Google Scholar]
- Giannelos, S.; Jain, A.; Borozan, S.; Falugi, P.; Moreira, A.; Bhakar, R.; Mathur, J.; Strbac, G. Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty. Energies 2021, 14, 7813. [Google Scholar] [CrossRef]
- Holttinen, H.; Kiviluoma, J.; Helistö, N.; Levy, T.; Menemenlis, N.; Jun, L.; Cutululis, N.; Koivisto, M.; Das, K.; Orths, A.; et al. Design and Operation of Energy Systems with Large Amounts of Variable Generation: Final Summary Report, IEA Wind TCP Task 25; VTT Technical Research Centre of Finland: Espoo, Finland, 2021. [Google Scholar] [CrossRef]
- Beulertz, D.; Charousset, S.; Most, D.; Giannelos, S.; Yueksel-Erguen, I. Development of a Modular Framework for Future Energy System Analysis. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Stochastic optimisation-based valuation of smart grid options under firm DG contracts. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–6 April 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option Value of Demand-Side Response Schemes Under Decision-Dependent Uncertainty. IEEE Trans. Power Syst. 2018, 33, 5103–5113. [Google Scholar] [CrossRef]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Investment Model for Cost-effective Integration of Solar PV Capacity under Uncertainty using a Portfolio of Energy Storage and Soft Open Points. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Amann, G.; Escobedo Bermúdez, V.R.; Boskov-Kovacs, E.; Gallego Amores, S.; Giannelos, S.; Iliceto, A.; Ilo, A.; Chavarro, J.R.; Samovich, N.; Schmitt, L.; et al. E-Mobility Deployment and Impact on Grids. In Impact of EV and Charging Infrastructure on European T&D Grids: Innovation Needs; Gallego Amores, S., Ed.; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- Becker, S.; Cheridito, P.; Jentzen, A. Deep optimal stopping. J. Mach. Learn. Res. 2019, 20, 1–25. [Google Scholar]
- Bertsekas, D.P. II: Approximate Dynamic Programming. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 2012. [Google Scholar]
- Bunn, D.W.; Oliveira, F.S. Agent-based analysis of technological diversification and specialization in electricity markets. Eur. J. Oper. Res. 2007, 181, 1265–1278. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making Under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010. [Google Scholar]
- Dong, D.; Chen, C.; Li, H.; Tarn, T.-J. Quantum Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part B. (Cybernetics) 2008, 38, 1207–1220. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. Available online:https://arxiv.org/abs/1509.02971 (accessed on 1 March 2025).
- Pannakkong, W.; Vinh, V.T.; Tuyen, N.N.M.; Buddhakulsomsiri, J.A. A reinforcement learning approach for ensemble machine learning models in peak electricity forecasting. Energies 2023, 16, 5099. [Google Scholar] [CrossRef]
- Shengguang, P. Overview of Meta-Reinforcement Learning Research. In Proceedings of the 2020 2nd International Conference on Information Technology and Computer Application (ITCA), Guangzhou, China, 18–20 December 2020; pp. 54–57. [Google Scholar] [CrossRef]
- Wiencek, R.; Ghosh, S. Deep Reinforcement Learning for Adaptive Optimization of PI Control for Microgrid Under Fault and Variable Loading. In Proceedings of the 2024 6th Global Power, Energy and Communication Conference (GPECOM), Budapest, Hungary, 4–7 June 2024; pp. 826–831. [Google Scholar]
- Su, W.; Li, Z.; Xu, M.; Kang, J.; Niyato, D.; Xie, S. Compressing Deep Reinforcement Learning Networks with a Dynamic Structured Pruning Method for Autonomous Driving. IEEE Trans. Veh. Technol. 2024, 73, 18017–18030. [Google Scholar]
- Luo, B.; Wu, Z.; Zhou, F.; Wang, B.C. Human-in-the-Loop Reinforcement Learning in Continuous-Action Space. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 15735–15744. [Google Scholar]
- Han, Y.; Wang, X.; He, M.; Wang, X.; Guo, S. Intrusion Detection for Encrypted Flows Using Single Feature Based on Graph Integration Theory. IEEE Internet Things J. 2024, 11, 17589–17601. [Google Scholar]
- Midhula, K.S.; Kumar, P.A.R. An Adaptive Congestion Control Protocol for Wireless Networks Using Deep Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2024, 21, 2027–2043. [Google Scholar]
- Niu, D.; Cheng, G.; Chen, Z. TDS-KRFI: Reference Frame Identification for Live Web Streaming Toward HTTP Flash Video Protocol. IEEE Trans. Netw. Serv. Manag. 2023, 20, 4198–4215. [Google Scholar]
- Li, Z.; Zhao, H.; Zhao, J.; Jiang, Y.; Bu, F. SAT-Net: A Staggered Attention Network using Graph Neural Networks for Encrypted Traffic Classification. J. Netw. Comput. Appl. 2024, 233, 104069. [Google Scholar]
- Hariri, A.M.A.; Potts, C.N. A Branch and Bound Algorithm to Minimize the Number of Late Jobs in a Permutation Flowshop. Eur. J. Oper. Res. 1989, 38, 228–237. [Google Scholar]
- Maravelias, C.T.; Grossmann, I.E. A hybrid milp/cp decomposition approach for the continuous time scheduling of multipurpose batch plants. Comput. Chem. Eng. 2004, 28, 1921–1949. [Google Scholar]
- Hooker, J.N. Planning and Scheduling by Logic-Based Benders Decomposition. Oper. Res. 2007, 55, 588–602. [Google Scholar] [CrossRef]
- Harjunkoski, I.; Grossmann, I.E. Decomposition techniques for multistage scheduling problems using mixed-integer and constraint programming methods. Comput. Chem. Eng. 2002, 26, 1533–1552. [Google Scholar] [CrossRef]
- Rebennack, S. Combining sampling-based and scenario-based nested Benders decomposition methods: Application to stochastic dual dynamic programming. Math. Program. 2016, 156, 343. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Modified cuckoo search algorithm for short-term hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2015, 65, 271. [Google Scholar] [CrossRef]
- Houben, R.; Bobekh, A.; Preuschoff, F.; Moser, A. Optimizing large-scale Integrated Energy Systems with Storage Facilities: A parallelized approach. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 24–30. [Google Scholar]
- Mehrtash, M.; Hobbs, B.F.; Mahroo, R.; Cao, Y. Does Choice of Power Flow Representation Matter in Transmission Expansion Optimization? A Quantitative Comparison for a Large-Scale Test System. IEEE Trans. Ind. Appl. 2024, 60, 1433–1441. [Google Scholar] [CrossRef]
- García-Cerezo, Á.; García-Bertrand, R.; Baringo, L. Computational Performance Enhancement Strategies for Risk-Averse Two-Stage Stochastic Generation and Transmission Network Expansion Planning. IEEE Trans. Power Syst. 2024, 39, 273–286. [Google Scholar] [CrossRef]
- Yu, N.; Qian, B.; Hu, R.; Chen, Y.; Wang, L. Solving open vehicle problem with time window by hybrid column generation algorithm. J. Syst. Eng. Electron. 2022, 33, 997–1009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).