1. Introduction
The Sulfur Recovery Unit with Hydrogen Extraction (SRUHE) is one of the key technological facilities at oil refineries, as it enables the conversion of harmful acidic gases and sulfur-containing hydrogen sulfide into valuable products: high-quality sulfur and hydrogen [
1,
2]. The sulfur produced is further used to manufacture pharmaceutical products, dyes, explosives, fertilizers, and other chemical products [
3,
4]. The hydrogen extracted in the sulfur production process is utilized for hydrogen energy [
5,
6]. Traditional deterministic models often fail to account for the uncertainty inherent in refinery processes, particularly in sulfur recovery and hydrogen extraction. By integrating fuzzy logic, the proposed system enhances adaptability to uncertain operating conditions, ensuring a more accurate and efficient optimization of SPUHE operations.
Thus, SRUHE not only enhances the economic performance of refineries by producing and selling sulfur and hydrogen, which are in high demand in various chemical, medical, construction, and energy industries [
6,
7] but also addresses environmental issues in oil refining by converting toxic hydrogen sulfide and other acidic gases into useful products.
Recently, the share of high-sulfur crude oil extracted in Kazakhstan and other countries has been increasing, leading to higher emissions of harmful and toxic sulfur-containing gases during processing. Therefore, improving the efficiency of SRUHE operations, based on advancements in modern science and information technologies, while ensuring strict environmental standards and reducing its impact on the environment, is a top priority. The SRUHE at oil refineries is a highly complex technological system, consisting of interconnected and interacting units where physical and chemical processes take place, many of which are still insufficiently studied, have parameters that are not measured, and are difficult to formalize, making mathematical modeling challenging [
8]. Thus, the main units of the SRUHE operate in conditions of data scarcity and uncertainty, as some critical parameters and indicators (such as sulfur quality and others) are not directly measurable but rather evaluated by decision-makers (DMs) and experts responsible for managing its operation modes. These immeasurable production indicators are assessed based on expert knowledge, experience, and intuition, using natural language, which introduces fuzziness. The optimization of SRUHE operating modes using modeling techniques is characterized by a vector of economic and environmental criteria, which are often conflicting in terms of finding effective solutions, making this a decision-making problem in a fuzzy environment. All of this highlights the importance and relevance of developing a system of interconnected models for the main SRUHE units under conditions of data scarcity and uncertainty, to achieve effective multi-criteria optimization and control of its operational modes. The urgency of this problem has significantly increased due to tightening environmental regulations, stricter industrial requirements, and the need to minimize environmental pollution. This situation motivates the current study, which aims to develop a system of models for the main interconnected units of the SRUHE at the Atyrau Oil Refinery (Atyrau, Kazakhstan), considering data scarcity and uncertainty. The developed model is then used to optimize and manage the operating conditions of the unit.
In practice, when studying and managing complex facilities such as SRUHE, uncertainty problems may arise due to the probabilistic, random, and/or fuzzy nature of the initial information. Uncertainty problems caused by the probabilistic nature of initial information obtained through instrument measurements can be resolved using probability theory and mathematical statistics methods, provided that a sufficient amount of statistical data are available [
9,
10,
11]. In cases where parameters cannot be measured, statistical data are unavailable, or data collection is impossible or impractical, and the cause of uncertainty is the fuzziness of available information, other approaches must be used, such as non-statistical methods for solving uncertainty problems. Fuzzy logic enhances the SPUHE modeling system by incorporating expert knowledge into process evaluation, enabling the assessment of qualitative sulfur properties and improving prediction reliability in cases of uncertain or incomplete data. Unlike traditional deterministic models, which struggle with qualitative variables, fuzzy models can systematically process linguistic assessments of sulfur quality, process stability, and operational efficiency. This ensures that expert insights are effectively utilized in decision-making, enhancing the robustness and adaptability of the SPUHE system under real refinery conditions. If parameter values are not measured but are assessed in a fuzzy manner by decision-makers (DMs) and experts, based on their knowledge and experience, then expert evaluation methods and fuzzy set theory are used to address the uncertainty problem of a fuzzy nature [
12,
13,
14,
15].
The goal of this study is to develop a system of models for the main interconnected units of the SRUHE at the Atyrau Oil Refinery (Atyrau, Kazakhstan), considering data scarcity and uncertainty using a systematic approach, which integrates both statistical and fuzzy methods for addressing uncertainty in initial information. Based on the developed SRUHE model system, the process of optimization and selection of effective operating modes is then implemented.
Currently, due to the increasing importance of effectively improving economic performance and enhancing the environmental sustainability of the oil refining sector, research has intensified in the field of optimizing sulfur production process management. The most effective approach to solving this problem is based on modern scientific advancements, specifically mathematical modeling and optimization methods, as well as information technology tools.
Let us present the main results of the literature review on the research topic. The authors of studies [
16,
17,
18,
19,
20] investigated the issues of modeling and optimizing sulfur production processes, the operation of sulfur production plants, and the Claus process technology. The authors of [
16,
17] studied and proposed an approach to the development of models and optimization based on the obtained sulfur production process models under deterministic conditions. Kazempour et al., in their works [
18,
19,
20], presented research results on the optimization of the Claus process based on models for extracting sulfur from sulfur-containing gases.
Zare in [
21], and Hashemi et al. in their studies [
22], analyzed the energy, exergy, and exergoeconomic aspects of the modified Claus process, which can be used to optimize the sulfur production process. Mehmood et al. in their research [
23] evaluated kinetic models for modeling Claus reaction furnaces in sulfur recovery plants under various feed conditions. The authors of [
24,
25] used computational fluid dynamics (CFD) to model and analyze sulfur extraction processes from acid gas and improve their efficiency. Ibrahim et al., in [
26,
27,
28] studied and assessed the performance of sulfur recovery units (SRU), the impact of feed composition on plant performance, and proposed an approach to multi-objective optimization of high-sulfur gas purification units.
The authors of [
29,
30,
31,
32] analyzed and compared technologies and methods for sulfur production and biological removal of hydrogen sulfide from pollutants. Zhencai et al., in [
33,
34] described the Frasch Method and sulfur and sulfuric acid production technologies.
The results of the literature review and other studies in the research field show that the main issues of improving sulfur production efficiency have been explored and addressed, including through the use of mathematical modeling and optimization methods in deterministic and statistical conditions. However, it is well known that real industrial sulfur production facilities generally operate under uncertainty due to random and fuzzy characteristics of available information. If uncertainty is caused only by the random and probabilistic nature of measurable information, then probabilistic methods can be used to solve these uncertainty problems, as mentioned earlier. In existing studies, while some research has been conducted on uncertainty problems in stochastic conditions, the full resolution of uncertainty problems in these conditions has not yet been achieved. Furthermore, research dedicated to studying and solving uncertainty problems due to the fuzziness of initial information, which often occurs in practice when modeling and optimizing sulfur production processes, is almost absent. In this regard, the main goal of the present study is to develop a system of models for the main interconnected units of a sulfur production facility, considering data scarcity and uncertainty in initial information based on previous research by the authors. Based on the obtained results, intelligent decision support systems (DSS) will then be developed for the effective management of operating modes of the sulfur production facility in a fuzzy environment.
2. Object, Materials and Methods
The object of study in this work is the main units of the SRUHE at Atyrau Refinery (Atyrau, Kazakhstan) which form a technological system characterized by a deficit and uncertainty of some initial information. The SRUHE is designed to obtain granulated high-quality sulfur from acid gases, the main components of which are hydrogen sulfide and other sulfur-containing gases harmful to the environment. The produced sulfur is used for the manufacture of medical products, dyes, fertilizers, and other demanded products, while the hydrogen released in this process is used for hydrogen energy production. During sulfur production, the quality of sulfur is described with uncertainty, which is expressed through linguistic variables. The sulfur quality is evaluated using the following categories: high, above average, average, below average, and low. These assessments are conducted with the participation of specialists, including process engineers, laboratory technicians, and refinery laboratory experts. To optimize the operating modes of sulfur production processes, a set of models for the main interconnected units of the SRUHE should be developed, allowing for systematic modeling and identifying the most efficient operating mode. Such a set of models for the main units of the study object is created by combining the developed models of these units, taking into account the technological scheme of sulfur and hydrogen production in the SRUHE.
The diagram of the study object, the sulfur production unit at Atyrau Refinery (Atyrau, Kazakhstan), is presented in
Figure 1. The main units of the SRUHE, shown in
Figure 1, represent the processes of liquid sulfur production, where sulfur from the sulfur pit (SD) is transferred to the crystallization unit, where it undergoes processing to form granulated sulfur.
The raw material for the SRUHE is hydrogen sulfide-containing acid gas, which is a harmful gas released during oil refining processes. From this gas, valuable and highly demanded products are obtained for various industries. The acid gas from the separator enters the thermoreactor (TR) for the thermal conversion process. From there, it flows into the Claus reactor (RC), where the catalytic conversion process takes place. The sulfur from the Claus reactor (RC) is then supplied to the parallel-connected RCBA-1 and RCBA-2 reactors, where the Cold Bed Absorption (CBA) process occurs at a lower temperature than in the catalytic conversion process. After the CBA process, liquid sulfur is discharged from RCBA-1 and RCBA-2 into the sulfur pit. From there, it is transferred to the sulfur crystallization unit, where it undergoes crystallization and granulation.
As part of the study, data on process parameters and operating modes of the main units of SRUHE at Atyrau Refinery (Atyrau, Kazakhstan) are used. These data are collected through passive and active experiments [
35,
36,
37] and analyzed using mathematical statistics methods [
9,
10,
11,
38]. Passive experiments include statistical data on key parameters and laboratory test results from process log sheets filled out by SRUHE operators (DMs). Additional data are obtained from the SRUHE process regulations at Atyrau Refinery (Atyrau, Kazakhstan) [
39].
The immeasurable qualitative characteristics of sulfur are assessed by decision-makers (DMs) and expert specialists from the central refinery laboratory in a fuzzy manner, based on their experience, knowledge, and intuition. To collect, formalize, and process this fuzzy information, the study applies expert evaluation methods (a modified Delphi Method) and fuzzy set theory [
12,
13,
14,
15,
40,
41,
42,
43,
44,
45]. This research will also utilize materials on the thermal conversion process occurring in the thermoreactor (TR), the catalytic conversion process occurring in the Claus reactor (RC) in the presence of a catalyst, and the conversion processes in the RCBA-1 and RCBA-2 reactors.
The volume and quality of the obtained sulfur depend on the values of the input and operating parameters of the main SRUHE reactor units TR, E-1, E-4, RC, RCBA-1, and RCBA-2, as well as on their operating modes. Therefore, to determine the optimal operating mode of the SRUHE, it is necessary to develop a system of model packages for its main interconnected units, which describe the dependencies of sulfur volume and quality on input and operating parameters. Then, using computer modeling based on the obtained system of models for various SRUHE operating modes, it is possible to select input and operating parameters that ensure the most efficient mode of operation. For example, an operating mode of the main SRUHE units that allows obtaining the maximum volume of sulfur with the best quality indicators, while complying with the technological regulations of the unit and other operational constraints.
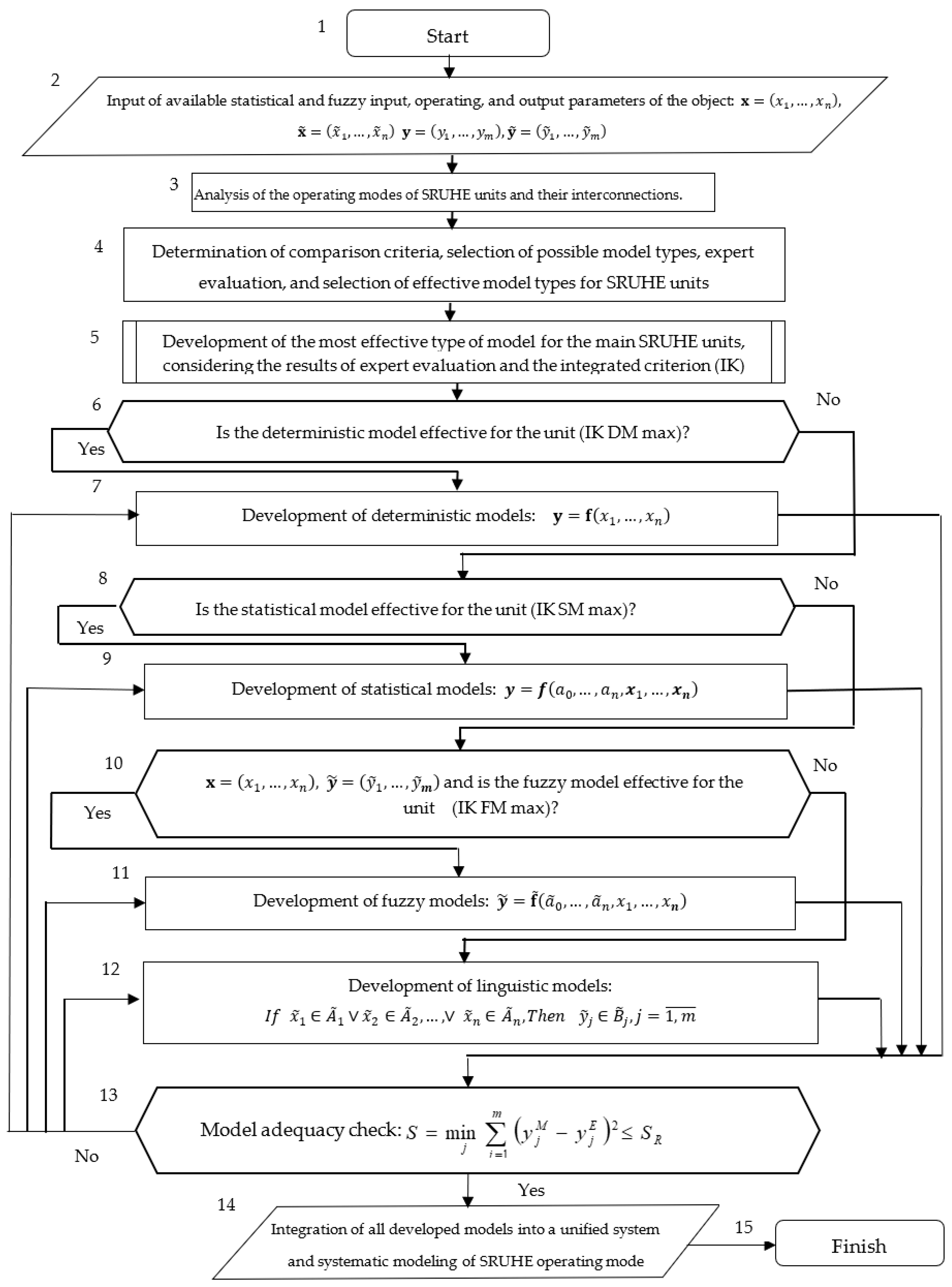
The block diagram of the proposed and used method for developing the system of models for the main SRUHE units is presented in
Figure 2.
The proposed method for developing a system of models for interconnected SRUHE units is based on available statistical and fuzzy information under conditions of data scarcity and uncertainty.
In Block 2, values are entered for the vector of available statistical and fuzzy input, operating, and output parameters of the SRUHE unit, represented as: and . At this stage, the input and operating parameters that influence the output parameters and define the operating modes and quality of the SRUHE performance are selected.
In Block 3, a systematic analysis of the operating modes of interconnected main SRUHE units is carried out, along with their formalized description.
In Block 4, a set of criteria is determined for comparing, evaluating, and selecting the most effective type of model for each SRUHE unit. Based on these criteria, an expert evaluation is conducted. The results of this expert evaluation are then processed to select the most effective types of models for the main SRUHE units that need to be developed.
From Block 5 to Block 12, the development of the selected effective model types for the main units (TR, E-1, E-4, RC, RCBA-1, and RCBA-2) of the SRUHE is carried out. In Block 5, the most effective model type for the main units of SRUHE is determined based on the results of expert evaluation processing and the value of the integrated criterion (IK), which is obtained by summing the local criteria.
To reduce the subjectivity of expert information obtained through the Delphi method, the following approach is implemented. After each round of individual assessment, each expert is presented with the evaluations of all other experts. Based on this analysis, each expert may either adjust their assessment to align more closely with others or justify the correctness of their original evaluation. Next, the degree of consensus among experts is assessed using a well-known methodology—calculating the concordance coefficient, which measures the consistency of expert opinions. The closer its value is to 1, the higher the level of agreement among experts, and vice versa. This round-based procedure is repeated until the concordance coefficient reaches 1 or approaches it, indicating a high level of consensus among all experts. This, in turn, significantly reduces the subjectivity of expert evaluations. To minimize the time required to reach a final decision with consensus among all experts, and to further reduce the subjectivity of expert assessments, it is necessary to automate the process of conducting rounds and calculating the concordance coefficient. This can be achieved by using computers connected to a shared network between experts and the organizers of the expert evaluation process.
In Block 6, the condition is checked again to determine whether the selected unit’s deterministic model is effective, i.e., whether IK DM max is achieved. If the condition is met, then in Block 7, the deterministic models for this unit are developed analytically using the formula: . Afterward, to verify the adequacy of the obtained model, the process moves to Block 13. If the condition is not met, then the process moves to Block 8.
In Block 8, the condition is checked to determine whether the statistical model is effective for the unit, i.e., whether IK ST max is achieved. If the condition is met, then in Block 9, the statistical models for this unit are developed using an experimental-statistical method, for example, with the structure: where —are unknown parameters to be identified. Afterward, to verify the adequacy of the obtained model, the process moves to Block 13. If the condition is not met, then the process moves to Block 10.
In Block 10, the following condition is checked: “Are the input and operating parameters of the unit crisp (precisely defined numerical values), while the output parameters are fuzzy (linguistically or uncertainly defined)? Additionally, does the fuzzy model satisfy the IK FM max criterion, confirming its effectiveness for this unit?” If the condition is met, then in Block 11, the fuzzy model for this unit is developed using the corresponding method, with the structure:
for example, based on the sequential inclusion regression method:
For each the parameters —are fuzzy parameters that need to be identified. They can be identified based on the α-level set and the modified least squares method. Afterward, to verify the adequacy of the obtained model, the process moves to Block 13.
If the condition in Block 10 is not met, then the process moves to Block 12 for the synthesis of linguistic models of the unit.
In Block 12, the linguistic model of the unit is synthesized based on the compositional rule of inference and the corresponding method, with the structure:
where
and
—are linguistic variables that estimate fuzzy values of the input and output parameters of the unit, respectively.
and
—are fuzzy subsets where
and
are determined, respectively.
—is the union operation over fuzzy sets, corresponding to the logical “and” operation For the synthesis of linguistic models, using expert evaluation methods involving decision-makers (DMs), the term-sets
T(
X,
Y), are defined, which describe the fuzzy parameters of the unit. For these parameters, membership functions are constructed as:
. T These membership functions can be built using the Fuzzy Logic Toolbox of the MATLAB R2018b system, for example, by selecting a Gaussian-type function (gaussmf). Using the compositional rule
we can determine
where
—is the fuzzy mapping that relates
and
For computer-based calculations, the fuzzy mapping is formalized through its membership function:
Then, the fuzzy values of the output parameters are determined in a formalized form based on the max-min product rule: where —represents the fuzzy input parameter values determined by experts. Thus, the crisp values of the output parameters —can be determined using the formula: In Block 13, the adequacy condition of the developed models of SRUHE units is checked based on the criterion of minimizing the squared difference between the output parameter values obtained from the models (through calculations) and the actual values determined experimentally.
If the adequacy condition is met, then in Block 14, in accordance with the technological scheme of the SRUHE and the sulfur production process, the developed models are combined into a unified system that enables systematic modeling of SRUHE operating modes. These models are then recommended for practical application. If the adequacy condition is not met, the causes of inadequacy are identified, and the process returns to the corresponding block to eliminate the causes and improve the model’s adequacy.
3. Results
Let us present the results of developing the system of models for the main units of the SRUHE, including the thermoreactor, condenser, electric heater, Claus reactors, and CBA reactors, based on the method proposed in
Section 2 for developing the system of models, which is used for optimizing the operating modes of the unit.
In Blocks 2 and 3 of the method, the collected statistical and fuzzy input and output parameters of the unit were defined and entered, and a systematic analysis of the operating modes of the main SRUHE units and their interconnections was conducted. In Block 4, the criteria for selecting the most effective model type included: Availability of the necessary initial information for model development. Adequacy of the model. Cost of model development. Efficiency of using the model for optimization. Possibility of integrating the developed models into the overall system. Based on these criteria and the expert evaluation, statistical models were selected as the most effective type for determining the product output from the thermoreactor (TR), Claus reactors (RC), and Cold Bed Absorption reactor (RCBA-2). For evaluating the quality characteristics of sulfur produced in the CBA reactors, fuzzy models were determined to be the most effective. The condenser (E-1) and electric heater (E-4) were modeled using statistical models, developed with the participation of the authors in study [
45].
3.1. System of Mathematical Models for the Thermoreactor TF, Claus Reactors RC, and CBA Reactors of SRUHE at Atyrau Refinery (Atyrau, Kazakhstan)
The development of the selected effective models for the thermoreactor, Claus reactors, and Cold Bed Absorption (CBA) reactors of the SRUHE was carried out considering the results of expert evaluation and the integrated criterion (IK), following Blocks 5–12 of the proposed method. The mathematical models of the thermoreactor, Claus reactors, and CBA reactors were developed based on collected and processed experimental-statistical data and expert information, which was processed using fuzzy set theory methods. As a result, the structure of the developed models, based on the sequential inclusion regression method [
46] was identified in the form of the following: Multiple nonlinear regression Equations (4)–(6) Fuzzy regression models (7):
In models (4)–(6), —represent the volumes of intermediate products and final products obtained from the thermoreactor, Claus reactors, and CBA reactors, respectively; —are the main fuzzy quality indicators of sulfur in liquid sulfur from the CBA reactor outlet; The unknown crisp and fuzzy parameters of models (5) to be identified are: , and , —The input and operating parameters of TR, RC, and CBA are: —raw material feed into TR; —temperature and pressure in TR; —combustion air consumption in TR; —raw material feed into RC; —temperature and pressure in RC; —raw material feed into RCBA; —temperature and pressure in RCBA.
In the fuzzy model system (7), the evaluated quality indicators of the obtained sulfur are: —represent: Mass fraction of sulfur; Ash content; Organic substances; Acids (converted to sulfuric acid equivalent); Water content. The input and operating parameters of CBA reactors that affect sulfur quality are: —raw material feed into RCBA; —temperature and pressure in RCBA.
Since the models describing product output from the reactors are multiple regression models, their unknown parameters (regression coefficients) were identified using experimental-statistical data and the least squares method, utilizing the REGRESS software package 3.1.
The results of parametric identification of the models, which determine the dependence of intermediate product output from TR and sulfur volume from RC and CBA reactors, are given in Equations (8)–(10):
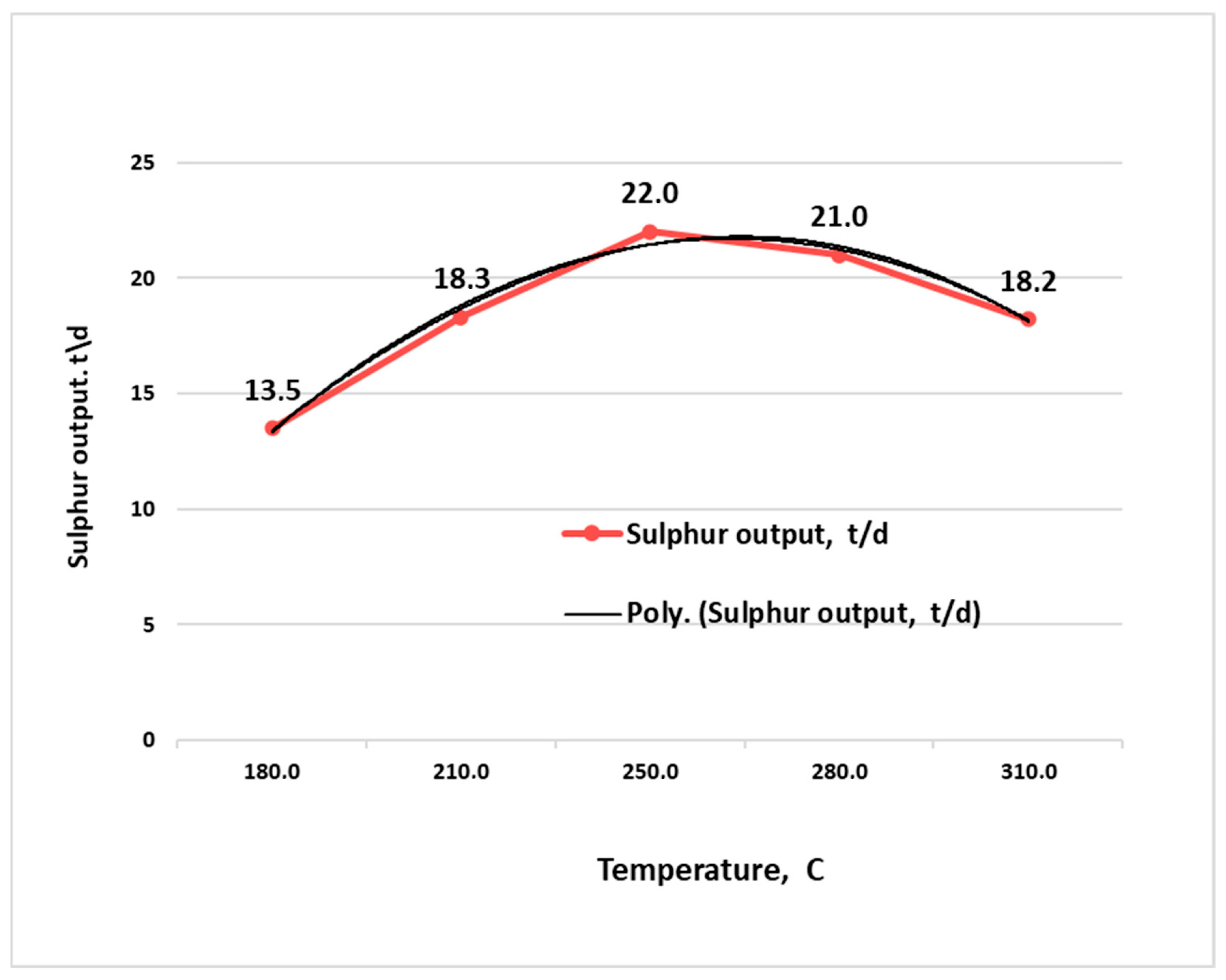
Figure 3 shows the graph of the dependence of sulfur output from CBA reactors on the temperature value
while keeping other input and operating parameters constant (
—raw material feed,
—temperature at the RCBA inlet,
—pressure in RCBA).
The unknown parameters of the fuzzy models (7), which evaluate the quality indicators of sulfur from the CBA reactor output, were identified based on the α-level set method and the modified least squares method. To identify the unknown fuzzy coefficients:
the fuzzy sets describing the product quality indicators were divided into the following levels:
For each level
the models of sulfur quality indicators can be represented as a system of crisp multiple regression equations. Thus, the identification task of the coefficients in these equations at the levels
is reduced to classical parameter estimation problems in multiple regression analysis. For the identification of parameters in these models, the REGRESS program, implementing the least squares method, can also be used. The obtained parameter values at levels:
were then combined into a single value using the fuzzy set theory formula:
Then, the models describing the fuzzy dependence of sulfur quality indicators, for example, the mass fraction of sulfur
on the input and operating parameters described above
have the following form:
Then, based on Equation (11), combining the values of fuzzy parameters at α-level sets—on the left (0.5, 0.8), the maximum value (1), and the right (0.5, 0.8)—a convenient model form for determining the sulfur fraction in the obtained sulfur on a computer is obtained:
The parametric identification of fuzzy models for evaluating sulfur quality indicators
and
was carried out analogously to the parametric identification of the fuzzy model for sulfur fraction evaluation
Then, as a result of combining the identified parameter values at the α-level sets based on Equation (11), the following models were obtained, allowing the determination of sulfur composition indicators on a computer: ash content
organic substances
; acid content (converted to sulfuric acid)
and water content in the produced sulfur
:
In the obtained models (8)–(10) and (13)–(17), after the parametric identification of regression coefficients, input parameters that do not influence or have negligible influence on the output parameters are not included.
Fuzzy information, i.e., formalized knowledge, experience, and intuition of SPUHE process operators and experts, enhances the accuracy and reliability of SPUHE models by eliminating uncertainties in the assessment of unmeasured sulfur quality indicators. Unlike deterministic and statistical models, which either assume precision or struggle with data inaccuracy, fuzzy logic enables the mathematical structuring, formalization, and resolution of the problem of determining fuzzy sulfur quality indicators and the efficiency of processes occurring in SPUHE. The integration of the fuzzy approach with other well-known methods within the proposed systematic approach improves the efficiency and accuracy of modeling, ensures adaptability in uncertain conditions, and enhances the reliability of process optimization for sulfur and hydrogen production in SPUHE under real refinery conditions.
For systematic modeling and optimization of the SRUHE operating modes, the developed reactor models were combined into a unified system, considering their interconnections, the sulfur production process, and the configuration of the main units in the sulfur production block with hydrogen separation, as shown in
Figure 1. In addition to the developed models (8)–(10) and (13)–(17) for the thermoreactor, Claus reactor, and CBA reactors, the modeling system also includes the condenser models E-1 and E-4 of Atyrau Refinery (Atyrau, Kazakhstan), which were previously developed in study [
45].
In the obtained system of reactor and condenser models, as shown in the scheme in
Figure 1, the interconnected main units of the SRUHE are replaced with their developed and utilized models. Thus, the outputs of one model—i.e., the simulation results of a given unit—are used as input data for the models of other units. For example: The simulation results of TR serve as input data for the condenser E-1 model. The simulation results of E-1 are then used as input for the condenser E-4 model. The outputs of the E-4 model—i.e., its simulation results—are used as input data for the Claus reactor RC model. The simulation results of RC are then used as input data for the CBA-1 and CBA-2 reactors.
We provide additional explanations regarding the results of model development, detailing the process of their creation. The structures of the statistical models (4)–(6) and fuzzy models (7) were identified using the sequential inclusion method of regressors in the form of nonlinear crisp and fuzzy regression equations. The unknown parameters of the statistical models (4)–(6) were identified based on collected and processed statistical data on the operating modes of the modeled SRUHE reactors using the least squares method with the REGRESS software package. The unknown fuzzy parameters of the fuzzy models (7) were identified using the α-level set approach and a modified least squares method, employing the REGRESS software package for each α value. The obtained set of crisp values of the identified fuzzy parameters for computer modeling was then combined into a single value based on formula (11) from fuzzy set theory.
3.2. Results of Sulfur Production Process Modeling Based on the SRUHE Reactor System Models
Through computer modeling, the operating modes of the interconnected models for the thermoreactor, Claus reactor, and CBA were simulated using the developed models (8)–(10) and (13)–(17) at various input operating parameter values. The optimal SRUHE operating modes were determined, ensuring: Maximum sulfur output Best quality indicators The software implementation of the developed models for computer modeling was performed in the Jupyter Notebook (Anaconda3) environment, using the Python 3.12.6. programming language.
The results of computer simulations of various SRUHE operating modes, the determination of the optimal mode, and a comparison with other studies and real-world data are presented in
Table 1. In compliance with GOST 127.2–93 standards [
47], the following sulfur quality indicators were monitored: Sulfur fraction Ash content Organic substances Acid content (converted to sulfuric acid) Water content in the produced sulfur. The real-world data were experimentally obtained during SRUHE operation at Atyrau Refinery (Atyrau, Kazakhstan), under the supervision of experienced operators (DMs).
The modeling results presented in
Table 1, obtained using the developed system of models for the main units, were compared with the results of known deterministic models and were found to match real data with high accuracy, as obtained by experienced DMs during the operation of the research facility. Additionally, the developed system of models for the main SRUHE units allows for the fuzzy description of qualitative indicators of the produced sulfur, which cannot be determined by traditional modeling methods.
The reliability of the obtained results, scientific statements, and conclusions is confirmed by: The correctness of the research methods used, based on the scientific principles of system analysis and mathematical modeling. The use of expert evaluation methods and fuzzy set theory. The sufficient convergence of the obtained modeling results with experimental and industrial results (relative error not exceeding 3%).
The developed models, based on the proposed approach using fuzzy logic, provide a more accurate representation of real refinery conditions compared to deterministic models. This is because they account for uncertain, hard-to-measure fuzzy parameters through expert knowledge and experience. Experimental validation under real operating conditions of the SPUHE unit at the Atyrau Refinery (Atyrau, Kazakhstan) demonstrated that our developed model system reduces relative error to ≤3%, whereas deterministic models often fail to capture the qualitative characteristics of sulfur, leading to higher errors. Additionally, a comparison of modeling results using the developed models and known deterministic models, presented in
Table 1, shows that the proposed models deliver better results, improve energy efficiency, and allow for the determination of fuzzy-evaluated qualitative sulfur indicators. The key input and operational parameters of the modeled objects were kept identical, while the temperature and pressure of the Claus reactors were optimized.
Unlike deterministic models, which strictly rely on measured numerical data, the developed models, through the integration of expert evaluation, enable the determination of fuzzy qualitative properties of sulfur. This allows for real-time adjustments of temperature and pressure in Claus reactors under uncertain conditions. Furthermore, a comparison of the results of the developed and known models indicates that the developed models reduce energy consumption by optimizing the adjustable parameters of sulfur production and hydrogen extraction processes. Additionally, a comparative analysis determined that the developed models improve sulfur recovery efficiency by 11.94% compared to deterministic models (
Table 1).
4. Discussion of Results
The proposed method for developing a system of models for interconnected units under conditions of information scarcity and uncertainty and the developed system of models for interconnected SPP reactors are based on: A systemic approach Experimental-statistical methods Expert evaluation methods Fuzzy set theory The developed system of models for the main interconnected units of the SRUHE enables systematic modeling of various operating modes of the SRUHE and determines the optimal operating mode, which allows maximization of sulfur production with the best quality indicators. The hydrogen released during the sulfur production process is subsequently used for hydrogen energy production.
The proposed systematic approach to modeling enhances sulfur production and hydrogen extraction processes in SPUHE by providing holistic optimization, eliminating uncertainties, and improving reliability and forecasting accuracy. By integrating fuzzy logic with deterministic and statistical models, this approach offers an adaptable and scalable framework for optimizing industrial processes under uncertain conditions. It enables refineries to minimize energy costs while simultaneously maximizing the efficiency of sulfur and hydrogen production and improving environmental sustainability.
The proposed method for developing a system of models for interconnected SRUHE units has synergistic effects and emergent system properties due to the comprehensive use of various methods, ensuring the development of effective and adequate models for SRUHE units. The obtained results can be exported and applied to develop modeling systems for other oil refining, petrochemical, and industrial facilities under conditions of information scarcity and uncertainty, demonstrating the practical significance of this work.
As a result of the analysis and discussion of the systematic modeling results for the SRUHE reactor operating modes, based on known deterministic models and the developed system of models (as presented in
Table 1), the following advantages of the proposed method and the developed system of models for SRUHE can be identified:
(1) The proposed method for developing a system of models for the main technological system units—using the SRUHE as an example under conditions of information scarcity and uncertainty—allows for the creation of a system of effective and adequate models for interconnected units in various technological systems. This advantage is ensured by the synergistic effect and emergent system properties of the developed model system, based on: A systemic approach Experimental-statistical methods Expert evaluation methods Fuzzy set theory The developed method, depending on the available information, allows for the creation of deterministic, statistical, fuzzy, or linguistic models of the studied objects, which are then integrated into a unified model system, considering the interconnections of objects and the processes occurring within them;
(2) The system of models for the thermoreactor, Claus reactors, and CBA at the Atyrau Refinery (Atyrau, Kazakhstan) SRUHE, developed using the proposed modeling method, enables: Systematic computer-based modeling of various SRUHE operating modes Determination of the optimal operating mode The optimal SRUHE operating mode is defined as the mode that ensures maximum production volume and the best sulfur quality indicators. Statistical models of SRUHE reactors (4)–(6), which determine the output volume of intermediate and final products, were developed using statistical methods based on experimental-statistical data. Fuzzy models (7) were synthesized based on fuzzy information from DMs and experts to evaluate fuzzy-defined quality indicators of sulfur from reactors and the CBA unit. The identification of unknown parameters in polynomial-type statistical models (4)–(6) was conducted using the least squares method, implemented in the REGRESS software package. The identification of fuzzy parameters in models evaluating fuzzy-defined sulfur quality indicators (7) was performed using the α-level set method and a modified least squares method. After parameter identification of the obtained crisp models at α-levels and aggregation of the identified unknown parameter values using expression (11), the final models (13)–(17) were obtained, which are suitable for computer-based modeling and sulfur quality assessment;
(3) Comparison of Simulation Results and Determination of the Optimal Operating Mode of the SRUHE at Atyrau Refinery (Atyrau, Kazakhstan) Based on the developed models, known deterministic models, and real experimental data obtained at the studied SRUHE (
Table 1), the following conclusions can be made:
- –
The final product output—sulfur from the CBA reactor outlet—shows higher agreement with real data compared to known models. This means that: The developed models demonstrate higher adequacy. Sulfur yield is increased by 2.45 t/day or 12.24%, ensuring higher efficiency of the SRUHE operation;
- –
The developed fuzzy models allow for the evaluation of qualitatively described sulfur characteristics, which are not determined by the known comparison models, including: Mass fraction of sulfur; Ash content; Organic substances; Acid content (converted to sulfuric acid); Water content in the produced sulfur;
- –
Table 1 shows that the best simulation and optimization results, based on the developed models, are achieved at lower temperature and pressure values in SRUHE reactors, compared to deterministic model results. This means that the proposed method of modeling and optimizing SRUHE operating modes is more energy-efficient compared to known methods, as it allows for better results while requiring lower energy consumption for temperature and pressure generation.
The interconnected reactor model system enhances the efficiency of sulfur production and hydrogen extraction processes in the Sulfur Production Unit with Hydrogen Extraction (SPUHE) by integrating deterministic, statistical, and fuzzy modeling approaches. Known deterministic and statistical models often face uncertainty issues due to a lack of reliable statistical data, the impracticality or economic infeasibility of obtaining such data, and the inherent fuzziness of available input information. These challenges complicate the effective modeling and optimization of sulfur production processes.
Our proposed systematic approach, based on expert evaluation methods and fuzzy set theory, systematically incorporates expert knowledge, experience, and intuition into the model, representing them as fuzzy information. This fuzzy logic-based approach enhances system adaptability by processing imprecise qualitative data, such as sulfur quality or process stability, which cannot be directly measured but are critical for decision-making. By utilizing fuzzy regression methods, the model provides more accurate predictions of sulfur yield and hydrogen extraction under various SPUHE operating conditions.
Moreover, the developed interconnected reactor model system ensures that dependencies between different technological units (thermal reactor, Claus reactor, and cold-bed absorption reactors) are taken into account, leading to a more comprehensive optimization strategy. Ultimately, the proposed systematic approach, which effectively integrates and utilizes available fuzzy information, enables real-time process adjustments, enhances operational efficiency, minimizes energy consumption, and improves product quality, making the SPUHE system more reliable and resilient under real refinery conditions.
The proposed systematic modeling approach brings significant benefits to the oil refining, hydrogen energy, and related industries by improving process optimization, increasing efficiency in sulfur and hydrogen production, and ensuring better compliance with environmental regulations. The integration of fuzzy logic with other methods enables more adaptive decision-making, leading to increased production volumes with superior quality, enhanced efficiency and reliability of developed models, and reduced operational costs in uncertain conditions. In oil refining, the proposed approach increases the yield of high-quality sulfur while minimizing energy consumption. Additionally, it improves hydrogen extraction efficiency, supporting sustainable hydrogen production for hydrogen energy applications. Industries that rely on high-purity sulfur and hydrogen, such as pharmaceuticals and fertilizers, also benefit from improved product quality and compliance with environmental standards.