Heat Transfer Analysis in Double Diaphragm Preforming Process of Dry Woven Carbon Fibres
Abstract
1. Introduction
2. Materials and Experimental Methods
2.1. Materials and Thermophysical Properties
2.2. Double Diaphragm Preforming (DDPF) Process of Woven Fabric Preforms
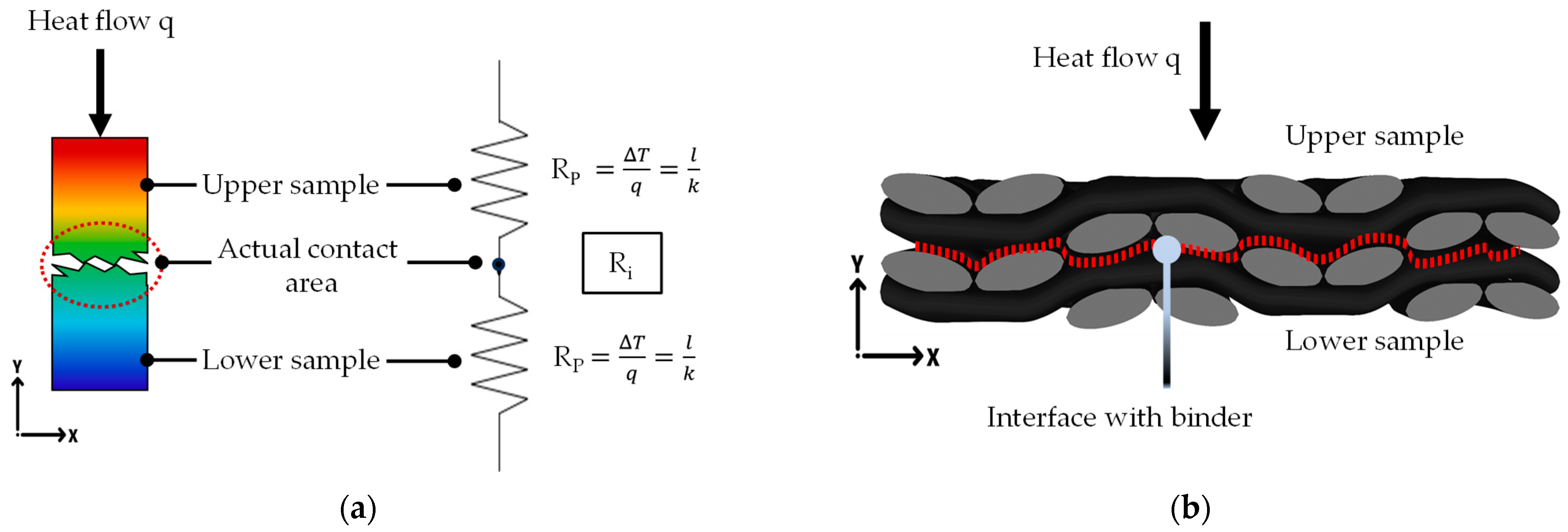
2.3. Compaction of Multilayer Coupon Preforms
2.4. TCC Parameter Tuning of Multilayer Coupon Models Under DDPF Process Conditions
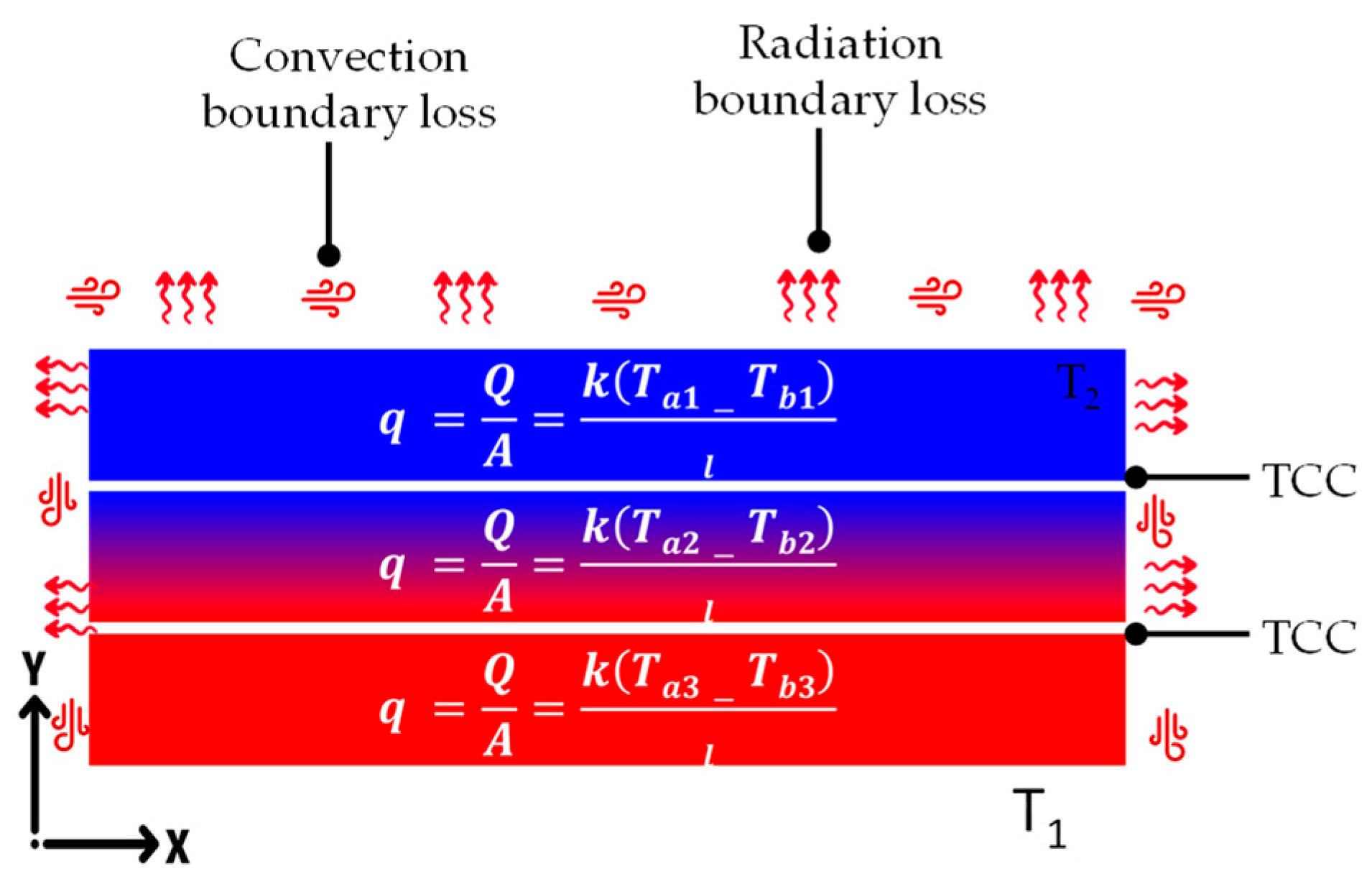
2.4.1. Empirical Relations for TCC Parameter Tuning in Multilayer Coupon Stacks
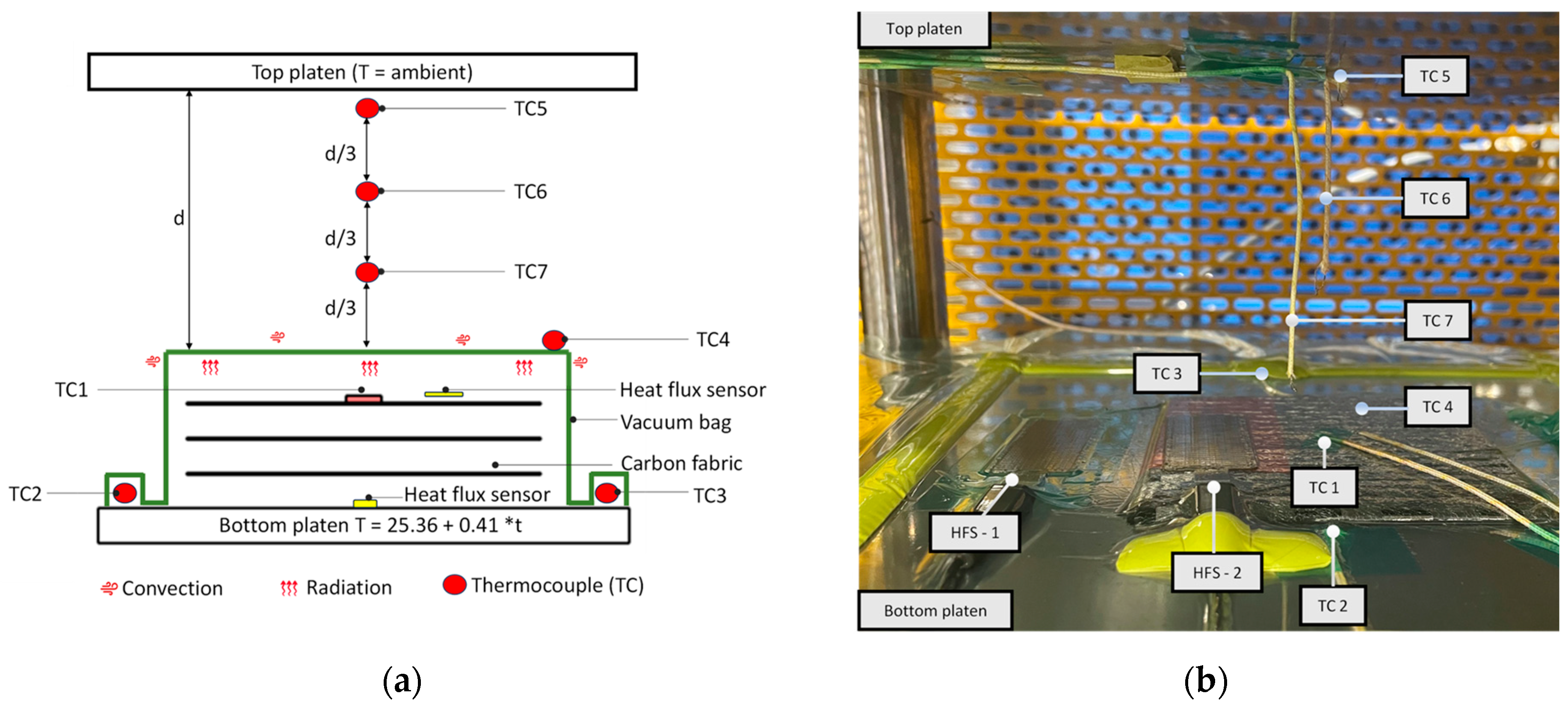
2.4.2. TCC Parameter Tuning in Multilayer Coupon Stacks—Experimental Validation
3. Numerical Methods for Heat Transfer Simulations
3.1. Heat Transfer Governing Equations
3.2. TCC Parameter Tuning in Multilayer Coupon Stacks
3.3. Homogenised Production-Scale Preform Models
4. Results and Discussion
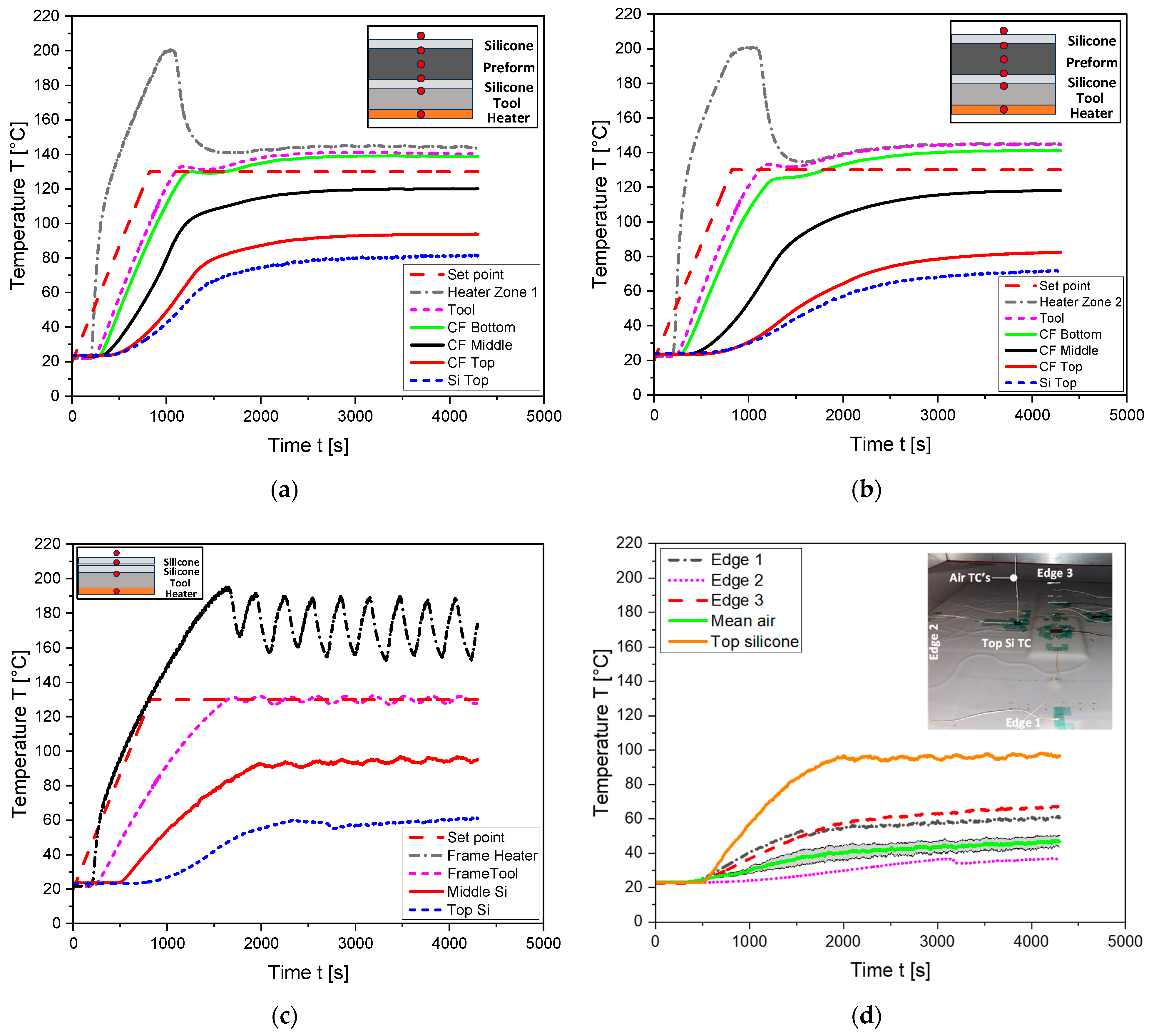
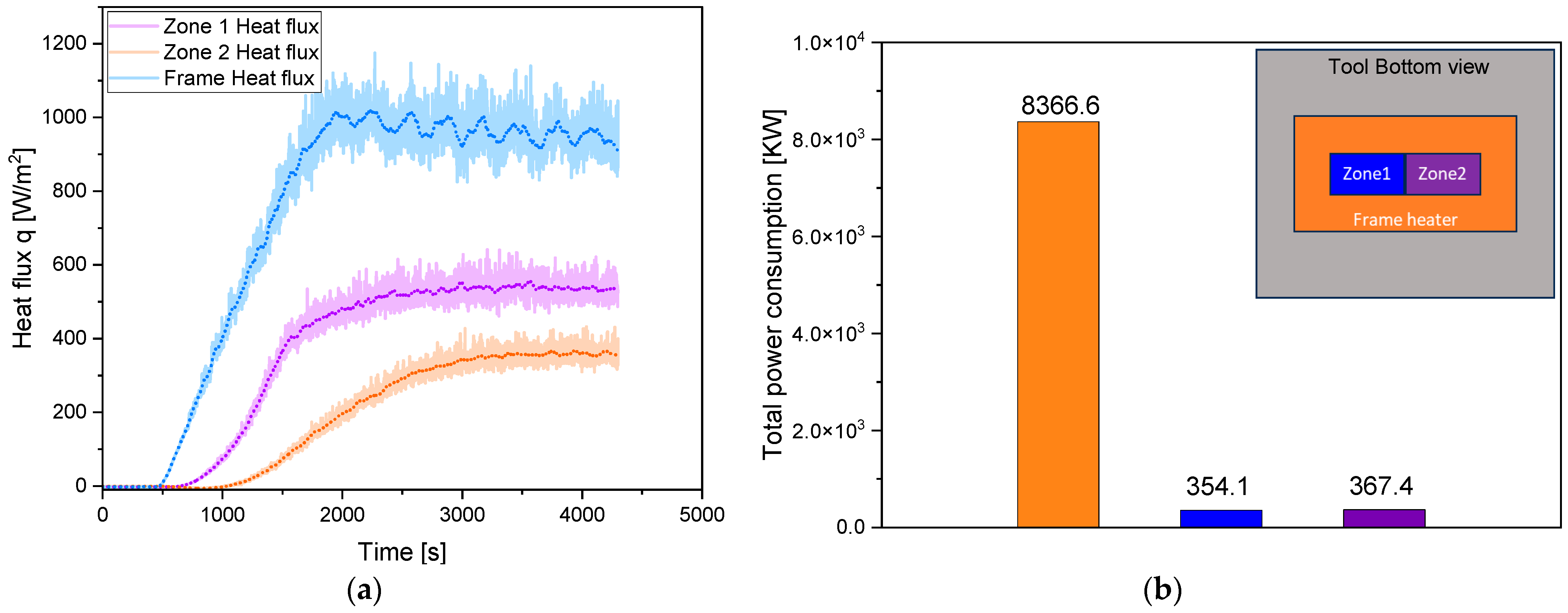
4.1. DDPF Process Experimental Results
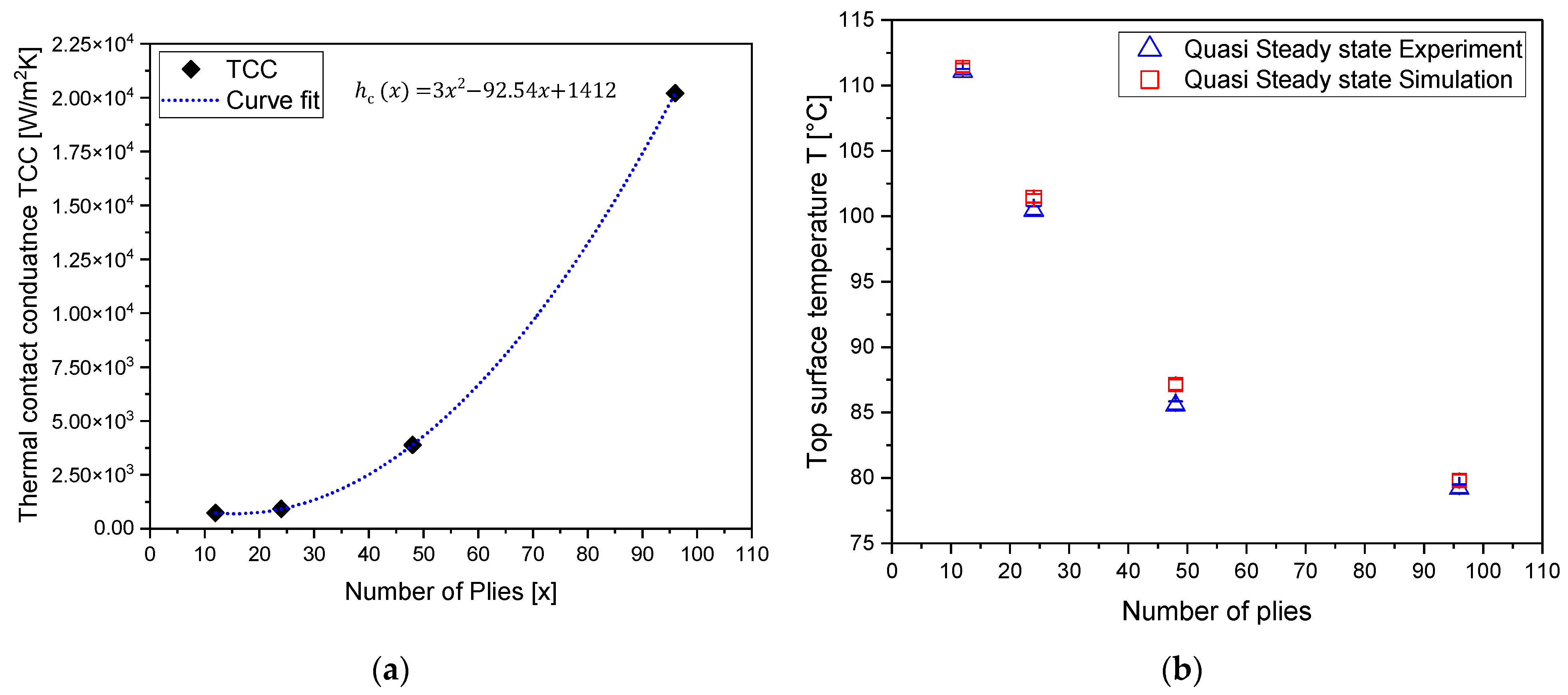
4.2. TCC Parameter Coupon Numerical Tuning and Experimental Validation Study
4.3. Homogenised Production-Scale Preform Model Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
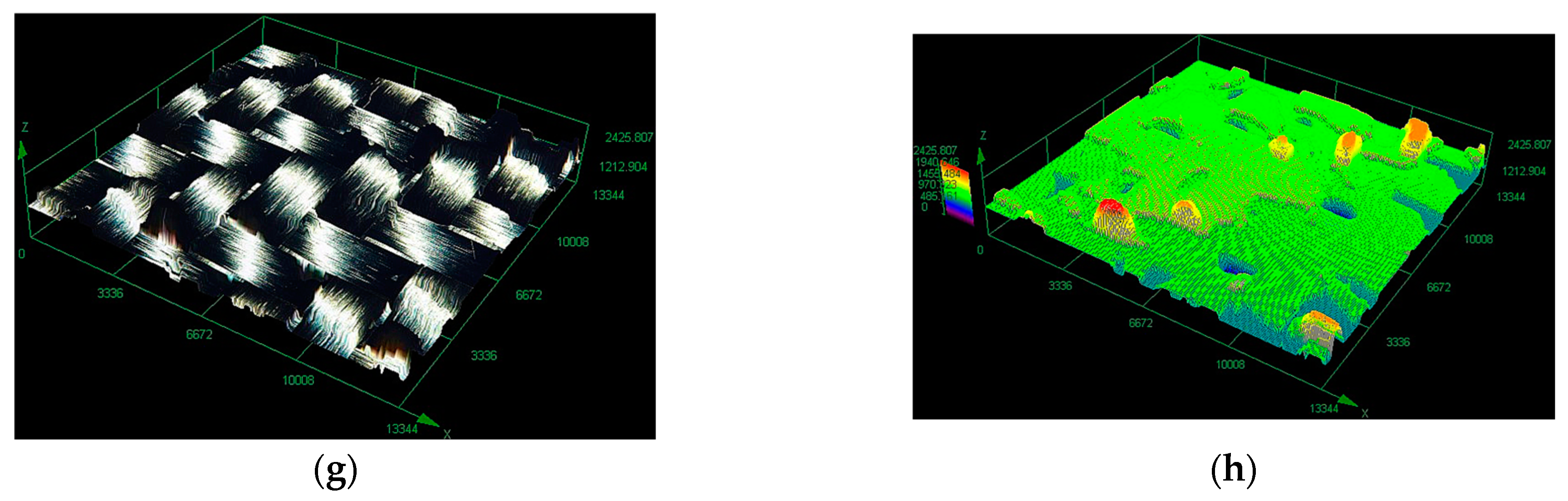
- Optical images and micrographs of coupon model surface asperities following de-compaction at the tool–material interface.

Appendix B
- Estimation of convection coefficient in natural heating.

References
- Lawrence, G.D.; Chen, S.; Warrior, N.A.; Harper, L.T. Preforming of Multi-Ply Non-Crimp Fabric Laminates Using Double Diaphragm Forming. In Proceedings of the Twenty-Third International Conference on Composite Materials, ICCM 23, Belfast, UK, 1 August 2023. [Google Scholar]
- Pantelakis, S.G.; Baxevani, E.A. Optimization of the Diaphragm Forming Process with Regard to Product Quality and Cost. Compos. Part Appl. Sci. Manuf. 2002, 33, 459–470. [Google Scholar] [CrossRef]
- Chen, S.; McGregor, O.P.L.; Harper, L.T.; Endruweit, A.; Warrior, N.A. Optimisation of Local In-Plane Constraining Forces in Double Diaphragm Forming. Compos. Struct. 2018, 201, 570–581. [Google Scholar] [CrossRef]
- Channer, K.J.; Cosgriff, W.; Smith, G.F.; Okoli, O.I. Development of the Double RIFT Diaphragm Forming Process. J. Reinf. Plast. Compos. 2002, 21, 1629–1635. [Google Scholar] [CrossRef]
- Solvay Unveils Double Diaphragm Forming (DDF) Automated Demonstrator Line. Available online: https://www.solvay.com/en/press-release/solvay-unveils-ddf-line (accessed on 20 June 2024).
- Hot Drape Forming—Preforming Solutions. Available online: https://old.pinetteemidecau.eu/en/equipment-and-systems/forming/preforming-solutions (accessed on 20 June 2024).
- Kunz, H.; Löchte, C.; Dietrich, F.; Raatz, A.; Fischer, F.; Dröder, K.; Dilger, K. Novel Form-Flexible Handling and Joining Tool for Automated Preforming. Sci. Eng. Compos. Mater. 2015, 22, 199–213. [Google Scholar] [CrossRef]
- Bian, X.X.; Gu, Y.Z.; Sun, J.; Li, M.; Liu, W.P.; Zhang, Z.G. Effects of Processing Parameters on the Forming Quality of C-Shaped Thermosetting Composite Laminates in Hot Diaphragm Forming Process. Appl. Compos. Mater. 2013, 20, 927–945. [Google Scholar] [CrossRef]
- Yu, F.; Chen, X.; Chen, S.; Harper, L.T. Numerical Study on the Formation of Defects During Double Diaphragm Forming Using a Biaxial Non-Crimp Fabric. In Proceedings of the 10th Chinese Society of Aeronautics and Astronautics Youth Forum; Chinese Society of Aeronautics and Astronautics, Ed.; Springer Nature: Singapore, 2023; pp. 392–402. [Google Scholar]
- Ning, H.; Vaidya, U.; Janowski, G.M.; Husman, G. Design, Manufacture and Analysis of a Thermoplastic Composite Frame Structure for Mass Transit. Compos. Struct. 2007, 80, 105–116. [Google Scholar] [CrossRef]
- Chen, S.; McGregor, O.P.L.; Endruweit, A.; Elsmore, M.T.; De Focatiis, D.S.A.; Harper, L.T.; Warrior, N.A. Double Diaphragm Forming Simulation for Complex Composite Structures. Compos. Part Appl. Sci. Manuf. 2017, 95, 346–358. [Google Scholar] [CrossRef]
- Thompson, A.J.; McFarlane, J.R.; Belnoue, J.P.-H.; Hallett, S.R. Numerical Modelling of Compaction Induced Defects in Thick 2D Textile Composites. Mater. Des. 2020, 196, 109088. [Google Scholar] [CrossRef]
- Thompson, A.J.; Belnoue, J.P.-H.; Hallett, S.R. Modelling Defect Formation in Textiles during the Double Diaphragm Forming Process. Compos. Part B Eng. 2020, 202, 108357. [Google Scholar] [CrossRef]
- Wambua, P.M.; Anandjiwala, R. A Review of Preforms for the Composites Industry. J. Ind. Text. 2011, 40, 310–333. [Google Scholar] [CrossRef]
- Krebs, J.; Bhattacharyya, D.; Friedrich, K. Production and Evaluation of Secondary Composite Aircraft Components—A Comprehensive Case Study. Compos. Part Appl. Sci. Manuf. 1997, 28, 481–489. [Google Scholar] [CrossRef]
- Krebs, J.; Friedrich, K.; Bhattacharyya, D. A Direct Comparison of Matched-Die versus Diaphragm Forming. Compos. Part Appl. Sci. Manuf. 1998, 29, 183–188. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, L.; Mai, Y.W. Modelling and Finite Element Treatment of Intra-Ply Shearing of Woven Fabric. J. Mater. Process. Technol. 2003, 138, 47–52. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Liu, M.; Peng, X. Development and Verification of a Finite Element Model for Double Diaphragm Preforming of Unidirectional Carbon Fiber Prepreg. Compos. Part Appl. Sci. Manuf. 2020, 135, 105924. [Google Scholar] [CrossRef]
- Kondratiev, A.; Purhina, S.; Shevtsova, M.; Tsaritsynskyi, A. Thermodynamic Model of Self-Heating Mold for the Energy Efficient Composite Manufacturing. In Proceedings of the 2021 IEEE 2nd KhPI Week on Advanced Technology, Kharkiv, Ukraine, 13–17 September 2021; pp. 120–125. [Google Scholar] [CrossRef]
- Widmaier, N.; Radjef, R.; Middendorf, P.; Fox, B. Double Diaphragm Forming of Bindered Unidirectional Dry-Fibre Tapes: Experimental Analysis of Forming Temperature. In Proceedings of the 20th Australian International Aerospace Congress, Melbourn, Australia, 27 February 2023; Engineers Australia: Melbourne, Australia, 2023. [Google Scholar]
- Miris, G.; Ravandi, M.; Cardew-Hall, A.; Eisenbart, B.; Di Pietro, A. Efficient Numerical Analysis of In-Plane Compression-Induced Defects in Thick Multi-Ply Woven Textile Preforms during Double Diaphragm Forming. Compos. Part Appl. Sci. Manuf. 2024, 186, 108431. [Google Scholar] [CrossRef]
- Matsudaira, M.; Qin, H. Features and Mechanical Parameters of a Fabric’s Compressional Property. J. Text. Inst. 1995, 86, 476–486. [Google Scholar] [CrossRef]
- Chen, B.; Chou, T.-W. Compaction of Woven-Fabric Preforms in Liquid Composite Molding Processes: Single-Layer Deformation. Compos. Sci. Technol. 1999, 59, 1519–1526. [Google Scholar] [CrossRef]
- Chen, B.; Chou, T.W. Compaction of Woven-Fabric Preforms: Nesting and Multi-Layer Deformation. Compos. Sci. Technol. 2000, 60, 2223–2231. [Google Scholar] [CrossRef]
- El-Dessouky, H.M.; Lawrence, C.A. Ultra-Lightweight Carbon Fibre/Thermoplastic Composite Material Using Spread Tow Technology. Compos. Part B Eng. 2013, 50, 91–97. [Google Scholar] [CrossRef]
- Ohlsson, F. An Introduction to Spread Tow Reinforcements. Part 2: Design and Applications. Reinf. Plast. 2015, 59, 228–232. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, H.; Zhao, X.; Zhang, N. Simulation of the Effects of Structural Parameters of Glass Fiber Fabric on the Thermal Insulation Property. Text. Res. J. 2018, 88, 1954–1964. [Google Scholar] [CrossRef]
- Snape, A.E.; Turner, J.L.; El-Dessouky, H.M.; Saleh, M.N.; Tew, H.; Scaife, R.J. Stabilising and Trimming 3D Woven Fabrics for Composite Preforming Applications. Appl. Compos. Mater. 2018, 25, 735–746. [Google Scholar] [CrossRef]
- Wu, W.; Jiang, B.; Xie, L.; Klunker, F.; Aranda, S.; Ziegmann, G. Effect of Compaction and Preforming Parameters on the Compaction Behavior of Bindered Textile Preforms for Automated Composite Manufacturing. Appl. Compos. Mater. 2013, 20, 907–926. [Google Scholar] [CrossRef]
- Wei, K.; Liang, D.; Mei, M.; Wang, D.; Yang, X.; Qu, Z. Preforming Behaviors of Carbon Fiber Fabrics with Different Contents of Binder and under Various Process Parameters. Compos. Part B Eng. 2019, 166, 221–232. [Google Scholar] [CrossRef]
- Bulat, M.; Heieck, F. Binder Application Methods for Textile Preforming Processes. LTH Faserverbund-Leichtbau; FL 21 200-02; Luftfahrttechnisches Handbuch: Braunschweig, Germany, 2015; pp. 1–16. [Google Scholar]
- Tonejc, M.; Ebner, C.; Fauster, E.; Schledjewski, R. Influence of Test Fluids on the Permeability of Epoxy Powder Bindered Non-Crimp Fabrics. Adv. Manuf. Polym. Compos. Sci. 2019, 5, 128–139. [Google Scholar] [CrossRef]
- Terekhov, I.V.; Chistyakov, E.M. Binders Used for the Manufacturing of Composite Materials by Liquid Composite Molding. Polymers 2021, 14, 87. [Google Scholar] [CrossRef]
- Dandangi, S.; Ravandi, M.; Naser, J.; Di Pietro, A. Thermophysical Characterization of Materials for Energy-Efficient Double Diaphragm Preforming. Energies 2024, 17, 3758. [Google Scholar] [CrossRef]
- Estrada, G.; Line Vieux-Pernon, C.É.; Advani, S.G. Experimental Characterization of the Influence of Tackifier Material on Preform Permeability. J. Compos. Mater. 2002, 36, 2297–2310. [Google Scholar] [CrossRef]
- Nezami, F.N.; Gereke, T.; Cherif, C. Isothermal Multisection Tooling for the Automated Preforming of Carbon Fiber Composite Structures. Key Eng. Mater. 2014, 611–612, 349–355. [Google Scholar] [CrossRef]
- Weiland, J.S.; Hubert, P.; Hinterho lzl, R. Thermal Dimensioning of Manufacturing Moulds with Multiple Resistively Heated Zones for Composite Processing. J. Compos. Mater. 2017, 51, 3969–3986. [Google Scholar] [CrossRef]
- Aranda, S.; Klunker, F.; Ziegmann, G. Influence of the Binding System on the Compaction Behaviour of NCF Carbon Fibre Reinforcements. In Proceedings of the ICCM 18: International Conferences on Composite Materials, Jeju, Republic of Korea, 21–26 August 2011; ICCM: Jeju, Republic of Korea, 2011. [Google Scholar]
- Schnurr, R.; Gabriel, F.; Beuscher, J.; Dröder, K. Model-Based Heating and Handling Strategy for Pre-Assembled Hybrid Fibre-Reinforced Metal-Thermoplastic Preforms. In Proceedings of the 2nd CIRP Conference on Composite Material Parts Manufacturing, Sheffield, UK, 10 October 2019; Advanced Manufacturing Research Centre: Sheffield, UK, 2019. [Google Scholar]
- Zinnecker, V.; Cardew-Hall, A.; Reghat, M.; Ravandi, M.; Di, P.A. Mechanical Characterisation of Influencing Material Properties of Dry Carbon Fibre Reinforcement in a Double Diaphragm Forming Process. In Proceedings of the AIAC 2023: 20th Australian International Aerospace Congress, Melbourne, Australia, 16 June 2023; Engineers Australia: Melbourne, Australia, 2023; pp. 569–574. [Google Scholar]
- Miris, G.; Ravandi, M.; Zinnecker, V.; Eisenbart, B.; Di, P.A. Process Modelling of an Aero-Grade Hyperelastic Membrane for Double Diaphragm Forming Operations. In Proceedings of the AIAC 2023: 20th Australian International Aerospace Congress, Melbourne, Australia, 16 June 2023; Engineers Australia: Melbourne, Australia, 2023; pp. 563–568. [Google Scholar]
- Reghat, M.; Ravandi, M.; Zinnecker, V.; Di Pietro, A. Through-Thickness Thermal Conductivity Characterisation of Dry Carbon Fibre Fabric. Mater. Lett. 2024, 361, 136116. [Google Scholar] [CrossRef]
- Kearney, P.; Lekakou, C.; Belcher, S. Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping. J. Compos. Sci. 2022, 6, 155. [Google Scholar] [CrossRef]
- Zhou, T.; Zhao, Y.; Rao, Z. Fundamental and Estimation of Thermal Contact Resistance between Polymer Matrix Composites: A Review. Int. J. Heat Mass Transf. 2022, 189, 122701. [Google Scholar] [CrossRef]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement Techniques for Thermal Conductivity and Interfacial Thermal Conductance of Bulk and Thin Film Materials. J. Electron. Packag. 2016, 138, 040802. [Google Scholar] [CrossRef]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal Conductivity Measurement Techniques for Characterizing Thermal Energy Storage Materials—A Review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Mohammadi, M.; Banks-Lee, P.; Ghadimi, P. Determining Radiative Heat Transfer Through Heterogeneous Multilayer Nonwoven Materials. Text. Res. J. 2003, 73, 896–900. [Google Scholar] [CrossRef]
- Guo, J.; Chen, X.N.; Qu, Z.G.; Ren, Q.L. Reverse Identification Method for Simultaneous Estimation of Thermal Conductivity and Thermal Contact Conductance of Multilayered Composites. Int. J. Heat Mass Transf. 2021, 173, 121244. [Google Scholar] [CrossRef]
- Yoshihiro, Y.; Hiroaki, Y.; Hajime, M. Effective Thermal Conductivity of Plain Weave Fabric and Its Composite Material Made from High Strength Fibers. J. Text. Eng. 2008, 54, 111–119. [Google Scholar]
- Zhang, H.; Wu, K.; Xiao, G.; Du, Y.; Tang, G. Experimental Study of the Anisotropic Thermal Conductivity of 2D Carbon-Fiber/Epoxy Woven Composites. Compos. Struct. 2021, 267, 113870. [Google Scholar] [CrossRef]
- Macías, J.D.; Bante-Guerra, J.; Cervantes-Alvarez, F.; Rodrìguez-Gattorno, G.; Arés-Muzio, O.; Romero-Paredes, H.; Arancibia-Bulnes, C.A.; Ramos-Sánchez, V.; Villafán-Vidales, H.I.; Ordonez- Miranda, J.; et al. Thermal Characterization of Carbon Fiber-Reinforced Carbon Composites (C/C). Appl. Compos. Mater. 2019, 26, 321–337. [Google Scholar] [CrossRef]
- Puszkarz, A.K.; Machnowski, W.; Błasińska, A. Modeling of Thermal Performance of Multilayer Protective Clothing Exposed to Radiant Heat. Heat Mass Transf. Waerme Stoffuebertragung 2020, 56, 1767–1775. [Google Scholar] [CrossRef]
- Renard, M.; Puszkarz, A.K. Modeling of Heat Transfer through Firefighters Multilayer Protective Clothing Using the Computational Fluid Dynamics Assisted by X-Ray Microtomography and Thermography. Materials 2022, 15, 5417. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Wang, L.L.; Cheng, Q.; Zhu, N.; Liu, Y. Thermal Analysis of Biomimic Woven Fabric Based on Finite Element Method. J. Therm. Anal. Calorim. 2015, 121, 737–742. [Google Scholar] [CrossRef]
- Yang, Y. Thermal Conductivity of Carbon Fibre Fabrics and Multi-Scale Composites with Heat Transfer Simulations for RFI Manufacturing. Master’s Thesis, Université d’Ottawa/University of Ottawa, Ottawa, ON, Canada, 2013. [Google Scholar]
- Ma, Q.; Wang, K.; Wang, S.; Zhou, H.; Jin, L.; Yi, H.; Wu, X. Fea-Based Structural Heat Transfer Characteristic of 3-D Orthogonal Woven Composite Subjected to the Non-Uniform Heat Load. Autex Res. J. 2021, 23, 110–115. [Google Scholar] [CrossRef]
- Siddiqui, M.O.R.; Sun, D.; Butler, I.B. Geometrical Modelling and Thermal Analysis of Nonwoven Fabrics. J. Ind. Text. 2018, 48, 405–431. [Google Scholar] [CrossRef]
- Yu, H.; Heider, D.; Advani, S. Comparison of Two Finite Element Homogenization Prediction Approaches for through Thickness Thermal Conductivity of Particle Embedded Textile Composites. Compos. Struct. 2015, 133, 719–726. [Google Scholar] [CrossRef]
- Penide-Fernandez, R.; Sansoz, F. Anisotropic Thermal Conductivity under Compression in Two-Dimensional Woven Ceramic Fibers for Flexible Thermal Protection Systems. Int. J. Heat Mass Transf. 2019, 145, 118721. [Google Scholar] [CrossRef]
- Iqbal, K.; Sun, D.; Stylios, G.K.; Lim, T.; Corne, D.W. FE Analysis of Thermal Properties of Woven Fabric Constructed by Yarn Incorporated with Microencapsulated Phase Change Materials. Fibers Polym. 2015, 16, 2497–2503. [Google Scholar] [CrossRef]
- Yang, Y.; Qian, J.; Chen, Y. Multi-Scale Modeling and Thermal Transfer Properties of Electric Heating Fabrics System. Int. J. Cloth. Sci. Technol. 2019, 31, 825–838. [Google Scholar] [CrossRef]
- Gou, J.J.; Zhang, H.; Dai, Y.J.; Li, S.; Tao, W.Q. Numerical Prediction of Effective Thermal Conductivities of 3D Four-Directional Braided Composites. Compos. Struct. 2015, 125, 499–508. [Google Scholar] [CrossRef]
- Liu, T.; Chen, M.; Dong, J.; Sun, R.; Yao, M. Numerical Simulation and Experiment Verified for Heat Transfer Processes of High-Property Inorganic Fiber Woven Fabrics. Text. Res. J. 2022, 92, 2368–2378. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Li, Y.; Wang, H.; Wang, P.; Zhang, Y. The Through-Thickness Thermal Conductivity and Heat Transport Mechanism of Carbon Fiber Three-Dimensional Orthogonal Woven Fabric Composite. J. Text. Inst. 2024, 115, 308–315. [Google Scholar] [CrossRef]
- Hind, S.; Robitaille, F. Measurement, Modeling, and Variability of Thermal Conductivity for Structural Polymer Composites. Polym. Compos. 2010, 31, 847–857. [Google Scholar] [CrossRef]
- Verma, N.N.; Mazumder, S. Extraction of Thermal Contact Conductance of Metal-Metal Contacts from Scale-Resolved Direct Numerical Simulation. Int. J. Heat Mass Transf. 2016, 94, 164–173. [Google Scholar] [CrossRef]
- Siddappa, P.G.; Tariq, A. Contact Area and Thermal Conductance Estimation Based on the Actual Surface Roughness Measurement. Tribol. Int. 2020, 148, 106358. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, F.; Zhuang, X.; Zhao, Z. Calibration of Thermal Contact Conductance for Precision Forming. Procedia Manuf. 2020, 50, 459–463. [Google Scholar] [CrossRef]
- Yuan, W.B.; Yu, N.; Li, L.Y.; Fang, Y. Heat Transfer Analysis in Multi-Layered Materials with Interfacial Thermal Resistance. Compos. Struct. 2022, 293, 115728. [Google Scholar] [CrossRef]
- Levy, A.; Heider, D.; Tierney, J.; Gillespie, J.W. Inter-Layer Thermal Contact Resistance Evolution with the Degree of Intimate Contact in the Processing of Thermoplastic Composite Laminates. J. Compos. Mater. 2014, 48, 491–503. [Google Scholar] [CrossRef]
- Ding, C.; Wang, R. Experimental Investigation of Thermal Contact Conductance across GFRP–GFRP Joint. Heat Mass Transf. 2015, 51, 433–439. [Google Scholar] [CrossRef]
- Aalilija, A.; Gandin, C.A.; Hachem, E. A Simple and Efficient Numerical Model for Thermal Contact Resistance Based on Diffuse Interface Immersed Boundary Method. Int. J. Therm. Sci. 2021, 166, 106817. [Google Scholar] [CrossRef]
- Mohebbi, F.; Sellier, M.; Rabczuk, T. Estimation of Linearly Temperature-Dependent Thermal Conductivity Using an Inverse Analysis. Int. J. Therm. Sci. 2017, 117, 68–76. [Google Scholar] [CrossRef]
- Chanda, S.; Balaji, C.; Venkateshan, S.P. Non-Intrusive Measurement of Thermal Contact Conductance at Polymer-Metal Two Dimensional Annular Interface. Heat Mass Transf. 2019, 55, 327–340. [Google Scholar] [CrossRef]
- Liu, F.-B. A Hybrid Method for the Inverse Heat Transfer of Estimating Fluid Thermal Conductivity and Heat Capacity. Int. J. Therm. Sci. 2011, 50, 718–724. [Google Scholar] [CrossRef]
- Saunders, R.A.; Lekakou, C.; Bader, M.G. Compression and Microstructure of Fibre Plain Woven Cloths in the Processing of Polymer Composites. Compos. Part Appl. Sci. Manuf. 1998, 29, 443–454. [Google Scholar] [CrossRef]
- Ito, M.; Chou, T.-W. An Analytical and Experimental Study of Strength and Failure Behavior of Plain Weave Composites. J. Compos. Mater. 1998, 32, 2–30. [Google Scholar] [CrossRef]
- Holman, J.P. Heat Transfer-Si Units-Sie, 10th ed.; Tata McGraw-Hill Education: Blacklick, OH, USA, 2009; ISBN 10: 0073529362. [Google Scholar]
- Faghri, A.; Zhang, Y. Flow and Heat Transfer in Porous Media. In Fundamentals of Multiphase Heat Transfer and Flow; Faghri, A., Zhang, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 687–745. ISBN 978-3-030-22137-9. [Google Scholar]
- El-Hage, Y.; Hind, S.; Robitaille, F. Thermal Conductivity of Textile Reinforcements for Composites. J. Text. Fibrous Mater. 2018, 1, 2515221117751154. [Google Scholar] [CrossRef]







| Material (Units) | Conductivity | Specific Heat | Density |
|---|---|---|---|
| (kT) W/m °C | (cP) J/g °C | (ρ) kg/m3 | |
| Carbon fibre (CF) + 3.6 wt% binder | 0.0835 | (0 ≤ T ≤ 85 °C) | Vf1 × PCF |
| (85 ≤ T ≤ 150 °C) | |||
| Silicone | 0.238 | (0 ≤ T ≤ 200 °C) | 1150 |
| Parameter (Units) | Magnitude | Standard Deviation |
|---|---|---|
| Contact area (mm2) | 14,609.57 | 1828.15 |
| MTS compaction load (kN) | 1.48 | 0.185 |
| Equivalent vacuum pressure (MPa) | 0.1013 | 0.012 |
| Ply Count (n) | Preform Thickness (H) | Per Layer Thickness (l) | Areal Weight * | Fabric Density | Fibre Density * | Volume Fraction |
|---|---|---|---|---|---|---|
| mm | mm | g/m2 | kg/m3 | kg/m3 | ||
| 12 | 2.82 | 0.235 | 204 | 865.99 | 1800 | 0.48 |
| 24 | 5.17 | 0.215 | 204 | 946.54 | 1800 | 0.52 |
| 48 | 10.41 | 0.217 | 204 | 940.11 | 1800 | 0.52 |
| 96 | 20.21 | 0.211 | 204 | 968.81 | 1800 | 0.53 |
| Mean | 929.5 | 0.51 |
| Parameter | Symbol (Units) | 12—Ply | 24—Ply | 48—Ply | 96—Ply | |
|---|---|---|---|---|---|---|
| Material inputs | Ply conductivity * | k (W/m °C) | 0.835 | |||
| Density | ρ (kg/m3) | 865.9 | 946.5 | 940.1 | 968.8 | |
| Specific heat * | Vf × cp (J/kg °C) | 48% | 52% | 52% | 53% | |
| Process step definitions | Step time | t (s) | 3200 | 3250 | 4500 | 4600 |
| Min increment | tmin (s) | 5.00 × 10−5 | ||||
| Interaction definitions | TCC | hc (W/m2 °C) | x1 | x2 | x3 | x4 |
| No. of contact interactions | - | 11 | 23 | 47 | 95 | |
| Emissivity | ε (N/a) | 0.3 | ||||
| Convection | h (W/m2 °C) | 3.3 | ||||
| Mesh | Edge seeds | Thickness | 4 | |||
| Element type | Quad Shell | DC2D4 | ||||
| Total elements in assembly | N/A | 11,200 | 22,400 | 44,800 | 89,600 | |
| Parameter | Symbol (Units) | 30-ply | 60-ply | Silicone | Tool | Heaters | |
|---|---|---|---|---|---|---|---|
| Material inputs | Bulk conductivity | Ke (W/m °C) | 0.078 | 0.076 | 0.238 | 55 * | 0.216 * |
| Density | ρ (kg/m3) | 925 | 946.5 | 1150 * | 7870 * | 1249.6 * | |
| Specific heat | Vf × cp (J/kg °C) | 51.4% | 52.6% | Measured | 508 * | 1880 * | |
| Step definitions | Step time | t (s) | 4500 | ||||
| Min increment | tmin (s) | 0.001 | |||||
| Max increment | tmax (s) | 10 | |||||
| Interaction Mesh | Emissivity | ε | - | - | 0.85 | 0.3 | - |
| Convection | h (W/m2 °C) | - | - | 7 | 4 | - | |
| Edge seeds | Thickness | 8 | 8 | 6 | 6 | 8 | |
| Nodes | - | 5940 | 5940 | 220,624 | 11,970 | 42,678 | |
| Mesh | Edge seeds | Thickness | 8 | 8 | 6 | 6 | 8 |
| Nodes | - | 5940 | 5940 | 220,624 | 11,970 | 42,678 | |
| Elements | - | 4816 | 4816 | 191,096 | 9768 | 35,704 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dandangi, S.; Ghanei, S.; Ravandi, M.; Naser, J.; Di Pietro, A. Heat Transfer Analysis in Double Diaphragm Preforming Process of Dry Woven Carbon Fibres. Energies 2025, 18, 1471. https://doi.org/10.3390/en18061471
Dandangi S, Ghanei S, Ravandi M, Naser J, Di Pietro A. Heat Transfer Analysis in Double Diaphragm Preforming Process of Dry Woven Carbon Fibres. Energies. 2025; 18(6):1471. https://doi.org/10.3390/en18061471
Chicago/Turabian StyleDandangi, Srikara, Sadegh Ghanei, Mohammad Ravandi, Jamal Naser, and Adriano Di Pietro. 2025. "Heat Transfer Analysis in Double Diaphragm Preforming Process of Dry Woven Carbon Fibres" Energies 18, no. 6: 1471. https://doi.org/10.3390/en18061471
APA StyleDandangi, S., Ghanei, S., Ravandi, M., Naser, J., & Di Pietro, A. (2025). Heat Transfer Analysis in Double Diaphragm Preforming Process of Dry Woven Carbon Fibres. Energies, 18(6), 1471. https://doi.org/10.3390/en18061471







