Energy Trading Strategies for Integrated Energy Systems Considering Uncertainty
Abstract
1. Introduction
- (1)
- A four-level robust optimization model is developed for the IES to improve the stability of system’s operation. This model comprehensively considers the probability distribution scenarios of renewable energy and the uncertainty of its output, while employing multiple interval uncertainty sets to ensure that the scheduling results are closer to actual conditions.
- (2)
- A column-and-constraint generation (C&CG) algorithm based on an alternating iteration strategy (AIS) is proposed to address the issue of excessive iterations due to the nonlinear terms in the subproblems. This method effectively reduces the number of iterations and ensures efficient problem-solving.
- (3)
- The Nash–Harsanyi method is used to resolve the issue of benefit allocation among multiple IESs. This method considers the bargaining power of each IES, effectively encouraging active participation in energy cooperation.
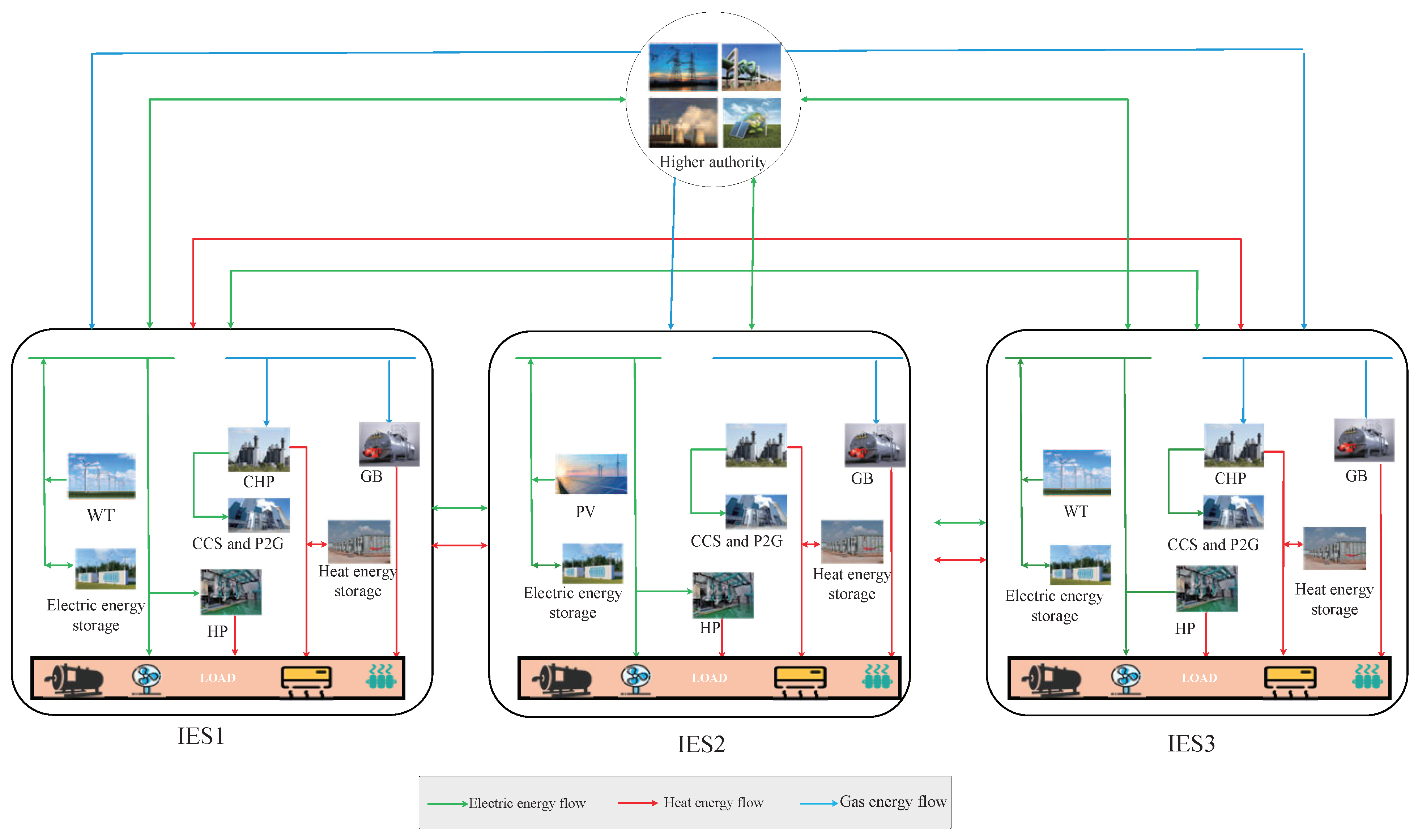
2. System Model
2.1. Model Constraints
- (1)
- CHP model.
- (2)
- GB model.
- (3)
- HP model.
- (4)
- Energy trading with the grid model.
- (5)
- Energy storage model.
- (6)
- CCS and P2G model
- (7)
- Power balance constraint
2.2. Objective Function
3. Development and Solution of Four-Level Robust Optimization Model
3.1. Construction of Uncertainty Set
3.2. Four-Level Robust Model
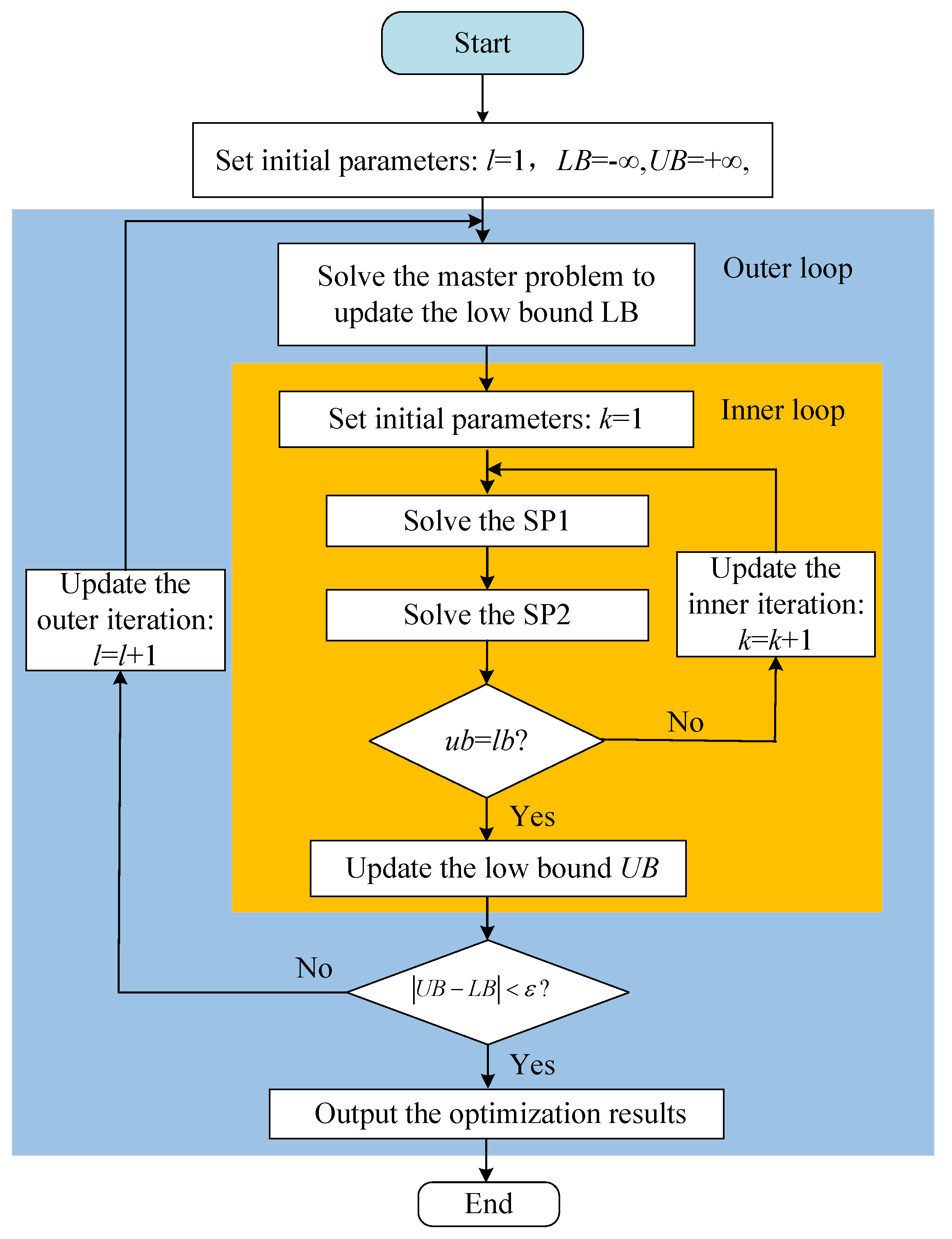
3.3. Solution Method
- (1)
- Master problem
- (2)
- Subproblem
- (a)
- -fixed bi-lever subproblem (SP1)
- (b)
- u-fixed bi-level subproblem (SP2):
4. Establishment and Solution of Cooperative Model
4.1. Model Establishment
4.2. Equivalent Model
- (1)
- Marginal contribution rate:
- (2)
- Energy trading contribution rate:
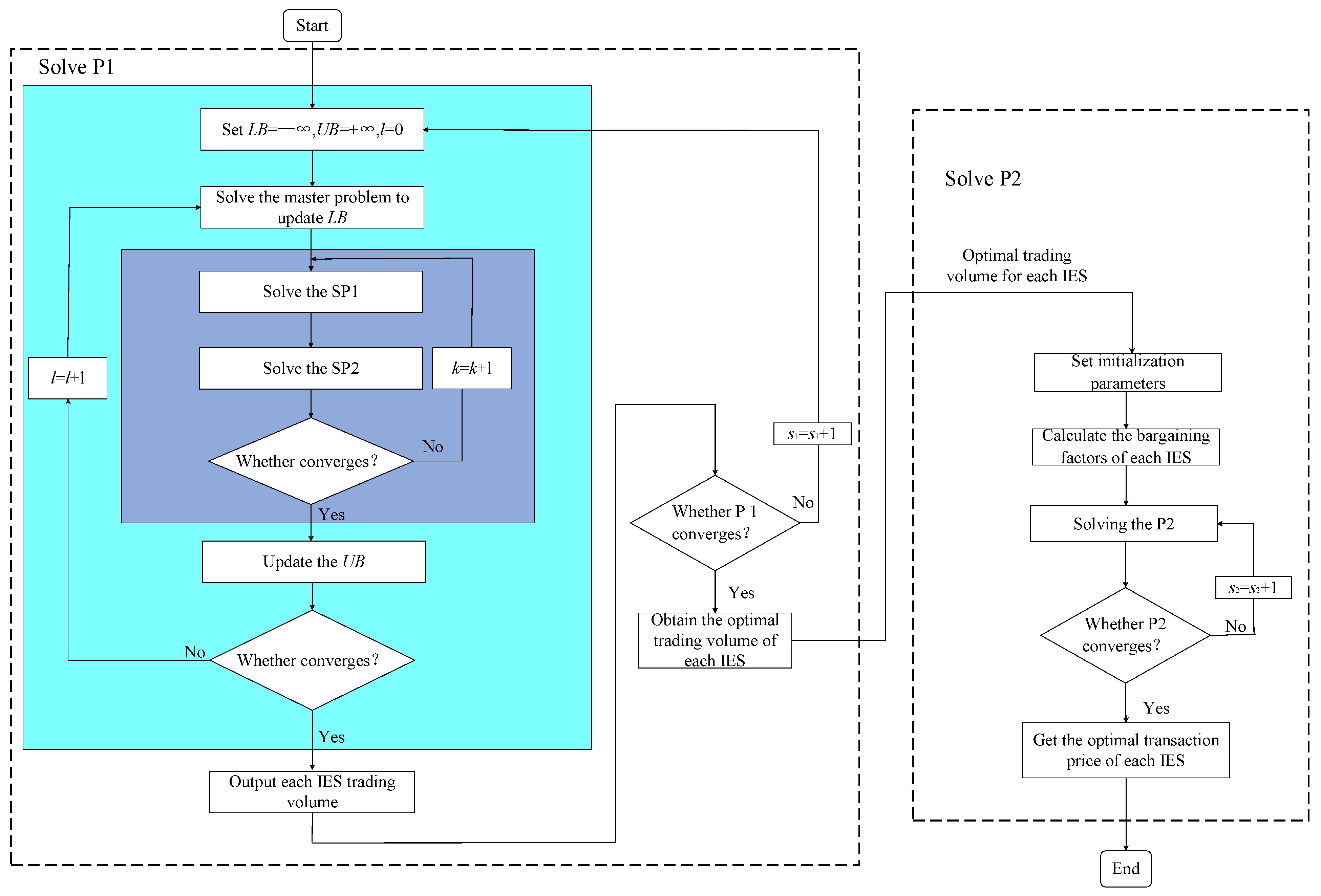
4.3. Model Solution Method
5. Case Study
5.1. Test System Description
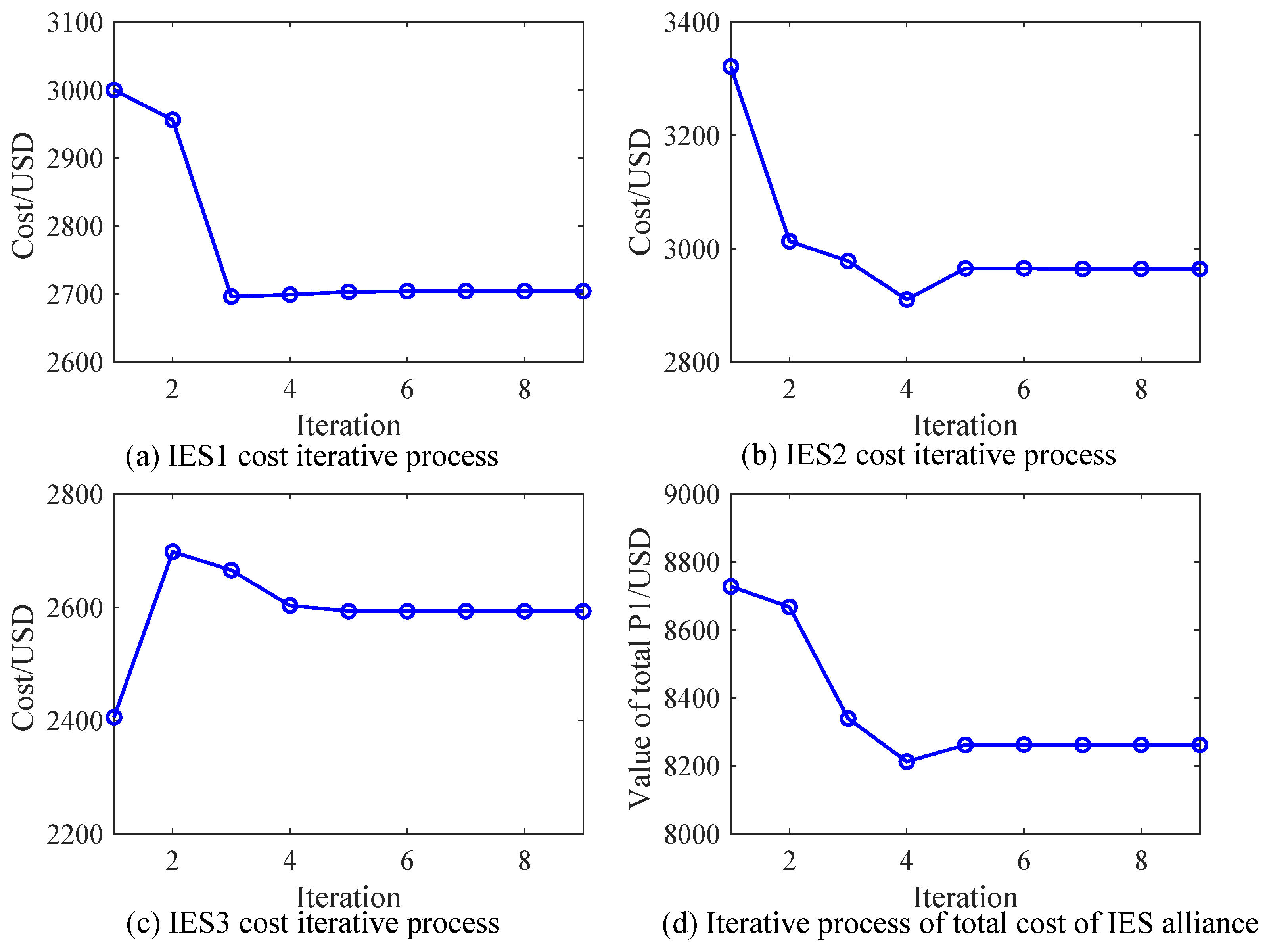
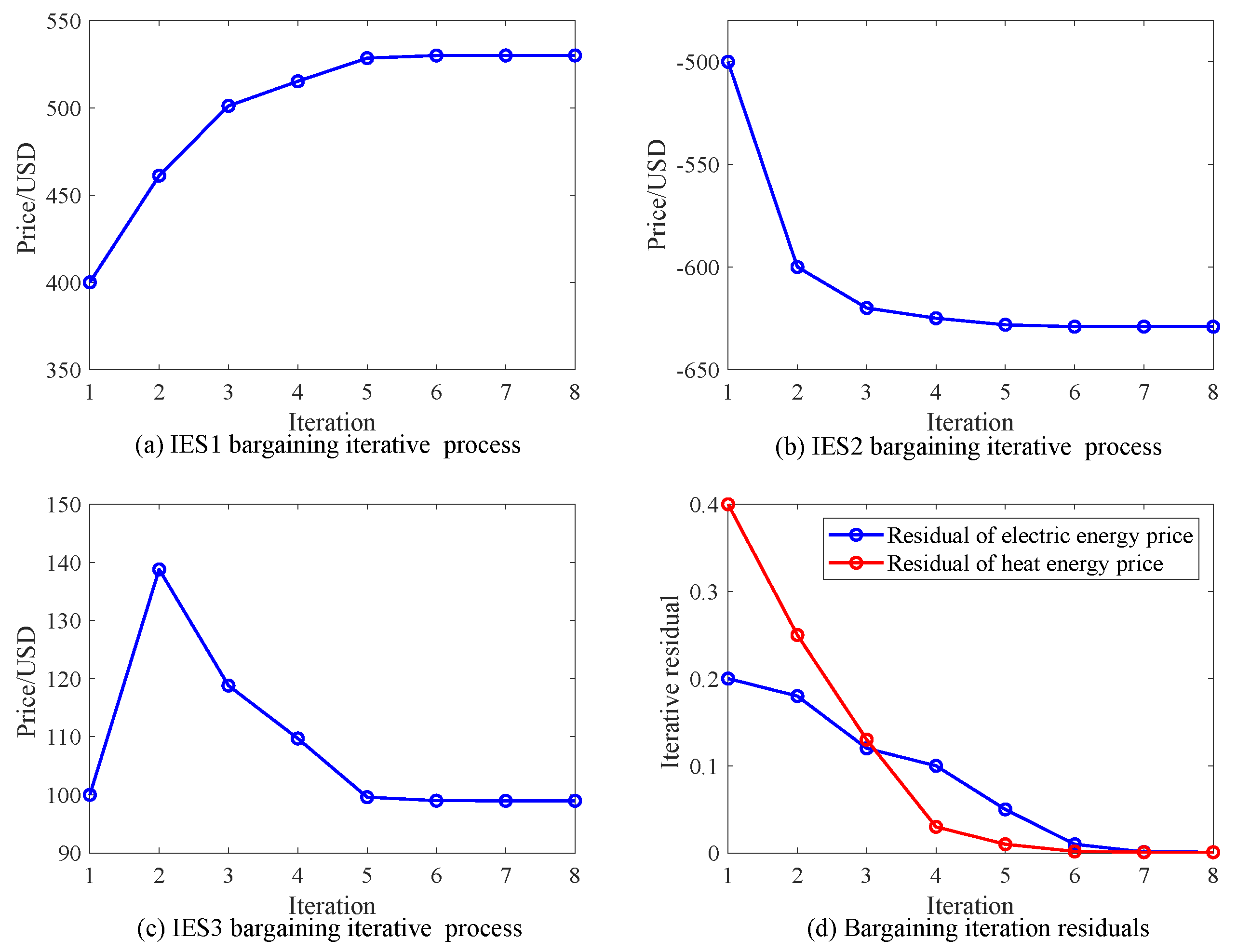
5.2. Algorithm Convergence Analysis
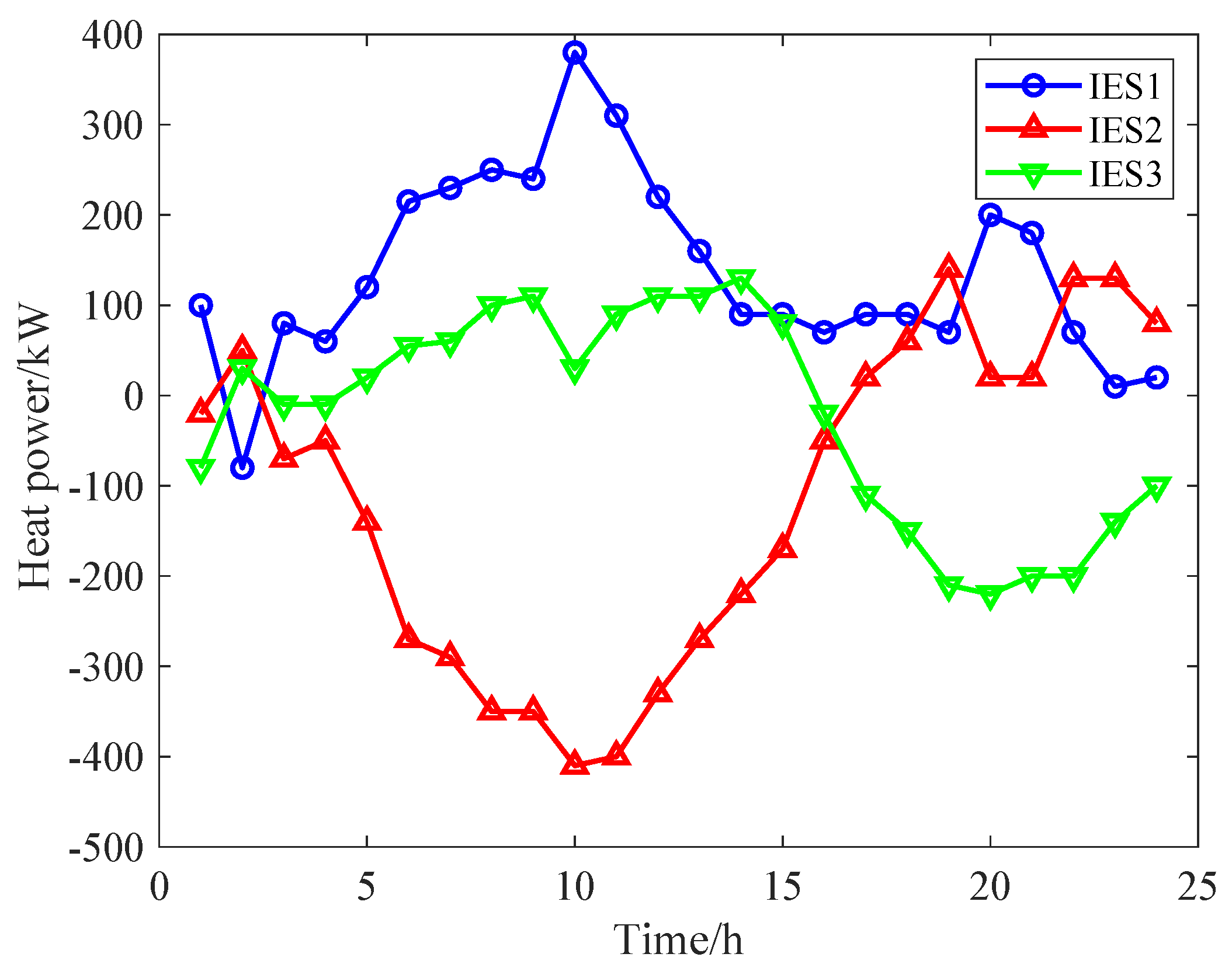
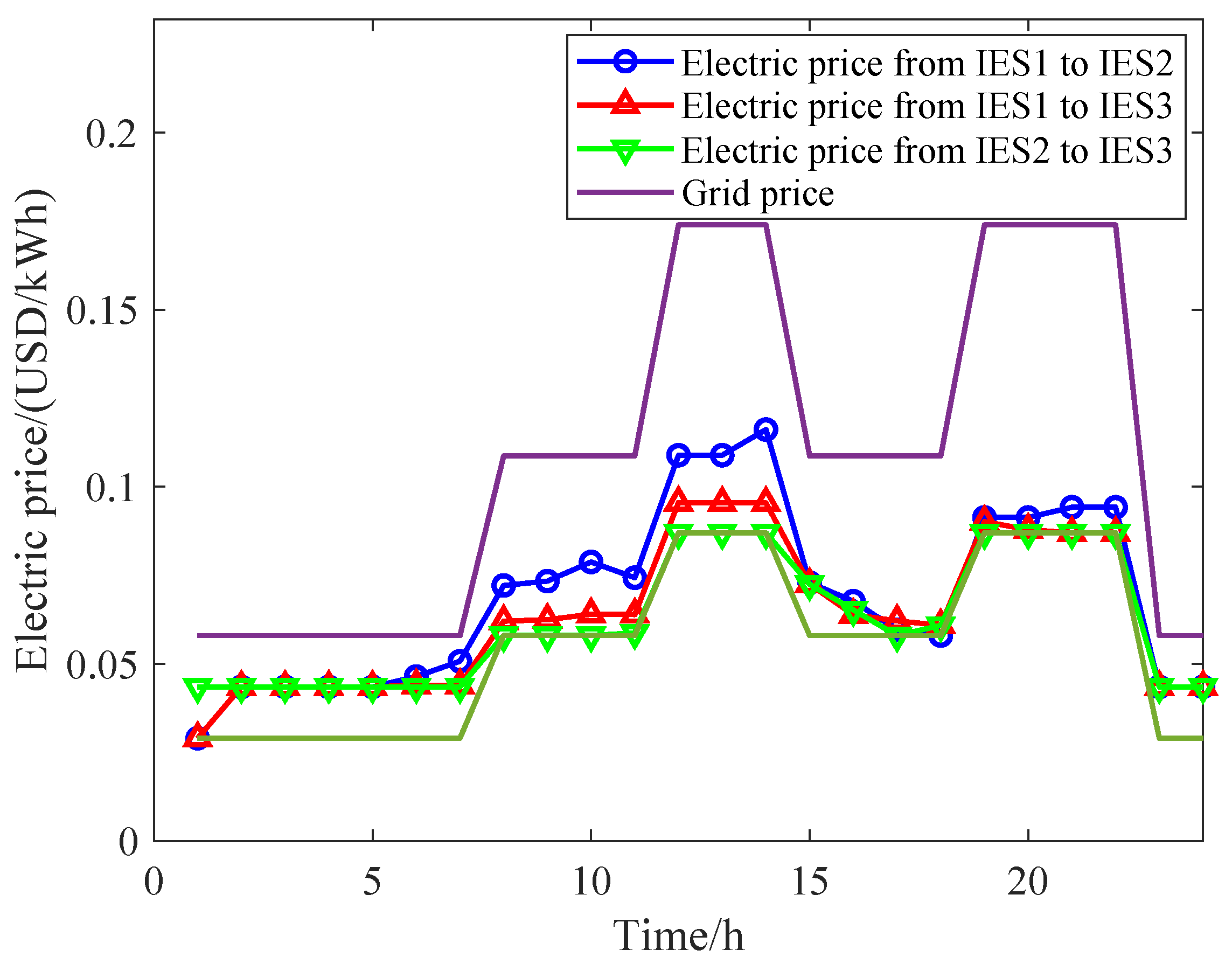
5.3. Optimization Results of Nash Bargaining
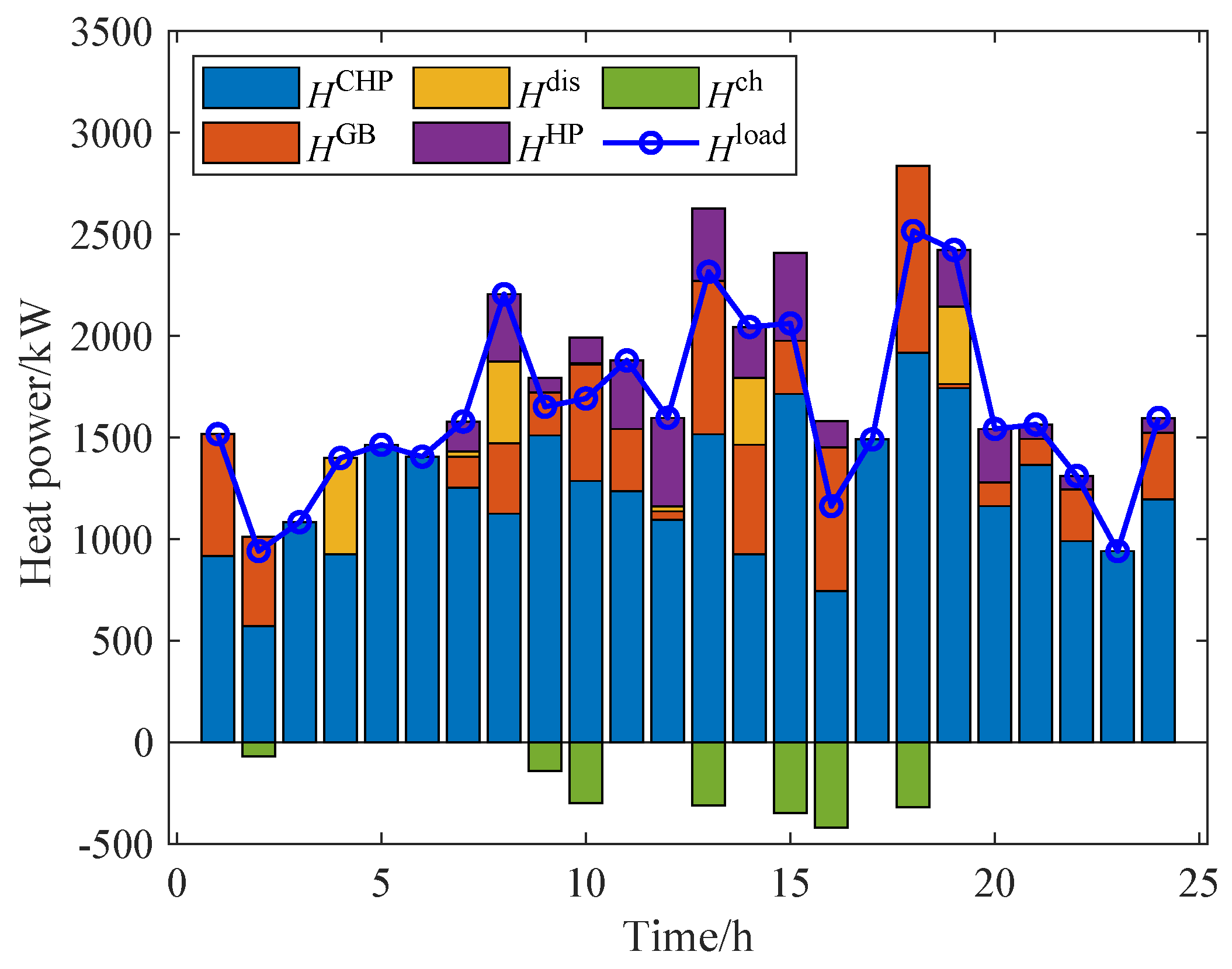
5.4. Benefit and Cost Analysis
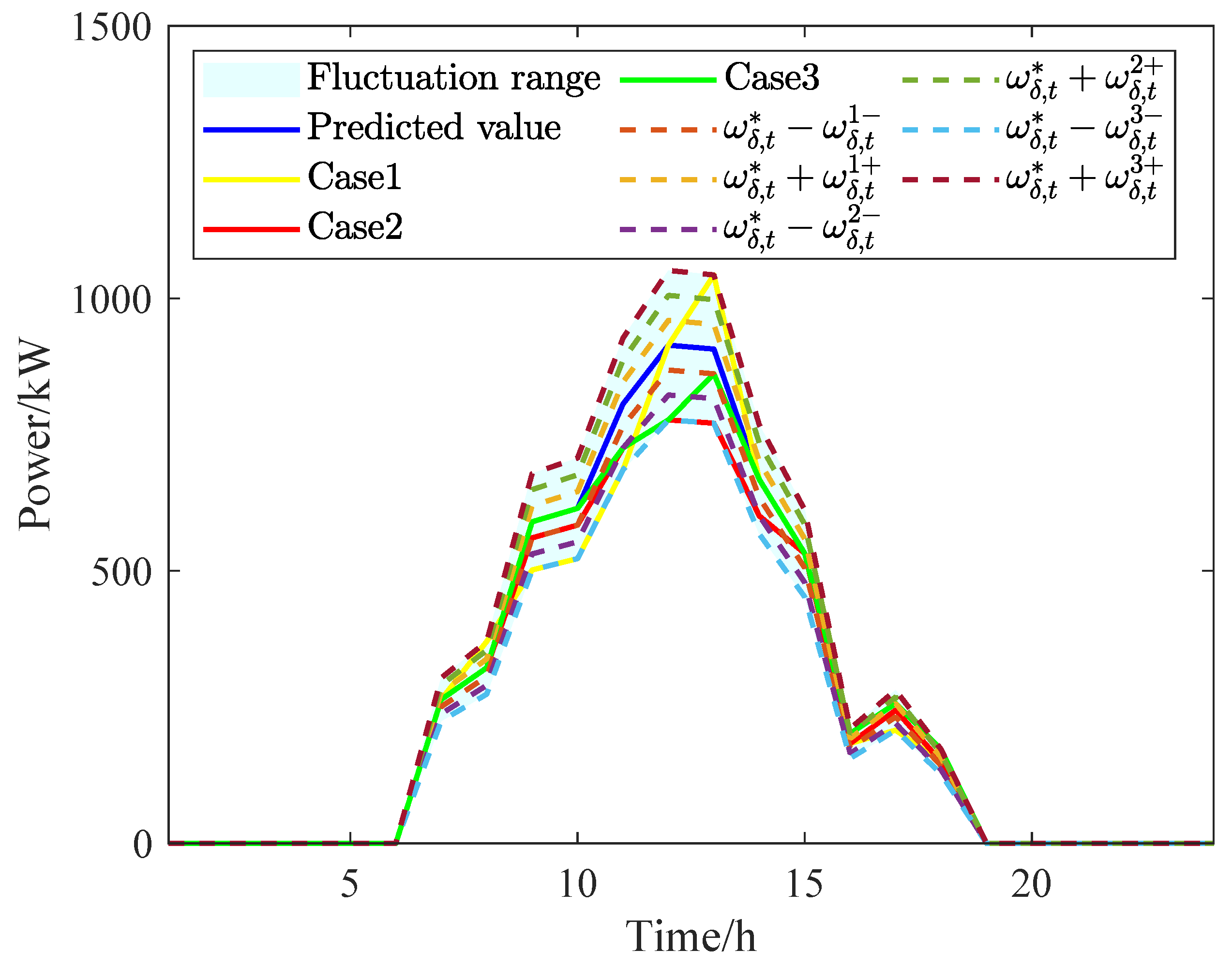
5.5. Uncertainty Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yang, H.; Chu, Y.; Ma, Y.; Zhang, D. Operation strategy and optimization configuration of hybrid energy storage system for enhancing cycle life. J. Energy Storage 2024, 95, 112560. [Google Scholar] [CrossRef]
- Liu, S.; Shen, J.; Zhang, J. A novel configuration optimization approach for IES considering exergy-degradation and non-energy costs of equipment. Energy 2024, 312, 133600. [Google Scholar] [CrossRef]
- Chu, X.; Fu, L.; Liu, Q.; Yu, S. Optimal allocation method of oxygen enriched combustion-carbon capture low-carbon integrated energy system considering uncertainty of carbon-source-load. Int. J. Electr. Power Energy Syst. 2024, 162, 110220. [Google Scholar] [CrossRef]
- Ghafoor, A.; Aldahmashi, J.; Apsley, J.; Djurović, S.; Ma, X.; Benbouzid, M. Intelligent Integration of Renewable Energy Resources Review: Generation and Grid Level Opportunities and Challenges. Energies 2024, 17, 4399. [Google Scholar] [CrossRef]
- Wu, X.; Yang, L.; Zheng, B. Joint capacity configuration and demand response optimization of integrated energy system considering economic and dynamic control performance. Energy 2024, 301, 131723. [Google Scholar] [CrossRef]
- Ren, X.Y.; Li, L.L. Optimization and performance analysis of integrated energy systems considering hybrid electro-thermal energy storage. Energy 2024, 2024, 134172. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Z.; Shi, Z. Low carbon economic dispatch of integrated energy systems considering utilization of hydrogen and oxygen energy. Int. J. Electr. Power Energy Syst. 2024, 158, 109923. [Google Scholar] [CrossRef]
- Dou, J.; Wang, X.; Liu, Z.; Sun, Q.; Wang, X.; He, J. Towards Pareto-optimal energy management in integrated energy systems: A multi-agent and multi-objective deep reinforcement learning approach. Int. J. Electr. Power Energy Syst. 2024, 159, 110022. [Google Scholar] [CrossRef]
- Li, J.; Wu, Y.; Ma, S.; Zhang, J.; Sun, X. Multi-objective optimization scheduling of integrated energy systems considering regional time-of-use electricity prices and weight sensitivity. Electr. Power Syst. Res. 2024, 236, 110905. [Google Scholar] [CrossRef]
- Zhou, C.; Zheng, C.B. Energy Trading Strategy for Heat and Electricity-Coupled Microgrid Based on Cooperative Game. Appl. Sci. 2022, 12, 6568. [Google Scholar] [CrossRef]
- Chen, J.; Tang, Z.; Huang, Y.; Qiao, A.; Liu, J. Asymmetric Nash bargaining-based cooperative energy trading of multi-park integrated energy system under carbon trading mechanism. Electr. Power Syst. Res. 2024, 228, 110033. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Q.; Ren, H.; Li, Q.; Zhou, W. A multi-agent distributed electricity-carbon shared trading strategy considering regional carbon inclusion. Renew. Energy 2024, 239, 122075. [Google Scholar] [CrossRef]
- Chen, W.; Wang, J.; Yu, G.; Chen, J.; Hu, Y. Research on day-ahead transactions between multi-microgrid based on cooperative game model. Appl. Energy 2022, 316, 119106. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, B.; Liu, N.; Wu, Q.; Voropai, N.; Li, C.; Barakhtenko, E. Peer-to-peer multienergy and communication resource trading for interconnected microgrids. IEEE Trans. Ind. Inform. 2020, 17, 2522–2533. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Song, W.; Li, Q. Stochastic cooperative bidding strategy for multiple microgrids with peer-to-peer energy trading. IEEE Trans. Ind. Inform. 2021, 18, 1447–1457. [Google Scholar] [CrossRef]
- Singh, K.; Gadh, R.; Singh, A.; Dewangan, C.L. Design of an optimal P2P energy trading market model using bilevel stochastic optimization. Appl. Energy 2022, 328, 120193. [Google Scholar] [CrossRef]
- Khan, S.S.; Ahmad, S.; Naeem, M. On-grid joint energy management and trading in uncertain environment. Appl. Energy 2023, 330, 120318. [Google Scholar] [CrossRef]
- Gao, J.; Shao, Z.; Chen, F.; Chen, Y.; Lin, Y.; Deng, H. Distributed robust operation strategy of multi-microgrid based on peer-to-peer multi-energy trading. Iet Energy Syst. Integr. 2023, 5, 376–392. [Google Scholar] [CrossRef]
- Siqin, Z.; Niu, D.; Wang, X.; Zhen, H.; Li, M.; Wang, J. A two-stage distributionally robust optimization model for P2G-CCHP microgrid considering uncertainty and carbon emission. Energy 2022, 260, 124796. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Zhao, Q.; Dong, S.; Li, H. Optimal dispatch of integrated energy station considering carbon capture and hydrogen demand. Energy 2023, 269, 126981. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Y.; Cao, Y.; Tan, Y.; Peng, Y.; Zhou, Y.; Nakanishi, Y.; Li, Z. Robust coordinated optimization with adaptive uncertainty set for a multi-energy microgrid. IEEE Trans. Sustain. Energy 2022, 14, 111–124. [Google Scholar] [CrossRef]
- Gao, J.; Shao, Z.; Chen, F.; Lak, M. Robust optimization for integrated energy systems based on multi-energy trading. Energy 2024, 308, 132302. [Google Scholar] [CrossRef]





| Ref | Bargaining Power | Uncertainties | Probability Distribution Scenarios | Privacy Protection |
|---|---|---|---|---|
| [5] | × | × | × | × |
| [6] | × | × | × | × |
| [7] | × | √ | × | × |
| [8] | × | × | × | × |
| [9] | × | × | × | × |
| [10] | × | × | × | √ |
| [11] | √ | × | × | √ |
| [12] | × | × | × | √ |
| [13] | × | × | × | √ |
| [14] | × | × | × | √ |
| [15] | × | × | √ | × |
| [16] | × | × | √ | × |
| [17] | × | √ | × | × |
| [18] | √ | √ | × | √ |
| [19] | × | √ | × | × |
| Proposed strategy | √ | √ | √ | √ |
| Parameters | Value |
|---|---|
| , | 0.35, 0.9 |
| , | 0.9, 4.5 |
| , | 0.01, 0.01 |
| , | 100, 100 |
| 2500 | |
| 2500 | |
| 1000 | |
| 2000 | |
| 2.7 | |
| , | 0.4, 0.2 |
| g | 0.1 |
| , | 0.5, 0.55 |
| IES Number | IES1 | IES2 | IES3 |
|---|---|---|---|
| Cost before cooperation/USD | 2630.1 | 3912.5 | 2880.3 |
| Final cost/USD | 2174.2 | 3593.4 | 2495.1 |
| Increase value/USD | 455.9 | 319.1 | 385.2 |
| Methods | IESs Number | Revenue/USD | Increased Percentage |
|---|---|---|---|
| Nash solution | IES1 | 303.1 | 33.2% |
| IES2 | 305.2 | 33.4% | |
| IES3 | 303.9 | 33.3% | |
| Shapley value method | IES1 | 478.2 | 41.7% |
| IES2 | 273.5 | 23.9% | |
| IES3 | 394.1 | 34.4% | |
| Method of this paper | IES1 | 455.9 | 39.3% |
| IES2 | 319.1 | 27.5% | |
| IES3 | 385.2 | 33.2% |
| C&CG (Gap = 0) | C&CG (Default Gap) | C&CG-AIS | |
|---|---|---|---|
| Solver | Baron | Baron | Gurobi |
| Solving time/s | — | 4351.19 | 56.38 |
| Cost/USD | — | 2618.8 | 2630.1 |
| Outer/inner loop iterations | — | 3/— | 3/(2;3;2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Shao, Z.; Chen, F.; Lak, M. Energy Trading Strategies for Integrated Energy Systems Considering Uncertainty. Energies 2025, 18, 935. https://doi.org/10.3390/en18040935
Gao J, Shao Z, Chen F, Lak M. Energy Trading Strategies for Integrated Energy Systems Considering Uncertainty. Energies. 2025; 18(4):935. https://doi.org/10.3390/en18040935
Chicago/Turabian StyleGao, Jin, Zhenguo Shao, Feixiong Chen, and Mohammadreza Lak. 2025. "Energy Trading Strategies for Integrated Energy Systems Considering Uncertainty" Energies 18, no. 4: 935. https://doi.org/10.3390/en18040935
APA StyleGao, J., Shao, Z., Chen, F., & Lak, M. (2025). Energy Trading Strategies for Integrated Energy Systems Considering Uncertainty. Energies, 18(4), 935. https://doi.org/10.3390/en18040935






