Novel Topological Aggregation Method for Grid-Forming Converters of Renewable Energy with Threshold Correction
Abstract
1. Introduction
2. Principle of Virtual Synchronous Generator (VSG)
2.1. Power Control Loop of the VSG
2.1.1. Active Power–Frequency Control
2.1.2. Reactive Power–Voltage Control
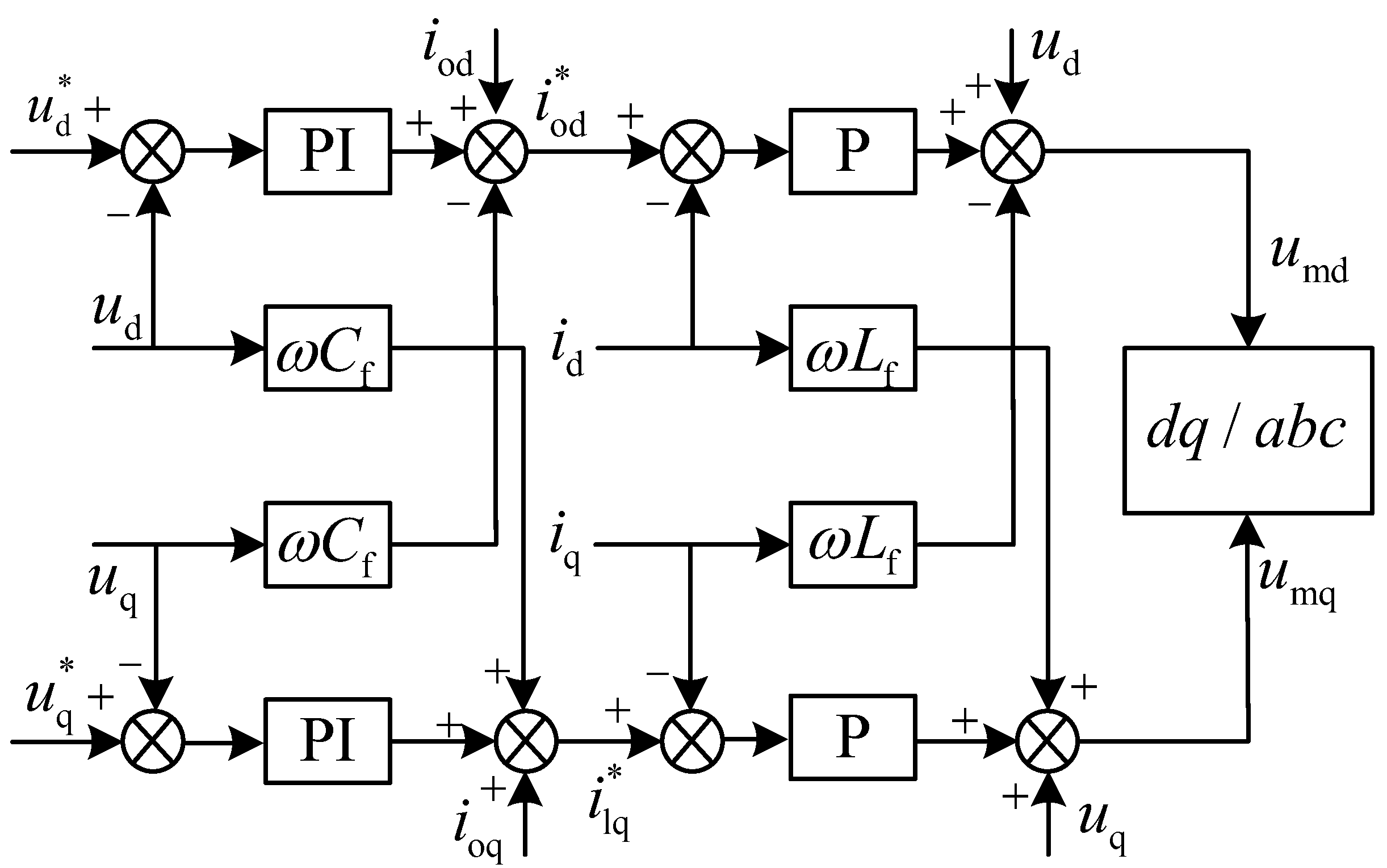
2.1.3. Voltage–Current Dual-Loop Control
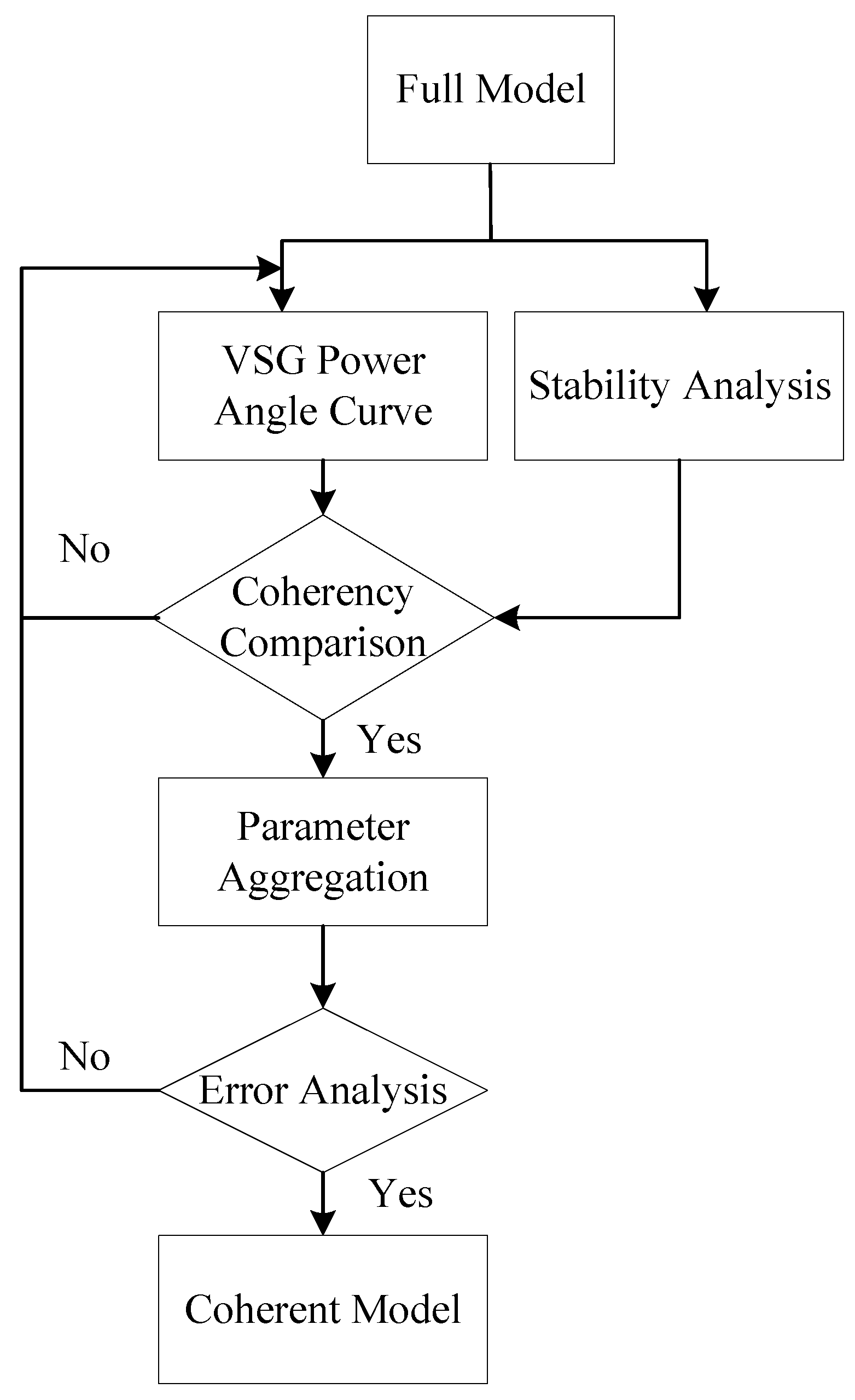
3. Coherent Identification Method Based on Stability Margin Correction
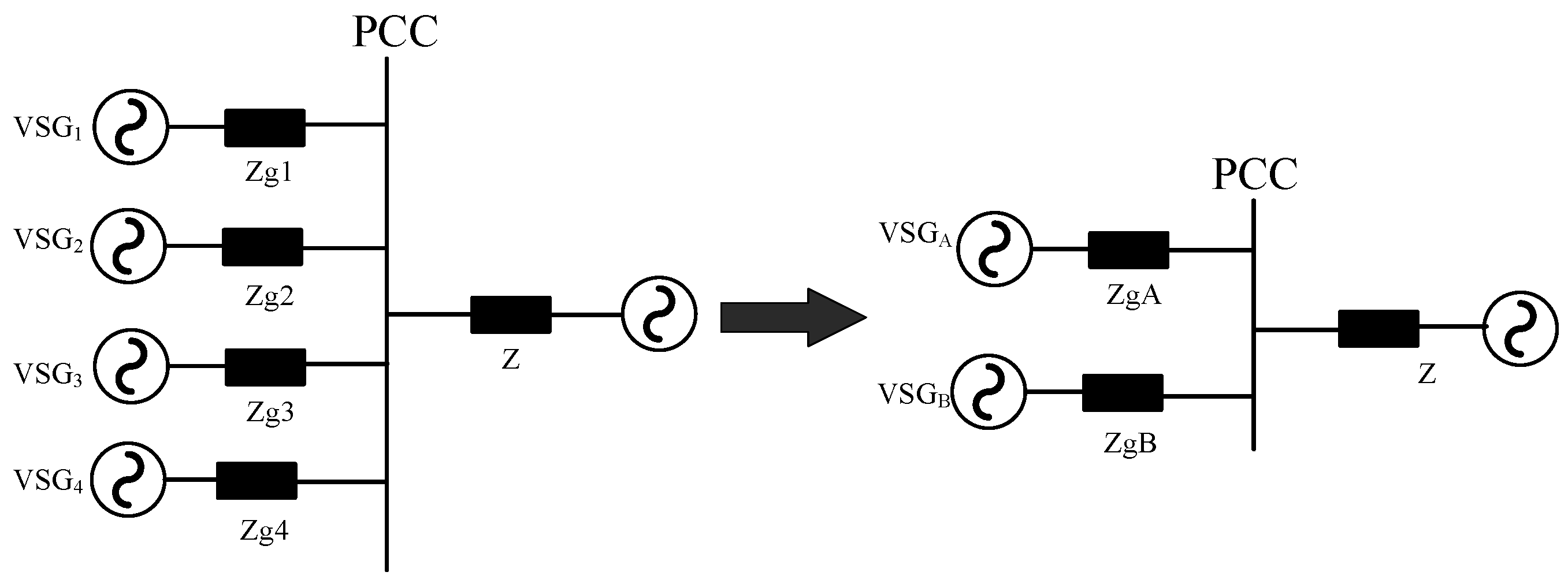
3.1. Homological Equivalence Method for VSGs
3.2. Time Window Determination
3.3. Threshold Determination
4. VSG Equivalent Aggregation Modeling
4.1. Aggregation of Control Parameters for Homological VSGs
4.1.1. Aggregation of Active Power Loop Control Parameters
4.1.2. Aggregation of Reactive Power Loop Control Parameters
4.1.3. Aggregation of Voltage–Current Dual-Loop Control Parameters
4.2. Aggregation of Main Circuit Parameters
5. Simulation Verification
5.1. Original System Parameters
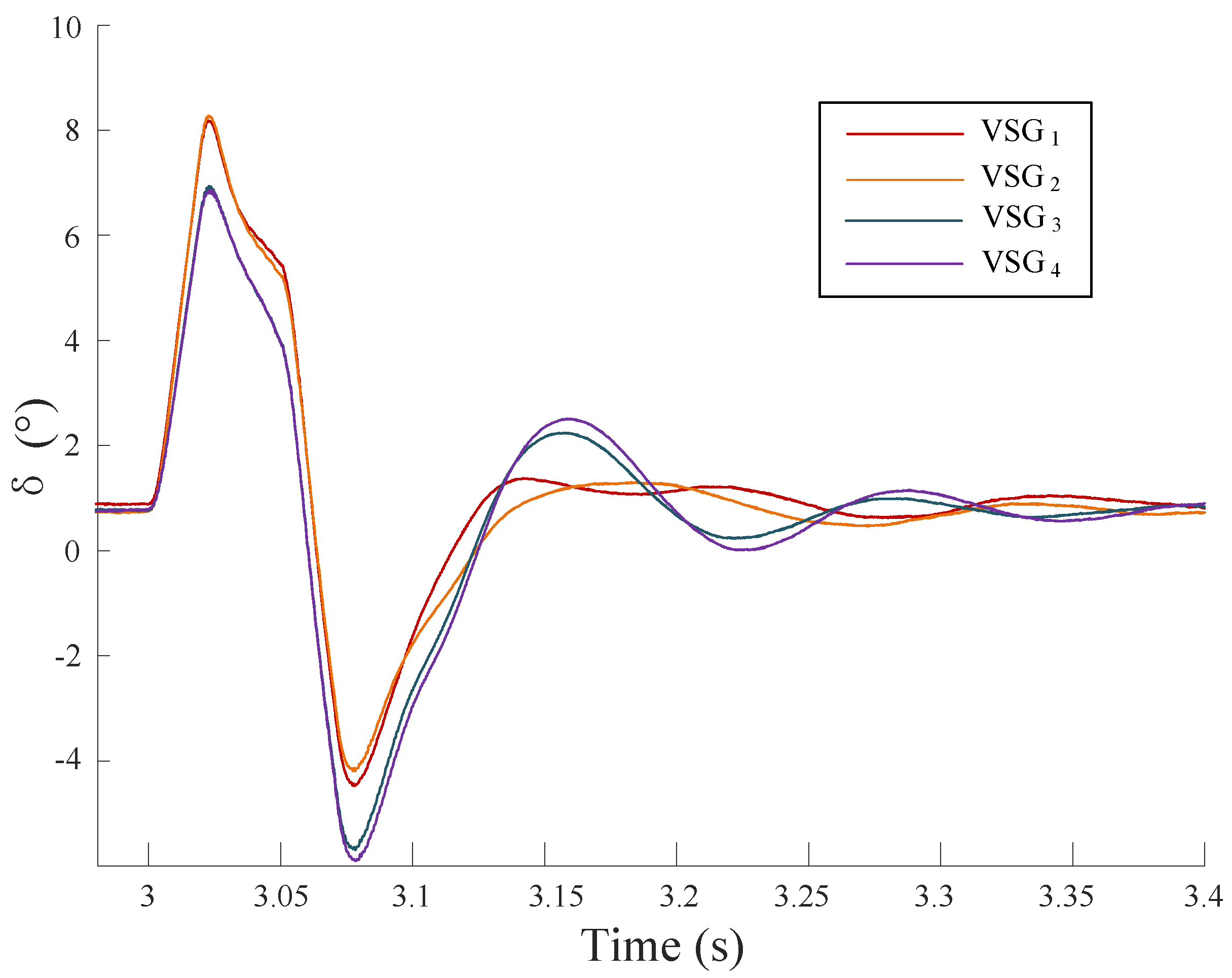
5.2. Corrected Homological Determination and Parameter Aggregation
5.3. Case Validation
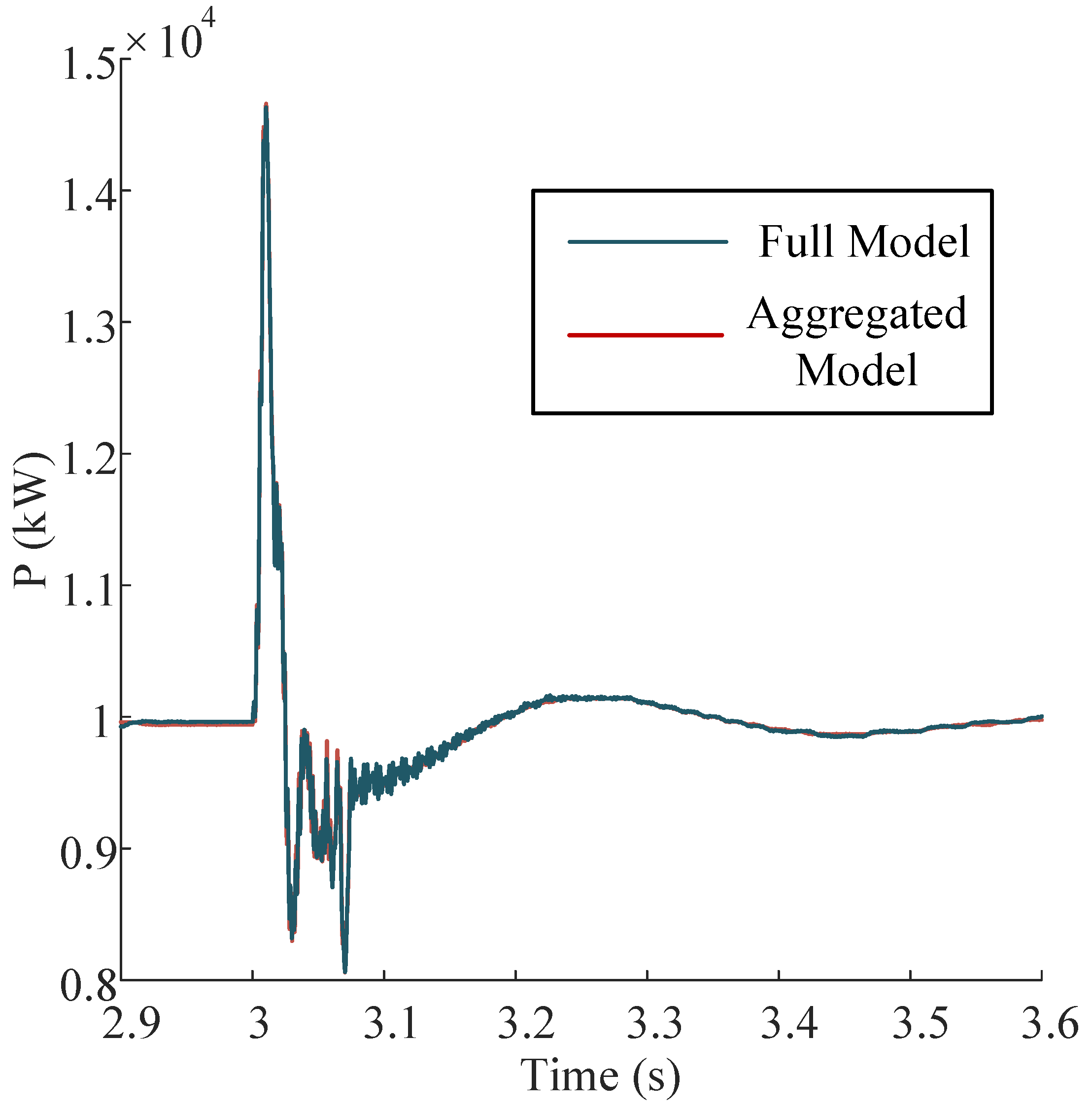
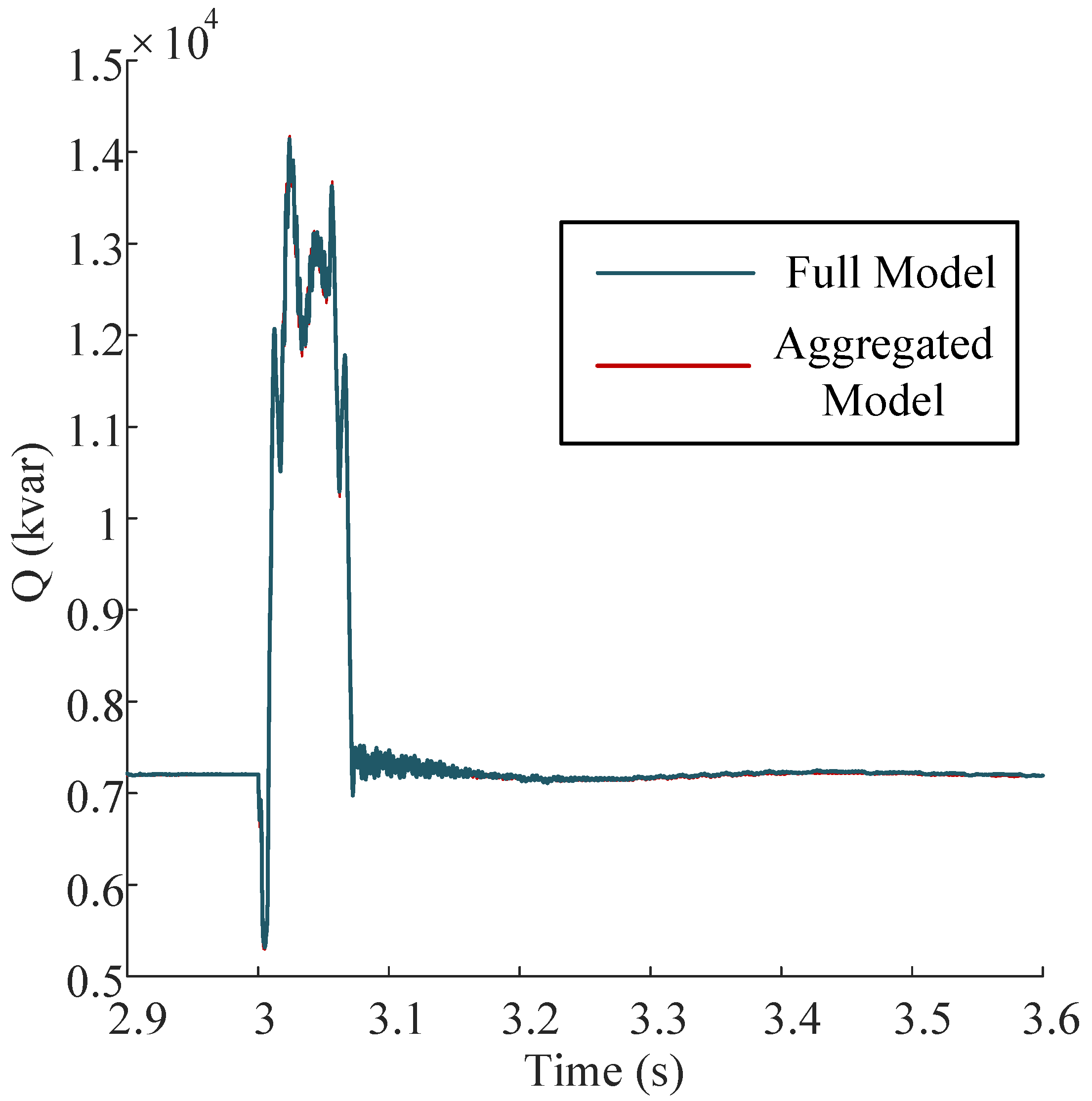
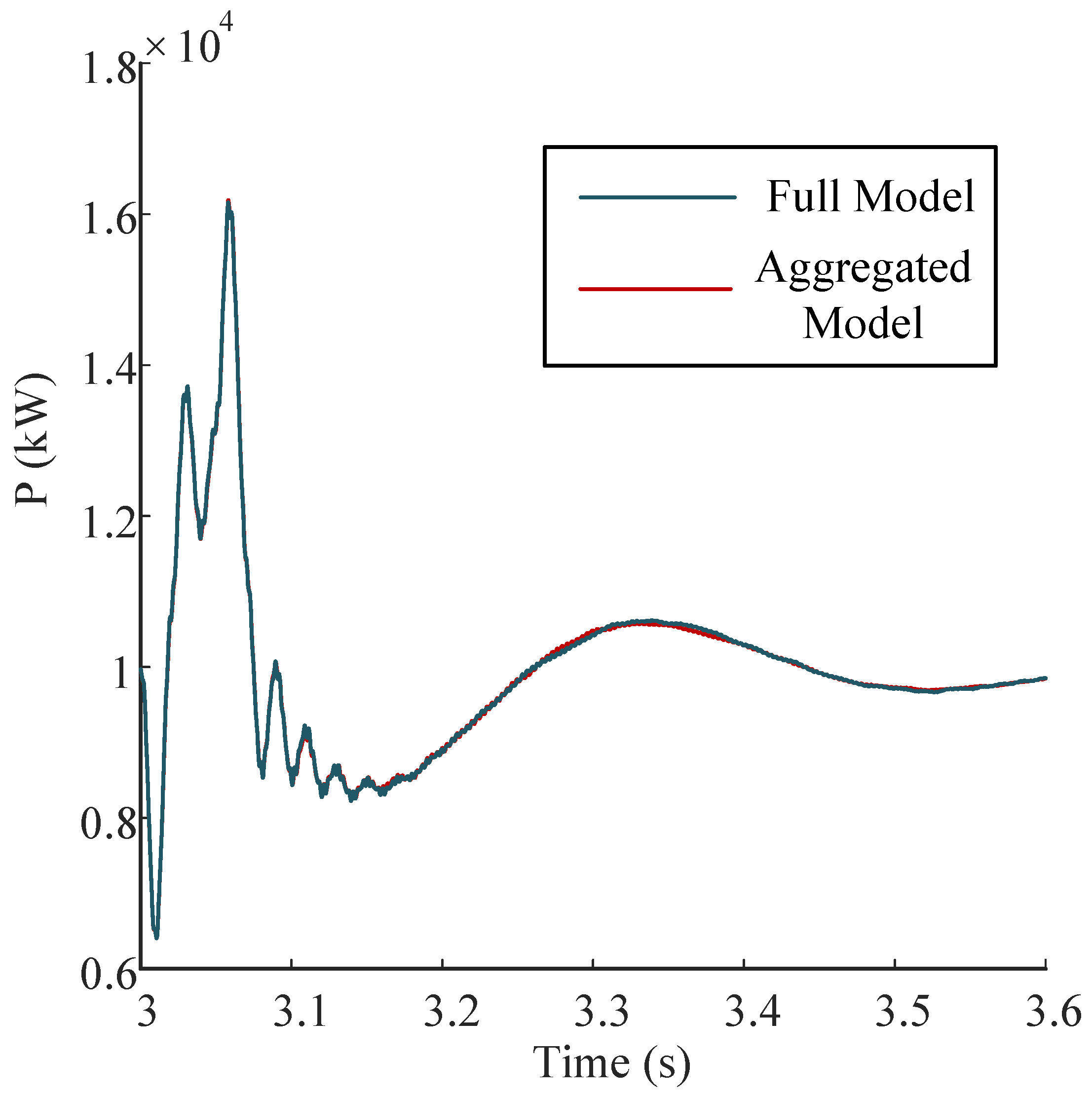
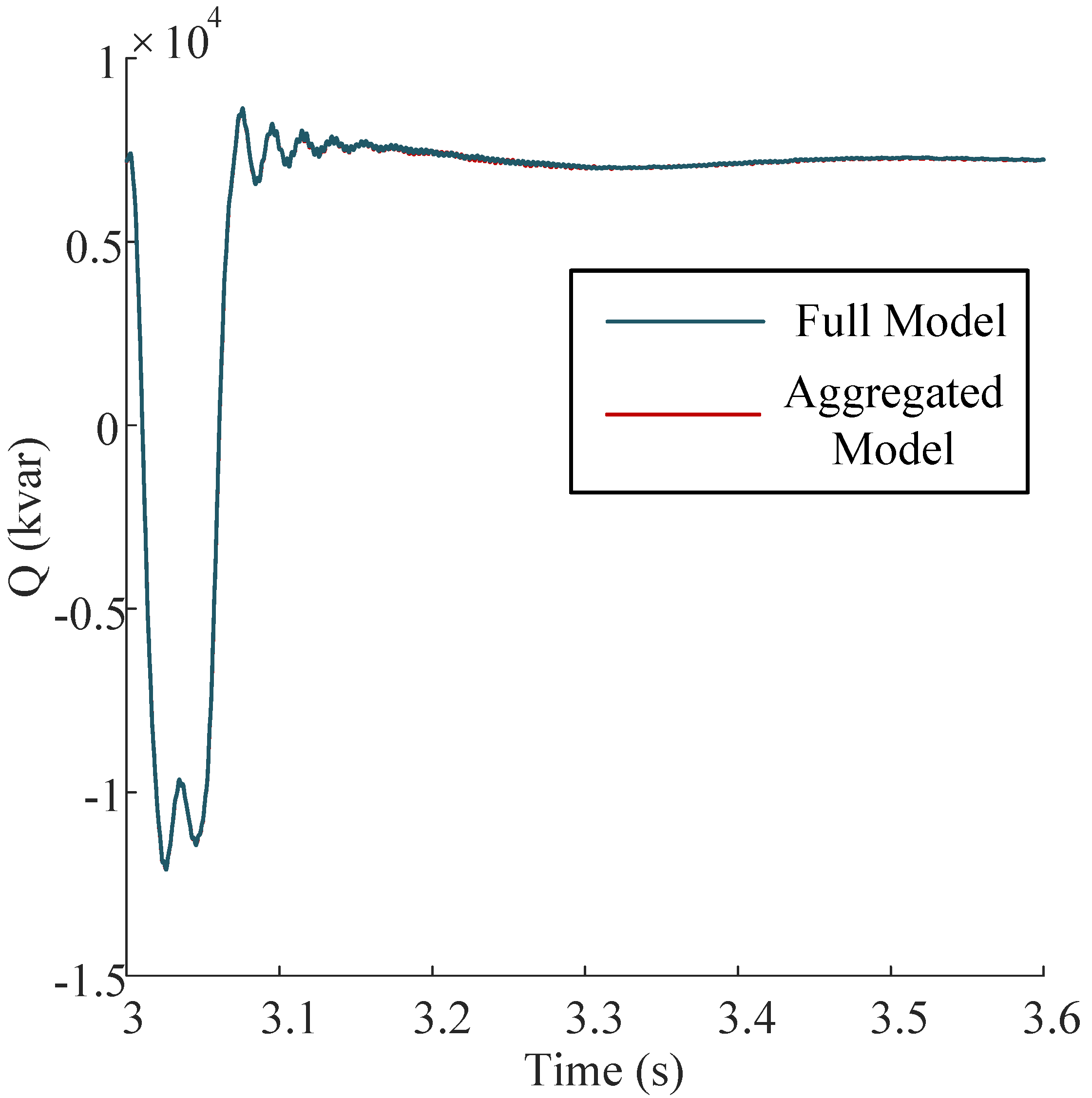
5.3.1. Case 1: Single-Phase Ground Fault
5.3.2. Case 2: 50% Voltage Sag
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Lee, S.T.Y.; Schweppe, F.C. Distance Measures and Coherency Recognition for Transient Stability Equivalents. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1550–1557. [Google Scholar] [CrossRef]
- Xu, J.; Gole, A.M.; Zhao, C. The Use of Averaged-Value Model of Modular Multilevel Converter in DC Grid. IEEE Trans. Power Deliv. 2015, 30, 519–528. [Google Scholar] [CrossRef]
- Chen, Z.; Ren, B.; Xu, J.; Wang, K.; Li, G.; Li, Q. Generalized Composite Load Aggregation Considering Different Distributed PV Systems based on Improved K-means Algorithm. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 18–20 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 296–301. [Google Scholar]
- Li, C.; Xu, J.; Zhao, C. A Coherency-Based Equivalence Method for MMC Inverters Using Virtual Synchronous Generator Control. IEEE Trans. Power Deliv. 2016, 31, 1369–1378. [Google Scholar] [CrossRef]
- Ding, Y.; Gao, F.; Hou, K.; Jiang, Y.; Zhong, X.; Yin, H. Transient Stability Analysis and Enhancement of an Islanded Microgrid with Grid-forming Converters and Grid-following Converters. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 21–23 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1362–1367. [Google Scholar]
- del Rivero, D.; García, P.; Blanco, C.; Navarro-Rodríguez, Á. Control of Aggregated Virtual Synchronous Generators for PV Plants Considering Communication Delays. IEEE Trans. Ind. Appl. 2024, 60, 6512–6523. [Google Scholar] [CrossRef]
- Nia, A.A.; Shabanikia, N.; Khajehoddin, S.A. Weighted Dynamic Aggregation Modeling of DC Microgrid Converters with Droop Control. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 700–706. [Google Scholar]
- Zhao, F.; Du, Z. Aggregation Model of Variable Frequency Motors and the Analysis of Active Power and Reactive Power Demand under Transient State. In Proceedings of the 2018 IEEE 3rd International Conference on Cloud Computing and Internet of Things (CCIOT), Dalian, China, 19–21 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 360–363. [Google Scholar]
- Zha, X.; Liao, S.; Huang, M.; Yang, Z.; Sun, J. Dynamic Aggregation Modeling of Grid-Connected Inverters Using Hamilton’s-Action-Based Coherent Equivalence. IEEE Trans. Ind. Electron. 2019, 66, 6437–6448. [Google Scholar] [CrossRef]
- Hart, P.J.; Lasseter, R.H.; Jahns, T.M. Coherency Identification and Aggregation in Grid-Forming Droop-Controlled Inverter Networks. IEEE Trans. Ind. Appl. 2019, 55, 2219–2231. [Google Scholar] [CrossRef]
- Yi, X.; Shen, C.; Peng, Y.; Huang, W.; Shuai, Z.; Lou, G. Aggregation Reduced-order Modeling of Multi-converter Systems Based on Coherency Equivalence Method. Proc. CSEE 2022, 42, 5644–5674. [Google Scholar]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F. Large Signal Synchronizing Instability of PLL-Based VSC Connected to Weak AC Grid. IEEE Trans. Power Syst. 2019, 34, 3220–3229. [Google Scholar] [CrossRef]
- Shen, C. Transient Stability and Current Injection Design of Paralleled Current-Controlled VSCs and Virtual Synchronous Generators. IEEE Trans. Smart Grid 2021, 12, 1118–1134. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Reduced-Order and Aggregated Modeling of Large-Signal Synchronization Stability for Multiconverter Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3150–3165. [Google Scholar] [CrossRef]
- Shuai, Z.; Peng, Y.; Liu, X.; Li, Z.; Guerrero, J.M.; Shen, Z.J. Dynamic Equivalent Modeling for Multi-Microgrid Based on Structure Preservation Method. IEEE Trans. Smart Grid 2019, 10, 3929–3942. [Google Scholar] [CrossRef]
- Xu, C.; Zou, Z.; Yang, J.; Wang, Z.; Chen, W.; Buticchi, G. Transient Stability Analysis and Enhancement of Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 1396–1408. [Google Scholar] [CrossRef]


| Parameter (Unit) | Value |
|---|---|
| Nominal Voltage U (V) | 380 |
| Equivalent Inductance L (mH) | 0.0032 |
| Equivalent Resistance R () | 0.1 |
| Parameter (Unit) | VSG1 | VSG2 | VSG3 | VSG4 |
|---|---|---|---|---|
| (V) | 600 | 600 | 600 | 600 |
| (kW) | 6 | 5 | 5 | 5 |
| (kvar) | 0 | 0 | 0 | 0 |
| () | 0.7 | 0.75 | 0.8 | 0.82 |
| (mH) | 18 | 19 | 20 | 30 |
| () | 0.05 | 0.04 | 0.04 | 0.01 |
| (mH) | 4.4 | 4.5 | 4.6 | 4.4 |
| C (μF) | 20 | 20 | 20 | 30 |
| J | 0.1 | 0.12 | 0.18 | 0.17 |
| 4 | 4.2 | 2.6 | 2.5 | |
| 950 | 960 | 1009 | 1000 | |
| 155 | 157 | 160 | 165 |
| VSG | (°) | (V) | |
|---|---|---|---|
| VSG1 | 0.038 | 379.721 | −0.064 |
| VSG2 | 0.033 | 379.798 | −0.056 |
| VSG3 | 0.033 | 379.788 | −0.023 |
| VSG4 | 0.032 | 379.806 | −0.023 |
| Parameter | Value |
|---|---|
| −0.023 | |
| −0.042 | |
| 0.54 |
| VSG | VSG1 | VSG2 | VSG3 | VSG4 |
|---|---|---|---|---|
| VSG1 | 0 | 0.2192 | 0.82266 | 0.60499 |
| VSG2 | 0.2192 | 0 | 1.0419 | 0.82418 |
| VSG3 | 0.82266 | 1.0419 | 0 | 0.21767 |
| VSG4 | 0.60499 | 0.82418 | 0.21767 | 0 |
| Parameter | VSGA | VSGB |
|---|---|---|
| (V) | 600 | 600 |
| (kW) | 6 | 5 |
| (kvar) | 0 | 0 |
| () | 0.7 | 0.75 |
| (mH) | 18 | 19 |
| () | 0.05 | 0.04 |
| (mH) | 4.4 | 4.5 |
| C (μF) | 20 | 20 |
| J | 0.1 | 0.12 |
| 4 | 4.2 | |
| 950 | 960 | |
| 155 | 157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, H.; Yu, S.; Gong, W.; Mei, S.; Ma, M.; Han, D. Novel Topological Aggregation Method for Grid-Forming Converters of Renewable Energy with Threshold Correction. Energies 2025, 18, 773. https://doi.org/10.3390/en18040773
Zhai H, Yu S, Gong W, Mei S, Ma M, Han D. Novel Topological Aggregation Method for Grid-Forming Converters of Renewable Energy with Threshold Correction. Energies. 2025; 18(4):773. https://doi.org/10.3390/en18040773
Chicago/Turabian StyleZhai, Haibao, Shaoqi Yu, Weizheng Gong, Sihan Mei, Meiling Ma, and Dong Han. 2025. "Novel Topological Aggregation Method for Grid-Forming Converters of Renewable Energy with Threshold Correction" Energies 18, no. 4: 773. https://doi.org/10.3390/en18040773
APA StyleZhai, H., Yu, S., Gong, W., Mei, S., Ma, M., & Han, D. (2025). Novel Topological Aggregation Method for Grid-Forming Converters of Renewable Energy with Threshold Correction. Energies, 18(4), 773. https://doi.org/10.3390/en18040773






