A Flexible Interconnected Distribution Network Power Supply Restoration Method Based on E-SOP
Abstract
1. Introduction
- (1)
- Development of a comprehensive E-SOP loss model with convex relaxation treatment;
- (2)
- Implementation of an Improved Whale Optimization Algorithm (IWOA) integrated with second-order cone transformation for FIDN fault recovery optimization;
- (3)
- Demonstration of enhanced power supply restoration capabilities in complex fault scenarios.
2. E-SOP Model Analysis
3. Power Supply Restoration Model with E-SOP and Its Cone Programming Transformation
3.1. Objective Functions
3.2. System Constraints
- (a)
- Establishing operational constraints for a SOP ensures its proper functioning and facilitates the maintenance of power balance within the system. These constraints serve as essential criteria for stable and reliable operation. SOP constraints encompass active power balance, power loss limitations, and capacity constraints, expressed by the following equations:
- (b)
- The implementation of ESS constraints ensures their safe operation, maintains energy storage capacity within reasonable limits, and guarantees normal system operation. The ESS constraints can be classified into three categories: power balance constraints, charging/discharging constraints, and capacity constraints, which are formulated as follows:
- (c)
- Power Flow Constraints
- (d)
- System Operational Security Constraints
- (e)
- System Operational Security Constraints
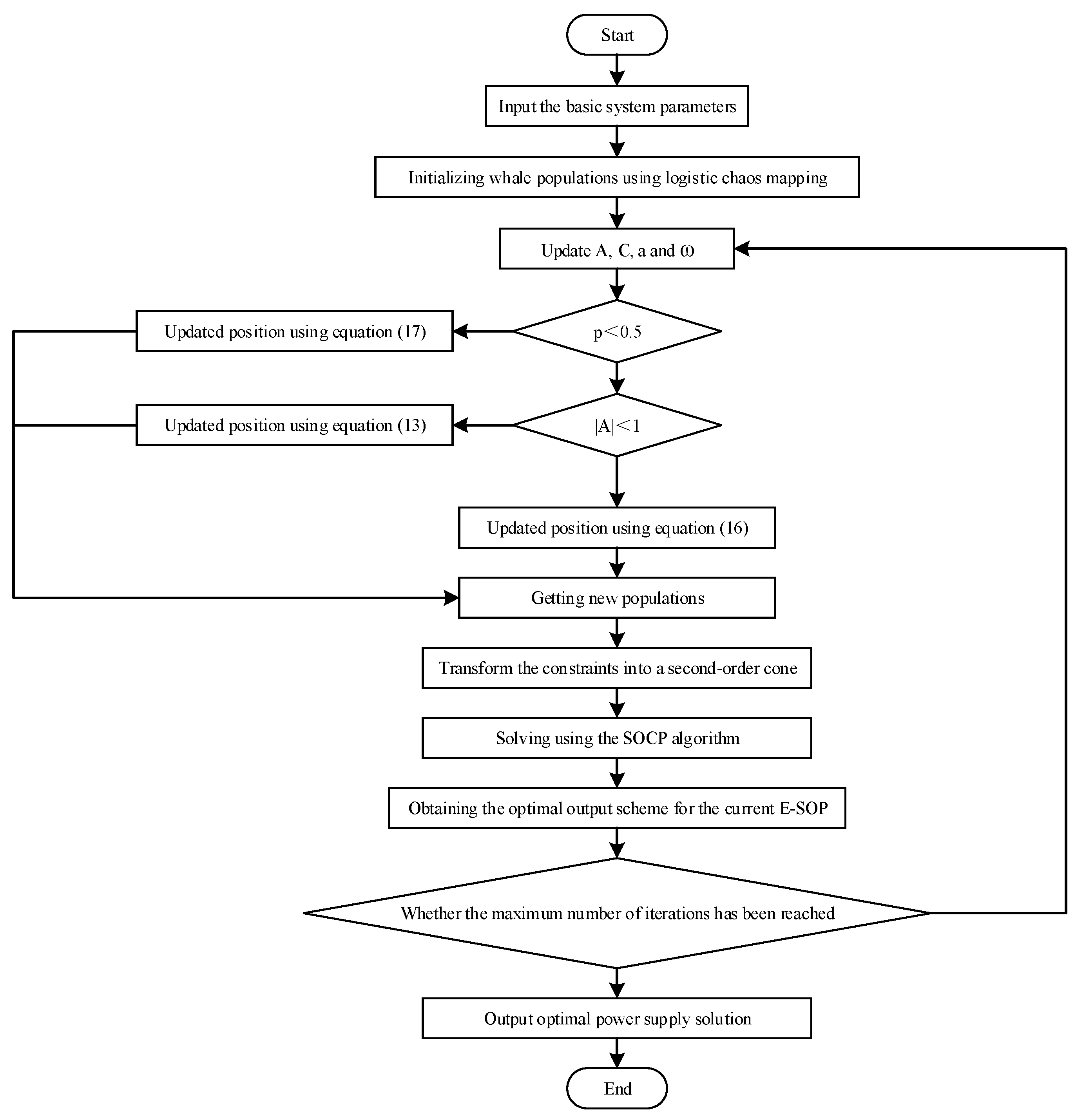
3.3. Improved Whale Optimization Algorithm
- (a)
- Encircling Prey
- (b)
- Bubble-Net Feeding
- (c)
- Prey Searching
- (a)
- Logistic Chaotic Mapping
- (b)
- Position Update Weight Strategy
3.4. Second-Order Cone Model and Convex Relaxation Transformation
4. Power Supply Restoration Model Based on E-SOP
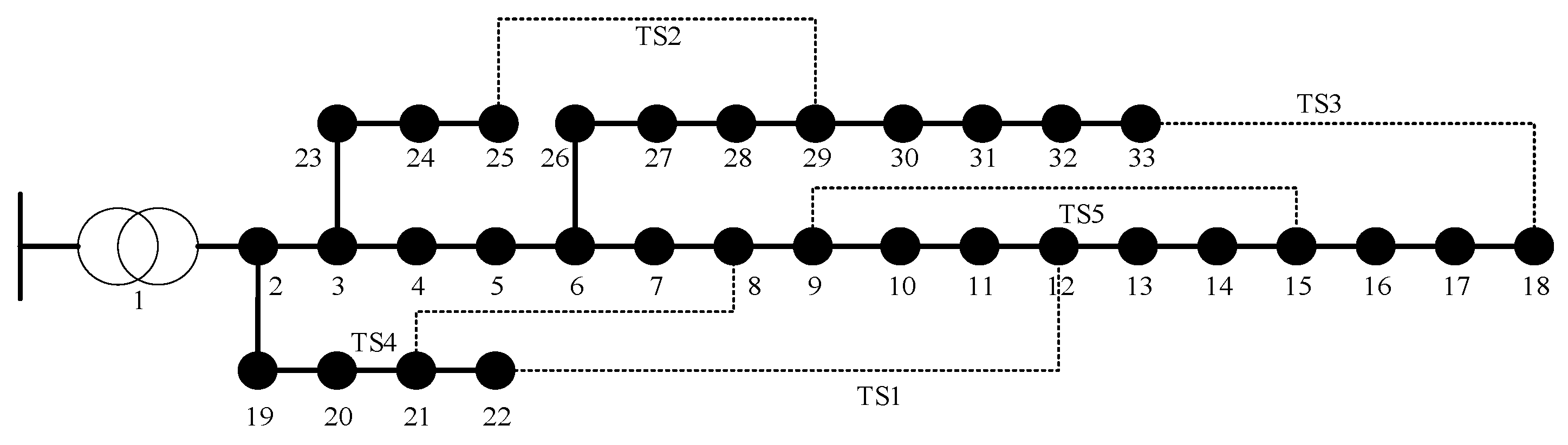
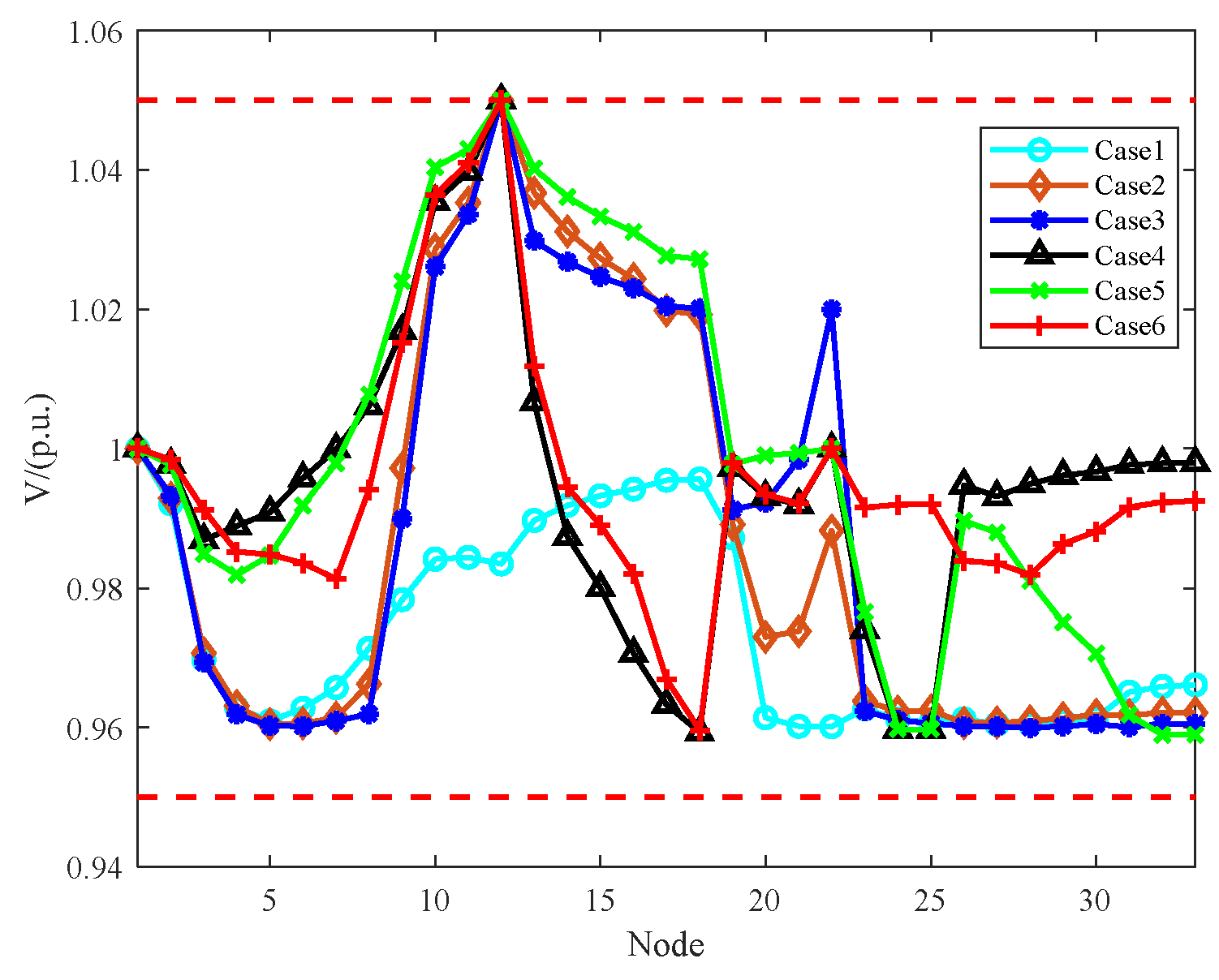
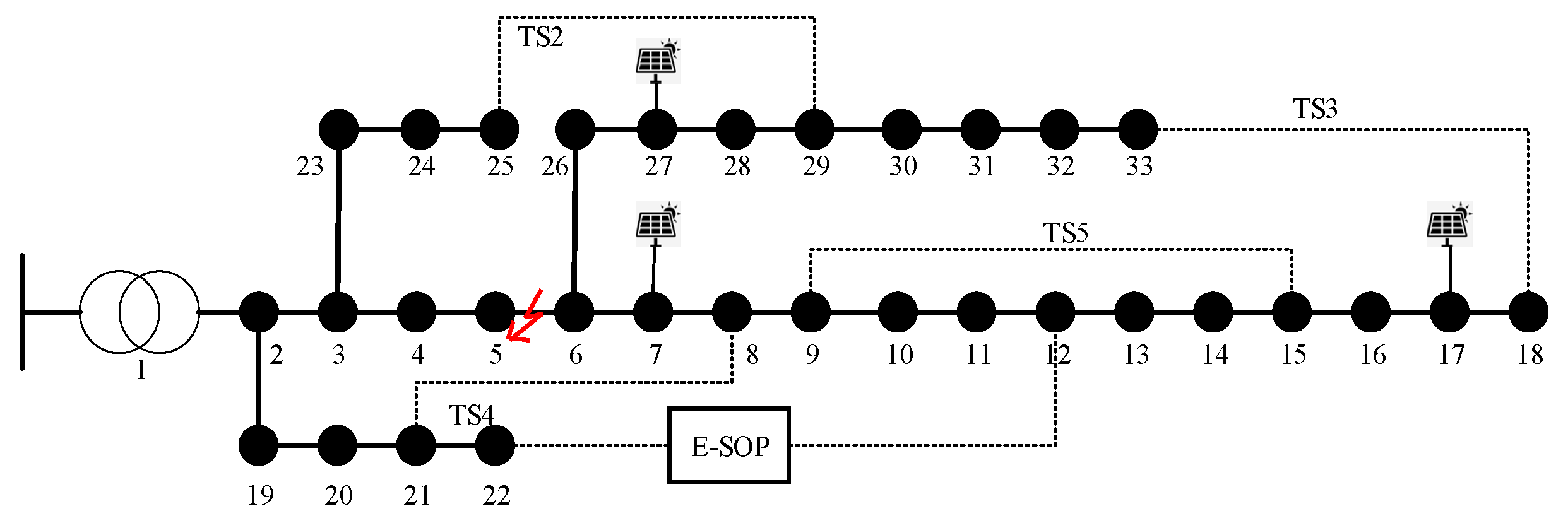
5. Case Study Analysis
5.1. Case Study Analysis (1)
5.2. Case Study Analysis (2)
6. Conclusions
- (a)
- As a novel flexible regulation device, an E-SOP effectively enhances the power supply restoration capability of flexible interconnected distribution networks. Compared to traditional switching schemes and network reconfiguration approaches, E-SOP-based restoration demonstrates superior advantages. However, the restoration’s effectiveness is generally constrained by the device placement location and capacity limitations;
- (b)
- Incorporating intelligent algorithms into the E-SOP-based power supply restoration process significantly improves the restoration capability of distribution networks while achieving enhanced voltage control performance. Experimental results demonstrate that the proposed hybrid IWOA–second-order cone optimization method achieves superior restoration outcomes and exhibits improved stability across multiple independent runs, indicating that the proposed method better mitigates the impact of initial value selection;
- (c)
- The integration of distributed generation provides effective power support to outage areas, further enhancing system fault recovery performance. Case studies reveal that after photovoltaic integration, all restoration schemes achieve significantly improved recovery rates, particularly the IWOA–second-order cone hybrid algorithm approach, which achieves a system recovery rate of 93.0%. This indicates that the coordinated optimization of multiple flexible resources plays a crucial role in enhancing distribution networks’ self-healing capabilities.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IWOA | Improved Whale Optimization Algorithm |
| E-SOP | soft open point with energy storage |
| DG | distributed generation |
| FIDN | flexible interconnected distribution networks |
| FID | flexible interconnection devices |
| SOP | soft open point |
| VSC | voltage source converters |
| B2B VSC | back-to-back voltage source converters |
| IPSO | Improved Particle Swarm Algorithm |
| ESS | energy storage system |
| WOA | Whale Optimization Algorithm |
References
- Xia, W.; Ren, Z.; Qin, H.; Dong, Z.Y. A coordinated operation method for networked hydrogen-power-transportation system. Energy 2024, 296, 131026. [Google Scholar] [CrossRef]
- Pamshetti, V.B.; Singh, S.; Thakur, A.K.; Singh, S.P. Multistage coordination Volt/VAR control with CVR in active distribution network in presence of inverter-based DG units and soft open points. IEEE Trans. Ind. Appl. 2021, 57, 2035–2047. [Google Scholar] [CrossRef]
- Wang, C.; Sun, J.J.; Huang, M.; Zha, X.; Hu, W. Two-stage optimization for active distribution systems based on operating ranges of soft open points and energy storage system. J. Mod. Power Syst. Clean Energy 2023, 11, 66–79. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Coordinated control method of voltage and reactive power for active distribution networks based on soft open point. IEEE Trans. Sustain. Energy 2017, 8, 1430–1442. [Google Scholar] [CrossRef]
- Xu, Z.P.; Liang, Y.S.; Li, H.F.; Gang, W.; Jia, L. Cloud-Edge Collaborative Optimization Algorithm for Fault Restoration of Flexible Interconnected Distribution Network. Autom. Electr. Power Syst. 2023, 47, 171–184. [Google Scholar]
- Liao, B.L.; Gao, Z.L.; Tang, J.Q.; Wu, Y.H.; Cheng, J. Active distribution network centralized direction protection based on graph theory. Smart Power 2019, 47, 55–62. [Google Scholar]
- Li, P.; Ji, H.R.; Wang, C.S.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Optimal Operation of Soft Open Points in Active Distribution Networks Under Three-Phase Unbalanced Conditions. IEEE Trans. Smart Grid 2019, 10, 380–391. [Google Scholar] [CrossRef]
- Xu, B.; Xiong, G.J.; Ye, F.H. A Flexible Interconnection Strategy for Distribution Networks Based on Intelligent Soft-Open Point Configuration. Power Syst. Clean Energy 2023, 39, 86–96. [Google Scholar]
- Li, P.; Song, G.Y.; Ji, H.R.; Zhao, J.; Wang, C.; Wu, J. A Supply Restoration Method of Distribution System Based on Soft Open Point. In Proceedings of the IEEE Innovative Smart Grid Technologies, Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 535–539. [Google Scholar]
- Sun, S.; Cong, W.; Sheng, Y.; Chen, M.; Wei, Z. Distributed Power Service Restoration Method of Distribution Network with Soft Open Point. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System, Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; pp. 1616–1621. [Google Scholar]
- Yu, Y.W.; Yuan, X.F.; Xiong, W. A Power Supply Restoration Method for the Flexible Interconnected Distribution Network with Multi-Terminal Soft Open Point. Power Syst. Clean Energy 2021, 37, 75–85+90. [Google Scholar]
- Song, Y.; Sun, C.B.; Li, P.; Kai, Y.; Guanyu, S.; Chengshan, W. SOP Based Supply Restoration Method of Active Distribution Networks Using Soft Open Point. Proc. CSEE 2018, 38, 4390–4398+4639. [Google Scholar]
- Zhao, Y.; Xiong, W.; Yuan, X.; Zou, X. A fault recovery strategy of flexible interconnected distribution network with SOP flexible closed-loop operation. Int. J. Electr. Power Energy Syst. 2022, 142, 108360. [Google Scholar] [CrossRef]
- Ji, H.; Wang, C.; Li, P.; Song, G.; Wu, J. SOP-based islanding partition method of active distribution networks considering the characteristics of DG, energy storage system and load. Energy 2018, 155, 312–325. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Y.; Ming, W.; Yang, P.; Wu, J. An overview of soft open points in electricity distribution networks. IEEE Trans. Smart Grid 2022, 13, 1899–1910. [Google Scholar] [CrossRef]
- Huang, Z.T.; Xu, Y.H.; Chen, L.; Ye, X. Coordinated planning method considering flexible resources of active distribution network and soft open point integrated with energy storage system. IET Gener. Transm. Distrib. 2023, 17, 5273–5285. [Google Scholar] [CrossRef]
- Li, Y.; Ling, F.; Qiao, X.B.; Zhong, J.J.; Cao, Y.J. Day-Ahead and Intra-Day Optimization of Flexible Interconnected Distribution System with Self-Energy Storage Based on the Grid-Side Resource Coordination. Trans. China Electrotech. Soc. 2024, 39, 758–773+923. [Google Scholar]
- Hu, Y.F.; Qian, F.; Li, H.L.; Liu, S.; Zhang, Q. Island fault recovery method of distribution network based on flexible interconnection device with energy storage. Distrib. Util. 2024, 41, 21–27. [Google Scholar]
- Sarantakos, I.; Peker, M.; Zografou-Barredo, N.-M.; Deakin, M.; Patsios, C.; Sayfutdinov, T. A robust mixed-integer convex model for optimal scheduling of integrated energy storage-soft open point devices. IEEE Trans. Smart Grid 2022, 13, 4072–4087. [Google Scholar] [CrossRef]
- He, J.F.; Zhang, Y.Z.; Zhang, T.; Mo, S.; Lu, Z.J. Multi-Time Scale Reactive Power Optimization Method for Flexible Interconnected Distribution Networks with Self-Energy Storage. South. Power Syst. Technol. 2024. Available online: http://kns.cnki.net/kcms/detail/44.1643.tk.20240730.1606.015.html (accessed on 27 January 2025).
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wu, X.L.; Hu, S.; Cheng, W. Multi-Objective Signal Timing Optimization Based on Improved Whale Optimization Algorithm. J. Kunming Univ. Sci. Technol. (Nat. Sci.) 2021, 46, 134–141. [Google Scholar]
- Ji, H.; Wang, C.; Li, P.; Zhao, J.; Song, G.; Wu, J. Quantified flexibility evaluation of soft open points to improve distributed generator penetration in active distribution networks based on difference-of-convex programming. Appl. Energy 2018, 218, 338–348. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, Y.; Li, Z.; Xie, D.; Ghias, A.M.M. Resilience enhancement of a multi-energy distribution system via joint network reconfiguration and mobile sources scheduling. CSEE J. Power Energy Syst. 2024, 12, 1–12. [Google Scholar] [CrossRef]

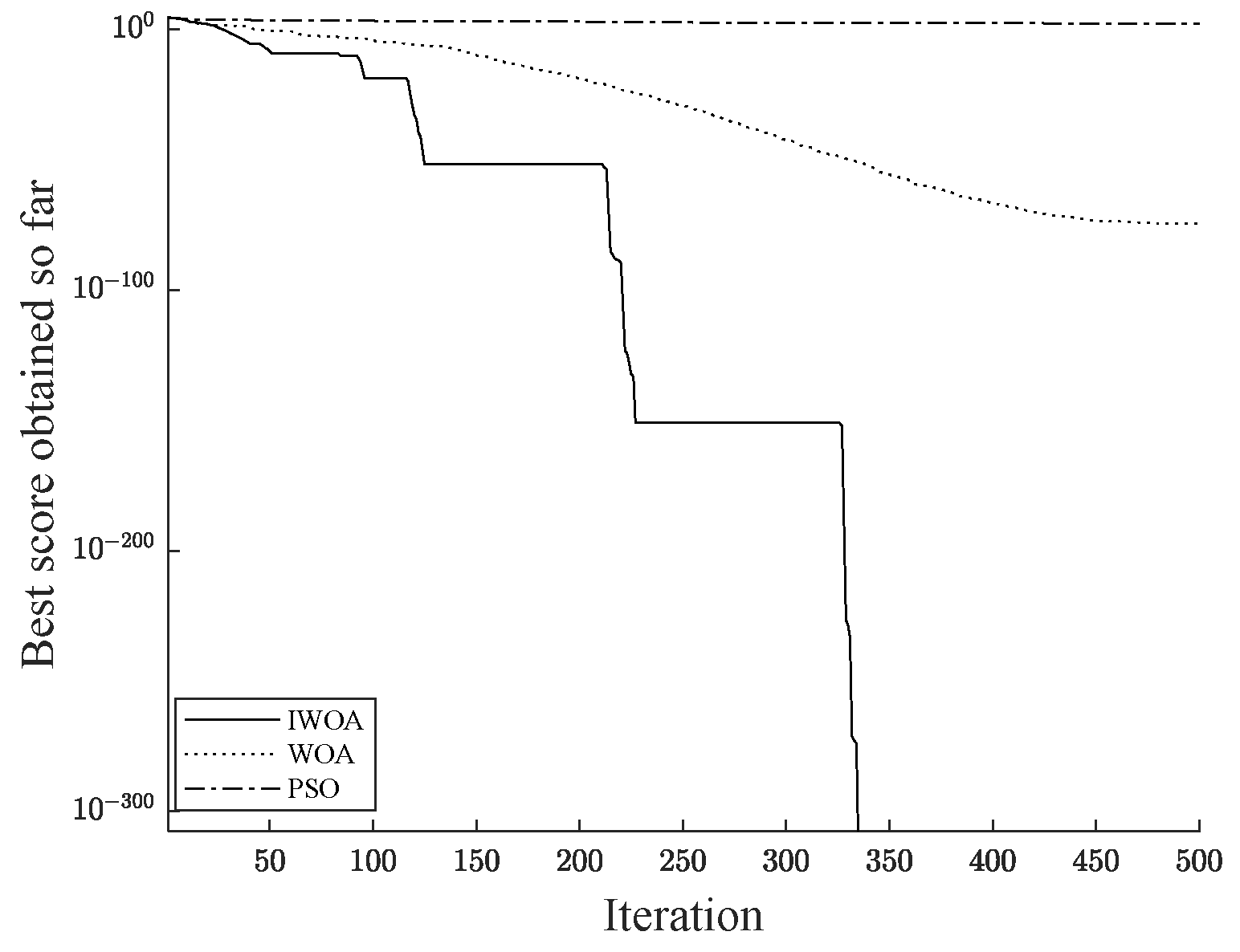

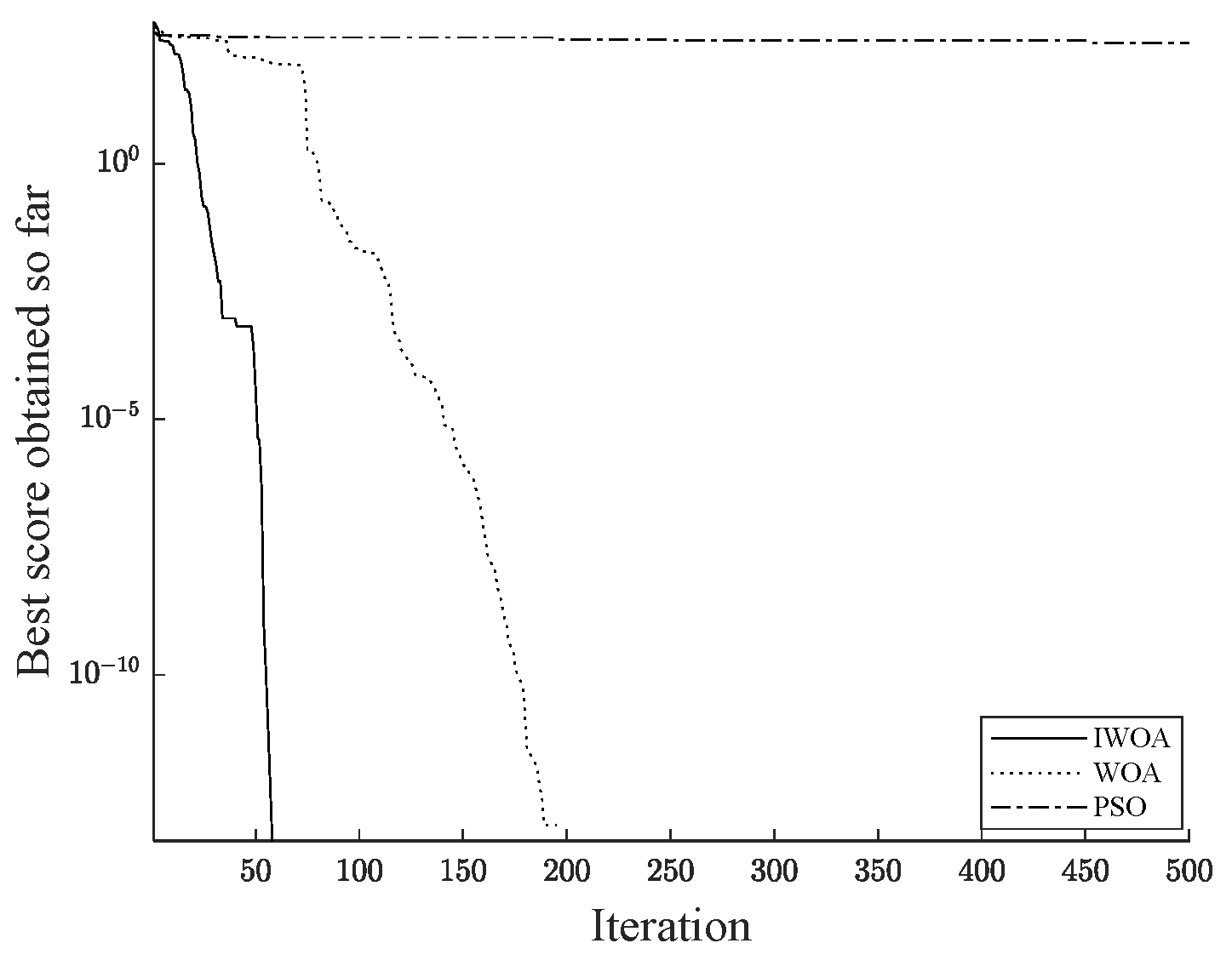



| Algorithm | Best Obtained Value | Worst Obtained Value | Mean Value | Standard Deviation | |
|---|---|---|---|---|---|
| IWOA | 0 | 0 | 0 | 0 | |
| f1 | WOA | 5.84 × 10−84 | 1.42 × 10−72 | 1.35 × 10−73 | 4.12 × 10−73 |
| PSO | 35 | 1.17 × 103 | 4.35 × 102 | 2.73 × 102 | |
| IWOA | 0 | 0 | 0 | 0 | |
| f2 | WOA | 3.54 × 10−57 | 6.1 × 10−50 | 3.61 × 10−51 | 1.35 × 10−50 |
| PSO | 6.63 | 47.7 | 20.5 | 11.5 | |
| IWOA | 0 | 0 | 0 | 0 | |
| f3 | WOA | 0 | 0 | 0 | 0 |
| PSO | 1.56 × 102 | 2.46 × 102 | 1.95 × 102 | 26.8 |
| Case | Power Outage/kW | Restored Load/kW | Recovery Rate/% | Computation Time/s | Power Loss Node |
|---|---|---|---|---|---|
| 1 | 620.0 | 30.17 | 0.55 | 7–11, 13–18, 31–33 | |
| 2 | 1275.0 | 62.04 | 0.70 | 9, 13–18, 32, 33 | |
| 3 | 1373.5 | 66.84 | 0.56 | 14–18, 32, 33 | |
| 4 | 2055 | 1432.3 | 69.70 | 2.49 | 8, 12, 13, 15, 17, 28, 29 |
| 5 | 1510.1 | 73.48 | 2.44 | 12, 15–18, 27, 31 | |
| 6 | 1642.2 | 79.91 | 2.37 | 11, 13, 15, 17, 27, 29 |
| Node | 7 | 17 | 27 |
| Load/kW | 300 | 200 | 200 |
| Case | Power Outage/kW | Restored Load/kW | Recovery Rate/% |
|---|---|---|---|
| 1 | 815.0 | 46.97 | |
| 2 | 1425.0 | 69.34 | |
| 3 | 1489.6 | 72.49 | |
| 4 | 2055 | 1733.6 | 84.36 |
| 5 | 1850.3 | 90.04 | |
| 6 | 1911.2 | 93.0 |
| Case | Best Obtained Value/% | Mean Value/% | Standard Deviation |
|---|---|---|---|
| 4 | 84.36 | 80.3 | 4.55 |
| 5 | 90.04 | 86.5 | 2.47 |
| 6 | 93.0 | 91.2 | 1.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Wang, C.; Qiu, W.; Xiao, H.; Hu, W. A Flexible Interconnected Distribution Network Power Supply Restoration Method Based on E-SOP. Energies 2025, 18, 954. https://doi.org/10.3390/en18040954
Jiang L, Wang C, Qiu W, Xiao H, Hu W. A Flexible Interconnected Distribution Network Power Supply Restoration Method Based on E-SOP. Energies. 2025; 18(4):954. https://doi.org/10.3390/en18040954
Chicago/Turabian StyleJiang, Lin, Canbin Wang, Wei Qiu, Hui Xiao, and Wenshan Hu. 2025. "A Flexible Interconnected Distribution Network Power Supply Restoration Method Based on E-SOP" Energies 18, no. 4: 954. https://doi.org/10.3390/en18040954
APA StyleJiang, L., Wang, C., Qiu, W., Xiao, H., & Hu, W. (2025). A Flexible Interconnected Distribution Network Power Supply Restoration Method Based on E-SOP. Energies, 18(4), 954. https://doi.org/10.3390/en18040954






