Low-Carbon Economic Dispatch Model for Virtual Power Plants Considering Multi-Type Load Demand Response

Abstract

Maximizing the optimal scheduling capability of a virtual power plant (VPP) over its aggregated resources is crucial for increasing its revenue. However, the limited dispatchable resources in single-energy VPPs hinder maximum economic efficiency. To address this issue, in this paper, a multienergy virtual power plant (MEVPP), which aggregates distributed electrical, thermal, and demand-side flexible resources, is introduced. Furthermore, a low-carbon economic dispatch strategy model is proposed for the coordinated operation of the MEVPP with shared energy storage. First, an MEVPP model incorporating shared energy storage is constructed, with equipment modeling developed from both electrical and thermal dimensions. Second, a low-carbon dispatch strategy that incorporates multiple types of demand responses is formulated, accounting for the effects of electrical and thermal demand responses, as well as carbon emissions, on dispatch. The simulation results demonstrate that, compared with models that do not consider the multienergy demand response, the proposed model reduces system operating costs to 54.2% and system carbon emissions to 42%. Additionally, the MEVPP can leverage energy storage by charging during low-price periods and discharging during high-price periods, thereby enabling low-carbon and economically viable system operation. This study offers valuable insights for the optimized operation of MEVPP systems.

1. Introduction

With the proposal of “dual carbon” goals, the proportion of distributed energy resources (DERs) connected to the power grid continues to increase. Their inherent randomness and output fluctuations pose significant challenges to the security and stability of the power system. In this context, VPP technology addresses this problem by integrating these decentralized and independently operated DERs into an aggregated entity [1,2], enabling coordinated control over power generation, storage, and consumption [3], thereby mitigating the impact of DERs’ uncertainties on the grid. Consequently, the optimal dispatch of VPPs has become a key focus of current research [4,5].

VPPs can be categorized into external-dispatch VPPs and internal-dispatch VPPs. External dispatch refers to the participation of the VPP in the centralized dispatch of the power grid as a single entity [6,7,8]. Internal optimal dispatch involves the VPP coordinating and controlling its internal DERs according to schedules issued by the dispatch organization. Research on scheduling strategies for maximizing VPP revenue focuses primarily on internal optimal dispatch. Reference [9] used a fully distributed dispatch method to achieve maximum economic benefit. Reference [10] introduced a decentralized economic dispatch method and architecture for VPPs that are applicable to massive DERs. However, the computational load and model complexity of the distributed algorithms in these two references are high; when the types and quantity of resources aggregated by the VPP are excessive, the difficulty of solving the optimization model increases significantly. Reference [11] established a two-stage optimal scheduling framework. This model leverages the inherent complementary characteristics of the wind and photovoltaic power outputs to effectively increase the operational revenue of the VPP. Nonetheless, the aforementioned studies consider only traditional single-energy (electrical) VPPs and lack the integration of cooling and heating complementarity, which, to some extent, limits the potential revenue of the VPP.

Multienergy virtual power plants (MEVPs) can aggregate additional forms of energy, such as electrical and thermal energy, enabling the complementary use of multiple types of energy resources and thereby achieving the efficient management and utilization of multiple energy sources. Reference [12] established a VPP comprising wind turbines and combined heat and power (CHP) units and verified the effectiveness of the thermoelectric coupling mode in reducing system operational costs. Furthermore, for systems with a high penetration of renewable energy, studies have shown that configuring electric boilers [13], thermal storage devices [14], or a combination of both [15] can increase system flexibility and reduce costs. The aforementioned studies demonstrate that extending VPPs to MEVPPs can improve the system’s economic efficiency; however, the dispatch mechanisms of MEVPPs need further investigation. In this regard, reference [16] explored an electricity–gas coupled VPP and established a dual-objective optimization model that simultaneously pursues maximum operational profit and minimum risk. However, the primary focus of this study was recycling within the electricity–gas conversion process, leaving the electricity–thermal coupling aspect for further exploration. Reference [17] employed scenario generation and reduction techniques to address the uncertainties of wind and photovoltaic power outputs and established a two-stage collaborative optimization model for a combined cooling, heating, and power (CCHP) VPP under multiple scenarios. However, this model did not fully account for the uncertainties in wind and PV power outputs when addressing the economic dispatch of the MEVPP, nor did it consider the role of demand-side resources. Reference [18] considered multiple uncertainties on both the supply and demand sides and adopted a two-stage robust stochastic optimization method for dispatch decisions. Reference [19] proposed a scenario optimization method that enables the MEVPP to perform coordinated dispatch in terms of both active and reactive power.

The studies mentioned above focused primarily on the economic aspect of MEVPP operation and overlooked the impact of carbon emissions on MEVPP operational strategies. To address this gap, reference [20] established an optimal dispatch model for a CCHP VPP that considers carbon trading costs. However, this study simplified the resources aggregated by the MEVPP and failed to consider the impact of key DERs, such as energy storage and demand response, on the optimization results. References [21,22] introduced a carbon trading mechanism into the MEVPP and employed a robust optimization method to address multiple uncertainties. However, this method, which makes decisions on the basis of the worst-case scenario, may lead to overly conservative dispatch schemes. Reference [23] designed an MEVPP architecture that incorporates thermal power units and a carbon capture system. This model performed well in synergistically reducing operational costs and carbon emissions, but its demand response model was oversimplified.

In summary, current academic research on MEVPPs predominantly focuses on the supply side, while the integration of demand-side flexibility resources into its low-carbon economic dispatch remains underexplored. To bridge this research gap, in this paper, a low-carbon economic dispatch model for MEVPPs that is compatible with multiple energy types and demand-side responses is proposed. This model uses shared electrical energy storage and shared thermal storage equipment to manage the charging and discharging operations of electrical and thermal energy. The effectiveness of the proposed model is validated using an IEEE 33-bus power system and a 20-node Belgian gas network.

Compared with existing studies, the novelty of this paper lies in three aspects: First, a MEVPP system model is constructed, which includes shared energy storage system, shared thermal storage system, wind power, photovoltaics, gas turbines, and gas boilers. Second, a multi-type demand response model incorporating shiftable, transferable, and reducible loads is considered, with detailed modeling for each type of demand response. Finally, a low-carbon economic dispatch model for the MEVPP is established, and a two-stage approach is adopted to account for the carbon emission costs of the MEVPP.

2. Multienergy Virtual Power Plant and Load Model

2.1. MEVPP Aggregation Mechanism and Model

The abbreviations of the key nouns in this paper are shown in Table 1:

Table 1. Abbrevuatuons.

VPP	virtual power plant	CNY	Chinese Yuan
MEVPP	multi-energy virtual power plant	ESS	Energy storagy system
DERs	distributed energy resources	TSS	Themal storagy system
CHP	combined heat and power	MT	microturbine
CCHP	combined cooling, heating, and power	GB	Gas-fired boiler
PV	photovoltaic	EL	Electrical load
WT	Wind power	TL	Themal load

The main symbols and variable declarations in the formula are shown in Table 2:

Table 2. The symbols and variable declarations.

$w_{\mathrm{SW}}$	the subjective weight vector	$P_{ch}(t)$	the charging power of the shared energy storage station
$w_{\mathrm{OW}}$	the objective weight vector	$P_{dis}(t)$	the discharging power of the shared energy storage station
$\omega$	the weight coefficient vector	$U_{ch}$	the binary variables indicating the charging states of the shared energy storage station
$\vartheta$	the linear weighting coefficient	$U_{dis}$	the binary variables indicating the discharging states of the shared energy storage station
$z_i^{\mathrm{O}}$	the final evaluation score of user i	$P_{\max }$	the upper limit for the charging/discharging power of the shared energy storage station
$z_i^{\mathrm{l}}$	the initial score matrix of user i	$y_t$	the time series value at time t
$L_{\mathrm{shift}}$	shiftable loads vector	${\varphi }_i$	the autoregressive parameter
$L_{\mathrm{shift}}^{*}$	shiftable loads vector before scheduling	${\theta }_j$	the moving average parameter
$P_{t_S}^{\mathrm{shift}}$	the power shifted at time $t_S$	${\alpha }_t$	The gaussian white noise
$\left[t_{\mathrm{sh}-},t_{\mathrm{sh}+}\right]$	the shift interval	$f_{{\mathrm{CO}}_2}$	the carbon trading cost of the MEVPP
$S_{\mathrm{shift}}$	the set of start times	$E_{\mathrm{out}}$	the total carbon emissions on the operating day
$F_{\mathrm{shift}}$	the compensation cost	$E_{\mathrm{all}}$	the allocated carbon quota
$P_{\mathrm{sum}}^{\mathrm{shift}}$	the total amount of load	$C_t$	the carbon price on the operating day
$\alpha \beta \gamma$	The binary variable	$\mathsf{\Omega }$	the total number of DERs
$\left[t_{\mathrm{tr}-},t_{\mathrm{tr}+}\right]$	the transfer interval	$c_i^{\mathrm{pre}}$	the carbon emission coefficients of device i during the production stages
$L_{\mathrm{tran}}$	the transferable Loads vector	$c_i^{\mathrm{run}}$	the carbon emission coefficients of device i during the operation stages
$P_t^{\mathrm{tran}}$	the transferable power at time t	$P_i$	the power output of device i
$P_{\min }^{\mathrm{tran}}$	the minimum transferable power	$f_{\mathrm{VPP}}$	the operating cost of MEVPP
$P_{\min }^{\mathrm{tran}}$	the maximum transferable power	$f_{{\mathrm{CO}}_2}$	the carbon market transaction costs
$T_{\min }^{\mathrm{tran}}$	the minimum continuous operation time	$F_{\mathrm{NET}}$	the cost of electricity purchased from the grid
$F_{\mathrm{tran}}$	the transfer compensation cost	$F_{\mathrm{DG}}$	the cost of wind and photovoltaic power generation
$F_{\mathrm{cost}}^{\mathrm{tran}}$	the compensation price per unit power load	$F_{\mathrm{MT}}$	the operating cost of gas turbines
$L_{\mathrm{cut}}$	the curtailable load vector	$F_{\mathrm{GB}}$	the operating cost of gas boilers
${\theta }_{\tau }$	the load reduction coefficient in period $\tau$	$F_{\mathrm{ESS}}$	the cost associated with charging and discharging utilizing shared energy storage
$P_{\tau }^{\mathrm{cut}*}$	the power of $L_{\mathrm{cut}}$ in period $\tau$ before scheduling	$F_{\mathrm{TSS}}$	the cost of charging and discharging heat using shared thermal storage systems
$P_{\tau }^{\mathrm{cut}}$	the power of $L_{\mathrm{cut}}$ in period $\tau$ after scheduling	$F_{\mathrm{L}}$	the total cost of demand response
$T_{\min }^{\mathrm{cut}}$	The minimum consecutive reduce periods	$K_{\mathrm{NET}}\left(t\right)$	the electricity price on the operating day at time t
$T_{\max }^{\mathrm{cut}}$	The maximum consecutive reduce periods	$P_{\mathrm{NET}}\left(t\right)$	the power of electricity purchased from or sold to the grid at time t
$N_{\max }$	the upper limit for the number of reduce events	$K_{\mathrm{W}}\left(t\right)$	the cost coefficients of wind units at time t
$F_{\mathrm{ess}}$	the shared energy storage cost paid by MEVPP	$K_{\mathrm{PV}}\left(t\right)$	the cost coefficients of photovoltaic units at time t
$\delta \left(t\right)$	the duration of a single dispatch period	$K_{\mathrm{MT}}\left(t\right)$	the cost coefficient of gas turbines at time t
$P_{\mathrm{ess},i}^{dis}(t)$	the discharge power	$P_{\mathrm{MT}}\left(t\right)$	the output power of gas turbines at time t
$P_{\mathrm{ess},i}^{ch}(t)$	the charge power	$K_{\mathrm{GB}}\left(t\right)$	the cost coefficient of gas boilers at time t
$P_{\mathrm{ess}}^{\max }$	the upper limit for the charging/discharging power of the shared energy storage	$P_{\mathrm{GB}}\left(t\right)$	the output power of gas boilers at time t
$U_{\mathrm{ess},i}^{ch}$	the binary variables indicating the charging states of user i	$K_{\mathrm{ESS},t}$	the costs associated with the charging/discharging power of shared energy storage system at time t
$U_{\mathrm{ess},i}^{dis}$	the binary variables indicating the discharging states of user i	$K_{TSS,t}$	the costs associated with the charging/discharging power of shared thermal storage system at time t
$E_{\max }$	the upper SOC limit	$P_{TSS}\left(t\right)$	the charging/discharging power of the shared thermal storage system at time t
$E_{\min }$	the lower SOC limit	$P_{\mathrm{LOAD}}(t)$	the electrical load demands at time t
$E(t)$	the state of charge of the energy storage station at time t	$Q_{\mathrm{LOAD}}(t)$	the thermal load demands at time t
${\eta }^{ch}$	the charging and efficiencies	$P_{pred}$	the forecasted output of wind and photovoltaic power
${\eta }^{dis}$	the discharging efficiencies	$P_{\mathrm{N}}$	the rated power of the gas turbine and gas boiler

In the context of massive and highly heterogeneous distributed energy resources (DERs), feature identification and classification form the foundation of MEVPP aggregation. On the basis of the core parameters describing DER characteristics, in this paper, a DER parameter dataset is constructed, and feature extraction and classification of DERs are performed according to the external characteristic requirements of the MEVPP.

The screening criteria for electricity and heat users include the following: rated power, load characteristic curve, shiftable load, transferable load, curtailable load, response time, response duration, responsive capacity, and response time period.

For distributed photovoltaic and distributed wind power, the screening criteria include the rated power, output characteristic curve, reserve capacity, and ramping rate.

For gas turbines and gas boilers, the screening criteria include the following: rated power, upper and lower output limits, output ramp rate limits, and minimum uptime/downtime.

After feature extraction, the MEVPP employs a combined subjective–objective weighting method to determine the weight of each indicator, thereby screening high-quality DERs for aggregation. Taking electricity and heat users as an example, the procedure is as follows:

• The subjective weighting method is employed to determine the subjective weight vector ${\omega }_{\mathrm{SW}}$ of the various criteria: Subjective weight coefficients are assigned on the basis of the importance the MEVPP places on each indicator when users participate in demand response.
• The objective weighting method is employed to determine the objective weight vector ${\omega }_{\mathrm{SW}}$ of the various criteria: The weight ${\omega }_{\mathrm{SW}}$ is adjusted by fully considering the differences among various types of user responses, thereby reducing the weight of evaluation indicators with low variability and making the evaluation model more targeted.
• Determine the weight coefficient vector $\omega$ for scoring demand response users by integrating the subjective indicator weight vector ${\omega }_{\mathrm{SW}}$ and the objective indicator weight vector ${\omega }_{\mathrm{OW}}$ using the linear weighting method:

  $$\omega =\vartheta {\omega }_{\mathrm{SW}}+(1-\vartheta ){\omega }_{\mathrm{OW}}$$

  (1)

  where $\vartheta$ represents the linear weighting coefficient.it is selected by comprehensively considering economic benefits, electrical distance, and the influence of both electrical distance and carbon balance potential on aggregation; its value is typically taken as 0.5 [24].
• Calculate the DER evaluation score on the basis of the performance evaluation indicator weight vector $\omega$ and the normalized scores of each performance indicator for the users:

  $$z_i^{\mathrm{O}}={\omega }^{\mathrm{T}}{z}_i^{\mathrm{l}}$$

  (2)

  where $z_i^{\mathrm{O}}$ and $z_i^{\mathrm{l}}$ denote the final evaluation score of user i and the initial score matrix of their respective indicators, respectively. ${\omega }^{\mathrm{T}}$ is defined as the transpose of the weight vector coefficient $\omega$.
• The MEVPP selects high-quality DERs for aggregation on the basis of their comprehensive performance evaluation scores.

The same procedure is subsequently applied to evaluate and select wind power units, photovoltaic units, gas turbines, and gas boilers. The final aggregated DERs form the MEVPP, as illustrated in Figure 1.

Figure 1. MEVPP structure diagram.

2.2. Analysis of User-Side Load Characteristics

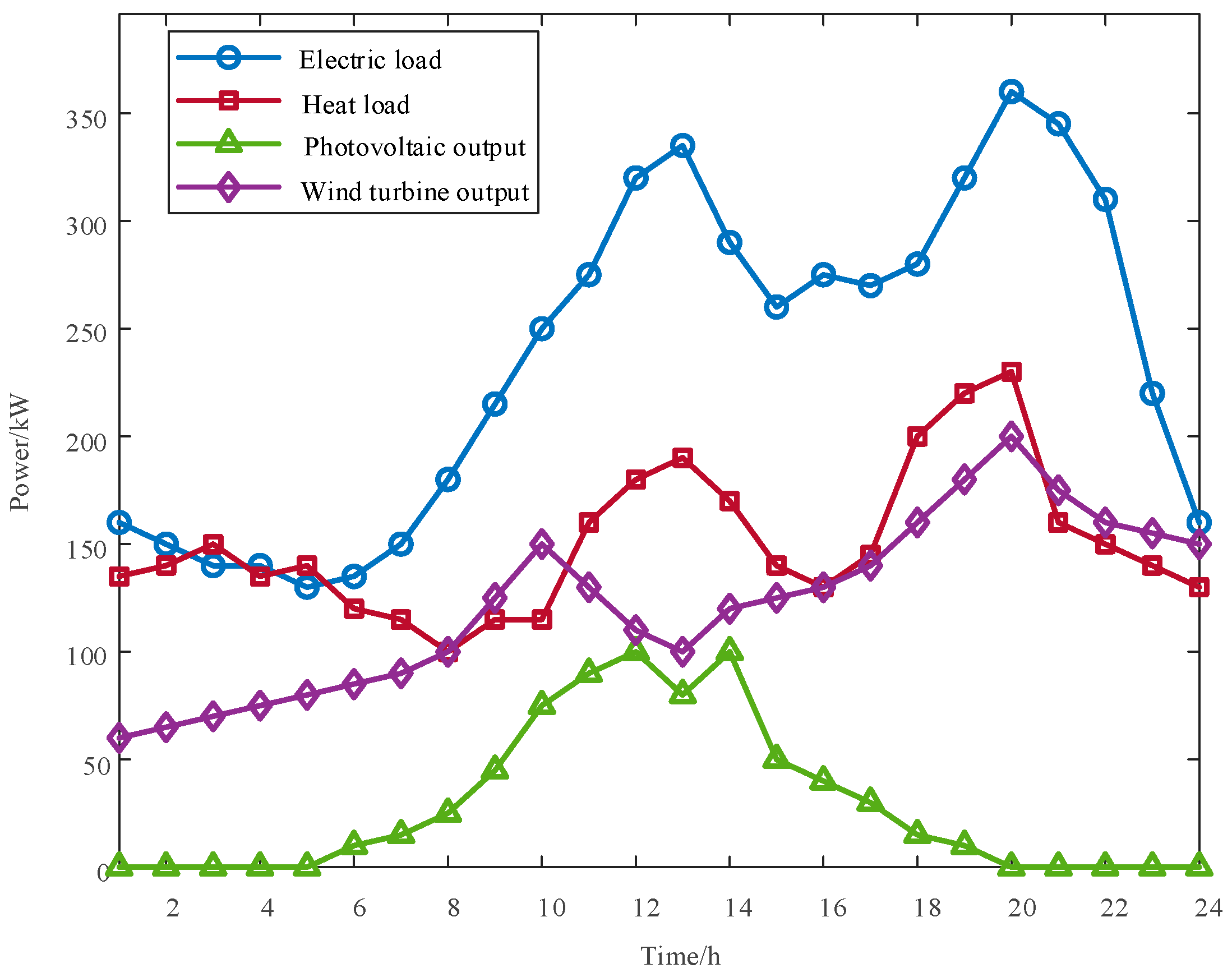
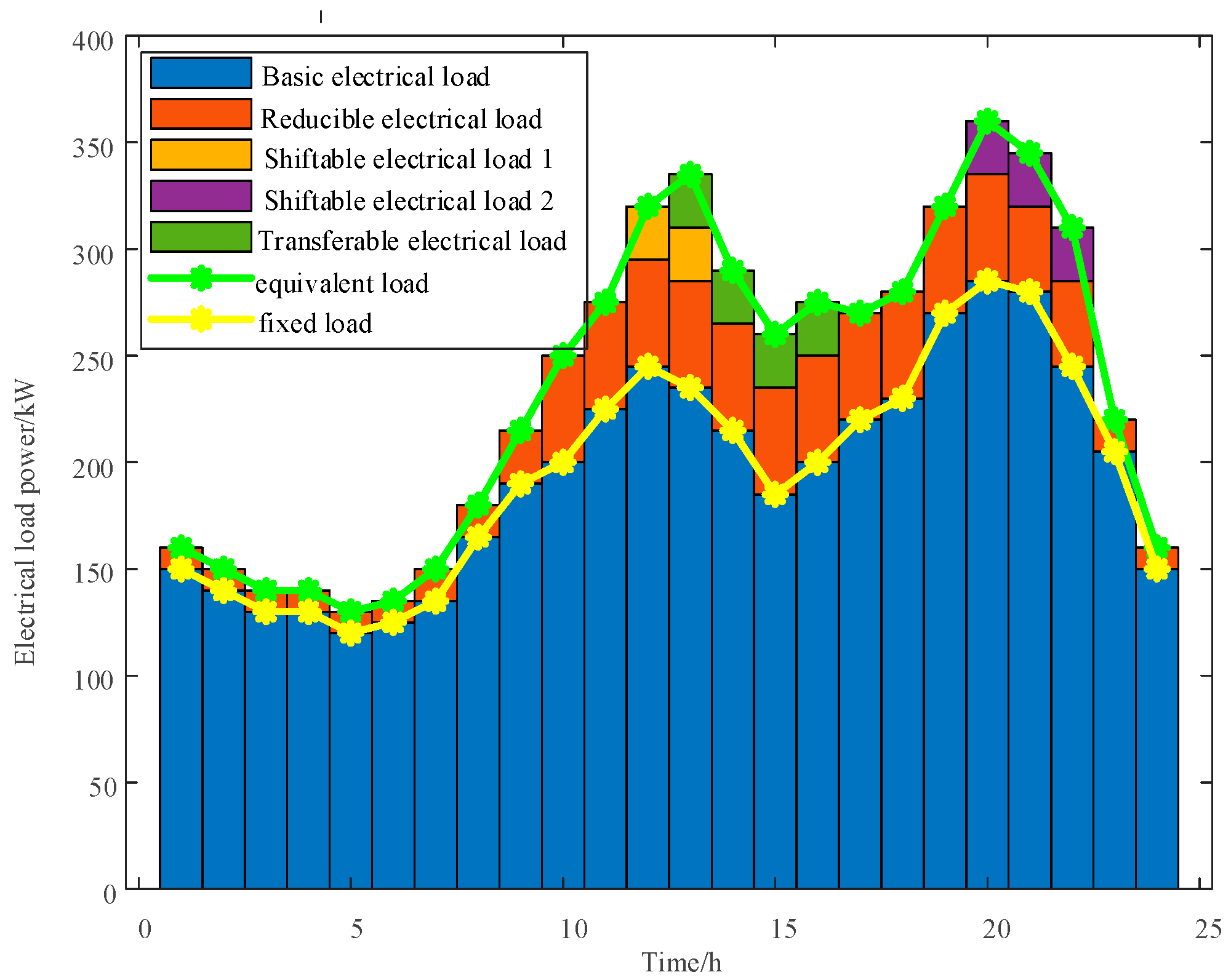
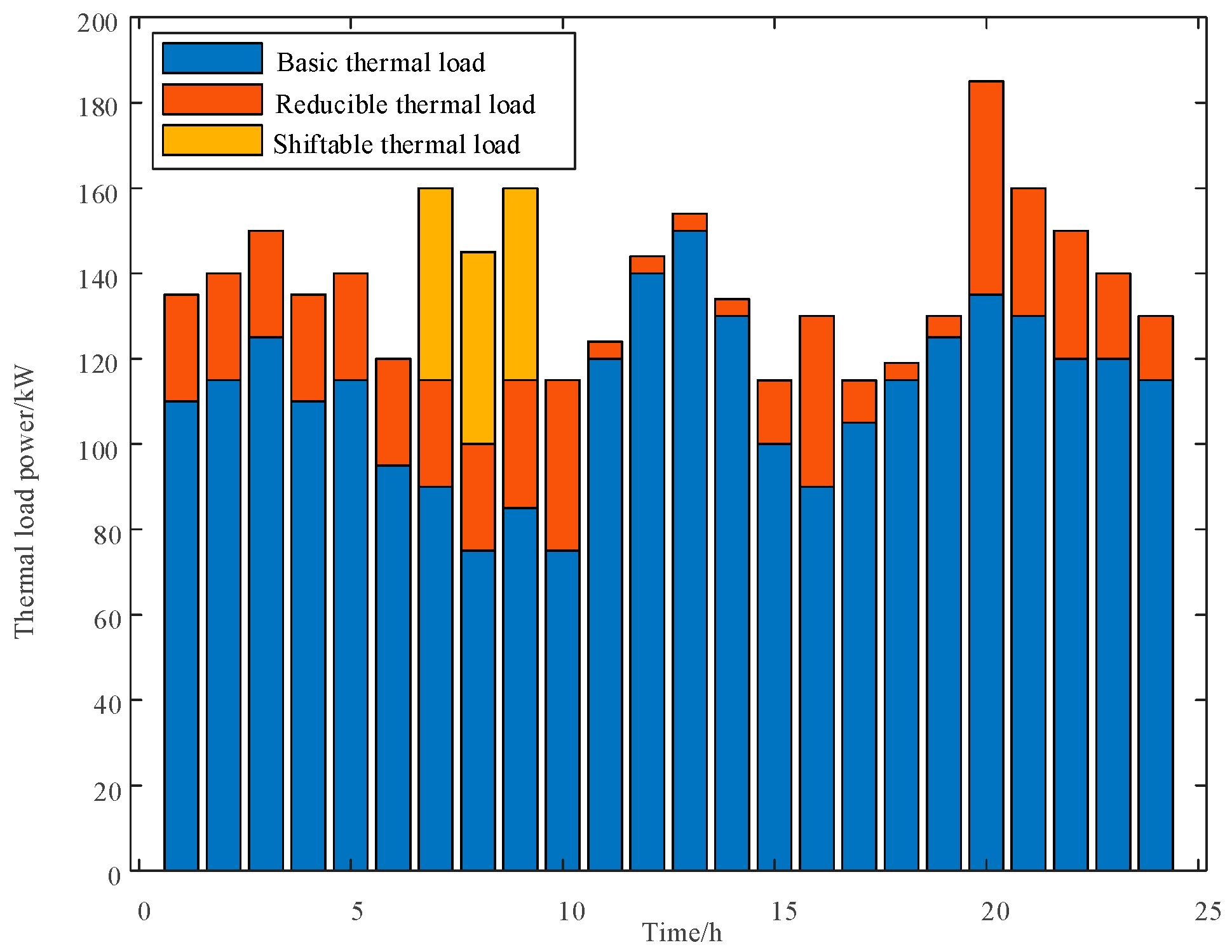
In the MEVPP constructed in this paper, the user-side loads include electrical loads and thermal loads. On the basis of their response characteristics, the user-side loads are recategorized as follows: rigid loads (must be satisfied and do not participate in dispatch), time-shiftable loads (whose operating time can be shifted but with a fixed power curve shape), power-adjustable loads (whose power can be adjusted within a certain range while maintaining constant total energy consumption), and interruptible loads (which can be partially curtailed during specific periods). Because thermal loads are generally more sensitive than electrical loads, curtailable electrical loads, curtailable thermal loads, shiftable electrical loads, shiftable thermal loads, and transferable electrical loads were comprehensively considered in this study. For example, the mathematical modeling of electrical loads is described below:

2.2.1. Shiftable Loads

In the model of this analysis, the dispatch duration for all types of demand-side response resources is 1 h. The loads vector $L_{\mathrm{shift}}^{*}$ of shiftable loads vector $L_{\mathrm{shift}}$ before scheduling is denoted as follows:

$$L_{\mathrm{shift}}^{*}=\left(0,\dots ,P_{t_S}^{\mathrm{shift}},P_{t_S+1}^{\mathrm{shift}},\dots ,P_{t_D}^{\mathrm{shift}}\dots ,0\right)$$

(3)

where $t_S$ represents the start time interval and $t_D$ represents the response duration, $P_{t_S}^{\mathrm{shift}}$ represents the power shifted at time $t_S$.

Let $\left[t_{\mathrm{sh}-},t_{\mathrm{sh}+}\right]$ be the shift interval. Considering both the start time and duration of $L_{\mathrm{shift}}$, a binary variable $\alpha$ is introduced to indicate the state of $L_{\mathrm{shift}}$. The values of 0 and 1 for $\alpha$ represent the nonshifted and shifted states, respectively. Let $S_{\mathrm{shift}}$ denote the set of start times for the shift:

$$S_{\mathrm{shift}}=\left[t_{\mathrm{sh}-},t_{\mathrm{sh}+}-t_D+1\right]\cup \left\{t_S\right\}$$

(4)

If $\tau =t_S$, the load remains unchanged during that period. If $\tau \in \left[t_{sh-},t_{sh+}-t_D+1\right]$ and $\tau \ne t_S$, then the power distribution vector $L_{\mathrm{shift}}$ shifted from the start time interval $t_S$ to the start time interval $\tau$ of $L_{\mathrm{shift}}^{*}$ is as follows:

$$L_{\mathrm{shift}}=\left(0,\dots ,P_{\tau }^{\mathrm{shift}},P_{\tau +1}^{\mathrm{shift}},\dots ,P_{\tau +t_D-t_S}^{\mathrm{shift}}\dots ,0\right)$$

(5)

The compensation cost $F_{\mathrm{shift}}$ to be paid to the user after the shift can be expressed as follows:

$$F_{\mathrm{shift}}=F_{\mathrm{cost}}^{\mathrm{shift}}\cdot P_{\mathrm{sum}}^{\mathrm{shift}}\cdot {\displaystyle \sum _{t=t_{sh-}}^{t_{sh-}-t_D+1}{\alpha }_t}$$

(6)

where $F_{\mathrm{cost}}^{\mathrm{shift}}$ represents the unit price for the demand response and $P_{\mathrm{sum}}^{\mathrm{shift}}$ represents the total amount of load participating in the demand response.

2.2.2. Transferable Loads

Let $\left[t_{\mathrm{tr}-},t_{\mathrm{tr}+}\right]$ be the transfer interval, and introduce a binary variable $\beta$ to represent the state of the transferable Loads vector $L_{\mathrm{tran}}$. For transferable loads, the maximum and minimum power constraints must be satisfied:

$${\beta }_{\tau }{P}_{\min }^{\mathrm{tran}}\le P_t^{\mathrm{tran}}\le {\beta }_{\tau }{P}_{\max }^{\mathrm{tran}}$$

(7)

where $P_{\min }^{\mathrm{tran}}$ and $P_{\max }^{\mathrm{tran}}$ represent the minimum and maximum transferable power, respectively.

In this study, a constraint on the duration of the transferable load is introduced to prevent the load from being transferred across multiple time intervals, thereby reducing equipment wear, as shown in the following formula:

$${\displaystyle \sum _{\tau =t}^{t+T_{\min }^{\mathrm{tran}}-1}{\beta }_{\tau }}\ge T_{\min }^{\mathrm{tran}}\left({\beta }_{\tau }-{\beta }_{\tau -1}\right)$$

(8)

where $T_{\min }^{\mathrm{tran}}$ represents the minimum continuous operation time.

After the user performs the transferable load response, the MEVPP should pay the transfer compensation cost $F_{\mathrm{tran}}$:

$$F_{\mathrm{tran}}=F_{\mathrm{cost}}^{\mathrm{tran}}{\displaystyle \sum _{t=t_{tr-}}^{t_{tr+}}\left({\beta }_{\tau }{P}_t^{\mathrm{tran}}\right)}$$

(9)

where $F_{\mathrm{cost}}^{\mathrm{tran}}$ represents the compensation price per unit power load transfer that the MEVPP needs to pay, $P_t^{\mathrm{tran}}$ represents the transferable power at time t.

2.2.3. Reducible Loads

Reducible loads represent the amount of load reduction by the user during a certain period. A binary variable $\gamma$ is introduced to represent the state of the reducible load vector $L_{\mathrm{cut}}$.

The load after participation in the demand response can be expressed as follows:

$$P_{\tau }^{\mathrm{cut}}=\left(1-{\theta }_{\tau }{\gamma }_{\tau }\right)P_{\tau }^{\mathrm{cut}*}$$

(10)

where ${\theta }_{\tau }$ represents the load reduction coefficient in period $\tau$, ${\theta }_{\tau }\in \left[0,1\right]$, $P_{\tau }^{\mathrm{cut}*}$ represents the power of $L_{\mathrm{cut}}$ in period $\tau$ before scheduling, $P_{\tau }^{\mathrm{cut}}$ represents the power of $L_{\mathrm{cut}}$ in period $\tau$ after scheduling.

In the model developed in this paper, constraints on the consecutive reduce duration and the number of reduce events are added to increase users’ comfort. This part of the model can be expressed as follows:

• Lower limit constraint on consecutive reduction periods

  $${\displaystyle \sum _{t=1}^{t+T_{\min }^{\mathrm{cut}}-1}{\gamma }_t}\ge T_{\min }^{\mathrm{cut}}$$

  (11)
• Upper limit constraint on consecutive reduction periods

  $${\displaystyle \sum _{t=1}^{t+T_{\max }^{\mathrm{cut}}+1}(1-{\gamma }_t)}\ge 1$$

  (12)
• Constraint on the number of reduction events

  $${\displaystyle \sum _{t=1}^{24}{\gamma }_t}\le N_{\max }$$

  (13)

  $$F_{\mathrm{cut}}=F_{\mathrm{cost}}^{\mathrm{cut}}{\displaystyle \sum _{t=1}^T{\gamma }_t\left(P_t^{\mathrm{cut}}-P_t^{\mathrm{cut}*}\right)}$$

  (14)

  where $T_{\min }^{\mathrm{cut}}$ and $T_{\max }^{\mathrm{cut}}$ represent the minimum and maximum consecutive reduce periods, respectively; $N_{\max }$ is the upper limit for the number of reduce events; $F_{\mathrm{cost}}^{\mathrm{cut}}$ represents the price per unit power load transfer that the MEVPP needs to pay; $F_{\mathrm{cut}}$ represents the total cost of reducible loads.

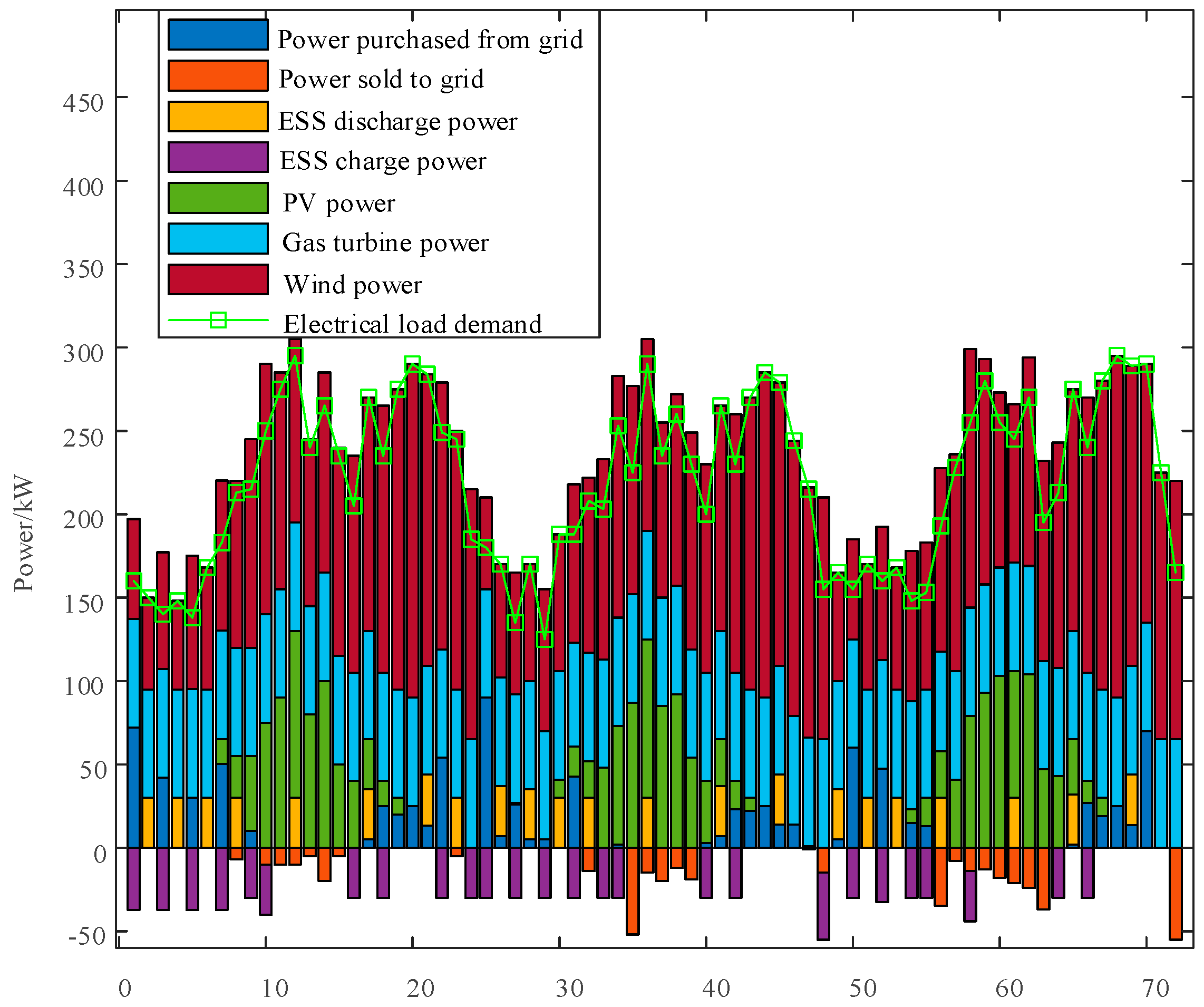
2.3. Shared Energy Storage Model

When the MEVPP is connected to a shared energy storage station for low-carbon dispatch, the service fee paid to the shared energy storage station must be considered.

$$F_{\mathrm{ess}}={\displaystyle \sum _{t=1}^T\delta \left(t\right)}\cdot \left[P_{\mathrm{ess},i}^{ch}(t)+P_{\mathrm{ess},i}^{dis}(t)\right]\cdot \Delta t$$

(15)

where $F_{\mathrm{ess}}$ represents the shared energy storage cost paid by MEVPP, $\delta \left(t\right)$ represents the service fee paid by the MEVPP to the energy storage station, $P_{\mathrm{ess},i}^{dis}(t)$ represents the discharge power utilized by the MEVPP from the shared energy storage, $P_{\mathrm{ess},i}^{ch}(t)$ represents the charge power utilized by the MEVPP from the shared energy storage station, and $\Delta t$ indicates the duration of a single dispatch period—in this paper, this parameter is assigned a value of 1 h.

The constraints include those for the charging and discharging of the shared energy storage, the state of charge (SOC) constraint, and the upper and lower power limits, which can be specifically expressed as follows:

• Charging/Discharging power constraint for users of the shared energy storage station

  $$\left\{\begin{array}{l}0\le P_{\mathrm{ess},i}^{ch}\le P_{\mathrm{ess}}^{\max }{U}_{\mathrm{ess},i}^{ch}\\ 0\le P_{\mathrm{ess},i}^{dis}\le P_{\mathrm{ess}}^{\max }{U}_{\mathrm{ess},i}^{dis}\\ U_{\mathrm{ess},i}^{ch}+U_{\mathrm{ess},i}^{dis}\le 1\\ U_{\mathrm{ess},i}^{ch}\in \left\{0,1\right\},U_{\mathrm{ess},i}^{dis}\in \left\{0,1\right\}\end{array}\right.$$

  (16)

  where $P_{\mathrm{ess}}^{\max }$ represents the upper limit for the charging/discharging power of the shared energy storage and $U_{\mathrm{ess},i}^{ch}$ and $U_{\mathrm{ess},i}^{dis}$ are binary variables indicating the charging and discharging states of user i, respectively.
• SOC constraint for the shared energy storage station

  $$\left\{\begin{array}{l}E(t)=E(t-1)+[{\eta }^{ch}{P}_{ch}(t)-{\displaystyle \frac{P_{dis}(t)}{{\eta }^{dis}}}]\\ E_{\min }\le E(t)\le E_{\max }\end{array}\right.$$

  (17)

  where $E_{\max }$ is the upper SOC limit, and $E_{\min }$ is the lower SOC limit; $E(t)$ is the state of charge of the shared energy storage station at time t; ${\eta }^{ch}$ and ${\eta }^{dis}$ are the charging and discharging efficiencies of the shared energy storage station, respectively; $P_{ch}(t)$ and $P_{dis}(t)$ represent the charging and discharging power of the shared energy storage station.
• Charging/Discharging power constraint for the shared energy storage station

  $$\left\{\begin{array}{l}0\le P_{ch}(t)\le P_{\max }{U}_{ch}\\ 0\le P_{dis}(t)\le P_{\max }{U}_{dis}\\ U_{ch}+U_{dis}\le 1\\ U_{ch}\in \left\{0,1\right\},U_{\mathrm{dis}}\in \left\{0,1\right\}\end{array}\right.$$

  (18)

  where $U_{ch}$ and $U_{dis}$ are binary variables, which indicate the charging/discharging state, and $P_{\max }$ is the upper limit for the charging/discharging power.
• Charging/Discharging power balance constraint for the shared energy storage station
  The sum of the charging/discharging powers from all users utilizing the shared energy storage station equals the total charging/discharging power of the energy storage station.

  $${\displaystyle \sum _{i=1}^N[P_{\mathrm{ess},i}^{dis}(t)-P_{\mathrm{ess},i}^{ch}(t)]=P_{dis}(t)}-P_{ch}(t)$$

  (19)

The model for the shared thermal storage device is identical to that of the shared electrical energy storage device. Owing to space limitations, this parameter will not be elaborated upon further here.

3. Scenario Generation Based on the ARMA Method and Scenario Reduction

In this paper, the MEVPP aggregator encompasses entities with uncertain outputs, such as wind power, photovoltaic generation, and electric heating loads. Furthermore, uncertainties exist in the spot market electricity price and carbon trading price. Consequently, when formulating a dispatch plan, the MEVPP must first address these uncertainties. This paper employs scenario generation and reduction techniques to handle these uncertainties, describing them with a classical scenario set containing probabilistic information. Taking photovoltaic as an example, the remaining uncertainty processing methods are the same as this.

First, an Auto-Regressive Moving Average (ARMA) model is adopted to generate sampled scenarios for wind and photovoltaic power output:

$$y_t={\displaystyle \sum _{i=1}^a{\varphi }_i{y}_{t-i}}+{\alpha }_t-{\displaystyle \sum _{j=1}^b{\theta }_j{\alpha }_{t-i}}$$

(20)

where $y_t$ represents the time series value at time t, ${\varphi }_i$ is the autoregressive parameter, ${\theta }_j$ is the moving average parameter, and ${\alpha }_t$ is gaussian white noise.

After generating the initial scenario set, this paper utilizes the fast forward selection technique based on probability distance for scenario reduction. The steps are as follows:

Step 1: Calculate the minimum geometric distance between each pair of scenarios s and s’ in set S.

Step 2: Identify the scenario d that has the smallest sum of probability distances to the remaining scenarios.

Step 3: Replace scenario d in S with scenario r, which is the geometrically closest scenario to d in S. Then, add the probability of d to that of r, forming a new scenario set S’.

Step 4: Determine whether the number of remaining scenarios meets the requirement. If not, repeat the above steps; if so, conclude the scenario reduction process.

4. Carbon Trading Mechanism Cost Model

4.1. Carbon Trading Mechanism

Carbon trading is a market-based environmental and economic policy, the core of which involves commodifying carbon emission rights and permitting their trade in designated markets. The governing regulatory authority first allocates an initial carbon quota to compliance entities. If an entity’s actual carbon emissions are lower than its allocated quota, the surplus can be sold on the market for profit; conversely, if emissions exceed the quota, the entity must purchase additional allowances to fulfill its compliance obligations. The aim of this mechanism is to incentivize the optimization of energy structures and the improvement of energy efficiency through economic means, thereby achieving greenhouse gas emission reduction. Due to the currently limited liquidity in China’s carbon market and relatively stable carbon price fluctuations [25], hence, a widespread approach in electricity-carbon market coupling studies is to treat carbon market transactions at a daily resolution, thereby resolving temporal scale inconsistencies [26].

4.2. Carbon Trading Cost Calculation

On the basis of the above analysis, the carbon trading cost of the MEVPP in this study can be modeled as follows:

$$f_{{\mathrm{CO}}_2}=C_t\left(E_{\mathrm{out}}-E_{\mathrm{all}}\right)$$

(21)

where $f_{{\mathrm{CO}}_2}$ represents the carbon trading cost of the MEVPP; a positive value of $f_{{\mathrm{CO}}_2}$ indicates excess emissions, whereas a negative value reflects a reduction in emissions; $E_{\mathrm{out}}$ denotes the total carbon emissions on the operating day; $E_{\mathrm{all}}$ is the allocated carbon quota; and $C_t$ indicates the carbon price on the operating day.

In the MEVPP, carbon emissions from different types of equipment occur at different stages. Carbon emissions from gas turbines and gas boilers are primarily concentrated during the operational phase [27], whereas equipment such as energy storage systems, photovoltaics, and wind power generate negligible carbon emissions during operation, which can be disregarded. However, significant indirect carbon emissions arise during the construction and transportation phases of these facilities. Therefore, such emissions should be accounted for in the total carbon emissions of the system [28]. To increase the accuracy of carbon emission accounting, a two-stage carbon emission calculation method is introduced as follows:

$$E_{\mathrm{out}}={\displaystyle \sum _{i=\mathsf{\Omega }}\left(c_i^{\mathrm{pre}}+c_i^{\mathrm{run}}\right)}{P}_i$$

(22)

where $\mathsf{\Omega }$ represents the total number of distributed energy resources (DERs) aggregated in the MEVPP; $c_i^{\mathrm{pre}}$ and $c_i^{\mathrm{run}}$ denote the carbon emission coefficients of device i during the production and operation stages, respectively; and $P_i$ represents the power output of device i.

5. MEVPP Low-Carbon Economic Dispatch Model

5.1. Objective Function

The objective function of the proposed model is to minimize the sum of the MEVPP’s operating costs and carbon trading costs for the operating day:

$$\min f=f_{\mathrm{VPP}}+f_{{\mathrm{CO}}_2}$$

(23)

$$f_{\mathrm{VPP}}=F_{\mathrm{NET}}+F_{\mathrm{DG}}+F_{\mathrm{MT}}+F_{\mathrm{GB}}+F_{\mathrm{ESS}}+F_{TSS}+F_{\mathrm{L}}$$

(24)

in which

$$F_{\mathrm{NET}}={\displaystyle \sum _{t=1}^T{K}_{\mathrm{NET}}\left(t\right)}{P}_{\mathrm{NET}}\left(t\right)$$

(25)

$$F_{\mathrm{DG}}={\displaystyle \sum _{t=1}^T\left[K_{\mathrm{W}}\left(t\right)P_{\mathrm{W}}\left(t\right)+K_{\mathrm{PV}}\left(t\right)P_{\mathrm{PV}}\left(t\right)\right]}$$

(26)

$$F_{\mathrm{MT}}={\displaystyle \sum _{t=1}^T{K}_{\mathrm{MT}}\left(t\right)}{P}_{\mathrm{MT}}\left(t\right)$$

(27)

$$F_{\mathrm{GB}}={\displaystyle \sum _{t=1}^T{K}_{\mathrm{GB}}\left(t\right)}{P}_{\mathrm{GB}}\left(t\right)$$

(28)

$$F_{\mathrm{ESS}}={\displaystyle \sum _{t=1}^T{K}_{\mathrm{ESS},t}(P_{\mathrm{ess},i}^{dis}(t)+P_{\mathrm{ess},i}^{ch}(t)})$$

(29)

$$F_{TSS}={\displaystyle \sum _{t=1}^T{K}_{TSS,t}}\left|P_{TSS}\left(t\right)\right|$$

(30)

where $f_{\mathrm{VPP}}$ represents the operating cost of MEVPP. $f_{{\mathrm{CO}}_2}$ represents the carbon market transaction costs. $F_{\mathrm{NET}}$ denotes the cost of electricity purchased from the grid, $F_{\mathrm{DG}}$ represents the cost of wind and photovoltaic power generation, $F_{\mathrm{MT}}$ indicates the operating cost of gas turbines, $F_{\mathrm{GB}}$ refers to the operating cost of gas boilers, $F_{\mathrm{ESS}}$ stands for the cost associated with charging and discharging utilizing shared energy storage, $F_{TSS}$ represents the cost of charging and discharging heat using shared thermal storage systems, $F_{\mathrm{L}}$ denotes the total cost of demand response, $K_{\mathrm{NET}}\left(t\right)$ signifies the electricity price on the operating day at time t, $P_{\mathrm{NET}}\left(t\right)$ indicates the power of electricity purchased from or sold to the grid at time t, $K_{\mathrm{W}}\left(t\right)$ and $K_{\mathrm{PV}}\left(t\right)$ denote the cost coefficients of wind and photovoltaic units at time t, $P_{\mathrm{W}}\left(t\right)$ and $P_{\mathrm{PV}}\left(t\right)$ represent the output power of wind and photovoltaic units at time t, $K_{\mathrm{MT}}\left(t\right)$ denotes the cost coefficient of gas turbines at time t, $P_{\mathrm{MT}}\left(t\right)$ indicates the output power of gas turbines at time t, $K_{\mathrm{GB}}\left(t\right)$ represents the cost coefficient of gas boilers at time t, $P_{\mathrm{GB}}\left(t\right)$ denotes the output power of gas boilers at time t, $K_{\mathrm{ESS},t}$ and $K_{TSS,t}$ represent the costs associated with the charging/discharging power of shared energy storage and shared thermal storage systems at time t, respectively, and $P_{TSS}\left(t\right)$ denotes the charging/discharging power of the shared thermal storage system at time t, with absorption considered positive and release considered negative.

5.2. Constraints

In conducting low-carbon economic dispatch, the MEVPP must satisfy the load balance constraints, the upper and lower output limits of each unit, and the constraints on the charging and discharging capacities utilizing shared energy storage systems. Among these constraints, the load balance constraints and the output limits of the units are expressed in Equations (31)–(34), and the charging and discharging constraints of the shared energy storage systems are given in Equations (15)–(19):

• Power balance constraints

  $$P_{\mathrm{NET}}(t)+P_{\mathrm{W}}(t)+P_{\mathrm{PV}}(t)+P_{\mathrm{MT}}(t)-F_{\mathrm{ESS}}(t)=P_{\mathrm{LOAD}}(t)$$

  (31)

  $$Q_{\mathrm{HT}}(t)+Q_{\mathrm{GB}}(t)-Q_{\mathrm{HST}}(t)=Q_{\mathrm{LOAD}}(t)$$

  (32)

  where, $P_{\mathrm{LOAD}}(t)$ and $Q_{\mathrm{LOAD}}(t)$ represent the electrical and thermal load demands at time t, respectively.
• Upper and lower output limits of units
  The output of each renewable energy unit and energy conversion equipment must satisfy the upper and lower limit constraints:

  $$0\le P_{\mathrm{W}/\mathrm{PV}}(t)\le P_{pred}$$

  (33)

  $$0\le P_{\mathrm{WT}/\mathrm{GB}}(t)\le P_{\mathrm{N}}$$

  (34)

  where $P_{pred}$ represents the forecasted output of wind and photovoltaic power and $P_{\mathrm{N}}$ denotes the rated power of the gas turbine and gas boiler, respectively.

6. Case Study

6.1. Basic Data

The model proposed in this paper is a linear model. The numerical testing was conducted on a platform equipped with an NVIDIA GeForce GTX 1050Ti graphics card (NVIDIA, Santa Clara, CA, USA) and an Intel(R) Core(TM) i7-10700 CPU, using MATLAB 2022a, with the Cplex solver 12.10 employed for solution.

Resources from the regional electricity distribution network and gas network in a specific area were aggregated to form the MEVPP. The energy sources within the MEVPP include wind and photovoltaic (PV) units, gas boilers, and gas turbines. Furthermore, the MEVPP can interact electrically and thermally with shared energy storage and shared thermal storage systems. This study adopts a single-node equivalent model based on energy balance, aiming to analyze the system-level energy-carbon coordinated optimization mechanism. For the time being, it does not take into account network constraints such as power grid power flow and gas flow in natural gas pipelines. In this study, a 24 h operational cycle is modeled for the next day, with a 1 h time interval, the carbon market trading time interval is also 1 h. The generated typical scenarios are shown in Figure 2. In this paper, a stepwise carbon pricing mechanism is adopted for carbon market transactions. Specifically, when carbon emissions are less than 120 kg, the unit price is 0.15 CNY/kg; for the part of emissions exceeding 120 kg, the unit price is 0.4 CNY/kg. The operational participation of the MEVPP is detailed in Table 3.

Figure 2. Typical scenario diagram. (a) Photovoltaic power. (b) Wind power. (c) Electric load power. (d) Heat load power. (e) Electricity purchase price. (f) Electricity sale price.

Table 3. MEVPP operating parameters.

Type	Minimum Power Limit/kW	Maximum Power Limit/kW	Marginal Operating Cost/(CNY/kWh)
Distribution network			Operating day electricity price
Photovoltaic units	0	Predicted power	0.08
Wind turbine	0	Predicted power	0.12
Gas boiler	0	105	Operating day gas price
Gas turbine	0	205	Operating day gas price

The daily load curves and the forecasted output data for the renewable energy units are shown in Figure 3.

Figure 3. Electric heat load and wind solar output curve.

On the basis of the carbon emission accounting method for energy equipment proposed in this paper, the carbon emissions and corresponding carbon allowances for each energy unit within the MEVPP on the operating day are calculated and presented in Table 4. The carbon price for the operating day is set at 150 CNY/t.

Table 4. Carbon emission factors and allowance factors.

Type of Energy Source	${\mathit{c}}_{\mathit{i}}^{\mathbf{run}}$ $\mathbf{g}/(\mathbf{kW}\cdot \mathbf{h})$	${\mathit{c}}_{\mathit{i}}^{\mathbf{pre}}$ $\mathbf{g}/(\mathbf{kW}\cdot \mathbf{h})$	Carbon Quota $\mathbf{g}/(\mathbf{kW}\cdot \mathbf{h})$	Total Carbon Emission Coefficient $\mathbf{g}/(\mathbf{kW}\cdot \mathbf{h})$
converted carbon emissions from the grid	0	1302	797	1302
Gas turbine/gas boiler	447	115	423	562
photovoltaic power generation	0	55	79	55
wind-generated electricity	0	44	79	44
Energy storage/heat storage system	0	91	0	91

Before low-carbon economic dispatch is conducted, the baseline data for various types of flexible electrical loads and flexible thermal loads are presented in Table 5, Table 6 and Table 7 and Figure 4 and Figure 5, respectively.

Table 5. Shiftable load parameters.

Type	${\mathit{t}}_{\mathbf{sf}-}$	${\mathit{t}}_{\mathbf{sf}+}$	${\mathit{t}}_{\mathbf{D}}/\mathbf{h}$	${\mathit{F}}_{\mathrm{cost}}^{\mathbf{shift}}/\mathbf{CNY}\cdot {(\mathbf{kW}\cdot \mathbf{h})}^{-1}$
Shiftable electrical load 1	5:00	21:00	2	0.2
Shiftable electrical load 2	7:00	23:00	3	0.2
Shiftable thermal load	5:00	21:00	3	0.1

Table 6. Transferable load parameters.

Type	${\mathit{T}}_{\mathbf{min}}^{\mathbf{tran}}/\mathbf{h}$	${\mathit{P}}_{\mathbf{min}}^{\mathbf{tran}}~{\mathit{P}}_{\mathbf{max}}^{\mathbf{tran}}$	${\mathit{t}}_{\mathit{t}\mathit{r}-}~{\mathit{t}}_{\mathit{t}\mathit{r}+}$	${\mathit{F}}_{\mathrm{cost}}^{\mathrm{tran}}/\mathrm{CNY}\cdot {(\mathbf{kW}\cdot \mathbf{h})}^{-1}$
Transferable electrical load	2	8~26.7 kW	4:00–22:00	0.3

Table 7. Reducible load parameters.

Type	${\mathit{T}}_{\mathbf{min}}^{\mathbf{cut}}/\mathbf{h}$	${\mathit{T}}_{\mathbf{max}}^{\mathbf{cut}}/\mathbf{h}$	${\mathit{N}}_{\mathbf{max}}$	${\mathit{F}}_{\mathbf{cost}}^{\mathbf{cut}}/\mathbf{CNY}\cdot {(\mathbf{kW}\cdot \mathbf{h})}^{-1}$
Reducible electrical load	2	5	8	0.4
Reducible thermal load	2	5	8	0.2

Figure 4. Electrical Load Distribution Before Optimization.

Figure 5. Thermal Load Distribution Before Optimization.

6.2. Analysis of Simulation Results

6.2.1. Analysis of the Power Output of Each Device

Low-carbon economic dispatch of the MEVPP system is performed, considering various types of flexible loads and shared energy storage devices. The resulting outcomes for the different demand response types and the output profiles of the various equipment units are shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.

Figure 6. Electrical Load Distribution After Optimization.

Figure 7. Thermal Load Distribution After Optimization.

Figure 8. Comparison of the Electrical Load Profiles Before and After Optimization.

Figure 9. Comparison of Thermal Load Profiles Before and After Optimization.

Figure 10. Electrical Power Balance Diagram after Low−Carbon Economic Dispatch.

Figure 11. Thermal Power Balance Diagram after Low-Carbon Economic Dispatch.

Within the simulation parameters defined in this study, the time periods 0:00–7:00 are designated as the off-peak electricity price periods; 8:00–10:00, 16:00–18:00, and 22:00–24:00 are designated as the mid-peak periods; and 11:00–15:00 and 19:00–21:00 are designated as the on-peak periods. The electrical load profile after the low-carbon economic dispatch is shown in Figure 6, and the thermal load profile is shown in Figure 7.

Analysis of Figure 6 reveals that following the implementation of the low-carbon economic dispatch, the shiftable loads are shifted from their initial concentration in the on-peak and mid-peak periods to the off-peak and mid-peak periods. Similarly, the two categories of shiftable loads are relocated from the predispatch on-peak and mid-peak periods to the mid-peak and off-peak periods, respectively. The transferable loads are moved from the mid-peak and on-peak periods to the off-peak period. By managing this demand response shift, the MEVPP reduces associated costs, thereby increasing the overall economic efficiency of the system.

A direct comparison of the load profiles before and after optimization is shown in Figure 8. The results demonstrate that the MEVPP optimization successfully minimizes the load during all on-peak and some mid-peak periods by shifting shiftable and transferable loads to off-peak periods, all while adhering to all system constraints. This approach achieves the dual objectives of maintaining user comfort and maximizing system revenue while reducing carbon emissions.

A comparison between Figure 5 and Figure 7 indicates an analogous strategy for thermal loads: the MEVPP shifts shiftable thermal loads from on-peak to off-peak and mid-peak periods, significantly reducing the shiftable thermal load during peak times, with the majority being shifted to the off-peak period. This effect is clearly illustrated in Figure 9, which shows a pronounced reduction in the thermal load during on-peak periods and a decrease in some mid-peak periods post optimization. Conversely, the load increases during periods 7–9, corresponding directly to the time intervals to which the shiftable thermal loads were relocated.

The output power of various units within the MEVPP following the implementation of low-carbon economic dispatch is shown in Figure 10. The results demonstrate that to optimize the economic and low-carbon performance for the overall system, the MEVPP prioritizes maximizing the utilization of electrical energy generated by the wind turbine and photovoltaic units. During periods 11, 13–15, and 24, surplus power is sold back to the main grid. When the output from the renewable units is insufficient to meet the load demand, the MEVPP preferentially dispatches the gas turbine for power supply because of its relatively low generation cost and carbon emissions. If the load demand increases beyond the combined capacity of these three aforementioned sources, the MEVPP then purchases electricity from the grid.

Concurrently, the MEVPP utilizes a shared energy storage device for charging and discharging operations. Specifically, while maintaining the electrical power balance of the system, it strategically charges the storage during low electricity price periods and discharges it during high price periods. Furthermore, this operational strategy increases the overall economic benefit of the MEVPP.

The thermal outputs of the various equipment units following low-carbon economic dispatch are shown in Figure 11. As shown in the figure, the majority of the thermal energy required by the MEVPP is supplied by the gas turbine because of its relatively low operational cost. When the output of the gas turbine reaches its maximum capacity and remains insufficient to meet the thermal load demand, the gas boiler is activated to provide supplementary power. Concurrently, the MEVPP utilizes the shared thermal storage system by storing thermal energy during periods of lower heating costs and discharging it during periods of higher costs. This operational strategy increases the system’s economic efficiency and contributes to a reduction in carbon emissions.

The carbon emissions generated by the operation of various equipment units in fulfilling the system’s electrical and thermal power balance requirements are shown in Figure 12. Because the carbon emissions associated with electricity purchased from the grid are allocated to the MEVPP and the carbon emission factors of the gas turbine and gas boiler are relatively high, periods characterized by significant power output from these three sources consequently exhibit elevated carbon emission levels.

Figure 12. Total carbon emissions during each period.

6.2.2. Analysis of Scheduling Results in Different Scenarios

To further investigate the optimization effect of the proposed model on the MEVPP dispatch operation, two additional models are established for comparative analysis against the model presented in this paper. Analysis of Dispatch Results for the Six Scenarios are shown in Table 8. Six distinct scenarios are defined for this comparison: Scenario 1: Considering shared electrical energy storage system and shared thermal energy storage system, but carbon trading is not considered, and flexible electrical/thermal loads are not incorporated. Scenario 2: Considering shared electrical energy storage system and shared thermal energy storage system, but carbon trading is considered, but flexible electrical/thermal loads are not incorporated. Scenario 3: Both shared electrical energy storage system, shared thermal energy storage system, carbon trading and flexible electrical/thermal loads are considered. Scenario 4: Both shared electrical energy storage system, shared thermal energy storage system, carbon trading and flexible electrical/thermal loads are considered, the optimization horizon is extended from one day to three days, the comparison of electrical load and thermal load before and after optimization is shown in Figure 13 and Figure 14, respectively, the electrical power balance and thermal power balance after low-carbon economic dispatch is shown in Figure 15 and Figure 16, respectively. Scenario 5: Both shared electrical energy storage system, shared thermal energy storage system, carbon trading and flexible electrical/thermal loads are considered; however, wind power and photovoltaic output are extreme scenarios. The extreme scenarios of wind and photovoltaic output are shown in Table 9. Scenario 6, Both shared electrical energy storage system, shared thermal energy storage system, carbon trading and flexible electrical/thermal loads are considered, the number of wind turbines is increased from one to two, and the number of photovoltaic units from one to three. The charge/discharge power limit and capacity of the energy storage equipment are expanded by a factor of 2, the total output of the wind turbines and photovoltaic units in Scenario 6 at each time interval is presented in Table 10.

Table 8. Analysis of Dispatch Results for the Six Scenarios.

Scenario	Operating Cost/CNY	Carbon Transaction Cost/CNY	Total Cost/CNY	Total Renewable Energy Output/kWh	Total Carbon Emissions Traded/t	Total Carbon Emissions/t
1	84,812.92	0	84,812.92	2768.07	0	0.765
2	89,085.47	183.38	89,268.85	2770	0.761	0.761
3	48,277.24	58.56	48,335.80	3598	0.320	0.320
4	144,783.26	224.14	144,787.40	10,831	0.846	0.846
5	61,880.39	143.46	62,023.85	2703	0.628	0.628
6	24,405.31	395.64	24,800.95	6464.88	1.468	1.468

Figure 13. Comparison of Electrical Load Profiles Before and After Optimization.

Figure 14. Comparison of Thermal Load Profiles Before and After Optimization in scenario 4.

Figure 15. Electrical Power Balance Diagram after Low−Carbon Economic Dispatch in scenario 4.

Figure 16. Thermal Power Balance Diagram after Low−Carbon Economic Dispatch in scenario 4.

Table 9. Extreme Scene of Wind and Photovoltaic output.

Time/h	Wind/kW	Photovoltaic/kW	Time/h	Wind/kW	Photovoltaic/kW	Time/h	Wind/kW	Photovoltaic/kW
1	60	0	9	125	40	17	140	20
2	65	0	10	50	60	18	60	10
3	70	0	11	30	15	19	80	5
4	75	0	12	110	10	20	200	0
5	80	0	13	100	20	21	175	0
6	85	5	14	120	20	22	160	0
7	90	10	15	125	30	23	155	0
8	100	20	16	30	25	24	150	0

Table 10. Total Output of Wind and Photovoltaic Units in Scenario 6.

Time/h	Wind/kW	Photovoltaic/kW	Time/h	Wind/kW	Photovoltaic/kW	Time/h	Wind/kW	Photovoltaic/kW
1	60	0	9	125	40	17	140	20
2	65	0	10	50	60	18	60	10
3	70	0	11	30	15	19	80	5
4	75	0	12	110	10	20	200	0
5	80	0	13	100	20	21	175	0
6	85	5	14	120	20	22	160	0
7	90	10	15	125	30	23	155	0
8	100	20	16	30	25	24	150	0

Table 8 shows the operating costs, new energy consumption, and total carbon emissions of the three scenarios. Comparing Scenario 1 and Scenario 2, when the system considers carbon trading, the MEVPP will adjust the output of the equipment to comprehensively consider the economy and low carbon emissions, which will increase the operating cost of the system and increase the consumption of new energy. A comparison of Scenario 2 and Scenario 3 reveals that when the system considers the demand-side response of electricity and heat, the operating cost of the system is greatly reduced to approximately 54.2% of that when the demand response is not considered. Moreover, the carbon emissions decrease accordingly, which is 42% of that without considering the demand response, and the consumption of new energy further increases by 130%. This represents the upper limit of improvement under ideal conditions. In practice, however, the improvement capability will deteriorate when extreme scenarios of renewable energy output occur or when changes in energy storage capacity take place. Nevertheless, compared to scenarios without participation in demand response or carbon market trading, the operational costs will still be reduced. Scenarios 4 and 6 verify the scalability of the proposed model in this paper. Even when the optimization horizon is extended and the number of distributed generation (DG) units is increased, the proposed model still achieves excellent optimization performance.

In summary, the model proposed in this paper can reduce the carbon emissions of the system while improving the economy such that the entire system can achieve low-carbon economic operations.

7. Conclusions

To address the problem of insufficient research on VPP multienergy complementary low-carbon economic operations, in this paper, a MEVPP low-carbon economic operation model that comprehensively considers the multienergy demand response and electricity–heat shared energy storage is proposed. Through case analysis, the following conclusions can be drawn:

• Compared with not considering the multienergy demand response, the model proposed in this paper can reduce the system operating cost to 54.2%, reduce the system carbon emission to 42%, and realize the low-carbon economic operation of the system.This represents the upper limit of improvement under ideal conditions. In practice, how-ever, the improvement capability will deteriorate when extreme scenarios of renewable energy output occur or when changes in energy storage capacity take place. Nevertheless, compared to scenarios without participation in demand response or carbon market trading, the operational costs will still be reduced.
• The MEVPP uses shared storage equipment to discharge during the peak load period and charge during the low load period, thereby reducing the operating cost of the system.

With the continuous advancement of the electricity market and construction of the carbon trading market, the time scale of trading will be increased. In the future, the multitime-scale low-carbon economy optimization problem of the MEVPP will be further studied.