Ultra-Short-Term Multi-Step Photovoltaic Power Forecasting Based on Similarity-Based Daily Clustering

Abstract

Photovoltaic (PV) power generation is inherently intermittent and volatile, complicating power system operation and control. Accurate forecasting is crucial for proactive grid responses and optimal energy resource scheduling. This study proposes a novel hybrid forecasting model that achieves high-precision PV power forecasting by integrating similar-day clustering, generating extreme weather samples, and optimizing the Bidirectional Temporal Convolutional Network (BiTCN) and Bidirectional Gated Recurrent Unit (BiGRU) model via the Animated Oat Optimization (AOO) algorithm. The proposed method outperforms other models in the three evaluation metrics of mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R²). The innovations lie in the integration of similar-day clustering with deep learning and the application of AOO for hyperparameter optimization, which significantly enhances forecasting accuracy and robustness.

1. Introduction

Solar energy is increasingly being utilized on a global scale, largely because it stands out as an abundant and environmentally sustainable renewable option. As a key candidate to meet future energy demands, photovoltaic (PV) power generation has attracted significant attention in modern power grids for its efficient use of solar energy. It is projected that by 2025, PV generation will supply one-quarter of the world’s electricity demand [1]. However, the intermittent nature of solar energy necessitates that the generated electricity be either consumed immediately or stored in costly battery systems. To maintain a stable energy supply and enable effective resource planning, achieving high accuracy in PV power forecasting is critical.

The primary approaches for predicting PV power currently encompass physical models, statistical and probabilistic methods, and machine learning models. Physical models do not rely on historical data but rather compute PV power output directly using meteorological information (e.g., weather forecasts, satellite cloud maps) and system parameters such as PV panel installation angles and surface temperatures. In studies based on physical modeling, Zhi et al. [2] constructed a model based on physical principles for PV power forecasting, which incorporates both meteorological parameter prediction and an enhanced MPPT algorithm. Experimental results under various weather conditions demonstrated low prediction error, thereby improving both accuracy and applicability. El Ainaoui et al. [3] introduced new mathematical formulations using implicit single-diode models (SDM) and explicit Das models (DM) to describe variations in model parameters with temperature and irradiance. Field tests at the Moroccan Green Energy Park showed that their method could effectively predict PV performance, achieving an NRMSE below 4.16%, contributing to PV system optimization and enhanced grid stability. Zaimi et al. [4] proposed two new techniques for identifying the physical parameters of single-diode circuit models, which rely on establishing correlations between key photovoltaic indicators and quality factors. Manufacturer data were utilized to determine temperature and radiation coefficients, investigating the influence of environmental factors on model parameters. Testing on KC130GT and SM55 photovoltaic panels validated the effectiveness of the methods and models, providing support for photovoltaic system performance prediction. Tifidat et al. [5] proposed a novel simulation approach for PV module performance based on the single-diode model. By combining numerical and analytical techniques, they reduced the number of unknown parameters and eliminated the need for approximation and iteration, relying only on data under standard test conditions and simplifying the modeling process. Comparative experiments on PV modules using various technologies showed lower error and faster convergence compared to other methods, providing an effective tool for dynamic performance evaluation and design. Although physical modeling does not require historical data and is applicable to any prediction horizon, it faces practical challenges. A major constraint is the need for highly detailed, site-specific parameters tailored to large-scale PV plants, which makes these models less suitable for residential rooftop PV systems [6]. Furthermore, compared to data-driven methods, physical models demand more domain knowledge, as they rely on solving complex differential equations based on mathematical descriptions of photovoltaic conversion. This not only imposes high computational costs but also leads to longer runtimes to achieve accurate results. Despite a solid understanding of the underlying physical phenomena and accurate modeling, even mature and well-studied models can introduce errors [7]. Many fail to account for localized effects such as system faults, cloud movement, partial shading, or snow accumulation—factors that data-driven methods are better equipped to handle [8].

Statistical approaches rely on the analysis of historical data to construct a functional relationship between past and predicted values. Classical statistical techniques such as vector autoregression (VAR) [9] and autoregressive integrated moving average (ARIMA) models [10] were dominant in early studies. Li et al. [11] proposed an autoregressive moving average model with exogenous inputs (ARMAX), incorporating meteorological features to forecast power output. By using easily obtainable parameters such as temperature, precipitation, sunshine duration, and humidity, the model retained the simplicity of ARIMA without relying on solar irradiance forecasts. It also proved to be more general and flexible in practical applications. Based on real-world data from a 2.1 kW grid-connected PV system, the ARMAX model significantly outperformed ARIMA in prediction accuracy. Despite advantages such as structural simplicity and fast computation, statistical models struggle to capture the volatile and dynamic nature of PV data, limiting their predictive performance [12].

In recent years, machine learning has been widely applied in PV power forecasting due to its ease of modeling, high accuracy, and strong generalization capability. Sulaiman et al. [13] successfully applied neural network (NN) models for forecasting the power generation of rooftop PV systems. The authors reported superior accuracy and consistency over alternative approaches. For day-ahead forecasting in a real microgrid, an integrated model (WT-PSO-SVM) was formulated by Eseye et al. [14], which merges wavelet transform, particle swarm optimization, and support vector machine. Wavelet transform was used for preprocessing, and particle swarm optimization for hyperparameter tuning, resulting in improved prediction performance. Wolff et al. [15] evaluated support vector regression (SVR) against physical models by utilizing a fused dataset, which included PV power observations, numerical weather prediction (NWP), and cloud motion vector (CMV) information. SVR showed excellent performance in real microgrid environments. Machine learning models have shown significant promise for PV forecasting; however, their effectiveness is often constrained when it comes to fully modeling the intricate nonlinear dynamics between weather conditions and PV power. It often struggles to capture dynamic phenomena such as sudden cloud cover changes and component degradation, and lacks long-range modeling capabilities, which constrain further accuracy improvements. Overcoming these limitations calls for models with stronger feature extraction and time-series modeling capabilities, paving the way for deep learning applications in PV forecasting.

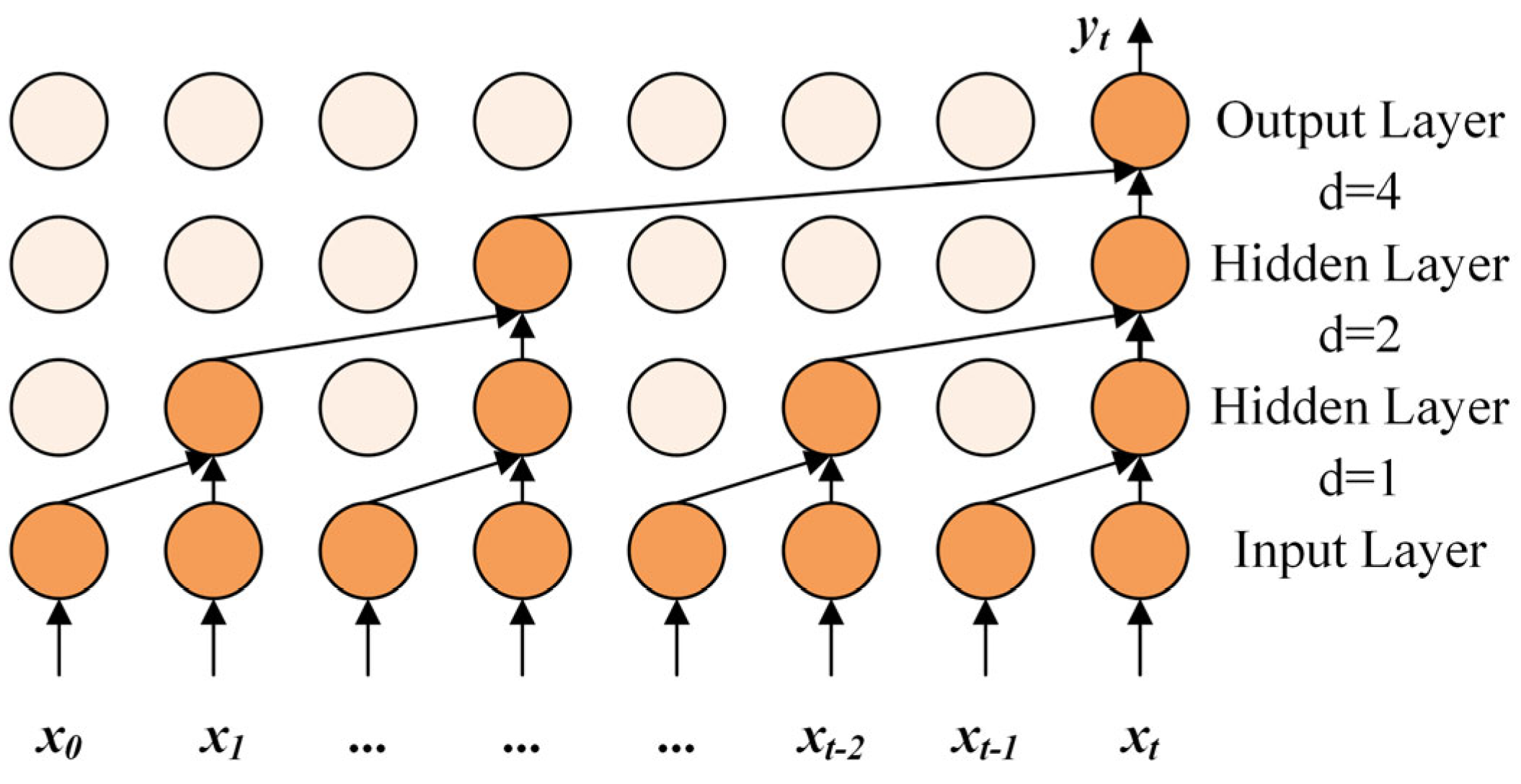
Owing to its powerful strengths in feature extraction, nonlinear modeling, and generalization, deep learning has emerged as an increasingly prominent subfield of machine learning. Recurrent neural networks (RNNs) [16] are frequently applied to time-series prediction problems. Lee et al. [17] utilized two types of RNNs to forecast PV power without requiring future meteorological information, achieving better results than traditional artificial neural networks (ANNs) and deep neural networks (DNNs). However, RNNs suffer from long-term dependency issues, leading to vanishing or exploding gradients. Hochreiter et al. [18] presented the long short-term memory (LSTM) network to tackle this issue. By leveraging a mechanism of input, forget, and output gates plus a memory cell, the LSTM network effectively overcomes long-term dependency issues, making it a broadly applied tool in PV forecasting. Hu et al. [19] further combined LSTM with self-attention mechanisms, integrating historical and forecast data. Their model, tested on real PV data from a building in Japan, exhibited strong accuracy and adaptability. Ahmed et al. [20] proposed an efficient and practical integrated forecasting method combining LSTM with live data from the Yulara PV plant in Australia. Other commonly used deep learning models include gated recurrent units (GRUs) [21] and convolutional neural networks (CNNs) [22]. Dai et al. [23] used LOWESS smoothing to extract PV features and proposed a CNN-BiGRU-Attention hybrid model optimized via ensemble learning. Chen et al. [24] employed a multi-task learning (MTL) scheme for TPA-LSTM to jointly forecast wind–solar. Their approach utilized the maximal information coefficient for feature selection and wind–PV correlation analysis. The MTL framework’s innovation lay in separating shared and task-specific components, which was further enhanced by a novel loss strategy balancing training speed and loss magnitude. Qu et al. [25] introduced an attention-based long- and short-term memory prediction model (ALSM) under a multi-related and target-variable prediction (MRTPP) scheme. The model combines CNN, LSTM, and attention mechanisms and was validated using historical PV system data from the DKSCA website. Results showed that the MRTPP-based ALSM outperformed traditional input–output schemes and various statistical and AI-based forecasting methods. Furthermore, improved LSTM-based algorithms are widely adopted in PV power forecasting. Bi-LSTM’s bidirectional learning enhances accuracy and convergence speed in time-series tasks [26,27], while GRU, by simplifying LSTM’s gate structure into a unified update gate, offers fewer parameters and easier training, contributing to its popularity [28,29,30,31,32,33].

In summary, while existing PV power forecasting methods have addressed many challenges, several issues remain. First, physics-based methods suffer from low prediction accuracy, poor generalization, and complex parameterization. Traditional statistical methods are inadequate in capturing key PV data characteristics. Moreover, conventional machine learning models are prone to gradient issues under long-term dependencies. Although hybrid models combining various algorithms have become mainstream in PV forecasting, they often focus solely on model structure, neglecting the role of meteorological data analysis. In response to these limitations, a deep learning-based PV power forecasting model that integrates similar-day clustering is proposed in this study, whose structure is illustrated in Figure 1. The main contributions are as follows:

−

To enhance the model’s adaptability in complex meteorological scenarios, the PV dataset is first processed using a K-medoids clustering algorithm based on Dynamic Time Warping (DTW) distance. This method allows the model to fully account for the impact of varying weather conditions on power generation.

−

The TimeGAN algorithm is employed to generate synthetic data samples under extreme weather conditions, aiming to mitigate model underfitting and enhance the model’s robustness in such scenarios.

−

The BiTCN and BiGRU algorithms are integrated to fully leverage their bidirectional structures for capturing latent information within the sequences. Meanwhile, to address the issue of excessive hyperparameters, the AOO algorithm is employed to optimize these parameters, thereby improving prediction accuracy and reducing manual tuning efforts.

−

The superior performance of the proposed method for photovoltaic power forecasting is validated through a comparative analysis against other models, utilizing Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and R² as the evaluation indicators.

The remainder of this article is organized as follows: Section 2 covers the theoretical foundations of the employed methods and the proposed model. Section 3 is then dedicated to the case study, data, and preprocessing. Section 4 describes the modeling process and presents a comprehensive analysis of the results. Lastly, Section 5 recaps the principal findings of this study and proposes potential avenues for subsequent research.

2. Methodology

The proposed AOO-BiTCN-BiGRU photovoltaic power forecasting framework centers on four core components: weather classification, sample augmentation, model optimization, and predictive modeling. Each component has a distinct role: (1) K-medoids clustering classifies similar days, enhancing the model’s adaptability to diverse weather patterns; (2) TimeGAN addresses sparse extreme weather samples by generating high-fidelity synthetic data to augment the training set; (3) The AOO algorithm optimizes hyperparameters of the BiTCN-BiGRU model to enhance performance; (4) BiTCN-BiGRU serves as the core prediction network, simultaneously capturing both local temporal features and long-term dependencies in PV power sequences. Through synergistic collaboration, these components ultimately achieve high-accuracy multi-step power forecasting.

2.1. DTW-K-Medoids Clustering Algorithm

This study utilizes a K-medoids clustering algorithm with the DTW distance metric for the efficient extraction of similar days [34]. The K-medoids algorithm addresses the limitations of the K-means algorithm in this research scenario, including its weak robustness to outliers and anomalies, distance distortion, and low interpretability of cluster centers. This approach is intended to fully categorize data samples based on power characteristics and to improve the model’s generalization and structural adaptability for PV power data. The main steps include data construction, DTW distance matrix calculation, and K-medoids clustering, which are outlined as follows:

2.1.1. Data Construction and Representation

The sampling time of the photovoltaic power time series is denoted as T, and the data includes historical records of N days. Each day is treated as a sample, and the sample matrix is constructed as follows:

$$P_i={\left[P_{i,1},P_{i,2},\dots ,P_{i,T}\right]}^T\in R^T, i=1,\dots ,N$$

(1)

In this context, P_i denotes the photovoltaic power value at each sampling point on the i-th day.

$$P=\left[\begin{array}{c}{P}_1^T\\ P_2^T\\ \begin{array}{c}⋮\\ P_N^T\end{array}\end{array}\right]=\left[\begin{array}{cccc}{P}_{1,1}& P_{1,2}& \dots & P_{1,T}\\ P_{2,1}& P_{2,2}& \dots & P_{2,T}\\ ⋮& ⋮& \ddots & ⋮\\ P_{N,1}& P_{N,2}& \dots & P_{N,T}\end{array}\right]\in R^{N\times T}$$

(2)

2.1.2. Definition of DTW Distance

To accurately measure the similarity between power curves on different days, Dynamic Time Warping (DTW) is introduced as a distance metric between samples. The DTW distance between any two daily power sequences, x₁ and y₁, is defined as:

$$x=\left[x_1,x_2,\dots ,x_T\right], y=\left[y_1,y_2,\dots ,y_T\right]$$

(3)

$$D_{DTW}\left(x,y\right)=\underset{\pi }{\mathit{min}}{\displaystyle \sum }_{\left(t_{x,}{t}_y\right)\in \pi }{\left(x_{t_x}-y_{t_y}\right)}^2 1\le t_x\le T,1\le t_y\le T$$

(4)

where π represents the set of paired time steps that satisfy the boundary constraints, monotonicity, and continuity conditions; $t_x$ and $t_y$ are the time indices of sequences and aligned on the warping path.

By calculating the DTW distance between all pairs of $P_i$ and $P_j$, a distance matrix is constructed:

$$D=\left[\begin{array}{cccc}{D}_{DTW}\left(P_1,P_1\right)& D_{DTW}\left(P_1,P_2\right)& \dots & D_{DTW}\left(P_1,P_N\right)\\ D_{DTW}\left(P_2,P_1\right)& D_{DTW}\left(P_2,P_2\right)& \dots & D_{DTW}\left(P_2,P_N\right)\\ ⋮& ⋮& \ddots & ⋮\\ D_{DTW}\left(P_N,P_1\right)& D_{DTW}\left(P_N,P_2\right)& \dots & D_{DTW}\left(P_N,P_N\right)\end{array}\right] D_{ij}=D_{DTW}\left(P_i,P_j\right)$$

(5)

2.1.3. K-Medoids Clustering

Given the number of clusters k, let $S=\left\{1,\dots ,N\right\}$ denote the set of sample indices and $C=\left\{C_1,\dots ,C_k\right\}\in S$ the indices of the medoids to be optimized. K-Medoids minimizes the sum of within-cluster DTW distances:

$$\underset{C}{\mathit{min}}{\displaystyle \sum }_{r=1}^k{\displaystyle \sum }_{i\in S_r}{D}_{DTW}\left(P_r,P_{C_r}\right)$$

(6)

where $S_r=\left\{i\in S|r=arg\underset{1\le l\le k}{\mathit{min}}{D}_{DTW}\left(P_i,P_{C_l}\right)\right\}$ represents the cluster for which $P_{C_r}$ serves as the medoid.

By iterating through different values of k, all historical daily samples are eventually categorized into 4 similar clusters, which are then used for subsequent modeling and prediction based on the categories.

2.2. TimeGAN

To address the scarcity of extreme weather data samples, this study employs TimeGAN, a framework introduced by Yoon et al. [35] that uses GANs for time-series generation. The model uniquely blends supervised and unsupervised learning, using embedding and recovery mechanisms alongside supervised losses. This approach allows it to learn the dynamic evolution and temporal consistency of data, not just static distributions, enabling the generation of high-quality, structurally similar sequences to augment the dataset.

As illustrated in Figure 2, TimeGAN’s architecture is constructed from four primary modules: an embedding network, a reconstruction network, a generator, and a discriminator. Operating as an autoencoder, the embedding network is responsible for transforming the high-dimensional input data into a low-dimensional latent representation, a process that inherently extracts the key features. The reconstruction network maps latent representations back to the original dimensions, optimized to minimize reconstruction error. Building upon this foundation, the model introduces a GAN architecture within the embedding space to jointly train the generator and discriminator, thereby capturing temporal dependencies within high-dimensional time series. This approach not only reduces the difficulty of adversarial training but also significantly enhances the model’s learning efficiency and generation quality.

2.3. AOO-BiTCN-BiGRU Network

TCNs are an enhanced CNN architecture well-suited for temporal problems, primarily due to their unique structure employing extended causal convolutions and residual blocks. As shown in Figure 3, the extension factor d grows exponentially with depth. This design allows the convolutions to expand their receptive field, sample inputs from preceding layers, and thereby extract features from time series data [36]. Residual connections directly link inputs to outputs, ensuring input information propagates to subsequent layers without excessive transformation, thereby mitigating information loss and vanishing gradient issues. This approach performs forward convolutional computations only on the input sequence, extracting forward data features while neglecting implicit information in the reverse direction. Hence, this study adopts the BiTCN network. The BiTCN network, illustrated in Figure 4, employs a bidirectional structure with a larger receptive field. The introduction of residual blocks mitigates issues like gradient vanishing and slow convergence associated with increased receptive fields. Consequently, the bidirectional temporal convolution architecture of BiTCN more effectively captures hidden features in both forward and backward directions, thereby better capturing long-term dependencies within sequences.

The BiGRU layer is employed to further process the output of the BiTCN, enhancing prediction accuracy by leveraging the precision of contextual information captured from both preceding and subsequent data. Figure 5A illustrates the BiGRU network. BiGRU is a dual-layer GRU network. The forward GRU layer processes features through forward propagation. This mines forward-related data correlations. The backward GRU layer trains the input sequence via backward propagation. This mines backward-related data correlations. This network architecture enables bidirectional feature extraction from inputs, better enhancing feature completeness and globality.

Figure 5B shows the structure of the GRU. The GRU receives two inputs. These are the hidden state $h_{t-1}$ from the previous time step and the input data $X_t$ from the current time step. Its output is the hidden state $h_t$ at the current time step. To reduce redundant data information during activation, the GRU performs preliminary parameter estimation before activation, thereby eliminating unnecessary computations. It also utilizes the mechanisms of the reset gate $r_t$ and the update gate $Z_t$ to update the state [37]. The core function of the reset gate lies in regulating the degree of forgetting historical state information. As the value of $r_t$ decreases, the amount of neglected information increases, expressed as follows:

$$r_t=\sigma \left(W_r\left[h_{t-1},X_t\right]+b_r\right)$$

(7)

The primary function of the update gate is to monitor the extent to which historical state information propagates to the current time point. As the $Z_t$ value increases, the amount of information transmitted from the previous moment to the present state correspondingly grows, as expressed by the following formula:

$$Z_t=\sigma \left(W_z\left[h_{t-1},X_t\right]+b_z\right)$$

(8)

Candidate latent states:

$${\tilde{h}}_t=\tan h\left(W\left[r_t{h}_{t-1},X_t\right]+b\right)$$

(9)

Implicit State at the Current Moment:

$$h_t=\left(1-Z_t\right)h_{t-1}+Z_t{\tilde{h}}_t$$

(10)

In these formulas, $W_r$ and $b_r$ are the reset gate weight and bias. ${\mathrm{W}}_{\mathrm{z}}$ and $b_z$ are the update gate weight and bias. $W$ and $b$ are the recurrent connection weight and bias.

The Animated Oat Optimization (AOO) algorithm is a novel intelligent optimization technique. Unlike previous algorithms, it draws inspiration from the three-stage motion mechanism of oat seeds propagating through “rolling-bouncing” in humid environments [38]. This mechanism ingeniously integrates global exploration with local exploitation within a two-stage framework. Figure 6 explains the algorithm’s underlying principles.

2.3.1. Initialization Phase

Before commencing the main strategy, the initial positions of the population must first be established:

$$X=\left[\begin{array}{cccccc}{x}_{1,1}& \dots & x_{1,j}& \dots & x_{1,Dim-1}& x_{1,Dim}\\ x_{2,1}& \dots & x_{2,j}& \dots & x_{2,Dim-1}& x_{2,Dim}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \dots & \dots & x_{i,j}& \dots & \dots & \dots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{N-1,1}& \dots & x_{N-1,j}& \dots & x_{N-1,Dim-1}& x_{N-1,Dim}\\ x_{N,1}& \dots & x_{N,j}& \dots & x_{N,Dim-1}& x_{N,Dim}\end{array}\right]$$

(11)

where $x_i$ denotes an individual in the i-th subgroup along with its location. $Dim$ indicates the dimensional size of the problem. N represents the total number of individuals in the subpopulation.

$$x_{i,j}=r\times \left(U{B}_j-L{B}_j\right)+L{B}_j,i=1,2,\dots ,N,j=1,2,\dots ,Dim$$

(12)

where $r$ represents a random value chosen from the range [0, 1]. The terms $U{B}_j$ and $L{B}_j$ define the problem’s boundaries for the j-th dimension. $U{B}_j$ is the upper limit. $L{B}_j$ is the lower limit.

2.3.2. Biological Parameter Mapping

The developed mathematical model quantifies the animated oat seed’s dispersal process. Several key biological characteristics are defined. These include the length and mass of the seed’s main awn. The eccentricity coefficient from the rolling process is also incorporated. The equations below are used to calculate these values:

$$\left\{\begin{array}{r}m=0.5\times \frac{r}{\mathit{dim}}\\ L=N\times \frac{r}{\mathit{dim}}\\ \mathrm{e}=0.5\times \frac{r}{\mathit{dim}}\\ c=1-{\left(\frac{t}{T}\right)}^3\end{array}\right.$$

(13)

where $m$, $L$, and $\mathrm{e}$ define the seed’s physical properties (mass, awn length, and eccentricity coefficient). $t$, $T$, and $c$ are the iteration control parameters (current iteration, max iterations, and dynamic adjustment factor).

2.3.3. Exploration Phase

To facilitate a wide-ranging exploration of the solution space, this random dispersal method governs position updates according to the following equations:

$$w={\displaystyle \frac{c}{\pi }}\times \left(2\times r_{dim}-1\right)\otimes UB$$

(14)

$$\{\begin{array}{c}{X}_{t+1}\left(i\right)={\displaystyle \frac{1}{N}}\times {\displaystyle {\displaystyle \sum }_{i=1}^N}{X}_t\left(i\right)+W,if mod \left(i,N/10\right)=0,\\ X_{t+1}\left(i\right)=X_{best}+W,if mod \left(i,N/10\right)=1,\\ X_{t+1}\left(i\right)=X_t\left(i\right)+W,else.\end{array}$$

(15)

where $UB$ defines the problem’s maximum boundary. $X_{t+1}\left(i\right)$ is the updated location for the i-th individual. $X_{best}$ tracks the best solution found so far in the population.

2.3.4. Development Stage

This stage implements two propagation methods based on obstacle encounters, each with an equal probability. The ‘no obstacle’ scenario, termed ‘hygroscopic rolling,’ is mathematically defined by the following eccentric rotation and torque equations:

$$A=UB-\left|{\displaystyle \frac{UB\times t\times \sin \left(2\times \pi \times r\right)}{T}}\right|$$

(16)

$$R=\left(m\times e+L^2\right)\times {\displaystyle \frac{r_{dim}\left(-A,A\right)}{dim}}$$

(17)

$$\mathrm{Levy}\left(\dim \right)=0.01\times {\displaystyle \frac{\mu \times \sigma }{{\left|\nu \right|}^{1/\beta }}}$$

(18)

$$\sigma ={\left({\displaystyle \frac{\Gamma \left(1+\beta \right)\times \sin \left(\frac{\pi \times \beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}}\right)}^{{\displaystyle \frac{1}{\beta }}}$$

(19)

$$X_t\left(i\right)=X_{best}+R+c\times Levy\left(dim\right)\otimes X_{best}$$

(20)

where $r_{dim}\left(-A,A\right)$ is a random matrix whose dimensions match the target problem. The Levy flight is controlled by several standard parameters. $\mu$ is the mean value used to adjust the step size. $\sigma$ is the scale parameter for the step length distribution. $\nu$ is the current velocity vector. $\beta$ is the stable distribution parameter which shapes the step’s randomness. Finally, $\Gamma$ is the standard gamma function.

In the event of an obstacle, the seed initiates an energy-driven ejection. This entire process is simulated as simplified projectile motion, with the position update defined as follows:

$$B=UB-\left|{\displaystyle \frac{UB\times t\times \cos \left(2\times \pi \times r\right)}{T}}\right|$$

(21)

$$\{\begin{array}{c}k=0.5+0.5\times r\\ x=3\times {\displaystyle \frac{r}{dim}}\\ \theta =\pi \times r\\ \alpha ={\displaystyle \frac{1}{\pi }}\times e^{{\displaystyle \frac{r^{\prime }}{T}}}\end{array}$$

(22)

$$J={\displaystyle \frac{2\times k\times x^2\times \sin \left(2\theta \right)}{mg}}\times {\displaystyle \frac{r_{dim}\left(-B,B\right)}{dim}}\times \left(1-\alpha \right)$$

(23)

$$X_t\left(i\right)=X_{best}+J+c\times Levy\left(dim\right)\otimes X_{best}$$

(24)

where $k$, $x$, $\theta$, and $\alpha$ represent the physical parameters for the projectile model (elasticity, length change, angle, and air resistance). $r’$ is a random number between 0 and $T$.

3. Data Analysis and Parameter Configuration

This section outlines the dataset employed in this study, the comparative methodology, evaluation metrics, parameter configurations, and feature relevance analysis. Furthermore, the experimental hardware configuration comprises a 3.7 GHz Intel^® Core^TM i9-10900K CPU, 96.00 GB of memory, and an NVIDIA^® GeForce RTX™ 5060 Ti graphics card. The TimeGAN algorithm was implemented in Python 3.10.15based on the PyTorch 2.7.0 framework with CUDA 12.8 support, whilst clustering and prediction algorithms were realized using MATLAB 2023a.

3.1. Data Information

The data for this study were sourced from figshare, a website that publicly shares various datasets [39]. The solar data was sourced from the China State Grid Renewable Energy Generation Forecasting Competition. This dataset originates from a 30 MW nominal capacity solar power station.

Table 1. Statistical overview of meteorological and PV power data.

Name	Unit	Min	Mean	Max	Std
Total Solar Irradiance	W/m2	0	163.24	1214.54	245.39
Direct Normal Irradiance	W/m2	0	142.02	1056.65	213.49
Global Horizontal Irradiance	W/m2	0	21.22	157.89	31.90
Air Temperature	°C	−8.04	18.01	47.63	8.56
Atmosphere	hPa	881.40	956.42	1037.78	30.54
Relative Humidity	%	11.83	71.71	100	18.50
Power	MW	0	4.23	29.41	6.52

and

Table 2. Power Generation and PV Panel Information of the Solar Energy Station.

PV Panel Model	Nominal Generation Output Capacity (MW)	Number of PV Panels Installations
HR-260P-18/Bbd	0.93	3567
HR-260P-18/Bbd	1.92	7234
GCL-M6/60G280	0.15	541
YL260P-29b	4.62	17,782
JC260m-24/Bb	6.96	26,763
CS6K-260P-PG	1.56	5986
CS6K-255P-PG	6.47	25,383
CS6K-250P-PG	0.30	1211
TSM-260PC05A	2.32	8908
SYP260P	4.24	16,326
JMPV-HM6VBM2/60-340	0.53	1559

illustrates its key characteristics. The dataset spans the period from 1 January 2019 to 31 December 2019, with a resolution of 15 min. Detailed feature information is presented in Table 1. Energy peaks around midday, with relatively lower levels at sunrise and in the afternoon, tending towards zero during night-time hours. Furthermore, a noticeable lag effect exists between certain meteorological factors and the PV data. As photovoltaic power output is zero at night, night-time data points were removed, retaining only data from 07:30 to 19:30. The dataset was subsequently partitioned into an 80% training set and a 20% validation set.

3.2. Comparative Methodology

To demonstrate the effectiveness of generated weather samples for photovoltaic power forecasting, this paper designed an ablation study comparing accuracy changes before and after data generation. Concurrently, to validate the efficacy of the AOO-BiTCN-BiGRU model for this task, we selected GRU, LSTM, TCN [40], and CNN models for comparative analysis.

3.3. Evaluation Metrics

To assess how well the predicted values matched the actual values, this study utilized three standard statistical metrics: MAE, RMSE, and the coefficient of determination (R²) [41,42,43].

The MAE quantifies the average magnitude of the errors between predicted and actual values:

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum }_{i=1}^n\left(Y_i-{\widehat{Y}}_I\right)$$

(25)

The RMSE is particularly sensitive to outliers. This is because its calculation squares each error, which gives large errors a disproportionately heavy weight:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum }_{i=1}^n{\left(Y_i-{\widehat{Y}}_I\right)}^2}$$

(26)

For the error metrics (MAE and RMSE), lower values signify superior predictive accuracy. Conversely, R² measures the quality of the model’s fit, where a value closer to 1 indicates a more accurate prediction:

$$R^2=1-{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i-{\widehat{Y}}_I\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i-{\overline{Y}}_I\right)}^2}}$$

(27)

where $Y_i$, ${\widehat{Y}}_I$, and ${\overline{ Y}}_I$ correspond to the actual, predicted, and mean values, respectively, and n is the total number of samples.

3.4. Parameter Configuration

For the DTW-based K-medoids algorithm, the sequence length was set to 49 points. Based on this data structure, the number of cluster categories was set to 4.

For the TimeGAN algorithm, the detailed parameter settings are presented in

Table 3. TimeGAN Hyperparameter Demonstration.

Hyperparameter	Search Scope	Value
Time Series Length	49	49
Batch Size	[64,128,256]	64
Max Steps	[3000–7000]	6500
Hidden Layer Size	[32,48,64]	64
Gamma	[0.5–1.0]	0.7

. Within this table, the middle column corresponds to the search range for each parameter, while the rightmost column indicates the final parameter values determined through experimental validation. It is worth noting that the algorithm generates a volume of synthetic samples consistent with the original dataset. To ensure comprehensive exploration of the solution space while balancing efficiency, the maximum number of iterations for the algorithm starts at 3000 and increments by 500 steps each time, ranging up to 7000.

Regarding parameter settings for the AOO-BiTCN-BiGRU model: the historical time step size is set to 49, the prediction step size to 4 (i.e., utilizing one day’s historical data to forecast the subsequent hour’s data); the filter size is set to 5; and the optimizer employs the Adam algorithm.

Dropout, a commonly used regularization technique in neural network training, primarily aims to suppress model overfitting. The selection of the Dropout rate necessitates consideration of the specific application scenario and model architecture, typically requiring cross-validation to determine the optimal value. This paper sets the Dropout rate at 0.1, a value that effectively avoids the reduced learning efficiency or underfitting issues caused by excessively high Dropout rates, while also preventing overfitting resulting from excessively low Dropout rates.

The parameter settings for the AOO optimization algorithm are as follows: population size of 4 and maximum iterations of 10. This algorithm primarily optimizes key parameters within the BiTCN-BiGRU model, specifically including the learning rate, number of neurons in the BiGRU layer, number of filters, and regularization parameters. The upper and lower limits for optimizing each parameter are detailed in

Table 4. Hyperparameter optimization scope.

Hyperparameter	Lower Limit	Upper Limit
Learning Rate	0.0001	0.01
Number of BiGRU Units	10	100
Number of Filters	20	120
L2 Regularization Parameter	0.00001	0.005

.

After AOO optimization, the final hyperparameter values used in the experiment are summarized in

Table 5. Optimized Hyperparameters of the AOO-BiTCN-BiGRU Model.

Hyperparameter	Sunny	Cloudy	Intermittent	Rainy
Learning Rate	5.3144 × 10−4	0.0036	0.0030	0.0030
Number of BiGRU Units	42	81	91	100
Number of Filters	110	20	120	56
L2 Regularization Parameter	0.0042	0.0043	0.0045	0.005

. These values are derived through iterative search and verification, ensuring they match the model structure and data characteristics to maximize predictive performance.

3.5. Feature Correlation Analysis

In this study, we employed the Pearson correlation coefficient method (PCC) [44] to analyze the degree of association between different variables. As a multifunctional analysis technique, PCC is calculated based on time-series data, focusing on linear correlations between data sequences. In the PCC calculation, we selected weather elements as the comparison series and PV output power as the baseline for comparison. The PCC calculation formula is as follows:

$${\rho }_{x,y}={\displaystyle \frac{cov\left(X,Y\right)}{{\sigma }_x{\sigma }_y}}={\displaystyle \frac{E\left(X-{\mu }_X\right)E\left(Y-{\mu }_Y\right)}{{\sigma }_X{\sigma }_Y}}$$

(28)

The PCC method was applied to calculate the pairwise correlations between seven meteorological factors and power in the original dataset, including total solar radiation (W/m²), direct normal radiation (W/m²), global horizontal radiation (W/m²), air temperature (°C), atmospheric pressure (hPa), relative humidity (%), and PV output power (MW). The PCC heat map is presented in Figure 7. Upon calculating the correlation coefficients, the degree of association between variables can be assessed via the value ranges. The heat map indicates that the factors exerting the greatest influence and exhibiting the highest correlation with PV output power are total solar radiation, direct normal radiation, and global horizontal radiation. Atmospheric pressure exerts the least influence and is therefore excluded. Consequently, the selected input variables for the model comprise total solar radiation, direct normal radiation, global horizontal radiation, air temperature, relative humidity, and PV output power.

4. Results and Discussion

The PV data exhibits strong periodicity. After excluding data points where nighttime power is zero, the remaining dataset contains a total of 49 time points per day (7:30–19:30). The model’s performance was validated on a specific task: predicting the subsequent 4 time steps (1 h) using data from the past 49 time steps (one day). A multi-output strategy was employed for this multi-step forecasting. Finally, comprehensive comparisons were conducted to analyze the model’s performance under varying conditions. This approach better captures dependencies between inputs and outputs, enabling simultaneous prediction of sequences across multiple time steps during model training. The experimental design comprises three parts: (i) K-medoids clustering algorithm evaluation, (ii) ablation experiments and (iii) comparative experiments.

4.1. Evaluation of the K-Medoids Clustering Algorithm

The clustering results, as shown in Figure 8, reveal that periods of stable irradiance (e.g., noon) form tighter clusters, while transitional periods (e.g., sunrise/sunset) exhibit higher variability. Clear-sky days yield the highest photovoltaic power data, whereas overcast days with insufficient light intensity produce relatively lower power, consistent with the physical dynamic characteristics of photovoltaic power generation.

To evaluate the effectiveness of the K-medoids clustering algorithm in capturing intrinsic patterns within photovoltaic power generation data simultaneously, we first visualized the high-dimensional data structure through multidimensional scaling (MDS) projection. MDS reduces feature dimensions while preserving pairwise distances between data points, enabling a qualitative assessment of cluster separability. As shown in Figure 9, the projected data exhibits a clear clustering structure. The boundaries between the four clusters are distinct, with only a few points located on either side of the boundaries. This indicates that the K-medoids algorithm effectively groups photovoltaic power sequences with similar temporal characteristics.

4.2. Ablation Experiments

To validate the efficacy of TimeGAN in augmenting extreme weather samples, we designed an ablation study. Initially, the model was trained using only the original 30 days of rainy-day samples. Following this, performance was assessed on the 17 rainy-day samples within the test set. Subsequently, 14 days of the synthetic data generated by TimeGAN were integrated with the original 30 days of samples, creating an augmented training set of 44 days. The original sequences and generated sequences are visualized in Figure 10. The predictive accuracy on the same 17-day test set was then re-evaluated using this combined dataset. The results (

Table 6. Ablation study results: TimeGAN augmentation for predictive performance.

Sample	Number of Test Samples	MAE	RMSE	R2
Original rainy day training dataset	17 days	0.6771	0.8931	0.7972
Combined training dataset	17 days	0.4091	0.5439	0.9358

) confirm that augmenting the data significantly boosts predictive performance: MAE dropped by 39.58%, RMSE decreased by 39.10%, and R² saw an increase of 0.1386. This clearly demonstrates that sample generation techniques enhance both model accuracy and generalization.

4.3. Comparative Experiments

In contrast to single-step methods that predict a singular future value, this work uses multi-step forecasting. This technique leverages past PV power and meteorological conditions to generate a sequence of predictions over a subsequent time horizon.

The detailed comparison results, summarized in

Table 7. Performance comparison (MAPE, RMSE, R²) of forecasting models under different weather conditions.

Day Weather	Error	Primary Model	GRU	LSTM	TCN	CNN
Sunny	MAE	1.3033	1.4435	1.3942	1.2312	1.8494
	RMSE	1.6750	1.8393	1.8723	1.5881	2.1863
	R2	0.9711	0.9620	0.9605	0.9759	0.9465
Cloudy	MAE	1.1224	1.2391	1.4297	1.4685	1.2614
	RMSE	1.5121	1.6604	1.8489	2.0003	1.6004
	R2	0.9356	0.9189	0.8963	0.8771	0.9337
Intermittent	MAE	0.8100	0.9394	0.8821	1.0269	0.8078
	RMSE	1.0448	1.1821	1.1078	1.3324	1.0381
	R2	0.9076	0.8723	0.8920	0.8397	0.9144
Rainy	MAE	0.4507	0.4410	0.5078	0.6148	0.6529
	RMSE	0.5802	0.5966	0.6959	0.8397	0.7806
	R2	0.9323	0.9272	0.8971	0.8468	0.8808
Average	MAE	0.9216	1.0158	1.0535	1.0854	1.1429
	RMSE	1.2030	1.3196	1.3812	1.4401	1.4014
	R2	0.9367	0.9201	0.9115	0.8849	0.9189

and Figure 11, indicate that the AOO-BiTCN-BiGRU model also achieved the highest accuracy in multi-step forecasting across four weather conditions. Results indicate that this model attained the highest average R² among the five models at 0.9367, while its MAE and RMSE values of 0.9216 and 1.2030, respectively, were the lowest among all models. Compared to other models, this model’s MAE and RMSE were 9.27% and 8.84% lower than the GRU model, 12.52% and 12.9% lower than the LSTM model, 15.09% and 16.46% lower than the TCN model, and 19.36% and 14.16% lower than the CNN model. Additionally, the AOO-BiTCN-BiGRU model achieved higher R² values than other models by 0.0166, 0.0252, 0.0518, and 0.0178, respectively. While some weather conditions showed slightly higher performance in comparison models, this discrepancy is attributed to the more complex bidirectional structure and larger parameter set of our model, with a large number of parameters. Consequently, its performance in predicting weather conditions with relatively smooth power fluctuations may not significantly outperform other models. However, the average accuracy of this model far exceeds that of the comparison models, indicating that while it demonstrates strong predictive capabilities under weather conditions with smooth power fluctuations, it also possesses robust representational power for weather conditions with intense fluctuations. These results demonstrate that the AOO-BiTCN-BiGRU model possesses strong generalization capabilities and significantly improves prediction accuracy.

The AOO-BiTCN-BiGRU model exhibits high reliability in multi-step photovoltaic power forecasting. This is visually confirmed by Figure 12, which depicts the alignment between the actual and forecasted power values throughout the prediction. The results indicate that this model effectively captures long-term dependencies in PV data, performing particularly well during rainy days with high volatility, where the curves exhibit fewer discrete values. Even when forecast values deviate from actual values, the model converges to the actual values faster and more accurately. The predictions from the AOO-BiTCN-BiGRU model are therefore shown to be balanced, lacking significant overestimation or underestimation biases. Regarding computational efficiency concerns, all models were trained on the unified hardware platform described above. Given that the structural complexity of photovoltaic time-series data is lower than that of multidimensional tensors in image data, the training duration of the proposed AOO-BiTCN-BiGRU model falls within a reasonable range: In single-category weather scenarios, sunny-day training took the longest, approximately 50 min (including hyperparameter optimization and model training), with the pure model training phase taking less than 2 min. The comparison model, featuring a simpler network architecture and requiring no additional hyperparameter tuning, completed sunny-day training within 30 s. Notably, during actual deployment, the model rapidly outputs predictions by loading pre-trained parameters alone, fully meeting the real-time requirements of power grid dispatch.

5. Conclusions

Accurately predicting PV power on an ultra-short timescale is vital for maintaining the stable operation of the power grid and executing peak shaving and valley filling operations. Such forecasting is critical for managing the equilibrium between supply and load, as well as for optimizing energy dispatch. While single-structure models are often challenged by highly volatile data and long-range temporal relationships, composite-structure models generally yield superior accuracy. The latter achieves this by utilizing more intricate neural network architectures capable of learning complex features and data patterns. To address this, our study enhances ultra-short-term PV forecasting accuracy by constructing a hybrid prediction model. This model integrates clustering, optimization, generative adversarial networks, and deep learning methods, thereby achieving high-precision forecasting and robust performance evaluation.

The main conclusions drawn from this work include:

A hybrid PV power forecasting model was developed that fully accounts for the influence of varying weather conditions on PV output. To significantly boost the model’s accuracy and adaptability across complex meteorological conditions, multi-dimensional meteorological data (such as temperature, humidity, wind speed, and solar irradiance) along with historical PV power data were incorporated.

Data generation via the TimeGAN algorithm mitigates model underfitting, thereby enhancing robustness under extreme weather conditions. Exploration of model parameter optimization methods reduces complexity and computational efficiency, ensuring practical feasibility for real-world forecasting.

Validation and evaluation using operational data from actual PV power plants analyzed prediction accuracy and reliability across different seasons and weather conditions. Comparative analysis assessed the hybrid model’s advantages over single-method approaches, providing a more reliable tool for PV power forecasting in photovoltaic-storage integrated charging stations.

In summary, the integrated PV power forecasting algorithm proposed herein achieves a higher level of accuracy compared to the other models. Its consideration of weather factors and generation of extreme weather samples significantly enhances PV power prediction accuracy, holding substantial practical value and real-world significance. Future research may deepen the exploration of the following areas: firstly, expanding data dimensions to incorporate PV module status (real-time temperature, dust coverage, degradation level) and regional microclimate data to reduce prediction errors; secondly, integrating reinforcement learning to optimize model parameter update mechanisms, enabling online adaptive optimization and enhancing long-term operational stability; thirdly, integrating the model with energy management strategies for photovoltaic-storage systems to construct an integrated ‘prediction-scheduling’ decision model, thereby facilitating renewable energy integration.