A Multi-Time Scale Optimal Dispatch Strategy for Green Ammonia Production Using Wind–Solar Hydrogen Under Renewable Energy Fluctuations

Abstract

This paper develops an optimal dispatch model for an integrated wind–solar hydrogen-to-ammonia system to address the mismatch between renewable-energy fluctuations and chemical production loads. The model incorporates renewable variability, electrolyzer dynamics, hydrogen-storage regulation, and ammonia-synthesis load constraints, and is solved using a multi-time-scale MILP framework. An efficiency-priority power allocation strategy is further introduced to account for performance differences among electrolyzers. Using real wind–solar output data, a 72-h case study compares three operational schemes: the Balanced Scheme, the Steady-State Scheme, and the Following Scheme. The proposed Balanced Scheme reduces renewable curtailment to 2.4%, lowers ammonia load fluctuations relative to the Following Scheme, and decreases electricity consumption per ton of ammonia by 19.4% compared with the Steady-State Scheme. These results demonstrate that the integrated dispatch model and electrolyzer-cluster control strategy enhance system flexibility, energy efficiency, and overall economic performance in renewable-powered ammonia production.

1. Introduction

The accelerating pace of global climate change is reshaping the world’s energy system. International agreements such as the Paris Agreement are driving countries toward carbon-neutral pathways, with wind and solar power becoming central to this transition [1]. Their levelized cost of electricity has fallen sharply in recent decades, enabling rapid growth in installed capacity. Yet this progress highlights a persistent challenge: the inherent mismatch between the variable, non-dispatchable output of renewables and the stable, continuous power demand of energy-intensive industries [2]. This intermittency creates grid-balancing difficulties and leads to renewable curtailment, undermining both economic returns and emission-reduction benefits. Since industry accounts for roughly one-quarter of global CO₂ emissions, effectively aligning volatile renewable supply with steady industrial demand is essential for deep decarbonization [3,4].

Within this context, green ammonia has gained prominence as a key vector in future renewable energy systems. It provides three essential functions: a zero-carbon fertilizer, a hydrogen carrier with substantially simpler storage and transport requirements compared to molecular hydrogen, and a carbon-free fuel for power generation and maritime transport [5,6,7]. The thermodynamic properties of ammonia, which allow it to be liquefied at −33 °C or at ambient temperature under modest pressure (around 8–10 bar), confer a critical logistical advantage over hydrogen, requiring less energy-intensive infrastructure. This versatility establishes “green ammonia”—produced exclusively via hydrogen from water electrolysis powered by renewables-as a critical vector for sector coupling, effectively converting variable electricity into a storable, transportable, and multi-purpose chemical fuel [8,9,10].

However, the century-old Haber–Bosch process presents a critical operational bottleneck. Conventional plants, optimized for steady-state, fossil-based feedstocks, exhibit limited flexibility. Their high-temperature, high-pressure conditions and catalyst sensitivity make them vulnerable to rapid load-following, risking unsafe pressure swings and catalyst deactivation. As a result, traditional synthesis loops are fundamentally incompatible with the fluctuating output of wind and solar power, calling for new system designs and operational strategies to ensure flexibility without sacrificing stability or economic viability [11,12].

The academic community has responded to this challenge with a rich body of literature, which can be broadly categorized into three streams [13,14,15]. The first stream focuses on system design and techno-economic analysis (TEA), employing optimization models to determine the optimal capacity of renewable generators, electrolyzers, and storage. Studies by authors like Zhang et al. and Fasihi et al. [16,17,18,19,20] have provided valuable insights into the levelized cost of green ammonia under various geographical and economic conditions, establishing the foundational business case for such projects. Zhou et al. [21] proposed a multi-stable flexible strategy and a PSO-MILP framework to balance economy, safety, and low-carbon performance under renewable fluctuations. Karrabi et al. [22] developed a solar-ammonia multi-generation model integrating molten salt storage and fuel cell vehicles, verifying its industrial feasibility. Florez et al. [23] optimized islanded green ammonia production, reporting a low levelized cost for 2030, while Laimon et al. [24] demonstrated how considering curtailed energy can reduce costs below market price. A second stream of research delves into process-level modeling and flexibility enhancement. Works such as those by Verleysen et al. and Allman & Daoutidis [25,26] have explored the dynamic response of the Haber–Bosch process itself, investigating the use of hydrogen buffers and advanced control strategies to absorb power fluctuations. The third stream concentrates on the operational scheduling and control of electrolyzers. Recognizing their fast response capabilities, researchers have developed sophisticated MILP and MINLP models, as seen in the work of Sánchez & Martín and Schulte Beerbühl et al. [27,28,29], to optimally manage electrolyzer clusters, treating them as a primary source of grid flexibility. Mewafy et al. [30] proposed a PSO method for hybrid microgrids that coordinates the sizing and operation of electrolyzers and fuel cells to minimize cost.

Despite recent progress, an important gap remains at the intersection of system-level scheduling and equipment-level operational heterogeneity [31,32,33,34,35,36,37]. Many techno-economic and scheduling studies assume an idealized, homogeneous electrolyzer cluster with constant aggregate efficiency, overlooking the fact that individual units inevitably degrade at different rates due to membrane fouling, catalyst wear, and manufacturing tolerances. Such heterogeneity can lead to significant energy losses if power is allocated without considering unit-specific performance. Conversely, studies focusing on electrolyzer-cluster management often treat the ammonia synthesis section as a static sink, ignoring its dynamic constraints and the need for coordinated buffer control. Therefore, a comprehensive optimization framework is needed—one that couples a system-wide dispatch model respecting reactor load-following limits with a fine-grained, efficiency-aware control strategy for the electrolyzer cluster. This integrated approach is key to improving flexibility, efficiency, and durability in renewable-powered ammonia plants.

To address these limitations, this paper proposes an integrated optimization framework that couples system-wide dispatch with an efficiency-aware power allocation strategy for electrolyzer clusters. The goal is to enhance the energy efficiency, operational stability, and overall economic performance of renewable-powered ammonia plants. The model is formulated as a Mixed-Integer Linear Programming (MILP) problem, incorporating renewable generation, electrolyzer dynamics, hydrogen storage, and ammonia synthesis load. A 72-h case study using real generation data is conducted to validate the framework, evaluating key indicators such as renewable utilization, curtailment rate, and specific energy consumption.

The main contributions of this work are summarized as follows:

(1)

A High-Fidelity Multi-Timescale MILP Dispatch Model: An integrated scheduling framework is developed, including the dynamic interactions among renewable energy generation, electrolytic cell, hydrogen storage and Haber–Bosch process, as well as the stability and ramping constraints of ammonia production. The model aims to realize the coordinated scheduling of each section in the wind–solar hydrogen production synthetic ammonia system, and maximize the economic profit while enhancing the stability of the synthetic ammonia production process.

(2)

A Novel Efficiency-Priority Power Allocation Strategy (EPPA): This strategy explicitly considers the efficiency difference between each unit and dynamically allocates higher power load to more efficient electrolyzers. This aims to maximize the total hydrogen production rate per unit power consumption of the cluster, thereby reducing the energy consumption ratio and reducing the degree of degradation of the electrolytic cell.

(3)

A Rigorous Multi-Dimensional Performance Validation: The proposed framework is rigorously validated via a 72-h case study using real wind–solar data. A comparative analysis against two benchmarks—a rigid “Steady-State Scheme” and a volatile “Following Scheme”—across multiple key performance indicators quantitatively demonstrates the superiority of the “Balanced Scheme” in balancing economic efficiency, renewable integration, and operational robustness.

The remainder of this paper is structured as follows: Section 2 details the methodology, including system modeling and the formulation of the MILP problem. Section 3 presents the case study and discusses the results. Finally, Section 4 concludes the paper and suggests directions for future research.

2. Methods and Modeling

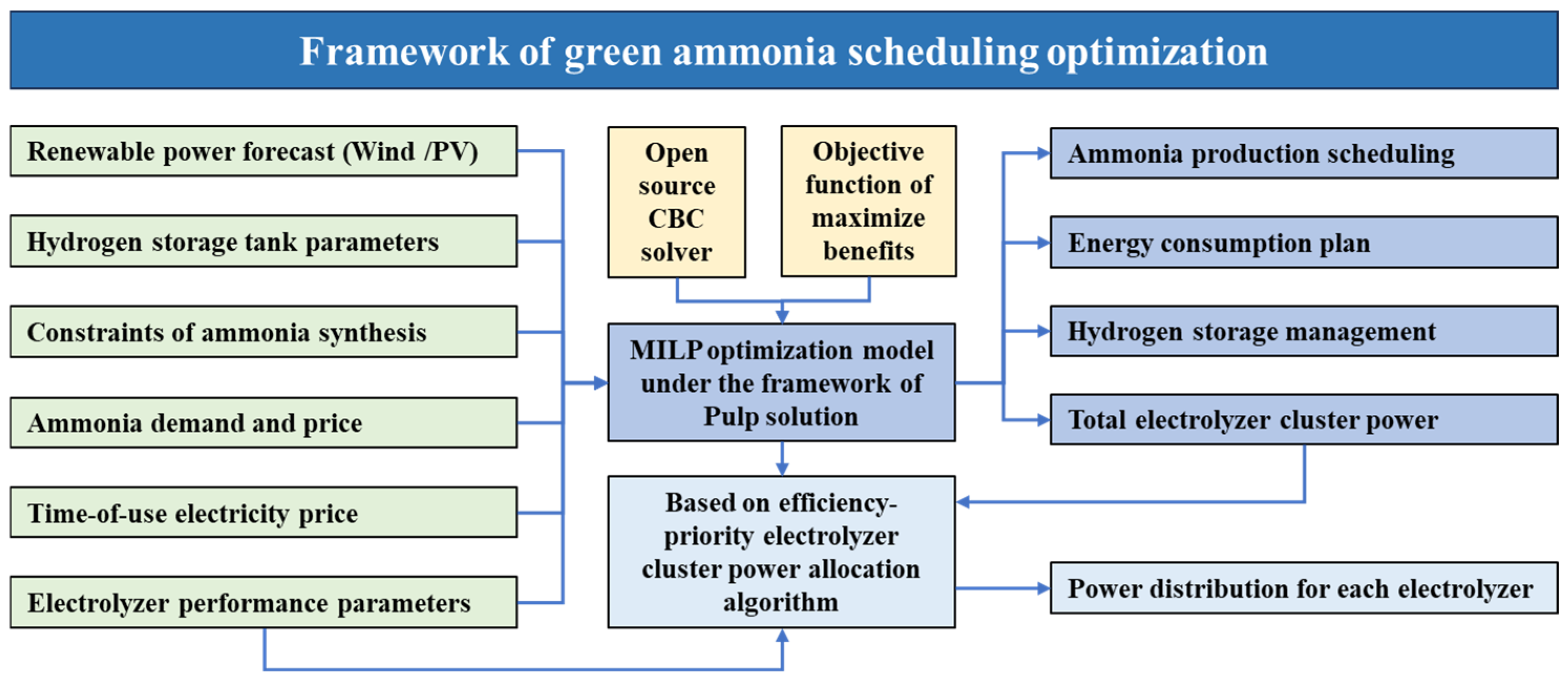
2.1. System Overview

The wind–solar hydrogen-to-ammonia system primarily consists of a wind–solar power generation unit, a water electrolysis hydrogen production section, an air separation nitrogen production section, a hydrogen storage section, and an ammonia synthesis section [38,39]. On the power supply side, the system integrates wind farms, photovoltaic (PV) power stations, and the power grid, achieving energy complementarity and power balance through a dynamically controllable electricity purchasing mechanism. When the output from wind and solar sources is insufficient, power can be flexibly purchased from the grid to supplement the system. This approach not only reduces the configuration costs of hydrogen storage and other energy storage devices but also maintains the minimum load level of the units under unexpected conditions, ensuring continuous and stable system operation [40]. The water electrolysis hydrogen production section typically employs Alkaline (ALK) electrolyzer technology, characterized by its maturity, low investment cost, and long lifespan, making it suitable for large-scale renewable energy hydrogen production scenarios [41,42]. The hydrogen storage section is equipped with hydrogen storage tanks to temporarily store the electrical energy converted into hydrogen energy, enabling energy time-shifting and balancing hydrogen supply and demand across different time scales [43]. The ammonia synthesis section utilizes the established Haber–Bosch process, which includes synthesis gas compression, the synthesis reaction, waste heat recovery, ammonia separation, and a recycle loop. The overall system structure is depicted in Figure 1.

The proposed optimal dispatch framework for the green ammonia system is illustrated in Figure 2. This framework adopts a hierarchical optimization architecture, achieving step-by-step optimization from system-level scheduling to equipment-level allocation. It is mainly composed of an input parameter module, a core optimization module, and an output results module.

The Input Parameter Module integrates key data sources, including:

(1)

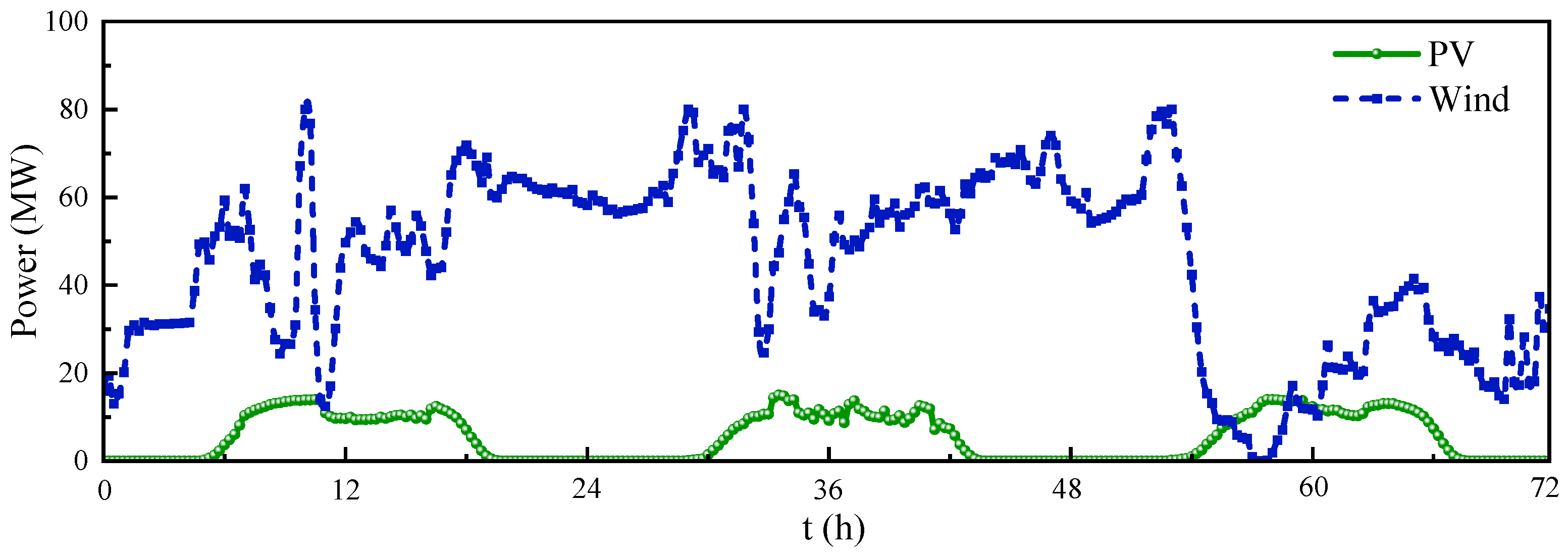
Renewable energy output forecast data, containing short-term power predictions for wind and PV;

(2)

Hydrogen storage parameters, covering operational boundaries such as tank capacity and charge/discharge rate limits;

(3)

Ammonia synthesis constraints, including process limitations like the reactor load adjustment range and minimum continuous operation time;

(4)

Market information, involving ammonia product demand and dynamic market prices;

(5)

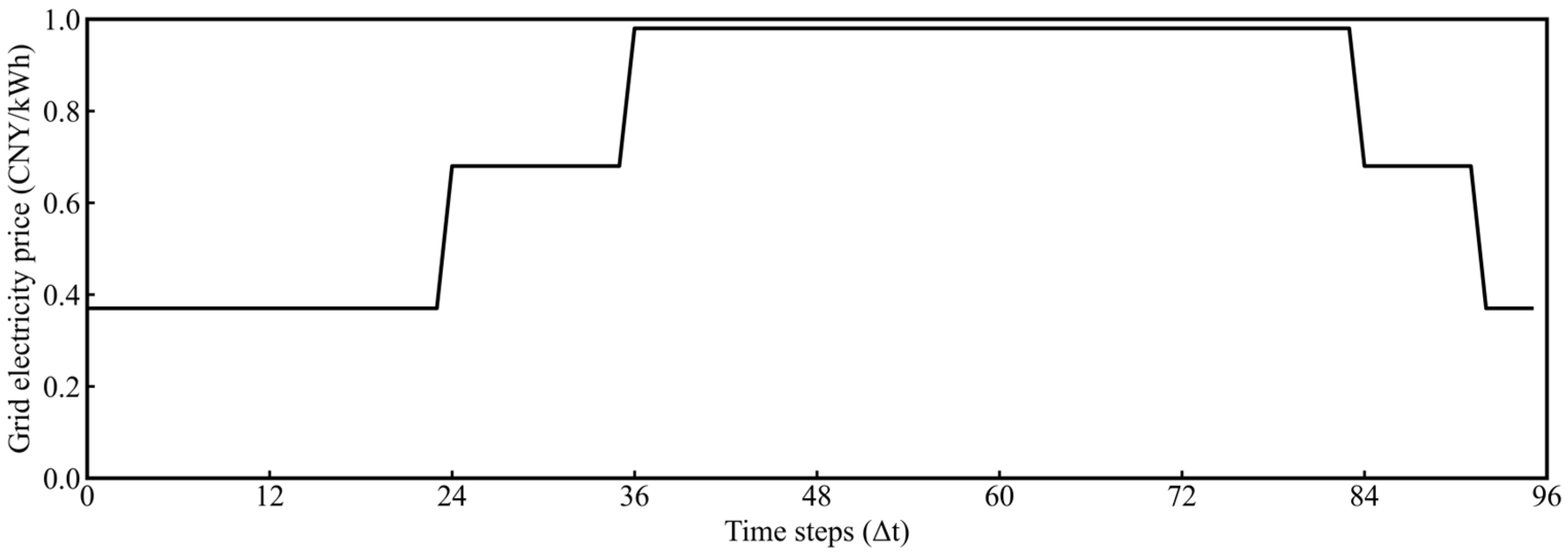
Time-of-use electricity prices, reflecting temporal economic signals for grid power purchase/sale;

(6)

Performance parameters, characterizing the capacity, efficiency characteristics, and operational status of the electrolyzer cluster.

The Core Optimization Module employs a two-level optimization strategy:

(1)

The upper level is an MILP optimization model based on the PuLP framework and the CBC solver^@. With the objective function of maximizing economic benefits, it comprehensively considers multiple constraints such as renewable energy consumption, hydrogen storage charge/discharge timing, and the load regulation capability of ammonia synthesis. It optimizes to obtain the ammonia production schedule, energy consumption plan, hydrogen storage dispatch strategy, and the total power demand of the electrolyzer cluster;

(2)

The lower level is an efficiency-priority power allocation algorithm for the electrolyzer cluster. Based on the total power demand output from the MILP model and the efficiency status of individual electrolyzers, it achieves optimal power distribution within the cluster to maximize overall hydrogen production efficiency and reduce system energy consumption.

The Output Results Module generates the following key decision variables: the ammonia production schedule, energy consumption plan, hydrogen storage management strategy, total power for the electrolyzer cluster, and the power allocation scheme for each individual electrolyzer.

Through this multi-level coupled optimization, the framework achieves coordinated optimization across the entire chain of the wind–solar hydrogen-to-ammonia system. It enhances the utilization rate of renewable energy and reduces comprehensive electricity costs while ensuring stable system operation, providing scientific decision support for the refined operation of the system.

2.2. Modeling of the Wind–Solar Hydrogen-to-Ammonia System

2.2.1. Wind–Solar Power Generation Section

The power supply side of the system comprises wind power generation, photovoltaic (PV) power generation, and grid power purchase. The overall system operates in a mode with a weak grid connection, prioritizing the supply of renewable electricity to internal loads. Surplus renewable power is curtailed, while any shortfall is supplemented by purchasing electricity from the grid. Wind and solar energy exhibit complementary characteristics on a temporal scale: wind power output is generally higher at night and in winter, whereas PV output is concentrated during daytime and summer. This complementarity can, to some extent, smooth out the fluctuations in renewable energy output.

The system’s energy balance relationship can be expressed as:

$$P_t^{Wind}+P_t^{PV}+P_t^{Grid}=P_t^{Ele,total}+P_t^{Aux}+P_t^{Windcut}+P_t^{PVcut}$$

(1)

where $P_t^{Wind}, P_t^{PV},$ and $P_t^{Grid}$ represent the wind power, PV power, and grid-purchased power at time t, respectively (MW); $P_t^{Ele,total}$, $P_t^{Aux}$, $P_t^{Windcut}$ and $P_t^{PVcut}$ represent the power for water electrolysis, auxiliary power consumption (for sections like hydrogen storage, air separation, and ammonia synthesis), curtailed wind power, and curtailed PV power at time t, respectively (MW).

2.2.2. Water Electrolysis Hydrogen Production Section

The hydrogen production process is the core of the green ammonia system, converting renewable electrical energy into chemical energy in the form of hydrogen. In large-scale green ammonia systems, the electrolyzer cluster typically consists of multiple electrolyzers. The load of each electrolyzer can be flexibly adjusted between 30% and 110% of its rated power, featuring minute or even second-level response characteristics. Since electrolyzers have fast response times and low inertia, their power regulation rate is much higher than that of the ammonia synthesis section. Therefore, the power ramp constraints of the hydrogen production section are neglected in the dispatch modeling of this paper.

The physical relationship of water electrolysis for hydrogen production can be described as:

$$F_t^{H_2,total}={\displaystyle \frac{P_t^{Ele,total}\Delta t}{c^{EHR}}}$$

(2)

$$P_{min}^{Ele,total}\le P_t^{Ele,total}\le P_{max}^{Ele,total}$$

(3)

where $F_t^{H_2,total}$ is the total hydrogen production from all electrolyzers at time t (Nm³); $P_t^{Ele,total}$ is the total hydrogen production power of all electrolyzers at time t (MW); $c^{EHR}$ is the rated hydrogen production power consumption (MWh/Nm³), treated as a constant coefficient; $\Delta t$ is the dispatch time step (h); $P_{\min }^{Ele,total}$ and $P_{\max }^{Ele,total}$ are the lower and upper limits for the total hydrogen production power of all electrolyzers, respectively (MW).

2.2.3. Hydrogen Storage Section

Due to the significant randomness and volatility of wind and solar power generation, directly using their output for the ammonia synthesis section could lead to frequent load fluctuations and system instability. Therefore, hydrogen storage tanks are configured as buffer units to achieve energy transfer and dynamic balance of hydrogen across the time dimension. When discharging, hydrogen from the storage tank needs to be compressed before being sent to the ammonia synthesis section. When charging, part or all of the hydrogen produced by the electrolyzers can be stored for later use.

The mass balance and logical constraints for hydrogen storage are as follows:

$$F_t^{H_2,total}=F_t^{H_2,use}+b_t^{charge}{V}_t^{H_2,in}-b_t^{release}{V}_t^{H_2,out}$$

(4)

$$b_t^{charge}+b_t^{release}+b_t^{idle}=1$$

(5)

$$V_{t+1}^{H_2}=V_t^{H_2}+\Delta t\left(V_t^{H_2,in}-V_t^{H_2,out}\right)$$

(6)

$$V_{min}^{H_2}\le V_t^{H_2}\le V_{max}^{H_2}$$

(7)

where $F_t^{H_2,use}$ represents the total hydrogen consumption by the ammonia synthesis section at time t (Nm³); $V_t^{H_2,in}$ and $V_t^{H_2,out}$ represent the hydrogen charging and discharging flow rates of the storage tank at time t, respectively (Nm³); $b_t^{charge}$, $b_t^{release}$ and $b_t^{idle}$ are binary variables indicating whether the storage tank is in charging, discharging, or idle state, respectively, constraining it from simultaneous charging and discharging. This ensures the tank can only be in one state at any given time; $V_{t+1}^{H_2}$ and $V_t^{H_2}$ represent the capacity of the hydrogen storage tank at time t + 1 and t, respectively (Nm³); $V_{min}^{H_2}$ and $V_{max}^{H_2}$ represent the lower and upper capacity limits of the hydrogen storage tank, respectively (Nm³).

2.2.4. Air Separation Nitrogen Production Section

The nitrogen required by the ammonia synthesis section is provided by an Air Separation Unit (ASU). Since the ammonia synthesis process requires a hydrogen-to-nitrogen molar ratio of approximately 3:1 [14], the nitrogen production from air separation can be linearly correlated with the hydrogen supply rate to simplify the model:

$$F_t^{N_2}={\displaystyle \frac{F_t^{H_2,use}}{c^{HNR}}}$$

(8)

where $F_t^{N_2}$ is the nitrogen demand at time t (Nm³); $c^{HNR}$ is the hydrogen-to-nitrogen ratio constant.

2.2.5. Ammonia Synthesis Section

The ammonia synthesis reaction is sensitive to temperature, pressure, and load changes. Typically, the unit is required to operate within a stable range near its rated load to avoid catalyst deactivation and equipment fatigue caused by frequent start-ups and shutdowns. Its dynamic operational constraints are as follows:

$$F_t^{N{H}_3}={\alpha }_{\mathrm{t}}{F}_k^{N{H}_3}$$

(9)

$${\alpha }_{min}\le {\alpha }_t\le {\alpha }_{max}$$

(10)

$$F_t^{N{H}_3}=F_{t-1}^{N{H}_3}+{\beta }_t{F}_k^{N{H}_3}\Delta t$$

(11)

$${\beta }_{min}\le {\beta }_t\le {\beta }_{max}$$

(12)

where $F_k^{N{H}_3}$ is the rated ammonia production rate (t/h); ${\alpha }_{\mathrm{t}}$ is the load factor of the ammonia synthesis unit; ${\beta }_t$ is the load ramp rate of the ammonia synthesis unit; $F_t^{N{H}_3}$ and $F_{t-1}^{N{H}_3}$ are the ammonia production rates at time t and t − 1, respectively (t/h); ${\alpha }_{min}$ and ${\alpha }_{max}$ represent the lower and upper limits of the ammonia synthesis unit load factor, respectively; typically set at 30% and 110% of the rated capacity to ensure operational stability and catalyst longevity. ${\beta }_{max}$ and ${\beta }_{min}$ represent the upper and lower limits of the load ramp rate coefficient, respectively. Generally the rate limit is ±10% per hour of the rated capacity.

Based on dynamic simulation and industrial data, the hydrogen consumption per ton of ammonia $F_t^{H_2,use}$ is linearly fitted as follows:

$$F_t^{N{H}_3}={\displaystyle \frac{F_t^{H_2,use}}{c^{HAR}}}$$

(13)

where $c^{HAR}$ represents the hydrogen consumption per ton of ammonia (t/Nm³).

2.3. Composite Optimization Objective Function

Based on the system model described above, this paper constructs a composite optimization objective function that simultaneously considers economic performance and operational stability. The objective function comprehensively accounts for four aspects: ammonia production revenue, electricity purchase cost, load fluctuation penalty, and power curtailment penalty. The overall form is as follows.

$$Obj=\left[-w_1{C}_{income,N{H}_3}+w_2{C}_{cost,Grid}+w_3{C}_{punish,load}+w_4{C}_{punish,cut}\right]$$

(14)

where $w_1,w_2,w_3,w_4$ are the weighting coefficients for each sub-objective function. The definitions of each sub-objective function are as follows:

(1)

Net Ammonia Production Revenue

This primarily includes revenue from ammonia sales, the cost of renewable electricity, and utility energy consumption:

$$C_{income,N{H}_3}={\displaystyle \sum }_t^T\left(c^{pr,N{H}_3}{F}_t^{N{H}_3}\Delta t-c^{pr,Res}\left(P_t^{Wind}+P_t^{PV}-P_t^{Windcut}-P_t^{PVcut}\right)\Delta t\right)$$

(15)

where $c^{pr,N{H}_3}$ is the selling price of ammonia (CNY/t); $c^{pr,Res}$ is the price of wind and solar green electricity (CNY/MWh).

(2)

Electricity Purchase Cost

$$C_{cost,Grid}=c_t^{pr,Grid}{P}_t^{Grid}\Delta t$$

(16)

where $c_t^{pr,Grid}$ is the time-of-use gird electricity price (CNY/MWh).

(3)

Ammonia Production Load Fluctuation Penalty Term

To avoid excessive equipment stress caused by frequent adjustments, a load smoothing constraint is set:

$$C_{punish,load}={\displaystyle \sum }_t^T\left(a\left|F_t^{N{H}_3}-F_{t-1}^{N{H}_3}\right|\right)$$

(17)

where $F_t^{N{H}_3}$ and $F_{t-1}^{N{H}_3}$ are the ammonia production rates at time t and t − 1, respectively (t); $a$ is the penalty coefficient for ammonia load fluctuation.

(4)

Power Curtailment Penalty Term

$$C_{punish,cut}={\displaystyle \sum }_t^T{c}^{pr,Res}\Delta t\left(P_t^{Windcut}+P_t^{PVcut}\right)$$

(18)

In summary, the main decision variables of the system include $P_t^{Grid}$, $P_t^{Ele,total}, P_t^{Aux}$, $P_t^{Windcut}, P_t^{PVcut}, P_t^{Ele,total}$, $F_t^{H_2,total}, F_t^{H_2,use}$, $b_t^{charge}, V_t^{H_2,in },b_t^{release}, V_t^{H_2,out}, F_t^{N{H}_3}$, etc., collectively denoted as x. The proposed dispatch problem is formulated as follows:

$$\begin{array}{l}\underset{x}{\min } (14)\\ s.t. (1)-(13).\end{array}$$

(19)

By optimizing and solving the above problem, flexible dispatch and economical operation of the wind–solar hydrogen-to-ammonia system can be achieved.

2.4. Electrolyzer Cluster Power Allocation Strategy

The flexible dispatch of the electrolyzer section plays a decisive role in the overall energy efficiency of the system. Through rational unit commitment combinations and power allocation strategies, the overall adjustable power range of the electrolyzer cluster can be expanded to approximately 5% to 110% of the system’s rated power, with response times on the scale of minutes or even seconds, significantly enhancing operational flexibility. In industrial practice, electrolyzers typically operate in a continuous hot-standby state with minimal cold starts; thus, load adjustment is achieved primarily through current regulation, and start-stop constraints are not considered here.

However, during long-term operation, performance degradation occurs in electrolyzer stacks, electrodes, and membrane assemblies, causing the electrical-to-hydrogen conversion efficiency to gradually diverge among different electrolyzers. If these degradation differences are not considered during power allocation, it can easily lead to a decrease in the system’s overall efficiency or overload operation of some units. Therefore, this paper proposes an efficiency-priority-based power allocation strategy for the electrolyzer cluster. Its core principle is to prioritize allocating load to electrolyzers with higher efficiency and lower degradation levels, under the premise of meeting the total hydrogen production power demand, in order to achieve optimal system energy consumption. The power allocation process for the electrolyzer cluster can be formalized as the following EPPA algorithm (Algorithm 1):

Algorithm 1. Efficiency-Priority Power Allocation Strategy for Electrolyzer Cluster

1: Precondition: Initialize electrolyzer parameters: rated power $P_{rated}$, efficiency ${\eta }_i$, time step $\Delta t$, and ratio limits $\left[r_{min},r_{max}\right]$. 2: Compute power bounds: $P_{min}=r_{min}{P}_{rated}, P_{max}=r_{max}{P}_{rated}$. 3: Sort electrolyzers by descending efficiency to obtain order $O=argsort(\eta )$. 4: For each time step $t$:    a. Set remaining hydrogen $R_t=H_{2,demand}(t)$.    b. For each electrolyzer $i\in O$: 5: Compute $H_{2,max,i}=P_{max}\Delta t{\eta }_i$. 6: If $R_t\ge H_{2,max,i}$, assign $P_i=P_{max}$. 7: Else $P_i=min(max(R_t/(\Delta t{\eta }_i),P_{min}),P_{max})$. 8: Compute $H_{2,i}=P_i\Delta t{\eta }_i$, update $R_t=R_t-H_{2,i}$.    c. If last unit output $H_{2,i}<P_{min}\Delta t{\eta }_i$, average with previous unit. 9: Return each electrolytic cell power $P_i(t)$ and hydrogen production $H_{2,i}(t)$.

3. Case Study

To validate the effectiveness and practicality of the proposed optimal dispatch model and the efficiency-priority power allocation strategy for the green ammonia system, a case study system with the following engineering parameters was constructed. The system is powered by a 20 MW photovoltaic (PV) power station and an 80 MW wind farm. The direct green electricity price is set at 0.20 CNY/kWh. The time-of-use grid electricity price is shown in Figure 3. The water electrolysis hydrogen production system is configured with 13 alkaline (ALK) electrolyzers, each with a rated hydrogen production capacity of 1000 Nm³/h, resulting in a total installed capacity of 65 MW. The hydrogen production power consumption is 0.005 MWh/Nm³. The maximum capacity of the hydrogen storage tank is 40,000 Nm³, with the initial inventory set to 10,000 Nm³. The number of electrolyzer units (13 × 5 MW) and the hydrogen storage capacity (40,000 Nm³) are selected based on typical engineering configurations of a 50,000-ton-per-year green ammonia system, ensuring a realistic balance between renewable supply, hydrogen production capacity, and the storage required to buffer approximately 3–4 h of operation for stable ammonia synthesis. The ammonia synthesis unit has a rated load of 6.25 t/h, with an allowable operating range of 30% to 110% of the rated load. The hydrogen consumption per ton of ammonia is 1963.41 Nm³. The selling price of the ammonia product is 3000 CNY/t. The penalty coefficient $a$ for ammonia load fluctuation is 100 CNY/(t/h).

The dispatch model was formulated as a Mixed-Integer Linear Programming (MILP) problem using the open-source optimization tool PuLP and solved with the COIN-OR CBC solver (version 2.10.3). The solver employs a branch-and-bound framework, where an upper bound is derived from integer-feasible solutions obtained through heuristics such as the feasibility pump, and a lower bound is provided by the continuous relaxation of the MILP. Convergence is achieved when the relative gap between these bounds falls below the default optimality tolerance of 0.0001. All computations were performed on a PC with an Intel^® Core™ i5-1135G7 processor (2.40 GHz) and 16 GB of RAM.

Based on the above parameter settings, the dispatch time step was set to 15 min, and the total simulation period was 72 h (288 time steps in total). The 72-h simulation window could capture representative wind–solar variability and short-term dynamic interactions while keeping the MILP model computationally tractable. The wind and solar power output curves are shown in Figure 4. To simplify the model complexity, except for the electrolyzer system, all other sections (including hydrogen storage, air separation, and ammonia synthesis compression units) were considered as auxiliary loads, with their power consumption set to 10% of the total electrolyzer power. The initial weight coefficients $w_1,w_2,w_3,w_4$ in the model were set to [1, 1, 1, 1]. Subsequently, Section 3.1 presents a comparative analysis of the system dispatch results under three typical operating schemes. Then, based on the total electrolyzer power and hydrogen demand obtained from the dispatch stage, Section 3.2 performs the electrolyzer cluster power allocation calculation to verify the effectiveness of the proposed efficiency-priority control strategy and the operational characteristics of the cluster.

3.1. Dispatch Results Analysis

To validate the effectiveness of the constructed optimization dispatch model for the renewable energy generation-electrolytic hydrogen production-ammonia synthesis system, this section compares and analyzes three operating schemes under the same wind and solar power forecast conditions over a fixed three-day period. The schemes are:

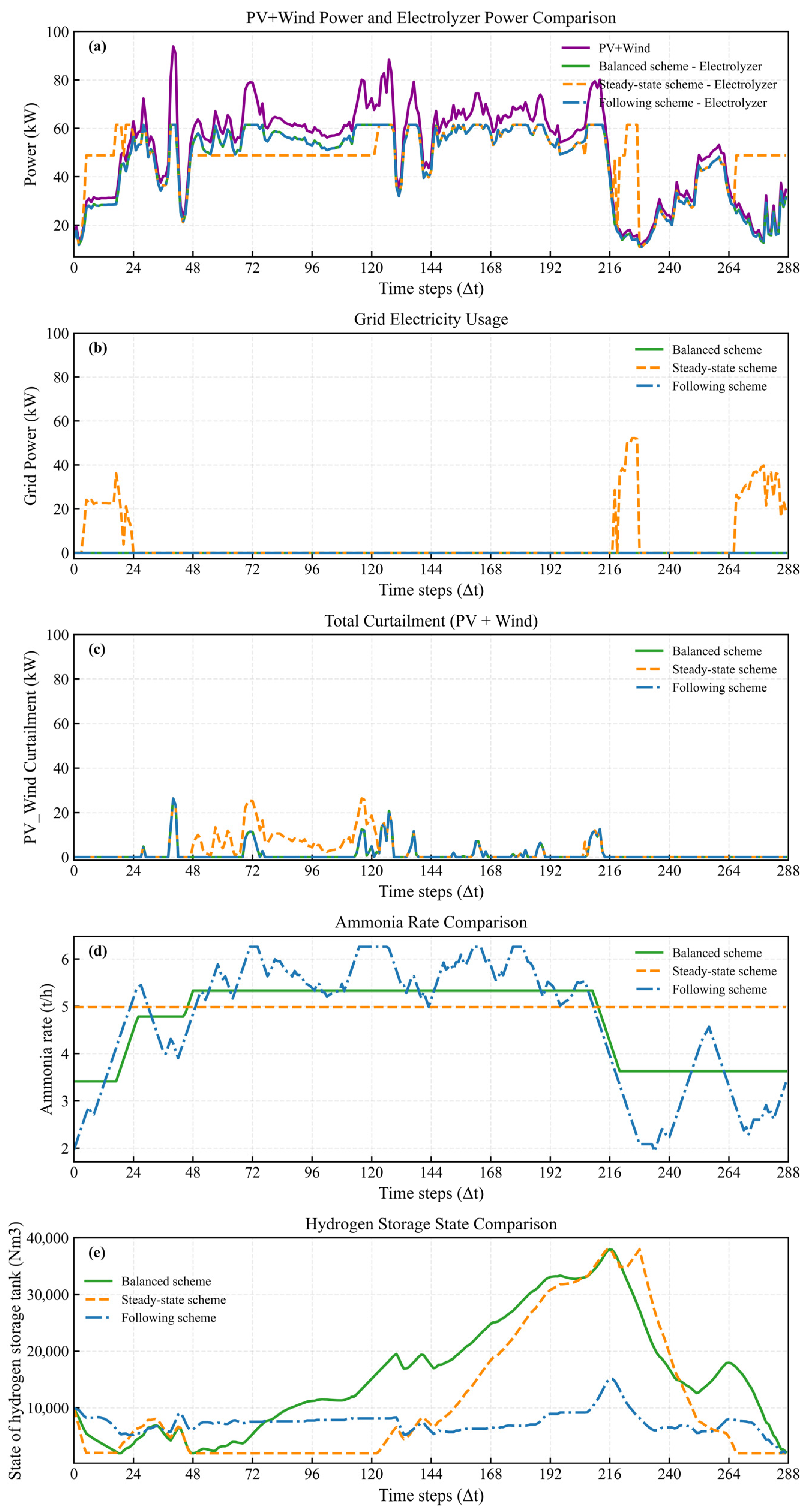
(1)

Balanced Scheme (Scheme A): achieves comprehensive coordination between renewable energy utilization and system load stability. All four sub-objectives in the composite optimization—ammonia revenue, electricity cost, load fluctuation penalty, and curtailment penalty—are considered, and the weight coefficients $w_1,w_2,w_3,w_4$ are set to [1, 1, 1, 1]. The reason for the equal weight of 1 is that all sub-goals are represented by the corresponding monetary unit (CNY) to ensure that each project contributes to the total cost based on its inherent economic impact, without arbitrary scaling.

(2)

Steady-State Scheme (Scheme B): corresponds to the traditional continuous, constant-load operation mode of chemical plants, primarily relying on the grid to compensate for renewable fluctuations. Since the load is constant and curtailment is not penalized, the weight coefficients $w_1,w_2,w_3,w_4$ are set to [1, 1, 0, 0].

(3)

Following Scheme (Scheme C): the system load varies with the fluctuations in renewable power output, without fully considering the dynamic constraints and equipment adaptability of the chemical process. Similar to Scheme B, only the economic objectives are considered, with weight coefficients $w_1,w_2,w_3,w_4$ are set to [1, 1, 0, 0].

Figure 5 shows the dynamic production curves for each scheme, including the (a) hydrogen production power, (b) grid Electricity usage, (c) PV + Wind curtailment, (d) ammonia rate and (e) state of hydrogen storage tank at each time step. The time periods Δt of 1–96, 97–192, and 193–288 represent Day 1, Day 2, and Day 3, respectively.

Table 1. Comparison of the main energy consumption and economic indicators under three operating schemes.

Indicator	Balanced Scheme	Steady-State Scheme	Following Scheme
Curtailed Energy (MWh)	90.43	241.0	90.43
Grid Electricity Usage (MWh)	0	363.75	0
Electrolyzer Power Consumption (MWh)	3287.03	3480.83	3287.03
Total Hydrogen Storage Throughput (104 Nm3)	11.8	10.94	5.76
Ammonia Production (t)	338.9	358.64	338.9
Unit Electricity Consumption Cost (CNY/t)	2187.15	2702.72	2187.15
Comprehensive Revenue (104 CNY)	27.55	10.66	27.55
Model solving time (s)	1.96	1.79	1.74

compares the main energy consumption and economic indicators of the three operating schemes.

From Figure 5a, it can be observed that the PV_Wind power generation curve exhibits significant diurnal fluctuation characteristics, with distinct PV output peaks during the daytime and primary reliance on wind power support at night. The three schemes show significant differences in their response to renewable power fluctuations: Under the Balanced Scheme (A) and the Following Scheme (C), the electrolyzer power curves almost overlap and both align well with the renewable power output. When the maximum electrolyzer power is reached, a small amount of curtailment inevitably occurs. The abandoned power of the three schemes can be corresponding as shown in Figure 5c.

The Steady-State Scheme (B), however, maintains a constant power operation. It purchases a significant amount of grid electricity to compensate when renewable generation is insufficient, while during peak generation periods, constrained by the rigid system load, a relatively large portion of wind and solar power is curtailed. For example, during periods 0–24, 216–228, and 264–288, the electrolyzer power curve of the Steady-State Scheme lies above the renewable generation curve, indicating substantial grid electricity purchase to supplement the load. In Figure 5b, it is shown that only the steady-state scheme (B) has a network electricity purchase, at times of 0–24, 216–228, 264–288. In contrast, during the 48–120 period, the power curve of the electrolytic cell in Figure 5a steady state scheme (B) is below the renewable power generation curve, indicating that there is a significant power reduction during this period, as shown in Figure 5c.

Figure 5d shows the variation trends of the ammonia production rate under the three schemes. The ammonia loads of the three schemes are within the upper (110%) and lower (30%) load limit constraints. The ammonia production rate in the Steady-State Scheme (B) remains constant at 4.98 t/h, consistent with traditional continuous operation. The Following Scheme (C) exhibits strong fluctuations within the allowable load-change range, with a peak-to-valley difference reaching 70% on Day 1. It also undergoes four instances of sustained increases or decreases exceeding 30% across the 288 time steps. Such operation in practice would disrupt thermal balance, affect catalyst activity, and accelerate equipment fatigue. In contrast, the Balanced Scheme (A) uses hydrogen storage to smooth the ammonia synthesis load. It slightly raises production during periods 20–28 and 46–50 to absorb more renewable power, and reduces load during period 212–222 in response to a subsequent drop in generation. The ammonia load curve under this scheme remains relatively stable even under significant renewable variation, thereby mitigating process disturbances.

Figure 5e shows the dynamic state of charge (SOC) of the hydrogen storage tank. Day 2 has the strongest renewable generation, which drops sharply after step 216. Between steps 96–216, both the Balanced and Steady-State Schemes increase their hydrogen inventory, preparing for the subsequent generation decline. Under the Balanced Scheme, the tank cycles frequently, with inventory varying between 2000 and 38,000 Nm³, demonstrating clear “peak shaving and valley filling” operation. The Steady-State Scheme, due to grid power support, involves less frequent storage cycling. The Following Scheme, though grid-free, maintains low inventory (<15,000 Nm³) with unstable storage dynamics as it closely tracks renewable output. Total hydrogen throughput (Table 1) further supports this: the Balanced Scheme reaches 118,000 Nm³, about twice that of the Following Scheme (57,600 Nm³), highlighting the critical role of hydrogen storage in energy buffering and load regulation for improved renewable utilization and flexibility.

Over the three-day period, total renewable energy generation was 3706.16 MWh. As shown in Table 1, the Steady-State Scheme consumed the most electrolyzer power (3480.83 MWh), about 5.9% higher than the Balanced Scheme (3287.03 MWh), due to its reliance on grid power to maintain a constant load. Both the Balanced and Following Schemes used no grid electricity, had a curtailment rate of 2.4%, and consumed the same amount of electrolyzer power (3287.03 MWh).

Although the Steady-State Scheme produced slightly more ammonia (358.64 t), its unit electricity cost was 2702.72 CNY/t—about 19% higher than the Balanced Scheme (2187.15 CNY/t). In terms of revenue, the Balanced and Following Schemes each achieved a comprehensive revenue of 275,500 CNY, far exceeding the Steady-State Scheme’s 106,600 CNY. Despite similar economic indicators, the Following Scheme suffers from large operational fluctuations and underused hydrogen storage, compromising long-term reliability. The Balanced Scheme, in contrast, maintains economic efficiency while balancing energy use and process stability, demonstrating superior overall performance and greater suitability for practical application. As shown in Table 1, all three schemes were solved within 2 s, demonstrating the high computational efficiency of the MILP framework, despite potential approximation errors from linearization.

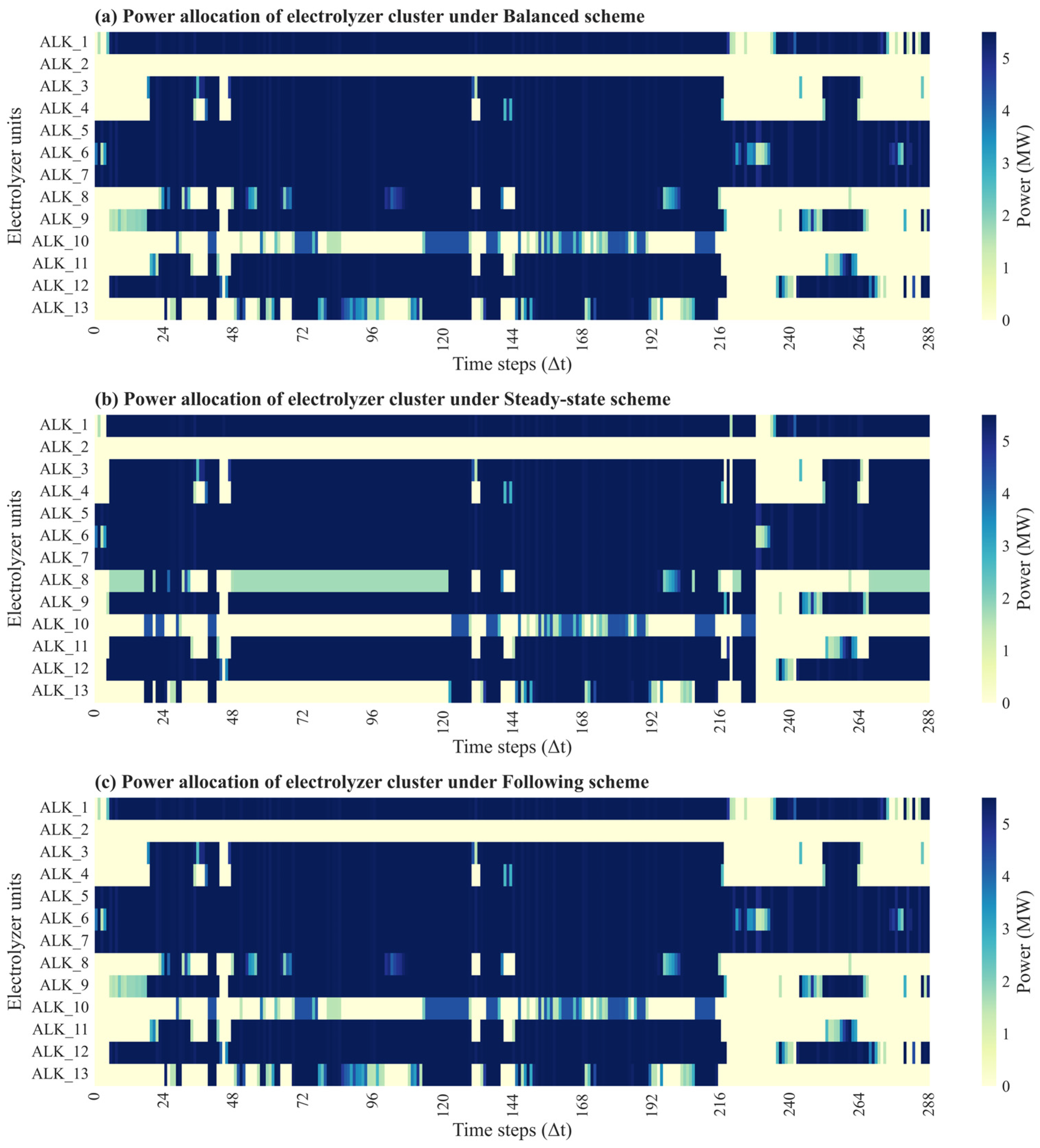
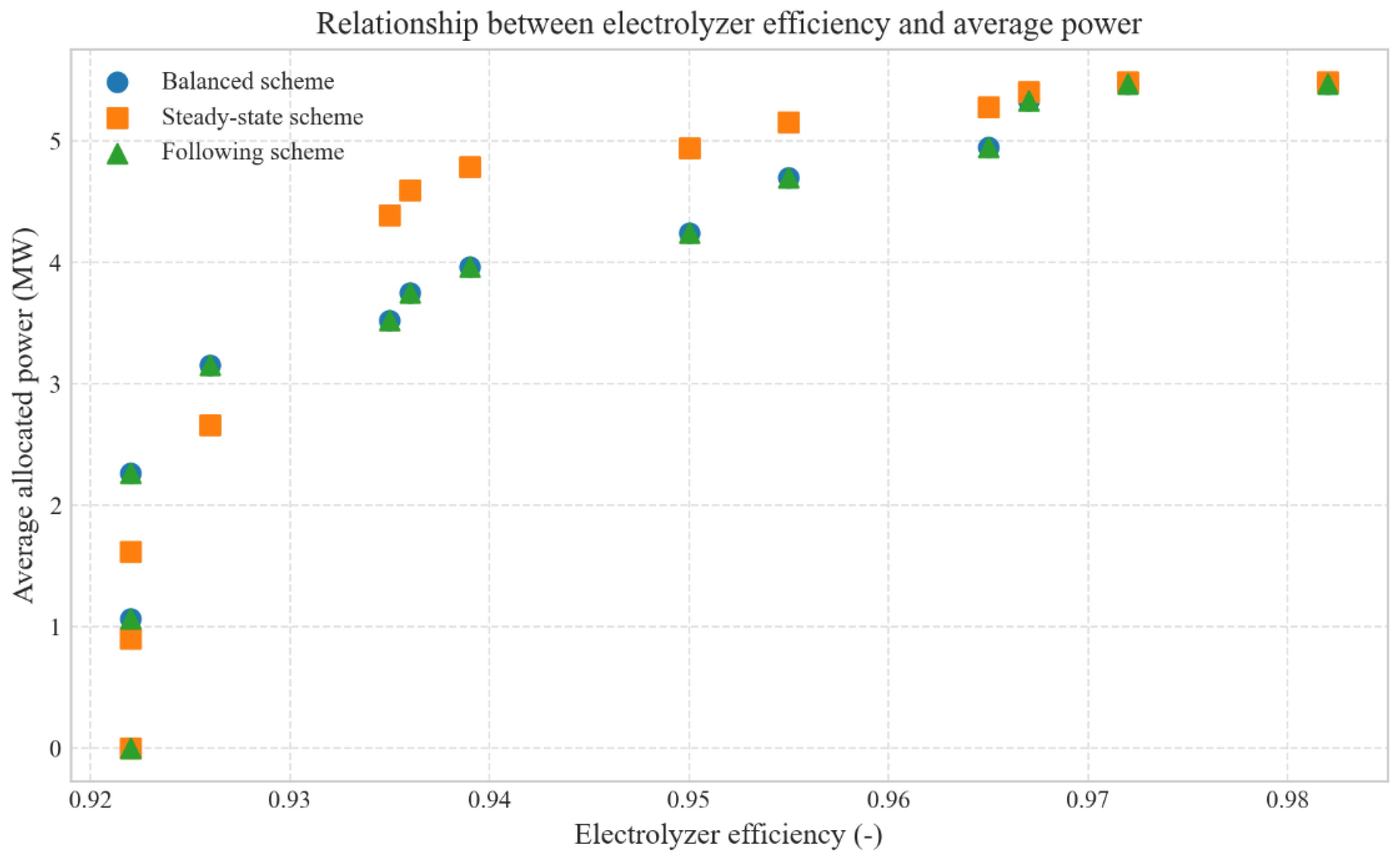
3.2. Analysis of Electrolyzer Cluster Control Effectiveness

The efficiencies ${\eta }_i$ for the 13 electrolyzers in the model are set to [0.965, 0.922, 0.939, 0.936, 0.972, 0.967, 0.982, 0.926, 0.950, 0.922, 0.935, 0.955, 0.922], respectively. To evaluate the effectiveness of the efficiency-based power allocation strategy, the power distribution among the 13 electrolyzers under the three operating schemes was analyzed, using the total hydrogen demand and electrolyzer efficiencies as boundary conditions. The results are shown in Figure 6 and Figure 7.

Figure 6 compares the electrolyzer power allocation under the three schemes using a heatmap, where color represents power level, the horizontal axis is time, and the vertical axis is the electrolyzer number. All three schemes show a clear layered structure: high-efficiency units (#5, #6, #7) consistently operate at the maximum load of 5.5 MW, indicated by the darkest shades, demonstrating the effectiveness of the efficiency-priority strategy. These units handle most of the load variations, while low-efficiency electrolyzers remain at low power or standby.

From time step 216 onward, renewable generation declines significantly, and the electrolyzer power allocation correspondingly adjusts. The heatmap also visually reflects the additional grid power purchases and curtailment in the Steady-State Scheme through color intensity differences.

Figure 7 further illustrates the linear relationship between electrolyzer efficiency and average allocated power, confirming that the efficiency-priority strategy successfully matches load to performance. In practice, electrolyzer efficiency can be updated in real time to maintain optimal operation. Since the power profiles of the Balanced and Following Schemes are nearly identical, their representations in Figure 6 and Figure 7 overlap considerably. Overall, the efficiency-based control strategy effectively balances system-level hydrogen demand with unit-level degradation, enabling dynamic, efficient, and coordinated operation.

4. Conclusions

This paper investigates the coordinated operation of a wind–solar–hydrogen–ammonia system under high renewable energy penetration. A mixed-integer linear programming (MILP) based dispatch model and an efficiency-priority power allocation strategy for electrolyzers are proposed, achieving multi-dimensional coupling and optimization of source-load-storage-chemical processes. The main conclusions are as follows:

(1)

Under fluctuating renewable generation, the Balanced Dispatch Scheme achieves high self-sufficiency, with a 2.4% curtailment rate and no grid electricity dependence. It effectively balances power fluctuation mitigation and load stability. Compared to the Steady-State Scheme, it reduces the unit electricity cost by about 19.4% and increases comprehensive revenue by approximately 169,000 CNY, significantly improving both economic performance and energy utilization efficiency.

(2)

Although the apparent revenue of the Following Scheme is similar to that of the Balanced Dispatch Scheme, its frequent load fluctuations lead to a significant increase in equipment start-stop cycles, posing potential issues such as reduced lifespan and worsened thermal stability. Consequently, it is unsuitable for long-term continuous chemical production.

(3)

The efficiency-priority power allocation strategy for electrolyzers effectively prevents overloading of some units and enhances the overall energy efficiency and operational stability of the hydrogen production system cluster.

(4)

The proposed scheduling framework has economy, flexibility and stability in the scenario of high penetration of renewable energy, which provides a systematic modeling idea and practical reference for the intelligent operation of green ammonia system, and is of great significance to promote the integration of new energy-chemical industry and low carbonization of industry.

(5)

Future research can extend this framework by incorporating electrolyzer degradation prediction models, adopting stochastic or robust optimization to better handle long-term renewable uncertainty, refining dynamic models of the ammonia synthesis loop, and developing real-time optimization or AI-assisted control strategies. These directions may further enhance system flexibility, operational reliability, and large-scale applicability of renewable-powered ammonia production.