Sensorless Field-Oriented Control of a Low-Speed Six-Phase Induction Generator

Abstract

This paper presents a sensorless control strategy for a six-phase induction generator (6PIG) operating at low speed (125 rpm). The proposed approach is based on the Model Reference Adaptive System (MRAS), with an initial estimation scheme developed using the reference model as the rotor flux. Simulation studies were conducted in MATLAB/Simulink 24.2.0.2740171 (R2024b) Update 1 and experimentally validated on a 24 kW–125 rpm 6PIG, to demonstrate the feasibility and performance of this method. A reactive power-based MRAS variant was also proposed to overcome the observed limitations. Comparative analysis showed a significant improvement in estimation accuracy and dynamic response compared with the flux-based MRAS. Robustness tests under fault conditions, such as opening phases, confirmed that the reactive power-based MRAS maintains a stable and accurate rotor speed estimation. These findings demonstrate the potential of reactive-power-based MRAS for the sensorless control of six-phase induction generators (6PIGs) in renewable energy systems.

1. Introduction

The growing demand for electrical energy and the need to reduce its environmental impact have encouraged the development and integration of renewable energy sources into power systems [1]. Induction generators are widely used among various electromechanical converters because of their robustness, low cost, easy maintenance, and suitability for wind and small hydro applications [2]. Unlike synchronous generators, they do not require a dedicated DC excitation system and can operate at variable speeds, making them ideal for renewable energy applications. Many wind and micro-hydropower systems rely on squirrel cage or slip ring induction generators because of their simple design and reliable performance [2]. Their durability, affordability, and low upkeep have established them as a cornerstone of sustainable power generation.

In this context, multiphase induction machines, particularly six-phase induction machines, have recently gained research attention. Compared with their conventional three-phase counterparts, six-phase configurations offer superior performance characteristics, including improved fault tolerance, reduced torque ripple and harmonic distortion, enhanced torque density and better thermal management [3,4]. Their capability to operate with dual three-phase converters and to be reconfigured from existing three-phase designs further enhances the reliability and flexibility of control. Consequently, six-phase induction machines are increasingly regarded as promising candidates for renewable energy applications, such as wind turbine generation and hybrid systems [5,6,7].

Efficient control of these machines usually requires accurate rotor speed or position information, often measured by mechanical sensors such as encoders or tachometers. Although these sensors provide accurate real-time feedback, they also have drawbacks such as high cost, complexity, sensitivity to harsh conditions, installation difficulties, and reduced reliability due to mechanical failures [8]. In remote or industrial settings, installing and maintaining such sensors becomes even more challenging [9]. Therefore, eliminating the physical speed sensor is highly appreciated. Thus, sensorless control strategies aim to estimate rotor variables using only electrical measurements, offering higher reliability, lower cost, reduced system complexity, and better robustness in harsh operating environments [10].

Instead of using direct measurements, sensorless control estimates rotor speed or position in real-time from stator voltages and currents combined with machine models. Over the past decade, several estimation techniques have been developed, including open-loop estimators, observers such as Luenberger or Kalman filters, sliding mode observers, high-frequency signal injection methods, and adaptive schemes [10].

However, sensorless systems remain sensitive to parameter variations, particularly stator and rotor resistances, and perform poorly at zero and very low speeds. To overcome these limitations, model-based estimation methods have received significant attention because they rely on mathematical representations of the machine and state observers to determine unmeasured quantities, such as flux and speed [11].

Among these, the Model Reference Adaptive System (MRAS) has become the most popular method due to its simplicity, robustness, and real-time adaptability [12]. Its principle relies on comparing a reference model with an adjustable model where the adaptation mechanism provides an estimation of the rotor speed or position. The most common approach uses the rotor flux as the reference variable. Although widely studied and validated, this approach suffers from reduced accuracy at low speeds, mainly due to weak flux sensitivity and back-EMF signals.

Numerous MRAS variants have been proposed, mainly differing in the output variable, such as rotor flux, back-EMF [13], reactive power [14], or stator currents. Rotor flux-based schemes are the most widely adopted because of their simplicity and stable performance under various operating conditions [13]. Early contributions, such as Schauder’s observer, laid the foundation for modern MRAS techniques with later integrated neural networks [15,16] or fuzzy logic.

Nevertheless, the performance of conventional rotor flux-based MRAS is poor near to standstill due to weak back-EMF signals, integrator drift, and sensitivity to model errors. Replacing the integrator with a low-pass filter mitigates drift but introduces phase lag, further degrading performance at low speeds [10,13]. Therefore, alternative MRAS strategies have been proposed using other measurable variables.

In addition, recent research has extended sensorless control techniques to multiphase induction machines, which inherently offer improved tolerance and reduce harmonic distortion. In [17], position control of a faulted six-phase induction machine using genetic algorithms was presented, demonstrating robust performance even under phase-loss conditions. In a related study, the same authors developed an intelligent sensorless speed control method that achieves accurate estimation without the use of mechanical sensors [18]. More recently, ref. [19] introduced a robust sensorless field control for six-phase induction motor drive designed to reduce common-mode voltage and enhance stability. These advances highlight the growing interest in fault-tolerant, low-speed, and multiphase sensorless systems, providing strong motivation for this work.

In this work, a rotor flux-based MRAS strategy is developed and applied to a low-speed six-phase induction generator (6PIG). A reactive power-based variant is introduced to overcome its limitations, with the objective of improving estimation accuracy and dynamic performance. This study also includes a robustness analysis under fault conditions to compare the performance of both methods. This contribution aims to provide a comprehensive evaluation and open up new perspectives for sensorless control of a low-speed six-phase induction generation in renewable energy applications, such as micro-hydropower.

The remainder of this paper is organized as follows: Section 2 presents the modeling and control of the 6PIG. The MRAS strategies are described in Section 3. Simulation and experimental results and comparative analysis, including robustness tests, are be provided in Section 4. Finally, Section 5 concludes and outlines future perspectives.

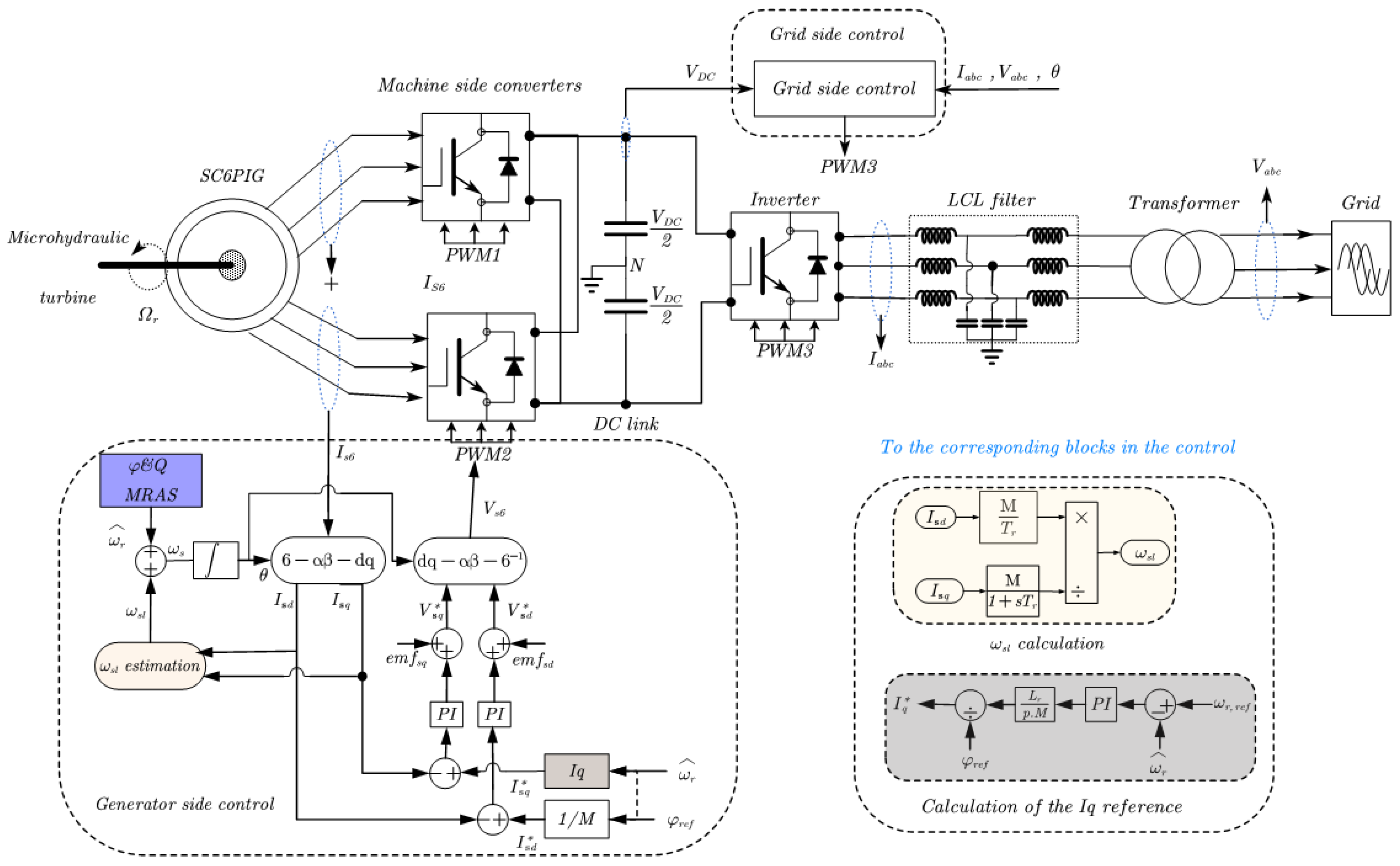
2. Modeling and Control of a Six-Phase Induction Generator (6PIG)

2.1. Modeling of the 6PIG

The squirrel cage six-phase induction generator (SC6PIG) consists of a stator with six identical windings, each shifted electrically by 60°, and a rotor made of conducting bars connected by a short-circuit ring. The configuration of the stator and rotor windings is illustrated in Figure 1.

The studied arrangement can be regarded as a symmetrical structure with a single neutral. The fundamental voltage, torque, and rotor speed equations expressed in the natural reference frame ($abcdef)$ [20] describe a simplified representation of the equivalent internal circuit model reported in [21]. The stator and rotor are characterized by their respective resistances, self-inductances and mutual inductances in this formulation.

The voltage and flux equations are derived from Equations (1) and (2), respectively,

$$\left\{\begin{array}{c}\left[V_{s6}\right]=\left[R_{s6}\right]\left[I_{s6}\right]+{\displaystyle \frac{d\left[{\varphi }_{s6}\right]}{dt}}\\ \left[V_{r6}\right]=\left[R_{r6}\right]\left[I_{r6}\right]+{\displaystyle \frac{d\left[{\varphi }_{r6}\right]}{dt}}\end{array}\right.$$

(1)

where $\left[V_{s6}\right]$ and $\left[V_{r6}\right]$ are the stator and rotor voltages and $\left[I_{s6}\right]$ and $\left[I_{r6}\right]$ are the stator and rotor currents, respectively, for the six-phases (a, b, c, d, e, f). $\left[R_{s6}\right]={diag}_6\left(R_s\right)$ and $\left[R_{r6}\right]={diag}_6\left(R_r\right)$ represent the stator and rotor resistance matrices, respectively.

The stator flux $\left[{\Phi }_{s6}\right]$ and rotor flux $\left[{\varphi }_{r6}\right]$ are given in Equation (2):

$$\left\{\begin{array}{c}\left[{\Phi }_{s6}\right]=\left[L_s\right]\left[I_{s6}\right]+\left[L_{sr}\right]\left[I_{r6}\right]\\ \left[{\varphi }_{r6}\right]={\left[L_{sr}\right]}^T\left[I_{s6}\right]+\left[L_r\right]\left[I_{r6}\right]\end{array}\right.$$

(2)

where $\left[L_s\right]$ and $\left[L_r\right]$ represent the stator and rotor inductance matrices, respectively, and $\left[L_{sr}\right]$ is the mutual inductance matrix between the stator and the rotor.

The electromagnetic torque, $T_e$, expressed as a function of the stator and the rotor currents, is given by Equation (3):

$$T_e=p{\left[I_{s6}\right]}^T{\displaystyle \frac{\mathit{\partial }\left[L_{sr}\right]}{\mathit{\partial }{ϴ}_r}}\left[I_{r6}\right]$$

(3)

where ${ϴ}_r$ represents the electrical rotor angle and $p$ denotes the number of pole pairs in the SC6PIG.

Based on (3), the rotor speed ${\Omega }_r$ which links the electrical and mechanical dynamics in the SC6PIG model is given by Equation (4):

$$J{\displaystyle \frac{d{\Omega }_r}{dt}}+f{\Omega }_r=T_e+T_L$$

(4)

where $J$ is the inertia, $f$ is the viscous friction coefficient and $T_L$ is the load torque.

2.2. Indirect Rotor Field-Oriented Control of the 6PIG

Field-oriented control (FOC) enables the independent regulation of the rotor flux and the electromagnetic torque, thereby improving the performance of the 6PIG. Briefly, the method relies on the rotating dq reference frame obtained from the natural frame through Clarke’s decoupling transformation matrix, denoted $T_6$, as defined in matrix (5) and derived from [22], while preserving the total power. This transformation depends on the number of active phases, N. As a result, the system is expressed in the $\mathsf{\alpha }\mathsf{\beta }{z}_i$, frame, where the $\mathsf{\alpha }\mathsf{\beta }$ components are responsible for power generation and the additional $z_i$ components (with to $z_i=N-$2) are associated with losses, which are neglected in this study.

$$T_6={\displaystyle \frac{1}{\sqrt{3}}}\left[\begin{array}{cccccc}1& \mathit{cos}\left(\theta \right)& \mathit{cos}\left(2\theta \right)& \mathit{cos}\left(3\theta \right)& \mathit{cos}\left(2\theta \right)& \mathit{cos}\left(\theta \right)\\ 0& \mathit{sin}\left(\theta \right)& \mathit{sin}\left(2\theta \right)& -\mathit{sin}\left(3\theta \right)& -\mathit{sin}\left(2\theta \right)& -\mathit{sin}\left(\theta \right)\\ 1& \mathit{cos}\left(2\theta \right)& \mathit{cos}\left(4\theta \right)& \mathit{cos}\left(6\theta \right)& \mathit{cos}\left(4\theta \right)& \mathit{cos}\left(2\theta \right)\\ 0& \mathit{sin}\left(2\theta \right)& \mathit{sin}\left(4\theta \right)& -\mathit{sin}\left(6\theta \right)& -\mathit{sin}\left(4\theta \right)& -\mathit{sin}\left(2\theta \right)\\ {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}\\ {\displaystyle \frac{1}{\sqrt{2}}}& -{\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& -{\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}& -{\displaystyle \frac{1}{\sqrt{2}}}\end{array}\right]$$

(5)

The phase angle $\theta$ equals ${\displaystyle \frac{\pi }{3}}$.

After applying the transformation, the stator voltages $V_s^{\alpha }$ and $V_s^{\beta }$, the rotor voltages $V_r^{\alpha }$ and $V_r^{\beta }$ and the stator fluxes $\left[{\varphi }_s^{\alpha }\right]$ and $\left[{\varphi }_s^{\beta }\right]$, as well as the rotor fluxes $\left[{\varphi }_r^{\alpha }\right]$ and $\left[{\varphi }_r^{\beta }\right]$, in the stationary reference frame can be expressed according to (6) and (7):

$$\left\{\begin{array}{c}\left[\begin{array}{c}{V}_s^{\alpha }\\ V_s^{\beta }\end{array}\right]=\left[\begin{array}{c}{R}_s\\ R_s\end{array}\right]\left[\begin{array}{c}{I}_s^{\alpha }\\ I_s^{\beta }\end{array}\right]+{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\varphi }_s^{\alpha }\\ {\varphi }_s^{\beta }\end{array}\right]\\ \left[\begin{array}{c}0\\ 0\end{array}\right]=\left[\begin{array}{c}{R}_r\\ R_r\end{array}\right]\left[\begin{array}{c}{I}_r^{\alpha }\\ I_r^{\beta }\end{array}\right]+{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\varphi }_r^{\alpha }\\ {\varphi }_r^{\beta }\end{array}\right]+\left[\begin{array}{cc}0& {\omega }_r\\ {-\omega }_r& 0\end{array}\right]\left[\begin{array}{c}{\varphi }_r^{\alpha }\\ {\varphi }_r^{\beta }\end{array}\right]\end{array}\right.$$

(6)

$$\left\{\begin{array}{c}\left[\begin{array}{c}{\varphi }_s^{\alpha }\\ {\varphi }_s^{\beta }\end{array}\right]=\left[\begin{array}{cc}{L}_s& 0\\ 0& L_s\end{array}\right]\left[\begin{array}{c}{I}_s^{\alpha }\\ I_s^{\beta }\end{array}\right]+\left[\begin{array}{cc}M& 0\\ 0& M\end{array}\right]\left[\begin{array}{c}{I}_r^{\alpha }\\ I_r^{\beta }\end{array}\right]\\ \left[\begin{array}{c}{\varphi }_r^{\alpha }\\ {\varphi }_r^{\beta }\end{array}\right]=\left[\begin{array}{cc}M& 0\\ 0& M\end{array}\right]\left[\begin{array}{c}{I}_s^{\alpha }\\ I_s^{\beta }\end{array}\right]+\left[\begin{array}{cc}{L}_r& 0\\ 0& L_r\end{array}\right]\left[\begin{array}{c}{I}_r^{\alpha }\\ I_r^{\beta }\end{array}\right]\end{array}\right.$$

(7)

where M is the mutual inductance, ${\omega }_r$ is the electrical rotor speed, $I_s^{\alpha }$ and $I_s^{\beta }$ are the stator currents, $I_r^{\alpha }$ and $I_r^{\beta }$ are the rotor currents and $R_s$ and $R_r$ are the stator and rotor resistances, respectively.

The transformation matrix $T_2$ given in Equation (8) is applied to express the machine equations in the synchronous rotating reference frame to control the 6PIG, where ${\theta }_s$ is the synchronous angle.

$$T_2=\left[\begin{array}{cc}cos{\theta }_s& sin{\theta }_s\\ -sin{\theta }_s& cos{\theta }_s\end{array}\right]$$

(8)

The stator voltages $V_s^d$ and $V_s^q$, and the rotor voltages $V_r^d$ and $V_r^q$, as well as the stator fluxes ${\varphi }_s^d$ and ${\varphi }_s^q$ and the rotor fluxes ${\varphi }_r^d$ and ${\varphi }_r^q$, in the rotating reference frame can be expressed as follows in Equations (9) and (10):

$$\left\{\begin{array}{c}\left[\begin{array}{c}{V}_s^d\\ V_s^q\end{array}\right]=\left[\begin{array}{c}{R}_s\\ R_s\end{array}\right]\left[\begin{array}{c}{I}_s^d\\ I_s^q\end{array}\right]+{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\varphi }_s^d\\ {\varphi }_s^q\end{array}\right]+\left[\begin{array}{cc}0& -{\omega }_r\\ {\omega }_r& 0\end{array}\right]\left[\begin{array}{c}{\varphi }_s^d\\ {\varphi }_s^q\end{array}\right]\\ \left[\begin{array}{c}{V}_r^d\\ V_r^q\end{array}\right]=\left[\begin{array}{c}{R}_r\\ R_r\end{array}\right]\left[\begin{array}{c}{I}_r^d\\ I_r^q\end{array}\right]+{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\varphi }_r^d\\ {\varphi }_r^q\end{array}\right]+\left[\begin{array}{cc}0& -\left({\omega }_s-{\omega }_r\right)\\ \left({\omega }_s-{\omega }_r\right)& 0\end{array}\right]\left[\begin{array}{c}{\varphi }_r^d\\ {\varphi }_r^q\end{array}\right]\end{array}\right.$$

(9)

$$\left\{\begin{array}{c}\left[\begin{array}{c}{\varphi }_s^d\\ {\varphi }_s^q\end{array}\right]=\left[\begin{array}{c}{L}_{ss}\\ L_{rs}\end{array} \begin{array}{c}{L}_{sr}\\ L_{ss}\end{array} \right]\left[\begin{array}{c}{I}_s^d\\ I_s^q\end{array}\right]\\ \left[\begin{array}{c}{\varphi }_r^d\\ {\varphi }_r^q\end{array}\right]=\left[\begin{array}{c}{L}_{ss}\\ L_{rs}\end{array} \begin{array}{c}{L}_{sr}\\ L_{ss}\end{array} \right]\left[\begin{array}{c}{I}_r^d\\ I_r^q\end{array}\right]\end{array}\right.$$

(10)

In indirect rotor field-oriented control (IRFOC), the rotor flux is aligned with the d-axis as follows:

$${\varphi }_{rd}={\varphi }_r^{*} and {\varphi }_{rq}=0$$

(11)

The synchonous angle ${\theta }_s$ [23] is obtained using Equation (12), where ${\omega }_{sl}$ represents the slip frequency and $T_r={\displaystyle \frac{L_r}{R_r}}$ is the time constant of the rotor.

$${\theta }_s=\int \left({\omega }_r+{\omega }_{sl}\right)dt\to \left\{\begin{array}{c}{\varphi }_r={\displaystyle \frac{M}{1+s{\tau }_r}}{I}_s^d\\ {\omega }_{sl}={\displaystyle \frac{M}{{\tau }_r{\varphi }_r}}{I}_s^q\end{array}\right.$$

(12)

To ensure full decoupling in the control of the 6PIG, regulation loops are designed for the stator currents $I_{sd}=i_s^d$ and $I_{sq}=i_s^q$.

$$\left\{\begin{array}{c}{V}_{sd}={\sigma L}_s{\displaystyle \frac{d{i}_{sd}}{dt}}+\left(R_s+{\displaystyle \frac{M^2{R}_r}{L_r^2}}\right)i_{sd}-{\omega }_s{\sigma L}_s{i}_{sq}+{\displaystyle \frac{{MR}_r}{L_r^2}}{\varphi }_{rq}\\ V_{sq}={\sigma L}_s{\displaystyle \frac{d{i}_{sq}}{dt}}+\left(R_s+{\displaystyle \frac{M^2{R}_r}{L_r^2}}\right)i_{sq}+{\omega }_s{\sigma L}_s{i}_{sd}+{\displaystyle \frac{M}{L_r}}{p\Omega \varphi }_r\end{array}\right.$$

(13)

The coefficient of dispersion $\sigma$ equals $1-{\displaystyle \frac{M^2}{L_s{L}_r}}$.

In the decoupled system, two additional inputs ($V_{s,dec}^d$, $V_{s,dec}^q$) are introduced to the control system, as shown in Equation (12):

$$\left\{\begin{array}{c}{V}_{s,dec}^d={\mathrm{V}}_{\mathrm{s}\mathrm{d}}+{emf}_s^d\\ V_{s,dec}^q={\mathrm{V}}_{\mathrm{s}\mathrm{q}}+{emf}_s^q\end{array}\right.$$

(14)

The compensation terms ${emf}_s^d$ and ${emf}_s^q$ are incorporated with opposite signs in the control to eliminate coupling between the d and q axes. These terms are defined in Equation (15) as follows:

$$\left\{\begin{array}{c}{emf}_s^d={\omega }_s{\sigma L}_s{i}_{sq}+{\displaystyle \frac{{MR}_r}{L_r^2}}{\varphi }_{rd}\\ {emf}_s^q=-{\omega }_s{\sigma L}_s{i}_{sd}-{\displaystyle \frac{M}{L_r}}{p\Omega \varphi }_r\end{array}\right.$$

(15)

The resulting transfer functions between the stator currents and the modified voltages are as follows:

$$\left\{\begin{array}{c}{i}_{sd}(s)={\displaystyle \frac{L_r^2}{R_s{L}_r^2+R_r{M}^2+{\sigma L}_s{L}_r^{2}s}}{V}_{s,dec}^d\\ i_{sq}(s)={\displaystyle \frac{L_r^2}{R_s{L}_r^2+R_r{M}^2+{\sigma L}_s{L}_r^{2}s}}{V}_{s,dec}^q\end{array}\right.$$

(16)

The proportional–integral (PI) controller parameters are given in (17), and these were determined using the Ziegler–Nichols tuning method. Specific values are provided in Appendix A.

$$\left\{\begin{array}{c}{K}_i^{dq}={\omega }_n^2·{\mathsf{\sigma }\mathrm{L}}_{\mathrm{s}}\\ K_p^{dq}=K_i^{dq}·\left({\displaystyle \frac{2\xi }{{\omega }_n}}-{\displaystyle \frac{{\mathrm{M}}^2}{{\mathrm{L}}_{\mathrm{r}}{\mathrm{T}}_{\mathrm{r}}{K}_i^{dq}}}-{\displaystyle \frac{{\mathrm{R}}_{\mathrm{s}}}{K_i^{dq}}}\right)\end{array}\right. \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} {\tau }_{PI}={\displaystyle \frac{K_p^{dq}}{K_i^{dq}}}$$

(17)

Figure 2 illustrates the overall structure of the proposed control system, which includes a SC6PIG for power generation, a back-to-back converter composed of two three-phase VSIs connecting the generator to the grid and/or local load through an LCL filter, and the control blocks for both the generator and grid sides.

This work focused on the generator side, where the proposed sensorless control replaces the encoder, as detailed in Figure 3 and Figure 4. In this scheme, the rotor speed (violet block) is estimated instead of measured. Slip frequency ${\omega }_{sl}$ (yellow block) is added to the rotor speed to obtain the synchronous speed.

The six-phase stator currents are transformed using the Clarke (5) and Park (8) transformations to derive the flux component $I_{sd}$ and torque component $I_{sq}$ (the reference is shown in the gray block), which are regulated by PI controllers. Subsequently, the resulting signals are converted back and applied to the inverter through a PWM modulator. The speed estimator calculates the rotor angle from the measured currents and voltages, ensuring precise and stable control without a mechanical sensor. The entire system has been modeled and simulated using MATLAB/Simulink^®.

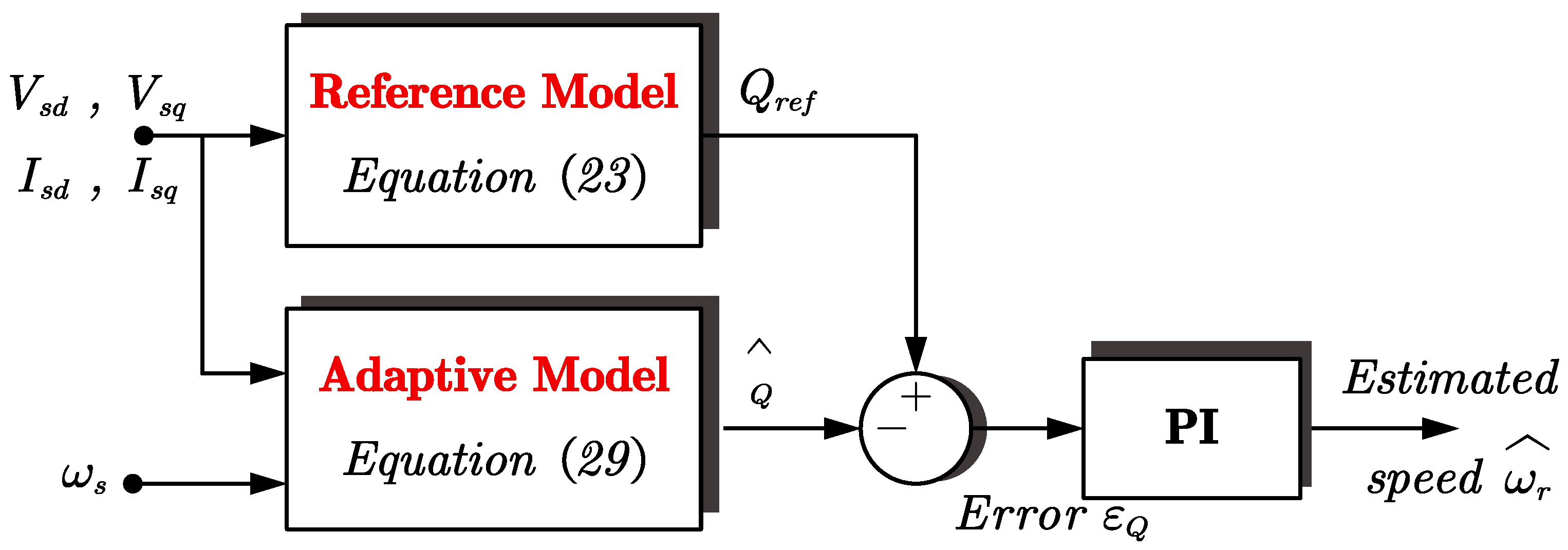
3. Sensorless Estimation Using Model Reference Adaptive System (MRAS)

The Model Reference Adaptive Reference System (MRAS) has become a key approach for the sensorless control of induction machines owing to its simple structure, low computational cost and robustness [24]. Its principle lies in the comparison between a reference model independent of the rotor speed and an adjustable model that depends on the estimated speed. The adaptation mechanism drives the error to zero, thus estimating the rotor speed.

In this study, two MRAS variants are addressed. The first model, which is widely reported in the literature, uses rotor flux as the reference model, whereas the second model, which is proposed here, relies on reactive power and is specially designed to enhance estimation accuracy at low speed.

3.1. Conventional Flux-Based MRAS

The reference model is derived from the stator voltage equations. Based on the flux (7), the following relation (18) can be expressed:

$$\left\{\begin{array}{c}{\phi }_{s\alpha }=\sigma L_s{I}_{s\alpha }+{\displaystyle \frac{M}{L_r}}{\phi }_{r\alpha }\\ {\phi }_{s\beta }={\sigma L}_s{I}_{s\beta }+{\displaystyle \frac{M}{L_r}}{\phi }_{r\beta }\end{array}\right.$$

(18)

By differentiating (18) and expressing the rotor fluxes from the derived expression, we obtain the following:

$$\left\{\begin{array}{c}\dot{{\phi }_{r\alpha }}={\displaystyle \frac{L_r}{M}}\left(\dot{{\phi }_{s\alpha }}-\sigma L_s{I}_{s\alpha }\right)\\ \dot{{\phi }_{r\beta }}={\displaystyle \frac{L_r}{M}}\left(\dot{{\phi }_{s\beta }}-{\sigma L}_s{I}_{s\beta }\right) \end{array}\right.$$

(19)

With Equation (6), the reference rotor flux in the stationary reference frame is given by the following:

$$\left\{\begin{array}{c}{\phi }_{r\alpha }=\int \left\{{\displaystyle \frac{L_r}{M}}\left(V_{s\alpha }-R_s{I}_{s\alpha }\right)-\sigma {\displaystyle \frac{L_r{L}_s}{M}}{\displaystyle \frac{d{I}_{s\alpha }}{dt}}\right\}dt\\ {\phi }_{r\beta }=\int \left\{{\displaystyle \frac{L_r}{M}}\left(V_{s\beta }-R_s{I}_{s\beta }\right)-\sigma {\displaystyle \frac{L_r{L}_s}{M}}{\displaystyle \frac{d{I}_{s\beta }}{dt}}\right\}dt\end{array}\right.$$

(20)

Unlike the reference model, the adaptive model depends on the rotor speed and stator currents. Based on (7), the rotor flux in the adaptive model, expressed in the same frame and dependent on the estimated rotor speed, is as follows:

$$\left\{\begin{array}{c}\widehat{{\phi }_{r\alpha }}=\int \left\{-{\displaystyle \frac{L_r}{R_r}}\widehat{{\phi }_{r\alpha }}-\widehat{{\omega }_r}\widehat{{\phi }_{r\beta }}-{\displaystyle \frac{{MR}_r}{L_r}}{I}_{s\alpha }\right\}dt\\ \widehat{{\phi }_{r\beta }}=\int \left\{-{\displaystyle \frac{L_r}{R_r}}\widehat{{\phi }_{r\beta }}+\widehat{{\omega }_r}\widehat{{\phi }_{r\alpha }}-{\displaystyle \frac{{MR}_r}{L_r}}{I}_{s\beta }\right\}dt\end{array}\right.$$

(21)

The adaptation mechanism in the MRAS scheme is designed to generate the estimated speed by reducing the error between the reference and estimated fluxes. This is most commonly achieved using a PI controller. However, some studies have employed artificial intelligence techniques, such as fuzzy logic, neural networks, and genetic algorithms. The speed tuning signal ${\epsilon }_{\phi }$ and estimated speed are expressed as:

$$\left\{\begin{array}{c}{\epsilon }_{\phi }={\phi }_{r\beta }\widehat{{\phi }_{r\alpha }}-{\phi }_{r\alpha }\widehat{{\phi }_{r\beta }}\\ \widehat{{\omega }_r}=\left(K_p^{\phi }+{\displaystyle \frac{K_i^{\phi }}{s}}\right){\epsilon }_{\phi }\end{array}\right.$$

(22)

The rotor flux-based MRAS compares two estimates of the rotor flux, one obtained from the stator voltage model (reference model) and the other from the rotor equations (adaptive model). The adaptation mechanism processes the error between these fluxes to adjust the rotor speed. Figure 3 illustrates the general scheme of the proposed approach.

3.2. Reactive Power-Based MRAS for Enhanced Low-Speed Estimation

The most common rotor flux-based MRAS strategy is that proposed by Schauder [25]. However, this method exhibits limitations at low and zero speeds due to pure flux integration and sensitivity to the stator resistance.

The instantaneous reactive power in the dq frame is defined as follows:

$$Q_{ref}=V_{sq}{I}_{sd}-V_{sd} I_{sq}$$

(23)

Based on Equation (13) and neglecting the resistances in the reactive power computation, the voltages in the steady state under FOC with ${\phi }_{rq}=0$ are given by the following:

$$\left\{\begin{array}{l}{V}_{sd}=-{\omega }_s{\sigma L}_s{i}_{sq}\\ V_{sq}={\omega }_s{\sigma L}_s{i}_{sd}+{\displaystyle \frac{M}{L_r}}{p\Omega \phi }_r\end{array}\right.$$

(24)

Thus, we can write the following:

$$\widehat{Q}=\underset{stator}{\underbrace{\left({\omega }_s{\sigma L}_s{i}_{sd}\right)i_{sd}+\left({\omega }_s{\sigma L}_s{i}_{sq}\right)i_{sq}}}+\underset{rotor}{\underbrace{{\displaystyle \frac{M}{L_r}}{p\Omega \phi }_r{i}_{sd}}}$$

(25)

The stator related term can be expressed as follows:

$$Q_s={\omega }_s{\sigma L}_s\left(i_{sd}^2+i_{sq}^2\right)$$

(26)

In the steady state, with ${\phi }_r=M{i}_{sd}$, the rotor related term becomes the following:

$$Q_r={\omega }_s{\displaystyle \frac{M^2}{L_r}}{i}_{sd}^2$$

(27)

This approach avoids the derivative terms present in the conventional model and leads to a compact representation. Consequently, the reactive power is obtained as follows:

$$\widehat{Q}=Q_s+Q_r={\sigma L}_s{\omega }_s\left(I_{sd}^2+I_{sq}^2\right)+{\omega }_s{\displaystyle \frac{M^2}{L_r}}{I}_{sd}^2$$

(28)

This expression highlights the contribution of both the stator leakage term and the mutual interaction between stator currents and rotor flux while ensuring a formulation that is more suitable for the MRAS observer’s practical implementation.

In the final expression, only the slip-dependent term $\left({\omega }_s - {\omega }_r\right)$ is kept since it represents the reactive exchange. The component proportional to ${\omega }_r$ is linked to active power production and is therefore excluded from the reactive part.

$$\widehat{Q}={\sigma L}_s{\omega }_s\left(I_{sd}^2+I_{sq}^2\right)+{\displaystyle \frac{M^2}{L_r}}({\omega }_s{ - {\omega }_r)I}_{sd}^2$$

(29)

The error between instantaneous and adaptive reactive power is given by the following:

$$\left\{\begin{array}{c}{\epsilon }_Q=\widehat{Q}-Q\\ \widehat{{\omega }_r}=\left(K_p^Q+{\displaystyle \frac{K_i^Q}{s}}\right){\epsilon }_Q\end{array}\right.$$

(30)

In the reactive power-based MRAS, the estimated reactive power is derived from the stator currents and voltages in the dq frame. The reference model provides the instantaneous reactive power, whereas the adaptive model introduces the estimated speed through the rotor equations. The adaptation mechanism minimizes the difference between the two to yield the rotor speed estimation. Figure 4 shows the corresponding block diagram.

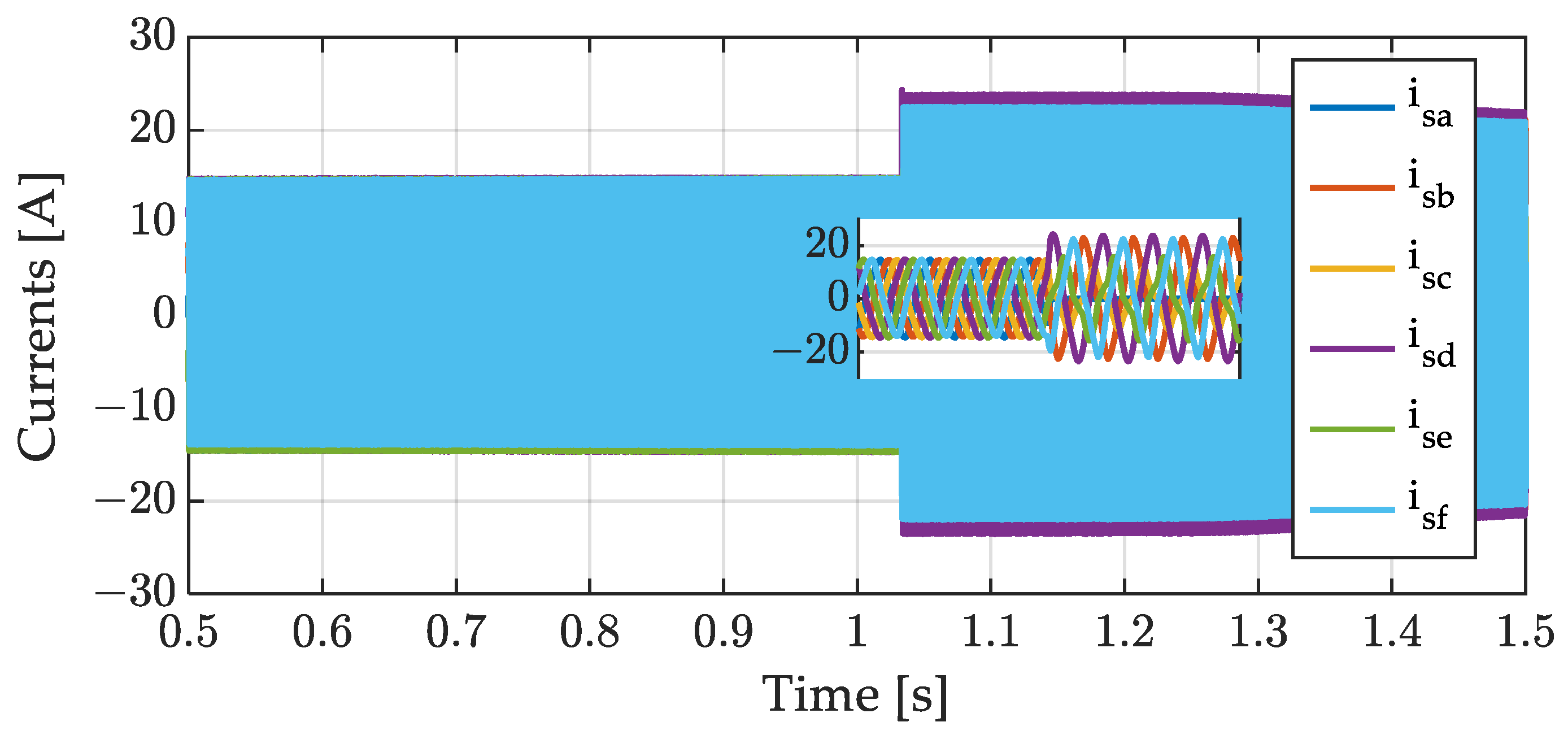
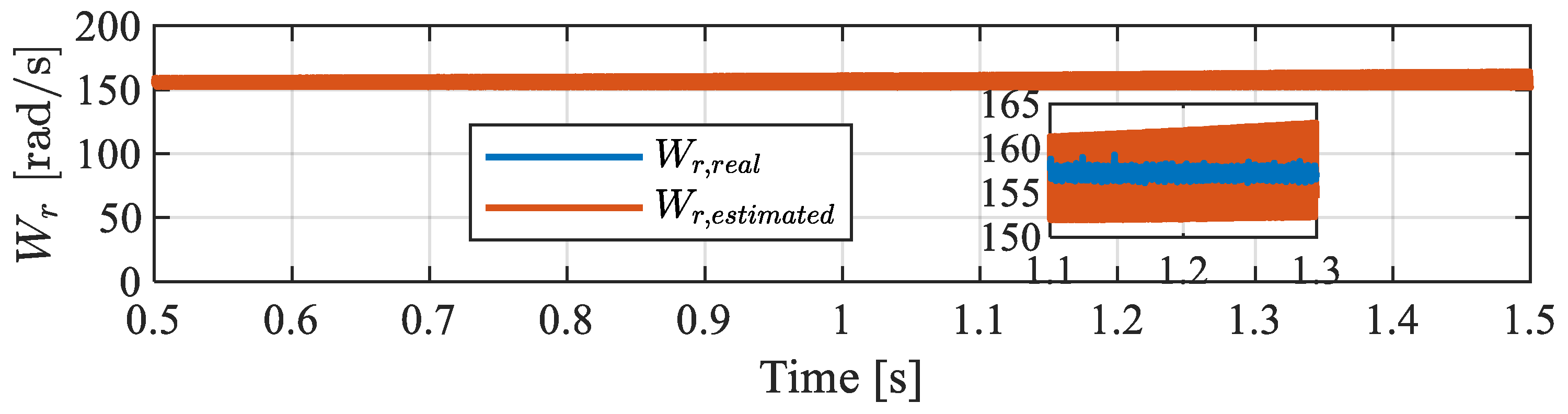
4. Simulations and Experimental Results

This section presents the simulation and experimental results of the flux and reactive power-based MRAS control schemes. The analysis evaluates the estimation and the stability of the proposed approach while highlighting the consistency between numerical and experimental outcomes.

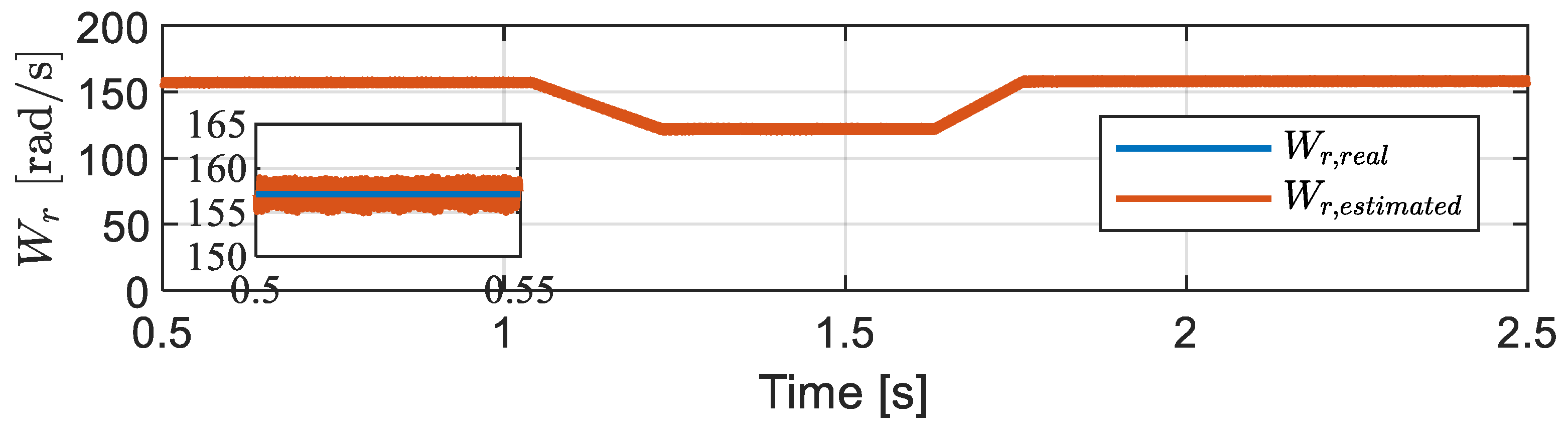
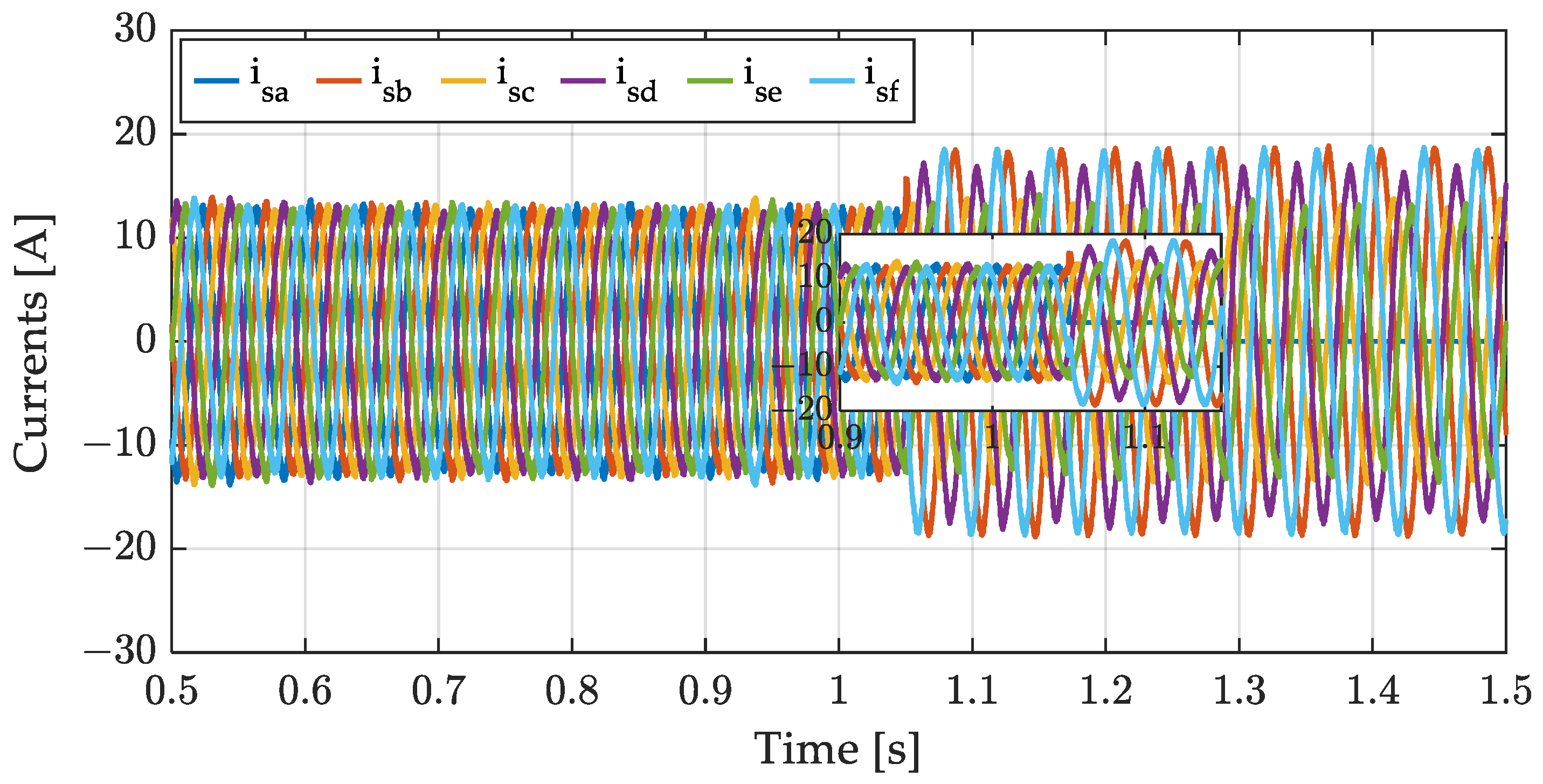
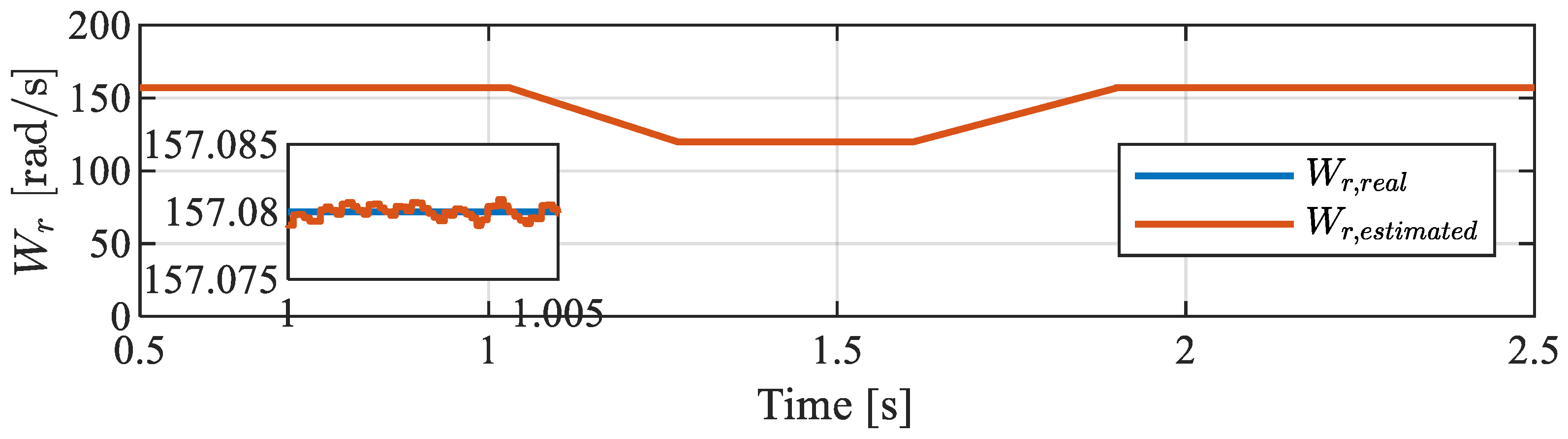
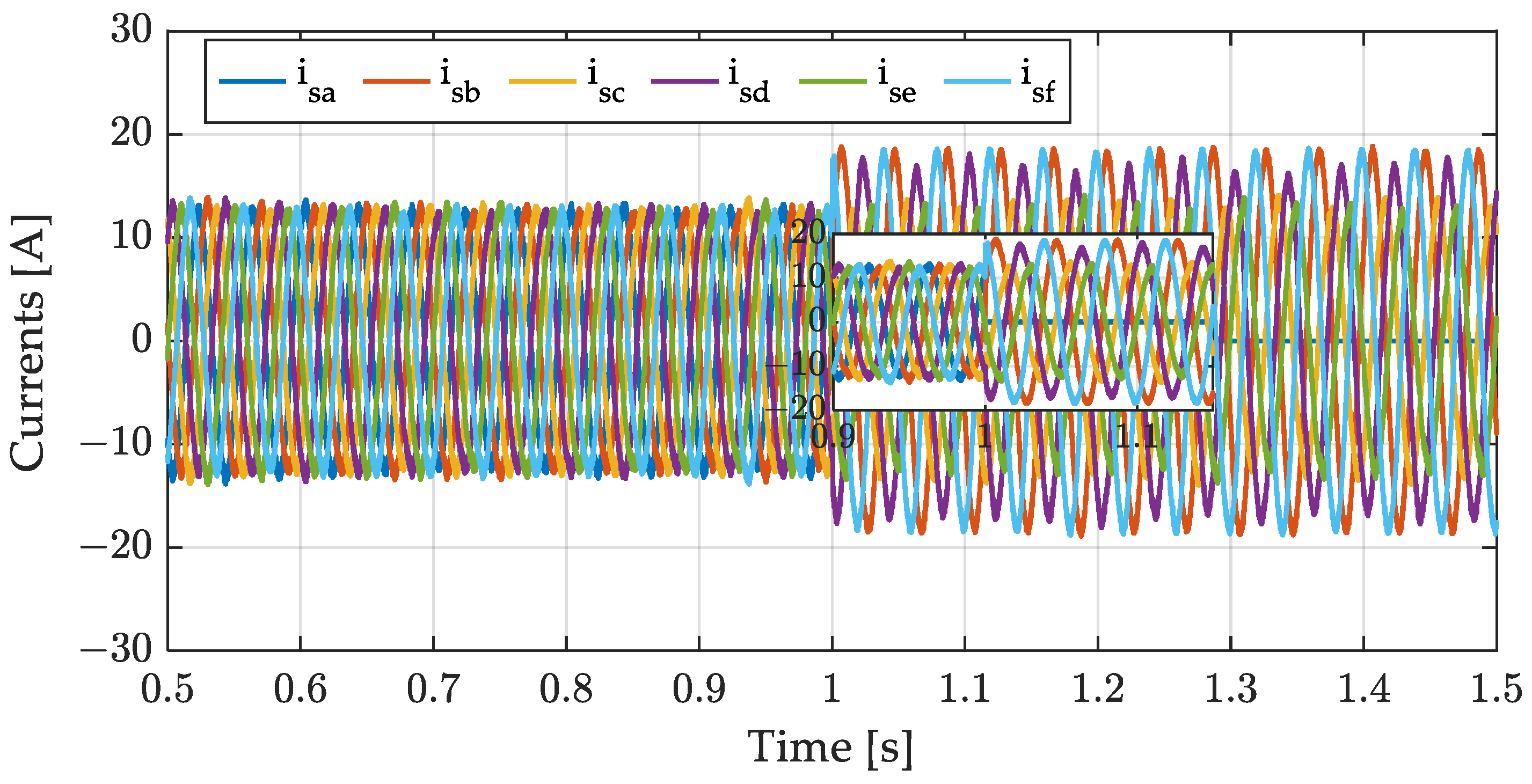
4.1. Simulations Results

a. 

Flux-based MRAS

Figure 5 shows the real (in blue) and estimated (in red) speeds obtained using the flux-based MRAS observer. The reference profile is defined as follows: the rotor speed is held constant at ${\omega }_m$= 13.09 rad/s (125 rpm) until t = 1.04 s, decreases linearly with a slope of $-$15.39 $\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$ until ${\omega }_m$= 10.17 rad/s at t = 1.23 s, remains constant until t = 1.63 s and then finally increases linearly with a slope of $+$23.08 $\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$ to reach ${\omega }_m$= 13.09 rad/s at t = 1.76 s.

Although the estimated speed follows the reference, the estimated rotor speed (${\omega }_r, estimated$) presents high magnitudes of oscillations compared with the actual rotor speed (${\omega }_r, real$). These fluctuations are particularly pronounced at low-speed operation, where the sensitivity to the flux variation reduces the estimation reliability, degrading observer accuracy, and potentially affecting the overall system stability.

Now, the robustness of the method is tested by opening phase “a” at time t = 1.05 s. Figure 6 represents the stator currents in this case, whereas Figure 7 depicts the real and estimated speed under phase loss. After the fault, the estimated speed exhibits increasing oscillations (Figure 5 and Figure 7), indicating that the MRAS scheme is slightly sensitive to phase loss.

b. 

Reactive power-based MRAS

Figure 8 depicts the real rotor mechanical speed (in blue) and the estimated speed (in red) obtained using the reactive power-based MRAS observer when the reference speed is varied. Considering a 6PIG with p = 12 pole pairs, the corresponding mechanical speed profile evolves as follows: it remains constant at ${\omega }_r$= 13.09 rad/s until t = 1.03 s and decreases linearly with a slope of $-$12.85 $\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$ until it reaches 10.00 rad/s at t = 1.27 s. The speed remains constant at this value from t = 1.27 s to 1.61 s before increasing linearly with a slope of 10.66 $\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$ from t = 1.61 s to 1.90 s, returning to 13.09 rad/s. The estimated rotor speed (${\omega }_r, estimated$) exhibits excellent tracking performance with noticeably fewer oscillations compared to the flux-based approach, as shown in the zoomed-in views. These results confirm the improved stability and dynamic response of the reactive power-based MRAS under varying speed conditions.

To evaluate the robustness of the reactive power-based MRAS, phase “a” is disconnected at approximately t = 1 s, as in the previous method. Figure 9 shows the stator currents in this case, whereas Figure 10 depicts the real and estimated speed under phase loss. Figure 9 shows that the stator current waveforms clearly reflect the phase loss. Immediately after the fault, the estimated rotor speed exhibits more oscillations than in the healthy condition, as shown in Figure 8 and Figure 10. Nevertheless, these ripples remain low-magnitude ones.

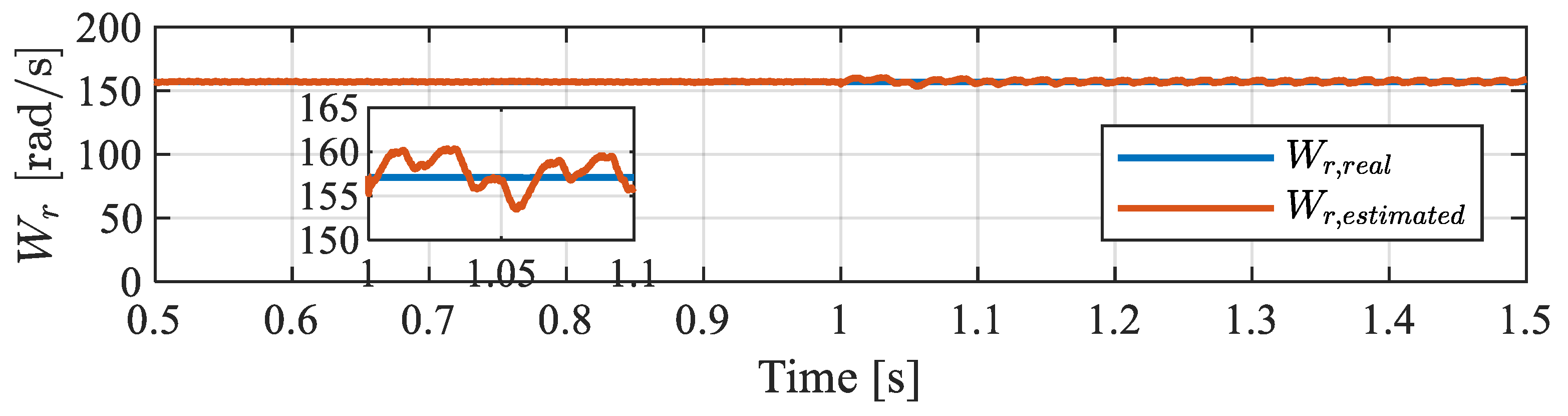
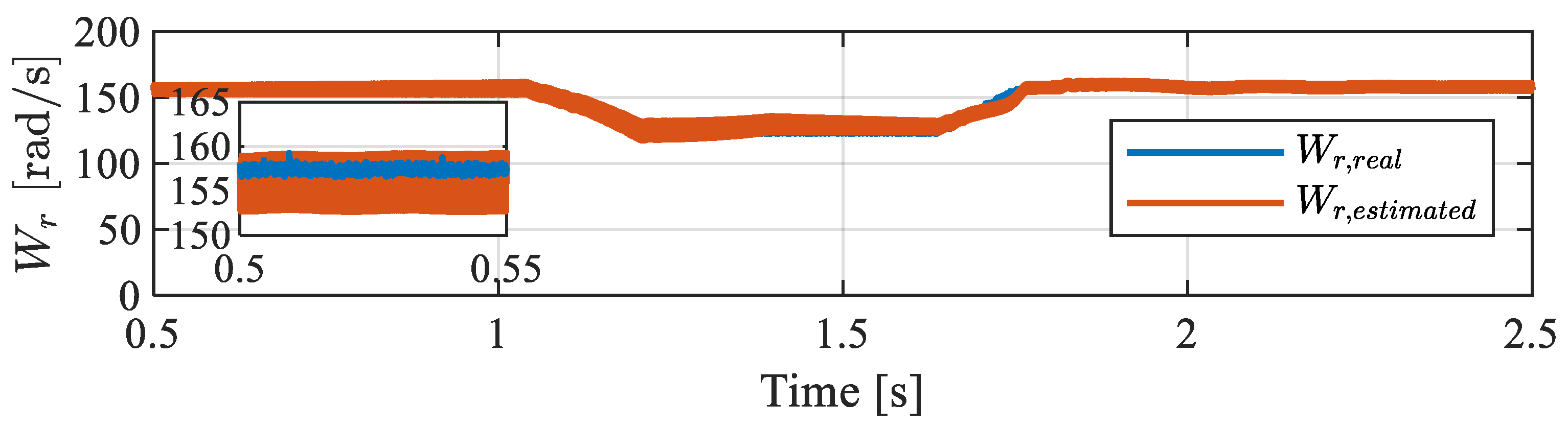
4.2. Experimental Results

Figure 11 shows the test bench designed to emulate the behavior of a microhydraulic or wind energy system. The setup features a 45 kW 3-phase induction machine coupled with a gearbox, forming a gearmotor that replicates the kinetic energy of flowing water or wind forces. The gearmotor is driven by a LEROY SOMER^® variable speed drive operating under a voltage/frequency (V/f) control scheme, allowing the generator speed to be varied from 0 to 133 rpm. The rotor position is measured using an optical encoder that provides 4096 pulses per revolution. The gearmotor is coupled to a torque sensor with data acquisition handled by a MAGTROL system (Model 3411), and it drives a 24 kW, 125 rpm, 24-pole, 230 V squirrel cage 6-phase induction generator (SC6PIG). Electrical power is extracted via two 3-phase back-to-back converters controlled in real time by an industrial PC from Triphase^®. All measurements are sampled at a frequency of 8 kHz, enabling high-resolution current and power analysis using a National Instruments^® DAQ system.

The experimental results were obtained under the same scenario as the simulation results were for both observers and generally confirm the trends observed in the simulation.

a. 

Flux-based MRAS

Figure 12 depicts the real (blue) and the estimated (red) speeds with flux-based MRAS when the reference is modified. The estimated rotor speed can follow the real speed, as already observed in the simulation results of Figure 5. Figure 13 presents the ripples affecting the estimation speed in healthy mode. These oscillations are consistent with the behavior shown in the simulation, confirming that the flux-based MRAS is sensitive to flux variation in the healthy mode.

The robustness of the method is tested by opening phase a at time t = 1.05 s, as in the simulation. Figure 14 represents the stator currents in this case, whereas Figure 15 depicts the real and estimated speed under phase loss.

The effect of the fault is clearly visible in the current waveform, which agrees well with the simulated behavior shown in Figure 6.

The estimated speed exhibits growing oscillations after fault, confirming the sensitivity of the observer to the phase loss. This behavior is consistent with the simulation results shown in Figure 7, where the degradation in the estimation is progressive rather than abrupt. Figure 16 highlights the ripples in the estimated speed under the fault conditions. Compared to the healthy case (Figure 12), these oscillations are amplified after the fault, indicating that the MRAS becomes less reliable and more unstable when the system is unbalanced.

Overall, the experimental results in Figure 13, Figure 14, Figure 15 and Figure 16 strongly correlate with the simulation results in Figure 5, Figure 6 and Figure 7, validating the analysis. Both the simulation and experimental results confirm that while the flux-based MRAS can track the rotor speed, it remains sensitive to phase loss, degrading the estimation accuracy and compromising the method’s overall stability.

Figure 17 shows the temporal evolution of the error metrics (RMS, NRMSE, and MAE) for the flux-based MRAS method. In the healthy region (0.5–1.0 s), the error values remain moderate. When the fault occurs (from t = 1.0 s onward), a rapid and continuous increase in the errors is observed without noticeable peaks. In the faulty condition, these values gradually increase, highlighting the sensitivity of this method to slow variations and conditions.

b. 

Reactive power-based MRAS

Figure 18 depicts the real (blue) and the estimated (red) experimental speeds with reactive power-based MRAS when the reference is modified to test the observer’s tracking performance. As in the simulation (Figure 8), the reactive power-based MRAS demonstrated excellent tracking capacities with significantly fewer oscillations than the flux-based approach.

This improved experimental performance can be attributed to the real dynamics of the generator, which provide smoother torque interaction and more favorable coupling between flux and reactive power, thereby reducing the phase lags observed in the simulated model.

Phase “a” is experimentally disconnected at time t = 1.015 s to evaluate the robustness. Figure 19 represents the experimental stator currents in this case, while Figure 20 depicts the real and estimated experimental speed under phase loss. The estimated speed (Figure 20) exhibits a transient peak and increased oscillations when the phase is opened, which are also reflected in the ripples (Figure 21). Despite these disturbances, the performance of the reactive power-based MRAS observer remains much better than that of the flux-based observer.

Figure 22 presents the same error metrics for the reactive power-based MRAS. The errors are low and stable in the healthy interval. When the fault occurs, only a slight increase is observed and the overall values remain significantly lower than those of the flux-based method (Figure 17). This behavior confirms the higher robustness and steady estimation capability of the reactive power-based approach under faulty operation.

In summary, the experiments validate the simulation results while revealing the influence of practical conditions on system dynamics. The reactive power-based MRAS is more robust and reliable than the flux-based MRAS even under speed variations and fault conditions.

The ripple measurements in both healthy and faulted conditions (

Table 1. Ripple under both methods in healthy and faulted mode (experimentation).

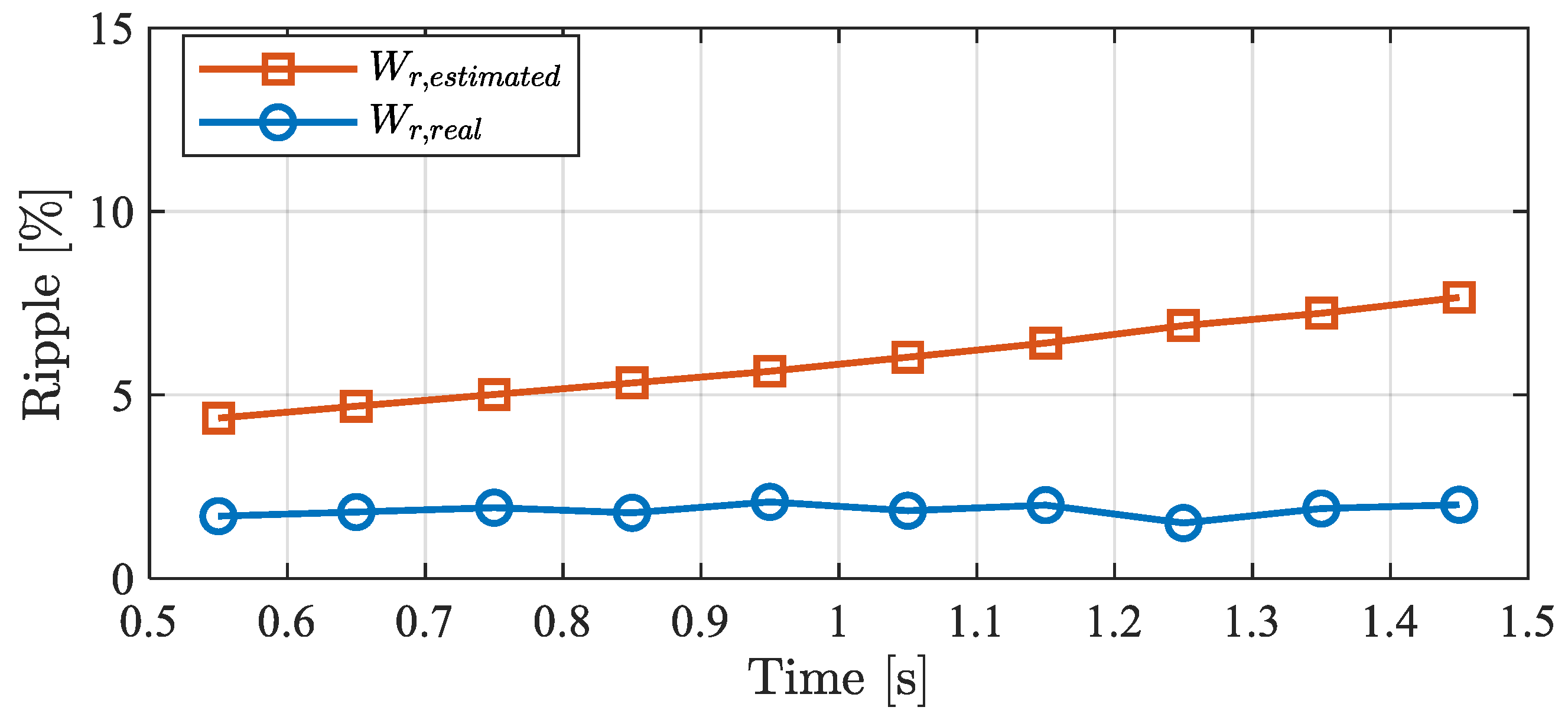
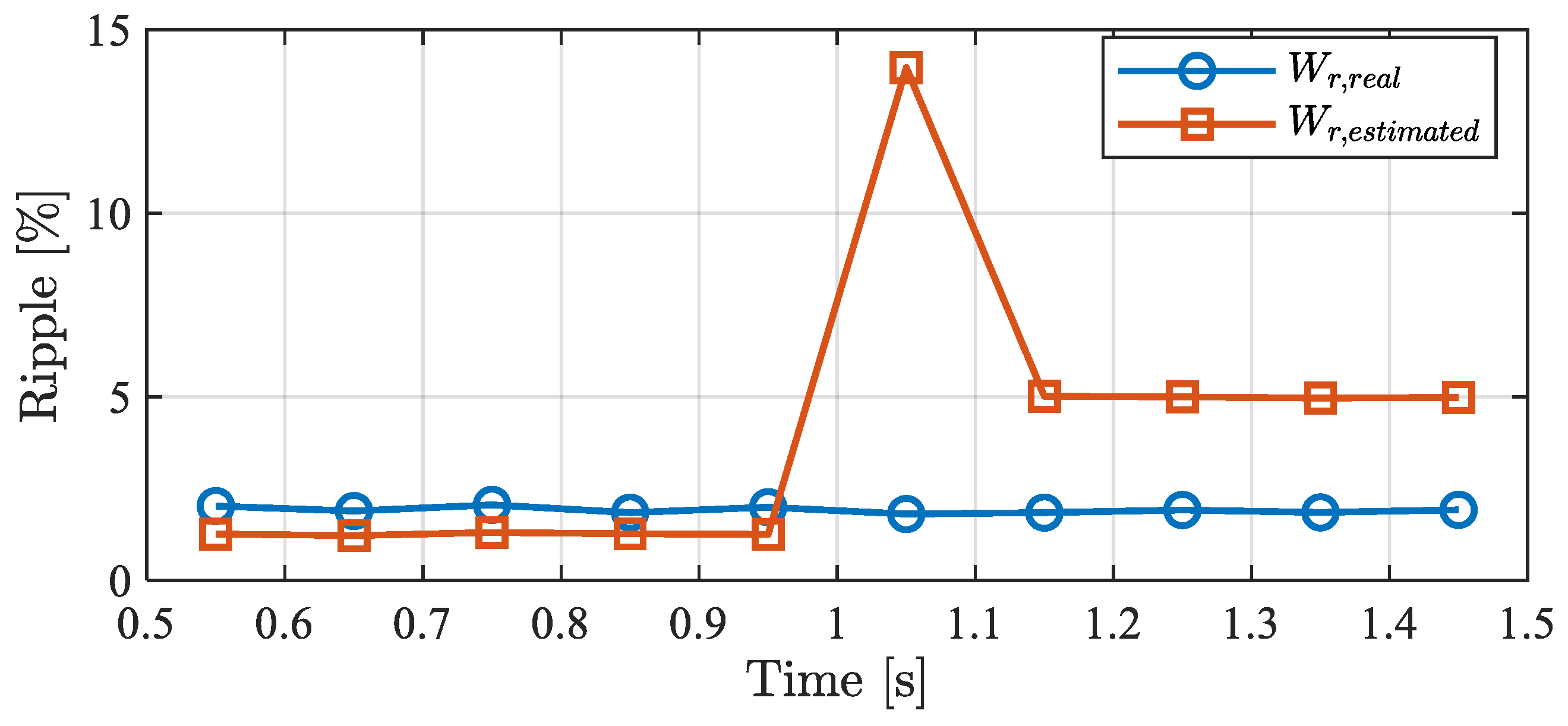
MRAS Methods	Flux-Based		Reactive Power-Based
Mode	Healthy	Faulty	Healthy	Faulty
Ripple ${\omega }_{r, estimated}$ (%)	4.69	7.23	1.27	4.97

) clearly demonstrate that the reactive power-based MRAS maintains lower oscillations and better tracking than the flux-based approach.

The data presented in

Table 2. Evolution of MRAS observer error metrics under healthy and faulty operating modes (experimentation).

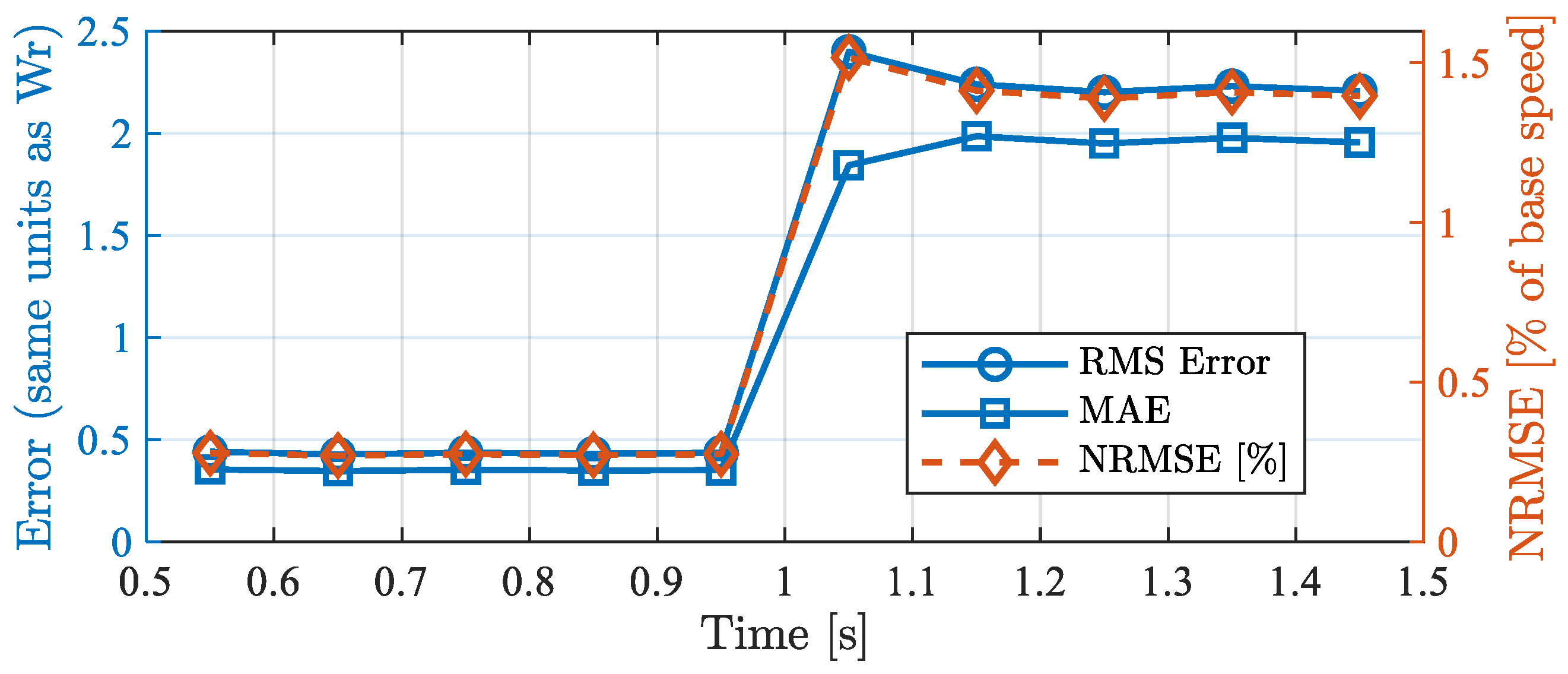
MRAS Methods	Mode	Interval	RMS Error	NRMSE (% Base)	MAE
Flux-based	Healthy	0.5–1.0 s	2.91	1.83	2.41
	Faulty	1.0–1.5 s	3.75	2.40	3.27
Reactive power-based	Healthy	0.5–1.0 s	0.42	0.27	0.35
	Faulty	1.0–1.5 s	2.20	1.40	1.96

are obtained from Figure 17 and Figure 22 and compare the performance of the two MRAS observer methods (flux-based and reactive power-based) over different time intervals in both healthy and faulty modes. In the healthy mode, both methods show low errors, but the reactive power-based method is significantly more accurate (RMS error 0.42 vs. 2.91). This trend continues with lower error values for the reactive power-based method (RMS error 2.20 vs. 3.75) under faulty (phase “a” opened) conditions, indicating more precise and consistent estimation.

When considering the entire signal, the global metrics show that the flux-based method presents an RMS error = 43.73, an NRMSE = 21.87%, and a Mean Absolute Error (MAE) = 17.17, while the reactive power-based method has an RMS error = 39.43, an NRMSE = 24.87%, and a MAE = 12.16. These results indicate that although the flux-based method performs slightly better in terms of average NRMSE over the full signal, the reactive power-based method maintains a lower MAE and shows more consistent performance across critical intervals.

5. Conclusions

This paper focused on sensorless control strategies based on flux and reactive power estimations applied to a low-speed six-phase induction generator (6PIG) using a Model Reference Adaptive System (MRAS) framework. Both the simulation and experimental results were analyzed under healthy and faulty (open-phase fault) conditions.

Numerical evaluations showed that the flux-based MRAS method exhibits higher estimation errors, with global values of RMS error = 43.73, NRMSE = 21.87% and MAE = 17.17, as well as larger ripples and noticeable delays compared to the real rotor speed. In contrast, the reactive power-based MRAS achieved lower errors (RMS error = 39.43, NRMSE = 24.87%, MAE = 12.16) and provided more accurate and stable rotor speed tracking with reduced ripples even in faulty conditions. The experimental results confirm this, showing slightly increased ripples due to prototype uncertainties. Overall, the reactive power-based approach demonstrated superior robustness, precision, and reliability across all tested scenarios.

Future work will focus on extending this study by comparing the proposed MRAS estimators with other advanced observers such as Extended Kalman Filters, sliding mode observers or Nonlinear Adaptive Schemes. Moreover, the integration of AI-based techniques, including fuzzy logic systems, artificial neural networks, and genetic algorithms, could further improve the adaptability, accuracy, and fault tolerance of sensorless control, particularly under low-speed and faulty operating conditions.