Smooth Droop Control Strategy for Multi-Functional Inverters in Microgrids Considering Unplanned Off-Grid Transition and Dynamic Unbalanced Loads
Abstract
1. Introduction
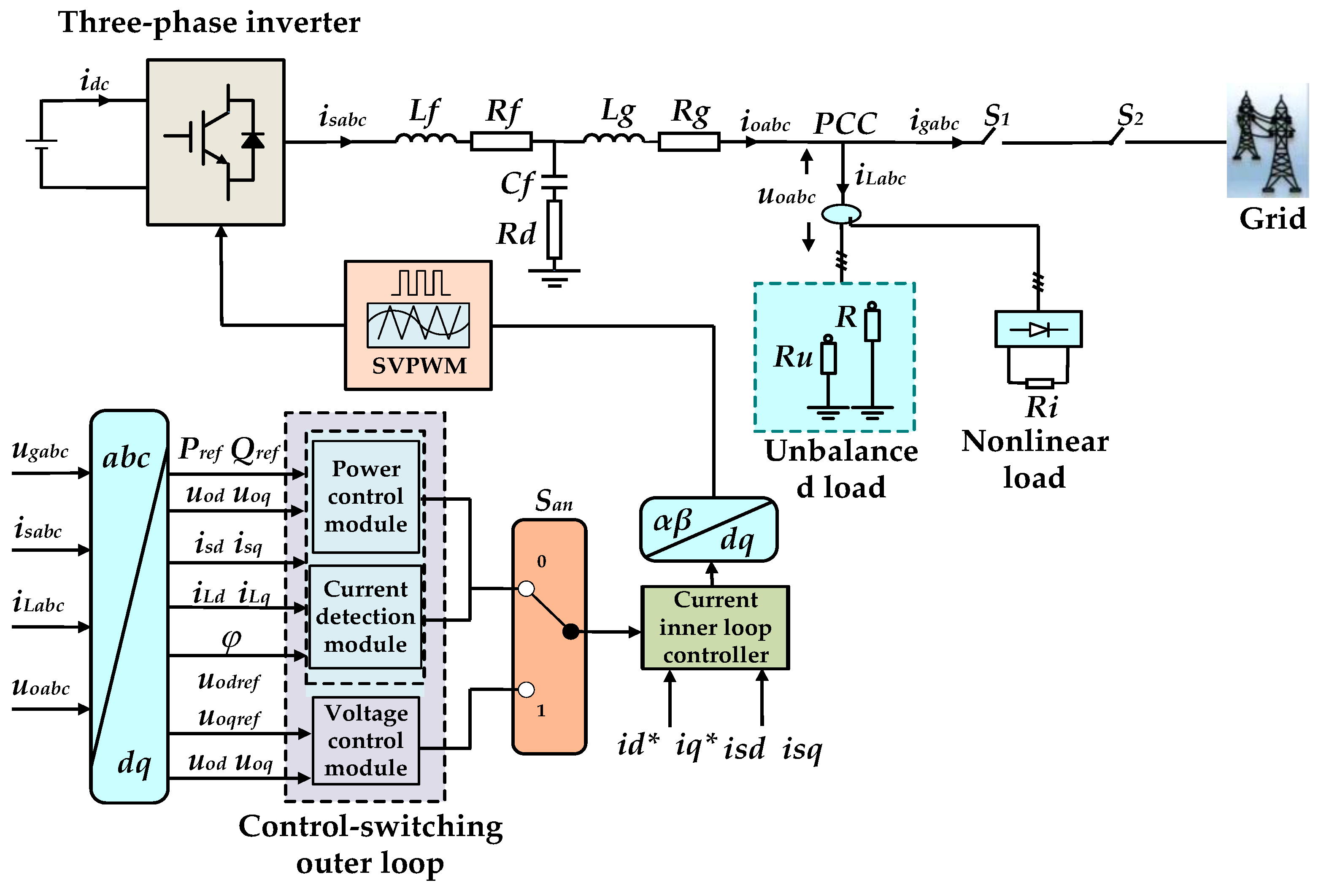
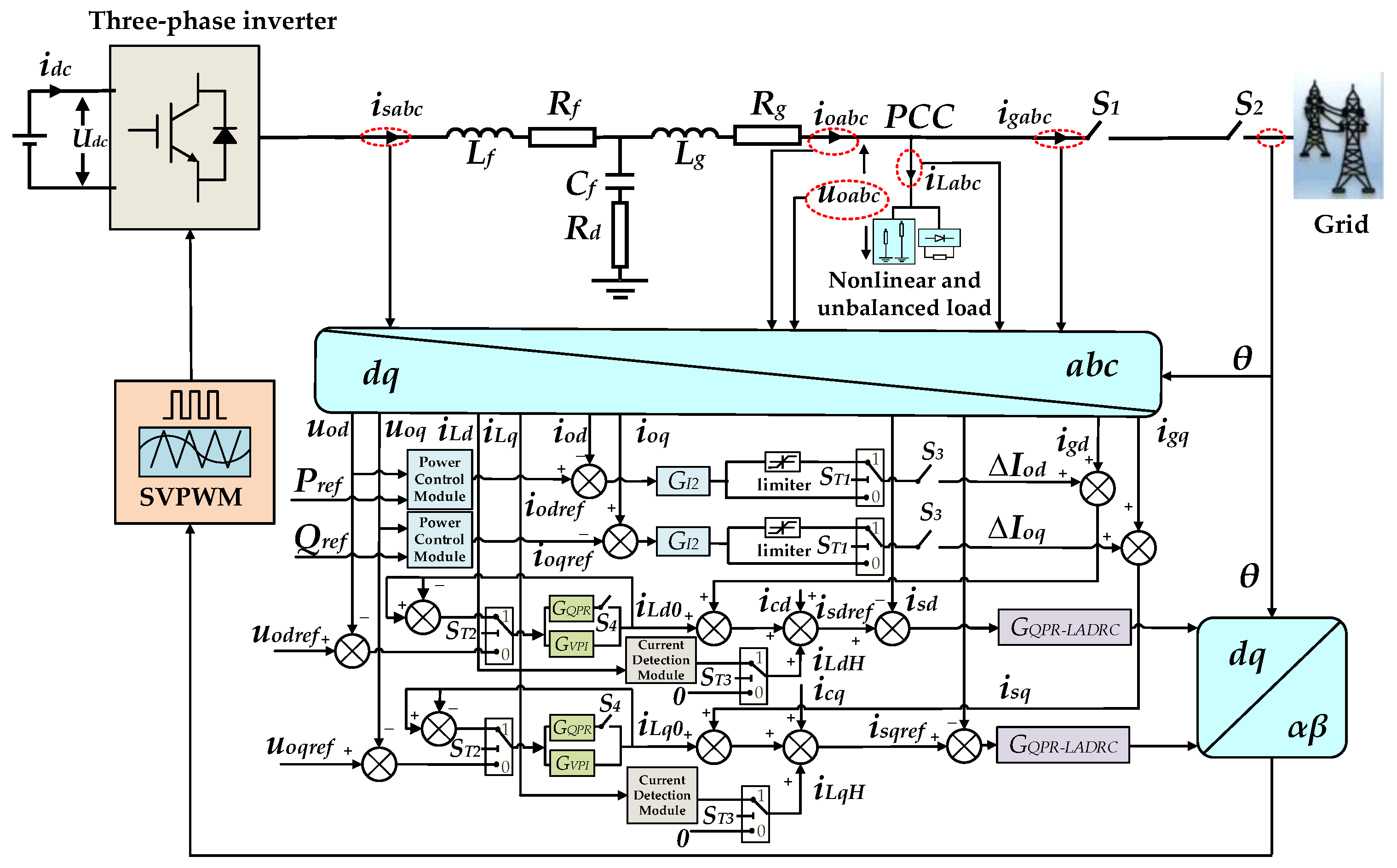
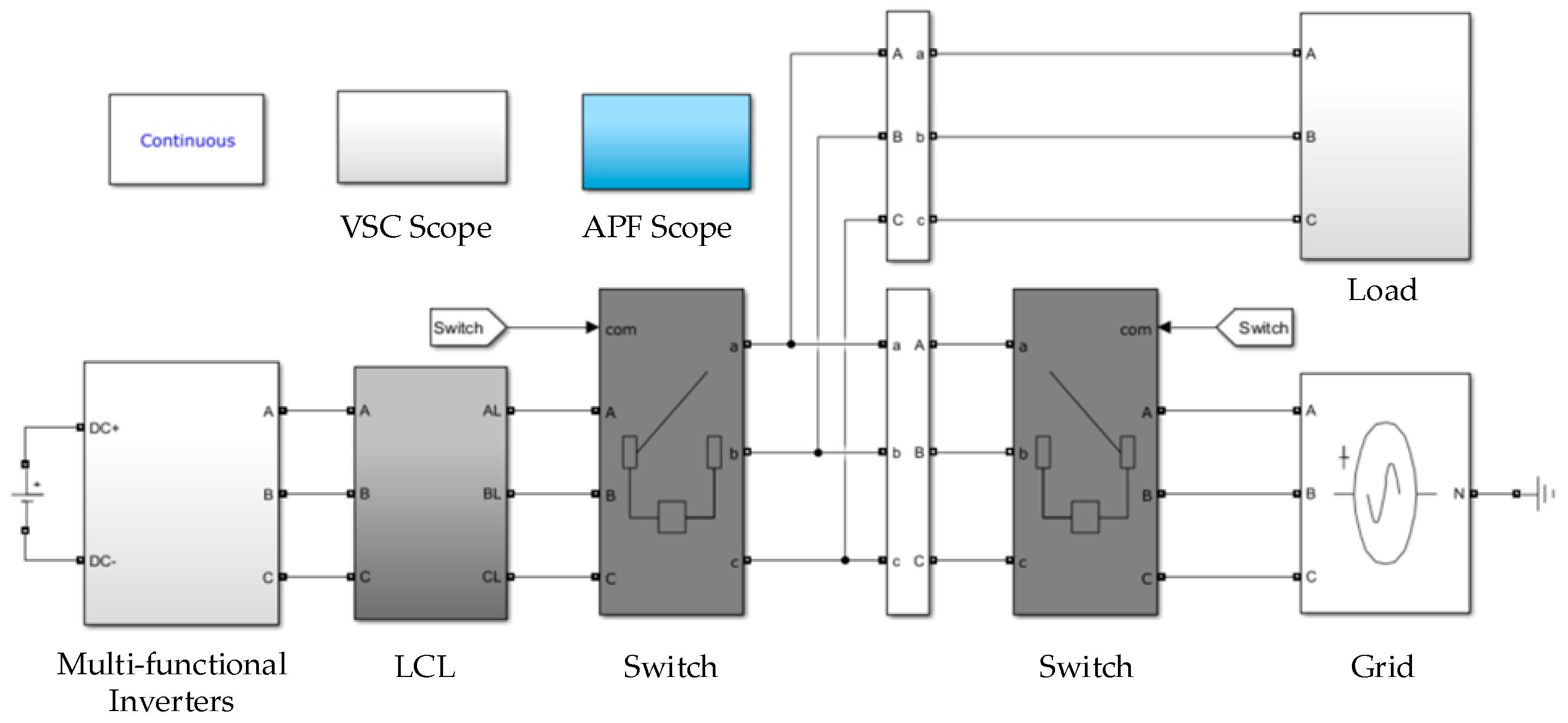
2. Microgrid Structure and Basic Principles of Grid-Connected and Off-Grid Switching
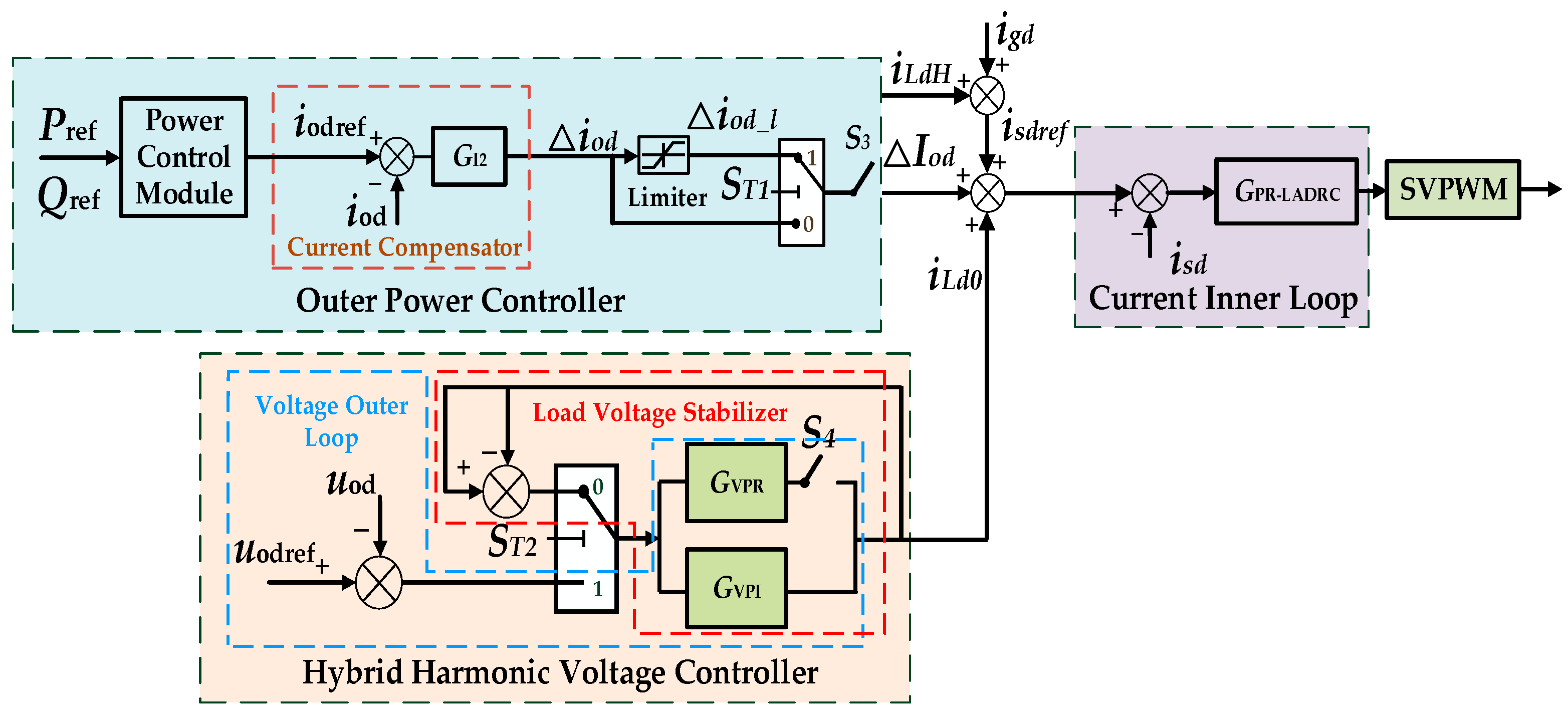
3. Improved PQ/VF Control
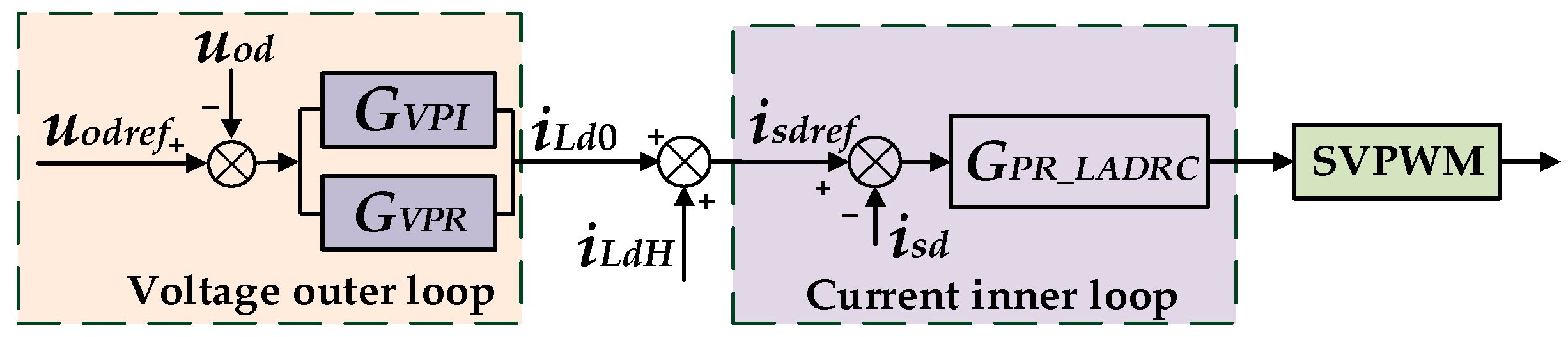
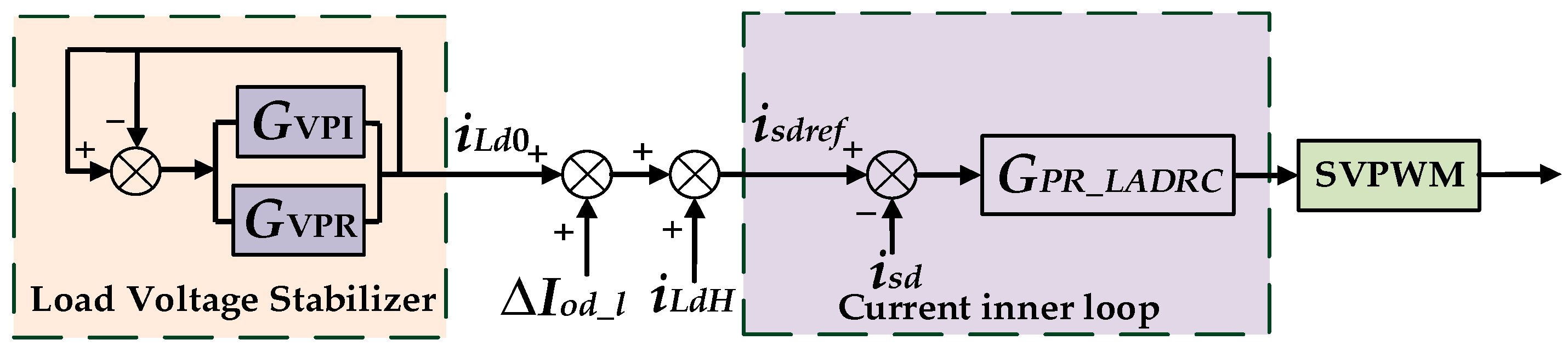
3.1. Load Voltage Regulator
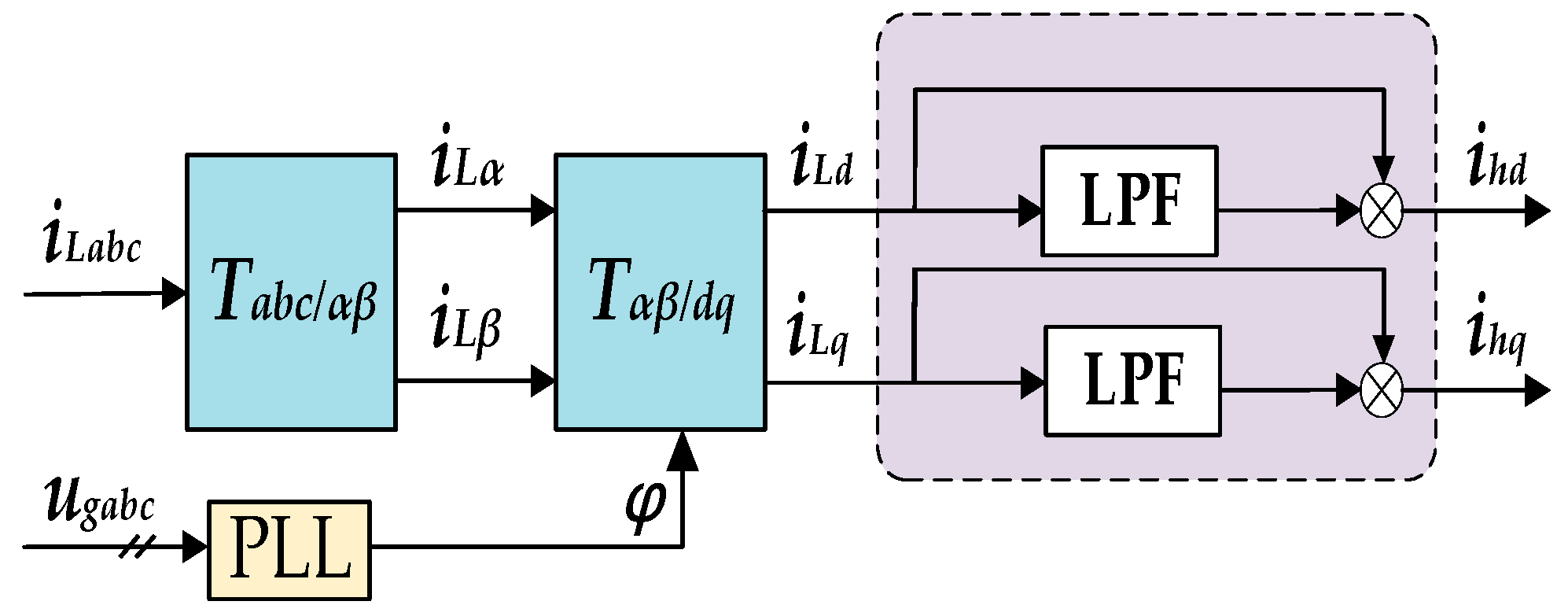
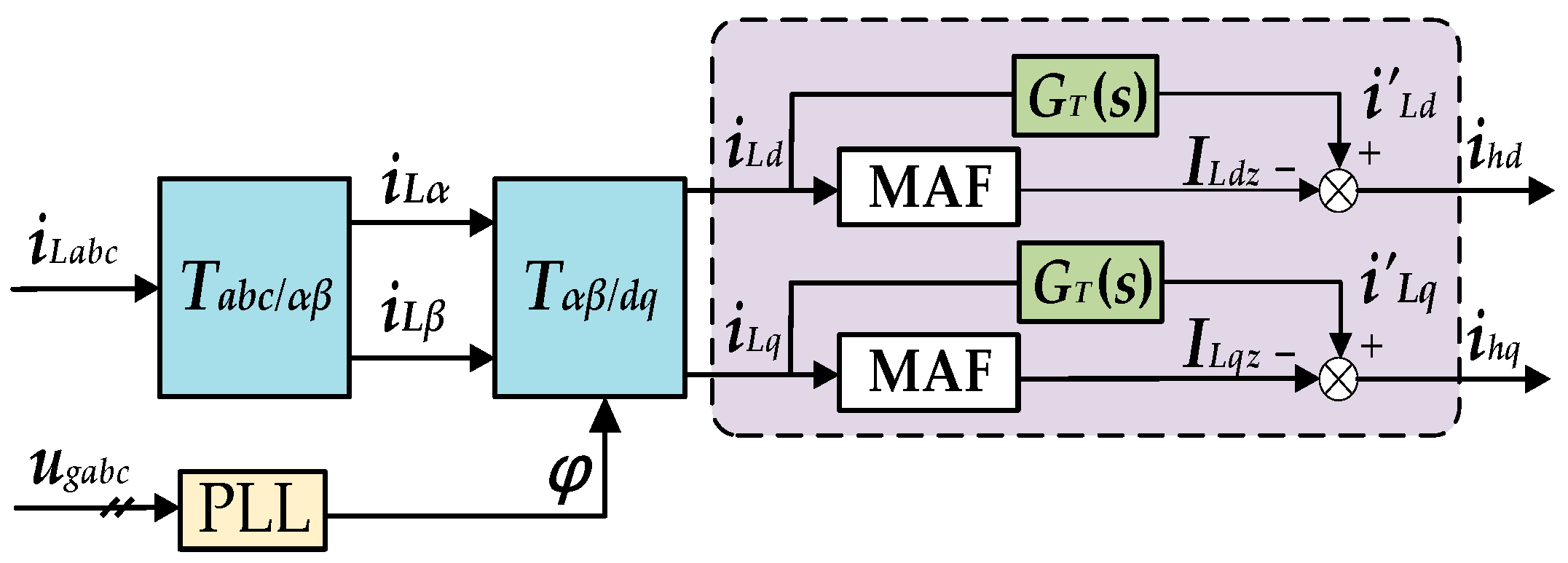
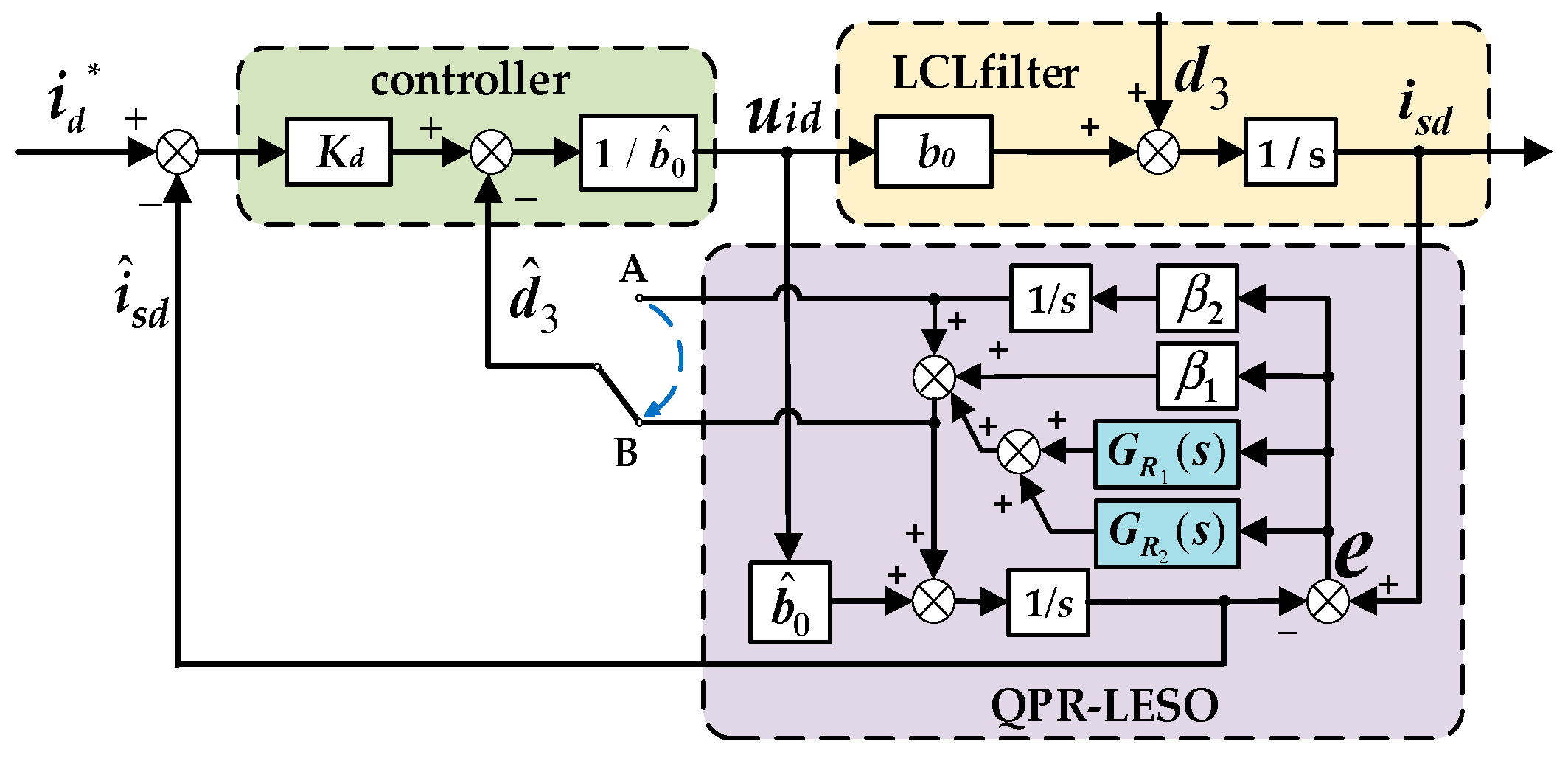
3.2. Composite Controller Combining PI and QPR
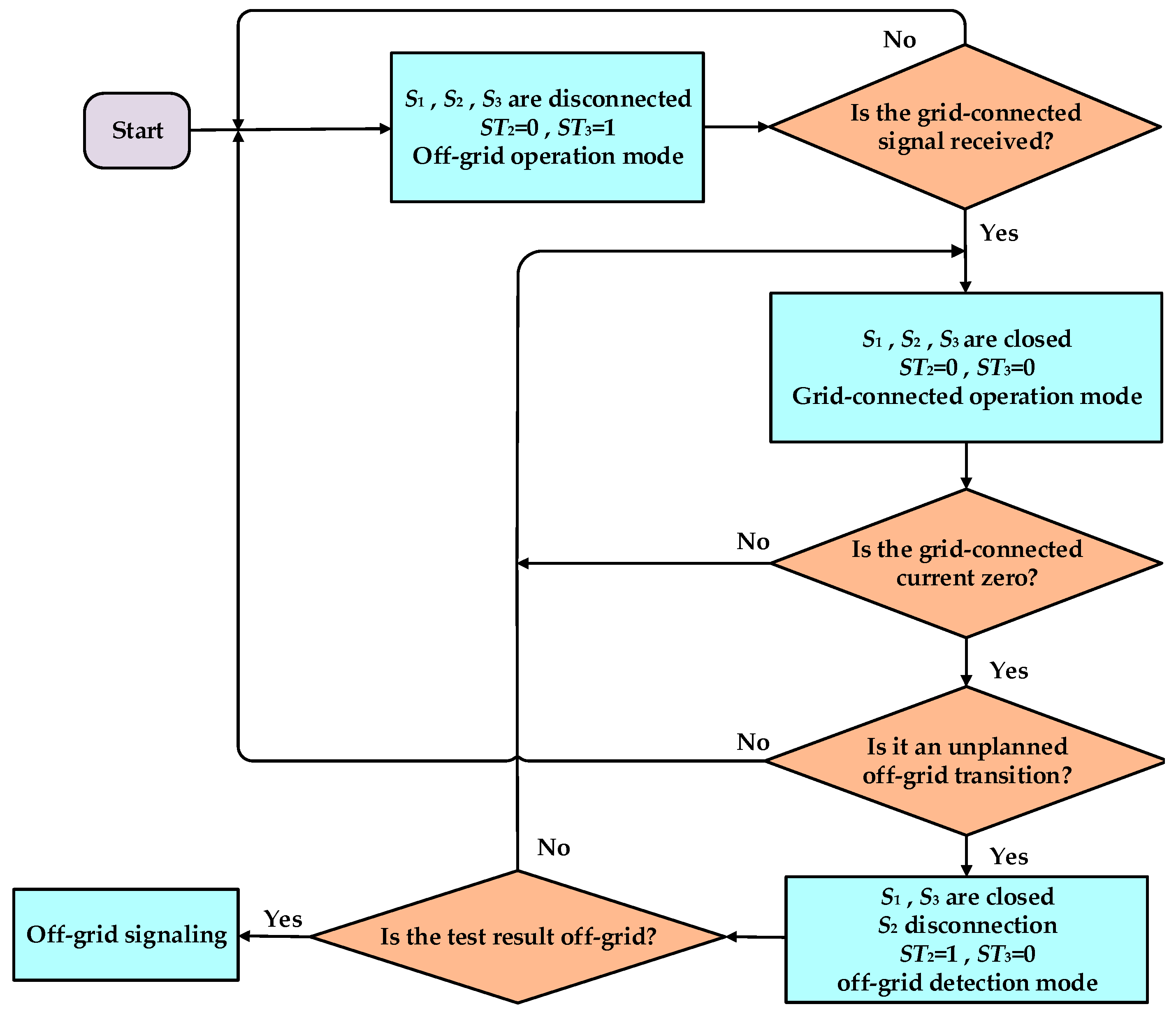
4. Analysis of Operating Modes
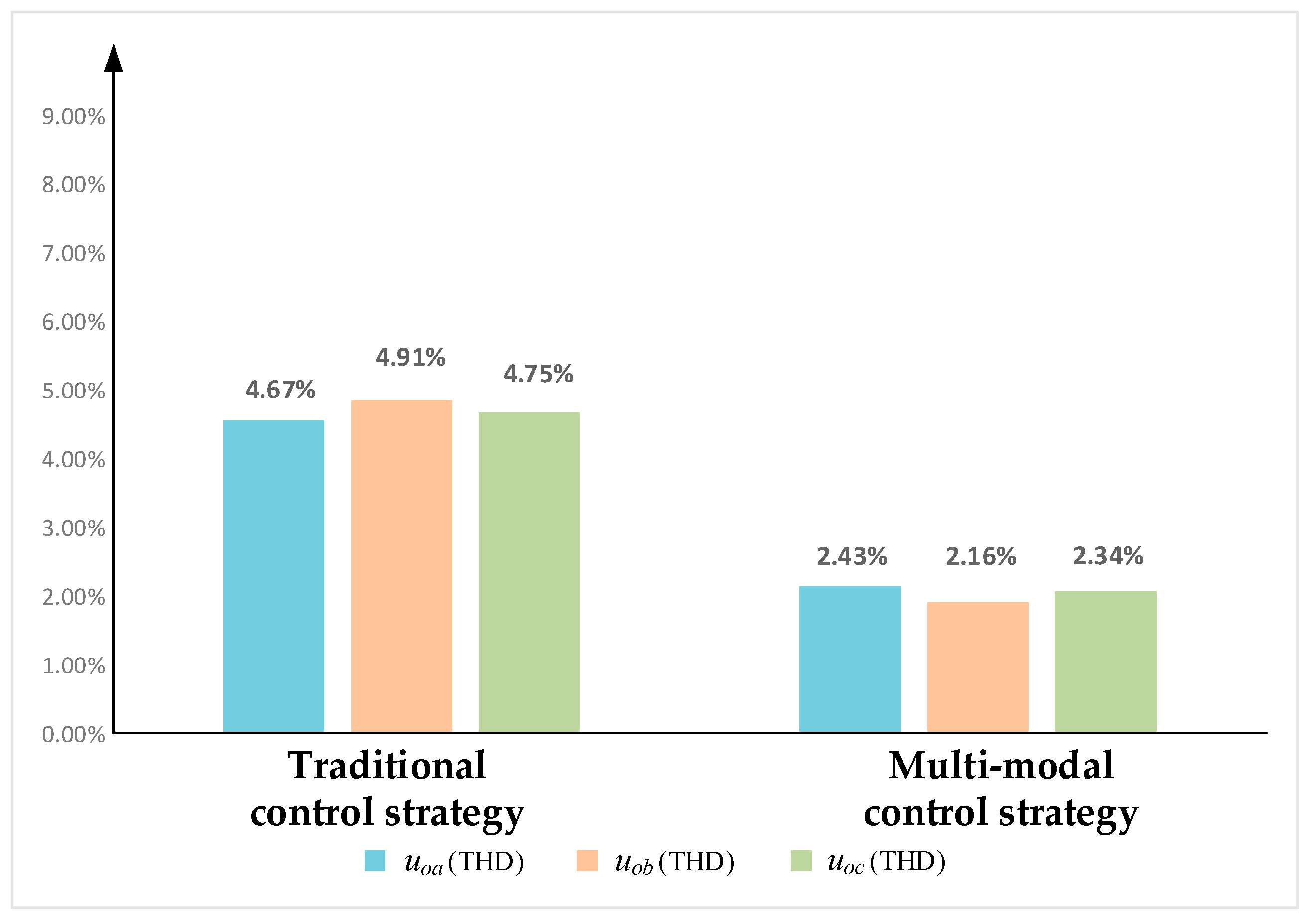
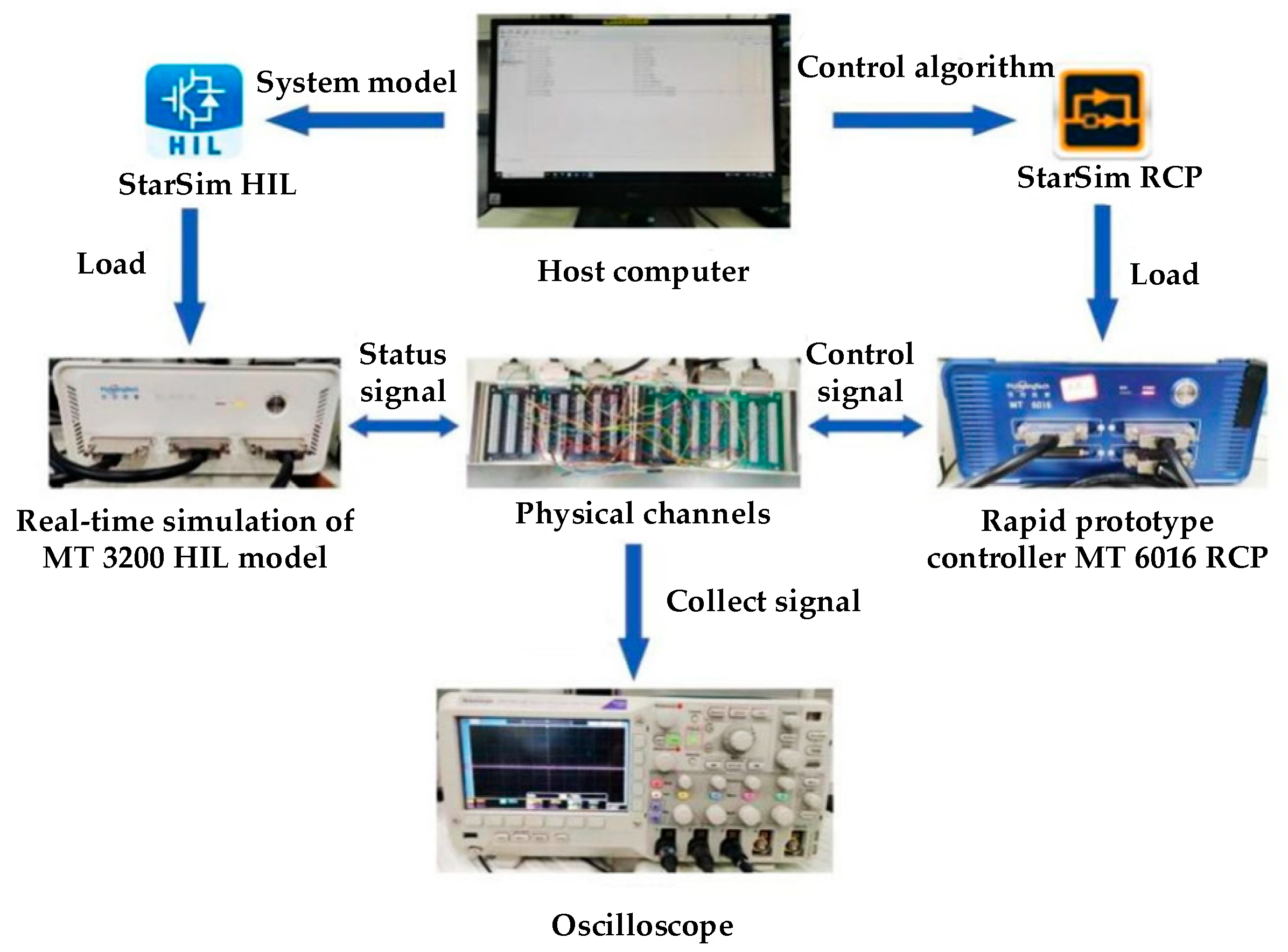
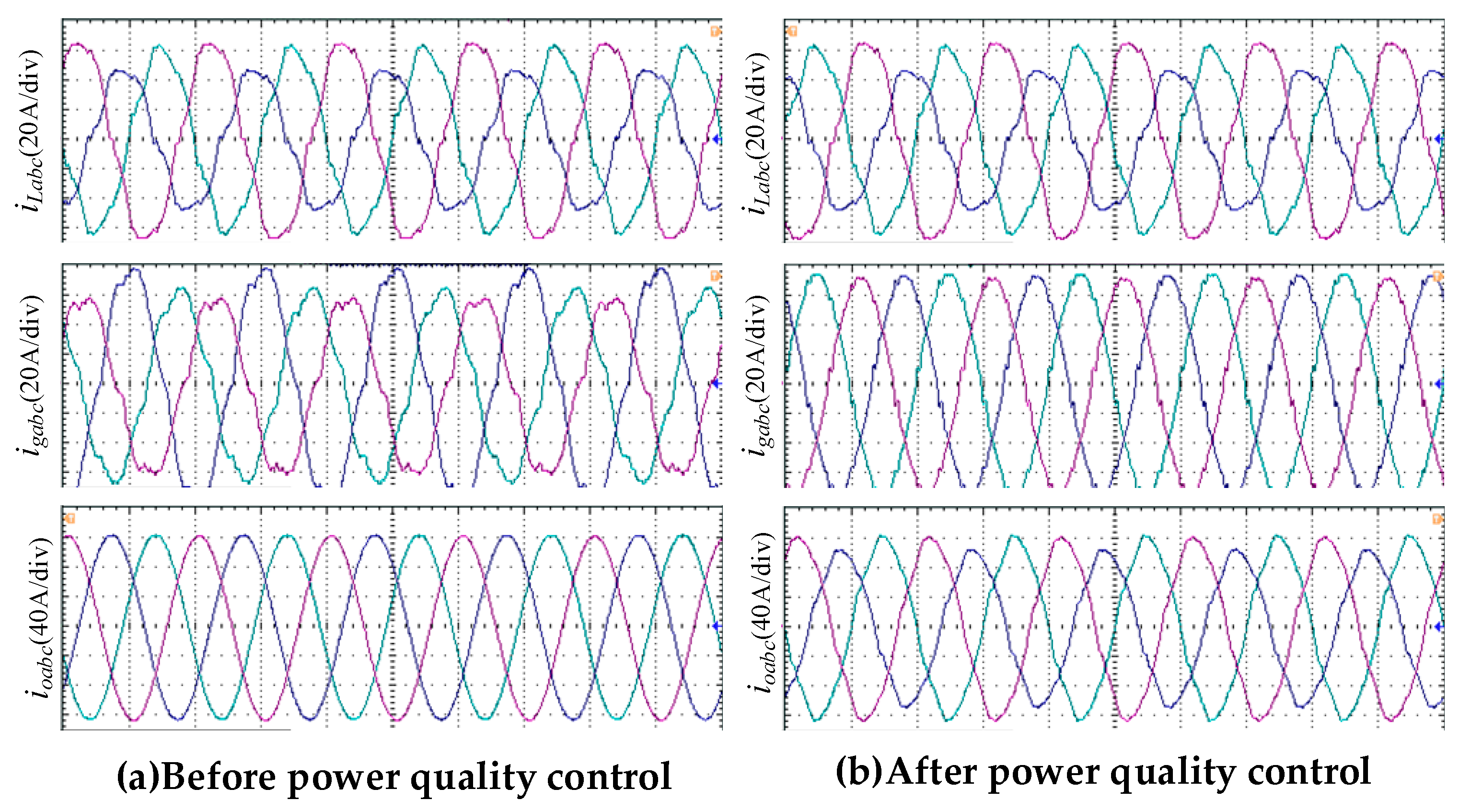
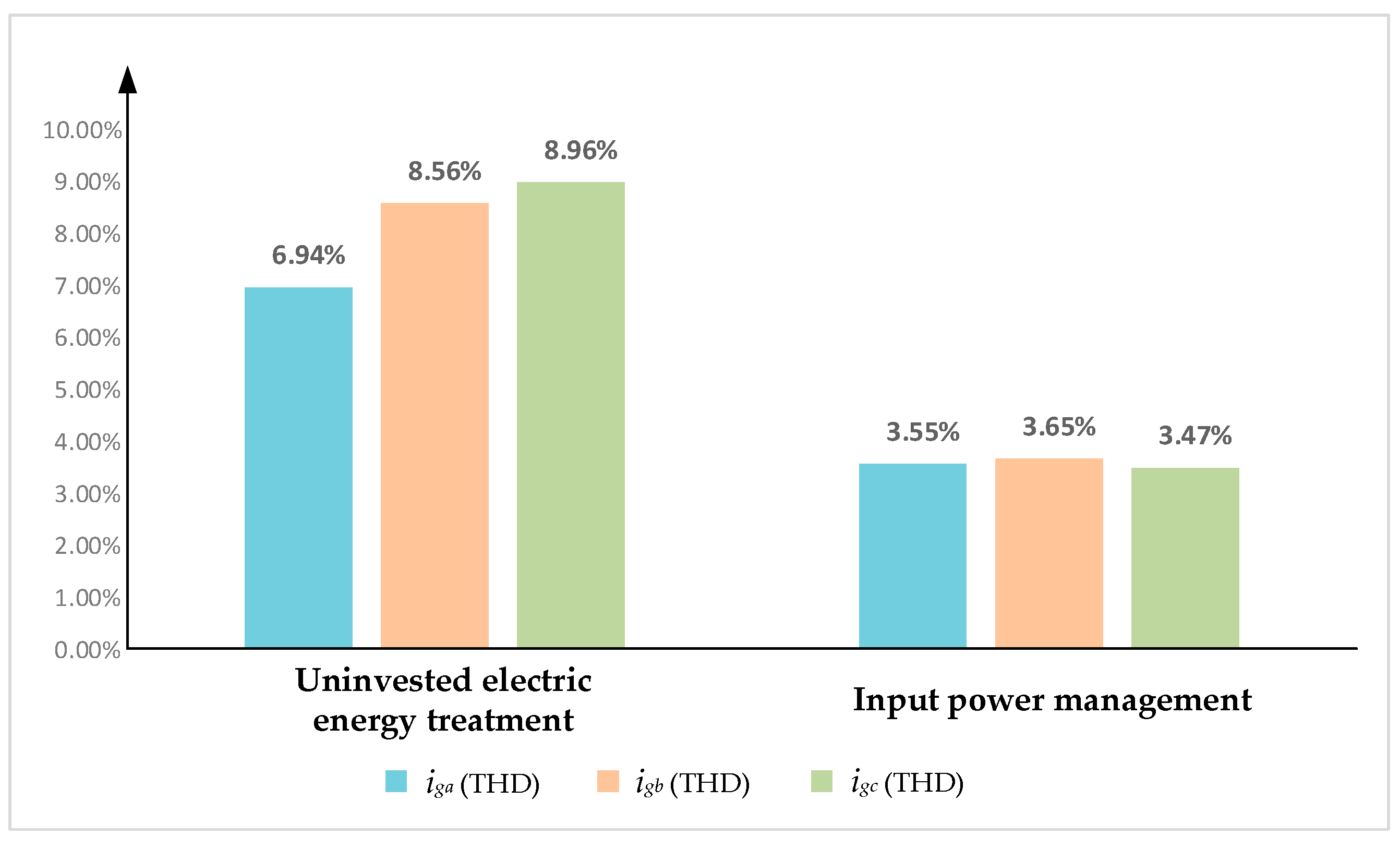
5. Simulation and Experimental Results
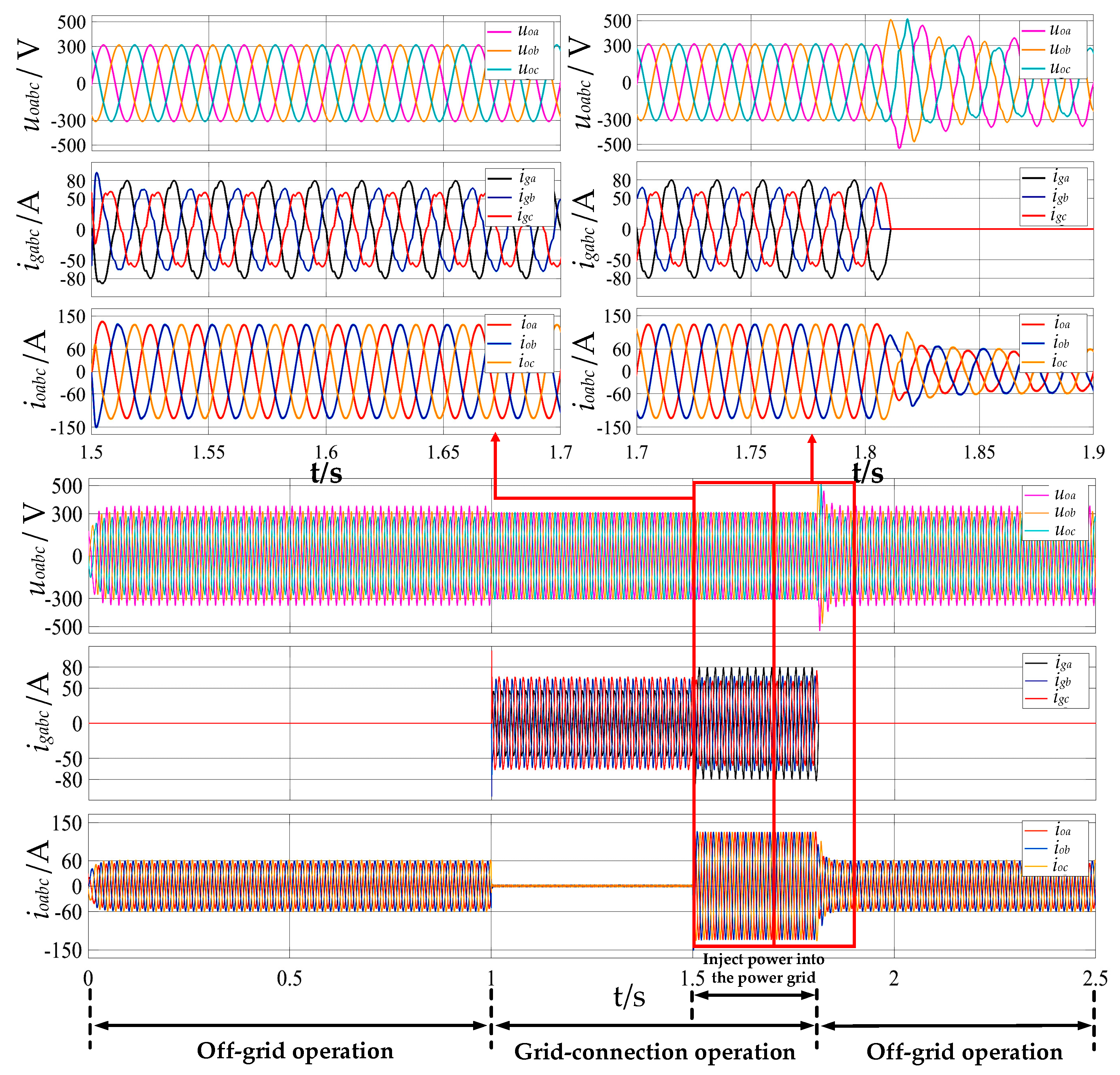
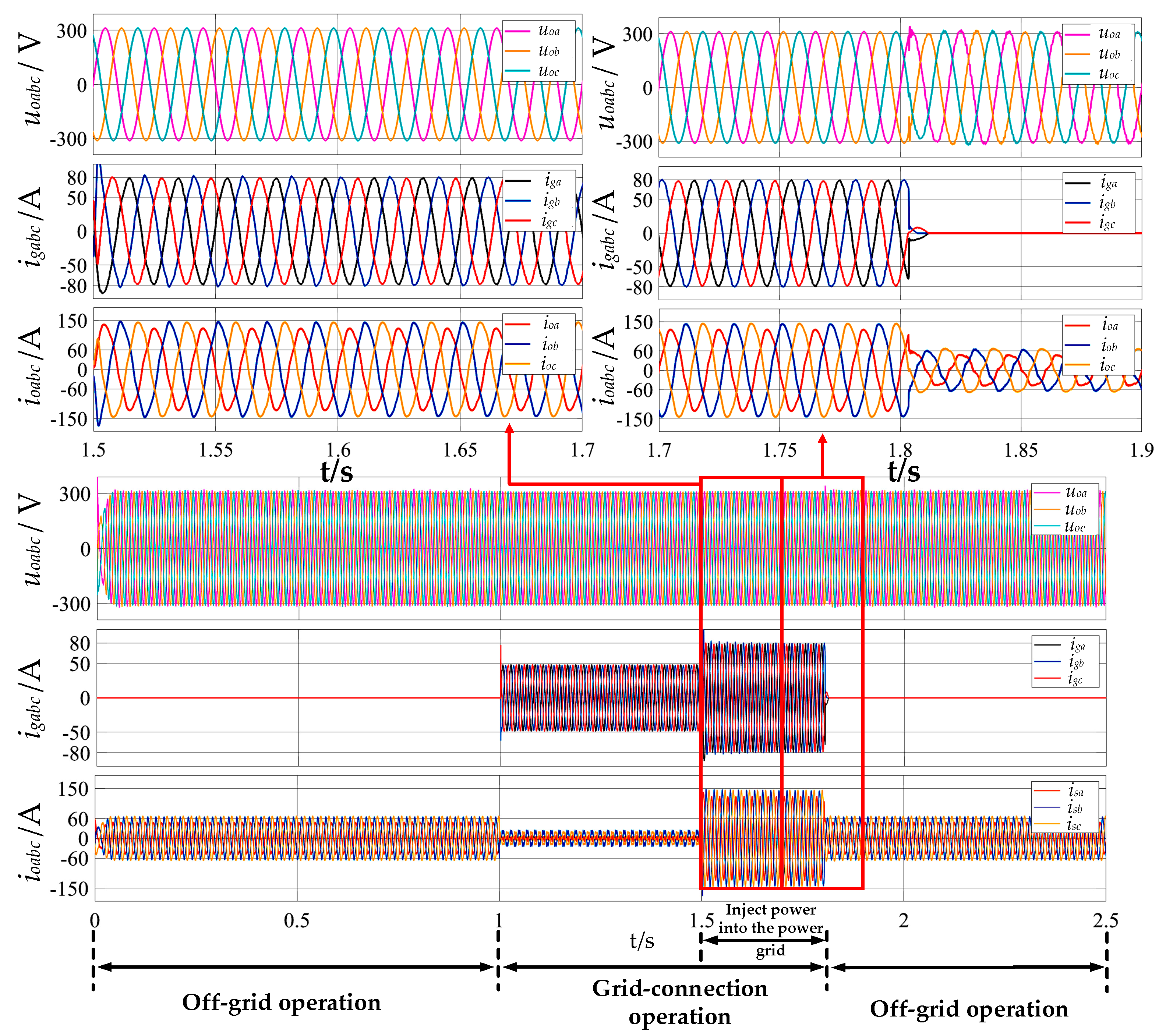
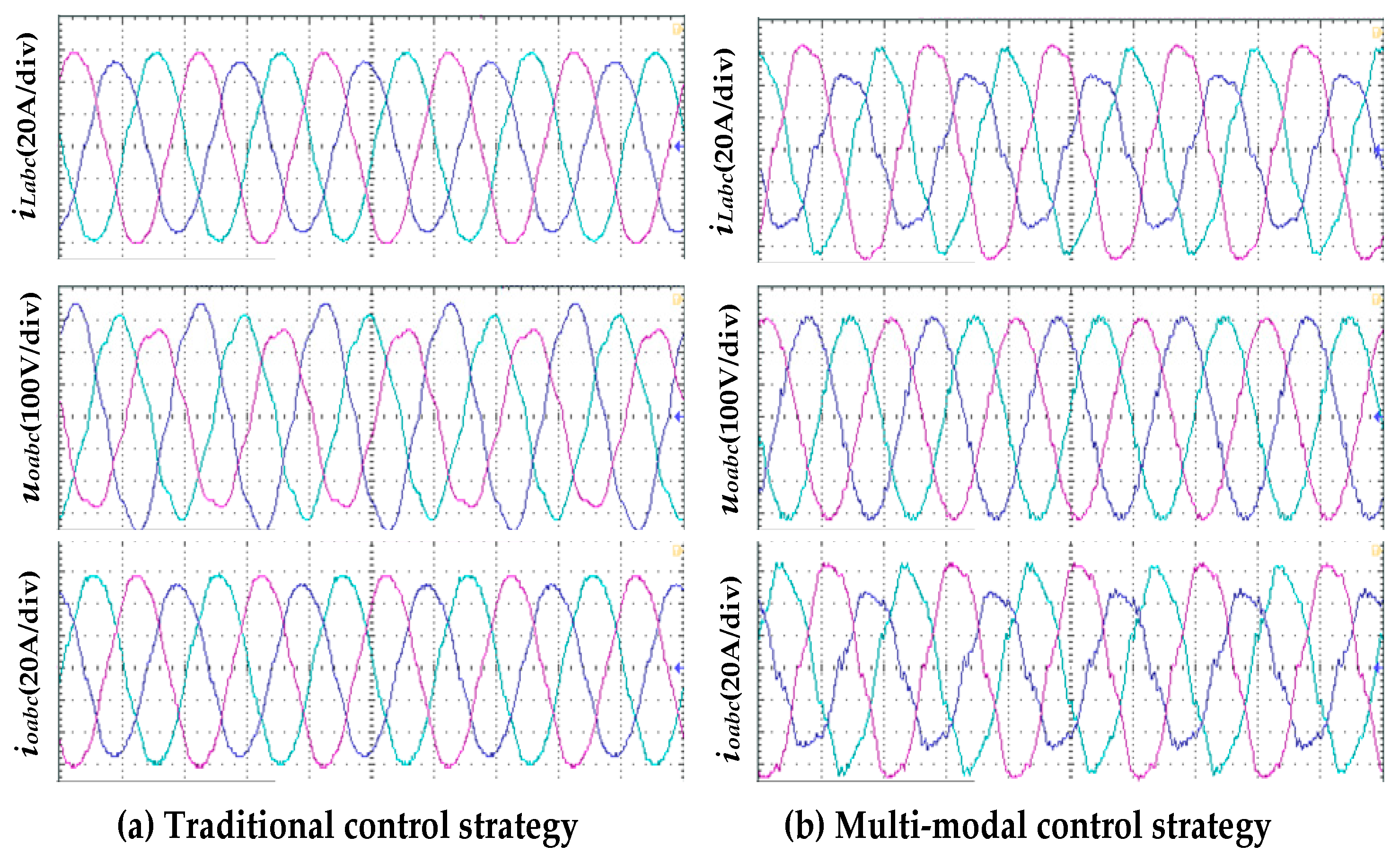
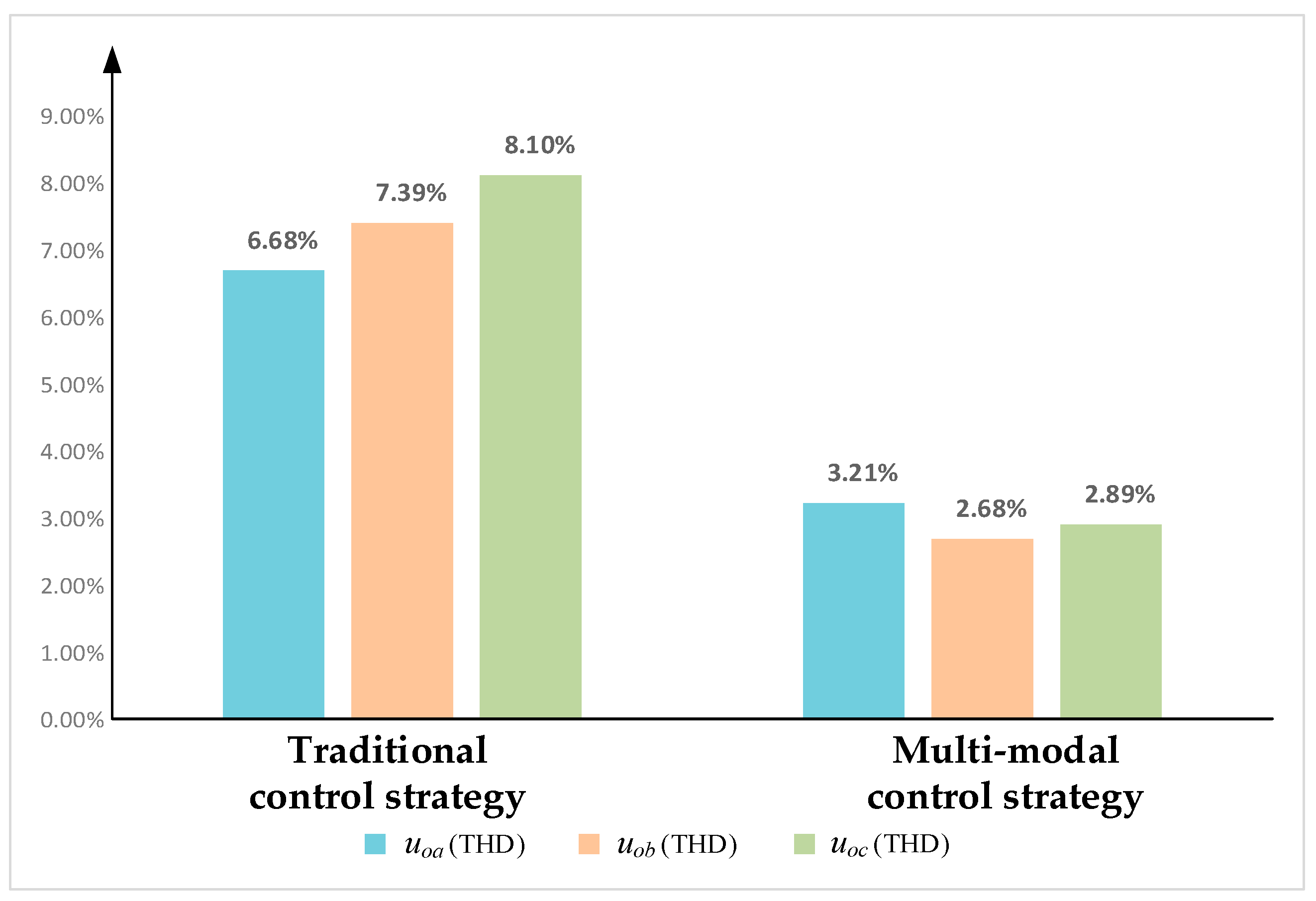
5.1. Simulations of Full-Mode Operation of Conventional Switching Strategy for Inverters
5.2. Simulations of Full-Mode Operation of the Inverter with Proposed Multi-Modal Control Strategy
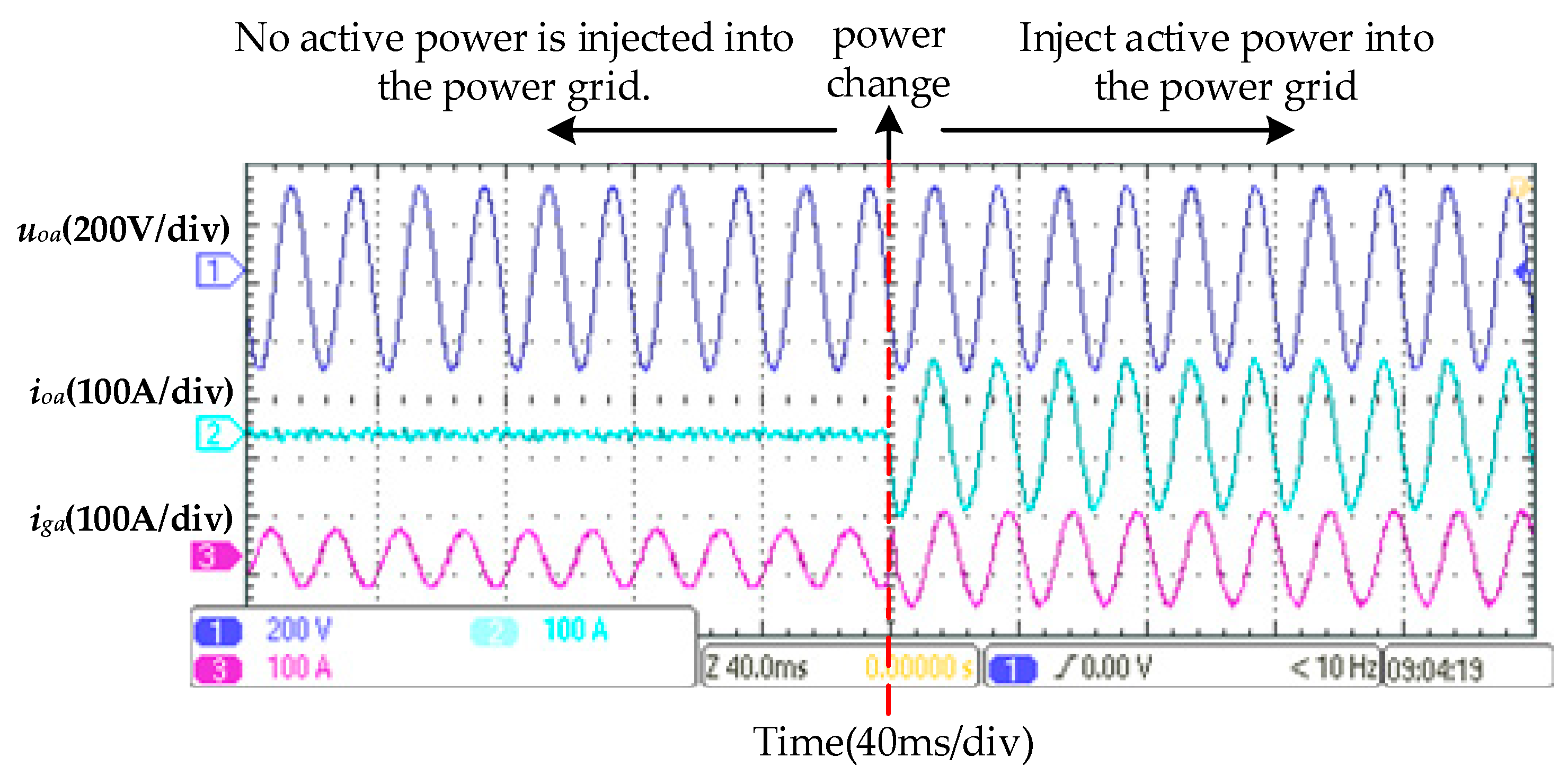
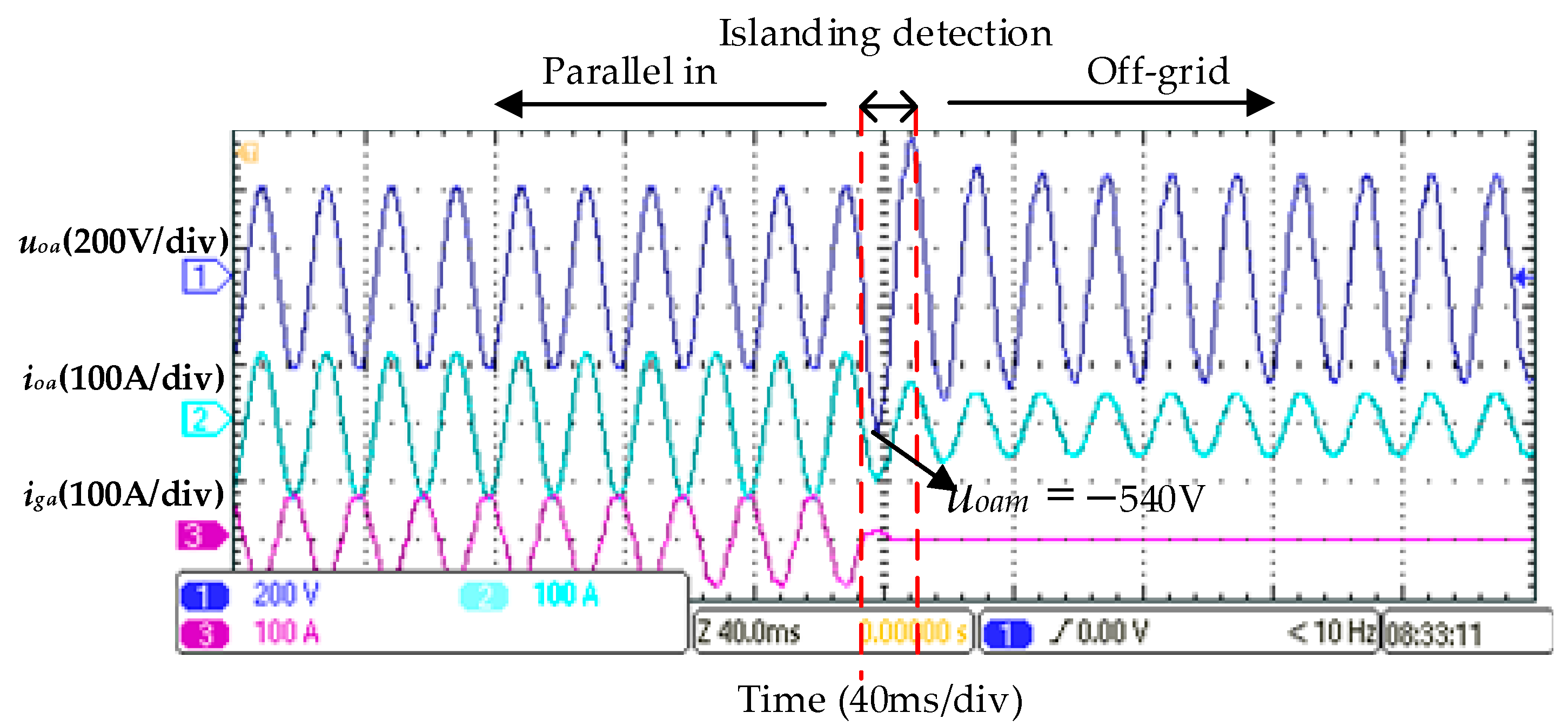
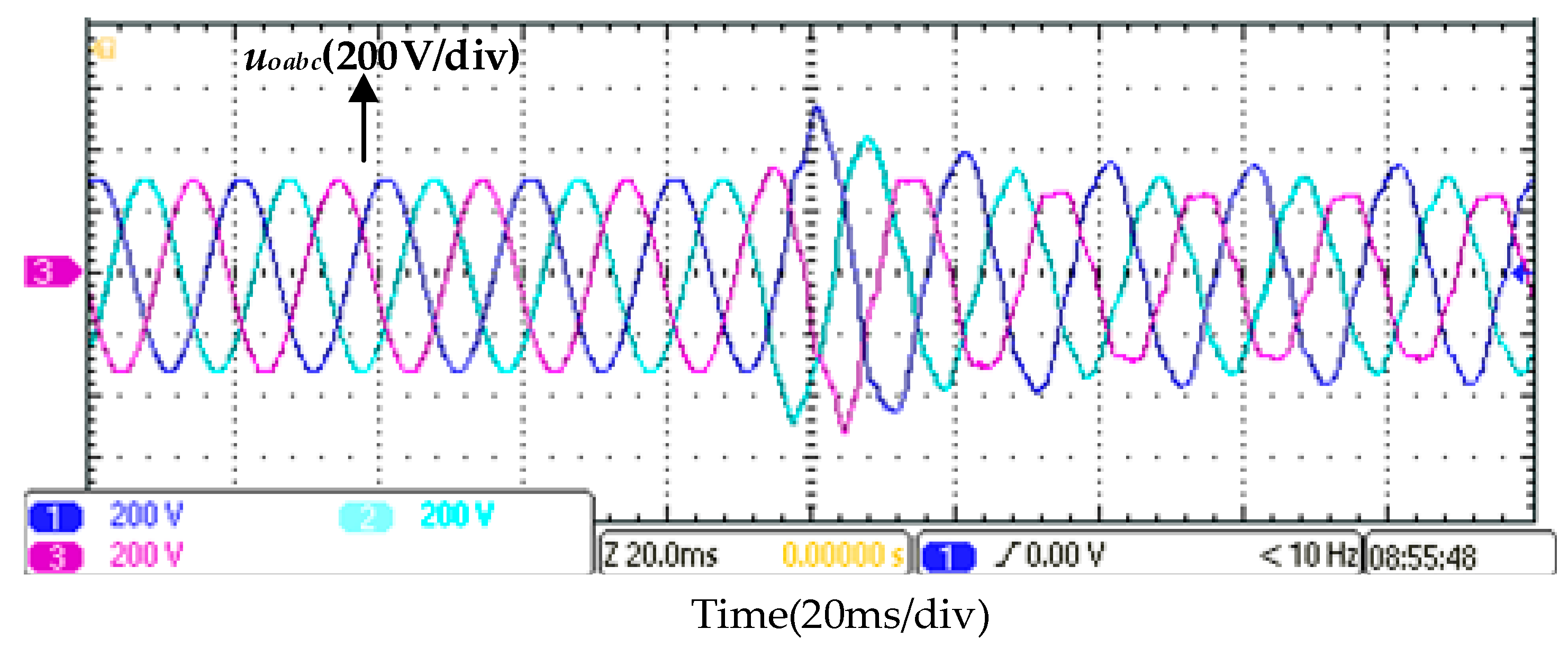
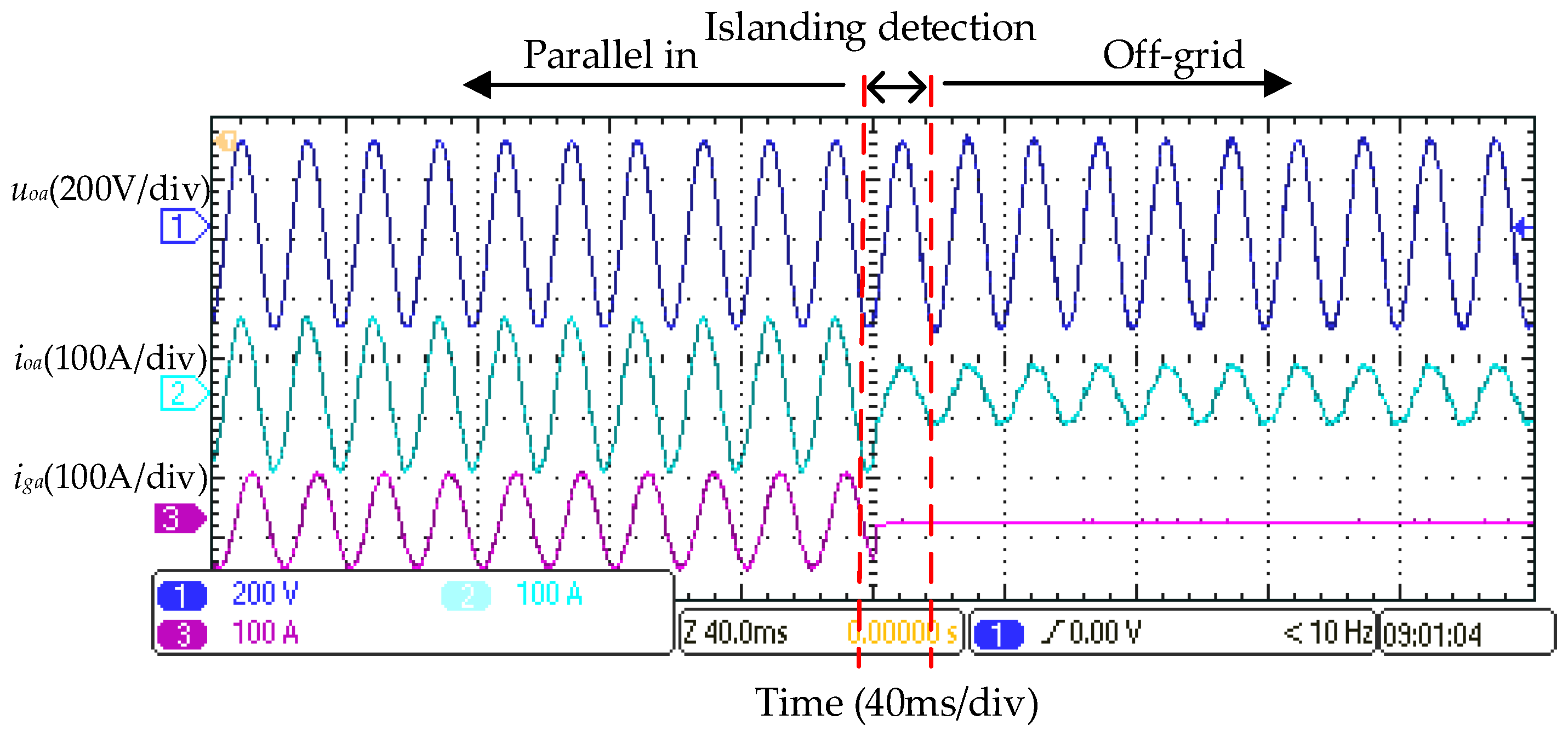
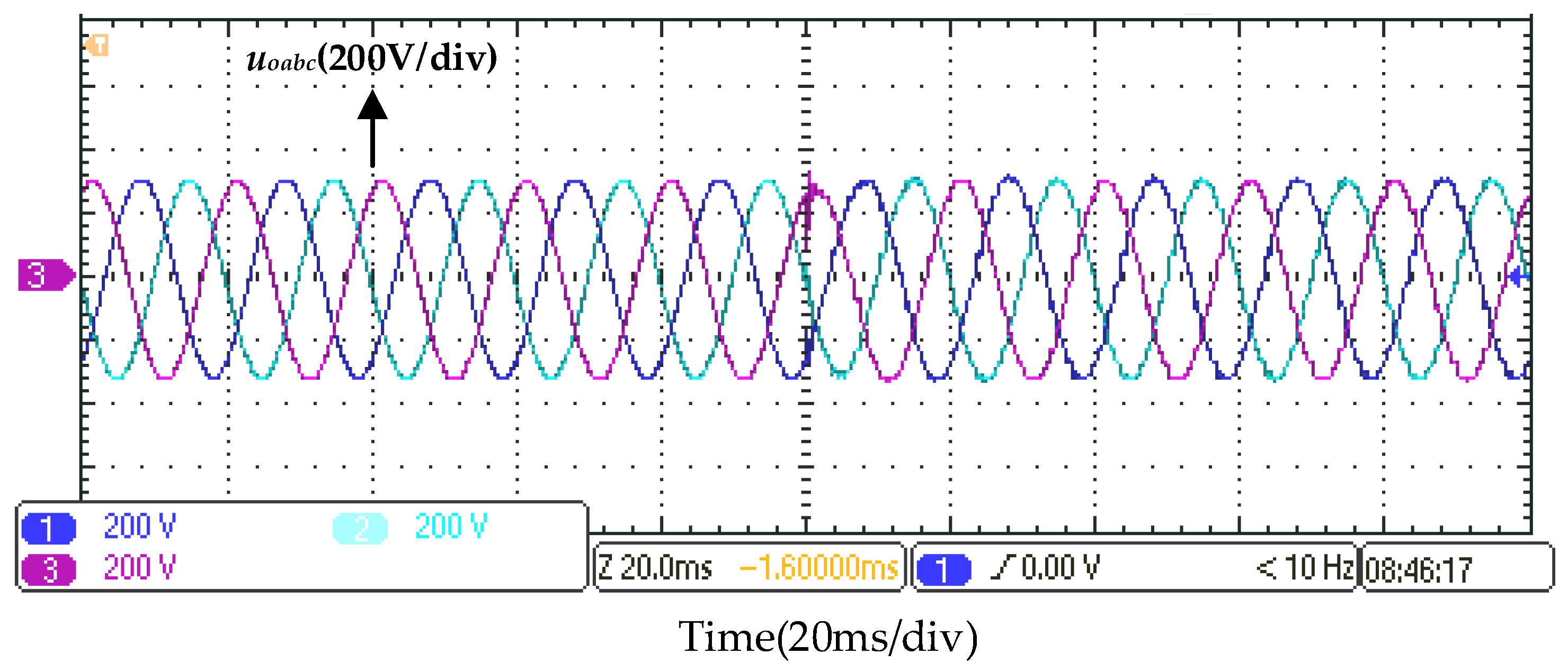
6. Experiments
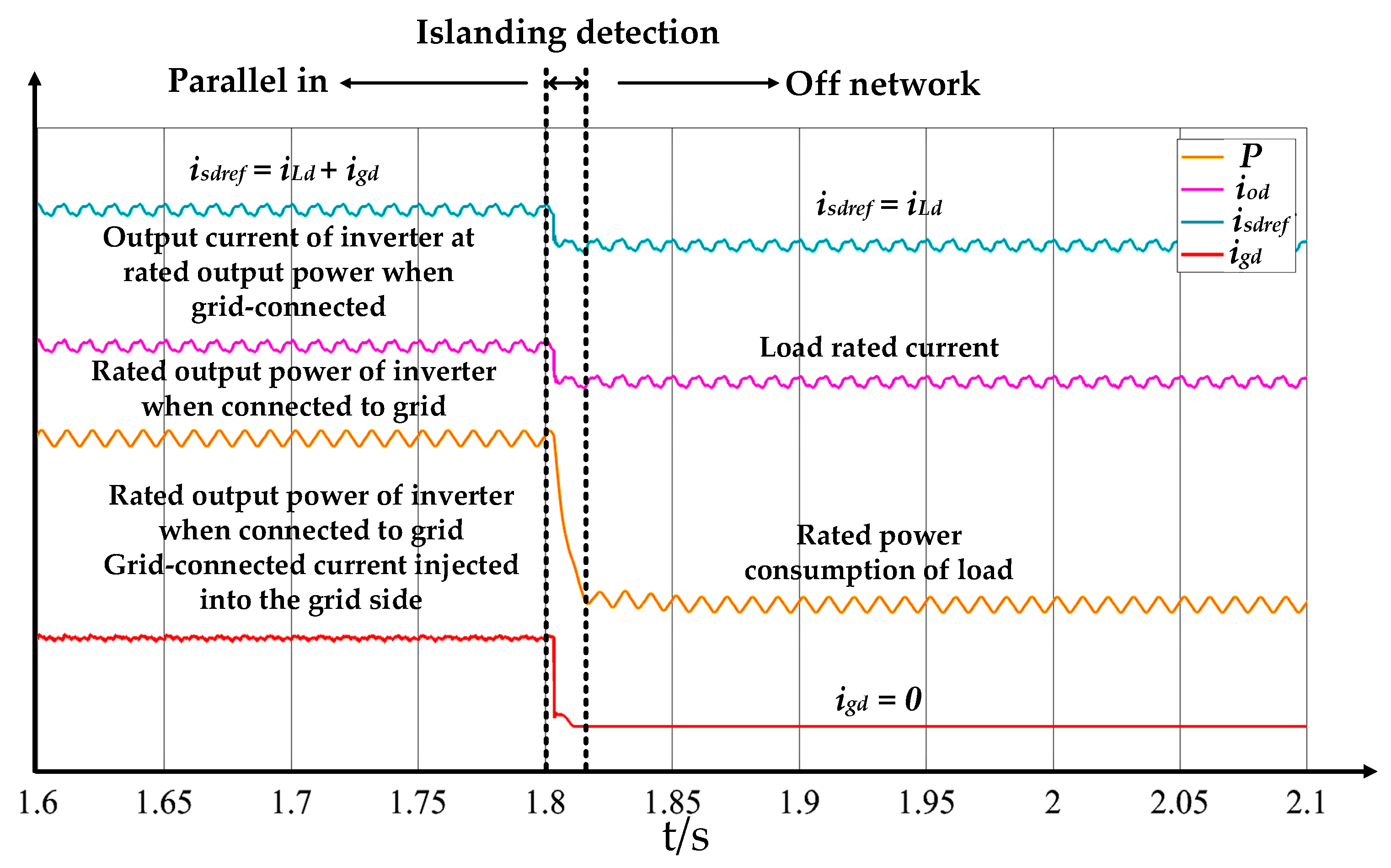
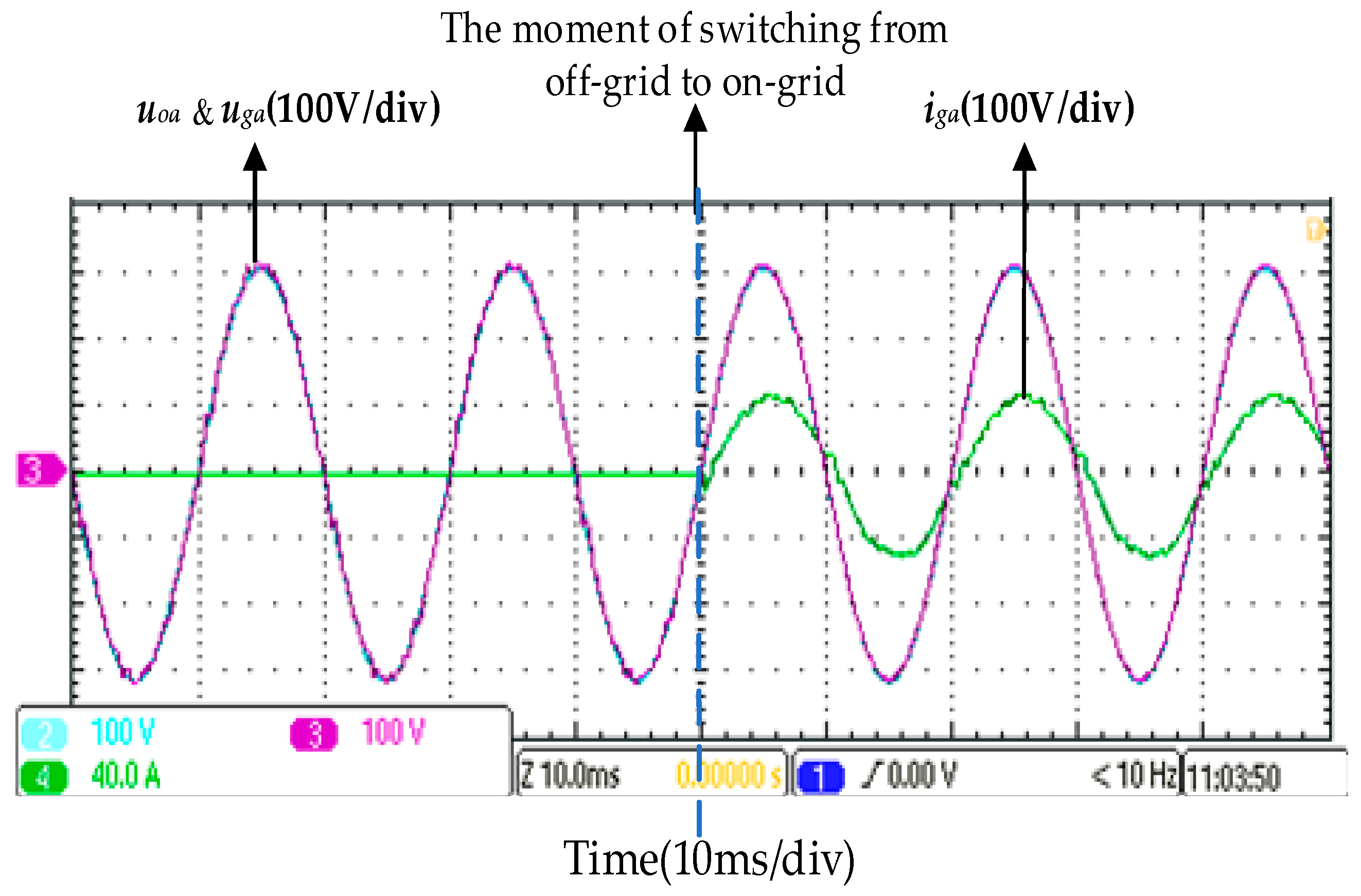
6.1. Experimental Verifications of Switching from Off-Grid Mode to Grid-Connected Mode of Multi-Functional Inverter
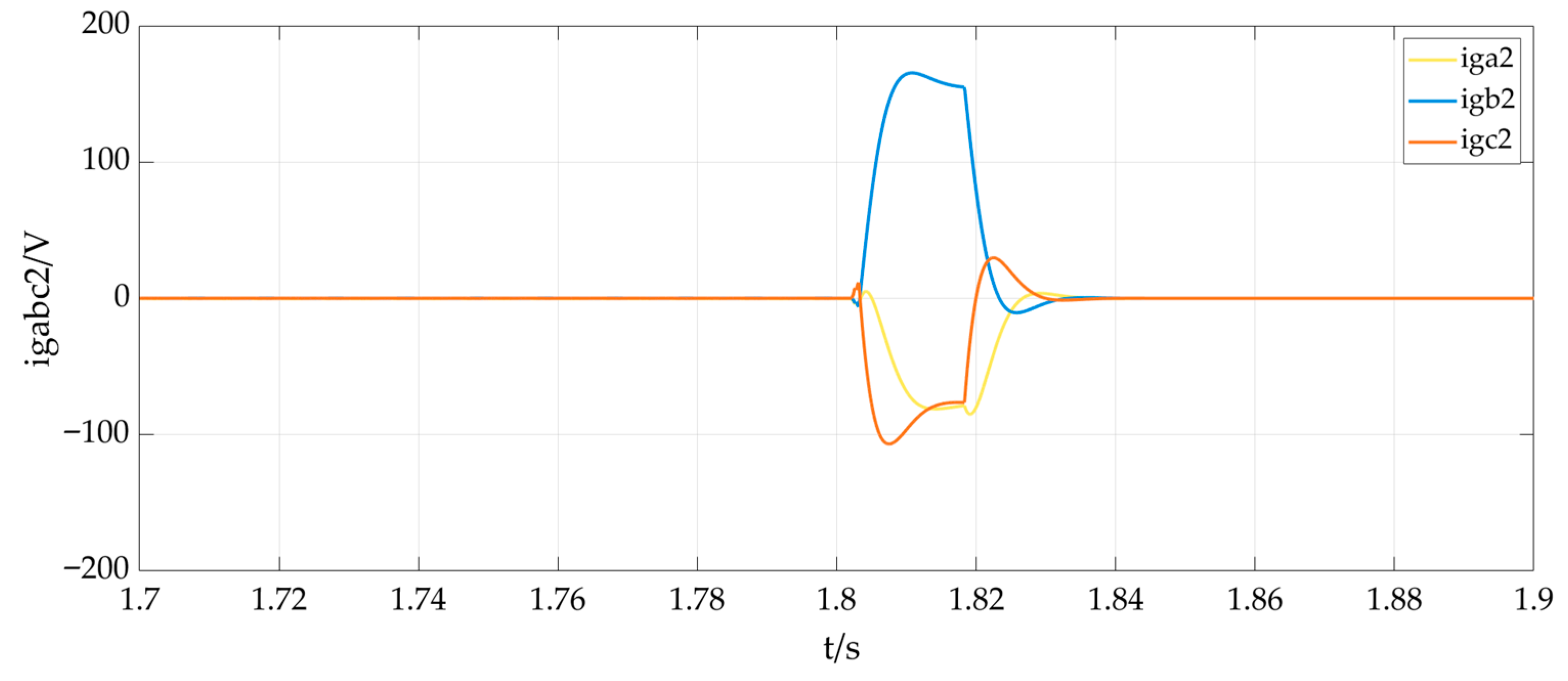
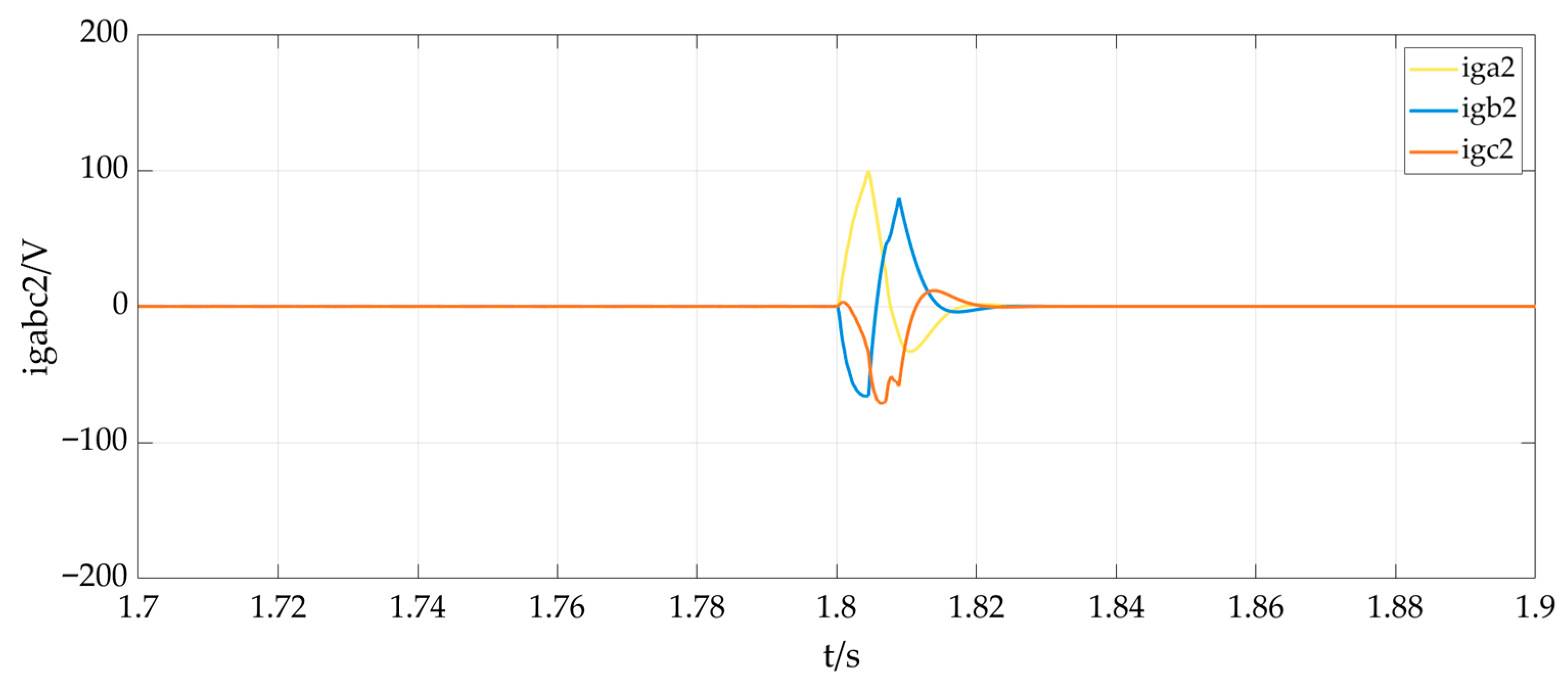
6.2. Experimental Verifications of Smooth Unplanned Transition from Grid-Connected Mode to Off-Grid Mode for Multi-Functional Inverter
7. Summary and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sunjaq, A.; Chen, P.; Bongiorno, M. Frequency control by BESS for smooth Island transition of a hydro-powered microgrids. IET Smart Grid 2024, 7, 63–77. [Google Scholar] [CrossRef]
- IEC TS 62898-1:2017+AMD1:2023 CSV; Microgrids—Part 1: Guidelines for microgrid projects planning and specification. International Electrotechnical Commission: Geneva, Switzerland, 2023.
- Shanzah, N.; Sadiq, A. Intelligent islanding detection in smart microgrids using variance autocorrelation function-based modal current envelope. IET Smart Grid 2024, 7, 1019–1035. [Google Scholar]
- Mehdi, B. Control method for improvement of power quality in single interlinking converter hybrid AC-DC microgrids. IET Smart Grid 2021, 4, 414–428. [Google Scholar]
- Nwaulu, E.; Masaud, T.M. Stochastic risk-managed reserve dispatch for seamless microgrids islanding during unplanned events. J. Eng. 2025, 2025, e70035. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J. Indirect current control based seamless transfer of three-phase inverter in distributed generation. IEEE Trans. Power Electron. 2014, 29, 3368–3383. [Google Scholar] [CrossRef]
- Deng, Y.; Tao, Y.; Chen, G.; Li, G.; He, X. Enhanced power flow control for grid-connected droop-controlled inverters with improved stability. IEEE Trans. Ind. Electron. 2016, 64, 5919–5929. [Google Scholar] [CrossRef]
- Ashabani, S.M.; Mohamed, Y.A.-R.I. A flexible control strategy for grid-connected and islanded microgrids with enhanced stability using nonlinear microgrids stabilizer. IEEE Trans. Smart Grid 2012, 3, 1291–1301. [Google Scholar] [CrossRef]
- Ankita, S.; Rajasekharareddy, C.; Kumar, K.V.P. Model Predictive Control of MMC-based Medium Voltage microgrids for grid Connected and Islanded Operation. IEEE Trans. Ind. Appl. 2025, 61, 5751–5766. [Google Scholar] [CrossRef]
- Hmad, J.; Houari, A.; Trabelsi, H.; Machmoum, M. Fuzzy logic approach for smooth transition between grid-connected and stand-alone modes of three-phase DG-inverter. Electr. Power Syst. Res. 2019, 175, 105892. [Google Scholar] [CrossRef]
- Ghanbarian, M.M.; Nayeripour, M.; Rajaei, A.; Mansouri, M. Design and implementation of a new modified sliding mode controller for grid-connected inverter to controlling the voltage and frequency. ISA Trans. 2016, 61, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, X. Unplanned off-grid switching strategy considering BES rate characteristic and dynamic PQ control. Dianli Xitong Baohu yu Kongzhi/Power Syst. Prot. Control. 2022, 50, 100–107. [Google Scholar]
- Wang, J.; Blake, L.; Andrey, B. Design of a Non-PLL grid-forming Inverter for Smooth microgrids Transition Operation. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting, Montreal, QC, Canada, 2–6 August 2020. [Google Scholar]
- Wang, G.; Wang, X.; Gao, X. Improved Seamless Switching Control Strategy for AC/DC Hybrid microgrids. IEEE Access 2021, 9, 55790–55801. [Google Scholar] [CrossRef]



| Parameter Name | Parameter Symbols | Numerical Values |
|---|---|---|
| Inverter-side filter inductance | Ls | 1.5 mH |
| Filter capacitor | C | 16.5 μF |
| Grid-side filter inductance | Lg | 0.45 mH |
| DC-side voltage | Udc | 750 V |
| Grid phase voltage | Ug | 220 V |
| Grid frequency | f | 50 Hz |
| Grid-connected inverter capacity | Cg | 60 kW |
| Switching frequency | fs | 10 kHz |
| Asymmetric resistive loads active | P1, P2, P3 | 3 kW, 6 kW, 9 kW |
| Non-linear load DC-side resistance | Ri | 20 Ω |
| Damping resistance | Rc | 1.5 Ω |
| Linear load active | P4 | 5 kW |
| Resonance frequency (one) | ωn1 | 200 πrad/s |
| Resonance frequency (two) | ωn2 | 600 πrad/s |
| Gains | Kr1 Kr2 | 2000 rad/s |
| Observer gain one | β1 | 4000 rad/s |
| Observer gain two | β2 | 4,000,000 rad/s |
| P gain | kp | 0.1 |
| I gain | ki | 20 |
| Filtering inductor Ls1 | Ls1 | 2 mH |
| Filtering inductor Ls2 | Ls2 | 1 mH |
| Filtering capacitor Cf1 | Cf | 16.5 μF |
| Bandwidth | Ωc1 ωc2 | 25 |
| Overall controller bandwidth | Kd | 35 |
| Disturbance Compensation Coefficient | b0 | 476.2 |
| Observer bandwidth | ωe | 2000 rad/s |
| Limiter coefficient of voltage | αv | 1.6 |
| Limiter coefficient of current | ILIMIT | ±50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Zhang, H.; Su, X.; Gao, Y.; Zheng, K.; Long, C.; Liu, X. Smooth Droop Control Strategy for Multi-Functional Inverters in Microgrids Considering Unplanned Off-Grid Transition and Dynamic Unbalanced Loads. Energies 2025, 18, 6161. https://doi.org/10.3390/en18236161
Shen J, Zhang H, Su X, Gao Y, Zheng K, Long C, Liu X. Smooth Droop Control Strategy for Multi-Functional Inverters in Microgrids Considering Unplanned Off-Grid Transition and Dynamic Unbalanced Loads. Energies. 2025; 18(23):6161. https://doi.org/10.3390/en18236161
Chicago/Turabian StyleShen, Jinhao, Hua Zhang, Xueneng Su, Yiwen Gao, Kun Zheng, Cheng Long, and Xinbo Liu. 2025. "Smooth Droop Control Strategy for Multi-Functional Inverters in Microgrids Considering Unplanned Off-Grid Transition and Dynamic Unbalanced Loads" Energies 18, no. 23: 6161. https://doi.org/10.3390/en18236161
APA StyleShen, J., Zhang, H., Su, X., Gao, Y., Zheng, K., Long, C., & Liu, X. (2025). Smooth Droop Control Strategy for Multi-Functional Inverters in Microgrids Considering Unplanned Off-Grid Transition and Dynamic Unbalanced Loads. Energies, 18(23), 6161. https://doi.org/10.3390/en18236161







