Analysis of the Demagnetization of a PMSG Using a Coupled Electromagnetic–Fluid–Thermal Numerical Model
Abstract
1. Introduction
2. Electromagnetic Model
2.1. Electromagnetic Problem Formulation
2.2. Electromagnetic Losses
2.2.1. Core Losses
2.2.2. PM Losses
2.2.3. Winding Losses
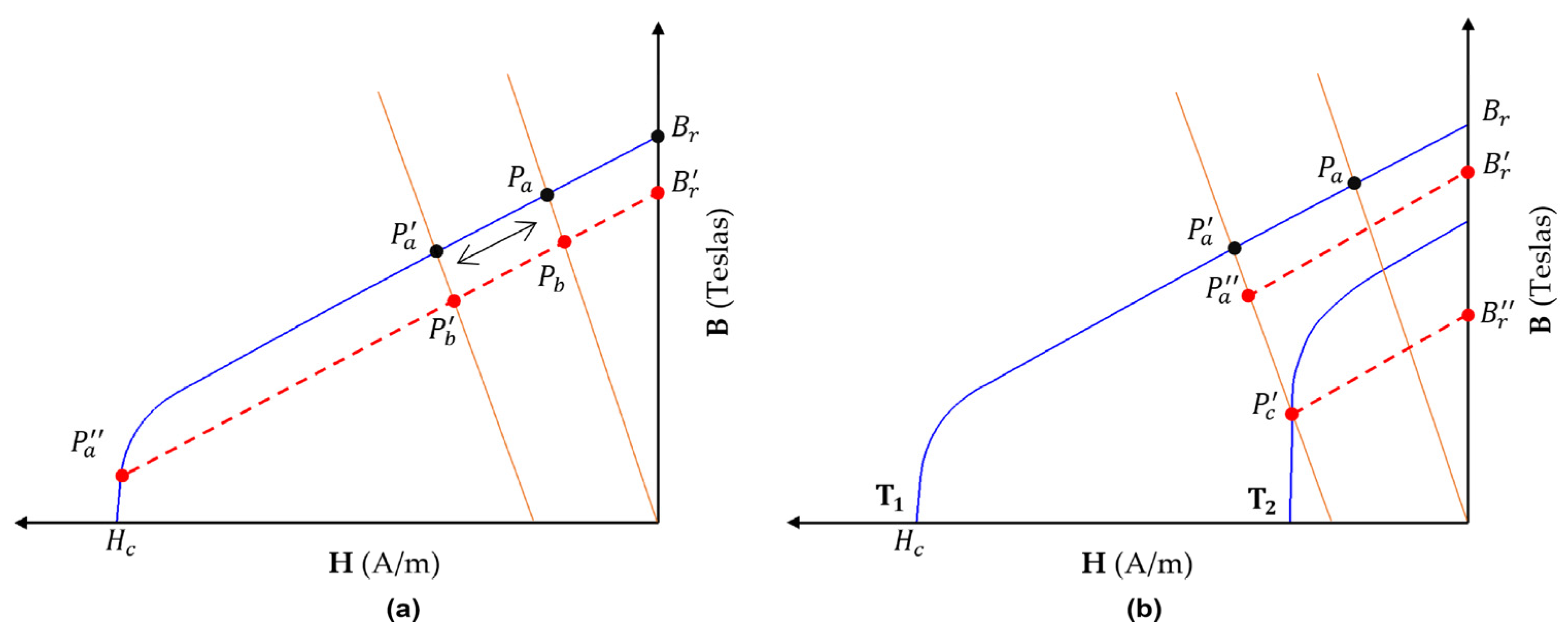
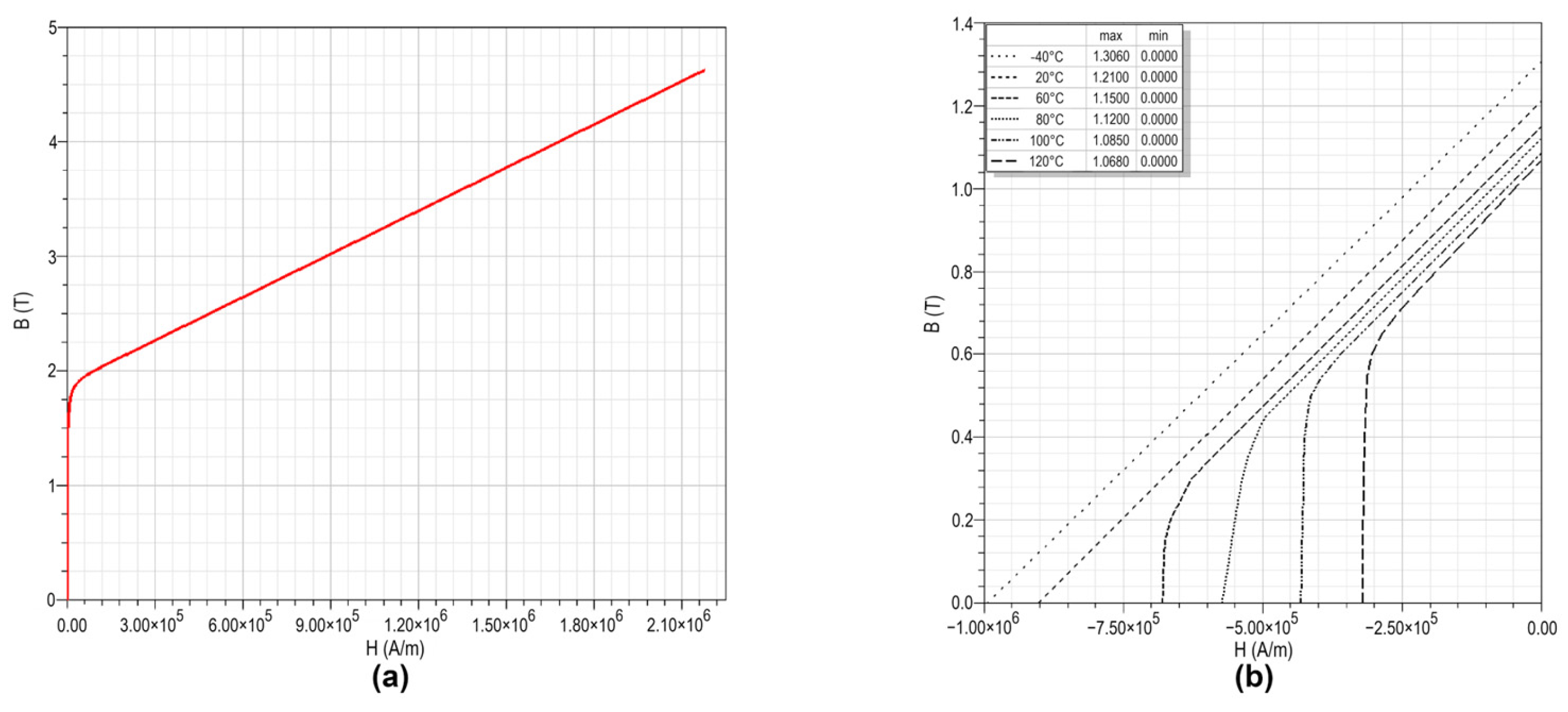
2.3. Demagnetization Phenomenon
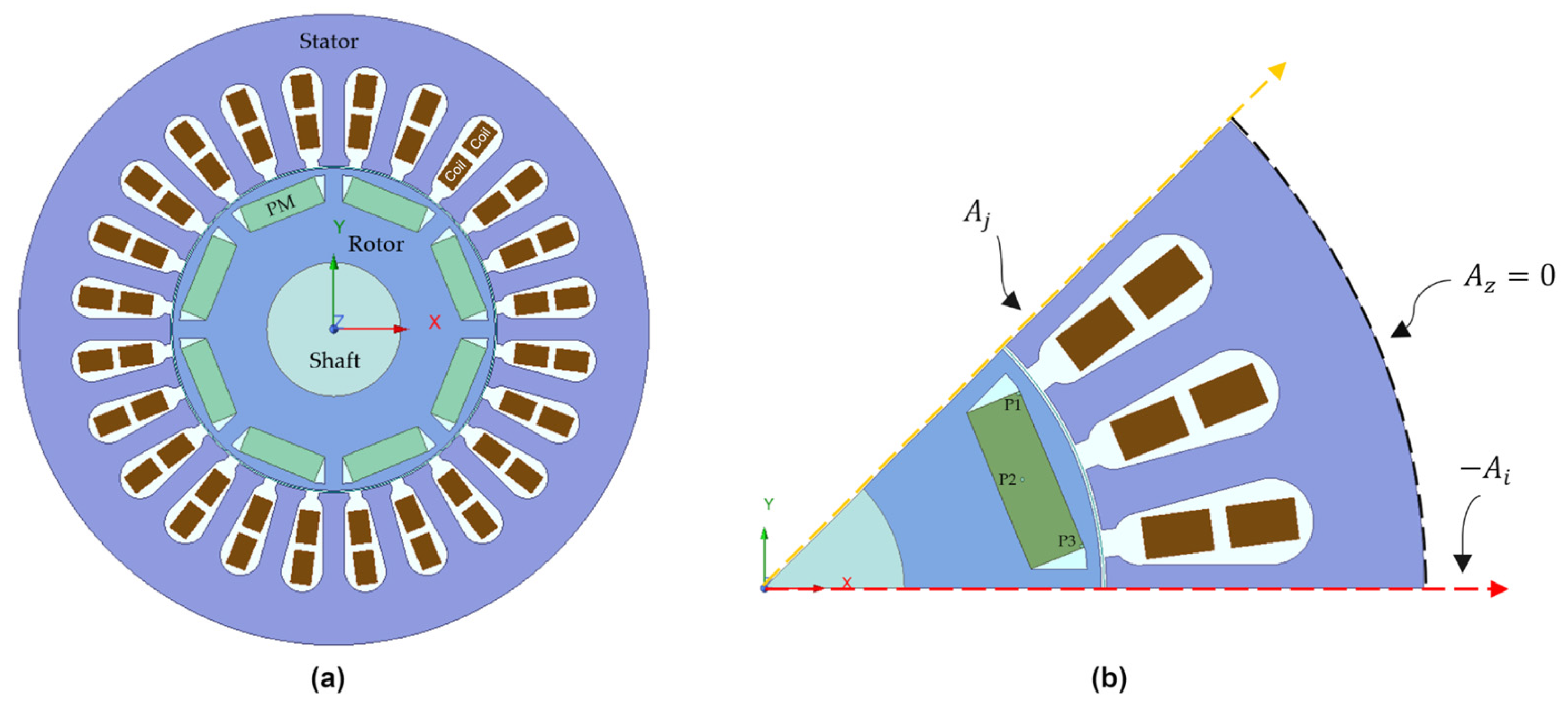
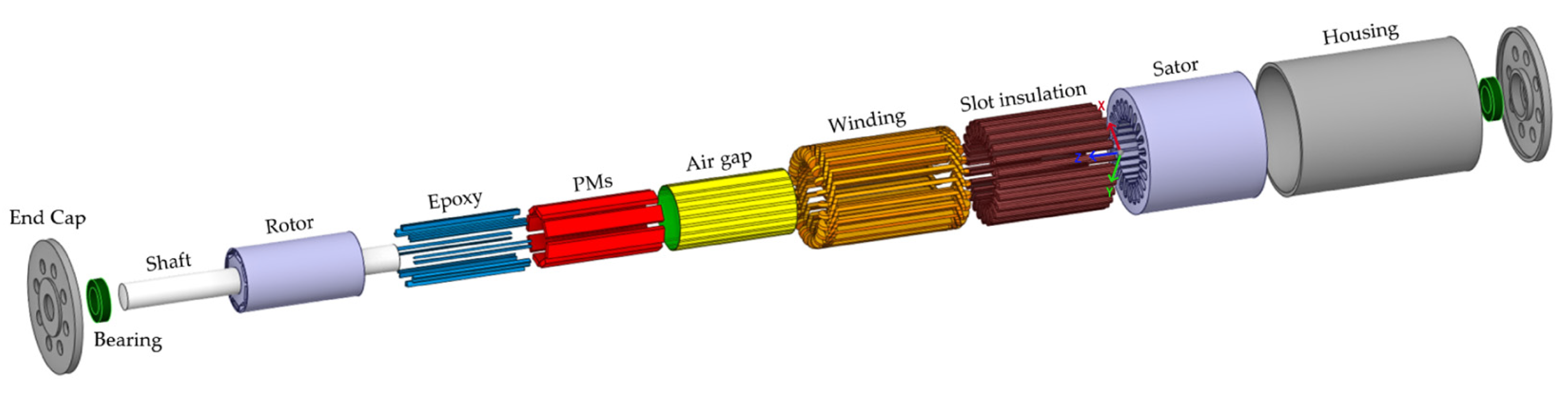
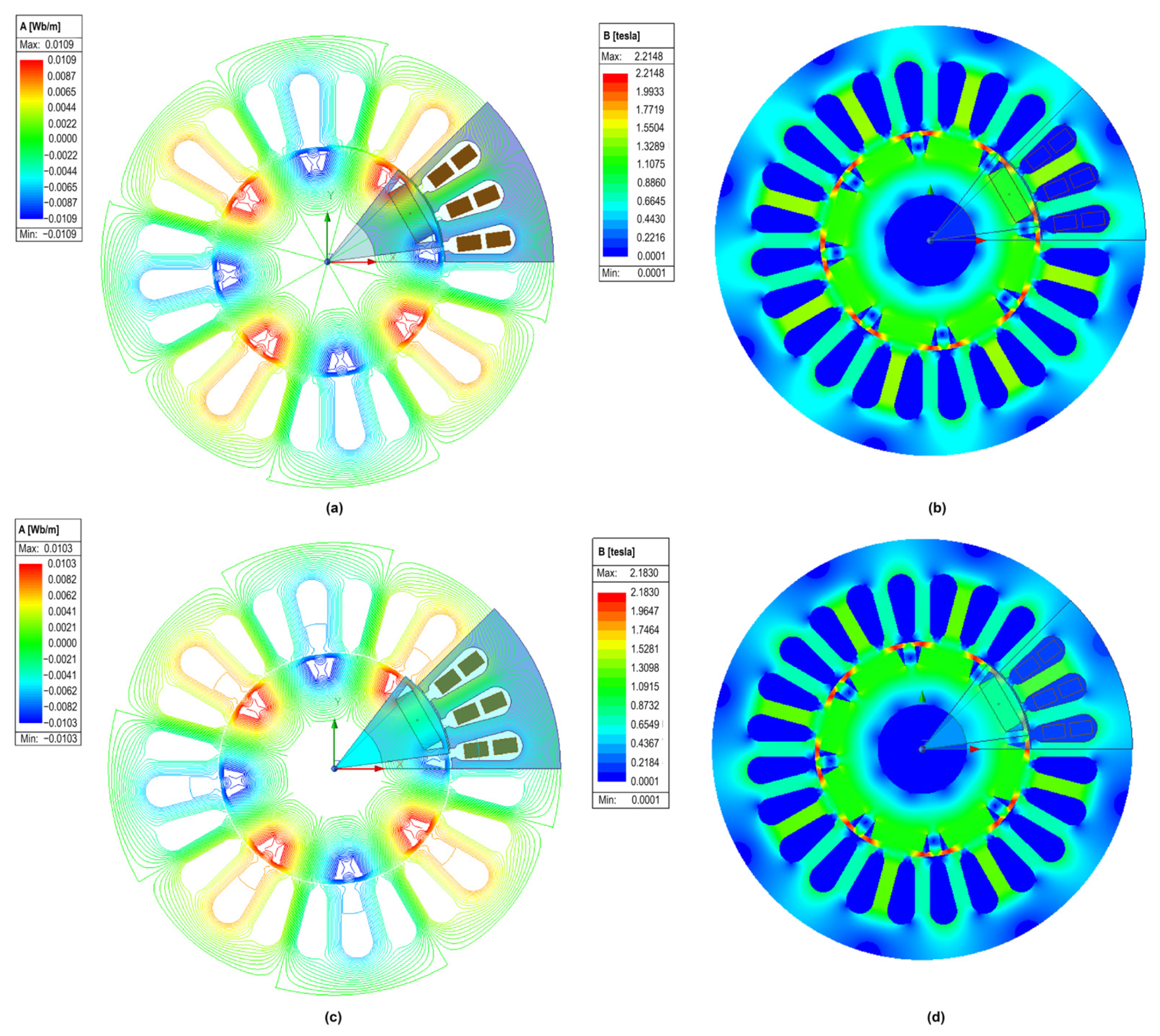
2.4. Electromagnetic Model of the PMSG
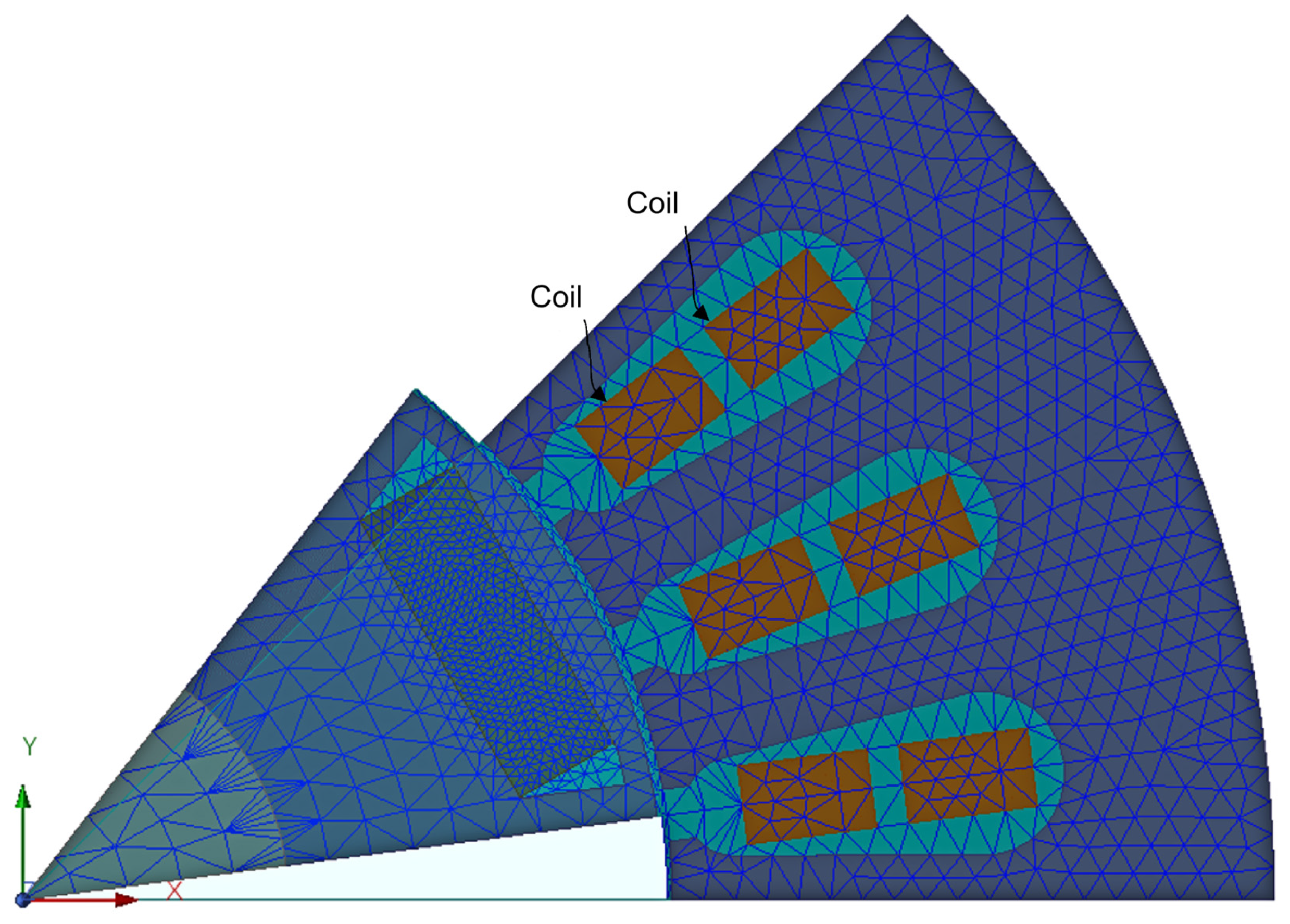
2.5. Electromagnetic Meshing
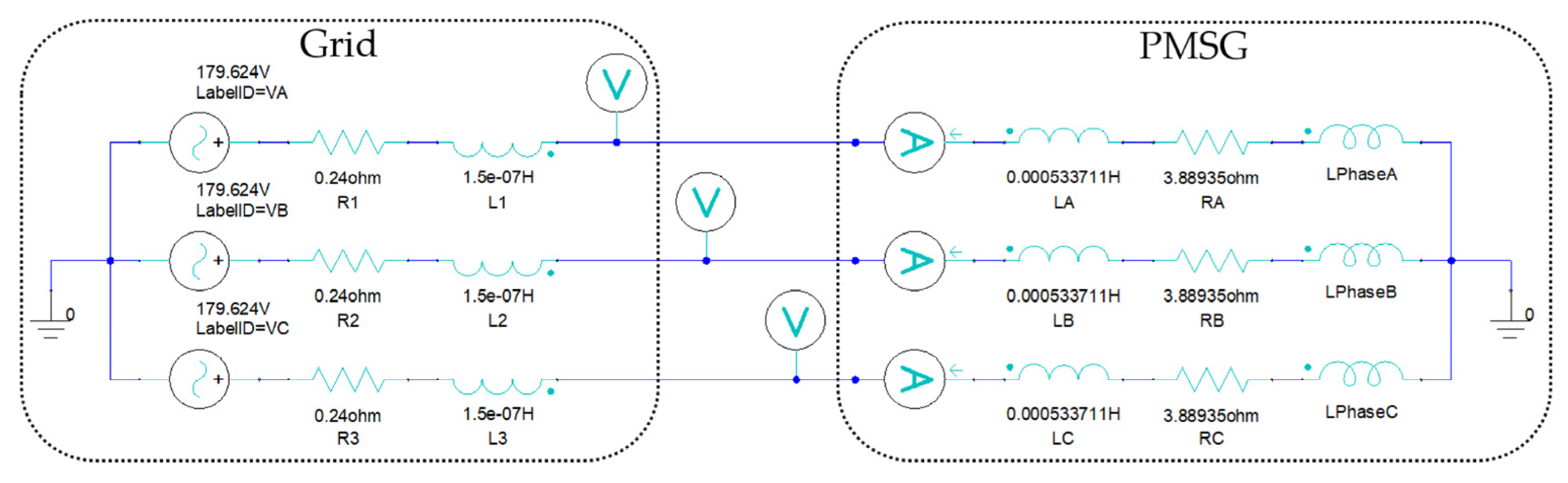
2.6. External Circuit
3. CFD Model of the PMSG
3.1. Governing Equations
3.2. k-w SST Turbulence Model
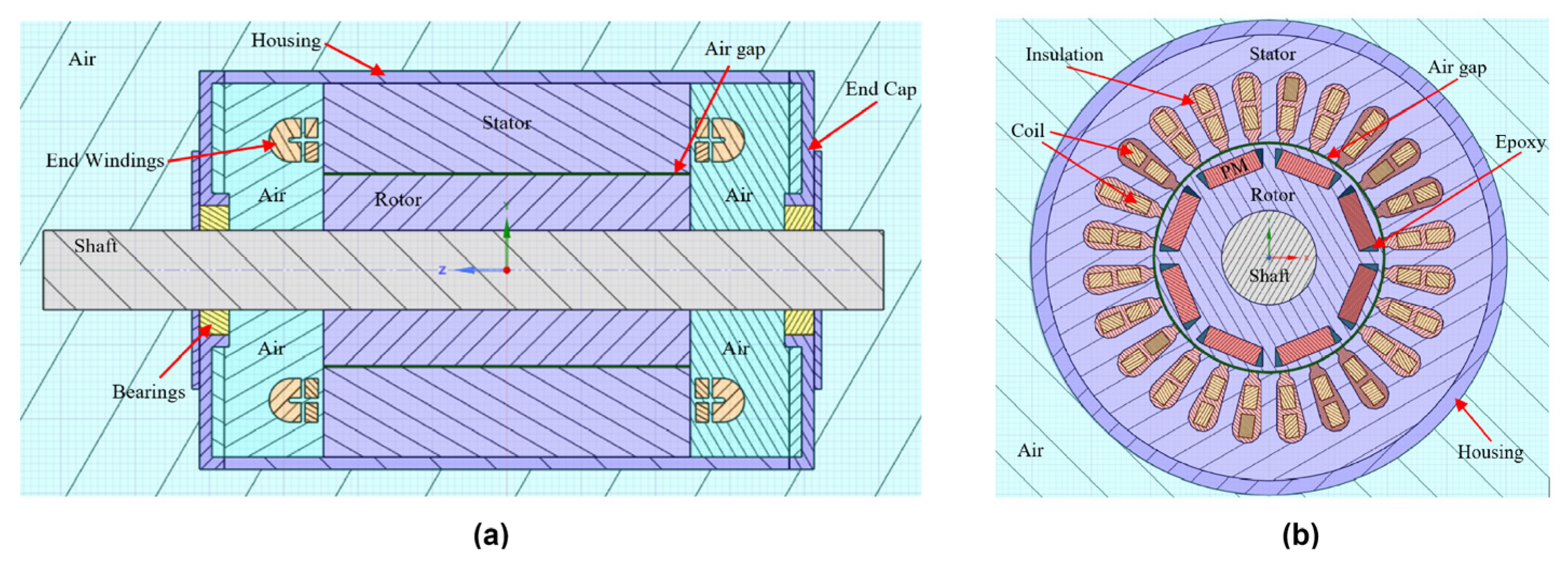
3.3. Geometry and Thermophysical Properties
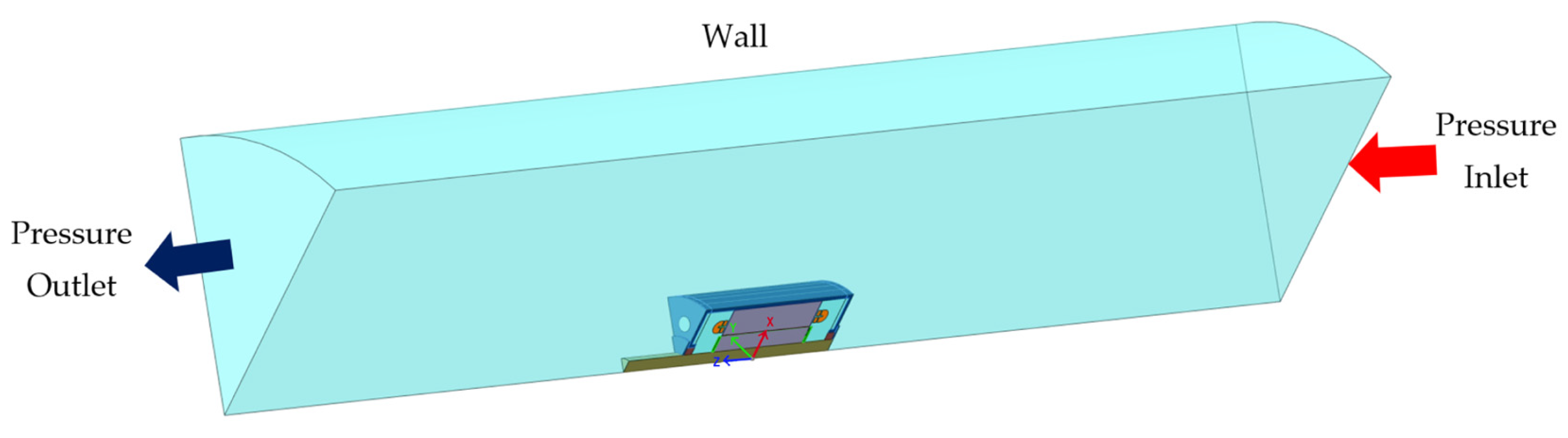
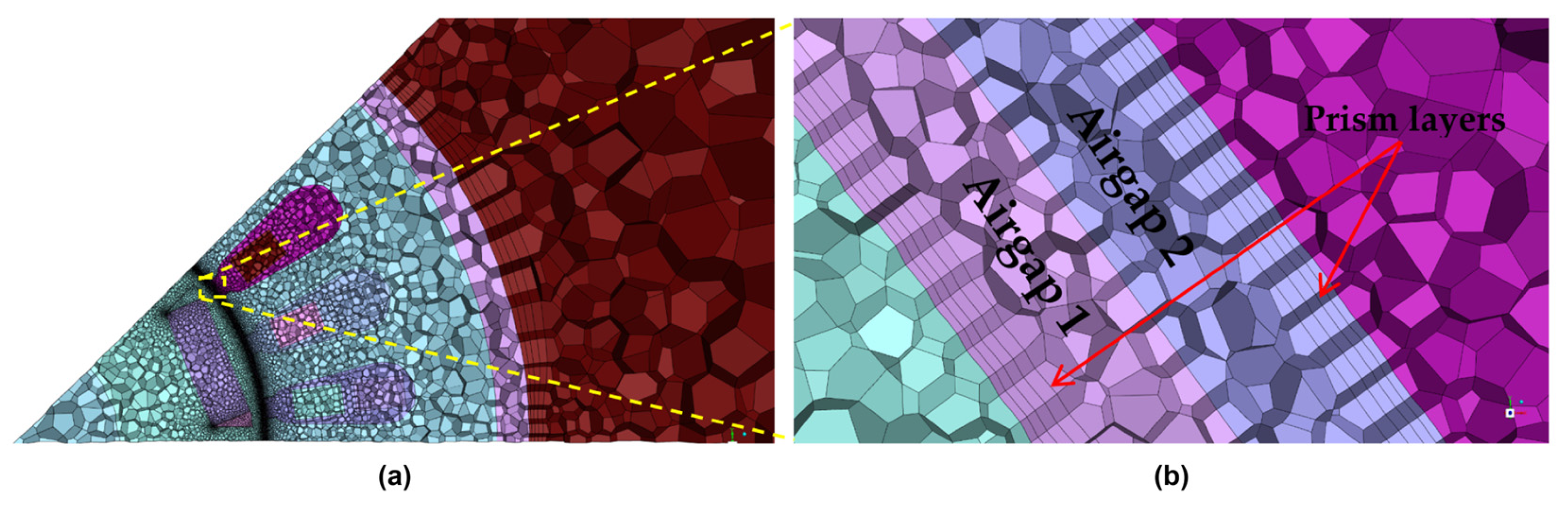
3.4. Boundary Conditions and Mesh
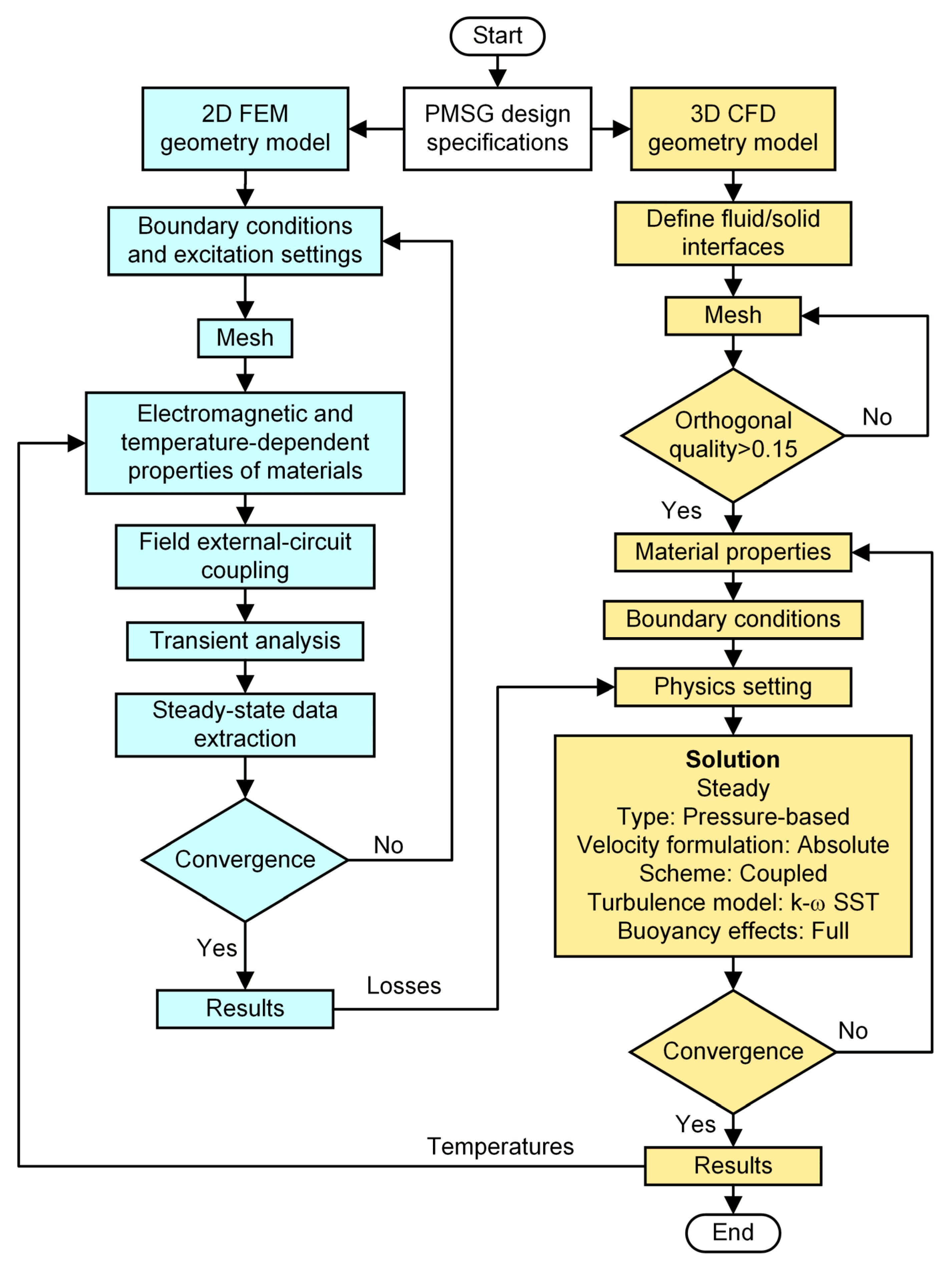
4. Multi-Physic Coupling Analysis Methodology
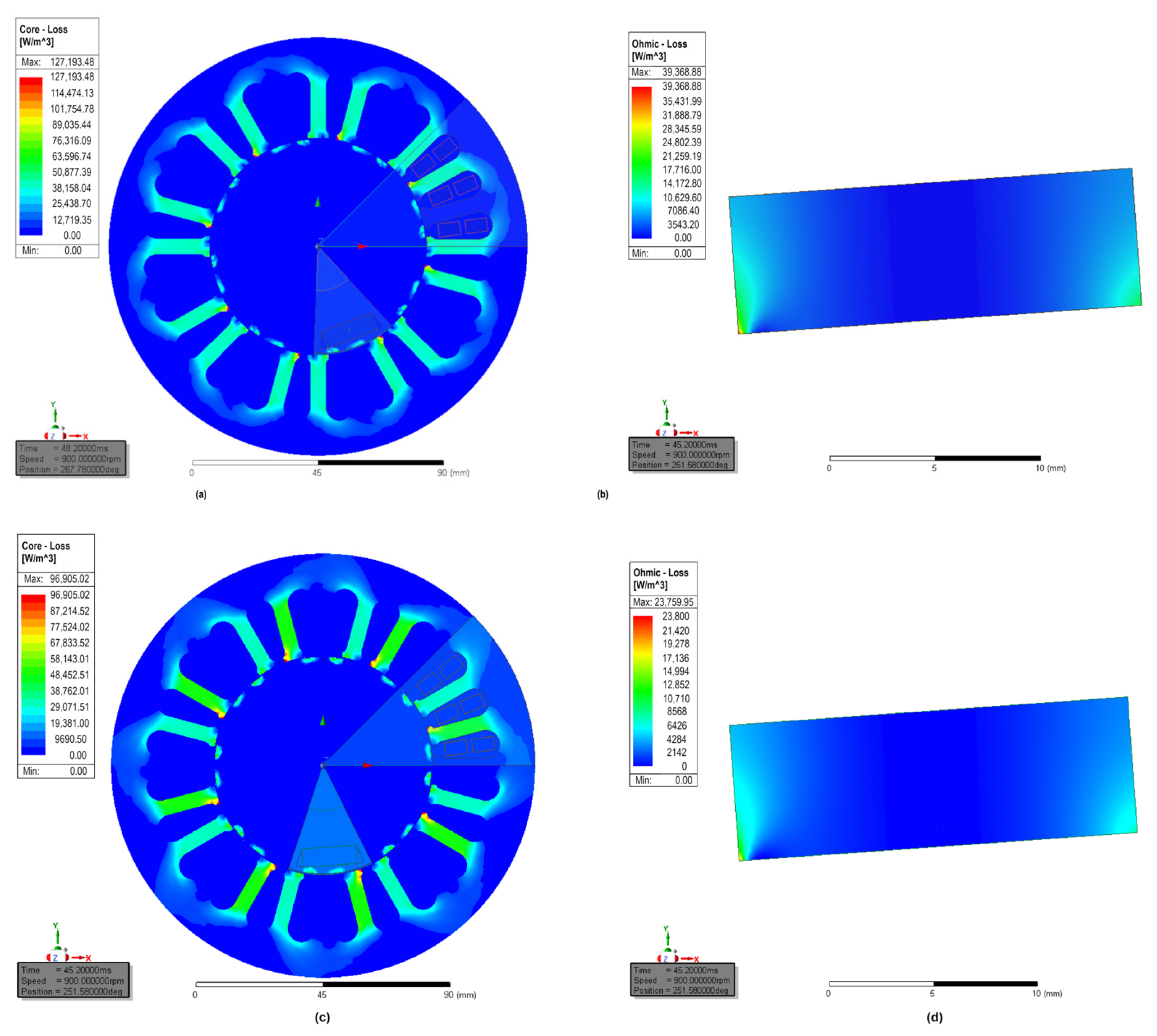
4.1. Loss Calculation for Case 1 and Case 2
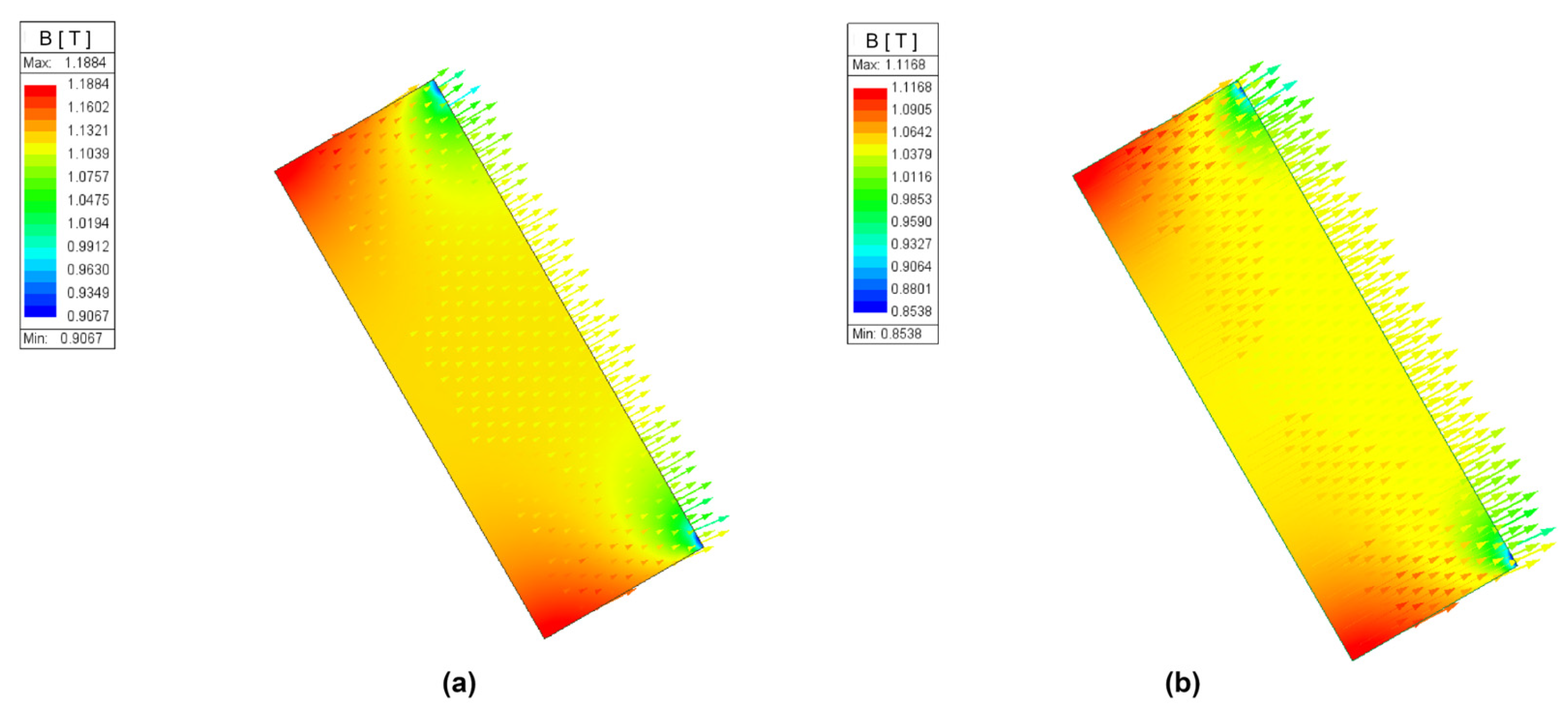
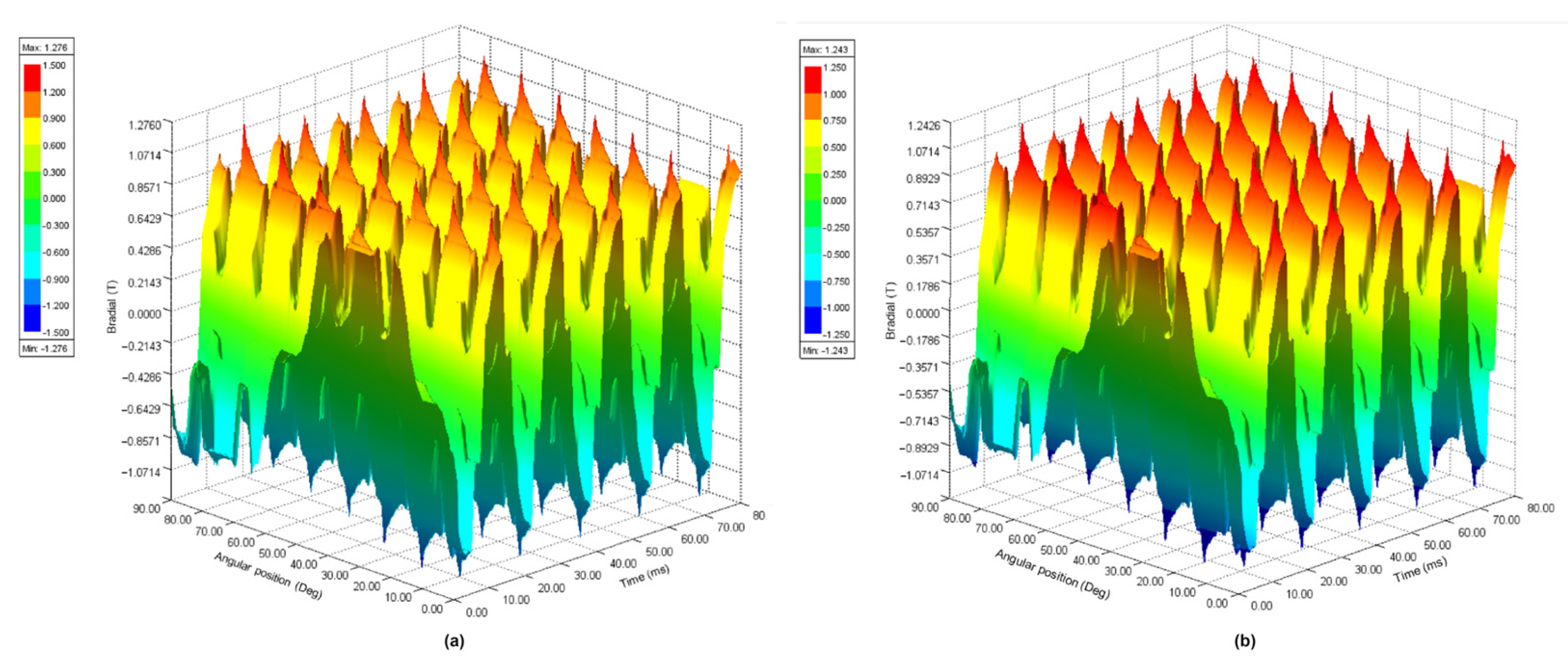
4.2. Reversible Demagnetization for Case 1 and Case 2
5. FEM-CFD Analysis
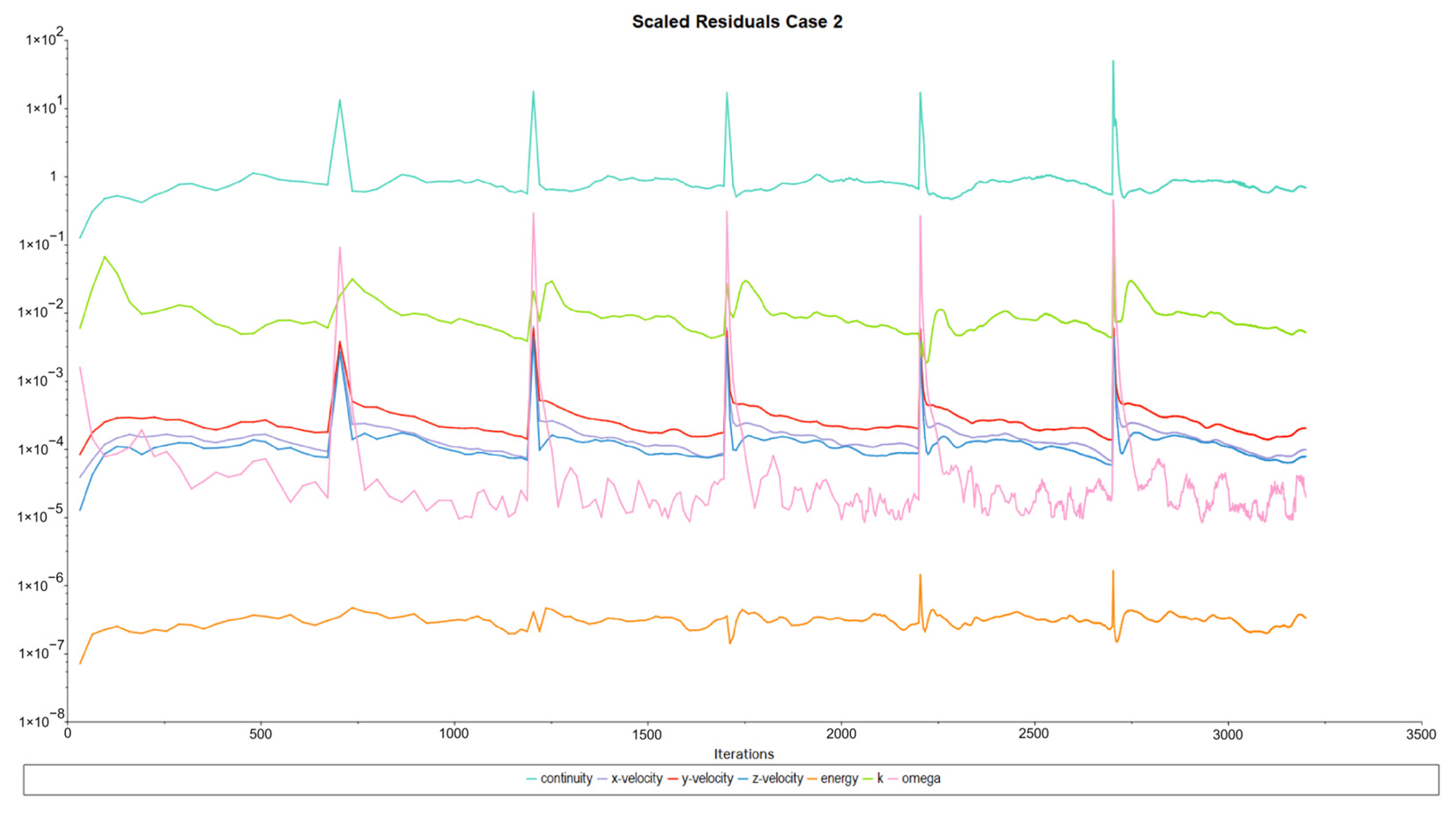
5.1. Convergence for Case 2
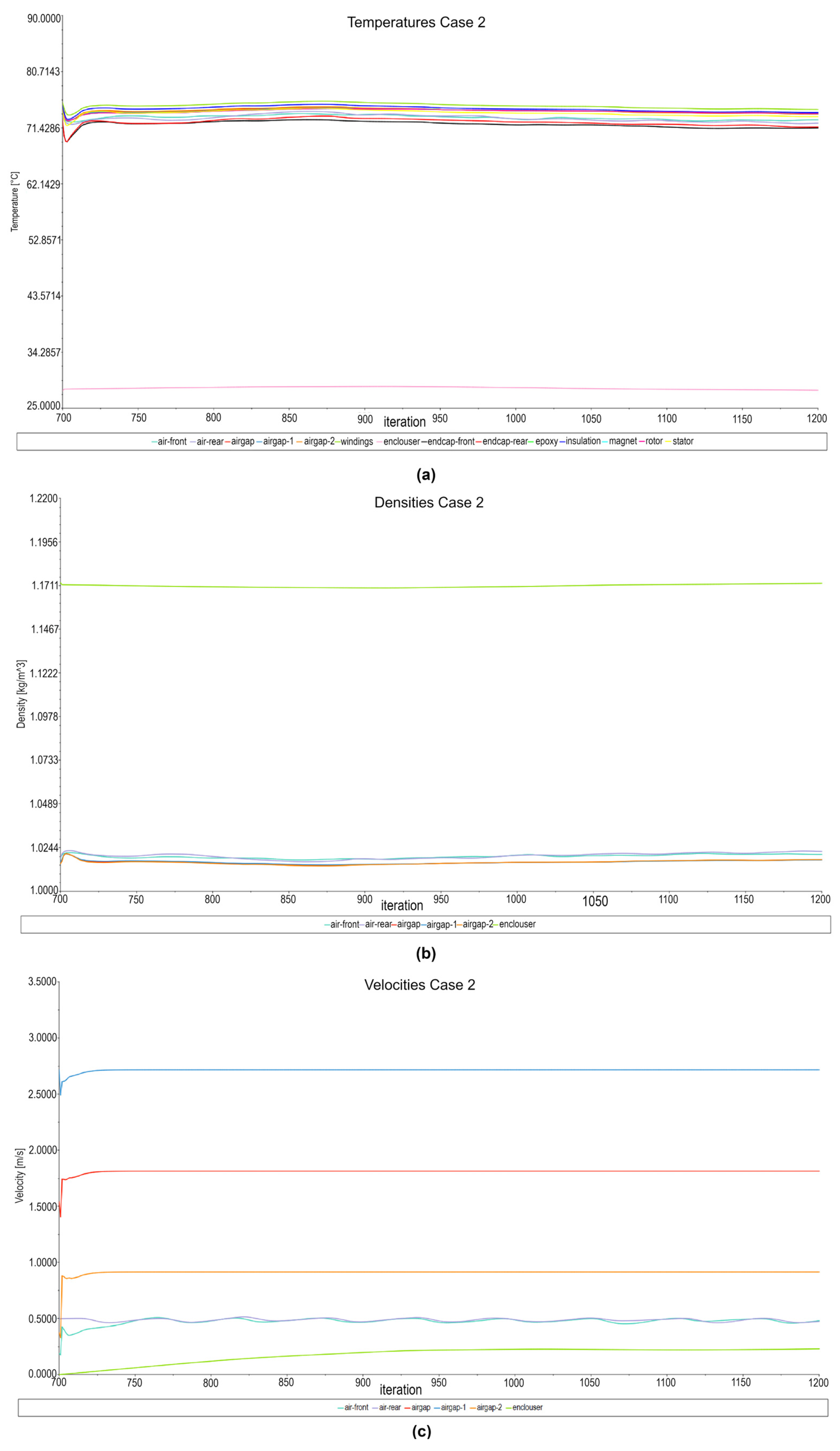
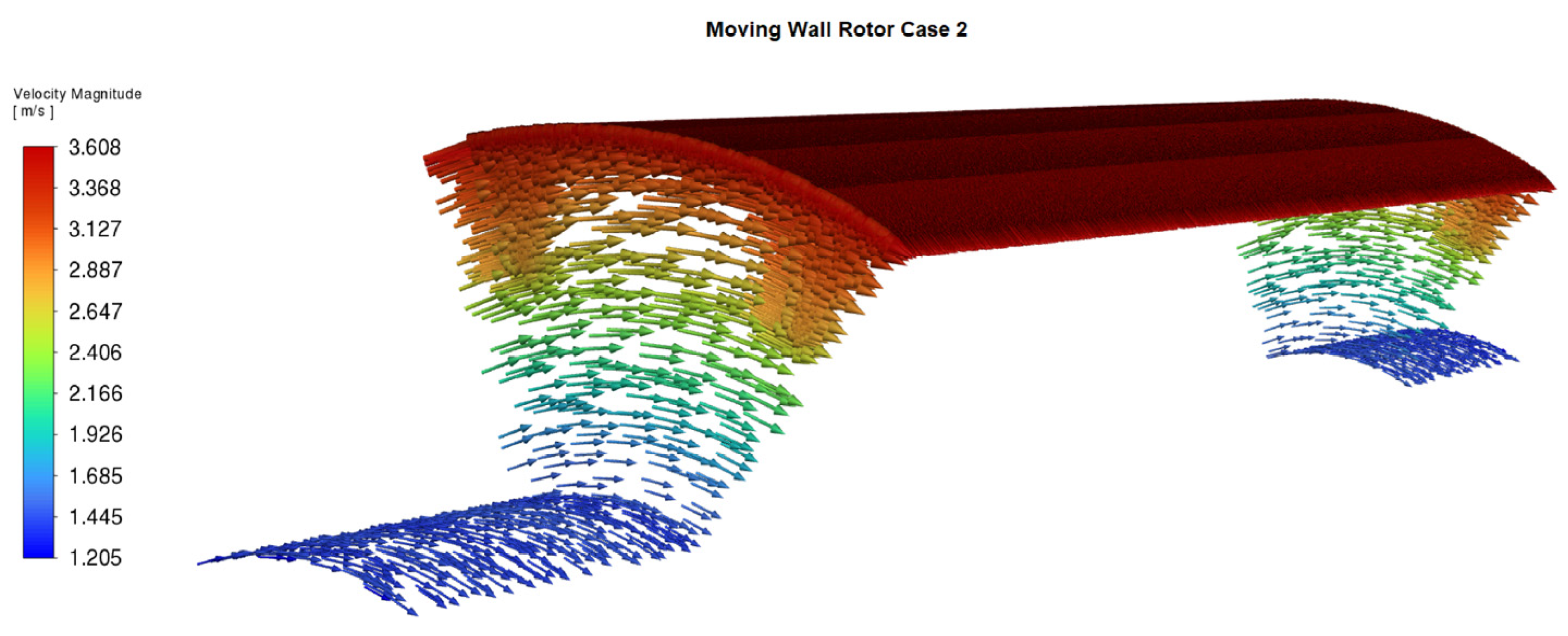
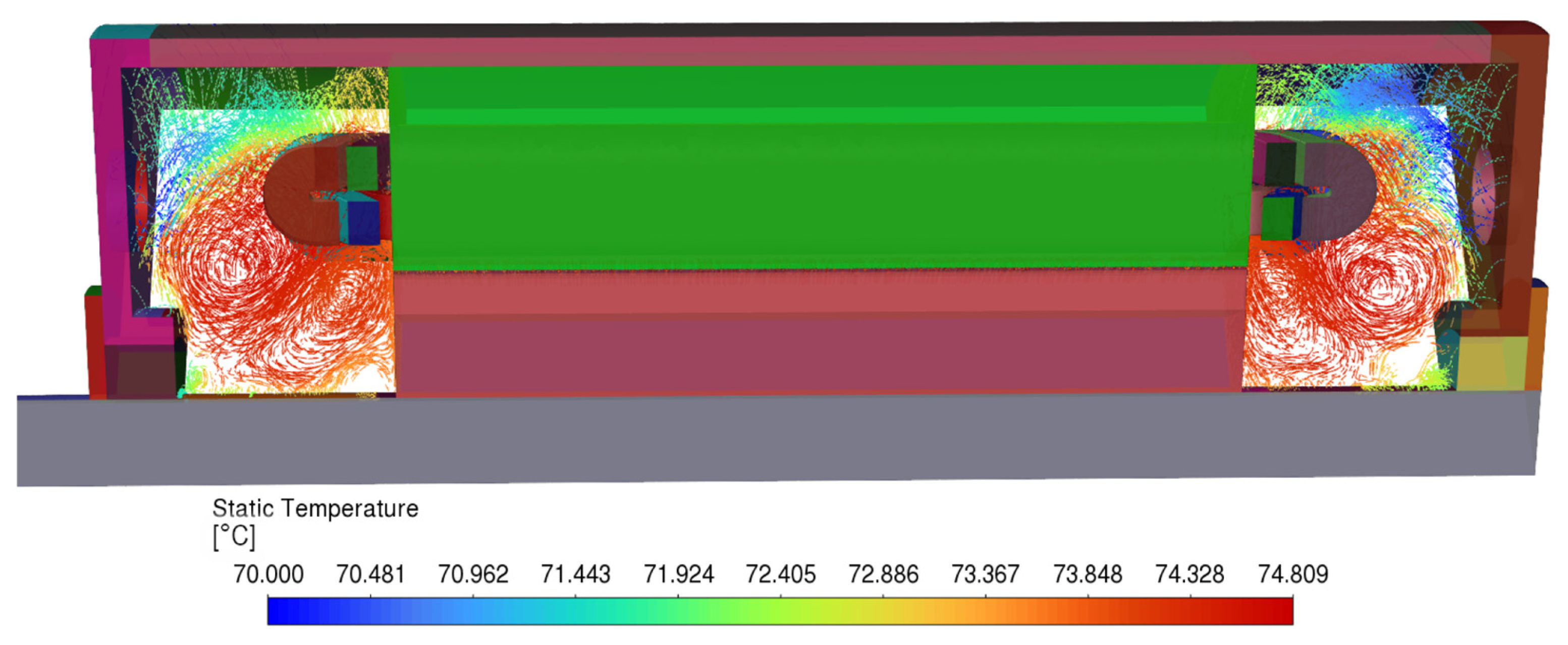
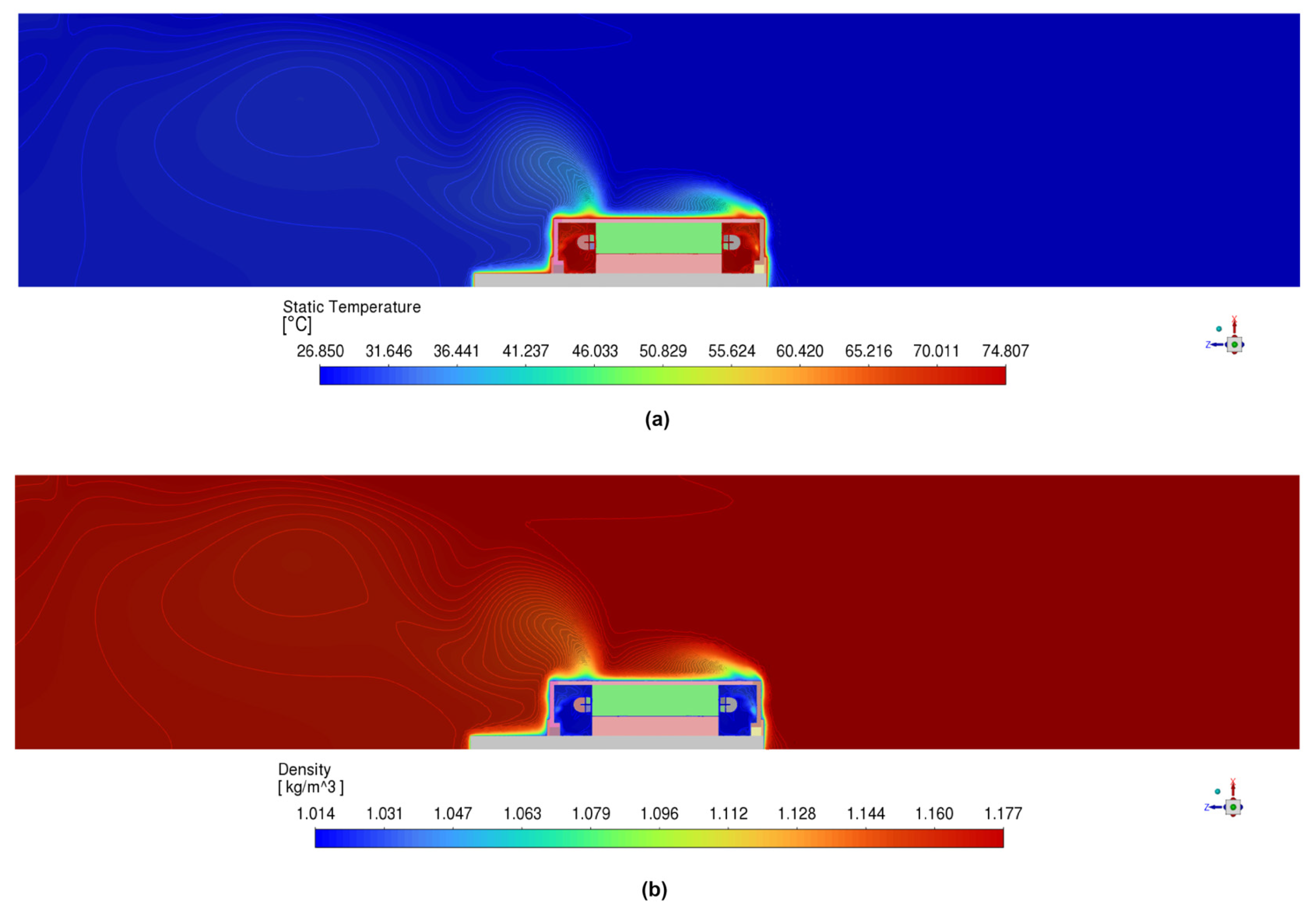
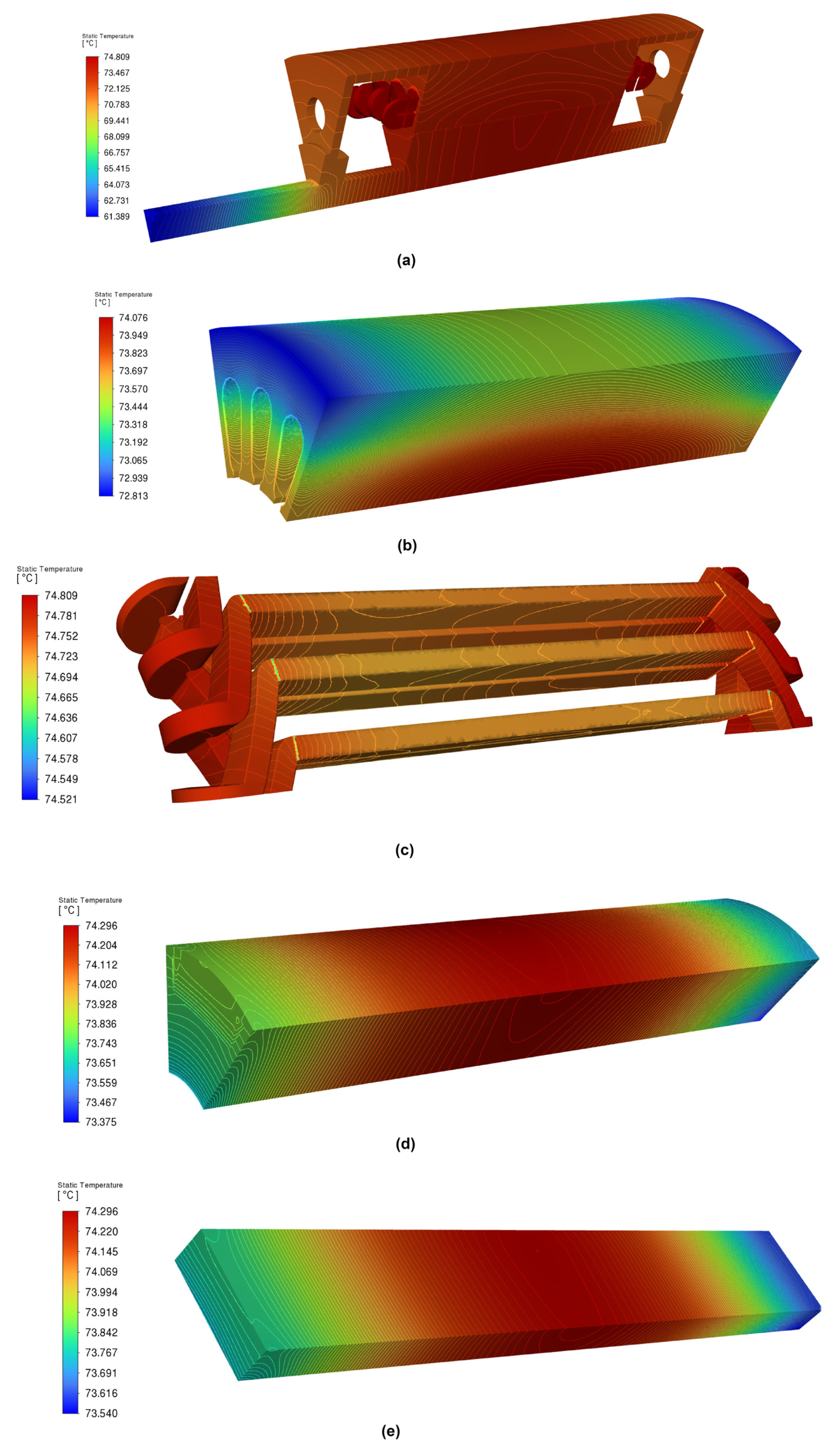
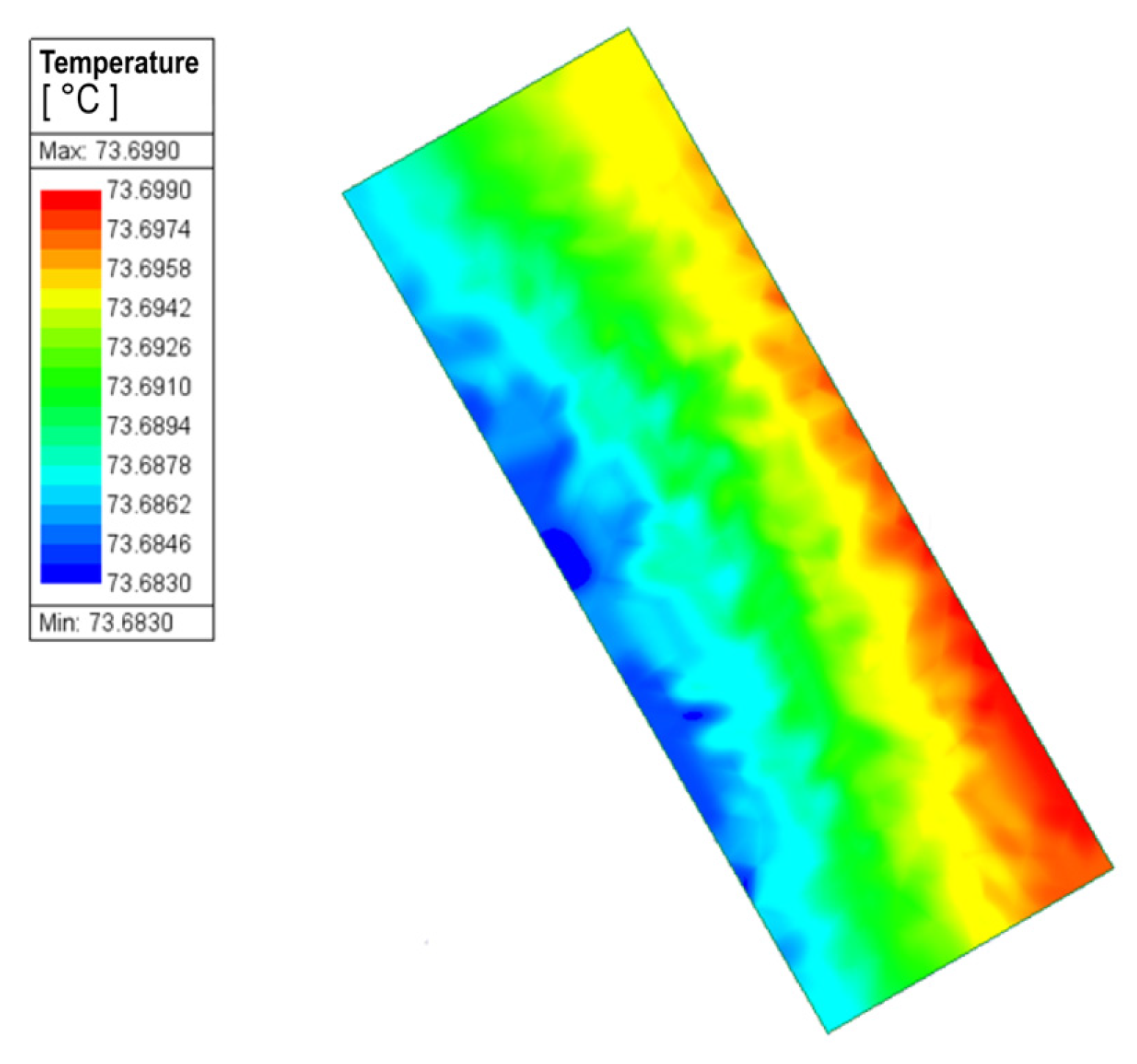
5.2. Thermal Field Results for Case 2
6. Conclusions
- The total electromagnetic losses for Case 1 without thermal coupling showed a slight increase of ~3.5% compared to the coupled Case 2, while parasitic losses in the PM differed by only ~25%.
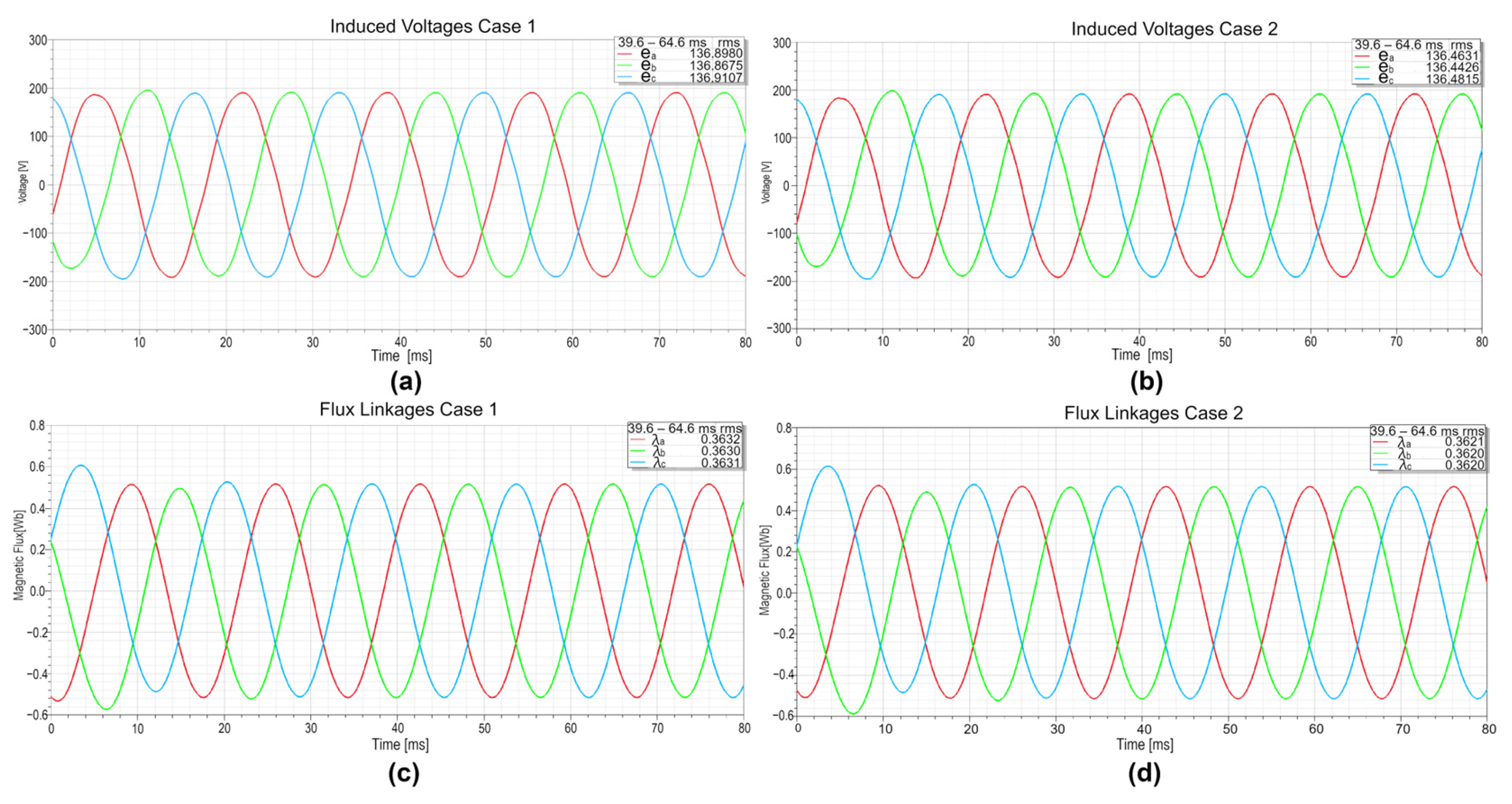
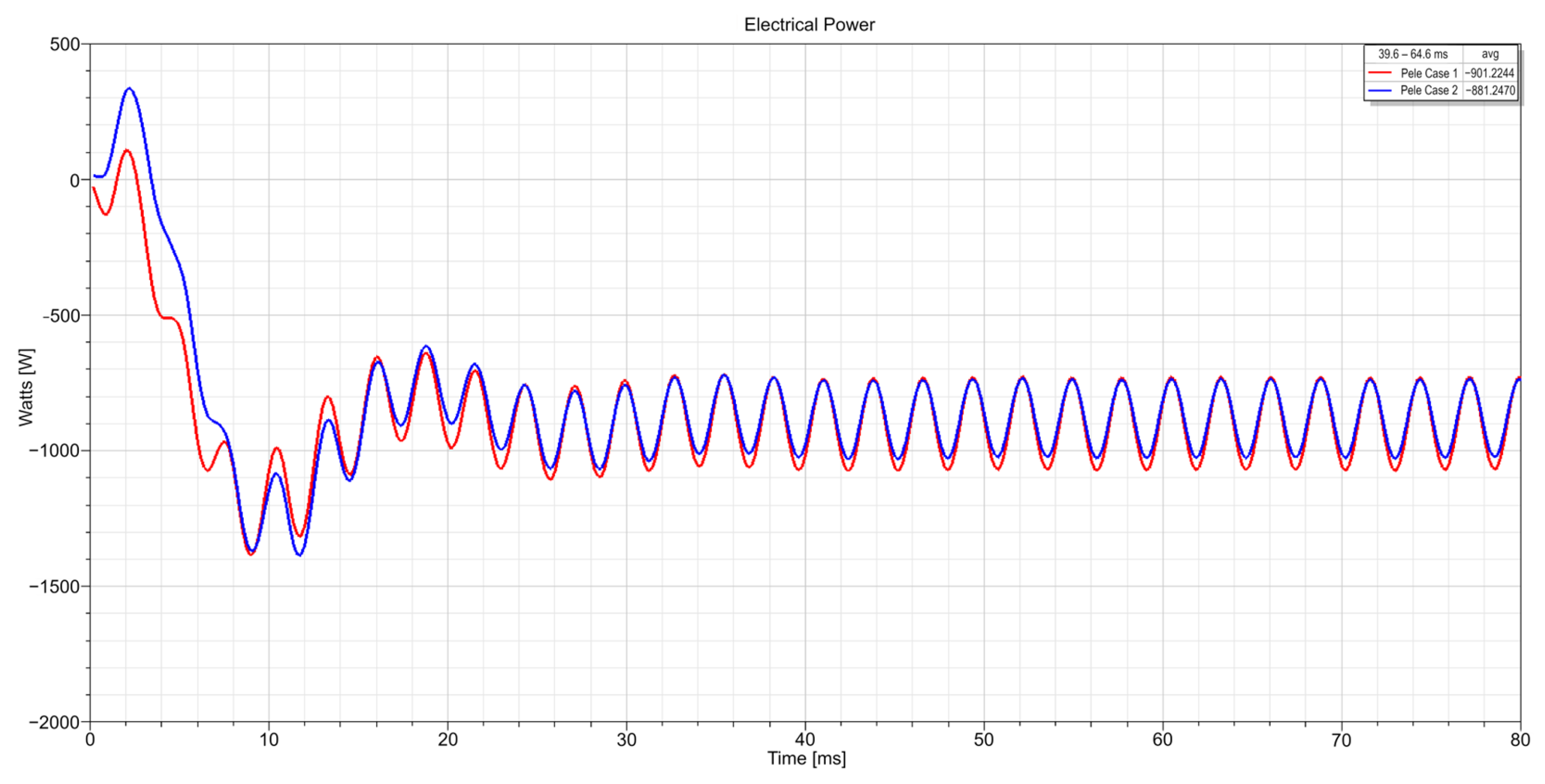
- Induced voltages decreased by ~0.43 V in Case 2 compared to Case 1.
- Case 1 met the design requirements for nominal electrical power generation of 900 W at a constant temperature of 70 °C, whereas Case 2 experienced a slight reduction of ~2.22% (881.24 W).
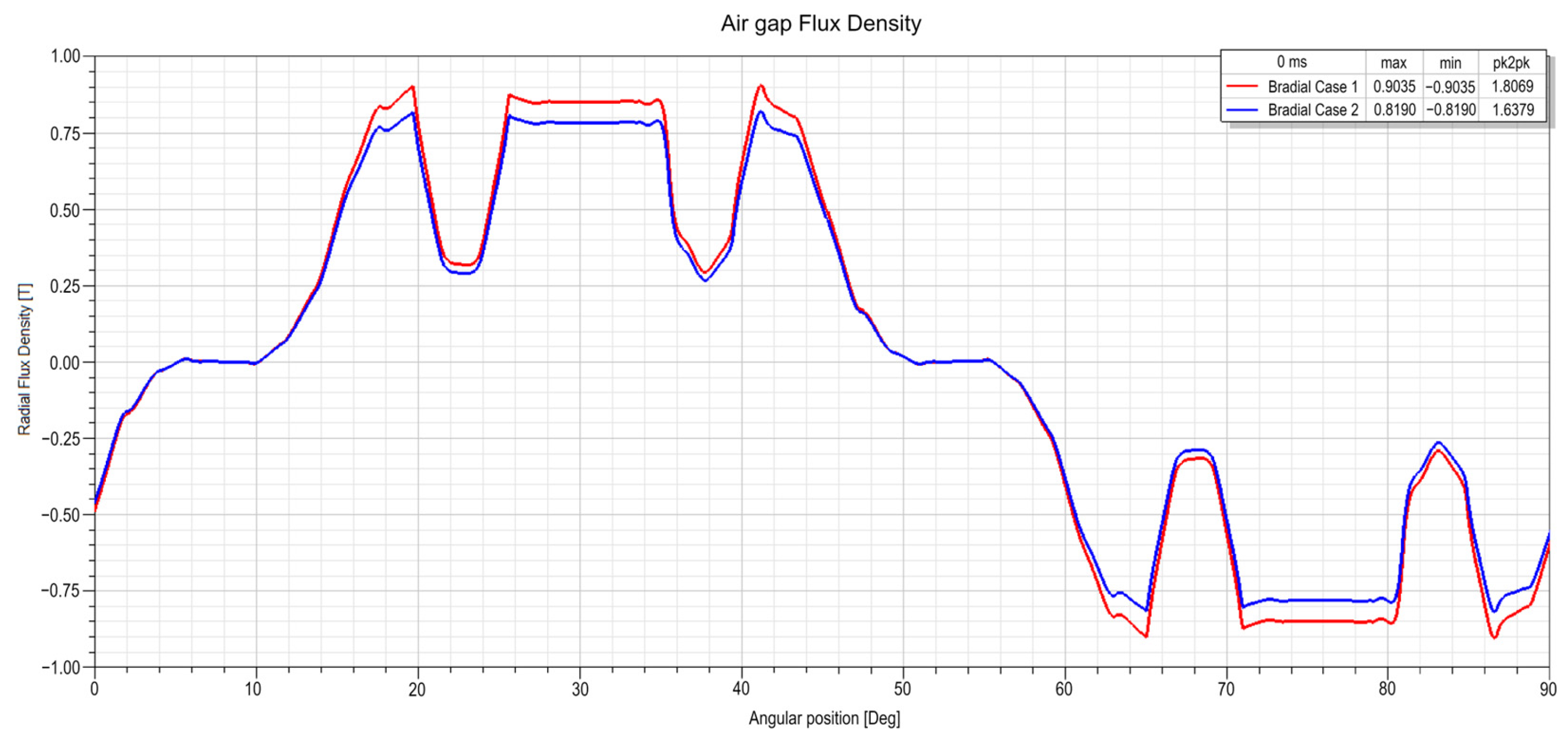
- Air gap magnetic flux decreased in Case 2 due to the PM temperature rise, reducing losses, induced voltages, and generated electrical power compared to Case 1.
- For Case 1 and Case 2, evaluation of the PM critical points on the demagnetization curve showed no risk of irreversible demagnetization due to temperature rise, indicating satisfactory PMSG design and PM selection.
- Natural convection, velocity, density, turbulence, and heat transfer effects between solid and fluid regions in the end windings, air gap, and exterior of the PMSG were accurately captured.
- Residuals and flow monitors were used as convergence criteria, showing satisfactory behavior for numerical stability and convergence in the CFD model for Case 2.
- PM temperature increase in Case 2, according to the CFD model, was approximately 4 °C in the bidirectional coupling, compared to the design temperature in Case 1 of 70 °C using the FEM model without thermal coupling, allowing for a more precise electrothermal analysis.
- When interpolating temperatures from the CFD domain to the FEM domain for Case 2, the difference was 0.81%, demonstrating satisfactory discretization levels of the PM in both domains (Electromagnetic and CFD).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMSG | Permanent Magnet Synchronous Generator |
| WECS | Wind Energy Conversion Systems |
| GWEC | Global Wind Energy Council |
| DFIG | Double Field Induction Generator |
| PM | Permanent Magnet |
| NdFeB | Neodymium-Iron-Boron |
| FEM | Finite Element Method |
| FEA | Finite Element Analysis |
| CFD | Computational Fluid Dynamics |
| FVM | Finite Volume Method |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| EMC | Equivalent Magnetic Circuit |
| PNM | Permeance Network Model |
| LPTN | Lumped Thermal Network |
| THD | Total Harmonic Distortion |
| IPMSGM | Internal Permanent Magnet Synchronous Motor |
| SPMSG | Surface Permanent Magnet Synchronous Generator |
| HSPMM | High-Speed Permanent Magnet Machines |
| LSPMSM | Line Start Permanent Magnet Synchronous Motor |
| STT | Shear Stress Transport |
References
- Abo-Khalil, A.G.; Alobaid, M. Optimized Control for PMSG Wind Turbine Systems under Unbalanced and Distorted Grid Voltage Scenarios. Sustainability 2023, 15, 9552. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-Power Wind Energy Conversion Systems: State-of-the-Art and Emerging Technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Fang, H.; Wang, D. A Novel Design Method of Permanent Magnet Synchronous Generator from Perspective of Permanent Magnet Material Saving. IEEE Trans. Energy Convers. 2017, 32, 48–54. [Google Scholar] [CrossRef]
- Wu, D.; Seo, G.-S.; Xu, L.; Su, C.; Kocewiak, L.; Sun, Y.; Qin, Z. Grid Integration of Offshore Wind Power: Standards, Control, Power Quality and Transmission. IEEE Open J. Power Electron. 2024, 5, 583–604. [Google Scholar] [CrossRef]
- Faiz, J.; Mazaheri-Tehrani, E. Demagnetization Modeling and Fault Diagnosing Techniques in Permanent Magnet Machines Under Stationary and Nonstationary Conditions: An Overview. IEEE Trans. Ind. Appl. 2017, 53, 2772–2785. [Google Scholar] [CrossRef]
- Hernandez, C.; Lara, J.; Arjona, M.A.; Martinez, F.J.; Moron, J.E.; Escarela-Perez, R.; Sykulski, J. Electromagnetic Optimal Design of a PMSG Considering Three Objectives and Using NSGA-III. IEEE Trans. Magn. 2022, 58, 1–4. [Google Scholar] [CrossRef]
- Chen, J.; Nayar, C.V.; Xu, L. Design and Finite-Element Analysis of an Outer-Rotor Permanent-Magnet Generator for Directly Coupled Wind Turbines. IEEE Trans. Magn. 2000, 36, 3802–3809. [Google Scholar] [CrossRef]
- Duan, G.; Wang, H.; Guo, H.; Gu, G. Direct Drive Permanent Magnet Wind Generator Design and Electromagnetic Field Finite Element Analysis. IEEE Trans. Appl. Supercond. 2010, 20, 1883–1887. [Google Scholar] [CrossRef]
- Ibrayeva, A.; Eriksson, S. Dynamic Modeling of a Generator with Anisotropic Nonlinear Permanent Magnets in Finite Element Method Software. IEEE Trans. Magn. 2023, 59, 1–8. [Google Scholar] [CrossRef]
- Chan, T.-F.; Wang, W.; Lai, L.-L. Permanent-Magnet Synchronous Generator Supplying an Isolated Load. IEEE Trans. Magn. 2010, 46, 3353–3356. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Marignetti, F. The Demagnetization Phenomenon in PM Machines: Principles, Modeling, and Design Considerations. IEEE Access 2023, 11, 47750–47773. [Google Scholar] [CrossRef]
- Choi, G. Analysis and Experimental Verification of the Demagnetization Vulnerability in Various PM Synchronous Machine Configurations for an EV Application. Energies 2021, 14, 5447. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Bracken, E. Generalized Algorithm to Deal with Temperature-Dependent Demagnetization Curves of Permanent Magnets for FEA. IEEE Trans. Magn. 2021, 57, 1–6. [Google Scholar] [CrossRef]
- Zhou, P.; Lin, D.; Xiao, Y.; Lambert, N.; Rahman, M.A. Temperature-Dependent Demagnetization Model of Permanent Magnets for Finite Element Analysis. IEEE Trans. Magn. 2012, 48, 1031–1034. [Google Scholar] [CrossRef]
- Ruoho, S.; Dlala, E.; Arkkio, A. Comparison of Demagnetization Models for Finite-Element Analysis of Permanent-Magnet Synchronous Machines. IEEE Trans. Magn. 2007, 43, 3964–3968. [Google Scholar] [CrossRef]
- Hamidizadeh, S.; Alatawneh, N.; Chromik, R.R.; Lowther, D.A. Comparison of Different Demagnetization Models of Permanent Magnet in Machines for Electric Vehicle Application. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, P.; Wang, M.; Liu, Y.; Fu, Z.; Sui, Y. Demagnetization and Permanent-Magnet Minimization Analyses of Less-Rare-Earth Interior Permanent-Magnet Synchronous Machines Used for Electric Vehicles. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Attestog, S.; Van Khang, H.; Robbersmyr, K.G. Modelling Demagnetized Permanent Magnet Synchronous Generators Using Permeance Network Model with Variable Flux Sources. In Proceedings of the 2019 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG), Paris, France, 15–19 July 2019; pp. 1–4. [Google Scholar]
- Zhang, Y.; McLoone, S.; Cao, W. Electromagnetic Loss Modeling and Demagnetization Analysis for High Speed Permanent Magnet Machine. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Wu, S.; Wu, S.; Zhao, W.; Cui, S. Demagnetization Research on PMs in the Halbach Magnetized Pulsed Alternator. CES Trans. Electr. Mach. Syst. 2019, 3, 170–177. [Google Scholar] [CrossRef]
- Baranski, M.; Szelag, W.; Lyskawinski, W. Experimental and Simulation Studies of Partial Demagnetization Process of Permanent Magnets in Electric Motors. IEEE Trans. Energy Convers. 2021, 36, 3137–3145. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and Modern Approaches for Thermal Analysis of Electrical Machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Zhu, Z.-Q.; Liang, D. Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures. Energies 2022, 15, 8189. [Google Scholar] [CrossRef]
- Staton, D.A.; Cavagnino, A. Convection Heat Transfer and Flow Calculations Suitable for Electric Machines Thermal Models. IEEE Trans. Ind. Electron. 2008, 55, 3509–3516. [Google Scholar] [CrossRef]
- Boglietti, A.; Carpaneto, E.; Cossale, M.; Vaschetto, S. Stator-Winding Thermal Models for Short-Time Thermal Transients: Definition and Validation. IEEE Trans. Ind. Electron. 2016, 63, 2713–2721. [Google Scholar] [CrossRef]
- Feng, J.; Liang, D.; Zhu, Z.Q.; Guo, S.; Li, Y.; Zhao, A. Improved Low-Order Thermal Model for Critical Temperature Estimation of PMSM. IEEE Trans. Energy Convers. 2022, 37, 413–423. [Google Scholar] [CrossRef]
- Mezani, S.; Takorabet, N.; Laporte, B. A Combined Electromagnetic and Thermal Analysis of Induction Motors. IEEE Trans. Magn. 2005, 41, 1572–1575. [Google Scholar] [CrossRef]
- Yeo, H.-K.; Park, H.-J.; Seo, J.-M.; Ro, J.-S.; Jung, H.-K. Coupled Electromagnetic-Thermal Analysis of a Surface-Mounted Permanent-Magnet Motor with Overhang Structure. In Proceedings of the 2016 IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 13–16 November 2016. [Google Scholar]
- Kasprzak, M.; Jiang, J.W.; Bilgin, B.; Emadi, A. Thermal Analysis of a Three-Phase 24/16 Switched Reluctance Machine Used in HEVs. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Shi, Y.; Wang, J.; Wang, B. Transient 3-D Lumped Parameter and 3-D FE Thermal Models of a PMASynRM Under Fault Conditions with Asymmetric Temperature Distribution. IEEE Trans. Ind. Electron. 2021, 68, 4623–4633. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, B.; Qu, R.; Li, D.; Li, J.; Huo, Y. Comparative Thermal Analysis of IPMSMs with Integral-Slot Distributed-Winding (ISDW) and Fractional-Slot Concentrated-Winding (FSCW) for Electric Vehicle Application. IEEE Trans. Ind. Appl. 2019, 55, 3577–3588. [Google Scholar] [CrossRef]
- Qi, J.; Hua, W.; Zhang, H. Thermal Analysis of Modular-Spoke-Type Permanent-Magnet Machines Based on Thermal Network and FEA Method. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Bastos, J.P.; Cabreira, M.F.R.R.; Sadowski, N.; Arruda, S.R.; Nau, S.L. A Thermal Analysis of Induction Motors Using a Weak Coupled Modeling. IEEE Trans. Magn. 1997, 33, 1714–1717. [Google Scholar] [CrossRef]
- Lundmark, S.T.; Grunditz, E.A.; Thiringer, T.; Andreasson, A.; Bergqvist, A.; Orbay, R.; Jansson, E. Heat Transfer Coefficients in a Coupled 3-D Model of a Liquid-Cooled IPM Traction Motor Compared with Measurements. IEEE Trans. Ind. Appl. 2021, 57, 4805–4814. [Google Scholar] [CrossRef]
- Gai, Y.; Kimiabeigi, M.; Chuan Chong, Y.; Widmer, J.D.; Deng, X.; Popescu, M.; Goss, J.; Staton, D.A.; Steven, A. Cooling of Automotive Traction Motors: Schemes, Examples, and Computation Methods. IEEE Trans. Ind. Electron. 2019, 66, 1681–1692. [Google Scholar] [CrossRef]
- Huang, C.; Xiong, L.; Hu, L.; Gong, Y. Thermal Design and Analysis of Oil-Spray-Cooled In-Wheel Motor Using a Two-Phase Computational Fluid Dynamics Method. World Electr. Veh. J. 2023, 14, 184. [Google Scholar] [CrossRef]
- Gebauer, M.; Blejchař, T.; Brzobohatý, T.; Nevřela, M. Conjugate Heat Transfer Model for an Induction Motor and Its Adequate FEM Model. Symmetry 2023, 15, 1294. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, J.; Chen, P.; Li, Z. Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load. Energies 2018, 11, 2024. [Google Scholar] [CrossRef]
- Chari, M.V.K.; Salon, S.J. Numerical Methods in Electromagnetism; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Hameyer, K.; Belmans, R. Numerical Modelling and Design of Electrical Machines and Devices; WIT Press: Southampton, UK, 1999. [Google Scholar]
- Ansys Inc. Ansys Maxwell User’s Guide 2023 R2; Ansys: Canonsburg, PA, USA, 2023. [Google Scholar]
- Lin, D.; Zhou, P.; Fu, W.N.; Badics, Z.; Cendes, Z.J. A Dynamic Core Loss Model for Soft Ferromagnetic and Power Ferrite Materials in Transient Finite Element Analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
- Fu, X.; Lin, M.; Yu, H.; Hao, L.; Xu, D.; Jin, P.; Zou, J. Calculation and Analysis of Iron Loss in Homopolar Inductor Alternator. IEEE Trans. Magn. 2012, 48, 3466–3469. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.; Lei, G.; Zhu, J. Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network. Magnetism 2023, 3, 327–342. [Google Scholar] [CrossRef]
- Su, W.-M.; Mao, S.-H.; Wang, P.-J. Estimation of the Core Losses of Induction Machines Based on the Corrected Epstein Test Method. IEEE Trans. Magn. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Wang, P.; Liu, L.; Xu, Q.; Che, S.; Zhang, L.; Du, S.; Zhang, H.; Sun, H. Loss Calculation and Thermal Analysis of Ultra-High Speed Permanent Magnet Motor. Heliyon 2022, 8, e11350. [Google Scholar] [CrossRef]
- Oh, S.Y.; Cho, S.-Y.; Han, J.-H.; Lee, H.J.; Ryu, G.-H.; Kang, D.; Lee, J. Design of IPMSM Rotor Shape for Magnet Eddy-Current Loss Reduction. IEEE Trans. Magn. 2014, 50, 841–844. [Google Scholar] [CrossRef]
- Kim, B.-C.; Lee, J.-H.; Kang, D.-W. A Study on the Effect of Eddy Current Loss and Demagnetization Characteristics of Magnet Division. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Kral, C.; Sprangers, R.; Waarma, J.; Haumer, A.; Winter, O.; Lomonova, E. Modeling Demagnetization Effects in Permanent Magnet Synchronous Machines. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Bianchi, N. Electrical Machine Analysis Using Finite Elements; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-21929-5. [Google Scholar]
- Ansys Inc. Ansys Fluent Theory Guide, Release 2023 R2; Ansys: Canonsburg, PA, USA, 2023. [Google Scholar]
- Guo, C.; Long, L.; Wu, Y.; Xu, K.; Ye, H. Electromagnetic-Thermal Coupling Analysis of a Permanent-Magnet in-Wheel Motor with Cooling Channels in the Deepened Stator Slots. Case Stud. Therm. Eng. 2022, 35, 102158. [Google Scholar] [CrossRef]
- Melka, B.; Smolka, J.; Hetmanczyk, J.; Bulinski, Z.; Makiela, D.; Ryfa, A. Experimentally Validated Numerical Model of Thermal and Flow Processes within the Permanent Magnet Brushless Direct Current Motor. Int. J. Therm. Sci. 2018, 130, 406–415. [Google Scholar] [CrossRef]
- Arbab, N.; Wang, W.; Lin, C.; Hearron, J.; Fahimi, B. Thermal Modeling and Analysis of a Double-Stator Switched Reluctance Motor. IEEE Trans. Energy Convers. 2015, 30, 1209–1217. [Google Scholar] [CrossRef]
- Ahmed Abdelrahman, S.; Bilgin, B. Computationally Efficient Surrogate-Based Magneto-Fluid-Thermal Numerical Coupling Approach for a Water-Cooled IPM Traction Motor. IEEE Access 2022, 10, 83692–83704. [Google Scholar] [CrossRef]



| Part Name | Value |
|---|---|
| Rated output power | 900 W |
| Rated voltage | 220 V |
| Number of phases | 3 |
| Rated frequency | 60 Hz |
| Rated speed | 900 rpm |
| Load type | Infinite Bus |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Axial length | 148 mm | Stacking factor | 0.97 |
| Air gap | 0.6 mm | Conductors per slot | 58 |
| Number of slots | 24 | Internal diameter rotor | 32 mm |
| Number of poles | 8 | External diameter rotor | 77.08 mm |
| Internal diameter stator | 78.2 mm | Magnet width | 19.25 mm |
| External diameter stator | 150.7 mm | Magnet thickness | 6.55 mm |
| Parameter | Value |
|---|---|
| Residual induction () | 1.21 T |
| Coercivity () | −907 kA/m |
| BHmax | 283 kJ/m3 |
| Temp. coeff. of (20–80 °C) | −0.12%/°C |
| Temp. coeff. of (20–80 °C) | −0.62%/°C |
| Curie temperature () | 310 °C |
| Conductivity | 555,556 S/m |
| Components | Material | Density [kg/m3] | Specific Heat [J/kg/°C] | Thermal Conductivity [W/m∙°C] |
|---|---|---|---|---|
| Housing and end caps | Aluminum alloy | 2719 | 871 | 202.4 |
| Stator and rotor | M22-26G | 8030 | 502.48 | |
| Winding | Copper | 8978 | 381 | 387.6 |
| Slot insulation | Insulation | 700 | 2310 | 0.22 |
| PMs | NdFeB-N35 | 7449.8 | 460.548 | 6.7409 |
| Air gap, end windings, and enclosure | Air | Incompressible ideal law | 1006.43 | 0.0242 |
| Shaft | Steel | 8030 | 502.48 | 16.27 |
| Rotor nonmagnetic filler | Epoxy | 1200 | 1500 | 0.22 |
| Region | Number of Cells | Min. Orthogonal Quality |
|---|---|---|
| Stator | 1,492,904 | 0.5000 |
| Rotor | 2,292,503 | 0.5000 |
| Windings | 99,073 | 0.5071 |
| PM | 196,999 | 0.5042 |
| Air gap 1 | 3,833,264 | 0.5008 |
| Air gap 2 | 3,936,312 | 0.3848 |
| Air end windings | 70,9307 | 0.3017 |
| Air ventilation holes | 17,044 | 0.5688 |
| Shaft | 15,568 | 0.5111 |
| End caps and bearings | 51,701 | 0.5000 |
| Housing | 46,802 | 0.5484 |
| Insulation slots | 740,335 | 0.4922 |
| Enclosure | 159,641 | 0.4769 |
| Rotor nonmagnetic filler | 154,445 | 0.5000 |
| Losses (W) | Case 1 | Case 2 |
|---|---|---|
| Stator Hysteresis | 12.200 | 12.1863 |
| Stator Eddy Current | 3.1010 | 3.0396 |
| Stator Excess | 0.2209 | 0.2187 |
| Rotor Hysteresis | 0.2175 | 0.2268 |
| Rotor Eddy Current | 0.3878 | 0.3962 |
| Rotor Excess | 0.0238 | 0.0250 |
| Winding | 71.2103 | 68.3012 |
| PM Eddy Current | 0.4014 | 0.3000 |
| Total PMSG Loss | 87.7623 | 84.6938 |
| Components | Case 2 | ||
|---|---|---|---|
| Min (°C) | Max (°C) | Avg (°C) | |
| Winding | 74.7115 | 74.8093 | 74.7474 |
| Stator | 72.8220 | 74.0731 | 73.5120 |
| Rotor | 73.3997 | 74.2963 | 74.0520 |
| PM | 73.5435 | 74.2955 | 74.0635 |
| Shaft | 61.4201 | 74.2725 | 71.1520 |
| Air gap | 73.6005 | 74.2930 | 74.0013 |
| Epoxy | 73.5573 | 74.2939 | 74.0647 |
| Slot insulation | 73.1188 | 74.7759 | 74.2116 |
| Enclosure | 26.8499 | 72.2899 | 27.9229 |
| Air-front | 59.3990 | 74.7901 | 73.0421 |
| Air-rear | 45.2815 | 74.8075 | 72.6266 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morón-Monreal, J.E.; Martinez-Rios, F.J.; Hernandez, C.; Arjona, M.A. Analysis of the Demagnetization of a PMSG Using a Coupled Electromagnetic–Fluid–Thermal Numerical Model. Energies 2025, 18, 6149. https://doi.org/10.3390/en18236149
Morón-Monreal JE, Martinez-Rios FJ, Hernandez C, Arjona MA. Analysis of the Demagnetization of a PMSG Using a Coupled Electromagnetic–Fluid–Thermal Numerical Model. Energies. 2025; 18(23):6149. https://doi.org/10.3390/en18236149
Chicago/Turabian StyleMorón-Monreal, Jorge E., Francisco J. Martinez-Rios, Concepcion Hernandez, and Marco A. Arjona. 2025. "Analysis of the Demagnetization of a PMSG Using a Coupled Electromagnetic–Fluid–Thermal Numerical Model" Energies 18, no. 23: 6149. https://doi.org/10.3390/en18236149
APA StyleMorón-Monreal, J. E., Martinez-Rios, F. J., Hernandez, C., & Arjona, M. A. (2025). Analysis of the Demagnetization of a PMSG Using a Coupled Electromagnetic–Fluid–Thermal Numerical Model. Energies, 18(23), 6149. https://doi.org/10.3390/en18236149






