Modelling of Insulation Thermal Ageing: Historical Evolution from Fundamental Chemistry Towards Becoming an Electrical Machine Design Tool

Abstract

Electrical insulation systems (EISs) are the principal reliability bottleneck of modern electrical machines (EMs). Among the many stresses acting on insulation, thermal stress is the most pervasive because it accelerates chemical reactions that progressively erode dielectric and mechanical integrity, ultimately dictating service life. As EMs migrate into compact, high-power-density platforms—automotive, aerospace, and industrial drives—designers need lifetime models that are not merely explanatory but actionable, linking operating temperatures and missions to quantified ageing and risk. This review article traces the evolution of thermal-ageing modelling from fundamental chemistry to a practical design tool. The historical empirical lineage of Arrhenius equation, Arrhenius–Dakin model, and Montsinger model is first revisited, clarifying their assumptions, parameter definitions, and the construction of thermal endurance curves. A discussion then follows on extensions that address deviations from first-order kinetics and demonstrate how variable temperature histories can be incorporated through cumulative damage formulations suitable for duty-cycle analysis. Since models are required to be anchored in data, accelerated thermal ageing (ATA) practices on representative specimens are outlined, alongside a description of the Weibull post-processing for deriving percentile lifetimes aligned with design targets. Building upon these foundations, the Physics-of-Failure (PoF) approach is introduced as a reliability-oriented design (ROD) methodology, in which validated lifetime models guide material selection and geometry optimisation while supporting prognostics and health management during operation. The emerging trend towards a hybrid PoF–AI approach is also discussed, which integrates artificial intelligence to identify nonlinear degradation patterns and drifting parameter relationships beyond the reach of empirical models, with physical constraints ensuring that predictions remain consistent with known ageing mechanisms. Such integration enables the learning process to adapt to operational variability and coupled stress effects, thereby improving both the accuracy and physical interpretability of lifetime estimation. The review aims to provide a concise view of models, tests, and workflows that convert thermal-ageing knowledge into robust, design-time decisions. By linking empirical and physics-based insights with modern data-driven learning, these developments support proactive maintenance, sustainable asset management, and extended operational lifetimes for next-generation EMs.

1. Introduction

Electrical insulation materials are designed to provide effective galvanic separation between conductors operating at different voltage potentials. This separation is essential for maintaining the safety and efficiency of electrical systems, thereby safeguarding both personnel and equipment from electrical hazards. During service, however, insulation materials are subjected to a variety of stresses that cause ageing [1,2]. In the context of wound components, ageing is commonly defined as the gradual loss of the material’s capacity to perform its intended electrical and mechanical functions [3]. Among the stresses that drive the ageing process, thermal stress stands out as one of the most weighty for being a major contributor to long-term degradation through wear and tear—a critical concern in the reliability and longevity of electrical insulation systems (EISs). The effects of thermal stress are primarily attributed to temperature-activated chemical reactions, which progressively compromise the insulation’s structural and dielectric integrity [4].

In high-voltage power systems, the vulnerability of insulation materials to thermal stress is pronounced, as prolonged exposure to elevated temperatures is common under continuous operation and high electrical loads [5,6]. The onset of accelerated thermal ageing mechanisms begins when operating temperatures exceed the rated thermal threshold (insulation thermal class, e.g., Class H, 180 °C). In the early stages, the degradation effects may be subtle and partially reversible, including minor reductions in mechanical strength or slight alterations in dielectric behaviour [7,8]. However, with sustained exposure to high temperatures, the rate of chemical reactions increases significantly [9]. As a result, insulation materials become susceptible to oxidation, cross-linking, and chain scission, during which oxygen molecules react with the polymer chains, initiating irreversible chemical changes [10,11].

In advanced stages of thermal ageing, degradation accelerates and manifests in physical damage due to the breakdown of molecular bonds [12]. The subsequent development of cracks and voids compromises structural cohesion and distorts the local electric field, creating conditions conducive to partial discharge (PD) inception and further propagation of deterioration [13]. Such detrimental phenomena not only lead to delamination and loss of tensile strength but also increase the risk of electrical tracking and internal arcing [14,15]. Additionally, mechanical vibrations may exacerbate insulation detachment, exposing live conductors and promoting short-circuit events, particularly in environments subject to dynamic mechanical loads [16,17]. Ultimately, insulation materials become brittle and may disintegrate, at which point catastrophic failure becomes likely and irreversible [18,19].

The implications of thermal ageing extend beyond the degradation of individual insulation components [20]. The repercussions of their incremental weakening can trigger cascading failures capable of undermining the EIS as a whole, compromising the functional reliability of the device in which it is embedded [21]. Once the integrity of the EIS is eroded, the host unit—such as a rotating electrical machine (EM) or a power converter/inverter—becomes susceptible to failure, and the ensuing disruptions can propagate upward, jeopardising the resilience of large-scale equipment and even the stability of entire power networks. In extreme circumstances, a chain of failure events can result in significant repair costs, unexpected system outages, safety risks to operating personnel, and substantial disruptions in industrial or critical service operations. These outcomes are particularly problematic in transport applications and grid-level energy infrastructure, where system reliability is paramount [22,23].

Given the intricate interplay between chemical reactions, thermally induced mechanical fatigue, and dielectric breakdown phenomena, a predictive understanding of insulation behaviour under thermal stress becomes essential. Consequently, the interdependence and coupling of the degradation mechanisms necessitate the development of quantitative thermal-ageing models capable of forecasting insulation performance over the EM’s operational lifetime. The availability of validated models is crucial not only for predicting the remaining service life of insulation at both component and system levels but also for supporting proactive maintenance and asset management [24]. Such models enable condition-based strategies that help avoid premature replacement or unexpected failure, aligning with the principles of reliability-oriented design (ROD). They also assist engineers in making informed choices regarding material selection, thermal class assignment, and operational margins during the design phase. Furthermore, as EMs are increasingly integrated into high-demand and thermally constrained environments, accurate insulation lifetime modelling is becoming essential for ensuring availability, functional safety, and cost-effective operation across the machine lifecycle [25].

Over the decades, several models have been developed to simulate insulation degradation under thermal stress, including physical, thermodynamic, and empirical (or phenomenological) models [26]. Physical models aim to capture underlying physical and chemical mechanisms at the microscale, such as reaction kinetics, material diffusion, and localised effects of coupled stresses, in order to represent the fundamental pathways through which degradation evolves over time [27]. Thermodynamic models, by contrast, characterise ageing in terms of entropy generation and irreversible energy dissipation, providing a macroscopic framework that links degradation to the broader principles of energy balance and disorder [28]. However, both model types are often highly complex, require extensive material parameterisation and involve significant computational resources, thereby introducing serious challenges when integrated in EM design. As such, only the Eyring thermodynamic model is presented and the process of simplifying it into an equivalent empirical model.

On the other hand, empirical models have gained widespread utilisation due to their practicality, greater computational efficiency and relatively straightforward implementation [29]. They rely on experimental data to establish correlations between thermal stress and material ageing, often focusing on measurable parameters such as temperature, time, and degradation indicators (i.e., diagnostic markers) [30]. While they are constrained to the specific conditions under which the data were collected, they remain highly relevant for industrial applications due to their scalability, ease of calibration, and ability to provide actionable lifetime predictions [6]. Despite longstanding and extensive empirical research, a unified and quantitatively validated framework that connects molecular-level degradation chemistry with statistical lifetime modelling and design integration remains absent in the literature.

This work aims to provide a concise outline of classical empirical models, with emphasis on their theoretical foundations and historical development. The discussion is organised in order to trace the evolution of the empirical models from fundamental chemical principles, as described by the Arrhenius equation, to their present role as a design tool for predicting insulation lifetime within the ROD of modern EMs. Particular attention is given to the Arrhenius–Dakin and the Montsinger lifetime models, and the Eyring lifetime model for higher-order reaction kinetics, along with the empirical interpretation of transition-state theory. The scope also extends to thermal ageing conditions under variable temperature profiles, the Physics-of-Failure (PoF) approach as part of the ROD, accelerated thermal ageing (ATA) tests on representative specimens, and the use of Weibull statistical analysis to post-process datasets.

In addition, the work highlights notable emerging trends in insulation lifetime modelling. With the increasing availability of experimental and field data, advanced approaches such as artificial intelligence (AI) can be employed to identify complex, nonlinear relationships between thermal stress and insulation degradation. These data-driven techniques complement the traditional PoF approach and provide opportunities for more accurate and generalisable lifetime predictions. Parallel efforts are also directed towards the development of adaptive or dynamic lifetime models for fluid-based EISs, which can capture changes in fluid chemistry and operating conditions over the service life of EMs in transport applications. Collectively, the identified trends are expected to enhance predictive accuracy and broaden the applicability of lifetime models under increasingly demanding operating environments.

2. Arrhenius Equation

In 1887, the Swedish chemist Svante Arrhenius unified the concepts of the Maxwell–Boltzmann distribution law of molecular energies and the activation energy of chemical reactions into one of the most impactful relationships in physical chemistry, known as the “Arrhenius equation” [31]. Since its introduction, this equation has served as a cornerstone for understanding the temperature dependence of chemical reaction rates across various scientific disciplines and has played a pivotal role in advancing research on the thermal ageing of EISs.

The mathematical representation of the Arrhenius equation is expressed by (1) [32,33,34]:

$$k=A\prime \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{E_a}{k_B\theta }}\right)$$

(1)

where $k$ is the rate constant of the chemical reaction that reflects the probability of a chemical reaction occurring per unit of time, the pre-exponential factor $A\prime$ is the frequency factor that describes the frequency of collisions between reacting molecules that have the proper orientation to result in a reaction ($A\prime$ is sometimes called the Arrhenius factor/constant and is calculated in per unit of time also), $E_a$ is the activation energy (thermal energy) in Joules per molecule or sometimes in electronvolts (eV) per molecule, required for the chemical reaction to occur, $k_B$ is the Boltzmann constant ($1.3806\times {10}^{-23} {\mathrm{J}\mathrm{K}}^{-1}$), and $\theta$ is the operating absolute (i.e., thermodynamic) temperature in Kelvin. The constant $k_B$ can be replaced by the universal gas constant $R$ ($8.3145 {\mathrm{J}\mathrm{K}}^{-1}{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) when shifting from a microscopic (per molecule) to a macroscopic (per mole) scale. In such a case, the activation energy is multiplied by Avogadro’s number $N_A$ ($6.0221\times {10}^{23} {\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) in order to be expressed on a per-mole basis. Equation (1) captures the interplay of key factors in chemical reactions. It succinctly shows that as the temperature rises, the chemical reaction rate constant increases exponentially. The temperature dependence can be further investigated from both chemical and mathematical perspectives.

From a chemical standpoint, the Arrhenius method underscores the importance of activation energy, which represents the minimum amount of energy required for reacting molecules to stretch, bend, and ultimately break their bonds. When the kinetic energy of colliding molecules exceeds this energy threshold, the likelihood of a successful chemical reaction increases considerably. Conversely, if the molecules possess insufficient kinetic energy due to slower motion, they simply rebound off each other without initiating a reaction. While the chemical analysis provides valuable insight into the molecular interactions driving chemical reaction kinetics, a detailed mathematical examination reveals the quantitative relationship between temperature and chemical reaction rates. Specifically, a smaller ratio of activation energy to Boltzmann constant $E_a/k_B\theta$, resulting from lower activation energy coupled with higher operating temperatures, yields a dramatically faster chemical reaction, as indicated by the negative sign in the equation’s exponent. Hence, it is evident that the exponential relationship highlights the profound impact of temperature changes on chemical reaction rates; even a modest increase in temperature can dramatically accelerate the reaction by enabling a large proportion of molecules to surpass the activation energy threshold.

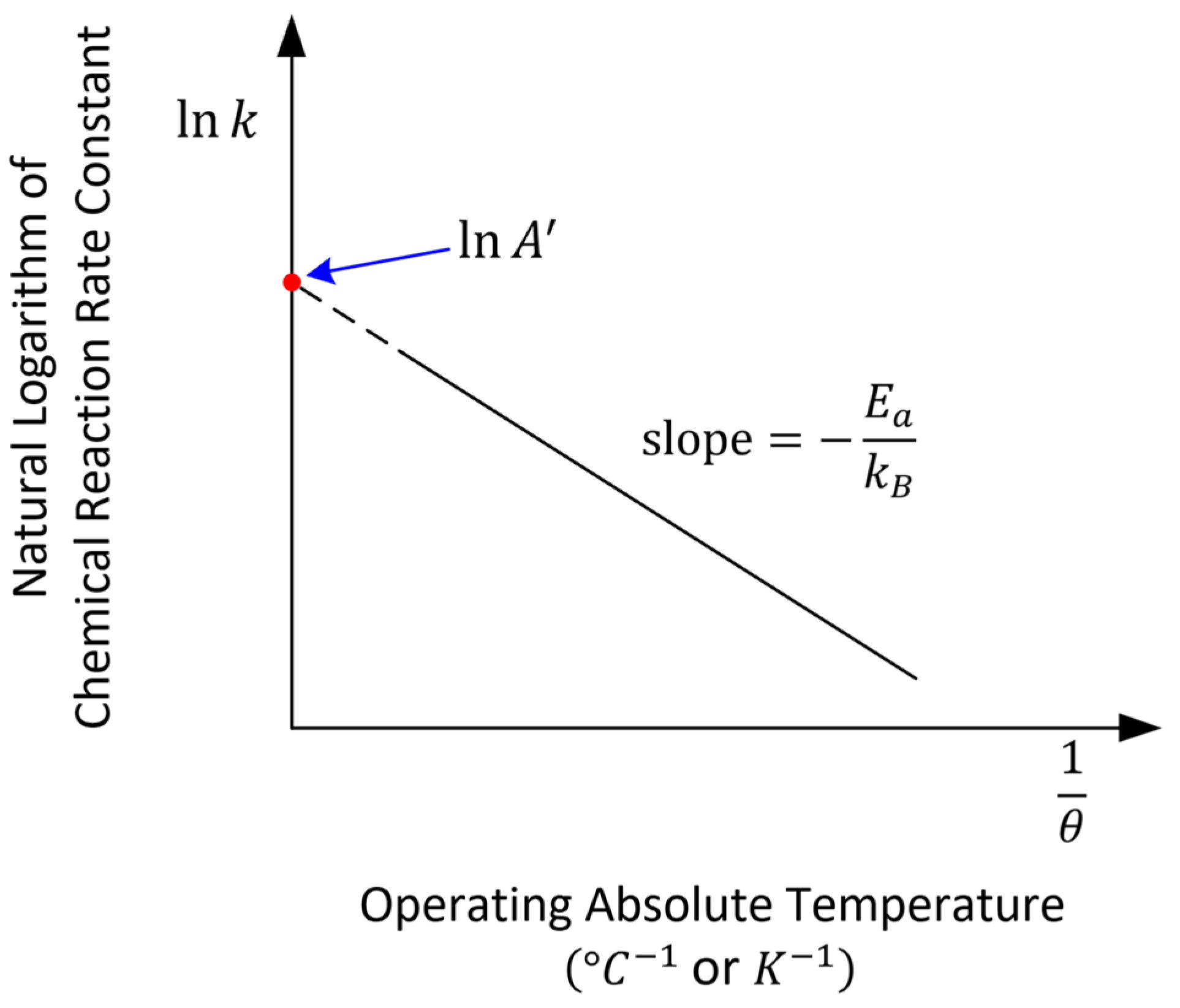
In practice, the logarithmic form (2) of the Arrhenius Equation (1) is typically used, which transforms the exponential relationship into a linear relationship [35,36,37] and is more convenient for data analysis purposes:

$$\ln k=-{\displaystyle \frac{E_a}{k_B\theta }}+\ln A\prime$$

(2)

Plotting the natural logarithm of the chemical reaction rate constant ($\ln k$) against the reciprocal of the operating absolute temperature ($1/\theta$) produces a straight line [30,38] with a slope equal to $-E_a/k_B$ [34,39], and the y-intercept is $\ln A\prime$ when $\theta$ tends to infinity. This graphical representation, shown in Figure 1 and commonly referred to as the Arrhenius plot or thermal endurance curve, facilitates determining the activation energy $E_a$ and the frequency factor $A\prime$ from experimental $k$-values obtained at various temperatures.

For a given end-of-life criterion (i.e., tensile strength reduction, loss of dielectric strength, breakdown resistance, PD inception, etc.), the thermal endurance plot allows for the prediction of the insulation’s remaining lifetime for any operating temperature within the model’s specified limits.

To better ground this relationship quantitatively, representative $E_a$ values of typical insulation materials used in EMs are summarised in

Table 1. Representative activation energy ranges of typical insulation materials used in EMs.

Insulation Material/System	Typical Application	$\mathbf{Indicative} {\mathit{E}}_{\mathit{a}}$ Values $(\mathbf{k}\mathbf{J}{ \mathbf{m}\mathbf{o}\mathbf{l}}^{-1}$)
Polyimide (PI)	High-temperature wire enamel, film insulation	180–240 [40,41]
Epoxy resin	Encapsulation, potting, and impregnation of windings	110–170 [42,43]
Polyester-imide	Magnet wire overcoat, varnishes	150–200 [44]
Polyurethane (PU)	Flexible coating, impregnating varnishes	80–120 [45]
Polyethylene terephthalate (PET)	Laminates, slot liners, films	90–130 [46]
Polyether–ether–ketone (PEEK)	Advanced high-temperature winding insulation	200–250 [47]
Polyamide–imide (PAI)	Dual-coat enamels, high-temperature magnet wire	160–210 [40]
Polyethylene (PE)	Cable insulation, low-voltage systems	80–100 [48]
Phenolic resin (Phenol–formaldehyde)	Slot liners, bonding resins	100–140 [49]
Silicone (PDMS-based elastomers)	High-flexibility coatings and potting compounds	90–130 [50]

. These values define the temperature sensitivity of the degradation process. In most practical applications, $E_a$ is expressed in kilojoules per mole of reacting material, since the Arrhenius Equation (1) for bulk systems employs the universal gas constant $R$. It reflects the average thermal energy required for one mole of reacting molecular units to reach the transition state. An increase in $E_a$ results in a sharp decrease in the reaction rate constant $k$ and a flatter Arrhenius slope, corresponding to enhanced thermal stability and extended service life at a given operating temperature.

The reported values in Table 1 vary with material formulation, filler content, curing conditions, and the specific thermal ageing protocols used in each study. For instance, polyimide (PI) and polyether–ether–ketone (PEEK) materials are characterised by relatively high $E_a$ values and, therefore, exhibit greater resistance to thermally activated degradation and slower ageing under identical thermal stress than other insulation materials, owing to the larger energy barrier that must be overcome by the reacting molecules to initiate degradation.

Having established the quantitative significance of activation energy, it is important to examine the underlying kinetic assumptions upon which the Arrhenius equation is based. The relationship describes insulation thermal ageing as a first-order chemical reaction, in which the degradation rate is assumed to depend linearly on the concentration of one reactant species undergoing a dominant reaction [51]. Within this framework, while the first-order approximation is clearly brought out, the simplification of a single reactant and a single effective reaction dominating the overall kinetics constitutes an engineering abstraction, rather than a complete representation of polymer degradation chemistry. Nevertheless, it affords a tractable description that captures the dominant degradation mechanism within the experimentally investigated temperature range.

In practice, however, multiple degradation mechanisms, often concurrent or overlapping, may be activated either simultaneously or sequentially under different thermal environments [52]. While each mechanism is characterised by its own $E_a$, the overall degradation process within the first-order approximation is governed by an effective $E_a$ that is treated as constant over the applicable temperature range. A linear Arrhenius relationship, therefore, indicates the dominance of a single mechanism with a temperature-independent effective $E_a$, whereas curvature or change in the slope reveal transitions between mechanisms and a change in temperature-dependent effective $E_a$.

Despite certain inherent simplifications, the Arrhenius equation remains a valid and widely used approach for estimating insulation lifetime and conducting accelerated-ageing analysis. Since its introduction in the late nineteenth century, it continues to serve as the most established equation for relating temperature to chemical reaction kinetics through the concept of activation energy. Its principle is substantiated by the numerous modifications that exist in the literature and have been proposed over the years [8], each developed to extend its applicability to a broader spectrum of materials and operating conditions. Notable examples include the Dakin’s modification and the reduction of the Eyring model, both of which are discussed in the following sections.

3. Arrhenius–Dakin and Montsinger Models

The transition from the fundamental Arrhenius equation to later empirical lifetime models evolved through progressive refinement. As the polymeric composition of EISs became increasingly complex and were experimentally aged under elevated temperatures, it became evident that the theoretical Arrhenius relationship required empirical adjustment to more accurately fit measured trends obtained from ATA tests. This refinement preserved the exponential temperature dependence but introduced calibration constants and empirical coefficients that linked lifetime predictions directly to observable end-of-life criteria. Subsequent developments in the early twentieth century were shaped by systematic experimental studies of insulation, leading to the classical works of Steinmetz, Lamme, Montsinger, and Dakin, which collectively established the modern foundations of thermal ageing modelling.

In 1913, Steinmetz and Lamme provided one of the initial systematic examinations of the relationship between insulation life and temperature, building on the growing interest in understanding insulation durability under thermal stress [53]. Their research, focusing on commonly used Class A insulation materials such as paper, cotton, natural oil resins, and gums, indicated that these materials exhibit very long life when ultimate temperatures do not exceed approximately 90 °C, retain comparatively long life around 100 °C, but deteriorate rapidly at higher temperatures, with mechanical weakening becoming severe near 125 °C. They further suggested that intermittent cooling during thermal cycling could mitigate the effects of ageing by allowing partial recovery of mechanical properties. However, notwithstanding these observations, their work primarily relied on qualitative assessments and empirical judgement, leaving the underlying degradation mechanisms due to thermal stress largely unexplored.

By the late 1920s, a deeper understanding of insulation thermal ageing began to emerge, culminating in Montsinger’s seminal publication in 1930 [54]. His experiments focused on varnished cambric insulation (yellow and black, about 0.012 inches thick), tested under thermal stress in both air and oil—materials and conditions representative of power transformer applications at the time. Montsinger challenged the notion of a temperature threshold, directly contrasting with Steinmetz’s and Lamme’s earlier views. Arguing that insulation thermal ageing is a continuous, temperature-dependent process governed by mechanical deterioration, he dismissed electrical strength as a reliable indicator of insulation health. Consistent with this view, his conclusion was corroborated by observations that the tensile strength of varnished cambric materials subjected to thermal stress declined faster in oil compared to air, independent of electrical breakdown tests. Drawing on nine years of experimental data, he established that the ageing rate is roughly doubled for every 8 °C increase in temperature and halved for an equivalent decrease (later generalised as the “ten-degree rule”). Montsinger’s rule was therefore empirical in nature and grounded in mechanical deterioration, treating lifetime reduction as a direct function of thermal exposure and providing a pragmatic tool for determining safe transformer loading levels.

While Montsinger’s rule offered a valuable practical framework, it lacked a physical-chemical basis and considered ageing primarily as an empirical outcome of thermal stress. Dakin’s later work provided the missing theoretical foundation for insulation lifetime prediction by relating thermal ageing to chemical reactions at the molecular level. In 1948, he demonstrated that thermal degradation arises from the chemical reaction process captured by the Arrhenius equation, having recognised that each insulation material possesses unique activation energy determining its ageing rate [3]. His investigations were carried out on cellulosic materials such as manila paper, pressboard, and cloth sealed in oil, as well as organic varnishes widely used in power transformers, cables, and capacitor insulation systems at the time. Dakin’s interpretation introduced a reaction-rate perspective, in which insulation ageing is modelled as a sequence of temperature-dependent oxidation, depolymerisation, and plasticiser loss reactions. By linking the observed deterioration of mechanical and electrical properties to underlying chemical kinetics, he established the first unified, quantitative framework for analysing thermal ageing across different insulation materials.

To clarify how the early formulations evolved from qualitative observation to quantitative modelling, a concise comparison of the main assumptions and conceptual bases of Steinmetz and Lamme, Montsinger, and Dakin is summarised in

Table 2. Comparative overview of early insulation thermal ageing formulations.

Researcher(s) & Year	Core Assumptions	Formulation	Testing Basis	Primary Focus	Main Limitations
Steinmetz & Lamme (1913) [53]	Long life below $~$90 °C; comparatively long life around 100 °C; rapid mechanical deterioration above $~$125 °C.	Qualitative temperature–life assessment based on observed durability limits (no kinetic formulation).	Empirical observations and early tests on Class A materials.	Identification of practical operating temperature limits and qualitative understanding of insulation durability under thermal stress.	Absence of reaction kinetics; reliance on qualitative judgement with no experimental validation of a temperature threshold.
Montsinger (1930) [54]	Ageing proceeds continuously with time and accelerates with increasing temperature (no threshold).	Lifetime halves for a fixed temperature interval.	Long-term tests on varnished cambric (air vs. oil).	Empirical lifetime prediction and practical rules for permissible transformer overloading	Assumes a fixed temperature–life slope for all materials; lacks activation-energy concept; not material-specific.
Dakin (1948) [3]	Ageing governed by temperature–activated chemical reactions; each material characterised by its own activation energy.	Arrhenius rate equation; lifetime derived from reaction kinetics.	Controlled ATA on cellulose, varnishes; analysis of material-specific activation energies.	Material-specific modelling and physical interpretation of ageing rate.	Assumes constant mechanism; accuracy reduced when multiple degradation modes coexist.

.

Where Montsinger relied on observed empirical trends, Dakin’s model quantified them through chemical-rate theory and activation energy. In doing so, he replaced the approximate “ten-degree rule” with a physically grounded exponential relationship of the Arrhenius law, yielding more accurate and material-specific life predictions. Building upon this foundation, Dakin developed an empirical model that treats thermal ageing as a single degradation process and is formulated with a quantifiable relationship between insulation lifetime and thermal stress, as given in (3). In this model, electrical, mechanical and environmental ageing are assumed to have no real impact during normal operation [55]:

$$L\left(\theta \right)=A \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{B}{\theta }}\right)$$

(3)

where $L$, as a function of operating absolute temperature $\theta$, represents the expected lifetime of insulation material (in hours, h) and is inversely proportional to the chemical reaction rate constant $k$ of the Arrhenius Equation (1) through a constant $C$ [56], i.e., $L\left(\theta \right)=C/k$. The constant $C$ serves as an empirical scaling factor introduced to align theoretical degradation kinetics with observed lifetime data. It reflects the specific failure criterion used in testing and ensures that the predicted lifetime corresponds to the experimentally defined end-of-life condition for a given EIS. Similarly, the pre-exponential factor $A$ is related to the reciprocal of its counterpart $A\prime$ through the same constant and is equal to the ratio $C/A\prime$, and the coefficient $B$ is equal to the ratio of activation energy to Boltzmann constant $E_a/k_B$.

In 1981, Simoni presented an extended version of the Dakin model to account for the lifetime $L_0$ at the reference absolute temperature ${\theta }_0$, which is the temperature that corresponds to the thermal class of insulation [57]. The study focused on polymeric EISs, including thermoplastics such as polyethylene and ethylene-propylene rubber, thermosetting resins such as epoxy and polyurethane, and composite laminates such as Nomex–Mylar–Nomex, all of which were widely applied in rotating EMs, power cables, capacitors, and related high-voltage equipment. Assuming that the operating absolute temperature $\theta$ in (3) is equal to the reference absolute temperature ${\theta }_0$, the reference lifetime $L_0$ is derived, as shown in (4):

$$L_0=A \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{B}{{\theta }_0}}\right)$$

(4)

Dividing (3) by (4) and then rearranging to solve for $L\left(\theta \right)$, or solving (4) for $A$ and then substituting into (3), allows for determining Simoni’s version of the Dakin model, as expressed in (5):

$$L\left(\theta \right)=L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left({\displaystyle \frac{1}{{\theta }_0}}-{\displaystyle \frac{1}{\theta }}\right)\right]$$

(5)

Equation (5) is widely known as the Arrhenius–Dakin model. This functional representation of the insulation lifetime can be further simplified into a compact form as in (6) [57]:

$$L\left(\theta \right)=L_0 \mathrm{e}\mathrm{x}\mathrm{p} \left[-B\Delta \left({\displaystyle \frac{1}{\theta }}\right)\right]$$

(6)

$$\Delta \left({\displaystyle \frac{1}{\theta }}\right)={\displaystyle \frac{1}{{\theta }_0}}-{\displaystyle \frac{1}{\theta }}$$

(7)

From $\Delta \left(1/\theta \right)$, the difference between the reciprocal of the reference absolute temperature and the reciprocal of the operating absolute temperature, given by (7), it follows that the Arrhenius–Dakin model predicts an exponential reduction in EIS lifetime when the operating absolute temperature exceeds the reference absolute value, ultimately accelerating the onset of failure. In analogy with the linearised Arrhenius Equation (2), the logarithmic form of (6), which also conforms to the Arrhenius law, can be written as in (8):

$$\ln L\left(\theta \right)=-B\Delta \left({\displaystyle \frac{1}{\theta }}\right)+\ln L_0$$

(8)

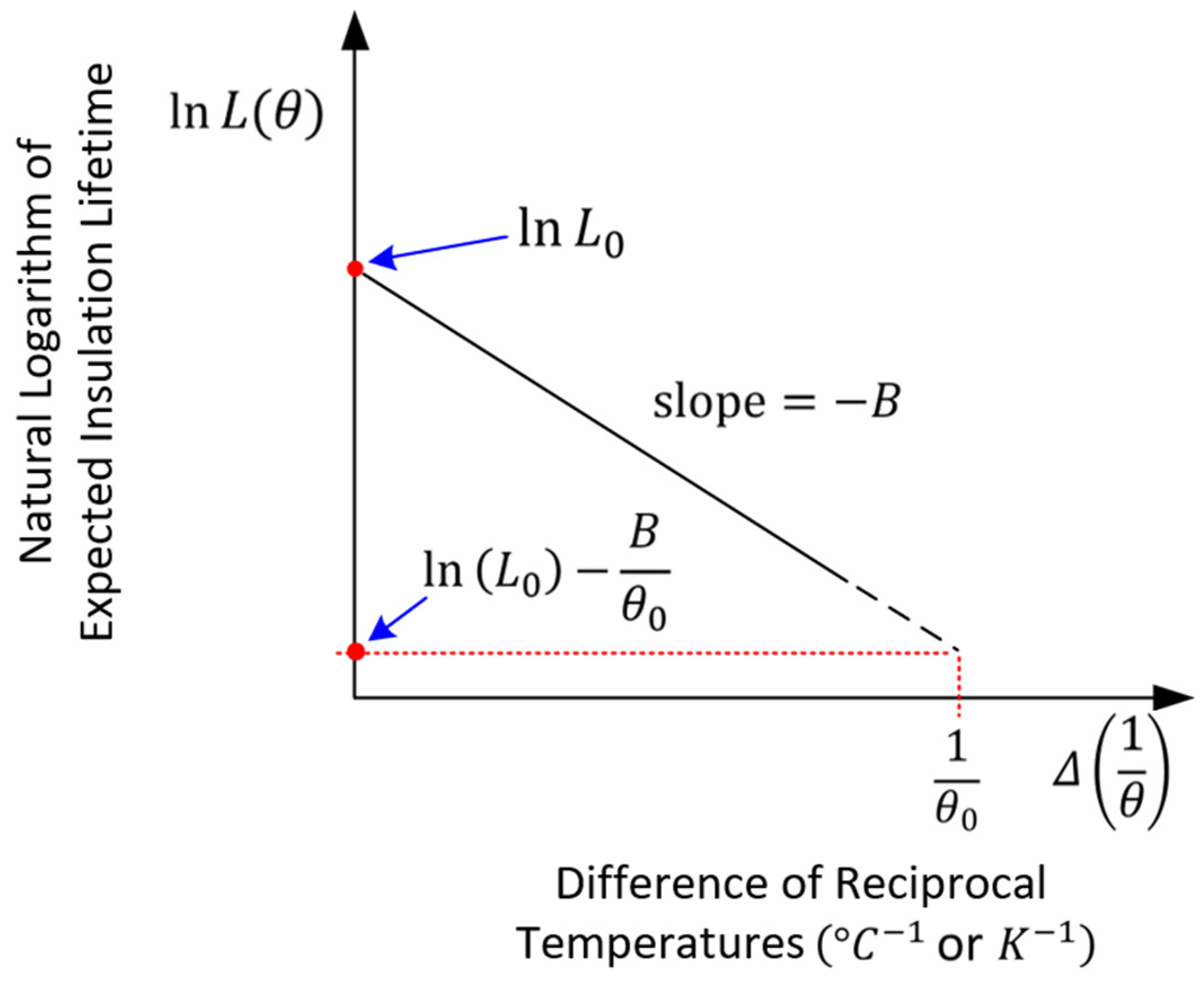
Similarly, a thermal endurance curve can be derived from (8) by plotting the natural logarithm of the insulation lifetime $\ln L\left(\theta \right)$ against the difference in reciprocal temperatures $\Delta \left(1/\theta \right)$ [39,56,57,58] as depicted in Figure 2:

The relationship between $\ln L\left(\theta \right)$ and $\Delta \left(1/\theta \right)$ exhibits straight-line behaviour. In practice, this is typically represented on a semi-logarithmic graph, where the vertical axis is the lifetime displayed on a logarithmic scale and the horizontal axis is the difference in reciprocal temperatures represented linearly. The slope of the line is given by the coefficient $-B$ [59], while the intercept on the y-axis is equal to $\ln L_0$. The parameter $A$ can then be obtained by substituting the values of the parameters $B$ and $L_0$ into Equation (4) and rearranging accordingly. Hence, the material-dependent constants $A$, $B$ and $L_0$ are explicitly determined, each carrying a distinct physical meaning tied to the degradation kinetics of the EIS.

The thermal endurance curve illustrated in Figure 2 is defined for $\theta \ge {\theta }_0$, where the horizontal axis spans between two limiting cases. When the operating absolute temperature $\theta$ is equal to the reference absolute temperature ${\theta }_0$, $\Delta \left(1/\theta \right)=0$, the difference is zero, meaning that the lifetime is equal to $L_0$, which corresponds to the reference lifetime (i.e., rated thermal endurance) of the EIS. As the operating absolute temperature tends to infinity ($\theta \to \infty$), $\Delta \left(1/\theta \right)$ progressively increases, approaching an upper bound of $1/{\theta }_0$. In this extreme condition, the lifetime decreases linearly and its logarithm reduces to $\ln \left(L_0\right)-B/{\theta }_0$, indicating the minimum extrapolated lifetime predicted by the Arrhenius–Dakin model. By examining the limiting cases, it is made clear that deviations in temperature from the reference point are directly linked to quantifiable reductions in lifetime, thereby providing a simple yet effective way to characterise accelerated thermal ageing.

An important extension of the Arrhenius–Dakin model is the formulation of the Montsinger model. In this context, the temperature difference between the operating condition and the reference point is defined as $\Delta \theta =\theta -{\theta }_0$. By equating this difference to the halving interval in Celsius (HIC)—defined as the temperature increase that leads to a 50% reduction in EIS lifetime, i.e., $L\left({\theta }_0+\Delta \theta \right)=L\left({\theta }_0+HIC\right)=L_0/2$—and substituting into (5), the expression simplifies to give (9):

$$B={\displaystyle \frac{{\theta }_0\theta \ln 2}{HIC}}$$

(9)

Substituting again into (5) for $B$, allows for determining the Montsinger model, given by (10):

$$L\left(\theta \right)=L_0{2}^{{\displaystyle \frac{{\theta }_0-\theta }{HIC}}}$$

(10)

Equation (10) represents a power-law model with base two. The frequently cited “ten-degree rule” arises as a specific case when HIC is fixed at 10 °C (or 10 K). Generally, HIC may be assigned other values, typically within the range of 8–15 °C [60], depending on the insulation material. In line with the Arrhenius equation and the Arrhenius–Dakin model, the Montsinger model is constructed on the assumption of first-order kinetics, with degradation governed by a single dominant chemical reaction and a constant activation energy. Possible threshold effects, arising from thermal ageing not occurring below certain temperatures, are neglected, while the potential contribution of concurrent secondary chemical reactions is similarly overlooked [55]. Consequently, the apparent linearity in Arrhenius coordinates is not intrinsic to the model itself but rather a direct outcome of the assumptions made, thus rendering the model highly sensitive to the quality of lifetime data obtained from ATA tests.

Even small deviations or experimental scatter in ATA test results can produce disproportionately large errors in the fitted slope ($-B$) and the y-intercept ($\ln L_0$), leading to significant uncertainty when extrapolating lifetime predictions towards service temperatures. The assumption of perfect linearity magnifies this sensitivity, particularly when only three temperature points are used to define the endurance line. Any variations arising from material heterogeneity, specimen-to-specimen differences, or failure criterion selection propagate into the estimated activation energy and the thermal index (i.e., the maximum temperature at which the EIS can endure 20,000 h, about 2.28 years, of continuous operation with acceptable degradation of its critical properties [17]). To mitigate such effects, statistical post-processing, most notably through Weibull statistical analysis, is required to distinguish intrinsic material behaviour from random data scatter and derive percentile-based lifetime estimations that capture the statistical variability more accurately in the experimental data.

4. Higher-Order Chemical Reaction

The validity of the Arrhenius–Dakin and Montsinger models, as well as any other Arrhenius-based models, becomes limited when higher-order chemical reactions govern the thermal ageing process [61]. A change in reaction order often indicates that a different degradation mechanism has become dominant under different operating conditions. By definition, the order of a chemical reaction specifies how the overall reaction rate depends on the concentration(s) of the reactant(s); for higher-order kinetics, the dependence is nonlinear and reflects the increased complexity of the contributing degradation mechanisms.

Since the empirical models discussed in the previous section rely on a first-order assumption, their ability to provide accurate lifetime predictions is compromised when EISs exhibit higher-order kinetics. At very high temperatures, deviations from first-order behaviour occur because degradation rates no longer scale linearly with the concentration of the reacting material, signalling the emergence of alternative degradation pathways that prevail under the new operating conditions. For instance, at around 290 °C, organic EISs undergo a glass transition, which substantially alters the dominant degradation mechanism—from primarily oxidative chain scission at lower temperatures to a combination of cross-linking between polymer chains, accelerated oxidation due to higher diffusion of oxygen, volatilisation of low-molecular-weight fragments, and structural damage arising from increased molecular mobility. In such cases, alternative formulations such as the Eyring model [62], expressed in (11), can be employed in place of the Arrhenius–Dakin and Montsinger models [63,64].

$$L\left(\theta \right)={\displaystyle \frac{C_E{h}_p}{k_B\theta }} \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{\Delta G}{k_B\theta }}\right)$$

(11)

The Eyring model, derived from transition-state theory developed in the 1930s, represents a major advancement in the analysis of temperature-dependent ageing process by introducing a more comprehensive set of parameters. In this formulation, $C_E$ is a material constant, $h_p$ is Planck’s constant ($6.6261\times {10}^{-34} \mathrm{J}\mathrm{s}$), $\theta$ is the operating absolute temperature, $k_B$ is Boltzmann’s constant ($1.3806\times {10}^{-23} {\mathrm{J}\mathrm{K}}^{-1}$), and $\Delta G$ is the Gibbs free energy of activation. The model explicitly accounts for the contributions of activation enthalpy $\Delta H$ and activation entropy $\Delta S$ through the relationship $\Delta G=\Delta H-\theta \Delta S$ [63]. The enthalpy term denotes the thermal energy (heat) required for molecules to surmount the energy barrier, whereas the entropy term quantifies the degree of molecular disorder associated with the transition state.

Due to the adaptability of the thermodynamic parameters $\Delta H$ and $\Delta S$ to higher-order kinetic transitions, the Eyring model can capture possible variations in effective activation energy across temperature ranges, while also improving the accuracy of lifetime extrapolations into both low- and high-temperature regimes on the Arrhenius plot. In addition, it inherently accommodates nonlinear reaction-rate dependence without requiring explicit parameter changes, whereas Arrhenius-based models typically necessitate separate modifications for each reaction order, which limits their versatility.

For EISs subjected to variable temperature profiles, fluctuations in thermal operating conditions may trigger competition between degradation mechanisms (e.g., oxidation vs. thermal decomposition), accompanied by shifts in the apparent chemical reaction order. To address this, the Eyring model is well-suited to capture changes in degradation mechanisms, owing to its thermodynamic formulation that accounts for variations in enthalpy and entropy. Nevertheless, despite its theoretical advantages, the model has seen limited practical adoption. Implementation is hindered by the need for an accurate determination of $C_E$, $\Delta H$ and $\Delta S$ for the selected insulation material, as well as by the higher data requirements and computational complexity. Moreover, the inherent complexity of EISs in EMs reduces the model’s practicality for ROD. Thus, Arrhenius-based models are explicitly recommended by international standards [65].

Although classical empirical models remain the preferred choice, the relationship between the Eyring model and the Arrhenius law is of particular interest, as it demonstrates that the Eyring formulation can be mathematically reduced to an Arrhenius-like expression. This reduction provides a conceptual bridge between a thermodynamically rigorous framework and the Arrhenius-based models endorsed by standards. The link is established by substituting the enthalpic and entropic contributions of the Gibbs free energy of activation into (11) to expand the numerator of the exponential index as shown in (12):

$$L\left(\theta \right)={\displaystyle \frac{C_E{h}_p}{k_B\theta }} \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{\Delta H-\theta \Delta S}{k_B\theta }}\right)$$

(12)

Equation (12) can be decomposed as in (13):

$$L\left(\theta \right)={\displaystyle \frac{C_E{h}_p}{k_B\theta }} \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{\Delta H}{k_B\theta }}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\Delta S}{k_B}}\right)$$

(13)

Grouping the temperature-independent terms into a constant $A$ gives (14):

$$A={\displaystyle \frac{C_E{h}_p}{k_B}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\Delta S}{k_B}}\right)$$

(14)

Then, replacing the grouped terms in (13) with the constant $A$ defined in (14) reduces the Eyring model to the Arrhenius-like form expressed in (15):

$$L\left(\theta \right)=A{ \theta }^{-1} \mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{\Delta H}{k_B\theta }}\right)$$

(15)

The activation enthalpy $\Delta H$ plays a role analogous to the activation energy $E_a$ in the Dakin model (3), while the term $1/\theta$ introduces a weak temperature dependence within the pre-exponential factor. The Eyring model can be interpreted as a physically derived Arrhenius-like model that incorporates both enthalpic and entropic effects, with the entropic contribution absorbed into the constant $A$.

Table 3. Comparison of applicability between Arrhenius and Eyring models for insulation ageing analysis.

Aspect	Arrhenius-Based Models	Eyring Model
Underlying principle	Empirical relationship between reaction rate (or lifetime) and absolute temperature based on a single activation energy.	Thermodynamically derived rate theory incorporating both enthalpic (ΔH) and entropic (ΔS) contributions to the activation process.
Typical kinetic order	Assumes first-order degradation kinetics with a single dominant reaction mechanism.	Accommodates higher-order, competing, or coupled reactions that cause deviations from first-order behaviour.
Assumptions	Activation energy is constant across the examined temperature range; one degradation pathway dominates.	Activation enthalpy and entropy vary with temperature; multiple mechanisms or relaxation processes coexist.
Temperature range of validity	Moderate temperature range below secondary transitions (e.g., oxidation onset, glass transition, volatilisation).	Extended range encompassing high-temperature regimes, near-transition conditions, or when nonlinear Arrhenius behaviour is observed.
Physical interpretation	Describes degradation rate or lifetime through a purely energetic barrier.	Captures both energetic and configurational effects, allowing thermodynamic insight into molecular mobility and disorder.
Experimental requirements	Requires limited ageing data (typically 3–4 temperature points) for parameter estimation.	Requires extensive, high-resolution data to extract ΔH and ΔS with statistical confidence.
Model linearity	Produces a linear lifetime–temperature relationship in Arrhenius coordinates	Produces curvature or slope variation reflecting temperature-dependent kinetics or entropic effects.
Preferred use	Engineering design, qualification testing, and estimation of lifetime within declared thermal class ratings.	Research-level analysis, mechanistic studies, or advanced modelling under variable or extreme thermal conditions.
Limitations	Cannot describe nonlinear kinetics or multiple degradation pathways; assumes constant activation energy.	Increased complexity and parameter sensitivity; limited routine application in reliability-oriented design.
Interpretation in practice	Effective when degradation is dominated by a single thermal process and data scatter is minimal.	Necessary when lifetime data show curvature (“knee”) or strong deviations from linear Arrhenius behaviour due to competing mechanisms.

lists its advantage over purely empirical Arrhenius-based models, as it provides a deeper thermodynamic basis while still retaining the familiar exponential temperature dependence.

As discussed, while classical models based on the Arrhenius law provide a practical basis for insulation lifetime prediction under first-order kinetics, their validity diminishes when thermal ageing is governed by higher-order reactions. The Eyring model offers a thermodynamically grounded alternative by capturing enthalpic–entropic effects and variations in activation energy; however, its extensive data and parameter requirements restrict its routine application in ROD. Variable operating temperature conditions pose an additional challenge for classical models; the absence of standardised ATA protocols and the presence of transient, highly variable thermal stresses necessitate the use of cumulative damage formulations that translate time-dependent temperature history into loss-of-life estimates suitable for mission-profile evaluation.

5. Variable Operating Temperature

ATA tests are conventionally performed under constant operating temperature conditions, where experimental data such as time-to-failure or diagnostic markers (e.g., insulation resistance (IR), insulation capacitance (IC), dielectric strength, dielectric dissipation factor ($\tan \delta$), PD inception voltage (PDIV)) are collected at fixed thermal loads. This practice reflects the absence of standardised protocols for conducting ATA tests under variable operating temperature conditions. In contrast, EISs in service rarely operate under steady thermal environments. Modern applications, particularly mobile platforms such as traction motors and electromechanical actuators (EMAs) in transportation, are instead characterised by fluctuating temperature profiles associated with mission-specific load cycles. Unlike continuous service scenarios dominated by constant thermal stress, insulation in temporary overload or intermittent duty cycles is exposed to transient and highly variable thermal stresses [34]. Such operational realities highlight the limitations of constant-temperature testing and emphasise the need for more advanced modelling strategies capable of addressing variable temperature profiles in order to achieve reliable lifetime prediction of EISs.

The classical Dakin–Arrhenius lifetime model (5) provides a robust description of insulation ageing under constant thermal stress but becomes inadequate when applied to EISs subjected to variable temperature profiles. Under service operating conditions, the insulation lifetime is no longer governed by a single fixed temperature; rather, it depends on the time-dependent temperature history $\theta \left(t\right)$. Therefore, lifetime prediction must be expressed as a composite function of $\theta \left(t\right)$, as shown in (16):

$$L\left(\theta \left(t\right)\right)=L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left({\displaystyle \frac{1}{{\theta }_0}}-{\displaystyle \frac{1}{\theta \left(t\right)}}\right)\right]$$

(16)

To extend the applicability of lifetime modelling under fluctuating thermal loads, the Miner cumulative damage law is commonly employed. In this approach, variable temperature profiles are discretised into infinitesimal time intervals $dt$, within which the temperature can be reasonably approximated as constant. For each of these intervals, the corresponding infinitesimal loss of life fraction is expressed as $dLF\left(\theta \left(t\right)\right)$. In the case of a generic variable temperature profile ${\theta }_j\left(t\right)$, assumed to be a continuous function of time with period $T$, the infinitesimal loss of life fraction $dLF\left({\theta }_j\left(t\right)\right)$ is given by (17):

$$dLF\left({\theta }_j\left(t\right)\right)={\displaystyle \frac{dt}{L\left({\theta }_j\left(t\right)\right)}}$$

(17)

The cumulative damage accumulated over a defined operating time interval [$t_1, t_2$] is then obtained by integrating the infinitesimal loss of life $dLF\left({\theta }_j\left(t\right)\right)$ over the corresponding time span. This leads to the expression for the cumulative loss of life fraction, as shown in (18):

$$LF{\left({\theta }_j\left(t\right)\right)}_{[\mathrm{t}1,\mathrm{t}2]}={\int }_{t_1}^{t_2}dLF\left({\theta }_j\left(t\right)\right)={\int }_{t_1}^{t_2}{\displaystyle \frac{dt}{L\left({\theta }_j\left(t\right)\right)}}$$

(18)

By substituting the generic variable temperature profile ${\theta }_j\left(t\right)$ into (16), and subsequently inserting the resulting expression into (18), the cumulative loss of life fraction is obtained as given by (19):

$$LF{\left({\theta }_j\left(t\right)\right)}_{[\mathrm{t}1,\mathrm{t}2]}={\int }_{t_1}^{t_2}{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_j\left(t\right)}\right)\right]}}$$

(19)

This framework provides a practical means of incorporating variable temperature effects into insulation lifetime models, thereby extending the applicability of Arrhenius-based models to mission-dependent operating conditions.

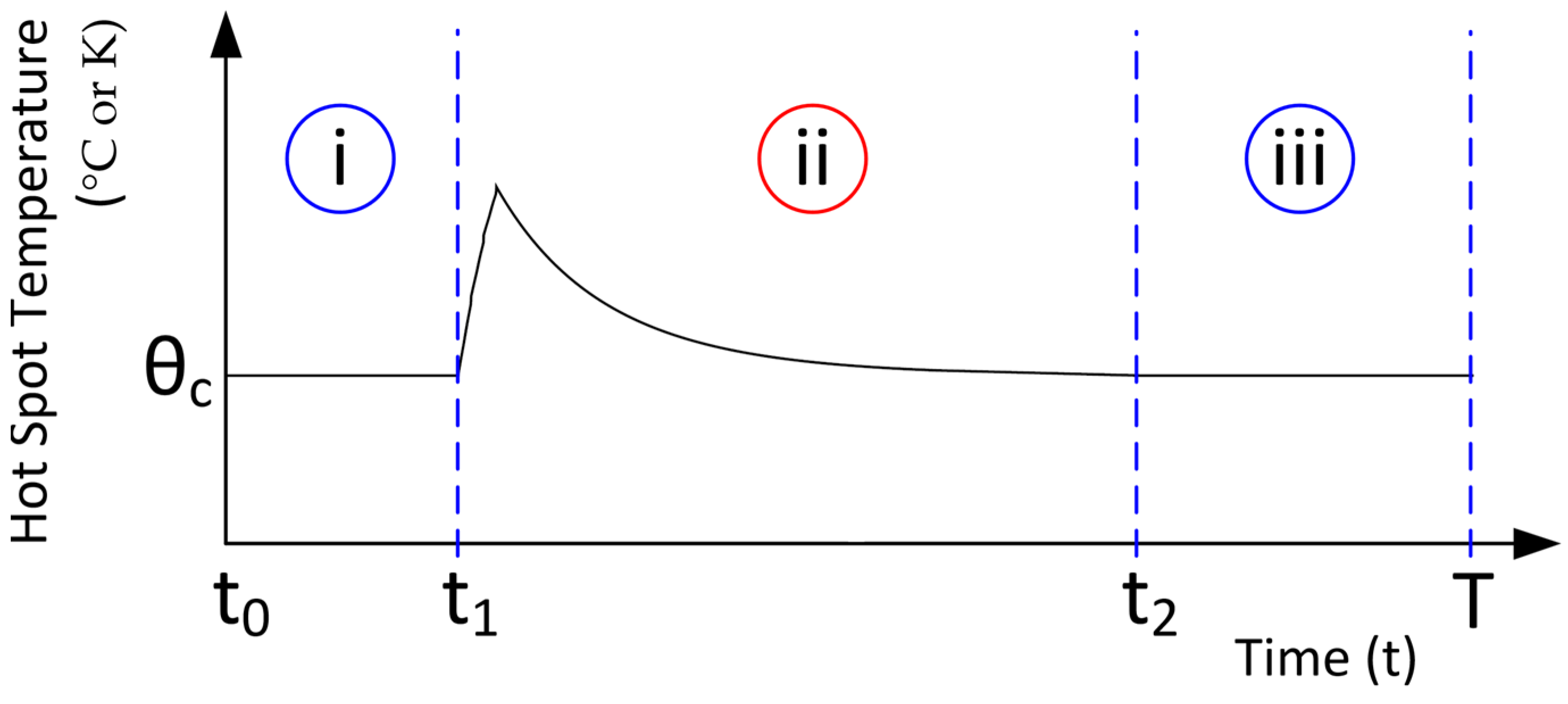
A cycle of temporary thermal overload is presented in Figure 3, where the winding hotspot temperature rises above a steady-state level for a limited interval [$t_1, t_2$]. Outside the overload interval, the temperature remains constant at ${\theta }_c$, and the cycle can be divided into three regimes: two segments at constant temperature ${\theta }_c$ (i and iii), and one segment of transient overload (ii) during which the temperature rises to its peak.

The depicted operating profile is representative of electric vehicle traction motor operation under mission-specific driving cycles, where short-term overloads caused by acceleration or hill climbing lead to rapid increases in winding temperature, followed by recovery towards the steady-state thermal equilibrium [67]. The cumulative loss of life fraction for one thermal cycle can therefore be estimated as the sum of ageing contributions from each regime. By setting ${\theta }_j\left(t\right)={\theta }_c$ in (19) for regimes (i) and (iii), and combining these with the expression from (19) applied to regime (ii), while adjusting the integration limits accordingly, the resulting equation is given by (20):

$$LF{\left({\theta }_j\left(t\right)\right)}_{cycle}={\int }_{t_0}^{t_1}{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_c}\right)\right]}}+{\int }_{t_1}^{t_2}{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_j\left(t\right)}\right)\right]}}+{\int }_{t_2}^T{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_c}\right)\right]}}$$

(20)

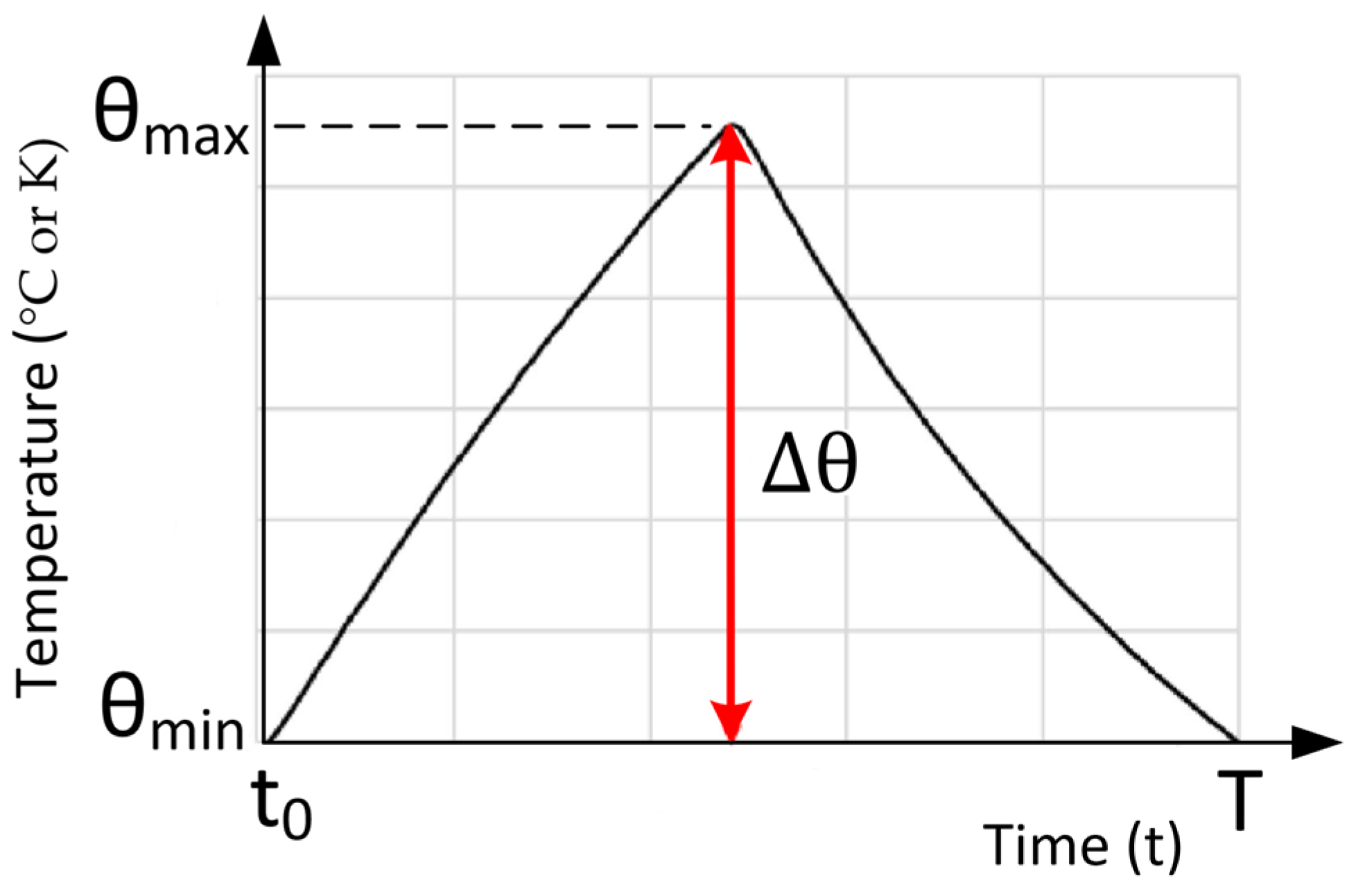
A variable temperature profile for EMs operating under intermittent service loads is illustrated in Figure 4. Unlike the temporary overload case in Figure 3, which reflects short-term excursions above a steady thermal level, intermittent service is characterised by continuous heating and cooling within each cycle.

This operating profile was reported in the study of short-duty-cycle aerospace motors, where insulation ageing was experimentally investigated under dynamic temperature conditions representative of EMAs for landing gear systems [68]. In this scenario, the winding hotspot temperature oscillates between ${\theta }_{min}$ and ${\theta }_{max}$ over the cycle duration $T$, with the amplitude of thermal excursions $\Delta \theta$ defined by the load pattern. Such a profile captures the cumulative effect of repeated thermal ramps, which impose additional ageing stresses compared to constant or single-overload conditions. The lifetime modelling is expressed in (21), where the infinitesimal loss of life fraction $dLF\left({\theta }_j\left(t\right)\right)$ is integrated across the entire thermal cycle to evaluate the periodic cumulative ageing damage:

$$LF{\left({\theta }_j\left(t\right)\right)}_{cycle}={\int }_{t_0}^T{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_j\left(t\right)}\right)\right]}}$$

(21)

Given that both temperature profiles exhibit periodicity and recur for $N$ identical cycles, the total lifetime of the EIS is given by (22):

$${L\left({\theta }_j\left(t\right)\right)}_{total}={\displaystyle \frac{T}{LF{\left({\theta }_j\left(t\right)\right)}_{cycle}}}$$

(22)

The treatment of variable operating temperatures establishes how time-dependent thermal profiles translate into cumulative loss of life and total lifetime, thereby extending Arrhenius-based models from constant operation to mission-driven operation.

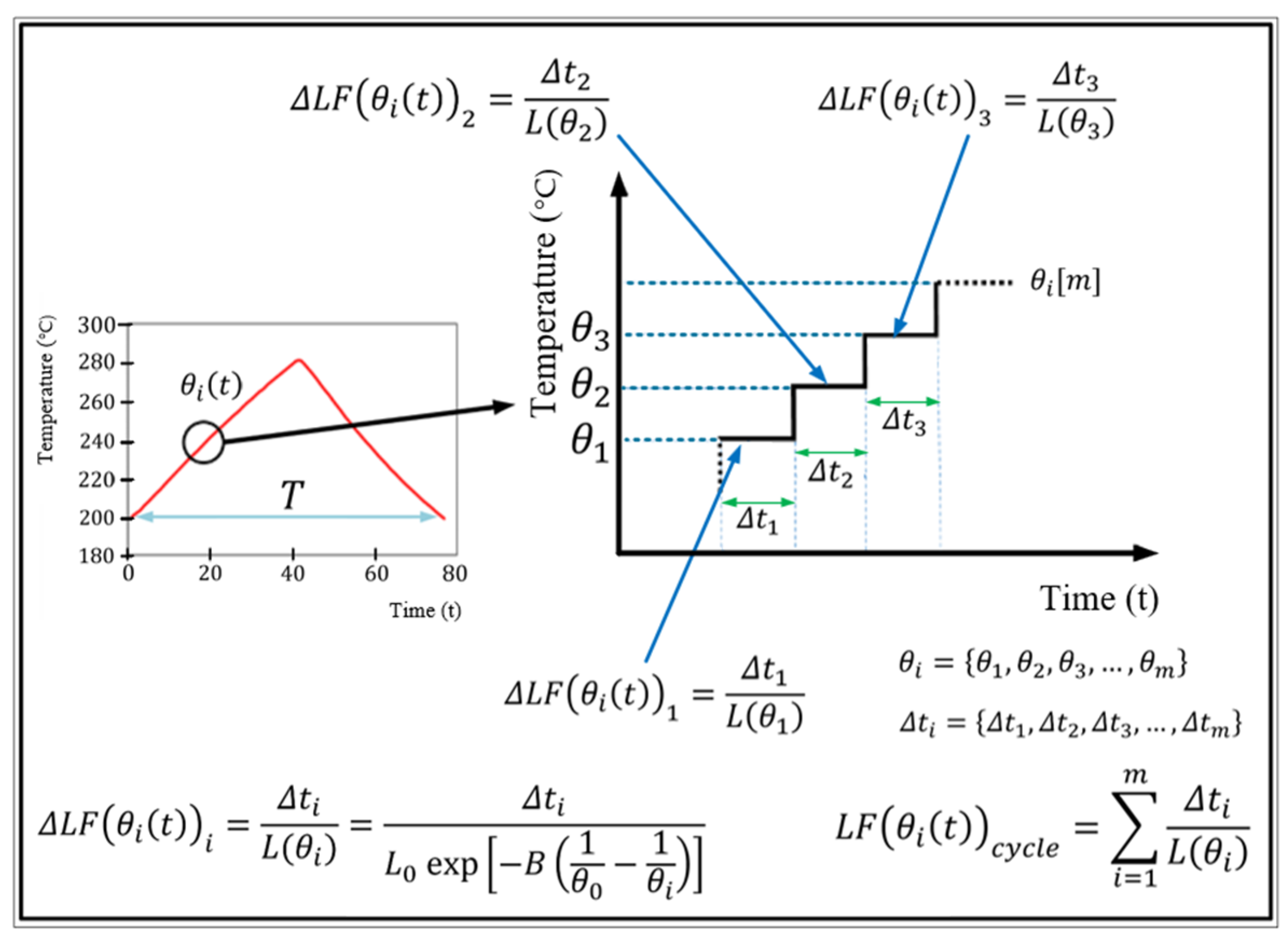
To illustrate the application of the Miner cumulative damage law under variable operating temperature conditions, the temperature profile ${\theta }_i\left(t\right)$ of a landing gear EMA spanning from 200 °C to 280 °C over a cycle duration of 77 s is represented in Figure 5. The cyclic temperature variation is discretised into $m$ isothermal segments (finite steps), where each $i$-th segment is defined by an instantaneous transient temperature ${\theta }_i$ (i.e., ${\theta }_i\left(t\right)={\theta }_i$), and its corresponding finite duration ${\Delta t}_i$. Figure 5 depicts part of the discretisation process, showing three representative temperature levels, ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$, along with their segment durations, ${\Delta t}_1$, ${\Delta t}_2$, and ${\Delta t}_3$.

The incremental loss of life fraction $\Delta LF{\left({\theta }_i\left(t\right)\right)}_i$ caused by thermal stress during a segment held at the constant temperature ${\theta }_i$ for the duration $\Delta t_i$ is expressed in (23):

$$\Delta LF{\left({\theta }_i\left(t\right)\right)}_i={\displaystyle \frac{{\Delta t}_i}{L\left({\theta }_i\right)}}$$

(23)

The piecewise lifetime $L\left({\theta }_i\right)$ of each segment has a constant value and can be predicted using the classical Dakin–Arrhenius lifetime model (5), which expands (23) into (24):

$$\Delta LF{\left({\theta }_i\left(t\right)\right)}_i={\displaystyle \frac{{\Delta t}_i}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_i}\right)\right]}}$$

(24)

It is important to note that the finite (discrete) time interval ${\Delta t}_i$ spent at a specific constant temperature ${\theta }_i$ carries the subscript $i$, since the durations of the isothermal segments can vary due to nonuniform sampling when the temperature rate varies resulting in irregular temperature ramps. However, for convenience, segments of equal duration are often adopted. Regardless of the sampling scheme, the cumulative loss of life fraction for a thermal cycle is obtained by summing over all segments as shown in (25):

$$LF{\left({\theta }_i\left(t\right)\right)}_{cycle}=\sum _{i=1}^m\Delta LF{\left({\theta }_i\left(t\right)\right)}_i=\sum _{i=1}^m{\displaystyle \frac{{\Delta t}_i}{L\left({\theta }_i\right)}}$$

(25)

Equation (25) represents the discrete form of the Miner law, which approximates the damage accumulated over a full duty cycle. An example of pseudocode outlining the step-by-step procedure used to compute the cumulative damage is given in Appendix A. To transition to the continuous form, the cycle is refined such that $\Delta t_i$ approaches zero ($\Delta t_i\to 0$). By invoking the Riemann sum formulation, the cumulative loss of life fraction given by (25) can be expressed as an integral in (26), (27):

$$LF{\left({\theta }_i\left(t\right)\right)}_{cycle}=\underset{\Delta t_i\to 0}{\lim }\sum _{i=1}^m{\displaystyle \frac{{\Delta t}_i}{L\left({\theta }_i\right)}}={\int }_0^T{\displaystyle \frac{dt}{L\left({\theta }_i\right(t\left)\right)}}$$

(26)

or equivalently, also using the Arrhenius–Dakin lifetime model (5),

$$LF{\left({\theta }_i\left(t\right)\right)}_{cycle}=\underset{\Delta t_i\to 0}{\mathit{lim}}\sum _{i=1}^m{\displaystyle \frac{{\Delta t}_i}{L\left({\theta }_i\right)}}={\int }_0^T{\displaystyle \frac{dt}{L_0 \mathrm{e}\mathrm{x}\mathrm{p}\left[-B\left(\frac{1}{{\theta }_0}-\frac{1}{{\theta }_i\left(t\right)}\right)\right]}}$$

(27)

The continuous form allows an instantaneous estimation of cumulative damage over a real duty cycle. During this transition, the finite time interval ${\Delta t}_i$ is replaced by the infinitesimal (differential) time element $dt$, representing the limit of ${\Delta t}_i$ as the partition width approaches zero. Consequently, the segment subscript $i$ is omitted in the continuous domain because each interval becomes infinitesimally small.

Differentiating Equation (26) with respect to time shown in (28) and rearranging (29) accordingly, gives the infinitesimal loss of life fraction $dLF\left({\theta }_i\left(t\right)\right)$ in (30).

$${\displaystyle \frac{d}{dt}}\left[LF{\left({\theta }_i\left(t\right)\right)}_{cycle}\right]={\displaystyle \frac{d}{dt}}\left[{\int }_0^T{\displaystyle \frac{dt}{L\left({\theta }_i\right(t\left)\right)}}\right]$$

(28)

$${\displaystyle \frac{dLF\left({\theta }_i\right(t\left)\right)}{dt}}={\displaystyle \frac{1}{L\left({\theta }_i\right(t\left)\right)}}$$

(29)

Rearranging differential expression (29) to get (30) corresponds to the earlier general formulation in (17). In (29) and (30), ${\theta }_i\left(t\right)$ denotes a specific variable temperature profile, while (17) applies to a generic variable temperature profile ${\theta }_j\left(t\right)$.

$$dLF({\theta }_i(t))={\displaystyle \frac{dt}{L\left({\theta }_i\right(t\left)\right)}}$$

(30)

The differential $dt$ can thus be regarded as the continuous counterpart of the finite time increment ${\Delta t}_i$. Conceptually, $dt$ represents the limiting case of ${\Delta t}_i$ as the time intervals become infinitesimally small, bridging the discrete and continuous formulations of the Miner cumulative damage law.

Yet, the analytical treatment of temperature alone cannot fully represent the multifactorial nature of insulation ageing. Variable thermal cycling also introduces significant thermo-mechanical stress (thermally induced mechanical stress) due to the mismatch in coefficients of thermal expansion between copper conductors and their surrounding materials, including the enamel coating, impregnation resins, slot liners, and steel laminations [69]. As the winding heats and cools, copper expands and contracts at a rate different from the surrounding materials, placing cyclic mechanical strain on the inter-turn enamel layers. This repeated mismatch leads to microcracking and delamination, ultimately accelerating enamel fatigue. Such thermo-mechanical degradation interacts synergistically with thermal oxidation and dielectric embrittlement, compounding the overall loss of insulation integrity. Within this context, multi-stress ageing must be considered, since electrical, mechanical, thermal, and environmental stressors interact in complex ways.

In practice, however, the dominant ageing factor concept is often adopted [38]; when thermal stress overwhelmingly dictates insulation ageing, secondary environmental factors can act as aggravating co-stressors. Moisture ingress promotes hydrolytic weakening of polyester-imide layers, vibration accelerates crack propagation along pre-existing defects, and surface contamination can intensify local electric-field enhancements conducive to partial discharge activity. Their influence may accelerate the overall degradation rate, particularly under high-humidity or mechanically dynamic conditions, where combined action amplifies the effects of thermal transient. It is therefore more accurate to regard secondary ageing factors as conditional accelerants that may become significant under adverse service conditions.

Having considered the role of secondary ageing factors, attention is now turned to thermo-mechanical stress, whose severity is strongly influenced by the thermal slew rate (thermal gradient), i.e., the rate of temperature change during heating and cooling. When winding hotspot temperatures fluctuate rapidly, steep spatial and temporal thermal gradients develop between copper conductors and surrounding insulation, intensifying the mismatch in thermal expansion. Recent accelerated ageing tests on enamelled coils exposed to cyclic profiles between 200 °C and 260 °C demonstrated that lifetime drastically decreases as the slew rate increases from 0.5 °C/s to 4 °C/s, as shown in Figure 6 [70]:

At the lowest thermal slew rate of 0.5 °C/s, specimens endured more than twice the service life compared with those subjected to 4 °C/s ramps, highlighting the role of rapid thermal transients in driving low-cycle thermo-mechanical fatigue of the polyamide-imide overcoat. The degree of deterioration was quantified by the time-to-failure at the 10th percentile of the Weibull lifetime distribution (B10), which corresponds to the time by which 10% of the tested specimens have failed (i.e., 10% cumulative probability). The relationship between thermal slew rate and insulation degradation rate is summarised in

Table 4. Effect of thermal slew rate on insulation lifetime degradation (adapted from [29]).

Thermal Slew Rate (°C/s)	Time to Failure (B10) (h)	Relative Degradation Rate (Compared to 0.5 °C/s)	Dominant Failure Mode	Main Degradation Mechanism
0.5	275	–	Delamination initiation after repeated cycles	Baseline thermo-mechanical fatigue
2.5	222	1.24 $\times$ faster degradation	Local enamel cracking and inter-turn stress accumulation	Accelerated strain energy accumulation per cycle
4	120	2.29 $\times$ faster degradation	Extensive microcracking, loss of adhesion, PD inception	Severe cyclic strain and thermal-mechanical coupling

.

The findings confirm that insulation degradation is not only governed by peak or average temperatures but also by the dynamics of thermal excursions, which impose additional mechanical hysteresis on the enamel and accelerate microcrack formation under mission-like load cycling.

Nonetheless, limiting the scope to thermal stress, the discussion now shifts to viewing insulation reliability from a physics perspective that informs the prototyping and qualification of EMs. The following section demonstrates how lifetime modelling grounded in PoF-consistent data from ATA tests can set design criteria, guide material and geometry choices, and, when combined with in-service monitoring data, enable condition-based maintenance for high-availability electrical drives.

6. Implementation of Physics of Failure into Reliability-Oriented Design and Health Management of Electrical Machines

The lifetime models discussed in the preceding sections describe how temperature governs insulation ageing through chemical reaction kinetics, providing the mathematical foundation for quantifying degradation under thermal stress. Their practical relevance, however, becomes evident only when they are embedded within an iterative workflow that applies the PoF approach to establish continuity between experimental ageing data and design optimisation, thereby positioning insulation lifetime prediction as a design-time reliability parameter within the development phase of EMs.

The PoF approach is a mechanistic reliability methodology that models the degradation of materials and components under field-representative operational and environmental stresses. Although not a new concept, PoF has already been successfully applied in the reliability assessment of power electronic components, where it underpins lifetime modelling of semiconductors, capacitors, and interconnects under thermal, electrical, and mechanical stresses [71]. Its relevance extends to EMs, where EISs are particularly vulnerable to failure due to continuous exposure to the same stresses over their service life. In contrast to methods that rely on assumed constant failure rates or outdated statistical handbooks, PoF offers a predictive framework for assessing insulation endurance by enabling reliability assessment based on root-cause degradation analysis and identifying dominant degradation mechanisms, in accordance with physical laws [72].

In EMs, EISs represent the primary reliability bottleneck, particularly in aerospace and automotive applications where strict constraints on weight, volume, and thermal efficiency are imposed. Traditional design practices address reliability concerns by introducing conservative safety factors and over-engineering, which often lead to excessive insulation thickness, reduced slot fill factors, and suboptimal thermal performance [73,74]. While precautionary, such conservative heuristics fail to capture the actual physics of insulation degradation under mission-specific stressors. ROD overcomes these limitations by elevating insulation reliability from a retrospective assessment to an explicit design objective, in addition to torque-speed characteristics, power capability, efficiency, dimensions, weight, and cost. Reflecting the change in design objective list, the PoF approach plays a pivotal role at the core of the ROD process by applying validated lifetime models to guide material selection and geometry optimisation.

As illustrated in Figure 7, the ROD process begins by setting quantifiable requirements and constraints to support preliminary EM sizing [75]. After the baseline for the iterative workflow is established, material selection and geometry optimisation are undertaken, followed by thermal simulations—typically carried out using lumped-parameter networks—generate temperature profiles that serve as inputs to the lifetime models, enabling the computation of cycles-to-failure or time-to-failure metrics of EIS at specified reliability percentiles. The results are then benchmarked against requirement thresholds and when discrepancies are identified, feedback within the loop drives iterative refinement through modifications in insulation grade and thermal conductivity, slot geometry, cooling architecture, or electromagnetic layout, until the design converges to the required performance and reliability levels.

Once all requirements and constraints are satisfied, prototypes are manufactured and qualified against international standards (e.g., IEC, IEEE), ensuring the transition to market-ready EMs. By employing predictions from PoF-grounded lifetime models early in the design cycle, the ROD process significantly reduces the risk of costly redesigns at later stages. More importantly, it guarantees that reliability is treated not as an afterthought, but as a central design driver.

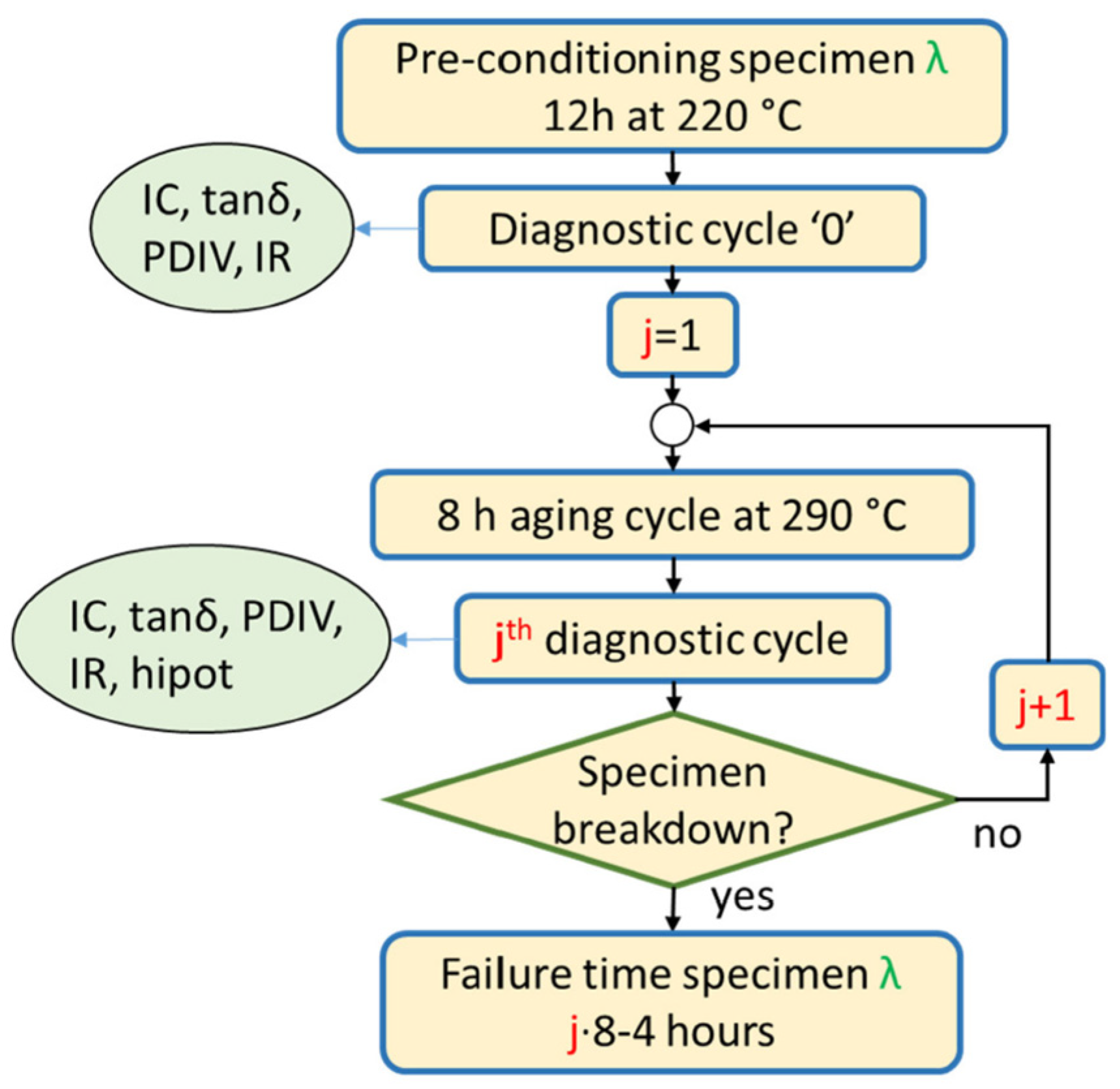
The implementation of PoF into the ROD process for EMs has been advanced through the development of a time-saving methodology for the thermal lifetime evaluation of low-voltage EMs, demonstrated on an aerospace PMSM employed in an EMA. Conventional thermal qualification of EISs, even when accelerated, typically demands thousands of ageing hours across multiple temperature levels, thereby delaying the transition from prototype to market-ready product. To shorten the qualification process, preliminary high-temperature ATA tests at 290 °C were performed on five motorettes (30 subcoils in total), as shown in Figure 8, during which IC, $\tan \delta$, PDIV, and IR were systematically monitored. Each specimen underwent 30 thermal cycles, every cycle consisting of 8 h of exposure at 290 °C followed by natural cooling to room temperature before dielectric measurements.

Before the start of the ageing process, all specimens underwent a pre-conditioning stage at 220 °C, the same as the insulation’s thermal-class temperature, for 12 h to remove volatile compounds and absorbed moisture from the enamel surface. Pre-conditioning ensures uniform dielectric conditions across all specimens, eliminating surface impurities and moisture that would otherwise cause high variability in insulation-capacitance readings. The first diagnostic session was carried out after this stage and defined as cycle “0”.

IR was discarded due to its non-monotonic behaviour, $\tan \delta$ was found to be strongly influenced by environmental conditions, and PDIV, although correlated with ageing, required more complex measurement setups. In contrast, IC exhibited a clear and monotonic trend with degradation, directly reflecting enamel thinning under thermal stress. On this basis, the percent differential insulation capacitance (ΔIC) was selected as the principal diagnostic marker for subsequent tests was defined in (31):

$$\Delta IC={\displaystyle \frac{{IC}_{HV}-{IC}_{LV}}{{IC}_{HV}}}\times 100$$

(31)

where ${IC}_{HV}$ and ${IC}_{LV}$ denote the insulation capacitance values measured above and below the partial discharge inception voltage (PDIV). The parameter ΔIC was normalised to its initial value ΔIC₀, measured after pre-conditioning, yielding the dimensionless ratio (ΔIC/ΔIC₀) used as the diagnostic ageing index. Four hours were subtracted from the total exposure time to exclude the incomplete final cycle once all subcoils had failed the hipot test, ensuring that only full exposure intervals were included in lifetime evaluation.

Thereafter, ATA tests were conducted on separate sets of five motorettes at 250 °C and 270 °C, comprising 5 and 10 cycles, respectively, closer to the insulation’s thermal class of 220 °C, and were terminated after a limited number of cycles (corresponding cycle durations were 120 h at 250 °C and 24 h at 270 °C), with time-to-failure extrapolated through Weibull-based statistical analysis rather than waiting for all specimens to fail. This procedure reduced the total qualification time by approximately 70% while maintaining predictive accuracy, as the resulting Arrhenius thermal endurance curve provided a thermal class of 207 °C, within 1% of the conventional full-duration method. In a broader sense, it demonstrates how PoF-based diagnostic marker selection and optimised ATA testing can substantially shorten qualification procedures while preserving reliability, thus embedding lifetime assessment directly into the early stages of EM design [80].

The application of the PoF approach extends beyond ROD into operational phases through prognostics and health management (PHM). In EMs, degradation of EISs is driven by mission-dependent stressors such as winding temperature fluctuations, load cycles, and ambient conditions. Capturing these effects requires PHM strategies that combine accelerated ageing data with in-service monitoring information, so that lifetime models are progressively updated during operation. Within this context, PoF provides the mechanistic link between stressors and insulation degradation, ensuring that diagnostic markers are rooted in the underlying failure physics rather than empirical correlations [81].

For instance, an investigation was conducted on inverter-fed low-voltage servomotors, in which ground-wall insulation was subjected to ATA tests. Following IEEE Std. 117 [76] procedures, four stator samples were cycled under PWM excitation in a controlled oven at 203 °C, 215 °C, 230 °C and 250 °C to replicate mission-relevant stress conditions. The ground-wall insulation health was continuously assessed through multi-frequency measurement of IC and $\tan \delta$, both of which directly reflect the molecular degradation of organic dielectrics via chain scission and cross-linking. In this way, the diagnostic markers were not statistical surrogates, but mechanistic indicators rooted in the PoF of insulation thermal ageing. Their temporal progression was coupled with the Arrhenius–Dakin model, with activation energy calibrated from ATA tests and dynamically updated in real-time using in situ measurements to refine lifetime predictions. The integration of test data with continuous monitoring enabled the extrapolation of remaining useful life (RUL) by fitting the normalised IC degradation trajectory with a polynomial function and projecting it to the critical threshold, where failure was consistently observed at about 70% of the initial value.

Table 5. A brief schematic or table summarising the diagnostic indicators.

Diagnostic Indicator	Physical Interpretation	Observed Failure/Alarm Limit
$\mathrm{Equivalent} \mathrm{Ground-Wall} \mathrm{Capacitance} ({\mathit{C}}_{\mathit{e}\mathit{q}}$)	Represents dielectric integrity of insulation. Capacitance decreases as polymer chains break during thermal ageing, reducing dielectric constant.	Failure occurs when normalised $C_{eq}$ decreases to ~0.70 ± 0.04 of initial value (≈69–73% threshold).
Dissipation Factor (tan δ)	Reflects dielectric losses and molecular mobility; increases with oxidation, moisture ingress, or cross-linking.	High dissipation (e.g., up to 60% at 250 °C) indicates unstable degradation regime; at lower temperatures (<230 °C), values stay within 0.5–4%.
$\mathrm{Equivalent} \mathrm{Parallel} \mathrm{Resistance} ({\mathit{R}}_{\mathit{e}\mathit{q}}$)	Represents insulation leakage path; decreases as conduction paths form due to carbonization or cracking.	Continuous reduction trend correlates with ageing rate; no fixed limit defined, but monotonic drop complements $C_{eq}$ decrease.
$\mathrm{Normalised} \mathrm{Capacitance} \mathrm{Variation} \mathrm{Rate} (\Delta {\mathit{C}}_{\mathit{e}\mathit{q}}$/Δt)	Captures rate of dielectric loss progression under constant temperature stress.	Increasing slope indicates accelerated degradation.

summarises the diagnostic indicators, their physical interpretation, and failure limits. This study illustrates how ATA testing, when integrated with PoF-grounded online diagnostics, yields a rigorous prognostic framework that elevates lifetime models from static design tools to adaptive decision-support systems for predictive maintenance in high-availability electrical drives [80].

In summary, the PoF approach serves as a rigorous structural element for the ROD of EMs by embedding lifetime models at the core of the iterative loop illustrated in Figure 6. By shifting from conservative heuristics to physics-based lifetime prediction, PoF ensures that insulation reliability is addressed proactively and quantitatively at an early stage, thereby reducing the risk of late-stage redesigns and unplanned failures. Beyond the design phase, PoF also establishes a framework for PHM, where the use of PoF-informed diagnostic markers enables lifetime prediction to be dynamically refined during service. ATA test results are transformed into practical prognostic tools for high-availability drives, and maintenance interventions are scheduled only when degradation indicators approach critical thresholds. In turn, unnecessary downtime is reduced, unexpected insulation failures are prevented, and lifecycle management in demanding applications is enhanced. Critically, ATA tests remain essential to the realisation of PoF, since they provide the empirical evidence required to identify degradation mechanisms and calibrate lifetime models. By using PoF methodologies to systematically apply ATA testing to EISs of EMs, these models are validated and subsequently integrated into the ROD process and PHM strategies. Thus, ATA testing does not stand apart from PoF, but rather enables the implementation of this approach across the entire lifecycle of EMs, highlighting its growing importance in supporting the electrification of transportation and other mission-critical applications.

6.1. Accelerated Thermal Ageing Tests

The evolution of empirical models for insulation lifetime assessment has always depended on high-quality experimental data, as numerical constants in degradation laws must be tuned against observed behaviour. At service conditions where temperatures remain below the declared thermal index, ageing proceeds at an imperceptibly slow rate, making direct observation over realistic timescales infeasible. ATA tests resolve this limitation by deliberately subjecting insulation specimens to temperatures well above nominal operating values. The imposed stress expedites the same chemical and physical degradation mechanisms (e.g., oxidation, chain scission, embrittlement, and microcrack propagation) that ultimately lead to electrical failure in the field [45]. In doing so, ATA tests condense years of degradation into months or weeks of experimentation, providing essential failure data for lifetime modelling within the PoF framework.

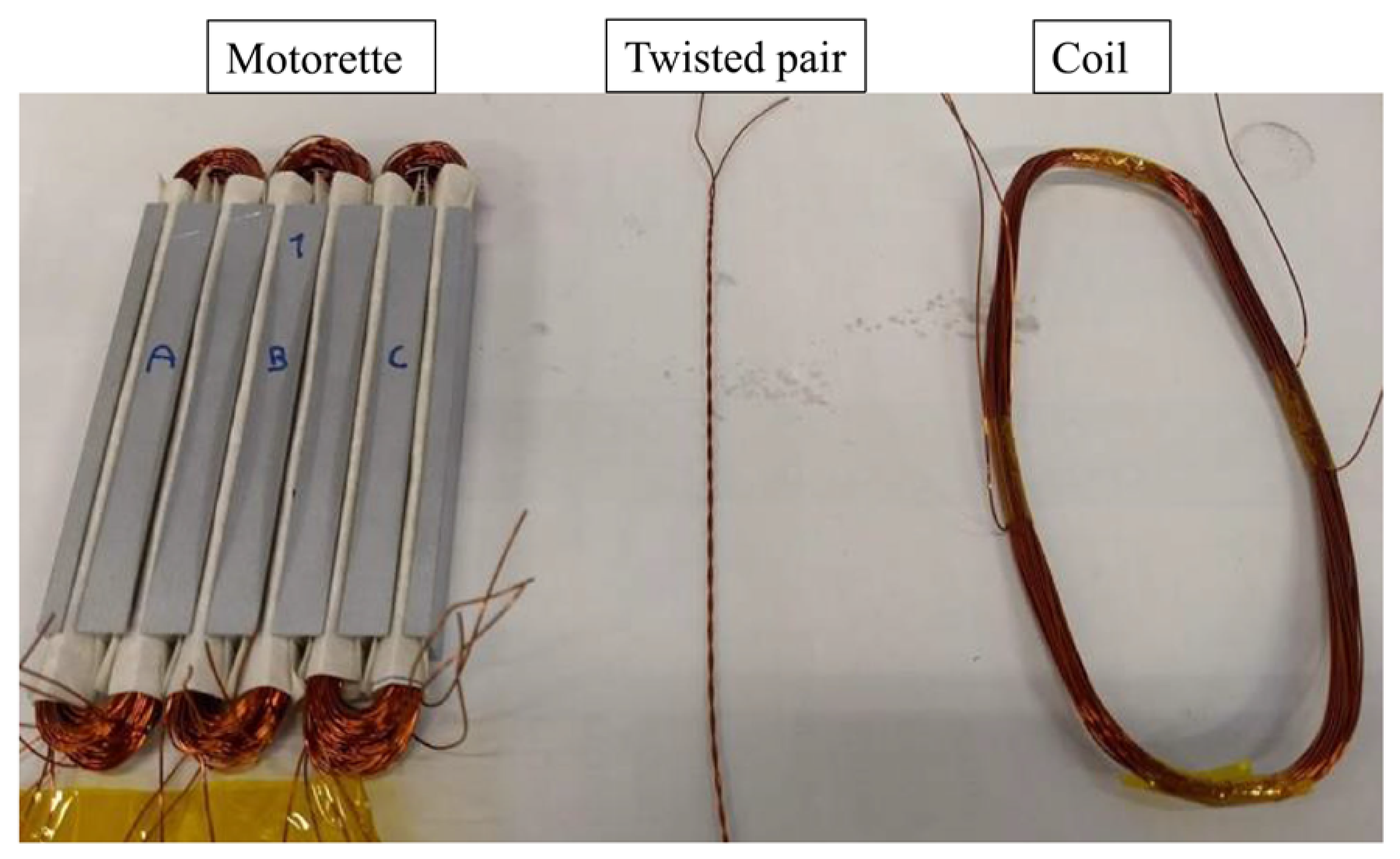
Selection of suitable specimens is a critical prerequisite for meaningful ATA testing. As illustrated in Figure 9, the most common specimen configurations include purpose-built twisted pairs, motorettes, and coils. Twisted pairs, consisting of two enamelled conductors helically wound together, have traditionally been employed for wire standardised insulation testing procedures. Their simplicity and low cost make them attractive, yet their diagnostic scope is restricted to inter-turn insulation, and their fragility renders handling difficult. They remain more appropriate for PD investigations than for comprehensive thermal ageing studies. Motorettes, in contrast, replicate a portion of the stator or rotor winding and enable simultaneous assessment of turn-to-turn, phase-to-phase, and phase-to-ground subsystems. Their geometry and construction closely mirror those of real machines, making them the preferred specimen type in most ATA test procedures. Coils, although not formally recognised in technical standards, have occasionally been used for comparative purposes, while complete machine testing offers the highest fidelity at the cost of significant resources.

The acceleration of thermal ageing depends not only on higher temperature but also on changes in the dominant degradation mechanisms [82]. In laboratory settings, pre-screening tests are often performed at several temperature levels to detect the onset of secondary mechanisms such as melting, glass transition, or volatilization [83]. The identified thresholds mark the upper temperature limits for accelerated thermal ageing, ensuring that subsequent ATA tests are conducted below these levels so that the produced degradation mechanisms remain consistent with those active under service conditions.

Experiments are typically performed on at least three sets of specimens, each maintained at a distinct constant temperature above thermal class separated by defined increments, often in the order of 20 °C. Exposure to multiple thermal stress levels permits lifetime extrapolation to realistic operating conditions [84]. This is justified because the imposed thermal ageing acceleration affects only the rate of chemical reaction, not its nature, which justifies extrapolating lifetime towards lower service temperatures within the same mechanism domain. Representativeness of the accelerated ageing process is ensured by reproducing the environmental factors that govern degradation kinetics. Airflow, oxygen concentration, and humidity are controlled through thermostatic chambers equipped with forced convection and drying systems, maintaining steady-state conditions comparable to the interior of EMs. The chamber temperature is stabilised within $\pm$1 °C, with relative humidity typically kept below 10% to suppress moisture-induced reactions. When tests are performed on impregnated or resin-coated specimens, ventilation rate and oxygen ingress are adjusted to emulate in-service diffusion rates through the insulation stack, ensuring that acceleration stems solely from temperature rather than extraneous chemical effects [82].

Replicating tests across several temperatures also reduces the influence of random variation, while larger specimen numbers mitigate measurement error and ensure statistical confidence [85]. In many studies, ten or more specimens per condition are employed, though higher numbers are preferred when available to capture material heterogeneity and random-winding effects. Diagnostic sessions are interspersed throughout the thermal exposure to monitor degradation progress. Standard practice includes insulation voltage-withstand tests or $\tan \delta$ measurements, with dielectric breakdown commonly adopted as the end-of-life criterion [86]. For systems verified as PD-free, breakdown testing at voltages near the inception level ensures that observed failures originate from thermal degradation rather than from electrical overstress. In PD-sensitive systems, the inception of PD itself may serve as the termination marker. Careful definition of diagnostic thresholds is therefore essential to ensure comparability across ATA test series. Key control parameters used to maintain experimental fidelity are summarised in

Table 6. Key control parameters in ATA testing to ensure physical representativeness and reliability.

Control Parameter	Typical Value/Setting	Purpose and Rationale
Temperature stability	$\pm$1 °C of setpoint	Maintains constant thermal stress across specimens and prevents artificial acceleration or cooling gradients.
Temperature increment between test levels	~20 °C	Enables extraction of activation energy for Arrhenius-based lifetime models and supports reliable extrapolation.
Relative humidity	$\le$10%	Minimises moisture-induced oxidation or hydrolysis not representative of sealed EM environments.
Airflow and oxygen concentration	Controlled forced convection; regulated O2 content	Reproduces internal ventilation and oxidation rates typical of service conditions; avoids over-oxidation.
Specimen diffusion environment	Adjusted for impregnated or resin-coated specimens	Emulates in-service diffusion rates of oxygen and vapours through insulation layers.
Recommended number of specimens per condition	$\ge$10	Improves statistical confidence and captures material variability and winding randomness.
Diagnostic interval	Periodic (predefined time steps or cycles)	Enables monitoring of degradation trends and early detection of anomalies.
End-of-life criterion	Dielectric breakdown or PD inception	Provides consistent and mechanistically relevant failure definition across test series.

.

Following the description of test protocols and specimen selection, the next step is to interpret the results from ATA tests and assess their contribution to lifetime modelling. Elevated thermal stress accelerates the degradation mechanisms without introducing spurious ageing phenomena, thereby preserving the validity of the test results. The experimental data obtained under accelerated conditions forms the empirical bridge between operational stressors and material degradation pathways. To translate raw failure-time records into accurate lifetime predictions, rigorous statistical post-processing is required after ATA testing [87]. This step not only accounts for data scatter, variability in specimen construction, and diagnostic uncertainties, but also reinforces the role of ATA testing in the realisation of the PoF approach. By ensuring that degradation mechanisms are faithfully captured in lifetime models, post-processing provides confidence that the models are correctly calibrated and validates their predictive capability. In this regard, ATA tests are established as the experimental foundation upon which Weibull analysis is performed.

6.2. Weibull Analysis

Post-processing of accelerated testing data requires a statistical analysis capable of describing a wide range of failure behaviours while also offering parameters with clear physical significance. By applying the Weibull distribution to experimental lifetime data, Weibull analysis fulfils these requirements and stands as the most commonly adopted statistical framework for insulation reliability assessment. The flexibility of the distribution allows for accommodating decreasing, constant, or increasing hazard rates, enabling the same probabilistic representation to represent early-life failures, random failures, and wear-out dominated failures [88]. Furthermore, its parameters not only quantify lifetime distribution but also provide insight into the underlying failure process itself, offering a direct link between statistical results and physical degradation laws.

The two-parameter Weibull cumulative distribution function (CDF) is given by (32) [55,75]:

$$F\left(t\right)=1- \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({\displaystyle \frac{t}{\alpha }}\right)}^{\beta }\right] ,t, \alpha , \beta >0$$

(32)

The function describes the probability $F\left(t\right)$ that a specimen has failed by time $t$. The scale parameter α represents the characteristic lifetime at which 63.2$\%$ of specimens have failed, providing a direct statistical analogue to the “most probable” failure time. The shape parameter β quantifies the distribution’s spread and indicates the prevailing failure mode. When $\beta >1$, failures are predominantly driven by wear-out mechanisms, reflecting the gradual accumulation of degradation until a critical threshold is reached. A value of $\beta =1$ corresponds to a constant failure rate, consistent with random, time-independent failures. When $\beta <1$, early-life or infant mortality failures dominate, often signalling manufacturing defects or latent material flaws.

To enable parameter estimation, the Weibull cumulative distribution function is recast into the linear form expressed in (33) [75,89]:

$$\ln \left[-\ln \left(1-F\left(t\right)\right)\right]=\beta \ln t-\beta \ln \alpha$$

(33)

Linearisation allows scattered time-to-failure data to be approximated by a straight line on double-logarithmic axes. Raw failure times obtained from accelerated tests are first ranked in ascending order, after which cumulative probabilities of failure are assigned to each ranked time. Median rank estimator is most commonly leveraged for this step, as it provides reliable probability assignments even when datasets are small—a frequent constraint in ATA tests due to their cost and complexity. The Benard’s approximation is employed for the median rank estimator to obtain the Weibull CDF $\widehat{F}\left(t_i\right)$ as shown in (34) [75]:

$$\widehat{F}\left(t_i\right)={\displaystyle \frac{i-0.3}{N+0.4}}$$

(34)

where $t_i$ represents the time to failure for the $i_{th}$ sample and $N$ is the total number of samples. The resulting probability-time pairs form the data points used to construct the linearised Weibull probability plot. Regression analysis, typically least squares, is subsequently applied to fit the best straight line through these points, allowing for a statistically robust calculation of the parameters $\alpha$ and $\beta$ [90]. Once $\alpha$ and $\beta$ are determined for each test temperature, percentile lifetimes such as B10 and B50 can be calculated. They represent the time to failure by which 10% and 50$\%$ of the entire population of similar EISs are expected to have failed, respectively, and are invaluable for ROD decisions.

A clear application example of the linearisation procedure is provided by a Weibull probability plot obtained at 250 °C, where the ranked failure times of motorette specimens have been fitted with a straight line together with 95$\%$ confidence intervals. As shown in Figure 10, the fitted distribution yields a B10 percentile lifetime of approximately 630 h and a B50 lifetime of around 1161 h. These values indicate that under the applied accelerated ageing conditions, 10$\%$ of the specimen population is statistically expected to fail by about 630 h, whereas half of it is projected to fail by 1161 h. The inclusion of confidence bounds further quantifies the uncertainty associated with the parameter estimation, ensuring that the derived lifetimes are not interpreted as exact but as statistical expectations within defined probability limits.

From the transformation of the Weibull cumulative distribution function given by (24), the vertical cumulative-percentage-axis of the plot in Figure 9 can be expressed as $\ln \left[-\ln \left(1-F\left(t\right)\right)\right]$, while the horizontal time-to-failure-axis corresponds to $\ln t$. Under the double-logarithmic scaling, it is evident that the Weibull distribution reduces to a straight line. The slope of this line directly yields the shape parameter $\beta$, whereas the intercept with the percentage-axis equals $-\beta \ln \alpha$.

The statistical confidence of Weibull-derived parameters directly influences the reliability of percentile lifetime predictions [91]. Confidence intervals for both the scale parameter $\alpha$ and the shape parameter $\beta$ are determined from the covariance matrix of the regression fit or through Monte Carlo resampling of the failure data [92]. Propagation of these parameter uncertainties into lifetime estimation defines upper and lower confidence bounds for the B10 and B50 percentile lifetimes, which represent the shortest and longest lifetimes that remain statistically consistent with the experimental data. Differences between the bounds can reach several-fold when limited datasets are used, reflecting the sensitivity of percentile lifetimes to data variability [93]. In Figure 9, B10 and B50 are shown as single-point estimates obtained from the best-fit Weibull distribution. The red outer lines represent the confidence bands of the fitted distribution, which define the uncertainty envelope of the cumulative failure probability and provide the basis for deriving the percentile confidence bounds [94].

The calculation of percentile lifetimes across multiple test temperatures provides the means to construct multi-percentile thermal endurance curves, where lifetime is plotted against the difference between the reciprocal of the reference absolute temperature and the reciprocal of the operating absolute temperature ($L\left(\theta \right) vs. \Delta (1/\theta )$) with the horizontal axis labelled as $\Delta (1/\theta )$ or $\Delta \left(\theta \right)$ [57], in order to characterise insulation performance over a range of reliability levels. 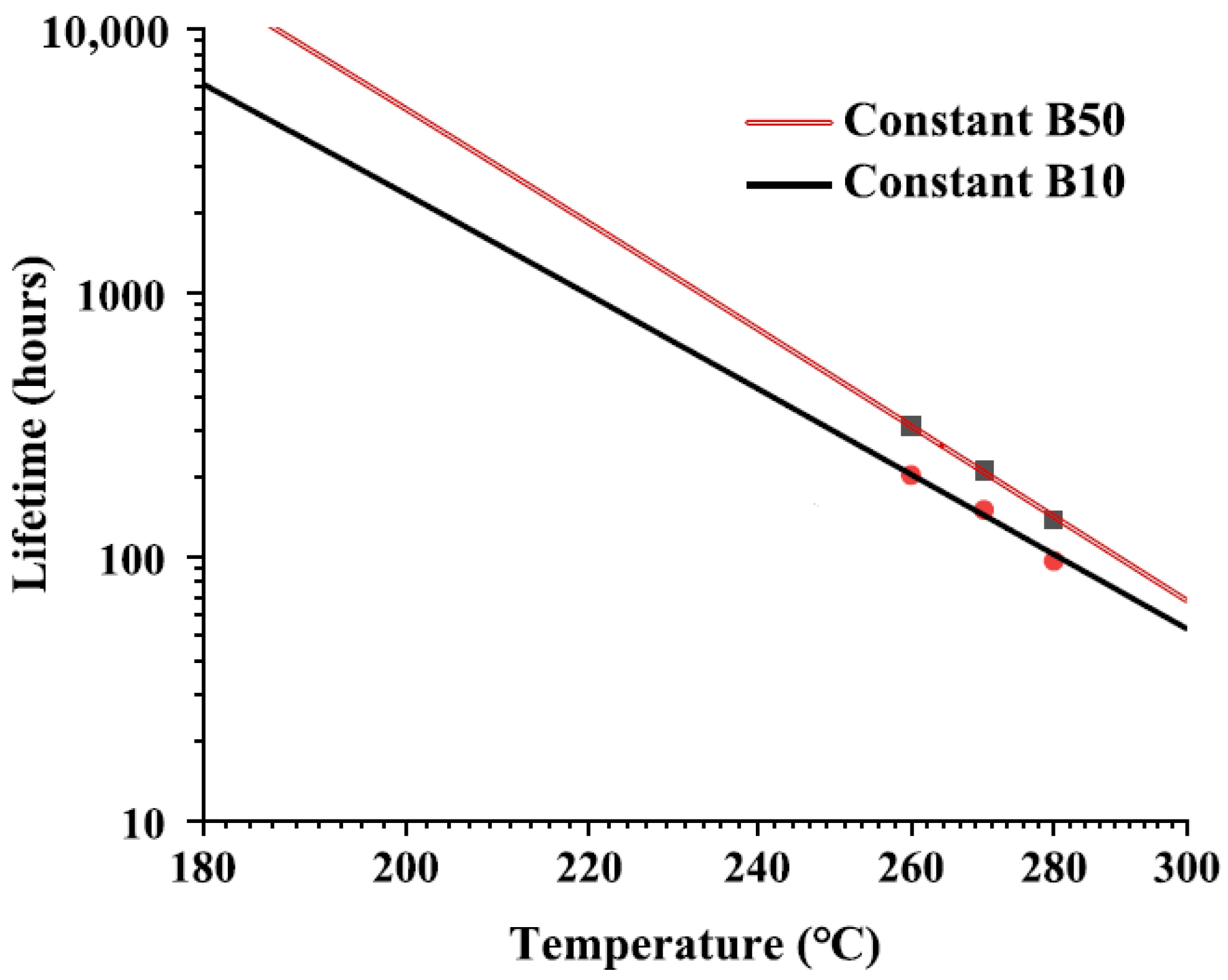An example is shown in Figure 11, where the B10 and B50 curves were constructed by interpolating percentile lifetime values derived from Weibull probability plots of motorette specimens subjected to accelerated ageing at 260 °C, 270 °C, and 280 °C.

Once the interpolated thermal endurance curves from constant temperature ageing were established, they were extrapolated both towards higher temperatures, up to 300 °C, and lower service-relevant temperature ranges, enabling lifetime prediction beyond the experimental dataset.

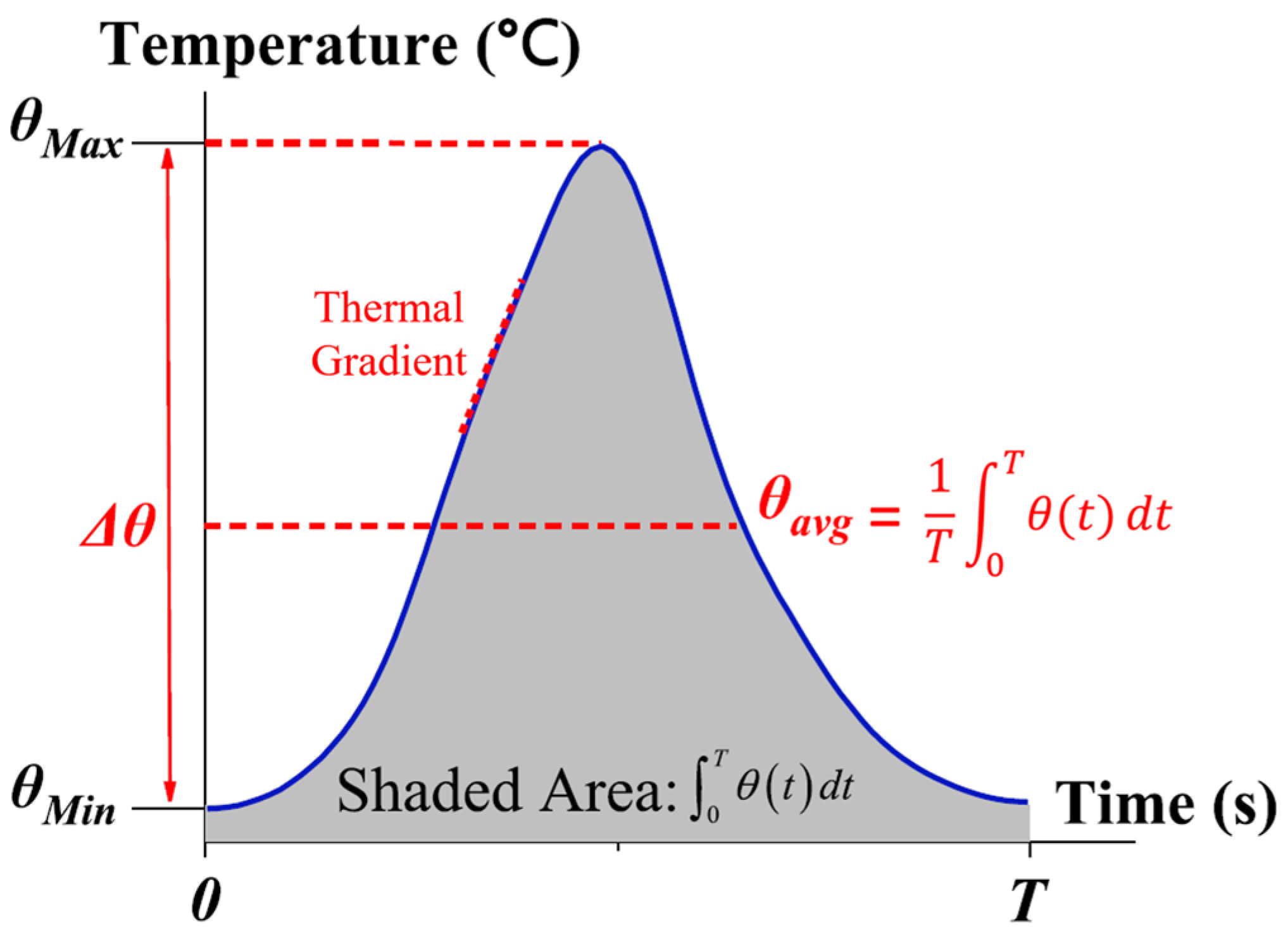
In the case of thermal ageing caused by fluctuations in temperature, the periodic temperature profile is typically reduced to a single equivalent average temperature ${\theta }_{avg}$, calculated over the thermal cycle period as shown in Figure 12. The measured time-to-failure data are then post-processed with Weibull analysis to calculate percentile lifetime values at ${\theta }_{avg}$.

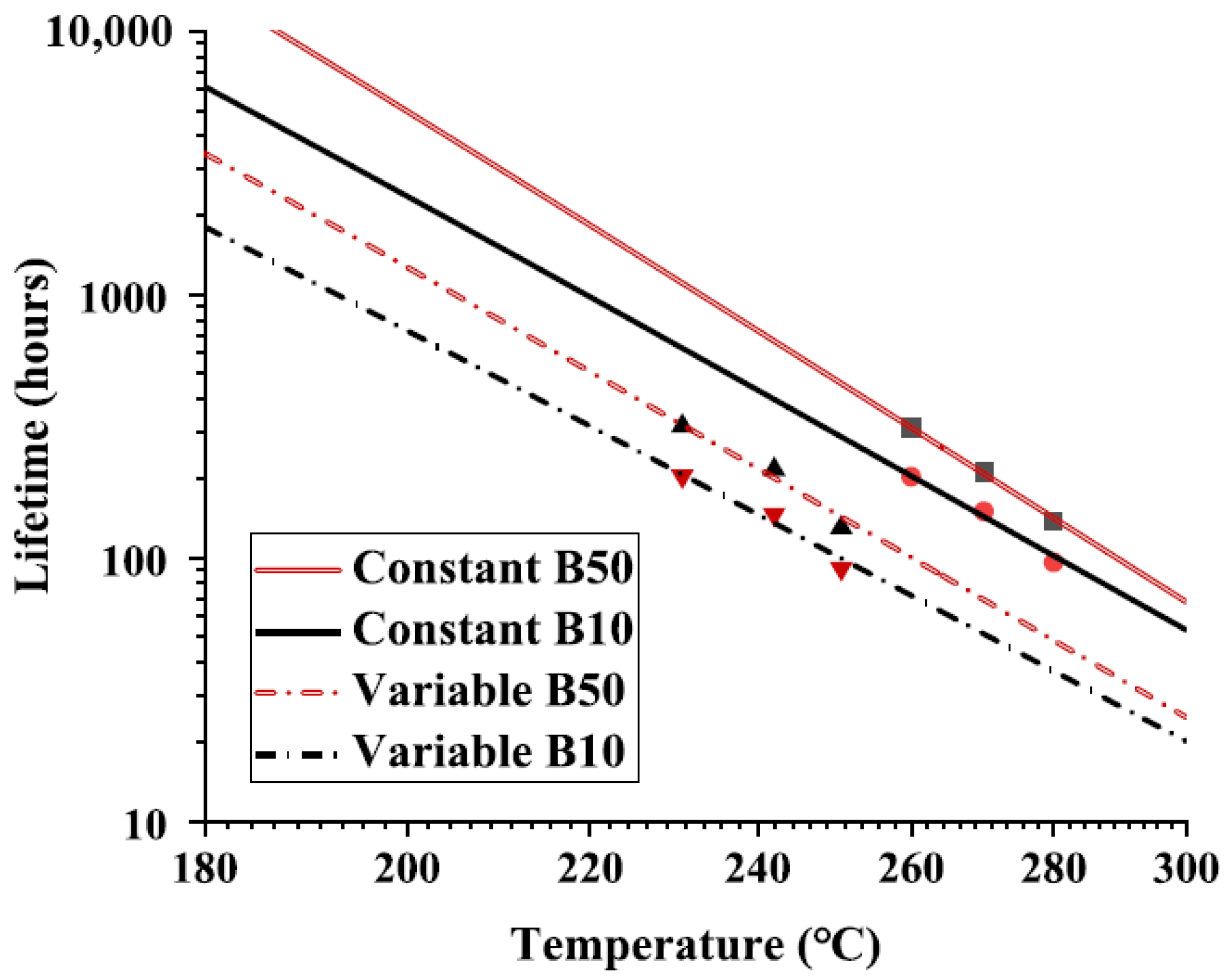
The percentile lifetime values for variable-temperature ageing were calculated at three equivalent average temperatures, reflecting the periodic cycling between 220 and 260 °C, 230–270 °C, and 240–280 °C. These three operating windows provide the representative data points from which the variable-temperature B10 and B50 curves were constructed, as illustrated in Figure 13:

The axes that were used to extrapolate thermal endurance curves from interpolated data under variable-temperature ageing were the same as that employed for constant-temperature ageing, thereby allowing direct comparisons. For meaningful assessment, identical percentiles should be selected for both constant- and variable-temperature ageing datasets.

The concept of equivalent average temperature provides a convenient means of relating variable-temperature ageing to an equivalent isothermal exposure, simplifying the estimation of cumulative degradation over non-uniform thermal cycles [96]. The approach allows accelerated testing under variable conditions to be expressed in terms of an equivalent single-temperature exposure, facilitating direct comparison with conventional ageing data. It is inherently assumed that thermal ageing remains the predominant degradation mechanism and that temperature governs the overall rate of material deterioration [97]. Mechanical fatigue, vibration-induced stress, or electric field effects that may occur concurrently during thermal cycling are not explicitly accounted for in the equivalent temperature formulation. Their contribution is generally minor under moderate operating conditions but can become significant in applications involving strong electro-mechanical coupling or repetitive start-stop cycles. Awareness of this limitation is, therefore, essential to ensure the correct interpretation of results and to avoid overestimating lifetime when nonthermal factors are present [98].

The necessity of extrapolation of interpolated data arises because ATA tests are usually conducted at three elevated temperature levels, chosen to produce a straight line in Arrhenius coordinates. These temperature levels are considerably higher than the normal operating temperature of EISs, and therefore, extrapolation is an important step to “rescale” the experimental data and infer lifetimes at service conditions. The challenge lies in the assumption of linearity; while the Arrhenius relationship is expected to hold within the tested range, there is no guarantee that the temperature–lifetime correlation remains linear outside it [99]. Secondary degradation mechanisms, particularly those activated by temperatures approaching the glass transition of polymeric enamel coatings, can alter the dominant degradation pathway and undermine the validity of the extrapolation [100]. Given that the onset of secondary degradation mechanisms is often manifested by the appearance of a curvature or “knee” in the thermal endurance plot [76], which disrupts the linearity essential for meaningful interpolation, retaining anomalous data would distort the slope of the endurance line and lead to either over-optimistic or unduly conservative lifetime predictions. To preserve both statistical rigour and physical fidelity, only data points that preserve the linearity of the endurance relationship (i.e., they remain representative of the dominant degradation mechanism over the tested temperature range) should be carried forward for interpolation, while outliers associated with additional or overlapping degradation phenomena are excluded. Dataset filtering is indispensable for making certain that the resulting thermal lifetime models faithfully capture service-relevant ageing processes and provide reliable input for PoF-based ROD.

In summary, the systematic statistical treatment of accelerated testing data through Weibull analysis ensures that lifetime predictions inferred from extrapolated thermal endurance curves remain aligned with observed degradation mechanisms. Unlike the exponential distribution, which assumes a constant failure rate, or the lognormal distribution, which does not directly indicate failure mode, the Weibull distribution accommodates increasing, constant, and decreasing hazard rates within a single framework, making it well-suited for EIS ageing where different degradation mechanisms and failure behaviours may dominate across various stages of service life. Also, Weibull analysis contributes to the sustainability and efficiency of EISs. By integrating uncertainty-aware percentile lifetimes into ROD workflows, material utilisation can be optimised to reduce excessive safety margins, minimise resource waste, and extend insulation service intervals. In this way, statistical interpretation is translated into practical integration of reliability insights into EM design, converting empirical degradation data into informed lifecycle management decisions.

6.3. Validation and Refinement of Lifetime Models

Validation of already calibrated lifetime models is a critical step in ensuring that statistical predictions align with the degradation mechanisms assumed in model development for the same end-of-life criteria [101]. The percentile lifetimes, derived via Weibull analysis of the failure-time data gathered from ATA tests, are compared with the model’s predicted lifetimes for corresponding stress levels [102]. Strong agreement across all tested conditions validates that model parameters, such as the activation energy and the pre-exponential factor, are correctly calibrated [103].

When discrepancies arise, they may signal the need for model refinement. Such adjustments can involve recalibrating activation energy values, modifying stress exponent coefficients, or even re-evaluating the dominant degradation mechanism assumed in the model. The Weibull shape parameter $\beta$ plays an important investigative role in this case; for example, if the model assumes a wear-out dominated process, but the experimental $\beta$ value is close to or less than one, it may indicate that the observed population is affected by early-life failures or by overlapping degradation mechanisms, rather than a pure wear-out process. The scale parameter $\alpha$, in turn, determines the characteristic life of the population. Confidence intervals on parameters $\alpha$ and $\beta$ quantify the statistical uncertainty of the fitted model and define the range within which the predicted lifetimes are expected to fall; predictions consistently outside these bounds suggest that the model may be systematically biassed [102].

Utilising statistical post-processing to validate lifetime models provides a rigorous means of assessing whether predicted lifetimes are consistent with experimentally observed behaviour. The versatility of Weibull analysis enables the comparison of percentile lifetimes with model outputs, the evaluation of shape parameters to confirm assumed degradation modes, and the use of confidence intervals to define the statistical reliability of the predictions. When discrepancies are identified, the analysis informs parameter recalibration or reassessment of the dominant degradation mechanism, aimed at keeping Arrhenius-based models both physically meaningful and statistically robust for insulation reliability studies.

7. Towards Hybrid Physics-of-Failure and Artificial Intelligence Approach in Electrical Insulation Diagnostics, Prognostics, and Lifetime Management

PoF-informed models, long central to condition-based maintenance and failure analysis, link measurable stressors (thermal slew rates, electric-field intensity, vibration, and mechanical load) to material fatigue, dielectric deterioration, and reaction-kinetics-driven chemical change. Calibrated and subsequently validated through ATA tests and Weibull analysis, they provide a mechanistic basis for prediction and test design [104]. Yet despite this interpretability, classical formulations struggle to capture multi-stress coupling, regime changes, and nonlinear dynamics that arise under variable-temperature missions and nonstationary duty cycles [105]. In practice, fielded EISs are further challenged by sensor noise, interacting stresses, and distribution shift [106]. To address these gaps, recent work advances hybrid reliability frameworks that combine the PoF approach with AI, merging physics-based plausibility with data-adaptive inference [107].

AI offers tools for uncovering secondary or complex degradation patterns that are difficult to model analytically [108]. Trained on operational and laboratory data, these tools can flag incipient faults, estimate RUL, and adapt as conditions evolve [109]. Purely data-driven techniques, however, encounter limitations in extrapolation and transparency outside the training domain. Hybridisation resolves this tension by embedding physics into the learning pipeline through physics-informed features, structural constraints, or mechanistic priors, so that predictions respect known physical ageing laws while benefiting from data-driven efficiency and noise robustness [110]. In practice, this combination yields reliability assessments that retain mechanistic interpretability while remaining applicable to full-scale electrical assets.

A mechanism-guided intelligent enhancement method exemplifies the integration of physics-based modelling with learning-based diagnosis in the early detection of winding insulation degradation. The approach employs a distributed-parameter model of the stator winding to predict how incipient defects modify the common-mode impedance spectrum, a sensitive but often overlooked indicator of insulation health. Because early inter-turn or ground-wall defects introduce only minor spectral changes that can be masked by noise, a three-stage enhancement pipeline is applied, consisting of mechanism knowledge focusing, dynamic knowledge matching, and guided reconstruction. A latent-variable reconstruction model constrained by physical priors generates diagnostic samples that amplify weak yet mechanistically consistent features, which enables reliable detection of early degradation with limited data. Validation on a 4 kW permanent magnet synchronous motor drive system demonstrated a reduction of more than 60% in early ageing diagnosis error relative to direct diagnosis, simulated mechanism models, interpolation-based enhancement, deep generative reconstruction, and domain adaptation methods. By embedding physical knowledge into the learning pipeline, the study demonstrated that physics-guided AI can deliver more reliable insulation monitoring in electrical drives, offering practical benefits for transport and industrial applications where operational stresses and downtime risks are high [111].

Neural networks (NNs) have also been proposed as alternatives to conventional regression-based approaches for predicting the thermal lifetime of EM insulation. In one study, twisted-pair magnet wire specimens with a thermal class of 220 °C were prepared following ASTM D2307 [112] procedures, using round copper conductors of 0.4 mm diameter coated with a double-layer enamel of modified polyester and polyamide-imide. Thirty specimens were aged in a controlled oven at 250 °C, 270 °C, and 290 °C, with diagnostic measurements including IR, IC, and $\tan \delta$ taken after each cycle. Several neural network architectures were compared, among which a feedforward model trained with Bayesian Regularisation Backpropagation achieved the lowest error (<10%) and closely reproduced experimental degradation trends. The general architecture of the adopted network, shown in Figure 14, consists of a multilayer feedforward structure where IR values at successive ageing cycles serve as inputs to predict future degradation states. Weibull analysis confirmed close alignment between predicted and measured time-to-failure, while the estimated temperature index deviated by only 0.125% from the conventional Arrhenius extrapolation. In addition, the NN approach reduced the overall ATA test duration by 1680 h (57%) without compromising predictive accuracy, showing that supervised AI models can significantly accelerate the thermal qualification of EM insulation [113].

Beyond accelerated ageing prediction, NNs have also been employed for qualitative assessment of insulation condition in high-voltage wound-field synchronous generators. A framework was developed that combines IR, polarisation index, and PD measurements with operational data, including years of service and frequency of failures. Data collected from two synchronous generators rated at 202 MVA, 15.75 kV, and 7405 A at a power plant were expanded into 5000 patterns to address data scarcity. An NN trained with 5-fold cross-validation classified insulation health into four categories (Excellent, Good, Acceptable, Bad) and proposed appropriate maintenance actions. Although temperature was not included as a direct input, the model explicitly acknowledged the role of TEAM stresses—thermal, electrical, ambient, and mechanical stresses—in driving insulation ageing, with thermal stress implicitly reflected in the degradation of IR, polarisation index, and PD. The NN achieved a mean squared error of 0.0812, a mean absolute error of 0.255, and a root mean squared error of 0.285, closely matching observed data and confirming its potential as a decision-support tool for maintenance planning in large rotating EMs [114].

AI techniques have found particularly broad application in power transformers, where abundant condition-monitoring data enable advanced modelling. A notable example is an integrated health management framework that extends the PoF–AI approach from diagnostics to full asset-level lifecycle optimisation, combining chemical, physical, thermal, mechanical, and electrical indicators into a composite health index that captures both subsystem condition and overall insulation integrity. Pre-processing removes outliers through interquartile range filtering, reconstructs missing values with multilayer perceptrons, and normalises heterogeneous inputs for consistency. Building on this processed data, Support Vector Machines dynamically adjust the weighting of subsystem contributions under varying operating states, while Long Short-Term Memory networks capture temporal patterns to identify emerging fault modes such as PD, cellulose degradation, and oil overheating. The resulting health indices are then passed into cost models, which translate them into inspection, repair, or replacement decisions by balancing failure risk, depreciation, and blackout penalties against the costs of intervention. Case studies on five mineral oil-type power transformers in Iran and Iraq demonstrated higher diagnostic accuracy, a 15–20% extension in service life, and maintenance cost reductions of up to 30%, illustrating the effectiveness of combining physics-informed features with AI-driven decision layers for fleet management [115].

Holistic PoF–AI integration has also been implemented in continuous monitoring platforms for power transformers. The workflow begins with multi-source sensing, where ultra-high-frequency PD sensors, leakage-current probes, and frequency-response modules generate multimodal data streams. These signals are pre-processed through adaptive filtering and feature extraction to reduce noise and highlight degradation-relevant patterns. Deep learning models are then applied, with convolutional networks used to classify PD patterns, recurrent networks to capture temporal degradation dynamics, and ensemble models to enhance robustness, while expert rules ensure interpretability by linking detected features to the underlying degradation mechanisms. Validation included a digital twin of a power transformer, laboratory experiments on a 100-kVA transformer under controlled degradation scenarios, and preliminary field trials. Results showed that the system detected insulation deterioration two to eight months earlier than conventional offline methods and provided short-horizon RUL predictions. The modular architecture facilitates edge deployment (i.e., deployment near-sensor or near-device processing, rather than centralised cloud) and seamless integration with digital twin environments, enabling transformer lifetime extension, outage reduction, and fleet-level optimisation of maintenance planning [116].

The reviewed literature demonstrates that the hybrid PoF–AI approach is rapidly advancing the state of insulation diagnostics, prognostics, and lifetime management across both EMs and power transformers. In EMs, AI has been successfully applied to reduce the testing time required for thermal lifetime evaluation of enamel insulation, enhance early defect detection, and support qualitative health classification in large synchronous generators. In power transformers, AI integrates diverse diagnostic indicators into health indices that guide maintenance and lifecycle planning. Despite differences in scale and operating environments, a common paradigm emerges that embedding physics-informed constraints within AI models improves interpretability and stability, ensuring that predictions remain consistent with known degradation mechanisms while gaining the efficiency and adaptability of data-driven learning. The latest advances signal a shift toward practical, physics-aware AI solutions that can address the challenges of multi-stress ageing, nonstationary duty profiles, and complex failure modes in modern EISs.

The reviewed studies were selected because they represent the most mature and experimentally validated implementations of PoF–AI integration, where data-driven algorithms are explicitly linked to measurable physical quantities such as partial discharge behaviour, thermal endurance, and dielectric response. The PoF–AI framework is conceptually distinct from the classical electro-thermal ageing research of Simoni, Montanari, Mazzanti, Stone, and others, whose work established empirical lifetime laws under controlled laboratory conditions. The hybrid approach builds upon that experimental foundation by embedding mechanistic ageing models within adaptive learning algorithms capable of handling variable duty cycles and field data. The integration of physics-based reasoning with data-driven inference enhances interpretability and enables continuous lifetime prediction, transforming reliability analysis from empirical correlation toward real-time prognostics for modern EISs.

8. Trends and Modelling Implications for Hybrid PoF–AI Insulation Lifetime Prediction

The integration of the PoF approach with AI techniques is poised to shape, and in many cases define, the next generation of insulation thermal ageing models. Emerging high-power-density designs, compact packaging, and aggressive thermal management expose gaps in established PoF-informed models tuned for quasi-static laboratory conditions. While these models provide mechanistic grounding, data-driven approaches contribute adaptability to mission variability and robustness to measurement noise. Accurate life prediction arises only when learning algorithms are anchored in the interaction of materials, interface behaviour, manufacturing variability, and in-service parameter drift. Advances in insulation lifetime prediction, therefore, hinge on fusing mechanistic insight, probabilistic generalisation, and dynamic recalibration to reflect the environments in which modern EMs operate.

Among emerging thermal management strategies, direct liquid cooling stands out as a clear paradigm [117]. Oil-spray and immersion schemes with dielectric fluids, including automotive transmission fluids, are highly effective at levelling out coil temperature distributions in both axial and radial directions, damping thermal slew rates during load transients, and suppressing localised overheating in the end-winding regions [118]. Benefits on the thermal side arrive with new electro-chemical questions. Laboratory studies report marked reductions in PDIV under hot-spray conditions, as well as adhesion or local delamination issues for certain enamels and resins after prolonged exposure to heated fluid [119]. The magnitudes can vary with fluid volatility, contamination, geometry, and duty cycle, yet the direction of impact is consistent—electro-chemical interaction can accelerate or redirect dominant degradation mechanisms. Consequently, lifetime models tuned on “dry” specimens or specimens aged in chemically inert atmospheres (e.g., nitrogen or controlled air) can misstate risk and introduce systematic bias when EISs operate in chemically active coolant environments [120].

Model structure should evolve accordingly. Arrhenius parameters can be conditioned on measurable fluid state variables—acid number, water content, dielectric loss factor—so that activation energies and pre-exponential terms represent the current chemistry rather than a nominal baseline [119]. New equipment can be initialised with “unaged-fluid” parameters, and mid-life equipment can transition to parameter sets inferred from in-service fluid measurements. The identification and validation of these chemistry-conditioned parameters render co-stress accelerated testing essential. Thermal, electrical, and thermo-mechanical loads should be applied in the presence of representative fluids, while AI components learn residual nonlinearities and parameter drift under controlled chemistry [121]. PHM then closes the loop in the field by updating parameters online and propagating uncertainty to the decision layer used in maintenance planning.

Scaling from laboratory specimens to complete windings represents a second, equally practical challenge [122]. Standards legitimately permit representative specimens (e.g., twisted pairs, motorettes, coils, formettes, etc.) for qualification and screening because they reduce cost and isolate degradation mechanisms. Translation to full machine windings introduces a size effect and greater population heterogeneity [123]. Weibull analysis with a geometrical size factor offers a principled route to rescale thermal-life predictions from specimen dimensions to coils and complete stators. Validation of PoF-informed models on low-voltage, random-wound EMs has shown that coil lifetime distributions fall within bounds predicted by scaled twisted-pair data under matched thermal stress, enabling cost-effective pre-qualification earlier in development [124]. When extended to PHM frameworks, PoF-based relationships provide a scalable foundation for transferring diagnostic thresholds and degradation signatures to industrial EMs and fleet-scale applications. The scalability enables the consistent calibration of health indicators and fault precursors across different machine sizes, operating conditions, and mission profiles. It also allows condition-based maintenance strategies to remain physically traceable to the same active degradation mechanisms and interface-driven failure modes observed in controlled laboratory-scale experiments.

Insulation interfaces are frequent initiation sites for failure through shrinkage mismatch, loss of adhesion, or chemical incompatibility. Materials with excellent intrinsic thermal indices can underperform when resin wetting is poor or chemical exposure shifts dielectric properties. Selection for transportation platforms, therefore, weighs thermal class alongside adhesion, chemical resistance, cost, shrinkage at temperature, thermal performance, storage or hydrolysis issues, and compatibility with oil-based cooling. The comparative view in

Table 7. Indicative comparison of insulation materials used in oil-cooled and high-performance EMs for transport applications (partly derived from [125]).

Material	Thermal Class	Adhesion to Core (CU)	Resistance to Chemicals/Abrasion	Cost	Shrinkage Under Temperature	Thermal Performance	Storage Issues	Hydrolysis Issues	Volatile Organic Compound(s) (VOC)-Free
THEIC-PET + PAI	180 °C	Very Good	Yes	Relatively Low	Yes	Inadequate	No	No	No
PEI + PAI	200 °C	Very Good	Yes	Relatively Low	Yes	Fair	No	No	No
PAI	220 °C	Difficult	Yes	Low	Yes	Excellent	No	No	No
PI	>240 °C	Fair	Yes	High	No	Unnecessarily High	Yes	Yes	No
PEEK	>240 °C	Difficult	Yes	High	No	Unnecessarily High	No	No	Yes

illustrates typical trade-offs used in practice.

Shrinkage at temperature is a practical proxy for thermo-mechanical stress. EMs with highly dynamic loads benefit from low-shrinkage choices, considering also that copper tends to expand. Thermal classes above 240 °C can be unnecessarily high in automotive applications, since at very high temperatures, Joule losses are over-exacerbated. Hence, adoption is best reserved for harsh environments where the thermal margin is indispensable. Despite PEEK’s (polyether-ether-ketone) VOC (volatile organic compound(s))-free chemistry, which has been assumed to improve compatibility with oil cooling, adhesion and manufacturability within the chosen insulation stack must be verified at the system level.

Concurrent trends in power electronics raise the bar further. Wide-bandgap semiconductor devices (SiC, GaN), higher $dv/dt$, and tighter packaging amplify electro-thermal stress (thermally induced electrical stress) coupling within the stator end-region and across insulation interfaces. Such shifts in device and packaging technology compound the challenges posed by liquid-cooled environments and scaling effects, creating service conditions that are faster-changing, more spatially non-uniform, and more tightly coupled across physical domains than the assumptions underpinning classical lifetime models. Junction-to-winding transients propagate more aggressively, PD inception thresholds are approached earlier, and local hotspots emerge at resin-copper or resin-fluid interfaces where property mismatches are sharpest. As a result, the margin between design specification and onset of degradation becomes narrower, making predictive models more sensitive to both material variability and mission-profile uncertainties.

Taken together, these realities show that insulation lifetime prediction can no longer rely on single-stress Arrhenius extrapolations or inert specimen tests. Direct liquid cooling introduces chemistry-conditioned parameter drift, specimen-to-stator translation demands probabilistic scaling, and advanced semiconductor devices intensify coupled stresses at insulation interfaces. To remain predictive under such conditions, model structure must rest on four mutually reinforcing pillars: (i) co-stress accelerated data that capture the true service environment, (ii) probabilistic scaling with Weibull percentiles and size factors to bridge specimen and system levels, (iii) online parameter tracking keyed to fluid chemistry and ambient state, and (iv) AI components that learn residual nonlinearities within physics-constrained bounds. Embedding this hybrid framework into ROD and PHM enables early material screening, system-level qualification, and sustained reliability across transportation platforms where safety, cost, and availability are non-negotiable.

9. Conclusions

The modelling of insulation thermal ageing has evolved from its origins in fundamental chemistry to becoming a practical tool in the design and reliability assessment of EMs. Early empirical models, such as the Arrhenius–Dakin and Montsinger frameworks, established the conceptual basis for linking temperature to insulation lifetime shortening. Subsequent refinements have improved predictive fidelity while preserving accessibility for industrial use. ATA tests and Weibull-based statistical post-processing have further provided the experimental foundation for calibrating and validating these models, ensuring that degradation pathways can be quantified with statistical confidence.

In parallel, the adoption of the PoF approach has embedded lifetime prediction into ROD, moving away from safety-factor and over-engineering heuristics towards test-validated models. This integration allows insulation reliability to be treated as a main design objective, informing material selection and geometry optimisation while also supporting condition-based maintenance strategies through prognostics and health management. As in power electronics, where PoF has driven a paradigm shift in reliability practice, its application to EISs for EMs ensures that design and operational decisions are guided by physics-based evidence rather than assumptions of constant failure rates.

Prospectively, a hybrid approach that fuses PoF with AI offers a path to address the nonlinearities, coupled stresses, and mission-dependent variability that challenge traditional models. Physics-constrained learning, co-stress accelerated testing, and chemistry-conditioned parameter tracking are emerging as key enablers for robust lifetime prediction under complex service conditions. By uniting mechanistic interpretability with data-adaptive inference, the hybrid approach promises to enhance predictive accuracy, improve generalisability, and increase operator trust in prognostics for mission-critical applications.

In summary, the historical progression from chemical kinetics to hybrid PoF–AI frameworks illustrates a clear trajectory that insulation thermal ageing models have matured from explanatory mathematical equations into actionable design tools. Their continuing refinement will underpin the reliability, safety, and lifecycle optimisation of next-generation EMs deployed in increasingly demanding environments.