Wind-Induced Stability Identification and Safety Grade Catastrophe Evaluation of a Dish Concentrating Solar Thermal Power System
Abstract
1. Introduction
2. Fluid–Structure Coupling Simulation Model and Verification
2.1. Conservation Equations
- (1)
- Fluid control equations
- (2)
- Solid control equation
- (3)
- Fluid–structure coupling equation
- (1)
- Using computational fluid dynamics (CFD) software 2025 to solve the average wind pressure p(1) corresponding to the initial shape of the DSC of the DCSTPS;
- (2)
- Using a static calculation program to determine the deformation x(1) of a DSC of the DCSTPS under the average wind pressure p(1), which will cause a change in the surface wind pressure coefficient of the DSC of the DCSTPS;
- (3)
- Based on the deformation of x(1), using CFD software again to solve the average wind pressure p(2) of the disk solar concentrator of the DCSTPS, and obtaining the deformation x(2) of the DSC of the DCSTPS under the action of p(2). If x(1) ≈ x(2), p(2) is the average wind pressure corresponding to the average deformation of the DSC of the DCSTPS. Otherwise, repeating steps (1) and (2), and continuing to solve x(i) and its corresponding average wind pressure p(i) until x(i−1) ≈ x(i), then p(i) is the average wind pressure corresponding to the average deformation of the DSC of the DCSTPS.
2.2. Modal Analysis Equation
- (1)
- Free mode of the DCSTPS
- (2)
- Fluid–structure coupling mode of the DCSTPS
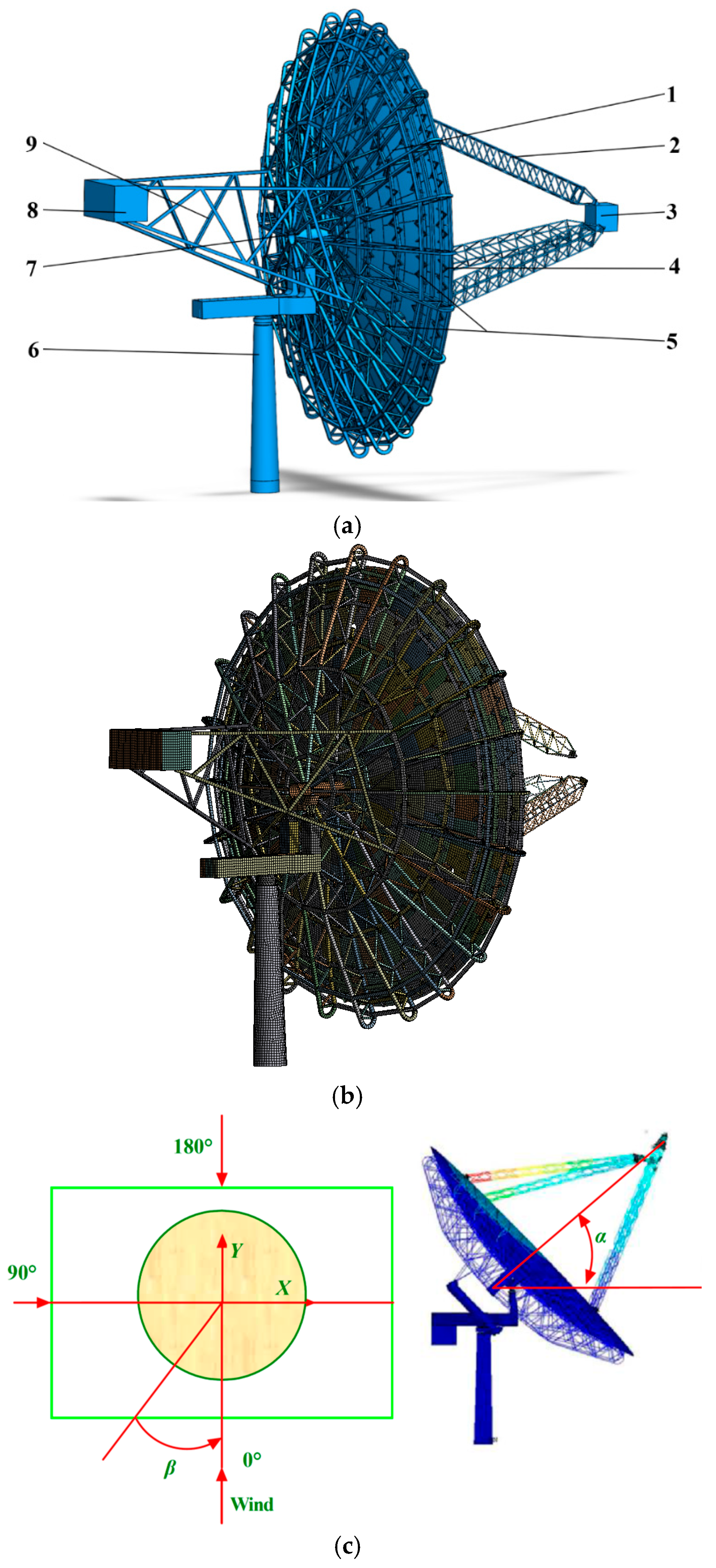
2.3. Simulation Conditions
- (1)
- Inlet of the DCSTPS: We consider that the fluid flow in this area of the DCSTPS is incompressible, and the initial wind speed is divided into constant wind speeds of 20 m/s, 22 m/s, and 25 m/s.
- (2)
- Boundary condition at the outlet of the DCSTPS: The boundary condition at the outlet is the pressure outlet, and the pressure is set to one standard atmospheric pressure, and the ambient temperature and ambient pressure are 298 K and 101.325 kPa, respectively.
- (3)
- Wall conditions in the CD of the DCSTPS: The radius of the DSC is 8.42 m and the maximum orthographic projection area is 222.5102 m2. The boundary conditions of the DCSTPS between the bottom of the CD and the surface of the DSC of the DCSTPS are set to smooth wall, and there is no velocity slip between the viscous fluids and smooth wall. The surface and the ground of the DSC are fixed and do not move, so a non-slip wall condition is set, and slip boundary conditions of the DCSTPS are used at the top, the front, and the back of the CD of the DCSTPS.
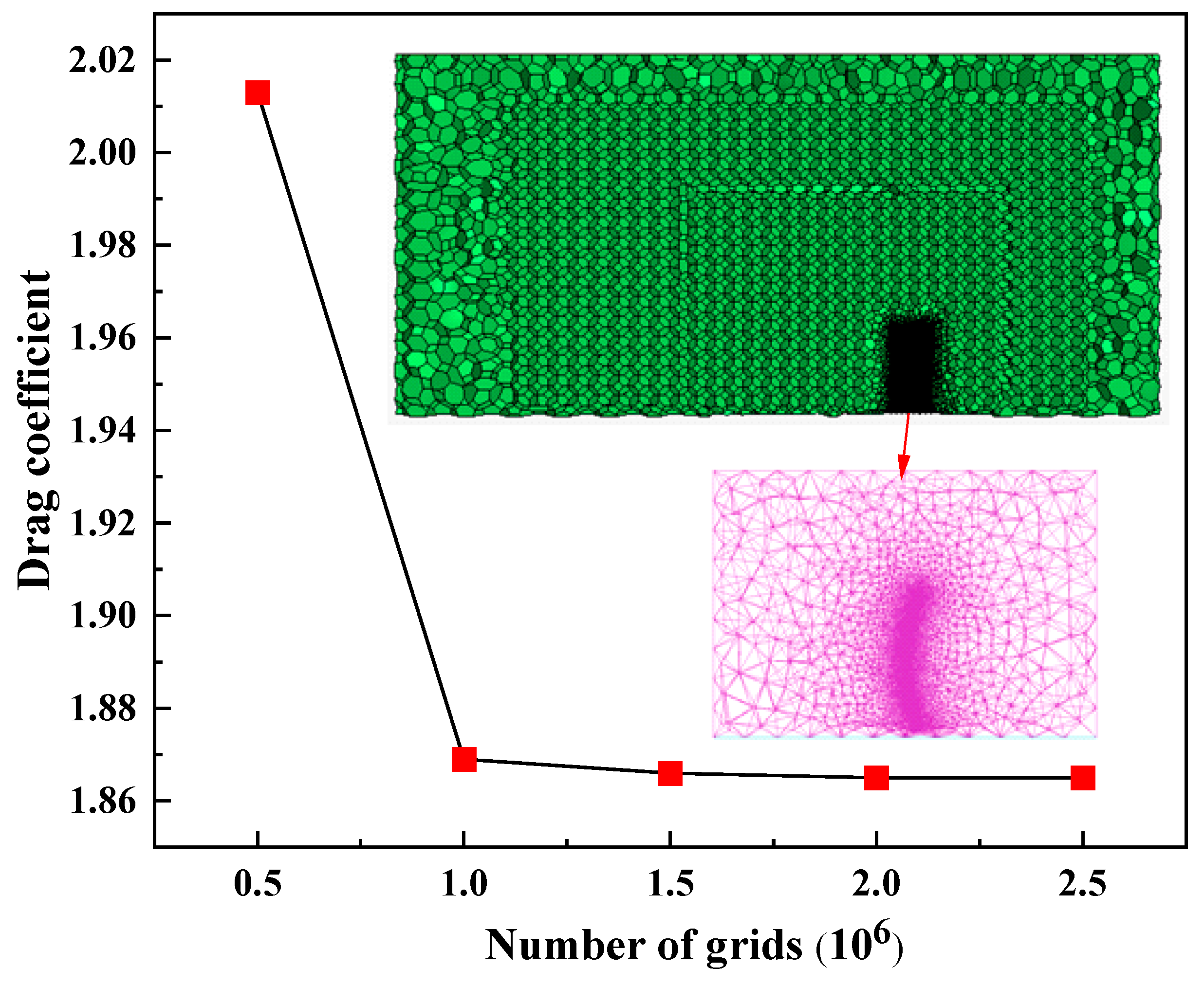
2.4. Grid Division and Grid Independence Verification
2.5. Model Validity Verification
3. Results and Discussion
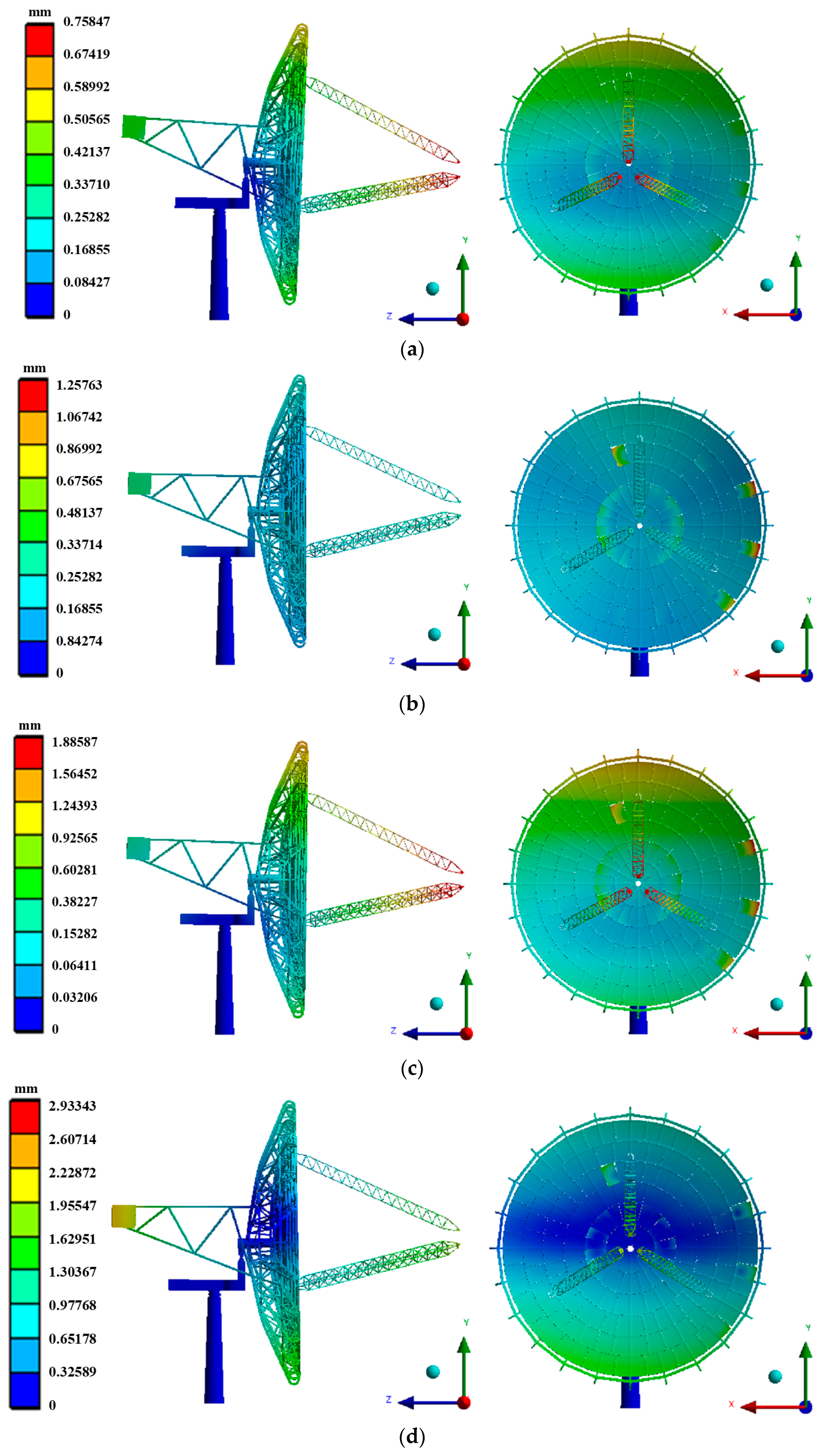
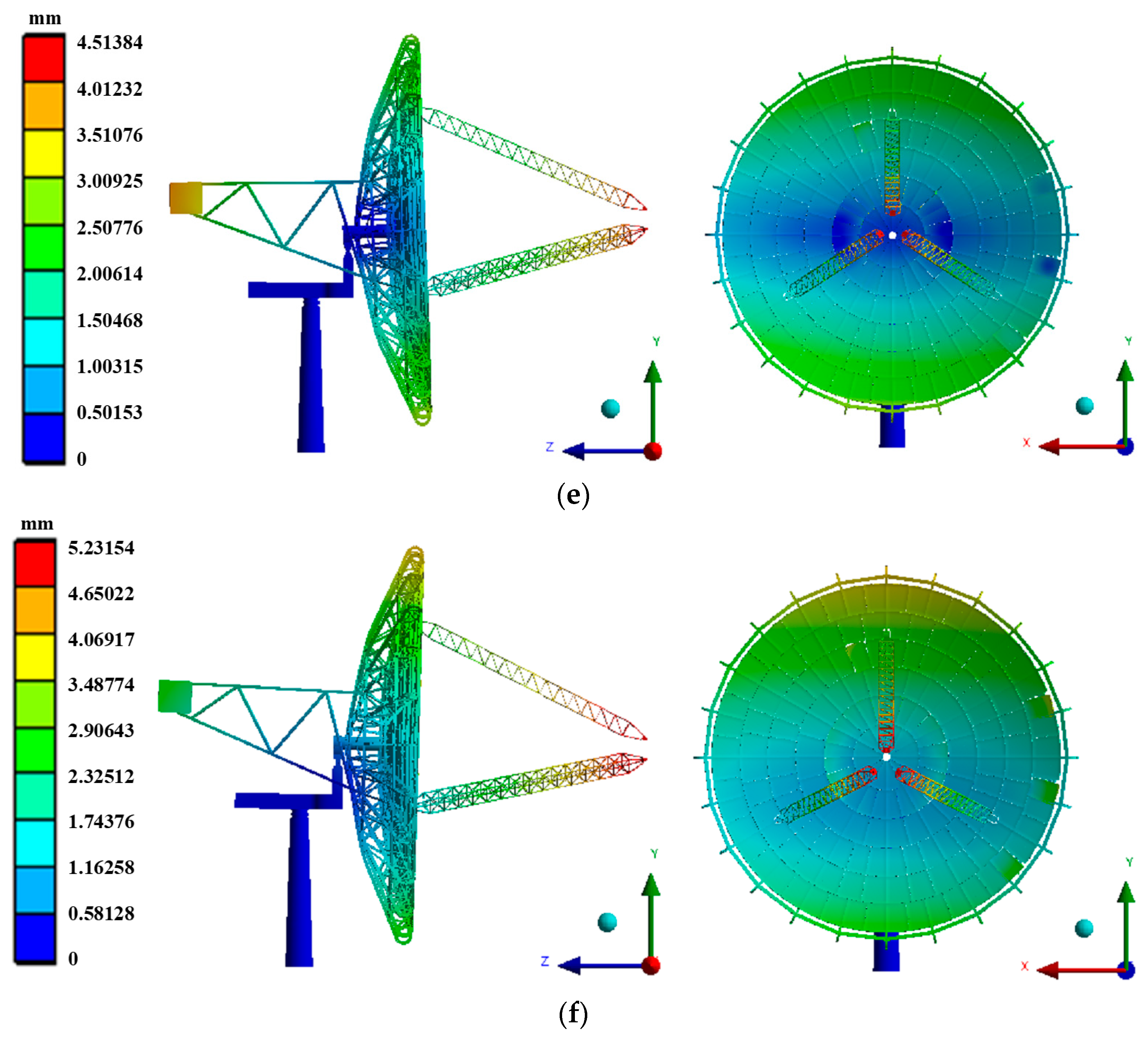
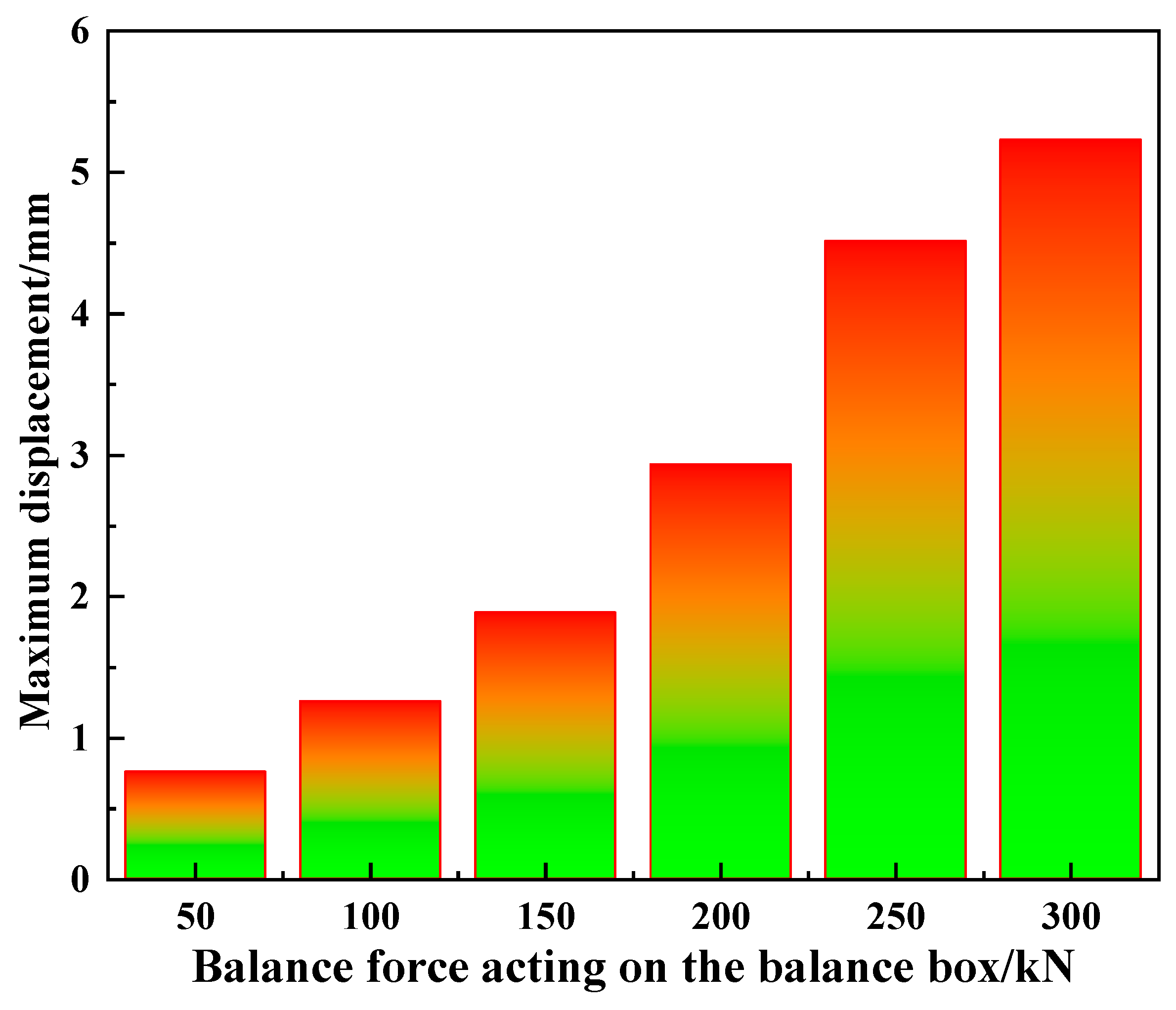
3.1. Static Analysis of the Dish Concentrating Solar Thermal Power System
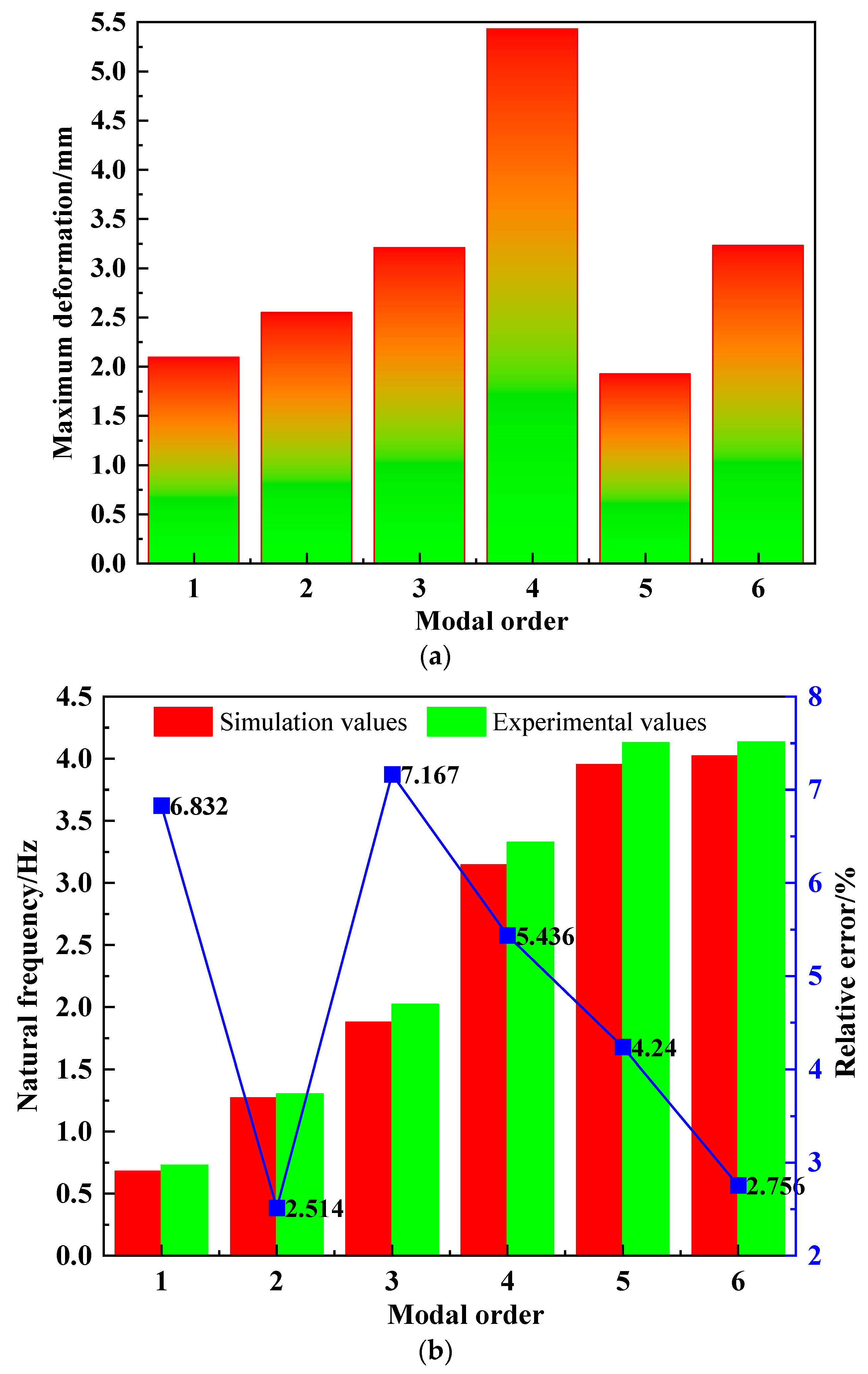
3.2. Modal Analysis
- (1)
- Compared with previous experimental values [40], the relative error is above 2.514–7.167%, indicating that the design of the balance box will reduce the natural frequency of the DCSTPS to a certain extent. At the same time, there are small differences in the material, structure, and other parameters between the established DCSTPS model and the experimental model [26], resulting in a small relative error, but the trend fluctuation of this relative error is not significant, which also proves the validity of the established DCSTPS model.
- (2)
- The fundamental natural frequency of the DCSTPS structure is 0.67910 Hz, and the natural frequency is much higher than the dominant frequency of the pulsating wind load (0.001~0.01 Hz), so the DCSTPS structure will not experience resonance phenomenon.
- (3)
- The most strongly vibrating parts of the DCSTPS structure are the edge area of the concentrator grid and the front and rear ends of the truss. The individual positions with protruding deformation are caused by an uneven distribution of model vibration, which belongs to the design problem of the DCSTPS model structure and has no impact on the overall mode of the DCSTPS in practice.
- (4)
- According to the modal analysis, the subsequent safety evaluation of the wind-induced vibration characteristic parameters of the DCSTPS model should focus on analyzing the edge position of the concentrator and the position with the strongest natural vibration, which will provide a basis for node selection.
3.3. Effects of Fluid–Structure Coupling on Natural Frequency and Maximum Deformation
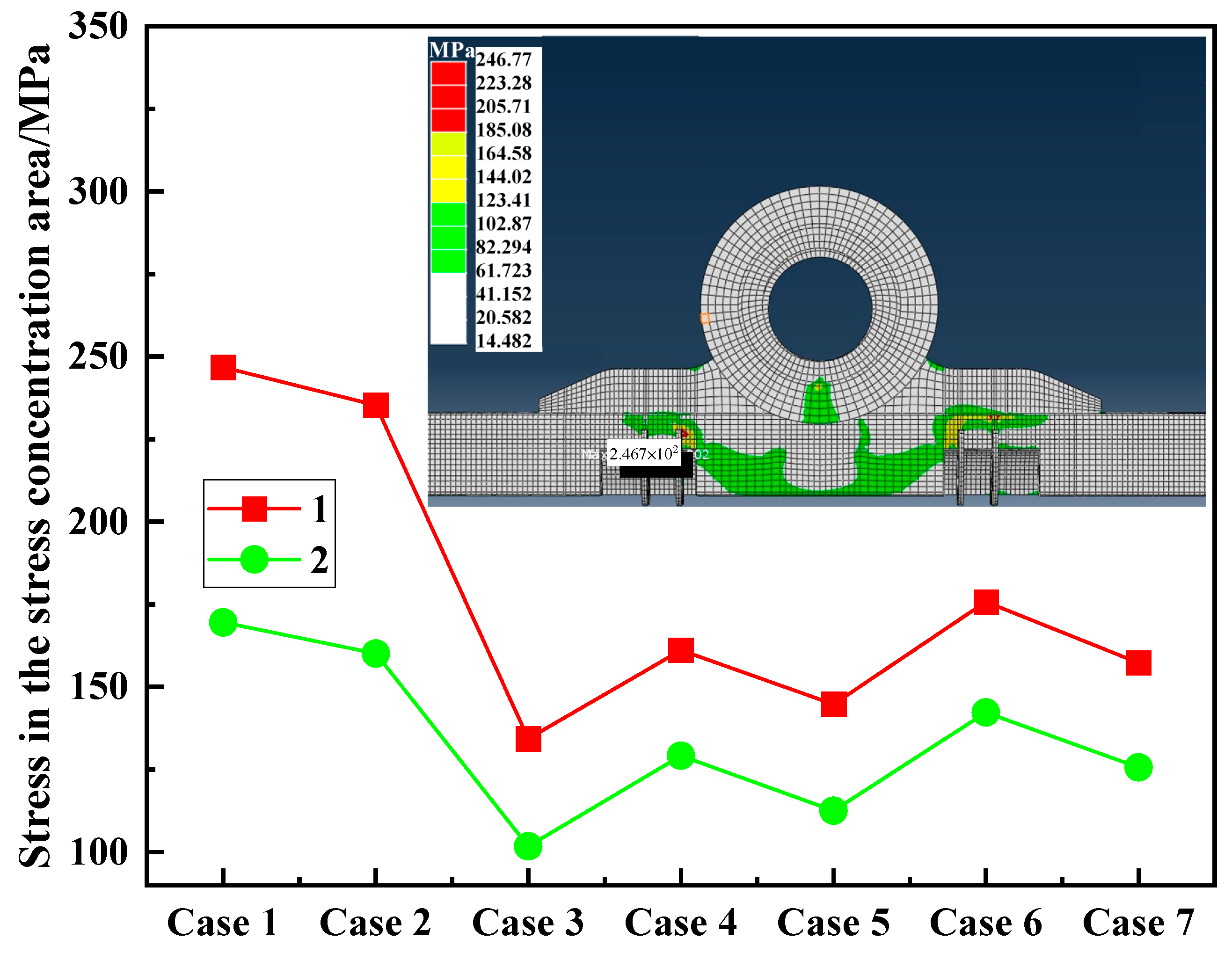
3.4. Safety Grade Evaluation of the Dish Concentrating Solar Thermal Power System Based on Catastrophe Modeling
- (1)
- Evaluation standards for safety grade of the DCSTPS
- (2)
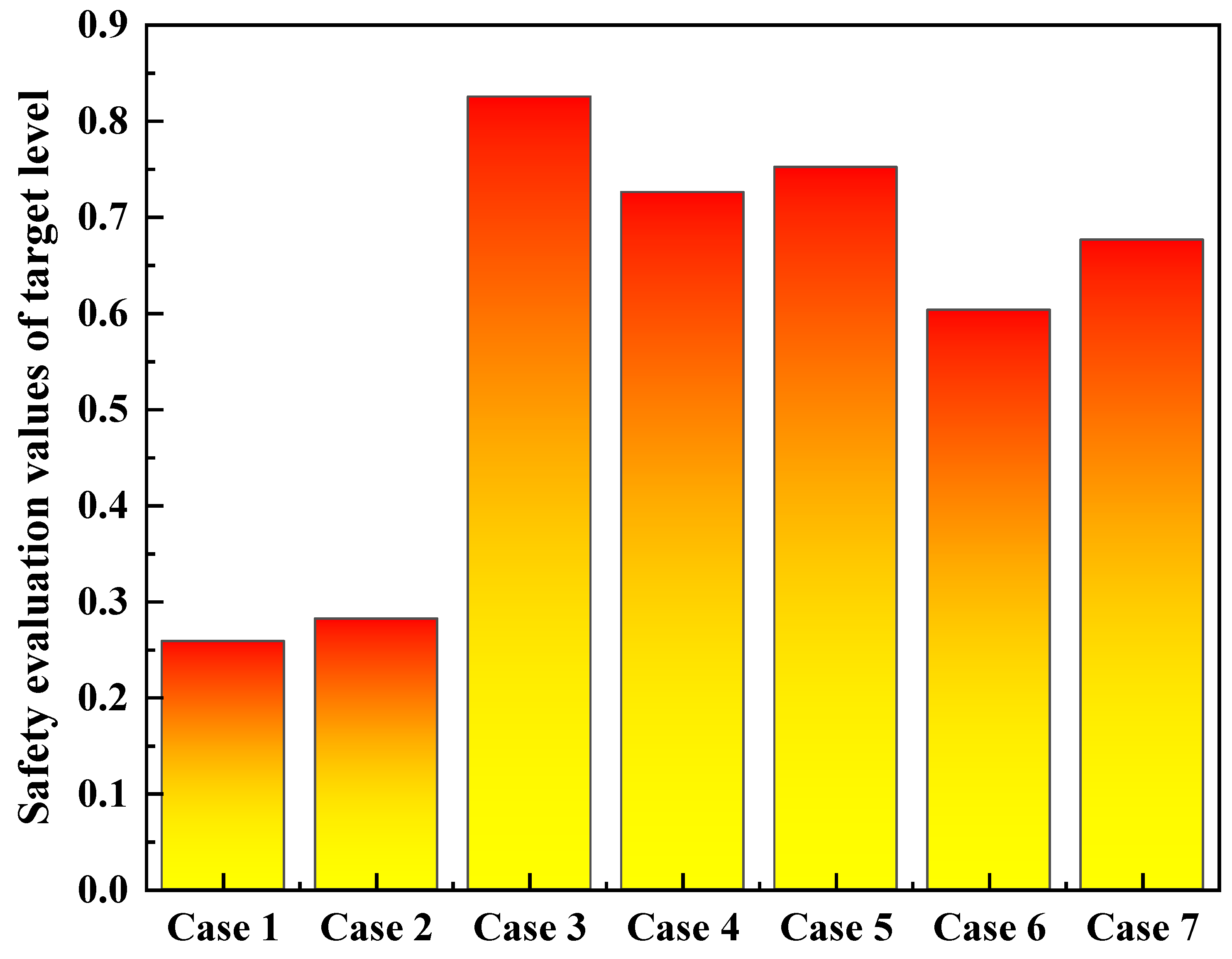
- Safety grades of the DCSTPS normalized by Catastrophe models
- (1)
- For case 1: xu = 0.9877; xv = 0.0173; xw = 0.1189.
- (2)
- Similarly, for case 2: xu = 1.0000, xv = 0.0224, xw = 0.1316; case 3: xu = 0.9262, xv = 0.5628, xw = 0.4819; case 4: xu = 0.9178, xv = 0.3828, xw = 0.6231; case 5: xu = 0.8352, xv = 0.4257, xw = 0.3420; case 6: xu = 0.8150, xv = 0.2198, xw = 0.2839; and case 7: xu = 0.8149, xv = 0.3097, xw = 0.4130.
4. Conclusions
- (1)
- According to the static analysis results, applying different forces to the balance box has a significant impact on the overall deformation of the DCSTPS model. Under α = 0° and β = 0°, the maximum displacement of the DCSTPS is basically at the connection between the cantilever and the Stirling generator, while the deformation of the support structure is mainly at the edges of the upper and lower parts of the concentrator.
- (2)
- According to the modal analysis results, the most strongly vibrating parts of the DCSTPS are the edge area of the concentrator grid and the front and rear ends of the truss grid. The fundamental natural frequency of the DCSTPS is 0.67910 Hz, and the natural frequency of the DCSTPS is much higher than the dominant frequency of the pulsating wind load (0.001~0.01 Hz), so the DCSTPS will not experience strong resonance phenomena.
- (3)
- The absolute values of the relative errors of the natural frequency of the DCSTPS and the maximum deformation of the DCSTPS decrease with the increase in the modal order considering the effect of FSC. This is mainly because the FSC has the effect of suppressing the deformation of higher order modes of the DCSTPS. Therefore, the fluid has a greater effect on the maximum deformation of a lower order DCSTPS, while having a smaller effect on the maximum deformation of a higher order DCSTPS. Additionally, considering the effect of FSC, the natural frequencies of all orders decrease, with the first-order natural frequency showing the most significant decrease.
- (4)
- Taking the safety grade evaluation index of the DCSTPS as the target layer, wind load, force load, and moment load as the criterion layer, and establishing relevant index layers below the criterion layer, a safety grade evaluation index system for the DCSTPS was ultimately established. On this basis, a safety grade evaluation of the DCSTPS was conducted based on the catastrophe theory. The results showed that the safety grade of the DCSTPS was 0.2586 and 0.2819 under case 1 and case 2. Through analysis and calculation, it was found that the membership value of the moment load was low, resulting in the stress on the connection seat of the altitude angle and the steering device of the base approaching the allowable stress of the material. This indicates that there are weak links in the system’s structural design, and such safety issues should be avoided in future design optimization work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
Greek Letters
References
- He, Y.L.; Qiu, Y.; Wang, K.; Yuan, F.; Wang, W.Q.; Li, M.J.; Guo, J.Q. Perspective of concentrating solar power. Energy 2020, 198, 117373. [Google Scholar] [CrossRef]
- Yu, Q.; Li, X.; Wang, Z.; Zhang, Q. Modeling and dynamic simulation of thermal energy storage system for concentrating solar power plant. Energy 2020, 198, 117183. [Google Scholar] [CrossRef]
- Shi, P.; Li, J.; Song, Y.; Xu, N.; Zhu, J. Cogeneration of clean water and valuable energy/resources via interfacial solar evaporation. Nano Lett. 2024, 19, 5673–5682. [Google Scholar] [CrossRef]
- Conceição, R.; González-Aguilar, J.; Merrouni, A.A.; Romero, M. Soiling effect in solar energy conversion systems: A review. Renew. Sustain. Energy Rev. 2022, 162, 112434. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Paneru, B.; Paneru, B.; Alexander, V.; Nova, S.; Bhattarai, N.; Poudyal, R.; Narayan Poudyal, K.; Dangi, M.B.; Boland, J.J. Solar energy for operating solar cookers as a clean cooking technology in South Asia: A review. Sol. Energy 2024, 283, 113004. [Google Scholar] [CrossRef]
- Ho, C.K. Advances in central receivers for concentrating solar applications. Sol. Energy 2017, 152, 38–56. [Google Scholar] [CrossRef]
- Gomez-Garcia, F.; Gonzalez-Aguilar, J.; Tamayo-Pacheco, S.; Olalde, G.; Romero, M. Numerical Analysis of Radiation Attenuation in Volumetric Solar Receivers Composed of a Stack of Thin Monolith Layers. Energy Procedia 2014, 57, 457–466. [Google Scholar] [CrossRef]
- Ho, C.K.; Khalsa, S.S.; Kolb, G.J. Methods for probabilistic modeling of concentrating solar power plants. Sol. Energy 2011, 85, 669–675. [Google Scholar] [CrossRef]
- Ho, C.K. A review of high-temperature particle receivers for concentrating solar power. Appl. Therm. Eng. 2016, 109, 958–969. [Google Scholar] [CrossRef]
- González-Pardo, A.; González-Aguilar, J.; Romero, M. Analysis of glint and glare produced by the receiver of small heliostat fields integrated in building façades. Methodology applicable to conventional central receiver systems. Sol. Energy 2015, 121, 68–77. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, L.; Zhang, H.; Ma, J.; Sambatmaryde, K. Performance analysis of a novel small-scale integrated solar-ORC system for power and heating. Sol. Energy 2024, 274, 112605. [Google Scholar] [CrossRef]
- Martínez-Hernández, A.; Conceição, R.; Asselineau, C.-A.; Romero, M.; González-Aguilar, J. Advanced surface reconstruction method for solar reflective concentrators by flux mapping. Sol. Energy 2023, 266, 112162. [Google Scholar] [CrossRef]
- Khan, M.I.; Asfand, F.; Al-Ghamdi, S.G.; Bicer, Y.; Khan, M.; Faqooq, M.; Pesyridis, A. Realizing the promise of concentrating solar power for thermal desalination: A review of technology configurations and optimizations. Renew. Sustain. Energy Rev. 2024, 208, 115022. [Google Scholar] [CrossRef]
- Rodriguez, J.; Canadas, I.; Monterreal, R.; Enrique, R.; Galindo, J. PSA SF60 solar furnace renewed. AIP Conf. Proc. 2019, 2126, 030046. [Google Scholar] [CrossRef]
- Broman, L.; Broman, A. Parabolic dish concentrators approximated by simple surfaces. Sol. Energy 1996, 57, 317–321. [Google Scholar] [CrossRef]
- Johnston, G.; Lovegrove, K.; Luzzi, A. Optical performance of spherical reflecting elements for use with paraboloidal dish concentrators. Sol. Energy 2003, 74, 133–140. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar thermal collectors and applications. Prog. Energy Combust. Sci. 2004, 3, 231–295. [Google Scholar] [CrossRef]
- Kumar, N.S.; Reddy, K.S. Comparison of receivers for solar dish collectors system. Energy Convers. Manag. 2008, 49, 812–819. [Google Scholar] [CrossRef]
- Chen, C.F.; Lin, C.H.; Jan, H.T. A solar concentrator with two reflection mirrors designed by using a ray tracing method. Opt. Int. J. Light Electron Opt. 2010, 121, 1042–1051. [Google Scholar] [CrossRef]
- Wu, W.; Wang, T.; Wang, X.; Wu, S.; Luo, Y.; Tian, X.; Zhang, Q. Hybird solar concentrator with zero self-absorption loss. Sol. Energy 2010, 84, 2140–2145. [Google Scholar] [CrossRef]
- Mlatho, J.S.P.; McPherson, M.; Mawire, A.; Heetkamp, V.R.J.J. Determination of the spatial extent of the focal point of a parabolic dish reflector using a red laser diode. Renew. Energy 2010, 35, 1982–1990. [Google Scholar] [CrossRef]
- Munir, A.; Hensel, O.; Scheffler, W. Design principle and calculations of a Scheffler fixed focus concentrator for medium temperature applications. Sol. Energy 2010, 84, 1490–1502. [Google Scholar] [CrossRef]
- Velazquez, N.; García-Valladares, O.; Sauceda, D.; Beltrán, R. Numerical simulation of a Linear Fresnel Reflector Concentrator used as direct generator in a Solar-GAX cycle. Energy Convers. Manag. 2010, 51, 434–445. [Google Scholar] [CrossRef]
- Zanganeh, G.; Bader, R.; Pedretti, A.; Pedretti, M.; Steinfeld, A. A solar dish concentrator based on ellipsoidal polyester membrane facets. Sol. Energy 2012, 86, 40–47. [Google Scholar] [CrossRef]
- Christo, F.C. Numerical modelling of wind and dust patterns around a full-scale paraboloidal solar dish. Renew. Energy 2012, 39, 356–366. [Google Scholar] [CrossRef]
- Liu, Z.; Lapp, J.; Lipiński, W. Optical design of a flat-facet solar concentrator. Sol. Energy 2012, 86, 1962–1966. [Google Scholar] [CrossRef]
- Sardeshpande, V.; Pillai, I.R. Effect of micro-level and macro-level factors on adoption potential of solar concentrators for medium temperature thermal applications. Energy Sustain. Dev. 2012, 16, 216–223. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, X.; Lu, Z.; Yu, W.; Wu, H. A review of available methods for surface shape measurement of solar concentrator in solar thermal power applications. Renew. Sustain. Energy Rev. 2012, 16, 2539–2544. [Google Scholar] [CrossRef]
- Ruelas, J.; Velazquez, N.; Cerezo, J. A mathematical model to develop a Scheffler-type solar concentrator coupled with a Stirling engine. Appl. Energy 2013, 101, 253–260. [Google Scholar] [CrossRef]
- Cheng, J.; Park, S.; Chen, C.L. Optofluidic solar concentrators using electrowetting tracking: Concept design and characterization. Sol. Energy 2013, 89, 152–161. [Google Scholar] [CrossRef]
- Ye, W.; Liu, J.; Gan, L.; Wang, H.; Qin, L.; Zang, Q.; Bordas, S.P. Fluid-structure coupling analysis in liquid-filled containers using scaled boundary finite element method. Comput. Struct. 2024, 303, 107494. [Google Scholar]
- Sun, Q.; Liu, B.; Wang, X.; Peng, W.; Lei, S. Fluid-structure coupling for particle deposition-resuspension predictions in tube bundle heat exchangers based on dynamic mesh method. Chem. Eng. Sci. 2024, 297, 120313. [Google Scholar] [CrossRef]
- John, G.S.; Lakshmanan, T. Cost optimization of dish solar concentrator system for improved scalability decisions. Renew. Energy 2017, 114, 600–613. [Google Scholar]
- Faddouli, A.; Hajji, M.; Fadili, S.; Hartiti, B.; Labrim, H.; Habchi, A. A comprehensive review of solar, thermal, photovoltaic, and thermoelectric hybrid systems for heating and power generation. Int. J. Green Energy 2024, 21, 413–447. [Google Scholar] [CrossRef]
- Pratik, N.A.; Ali, M.H.; Lubaba, N.; Hasan, N.; Asaduzzaman, M.; Miyara, A. Numerical investigation to optimize the modified cavity receiver for enhancement of thermal performance of solar parabolic dish collector system. Energy 2024, 290, 130133. [Google Scholar] [CrossRef]
- Yan, J.; Peng, Y.; Xie, X.; Liu, Y. Optical performance maintenance of solar dish collector system under service loads based on tracking compensation and receiver translational compensation methods. Energy 2024, 313, 134125. [Google Scholar] [CrossRef]
- Zuo, H.; Liu, G.; Zuo, W.; Wei, K.; Hu, W.; Tan, J.; Zhong, D. Catastrophic analysis on the stability of a large dish solar thermal power generation system with wind-induced vibration. Sol. Energy 2019, 183, 40–49. [Google Scholar] [CrossRef]
- Uzair, M.; Anderson, T.N.; Nates, R.J. The impact of the parabolic dish concentrator on the wind induced heat loss from its receiver. Sol. Energy 2017, 151, 95–101. [Google Scholar] [CrossRef]
- Zuo, H.; Tan, J.; Wei, K.; Huang, Z.; Zhong, D.; Xie, F. Effects of different poses and wind speeds on wind-induced vibration characteristics of a dish solar concentrator system. Renew. Energy 2021, 168, 1308–1326. [Google Scholar] [CrossRef]
- E, S.; Liu, Y.; Cui, Y.; Wu, A.; Yin, H. Effects of composite cooling strategy including phase change material and cooling air on the heat dissipation performance improvement of lithium ion power batteries pack in hot climate and its catastrophe evaluation. Energy 2023, 283, 129074. [Google Scholar] [CrossRef]






| Type of Catastrophe | Control Variable | State Variable | Primary Potential Functions | Divergence Equation |
|---|---|---|---|---|
| Cusp point-type model | 2 | 1 | V(x) = x4 + Ux2 + Vx | U = 6x2, V = 8x3 |
| Dovetail-type model | 3 | 1 | V(x) = x5 + Ux3 + Vx2 + Wx | U = 6x2, V = 8x3, W = 3x4 |
| Target Layer | Secondary Indicator Layer | Third Indicator Layer |
|---|---|---|
| Dish concentrating solar thermal power system safety evaluation index system | Wind load, u | Maximum surface wind pressure p (Pa), u1 |
| Air velocity (m/s), u2 | ||
| Force load, v | Lateral force (kN), v1 | |
| Drag (kN), v2 | ||
| Lift force (kN), v3 | ||
| Moment load, w | Pitch moment (N·m), w1 | |
| Rolling moment (N·m), w2 | ||
| Azimuth moment (N·m), w3 |
| Case | Altitude Angle α/° | Azimuth Angle β/° |
|---|---|---|
| 1 | 30 | 90 |
| 2 | 60 | 90 |
| 3 | 90 | 135 |
| 4 | 30 | 180 |
| 5 | 60 | 180 |
| 6 | 0 | 180 |
| 7 | 0 | 0 |
| Case | u1/Pa | u2/m·s−1 | v1/N | v2/N | v3/N | w1/N·m | w2/N·m | w3/N·m |
|---|---|---|---|---|---|---|---|---|
| 1 | 3.38 × 102 | 20.0 | 1.46 × 104 | 4.60 × 103 | −8.46 × 103 | 4.50 × 104 | −8.24 × 102 | 7.80 × 104 |
| 2 | 3.30 × 102 | 20.0 | 8.47 × 103 | 4.65 × 103 | −1.47 × 104 | 7.83 × 104 | −45.8 | 4.52 × 104 |
| 3 | 3.84 × 102 | 22.0 | −6.46 | 5.80 × 103 | −1.82 × 105 | 1.13 × 105 | −1.45 × 102 | 11.7 |
| 4 | 3.91 × 102 | 22.0 | 4.06 | 8.20 × 104 | 4.09 × 104 | 1.07 × 105 | 50.7 | 68. 9 |
| 5 | 4.73 × 102 | 25.0 | −22.4 | 4.24 × 104 | 5.50 × 104 | 1.76 × 105 | −4.07 × 102 | −2.61 × 102 |
| 6 | 4.96 × 102 | 25.0 | −84.0 | 1.28 × 105 | 2.80 × 103 | −5.60 × 104 | −16.3 | −1.80 × 103 |
| 7 | 4.97 × 102 | 25.0 | 21.9 | 1.55 × 105 | −1.83 × 103 | −4.16 × 104 | −29.4 | −4.03 × 102 |
| Case | u1 (−) | u2 (−) | v1 (−) | v2 (−) | v3 (−) | w1 (−) | w2 (−) | w3 (−) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.9755 | 1.0000 | 0.0003 | 1.0000 | 0.2160 | 0.9242 | 0.0198 | 0.0002 |
| 2 | 1.0000 | 1.0000 | 0.0005 | 0.9894 | 0.1246 | 0.5314 | 0.3557 | 0.0003 |
| 3 | 0.8579 | 0.9091 | 0.6285 | 0.7935 | 0.1003 | 0.3674 | 0.1119 | 1.0000 |
| 4 | 0.8424 | 0.9091 | 1.0000 | 0.0561 | 0.0446 | 0.3883 | 0.3210 | 0.1702 |
| 5 | 0.6976 | 0.8000 | 0.1812 | 0.1085 | 0.0332 | 0.2363 | 0.0400 | 0.0450 |
| 6 | 0.6643 | 0.8000 | 0.0483 | 0.0360 | 0.6537 | 0.7436 | 1.0000 | 0.0065 |
| 7 | 0.6640 | 0.8000 | 0.1851 | 0.0297 | 1.0000 | 1.0000 | 0.5530 | 0.0291 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, H.; Su, Y.; Liang, J.; Jia, G.; Chen, M.; Nie, D.; E, J. Wind-Induced Stability Identification and Safety Grade Catastrophe Evaluation of a Dish Concentrating Solar Thermal Power System. Energies 2025, 18, 6088. https://doi.org/10.3390/en18236088
Zuo H, Su Y, Liang J, Jia G, Chen M, Nie D, E J. Wind-Induced Stability Identification and Safety Grade Catastrophe Evaluation of a Dish Concentrating Solar Thermal Power System. Energies. 2025; 18(23):6088. https://doi.org/10.3390/en18236088
Chicago/Turabian StyleZuo, Hongyan, Yuhao Su, Jingwei Liang, Guohai Jia, Mang Chen, Duzhong Nie, and Jiaqiang E. 2025. "Wind-Induced Stability Identification and Safety Grade Catastrophe Evaluation of a Dish Concentrating Solar Thermal Power System" Energies 18, no. 23: 6088. https://doi.org/10.3390/en18236088
APA StyleZuo, H., Su, Y., Liang, J., Jia, G., Chen, M., Nie, D., & E, J. (2025). Wind-Induced Stability Identification and Safety Grade Catastrophe Evaluation of a Dish Concentrating Solar Thermal Power System. Energies, 18(23), 6088. https://doi.org/10.3390/en18236088








