Research on the Optimal Economic Proportion of Medium- and Long-Term Contracts and Spot Trading Under the Market-Oriented Renewable Energy Context
Abstract
1. Introduction
- (1)
- Most existing studies treat the proportion between MLT contracts and spot trading as an exogenously fixed policy parameter, lacking a systematic and quantitative analysis of its optimal endogenous level under different market conditions.
- (2)
- The modeling of key uncertainties—such as renewable generation, fuel prices, and load fluctuations—is often oversimplified, relying on deterministic or constant-volatility assumptions that fail to reflect the effects of extreme events and sudden shocks on contract structures.
- (3)
- Comparative analyses of different contract forms, such as financial Contracts for Difference (CfDs) and physical delivery contracts, remain limited, leaving unclear their relative advantages, efficiency, and suitability in high-renewable electricity markets.
- (4)
- Few studies incorporate advanced uncertainty-optimization perspectives, including stochastic, robust, or distributionally robust optimization, into electricity market modeling, leading to an incomplete understanding of how deep uncertainty and risk aversion jointly influence the optimal balance between MLT and spot trading.
2. The Model
2.1. Spot Market Clearing Mechanism
2.1.1. Cost Function and Generator Classification
2.1.2. Physical Constraints
2.1.3. Clearing Model
2.1.4. Price Formation Mechanism
2.1.5. Stochastic Environment Modeling and Randomization of the Price Process
2.2. Medium- and Long-Term Electricity Trading: A Bilateral Contract Mechanism Based on Nash Bargaining
2.2.1. Trading Structure and Variable Definition
2.2.2. Payoff Decomposition and Disagreement Point
- Spot Market Payoffs
- 2.
- Contract Cash Flows
- 3.
- Intertemporal Payoffs with Mean–Variance Risk Adjustment
- 4.
- Disagreement Point (No-Contract Baseline)
- 5.
- Nash Bargaining Model
- 6.
- Constraints
2.3. Optimization Model for the Optimal Economic Proportion of Medium- and Long-Term vs. Spot Trading
2.3.1. Volume Proportion (Contract Penetration Rate)
2.3.2. Economic Proportion (Effective Contract Penetration Rate)
3. Data and Algorithm
3.1. Data Sources and Characteristics
3.2. Algorithmic Procedure
4. Simulation Analysis
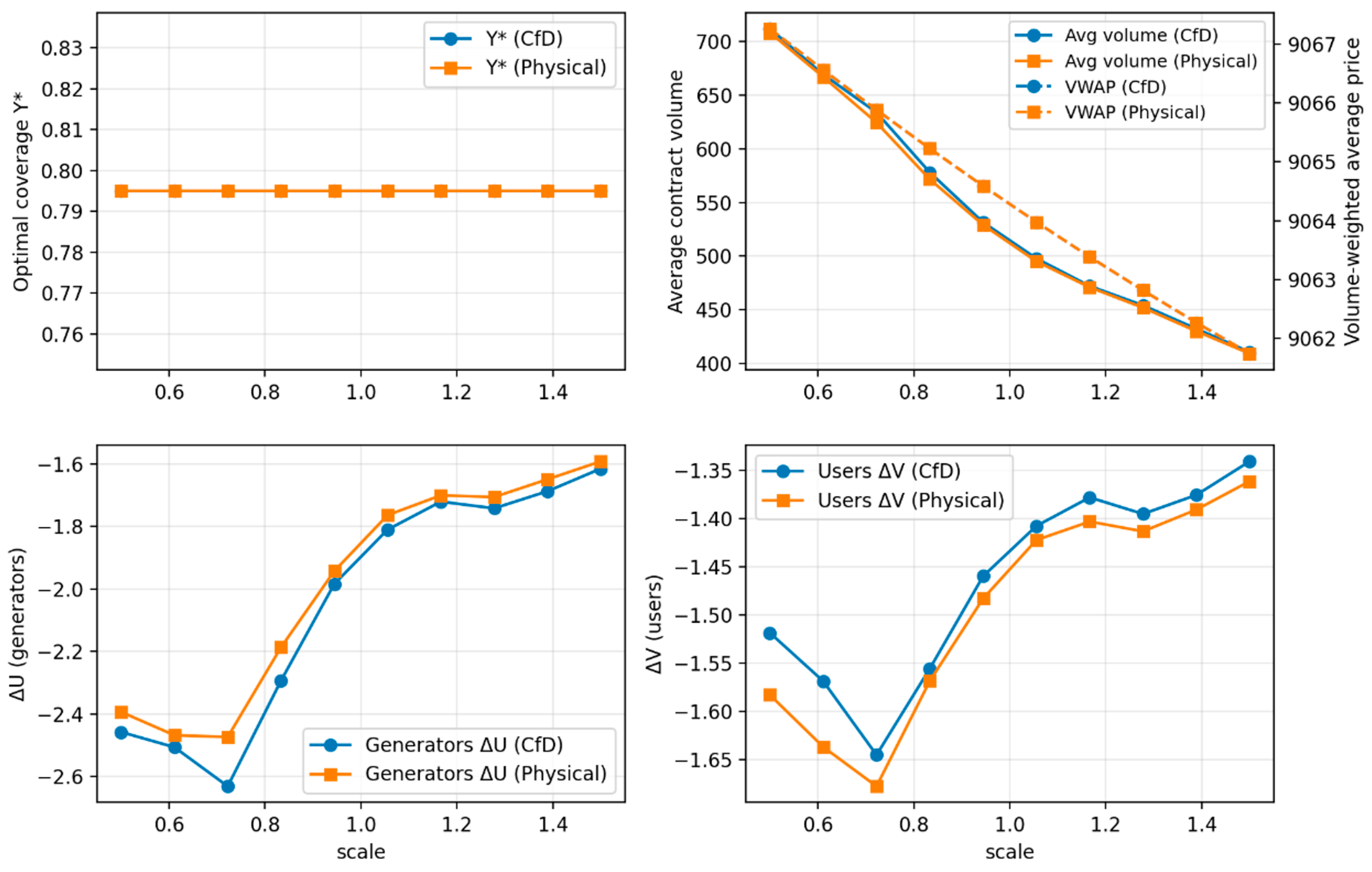
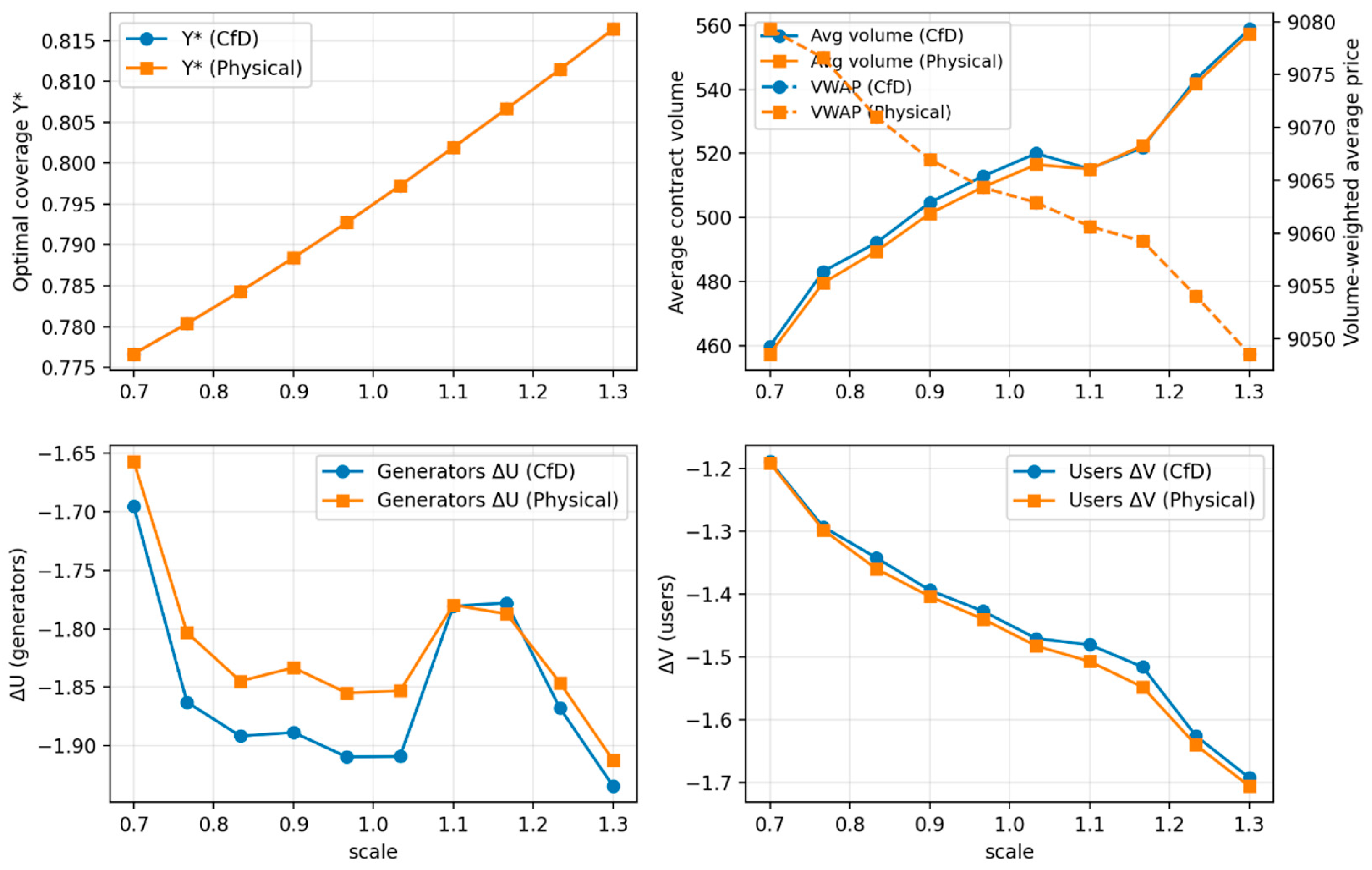
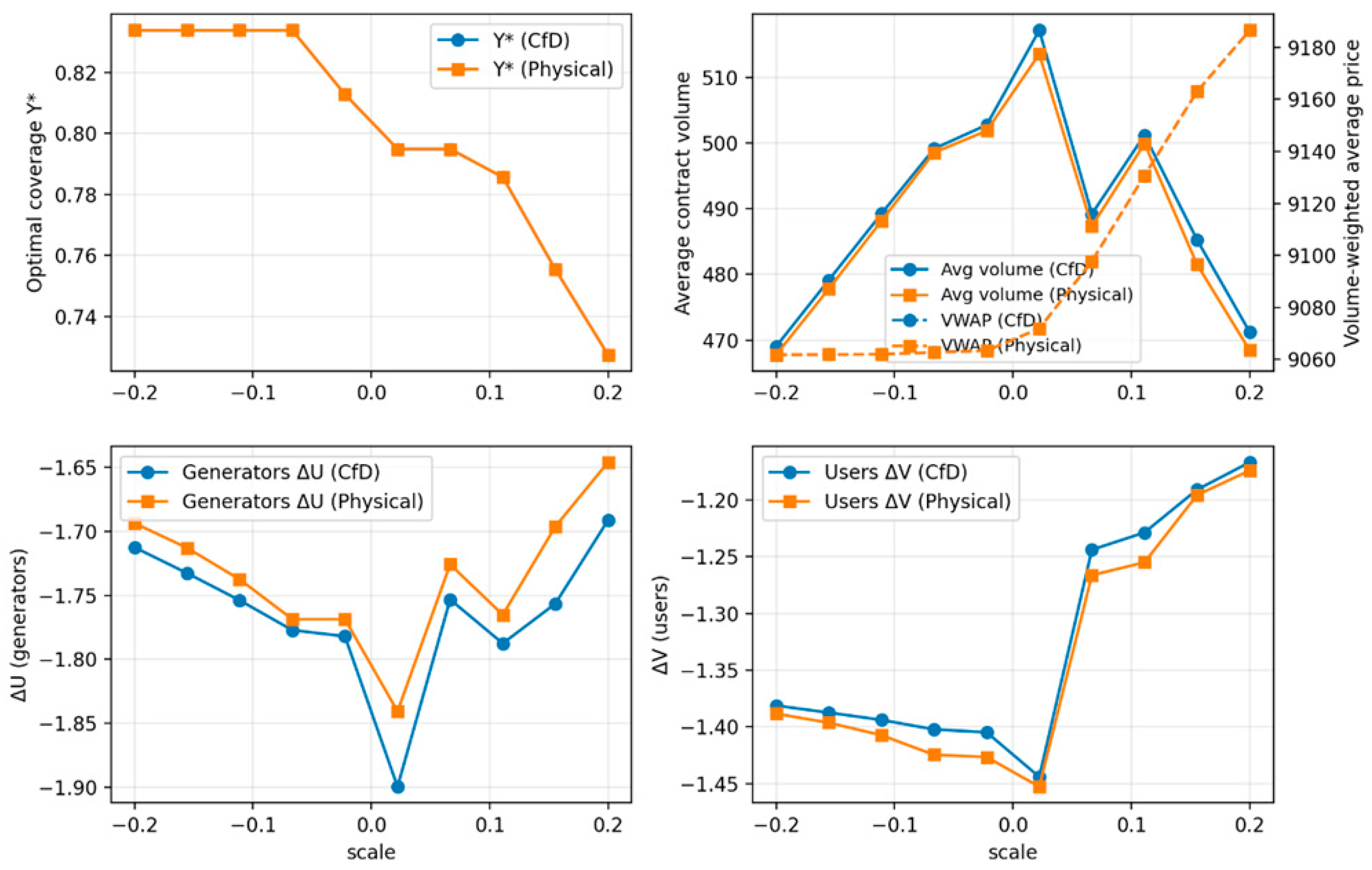
4.1. Sensitivity Analysis of Coal Price Volatility
4.2. Sensitivity Analysis of Wind and Solar Output Uncertainty
4.3. Sensitivity Analysis of Load Peak–Valley Variations
4.4. Sensitivity Analysis of Transmission Capacity Constraints
4.5. Sensitivity Analysis of Risk Aversion Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: End-to-End Solver (Spot–Contract Co-Optimization) |
| Inputs: (Enter the number of scenarios, time periods, and random number seed for the simulation.) (Mean-reverting parameter for fuel prices.) (Mean reversion and fluctuation parameters of wind power and photovoltaic power.) (Dynamic mean and fluctuation parameters of load demand.) (Grid topology data, including busbar set, line set, PTDF coefficient, and transmission capacity upper limit.) (Parameter information of the unit and the user, including capacity limit, heat rate, variable cost, etc.) (The risk aversion coefficient and negotiation weight of power generators and users.) Outputs: Output the optimal contract ratio, contract volume and price, as well as spot energy price, node electricity price and unit output. Steps: 1. Generate Monte Carlo scenario paths for fuel prices, wind speed, irradiance, and loads based on input parameters 2. The DC optimal power flow (DC-OPF) is run in all scenarios and time periods to obtain the energy price, node electricity price and maximum power generation. 3. Calculate the benchmark load demand as a reference path for the contract market. 4. Setting reference price: CfD uses the unified energy price of the entire network, and Physical uses the average of node electricity prices as the hub. 5. Searches for the optimal contract coverage ratio for financial contracts for difference (CfDs) and outputs the contract volume and price. 6. Searches for the optimal contract coverage ratio for physically delivered contracts (Physical) and outputs the contract volume and price. 7. Returns all results, including optimal contract solutions for CfDs and Physicals, as well as spot market clearing results. |
| Algorithm A2: Generate Scenarios (Fuel, RES, Demand) |
| Inputs: as in Algorithm A1
Outputs: |
| Algorithm A3: DCOPF_One Period (Cost-Minimizing, DC-flow) |
| Inputs: (thermal); (RES); demand ; GridData; Units
Outputs: , , 1: Variables: for all gens (net injection at bus b) (line flows), ≥0 (load shed), ≥0 (spillage) 2: Objective: 3: Constraints: 4: 5: 6: |
| Algorithm A4: Inner Nash_Quantities (Step-1 Quantities, Convex QP) |
| Inputs: coverage , demand path Outputs: |
| Algorithm A5: Inner Nash_Price Split (Step-2 Constant Price Splitting) |
| Inputs: ,, Units, RiskPref
Outputs: (constant bilateral prices) |
| Algorithm A6: Outer Search Y |
| Inputs: , , contract_type, GridData, Units, RiskPref Outputs: (Y*, Q*, F*) |
References
- Yang, Y.; Lo, K. China’s renewable energy and energy efficiency policies toward carbon neutrality: A systematic cross-sectoral review. Energy Environ. 2024, 35, 491–509. [Google Scholar] [CrossRef]
- De La Peña, L.; Guo, R.; Cao, X.; Ni, X.; Zhang, W. Accelerating the energy transition to achieve carbon neutrality. Resour. Conserv. Recycl. 2022, 177, 105957. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Andrews-Speed, P. Using diverse market-based approaches to integrate renewable energy: Experiences from China. Energy Policy 2019, 125, 330–337. [Google Scholar] [CrossRef]
- an, S.; Wang, W.; Li, X.; He, H.; Zhao, X. Research on cross-provincial power trading strategy considering the medium and long-term trading plan. Sci. Rep. 2024, 14, 30137. [Google Scholar]
- Khorasany, M.; Mishra, Y.; Ledwich, G. Market framework for local energy trading: A review of potential designs and market clearing approaches. IET Gener. Transm. Distrib. 2018, 12, 5899–5908. [Google Scholar] [CrossRef]
- Li, Y.; Xue, W.; Zhang, Y.; Zheng, X.; Yang, L. Promoting the sustainable development of the provincial electricity spot market: Supervision obstacle identification, analysis, and solutions based on the ISM-DEMATEL model. Front. Energy Res. 2025, 13, 1544722. [Google Scholar] [CrossRef]
- Powers, D. Fighting the Wrong Fight: Why the MLP Parity Act Is a Misguided Attempt at Achieving Renewable Energy Capital Raising Parity. Sustain. Dev. Law Policy 2017, 17, 5. [Google Scholar]
- Wang, M.; Song, Y.; Sui, B.; Wu, H.; Zhu, J.; Jing, Z.; Rong, Y. Comparative study of pricing mechanisms and settlement methods in electricity spot energy market based on multi-agent simulation. Energy Rep. 2022, 8, 1172–1182. [Google Scholar] [CrossRef]
- Li, X.; Wei, X.; Zhou, H.; Ding, Y.; Yang, B.; Wang, C. Study on Medium-and Long-term Market Trading Curve Adapted to Spot Market. In Proceedings of the 2024 7th International Conference on Energy, Electrical and Power Engineering (CEEPE), Yangzhou, China, 26–28 April 2024; pp. 1688–1693. [Google Scholar]
- Jing, Z.; Pan, J.; Ji, T. Medium and Long-Term Markets in a Hybrid Electricity Market: Definition, Challenges, and Recommendations to Guangdong Electricity Market. Chall. Recomm. Guangdong Electr. Market. 2024. [Google Scholar]
- Fu, X.; Wang, Z.; Guo, Y.; Li, W.; Tang, Z. Intra-provincial Medium-and Long-term Bidding Model Incorporating Inter-provincial Markets and Available Transmission Capacity. IEEE Trans. Energy Mark. Policy Regul. 2024, 3, 109–120. [Google Scholar] [CrossRef]
- Zhai, Z.; Zhang, L.; Wang, Y.; Hou, X.; Yang, Q. Optimization of Power Generation Structure and Electricity Transmission Pattern in China Based on the Electricity-Carbon Coordinated Market. Renew. Energy 2025, 252, 123359. [Google Scholar] [CrossRef]
- Liu, S.; Cai, B.; Gao, M.; Wu, Y.; Chen, K.; Zhu, X.; He, S. Empirical evidence for the edge of a centralized regional market over a cross-province balancing market in allocating electricity resources: A case study of Yunnan in China. Energy Rep. 2023, 9, 911–921. [Google Scholar] [CrossRef]
- Wang, M.; Xin, L.; Jin, Y.; Xu, J.; Chen, Y.; Wang, W.; Yang, B.; Wang, P. Two-Stage Bi-Level Multi-Objective Optimization Model for Equilibrium Analysis of Electricity and Carbon Markets. In Proceedings of the 2025 2nd International Conference on Smart Grid and Artificial Intelligence (SGAI), Changsha, China, 21–23 March 2025; pp. 452–457. [Google Scholar]
- Wang, P.; Wang, W.; Jiang, K.; Cheng, Y.; Zhang, T.; Li, X. Modeling the coupling of China’s multi-timescale electricity markets during the transition towards decarbonization and marketization. Energy 2025, 319, 134938. [Google Scholar] [CrossRef]
- Alishahi, E.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. A system dynamics approach for investigating impacts of incentive mechanisms on wind power investment. Renew. Energy 2012, 37, 310–317. [Google Scholar] [CrossRef]
- Ozcan, M. Assessment of renewable energy incentive system from investors’ perspective. Renew. Energy 2014, 71, 425–432. [Google Scholar] [CrossRef]
- Kim, Y.S.; Park, G.H.; Kim, S.W.; Kim, D. Incentive design for hybrid energy storage system investment to PV owners considering value of grid services. Appl. Energy 2024, 373, 123772. [Google Scholar] [CrossRef]
- Keppler, J.H. Rationales for capacity remuneration mechanisms: Security of supply externalities and asymmetric investment incentives. Energy Policy 2017, 105, 562–570. [Google Scholar] [CrossRef]
- Aquila, G.; de Oliveira Pamplona, E.; de Queiroz, A.R.; Junior, P.R.; Fonseca, M.N. An overview of incentive policies for the expansion of renewable energy generation in electricity power systems and the Brazilian experience. Renew. Sustain. Energy Rev. 2017, 70, 1090–1098. [Google Scholar] [CrossRef]
- Tarashandeh, N.; Karimi, A. Utilization of energy storage systems in congestion management of transmission networks with incentive-based approach for investors. J. Energy Storage 2021, 33, 102034. [Google Scholar] [CrossRef]
- Onofri, L. Contracts, investment incentives and efficiency in the restructured electricity market. Eur. J. Law Econ. 2003, 16, 23–28. [Google Scholar] [CrossRef]
- Onifade, T.T. Hybrid renewable energy support policy in the power sector: The contracts for difference and capacity market case study. Energy Policy 2016, 95, 390–401. [Google Scholar] [CrossRef]
- Kitzing, L.; Held, A.; Gephart, M.; Fabian, W.; Vasilios, A.; Corinna, K. Contracts-for-Difference to Support Renewable Energy Technologies: Considerations for Design and Implementation; European University Institute: Florence, Italy, 2024. [Google Scholar]
- Bunn, D.; Yusupov, T. The progressive inefficiency of replacing renewable obligation certificates with contracts-for-differences in the UK electricity market. Energy Policy 2015, 82, 298–309. [Google Scholar] [CrossRef]
- Beiter, P.; Guillet, J.; Jansen, M.; Wilson, E.; Kitzing, L. The enduring role of contracts for difference in risk management and market creation for renewables. Nat. Energy 2024, 9, 20–26. [Google Scholar] [CrossRef]
- Wild, P. Determining commercially viable two-way and one-way ‘Contract-for-Difference’ strike prices and revenue receipts. Energy Policy 2017, 110, 191–201. [Google Scholar] [CrossRef]
- Simshauser, P. On the stability of energy-only markets with government-initiated contracts-for-differences. Energies 2019, 12, 2566. [Google Scholar] [CrossRef]
- Liang, Z.; Yin, X.; Chung, C.Y.; Rayeem, S.K.; Chen, X.; Yang, H. Managing Massive RES Integration in Hybrid Microgrids: A Data-Driven Quad-Level Approach With Adjustable Conservativeness. IEEE Trans. Ind. Inform. 2025, 21, 7698–7709. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Wang, X.; Chen, S.; Zhang, C. Risk-based uncertainty set optimization method for energy management of hybrid AC/DC microgrids with uncertain renewable generation. IEEE Trans. Smart Grid 2019, 11, 1526–1542. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Shi, K.; Liang, Z.; Mo, W.; Hua, D. A multi-time reactive power optimization under interval uncertainty of renewable power generation by an interval sequential quadratic programming method. IEEE Trans. Sustain. Energy 2018, 10, 1086–1097. [Google Scholar] [CrossRef]
- Chakraborty, G.; Chandrashekhar, G.R.; Balasubramanian, G. Measurement of extreme market risk: Insights from a comprehensive literature review. Cogent Econ. Financ. 2021, 9, 1920150. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Chen, S.; Wang, Y.; Zhang, C.; Kang, C. Robust transmission expansion planning based on adaptive uncertainty set optimization under high-penetration wind power generation. IEEE Trans. Power Syst. 2020, 36, 2798–2814. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Zhang, J.H. A chance constrained transmission network expansion planning method with consideration of load and wind farm uncertainties. IEEE Trans. Power Syst. 2009, 24, 1568–1576. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Duan, C.; Lin, J.; Lyu, J. Distributionally robust optimal reactive power dispatch with Wasserstein distance in active distribution network. J. Mod. Power Syst. Clean Energy 2020, 8, 426–436. [Google Scholar] [CrossRef]
- Cao, X.; Sun, X.; Xu, Z.; Zeng, B.; Guan, X. Hydrogen-based networked microgrids planning through two-stage stochastic programming with mixed-integer conic recourse. IEEE Trans. Autom. Sci. Eng. 2021, 19, 3672–3685. [Google Scholar] [CrossRef]
- Zhao, N.; You, F. Sustainable power systems operations under renewable energy induced disjunctive uncertainties via machine learning-based robust optimization. Renew. Sustain. Energy Rev. 2022, 161, 112428. [Google Scholar] [CrossRef]
- Li, B.; Tan, Y.; Wu, A.-G.; Duan, G.-R. A distributionally robust optimization based method for stochastic model predictive control. IEEE Trans. Autom. Control 2021, 67, 5762–5776. [Google Scholar] [CrossRef]
- Aranha, A.S.; Street, A.; Fernandes, C.; Granville, S. Risk-constrained optimal dynamic trading strategies under short-and long-term uncertainties. IEEE Trans. Power Syst. 2022, 38, 1474–1486. [Google Scholar] [CrossRef]
- Poursoltani, M.; Delage, E. Adjustable robust optimization reformulations of two-stage worst-case regret minimization problems. Oper. Res. 2022, 70, 2906–2930. [Google Scholar] [CrossRef]
- Luo, F.; Mehrotra, S. Distributionally robust optimization with decision dependent ambiguity sets. Optim. Lett. 2020, 14, 2565–2594. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wang, S. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response. IEEE Trans. Smart Grid 2016, 8, 2637–2647. [Google Scholar] [CrossRef]
- Haar, L. Design flaws in united kingdom renewable energy support scheme. Energies 2021, 14, 1657. [Google Scholar] [CrossRef]
- Meyer-Brandis, T.; Tankov, P. Multi-factor jump-diffusion models of electricity prices. Int. J. Theor. Appl. Financ. 2008, 11, 503–528. [Google Scholar] [CrossRef]
- Mari, C.; Baldassari, C. Ensemble methods for jump-diffusion models of power prices. Energies 2021, 14, 2084. [Google Scholar] [CrossRef]
- Andersen, L.; Andreasen, J. Jump-diffusion processes: Volatility smile fitting and numerical methods for option pricing. Rev. Deriv. Res. 2000, 4, 231–262. [Google Scholar] [CrossRef]
- Maqbool, A.S.; Baetens, J.; Lotfi, S.; Vandevelde, L.; Van Eetvelde, G. Assessing financial and flexibility incentives for integrating wind energy in the grid via agent-based modeling. Energies 2019, 12, 4314. [Google Scholar] [CrossRef]
- Hussain, M.S.; Cho, K.; Park, S. Resource Adequacy and Integration of Renewables in Light of US, EU, and Pakistan’s Evolving Power Sector. Energies 2024, 17, 5051. [Google Scholar] [CrossRef]


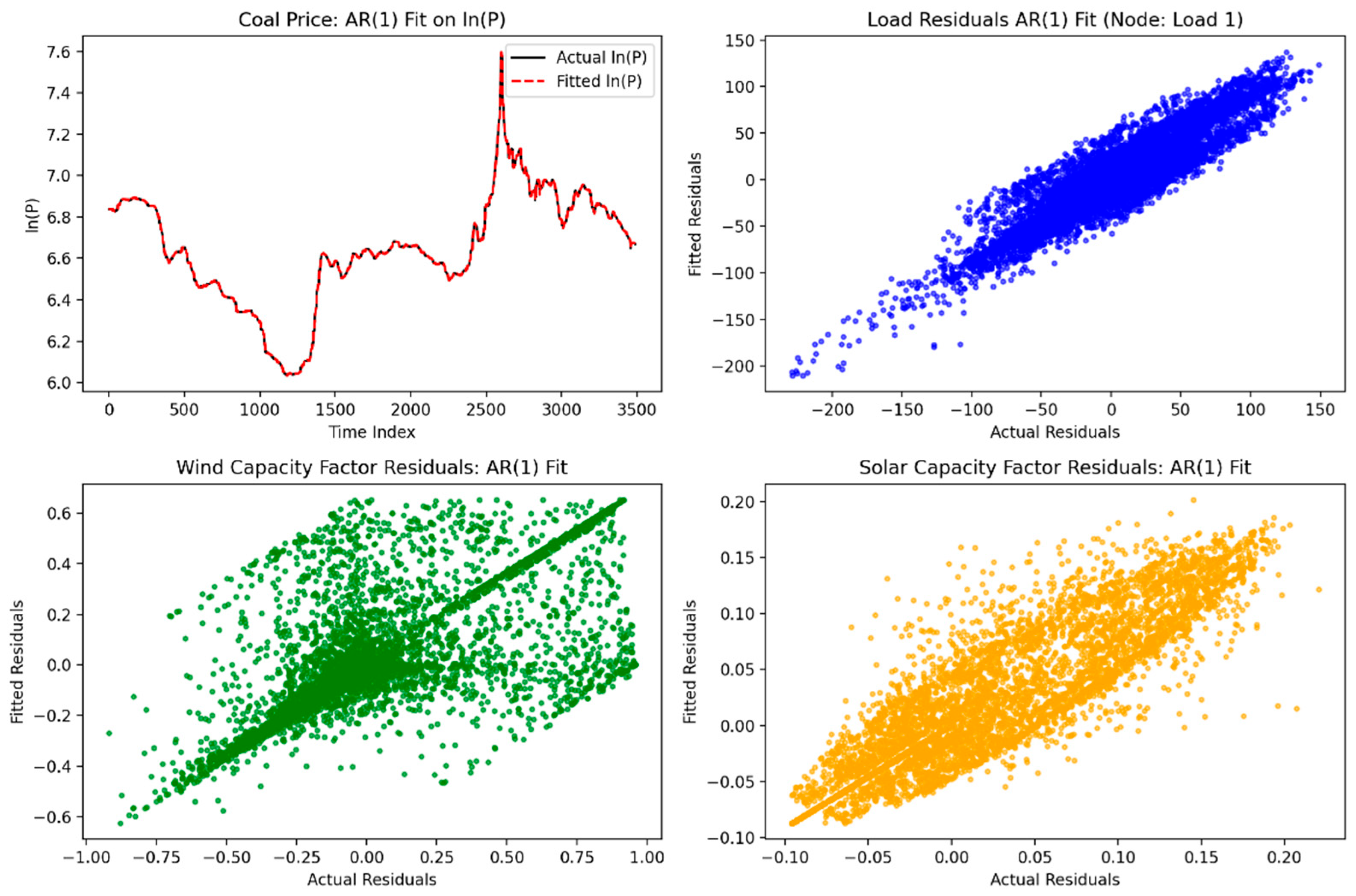


| Process | AR(1) | ||||
|---|---|---|---|---|---|
| Coal price | 0.0010 | 6.4933 | 0.0060 | 0.9193 | 0.9995 |
| wind | 0.3842 | 0.001 | 0.2642 | 0.6809 | 0.8637 |
| pv | 0.0899 | 0.001 | 0.0287 | 0.9139 | 0.8353 |
| load | 0.0841 | 23.5098 | 0.9193 | 0.8941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhao, X.; Yang, L.; Wu, M.; Yu, H. Research on the Optimal Economic Proportion of Medium- and Long-Term Contracts and Spot Trading Under the Market-Oriented Renewable Energy Context. Energies 2025, 18, 6085. https://doi.org/10.3390/en18236085
Wu Y, Zhao X, Yang L, Wu M, Yu H. Research on the Optimal Economic Proportion of Medium- and Long-Term Contracts and Spot Trading Under the Market-Oriented Renewable Energy Context. Energies. 2025; 18(23):6085. https://doi.org/10.3390/en18236085
Chicago/Turabian StyleWu, Yushi, Xia Zhao, Libin Yang, Mengting Wu, and Hongwei Yu. 2025. "Research on the Optimal Economic Proportion of Medium- and Long-Term Contracts and Spot Trading Under the Market-Oriented Renewable Energy Context" Energies 18, no. 23: 6085. https://doi.org/10.3390/en18236085
APA StyleWu, Y., Zhao, X., Yang, L., Wu, M., & Yu, H. (2025). Research on the Optimal Economic Proportion of Medium- and Long-Term Contracts and Spot Trading Under the Market-Oriented Renewable Energy Context. Energies, 18(23), 6085. https://doi.org/10.3390/en18236085






