Conducted Common-Mode Electromagnetic Interference Analysis of Gate Drivers for High-Voltage SiC Devices
Abstract
1. Introduction
2. Analysis of Common Current for Gate Driver
2.1. Modeling of Conduction Electromagnetic Interference in Gate Driver
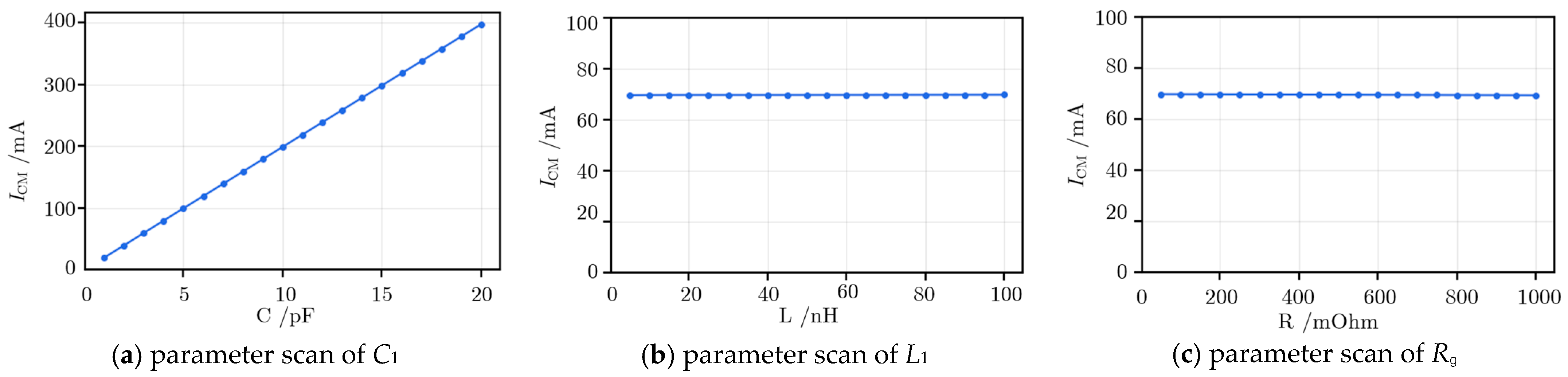
2.2. Characteristics of Common-Mode Current Magnitude in Drive Circuits
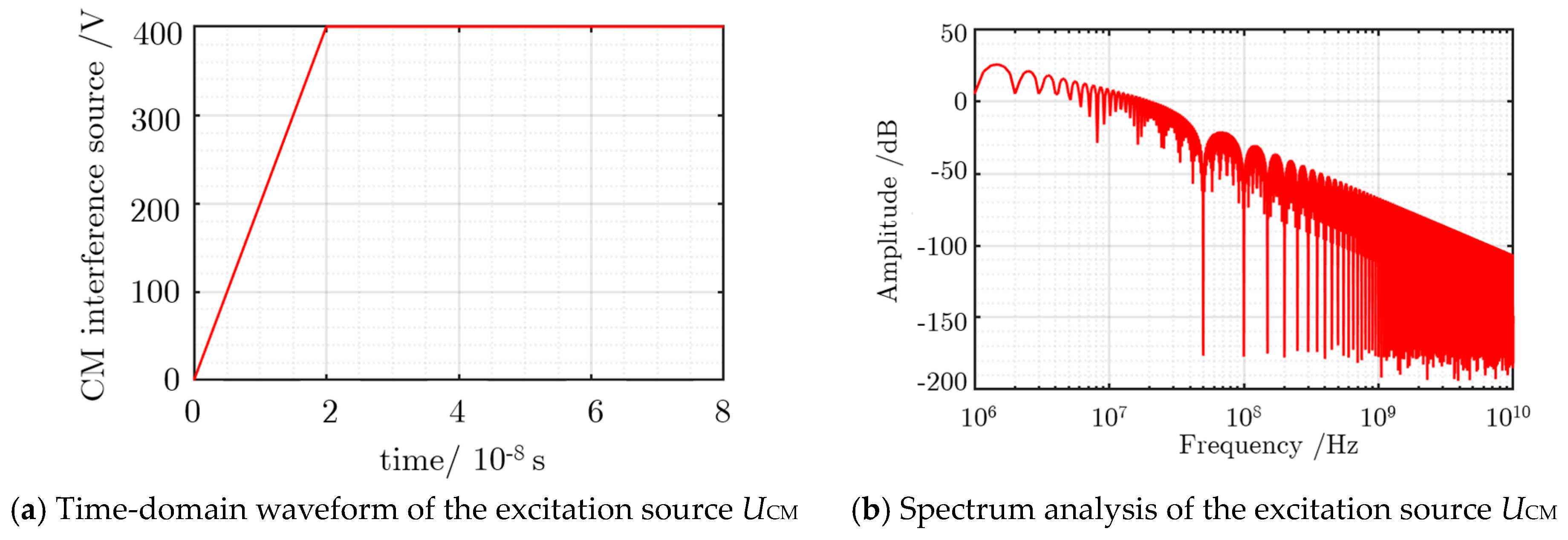
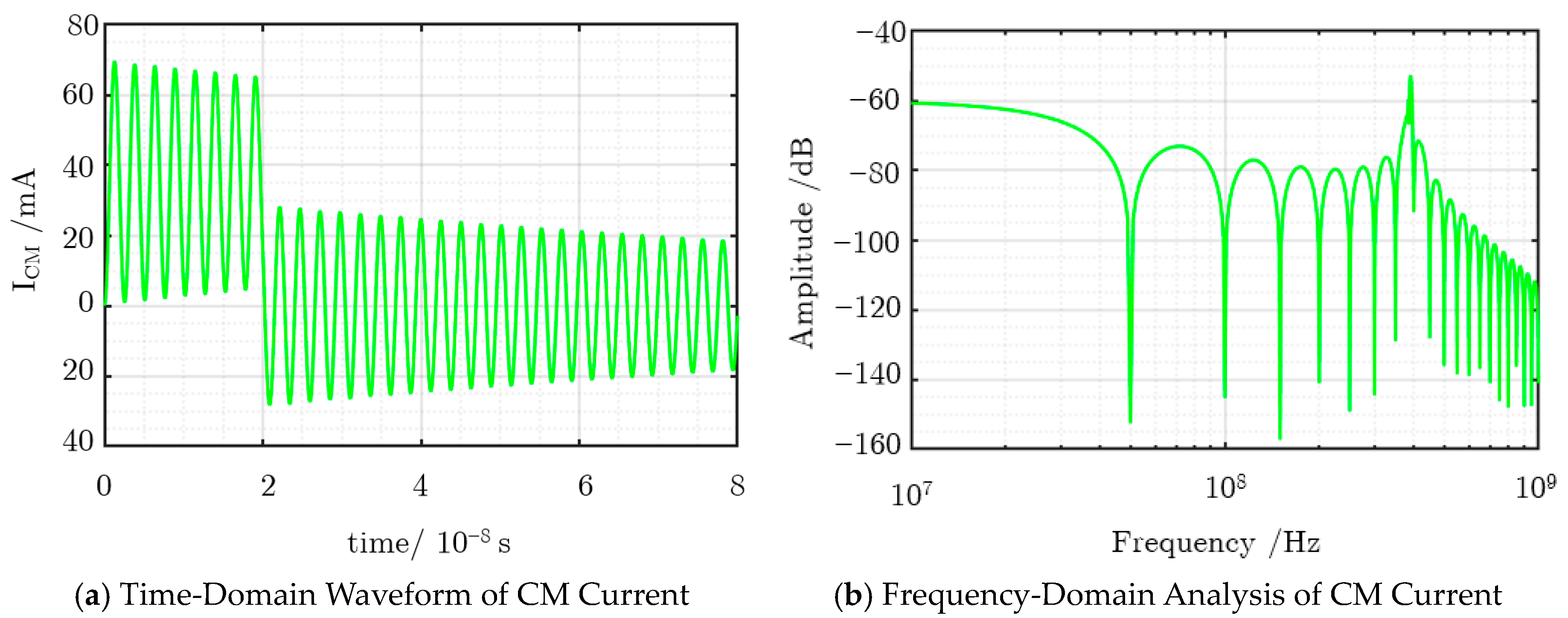
2.3. Simulation and Common-Mode Current Spectrum Analysis
3. Hardware Design of Half-Bridge Power Module
3.1. Selection of Power Device
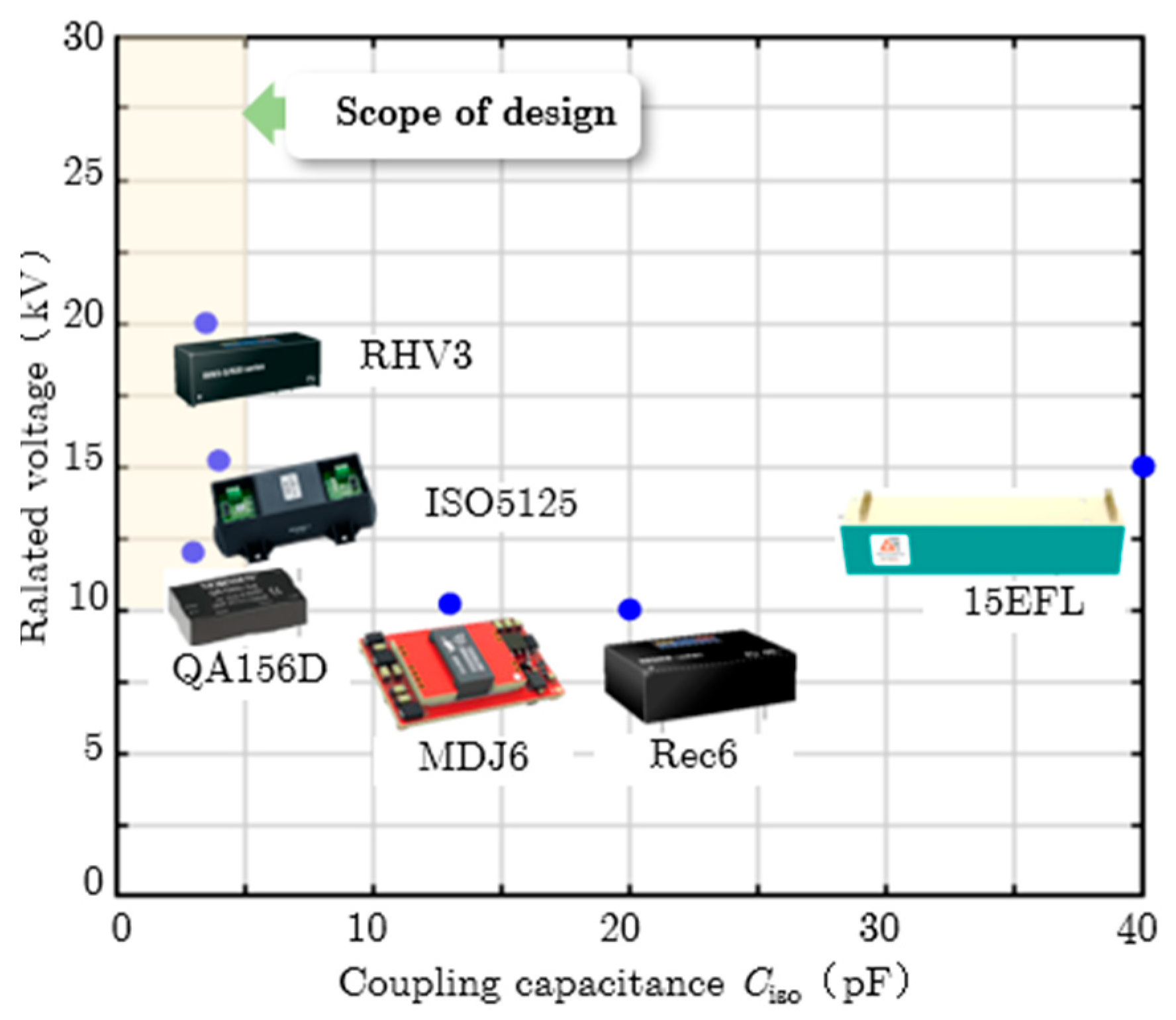
3.2. Selection of Isolated Power Supply
3.3. Gate Driver Design
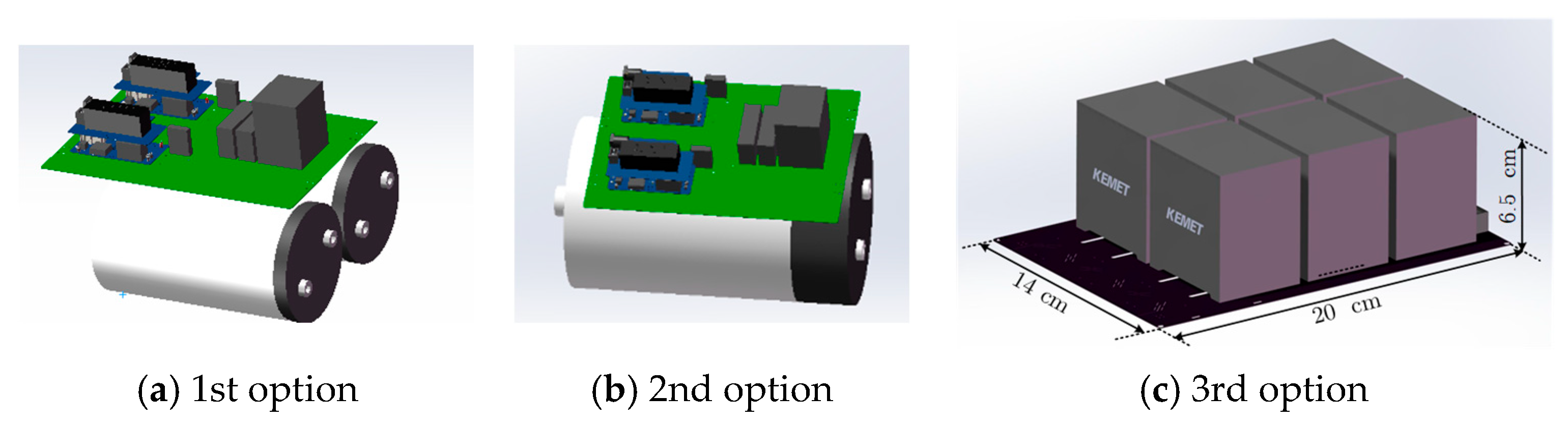
3.4. Selection of Capacitor
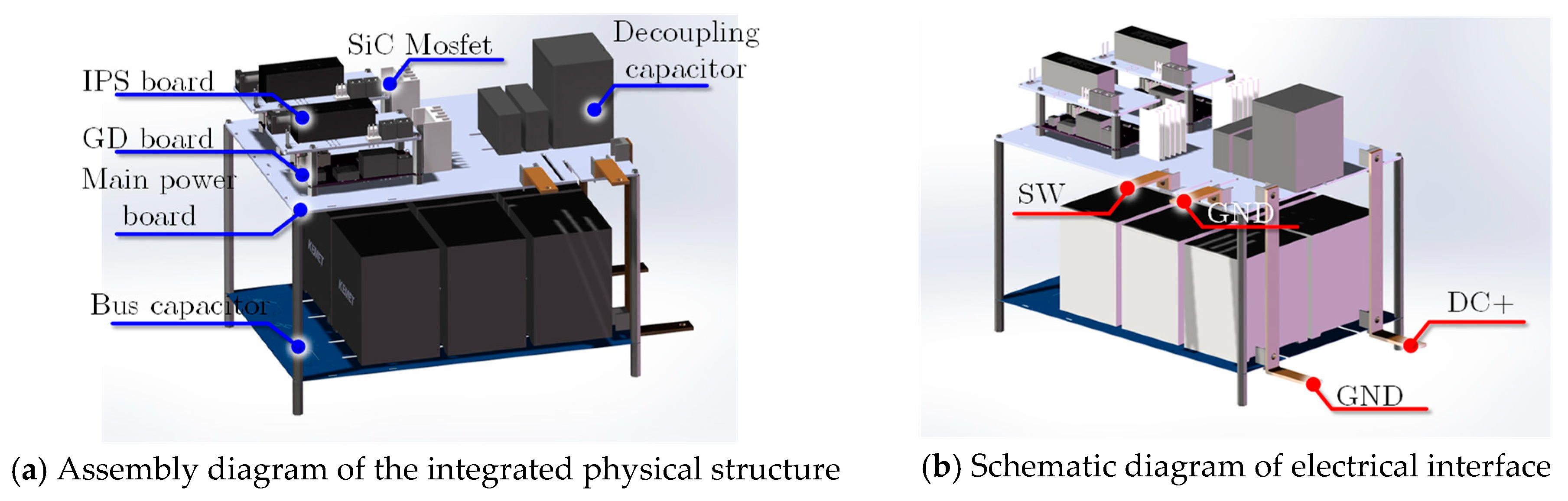
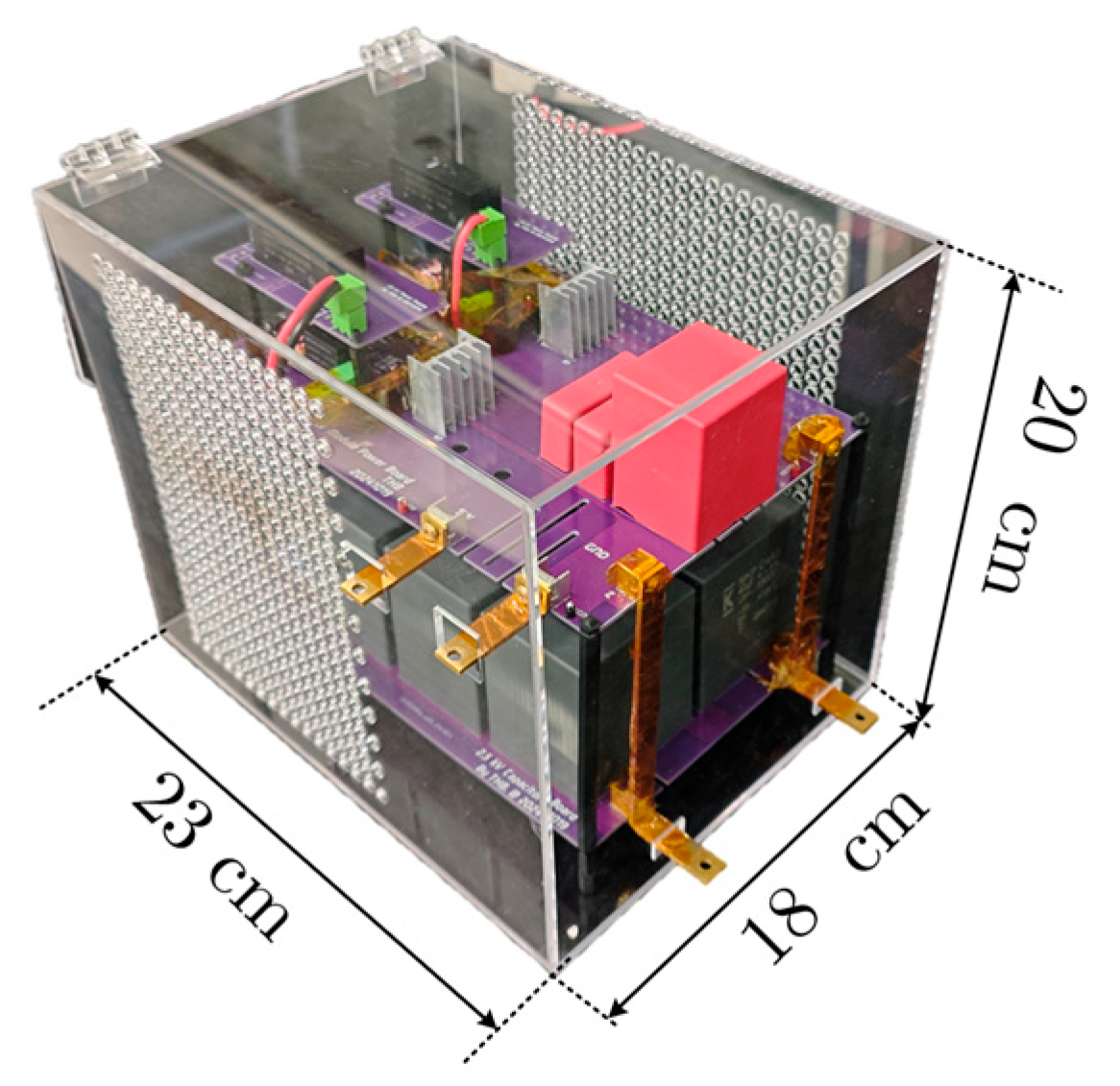
3.5. Module Integration
4. Experimental Validation
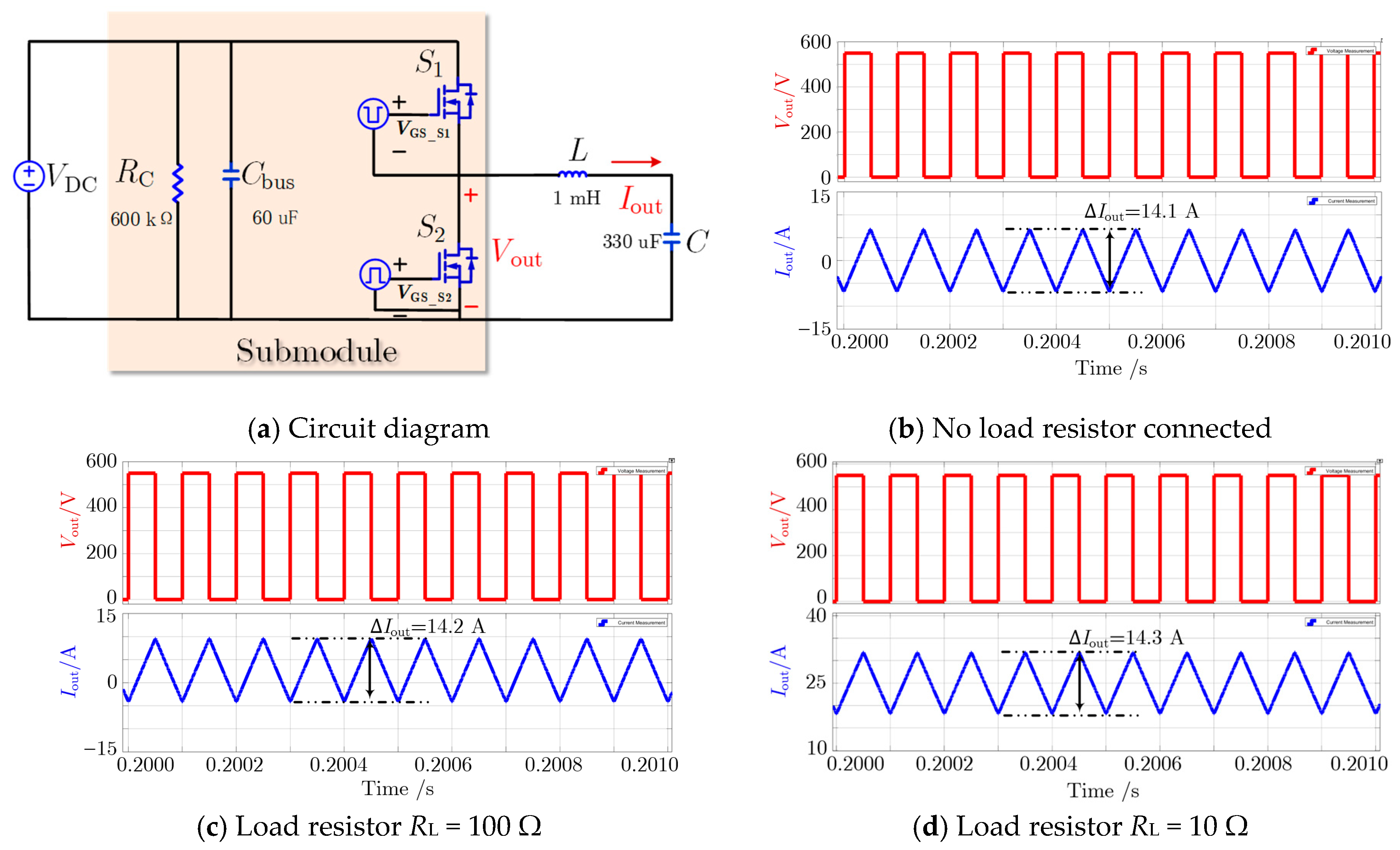
4.1. Buck Test
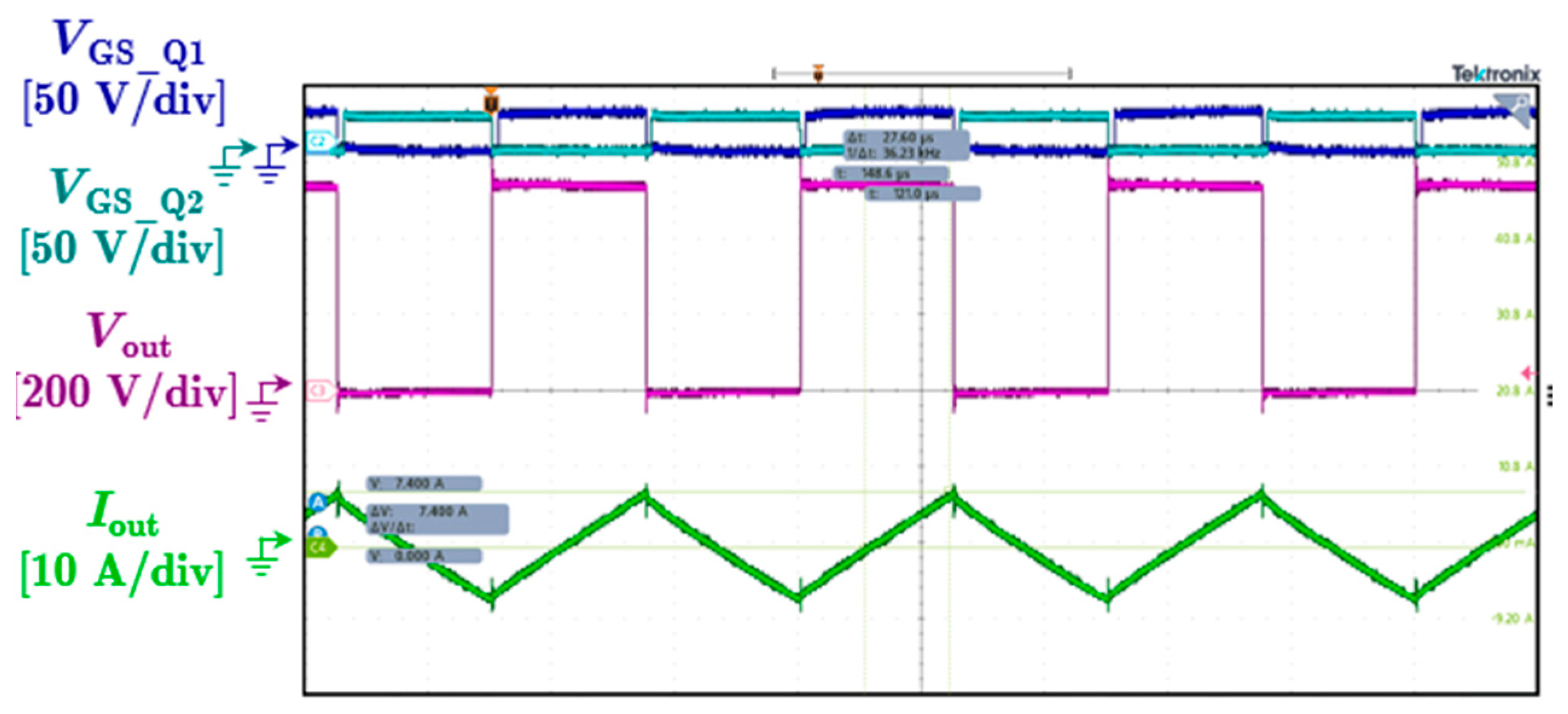
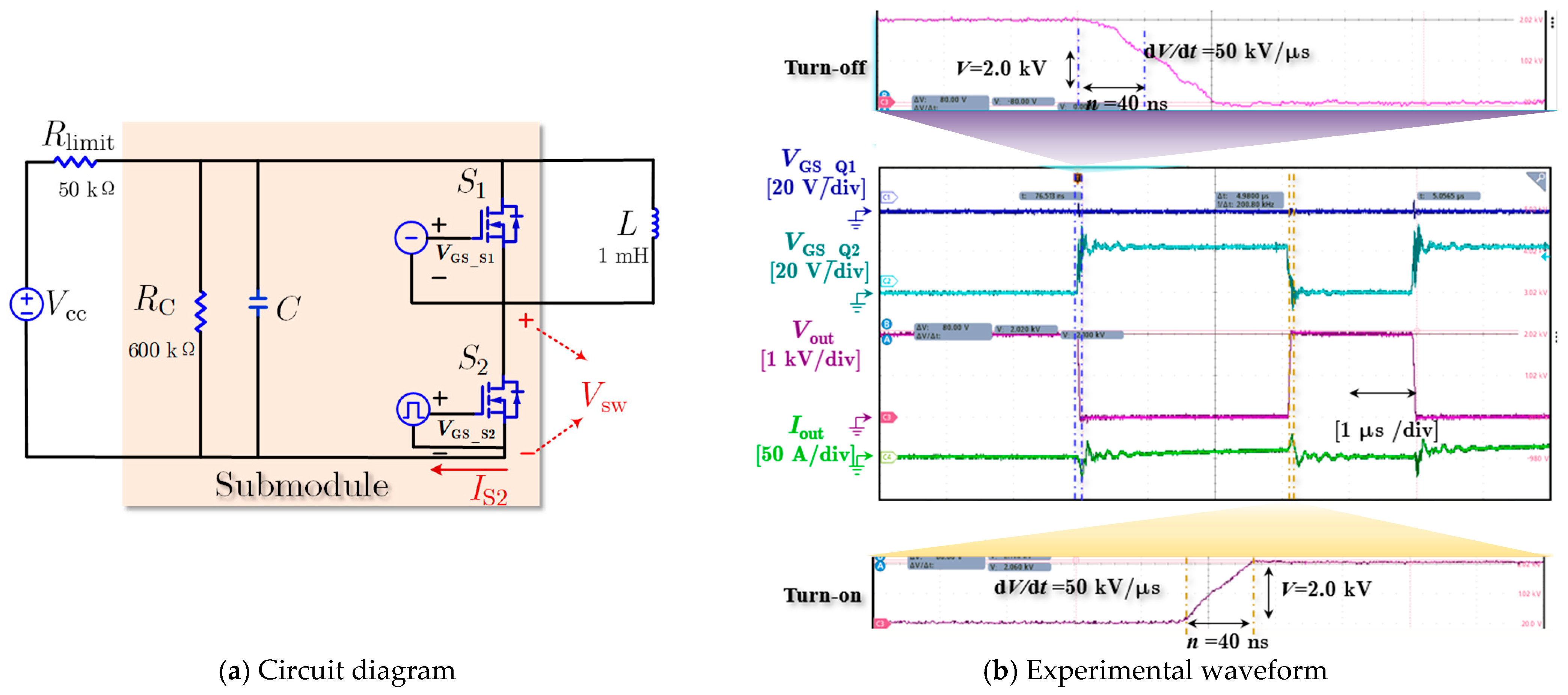
4.2. Double Pulse Test
4.3. Measurement of Common-Mode Current
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, J.; Ke, Z.; Al Sabbagh, M.; Li, H.; Arjun Potty, K.; Perdikakis, W.; Na, R.; Zhang, J.; Wang, J.; Xu, L. 7-kV 1-MVA SiC-Based Modular Multilevel Converter Prototype for Medium-Voltage Electric Machine Drives. IEEE Trans. Power Electron. 2020, 35, 10137–10149. [Google Scholar] [CrossRef]
- Zhao, Y.; Pan, J.; Yan, S.; Luo, Y.; Tang, H.; Li, J. Novel Voltage-Balance Control of Four-Level Hybrid-Clamped Converter with Open-Loop Optimized Common-Mode Voltage Injection. IEEE Trans. Power Electron. 2022, 37, 14045–14051. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, S.; Yin, F.; Wang, L. A High Misalignment-Tolerant Hybrid Coupler for Unmanned Aerial Vehicle WPT Charging Systems. IEEE Trans. Transp. Electrif. 2025, 11, 1570–1581. [Google Scholar] [CrossRef]
- Fu, X.; Yan, S.; Guo, Y.; Xiao, J.; Yang, J.; Ke, Z. Hardware Design of SiC-based 3 kV High-Power Four-Level Hybrid Clamped Converter. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024. [Google Scholar]
- Anurag, A.; Acharya, S.; Kolli, N.; Bhattacharya, S.; Weatherford, T.; Parker, A.A. A Three-Phase Active-Front-End Converter System Enabled by 10-kV SiC MOSFETs Aimed at a Solid-State Transformer Application. IEEE Trans. Power Electron. 2022, 37, 5606–5624. [Google Scholar] [CrossRef]
- Vechalapu, K.; Bhattacharya, S.; Van Brunt, E.; Ryu, S.-H.; Grider, D.; Palmour, J.W. Comparative evaluation of 15 kV SiC MOSFET and 15 kV SiC IGBT for medium voltage converter under same dv/dt conditions. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Cairnie, M.; Di Marino, C. 10 kV SiC MOSFET Power Module with Double-Sided Jet-Impingement Cooling. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023. [Google Scholar]
- Guo, Z.; Li, H.; Dong, X. A Self-Voltage Balanced Hybrid Three-Level MV Inverter Using 3.3-kV SiC MOSFET Module With False-Trigger-Proof Design. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 6854–6864. [Google Scholar] [CrossRef]
- Du, X.; Diao, F.; Zhao, Z.; Zhao, Y. An All Silicon Carbide 3 kV/540 V Series-Resonant Converter for Electric Aircraft Systems. IEEE Trans. Ind. Appl. 2022, 58, 7363–7372. [Google Scholar] [CrossRef]
- Mocevic, S.; Yu, J.; Xu, Y.; Stewart, J.; Wang, J.; Cvetkovic, I. Power Cell Design and Assessment Methodology Based on a High-Current 10-kV SiC MOSFET Half-Bridge Module. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3916–3935. [Google Scholar] [CrossRef]
- Anurag, A.; Acharya, S.; Kolli, N.; Bhattacharya, S. Gate Drivers for Medium-Voltage SiC Devices. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 2, 1–12. [Google Scholar] [CrossRef]
- Palmour, J.W.; Cheng, L.; Pala, V.; Brunt, E.V.; Lichtenwalner, D.J.; Wang, G. Silicon carbide power MOSFETs: Breakthrough performance from 900 V up to 15 kV. In Proceedings of the 2014 IEEE 26th International Symposium on Power Semiconductor Devices & I’s (ISPSD), Waikoloa, HI, USA, 15–19 June 2014. [Google Scholar]
- Rothmund, D.; Bortis, G.; Kolar, J.W. Accurate Transient Calorimetric Measurement of Soft-Switching Losses of 10-kV SiC mosfets and Diodes. IEEE Trans. Power Electron. 2018, 33, 5240–5250. [Google Scholar] [CrossRef]
- Anurag, A.; Acharya, S.; Gohil, G.; Bhattacharya, S. A Gate Driver Design for Medium Voltage Silicon Carbide Power Devices with High dv/dt. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Dalal, D.; Christensen, N.; Jørgensen, A.; Sønderskov, S.; Bęczkowski, S.; Uhrenfeldt, C.; Munk-Nielsen, S. Gate driver with high common mode rejection and self turn-on mitigation for a 10 kV SiC MOSFET enabled MV converter. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- Anurag, A.; Acharya, S.; Prabowo, Y.; Gohil, G.; Bhattacharya, S. Design Considerations and Development of an Innovative Gate Driver for Medium-Voltage Power Devices with High dv/dt. IEEE Trans. Power Electron. 2019, 34, 5256–5267. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Pawaskar, V.U.; Gohil, G. Isolated Gate Driver for Medium-Voltage SiC Power Devices Using High-Frequency Wireless Power Transfer for a Small Coupling Capacitance. IEEE Trans. Ind. Electron. 2021, 68, 10992–11001. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Alex Brothers, J.; Fu, L.; Perales, M.; Wu, J.; Wang, J. A Gate Drive with Power Over Fiber-Based Isolated Power Supply and Comprehensive Protection Functions for 15-kV SiC MOSFET. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 946–955. [Google Scholar] [CrossRef]
- Tang, H.; Fu, X.; Zhao, Y.; Du, Y.; Guo, Y.; Pan, J. Coupling Capacitance Characteristics and Design Optimization Method of CT-Type Isolated Power Supply for High-voltage SiC Devices. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023. [Google Scholar]
- Li, H.; Gao, Z.; Wang, F. Medium-Voltage Isolated Auxiliary Power Supply Design for High Insulation Capability, Ultra-Low Coupling Capacitance, and Small Size. IEEE Trans. Power Electron. 2023, 38, 7226–7240. [Google Scholar] [CrossRef]
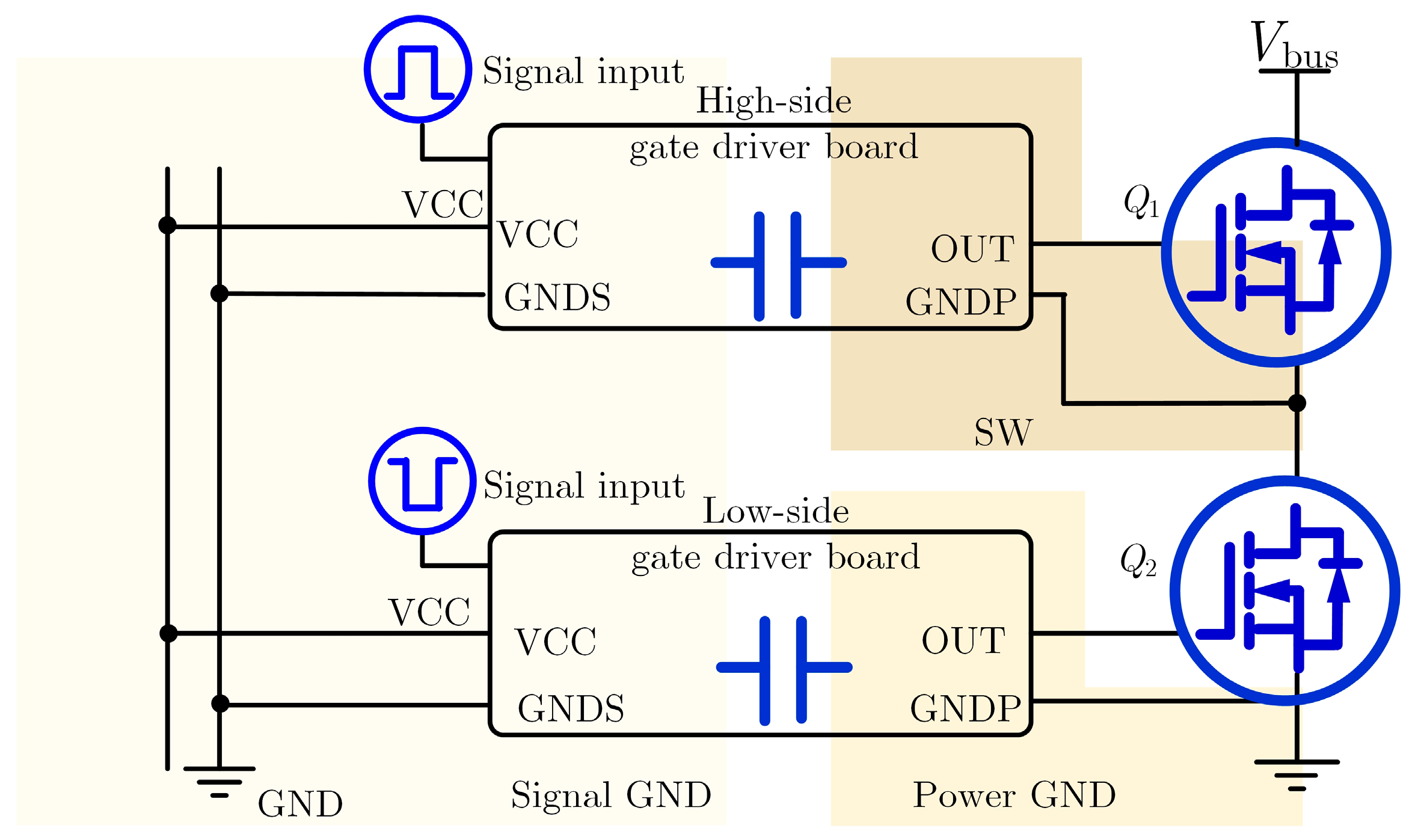


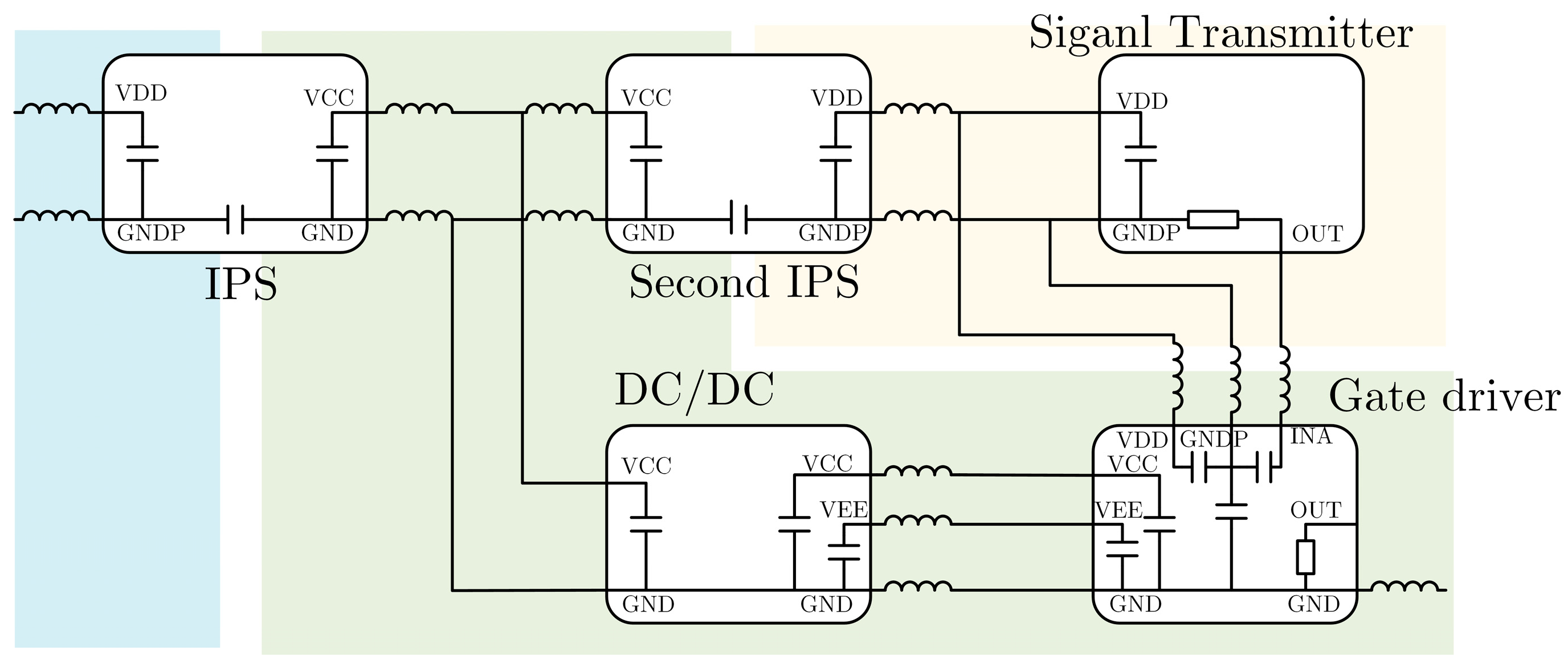
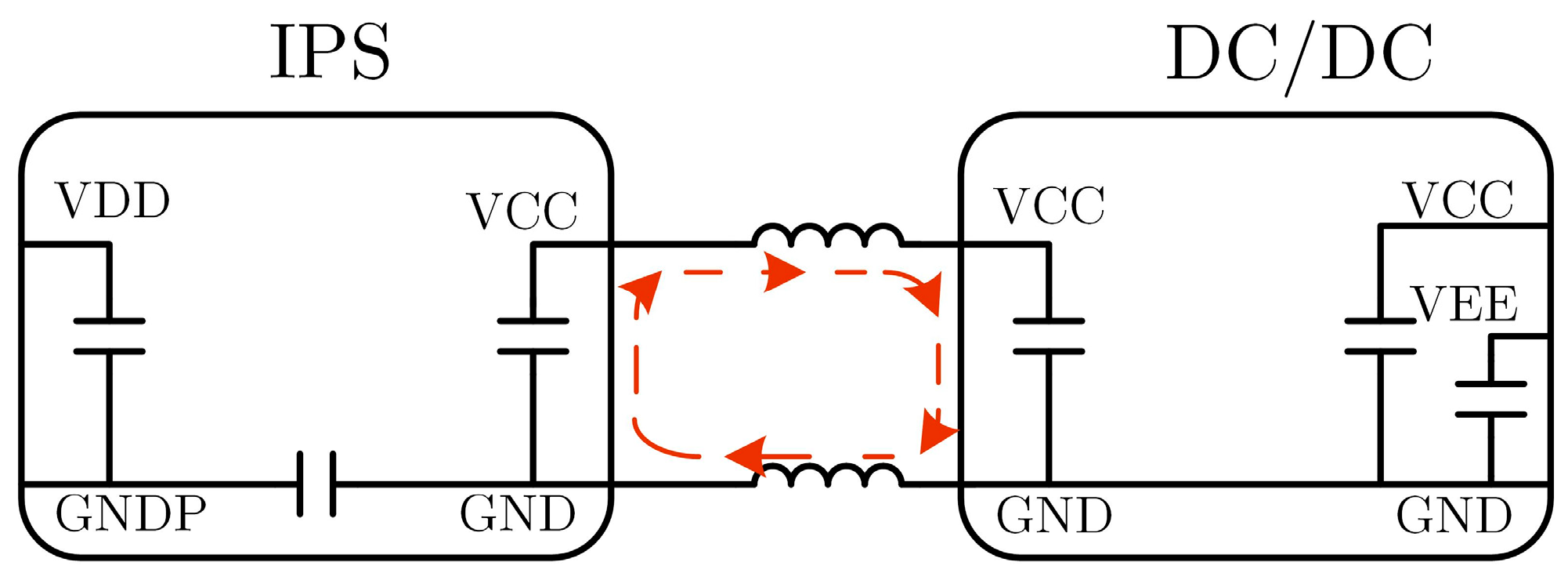
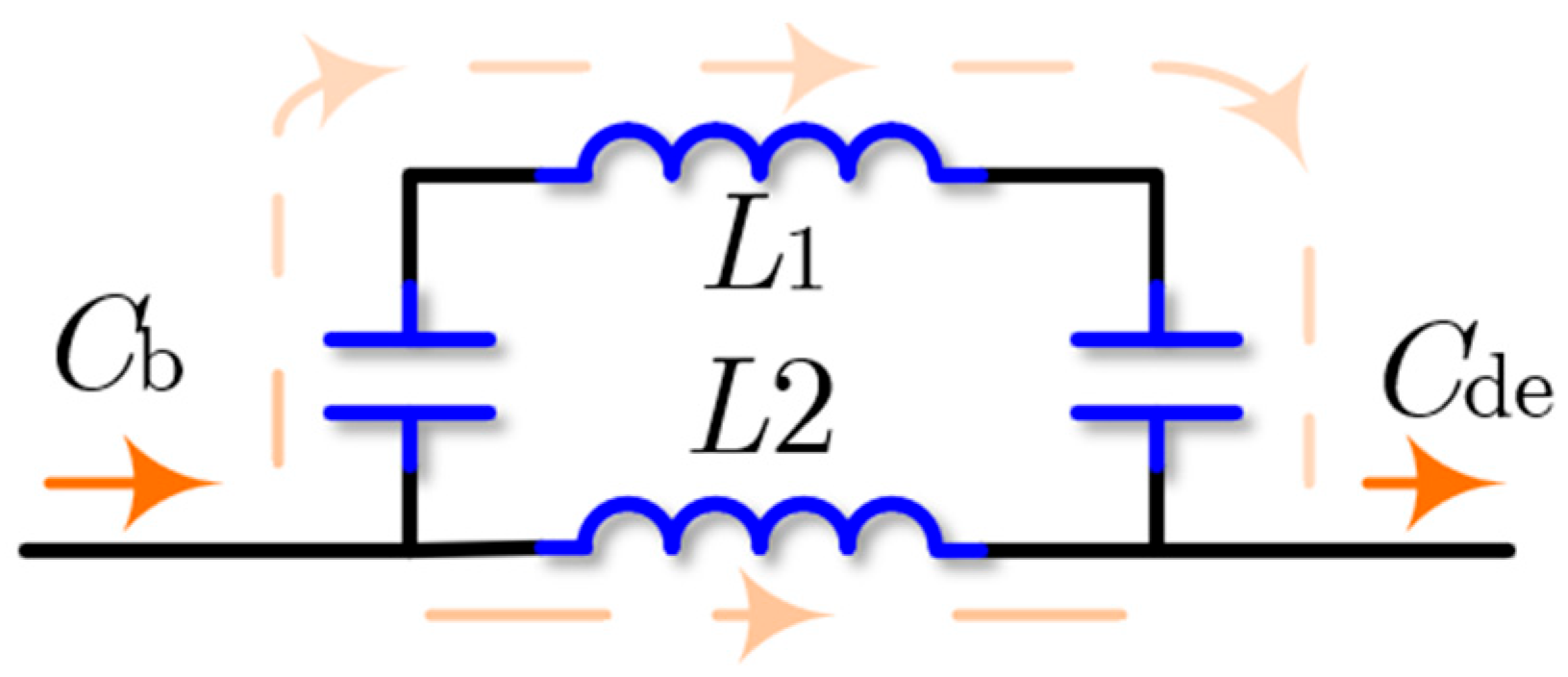
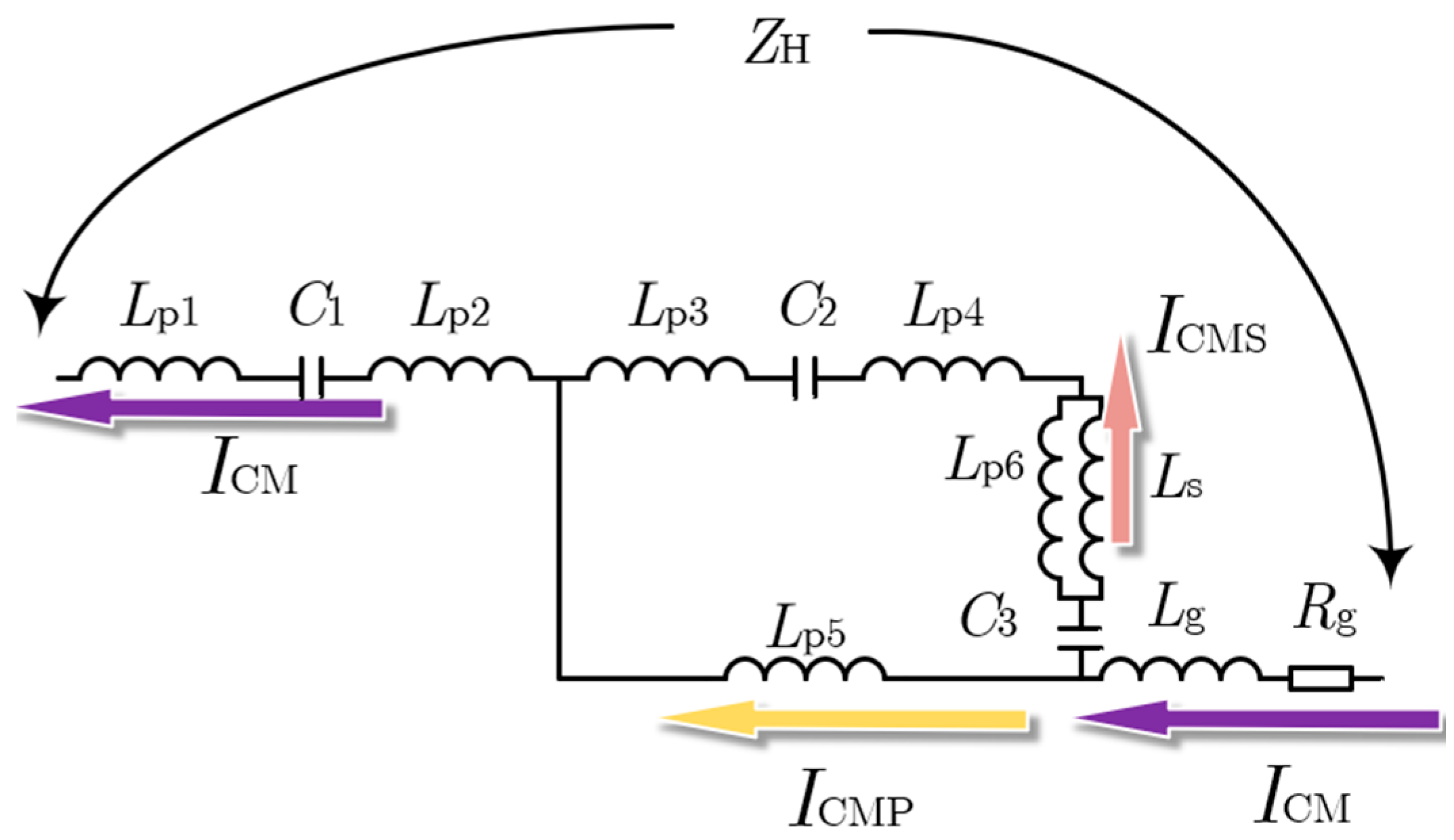
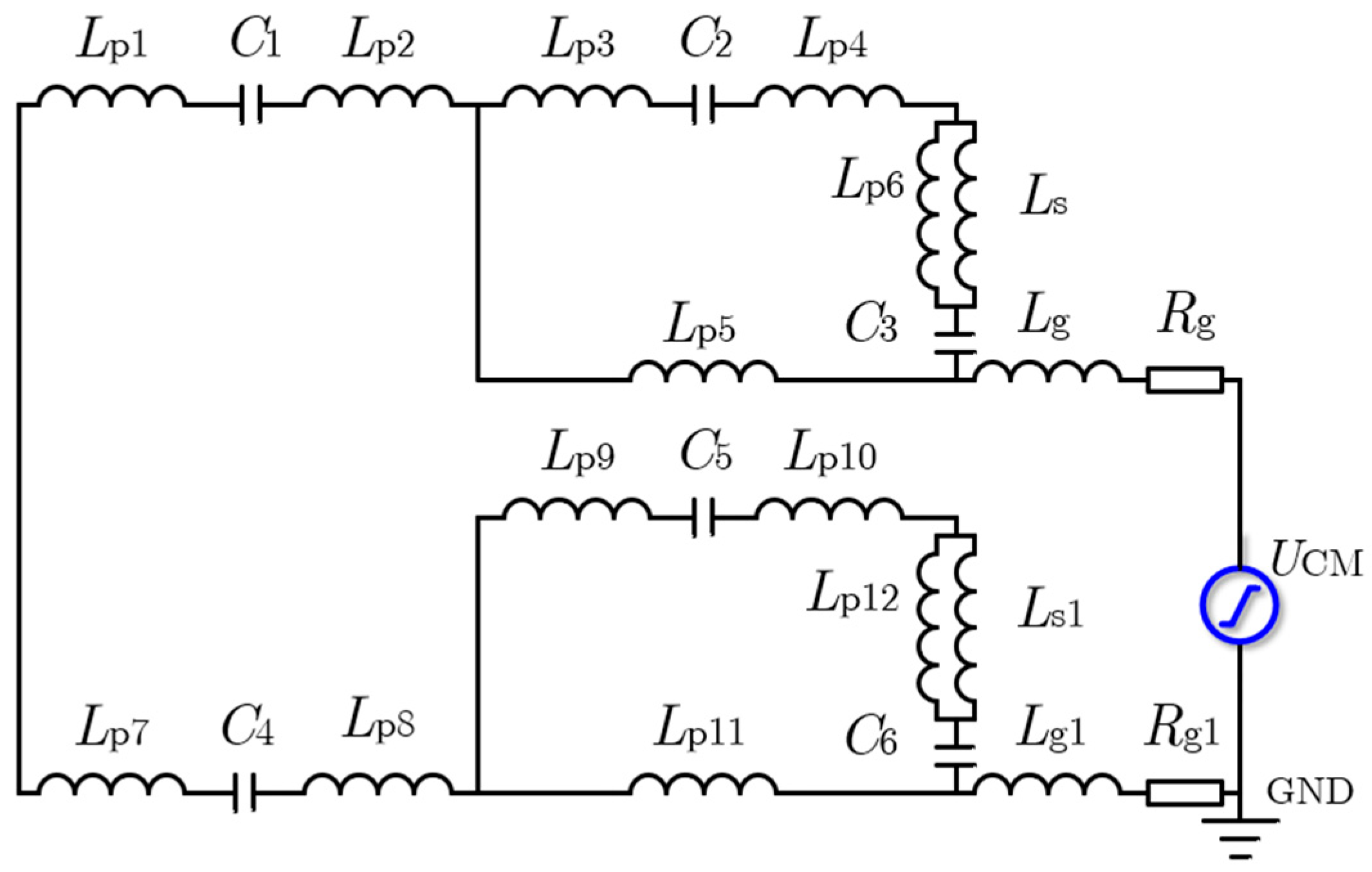

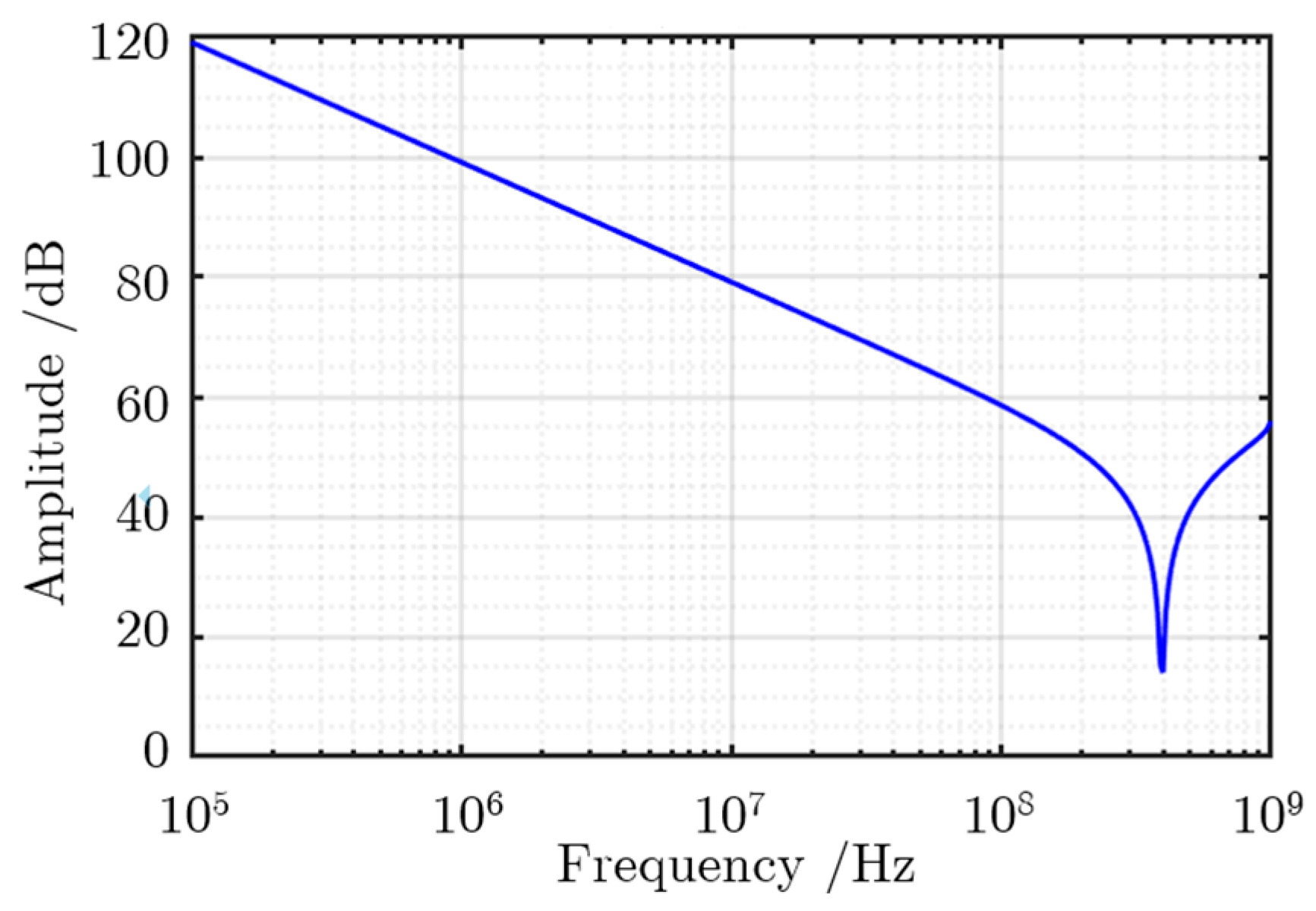
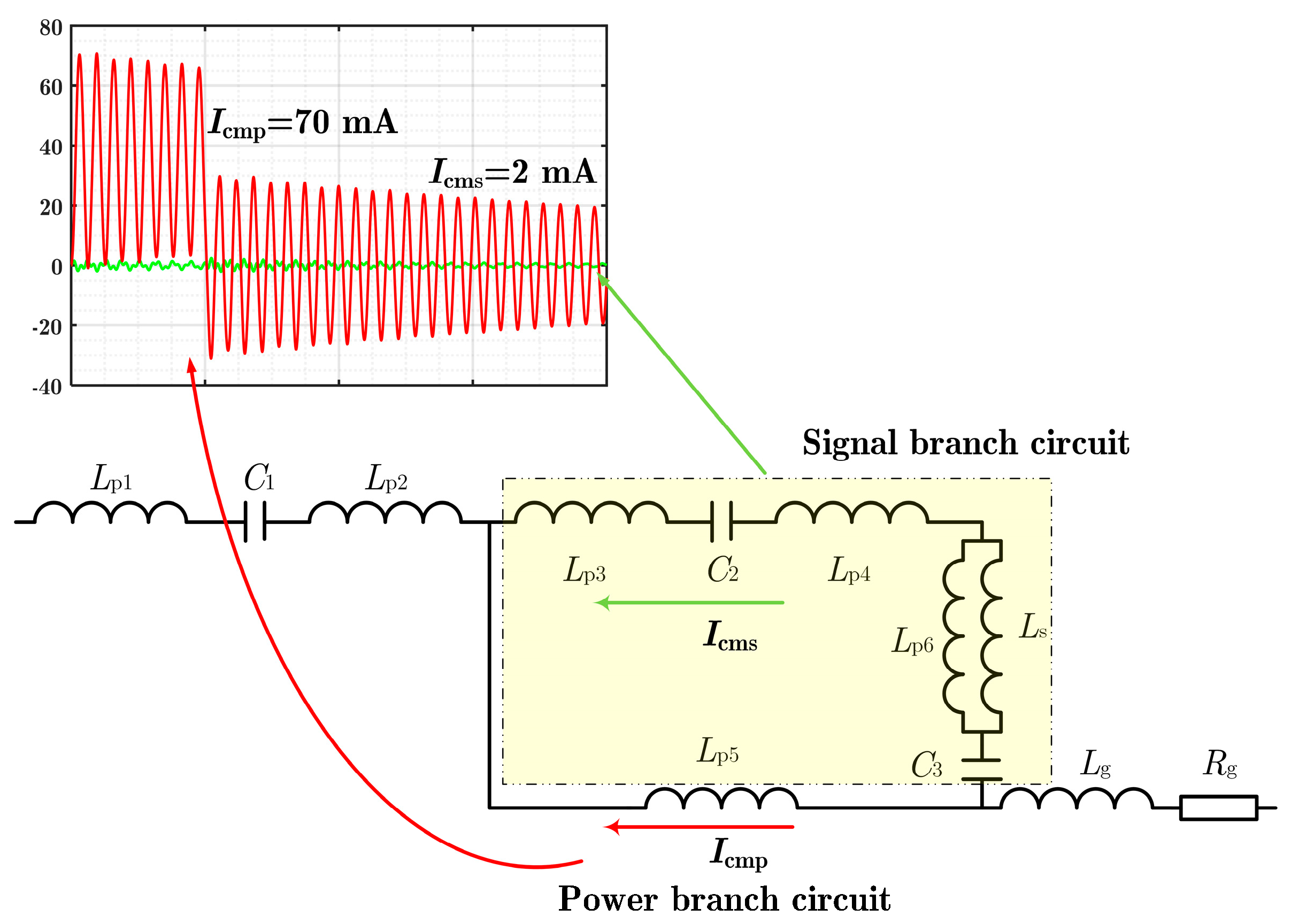
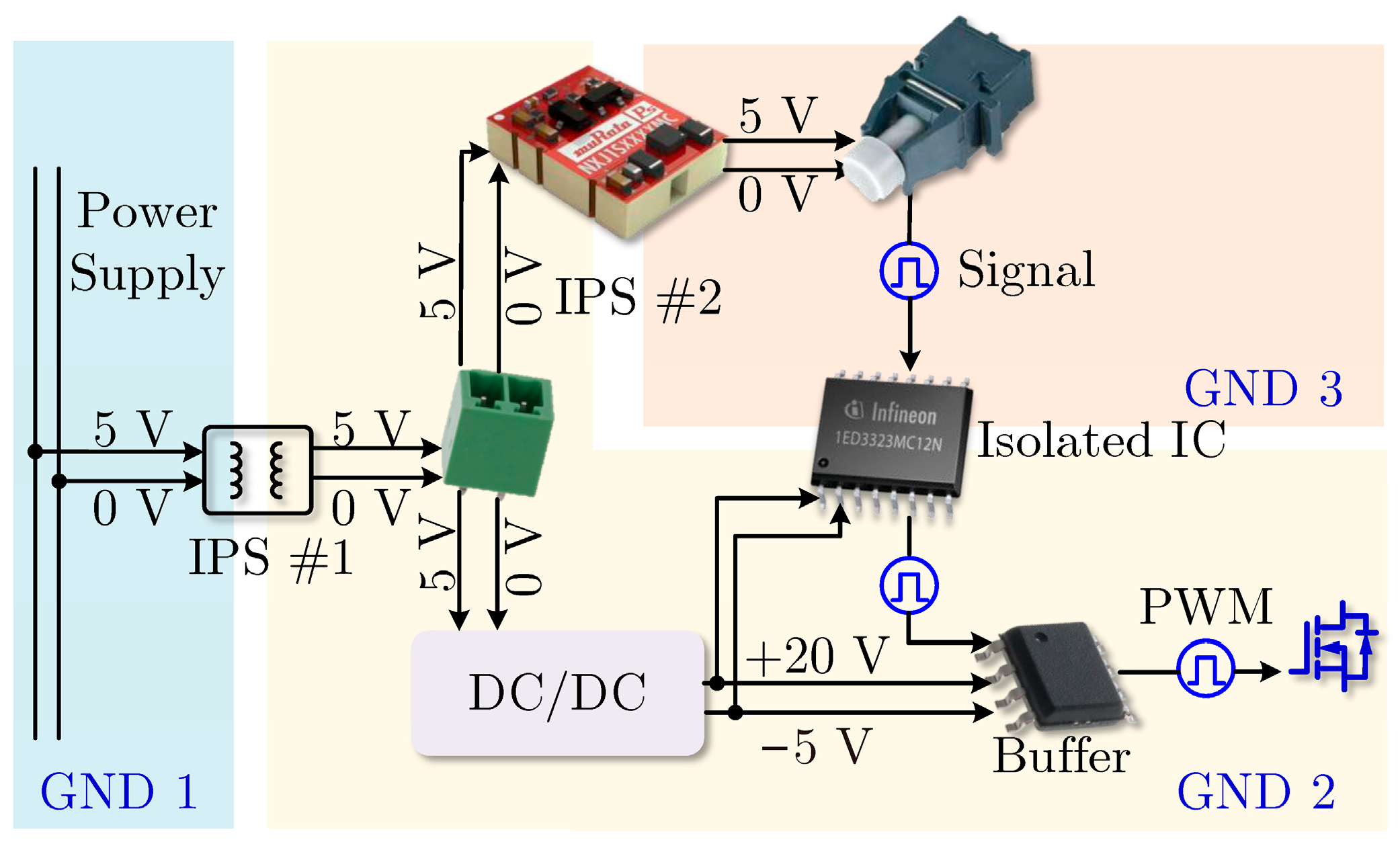



| Parameter | Physical Meaning | Parameter | Physical Meaning |
|---|---|---|---|
| Lp1 | Input parasitic inductor of IPS | Ls | Parasitic inductor between fiber optic and GD IC |
| Lp2 | Input parasitic inductor of DC/DC module | Lg | Parasitic inductor between GD IC and the source of MOSFET |
| Lp3 | Input parasitic inductor of Second IPS | C1 | Coupling capacitor of IPS |
| Lp4 | Parasitic inductor of fiber optic conversion circuit | C2 | Coupling capacitor of Second IPS |
| Lp5 | Output parasitic inductor of GD IC | C3 | Coupling capacitor of the GD IC |
| Lp6 | Input parasitic inductor of GD IC | Rg | Parasitic resistance between GD IC and the source of MOSFET |
| Parameters | Series | Value (pF) |
|---|---|---|
| C1 | NXE1S0505MC-R13 | 3 |
| C2 | 1ED332xMC12N | 1.4 |
| C3 | NXE1S0505MC-R13 | 3 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Lp1 | 3.73 nH | Lp6 | 5.9 nH |
| Lp2 | 11.35 nH | Ls | 7.7 nH |
| Lp3 | 3.31 nH | Lg | 26.8 nH |
| Lp4 | 8.18 nH | Rg | 0.36 ohm |
| Lp5 | 4.62 nH |
| Series | G2R1000MT33J | MSC400SMA330B4 | G2R120MT33J |
|---|---|---|---|
| Company | GeneSiC (Chantilly, VA, USA) | Microchip (Chandler, AZ, USA) | GeneSiC (Chantilly, VA, USA) |
| ID | 3 A | 11 A | 35 A |
| Qg | 21 nC | 37 nC | 145 nC |
| RDS(on) | 1000 mΩ | 400 mΩ | 120 mΩ |
| Cost | $18.69 | $32.11 | $92.99 |
| 1st Option | 2nd Option | 3rd Option | |
|---|---|---|---|
| Volt. [kV] | 3.0 | 3.0 | 3.0 |
| Cap. [μF] | 105.0 | 200.0 | 60.0 |
| Cur. [A] | 57.0 | 80.0 | 101.1 |
| ESL [nH] | 110.0 | 100.0 | 12.6 |
| ESR [mΩ] | 6.0 | 1.6 | 2.1 |
| Vol [L] | 2.3 | 3.3 | 1.8 |
| [1] | [2] | [3] | This Work | |
|---|---|---|---|---|
| Test voltage | 1.1 kV | 5.0 kV | 6.8 kV | 0.4 kV |
| dv/dt | 65.4 kV/μs | 65 kV/μs | 81 kV/μs | 20 kV/μs |
| The method used in paper | Customized isolated power supply | Customized isolated power supply | Customized isolated power supply and shielding techniques | The proposed method and commercial power supplies |
| Measured CM current on gate driver | 426 mA | 471 mA | 130 mA | 68 mA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, K.; Tang, H.; Cai, Z.; Zou, Y.; Pan, J. Conducted Common-Mode Electromagnetic Interference Analysis of Gate Drivers for High-Voltage SiC Devices. Energies 2025, 18, 6083. https://doi.org/10.3390/en18236083
Xiao K, Tang H, Cai Z, Zou Y, Pan J. Conducted Common-Mode Electromagnetic Interference Analysis of Gate Drivers for High-Voltage SiC Devices. Energies. 2025; 18(23):6083. https://doi.org/10.3390/en18236083
Chicago/Turabian StyleXiao, Kai, Haibo Tang, Zhihong Cai, Yansheng Zou, and Jianyu Pan. 2025. "Conducted Common-Mode Electromagnetic Interference Analysis of Gate Drivers for High-Voltage SiC Devices" Energies 18, no. 23: 6083. https://doi.org/10.3390/en18236083
APA StyleXiao, K., Tang, H., Cai, Z., Zou, Y., & Pan, J. (2025). Conducted Common-Mode Electromagnetic Interference Analysis of Gate Drivers for High-Voltage SiC Devices. Energies, 18(23), 6083. https://doi.org/10.3390/en18236083





