Incentive Mechanism Design for Privacy-Aware Energy Theft Detection Based on Contract Theory

Abstract

Energy theft remains a major source of non-technical losses in smart grids, leading to significant economic damage and operational risks. Traditional detection methods often rely on fine-grained user consumption data, raising serious privacy concerns and limiting user willingness to cooperate. To address this conflict between detection accuracy and privacy protection, this paper proposes a novel incentive mechanism based on contract theory. We first quantify privacy-preserving levels using the differential privacy framework and analyze the resulting degradation in energy theft detection performance due to added noise. Then, we design an optimal contract menu that encourages users to report more accurate data by compensating them for privacy losses, while accounting for information asymmetry regarding individual privacy preferences. The proposed mechanism is analyzed under both discrete and continuous user types, and the optimization problem is simplified by reducing the number of incentive compatibility and individual rationality constraints. Simulation results demonstrate the feasibility of the proposed mechanism and show how it balances detection performance, aggregation accuracy, and user privacy. This work offers a theoretically grounded and feasible solution to the privacy–detection trade-off in smart grid energy theft detection.

1. Introduction

Losses of energy in power systems encompass technical losses and non-technical losses (NTLs) [1,2], where technical losses denote energy losses caused by natural phenomena in the power system, such as dissipation of power lines and transformers, and NTLs, on the other hand, refer to non-natural losses due to actions external to the power system, such as unpaid electricity, metering inaccuracies, and fraudulent behavior of customers. In comparison with technical losses, NTLs are more difficult to estimate because the causes of NTLs are diversified and there is no helpful information to measure these losses. Among the various forms of NTLs, energy theft accounts for the majority, especially in developing countries [3]. Energy theft has been a major concern for utility companies around the world, wherein abnormal users can steal electricity for personal benefits. It has been reported that energy theft costs the utility companies about USD 6 billion every year in the USA alone [4], and up to nearly 50% of the electricity is obtained by theft in some developing countries [5]. There are various methods to conduct energy theft [6], including hidden connections in front of the meter, physical tampering with the meters, hacking the digital meter’s software, and so on. Energy theft will not only result in serious economic losses, but also cause a significant impact on the operation and even stabilization of the whole power system. Arango et al. [7] showed that energy theft results in power quality deviation problems. In addition, a large amount of unreported energy consumption might mislead the power system operator and then interrupt the power supply because the control center cannot schedule sufficient active and reactive power generation [8]. Therefore, the energy theft issue has been an urgent problem to be solved for utility companies.

Strict laws and regulations have been established against illegal consumption of electric energy around the world [6]. Relevant laws in Poland consider energy theft a crime punishable by imprisonment of 3 months to 5 years. In Austria, a criminal who steals energy worth more than EUR 40,000 will be sentenced to imprisonment of one to ten years. However, legal means alone fail to effectively prevent the occurrence of energy theft because fluke mind widely exists among people. To combat energy theft effectively, a lot of energy theft detection systems have been proposed to detect the abnormal power consumption of end users [9]. Nevertheless, most of the proposed detection methods require the fine-grained energy consumption data of end users [10], which gives rise to serious privacy concerns [11]. Specifically, it has been shown that the fine-grained energy consumption data can expose personal private data such as the occupation of a house and the living habits and even health condition of the residents, which may lead to certain criminal activities such as burglaries and robberies. A Non-intrusive Load Monitoring (NILM) algorithm is proposed by Hart [12] to monitor the running states of the appliances in the house, which can be utilized to infer further privacy information. What is worse, the widespread deployment of smart meters has increased the risk of power usage data leakage significantly because the emerging communication and computation technologies employed by smart meters also bring more vulnerabilities simultaneously. In DEFCON 2012, researchers demonstrated how to hack a smart meter through quick memory acquisition techniques and hardware bus sniffing, which exposed the vulnerability of smart meters. Even though most residential smart meters record and report the energy reading at lower frequencies, typically 15 min intervals, which is the de facto standard adopted by European and most Chinese utilities because it gives the operator enough granularity for load forecasting and fast anomaly detection while keeping communication and storage costs manageable, recent advances in NILM techniques have demonstrated that even such “low-rate” data can achieve good appliance-disaggregation accuracies [13]. Privacy concerns have hindered the application of new technologies in power systems. Several states in the USA have established corresponding smart meter privacy rules and guidelines through statute or regulatory proceedings. In 2014, California’s new privacy law covering smart meter privacy went into effect, which requires certain non-utility businesses to obtain the customers’ approval before sharing their power usage data. Therefore, the privacy issue for electricity users cannot be ignored and is to be addressed as a matter of urgency when proceeding with basic functions of power systems.

However, only a few works consider the energy theft detection and privacy issue simultaneously. Salinas et al. [14] proposed three energy theft detection algorithms based on peer-to-peer (P2P) computing to obtain the users’ “honesty coefficients” in a distributed manner in order that the private energy consumption data can be processed locally and personal privacy can be preserved. Richardson et al. [15] proposed a privacy-preserving method to detect manipulated distributed energy resource (DER) generation measurements by utilizing the geographical correlation property of photovoltaic (PV) energy output, and only a Euclidean distance measure, which cannot be used to infer detailed energy consumption or generation profiles, is communicated during the detection procedure. Salinas et al. [16] developed a privacy-preserving bias estimation algorithm to detect the energy thieves while preserving users’ privacy by decomposing the Kalman filter into two parallel and loosely coupled filters. However, existing works fail to give a quantified privacy-preserving level; thus customized services cannot be provided according to the different privacy requirements of end users. In addition, most of the existing works still require the collection of raw energy consumption data, whereas electricity users are sometimes reluctant to report the fine-grained energy consumption data because these data still have the possibility of being eavesdropped during communication and the users’ privacy losses are not compensated rationally.

Incentive-based methods have become widely adopted for reconciling the system utility and the preservation of privacy in diverse areas. Liu et al. [17] proposed an incentive mechanism for participants, aiming to protect them from privacy leakage, ensure the availability of sensing data, and maximize the utilities of both platforms and participants in crowdsensing. Based on auction theory, Fleischer and Lyu [18] designed a Bayesian incentive-compatible and privacy-preserving mechanism that guarantees accuracy and protects the privacy of both cost and data in data mining. Kim et al. [19] designed a novel incentive mechanism to attract more data owners to join in the federated learning process with the consideration of privacy preservation. Different from these works, we are devoted to balancing energy theft detection accuracy and electricity users’ privacy in smart grids. Since the utility company has no knowledge of the privacy preference of each user, information asymmetry between the utility company and the users should be addressed. Therefore, a contract-based incentive mechanism, which has been developed to tackle information asymmetry issue while balancing system utility and privacy preservation, needs to be adopted.

In this paper, we set up a novel data reporting framework, where electricity users can add noisy signals to their raw energy consumption data before reporting them to the utility company so that their privacy can be preserved. The magnitudes of added noisy signals can vary according to the users’ privacy preferences. However, one major problem is that the users tend to add more noise for a higher privacy-preserving level under the hypothesis of selfishness, which is in conflict with the utility company’s desire to collect more precise data to guarantee the performance of the energy theft detector and aggregation accuracy. Hence, an effective mechanism is needed to reconcile the conflict between the utility company and electricity users. The other problem is that the utility company has little knowledge about the privacy preferences of one specific user due to the information asymmetry. So the proposed mechanism also needs to meet the various privacy requirements without knowing the exact privacy preference of every individual user. To tackle the aforementioned challenges, we propose an incentive mechanism based on contract theory in this paper. In the smart grid scenario, the utility company will design a series of contracts for the electricity users to choose based only on the knowledge of the distribution of different privacy preferences. Each contract will give the end users some rewards to compensate for the privacy losses; thus their personal utility can be maximized, which means the users will be encouraged to report more precise data to the utility company. The design of the contracts will jointly consider the detector performance, economic benefit, and aggregation accuracy so that the disutility of the utility company will be minimized.

The contributions of our work are threefold: (1) We quantify the privacy-preserving level under the differential privacy paradigm, which makes it possible to offer customized privacy-preserving services to meet various privacy requirements at different levels. Based on this, we analyze the detection performance degeneration theoretically after noisy signals are added into the raw energy consumption data. (2) We propose an incentive mechanism based on contract theory to encourage the electricity users to report real consumption data in order that the disutility of power supplier can be minimized. We also generalize the relevant results to the case with continuous privacy preferences. (3) Simulation results are given to validate the feasibility of the proposed incentive mechanism.

The rest of this paper is organized as follows. We first present the basic concepts and system models in Section 2. Then we design the incentive mechanism based on contract theory to address the information asymmetry problem and maximize the utility of electricity suppliers in Section 3. Simulations and evaluations are illustrated in Section 4 to validate the theoretical results. Lastly, we conclude this paper in Section 5.

2. System Model

The utility company faces a population consisting of two user types: normal and abnormal. The normal users pay their entire bills, while the abnormal users intend to lower their billed energy below the amount they actually consume and can be regarded as malicious attackers. The attackers can conduct electricity theft through various methods, including bypassing or tampering with the meter’s current path, re-flashing the meter to transmit a fixed or scaled-down reading, and intercepting the data packet and replacing it with a lower value [20]. Considering that electricity users are limited in their resources and technical abilities, they cannot obtain the knowledge of system parameters like network topology or anomaly detection settings.

Let $\mathcal{N}$ denote the set of customers served by the utility company, which includes both normal users and abnormal users (attackers). The total number of end users is denoted as N. Let $x_n$ and $x_a$ denote the actual energy consumption of a normal user and an abnormal user during a certain time interval, respectively. Note that the energy consumption of the abnormal user consists of two parts, namely the billed consumption $x_a^b$ and unbilled consumption $x_a^u$; i.e., $x_a=x_a^b+x_a^u$. The utility company runs a simple diagnostic scheme for energy theft detection in which a consumer is classified as an abnormal user if the overall reported consumption within a certain period of time is below a pre-specified threshold, i.e., $x<\tau$ [21]. This detection scheme is straightforward yet effective in practice. The threshold $\tau$ can be determined by analyzing historical energy consumption data while considering a certain level of false alarm rate. Note that the utility company can learn the distribution of energy consumption of both normal users and abnormal users through analyzing the historical consumption data. The labeled historical consumption data for abnormal users can be obtained through costly, labour-intensive methods. To obtain the data, the utility personnel may have to install balance meters at distribution transformers to identify feeders with unmetered losses, conduct periodic on-site inspections of seals and wiring, or dispatch technicians to verify suspected meters. The small, high-quality labeled data set generated by these manual audits could allow the utility to calibrate an initial detection threshold and detect potential electricity theft behavior so that the electricity theft database will gradually be expanded as the detection system operates. For analytical convenience, we assume that the energy consumptions of the normal users and abnormal users follow an exponential distribution [22]:

$$pd f\left(x_n\right)={\displaystyle \frac{1}{q_n}}{e}^{-{\displaystyle \frac{x_n}{q_n}}}\mathrm{and}pd f\left(x_a^b\right)={\displaystyle \frac{1}{q_a}}{e}^{-{\displaystyle \frac{x_a^b}{q_a}}}$$

(1)

respectively, where $q_n$ and $q_a$ are corresponding scale parameters with $x_n,x_a^b\in (0,+\infty )$. Thus, the positive alarm rate $p_D$ and false alarm rate $p_F$ of the diagnostic scheme without a privacy-preserving mechanism can be expressed by

$$\begin{array}{cc}\hfill & p_D={\int }_0^{\tau }{\displaystyle \frac{1}{q_a}}{e}^{-{\displaystyle \frac{x_a^b}{q_a}}}d{x}_a^b=1-e^{-{\displaystyle \frac{\tau }{q_a}}}\hfill \\ \hfill & p_F={\int }_0^{\tau }{\displaystyle \frac{1}{q_n}}{e}^{-{\displaystyle \frac{x_n}{q_n}}}d{x}_n=1-e^{-{\displaystyle \frac{\tau }{q_n}}}\hfill \end{array}$$

(2)

respectively. It is worth noting that the energy theft detection algorithm considered in this paper is a straightforward average detector, wherein the detector would raise an alarm if the average power consumption during a time period is lower than a threshold. This average detector is quite simple but effective and sometimes even outperforms some more sophisticated algorithms such as CUSUM and EWMA. Detailed evaluation results can be found in Reference [21]. More complex scenarios where other energy consumption distributions and detection algorithms will be left as our future work.

2.1. Differential Privacy

In this paper, we adopt differential privacy to quantify the privacy-preserving level. The concept of differential privacy was originally proposed by Dwork [23], and it is designed to minimize the probability of identifying private records in the database while releasing useful statistical information about the database. This concept can be also utilized to quantify the privacy-preserving level in the smart grid domain [24,25]. The typical method to achieve differential privacy is to directly add some noisy signals to the raw energy consumption data in order that the running state of the appliances in the house will be masked by the noise [26]. The formal definition of differential privacy is given as follows.

Definition 1.

Let ϵ be a positive real number. A randomized algorithm A gives ϵ-differential privacy if for all databases $D_1$ and $D_2$ that differ in only one element, and all $S\in Range\left(A\right)$,

$$Pr[A\left(D_1\right)\in S]\le e^{ϵ}·Pr[A\left(D_2\right)\in S]$$

(3)

where $Range\left(A\right)$ denotes the output range of algorithm A.

This definition indicates that the result of a statistical query on these two adjacent databases shall be indistinguishable such that the private record that the two databases differ in will be unidentifiable. The parameter $ϵ$ is used to quantify the privacy protection level, and a smaller $ϵ$ means better privacy preservation.

One common way to achieve $ϵ$-differential privacy is by injecting stochastic noise with a pre-specified distribution into the original query $f\left(D\right)$. A typical distribution is the Laplace distribution, whose probability density function can be expressed as follows:

$$pd f\left(x\right)={\displaystyle \frac{1}{2b}}{e}^{{\displaystyle \frac{-|x-\mu |}{b}}},x\in (-\infty ,+\infty )$$

(4)

where $\mu$ is a location parameter and is usually set to be 0, while b is a scale parameter. Note that the distribution of the injected noise varies from scheme to scheme and can be designed optimally [27]. In this paper, we only consider the Laplace mechanism for the purpose of analytical tractability. The global sensitivity $\Delta f$ is defined as follows.

Definition 2.

For $f:D\to R^k$, the sensitivity of f is

$$\Delta f=\underset{D_1,D_2}{max}\parallel f\left(D_1\right)-f\left(D_2\right)\parallel$$

(5)

for all $D_1$ and $D_2$ that differ in only one element.

For Laplace mechanisms, which add noise to the query result of $f\left(D\right)$ with a Laplace distribution of $\mu =0$ and b, i.e.,

$$A\left(D\right)=f\left(D\right)+r,r\sim Lap\left(b\right),$$

(6)

algorithm A can achieve differential privacy according to Lemma 1 [24].

Lemma 1.

The algorithm A achieves ϵ-differential privacy if the noise signal from the Laplace distribution $Lap\left({\displaystyle \frac{\Delta f}{ϵ}}\right)$ is independently added to f by A.

It is worth noting that, in the context of smart meter privacy, the query function $f(·)$ denotes the reporting process of smart meter data because it indicates the sum of users’ energy consumption in a certain time interval, and sensitivity $\Delta f$ is the largest energy consumption among all the household appliances of the user. In this paper, we assume that all the normal users share the same sensitivity $\Delta f$. The notion of adjacent databases denotes two time intervals where the sets of running appliances differ in only one element. Then, if Laplacian noise is injected into the metering data, a malicious eavesdropper cannot figure out the on/off event of the appliances precisely such that the privacy of appliance usage can be protected effectively, and the protection level can be quantified by parameter $ϵ$. Throughout this paper, we only consider the scenario where the energy theft detection scheme is based on the consumption measurement during one time interval for analytical convenience. When the energy theft detection scheme is based on the overall consumption within multiple time intervals, similar results will be obtained as long as the distribution of the summation can be derived.

2.2. Energy Theft Detection Under Privacy Protection

Due to the fact that the attackers do not care about the privacy issues because their metering data cannot truly reflect the energy usage pattern, the distribution of the attackers’ metering data stays unchanged; i.e., the positive alarm rate of the detection scheme remains the same when a privacy protection mechanism is adopted. In contrast, the false alarm rate of the applied energy theft detection scheme will be affected by the stochastic noise and become

$$p_F^{\prime }=1-{\displaystyle \frac{q_n·e^{-\frac{\tau }{q_n}}-b·e^{-\frac{\tau }{b}}}{2(q_n-b)}}-{\displaystyle \frac{q_n·e^{-\frac{\tau }{q_n}}}{2(q_n+b)}}.$$

(7)

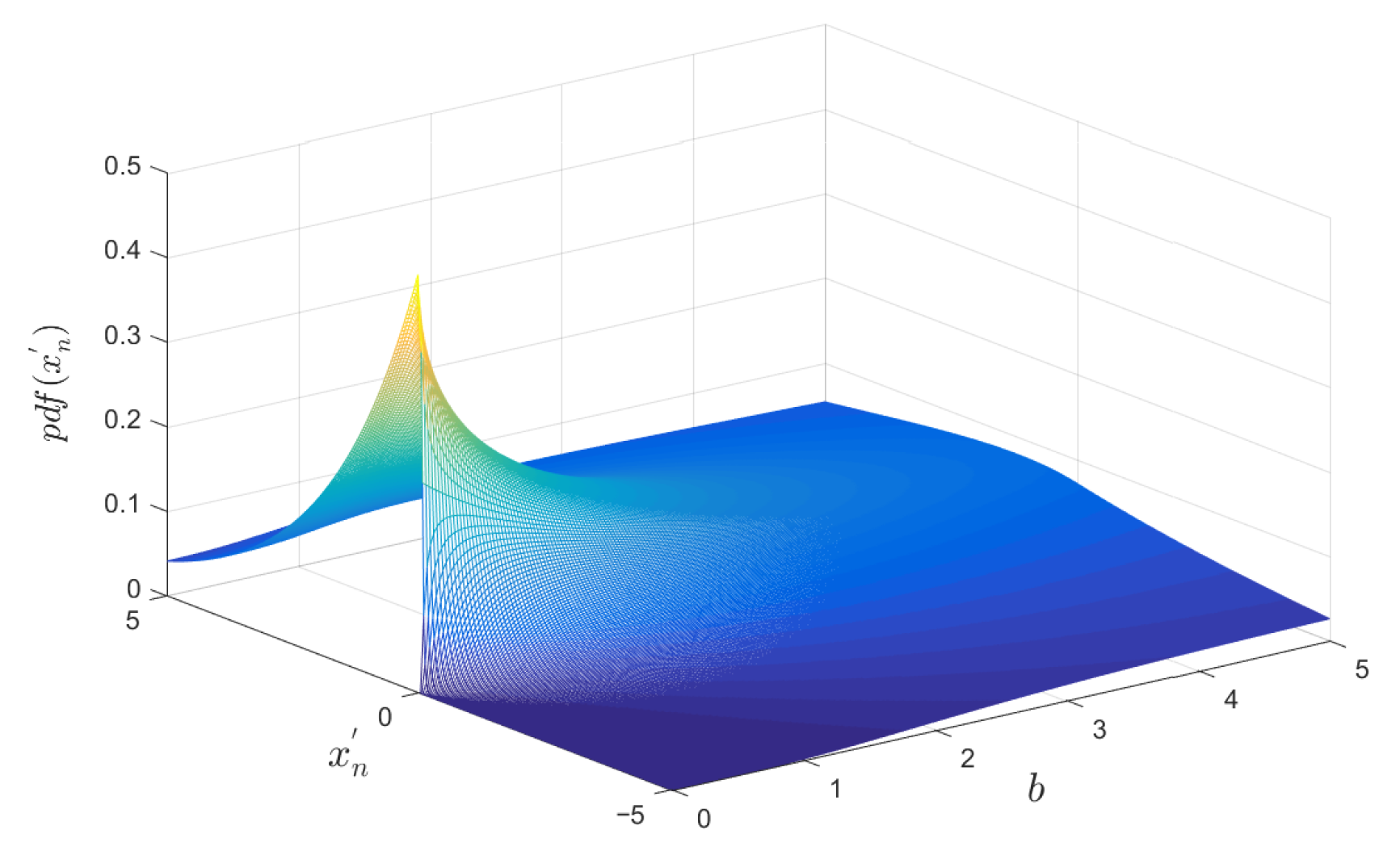
The detailed derivation process is provided in Appendix A. Let $x_n^{\prime }$ denote the reported energy consumption of a normal user; the probability density function of $x_n^{\prime }$ under varying b is demonstrated in Figure 1 and Figure 2. Figure 1 demonstrates the surface, which plots the probability density function of the reported consumption $x_n^{\prime }$ as a continuous function of the Laplace noise scale parameter b and the reported value $x_n^{\prime }$. The height of the surface at any point shows how likely it is that a normal user’s noisy reading will equal $x_n^{\prime }$ for that privacy setting. As b grows, the distribution becomes wider and lower, visually capturing the privacy–accuracy trade-off that is introduced by the privacy-preserving mechanism. 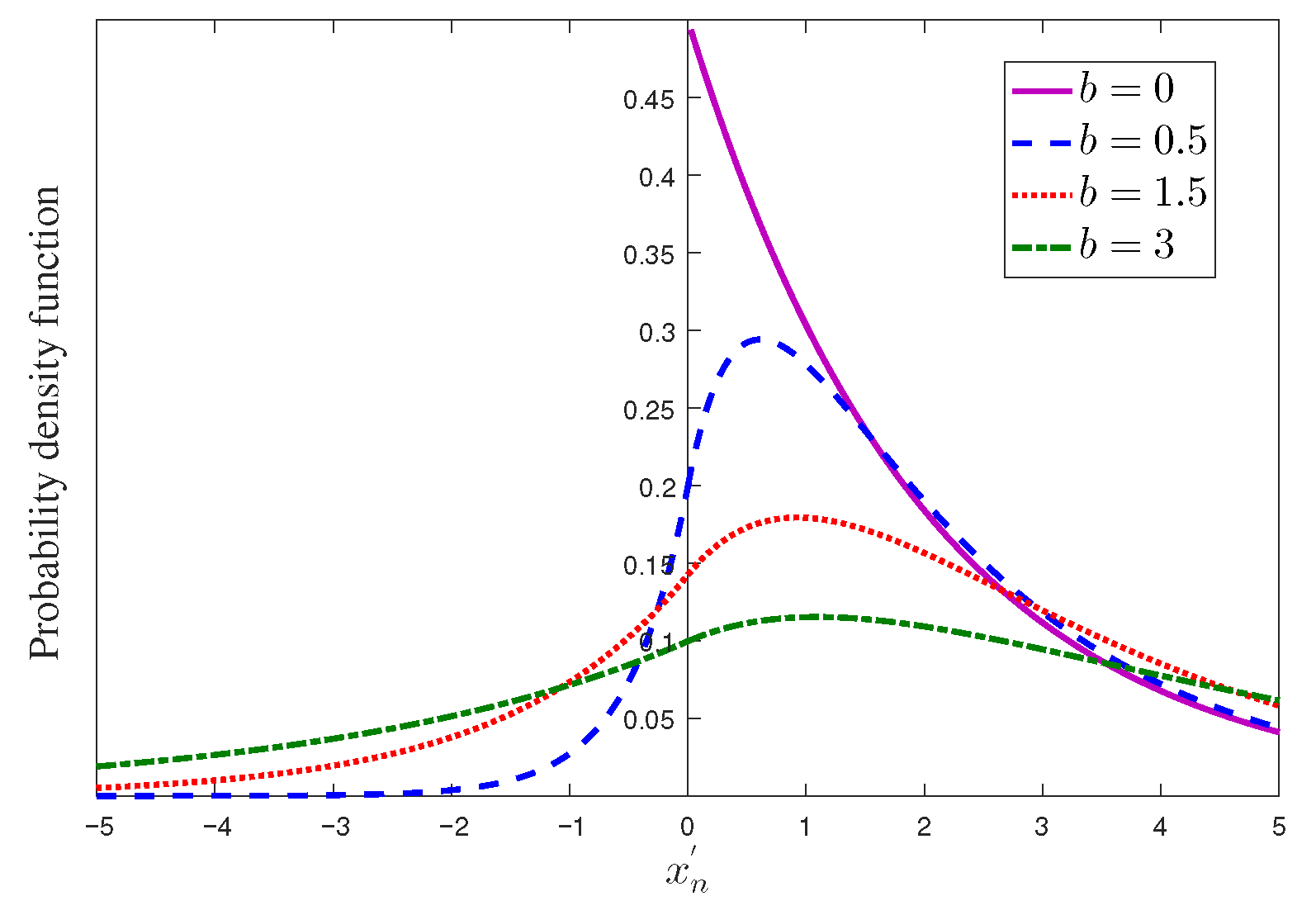To make the 3-D surface easier to read, Figure 2 displays four representative cross-sections at b = 0, 0.5, 1.5, and 3. In Figure 2, the blue, red, and green curves show the PDF of the meter reading after Laplace noise with scale parameter b = 0.5, 1.5, and 3 is added. 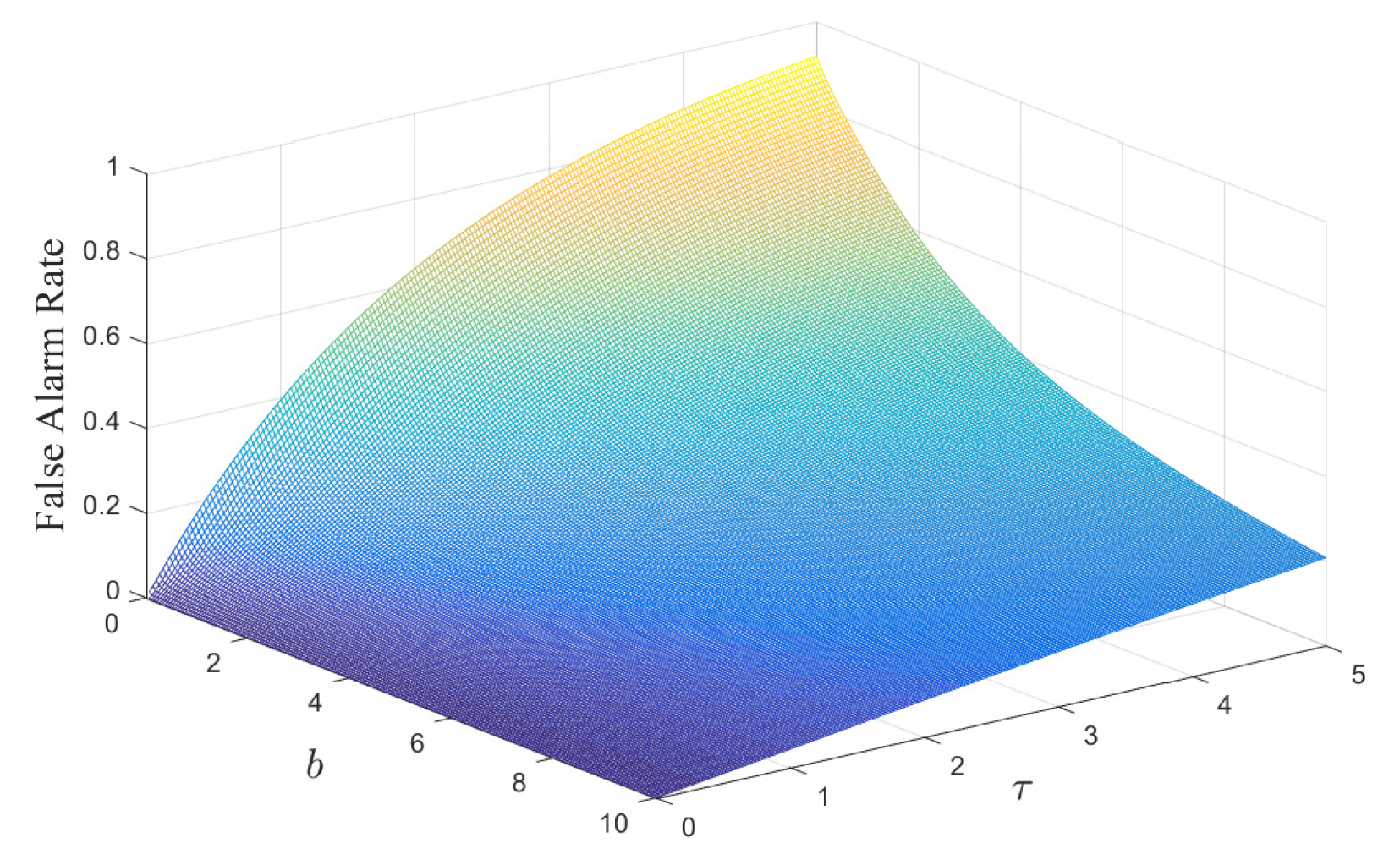The rightward shift and flattening as b increases again illustrate the privacy–accuracy trade-off and degradation of the false alarm rate. 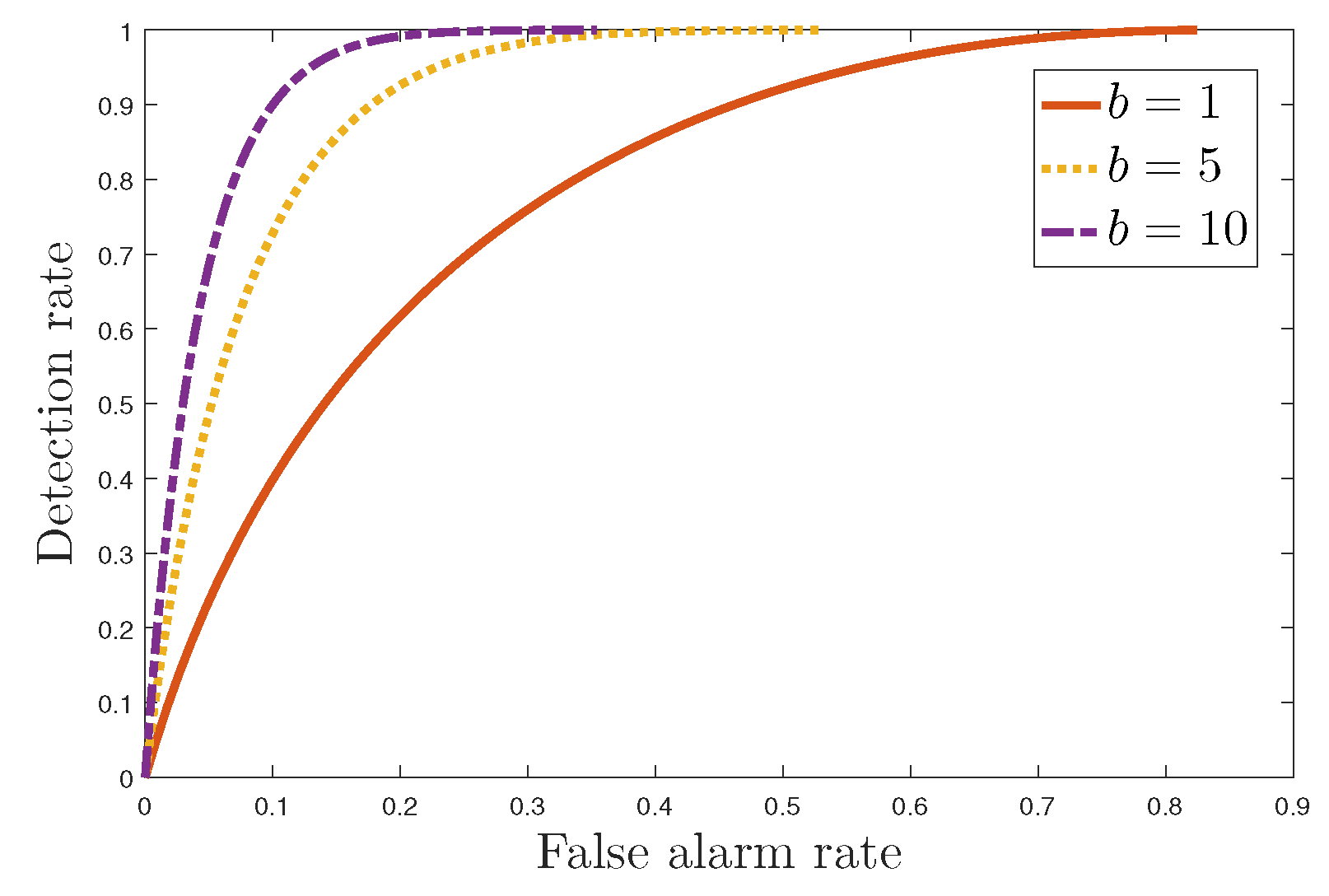The false alarm rate after the adoption of the privacy-preserving scheme is illustrated in Figure 3. In this figure, the monotonic degradation trends are clearly visible and visually reinforce the privacy–utility trade-off that an incentive mechanism must balance. The receiver operating characteristic (ROC) curve to model the trade-off between $p_D$ and $p_F$ is demonstrated in Figure 4. A higher false alarm rate significantly affects user satisfaction, as the normal user will frequently receive warnings about nonexistent energy theft. Therefore, we consider the false alarm rate as the cost brought by the detection scheme. One reasonable model of the relationship between false alarm rate $p_F$ and diagnostic scheme cost l is [21]

$$p_F={\displaystyle \frac{l}{1+l}}.$$

(8)

3. Contract Design

Through the above analysis, it can be seen that the privacy protection mechanism will have significant impacts on the performance of the diagnostic scheme, which introduces conflict with the user’s privacy demand. However, when the incentive mechanism is not involved, the user intends to add larger noisy signals due to selfishness. So the utility company needs to design an appropriate incentive mechanism to compensate the users’ privacy losses and optimize its profit under some practical constraints. We consider a scenario where there are multiple classes of electricity users and we utilize contract theory to design the incentive mechanism. In our privacy settings, each class of electricity users has different valuations for privacy. Generally speaking, the utility company cannot obtain the precise privacy preference of each individual user; i.e., information asymmetry exists between the utility company and electricity users. So we assume that the utility company only has knowledge about the distribution of each class of users, and the contract designed under complete information will also be studied as the benchmark, where the utility company knows the precise type of every user.

In this paper, we consider a simple privacy loss model [28]:

$$c=U(\theta ,ϵ)=\theta ·ϵ$$

(9)

where $\theta$ is the user’s privacy preference and a higher $\theta$ indicates greater valuation of personal privacy. $ϵ$ denotes the privacy-preserving level under the differential privacy paradigm, as Section II-A states. Note that the approach proposed in this paper can be applied to any form of privacy loss models as long as they have the following properties:

• Property 1: The privacy loss function $U(\theta ,ϵ):\Theta \times {\mathbb{R}}^{+}⟶\mathbb{R}$ is increasing in both $\theta$ and $ϵ$ and differentiable with respect to $ϵ$.
• Property 2: The marginal gain of increasing the privacy setting $ϵ$ with a higher privacy preference $\theta$ is greater than that with a lower privacy preference; i.e., $U({\theta }_1,ϵ)-U({\theta }_2,ϵ)$ is increasing in $ϵ$ when ${\theta }_1\ge {\theta }_2$.

In this paper, we assume that there are k classes of electricity users, denoted as $\Theta =({\theta }_1,{\theta }_2,\dots ,{\theta }_k)$, and each class-i has a proportion of ${\lambda }_i$ users. Also, let ${\lambda }_a$ denote the number of abnormal users. For analytical convenience, the elements in $\Theta$ are sorted in ascending order, i.e., ${\theta }_1\le {\theta }_2\le \dots \le {\theta }_k$. For each individual user, when the expected energy consumption is given, the utility function of electricity users can be defined as $o=p-c$, where p denotes the reward offered by the utility company for the privacy loss. And obviously, the following constraints can be set:

$$p_i-{\theta }_i·{ϵ}_i\ge 0,\forall i$$

(10)

where the subscript i denotes the index of the electricity user. The constraint (10) is also known as the individual rationality (IR) constraint. Also, as the type of contract is selected selfishly by the user, the contract designed for user i shall bring them the highest profit, i.e.,

$$p_i-{\theta }_i·{ϵ}_i\ge p_j-{\theta }_i·{ϵ}_j,\forall i\ne j.$$

(11)

Equation (11) is often called the incentive compatibility (IC) constraint. Note that there are $k·(k-1)$ IC constraints in total, which will significantly increase the computational complexity and reduce the scalability when k is large. However, we prove that the number of IC constraints can be somehow reduced.

Theorem 1.

When ${\theta }_1\le {\theta }_2\le ...\le {\theta }_k$, the monotonic property can be obtained as follows:

$${ϵ}_1\ge {ϵ}_2\ge ...\ge {ϵ}_k.$$

(12)

The theorem above is straightforward to prove, as we can obtain $p_i-{\theta }_i·{ϵ}_i\ge p_j-{\theta }_i·{ϵ}_j$ and $p_j-{\theta }_j·{ϵ}_j\ge p_i-{\theta }_j·{ϵ}_i$ for $\forall i,j\in \Theta$ based on the IC constraints. Then we have $({\theta }_i-{\theta }_j)·{ϵ}_j\ge ({\theta }_i-{\theta }_j)·{ϵ}_i$ by adding the two inequalities above. Therefore, it is obvious that ${ϵ}_i\le {ϵ}_j$ if ${\theta }_i\ge {\theta }_j$. When the privacy loss function is a general form denoted as $U(·)$, the monotonic property still holds. Detailed proof can be found in Appendix B.

Theorem 2.

For any privacy loss functions that satisfy Property 1 and Property 2, the $k·(k-1)$ IC constraints can be reduced to $3(k-1)$ constraints, as shown below:

$${ϵ}_i\ge {ϵ}_{i+1},\forall i,$$

$$p_i-U({\theta }_i,{ϵ}_i)\ge p_{i+1}-U({\theta }_i,{ϵ}_{i+1}),\forall i,$$

(13)

$$p_i-U({\theta }_i,{ϵ}_i)\ge p_{i-1}-U({\theta }_i,{ϵ}_{i-1}),\forall i.$$

The detailed proof of Theorem 2 is given in Appendix C.

Theorem 3.

For any privacy loss functions that satisfy Property 1 and Property 2, the k IR constraints can be reduced to one single constraint:

$$\begin{array}{c}\hfill p_k-U({\theta }_k,{ϵ}_k)\ge 0.\end{array}$$

(14)

Theorem 3 is straightforward to derive from the monotonic property of $U(·)$ and the IC constraints as $p_i-U({\theta }_i,{ϵ}_i)\ge p_k-U({\theta }_i,{ϵ}_k)\ge p_k-U({\theta }_k,{ϵ}_k)\ge 0$.

For a utility company, the objective of investment in energy theft detection can be described as follows:

$$O=\sum _{i=1}^k{\lambda }_i(l_i(b_i,{\tau }_i)+{\gamma }_1·p_i)-{\gamma }_1·{\lambda }_a·p_D·F$$

(15)

where $l_i(b_i,{\tau }_i)$ is the diagnostic scheme cost for electricity user i, as (8) shows, F refers to the fine imposed on detected abnormal users, and ${\gamma }_1$ is the weight coefficient. Furthermore, the utility company has a budget constraint on the privacy investment as follows:

$$\sum _{i=1}^k{\lambda }_i·p_i\le B$$

(16)

where B is the overall budget for the privacy investment. Moreover, the smart meter data are collected for not only energy theft detection but also other important applications such as demand response and state estimation. Hence, the accuracy of the aggregated data in a certain region has to be considered. In this paper, we adopt the notion of $(\alpha ,\delta )$-accuracy defined as follows.

Definition 3.

The aggregation of the smart meter data $\widehat{s}={\sum }_{i\in \mathcal{N}}{x}_{n,i}^{\prime }$ achieves $(\alpha ,\delta )$-accuracy if

$$Pr\left(\right|\widehat{s}-s|\le \alpha )\ge 1-\delta$$

(17)

where $s={\sum }_{i\in \mathcal{N}}{x}_{n,i}$ is the precise aggregation data without the noise.

From the definition of $(\alpha ,\delta )$-accuracy, we can see that $\alpha$ denotes the confidence interval and $1-\delta$ denotes the confidence level. Intuitively speaking, a smaller $\alpha$ means better data accuracy for any fixed $\delta$. Then the following theorem can be derived.

Theorem 4.

For a fixed confidence level $1-\delta$, the aggregation accuracy of the perturbed metering data can be found as

$$\alpha =\sqrt{{\displaystyle \frac{{\sum }_{i=1}^k{\lambda }_i·2b_i^2}{\delta }}}.$$

(18)

Detailed proof can be found in Appendix D.

From the above, we can derive the following primal optimization problem:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}(p_1,{ϵ}_1,{\tau }_1),\\ ...,\\ (p_k,{ϵ}_k,{\tau }_k)\end{array}}{min}& \sum _{i=1}^k{\lambda }_i(l_i(b_i,{\tau }_i)+{\gamma }_1{p}_i)-{\gamma }_1{\lambda }_a{p}_{D}F+{\gamma }_2\alpha \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& p_k-U({\theta }_k,{ϵ}_k)\ge 0,\hfill \\ \hfill & {ϵ}_i\ge {ϵ}_{i+1},\forall i,\hfill \\ \hfill & p_i-U({\theta }_i,{ϵ}_i)\ge p_{i\pm 1}-U({\theta }_i,{ϵ}_{i\pm 1}),\forall i,\hfill \\ \hfill & \sum _{i=1}^k{\lambda }_i·p_i\le B.\hfill \end{array}$$

(19)

where ${\lambda }_a$ is the total number of abnormal users.

We also investigate the optimal contract design for a more ideal scenario, where the utility company knows the precise privacy preference of each customer and can provide a specific privacy contract to them directly, instead of offering a series of contracts for customers to choose from. It is expected that the utility company will achieve higher welfare in this scenario, for there is no information asymmetry between the energy provider and users. In the evaluation part, we will also study the performance under such an ideal scenario and use it as a benchmark. The optimal contract design problem under complete information can be formulated as follows:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}(p_1,{ϵ}_1,{\tau }_1),\\ ...,\\ (p_k,{ϵ}_k,{\tau }_k)\end{array}}{min}& \sum _{i=1}^k{\lambda }_i\left(l_i(b_i,{\tau }_i)+{\gamma }_1{p}_i\right)-{\gamma }_1{\lambda }_a{p}_{D}F+{\gamma }_2\alpha \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& p_i-U({\theta }_i,{ϵ}_i)\ge 0,\forall i\hfill \\ \hfill & \sum _{i=1}^k{\lambda }_i·p_i\le B.\hfill \end{array}$$

(20)

It can be seen that, compared with the incomplete information scenario, the incentive compatibility constraints are ignored under complete information because of the information symmetry. Additionally, the k IR constraints cannot be reduced to one in this scenario because of the absence of IC constraints.

4. Generalization to the Continuous Scenario

In a more realistic scenario, the customers’ privacy preference $\theta$ could be continuous. In this section, we will study the optimal contract design with a continuous privacy preference.

Let $\lambda \left(\theta \right)$ denote the distribution density function of $\theta$, and assume $\theta$ is bounded by $[\underline{\theta },\overline{\theta }]$. Then we can formulate the optimal contract design problem as the following optimization problem:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}p\left(\theta \right),ϵ\left(\theta \right),\tau \left(\theta \right)\end{array}}{min}& {\int }_{\underline{\theta }}^{\overline{\theta }}\lambda \left(\theta \right)(l\left(b\left(\theta \right),\tau \left(\theta \right)\right)+{\gamma }_{1}p\left(\theta \right))d\theta -{\gamma }_1{\lambda }_a{p}_{D}F+{\gamma }_2\alpha \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& p\left(\theta \right)-U(\theta ,ϵ(\theta \left)\right)\ge 0,\hfill \\ \hfill & p\left(\theta \right)-U(\theta ,ϵ\left(\theta \right))\ge p\left({\theta }^{\prime }\right)-U(\theta ,ϵ\left({\theta }^{\prime }\right)),\forall {\theta }^{\prime }\ne \theta ,\hfill \\ \hfill & {\int }_{\underline{\theta }}^{\overline{\theta }}\lambda \left(\theta \right)·p\left(\theta \right)d\theta \le B\hfill \end{array}$$

(21)

where the aggregation accuracy $\alpha$ in continuous form can be described as follows:

$$\alpha =\sqrt{{\int }_{\underline{\theta }}^{\overline{\theta }}{\displaystyle \frac{\lambda \left(\theta \right)·2b^2\left(\theta \right)}{\delta }}d\theta }.$$

(22)

It can be found that the problem above cannot be solved due to the infinite number of constraints. Fortunately, we can reduce the IR and IC constraints similarly to the discrete case.

Theorem 5.

The monotonic property of $ϵ\left(\theta \right)$ in the continuous scenario can be obtained as follows:

$${\displaystyle \frac{dϵ}{d\theta }}\le 0$$

(23)

if the privacy loss function satisfies

$${\displaystyle \frac{{\partial }^{2}U(\theta ,ϵ\left(\theta \right))}{\partial ϵ\left(\theta \right)\partial \theta }}\ge 0.$$

(24)

It can be seen that the assumption about the second-order mixed partial derivative of the privacy loss function is a continuous version of Property 2. Detailed proof can be found in Appendix E.

Based on the monotonic property of $ϵ\left(\theta \right)$, we can obtain the following theorem.

Theorem 6.

For any privacy loss functions that satisfy Property 1 and the continuous version of Property 2, the infinitely many IC constraints can be reduced to

$$\begin{array}{ccc}\hfill & {\displaystyle \frac{dp\left(\theta \right)}{d\theta }}-{\displaystyle \frac{\partial U(\theta ,ϵ(\theta \left)\right)}{\partial ϵ\left(\theta \right)}}·{\displaystyle \frac{dϵ\left(\theta \right)}{d\theta }}=0,\hfill & \hfill {\displaystyle \frac{dϵ\left(\theta \right)}{d\theta }}\le 0.\end{array}$$

(25)

Detailed proof can be found in Appendix F.

Theorem 7.

For any privacy loss functions that satisfy Property 1 and the continuous version of Property 2, the infinitely many IR constraints can be reduced to

$$p\left(\overline{\theta }\right)-U(\overline{\theta },ϵ\left(\overline{\theta }\right))\ge 0.$$

(26)

The proof of Theorem 7 can be found in Appendix G.

From the discussion above, the optimal contract design problem with a continuous privacy preference can be formulated as follows:

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}p\left(\theta \right),ϵ\left(\theta \right),\tau \left(\theta \right)\end{array}}{min}& {\int }_{\underline{\theta }}^{\overline{\theta }}\lambda \left(\theta \right)(l\left(b\left(\theta \right),\tau \left(\theta \right)\right)+{\gamma }_{1}p\left(\theta \right))d\theta -{\gamma }_1{\lambda }_a{p}_{D}F+{\gamma }_2\alpha \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& p\left(\overline{\theta }\right)-U(\overline{\theta },ϵ\left(\overline{\theta }\right))\ge 0,\hfill \\ \hfill & {\displaystyle \frac{dϵ\left(\theta \right)}{d\theta }}\le 0,\hfill \\ \hfill & {\displaystyle \frac{dp\left(\theta \right)}{d\theta }}-{\displaystyle \frac{\partial U(\theta ,ϵ(\theta \left)\right)}{\partial ϵ\left(\theta \right)}}·{\displaystyle \frac{dϵ\left(\theta \right)}{d\theta }}=0,\hfill \\ \hfill & {\int }_{\underline{\theta }}^{\overline{\theta }}\lambda \left(\theta \right)·p\left(\theta \right)d\theta \le B\hfill \end{array}$$

(27)

The main notations used in this article are summarized in Appendix H.

5. Simulation

In this section, simulation results are illustrated to validate the feasibility of the proposed incentive mechanism. Specifically, we consider a scenario where there are 20 types of customers, who are uniformly distributed. The corresponding privacy preferences are taken from the interval [0,19]. The total number of electricity users is 200. The contract budget and fine for energy theft are set to be 100 and 1, respectively. The proportion of abnormal users is set to be 5%, and the confidence level in the definition of aggregation accuracy is set to be $1-\delta =0.9$. The privacy loss function is defined as a linear form, as Equation (9) shows.

We first show the monotonic decreasing property of $ϵ$, i.e., the monotonic increasing property of b, in Figure 5. In this figure and subsequent figures, the abscissa “Type of contracts” denotes the index of the menu ordered by ascending privacy preference. A higher index number corresponds to a user type with a stronger privacy preference. The red line with X marks denotes the optimally designed b under incomplete information, and the blue line with round marks denotes the optimally designed b under complete information. Interestingly, it can be seen that the designed b follows a monotonic increasing property under both scenarios, even though the IC constraints are removed under the complete information scenario. It is also worth noting that the pre-specified privacy preference of Type 1 users is 0, which means that they do not care about their privacy at all. And the corresponding scale parameter of the added noisy signal’s distribution is 0; i.e., the optimally designed contract for Type 1 users can only assure ∞-differential privacy, which is consistent with the intuition that users with a higher privacy preference intend to choose a higher privacy-preserving level. Additionally, Figure 5 also demonstrates that the utility company can provide a lower privacy-preserving level under complete information with the same contract budget so that higher aggregation accuracy can be achieved. This is mainly because the utility company has more information that is unknown under incomplete information to optimally design the contracts in this scenario.

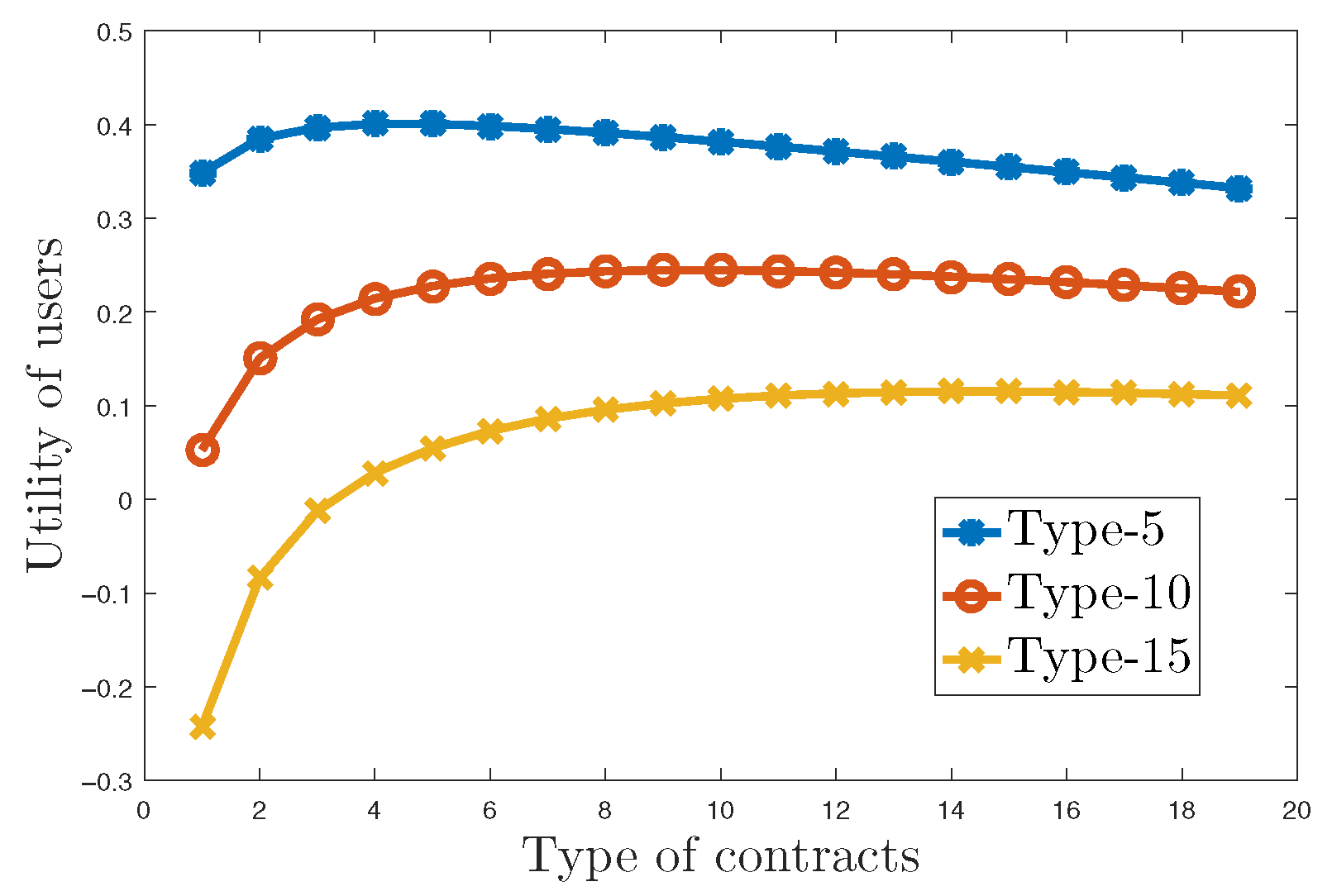
Figure 6 visualizes the incentive compatibility (IC) property derived in Theorem 2. It shows the utility value of Type 5, Type 10, and Type 15 users when they choose other types of contracts. Every curve is single-peaked, with its global maximum exactly at the index matching the user’s own type, demonstrating that truth-telling yields the highest payoff and that no participant benefits from pretending to belong to a different privacy class. In other words, the users can achieve the highest utility value when they choose the corresponding type of contract, which illustrates the incentive compatibility property. Furthermore, the users with low privacy preferences will always achieve a higher utility value than users with high privacy preferences when they choose the same contracts.

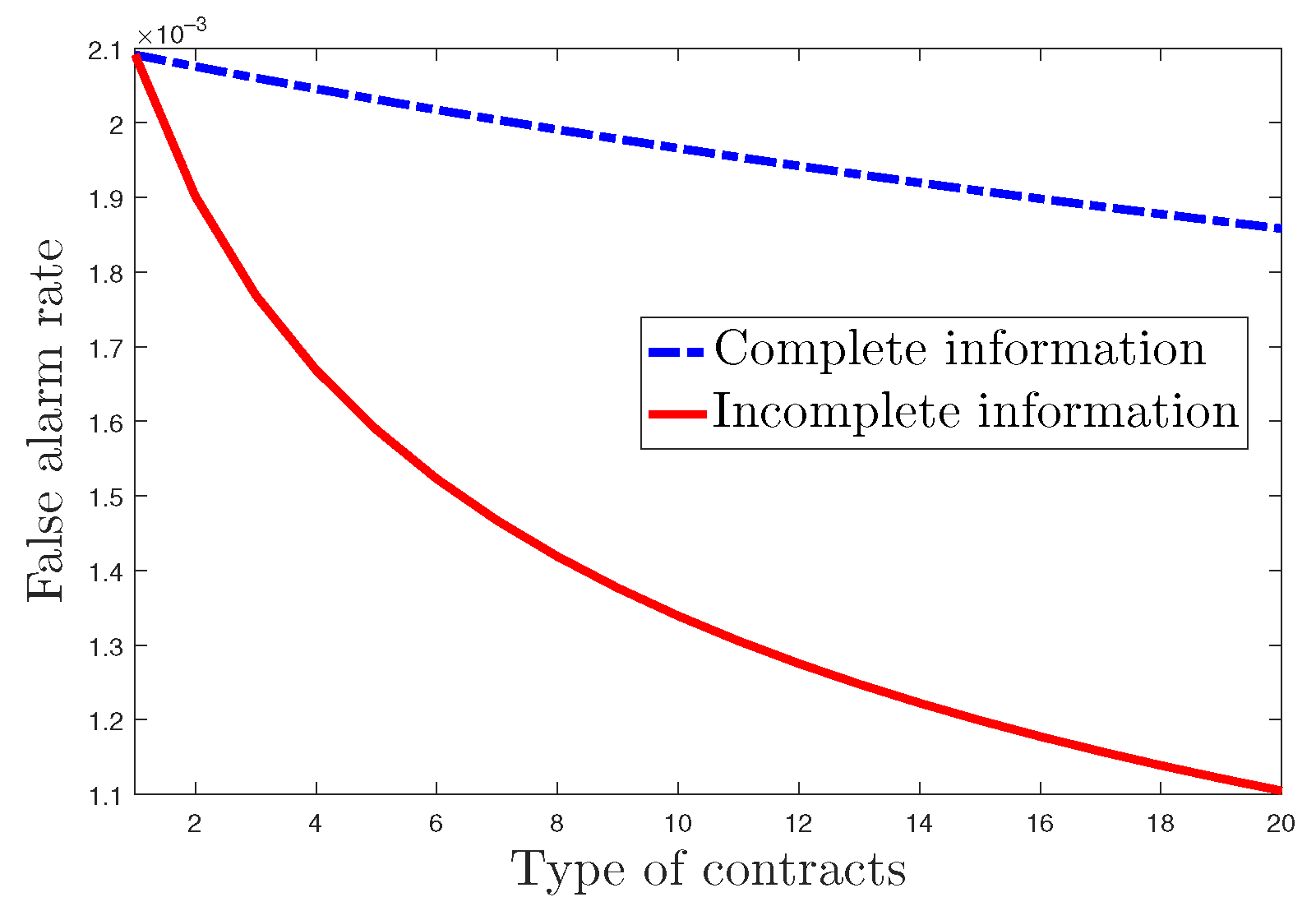
Figure 7 illustrates the performance of the energy theft detector under default settings. Combining Figure 4 and Figure 7, we can conclude that the proposed incentive mechanism can achieve good detection performance under both complete information and incomplete information.

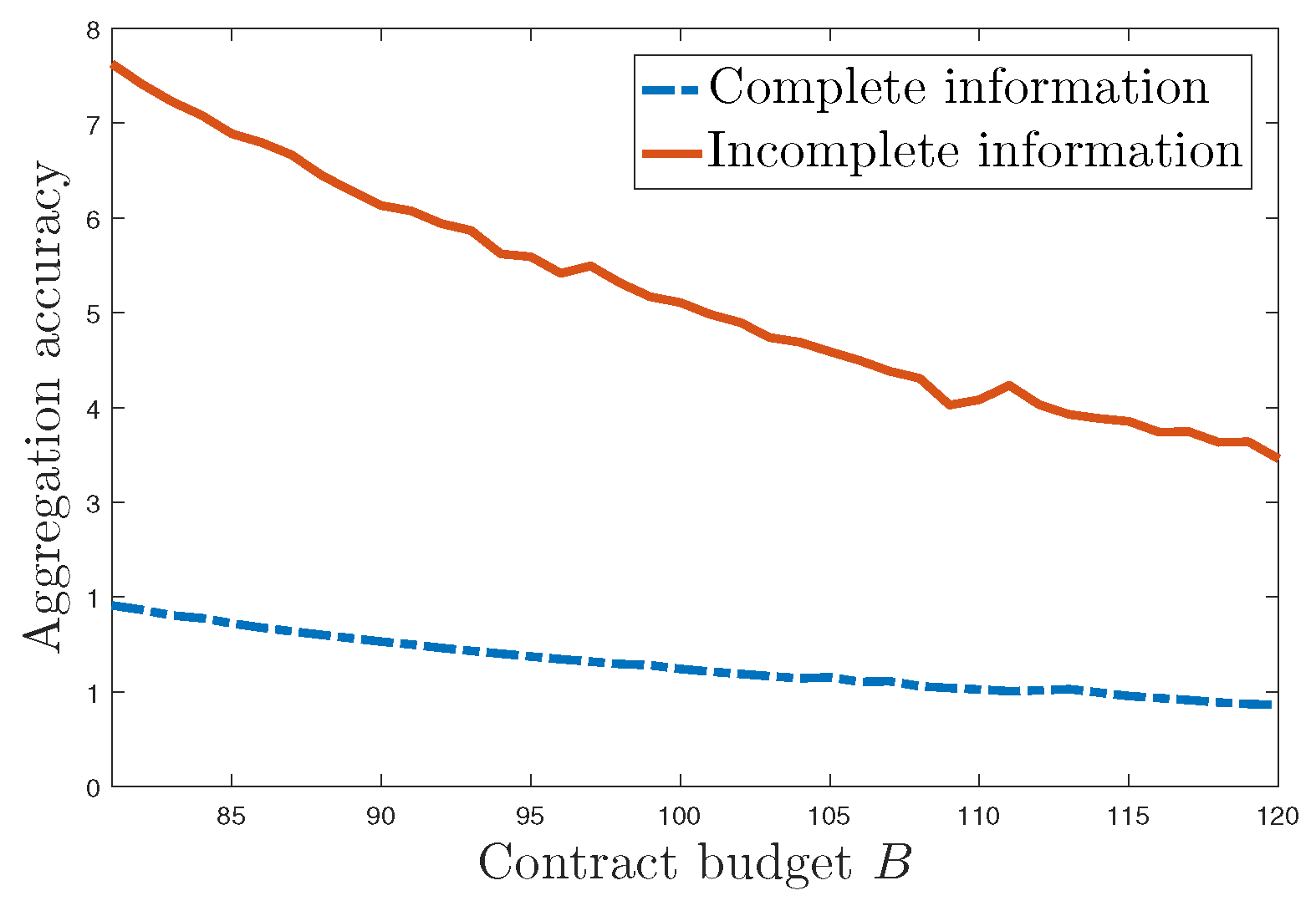
Figure 8 shows the aggregation accuracy under different settings of the contract budget B. A smaller $\alpha$ denotes better aggregation accuracy in our settings. It can be seen that $\alpha$ shows a tendency to decrease with the rise in the contract budget. This is because the utility company can buy more privacy from the users with a higher contract budget. In addition, under the default settings, the utility company can achieve higher aggregation accuracy under complete information than that under incomplete information, which is also on account of the information symmetry between the utility company and electricity users.

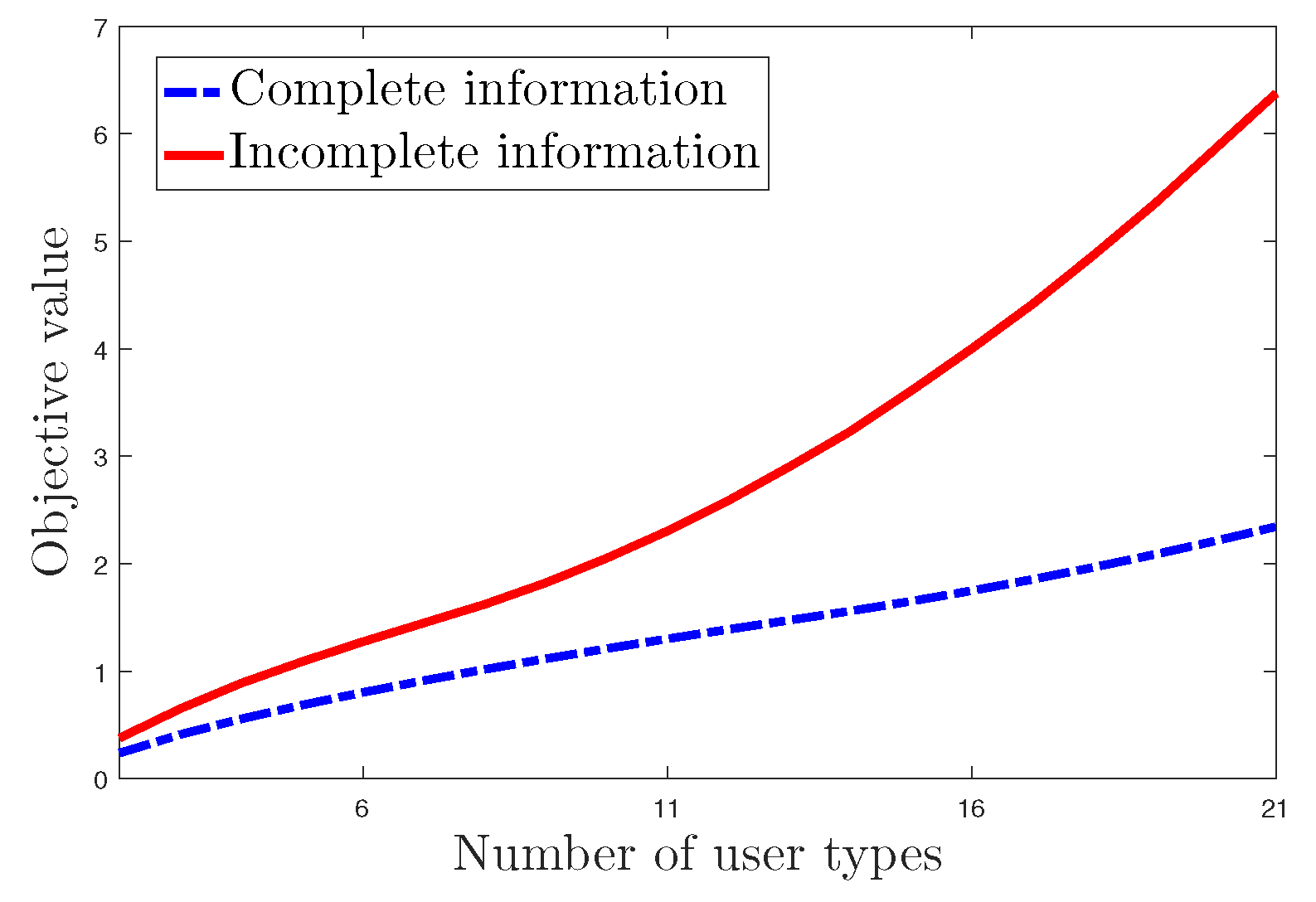
Figure 9 demonstrates the relationship between the objective value and the number of contract types. It can be seen that the utility company will achieve a higher objective value under incomplete information due to the information asymmetry. And interestingly, it seems that the objective value increases with the number of user types. Hence, in a practical scenario, the utility company has to comprehensively consider the diversity of users’ privacy requirements and its own utility, so that a trade-off between them can be achieved.

6. Conclusions

This paper has introduced a contract-theoretic incentive mechanism that allows a utility to balance energy theft detection accuracy against users’ privacy guarantees under information asymmetry. Our work provides quantified privacy measurement under the differential privacy paradigm and analyzes the energy theft detection performance degradation after the involvement of noise signals. Then an optimal contract design problem is proposed to minimize the loss of the utility company; meanwhile, the number of IR and IC constraints is reduced to decrease the complexity of problem solving. By deriving contract designs for both discrete and continuous privacy preferences, we showed how proper compensation persuades users to inject only the minimum noise required, thereby limiting the false alarm rate and aggregation error while maintaining detection power. Simulations confirm that the menu satisfies incentive compatibility and individual rationality and reveal the quantitative cost of incomplete information.

Despite these contributions, this study has some limitations. First, the detection module assumes a single-time-interval average detector and a Laplace noise mechanism; more sophisticated detectors (e.g., CUSUM) or other noise distributions (e.g., Gaussian) may yield different privacy–accuracy trade-offs. Second, user consumption is modeled as an exponential distribution calibrated to historical averages, which is an assumption that may not capture the diurnal volatility or correlation structures observed in real households. Finally, this paper focuses on static, one-shot contracts; dynamic or online contracts that adapt to seasonal load patterns or system parameters represent a natural extension. To deal with the dynamic situation, a feasible solution is to extend the proposed incentive design method into an online algorithm; i.e., the utility company continuously estimates each customer’s short-term consumption distribution and offers a dynamic threshold $\tau$ in real time. Theorems 2, 3, 6, and 7 can theoretically accelerate the computational speed of incentive mechanism design.

Looking forward, we identify these promising directions.

• Billing accuracy: Since Laplace noise directly distorts the energy reading used for tariff calculation, an immediate question is how much revenue loss the utility tolerates under the optimal contract. A follow-up study will incorporate metering-error-aware tariff design and quantify the upper bound of noise magnitude that keeps billing errors within regulatory tolerance.
• Multi-period contracting: Real-world consumers face time-of-use prices and shifting load profiles. Extending the current single-interval model to a multi-period setting (possibly using dynamic contract theory) will allow the utility to offer privacy-reward menus that vary with expected load, thereby reducing the total compensation budget while maintaining detection performance.
• Learning type distributions: At present, the utility is assumed to know the prior distribution of privacy preferences. Combining the contract framework with machine learning mechanisms can relax this assumption, enabling the utility to refine the menu based on revealed preferences over time and to bound the regret incurred by initial mis-estimation.
• Stronger attacker capability: In this paper, it is assumed that the abnormal users cannot obtain knowledge of system parameters like network topology or anomaly detection settings. It would be both challenging and interesting to investigate a more complex scenario, where abnormal users can manipulate noise levels to evade detection.

Addressing these open issues will move the proposed scheme closer to field deployment and provide regulators with a principled tool for simultaneously protecting consumer privacy and safeguarding grid revenue.