Broadband Response Enhancement of a Pitching Wave Energy Converter Using a Nonlinear Stiffness Mechanism Under Dry Friction Effects
Abstract
1. Introduction
2. Methodology
2.1. Experimental Set-Up
2.1.1. WEC Description
2.1.2. Wave Conditions
2.1.3. Data Processing and Analysis
2.2. Theoretical Model
2.2.1. Hydrodynamic Modeling
2.2.2. Equation of Motion
2.2.3. Coupled Multibody System
2.2.4. Linearization
2.2.5. Friction
- Initialize with the linear response (without friction).
- Compute using Equation (27).
- Update the response using:
- Repeat until is less than a specified tolerance, in this case .
2.2.6. Nonlinear Stiffness Mechanism Configuration
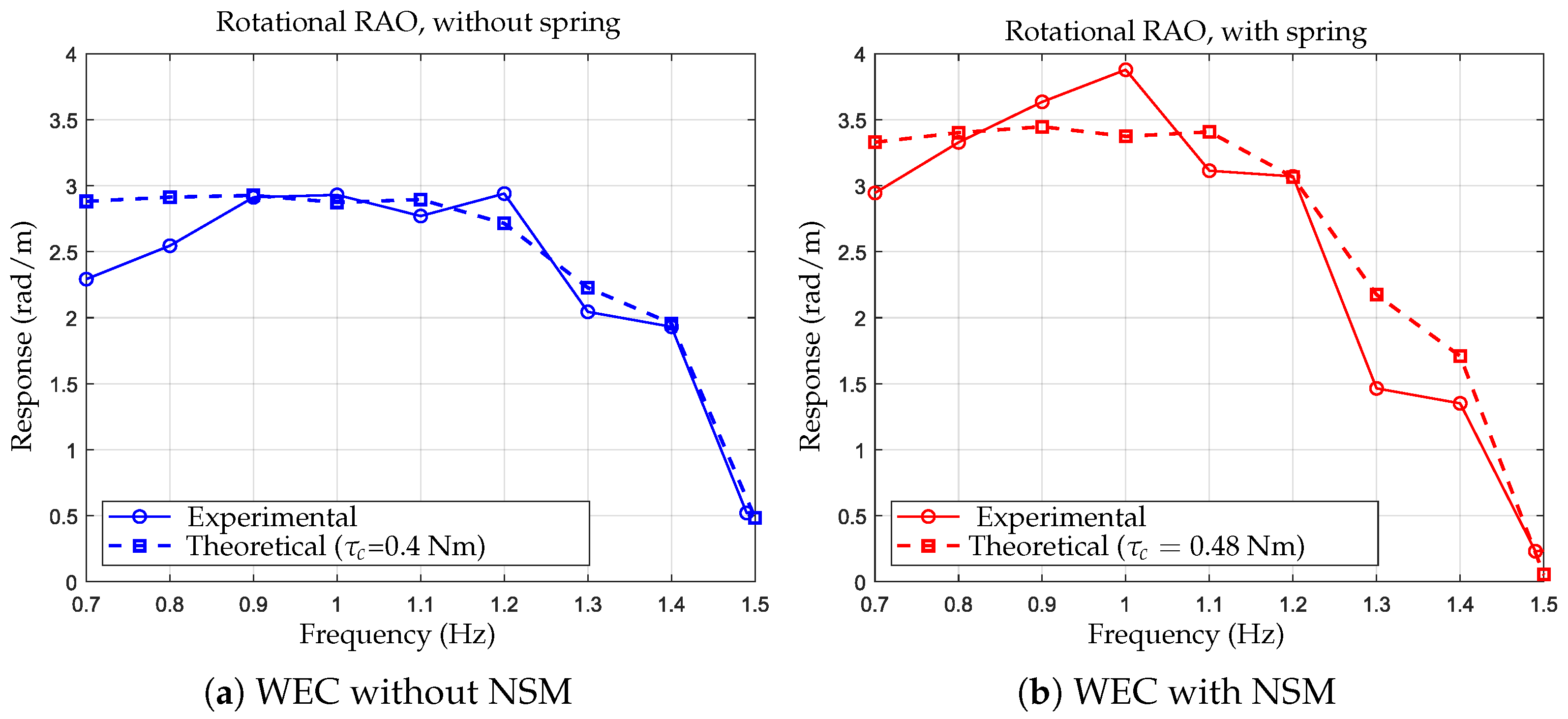
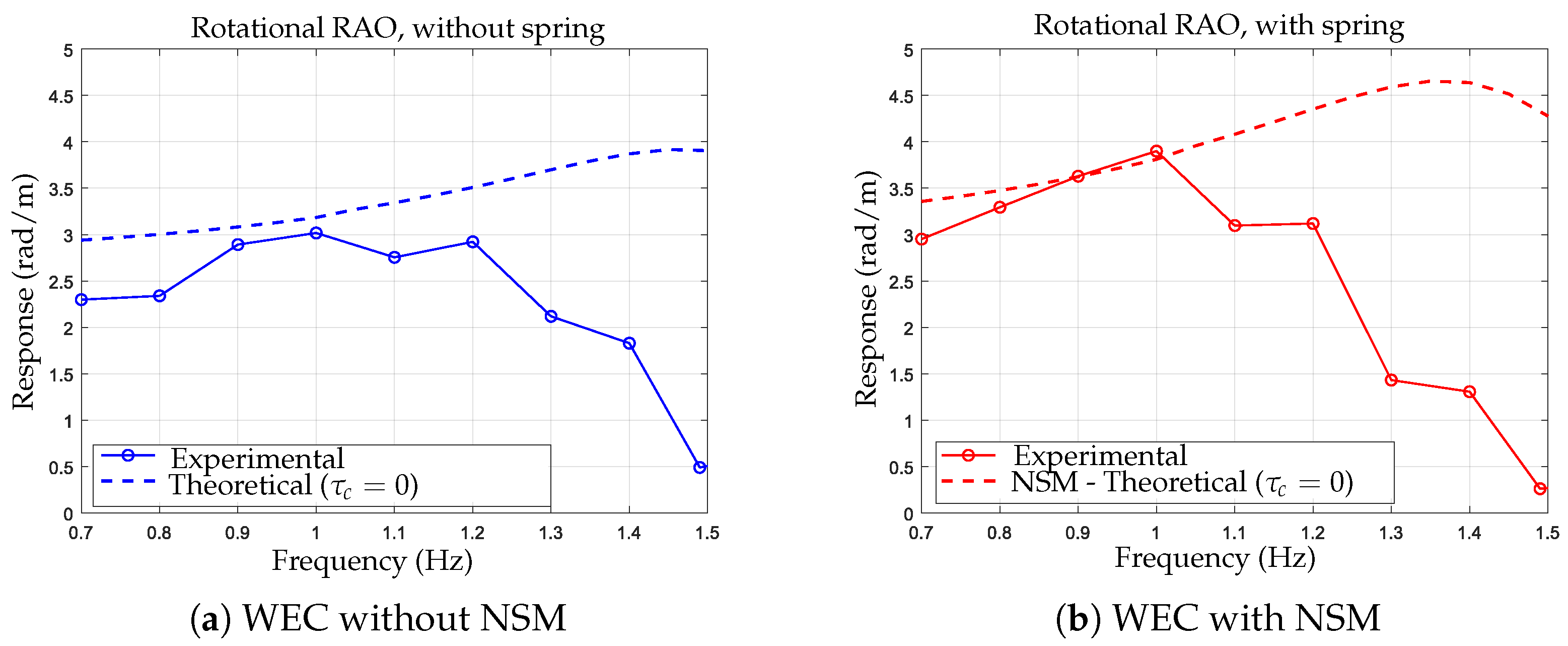
3. Results and Discussion
3.1. Hydrodynamic Coefficients
3.2. Theoretical-Experimental Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| NSM | Nonlinear Stiffness Mechanism |
| PA | Point Absorber |
| RAO | Response Amplitude Operator |
| FFT | Fast Fourier Transform |
| RMSE | Root Mean Square Error |
References
- Chen, C.; Pinar, M.; Stengos, T. Renewable energy and CO2 emissions: New evidence with the panel threshold model. Renew. Energy 2022, 194, 117–128. [Google Scholar] [CrossRef]
- Ramos, V.; Giannini, G.; Calheiros-Cabral, T.; López, M.; Rosa-Santos, P.; Taveira-Pinto, F. Assessing the effectiveness of a novel WEC concept as a co-located solution for offshore wind farms. J. Mar. Sci. Eng. 2022, 10, 267. [Google Scholar] [CrossRef]
- Guo, B.; Wang, T.; Jin, S.; Duan, S.; Yang, K.; Zhao, Y. A review of point absorber wave energy converters. J. Mar. Sci. Eng. 2022, 10, 1534. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Schubert, B.W. Performance enhancement of submerged wave energy converters using nonlinear stiffness. Appl. Ocean Res. 2021, 112, 102663. [Google Scholar]
- Zhang, X.; Zhang, H.; Zhou, X.; Sun, Z. Recent advances in wave energy converters based on nonlinear stiffness mechanisms. Appl. Math. Mech. 2022, 43, 1081–1108. [Google Scholar] [CrossRef]
- Wu, Z.; Levi, C.; Estefen, S.F. Wave energy harvesting using nonlinear stiffness system. Appl. Ocean Res. 2018, 74, 102–116. [Google Scholar] [CrossRef]
- Todalshaug, J.; Steinnásgeirsson, G.; Hjálmarsson, E.; Maillet, J.; Möller, P.; Pires, P.; Guerinel, M.; Lopes, M. Tank testing of an inherently phase controlled Wave Energy Converter. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar] [CrossRef]
- Khasawneh, M.A. Exploiting Non-Linearity to Improve the Performance of Point Wave Energy Absorbers. Ph.D. Thesis, ProQuest Dissertations Publishing, Ann Arbor, MI, USA, 2023. [Google Scholar]
- Xiao, L.; Zhang, X.; Yang, J. Numerical study of a wave energy converter with nonlinear snap-through stiffness in regular waves. In Proceedings of the 24th International Ocean and Polar Engineering Conference (ISOPE), Busan, Republic of Korea, 15–20 June 2014; pp. 883–890. [Google Scholar]
- Têtu, A.; Ferri, F.; Kramer, M.B.; Todalshaug, J.H. Physical and mathematical modeling of a wave energy converter equipped with a negative spring mechanism for phase control. Energies 2018, 11, 2362. [Google Scholar] [CrossRef]
- Younesian, D.; Alam, M.R. Multi-stable mechanisms for high-efficiency and broadband ocean wave energy harvesting. Appl. Energy 2017, 197, 292–302. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, X.; Xiao, L.; Li, X.; Chen, L. Application of an adaptive bistable power capture mechanism to a point absorber wave energy converter. Appl. Energy 2018, 228, 450–467. [Google Scholar] [CrossRef]
- Pierart, F.G.; Campos, P.G.; Basoalto, C.E.; Rohten, J.; Davey, T. Experimental Implementation of Reinforcement Learning Applied to Maximise Energy from a Wave Energy Converter. Energies 2024, 17, 5087. [Google Scholar] [CrossRef]
- McCarthy, J.; Ringwood, J.V. Modelling of friction and nonlinear damping in wave energy devices. J. Ocean Eng. Mar. Energy 2020, 6, 291–305. [Google Scholar]
- Pierart, F.G.; Fernandez, J.; Olivos, J.; Gabl, R.; Davey, T. Numerical Investigation of the Scaling Effects for a Point Absorber. Water 2022, 14, 2156. [Google Scholar] [CrossRef]
- Rao, S.S. Harmonically excited vibration. In Mechanical Vibrations, 5th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2011; pp. 113–180. [Google Scholar]



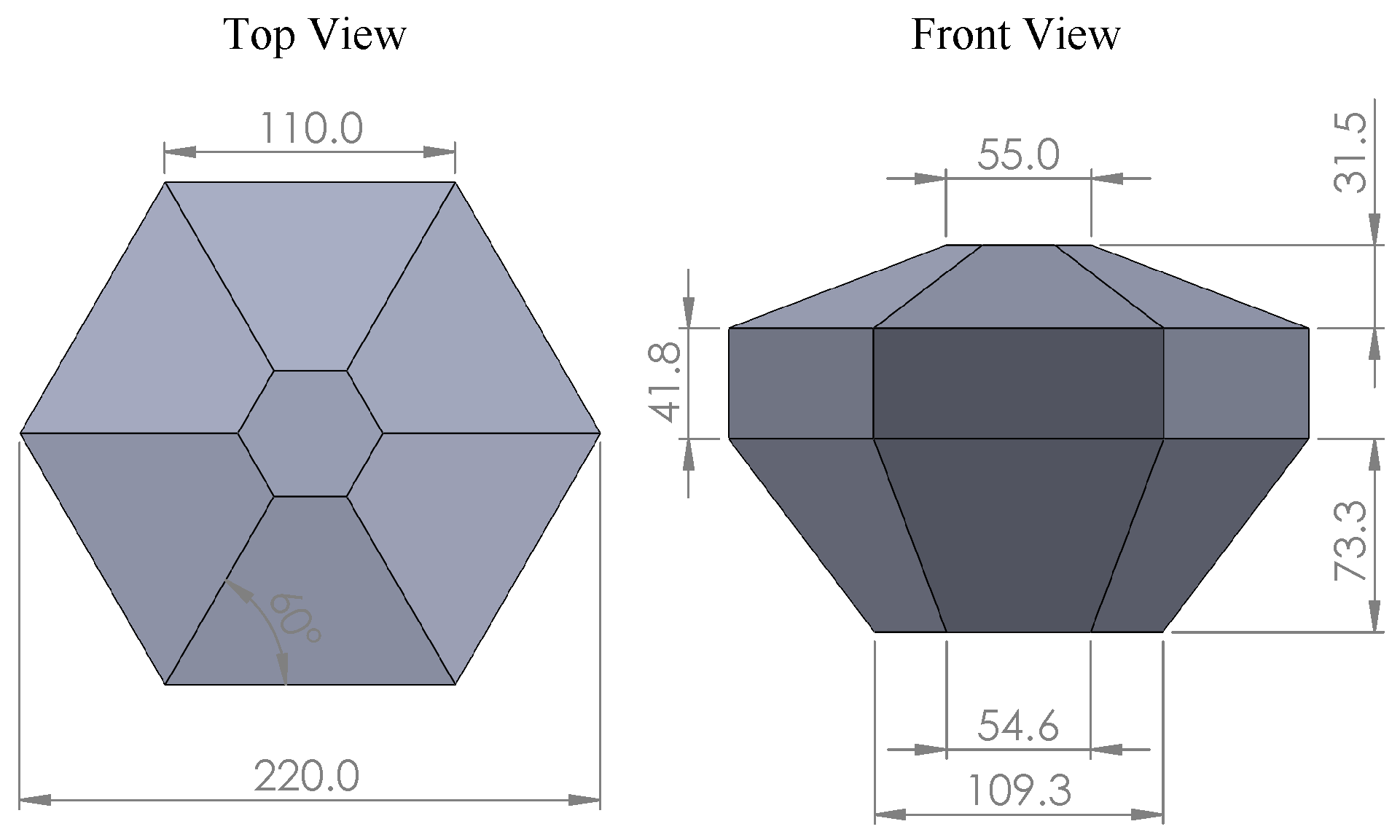
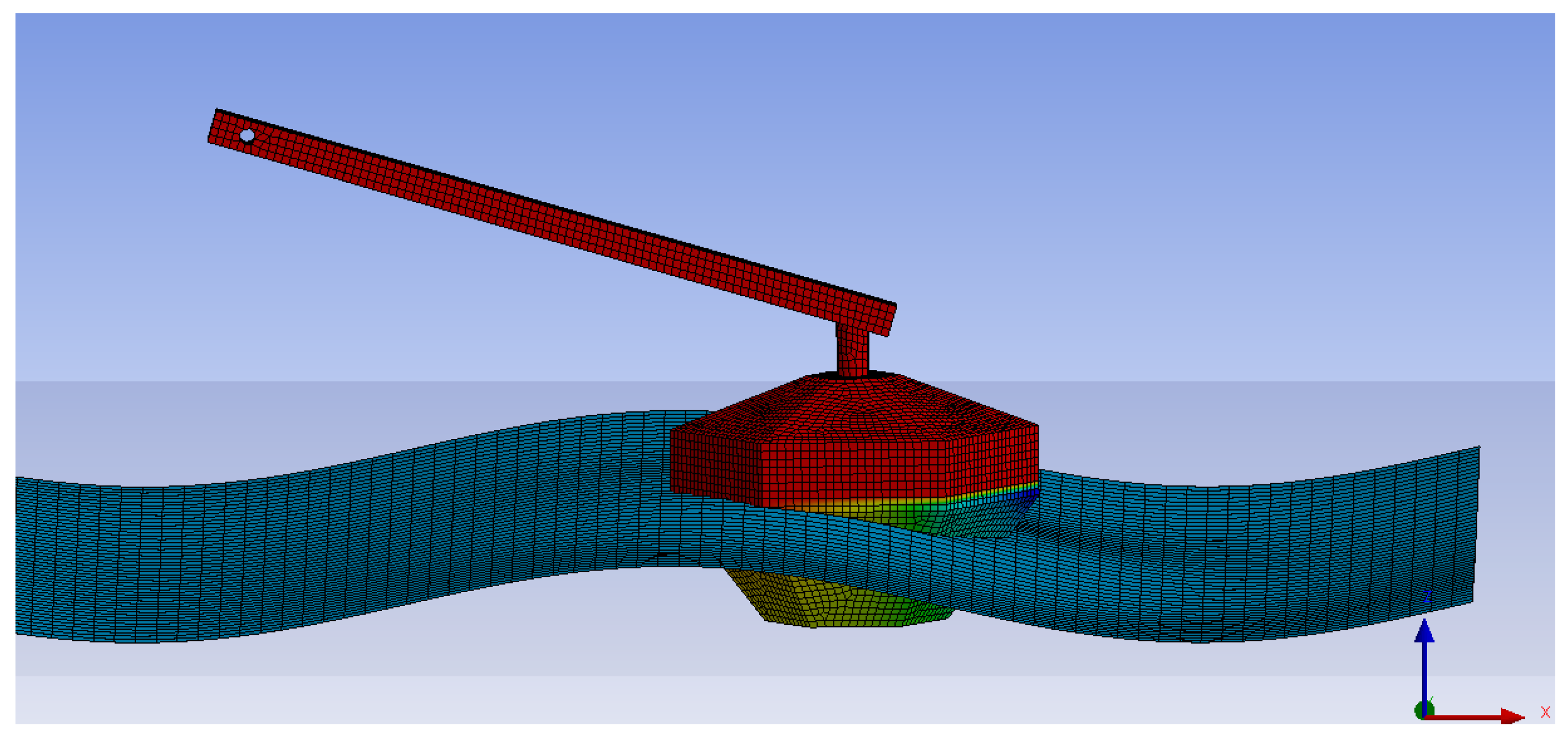
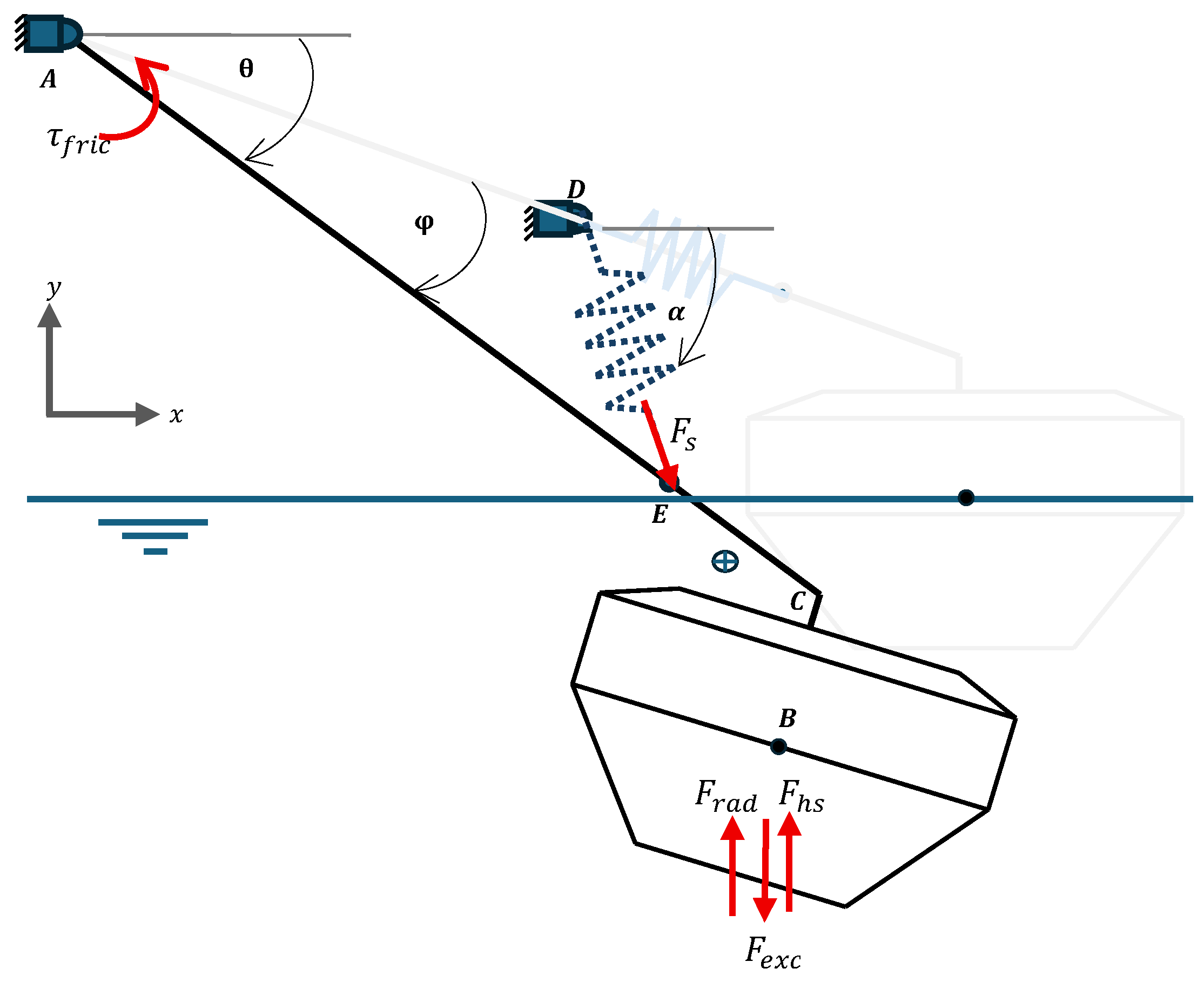
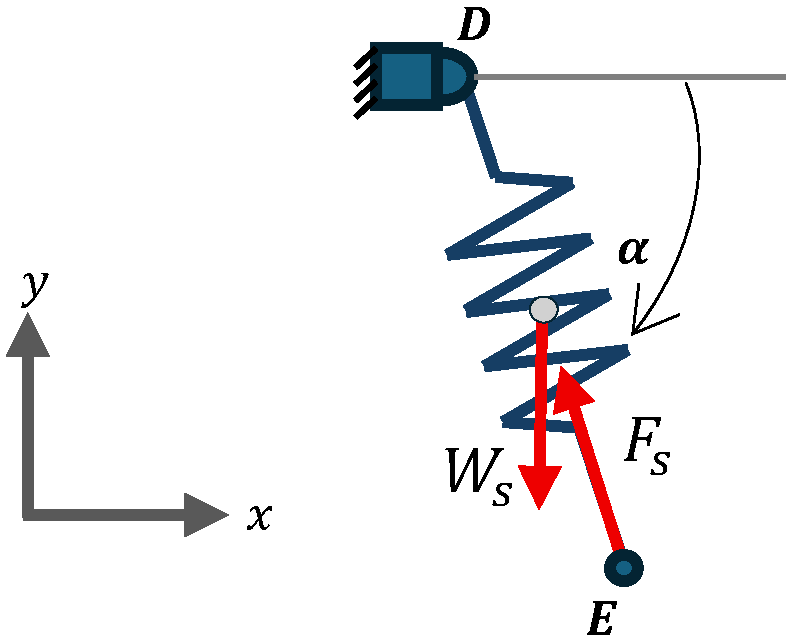

| Property | Description | Value | Unit |
|---|---|---|---|
| Mass of the lever arm and equipment | 1.216 | kg | |
| Mass of the buoy | 0.864 | kg | |
| Buoy volume | 0.0032 | m3 | |
| S | Buoy cross-sectional area | 0.0314 | m2 |
| Initial inclination angle | −0.20 | rad | |
| Distance between points A and C | 0.421 | m | |
| Distance between points C and Q | 0.031 | m | |
| Distance between points Q and B | 0.041 | m |
| Excitation Frequency, f (Hz) | Wavelength, (m) | Wave Height H (m) |
|---|---|---|
| 0.7 | 3.1863 | 0.1115 |
| 0.8 | 2.4395 | 0.0854 |
| 0.9 | 1.9275 | 0.0675 |
| 1.0 | 1.5613 | 0.0546 |
| 1.1 | 1.2903 | 0.0452 |
| 1.2 | 1.0842 | 0.0379 |
| 1.3 | 0.9239 | 0.0323 |
| 1.4 | 0.7966 | 0.0279 |
| 1.5 | 0.6939 | 0.0243 |
| Property | Description | Value | Unit |
|---|---|---|---|
| Distance between pivot A and point D | 0.223 | m | |
| Distance between pivot A and point E | 0.314 | m | |
| Natural length of the spring | 0.260 | m | |
| Spring stiffness | 430 | N/m |
| Configuration | Without Friction Model | With Friction Model |
|---|---|---|
| Without NSM | 1.310 | 0.256 |
| With NSM | 2.002 | 0.360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neira, B.; Pierart, F.G.; Villegas, C.; Cifuentes, C.; Barrientos, V.; Tampier, G.; Knobloch, T.; Corves, B.; Hüsing, M. Broadband Response Enhancement of a Pitching Wave Energy Converter Using a Nonlinear Stiffness Mechanism Under Dry Friction Effects. Energies 2025, 18, 6022. https://doi.org/10.3390/en18226022
Neira B, Pierart FG, Villegas C, Cifuentes C, Barrientos V, Tampier G, Knobloch T, Corves B, Hüsing M. Broadband Response Enhancement of a Pitching Wave Energy Converter Using a Nonlinear Stiffness Mechanism Under Dry Friction Effects. Energies. 2025; 18(22):6022. https://doi.org/10.3390/en18226022
Chicago/Turabian StyleNeira, Braulio, Fabián G. Pierart, Claudio Villegas, Cristian Cifuentes, Vicente Barrientos, Gonzalo Tampier, Thomas Knobloch, Burkhard Corves, and Mathias Hüsing. 2025. "Broadband Response Enhancement of a Pitching Wave Energy Converter Using a Nonlinear Stiffness Mechanism Under Dry Friction Effects" Energies 18, no. 22: 6022. https://doi.org/10.3390/en18226022
APA StyleNeira, B., Pierart, F. G., Villegas, C., Cifuentes, C., Barrientos, V., Tampier, G., Knobloch, T., Corves, B., & Hüsing, M. (2025). Broadband Response Enhancement of a Pitching Wave Energy Converter Using a Nonlinear Stiffness Mechanism Under Dry Friction Effects. Energies, 18(22), 6022. https://doi.org/10.3390/en18226022






