Novel GBest–Lévy Adaptive Differential Ant Bee Colony Optimization for Optimal Allocation of Electric Vehicle Charging Stations and Distributed Generators in Smart Distribution Systems
Abstract
1. Introduction
- Objective Function Formulation. The voltage profile, voltage deviation, and power losses are evaluated using the computationally efficient backward–forward sweep (BFS) load-flow method. This approach ensures an accurate and reliable assessment of distribution network performance.
- Optimization Technique. The GLAD-ABC algorithm is employed to determine the optimal allocation of EVCSs and DGs in the IEEE-33 and 69 bus distribution system. The proposed method evaluates the effectiveness of the distribution network and demonstrates its superiority over conventional techniques.
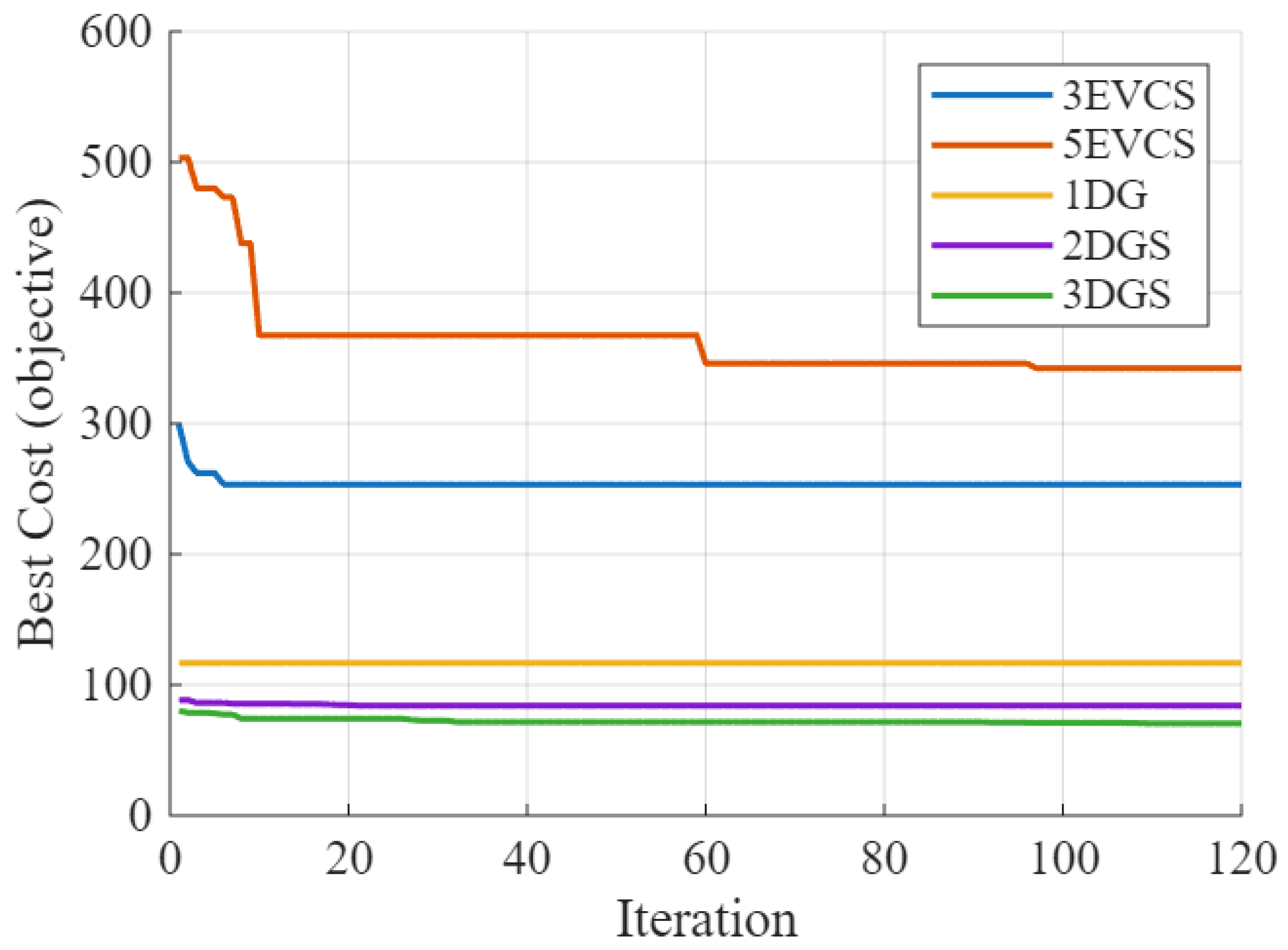
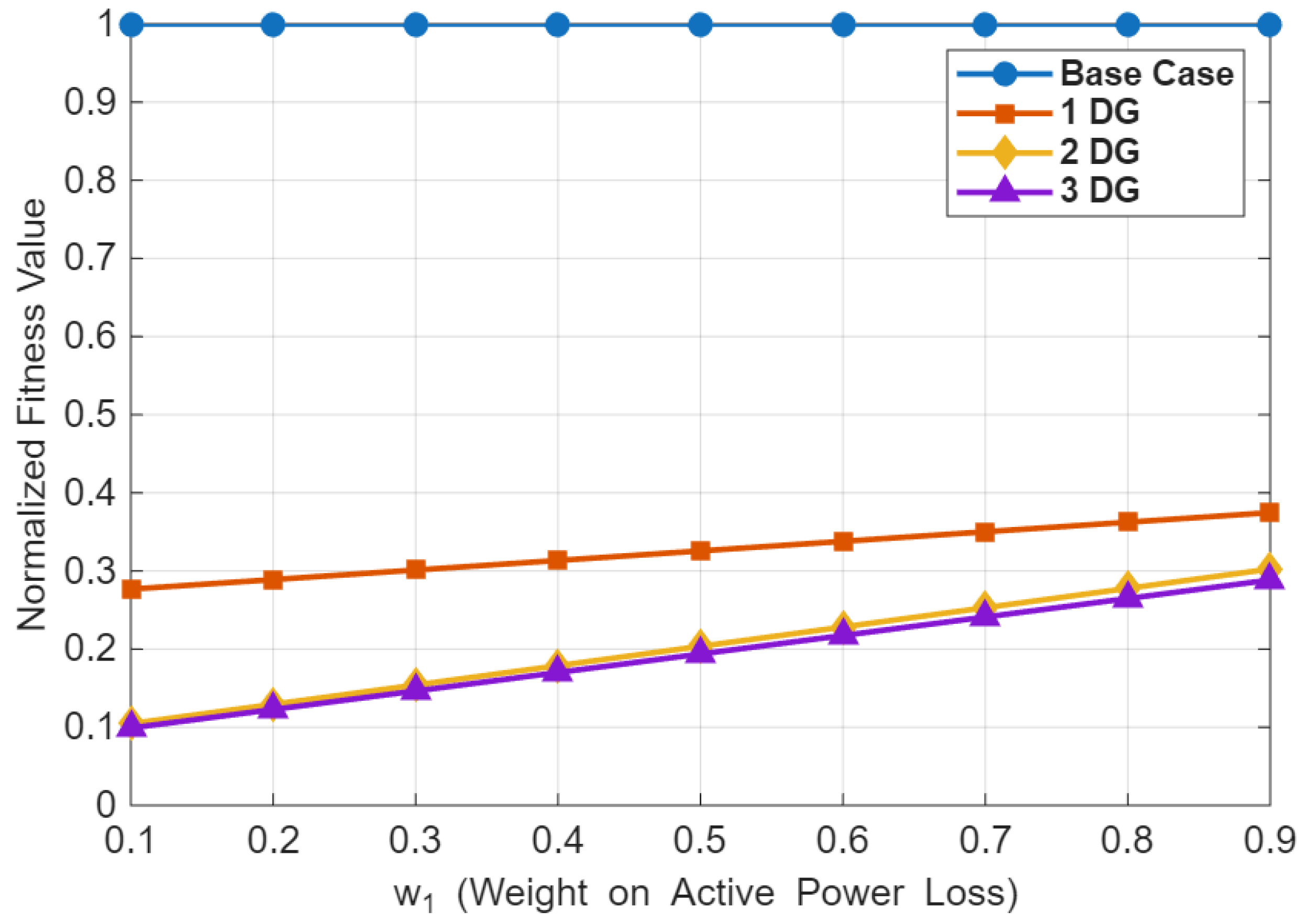
- The enhanced performance of the proposed optimizer is validated by comparing it with other up-to-date algorithms cited in the literature, delivering consistently lower active power losses alongside fast, stable convergence, indicating strong suitability for utility planning in EV-rich grids.
2. Literature Review
3. Problem Formulation
3.1. Objective Function
3.2. Operational Constraints
3.2.1. Equality Constraint
3.2.2. Inequality Constraints
- DG injection limits: The output of active and reactive power from distributed generation units is restricted to defined ranges.
- b.
- Voltage constraint: Maintain each bus voltage between 0.95 and 1.05 p.u. to preserve system stability.
- c.
- Current limit: No transmission or distribution line should carry a current exceeding its rated capacity.where and specify the lower and upper voltage levels at each bus within the system to ensure voltage stability. and represent the lower and upper active power level at the kth DG while and denote the minimum and maximum reactive power of the kth DG and and represent the actual and maximum limit of the current in the jth branch. The load-flow analysis is utilized to calculate the objective function.
3.3. Load-Flow Analysis
4. Design Methodology for EVCS and DG Placement
- (i)
- To maximize the voltage profile improvement of the network
- (ii)
- To minimize overall real and reactive power losses.
4.1. Artificial Bee Colony Optimization (ABC)
4.1.1. Initialization
4.1.2. Worker Bee Phase
4.1.3. Onlooker Bee Phase
4.1.4. Selection
4.2. GBest–Lévy Adaptive Differential Artificial Bee Colony (GLAD-ABC)
4.2.1. Initialization
4.2.2. Generation of Initial Scout Sources
4.2.3. Lévy Step Construction (Mantegna)
4.2.4. GLAD Scout Step Size
4.2.5. Generation of a New Scout Solution
4.2.6. Discovery/Abandonment Rule
4.2.7. Ending of GLAD-Scout Process
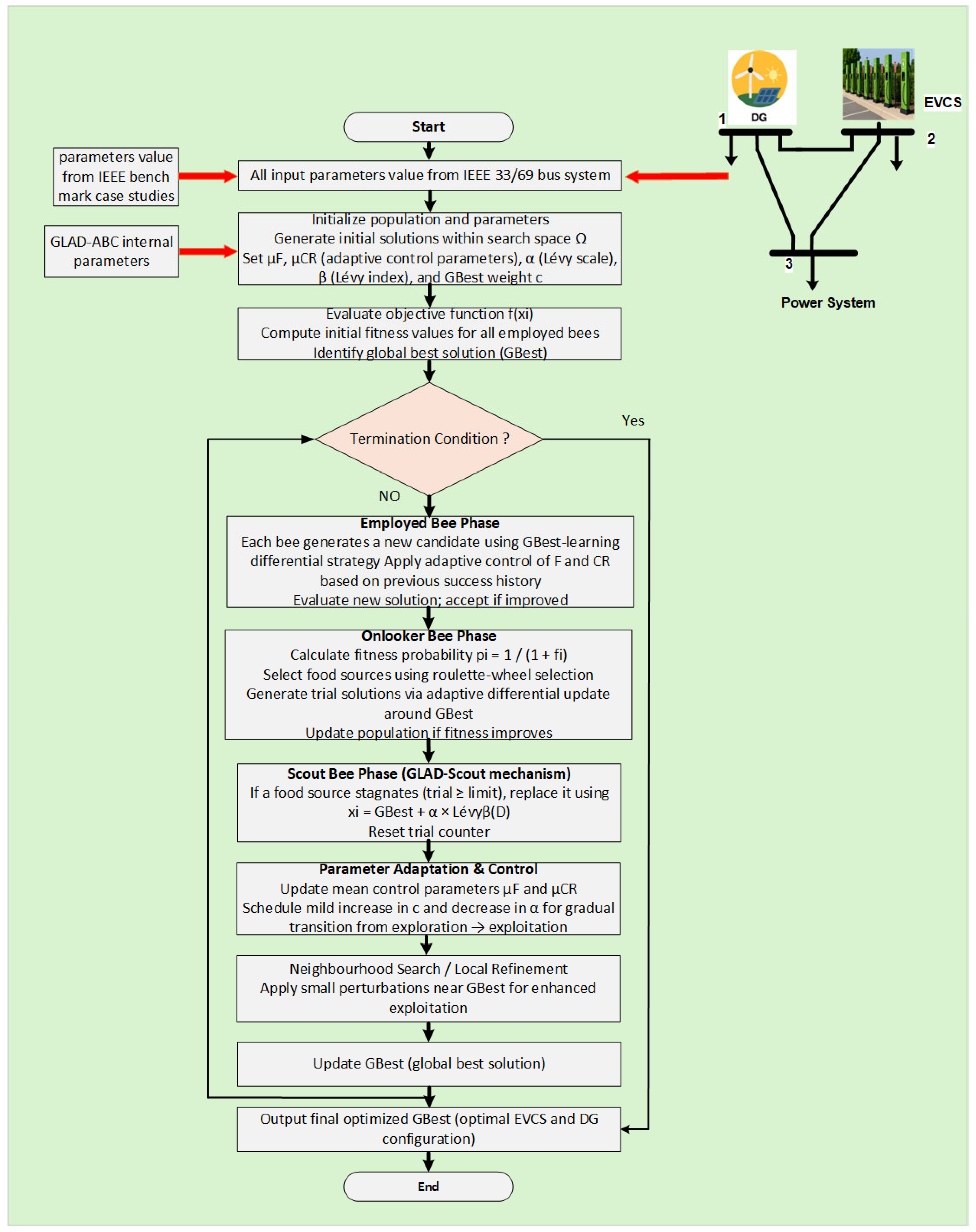
| Algorithm 1 Pseudocode of the GLAD-ABC. |
| Input: Objective f(·), bounds Ω, population size N, maxIter limit (trial counter threshold), β (Lévy index), initial params μF, μCR, c (GBest weight), α (Lévy scale) Output: Best solution gbest 1: Initialize population {xi}i = 1…N ~ Uniform(Ω) 2: Evaluate fi ← f(xi); gbest ← argmin fi 3: Set trial_i ← 0 for all i 4: for t = 1 … maxIter do 5: for i = 1 … N do 6: vi ← GLADStep (xi, gbest, μF, μCR, c, α, β, Ω) 7: if f(vi) ≤ f(xi) then xi ← ΠΩ (vi); trial_i ← 0; record (F, CR) success 8: else trial_i ← trial_i + 1 9: end if 10: end for 11: Update gbest ← argmin_i f(xi) 12: # -------- Onlooker-bee phase -------- 13: Compute fitness fit_i = 1/(1 + f(xi)) 14: Compute selection probabilities pi = fit_i/Σk fit_k 15: for k = 1 … N do 16: Select index i~Categorical({pi}) 17: vi ← GLADStep(xi, gbest, μF, μCR, c, α, β, Ω) 18: if f(vi) ≤ f(xi) then xi ← ΠΩ(vi); trial_i ← 0; record (F, CR) success 19: else trial_i ← trial_i + 1 20: end if 21: end for 22: Update gbest ← argmin_i f(xi) 23: # -------- Scout-bee phase (GLAD-scout) -------- 24: for i = 1 … N do 25: if trial_i ≥ limit then 26: xi ← ΠΩ (gbest + α · Levyβ(D)) 27: trial_i ← 0 28: end if 29: end for 30: Update μF, μCR from successful (F, CR) used this iteration 31: Optionally schedule c ↑ (mildly) and α ↓ (mildly) over t 32: end for 33: return gbest |
5. Result and Discussion
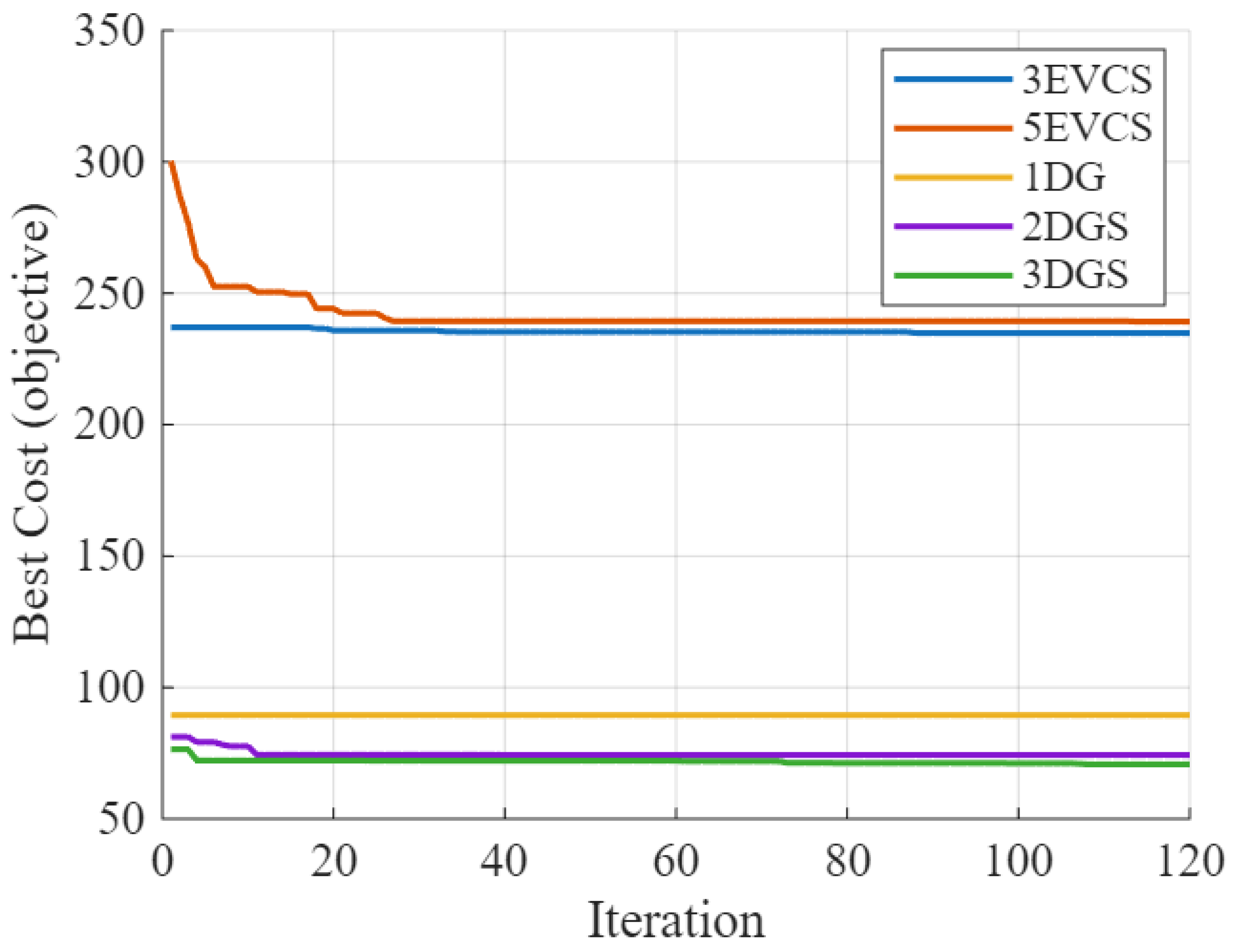
5.1. Results of IEEE-33 RDS
- Operational case 1. Load-flow analysis of base case for the existing load in IEEE-33 bus RDS.
- Operational case 2. Optimum allocation of three EVCSs within IEEE-33 bus RDS.
- Operational case 3. Optimum allocation of five EVCSs within IEEE-33 bus RDS.
- Operational case 4. Optimum placement of one DG within IEEE-33 bus RDS.
- Operational case 5. Optimum placement of two DGs within IEEE-33 bus RDS.
- Operational case 6. Optimum allocation of three DGs within IEEE-33 bus RDS.
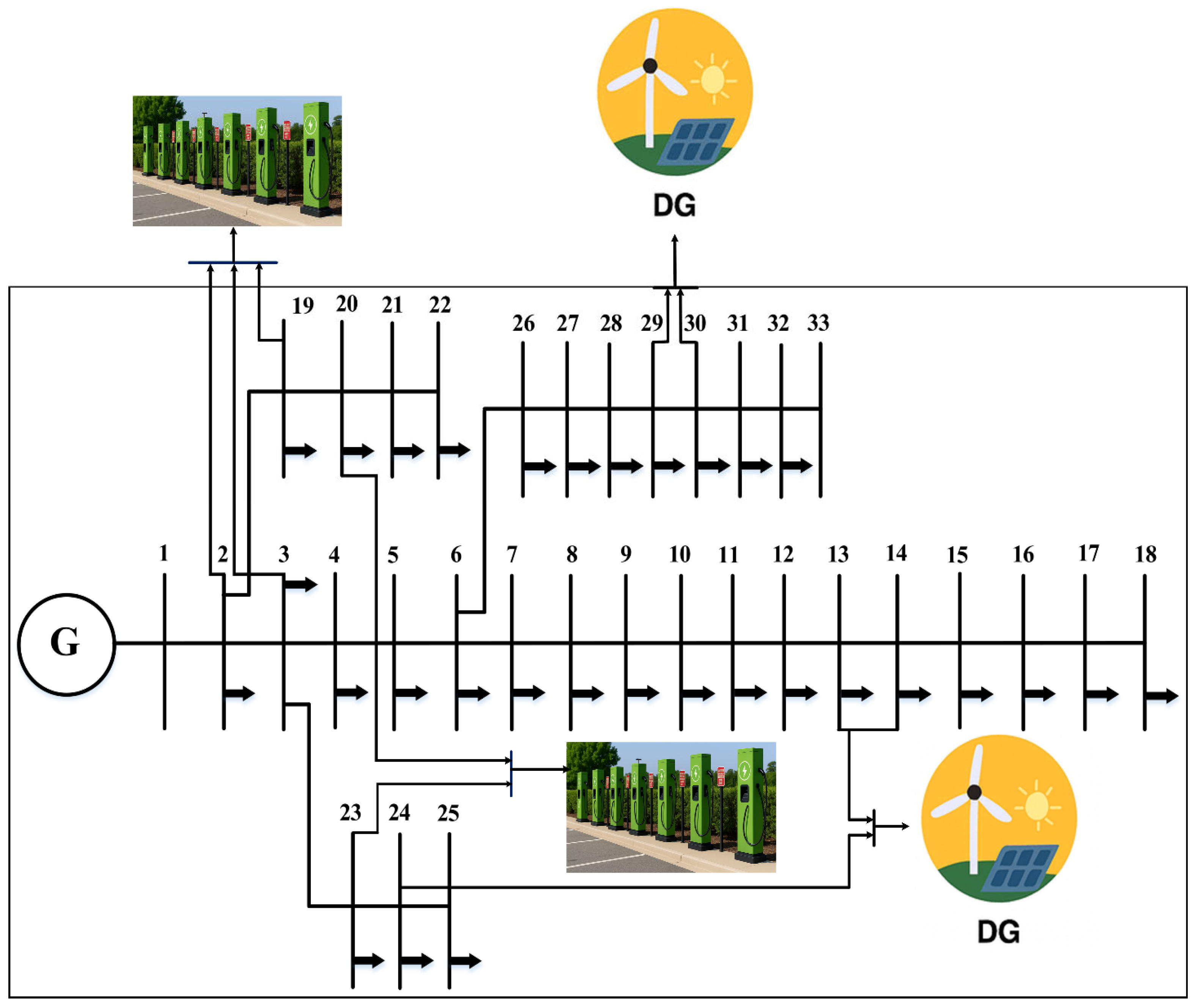
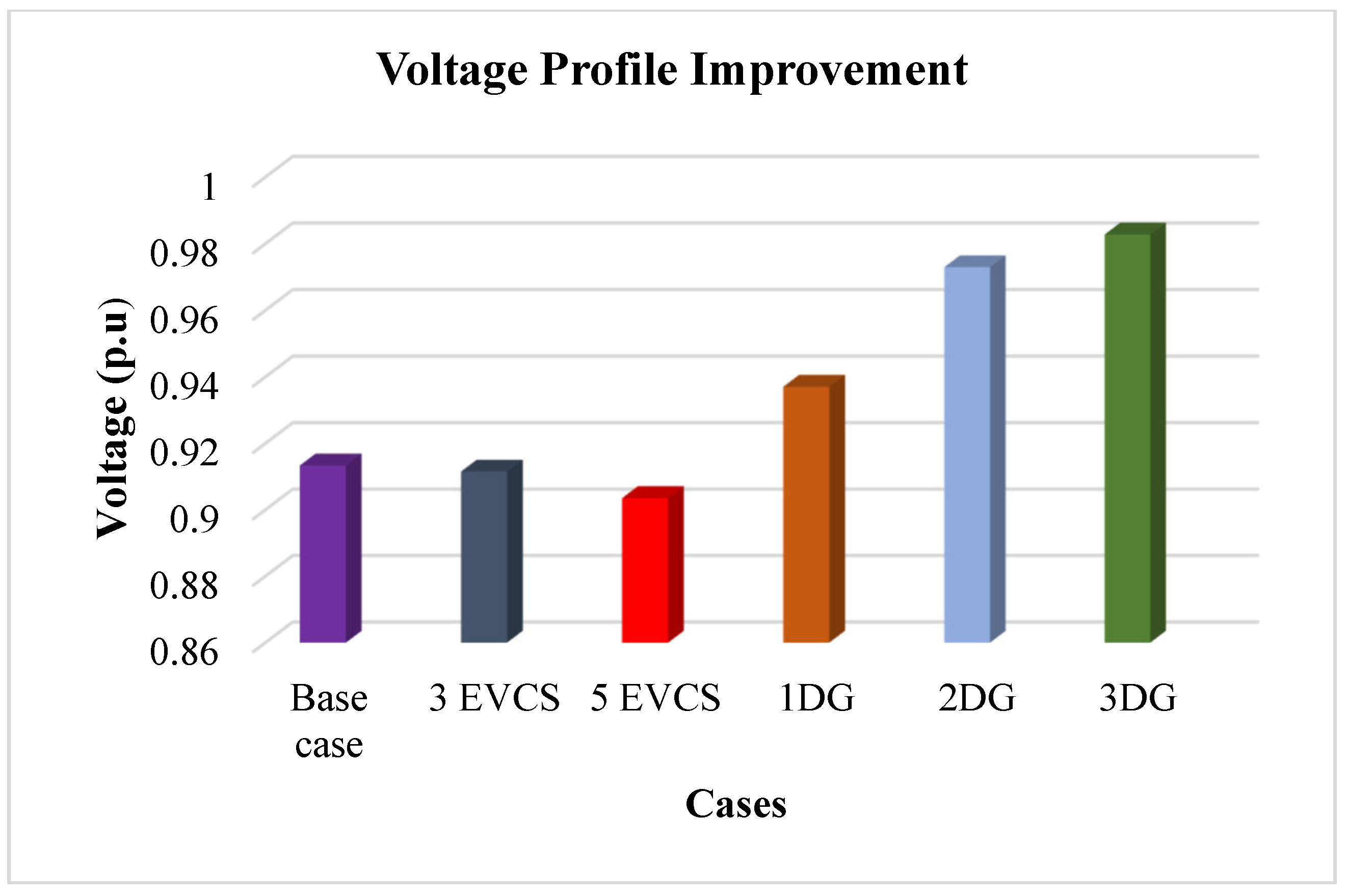
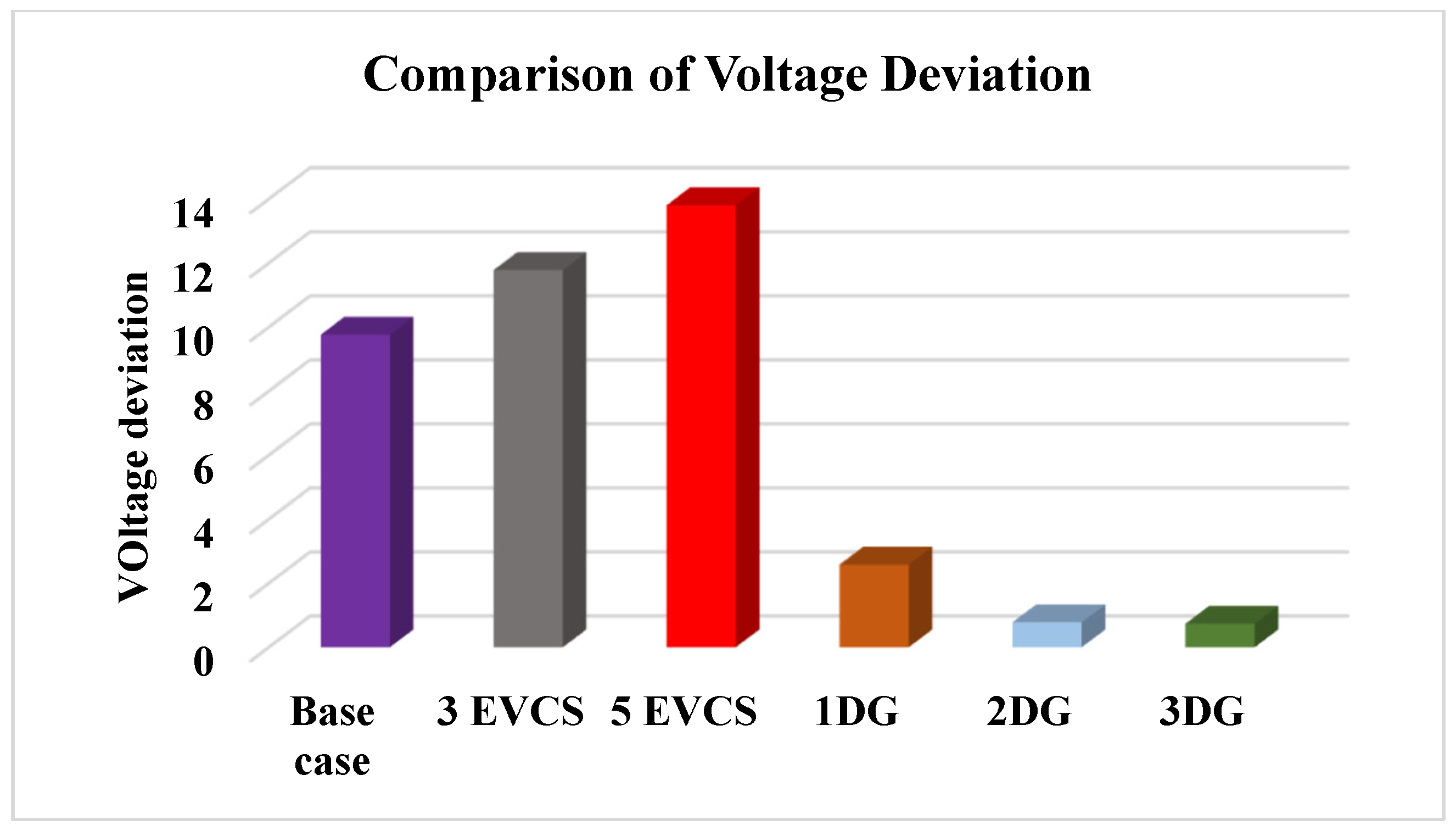
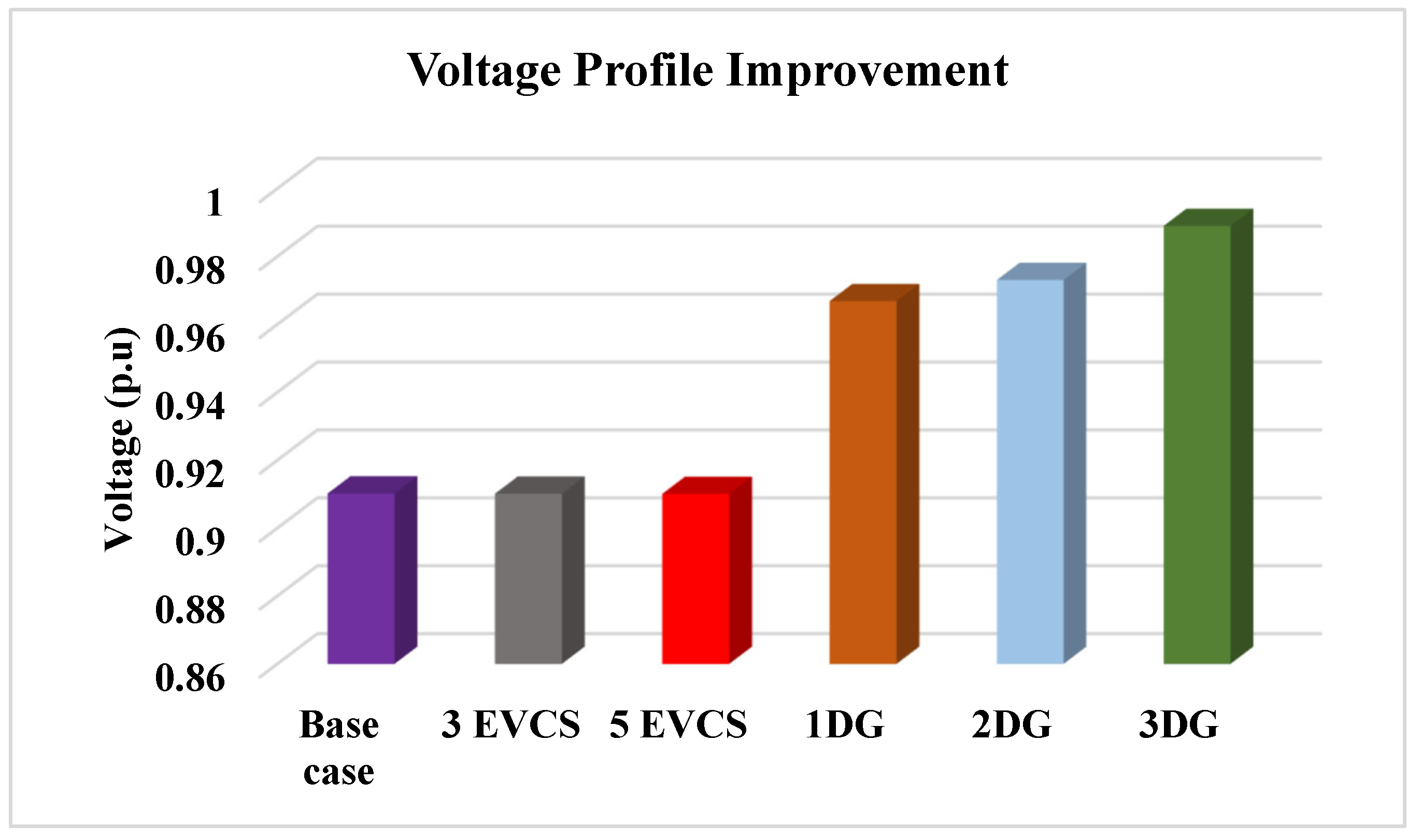
5.1.1. Impact of EVCSs and DGs on the Voltage Profile of IEEE-33 RDS
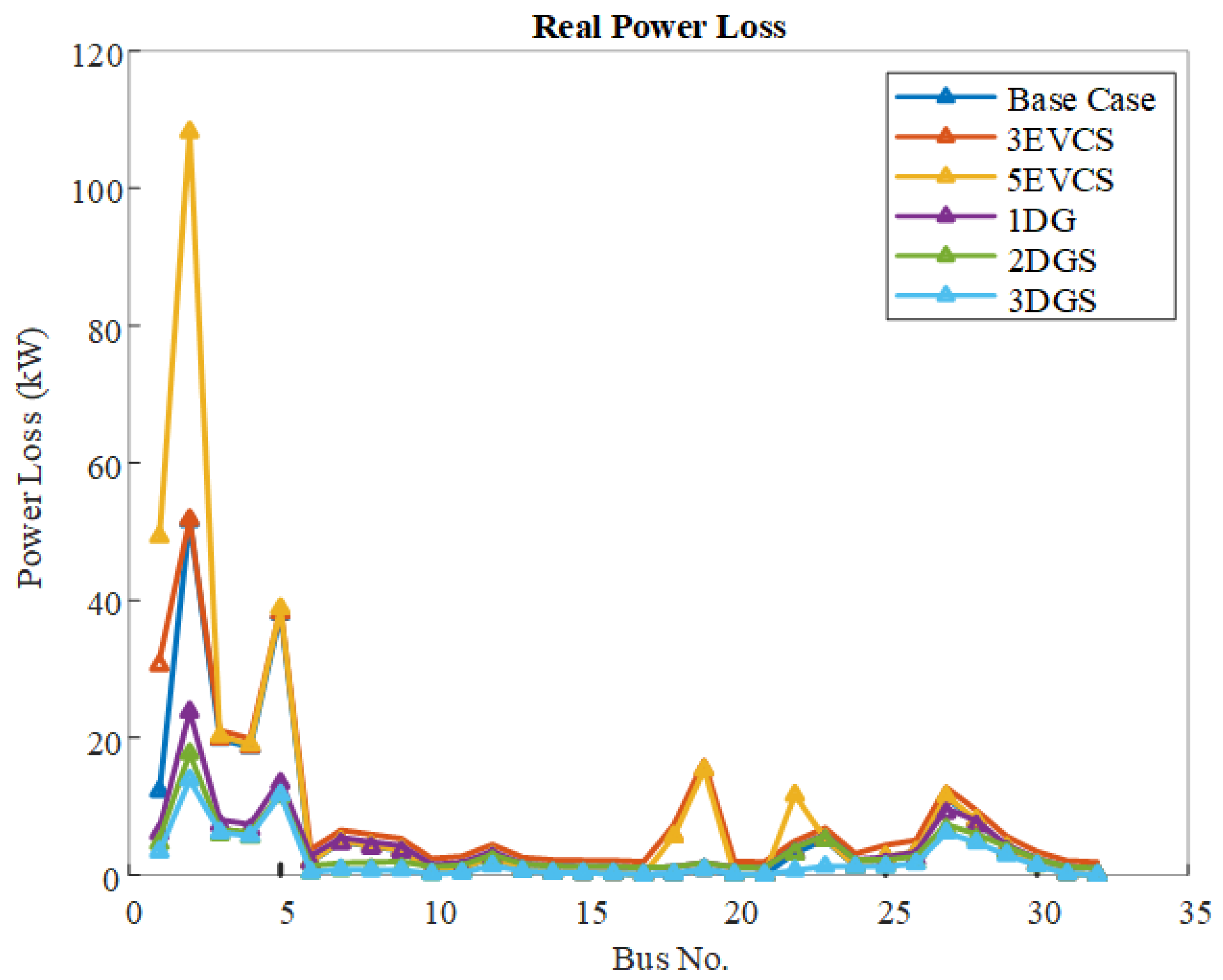
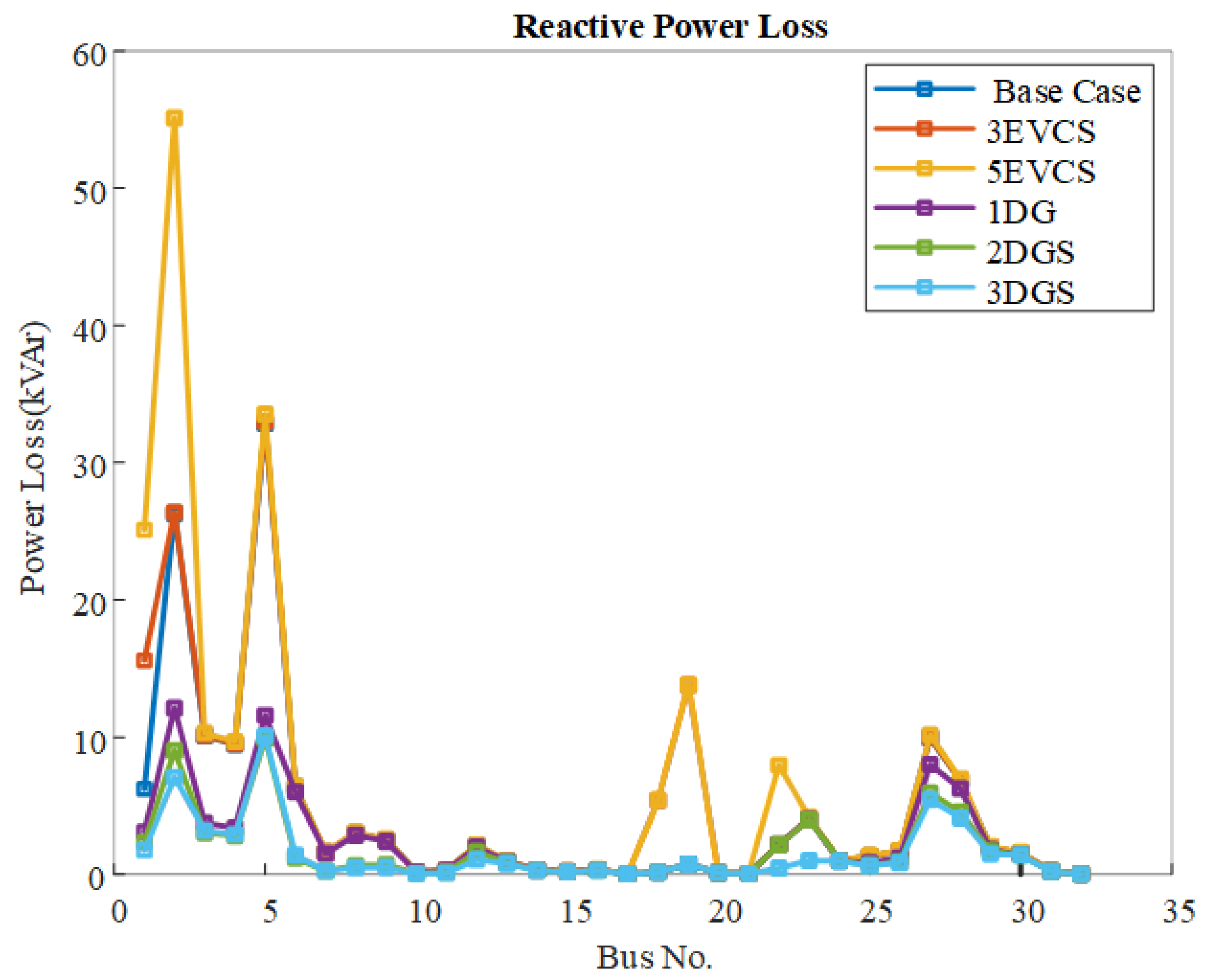
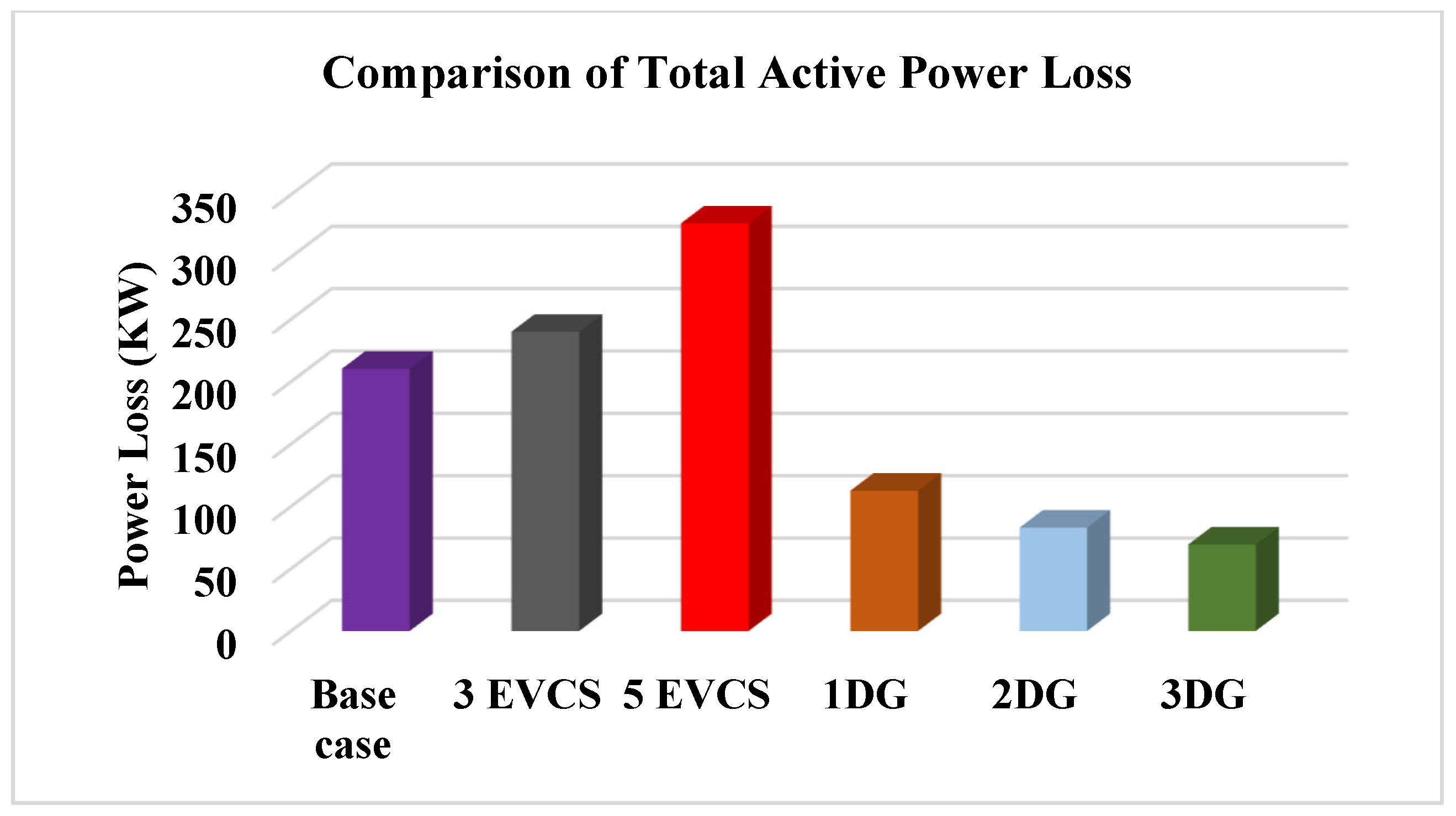
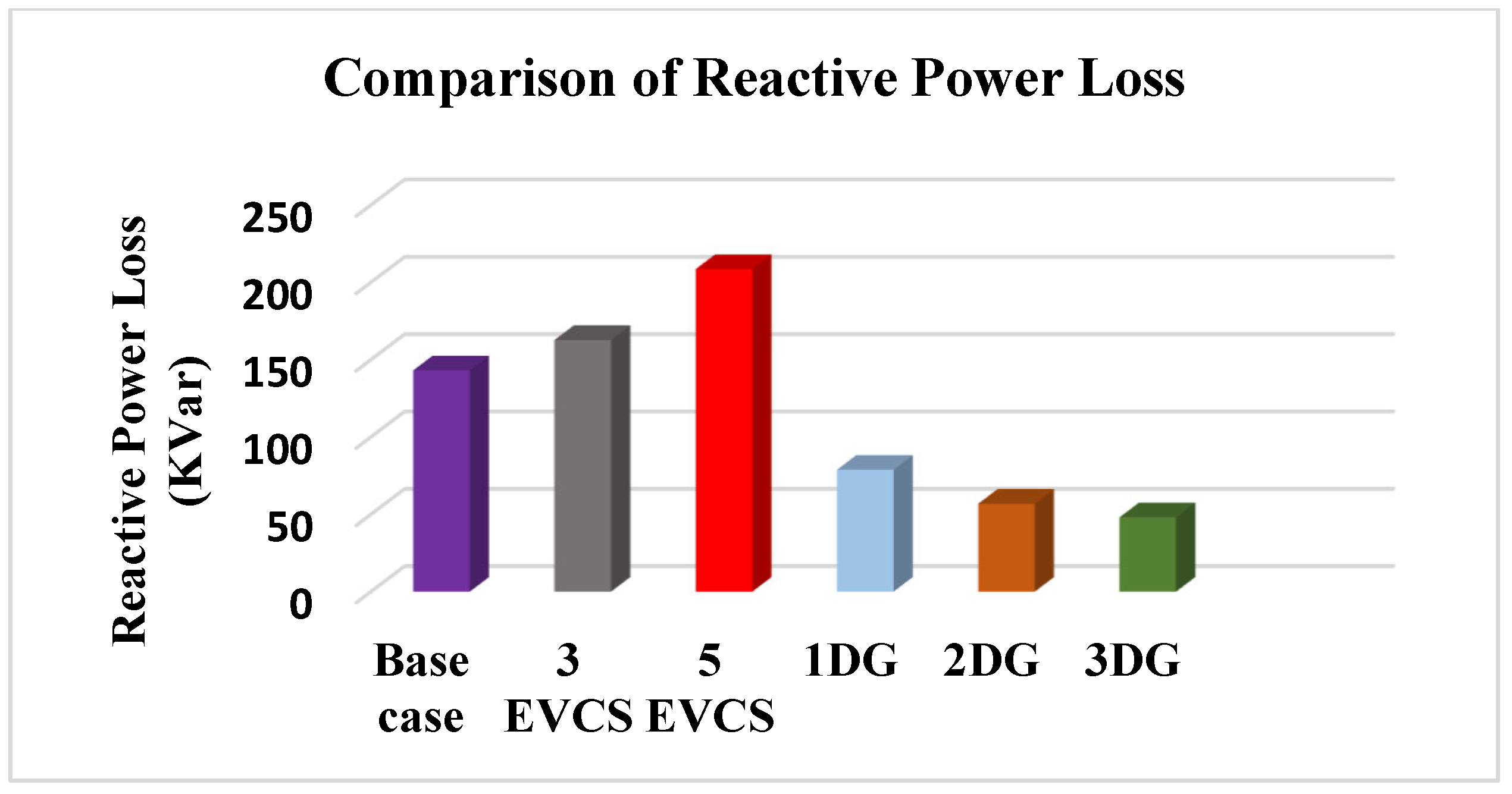
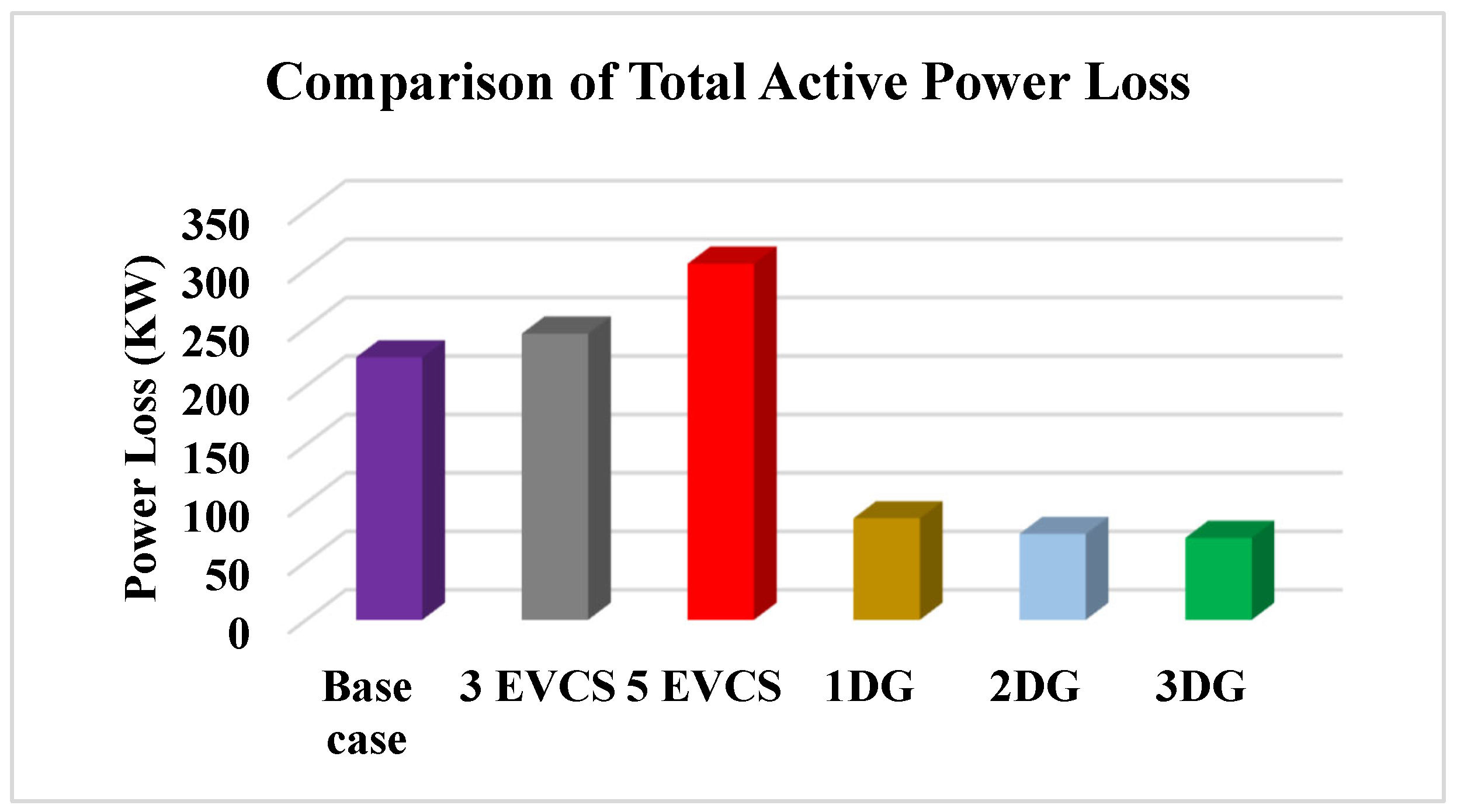
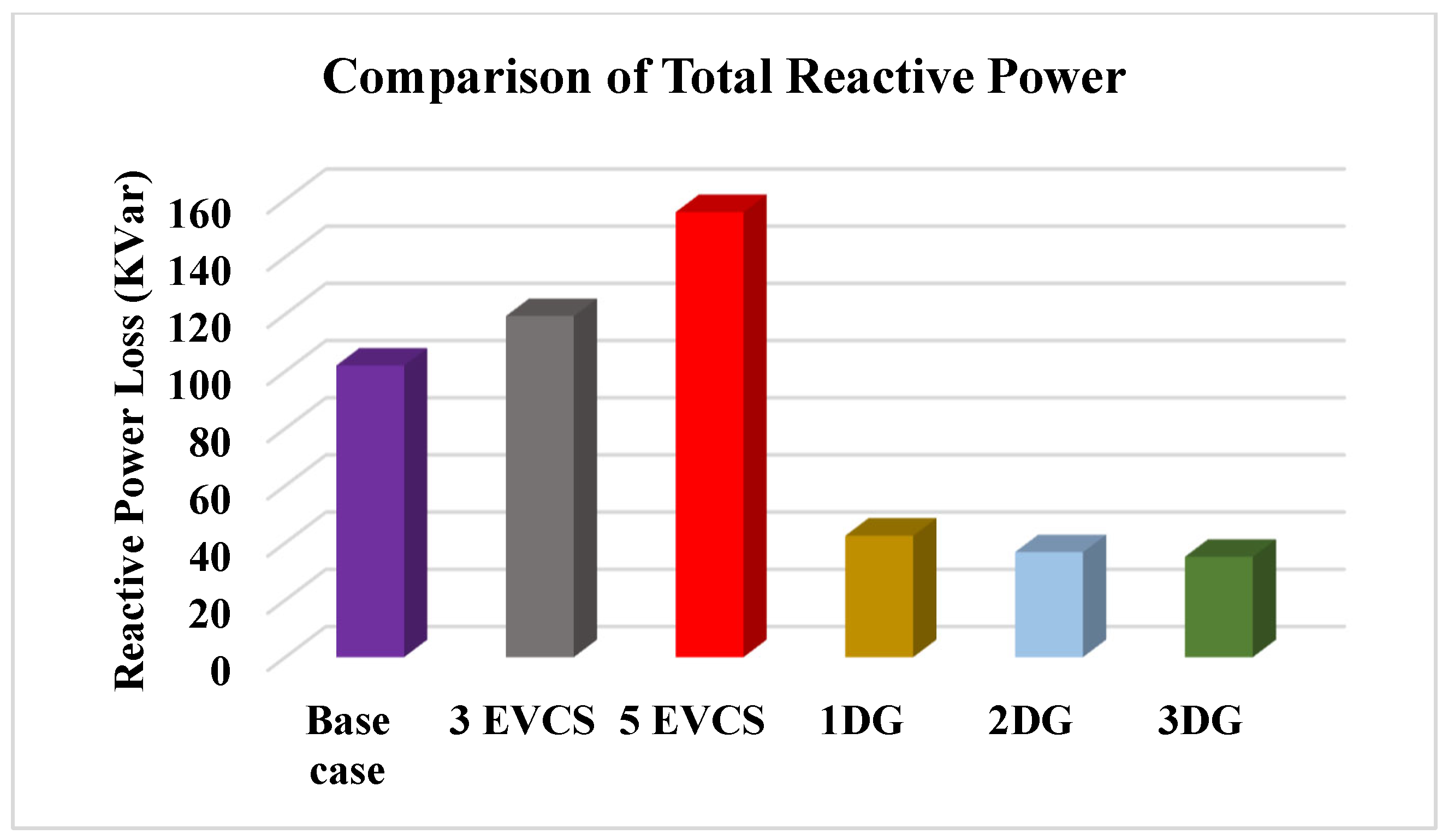
5.1.2. Impact of EVCSs and DGs on the Power Losses of IEEE-33 RDS
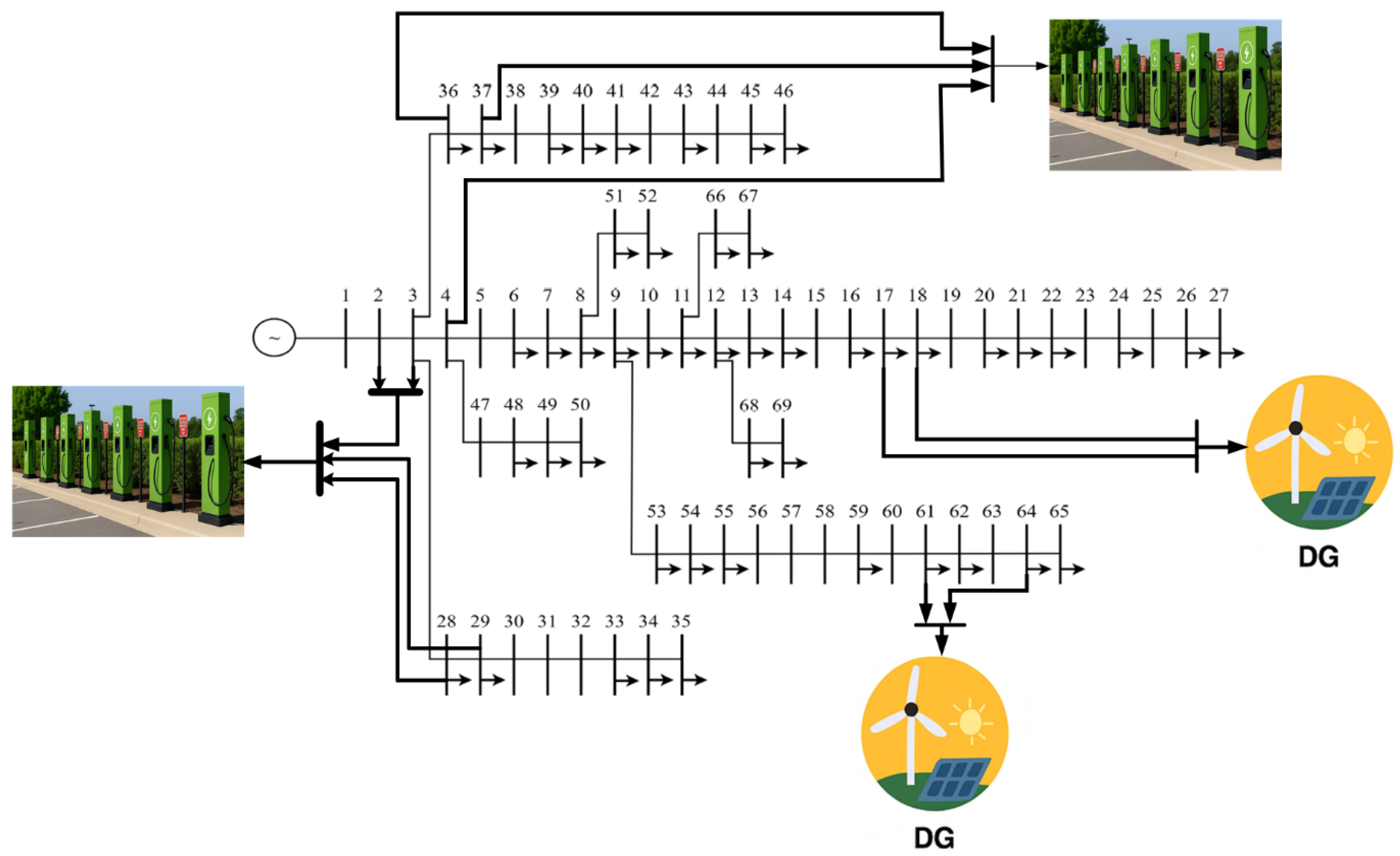
5.2. Results of IEEE-69 RDS
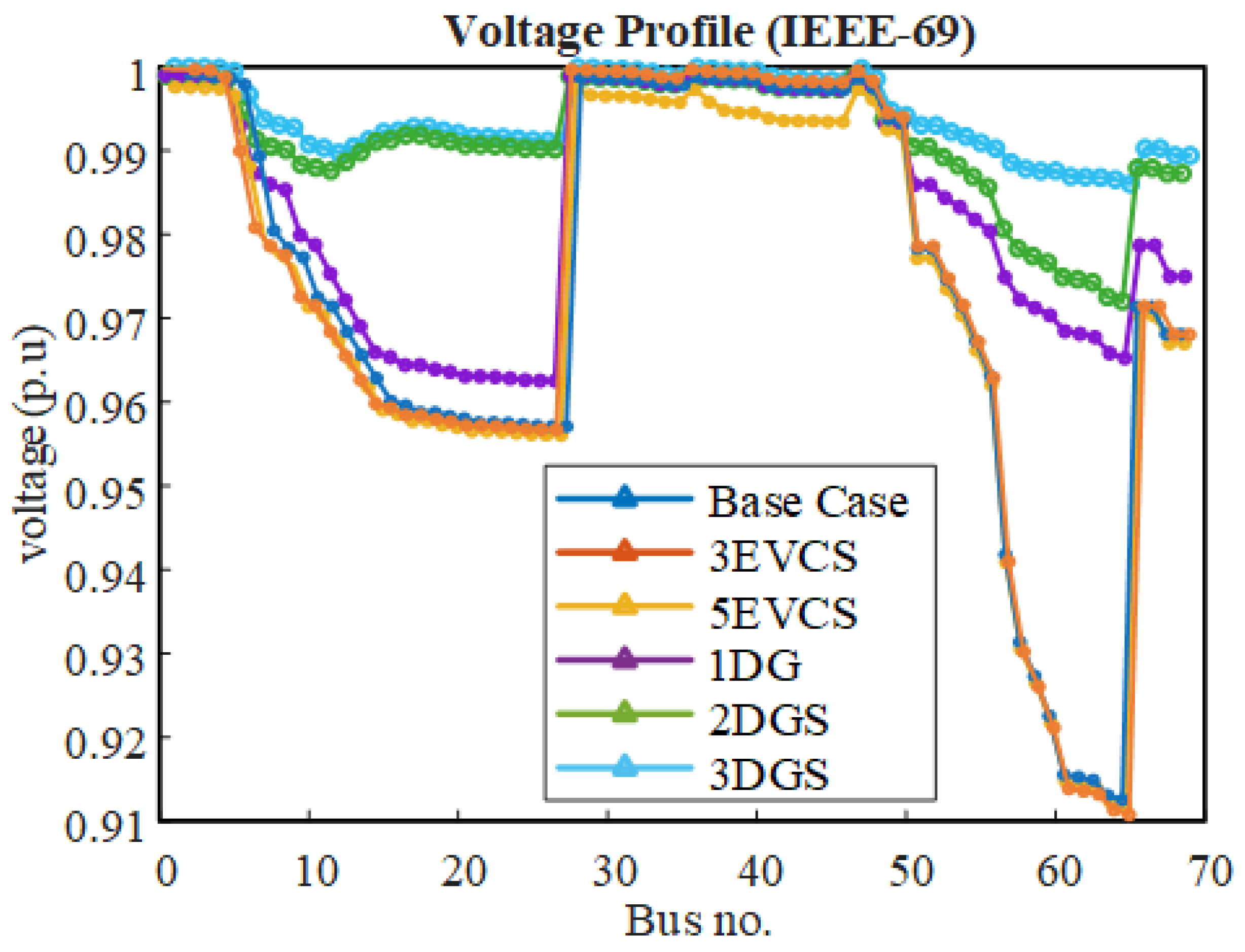
5.2.1. Impact of EVCSs and DGs on the Voltage Profile of IEEE-69 RDS
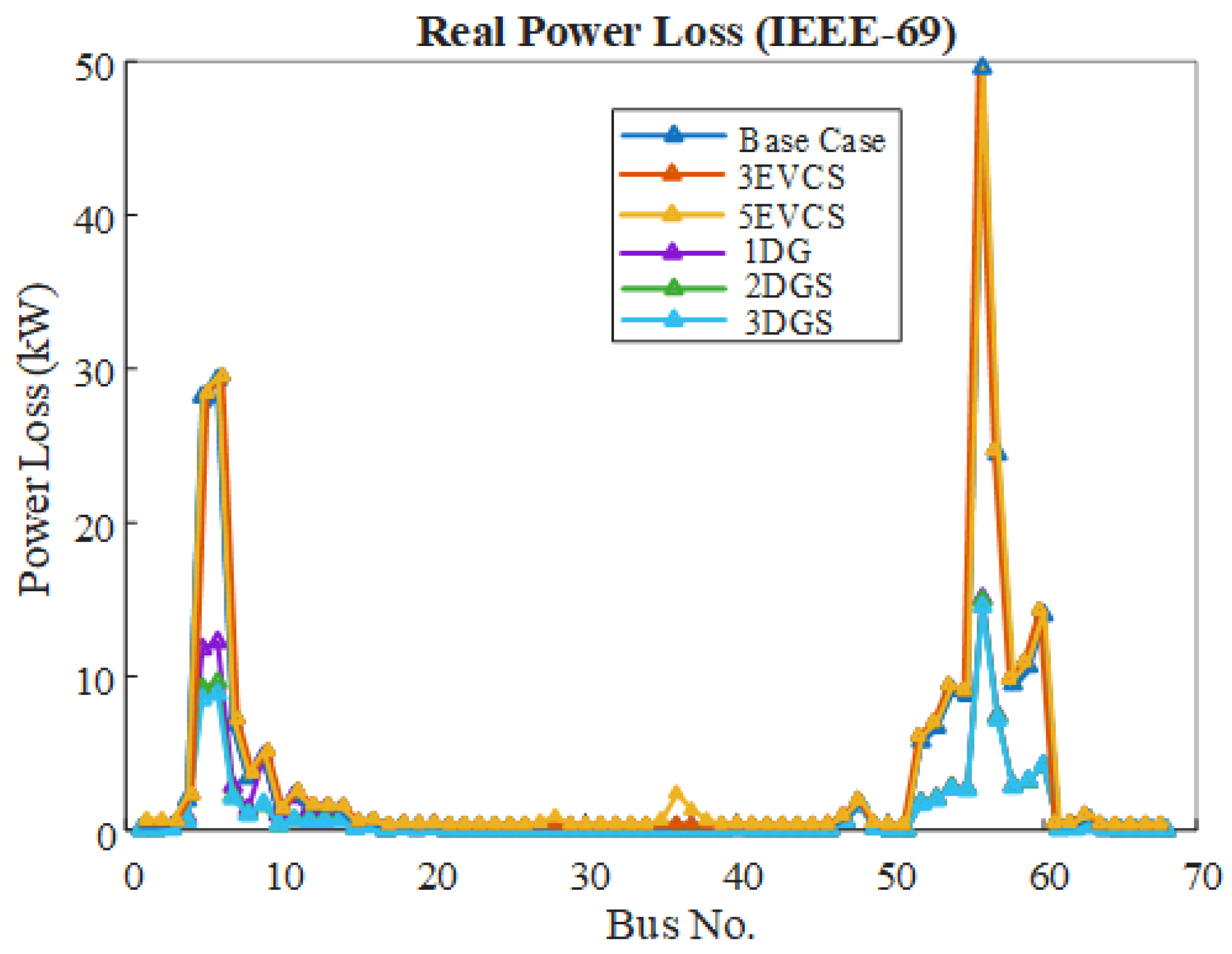
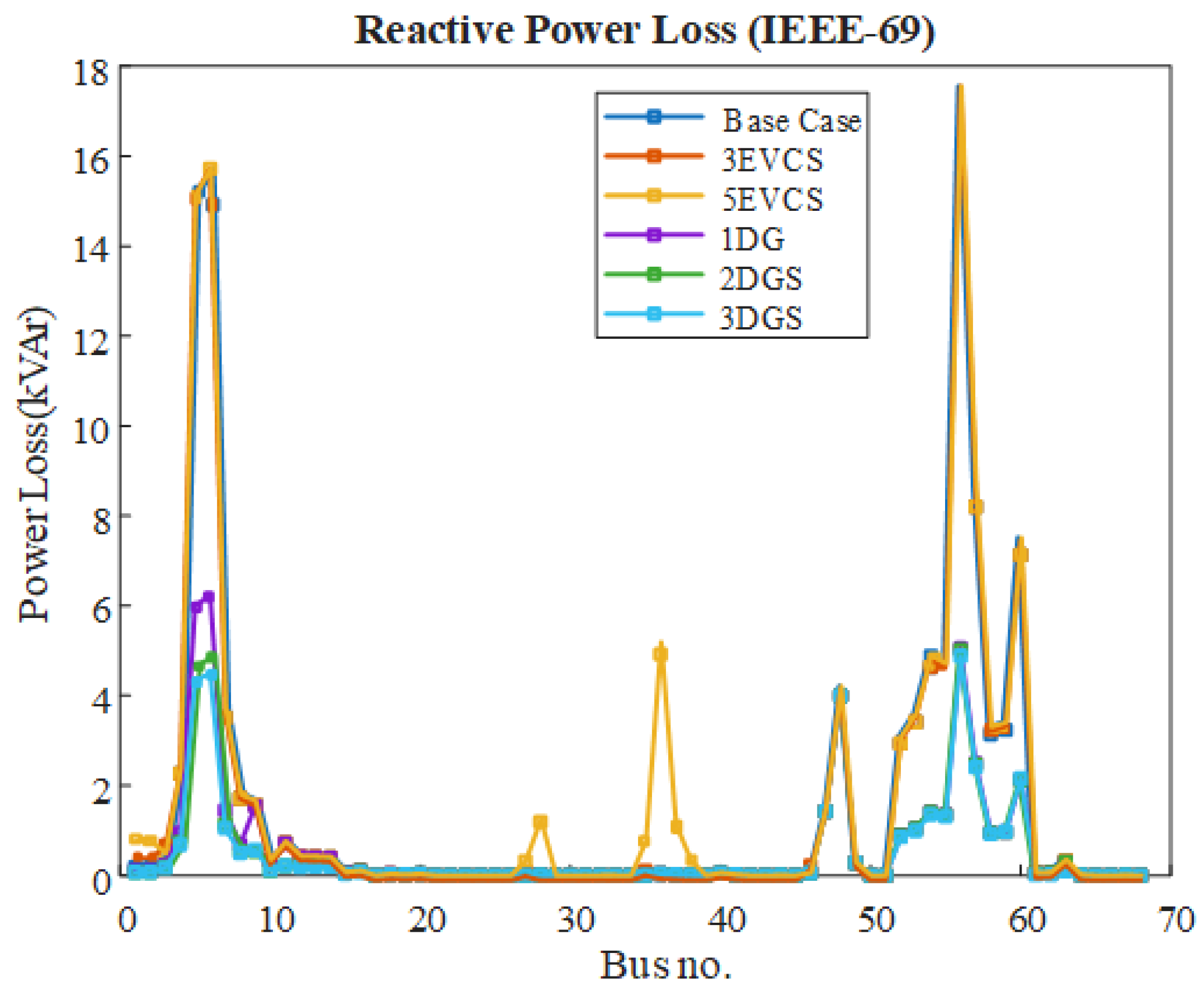
5.2.2. Impact of EVCSs and DGs on the Power Losses of IEEE-69 RDS
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Golla, N.k.; Sudabattula, S.K.; Suresh, V. Optimal Placement of Electric Vehicle Charging Station in Distribution System Using Meta-Heuristic Techniques. Math. Model. Eng. Probl. 2022, 9, 60–66. [Google Scholar] [CrossRef]
- Lei, X.; Yu, H.; Zhong, J.; Jia, Y.; Shao, Z.; Jian, L. Exploring electric vehicle’s potential as capacity reservation through V2G operation to compensate load deviation in distribution systems. J. Clean. Prod. 2024, 451, 141997. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M. Coordinated optimal planning of electric vehicle charging stations and capacitors in distribution systems with vehicle-to-grid facility. Preprint 2021. [Google Scholar] [CrossRef]
- Tomasov, M.; Motyka, D.; Kajanova, M.; Bracinik, P. Modelling effects of the distributed generation supporting e-mobility on the operation of the distribution power network. Transp. Res. Procedia 2019, 40, 556–563. [Google Scholar] [CrossRef]
- Waseem, M.; Huang, J.; Wong, C.-N.; Lee, C.K.M. Data-driven GWO-BRNN-based SOH estimation of lithium-ion batteries in EVs for their prognostics and health management. Mathematics 2023, 11, 4263. [Google Scholar] [CrossRef]
- Faddel, S.; Al-Awami, A.T.; Mohammed, O.A. Charge control and operation of electric vehicles in power grids: A review. Energies 2018, 11, 701. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Waseem, M.; Lin, Z.; Liu, S.; Sajjad, I.A.; Aziz, T. Optimal GWCSO-based home appliances scheduling for demand response considering end-users comfort. Electr. Power Syst. Res. 2020, 187, 106477. [Google Scholar] [CrossRef]
- Said, D.; Mouftah, H.T. A novel electric vehicles charging/discharging management protocol based on queuing model. IEEE Trans. Intell. Veh. 2019, 5, 100–111. [Google Scholar] [CrossRef]
- Said, D. A survey on information communication technologies in modern demand-side management for smart grids: Challenges, solutions, and opportunities. IEEE Eng. Manag. Rev. 2022, 51, 76–107. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of electric vehicle charging station load on distribution network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Pal, A.; Bhattacharya, A.; Chakraborty, A.K. Allocation of EV fast charging station with V2G facility in distribution network. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar]
- Wang, X.; Karki, R. Exploiting PHEV to augment power system reliability. IEEE Trans. Smart Grid 2016, 8, 2100–2108. [Google Scholar] [CrossRef]
- Pal, A.; Bhattacharya, A.; Chakraborty, A.K. Allocation of electric vehicle charging station considering uncertainties. Sustain. Energy Grids Netw. 2021, 25, 100422. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Farnoosh, A.; Chen, S.; Li, Y. GIS-based multi-objective particle swarm optimization of charging stations for electric vehicles. Energy 2019, 169, 844–853. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Charging station placement for electric vehicles: A case study of Guwahati city, India. IEEE Access 2019, 7, 100270–100282. [Google Scholar] [CrossRef]
- Liu, L.; Xie, F.; Huang, Z.; Wang, M. Multi-objective coordinated optimal allocation of DG and EVCSs based on the V2G mode. Processes 2020, 9, 18. [Google Scholar] [CrossRef]
- Alam, A.; Gupta, A.; Bindal, P.; Siddiqui, A.; Zaid, M. Power loss minimization in a radial distribution system with distributed generation. In Proceedings of the 2018 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 22–23 February 2018; pp. 21–25. [Google Scholar]
- Singh, D.; Singh, D.; Verma, K.S. GA based energy loss minimization approach for optimal sizing & placement of distributed generation. Int. J. Knowl.-Based Intell. Eng. Syst. 2008, 12, 147–156. [Google Scholar]
- Suresh, M.C.V.; Edward, B.J. Optimal placement of DG units for loss reduction in distribution systems using one rank cuckoo search algorithm. Int. J. Grid Distrib. Comput. 2018, 11, 37–44. [Google Scholar] [CrossRef]
- Rizwan, M.; Waseem, M.; Liaqat, R.; Sajjad, I.A.; Dampage, U.; Salmen, S.H.; Al Obaid, S.; Mohamed, M.A.; Annuk, A. SPSO based optimal integration of DGs in local distribution systems under extreme load growth for smart cities. Electronics 2021, 10, 2542. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A.S. Real-time coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. Bi-directional electric vehicle fast charging station with novel reactive power compensation for voltage regulation. Int. J. Electr. Power Energy Syst. 2015, 64, 300–310. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. PEVs modeling and impacts mitigation in distribution networks. IEEE Trans. Power Syst. 2012, 28, 1122–1131. [Google Scholar] [CrossRef]
- Reddy, M.S.K.; Selvajyothi, K. Optimal placement of electric vehicle charging station for unbalanced radial distribution systems. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 1731017. [Google Scholar] [CrossRef]
- Sanjay, R.; Jayabarathi, T.; Raghunathan, T.; Ramesh, V.; Mithulananthan, N. Optimal allocation of distributed generation using hybrid grey wolf optimizer. IEEE Access 2017, 5, 14807–14818. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric-vehicle charging stations in distribution systems. IEEE Trans. Power Deliv. 2012, 28, 102–110. [Google Scholar] [CrossRef]
- Fokui, W.S.T.; Saulo, M.J.; Ngoo, L. Optimal placement of electric vehicle charging stations in a distribution network with randomly distributed rooftop photovoltaic systems. IEEE Access 2021, 9, 132397–132411. [Google Scholar] [CrossRef]
- Onlam, A.; Yodphet, D.; Chatthaworn, R.; Surawanitkun, C.; Siritaratiwat, A.; Khunkitti, P. Power loss minimization and voltage stability improvement in electrical distribution system via network reconfiguration and distributed generation placement using novel adaptive shuffled frogs leaping algorithm. Energies 2019, 12, 553. [Google Scholar] [CrossRef]
- Altaf, M.; Yousif, M.; Ijaz, H.; Rashid, M.; Abbas, N.; Khan, M.A.; Waseem, M.; Saleh, A.M. PSO-based optimal placement of electric vehicle charging stations in a distribution network in smart grid environment incorporating backward forward sweep method. IET Renew. Power Gener. 2024, 18, 3173–3187. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, S.; Chanda, C.K. An analytical approach for allocation and sizing of distributed generations in radial distribution network. Int. Trans. Electr. Energy Syst. 2017, 27, e2322. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M.; Kothari, D.P. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int. J. Electr. Power Energy Syst. 2014, 63, 461–472. [Google Scholar] [CrossRef]
- Nagaballi, S.; Kale, V.S. Pareto optimality and game theory approach for optimal deployment of DG in radial distribution system to improve techno-economic benefits. Appl. Soft Comput. 2020, 92, 106234. [Google Scholar] [CrossRef]
- Pham, T.D.; Nguyen, T.T.; Dinh, B.H. Find optimal capacity and location of distributed generation units in radial distribution networks by using enhanced coyote optimization algorithm. Neural Comput. Appl. 2021, 33, 4343–4371. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Quasi-Oppositional Swine Influenza Model Based Optimization with Quarantine for optimal allocation of DG in radial distribution network. Int. J. Electr. Power Energy Syst. 2016, 74, 348–373. [Google Scholar] [CrossRef]
- Kamel, S.; Amin, A.; Selim, A.; Ahmed, M.H. Optimal placement of DG and capacitor in radial distribution systems considering load variation. In Proceedings of the 2019 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 21–23 September 2019; pp. 1–6. [Google Scholar]
- Balu, K.; Mukherjee, V. Optimal siting and sizing of distributed generation in radial distribution system using a novel student psychology-based optimization algorithm. Neural Comput. Appl. 2021, 33, 15639–15667. [Google Scholar] [CrossRef]
- Pamuk, N.; Uzun, U.E. Optimal allocation of distributed generations and capacitor banks in distribution systems using arithmetic optimization algorithm. Appl. Sci. 2024, 14, 831. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Comparison of different optimization techniques for optimal allocation of multiple distribution generation. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 317–323. [Google Scholar]
- McAsey, M.; Mou, L.; Han, W. Convergence of the forward-backward sweep method in optimal control. Comput. Optim. Appl. 2012, 53, 207–226. [Google Scholar] [CrossRef]
- Chang, G.W.; Chu, S.Y.; Wang, H.L. A simplified forward and backward sweep approach for distribution system load flow analysis. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–5. [Google Scholar]
- Karaboga, D. An Idea Based On Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Computer Engineering Department, Erciyes University: Kayseri, Turkey, 2005; pp. 1–10. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Basturk, B. An artificial bee colony (ABC) algorithm for numeric function optimization. In Proceedings of the IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 12–14 May 2006; Volume 2006, p. 12. [Google Scholar]
- Tu, J.; Yu, H.; Zhong, J.; Jian, L. User-needs-oriented shared DC charging resources optimal configuration and operation for improving EV penetration in old residential communities. Sustain. Cities Soc. 2024, 114, 105796. [Google Scholar] [CrossRef]





| Assumption | Description |
|---|---|
| Constant-Power | Each EVCS is modeled as a constant-power load during charging periods |
| Peak Demand | Maximum simultaneous charging of all connected EVs represents peak demand |
| Diversity Factor | A factor is applied to reflect stochastic arrival/departure of EVs. |
| Steady-State | Steady-state assumption is used for distribution-level planning analysis |
| Cases | Bus No. | Real Power Loss (KW) | Reactive Power Loss (Kvar) | Voltage Deviation (p.u) |
|---|---|---|---|---|
| Base case | - | 210.303 | 143.140 | 11.640 |
| 3 EVCSs | 2, 20, 19 | 240 | 162.782 | 12.376 |
| 5 EVCSs | 3, 20, 23, 2, 19 | 326.911 | 208.602 | 15.338 |
| 1 DG | 29 | 112.523 | 78.861 | 4.213 |
| 2 DGs | 13, 30 | 82.948 | 56.902 | 1.083 |
| 3 DGs | 30, 14, 24 | 69.397 | 48.086 | 1.013 |
| Techniques | DG Location | DG Size (MW) | Active Power Loss in KW with DG | Power Loss (Reduction %) |
|---|---|---|---|---|
| GA [30] | 29, 8, 32, 16 | 0.5, 0.5, 0.5, 0.5 | 78.920 | 62.52 |
| SA [30] | 30, 13 | 0.079, 0.445, 0.096 | 178.28 | 10.45 |
| AM [31] | 13, 29, 31 | 1.121, 1.027, 0.126 | 89.5 | 57.28 |
| FWA [32] | 14, 18, 32 | 0.5897, 0.1895, 1.0146 | 88.68 | 56.24 |
| MTLBO [33] | 23, 32, 15 | 1.066, 0.847, 0.885 | 80.22 | 62 |
| JAYA [33] | 29, 25, 12 | 0.921, 0.795, 1.110 | 76.66 | 63.6 |
| GWO [33] | 12, 25, 30 | 0.955, 0.889, 1.037 | 74.10 | 64.88 |
| COA [34] | 14, 25, 30 | 0.7096, 0.5954, 0.9972 | 76 | 63.98 |
| ECOA [34] | 14, 25, 30 | 0.7376, 0.6518, 1.0705 | 74.6 | 64.64 |
| SIMBO-Q [35] | 14, 24, 29 | 0.7638, 1.0415, 1.1352 | 73.4 | 65.20 |
| AA [36] | 13, 24, 30 | 0.79, 1.07, 1.012 | 72.89 | 65.45 |
| HHO [37] | 13, 24, 30 | 0.8173, 1.0829, 1.0465 | 72.80 | 65.4956 |
| SPBO [37] | 14, 24, 30 | 0.7723, 1.1059, 1.0685 | 72.79 | 65.5003 |
| AOA [38] | 14, 24, 30 | 0.7764, 1.0990, 1.0702 | 72.79 | 65.50 |
| Proposed GLAD-ABC | 14, 24, 30 | 0.771, 1.094, 1.096 | 69.397 | 67.0014 |
| Cases | Bus Number | Real Power (KW) | Reactive Power Loss (Kvar) | Voltage Deviation |
|---|---|---|---|---|
| Base case | - | 224.55 | 102.01 | 9.762 |
| 3 EVCSs | 28, 36, 47 | 244.836 | 119.331 | 11.782 |
| 5 EVCSs | 28, 36, 40, 47, 48 | 304.674 | 155.673 | 13.807 |
| 1 DG | 61 | 86.865 | 42.500 | 2.582 |
| 2 DGs | 17, 61 | 73.465 | 36.744 | 0.780 |
| 3 DGs | 15, 61, 64 | 70.078 | 35.111 | 0.736 |
| Techniques | DG Location | DG Size (MW) | Active Power Loss in KW with DG | Power Loss (Reduction %) |
|---|---|---|---|---|
| FWA [32] | 65, 61, 27 | 0.4085, 1.1986, 0.2258 | 77.85 | 65.39 |
| MTLBO [33] | 20, 62, 57 | 0.079, 0.445, 0.096 | 77.36 | 65.61 |
| JAYA [33] | 61, 50, 12 | 2.000, 0.100, 1.016 | 75.83 | 66.29 |
| GWO [33] | 61, 50, 12 | 2.000, 0.586, 0.792 | 73.43 | 67.36 |
| SIMBO-Q [35] | 61, 9, 17 | 1.500, 0.6189, 0.5297 | 71.3 | 68.3 |
| QOSIMBO-Q [35] | 9, 18, 61 | 0.8336, 0.4511, 1.500 | 71.0 | 68.43 |
| HHO [37] | 12, 61, 62 | 0.7341, 1.1912, 0.7623 | 74.14 | 67.046 |
| WOA [39] | 49, 18, 61 | 0.84046, 0.53352, 1.8084 | 70.19 | 68.40 |
| DA [39] | 66, 14, 61 | 0.84046, 0.533352, 1.8084 | 71.10 | 68.40 |
| Proposed GLAD-ABC | 15, 61, 64 | 0.548, 1.491, 0.296 | 70.08 | 68.7918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alatwi, A.M.; Albalawi, H.; Wadood, A.; Atawi, I.E.; Alatawi, K.S.S. Novel GBest–Lévy Adaptive Differential Ant Bee Colony Optimization for Optimal Allocation of Electric Vehicle Charging Stations and Distributed Generators in Smart Distribution Systems. Energies 2025, 18, 6018. https://doi.org/10.3390/en18226018
Alatwi AM, Albalawi H, Wadood A, Atawi IE, Alatawi KSS. Novel GBest–Lévy Adaptive Differential Ant Bee Colony Optimization for Optimal Allocation of Electric Vehicle Charging Stations and Distributed Generators in Smart Distribution Systems. Energies. 2025; 18(22):6018. https://doi.org/10.3390/en18226018
Chicago/Turabian StyleAlatwi, Aadel Mohammed, Hani Albalawi, Abdul Wadood, Ibrahem E. Atawi, and Khaled Saleem S. Alatawi. 2025. "Novel GBest–Lévy Adaptive Differential Ant Bee Colony Optimization for Optimal Allocation of Electric Vehicle Charging Stations and Distributed Generators in Smart Distribution Systems" Energies 18, no. 22: 6018. https://doi.org/10.3390/en18226018
APA StyleAlatwi, A. M., Albalawi, H., Wadood, A., Atawi, I. E., & Alatawi, K. S. S. (2025). Novel GBest–Lévy Adaptive Differential Ant Bee Colony Optimization for Optimal Allocation of Electric Vehicle Charging Stations and Distributed Generators in Smart Distribution Systems. Energies, 18(22), 6018. https://doi.org/10.3390/en18226018









