A New Method for PMU Deployment Based on the Preprocessed Integer Programming Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Power System and Its Observability
2.1.1. Observability Requirements
- (1)
- The algebra is considerable
- (2)
- The topology is considerable
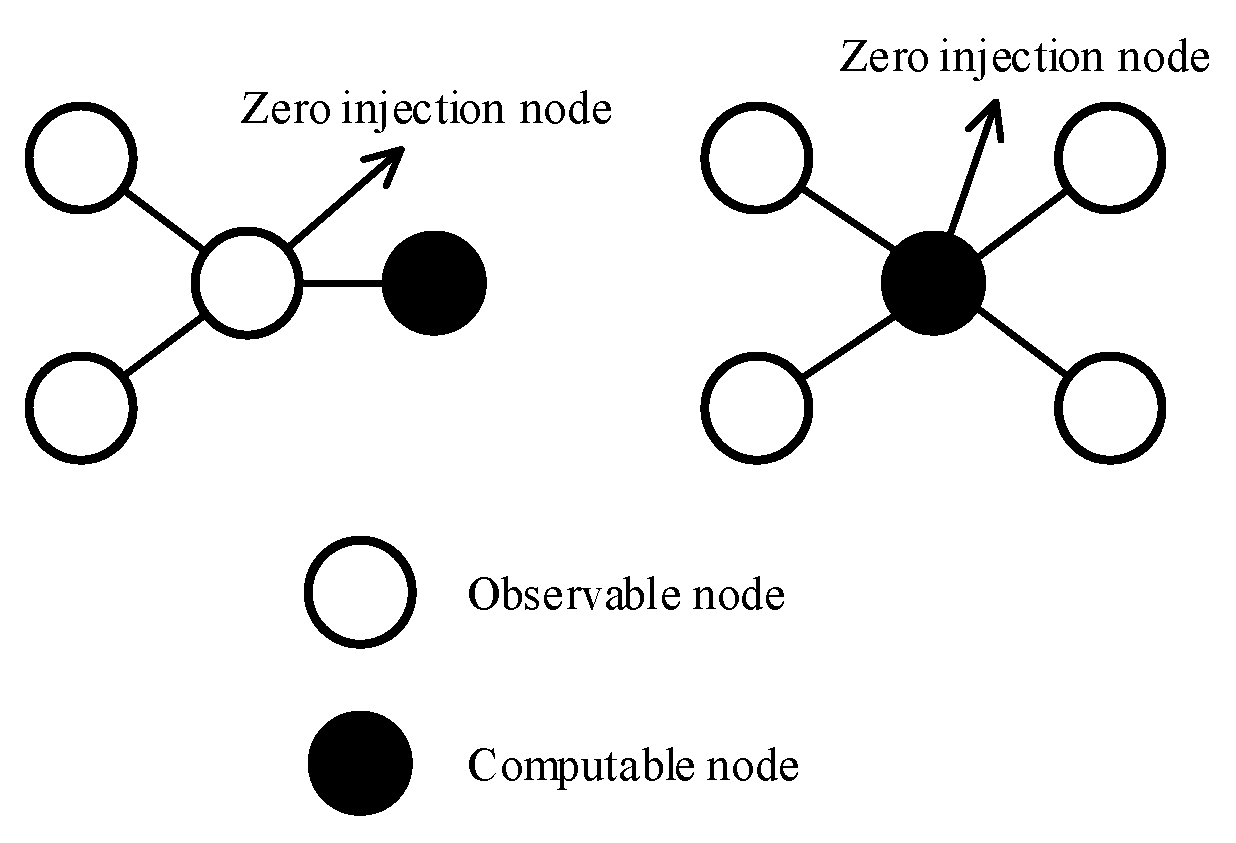
2.1.2. Configuration Rules Under Observable Conditions
- (1)
- When node i is configured with a PMU, the node itself can directly measure and achieve observability.
- (2)
- When node i is configured with a PMU, the state quantities of its adjacent nodes can be calculated, and the implementation of its adjacent nodes is considerable.
- (3)
- When node i is injected into a node with zero, in the set of N nodes formed by itself and adjacent nodes, as long as N − 1 nodes achieve observability, the remaining node can be calculated, and all N nodes achieve observability.
2.1.3. Average Channel Index
2.2. Improve the Integer Programming Deployment Method After Preprocessing
3. Simulation and Results
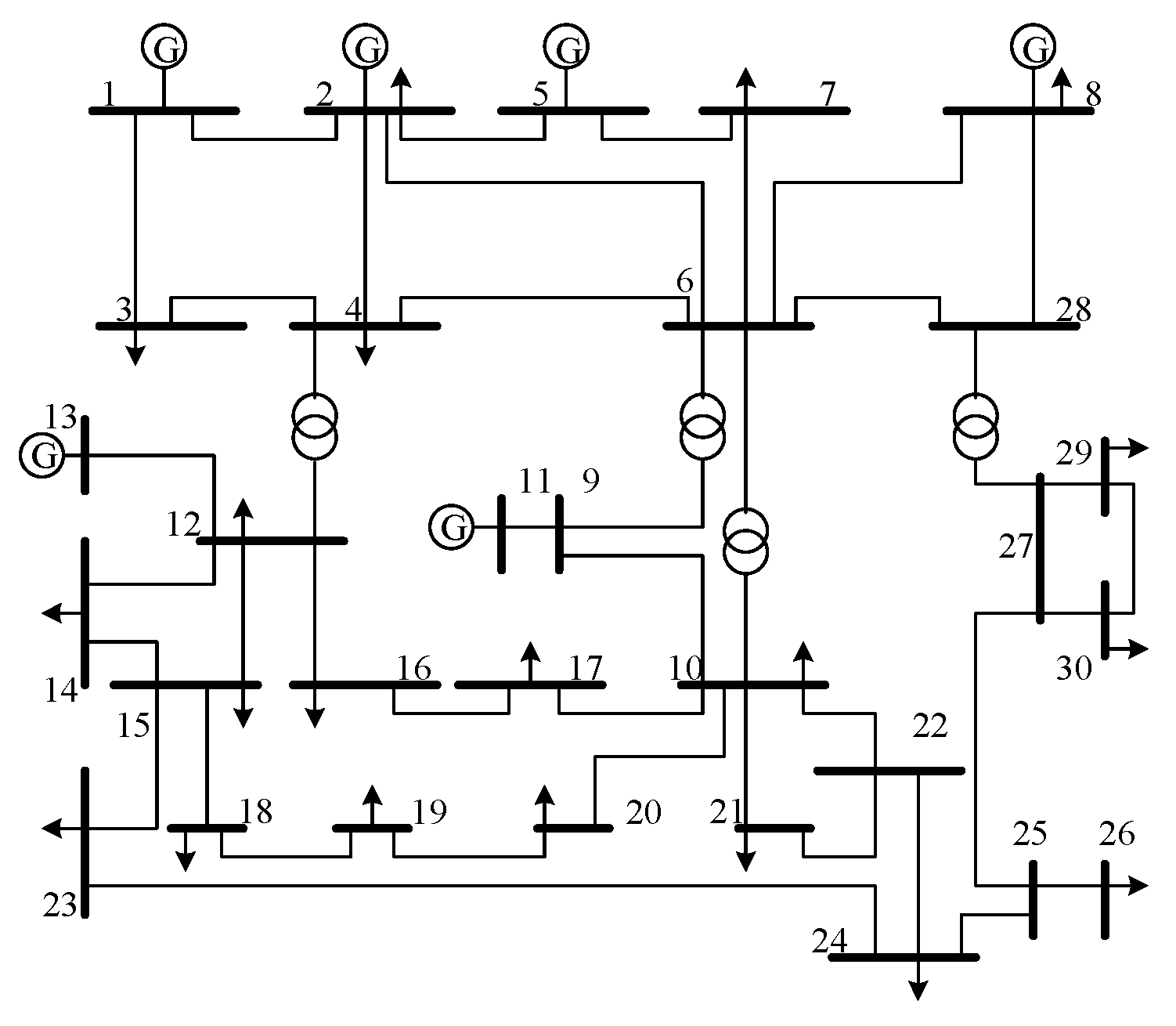
3.1. IEEE-14
3.2. IEEE-30
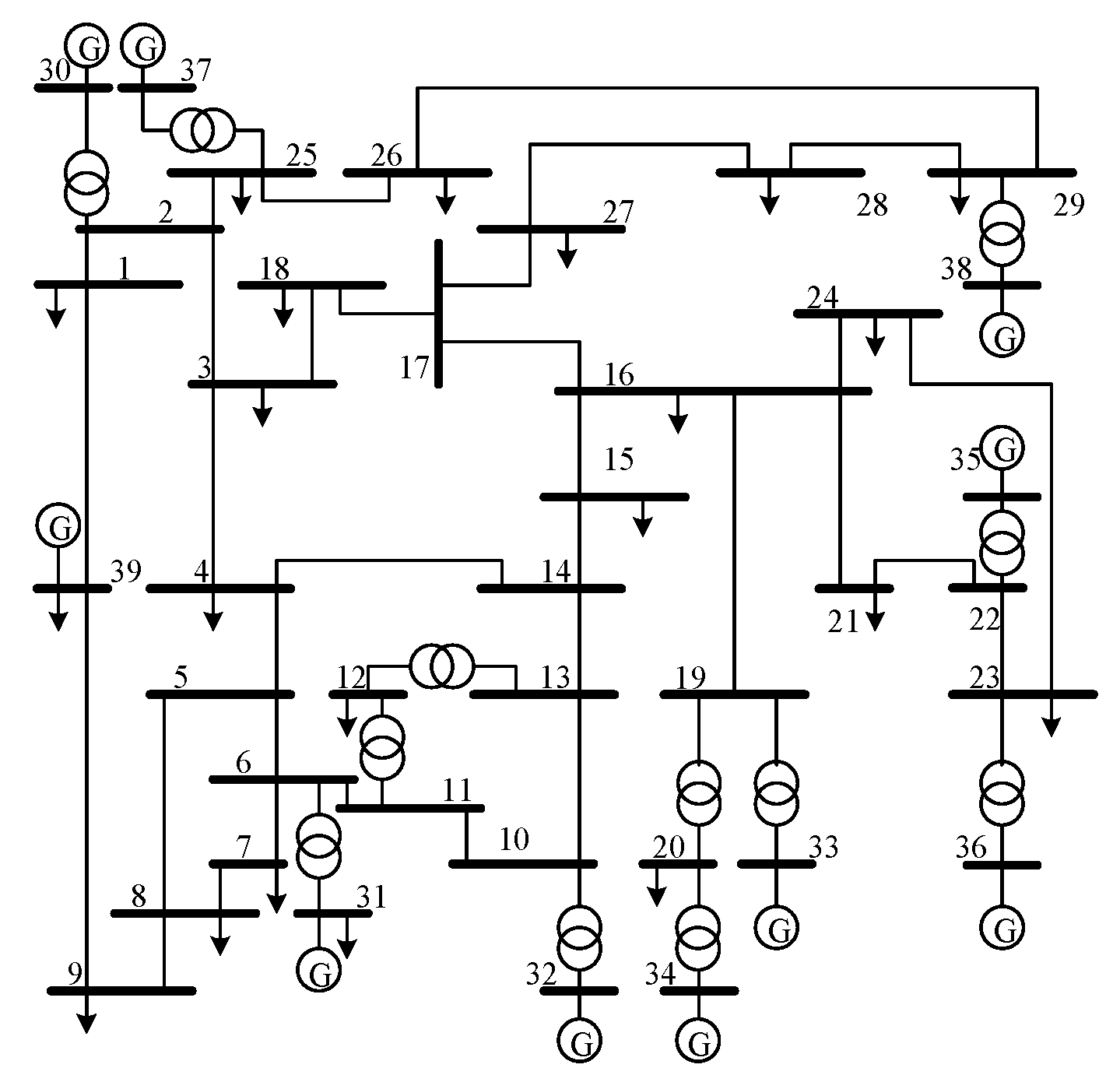
3.3. NE-39 Nodes
4. Discussion
5. Conclusions
- (1)
- In the test case of the IEEE-14 node model, it can be seen that compared with other deployment algorithms, the improved algorithm only takes 0.02 s to obtain the solution, and the number of deployed PMUs is only 3 to meet the global observability condition.
- (2)
- In the test case of the EIEE-30 node model, it can be seen that there are multiple solutions obtained by the improved algorithm. It only takes 0.02 s to obtain the optimal solution, and the number of deployed PMUs is only 7 to meet the global observability condition.
- (3)
- In the test case of the NE-39 node model, it can be seen that the improved algorithm only takes 0.03 s to obtain the solution, and the number of deployed PMUs only needs 9 to meet the global observability condition.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IEEE | Institute of Electrical and Electronic Engineers |
| NE | New England |
| PMU | Phasor Measurement Unit |
| SCADA | Supervisory Control and Data Acquisition |
| WAMS | Wide Area Measurement System |
References
- Xu, Y.; Liu, X.; Li, Z.; Lv, M. Influence of PMU quasi-real-time data on robust estimation of active distribution network. Electr. Power Autom. Equip. 2020, 40, 15–22. [Google Scholar] [CrossRef]
- Li, Z.; Cui, J.; Lu, H.; Zhou, F.; Diao, Y.; Li, Z. Prediction method for instrument transformer measurement error: Adaptive decomposition and hybrid deep learning models. Measurement 2025, 253, 117592. [Google Scholar] [CrossRef]
- Almasabi, S.; Mitra, J. A fault-tolerance based approach to optimal PMU placement. IEEE Trans. Smart Grid 2019, 10, 6070–6079. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, G.; Yang, D.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced detection of power transformer winding faults through 3D FRA signatures and image processing techniques. Electr. Power Syst. Res. 2025, 242, 111433. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, H.; Yang, D.; Wei, J.; Li, Z.; Guo, Z.; Zhang, S. Residual Magnetism Elimination Method for Large Power Transformers Based on Energy Storage Oscillation. IEEE Trans. Power Deliv. 2025, 40, 2759–2768. [Google Scholar] [CrossRef]
- Li, Z.; Cui, J.; Wei, Y.; Huang, Y.; Xie, H.; Yao, W. Calculation study of ion flow field in ±800 kV transmission lines under the effects of air pressure, temperature, humidity and improvement measures. Electr. Power Syst. Res. 2024, 234, 110574. [Google Scholar] [CrossRef]
- Li, Z.; Cui, J.; Lu, H.; Zhou, F.; Diao, Y.; Li, Z. Prediction model of measurement errors in current transformers based on deep learning. Rev. Sci. Instrum. 2024, 95, 044704. [Google Scholar] [CrossRef]
- Carvajal, G.; Carrión, D.; Jaramillo, M. Planning Scheme for Optimal PMU Location Considering Power System Expansion. Energies 2025, 18, 3283. [Google Scholar] [CrossRef]
- Ogbogu, C.E.; Thornburg, J.; Okozi, S.O. Smart Grid Fault Mitigation and Cybersecurity with Wide-Area Measurement Systems: A Review. Energies 2025, 18, 994. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, S.; Cai, Y.; Hui, Q.; Xu, J. Power system situation awareness method based on trend analysis. Electr. Meas. Instrum. 2024, 61, 99–106. [Google Scholar] [CrossRef]
- Liu, C.; Han, K.; Wang, Y.; Ye, Z. Multi-objective optimization of distributed multi-energy system considering shared energy storage. Electr. Meas. Instrum. 2024, 61, 88–96. [Google Scholar] [CrossRef]
- Zheng, J. The current situation and prospect of frontier electric power technologies. China Electr. Power 1999, 10, 11–16. [Google Scholar] [CrossRef]
- Wang, Z.; Ge, F.; Dai, C. Power system modeling and parameter identification based on PMU. Relay 2007, S1, 378–382. (In Chinese) [Google Scholar]
- Kong, X.; Wang, Y.; Yuan, X.; Yu, L. PMU optimal configuration considering multiple topological observability of distribution network based on customized genetic algorithm. Electr. Power Autom. Equip. 2020, 40, 66–72. [Google Scholar] [CrossRef]
- Al-Odienat, A.I.; Malahmeh, B.; Tarawneh, A.R. The optimal PMU placement in the power systems for the enhancement of state estimation. In Proceedings of the 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Istanbul, Turkey, 12–13 June 2020; pp. 1–6. [Google Scholar]
- Mishra, A.; de Callafon, R.A. Algebraic approach to PMU placement for minimum variance linear state estimation in power networks. IEEE Trans. Power Syst. 2022, 38, 4381–4390. [Google Scholar] [CrossRef]
- Zhang, W.; Qiu, Y.; Zheng, X. GPS and its application in power system. Power Grid Technol. 1996, 05, 38–40+45. (In Chinese) [Google Scholar]
- Xu, W.; Xue, Y.; Chen, S.; Ge, F. Difficulties and prospects in extracting knowledge from measured trajectories. Autom. Electr. Power Syst. 2009, 33, 1–7. [Google Scholar] [CrossRef]
- Chai, J.; Li, S.; He, H. Parameter estimation of transmission grid based on PMU and multiple time sections. Autom. Electr. Power Syst. 2009, 33, 49–52. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, M.H.; Li, V.O.; Leung, K.-C. Optimal PMU-communication link placement for smart grid wide-area measurement systems. IEEE Trans. Smart Grid 2018, 10, 4446–4456. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Watanabe, M.; Mitani, Y.; Othman, M.L. Multi-objective PMU placement optimization considering the placement cost including the current channel allocation and state estimation accuracy. Electr. Eng. Jpn. 2019, 207, 20–27. [Google Scholar] [CrossRef]
- Chen, X.; Sun, L.; Chen, T.; Sun, Y.; Rusli; Tseng, K.J.; Ling, K.V.; Ho, W.K.; Amaratunga, G.A. Full coverage of optimal phasor measurement unit placement solutions in distribution systems using integer linear programming. Energies 2019, 12, 1552. [Google Scholar] [CrossRef]
- Zheng, M. Research on Optimal Allocation of PMU Based on 0-1 Integer Programming. Master’s Degree, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Zhang, B. PMU-Based Distribution Network State Estimation and PMU Configuration Optimization. Master’s Degree, Zhejiang University, Hangzhou, China, 2020. [Google Scholar]
- Liu, X.; Jiang, Q.; Cao, Y. Optimal configuration method of PMU without loss of observability under N-1 condition. Proc. CSEE 2009, 29, 47–51. [Google Scholar] [CrossRef]
- He, K.; Zhang, Q.; Zheng, M. Optimal configuration method of PMU with minimum number of analog channels. Power Syst. Prot. Control 2015, 43, 14–18. [Google Scholar]
- Zhao, Y.; Yuan, P.; Ai, Q.; Lv, T. Optimal configuration of PMU considering topological constraints and using improved genetic algorithm. Power Grid Technol. 2014, 38, 2063–2070. [Google Scholar] [CrossRef]
- Tang, L.; Han, Y.; Zalhaf, A.S.; Zhou, S.; Yang, P.; Wang, C.; Huang, T. Resilience enhancement of active distribution networks under extreme disaster scenarios: A comprehensive overview of fault location strategies. Renew. Sustain. Energy Rev. 2024, 189, 113898. [Google Scholar] [CrossRef]
- Citroni, R.; Mangini, F.; Frezza, F. Efficient integration of ultra-low power techniques and energy harvesting in self-sufficient devices: A comprehensive overview of current progress and future directions. Sensors 2024, 24, 4471. [Google Scholar] [CrossRef]
- Niu, S.; Jia, Y.; Wang, W.; He, R.; Hu, L.; Liu, Y. Electricity consumption and human development level: A comparative analysis based on panel data for 50 countries. Int. J. Electr. Power Energy Syst. 2013, 53, 338–347. [Google Scholar] [CrossRef]
- Zhao, C.; Dong, K.; Wang, K.; Nepal, R. How does artificial intelligence promote renewable energy development? The role of climate finance. Energy Econ. 2024, 133, 107493. [Google Scholar] [CrossRef]
- Luo, K.; Lee, C.-C.; Zhuo, C. A pathway to coordinated regional development: Energy utilization efficiency and green development-Evidence from China’s major national strategic zones. Energy Econ. 2024, 131, 107402. [Google Scholar] [CrossRef]
- Ren, Z.; San, Y. Improvement of adaptive genetic algorithm and its application in system identification. J. Syst. Simul. 2006, 18, 41–43+66. [Google Scholar] [CrossRef]
- Dongjie, X.; Renmu, H.; Peng, W.; Tao, X. Comparison of several PMU placement algorithms for state estimation. In Proceedings of the 2004 Eighth IEE International Conference on Developments in Power System Protection, Amsterdam, The Netherlands, 5–8 April 2004; pp. 32–35. [Google Scholar]
- Wang, X.; Liu, Y.; Sheng, G.; Jiang, X.; Luo, L.; Zhang, X.; Liu, Z. A new method for PMU optimal configuration based on improved BPSO algorithm. Guangdong Electr. Power 2018, 31, 62–67. [Google Scholar]
- Jiang, Z.; Cao, Y.; Sun, W. Multi-objective optimal PMU configuration algorithm based on 01 integer programming. Power Syst. Prot. Control 2008, 21, 12–17. [Google Scholar] [CrossRef]
- Yan, L.; Liu, Z.; Ai, Y.; Luo, C.; Chen, B. A new method for optimal configuration of PMU measurement points based on 0-1 integer programming algorithm. Power Syst. Prot. Control 2017, 45, 101–106. [Google Scholar]
- Cao, P.; Liu, M. PMU optimization configuration method based on improved integer programming method combined with zero injection node. Power Syst. Prot. Control 2021, 49, 143–150. [Google Scholar] [CrossRef]
- Monticelli, A. State Estimation in Electric Power Systems: A Generalized Approach; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Krumpholz, G.; Clements, K.; Davis, P. Power system observability: A practical algorithm using network topology. IEEE Trans. Power Appar. Syst. 2007, PAS-99, 1534–1542. [Google Scholar] [CrossRef]


| Algorithm | PMU Deployment Quantity | PMU Deployment Node Location | Average Algorithm Time |
|---|---|---|---|
| Improved algorithm in the text | 3 | 2\6\9 | 0.02 s |
| Depth-first search algorithm | 6 | 2\4\6\8\10\14 | 0.004 s |
| Improve the simulated annealing algorithm | 4 | 2\6\7\9 | 0.03 s |
| Plan | PMU Deployment Location (First Line)/ Number of PMU Connection Channels (Second Line) | Average PMU Channel |
|---|---|---|
| 1 | 3\7\10\12\19\24\29 | 2.571 |
| 2\2\5\4\1\2\2 | ||
| 2 | 1\2\10\12\19\24\29 | 2.857 |
| 2\4\5\4\1\2\2 | ||
| 3 | 2\4\10\12\19\24\30 | 3.000 |
| 4\3\5\4\1\2\2 |
| Algorithm | PMU Deployment Quantity | PMU Deployment Node Location | Average Algorithm Time |
|---|---|---|---|
| Improved algorithm in the text | 7 | 3\7\10\12\ 19\24\29 | 0.02 s |
| Depth-first search algorithm | 10 | 1\5\6\10\11\12\ 18\24\26\27 | 0.004 s |
| Improve the simulated annealing algorithm | 7 | 1\5\10\12\ 18\24\27 | 0.1 s |
| Algorithm | PMU Deployment Quantity | PMU Deployment Node Location | Average Algorithm Time |
|---|---|---|---|
| Improved algorithm in the text | 9 | 3\6\13\16\20\23\25\29\39 | 0.03 s |
| Depth-first search algorithm | 16 | 2\4\6\8\10\12\16\18\20\ 22\26\33\36\37\38\39 | 0.004 s |
| Improve the simulated annealing algorithm | 12 | 2\8\10\11\16\22\ 26\34\36\37\38\39 | 0.2 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dan, H.; Li, Z.; Dou, H. A New Method for PMU Deployment Based on the Preprocessed Integer Programming Algorithm. Energies 2025, 18, 5966. https://doi.org/10.3390/en18225966
Dan H, Li Z, Dou H. A New Method for PMU Deployment Based on the Preprocessed Integer Programming Algorithm. Energies. 2025; 18(22):5966. https://doi.org/10.3390/en18225966
Chicago/Turabian StyleDan, Hanyuan, Zhenhua Li, and Hongda Dou. 2025. "A New Method for PMU Deployment Based on the Preprocessed Integer Programming Algorithm" Energies 18, no. 22: 5966. https://doi.org/10.3390/en18225966
APA StyleDan, H., Li, Z., & Dou, H. (2025). A New Method for PMU Deployment Based on the Preprocessed Integer Programming Algorithm. Energies, 18(22), 5966. https://doi.org/10.3390/en18225966






