Wide-Band Characteristic Analysis and Compensation Research of Electromagnetic Current Transformer
Abstract
1. Introduction
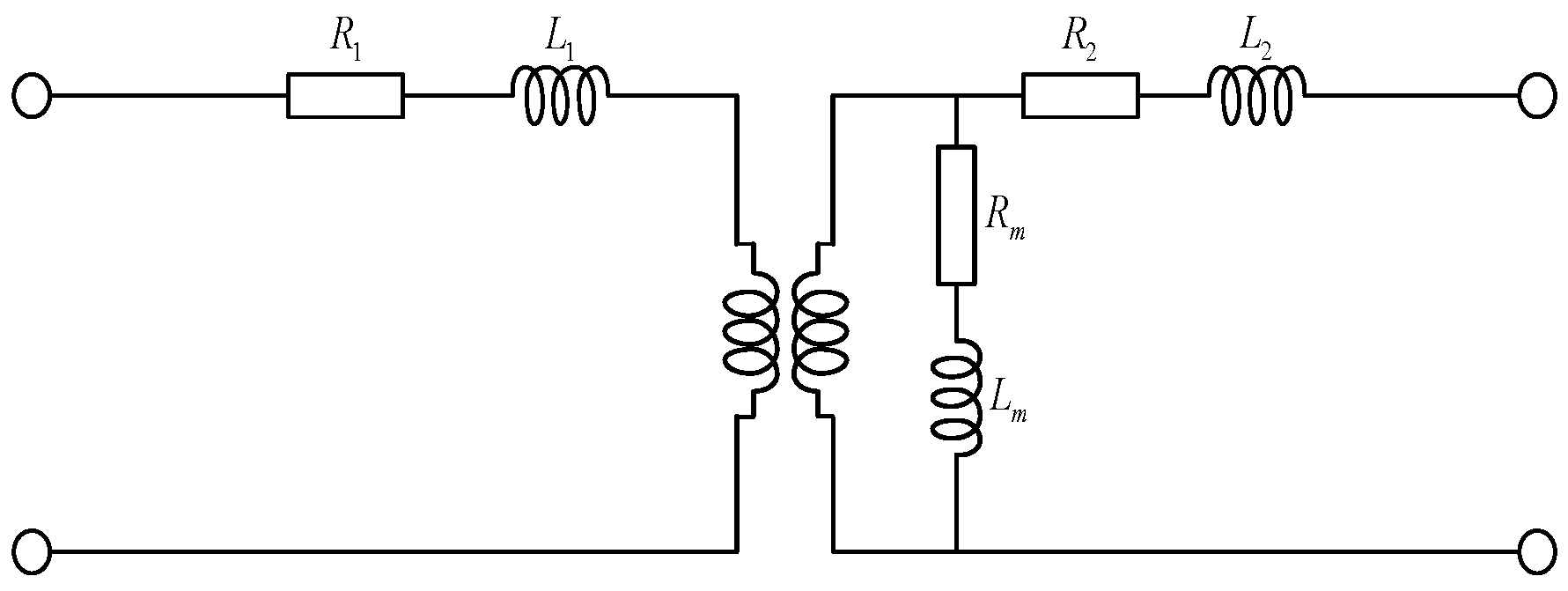
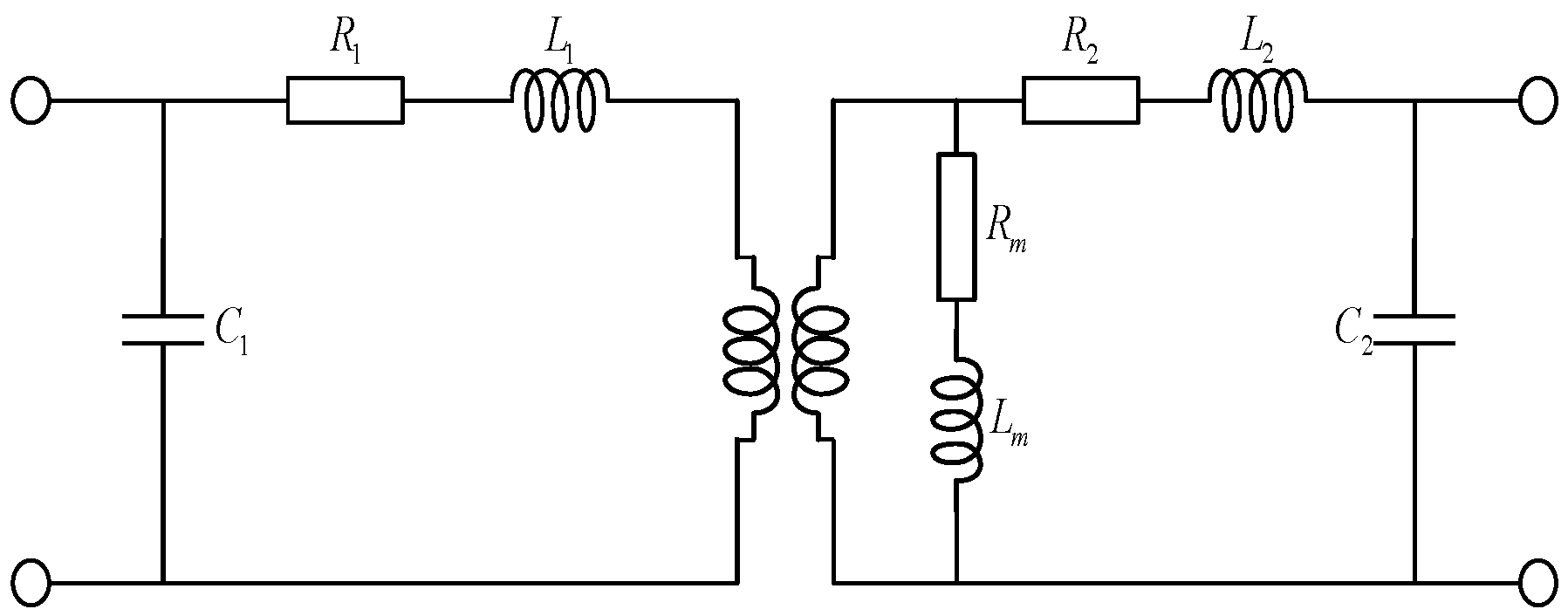
2. Wide-Band Modeling of Electromagnetic Current Transformer
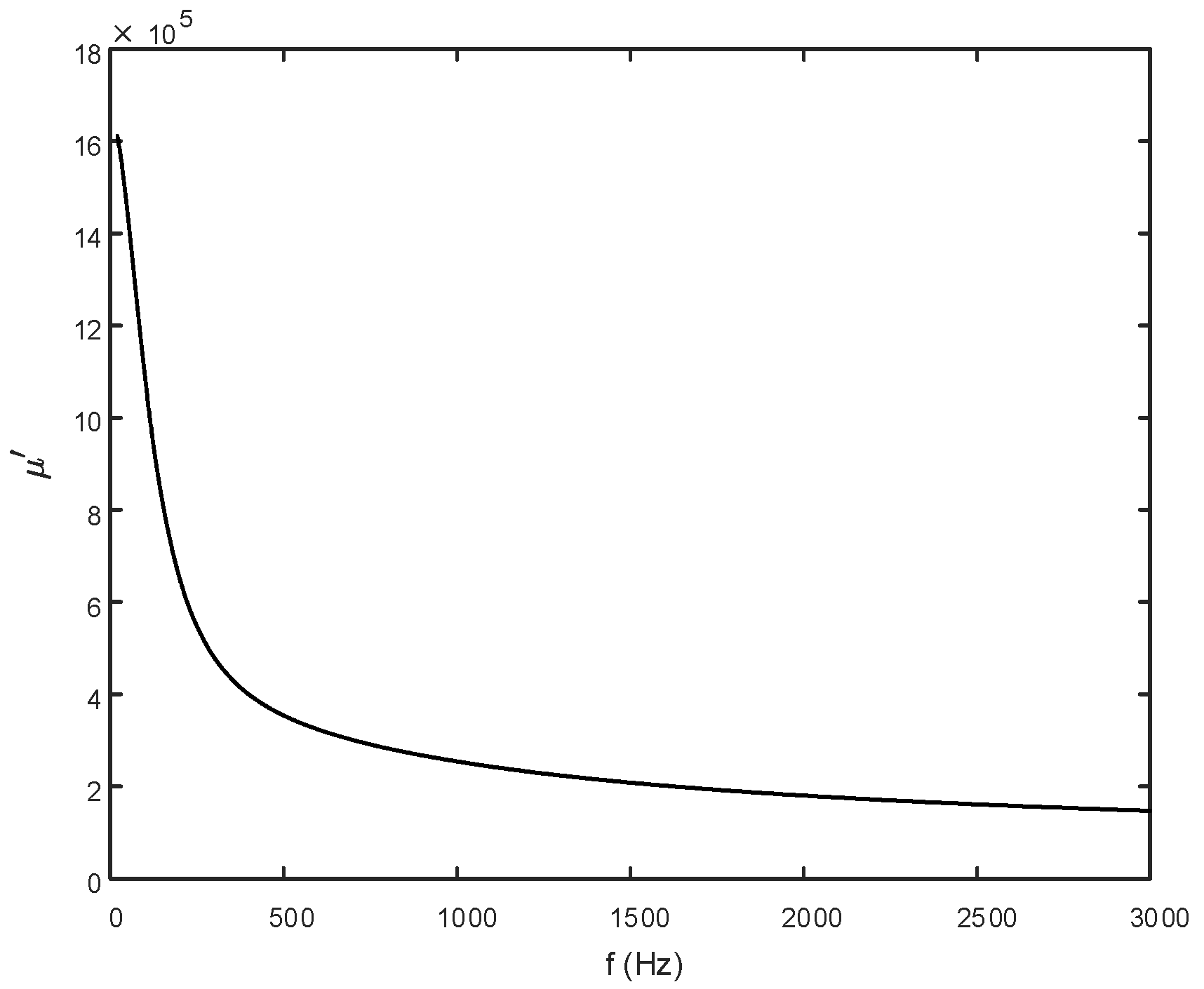
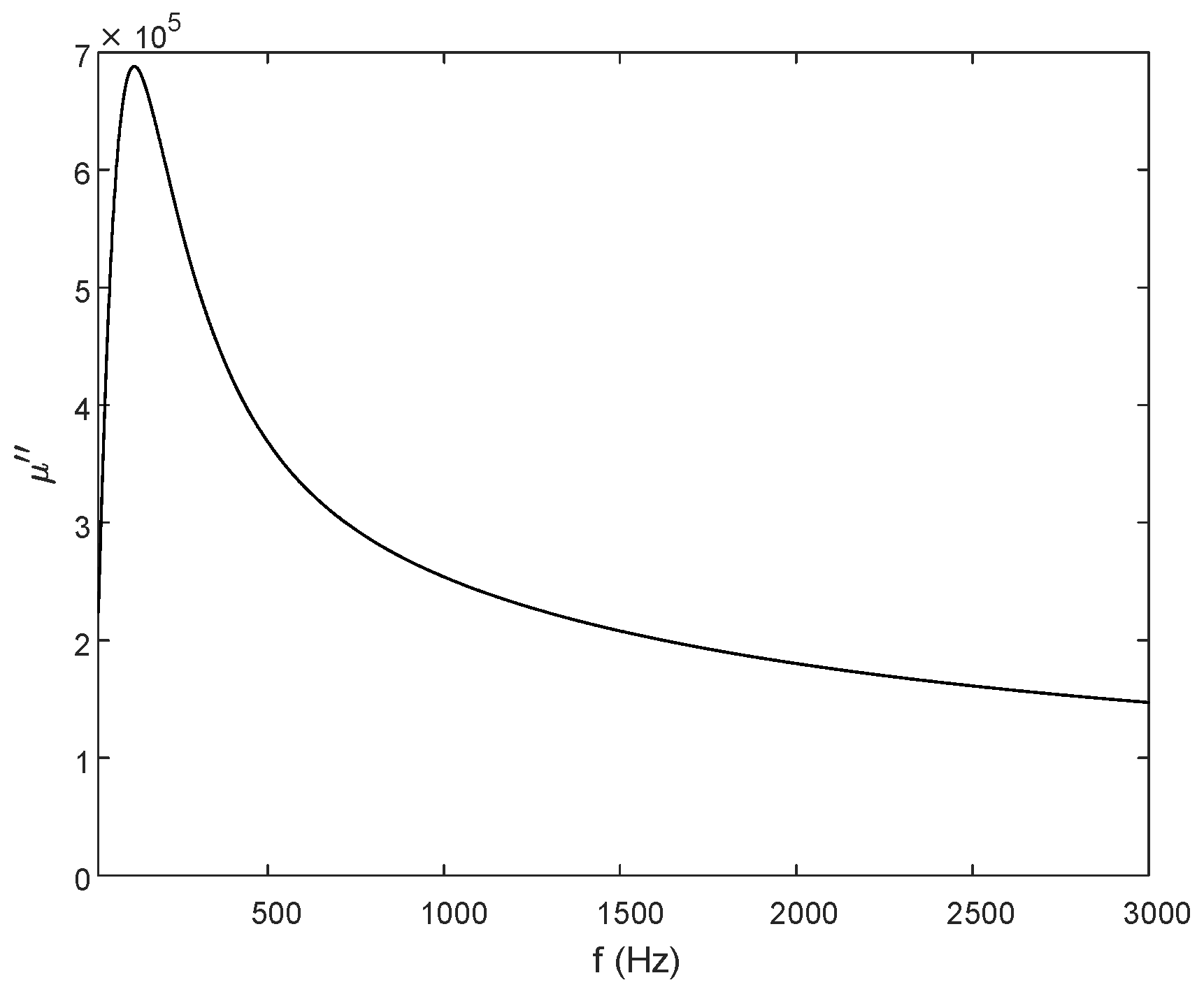
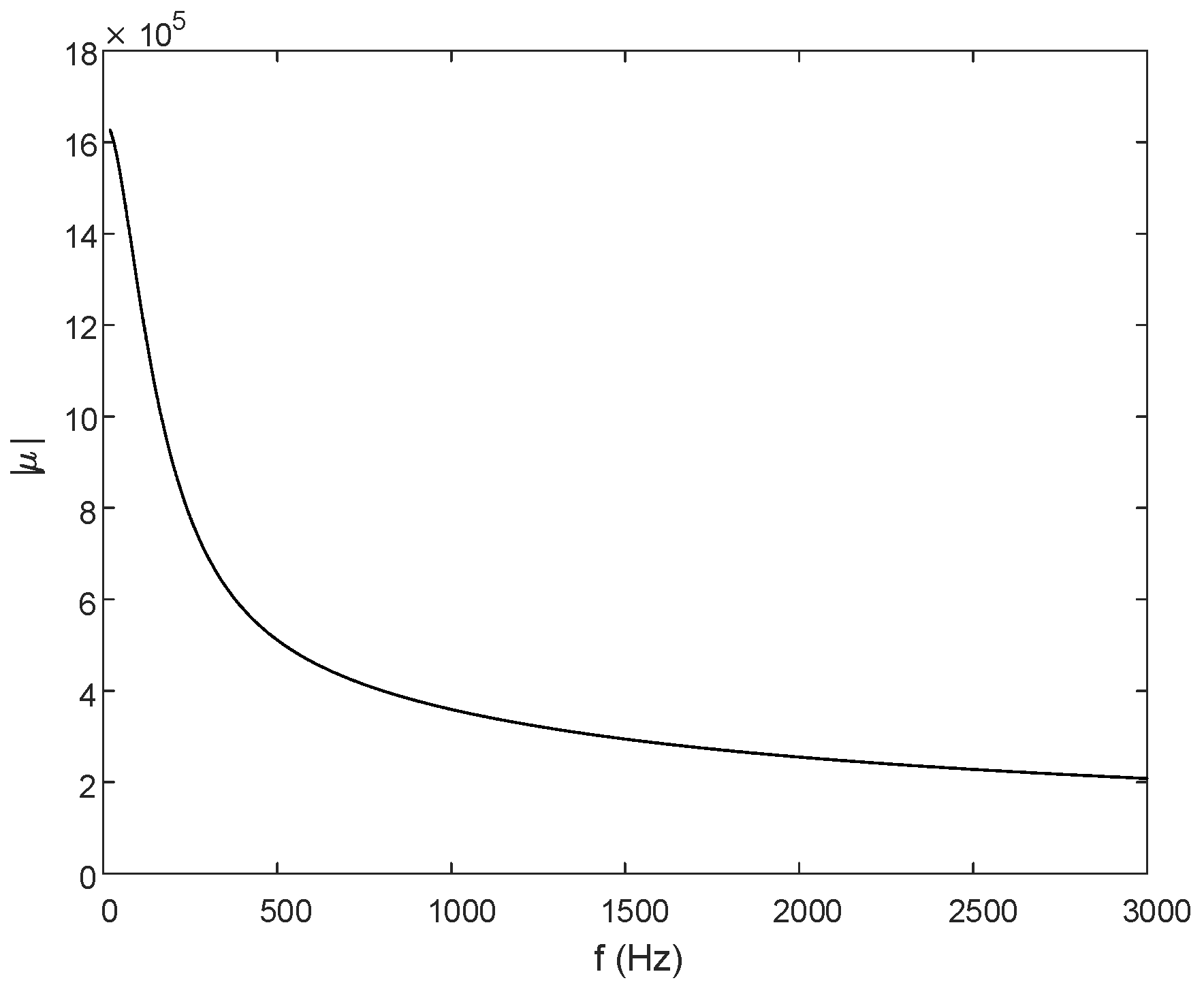
3. Study on the Frequency Characteristics of Complex Permeability of Ferromagnetic Materials
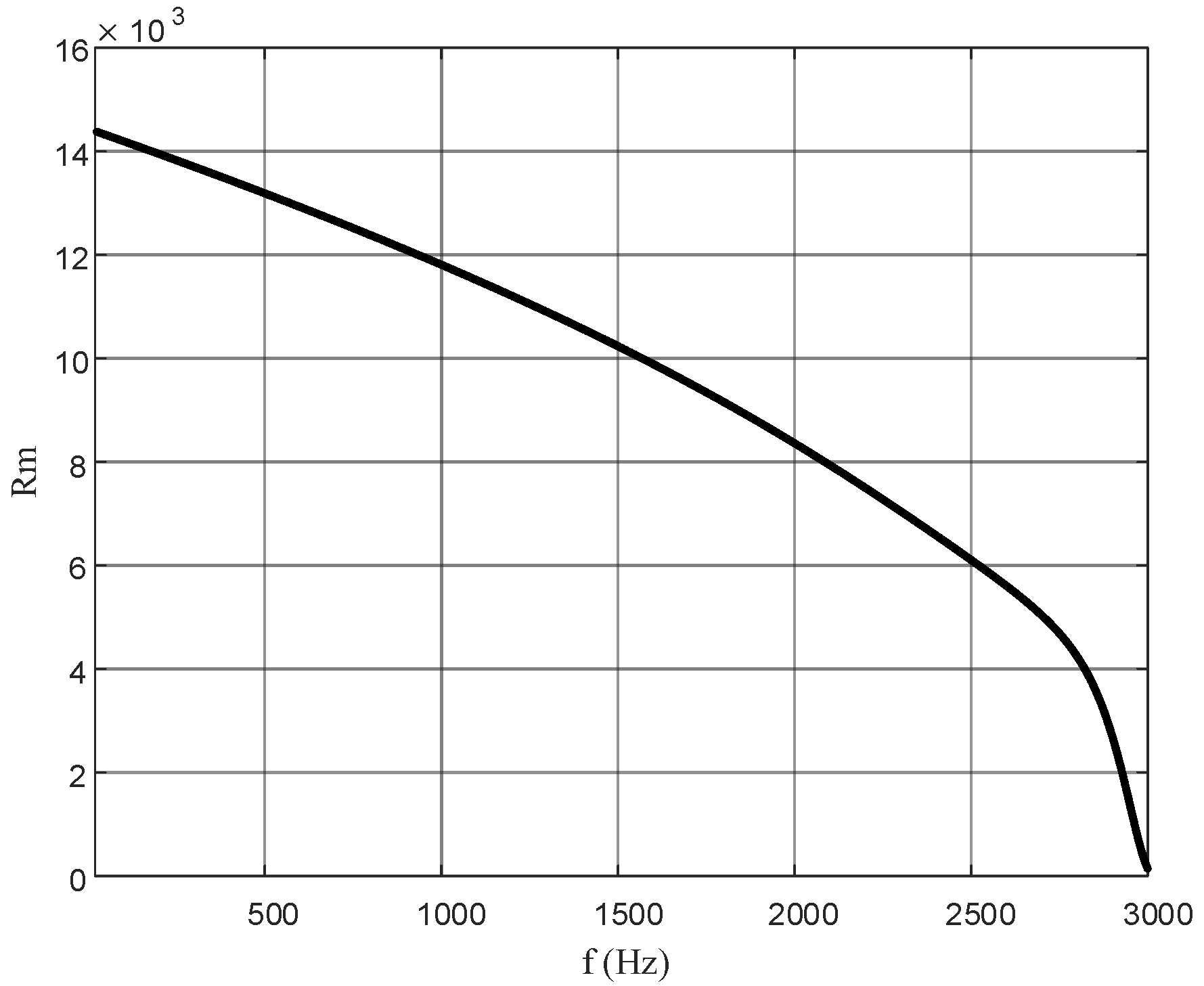
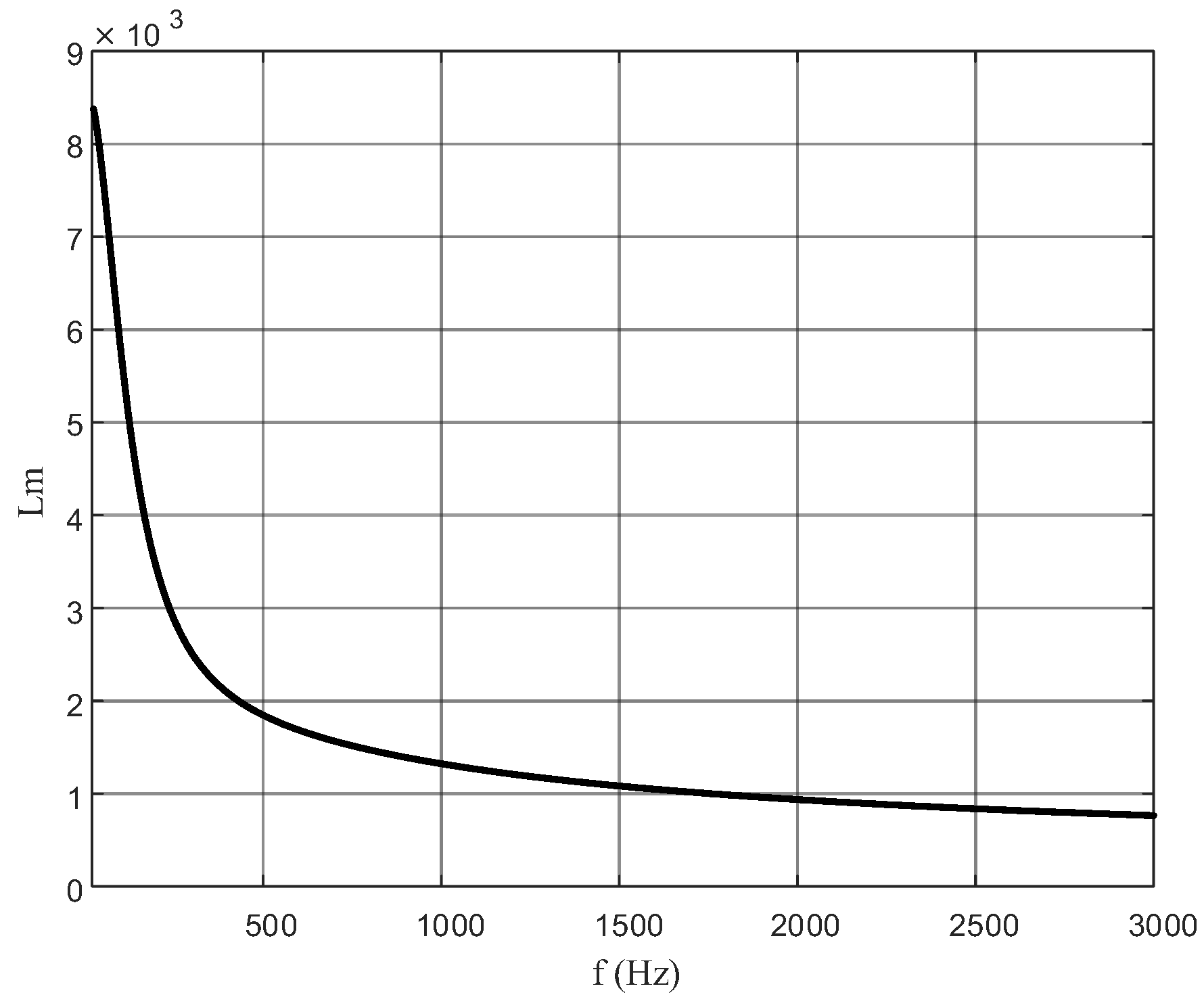
4. Frequency Characteristic Analysis of Current Transformer
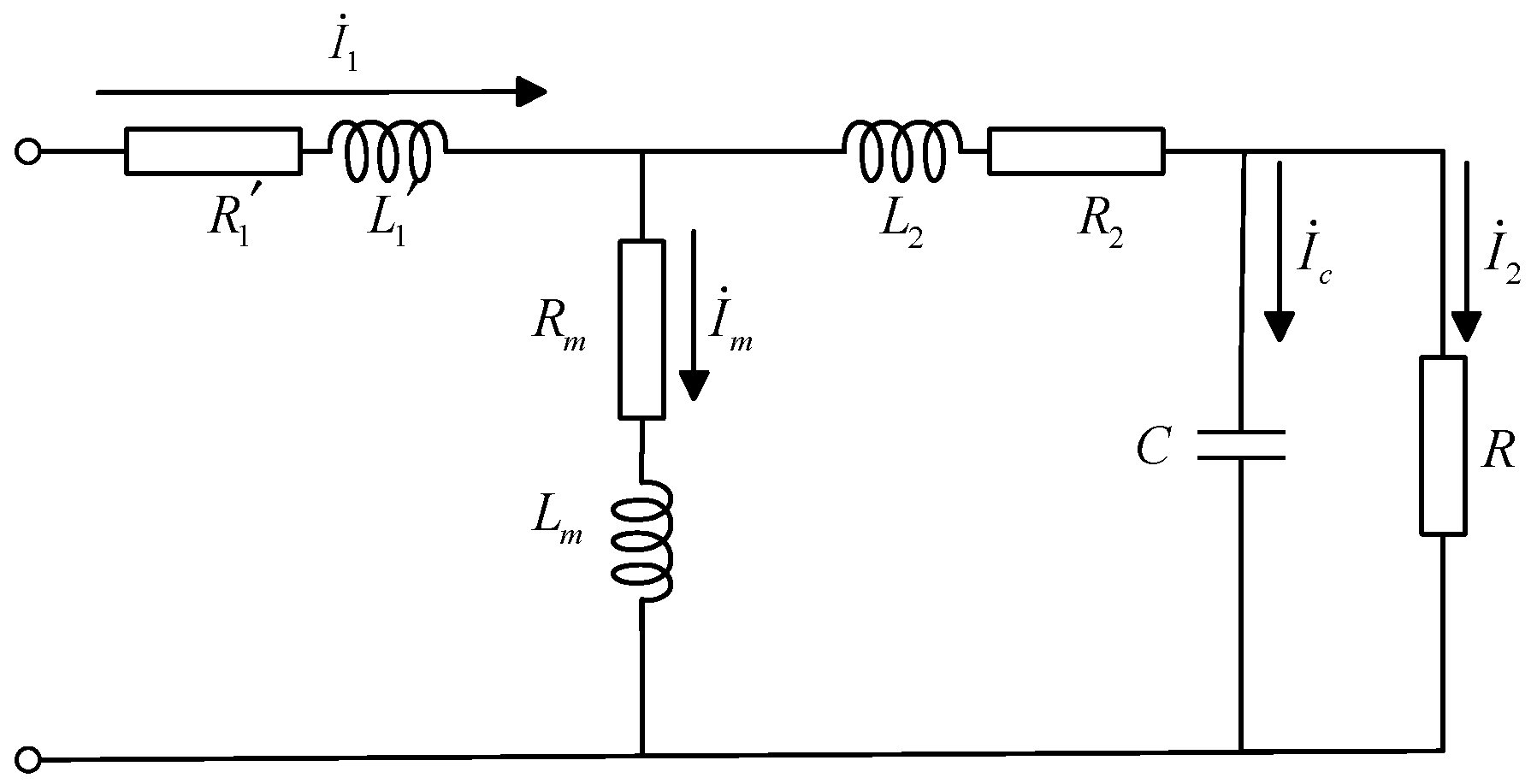
4.1. Mathematical Model of the Frequency Characteristics of Current Transformers
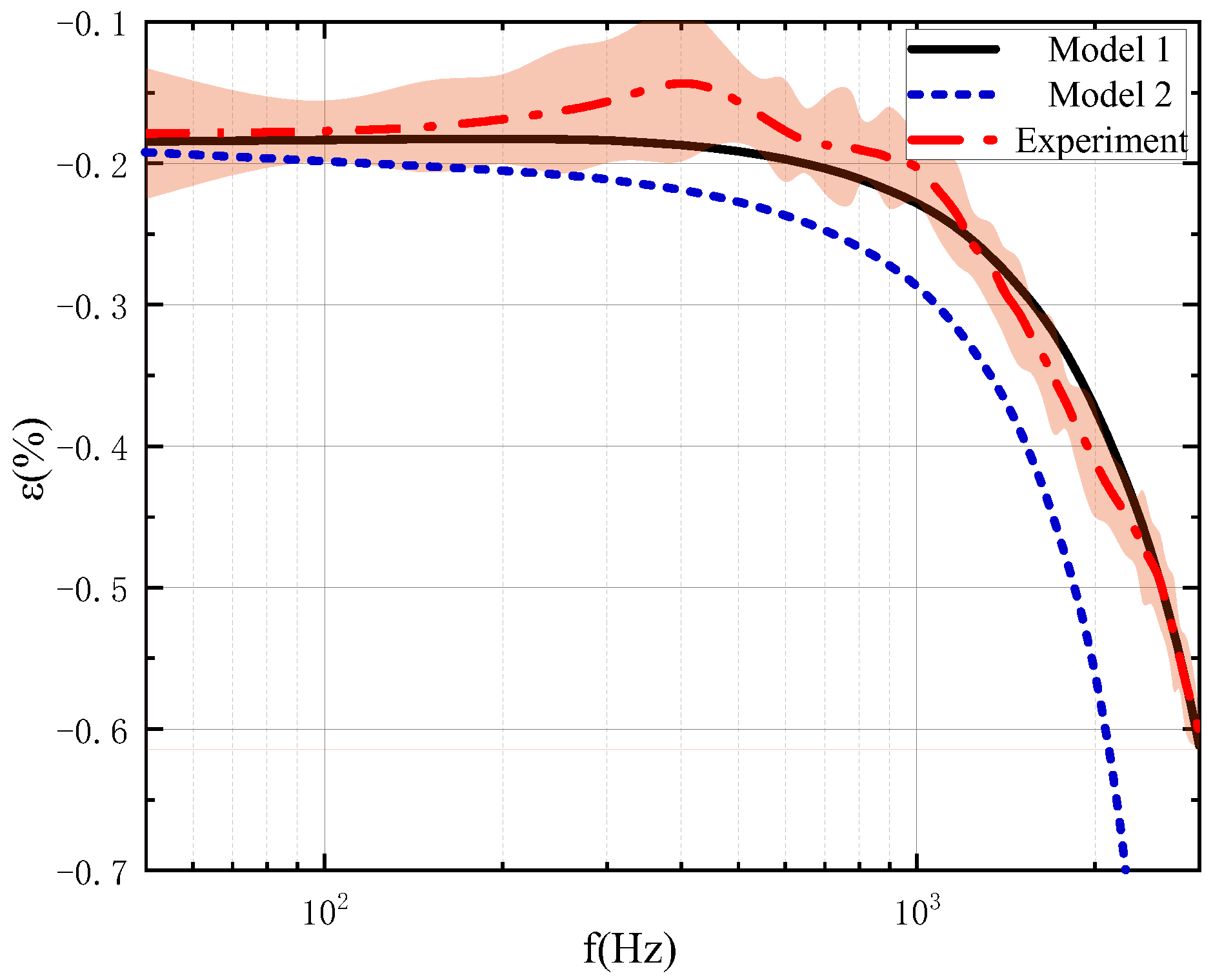
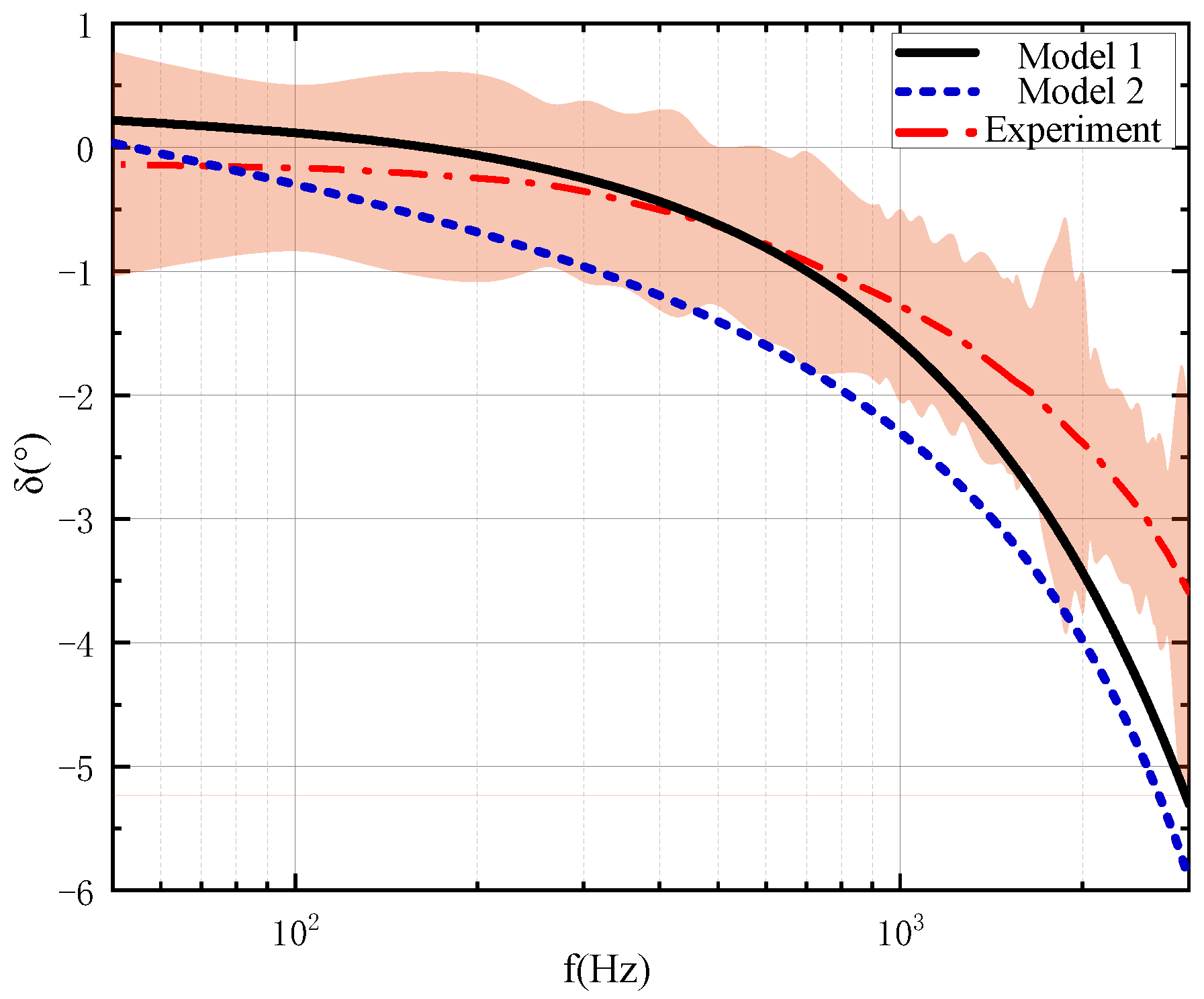
4.2. Comparative Analysis of the Experiment
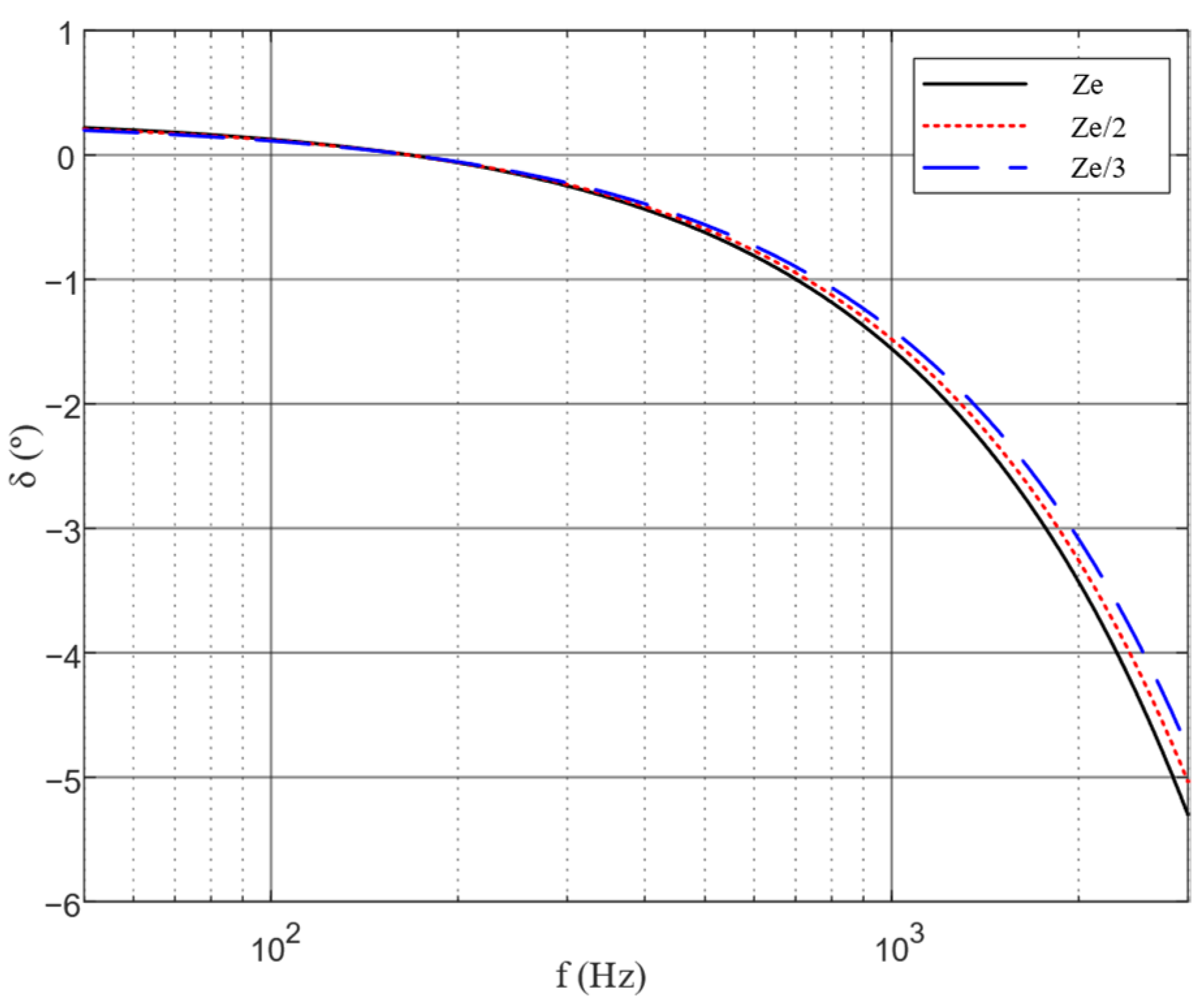
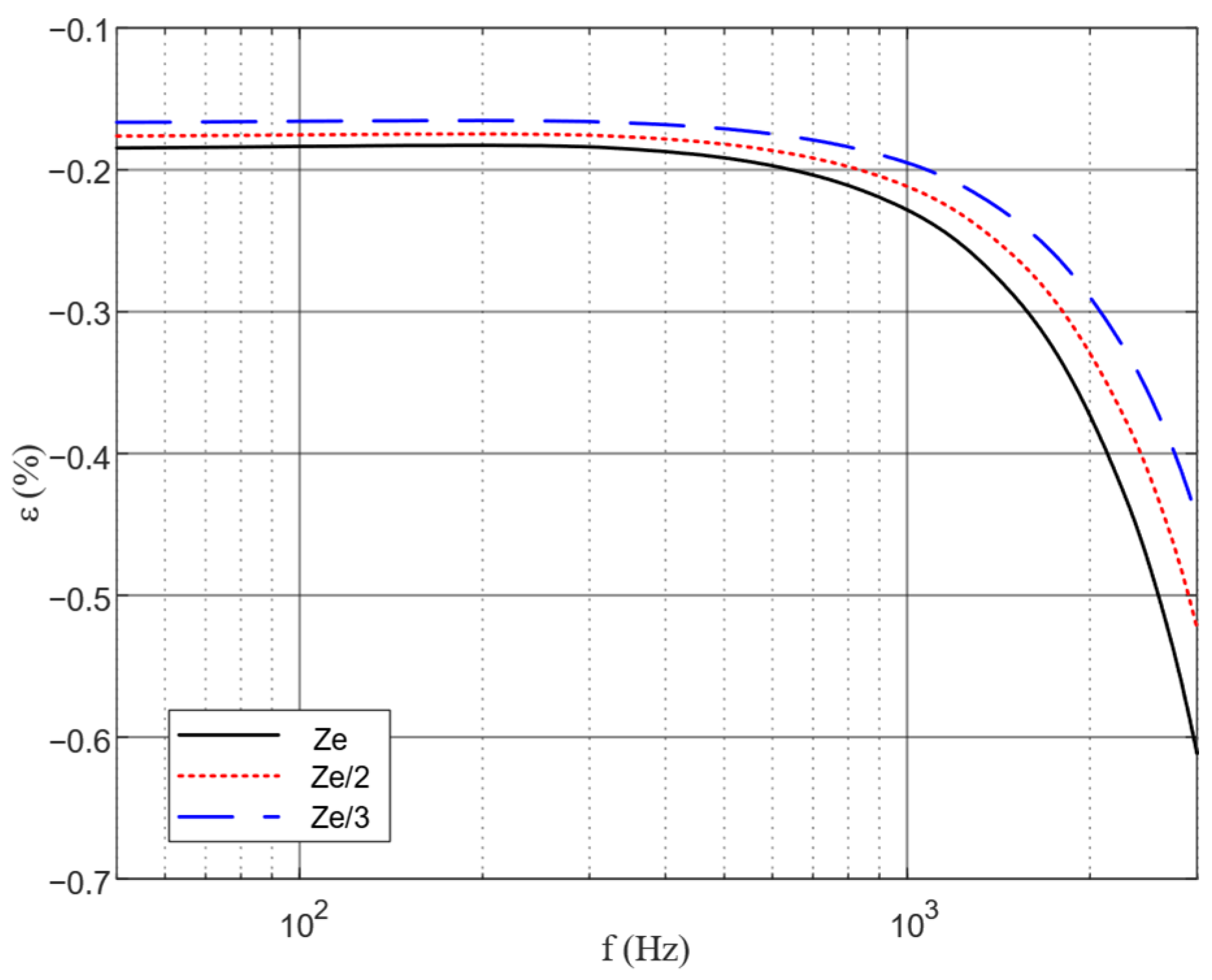
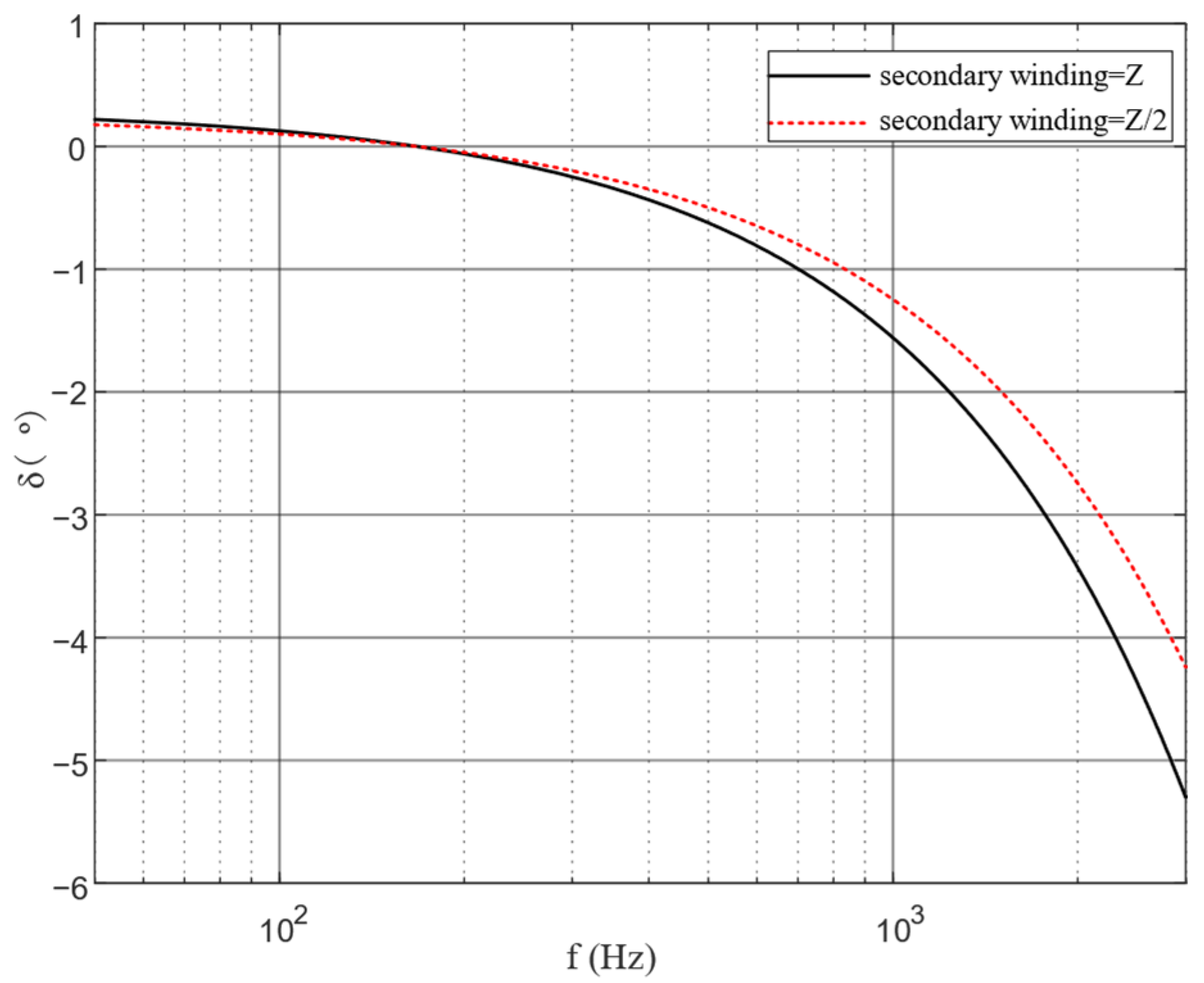
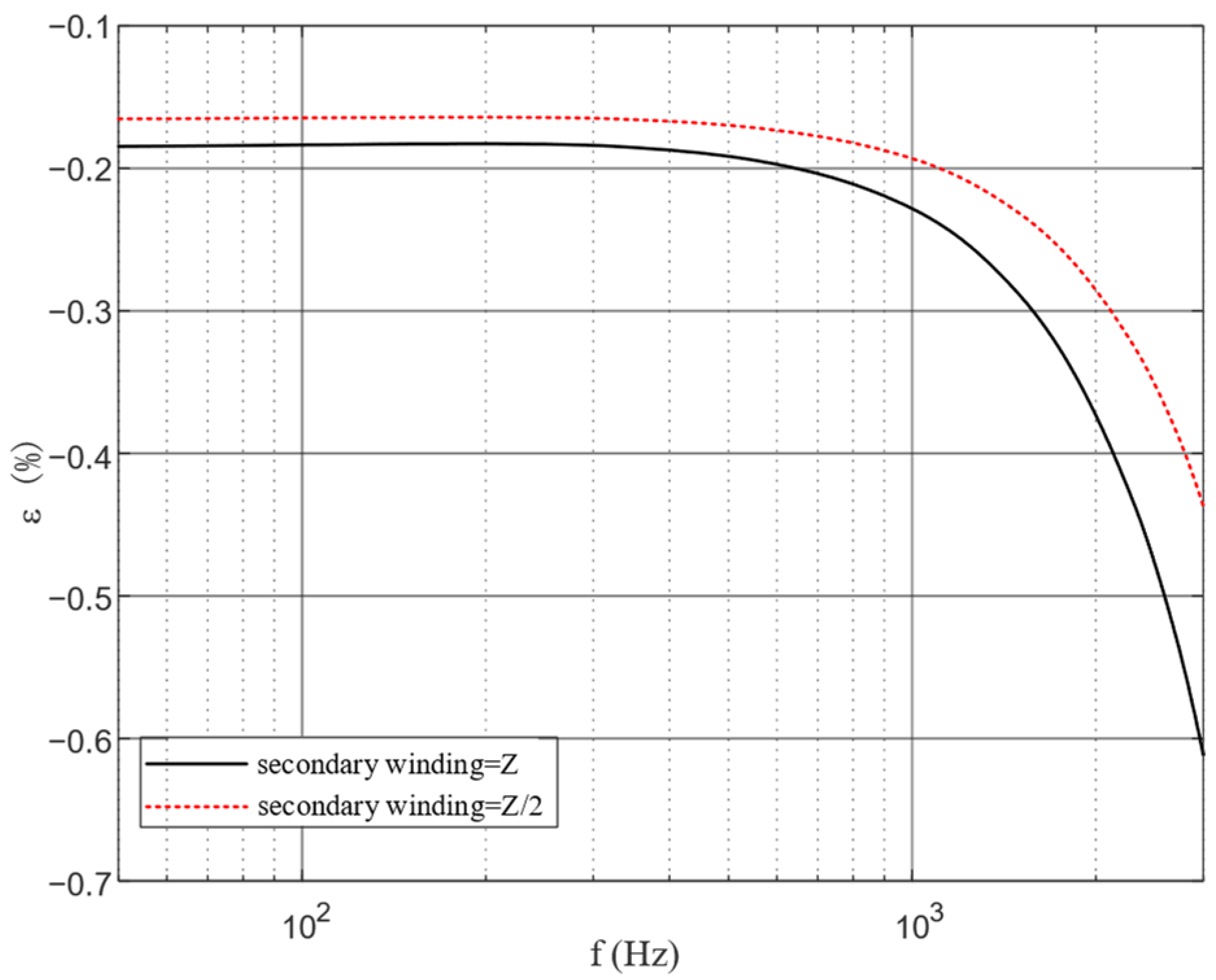
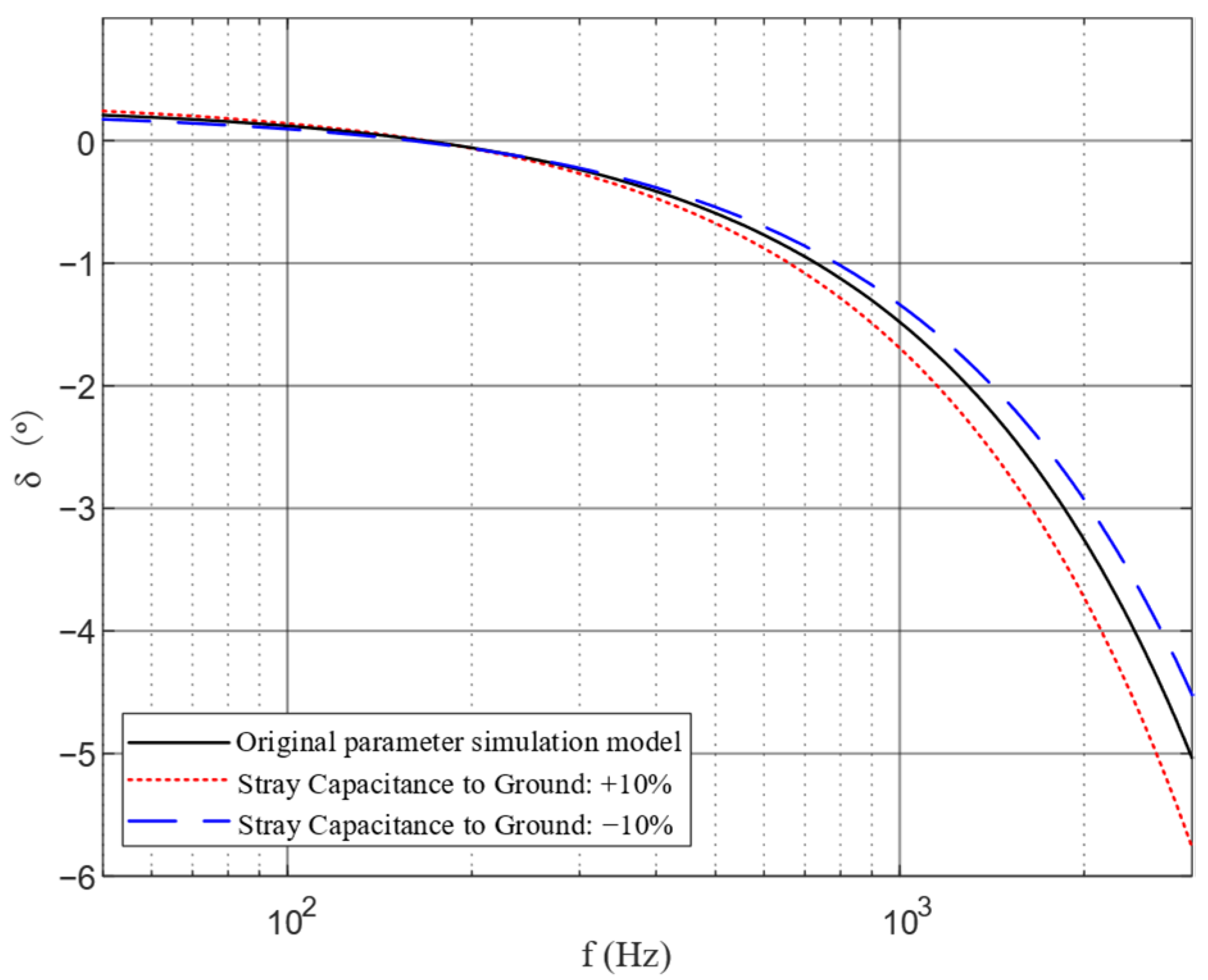
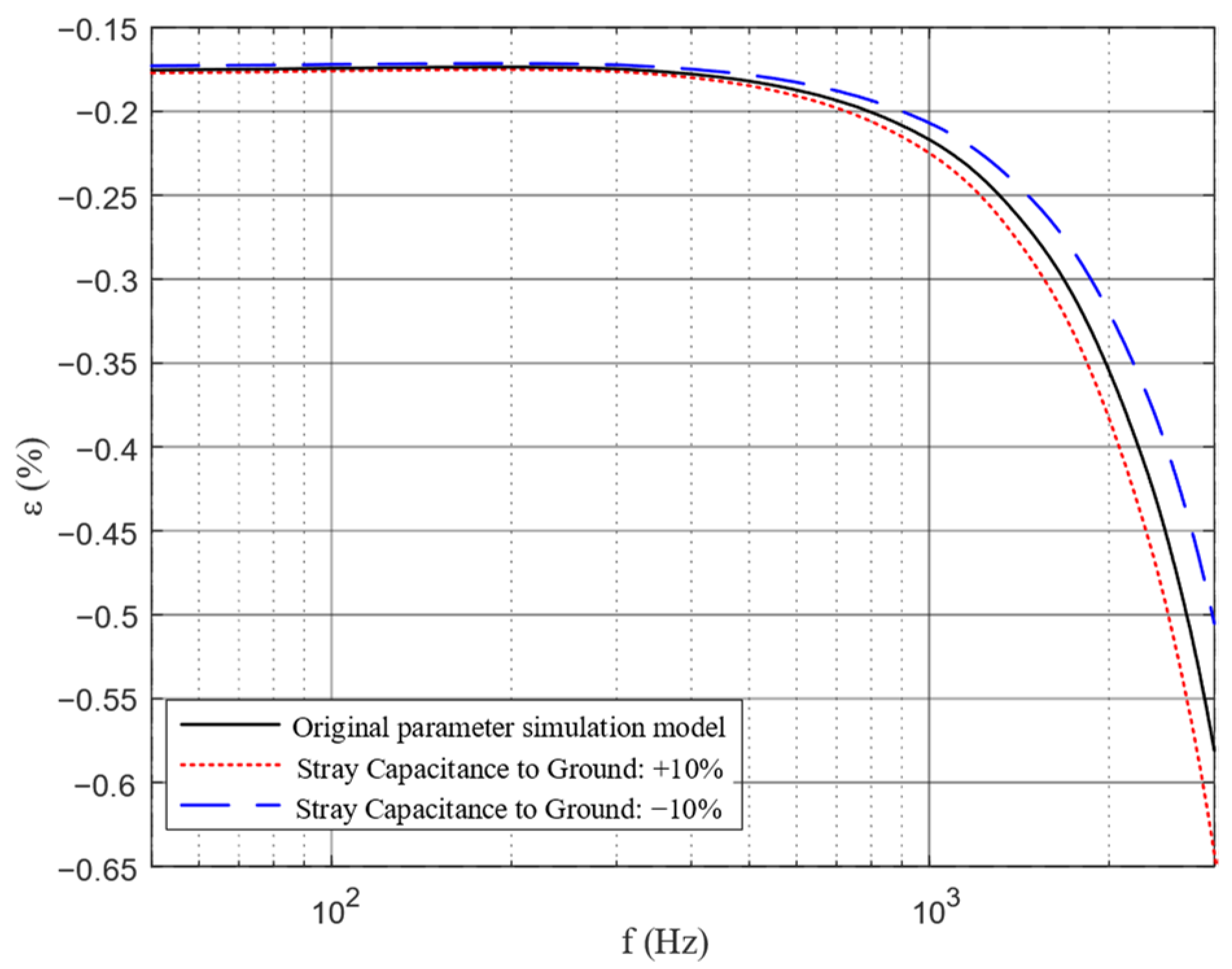
5. Frequency Characteristic Improvement and Frequency Band Broadening
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Danquah, O.J.; Mandava, S. Machine learning-based current transformer saturation detection for medium voltage in power grids system. Measurement 2025, 253, 117636. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, B.; She, X.; Wang, K.; Liu, A. A Family of Voltage Balancers with Fault-Tolerance and Interpolar Voltage Self-Balancing Ability for Bipolar DC Power Systems. IEEE Trans. Transp. Electrif. 2025, 11, 9864–9876. [Google Scholar] [CrossRef]
- Mahmoud, A.R. Digital protection scheme based on Durbin Watson and Pearson similarity indices for current signals practically applied to power transformers. Sci. Rep. 2025, 15, 12214. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Lin, S.; Zhou, Q.; Wu, G.; Li, X.; Liu, J.; Cheng, H. Frequency analysis and calculation of transformer neutral DC caused by metro stray currents. Int. J. Electr. Power Energy Syst. 2025, 166, 110531. [Google Scholar] [CrossRef]
- Rom, M.; Brom, D.V.E.H.; Houtzager, E.; van Leeuwen, R.; van der Born, D.; Rietveld, G.; Muñoz, F. Measurement System for Current Transformer Calibration from 50 Hz to 150 kHz Using a Wideband Power Analyzer. Sensors 2025, 25, 5429. [Google Scholar] [CrossRef]
- Yao, L.; Xu, L.J.; Li, S. Research on traceability technology of broadband standard current transformer based on digital comparison method. Electr. Meas. Instrum. 2024, 61, 97–103. (In Chinese) [Google Scholar]
- Kaczmarek, M.; Blus, K. Analytical Investigation of Primary Waveform Distortion Effect on Magnetic Flux Density in the Magnetic Core of Inductive Current Transformer and Its Transformation Accuracy. Sensors 2025, 25, 4837. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Yang, L.; Xiao, Y. Transfer characteristics of wide-range current transformer based on zero-flux theorem. South. Power Syst. Technol. 2024, 18, 150–158. (In Chinese) [Google Scholar]
- Feizbakhsh, A.; Naimi, M.H.; Vakilian, M. An accurate method for detection and compensation of current transformer saturation using unscented Kalman filter. Electr. Power Syst. Res. 2025, 249, 112015. [Google Scholar] [CrossRef]
- Lu, Y.Q.; Fan, S.T.; Li, X.Q. A new method for measuring frequency characteristics of industrial current transformers. J. Beijing Inst. Petrochem. Technol. 2009, 17, 45–48. (In Chinese) [Google Scholar]
- Cataliotti, A.; Cara, D.D.; Emanuel, E.A.; Nuccio, S. A novel approach to current transformer characterization in the presence of harmonic distortion. IEEE Trans. Instrum. Meas. 2009, 58, 1446. [Google Scholar] [CrossRef]
- GB/T 17215.302-2013; National Technical Committee 104 on Electricity Metering Equipment (SAC/TC 104). AC Electricity Metering Equipment—Particular Requirements—Part 2: Static Harmonic Meters for Active Energy (Classes 0, 2 S, 0, 5 S, 1 and 2). China Standards Press: Beijing, China, 2013.
- Li, Z.H.; Cui, J.X.; Lu, H.P.; Zhou, F.; Diao, Y.; Li, Z. Prediction method for instrument transformer measurement error: Adaptive decomposition and hybrid deep learning models. Measurement 2025, 253, 117592. [Google Scholar] [CrossRef]
- Yang, N.; Xiong, Z.; Ding, L.; Liu, Y.; Wu, L.; Liu, Z.; Shen, X.; Zhu, B.; Li, Z.; Huang, Y. A Game-Based Power System Planning Approach Considering Real Options and Coordination of All Types of Participants. Energy 2024, 312, 133400. [Google Scholar] [CrossRef]
- Li, Z.H.; Cui, J.X.; Wei, Y.K.; Huang, Y.-H.; Xie, H.-C.; Yao, W.-F. Calculation study of ion flow field in ±800 kV transmission lines under the effects of air pressure, temperature, humidity and improvement measures. Electr. Power Syst. Res. 2024, 234, 110574. [Google Scholar] [CrossRef]
- Yang, N.; Shen, X.; Liang, P.; Ding, L.; Yan, J.; Xing, C.; Wang, C.; Zhang, L. Spatial-temporal Optimal Pricing for Charging Stations: A Model-Driven Approach Based on Group Price Response Behavior of EVs. IEEE Trans. Transp. Electrif. 2024, 10, 8869–8880. [Google Scholar] [CrossRef]
- Yu, G.; Liu, C.; Tang, B.; Chen, R.; Lu, L.; Cui, C.; Hu, Y.; Shen, L.; Muyeen, S. Short term wind power prediction for regional wind farms based on spatial-temporal characteristic distribution. Renew. Energy 2022, 199, 599–612. [Google Scholar] [CrossRef]
- Li, Z.H.; Cui, J.X.; Lu, H.P.; Zhou, F.; Diao, Y.-L.; Li, Z.-X. Prediction model of measurement errors in current transformers based on deep learning. Rev. Sci. Instrum. 2024, 95, 044704. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Wu, H.D.; Yang, D.Q. Research on eliminating residual magnetism in large power transformers using energy storage oscillation. IEEE Trans. Power Deliv. 2025, 1–10, early Access. [Google Scholar]
- Zhao, X.Z.; Wu, G.; Yang, D.Q.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced detection of power transformer winding faults through 3D FRA signatures and image processing techniques. Electr. Power Syst. Res. 2025, 242, 111433. [Google Scholar] [CrossRef]
- Lou, W.; Lu, B.; Pan, Y.; Han, Z.; Wang, L. Numerical Analysis of Electric Field in Oil-Immersed Current Transformer with Metallic Particles Inside Main Insulation. Energies 2025, 18, 3628. [Google Scholar] [CrossRef]
- Kaczmarek, M. Operating Properties of the Inductive Current Transformer and Evaluation of Requirements for Its Compliance with the IEC 61869-1 WB2 Class Extension for Frequency up to 20 kHz. Energies 2025, 18, 2595. [Google Scholar] [CrossRef]
- Odinaev, I.; Aty, A.H.A.; Pazderin, A.; Safaraliev, M.; Matrenin, P.; Senyuk, M.; Menaem, A.A.; Kanan, M. Restoration of the current transformer secondary current under core saturation conditions based on ANN. Heliyon 2024, 10, e37960. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yin, X.; Wang, Q.; Peng, C.; Chen, H.; Lu, B.; Zhao, Q.; Tong, T.; Ding, C. Measurement equipment and result analysis of B-H curve of current transformer core material under mixing frequency. Rev. Sci. Instrum. 2024, 95, 084710. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Xiong, X.F.; Liao, R.J. Effect and analysis of leakage current on error characteristics of current transformer. Trans. China Electrotech. Soc. 2018, 33, 697–704. [Google Scholar]
- Qi, X.; Wan, B.; Zhang, J.; Wang, Q.; Chen, H.; Zhao, Q.; Wang, B. Active on-site calibration technology of current transformer based on non-rated frequency current injection. Rev. Sci. Instrum. 2024, 95, 074705. [Google Scholar] [CrossRef]
- You, H.; Gan, M.; Duan, D.; Zhao, C.; Lv, F.; Yuan, J. Approach of obtaining the error of current transformers through the measurement of turns correction factor and impedance. Sens. Actuators A Phys. 2024, 376, 115566. [Google Scholar] [CrossRef]
- Li, Y.M.; Jiang, J.P.; Jian, Y.W. Research on the influence of harmonics on the measurement of electromagnetic transformers. Electr. Technol. 2021, 22, 36–41. (In Chinese) [Google Scholar]
- Wang, S.Q.; Jiang, C.Y.; Nie, G.N. Research on wideband error calibration system of current transformer. High. Volt. Eng. 2024, 50, 5281–5288. (In Chinese) [Google Scholar]
- Zhang, Z.; Chen, B.; Tian, C.; Chen, Y.; Wang, Y. A novel measurement-protection-integrated current transformer based on hybrid core and magnetic field sensor. IET Electr. Power Appl. 2024, 18, 739–755. [Google Scholar] [CrossRef]

| Parameter Name and Symbol | Numerical Value |
|---|---|
| Core thickness b/m | 0.0634 |
| Insulation layer thickness ∆/mm | 1.7 |
| Core resistivity | |
| Conductivity of iron core | |
| The relative permeability of iron core | 0.03212 |
| Magnetic flux path length L/M | 0.78 |
| Primary side winding thickness | 0.62 |
| Secondary winding thickness | 12.58 |
| Winding height h/mm | 620 |
| The average winding turn length p/mm | 100 |
| Vacuum permeability |
| Parameter | Values |
|---|---|
| Transformer ratio | 1:300 |
| Secondary distributed capacitance C/pF | 60 |
| Secondary leakage inductance | 0.73 |
| Secondary leakage resistance | 0.08 |
| Accuracy level | 0.2 |
| Rated load | 20 |
| Current Frequency/Hz | Ratio Difference/(%) | Angle Difference/(°) |
|---|---|---|
| 50 | −0.1785 | −0.1457 |
| 100 | −0.1786 | −0.1693 |
| 150 | −0.1744 | −0.2085 |
| 200 | −0.1684 | −0.2556 |
| 250 | −0.1639 | −0.2948 |
| 300 | −0.1577 | −0.3576 |
| 350 | −0.1487 | −0.4361 |
| 400 | −0.1438 | −0.5145 |
| 450 | −0.1475 | −0.5694 |
| 500 | −0.1568 | −0.6479 |
| 550 | −0.1683 | −0.7028 |
| 600 | −0.1775 | −0.7891 |
| 700 | −0.1879 | −0.9225 |
| 800 | −0.1909 | −1.0716 |
| 900 | −0.1954 | −1.1814 |
| 1000 | −0.2022 | −1.2991 |
| 2000 | −0.4107 | −2.3584 |
| 3000 | −0.6032 | −3.5432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Li, Z.; Li, Z.; Zhang, L.; Yang, C. Wide-Band Characteristic Analysis and Compensation Research of Electromagnetic Current Transformer. Energies 2025, 18, 5862. https://doi.org/10.3390/en18215862
Wu X, Li Z, Li Z, Zhang L, Yang C. Wide-Band Characteristic Analysis and Compensation Research of Electromagnetic Current Transformer. Energies. 2025; 18(21):5862. https://doi.org/10.3390/en18215862
Chicago/Turabian StyleWu, Xingyan, Zhenhua Li, Zhenxing Li, Lei Zhang, and Chenyi Yang. 2025. "Wide-Band Characteristic Analysis and Compensation Research of Electromagnetic Current Transformer" Energies 18, no. 21: 5862. https://doi.org/10.3390/en18215862
APA StyleWu, X., Li, Z., Li, Z., Zhang, L., & Yang, C. (2025). Wide-Band Characteristic Analysis and Compensation Research of Electromagnetic Current Transformer. Energies, 18(21), 5862. https://doi.org/10.3390/en18215862






