A Multi-Head Attention-Based TimesNet for Heat Production Planning Under Unknown Future Demands
Abstract
1. Introduction
2. Literature Review
3. Problem Description
4. Proposed Method
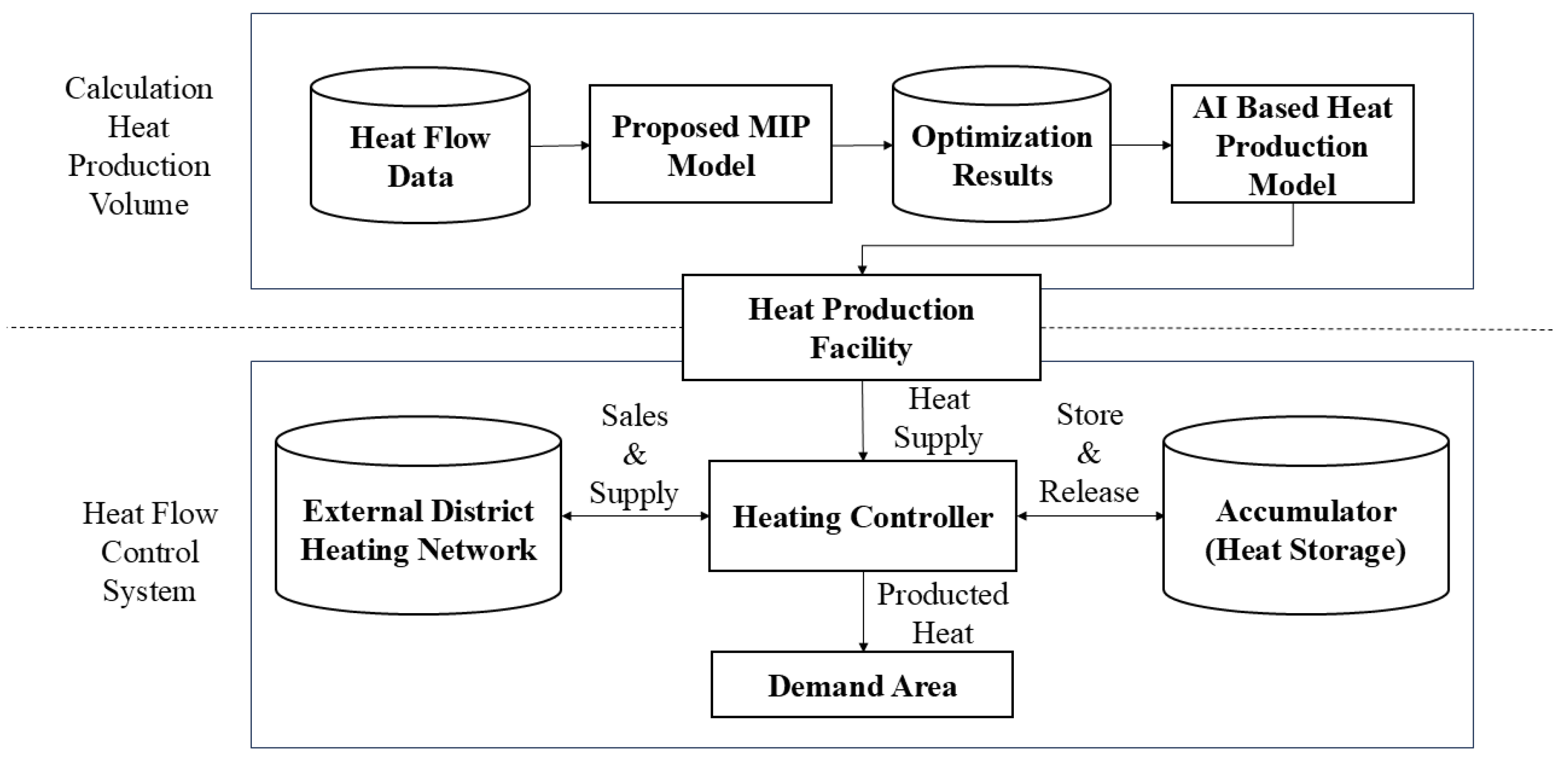
4.1. Overall Framework
4.2. Data Configuration and Inference Method
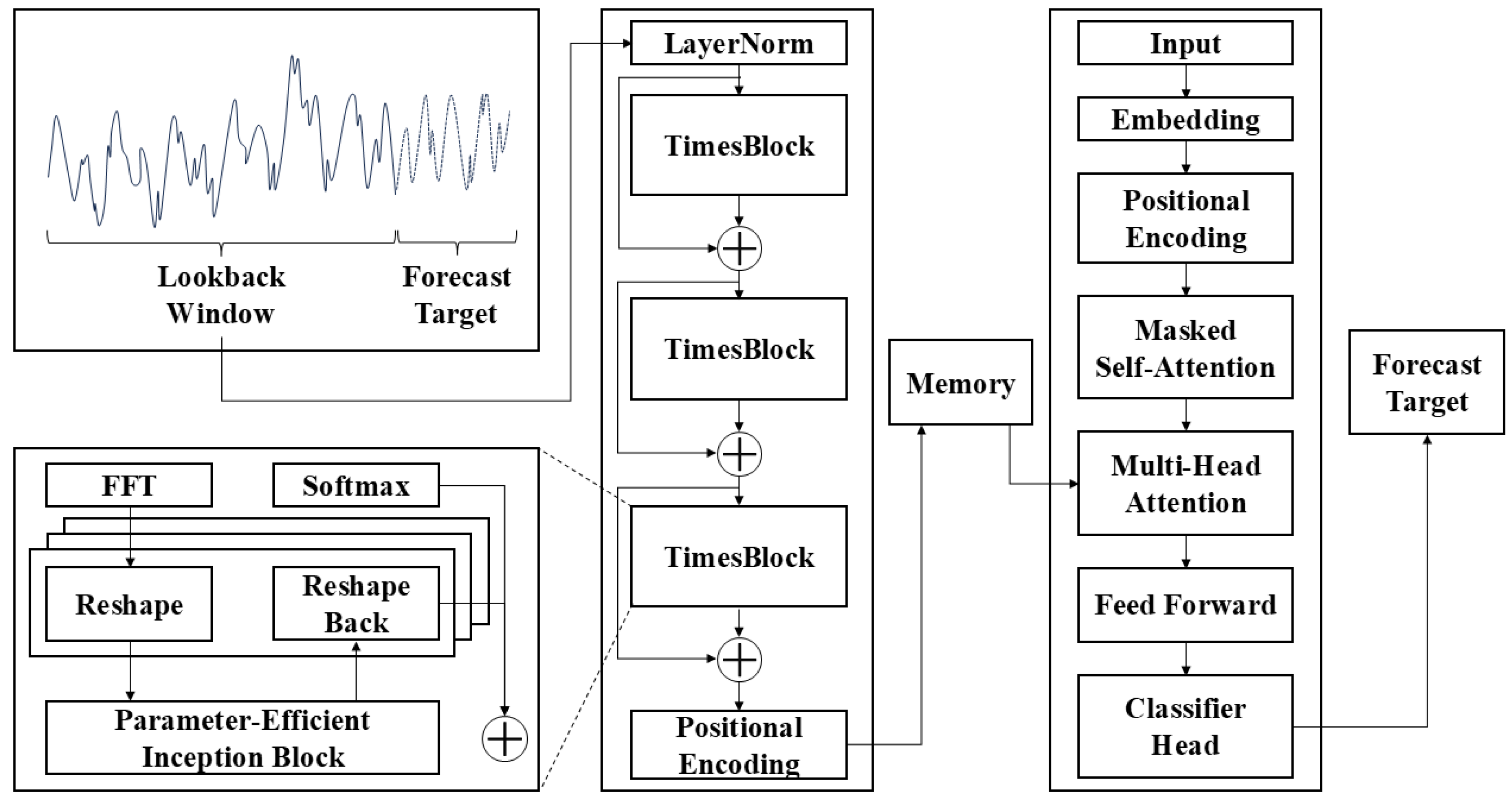
4.3. Proposed MATN-Based Heat Production Planning Model
4.4. Cost-Aware Loss Function
5. Computational Experiments
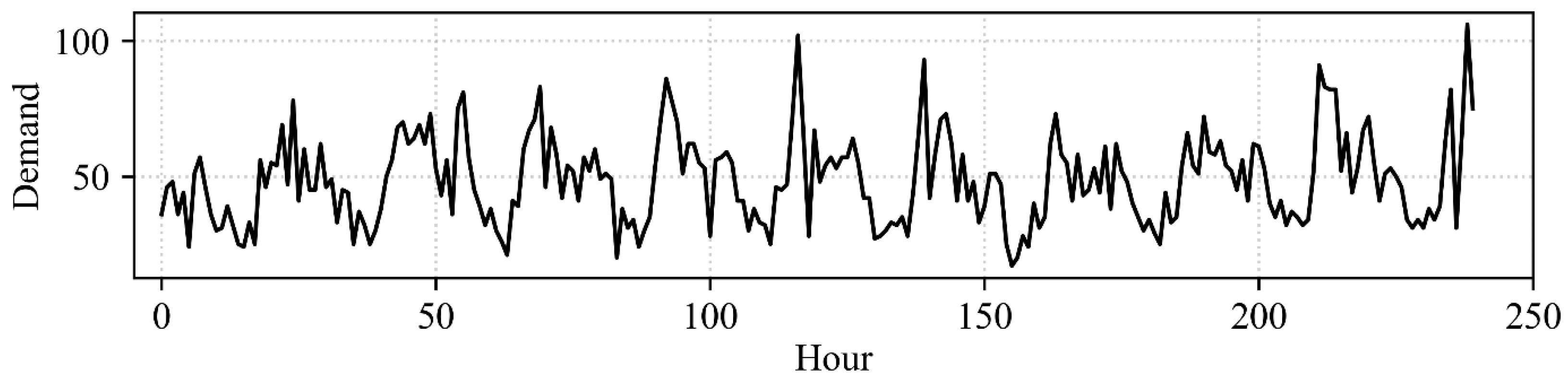
5.1. Datasets
5.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- IEA. District Heating—Energy System. Available online: https://www.iea.org/energy-system/buildings/district-heating (accessed on 15 October 2025).
- Pardo-Bosch, F.; Blanco, A.; Mendoza, N.; Libreros, B.; Tejedor, B.; Pujadas, P. Sustainable deployment of energy efficient district heating: City business model. Energy Policy 2023, 181, 113701. [Google Scholar] [CrossRef]
- Rušeljuk, P.; Lepiksaar, K.; Siirde, A.; Volkova, A. Economic Dispatch of CHP Units through District Heating Network’s Demand-Side Management. Energies 2021, 14, 4553. [Google Scholar] [CrossRef]
- Huang, S.; Tang, W.; Wu, Q.; Li, C. Network constrained economic dispatch of integrated heat and electricity systems. Energy 2019, 179, 464–474. [Google Scholar] [CrossRef]
- Siddique, M.B.; Zeng, T.; Yang, M.; Peng, S.; Gao, C.; Yang, Y. Dispatch strategies for large-scale heat pump based district heating under high renewable share and risk-aversion: A multistage stochastic optimization approach. Energy Econ. 2024, 136, 107764. [Google Scholar] [CrossRef]
- Li, J.; Xue, Y.; Du, Y.; Pan, Z.; Zhang, J.; Shao, Y.; Sun, H. Coordinated economic dispatch of the primary and secondary heating systems in district heating. Front. Energy Res. 2023, 10, 1005784. [Google Scholar] [CrossRef]
- Gadd, H.; Werner, S. Thermal energy storage systems for district heating and cooling. In Advances in Thermal Energy Storage Systems: Methods and Applications, 2nd ed.; Cabeza, L.F., Ed.; Woodhead Publishing/Elsevier: Oxford, UK, 2021; pp. 625–638. [Google Scholar] [CrossRef]
- Sihvonen, V.; Ollila, I.; Jaanto, J.; Grönman, A.; Honkapuro, S.; Riikonen, J.; Price, A. Role of power-to-heat and thermal energy storage in district heating systems. Energy 2024, 305, 132372. [Google Scholar] [CrossRef]
- Huo, S.; Wang, J.; Qin, Y.; Cui, Z. Operation optimization of district heating network under typical modes for improving the economic and flexibility performances of integrated energy system. Energy Convers. Manag. 2022, 267, 115904. [Google Scholar] [CrossRef]
- Benonysson, A.; Bøhm, B.; Ravn, H.F. Operational optimization in a district heating system. Energy Convers. Manag. 1995, 36, 297–314. [Google Scholar] [CrossRef]
- Franco, A.; Versace, M. Multi-objective optimization for the maximization of the operating share of cogeneration system in district heating network. Energy Convers. Manag. 2017, 139, 33–44. [Google Scholar] [CrossRef]
- Dorotić, H.; Pukšec, T.; Duić, N. Multi-objective optimization of district heating and cooling systems for a one-year time horizon. Energy 2019, 169, 319–328. [Google Scholar] [CrossRef]
- Rasoulian, H. Reliability, Availability and Resilience Assessment of Heating Systems. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2022. Available online: https://spectrum.library.concordia.ca/id/eprint/991121/ (accessed on 15 October 2025).
- Rafati, A.; Tahavori, M.; Shaker, H.R. Data-driven reliability analysis of district heating systems for asset management applications: A review. Sustain. Cities Soc. 2025, 118, 106052. [Google Scholar] [CrossRef]
- Protić, M.; Shamshirband, S.; Petković, D.; Abbasi, A.; Kiah, M.L.M.; Unar, J.A.; Živković, L.; Raos, M. Forecasting of consumers heat load in district heating systems using the support vector machine with a discrete wavelet transform algorithm. Energy 2015, 87, 343–351. [Google Scholar] [CrossRef]
- Fang, T.; Lahdelma, R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system. Appl. Energy 2016, 179, 544–552. [Google Scholar] [CrossRef]
- Reda, F.; Ruggiero, S.; Auvinen, K.; Temmes, A. Towards low-carbon district heating: Investigating the socio-technical challenges and opportunities. Smart Energy 2021, 4, 100054. [Google Scholar] [CrossRef]
- Danfoss. The Importance of System Boundaries When Evaluating the Energy Efficiency of District Heating Systems. 2025. Available online: https://www.danfoss.com/en/about-danfoss/articles/dhs/the-importance-of-system-boundaries-when-evaluating-the-energy-efficiency-of-district-heating-systems/ (accessed on 15 October 2025).
- Mertz, T.; Serra, S.; Henon, A.; Reneaume, J.-M. A MINLP optimization of the configuration and the design of a district heating network: Academic study cases. Energy 2016, 117, 450–464. [Google Scholar] [CrossRef]
- Weinand, J.M.; Kleinebrahm, M.; McKenna, R.; Mainzer, K.; Fichtner, W. Developing a combinatorial optimisation approach to design district heating networks based on deep geothermal energy. Appl. Energy 2019, 251, 113367. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Optimization of 4th generation distributed district heating system: Design and planning of combined heat and power. Renew. Energy 2019, 130, 371–387. [Google Scholar] [CrossRef]
- Lee, D.; Yoon, S.M.; Lee, J.; Kim, K.; Song, S.H. Applying deep learning to the heat production planning problem in a district heating system. Energies 2020, 13, 6641. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2017, 10, 3. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K. Recurrent neural network-based hourly prediction of photovoltaic power output using meteorological information. Energies 2019, 12, 215. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Vesterlund, M.; Toffolo, A.; Dahl, J. Optimization of multi-source complex district heating network, a case study. Energy 2017, 126, 53–63. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the International Conference on Learning Representations (ICLR 2023), Kigali, Rwanda, 1–5 May 2023; Available online: https://openreview.net/forum?id=ju_Uqw384Oq (accessed on 15 October 2025).
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS) 2017, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: New York, NY, USA, 2017. Available online: https://papers.neurips.cc/paper/7181-attention-is-all-you-need.pdf (accessed on 15 October 2025).
- Sameti, M.; Haghighat, F. Optimization approaches in district heating and cooling thermal network. Energy Build. 2017, 140, 121–130. [Google Scholar] [CrossRef]
- Jie, P.; Zhu, N.; Li, D. Operation optimization of existing district heating systems. Appl. Therm. Eng. 2015, 80, 20–28. [Google Scholar] [CrossRef]
- Talebi, B.; Mirzaei, P.A.; Bastani, A.; Haghighat, F. A review of district heating systems: Modeling and optimization. Front. Built Environ. 2016, 2, 22. [Google Scholar] [CrossRef]
- Lesko, M.; Bujalski, W.; Futyma, K. Operational optimization in district heating systems with the use of thermal energy storage. Energy 2018, 165, 902–915. [Google Scholar] [CrossRef]
- Qin, C.; Yan, Q.; He, G. Integrated energy systems planning with electricity, heat and gas using particle swarm optimization. Energy 2019, 188, 116044. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Haijian, Z.; Zhu, T. Optimization modeling for smart operation of multi-source district heating with distributed variable-speed pumps. Energy 2017, 138, 1247–1262. [Google Scholar] [CrossRef]
- Wu, C.; Gu, W.; Jiang, P.; Li, Z.; Cai, H.; Li, B. Combined economic dispatch considering the time-delay of district heating network and multi-regional indoor temperature control. IEEE Trans. Sustain. Energy 2017, 8, 1709–1719. [Google Scholar] [CrossRef]
- Riedmüller, S.; Rivetta, F.; Zittel, J. Long-Term Multi-Objective Optimization for Integrated Unit Commitment and District Heating Scheduling. arXiv 2024, arXiv:2410.06673. [Google Scholar]
- Sporleder, M.; Rath, M.; Ragwitz, M. Design optimization of district heating systems: A review. Front. Energy Res. 2022, 10, 971912. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Murele, O.C.; Silvente, J.; Zhakiyev, N.; Akhmetbekov, Y.; Tutkushev, D. Efficient planning of energy production and maintenance of large-scale combined heat and power plants. Energy Convers. Manag. 2018, 171, 1304–1317. [Google Scholar] [CrossRef]
- Sandberg, A.; Wallin, F.; Li, H.; Azaza, M. An analyze of long-term hourly district heat demand forecasting of a commercial building using neural networks. Energy Procedia 2017, 105, 3784–3790. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 7046–7051. [Google Scholar] [CrossRef]
- Rahman, A.; Smith, A.D. Predicting heating demand and sizing a stratified thermal storage tank using deep learning algorithms. Appl. Energy 2018, 228, 108–121. [Google Scholar] [CrossRef]
- Lu, K.; Meng, X.R.; Sun, W.X.; Zhang, R.G.; Han, Y.K.; Gao, S.; Su, D. GRU-based encoder–decoder for short-term CHP heat load forecast. IOP Conf. Ser. Mater. Sci. Eng. 2018, 392, 062173. [Google Scholar] [CrossRef]
- Lu, K.; Bi, Z.; Wang, X.; Meng, X.; Li, H.; Sun, W.; Zhu, Z.; Liu, Z. Short-term CHP heat load forecast method based on concatenated LSTMs. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 99–103. [Google Scholar] [CrossRef]
- Yu, J.; Shen, X.; Sun, H. Economic dispatch for regional integrated energy system with district heating network under stochastic demand. IEEE Access 2019, 7, 46659–46667. [Google Scholar] [CrossRef]
- Jiang, M.; Rindt, C.; Smeulders, D.M.J. Optimal planning of future district heating systems—A review. Energies 2022, 15, 7160. [Google Scholar] [CrossRef]
- Talebi, B.; Haghighat, F.; Tuohy, P.; Mirzaei, P.A. Optimization of a hybrid community district heating system integrated with thermal energy storage system. J. Energy Storage 2019, 23, 128–137. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Y.; Wang, Z.; Liu, X.; Liu, H.; Fu, Y. Explainable district heat load forecasting with active deep learning. Appl. Energy 2023, 350, 121753. [Google Scholar] [CrossRef]
- Van Dreven, J.; Boeva, V.; Abghari, S.; Grahn, H.; Al Koussa, J.; Motoasca, E. Intelligent approaches to fault detection and diagnosis in district heating systems. Electronics 2023, 12, 1448. [Google Scholar] [CrossRef]
- Weber, S.A.; Fischlschweiger, M.; Volta, D.; Geisler, J. Feature selection for specific prediction targets at the user level in district heating networks. Sci. Rep. 2025, 15, 29789. [Google Scholar] [CrossRef] [PubMed]
- Boutarene, A. Predicting Heat Load in District Heating Systems. Master’s Thesis, Stockholm University, Stockholm, Sweden, 2025. Available online: http://su.diva-portal.org/smash/get/diva2:1962718/FULLTEXT01.pdf (accessed on 15 October 2025).
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-line building energy optimization using deep reinforcement learning. arXiv 2017, arXiv:1707.05878. [Google Scholar] [CrossRef]
- Wei, T.; Wang, Y.; Hong, T. Deep reinforcement learning for building HVAC control. In Proceedings of the 4th ACM International Conference on Systems for Energy-Efficient Built Environments (BuildSys), Delft, The Netherlands, 8–9 November 2017. [Google Scholar] [CrossRef]
- Al Sayed, K.; Boodi, A.; Sadeghian Broujeny, R.; Beddiar, K. Reinforcement learning for HVAC control in intelligent buildings: A technical and conceptual review. J. Build. Eng. 2024, 95, 110085. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control using model predictive control—A review. Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Verheyen, J.; Thommessen, C.; Roes, J.; Hoster, H. Effects on the unit commitment of a district heating system due to seasonal aquifer thermal energy storage and solar thermal integration. Energies 2025, 18, 645. [Google Scholar] [CrossRef]
- Cui, M. District heating load prediction algorithm based on bidirectional long short-term memory network model. Energy 2022, 254, 124283. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Emadi, A. Lithium-ion battery pack robust state of charge estimation, cell inconsistency, and balancing: Review. IEEE Access 2021, 9, 50570–50582. [Google Scholar] [CrossRef]




| Notation | Description | Unit |
|---|---|---|
| t | Unit period for the planning | |
| T | End of the planning periods | |
| i | Production level | |
| K | Maximum number of production levels | |
| Heat production at time t | MWh | |
| If production level i is selected at t, set to 1. Otherwise, 0. | ||
| If the facility is operated at time t, it is set to 1. Otherwise, 0. | ||
| If the facility starts up at time t, it is set to 1. Otherwise, 0. | ||
| If the facility shuts down at time t, it is set to 1. Otherwise, 0. | ||
| Heat production volume at the production level i | MWh | |
| Heat inventory at the heat storage at time t | MWh | |
| Heat supply from external network at time t | MWh | |
| Heat sales to external network at time t | MWh | |
| Heat demand at time t | MWh | |
| Heat production cost at time t | USD/MWh | |
| Heat supply cost from external network at time t | USD/MWh | |
| Heat sales price to external network at time t | USD/MWh | |
| C | Heat inventory holding cost | USD/MWh |
| Min and Max capacity at heat production facility | MW | |
| Min and Max capacity at heat storage | MW | |
| Min operation time of the production facility | Hour | |
| Class weight for level in the weighted cross-entropy | ||
| Softmax probability that the model selects level at time |
| Categories | Descriptions | Number of Features |
|---|---|---|
| Inputs | , initial inventory at the beginning of time t | 1 |
| , heat production at time t − 1 | 1 | |
| heat demand data for the past 24 h | 24 | |
| , hourly production costs for the past 24 h | 24 | |
| Output | , target heat production level indicator at time t | i |
| Index | Number of Layer | Number of Head | Number of Top-k | Accuracy | Cost |
|---|---|---|---|---|---|
| A1 | 2 | 2 | 1 | 77.50% | 196,578.35 |
| A2 | 2 | 2 | 3 | 79.26% | 200,380.87 |
| A3 | 2 | 2 | 5 | 78.23% | 194,987.77 |
| A4 | 2 | 4 | 1 | 80.13% | 193,867.88 |
| A5 | 2 | 4 | 3 | 79.17% | 190,568.41 |
| A6 | 2 | 4 | 5 | 79.67% | 191,530.94 |
| A7 | 2 | 8 | 1 | 78.11% | 188,707.79 |
| A8 | 2 | 8 | 3 | 78.01% | 195,272.26 |
| A9 | 2 | 8 | 5 | 77.98% | 190,729.23 |
| A10 | 3 | 2 | 1 | 79.34% | 194,792.20 |
| A11 | 3 | 2 | 3 | 79.13% | 191,766.22 |
| A12 | 3 | 2 | 5 | 78.44% | 197,323.18 |
| A13 | 3 | 4 | 1 | 78.40% | 195,178.02 |
| A14 | 3 | 4 | 3 | 76.22% | 197,208.24 |
| A15 | 3 | 4 | 5 | 78.06% | 195,949.76 |
| A16 | 3 | 8 | 1 | 78.45% | 197,886.27 |
| A17 | 3 | 8 | 3 | 78.83% | 189,428.18 |
| A18 | 3 | 8 | 5 | 78.47% | 199,672.11 |
| A19 | 4 | 2 | 1 | 79.26% | 207,002.87 |
| A20 | 4 | 2 | 3 | 77.72% | 197,400.13 |
| A21 | 4 | 2 | 5 | 76.14% | 198,520.65 |
| A22 | 4 | 4 | 1 | 79.92% | 194,236.02 |
| A23 | 4 | 4 | 3 | 77.22% | 198,277.50 |
| A24 | 4 | 4 | 5 | 78.75% | 193,950.74 |
| A25 | 4 | 8 | 1 | 77.89% | 198,959.16 |
| A26 | 4 | 8 | 3 | 78.99% | 195,893.00 |
| A27 | 4 | 8 | 5 | 77.98% | 190,729.23 |
| Dataset | Total Operation Cost (USD) | Accuracy | |||
|---|---|---|---|---|---|
| MIP | DNN | MATN | DNN | MATN | |
| 1 | 198,658.39 | 220,812.98 | 209,543.83 | 76.79% | 80.00% |
| 2 | 184,608.80 | 203,229.94 | 189,407.38 | 77.00% | 80.58% |
| 3 | 165,845.17 | 179,442.22 | 167,510.09 | 76.89% | 82.25% |
| 4 | 196,220.41 | 216,606.60 | 206,143.42 | 77.26% | 78.42% |
| 5 | 199,945.69 | 215,901.00 | 203,376.74 | 76.51% | 79.25% |
| 6 | 170,035.34 | 184,604.26 | 172,773.43 | 76.60% | 81.00% |
| 7 | 160,868.08 | 173,123.14 | 163,521.72 | 76.95% | 83.33% |
| 8 | 190,647.88 | 211,028.40 | 194,658.41 | 76.99% | 82.08% |
| 9 | 195,720.11 | 211,283.42 | 203,182.63 | 77.63% | 78.33% |
| 10 | 163,526.79 | 176,477.69 | 164,288.45 | 68.50% | 82.08% |
| Avg | 182,607.67 | 199,250.96 | 187,440.61 | 77.72% | 80.73% |
| Data Set | MATN | DNN | ||||
|---|---|---|---|---|---|---|
| H = 4 | H = 12 | H = 24 | H = 4 | H = 12 | H = 24 | |
| 1 | 87.50% | 73.33% | 82.92% | 80.00% | 74.16% | 72.91% |
| 2 | 65.00% | 84.17% | 82.92% | 60.00% | 69.16% | 72.91% |
| 3 | 87.50% | 78.33% | 82.92% | 80.00% | 70.00% | 80.83% |
| 4 | 82.50% | 77.50% | 83.33% | 67.50% | 86.66% | 73.33% |
| 5 | 77.50% | 76.67% | 81.25% | 75.00% | 66.67% | 73.33% |
| 6 | 70.00% | 90.00% | 82.08% | 32.50% | 75.83% | 81.66% |
| 7 | 82.50% | 84.17% | 83.75% | 70.00% | 67.50% | 79.58% |
| 8 | 90.00% | 92.50% | 84.58% | 65.00% | 80.83% | 73.75% |
| 9 | 80.00% | 80.00% | 77.50% | 42.50% | 57.5% | 71.25% |
| 10 | 82.50% | 84.17% | 82.50% | 57.50% | 77.5% | 78.75% |
| Avg | 80.50% | 82.08% | 82.38% | 63.00% | 72.58% | 75.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lee, S.; Park, I.-B.; Kim, K. A Multi-Head Attention-Based TimesNet for Heat Production Planning Under Unknown Future Demands. Energies 2025, 18, 5963. https://doi.org/10.3390/en18225963
Kim J, Lee S, Park I-B, Kim K. A Multi-Head Attention-Based TimesNet for Heat Production Planning Under Unknown Future Demands. Energies. 2025; 18(22):5963. https://doi.org/10.3390/en18225963
Chicago/Turabian StyleKim, Jahun, Sangjun Lee, In-Beom Park, and Kwanho Kim. 2025. "A Multi-Head Attention-Based TimesNet for Heat Production Planning Under Unknown Future Demands" Energies 18, no. 22: 5963. https://doi.org/10.3390/en18225963
APA StyleKim, J., Lee, S., Park, I.-B., & Kim, K. (2025). A Multi-Head Attention-Based TimesNet for Heat Production Planning Under Unknown Future Demands. Energies, 18(22), 5963. https://doi.org/10.3390/en18225963






