Multiphase Flow and Heat Transfer of a Mine Return Air-Gravity Heat Pipe: Numerical Simulation and Experimental Validation
Abstract
1. Introduction
2. Experimental Setup
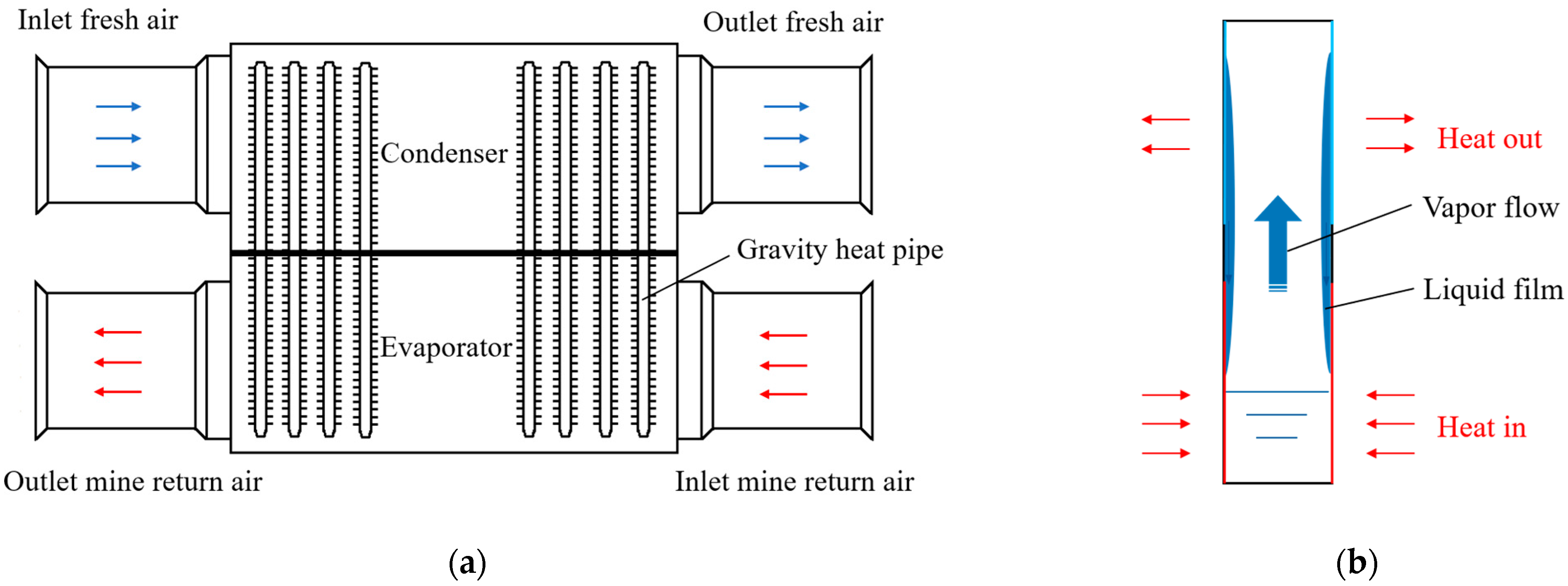
2.1. Description of Mine Return Air-Gravity Heat Pipe
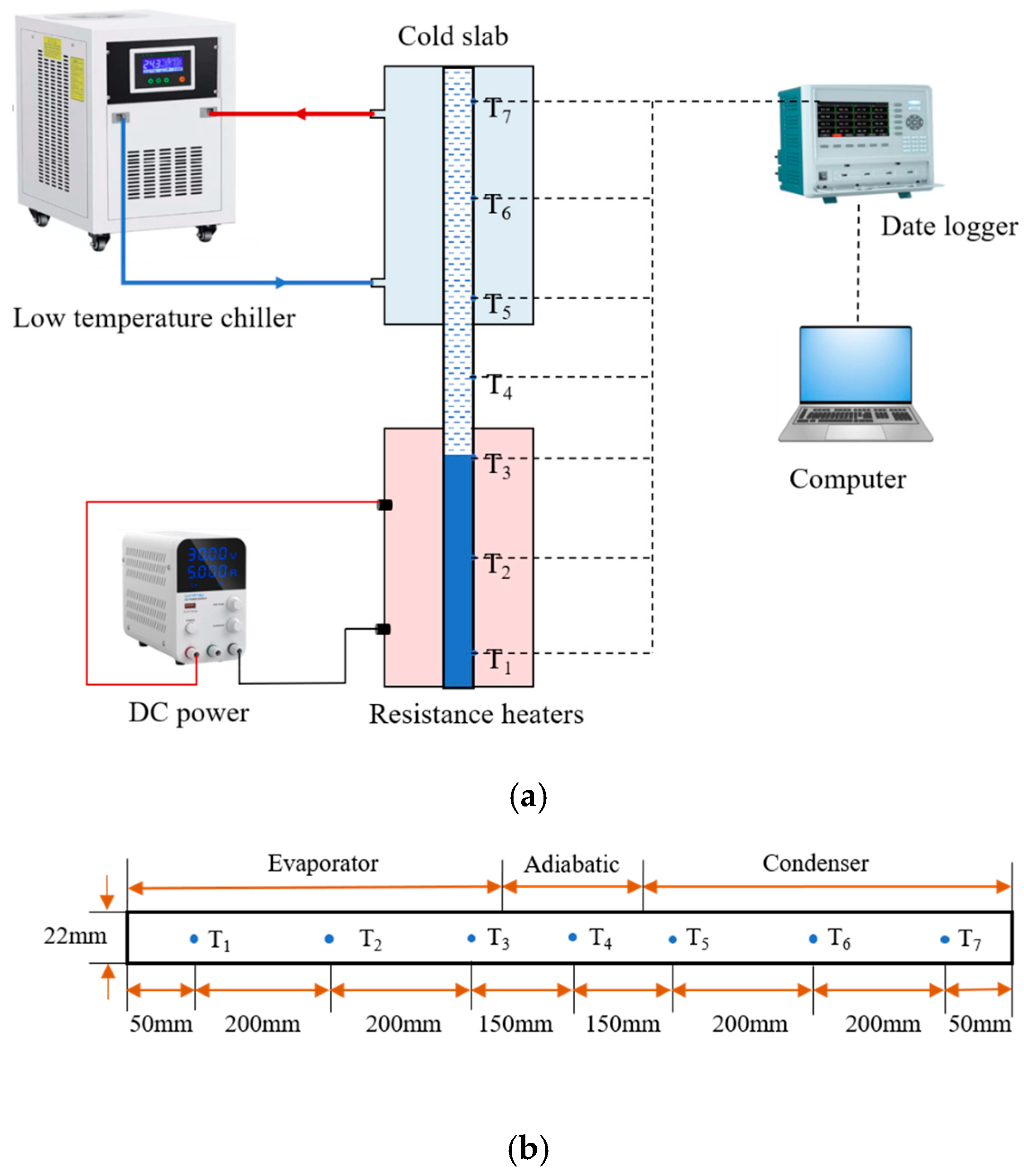
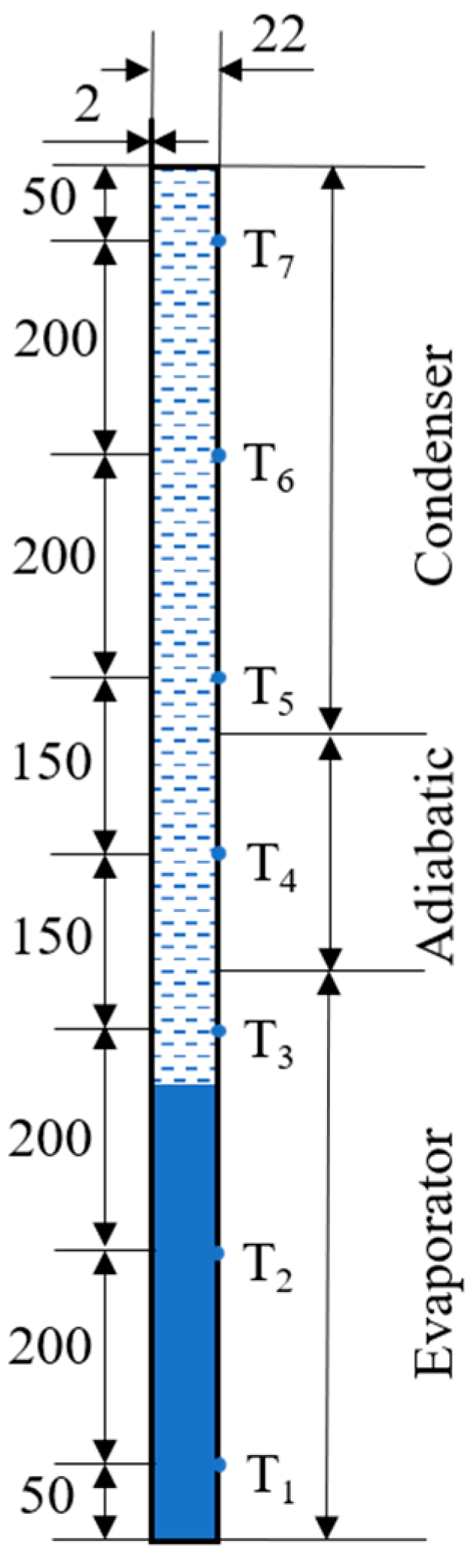
2.2. Experimental Apparatus and Procedure
2.3. Experimental Data Reduction
3. Numerical Simulation
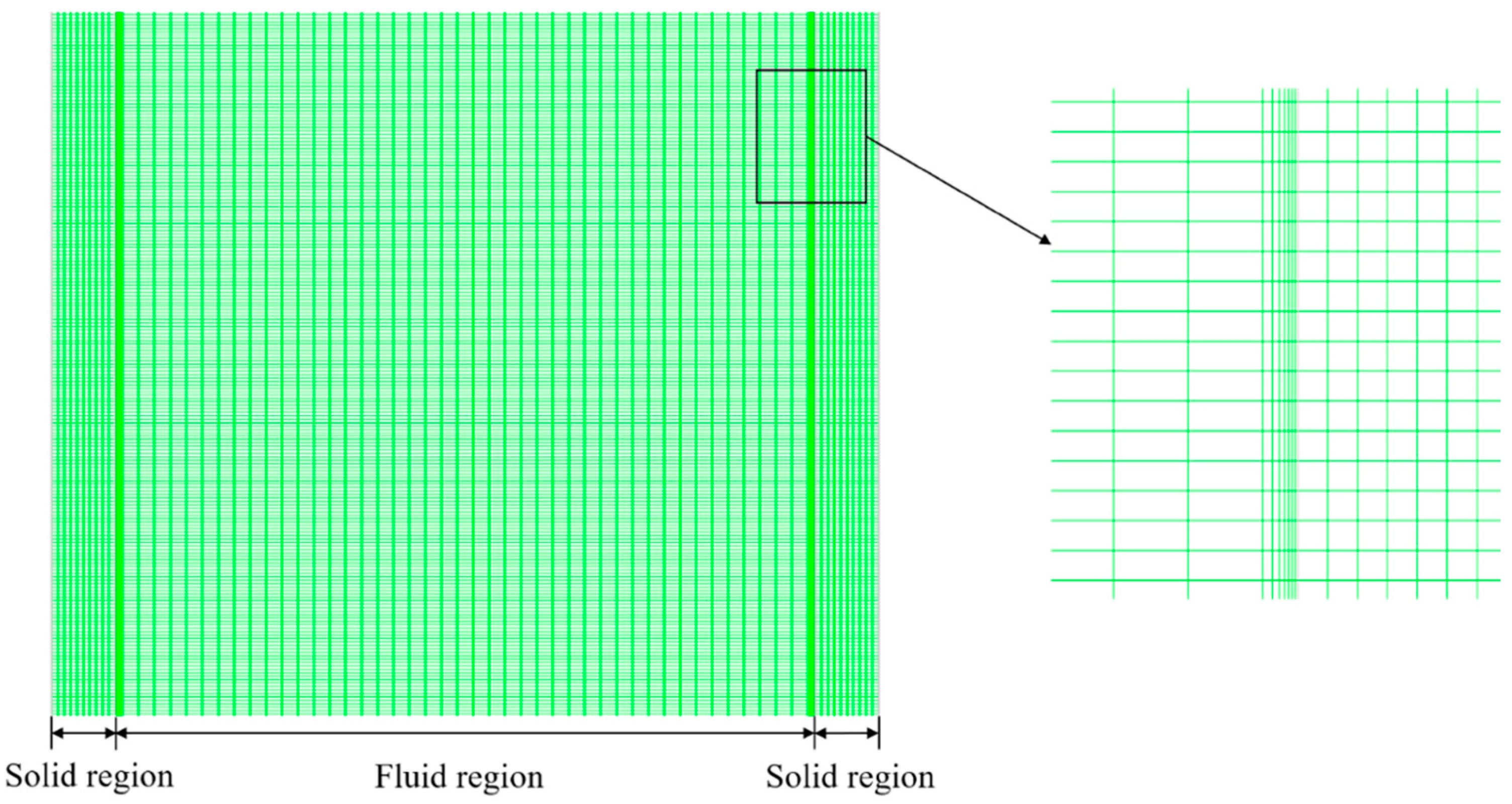
3.1. Physical Model and Computational Mesh
3.2. Governing Equations
3.3. Mass and Heat Transfer
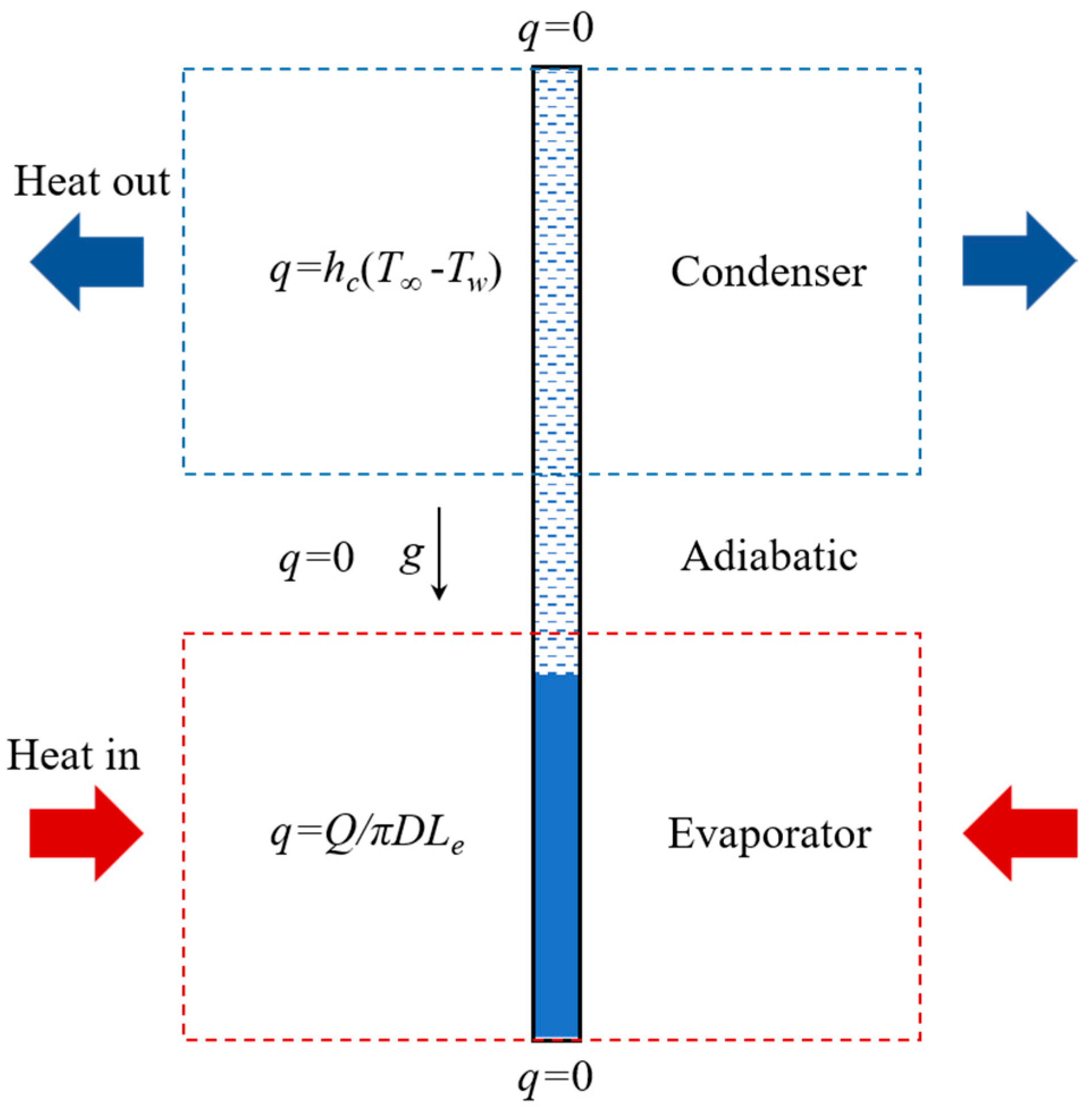
3.4. Boundary and Operating Conditions
4. Results and Discussion
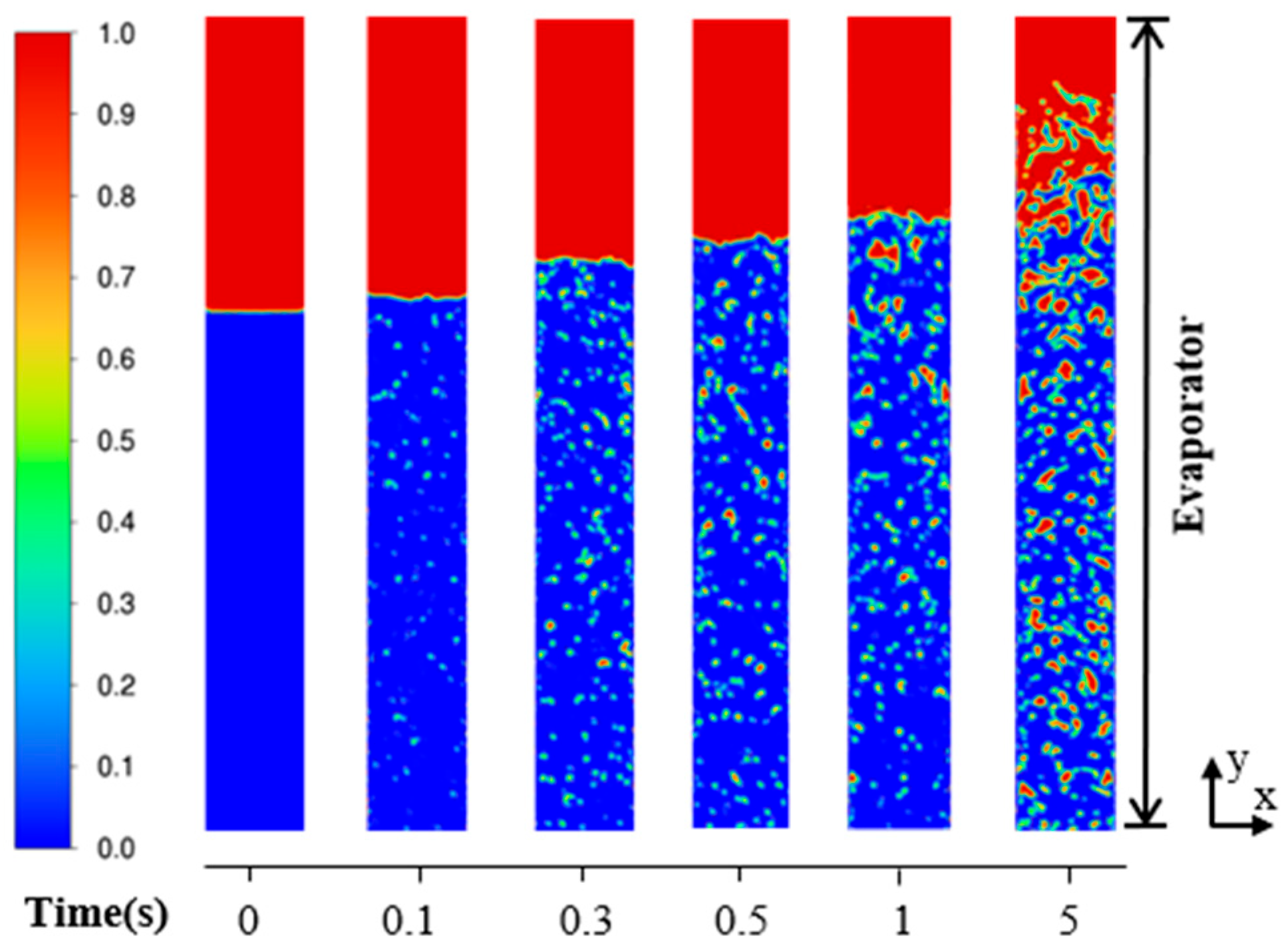
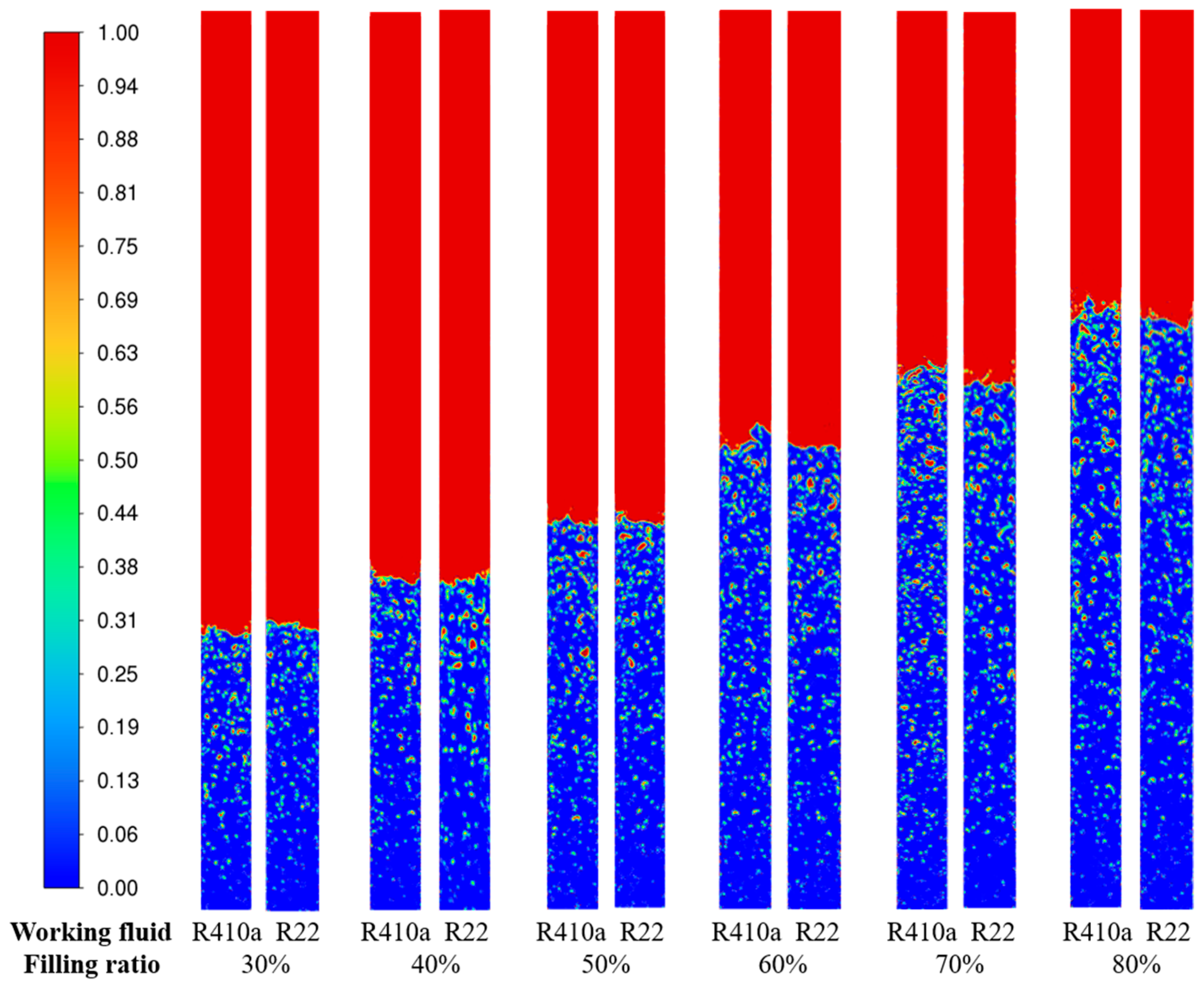
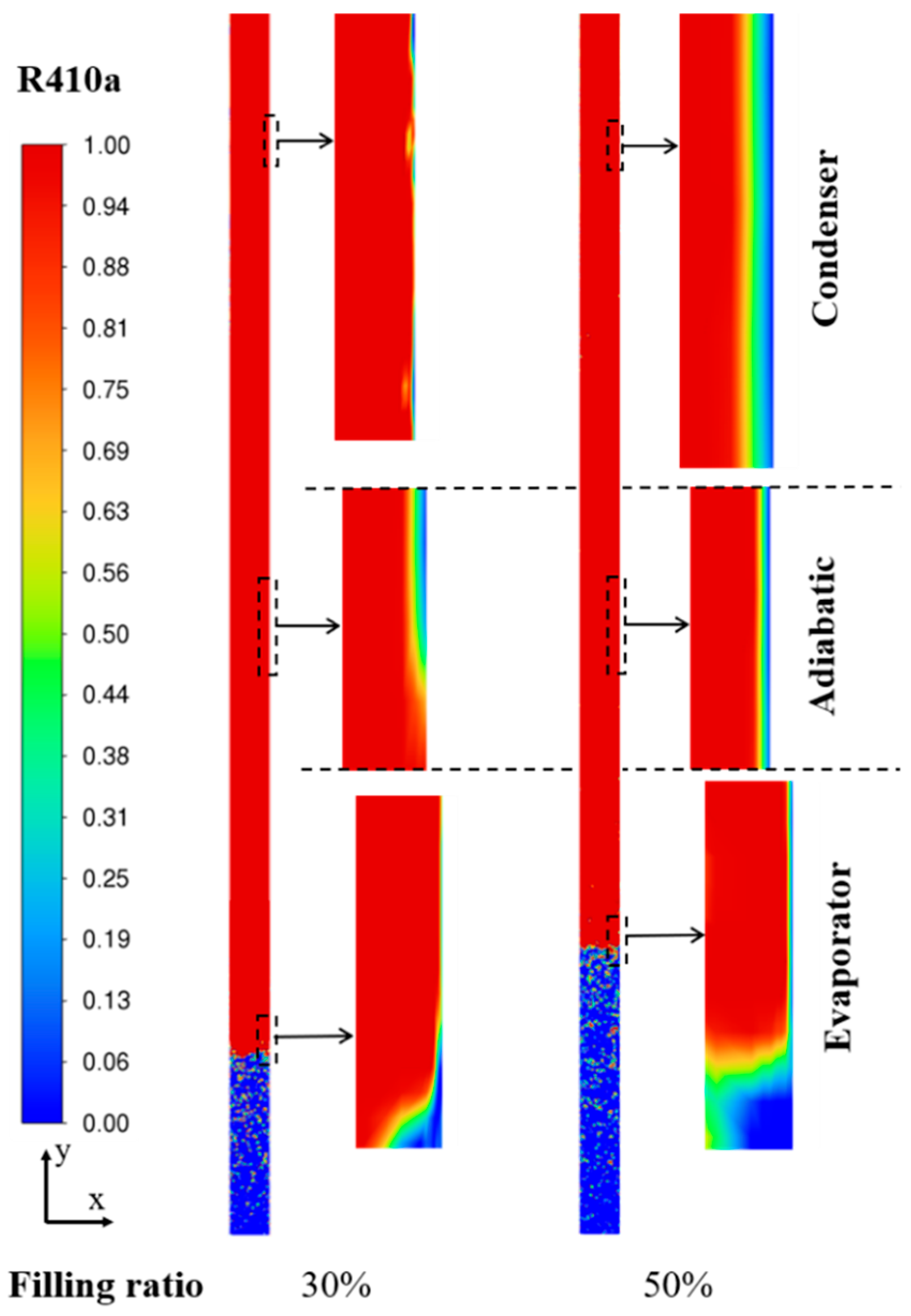
4.1. Two-Phase Flow Pattern Visualization
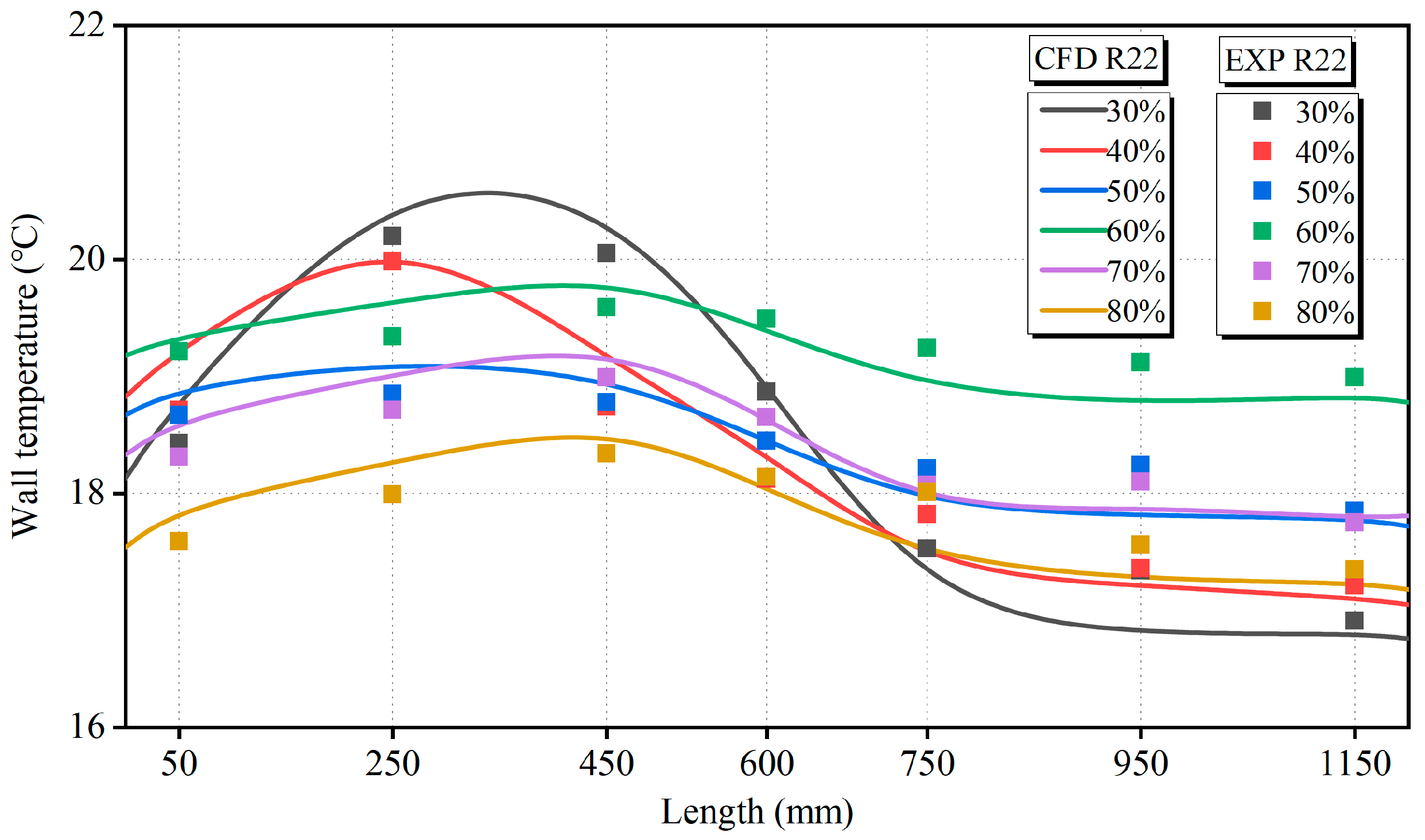
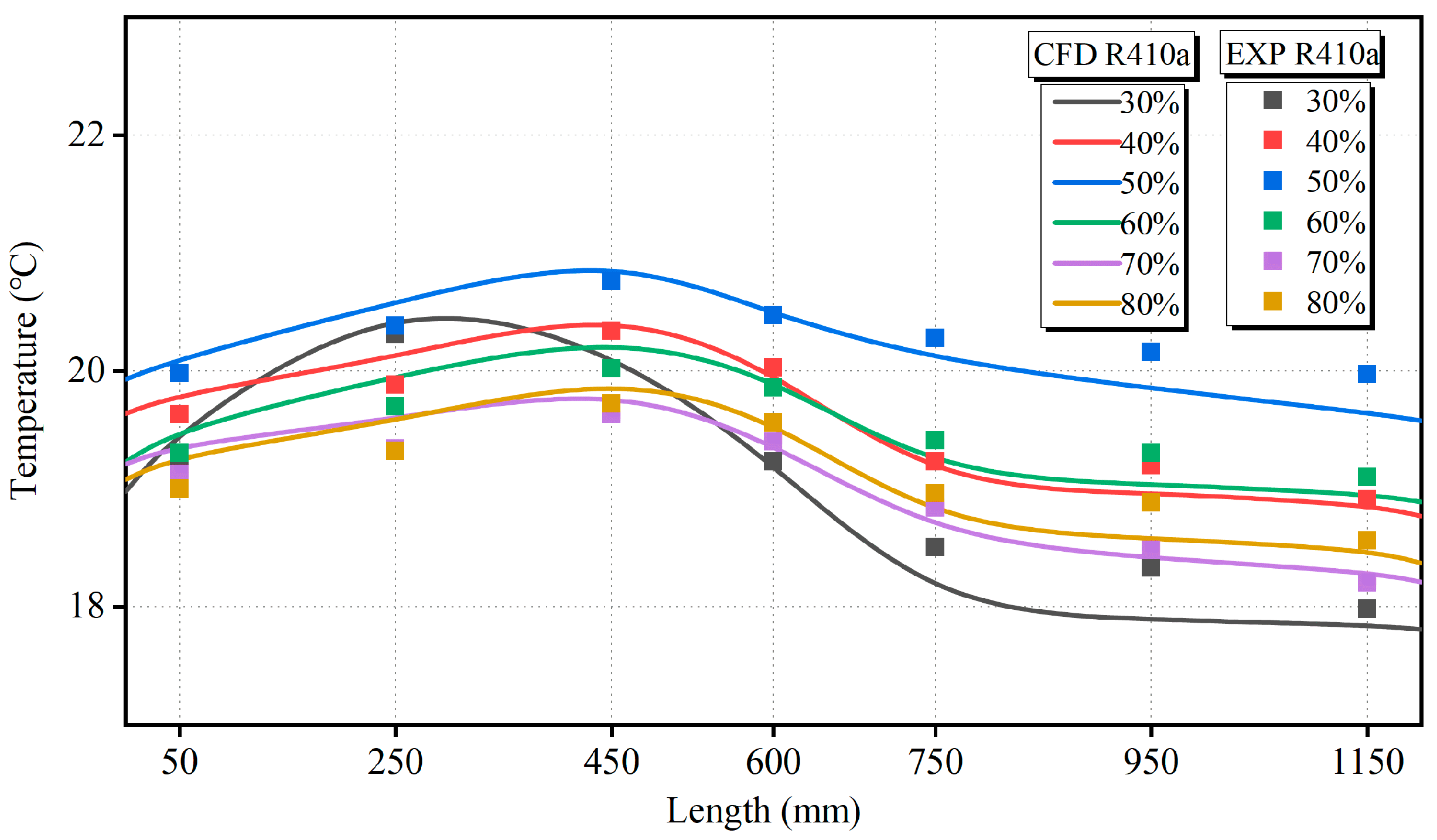
4.2. Heat Transfer Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaplunov, D.R.; Ryl’nikova, M.V.; Radchenko, D.N. Utilization of renewable energy sources in hard mineral mining. J. Min. Sci. 2015, 51, 111–117. [Google Scholar] [CrossRef]
- Gui, X. Research on numerical simulation of wind kinetic energy recovery power generation at mine return air Wellhead. Arab. J. Sci. Eng. 2021, 46, 12743–12754. [Google Scholar] [CrossRef]
- Baidya, D.; de Brito, M.A.R.; Sasmito, A.P.; Ghoreishi-Madiseh, S.A. Diesel generator exhaust heat recovery fully-coupled with intake air heating for off-grid mining operations: An experimental, numerical, and analytical evaluation. Int. J. Min. Sci. Technol. 2022, 32, 155–169. [Google Scholar] [CrossRef]
- de Brito, M.A.R.; Baidya, D.; Ghoreishi-Madiseh, S.A. Techno-economic feasibility assessment of a diesel exhaust heat recovery system to preheat mine intake air in remote cold climate regions. Int. J. Min. Sci. Technol. 2020, 30, 517–523. [Google Scholar] [CrossRef]
- Sbarba, H.D.; Fytas, K.; Paraszczak, J. Economics of exhaust air heat recovery systems for mine ventilation. Int. J. Min. Reclam. Environ. 2012, 26, 185–198. [Google Scholar] [CrossRef]
- Wan, L.-R.; Li, J.-L.; Wang, L.; Zhou, G.-Y. Research and application of the heat energy recycling technology in mine return air. In Proceedings of the 2012 International Conference on Communication, Electronics and Automation Engineering, Xi’an, China, 23–25 August 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 247–253. [Google Scholar]
- Faghri, A. Heat pipes: Review, opportunities and challenges. Front. Heat Pipes (FHP) 2014, 5. [Google Scholar] [CrossRef]
- Anand, R.; Li, A.; Huang, W.; Chen, J.; Li, Z.; Ma, Q.; Jiang, F. Super-long gravity heat pipe for geothermal energy exploitation-A comprehensive review. Renew. Sustain. Energy Rev. 2024, 193, 114286. [Google Scholar] [CrossRef]
- Lu, W.; Liu, Y.; Zhang, L.; Liu, F.; Wu, J.; Zhan, Z.; Zhang, X.; Zhang, H. Flow and heat transfer characteristics of a new coke oven gas ascension pipe heat exchanger: Experimental validation and numerical study. Therm. Sci. Eng. Prog. 2025, 60, 103386. [Google Scholar] [CrossRef]
- Peng, H.; Jia, X.L. Experimental study on heat energy recovery and utilization of coal gangue hill based on gravity heat pipe. Energy Rep. 2022, 8, 220–229. [Google Scholar] [CrossRef]
- Wang, G.; Bi, J.; Fan, Y.; Zhu, L.; Zhang, F.; Feng, D. Settlement characteristic of warm permafrost embankment with two-phase closed thermosyphons in Daxing’anling Mountains region. Sustainability 2022, 14, 12272. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Olabi, A.; Alami, A.H.; Al Radi, M.; Zwayyed, F.; Salamah, T.; Wilberforce, T.; Abdelkareem, M.A. Numerical simulation of heat pipes in different applications. Int. J. Thermofluids 2022, 16, 100199. [Google Scholar] [CrossRef]
- Li, Z.; Huang, W.; Chen, J.; Cen, J.; Cao, W.; Li, F.; Jiang, F. An enhanced super-long gravity heat pipe geothermal system: Conceptual design and numerical study. Energy 2023, 267, 126524. [Google Scholar] [CrossRef]
- Zeng, J.-L.; Liu, X.; Su, C.-Q.; Wang, Y.-P.; Xiong, X. Numerical investigation of a geothermal thermoelectric generator using gravity heat pipe structure. Energy Rep. 2023, 9, 1237–1246. [Google Scholar] [CrossRef]
- Lu, X.; Liu, J.; Tong, X.; Dai, R.; Xiao, Y.; Deng, J. Experimental investigation on thermal performance of gravity heat pipe with different pipe configurations. Case Stud. Therm. Eng. 2025, 65, 105695. [Google Scholar] [CrossRef]
- Chen, J.; Huang, W.; Cen, J.; Cao, W.; Li, Z.; Li, F.; Jiang, F. Heat extraction from hot dry rock by super-long gravity heat pipe: Selection of working fluid. Energy 2022, 255, 124531. [Google Scholar] [CrossRef]
- Chen, J.; Cen, J.; Huang, W.; Jiang, F. Multiphase flow and heat transfer characteristics of an extra-long gravity-assisted heat pipe: An experimental study. Int. J. Heat Mass Transf. 2021, 164, 120564. [Google Scholar] [CrossRef]
- Karpenko, M.; Bogdevičius, M. Investigation of hydrodynamic processes in the system—“pipeline-fittings”. In Proceedings of the International Conference TRANSBALTICA: Transportation Science and Technology, Vilnius, Lithuania, 18–19 September 2025; Springer International Publishing: Cham, Switzerland, 2019; pp. 331–340. [Google Scholar]
- Fadhl, B.; Wrobel, L.C.; Jouhara, H. CFD modelling of a two-phase closed thermosyphon charged with R134a and R404a. Appl. Therm. Eng. 2015, 78, 482–490. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, G.; Xu, H.; Zhou, J. Numerical investigation of effect of fill ratio and inclination angle on a U-shaped elliptical gravity heat pipe thermal performance. Therm. Sci. 2025, 23. [Google Scholar] [CrossRef]
- Jafari, D.; Filippeschi, S.; Franco, A.; Di Marco, P. Unsteady experimental and numerical analysis of a two-phase closed thermosyphon at different filling ratios. Exp. Therm. Fluid Sci. 2017, 81, 164–174. [Google Scholar] [CrossRef]
- Yao, H.; Yue, C.; Wang, Y.; Chen, H.; Zhu, Y. Numerical investigation of the heat and mass transfer performance of a two-phase closed thermosiphon based on a modified CFD model. Case Stud. Therm. Eng. 2021, 26, 101155. [Google Scholar] [CrossRef]
- Niu, Y. Research on thermal energy recycling utilization in high temperature mines. Procedia Eng. 2015, 121, 389–395. [Google Scholar] [CrossRef][Green Version]
- Kalantari, H.; Amiri, L.; Ghoreishi-Madiseh, S.A. Analysis of the performance of direct contact heat exchange systems for application in mine waste heat recovery. Int. J. Energy Res. 2022, 46, 290–307. [Google Scholar] [CrossRef]
- Ghoreishi-Madiseh, S.A.; Kalantari, H.; Kuyuk, A.F.; Sasmito, A.P. A new model to analyze performance of mine exhaust heat recovery systems with coupled heat exchangers. Appl. Energy 2019, 256, 113922. [Google Scholar] [CrossRef]
- Ran, Y.; Peng, J.; Tian, X.; Luo, D.; Zhao, J.; Pei, P. Technologies for heat hazard governance and thermal energy recovery in deep mines. Energies 2024, 17, 1369. [Google Scholar] [CrossRef]
- Bao, L.; Wang, J.; Wang, J.; Yu, Z. The heat recovery technologies of mine waste heat sources. World J. Eng. 2017, 14, 19–26. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhao, X.; Xue, G.; Dong, Z. Study on Heat Transfer Performance and Parameter Improvement of Gravity-Assisted Heat Pipe Heat Transfer Unit for Waste Heat Recovery from Mine Return Air. Energies 2023, 16, 6148. [Google Scholar] [CrossRef]
- Zhai, Y.; Ling, Z.; Zhao, X.; Dong, Z. Effects of Structure Parameters of Gravity-Type Heat Pipe on Heat Transfer Characteristics for Waste Heat Recovery from Mine Return Air. Energies 2024, 17, 6495. [Google Scholar] [CrossRef]
- Yang, H.; Yang, R.; Huo, Y. Utilization of low-temperature waste heat from mine return air based on separated heat pipe technology. J. Min. Sci. Technol. 2024, 9, 828–836. [Google Scholar]
- De Schepper, S.C.K.; Heynderickx, G.J.; Marin, G.B. Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker. Comput. Chem. Eng. 2009, 33, 122–132. [Google Scholar] [CrossRef]
- Fadhl, B.; Wrobel, L.C.; Jouhara, H. Numerical modelling of the temperature distribution in a two-phase closed thermosyphon. Appl. Therm. Eng. 2013, 60, 122–131. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties–REFPROP. NIST Stand. Ref. Database 2002, 23, v7. [Google Scholar]

| Mesh Size (Cells) | 245,664 | 327,552 | 436,740 | 545,925 |
|---|---|---|---|---|
| Te | 292.71 | 292.15 | 292.21 | 292.19 |
| Tad | 292.02 | 291.84 | 291.92 | 291.88 |
| Tc | 290.41 | 290.67 | 290.69 | 290.68 |
| Working Fluid | Density (ρl) | |||
|---|---|---|---|---|
| A0 | A1 | A2 | A3 | |
| R22 | 3728.422 | −21.669 | 0.07284 | −9.63 × 10−4 |
| R410a | 4649.71897 | −37.21881 | 0.14793 | −2.13 × 10−4 |
| Working Fluid | Surface Tension (σ) | |||
|---|---|---|---|---|
| B0 | B1 | B2 | B3 | |
| R22 | 0.0118 | −1.5175 × 10−5 | 1.5708 × 10−7 | 0 |
| R410a | 0.5191 | −6.72 × 10−5 | −6.52 × 10−7 | 1.18 × 10−9 |
| Properties | Working Fluid | |||
|---|---|---|---|---|
| R22-Liquid | R22-Vapor | R410a-Liquid | R410a-Vapor | |
| Density (kg/m3) | ρl | 34.36 | ρl | 49.5 |
| Thermal conductivity (W/m K) | 0.0875 | 0.0106 | 0.0942 | 0.0142 |
| Viscosity (kg/m s) | 2.11 × 10−4 | 1.24 × 10−5 | 1.95 × 10−4 | 1.41 × 10−5 |
| Specific heat (kJ/kg K) | 1.3618 | 0.8763 | 1.6843 | 1.1285 |
| Latent heat (kJ/kg) | 191.3 | 204.7 | ||
| Critical temperature (K) | 369.3 | 343.61 | ||
| Critical pressure (kPa) | 4990 | 4770 | ||
| Molecular weight (g/mol) | 86.47 | 72.59 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.; Meng, G.; Wang, A.; Cheng, X.; Yang, J. Multiphase Flow and Heat Transfer of a Mine Return Air-Gravity Heat Pipe: Numerical Simulation and Experimental Validation. Energies 2025, 18, 5942. https://doi.org/10.3390/en18225942
Song B, Meng G, Wang A, Cheng X, Yang J. Multiphase Flow and Heat Transfer of a Mine Return Air-Gravity Heat Pipe: Numerical Simulation and Experimental Validation. Energies. 2025; 18(22):5942. https://doi.org/10.3390/en18225942
Chicago/Turabian StyleSong, Binglin, Guoying Meng, Aiming Wang, Xiaohan Cheng, and Jie Yang. 2025. "Multiphase Flow and Heat Transfer of a Mine Return Air-Gravity Heat Pipe: Numerical Simulation and Experimental Validation" Energies 18, no. 22: 5942. https://doi.org/10.3390/en18225942
APA StyleSong, B., Meng, G., Wang, A., Cheng, X., & Yang, J. (2025). Multiphase Flow and Heat Transfer of a Mine Return Air-Gravity Heat Pipe: Numerical Simulation and Experimental Validation. Energies, 18(22), 5942. https://doi.org/10.3390/en18225942






