A Hybrid Strategy Integrating Artificial Neural Networks for Enhanced Energy Production Optimization
Abstract
1. Introduction
- Development of an improved hybrid control strategy that integrates an ANN/PE with a deep reinforcement learning framework to enhance the performance of photovoltaic energy optimization.
- Formulation of a systematic equilibrium-point selection method for ANN training, enabling accurate representation of the nonlinear behavior of photovoltaic systems and improving the network’s generalization capability under variable operating conditions.
- Design and validation of an ANN/PE-based MPPT controller capable of achieving faster convergence and reduced oscillations compared to the conventional Perturb and Observe (PO) method when subjected to variable irradiance profiles.
- Comprehensive comparative analysis between the proposed ANN/PE controller and classical MPPT techniques through detailed simulations, demonstrating superior tracking efficiency, dynamic stability, and adaptability to environmental changes.
2. Literature Review Energy Production Optimization
3. Optimization of Energy Production by Artificial Neural Network
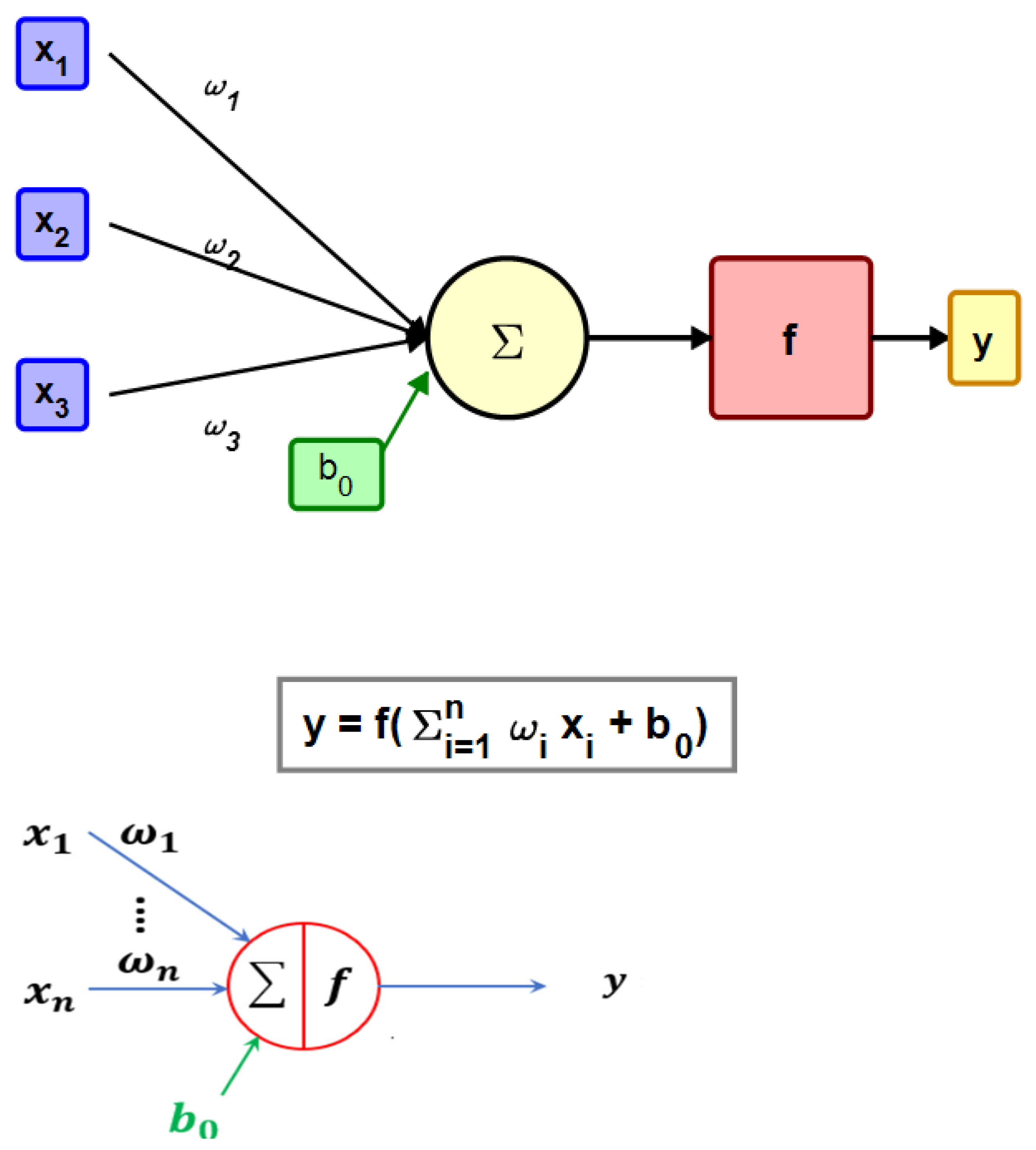
3.1. Artificial Neural Network Fundamentals
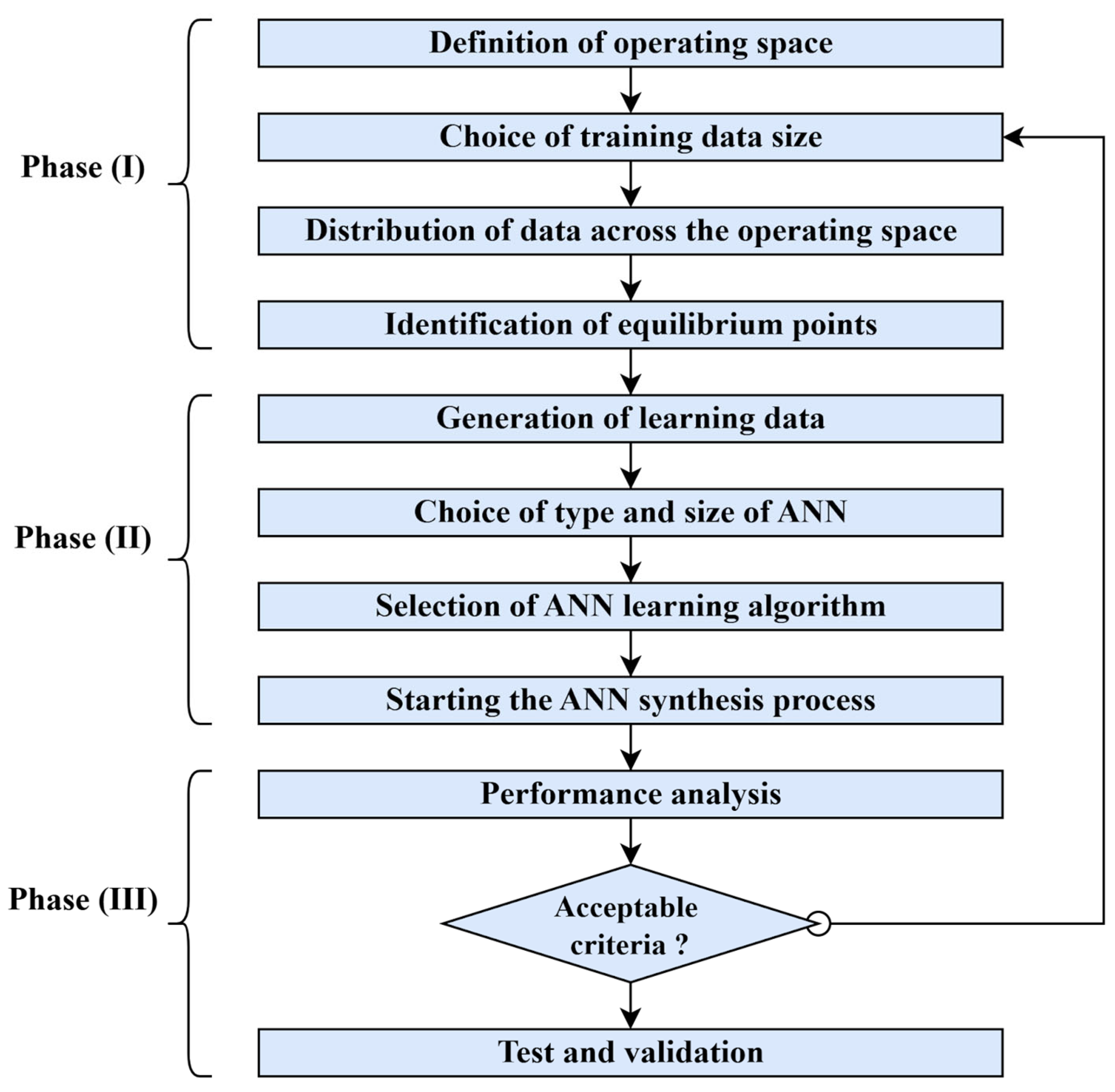
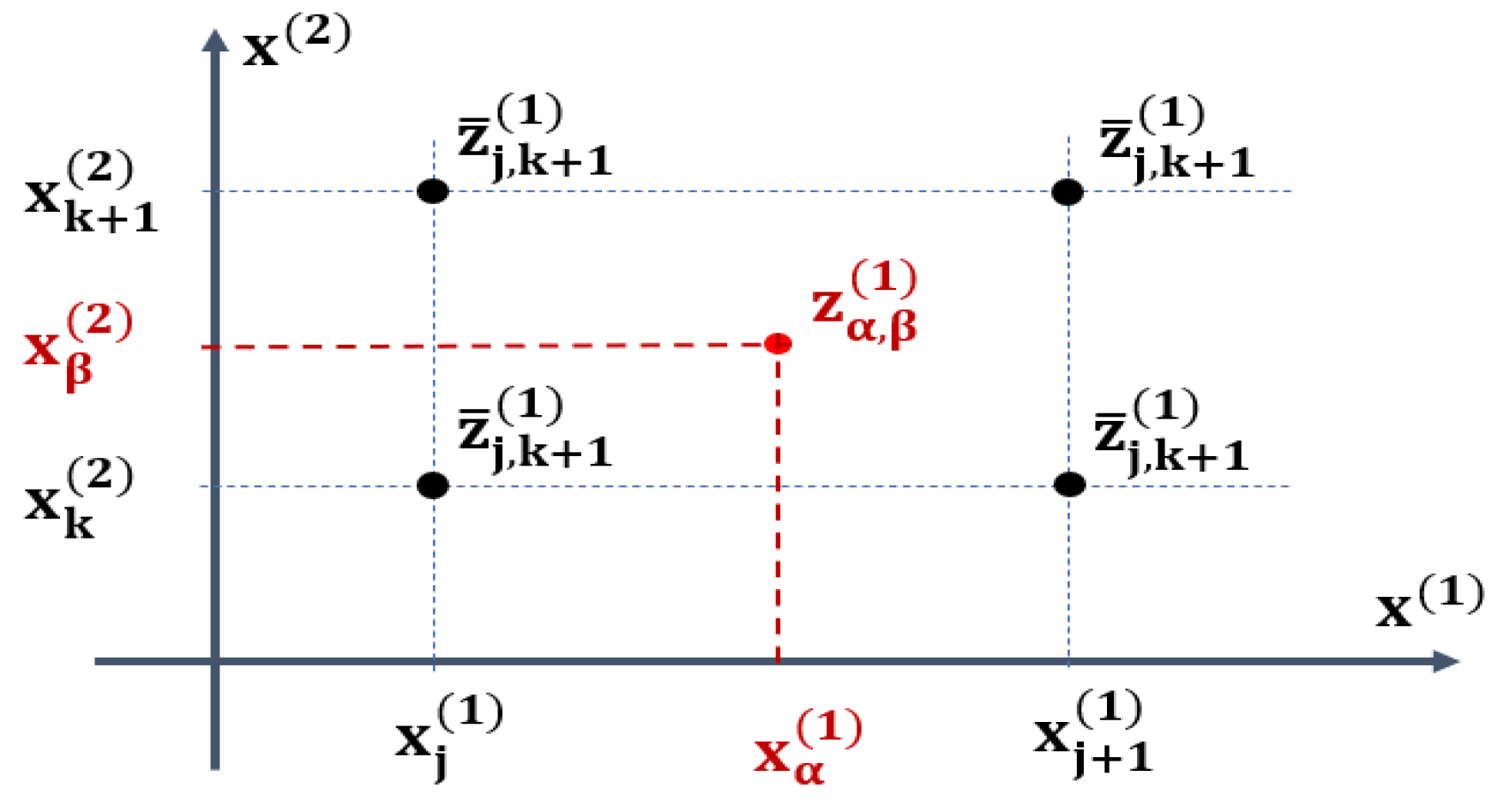
3.2. Procedure for Designing an ANN/PE Model
3.3. ANN/PE Network Structure and Training Process
4. Optimization of the Production of a Photovoltaic System by the ANN/PE Approach
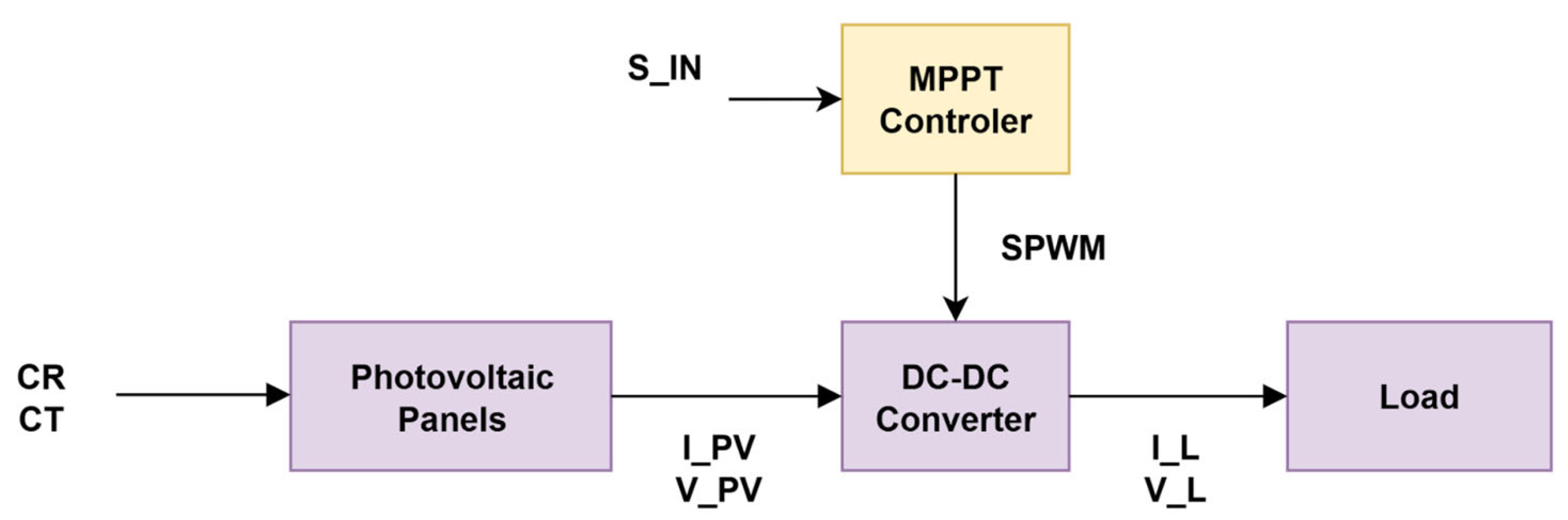
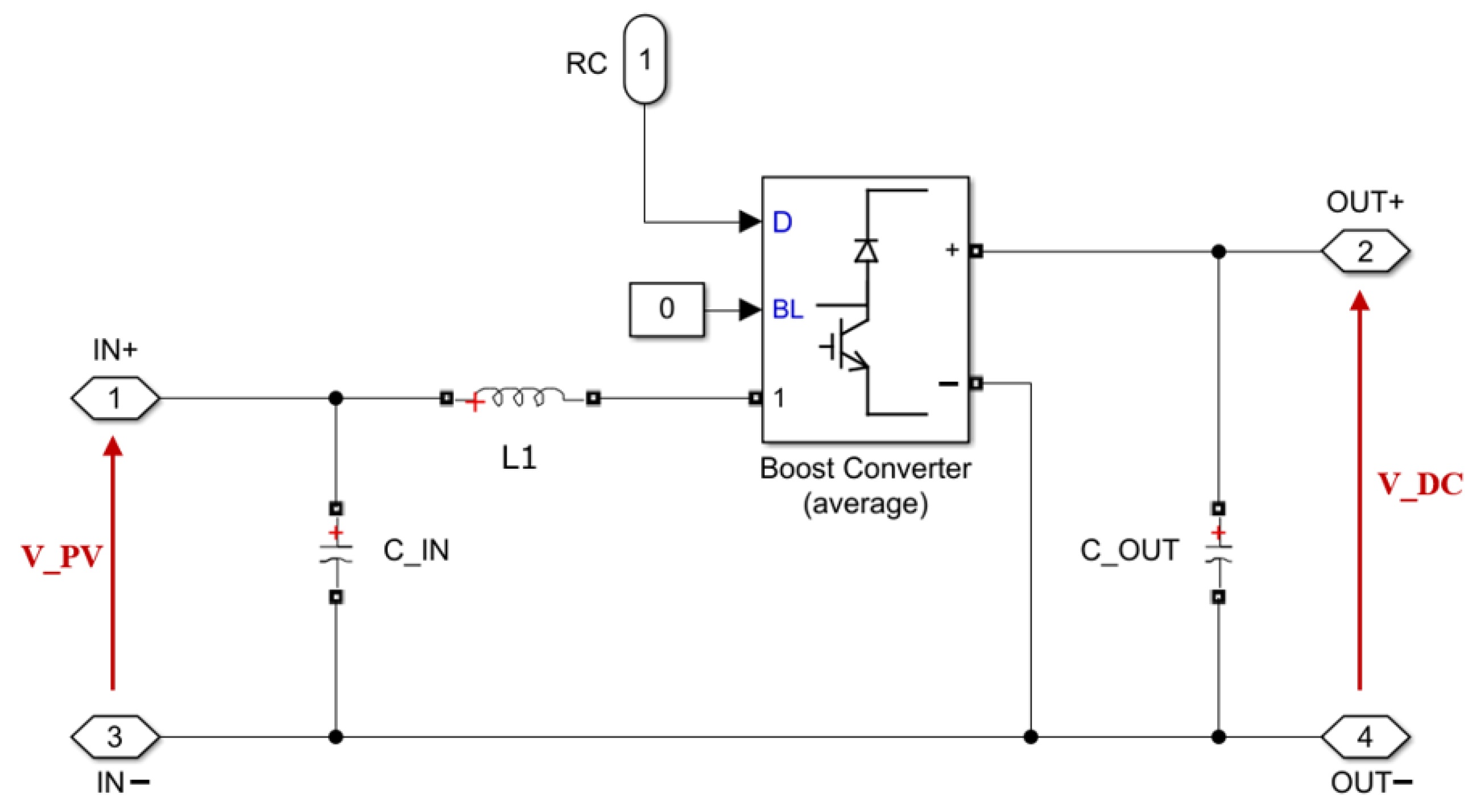
5. ANN/PE Controller Implementation for Isolated PV Systems
5.1. Synthesis of an ANN/PE Controller Based on Experimental Data
5.2. Synthesis of an ANN/PE Controller Based on Analytical Data
5.3. Comparative Studies of Two Approaches ANN/PE and MPPT/PO for the Control of an SPVI
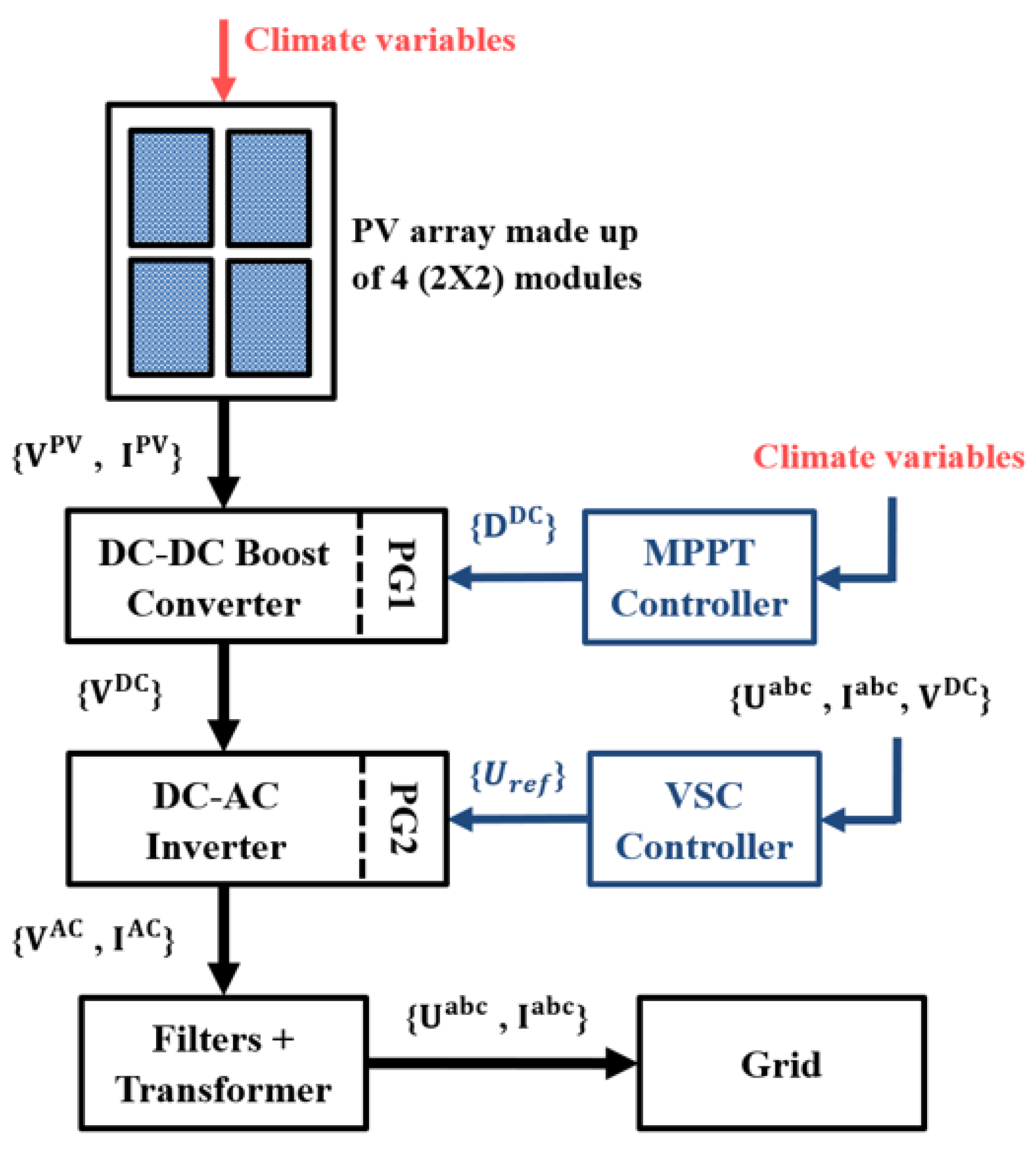
6. Hybrid Control of a Grid-Connected PV System
6.1. Hierarchical Control Structure Design
6.2. MPPT/PO and ANN/PE Sub-Controller Implementation
6.3. Hybrid Control Using Artificial Neural Networks for a Grid-Connected Photovoltaic System
6.4. Design of the ANN/PE Sub-Controller Using Supervised Learning
6.5. Design of the RL Main Controller Using Deep Reinforcement Learning
| Algorithm 1: Learning Scenario Generation for DRL Agent |
| Input: CRmin, CRmax, L |
| Output: Z_CR, CT1, CT2, CT3, CT4 |
| Initialization: ΔCR ← (CRmax − CRmin)/L |
| for i ← 1 to L do |
| CRi ← CRmin + (i −1) … ΔCR; |
| Z_CR[i] ← CRi; |
| CT1 ← random(5, 50); |
| CT2 ← CT1 + random(1, 5); CT3 ← CT2 + random(1, 5); |
| CT4 ← CT3 + random(1, 5); |
| end |
7. Discussion of Limitations and Practical Considerations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Komarova, A.V.; Filimonova, I.V.; Kartashevich, A.A. Energy consumption of the countries in the context of economic development and energy transition. Energy Rep. 2022, 8, 1309–1323. [Google Scholar] [CrossRef]
- Bazán Navarro, C.E.; Álvarez-Quiroz, V.J.; Sampi, J.; Arana Sánchez, A.A. Does economic growth promote electric power consumption? Implications for electricity conservation, expansive, and security policies. Electr. J. 2023, 36, 107164. [Google Scholar] [CrossRef]
- Bastida-Molina, P.; Hurtado-Pérez, E.; Moros Gómez, M.C.; Cárcel-Carrasco, J.; Pérez-Navarro, Á. Energy sustainability evolution in the Mediterranean countries and synergies from a global energy scenario for the area. Energy 2022, 252, 124045. [Google Scholar] [CrossRef]
- Smadi, T.A.; Handam, A.; Gaeid, K.S.; Al-Smadi, A.; Al-Husban, Y.; Khalid, A.S. Artificial intelligent control of energy management PV system. Results Control Optim. 2024, 14, 100356. [Google Scholar] [CrossRef]
- Wu, Z.; Adebayo, T.S.; Alola, A.A. Renewable energy intensity and efficiency of fossil energy fuels in the Nordics: How environmentally efficient is the energy mix? J. Clean. Prod. 2024, 438, 140824. [Google Scholar] [CrossRef]
- Merchán, R.P.; Santos, M.J.; Medina, A.; Calvo Hernández, A. High temperature central tower plants for concentrated solar power: 2021 overview. Renew. Sustain. Energy Rev. 2022, 155, 111891. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, L.; Gong, X.; Zhong, X.; Yin, Y. A genetic-simulated annealing algorithm for stochastic seru scheduling problem with deterioration and learning effect. J. Ind. Prod. Eng. 2023, 40, 163–177. [Google Scholar] [CrossRef]
- Trzmiel, G.; Jajczyk, J.; Szulta, J.; Chamier-Gliszczynski, N.; Woźniak, W. Modelling of Selected Algorithms for Maximum Power Point Tracking in Photovoltaic Panels. Energies 2025, 18, 5223. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Nazir, M.S.; Tao, H.; Cao, S.; Ji, R.; Jiang, M.; Yao, D.L. Integration of energy storage system and renewable energy sources based on artificial intelligence: An overview. J. Energy Storage 2021, 40, 102811. [Google Scholar] [CrossRef]
- Heydari, A.; Nezhad, M.M.; Keynia, F.; Fekih, A.; Shahsavari, N.; Garcia, D.A.; Piras, G. A combined multi-objective intelligent optimization approach considering techno-economic and reliability factors for hybrid-renewable microgrid systems. J. Clean. Prod. 2023, 383, 135428. [Google Scholar] [CrossRef]
- Neha, A.; Mukesh, P.; Seema, S. Multi objective optimization through experimental technical investigation of a green hydrogen production system. Environ. Dev. Sustain. 2024, 1–43. [Google Scholar] [CrossRef]
- Mazen, A.; El-mohandes, M.; Goda, M. An improved perturb-and-observe based MPPT method for PV systems under varying irradiation levels. Sol. Energy 2018, 171, 547–561. [Google Scholar]
- Sun, C.; Ling, J.; Wang, J. Research on a novel and improved incremental conductance method. Sci. Rep. 2022, 12, 15700. [Google Scholar] [CrossRef]
- Rezk, H.; Aly, M.; Al-Dhaifallah, M.; Shoyama, M. Design and hardware implementation of new adaptive fuzzy logic-based MPPT control method for photovoltaic applications. IEEE Access 2019, 7, 106427–106438. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Scelba, G. ANN based MPPT method for rapidly variable shading conditions. Appl. Energy 2015, 145, 124–132. [Google Scholar] [CrossRef]
- Sultana, Z.; Basha, C.H.; Irfan, M.M.; Alsaif, F. A novel development of optimized hybrid MPPT controller for fuel cell systems with high voltage transformation ratio DC–DC converter. Sci. Rep. 2024, 14, 8115. [Google Scholar] [CrossRef] [PubMed]
- Bemporad, A. Recurrent neural network training with convex loss and regularization functions by extended Kalman filtering. IEEE Trans. Autom. Control 2023, 68, 6970–6977. [Google Scholar] [CrossRef]
- Khan, H.; Hadeed, A.S.; Hussain, A.; Noman, A.M.; Murtaza, A.F.; Aboras, A.M. Improved RCC-based MPPT strategy for enhanced solar energy harvesting in shaded environments. IEEE Access 2024, 12, 41662–41676. [Google Scholar] [CrossRef]
- Guediri, M.; Ikhlef, N.; Bouchekhou, H.; Guediri, A.; Guediri, A. Optimization by Genetic Algorithm of a Wind Energy System applied to a Dual-feed Generator. Eng. Technol. Appl. Sci. Res. 2024, 14, 16890–16896. [Google Scholar] [CrossRef]
- Jia, X.; Xia, Y.; Yan, Z.; Gao, H.; Qiu, D.; Guerrero, J.M.; Li, Z. Coordinated operation of multi-energy microgrids considering green hydrogen and congestion management via a safe policy learning approach. Appl. Energy 2025, 401, 126611. [Google Scholar] [CrossRef]
- Qi, N.; Huang, K.; Fan, Z.; Xu, B. Long-term energy management for microgrid with hybrid hydrogen-battery energy storage: A prediction-free coordinated optimization framework. Appl. Energy 2025, 377, 124485. [Google Scholar] [CrossRef]
- Kurucan, M.; Özbaltan, M.; Yetgin, Z.; Alkaya, A. Applications of artificial neural network based battery management systems: A literature review. Renew. Sustain. Energy Rev. 2024, 192, 114191. [Google Scholar] [CrossRef]
- Das, S.; Amara, T.; Thiago, S.; Sai, S.K.; Banerjee, I. Recurrent Neural Networks (RNNs): Architectures, Training Tricks, and Introduction to Influential Research. In Machine Learning for Brain Disorders; Springer: Cham, Switzerland, 2023; pp. 117–138. [Google Scholar]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A review of the artificial neural network models for water quality prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Dao, D.V.; Adeli, H.; Ly, H.B.; Le, L.M.; Le, V.M.; Le, T.; Pham, B.T. A Sensitivity and Robustness Analysis of GPR and ANN for High-Performance Concrete Compressive Strength Prediction Using a Monte Carlo Simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Lachheb, A.; Chrouta, J.; Akoubi, N.; Ben Salem, J. Enhancing efficiency and sustainability: A combined approach of ANN based MPPT and fuzzy logic EMS for grid connected PV systems. Euro-Mediterr. J. Environ. Integr. 2025, 10, 3067–3079. [Google Scholar] [CrossRef]
- Abidi, H.; Sidhom, L.; Chihi, I. Systematic Literature Review and Benchmarking for Photovoltaic MPPT Techniques. Energies 2023, 16, 3565. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Rosas-Caro, J.C.; Valderrabano-Gonzalez, A.; Panda, G. Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems. IEEE Access 2023, 11, 31738–31763. [Google Scholar] [CrossRef]
- Sarvi, M.; Azadian, A. A comprehensive review and classified comparison of MPPT algorithms in PV systems. Energy Syst. 2022, 13, 887–916. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive review of Maximum Power Point Tracking (MPPT) Techniques used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Agrawal, R.; Sawle, Y.; Kumar, A. A Different approach for Maximum Power Point Tracking (MPPT) using impedance matching through non-isolated DC-DC converters in Solar Photovoltaic Systems. Electronics 2022, 11, 987. [Google Scholar] [CrossRef]
- Li, J.; Wu, Y.; Ma, S.; Chen, M.; Zhang, B.; Jiang, B. Analysis of photovoltaic array maximum power point tracking under uniform environment and partial shading condition: A review. Energy Rep. 2022, 8, 12698–12719. [Google Scholar] [CrossRef]
- Akoubi, N.; Ben Salem, J.; El Amraoui, L. Contribution on the combination of artificial Neural Network and incremental conductance method to MPPT Control Approach. In Proceedings of the 2022 8th International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 22–25 May 2022. [Google Scholar]
- Ali, K.; Ullah, S.; Clementini, E. Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions. Energies 2025, 18, 5134. [Google Scholar] [CrossRef]
- Rezaei, M.; Nezamabadi, H. A taxonomy of literature reviews and experimental study of deep reinforcement learning in portfolio management. Artif. Intell. Rev. 2025, 58, 28. [Google Scholar] [CrossRef]
- Jung, Y.; So, J.; Yu, G.; Choi, J. Improved perturbation and observation method (IP&O) of MPPT control for photovoltaic power systems. In Proceedings of the Conference Record of the Thirty-first IEEE Photovoltaic Specialists Conference, Orlando, FL, USA, 3–7 January 2005; pp. 1788–1791. [Google Scholar]
- Krishnaram, K.; Padmanabhan, T.S.; Alsaif, F.; Senthilkumar, S. Performance optimization of interleaved boost converter with ANN supported adaptable stepped-scaled P&O based MPPT for solar powered applications. Sci. Rep. 2024, 14, 8115. [Google Scholar]
- Borni, A.; Bouarroudj, N.; Bouchakour, A.; Zaghba, L. P&O-PI and fuzzy-PI MPPT Controllers and their time domain optimization using PSO and GA for grid-connected photovoltaic system: A comparative study. Int. J. Power Electron. 2017, 8, 300–322. [Google Scholar]
- Zhao, Y.; An, A.; Xu, Y.; Wang, Q.; Wang, M. Model predictive control of grid-connected PV power generation system considering optimal MPPT control of PV modules. Prot. Control. Mod. Power Syst. 2021, 6, 32. [Google Scholar] [CrossRef]
- Abadlia, I.; Hassaine, L.; Beddar, A.; Abdoune, F.; Bengourina, M.R. Adaptive fuzzy control with an optimization by using genetic algorithms for grid connected a hybrid photovoltaic–hydrogen generation system. Int. J. Hydrogen Energy 2020, 45, 22589–22599. [Google Scholar] [CrossRef]

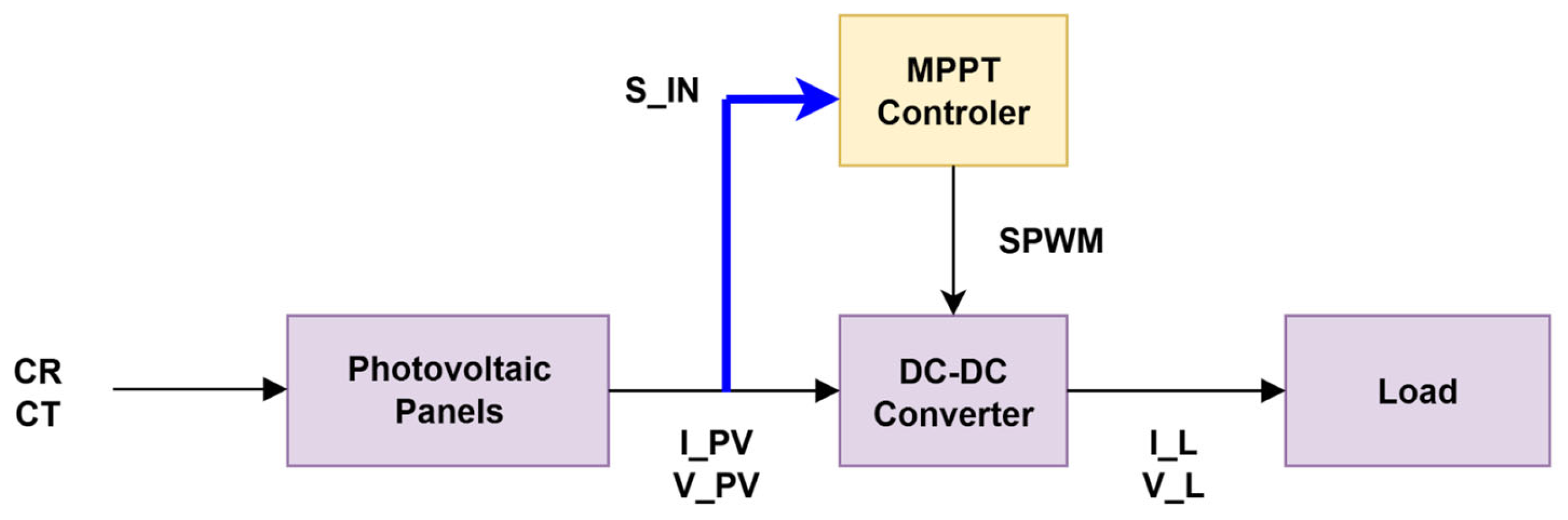



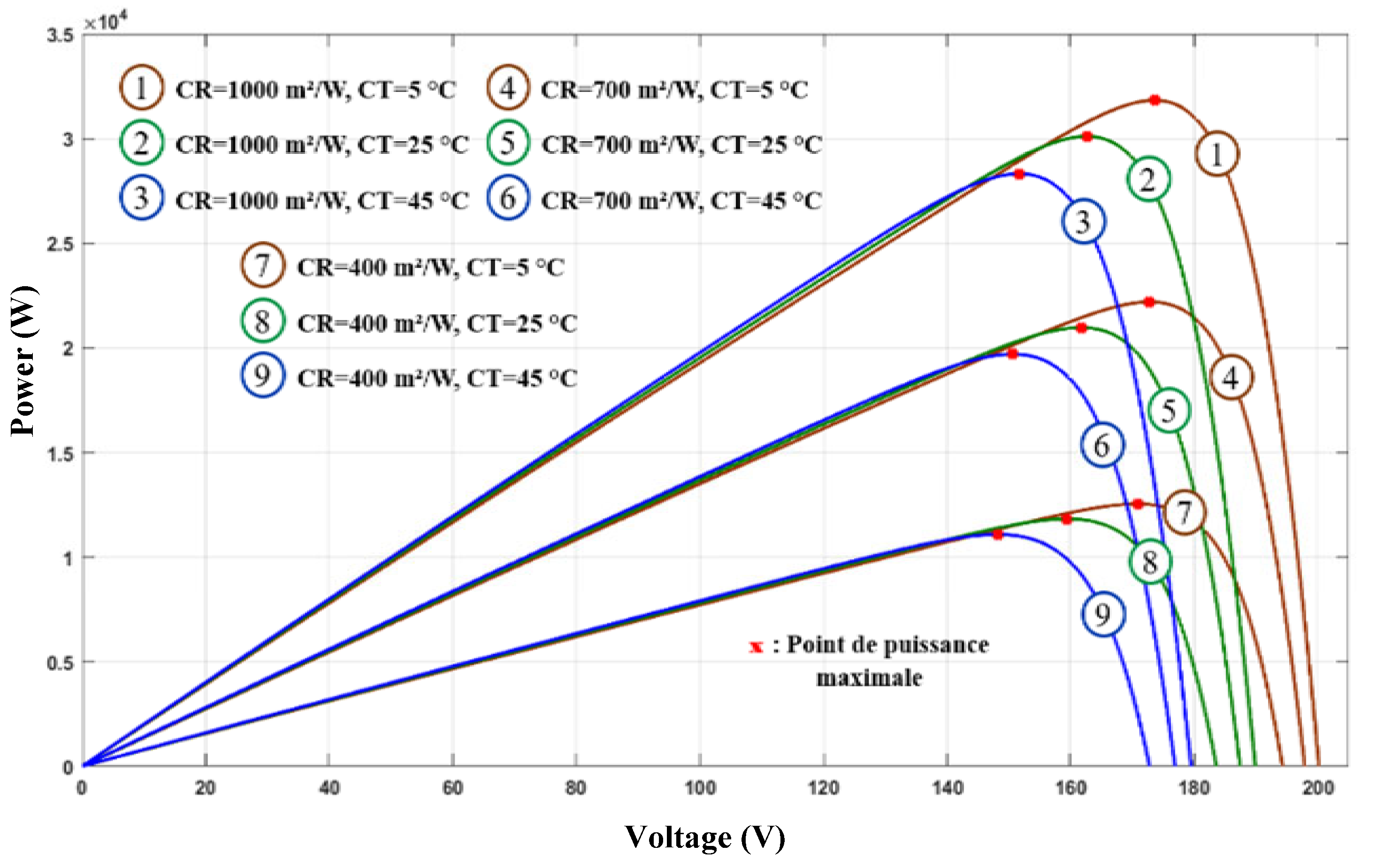
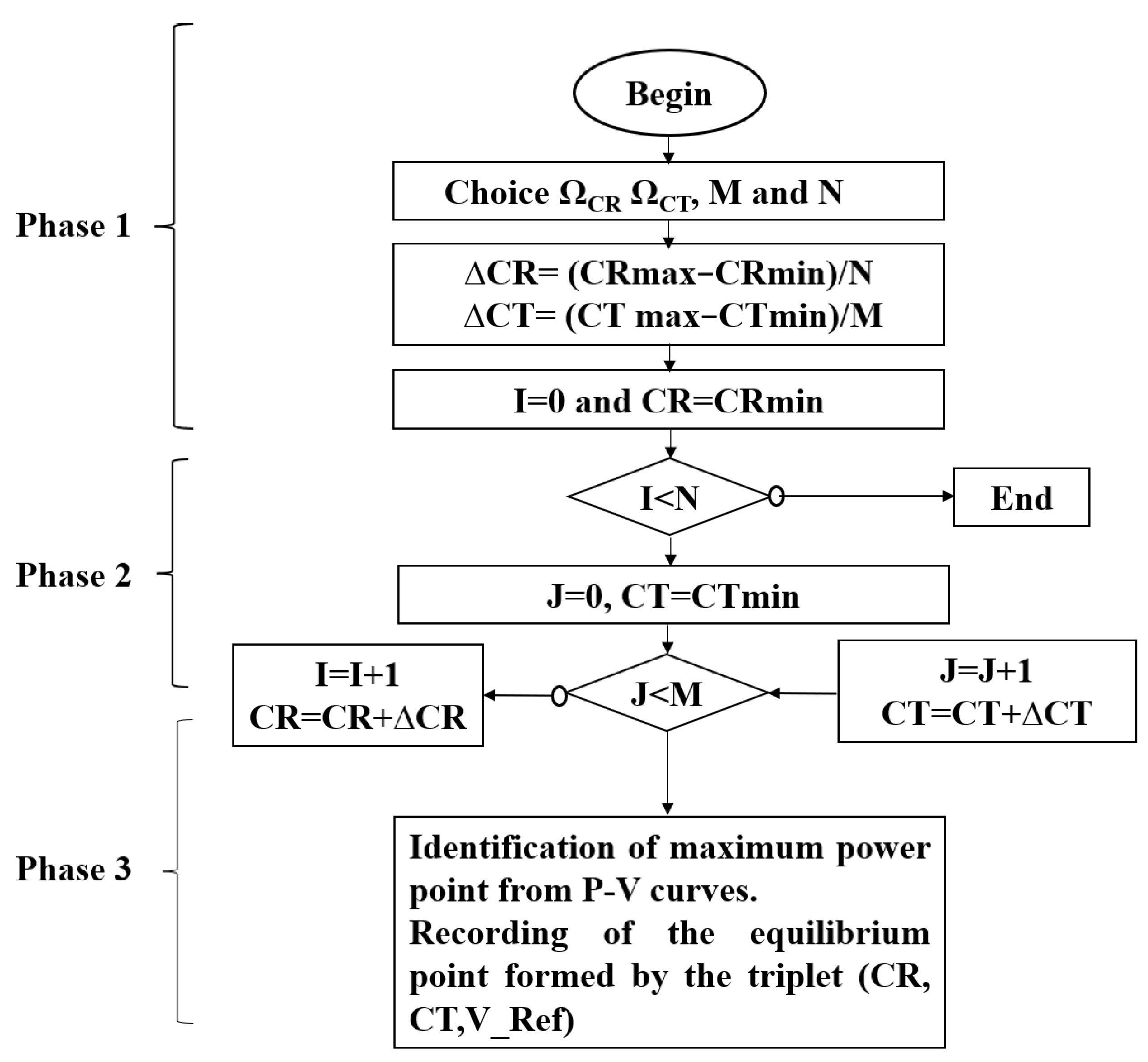
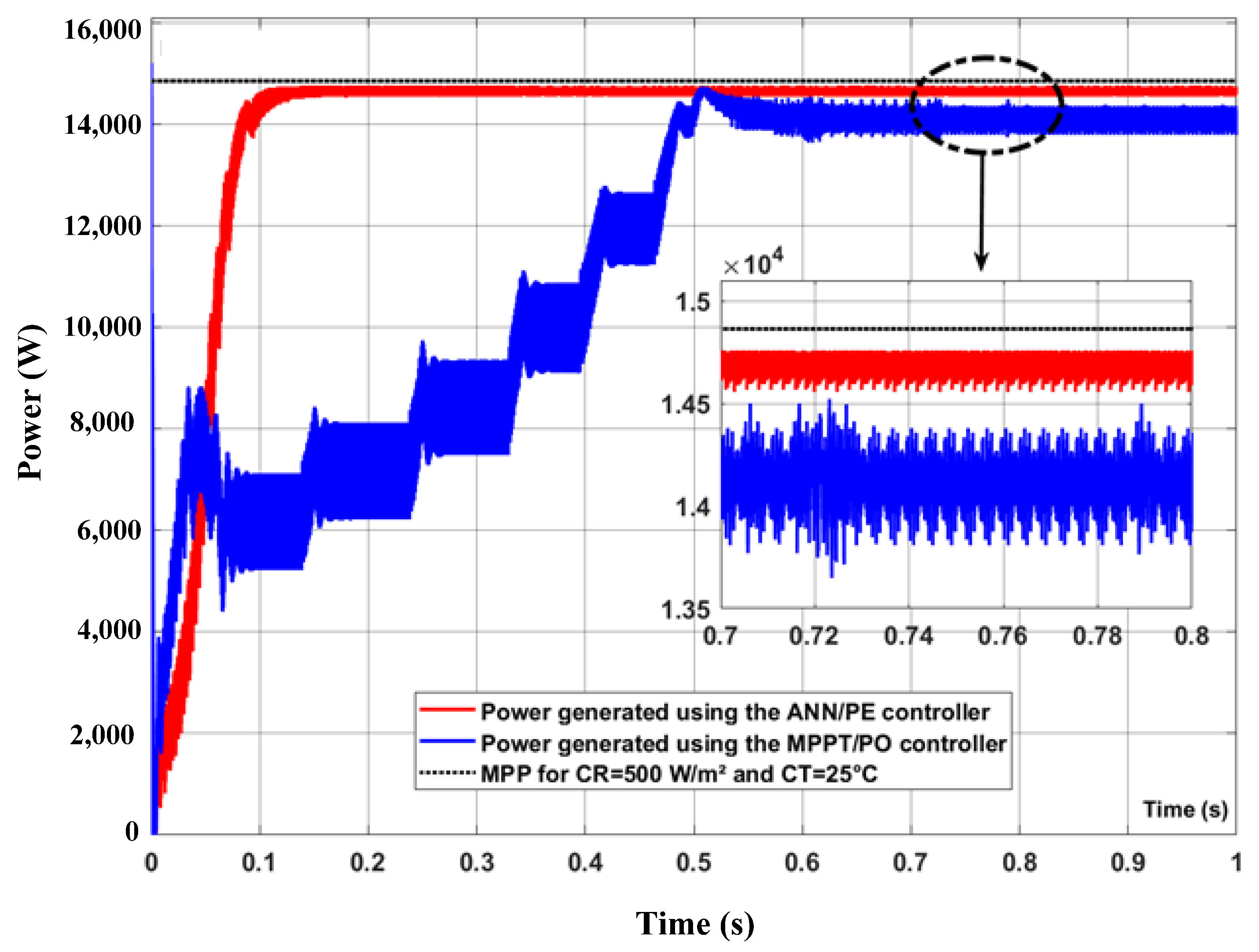

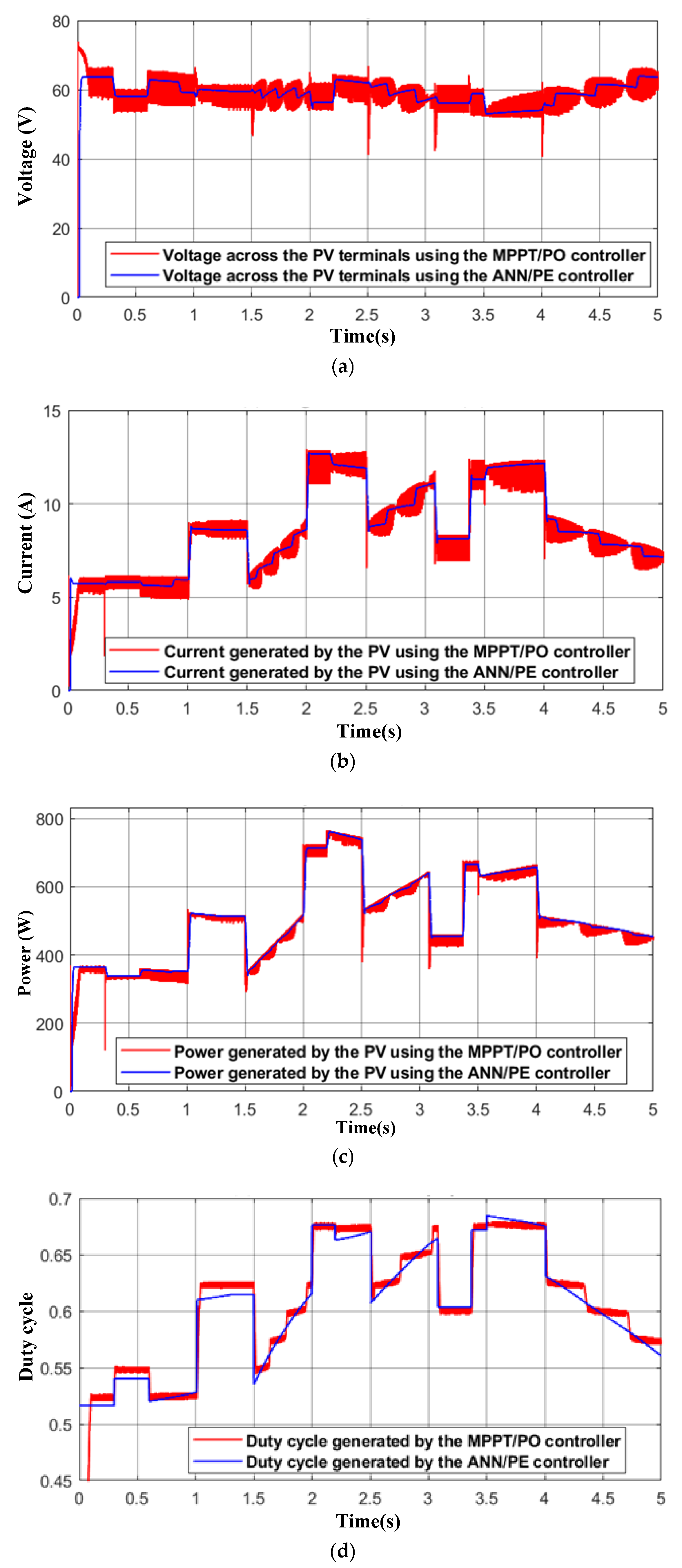

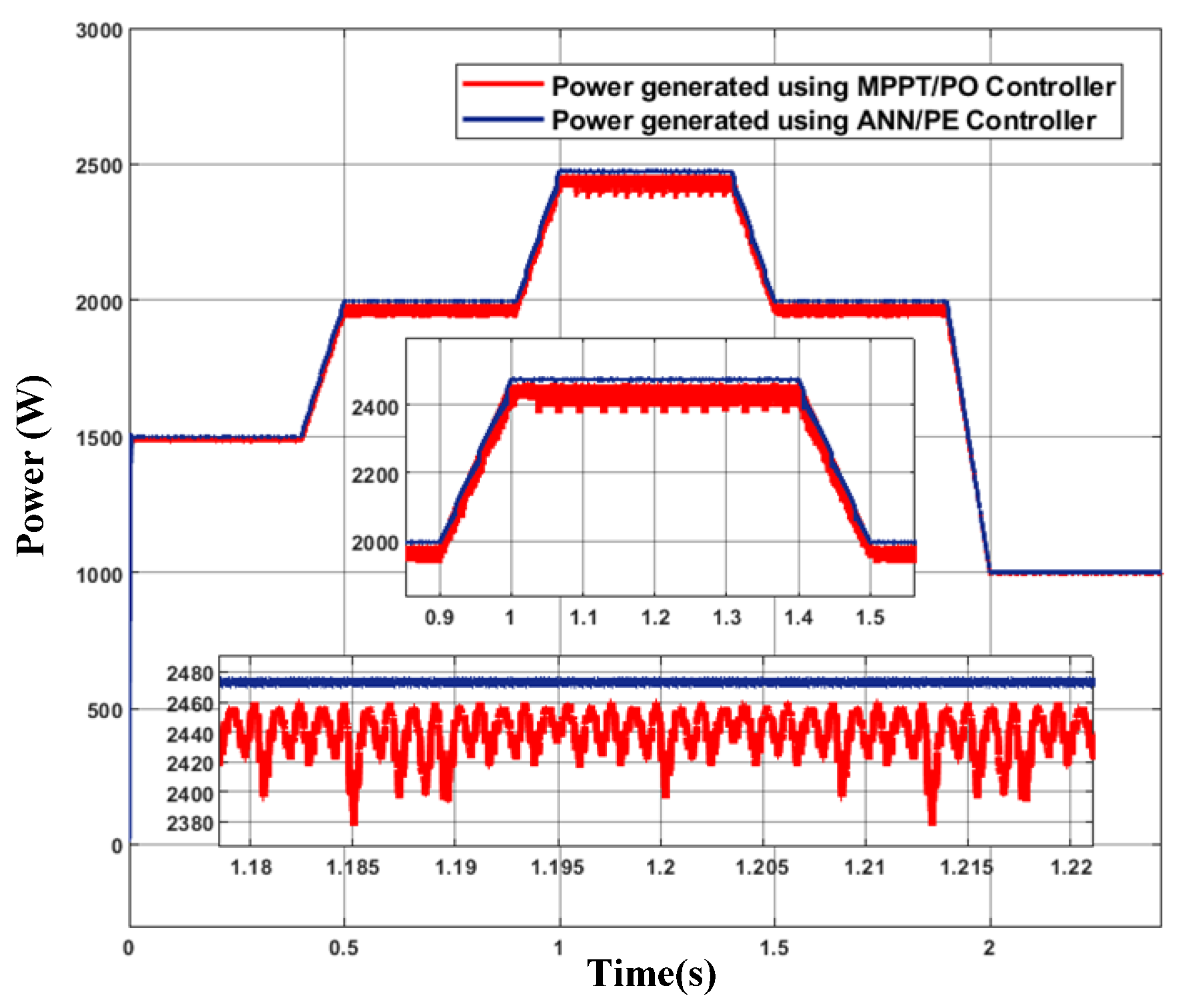
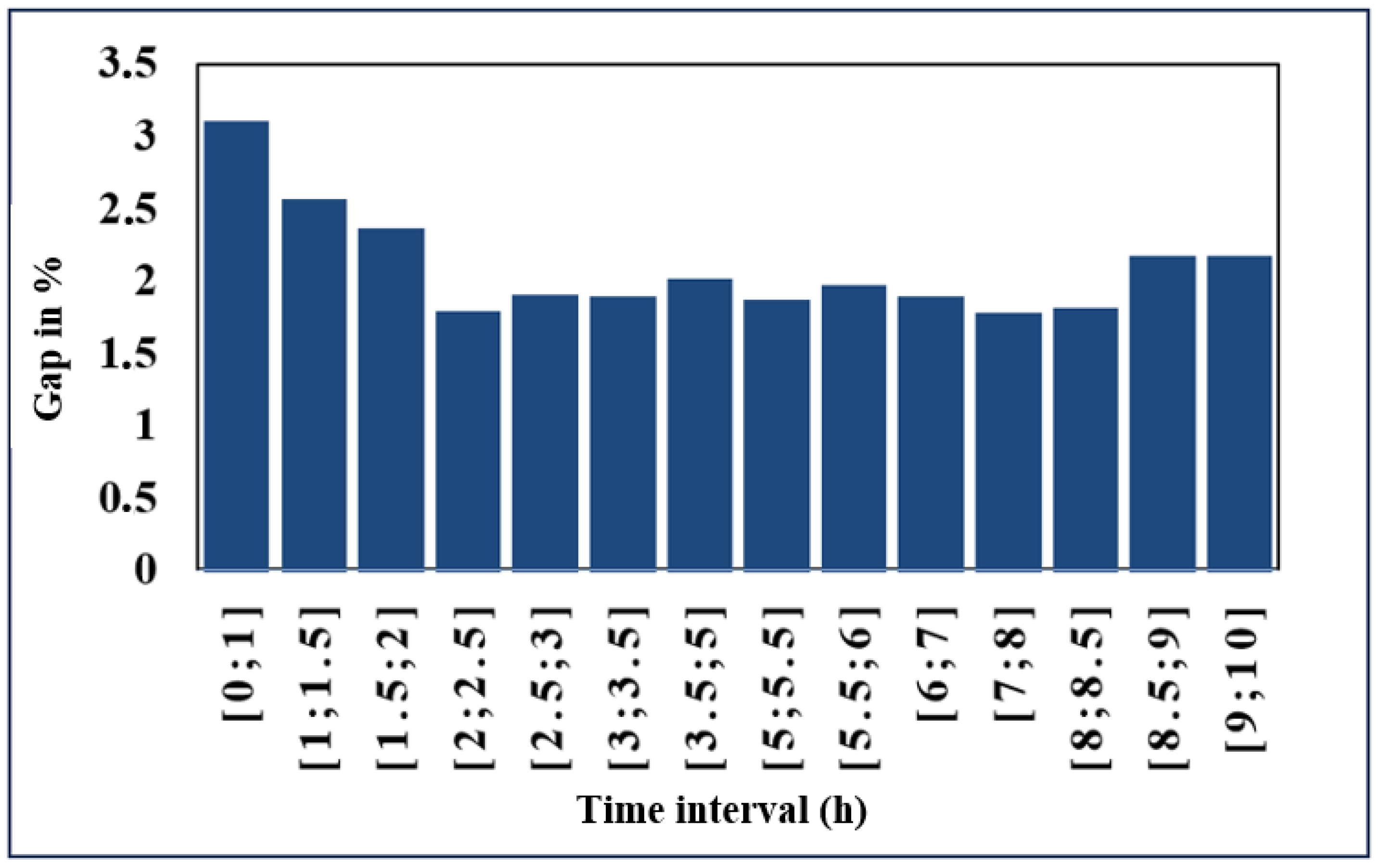
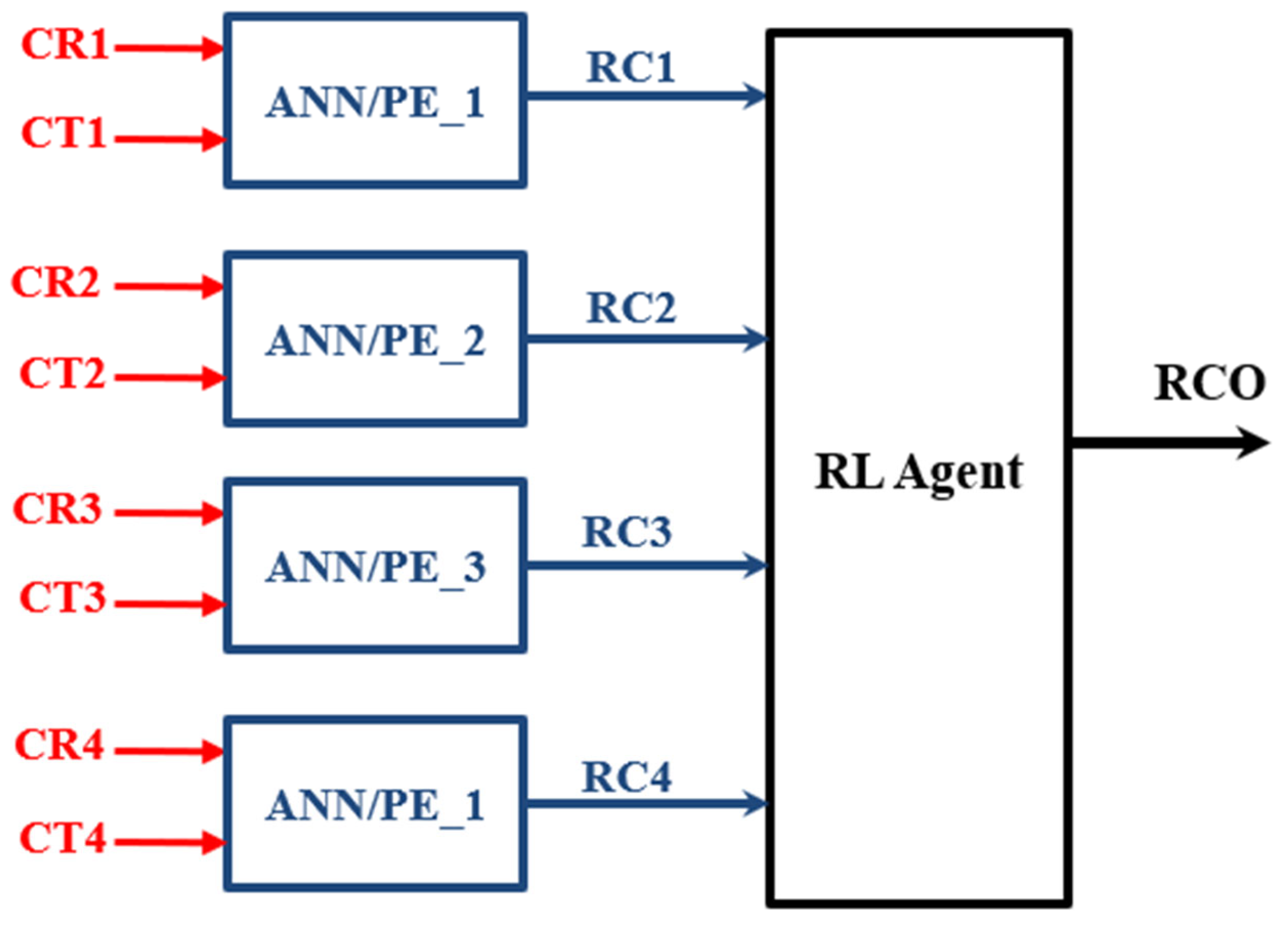
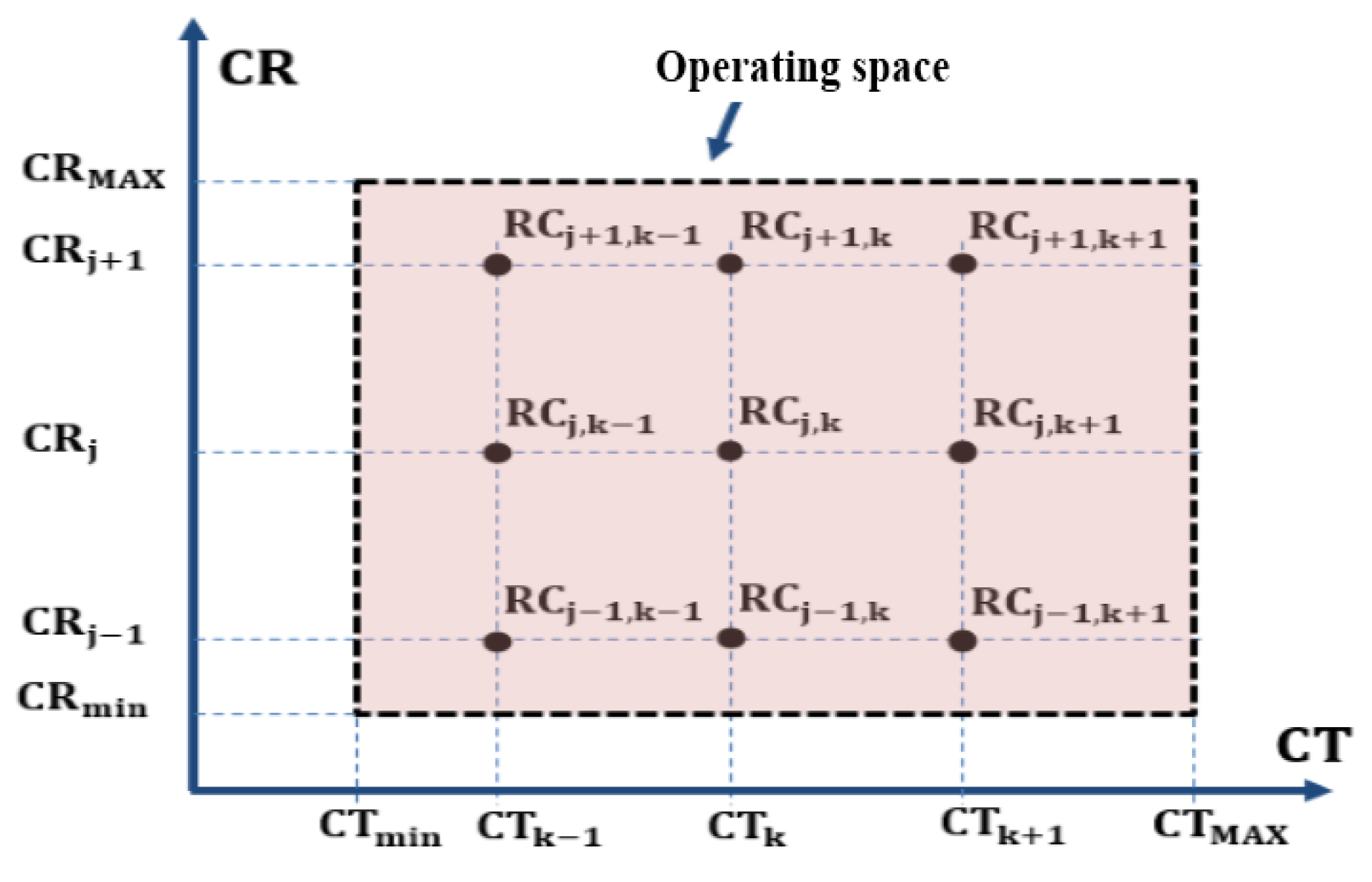
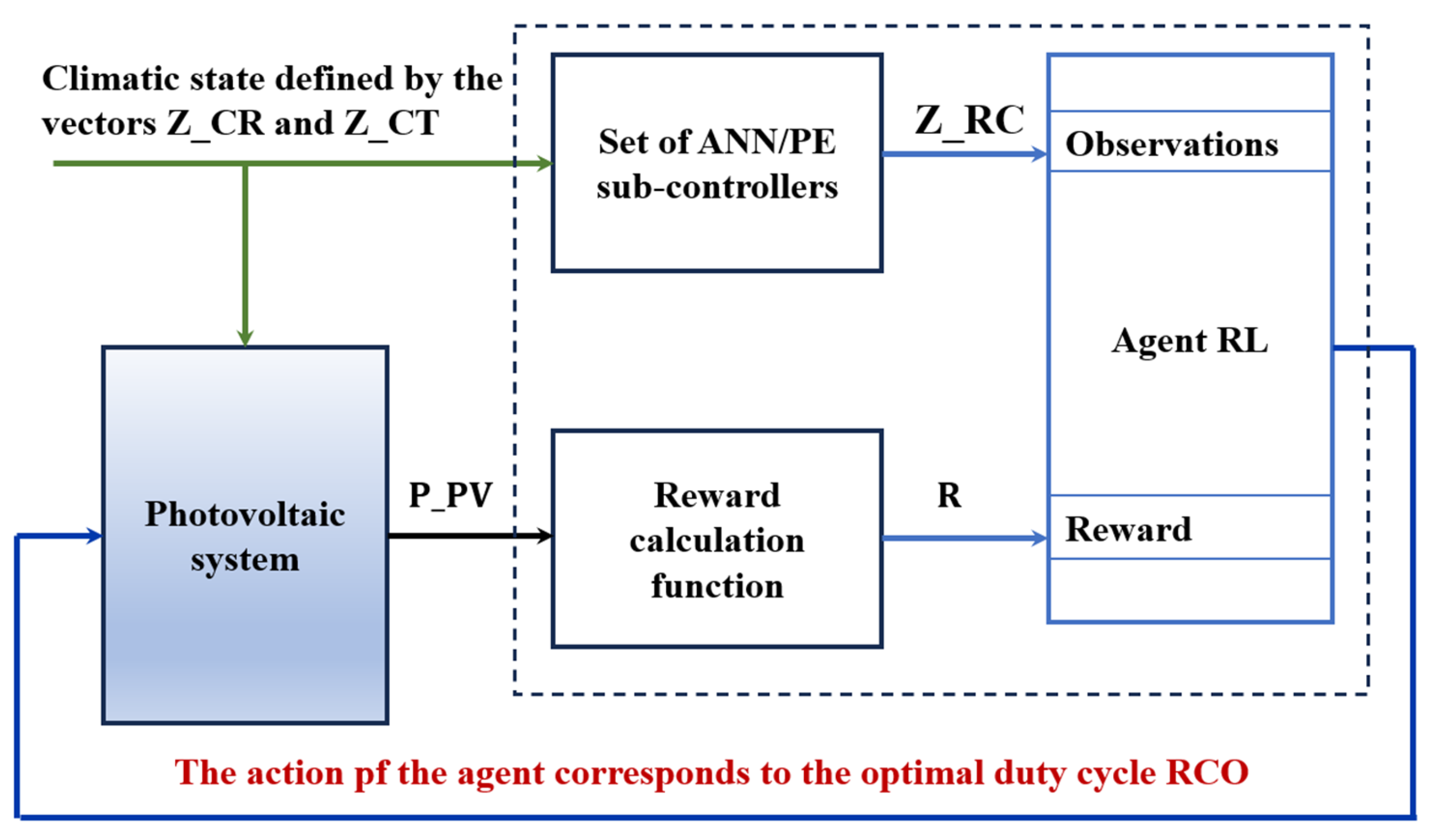
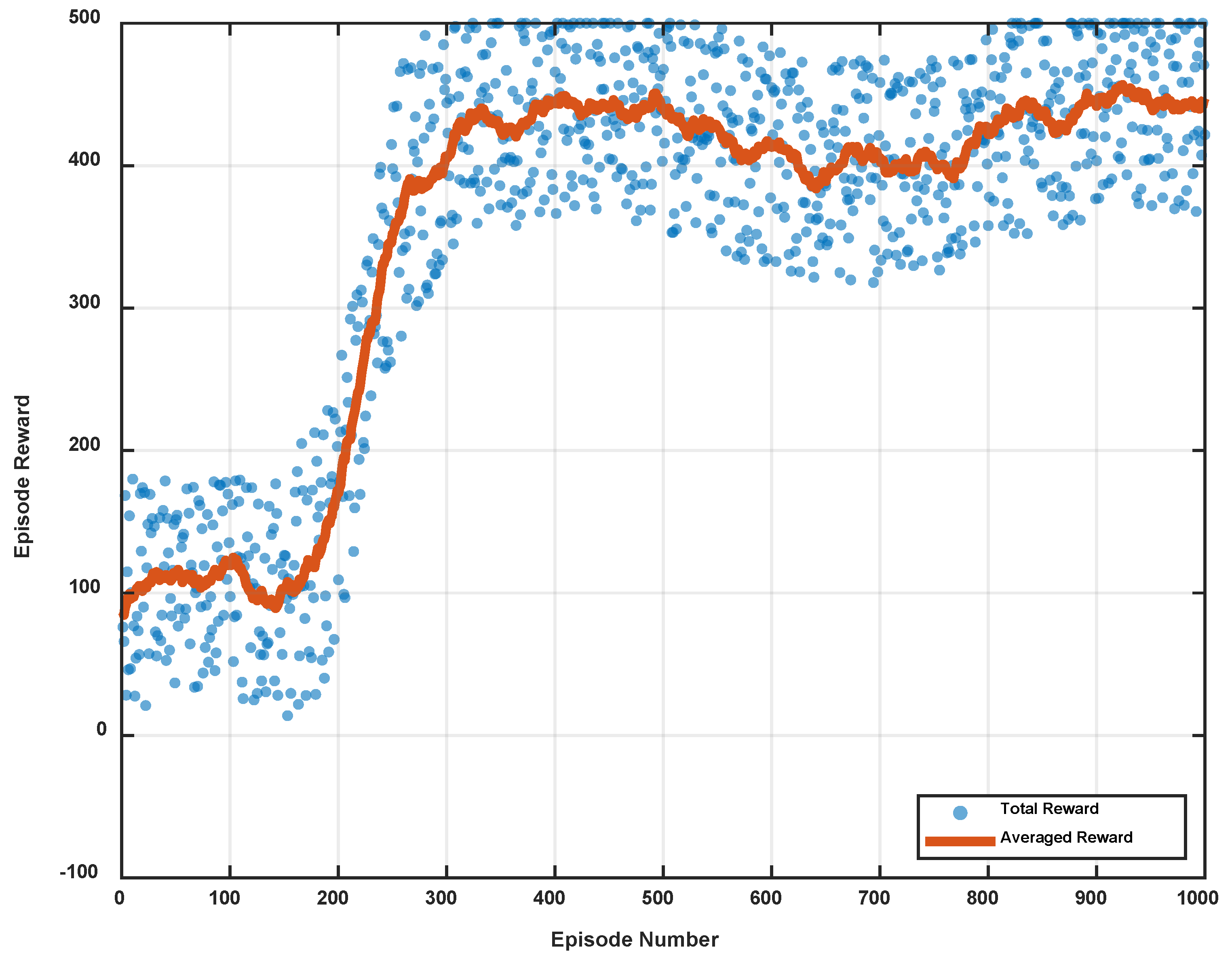
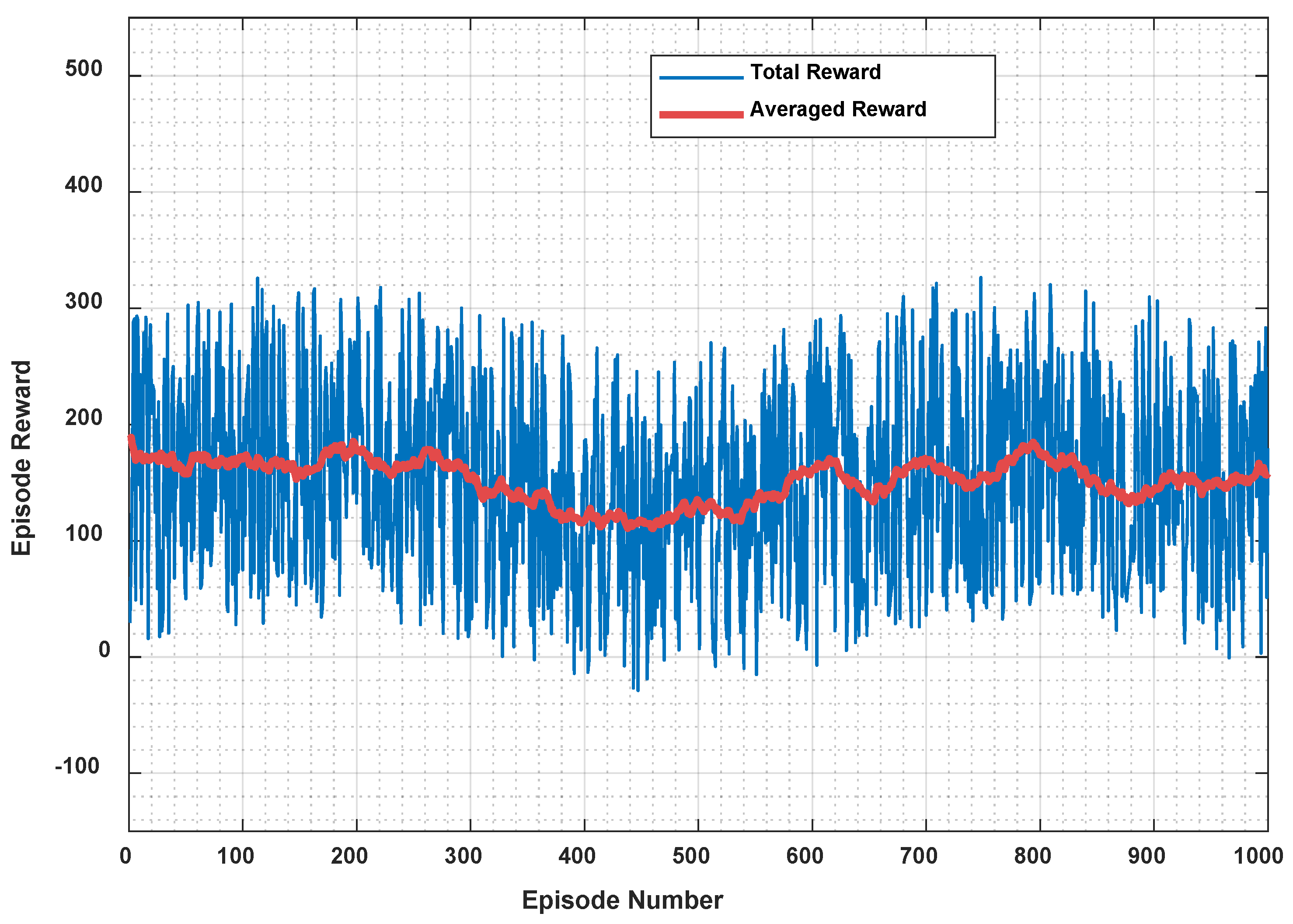

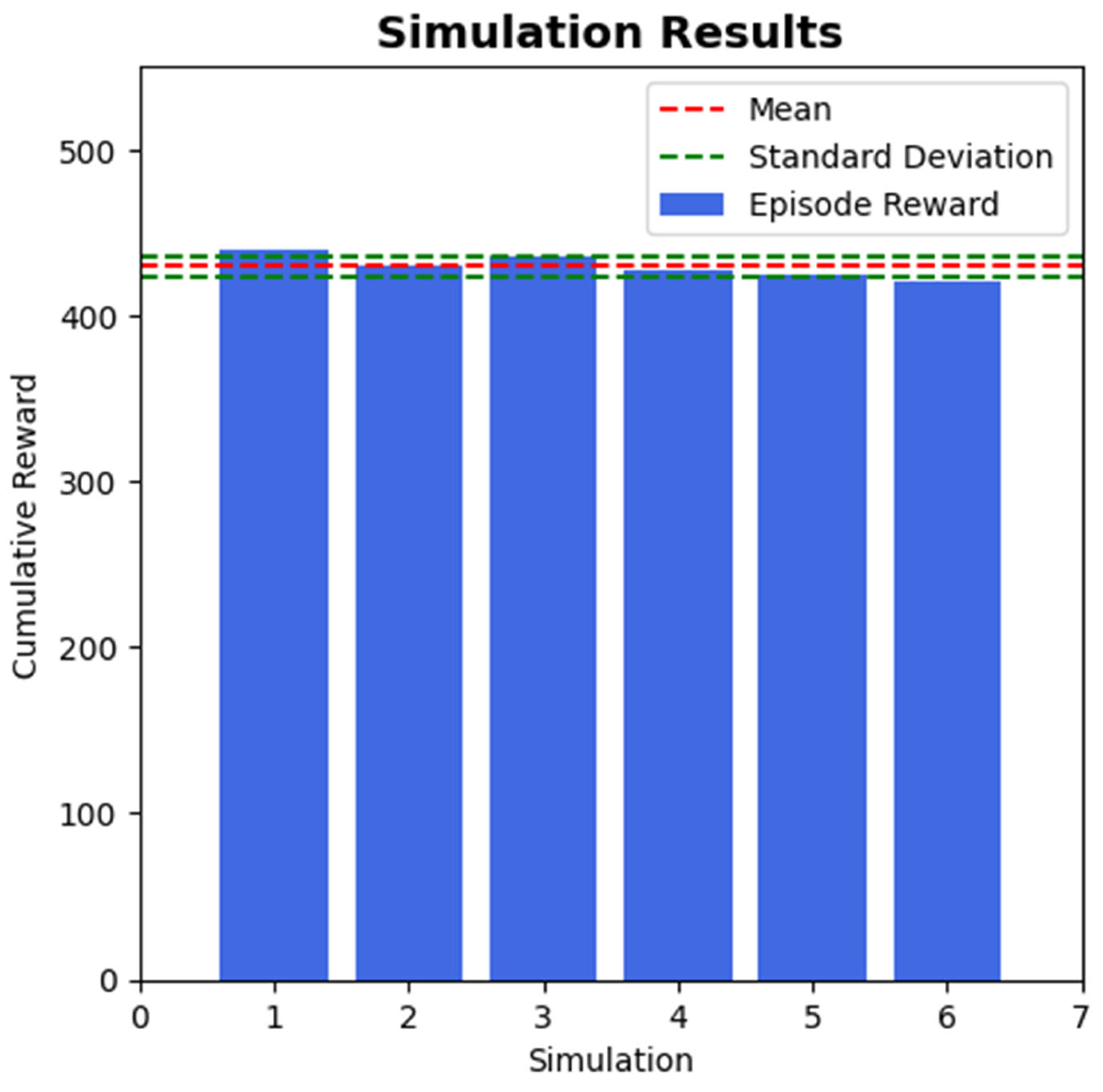
| Curve Number | CR (m2/W) | CT (°C) | P_PV_MAX (W) | V_Ref (V) |
|---|---|---|---|---|
| 1 | 1000 | 5 | 31,822.32 | 173.58 |
| 2 | 1000 | 25 | 30,097.44 | 162.62 |
| 3 | 1000 | 45 | 28,316.71 | 151.66 |
| 4 | 700 | 5 | 22,191.83 | 172.78 |
| 5 | 700 | 25 | 20,964.09 | 161.7 |
| 6 | 700 | 45 | 19,696.73 | 150.61 |
| 7 | 400 | 5 | 12,540.54 | 170.8 |
| 8 | 400 | 25 | 11,819.49 | 159.45 |
| 9 | 400 | 45 | 11,075.43 | 148.17 |
| Parameters | Value |
|---|---|
| N | 10 |
| M | 45 |
| CRmin (W/m2) | 100 |
| CRMAX (W/m2) | 1000 |
| CTmin (°C) | 0 |
| CTMax (°C) | 50 |
| ANN/PE Controller | ANN/PO Controller [32] | MPPT/PO Controller [31] | |
|---|---|---|---|
| Response time (s) | 6 | 12 | 30 |
| Maximum steady-state power value (W) | 14,750 | 14,630 | 14,520 |
| Minimum steady-state power value (W) | 14,600 | 13,680 | 13,680 |
| Value of the average power in steady state (W) | 14,660 | 14,530 | 14,110 |
| Steady-state ripple rate (%) | 1 | 2.1 | 5.95 |
| PV system efficiency (%) | 98.3 | 97.7 | 95 |
| DDGP Agent | TD3 Agent | |
|---|---|---|
| Average reward values | 423 | 435 |
| Maximum reward value | 436 | 444 |
| Minimum reward value | 408 | 427 |
| Control Strategy | Energy Loss (%) | Adaptation to Imbalance | Computational Complexity | Learning Requirement |
|---|---|---|---|---|
| PO + PI Control [38] | 1.95 | Poor | Low | None |
| IC + Model Predictive Control [39] | 1.6 | Moderate | High | Model-Based |
| Fuzzy Logic + Genetic Algorithm [40] | 1.35 | Good | Medium | Rule-based |
| ANN/PO + DDPG | 1.15 | Good | Medium | Data-driven |
| ANN/PE + TD3 | <1 | Excellent | Medium | Hybrid |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lachheb, A.; Akoubi, N.; Ben Salem, J.; El Amraoui, L.; BaQais, A. A Hybrid Strategy Integrating Artificial Neural Networks for Enhanced Energy Production Optimization. Energies 2025, 18, 5941. https://doi.org/10.3390/en18225941
Lachheb A, Akoubi N, Ben Salem J, El Amraoui L, BaQais A. A Hybrid Strategy Integrating Artificial Neural Networks for Enhanced Energy Production Optimization. Energies. 2025; 18(22):5941. https://doi.org/10.3390/en18225941
Chicago/Turabian StyleLachheb, Aymen, Noureddine Akoubi, Jamel Ben Salem, Lilia El Amraoui, and Amal BaQais. 2025. "A Hybrid Strategy Integrating Artificial Neural Networks for Enhanced Energy Production Optimization" Energies 18, no. 22: 5941. https://doi.org/10.3390/en18225941
APA StyleLachheb, A., Akoubi, N., Ben Salem, J., El Amraoui, L., & BaQais, A. (2025). A Hybrid Strategy Integrating Artificial Neural Networks for Enhanced Energy Production Optimization. Energies, 18(22), 5941. https://doi.org/10.3390/en18225941






