Simulation Study on Heat Transfer and Flow Performance of Pump-Driven Microchannel-Separated Heat Pipe System
Abstract
1. Introduction
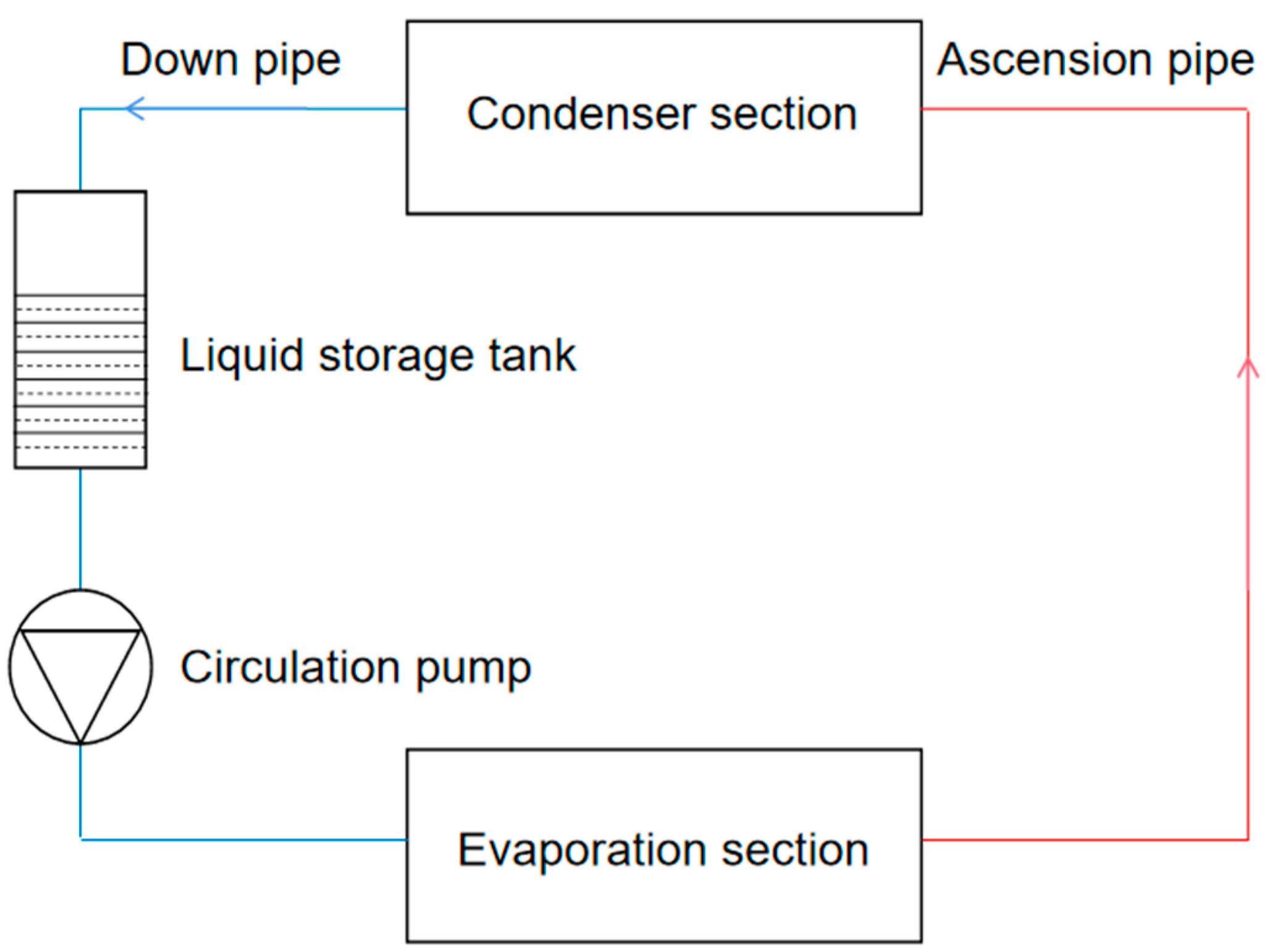
2. Steady State Mathematical Model of Pump-Driven Microchannel-Separated Heat Pipe
2.1. Evaporator Model
2.2. Condenser Model
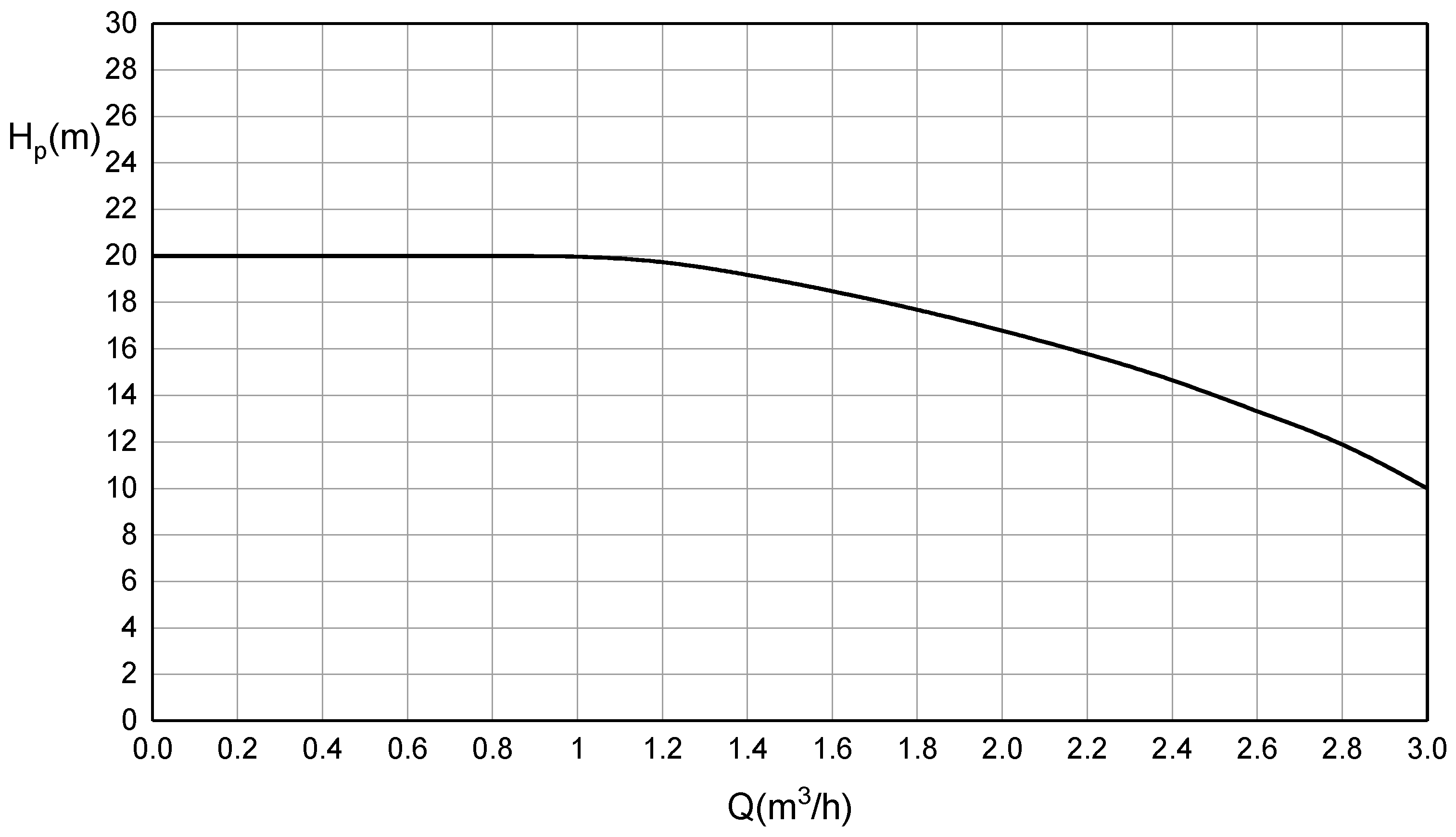
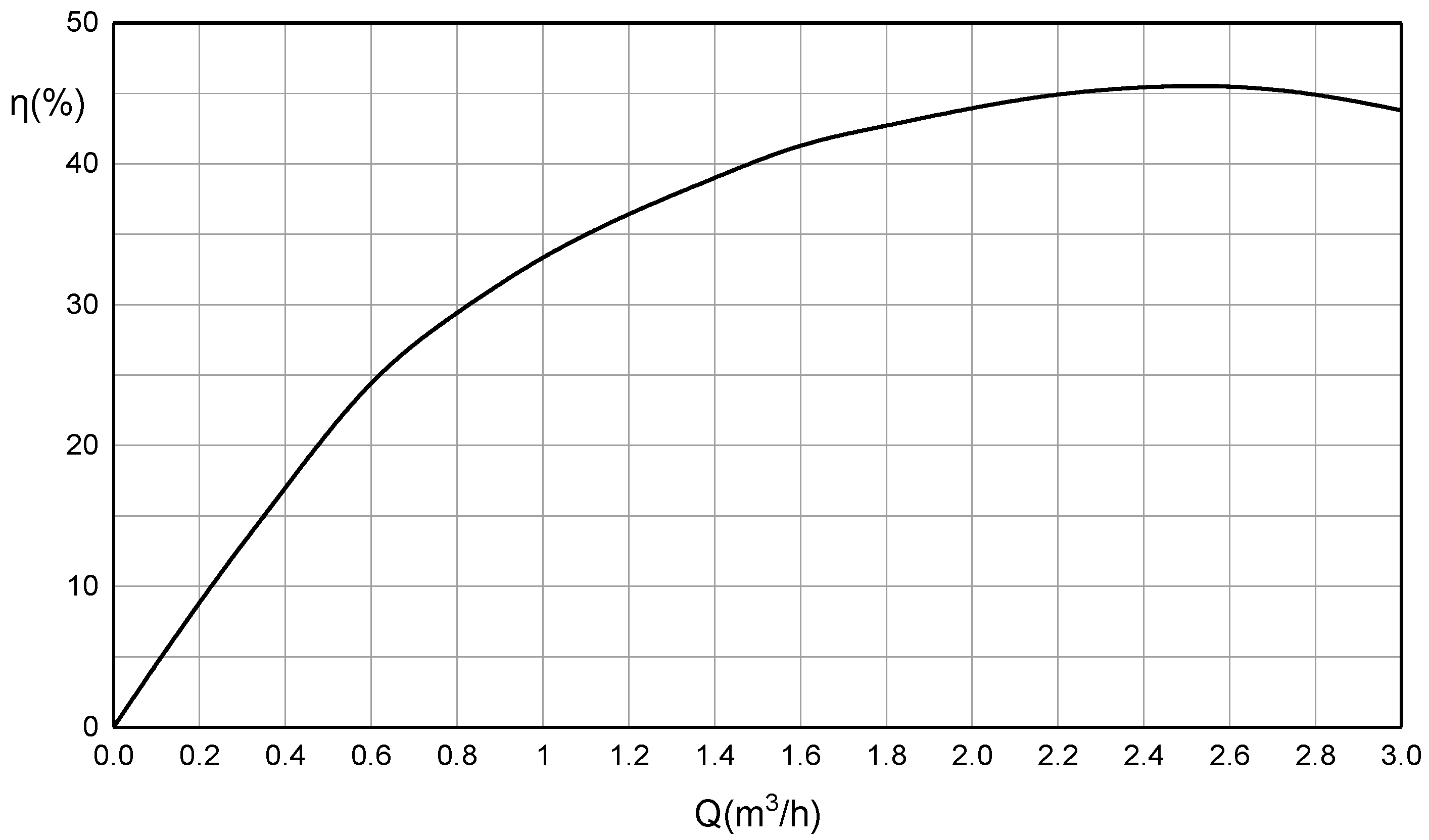
2.3. Pump Model
2.4. Model of Liquid Storage Tank
2.5. Calculation Procedure
- (1)
- Input liquid filling amount MFR, structural parameters of heat pipe system, ambient temperature, air volume at evaporator and condenser, and inlet air temperature;
- (2)
- Assumptions are made for evaporator inlet pressure p0, inlet enthalpy h0, and mass flow G0 to start calculation;
- (3)
- The refrigerant working medium parameters are brought into evaporator, riser, condenser, down pipe I, liquid storage tank, down pipe II, centrifugal pump, and down pipe III in turn for calculation to complete a cycle;
- (4)
- Analyze the difference between the outlet pressures p1 and p0 of the down pipe III; if the difference is within the allowable range, proceed to the next step; otherwise, adjust the mass flow rate G0 step by step, wherein the value is the previous assumed mass flow rate value plus 0.01 kg/s, returning to step (2);
- (5)
- Analyze the difference between h1 and h0 at the outlet of the down pipe III, if the difference is within the allowable range, proceed to the next step, otherwise adjust the inlet pressure h0 of the evaporator step by step, the value of which is the value of the previous assumed outlet enthalpy plus 0.1 kJ/kg, returning to step (2);
- (6)
- Analyze the difference between the total mass ∑Mi of each component of the system and the filling amount MFR, if the difference is within the allowable range, the calculation is complete, producing the parameters of each component and the parameters characterizing the heat transfer and flow of the evaporator and the condenser; otherwise adjust the inlet pressure p0 of the evaporator step by step, and the value of the inlet pressure p0 is the value of the previous assumed outlet enthalpy value plus 0.01 MPa, returning to step (2). Iterative cycles are also needed for the evaporator and condenser to discriminate the heat transfer quantity Q. Initial parameters for calculation procedure is show in Table 1.
3. Results and Discussion
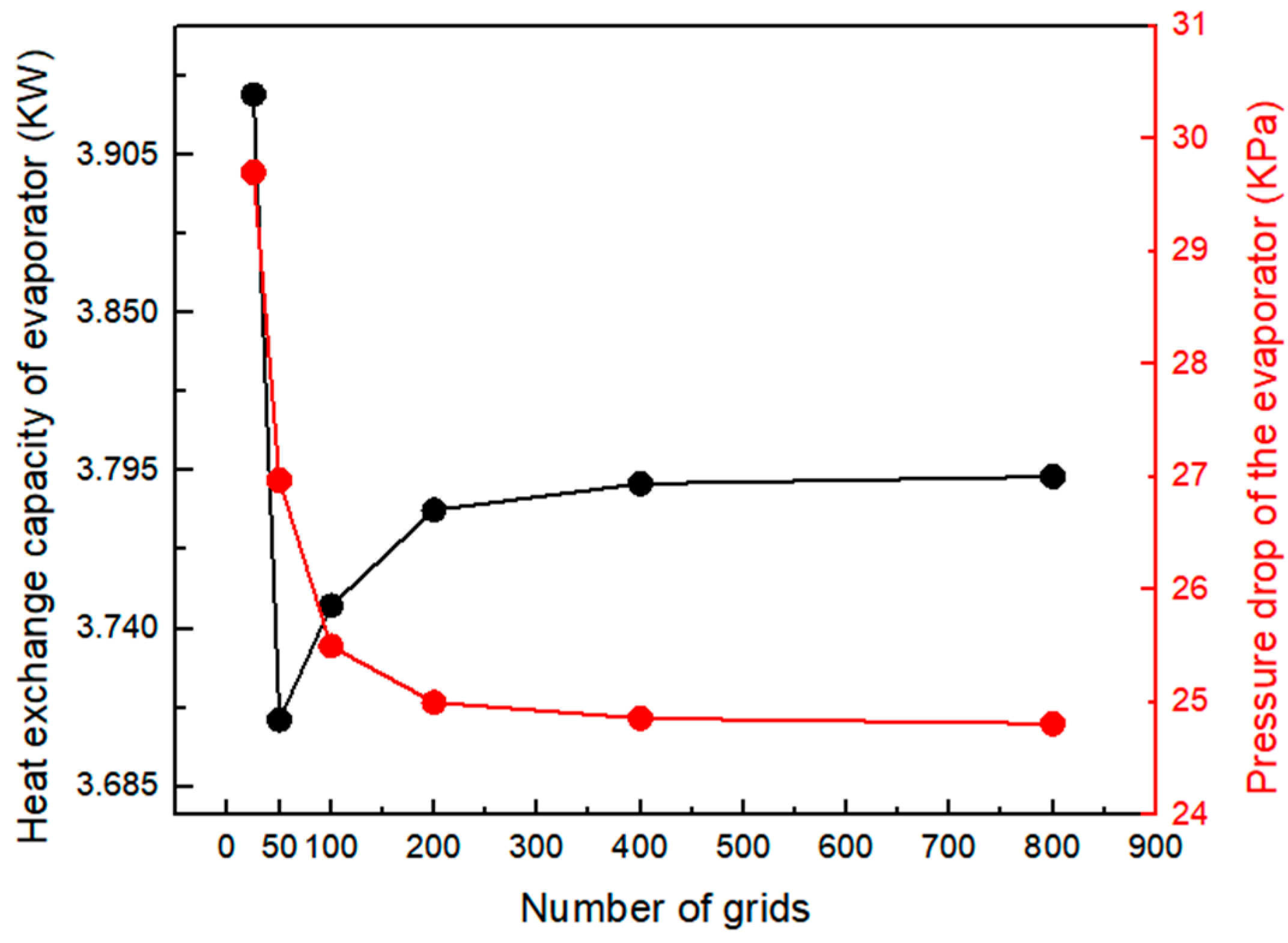
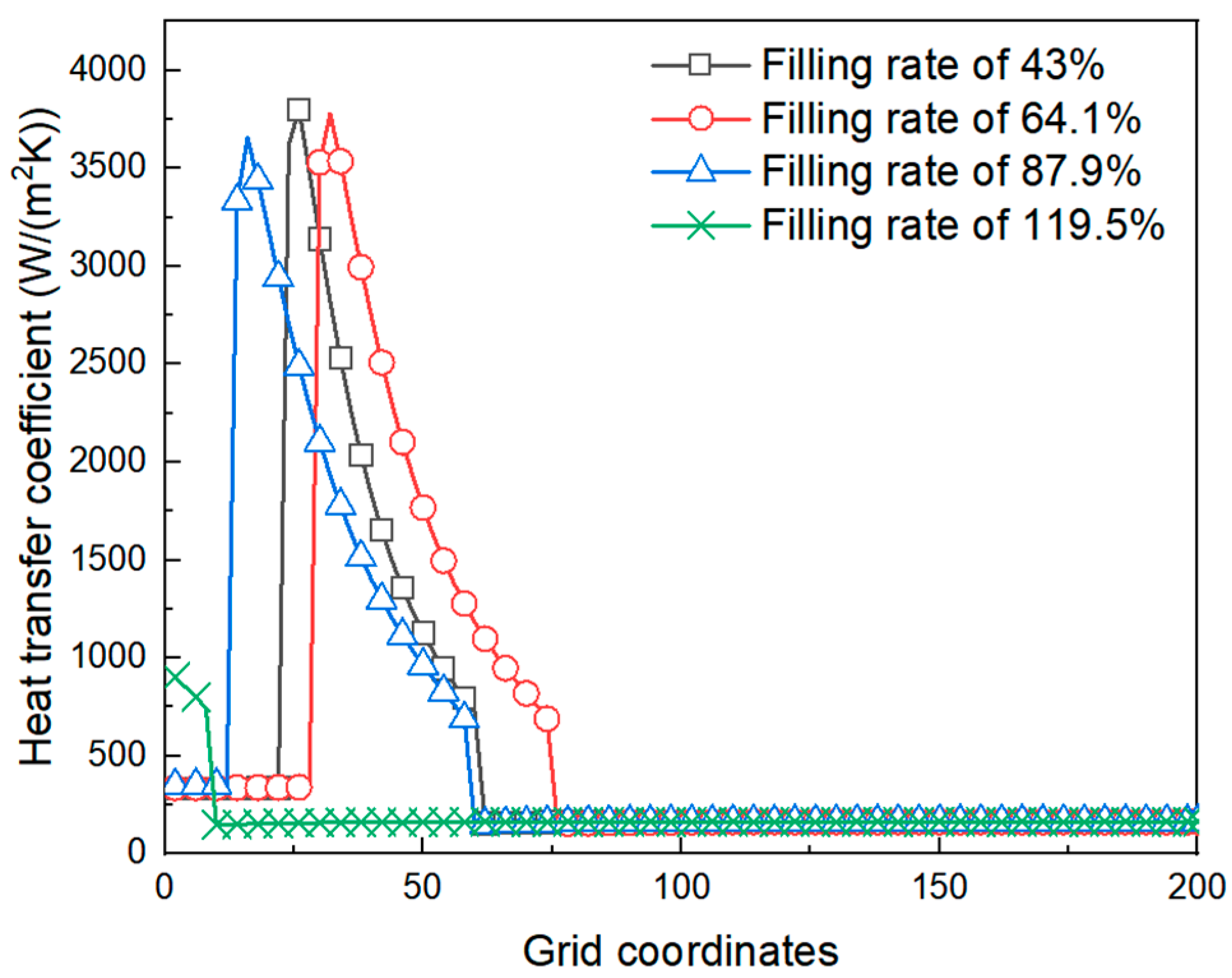
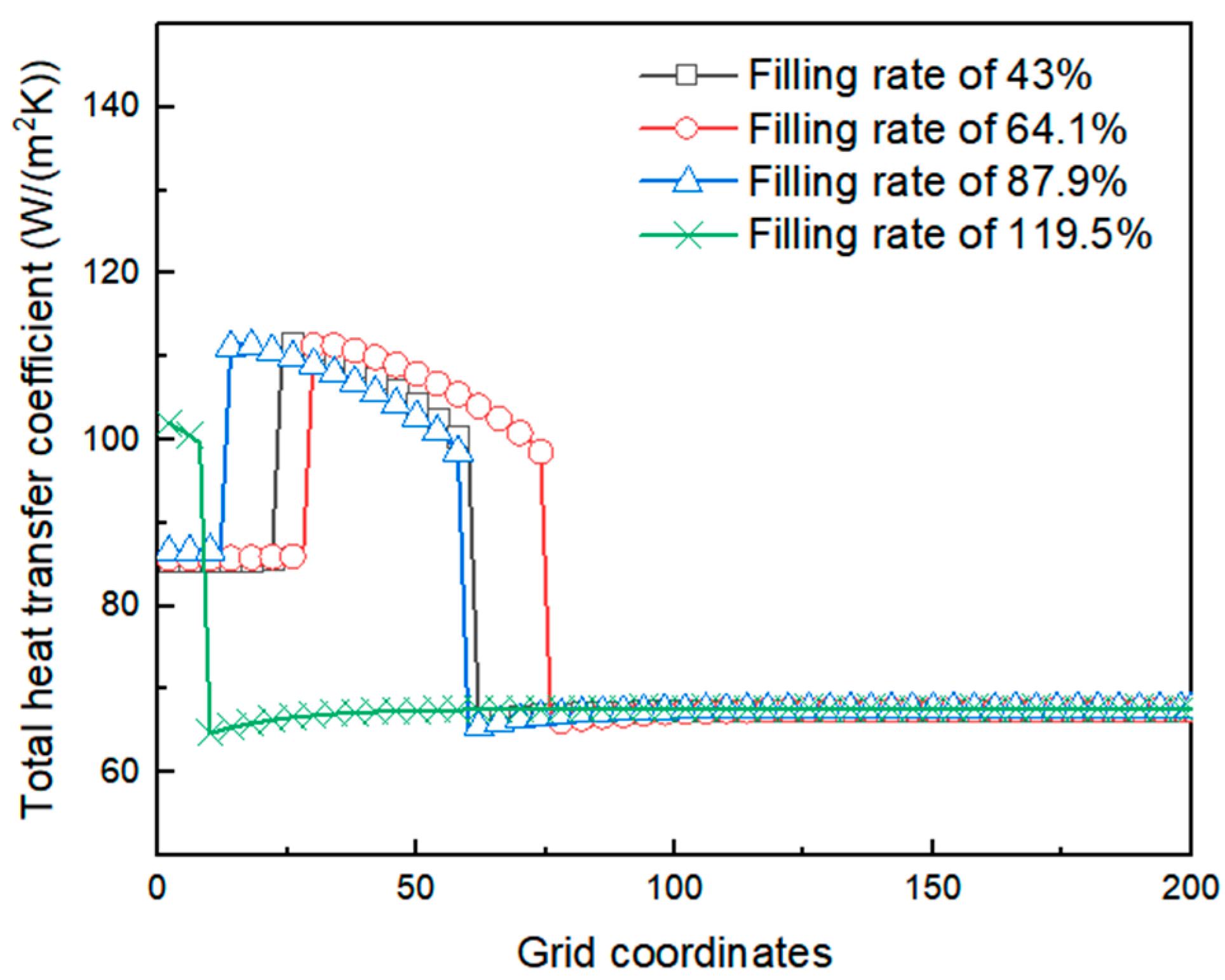
3.1. Verification of Grid Independence
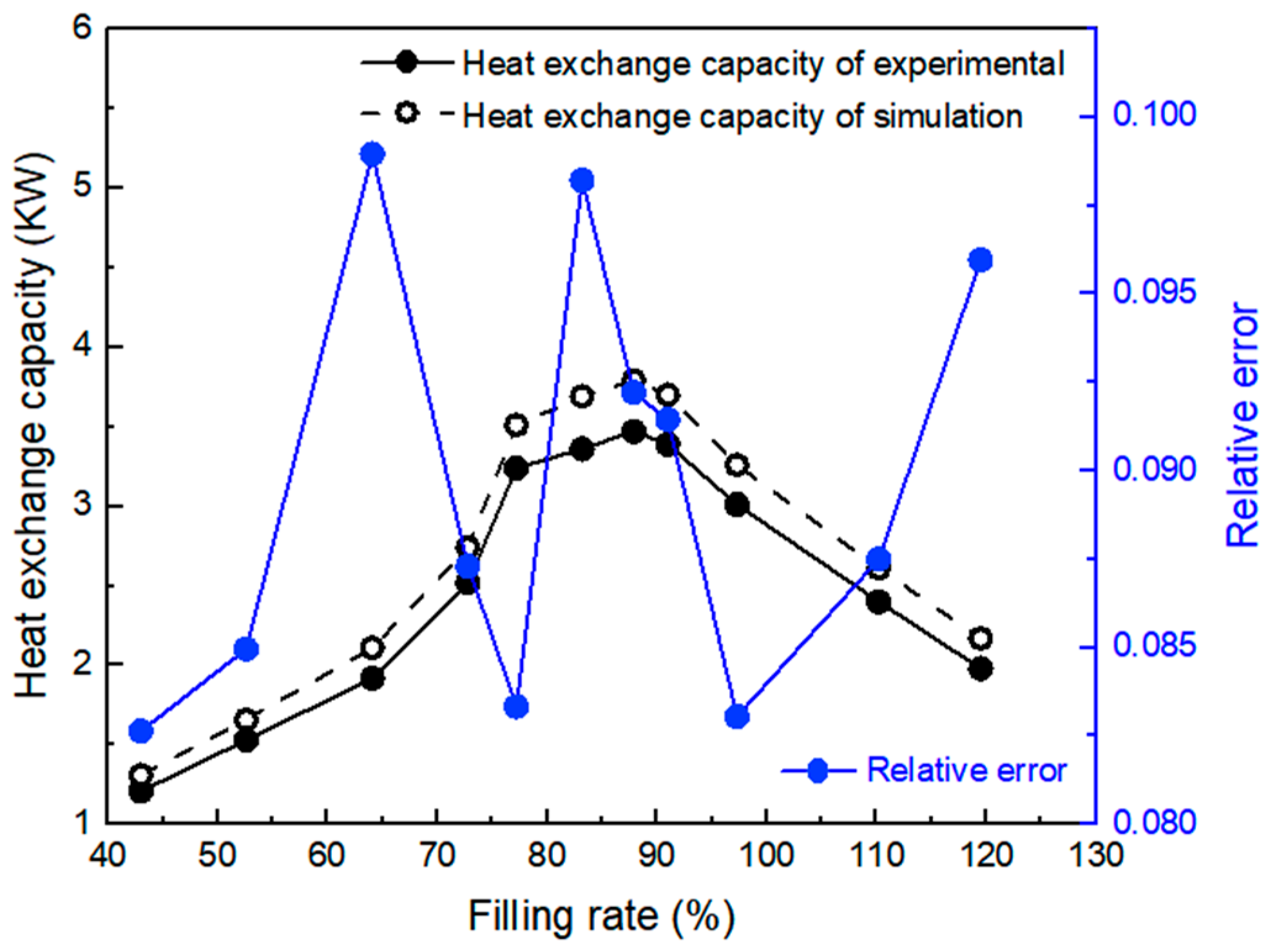
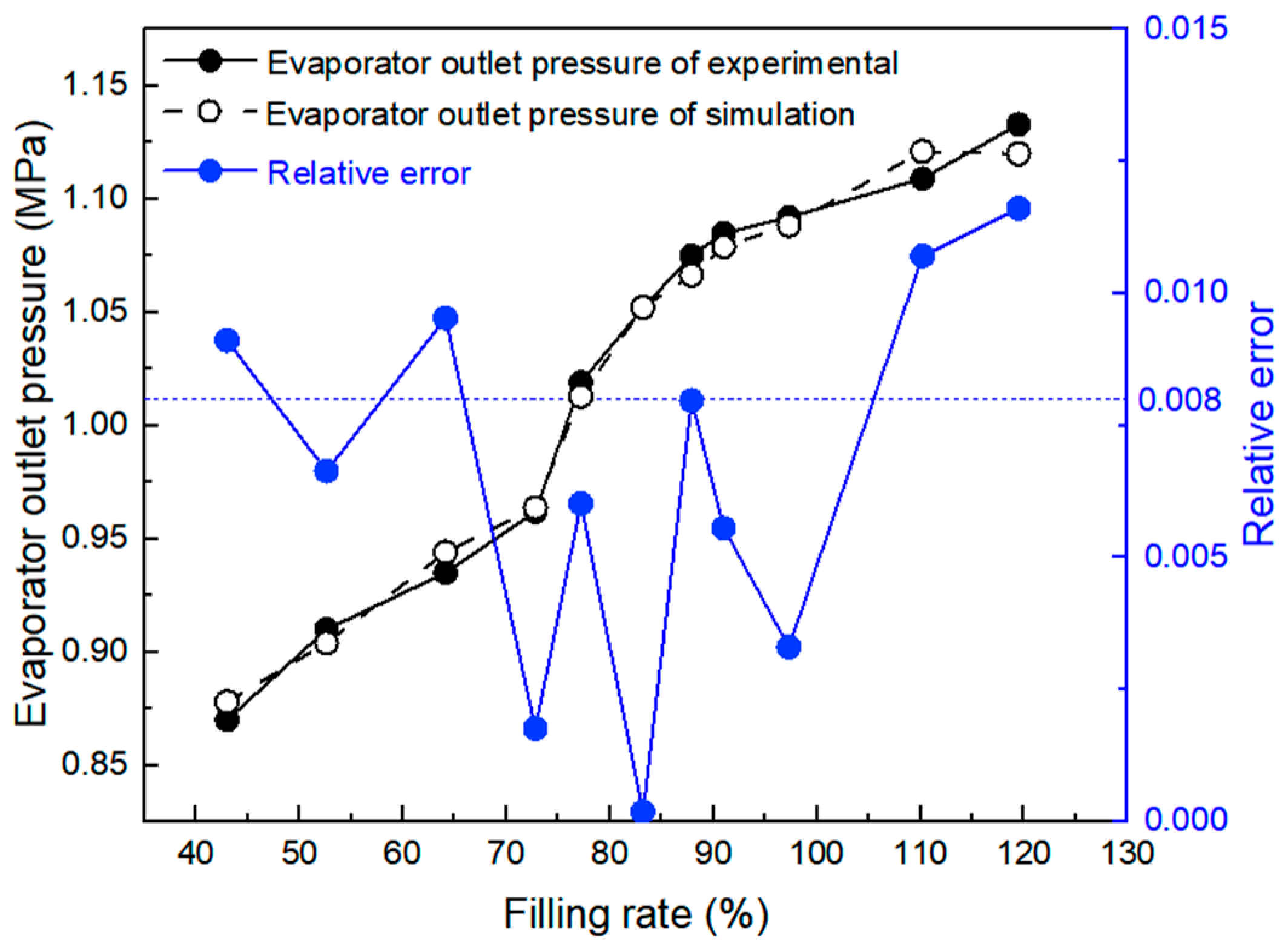
3.2. Comparison of Simulation and Experimental Results
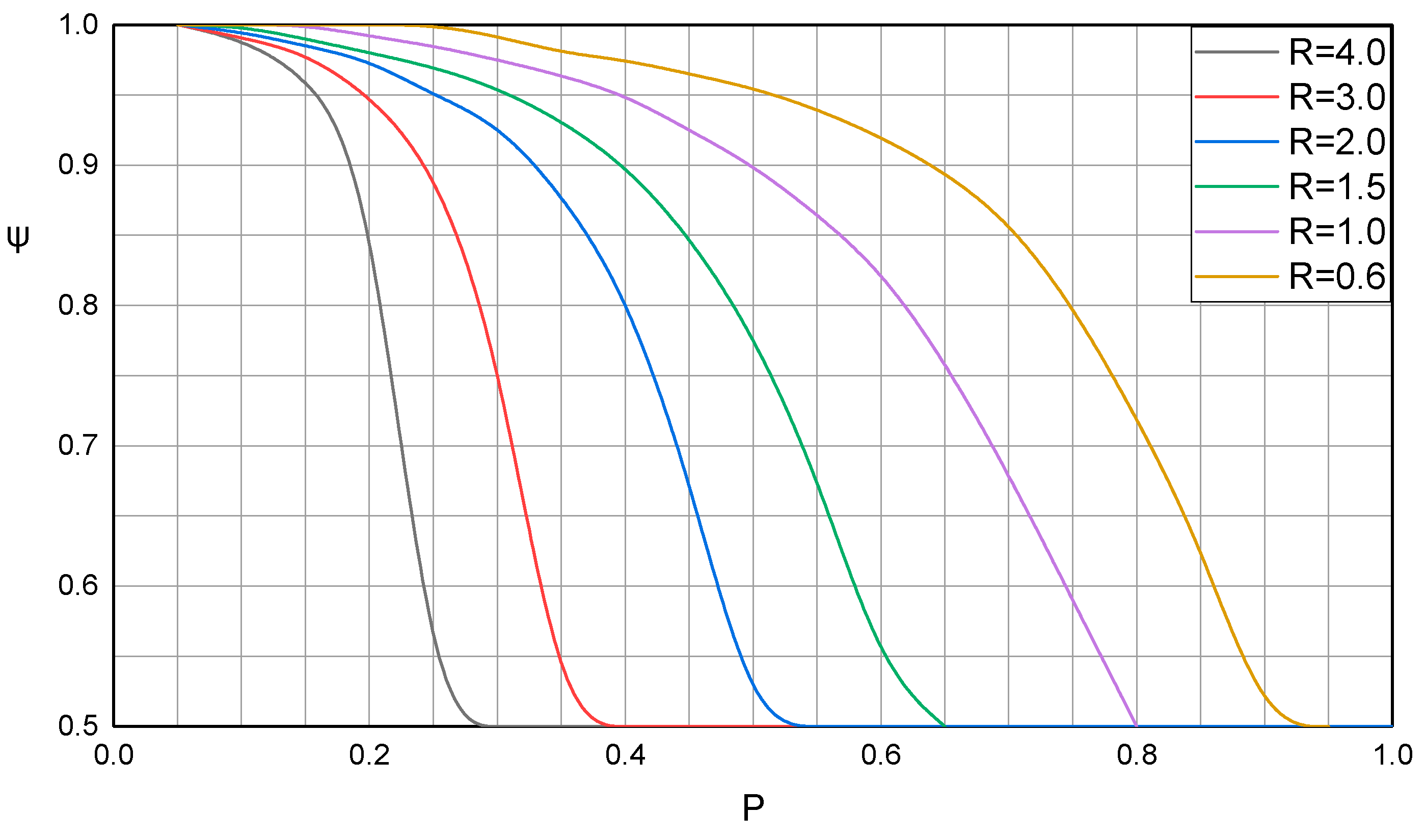
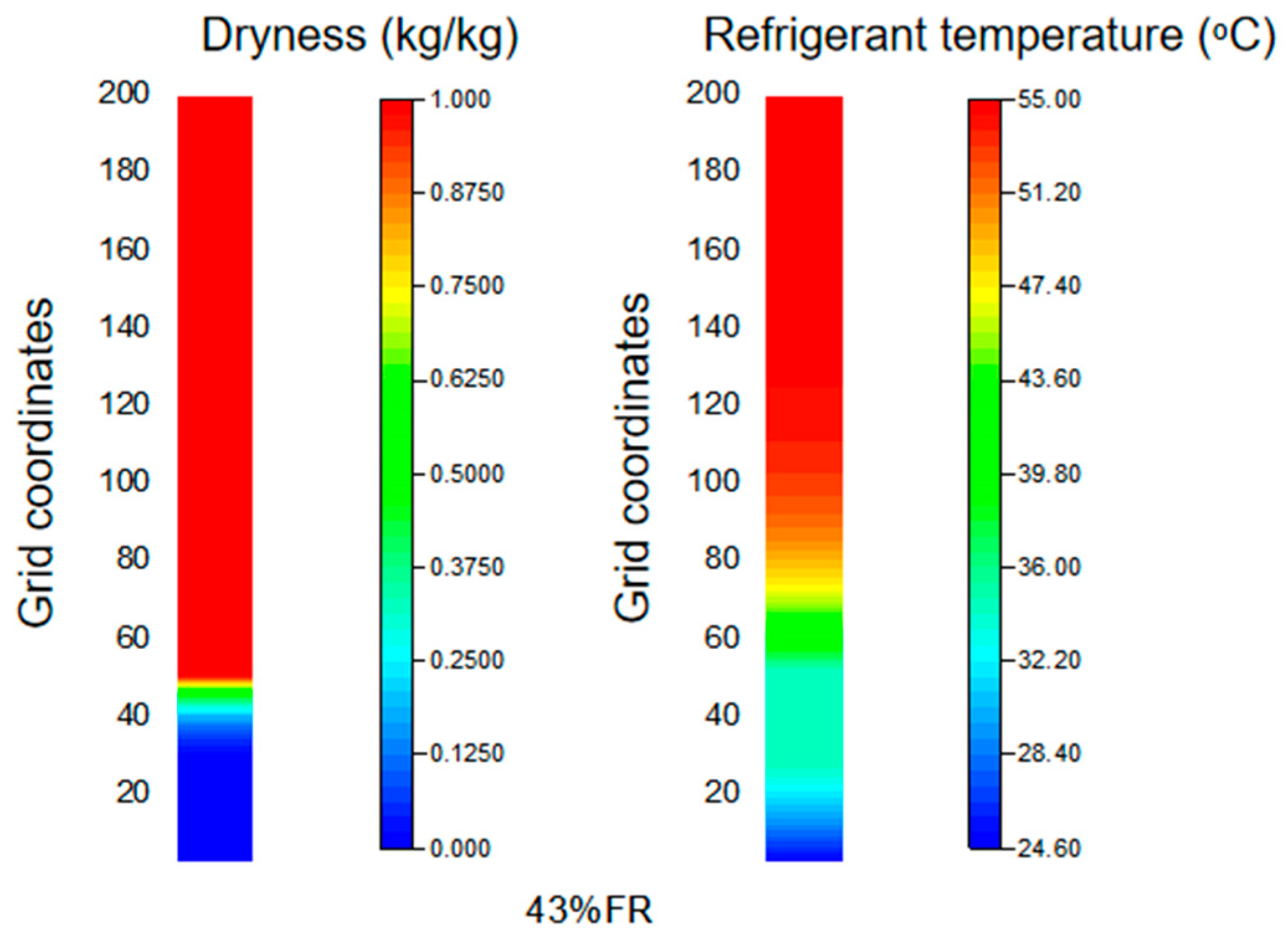
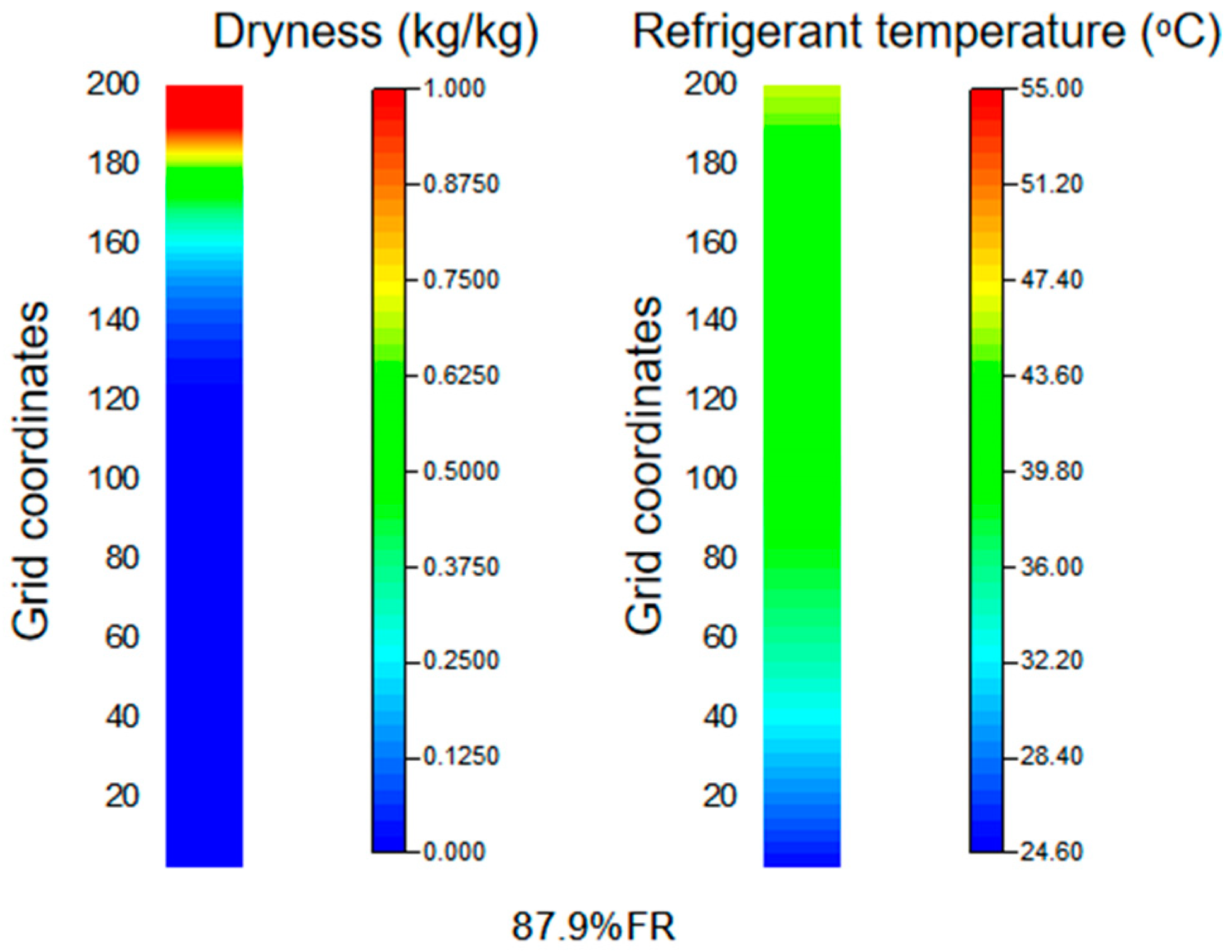
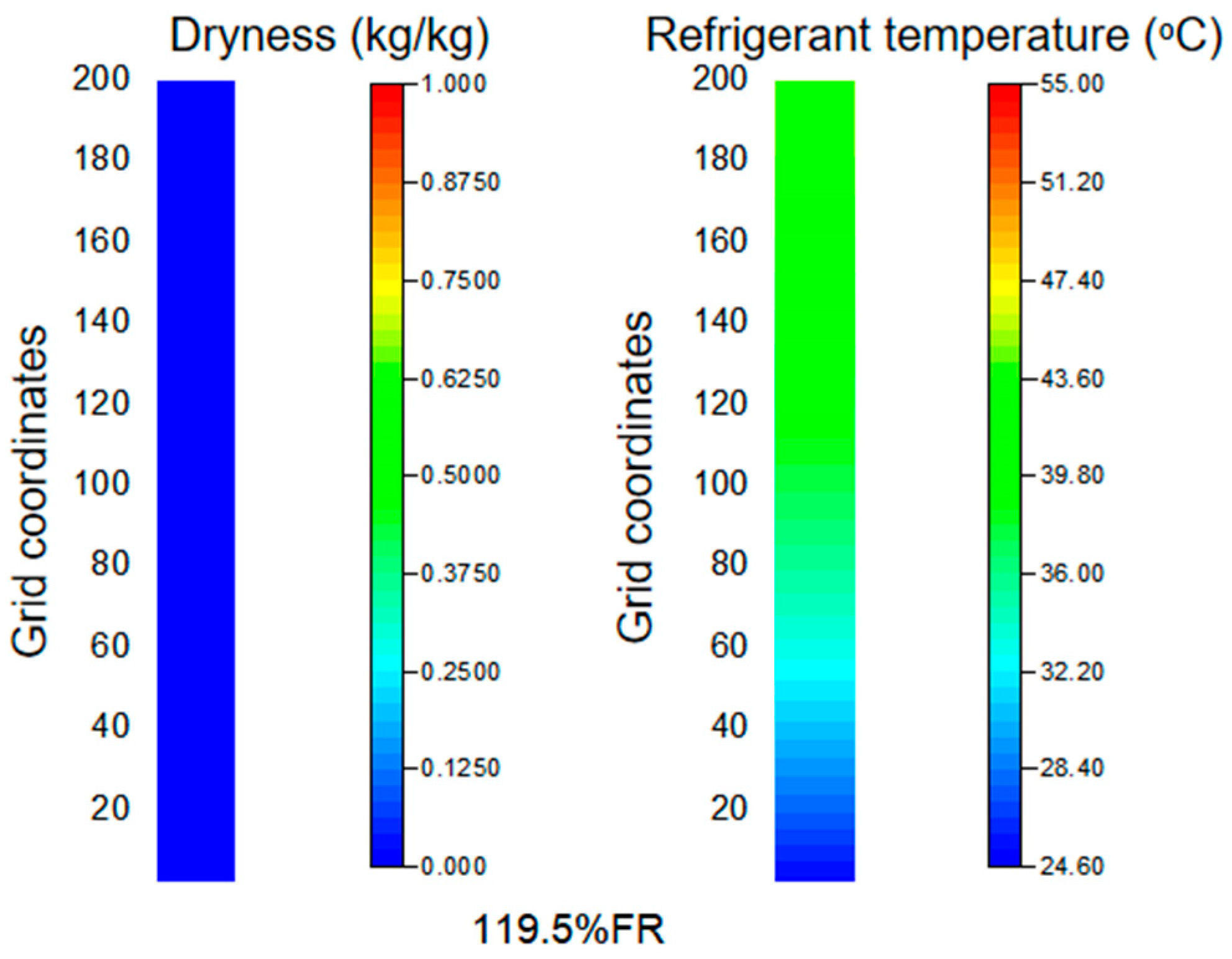
3.3. Analysis of Phase Change and Heat Transfer in Flat Tubes
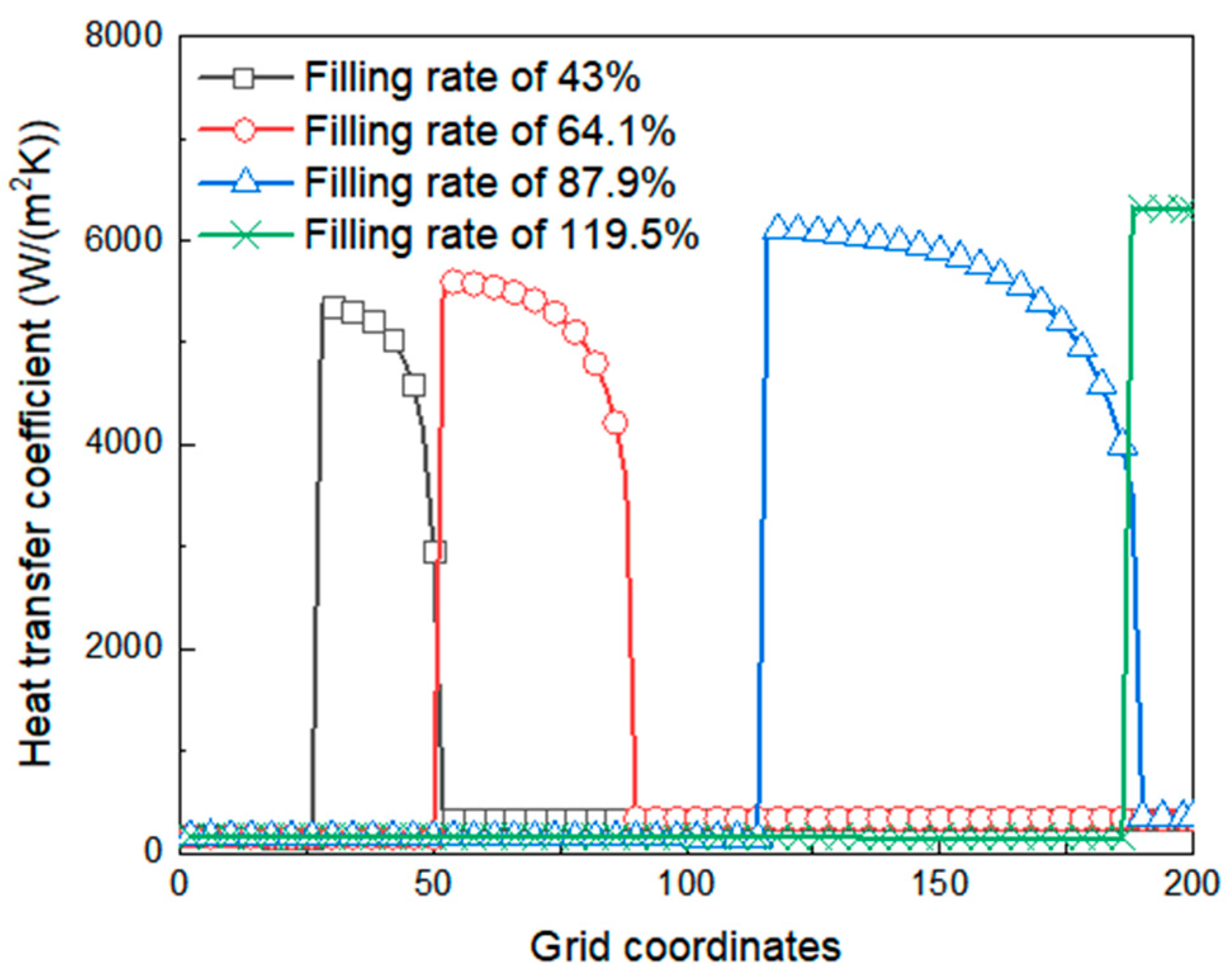
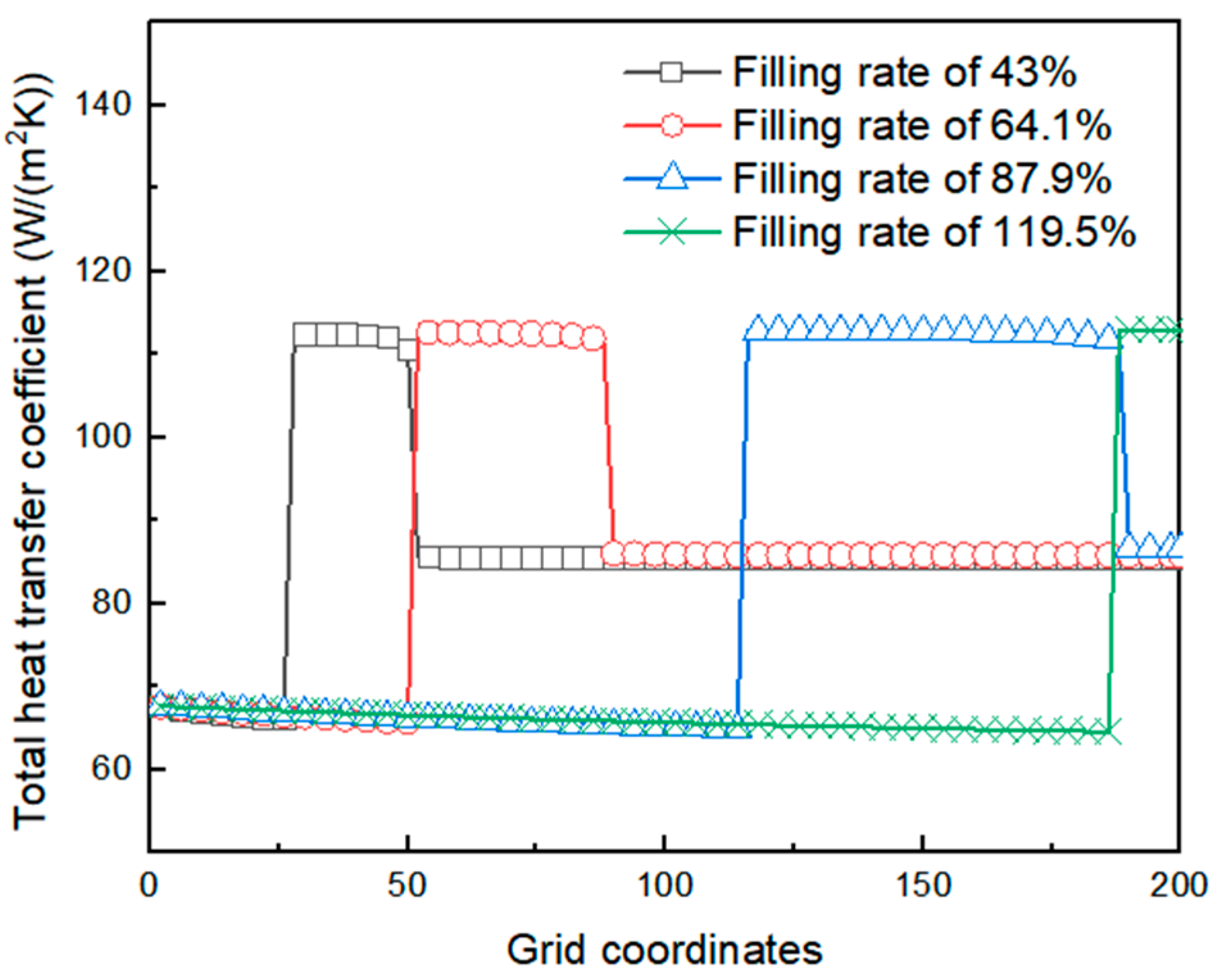
3.4. Heat Transfer Performance and Heat Transfer Mechanism Analysis
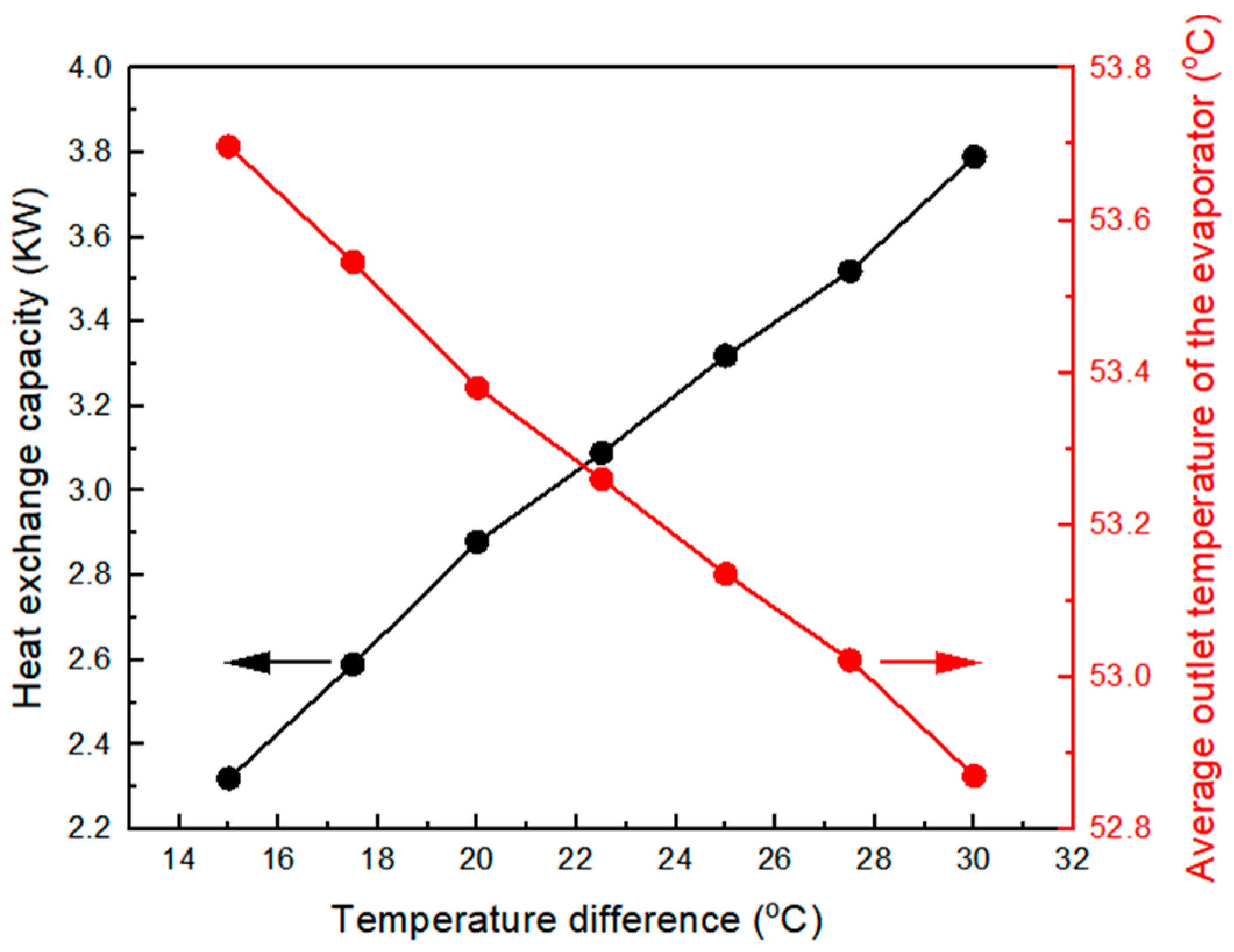
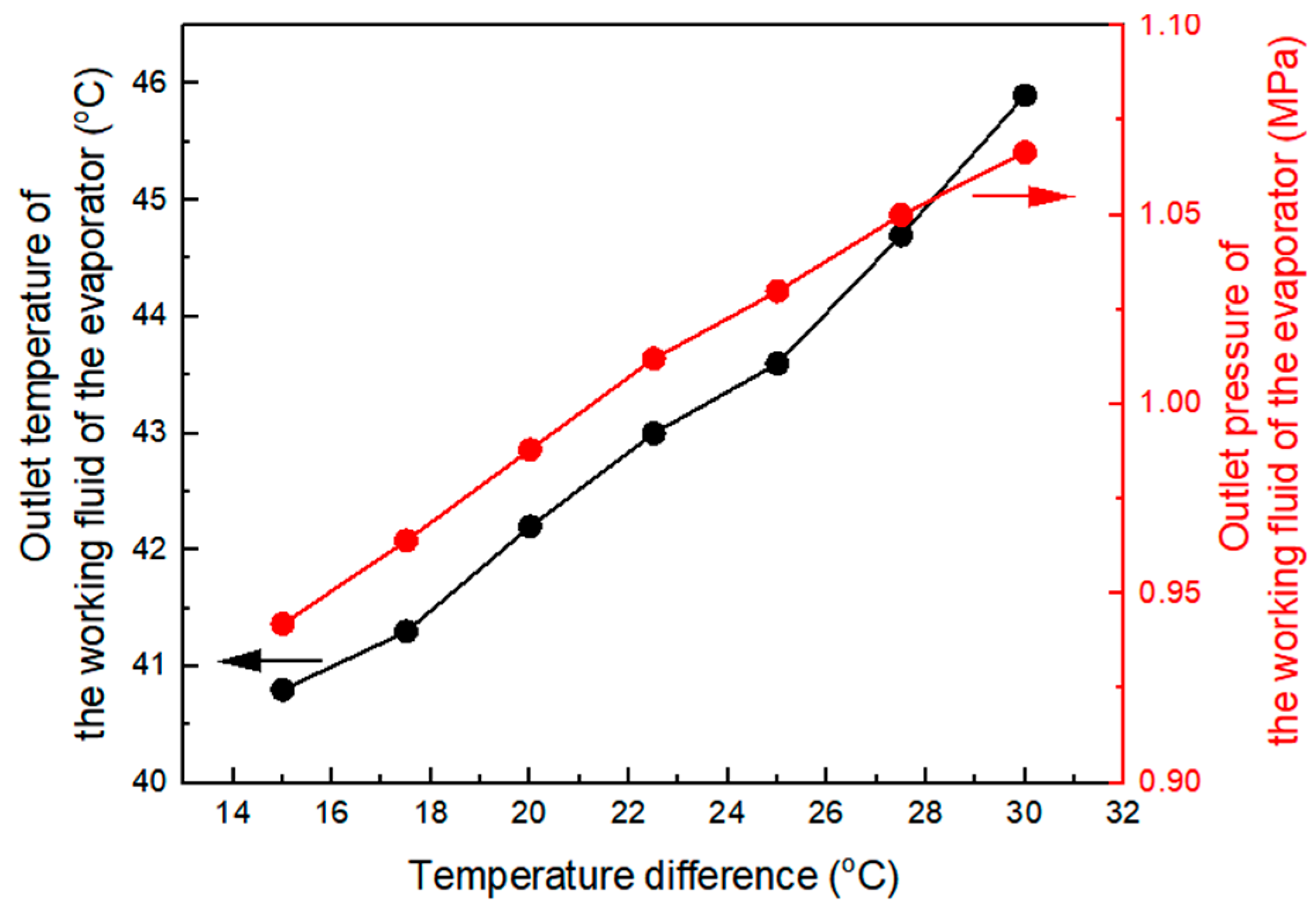
3.5. Effect of Temperature Difference on Heat Transfer Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weng, J.; Huang, Q.; Li, X.; Zhang, G.; Ouyang, D.; Chen, M.; Yuen, A.; Li, A.; Lee, E.; Yang, W.; et al. Safety issue on PCM-based battery thermal management: Material thermal stability and system hazard mitigation. Energy Storage Mater. 2022, 53, 580–612. [Google Scholar] [CrossRef]
- Samimi, F.; Babapoor, A.; Azizi, M.; Karimi, G. Thermal management analysis of a Li-ion battery cell using phase change material loaded with carbon fibers. Energy 2016, 96, 355–371. [Google Scholar] [CrossRef]
- Huang, Y.; Stonehouse, A.; Abeykoon, C. Encapsulation methods for phase change materials—A critical review. J. Heat Mass Transf. 2022, 200, 123458. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C.; Li, Y. Research and development of hydrogen energy safety. Emerg. Manag. Sci. Technol. 2022, 2, 1–9. [Google Scholar] [CrossRef]
- Dallaire, J.; Gosselin, L. Various ways to take into account density change in solid-liquid phase change models: Formulation and consequences. Int. J. Heat Mass Transf. 2016, 163, 672–683. [Google Scholar] [CrossRef]
- Chao, W.; Chen, L.; Kang, L. Method for quantitative expression of psychological safety and security distance (PSSD) using fuzzy theory. Emerg. Manag. Sci. Technol. 2022, 2, 1–8. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, Z.X.; Wang, T.; Han, Y.; Liu, H.; Miao, Z.; Huang, R.; Li, L. Directional thermal conductive PEG@BNNS composites enhanced tri-function passive radiative cooler for thermal management of high-power density devices. Compos. Sci. Technol. 2024, 258, 110889. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, J.; Gao, M.; Liu, M.; Tao, J. Review on loss prevention of chemical reaction thermal runaway: Principles and application. Emerg. Manag. Sci. Technol. 2022, 10, 1–8. [Google Scholar] [CrossRef]
- Lv, Y.F.; Yang, X.Q.; Zhang, G.Q. Durability of phase-change-material module and its relieving effect on battery deterioration during long-term cycles. Appl. Therm. Eng. 2020, 179, 115747. [Google Scholar] [CrossRef]
- Naghavi, M.S.; Ong, K.S.; Badruddin, I.A.; Mehrali, M.; Silakhori, M.; Metselaar, H.S.C. Theoretical model of an evacuated tube heat pipe solar collector integrated with phase change material. Energy 2015, 91, 911–924. [Google Scholar] [CrossRef]
- Hwang, F.S.; Confrey, T.; Reidy, C.; Picovici, D.; Callaghan, d.; Culliton, d.; Nolan, C. Review on battery thermal management system for electric vehicles. Renew. Sustain. Energy Rev. 2024, 192, 114171. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Yang, Y.C.; Qiu, H.H. A novel battery thermal management system utilizing ultrathin thermal ground planes for prismatic Lithium-ion batteries. Appl. Therm. Eng. 2023, 231, 120869. [Google Scholar] [CrossRef]
- Shen, J.B.; Wang, Y.P.; Yu, G.Z.; Li, H.G. Thermal Management of Prismatic Lithium-Ion Battery with Minichannel Cold Plate. J. Energy Eng. 2019, 146, 1943–7897. [Google Scholar] [CrossRef]
- Li, W.H.; Wang, X.; Cen, P.; Chen, Q.; Cordeiro, I.; Kong, L.; Lin, P.; Li, A. A Comparative Numerical Study of Lithium-Ion Batteries with Air-Cooling Systems towards Thermal Safety. Fire 2024, 7, 29. [Google Scholar] [CrossRef]
- Han, C.L.; Cheng, Y.J.; Wang, Z.R.; Zheng, Y.Y. A study on the cooling characteristics of radiator for battery hot spots based on temperature hydrogel adaptive valve. J. Energy Storage 2024, 102, 114107. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Cacua, K.; Buitrago-Sierra, R.; Herrera, B.; Pabon, E.; Sohel-Murshed, S. Nanofluids’ stability effects on the thermal performance of heat pipes: A critical review. J. Therm. Anal. Calorim. 2019, 136, 1597–1614. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Yue, M.; Chen, J.; Zhu, H.; Deng, Y.; Zhu, Y.; Zhang, F.; Wen, M.; Zhang, B.; Kang, S. Effects of the different air cooling strategies on cooling performance of a lithium-ion battery module with baffle. Appl. Therm. Eng. 2018, 144, 231–241. [Google Scholar] [CrossRef]
- Shen, X.Y.; Cai, T.A.; He, C.M.; Yang, Y.; Chen, M. Thermal analysis of modified Z-shaped air-cooled battery thermal management system for electric vehicles. J. Energy Storage 2023, 58, 106356. [Google Scholar] [CrossRef]
- Ren, D.S.; Feng, X.L.; Lu, L.G.; Ouyang, M.G.; Zheng, S.Q.; Li, J.Q.; He, X.M. An electrochemical-thermal coupled overcharge-to-thermal-runaway model for lithium ion battery. J. Power Sources 2017, 364, 328–340. [Google Scholar] [CrossRef]
- Wang, H.T.; Tao, T.; Xu, J.; Shi, H.; Mei, X.S.; Guo, P.A. Thermal performance of a liquid-immersed battery thermal management system for lithium-ion pouch batteries. J. Energy Storage 2022, 46, 103835. [Google Scholar] [CrossRef]
- Chen, D.F.; Jiang, J.C.; Kim, G.H.; Yang, C.B.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Ping, P.; Zhang, Y.; Kong, D.P.; Du, J. Investigation on battery thermal management system combining phase changed material and liquid cooling considering non-uniform heat generation of battery. J. Energy Storage 2021, 36, 102448. [Google Scholar] [CrossRef]
- Wiriyasart, S.; Hommalee, C.; Sirikasemsuk, S.; Prurapark, R.; Naphon, P. Thermal management system with nanofluids for electric vehicle battery cooling modules. Case Stud. Therm. Eng. 2020, 18, 100583. [Google Scholar] [CrossRef]
- Rao, Z.H.; Wang, S.F. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Ran, Y.; Su, Y.F.; Chen, L.; Yan, K.; Yang, C.X.; Zhao, Y. Investigation on thermal performance of water-cooled Li-ion cell and module with tree-shaped channel cold plate. Energy Storage 2022, 50, 104040. [Google Scholar] [CrossRef]
- Chen, X.C.; Yan, S.T.; Wang, D.; Han, J.Q.; Guang, Z.R.; Yin, Y.H.; Yang, S.T.; Dong, H.Y. A novel bionic lotus leaf channel liquid cooling plate for enhanced thermal management of lithium-ion batteries. Int. J. Heat Mass Transf. 2025, 236, 126246. [Google Scholar] [CrossRef]
- Liu, F.F.; Chen, Y.Y.; Qin, W.; Li, J. Optimal design of liquid cooling structure with bionic leaf vein branch channel for power battery. Appl. Therm. Eng. 2023, 218, 119283. [Google Scholar] [CrossRef]
- Liu, N.; Jiang, Y.M.; Liu, X.J.; Sun, Z.; Huang, J.B. Thermal performance analysis and structure optimization of bionic shark skin channel liquid cooling plate for lithium ion battery. Appl. Therm. Eng. 2025, 279, 127683. [Google Scholar] [CrossRef]
- Liang, L.; Zhao, Y.H.; Diao, Y.H.; Ren, R.Y.; Zhu, T.T.; Li, Y. Experimental investigation of preheating performance of lithium-ion battery modules in electric vehicles enhanced by bending flat micro heat pipe array. Appl. Energy 2023, 337, 120896. [Google Scholar] [CrossRef]
- Behi, H.; Behi, M.; Karimi, D.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van-Mierlo, J. Heat pipe air-cooled thermal management system for lithium-ion batteries: High power applications. Appl. Therm. Eng. 2021, 183, 116240. [Google Scholar] [CrossRef]
- Chen, K.; Hou, J.S.; Song, M.X.; Wang, S.F.; Wu, W.; Zhang, Y.L. Design of battery thermal management system based on phase change material and heat pipe. Appl. Therm. Eng. 2021, 188, 116665. [Google Scholar] [CrossRef]
- Zhang, D.; Li, G.; Liu, Y.Q.; Tian, X.L. Simulation and experimental studies of R134a flow condensation characteristics in a pump-assisted separate heat pipe. Int. J. Heat Mass Transf. 2018, 126, 1020–1030. [Google Scholar] [CrossRef]
- Ambrose, J.H.; Feild, A.R.; Holmes, H.R. A pumped heat pipe cold plate for high-flux applications. Exp. Therm. Fluid Sci. 1995, 10, 156–162. [Google Scholar] [CrossRef]
- Salvatore, V.; Valeria, P.; Davide, L.R.; Bonanno, A. Experimental assessment and numerical study of a pump-assisted loop heat pipe for high capacity thermal systems. Appl. Therm. Eng. 2020, 180, 115828. [Google Scholar] [CrossRef]
- Vachhani, M.; Sagar, K.R.; Patel, V.M.; Mehta, H. Novel integration of dual evaporator loop heat pipe for improved electric vehicle battery thermal regulation. Appl. Therm. Eng. 2024, 236, 121832. [Google Scholar] [CrossRef]
- Bivens, D.B.; Yokozeki, A. Heat transfer coefficient and transfer properties for alternative refrigerants. In Proceedings of the 1994 International Refrigeration Conference at Purdue, West Lafayette, IN, USA, 19–22 July 1994; pp. 299–304. [Google Scholar]
- Zhou, F.; Zhou, W.; Qiu, Q.F.; Yu, W.; Chu, X.Y. Investigation of fluid flow and heat transfer characteristics of parallel flow double-layer microchannel heat exchanger. Appl. Therm. Eng. 2018, 137, 616–631. [Google Scholar] [CrossRef]
- Chen, S.P.; Xu, P.; Shi, J.; Sheng, L.S.; Han, C.L.; Chen, Z.Q. Experimental study of a pump-driven microchannel-separated heat pipe system. Sustainability 2023, 15, 16839. [Google Scholar] [CrossRef]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Inlet pressure (MPa) | 0.01 | Inlet enthalpy (kJ/kg) | 0.1 |
| Inlet temperature of evaporator (°C) | 55 | Inlet temperature of condenser (°C) | 25 |
| Inlet flow rate of evaporator (m3/h) | 2500 | Inlet flow rate of condenser (m3/h) | 3000 |
| Filling rate (%) | 50 | Mass flow rate in heat pipe (kg/s) | 0.01 |
| Heat pipe diameter (mm) | 16 | Heat pipe length (mm) | 4000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Si, L.; Xu, C.; Yu, W.; Gao, H.; Han, C. Simulation Study on Heat Transfer and Flow Performance of Pump-Driven Microchannel-Separated Heat Pipe System. Energies 2025, 18, 5882. https://doi.org/10.3390/en18225882
Huang Y, Si L, Xu C, Yu W, Gao H, Han C. Simulation Study on Heat Transfer and Flow Performance of Pump-Driven Microchannel-Separated Heat Pipe System. Energies. 2025; 18(22):5882. https://doi.org/10.3390/en18225882
Chicago/Turabian StyleHuang, Yanzhong, Linjun Si, Chenxuan Xu, Wenge Yu, Hongbo Gao, and Chaoling Han. 2025. "Simulation Study on Heat Transfer and Flow Performance of Pump-Driven Microchannel-Separated Heat Pipe System" Energies 18, no. 22: 5882. https://doi.org/10.3390/en18225882
APA StyleHuang, Y., Si, L., Xu, C., Yu, W., Gao, H., & Han, C. (2025). Simulation Study on Heat Transfer and Flow Performance of Pump-Driven Microchannel-Separated Heat Pipe System. Energies, 18(22), 5882. https://doi.org/10.3390/en18225882






