Numerical Modeling and Multiscale Evaluation of Fe3O4–Graphene Oxide Nanofluids in Electromagnetic Heating for Colombian Heavy Oil Recovery
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of Nanofluid
3. Methodology
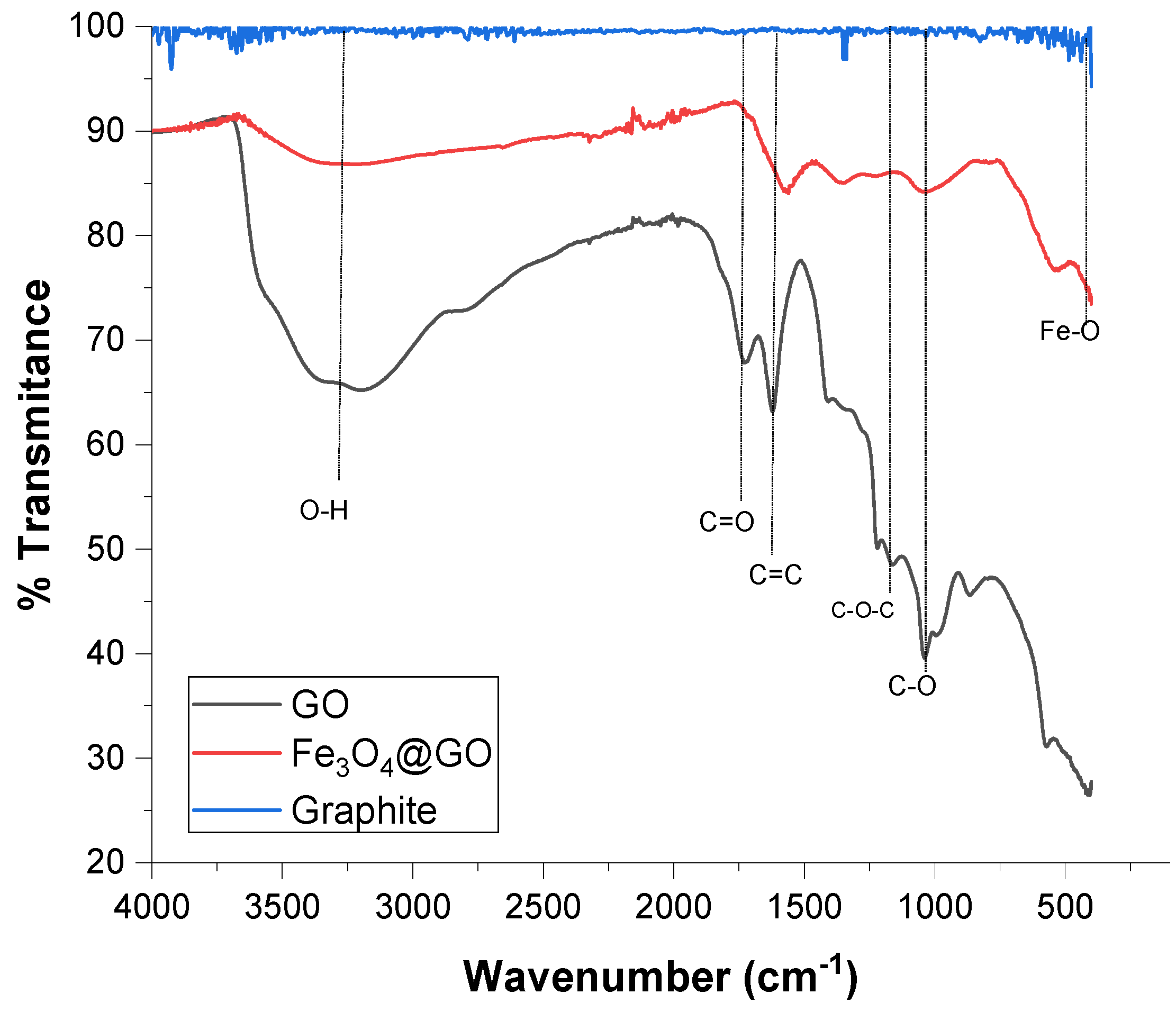
3.1. Characterization of the Graphene Oxide (GO) and Magnetic Graphene Oxide Fe3O4@GO)
3.2. Experimental Design to Evaluate Heat Transfer as a Function of Nanoparticle and Water Content in an EMH Process
- The base layer is the bed of river sand, which is compacted to form a level, uniform surface.
- A quartz tube is inserted above it to isolate the antenna.
- Then, the bottom control layer is placed, followed by the target layer, and finally the top control layer.
Simulation Matching for Data Processing
4. Results
4.1. Nanomaterial Characterization Results
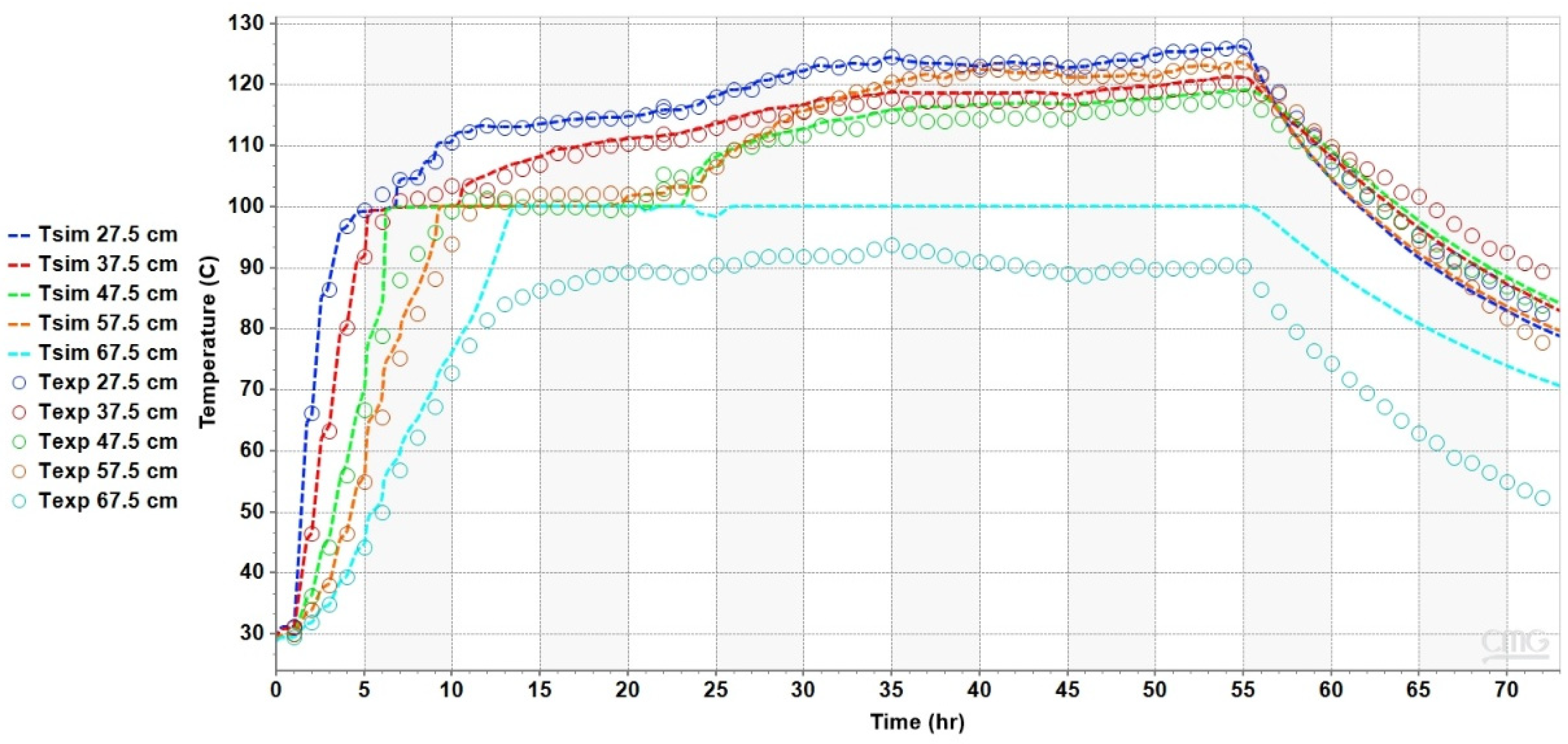
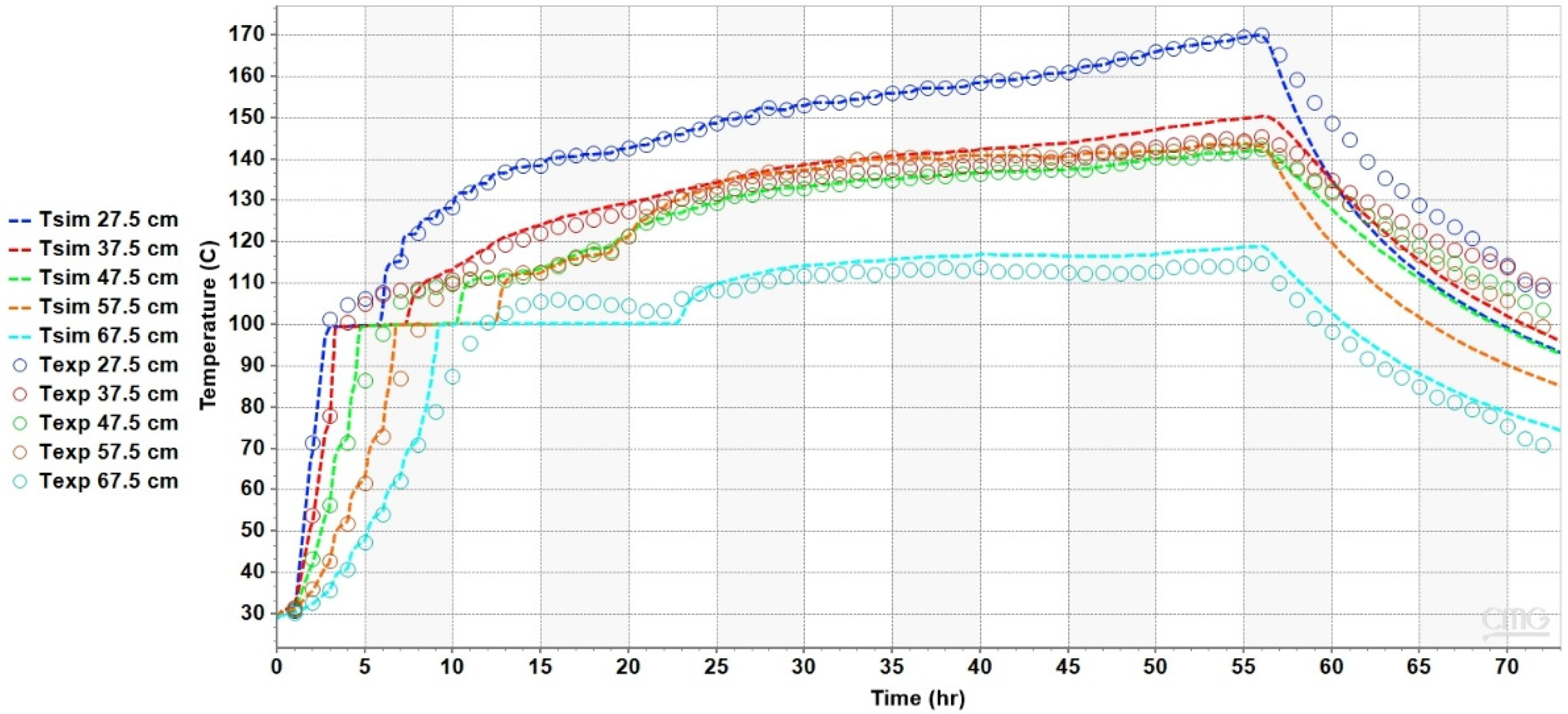
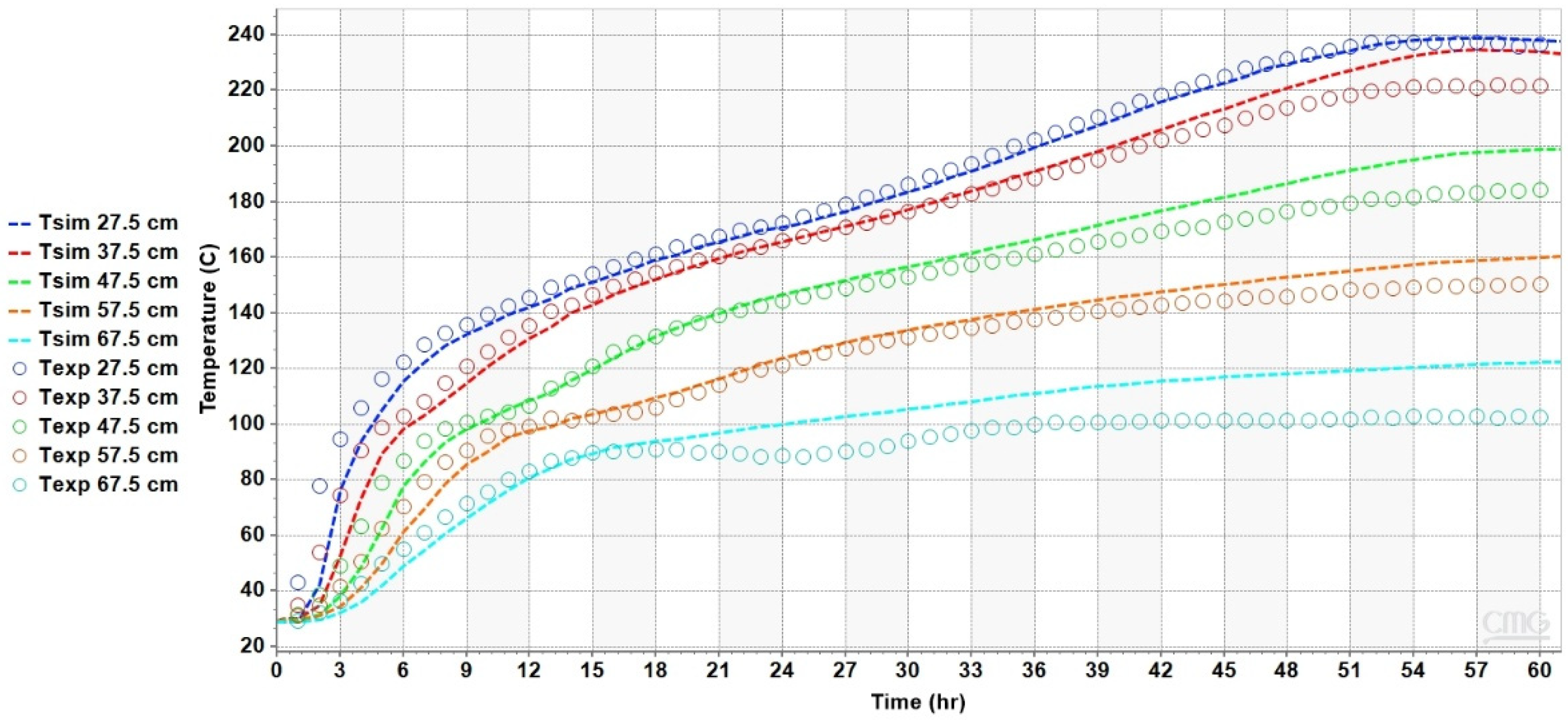
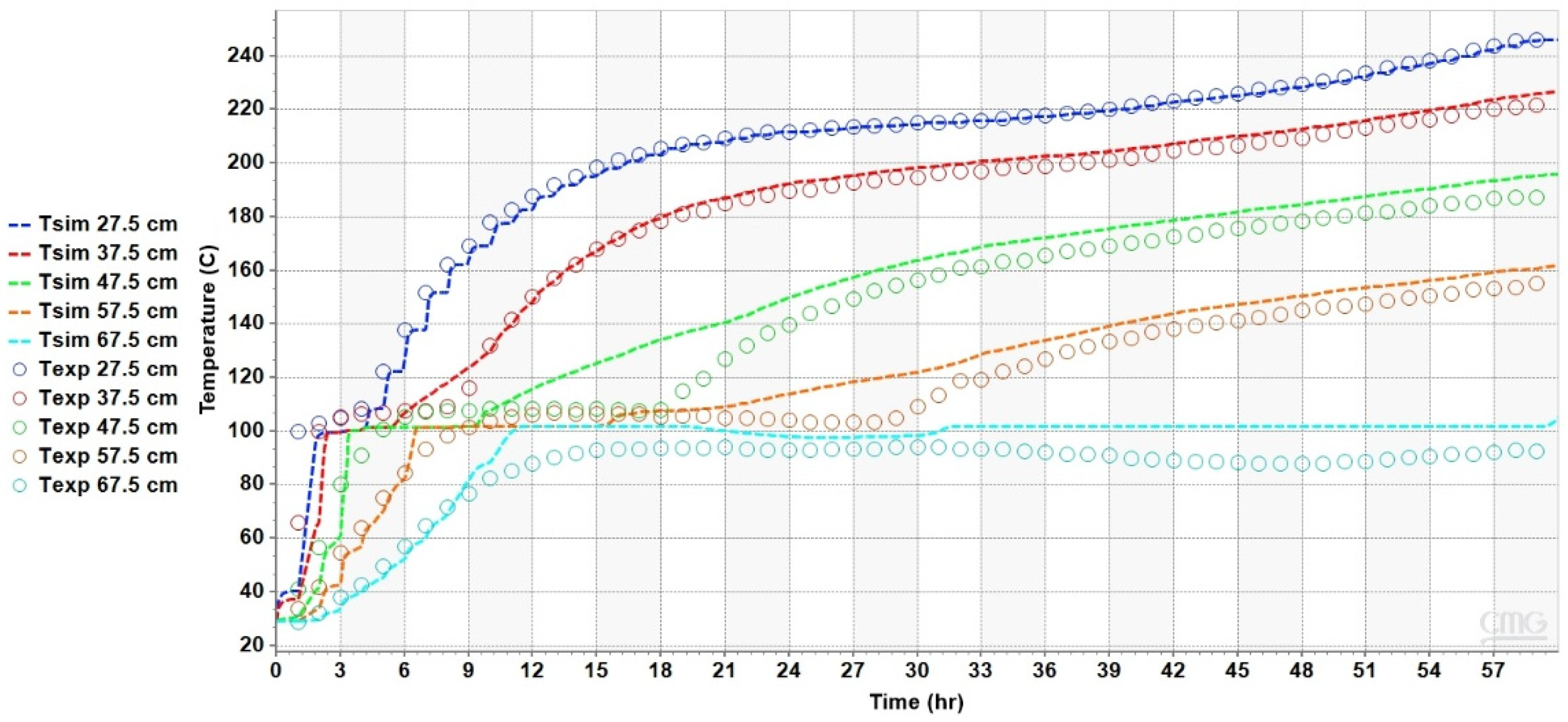
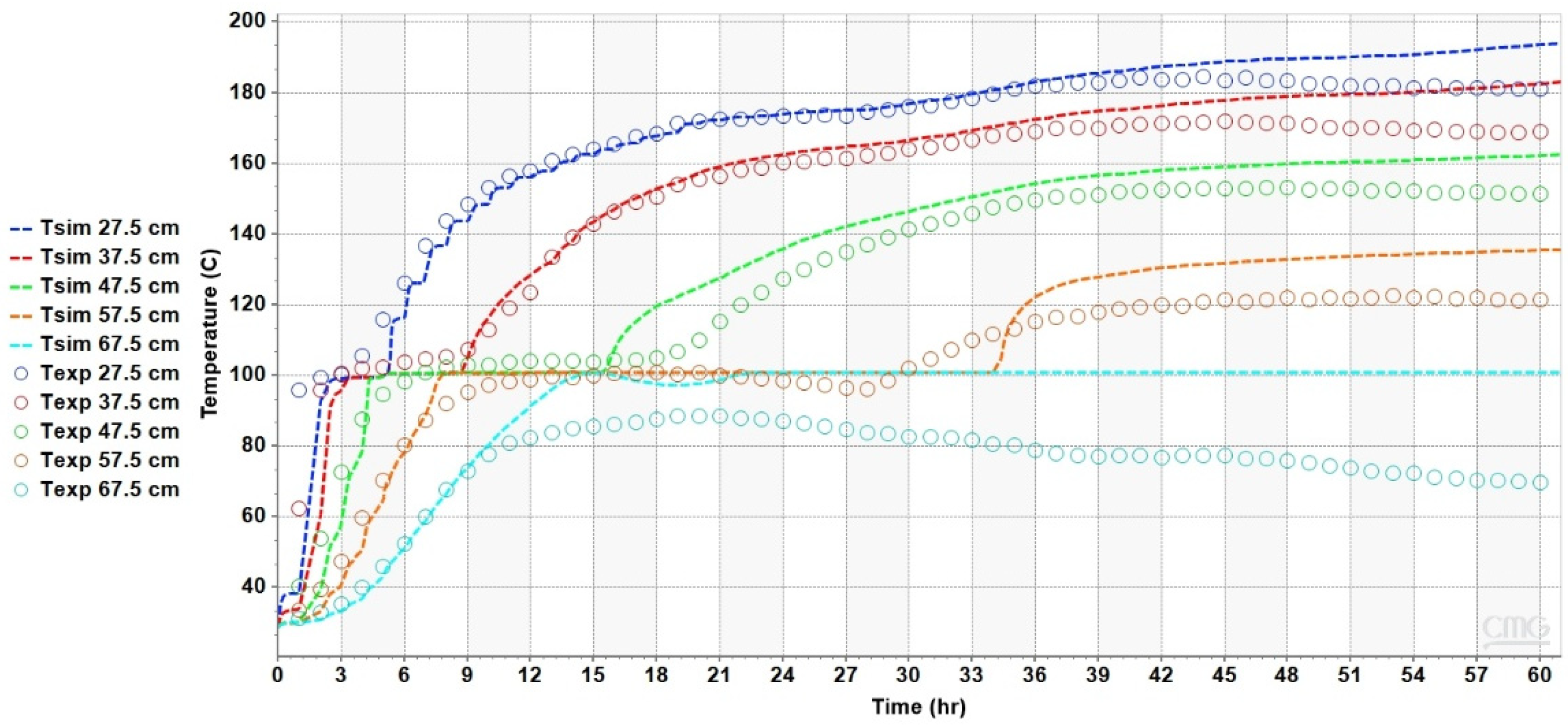
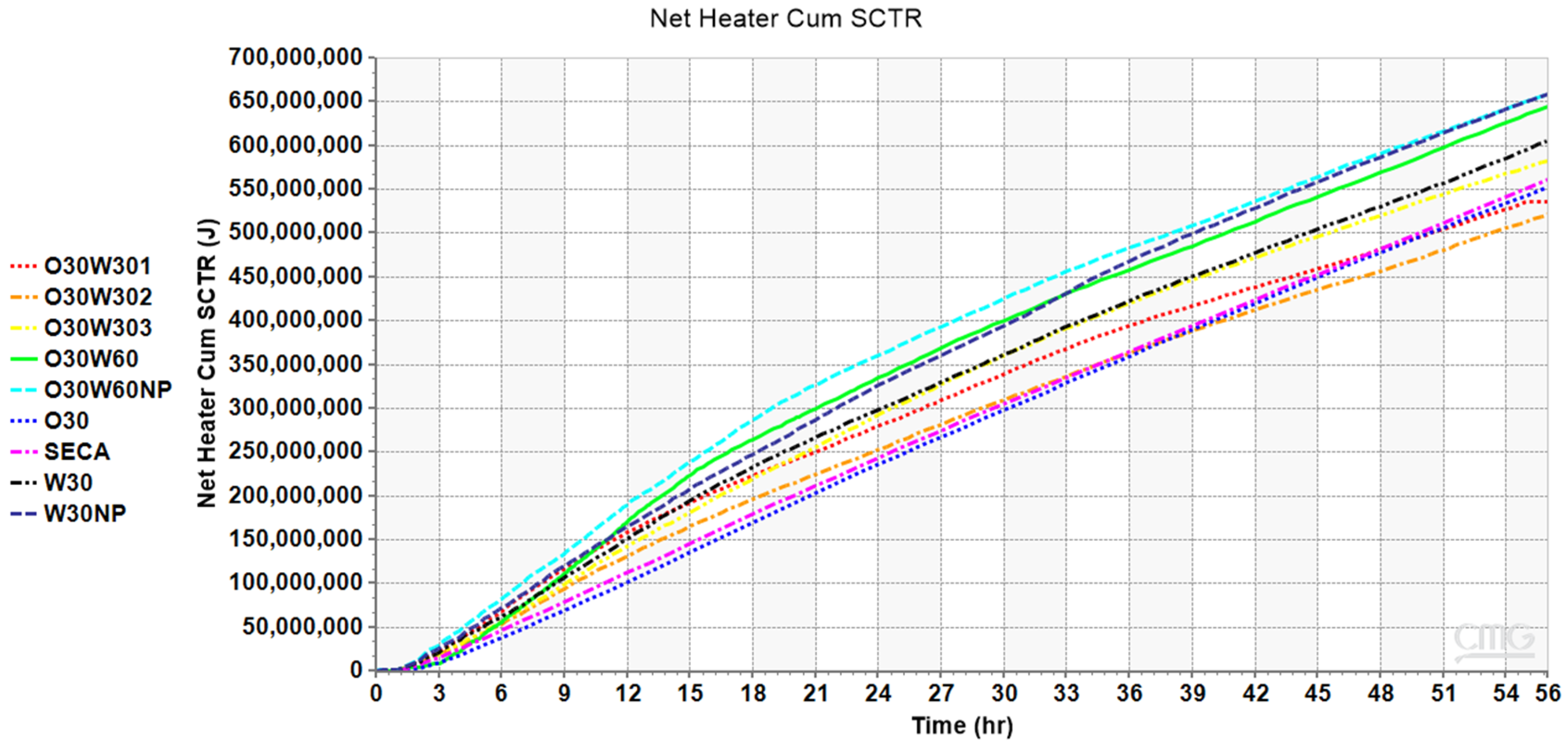
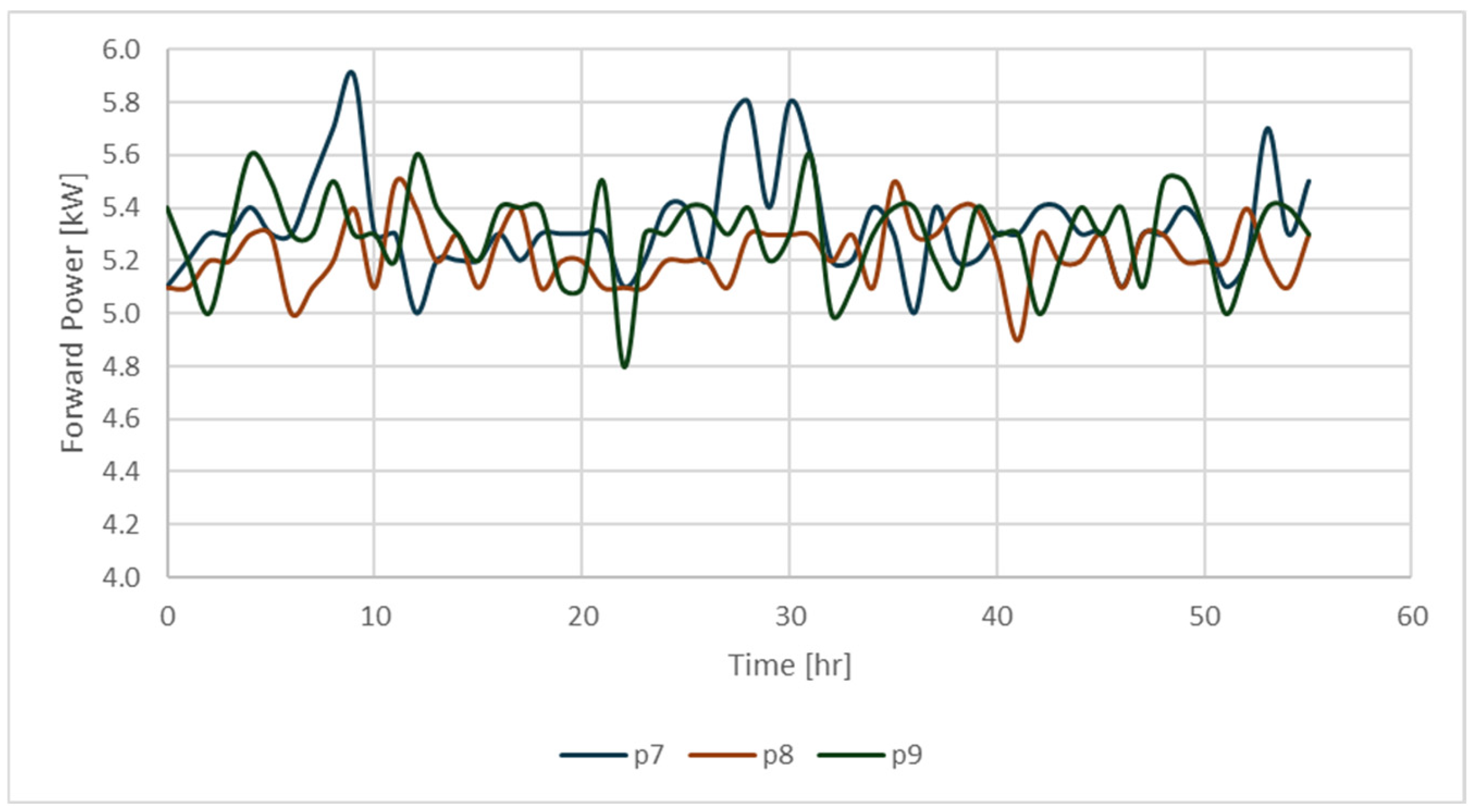
4.2. Results of the Heat Transfer Experiments
5. Analysis and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bjørnseth, F.; Gudmundsson, J.S. Heavy Oil Production Technology Challenges and the Effect of Nano Sized Metals on the Viscosity of Heavy Oil A Literature Review and an Experimental Study. Master’s Thesis, Norwegian University of Science and Technology (NTNU), Trondheim, Norway, 2013. [Google Scholar]
- Larter, S.R.; Head, I.M. Oil Sands and Heavy Oil: Origin and Exploitation. Elements 2014, 10, 277–283. [Google Scholar] [CrossRef]
- Guo, K.; Li, H.; Yu, Z. In-situ heavy and extra-heavy oil recovery: A review. Fuel 2016, 185, 886–902. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Hu, Z.; Xu, B.; Li, Y.; Pu, W.; Zhao, J. A review of in situ upgrading technology for heavy crude oil. Petroleum 2021, 7, 117–122. [Google Scholar] [CrossRef]
- Castañeda, L.; Muñoz, J.; Ancheyta, J. Combined process schemes for upgrading of heavy petroleum. Fuel 2012, 100, 110–127. [Google Scholar] [CrossRef]
- Wiehe, I.; Liang, K. Asphaltenes, resins, and other petroleum macromolecules. Fluid Ph. Equilib. 1996, 117, 201–210. [Google Scholar] [CrossRef]
- Sahni, A.; Kumar, M.; Knapp, R. Electromagnetic Heating Methods for Heavy Oil Reservoirs. In Proceedings of the SPE/AAPG Western Regional Meeting, Long Beach, CA, USA, 19–23 June 2000; pp. 1–10. [Google Scholar] [CrossRef]
- Ryles, R.G.; Cicchiello, J.V. New Polymers for EOR Applications. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, Oklahoma, 17–21 April 1986. [Google Scholar] [CrossRef]
- Spencer, H.W. Commercial application of radio frequency heating for heavy oil recovery in the Wildmere field, Alberta. J. Can. Pet. Technol. 1987, 26, 38–45. [Google Scholar] [CrossRef]
- Kasevich, R.S.; Price, S.L.; Faust, D.L.; Fontaine, M.F. Pilot Testing of a Radio Frequency Heating System for Enhanced Oil Recovery From Diatomaceous Earth. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, 25–28 September 1994. [Google Scholar] [CrossRef]
- Bottazzi, F.; Hanzlik, W.; Cardenas, E. Downhole electrical heating for heavy oil enhanced recovery: A successful application in offshore Congo. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13–15 January 2020. [Google Scholar] [CrossRef]
- Alomair, O.; Alarouj, M.; Althenayyan, A.; Alsaleh, A.; Mohammad, H.; Altahoo, Y.; Alhaidar, Y.; Alansari, S.; Alshammari, Y. Improving Heavy Oil Recovery by Unconventional Thermal Methods. In Proceedings of the SPE Kuwait International Petroleum Conference and Exhibition, Kuwait City, Kuwait, 12–14 December 2012. [Google Scholar] [CrossRef]
- Greff, J.; Babadagli, T. Use of nano-metal particles as catalyst under electromagnetic heating for in-situ heavy oil recovery. J. Pet. Sci. Eng. 2013, 112, 258–265. [Google Scholar] [CrossRef]
- Bera, A.; Babadagli, T. Status of electromagnetic heating for enhanced heavy oil/bitumen recovery and future prospects: A review. Appl. Energy 2015, 151, 206–226. [Google Scholar] [CrossRef]
- Kovaleva, L.; Davletbaev, A.; Babadagli, T.; Stepanova, Z. Effects of electrical and radio-frequency electromagnetic heating on the mass-transfer process during miscible injection for heavy-oil recovery. Energy Fuels 2010, 25, 482–486. [Google Scholar] [CrossRef]
- Hascakir, B.; Acar, C.; Akin, S. Microwave-assisted heavy oil production: An experimental approach. Energy Fuels 2009, 23, 6033–6039. [Google Scholar] [CrossRef]
- Sadeghi, A.; Hassanzadeh, H.; Harding, T.G. A comparative study of oil sands preheating using electromagnetic waves, electrical heaters and steam circulation. Int. J. Heat Mass Transf. 2017, 111, 908–916. [Google Scholar] [CrossRef]
- Bera, A.; Babadagli, T. Effect of native and injected nano-particles on the efficiency of heavy oil recovery by radio frequency electromagnetic heating. J. Pet. Sci. Eng. 2017, 153, 244–256. [Google Scholar] [CrossRef]
- Ovalles, C.; Vardeman, R.; Velasco, J.; Martínez, M. Opportunities of downhole dielectric heating in Venezuela: Three case studies involving medium, heavy, and extra-heavy crude oil reservoirs. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium and International Horizontal Well Conference, Calgary, Alberta, Canada, 4–7 November 2002; Society of Petroleum Engineers: Calgary, AB, Canada, 2002. [Google Scholar] [CrossRef]
- Hascakir, B. Microwave assisted gravity drainage of heavy oils. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 3–5 December 2008. [Google Scholar] [CrossRef]
- Hu, L.; Sun, Z.; Li, Y.; Chen, H. Experimental investigation of microwave-assisted thermal recovery in heavy oil reservoirs: Effects of frequency, salinity, and permeability. Fuel 2017, 207, 523–532. [Google Scholar] [CrossRef]
- Serga, V.; Burve, R.; Maiorov, M.; Krumina, A.; Skaudžius, R.; Zarkov, A.; Kareiva, A.; Popov, A.I. Impact of Gadolinium on the Structure and Magnetic Properties of Nanocrystalline Powders of Iron Oxides Produced by the Extraction-Pyrolytic Method. Materials 2020, 13, 4147. [Google Scholar] [CrossRef]
- Bleija, M.; Platnieks, O.; Macutkevič, J.; Banys, J.; Starkova, O.; Grase, L.; Gaidukovs, S. Poly(Butylene Succinate) Hybrid Multi-Walled Carbon Nanotube/Iron Oxide Nanocomposites: Electromagnetic Shielding and Thermal Properties. Polymers 2023, 15, 515. [Google Scholar] [CrossRef]
- Gerbreders, V.; Krasovska, M.; Sledevskis, E.; Mihailova, I.; Mizers, V. Co3O4 Nanostructured Sensor for Electrochemical Detection of H2O2 as a Stress Biomarker in Barley: Fe3O4 Nanoparticles-Mediated Enhancement of Salt Stress Tolerance. Micromachines 2024, 15, 311. [Google Scholar] [CrossRef]
- Zhang, T.; Zou, Q.; Cheng, Z.; Chen, Z.; Liu, Y.; Jiang, Z. Effect of particle concentration on the stability of water-based SiO2 nanofluid. Powder Technol. 2021, 379, 457–465. [Google Scholar] [CrossRef]
- Zou, Q.; Ma, T.; Liang, J.; Xu, B.; Ran, Q. Mesomechanical weakening mechanism of coal modified by nanofluids with disparately sized SiO2 nanoparticles. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2025, 188, 106056. [Google Scholar] [CrossRef]
- Zou, Q.; Zhang, T.; Ma, T.; Tian, S.; Jia, X.; Jiang, Z. Effect of water-based SiO2 nanofluid on surface wettability of raw coal. Energy 2022, 254, 124228. [Google Scholar] [CrossRef]
- Ma, T.; Zou, Q.; Wang, P.; Li, Q.; Fan, C.; Ran, Q.; Xu, B.; Huo, Z.; Zhang, J. Regulation mechanism of surfactant-SiO2 nanoparticle compound on mechanical property and microstructure of coal: Effect of the type of surfactant. Powder Technol. 2025, 466, 121459. [Google Scholar] [CrossRef]
- Gómez-Delgado, J.L.; Gutierrez-Niño, N.; Carrillo-Moreno, L.F.; Martínez-López, R.A.; Santos-Santos, N.; Mejía-Ospino, E. Experimental Assessment of Magnetic Nanofluid Injection in High-Salinity and Heavy-Crude-Saturated Sandstone: Mitigation of Formation Damage. Energies 2025, 18, 212. [Google Scholar] [CrossRef]
- Nguyen, N.; Chen, Z.; Almao, P.P.; Scott, C.E.; Maini, B. Reservoir Simulation and Production Optimization of Bitumen/Heavy Oil via Nanocatalytic in Situ Upgrading. Ind. Eng. Chem. Res. 2017, 56, 14214–14230. [Google Scholar] [CrossRef]
- Yamauchi, T. Electromagnetic Heating. In Soft Actuators; Asaka, K., Okuzaki, H., Eds.; Springer: Tokyo, Japan, 2014. [Google Scholar] [CrossRef]
- Al-Farsi, H.; Pourafshary, P.; Al-Maamari, R.S. Application of nanoparticles to improve the performance of microwave assisted gravity drainage (MWAGD) as a thermal oil recovery method. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 21–23 March 2016. [Google Scholar] [CrossRef]
- Davidson, A.; Huh, C.; Bryant, S.L. Focused Magnetic Heating Utilizing Superparamagnetic Nanoparticles for Improved Oil Production Applications. In Proceedings of the SPE International Oilfield Nanotechnology Conference and Exhibition, Noordwijk, The Netherlands, 12–14 June 2012. [Google Scholar]
- Bientinesi, M.; Petarca, L.; Cerutti, A.; Bandinelli, M.; De Simoni, M.; Manotti, M.; Maddinelli, G. A radiofrequency/microwave heating method for thermal heavy oil recovery based on a novel tight-shell conceptual design. J. Pet. Sci. Eng. 2013, 107, 18–30. [Google Scholar] [CrossRef]
- Salas-Chia, L.M.; Núñez-Mendez, K.S.; León, P.A.; Muñoz, S.F.; León, A.Y. Metodología para la simulación numérica de la adición de agentes catalíticos en procesos de inyección de vapor. Rev. ION 2022, 35, 17–32. [Google Scholar] [CrossRef]
- León Naranjo, P.A.; Muñoz Navarro, S.F.; León Bermudez, A.Y.; Bottia Ramirez, H. Efecto del uso de Catalizadores Sobre la Recuperación Mejorada de Crudos Pesados en Procesos de Inyección de Vapor; Universidad Industrial de Santander: Bucaramanga, Colombia, 2019; pp. 36–40. [Google Scholar]
- Sadeghi, A.; Hassanzadeh, H.; Harding, T.G.; MacFarlane, B.; Bashti, S.; Haghighat, P. Numerical modeling of electromagnetic-based thermal recovery techniques combined with solvent injection. Int. J. Heat Mass Transf. 2020, 151, 119393. [Google Scholar] [CrossRef]
- Zinnatullin, R.R.; Musin, A.A.; Kovaleva, L.A. Study of Heating of Oil Source Rocks in a High-Frequency Electromagnetic Field by the Method of Physico-Mathematical Modeling. High Temp. 2022, 60, 136–139. [Google Scholar] [CrossRef]
- Zinnatullin, R.R.; Musin, A.A.; Gaisin, I.V.; Usmanov, B.A. Physical and Mathematical Modeling of the Temperature Distribution Along the Length of Oil Source Rocks under Microwave Irradiation. High Temp. 2023, 61, 138–141. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Ching, D.L.C.; Sakidin, H.; Muthuvalu, M.S.; Zafar, M.; Haruna, A.; Merican, Z.M.A.; Azad, A.S. A New 3D Mathematical Model for Simulating Nanofluid Flooding in a Porous Medium for Enhanced Oil Recovery. Materials 2023, 16, 5414. [Google Scholar] [CrossRef]
- Dong, X.; Duan, Z.; Nie, T.; Gao, D. An analytical model for reservoir temperature during electromagnetic heating based on power transmission. Appl. Therm. Eng. 2023, 219, 119441. [Google Scholar] [CrossRef]
- Sun, C.; Liu, W.; Wang, B.; Ma, T.; Guo, C. Modeling microwave heating for enhanced shale gas recovery: Fully coupled two-phase flows with heat transfer and electromagnetism in deformable reservoirs. Appl. Therm. Eng. 2024, 248, 123190. [Google Scholar] [CrossRef]
- Yang, S.; Wang, H.; Lou, X.; Li, Z.; Pan, Y.; Zhao, X. The study of core and particle model of Fushun oil shale based on microwave field. J. Anal. Appl. Pyrolysis 2024, 179, 106496. [Google Scholar] [CrossRef]
- Chen, H.-W.; Zhang, S.-S.; Li, Y.; Xu, C.; Qin, S.-X. Multi-Physical Field Numerical Simulation of Electromagnetic Heating in Heavy Oil Reservoirs With Different Well Configurations. J. Therm. Sci. Eng. Appl. 2024, 16, 031006. [Google Scholar] [CrossRef]
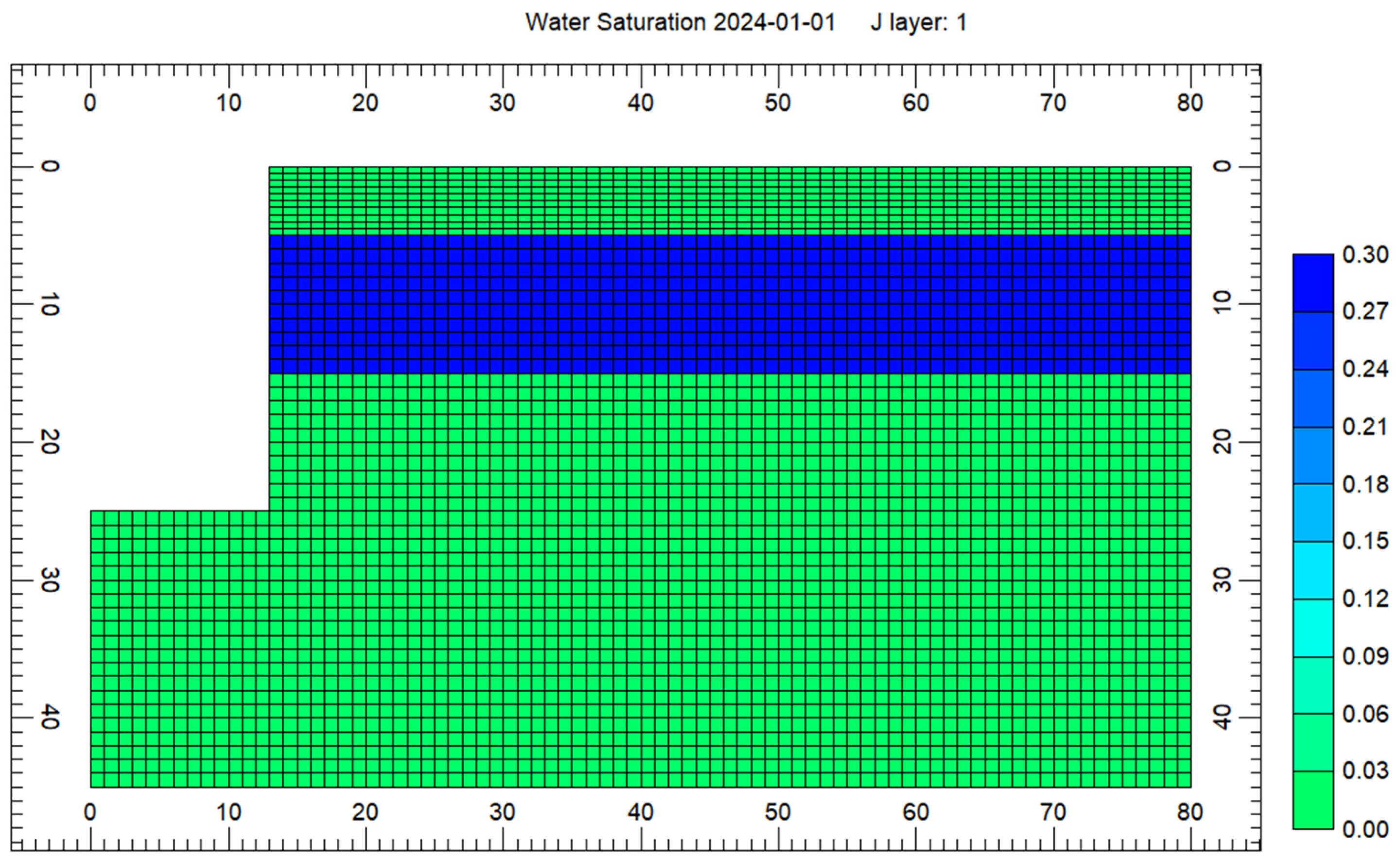






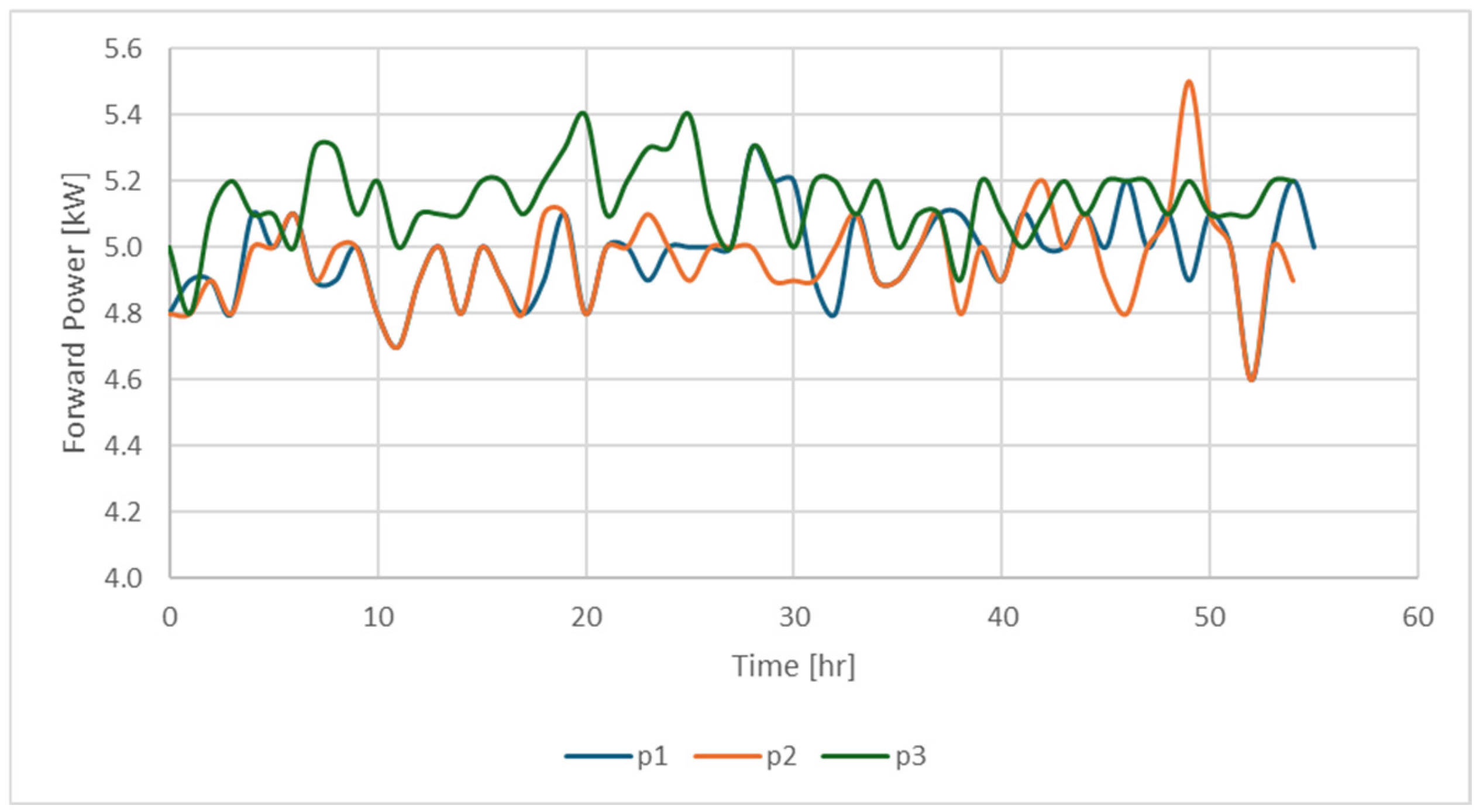
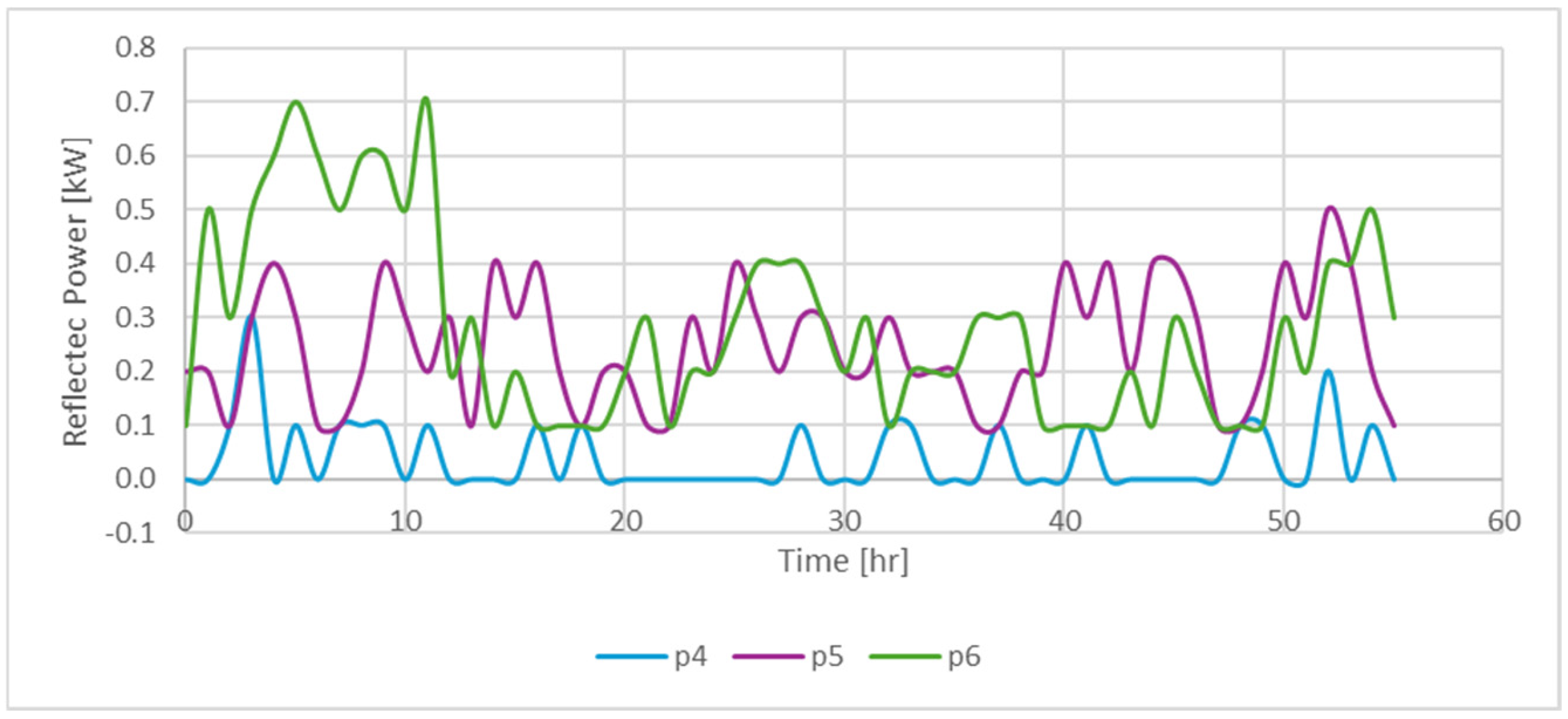
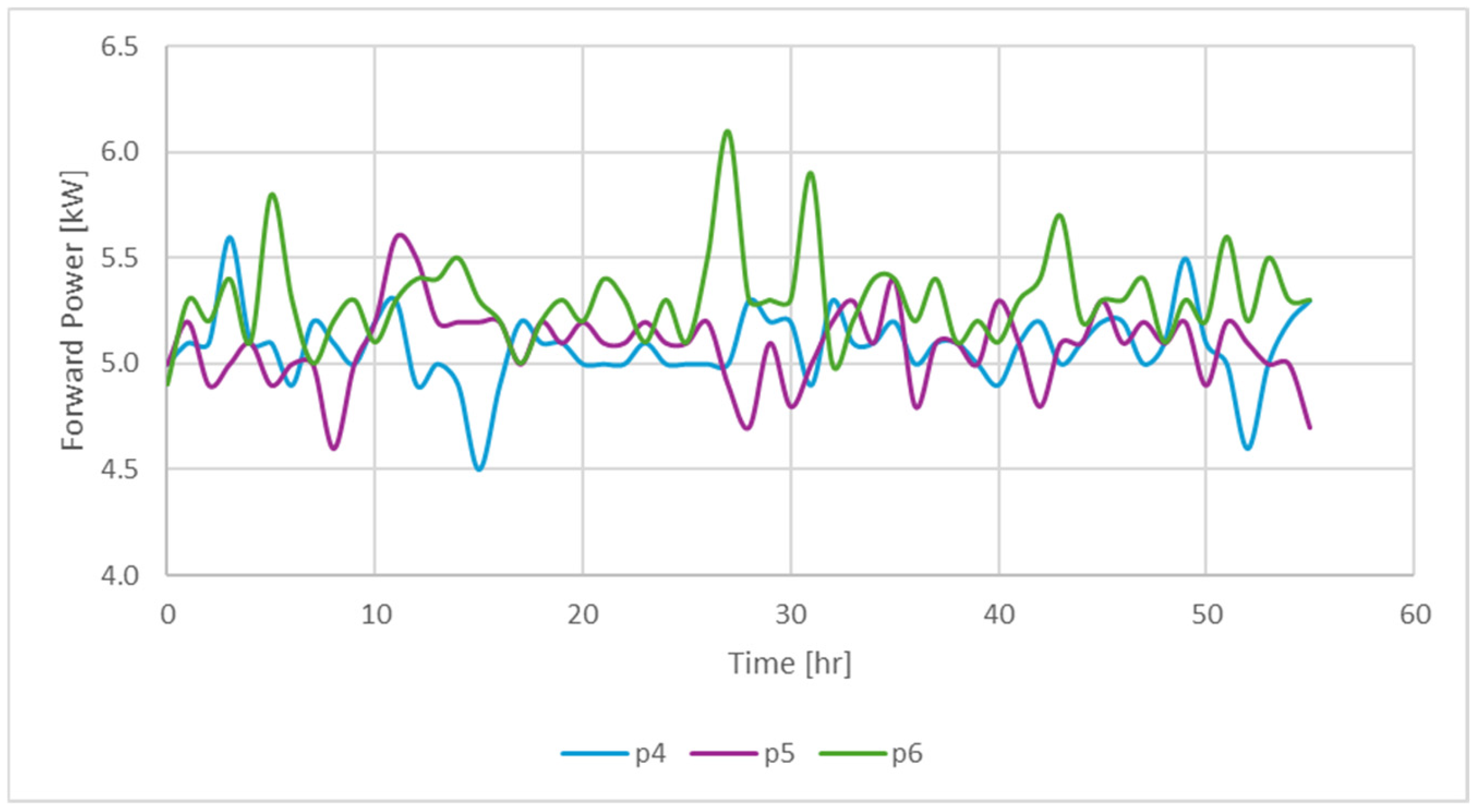
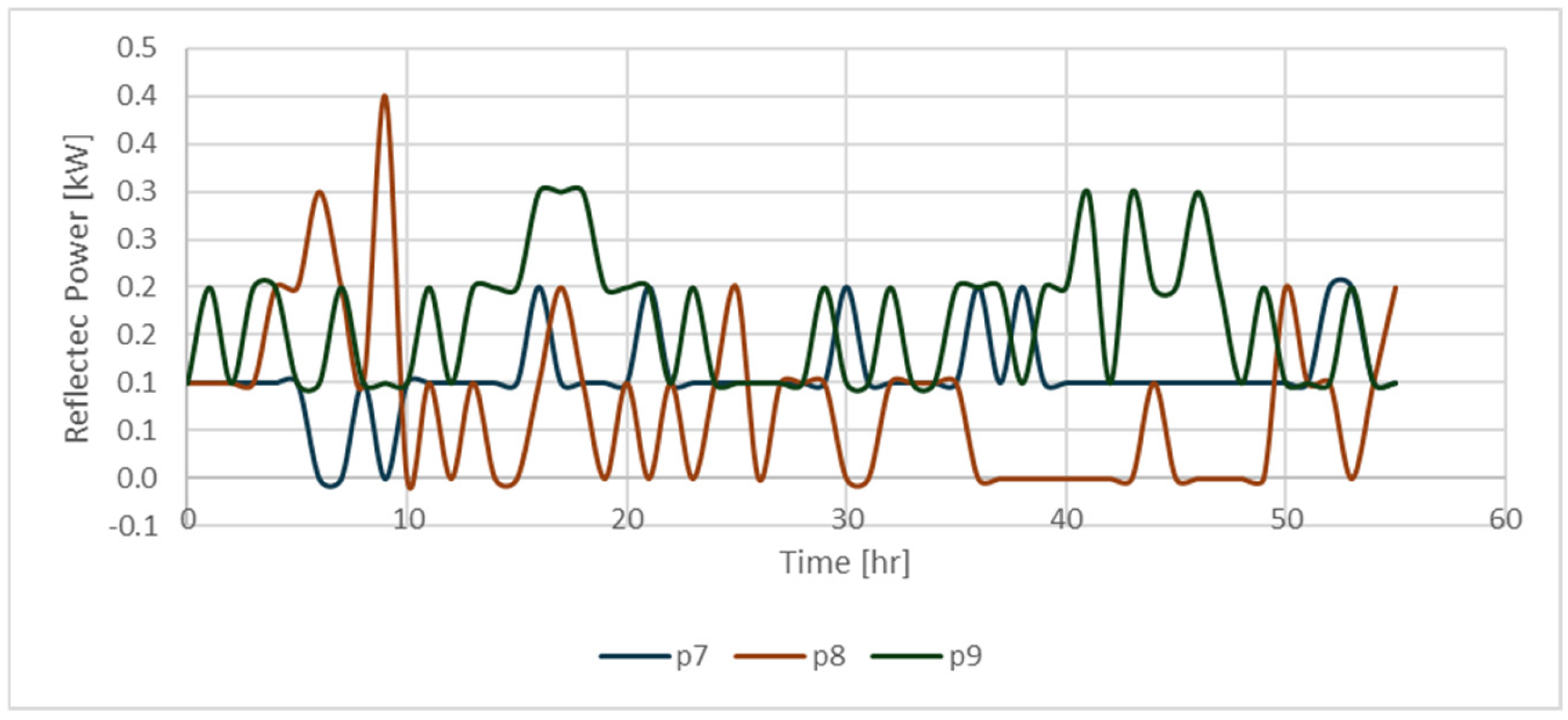
| Code for Identification of the Sample | Exp No. | Sw (%) | So (%) | Sg (%) | Presence of 500 ppm of Nanofluid |
|---|---|---|---|---|---|
| O30W301 | 1 | 0.3 | 0.3 | 0.4 | NO |
| O30W302 | 2 | 0.3 | 0.3 | 0.4 | NO |
| O30W303 | 3 | 0.3 | 0.3 | 0.4 | NO |
| O30W60 | 4 | 0.6 | 0.3 | 0.1 | NO |
| O30W60NP | 5 | 0.6 | 0.3 | 0.1 | YES |
| O30 | 6 | 0 | 0.3 | 0.7 | NO |
| DRY | 7 | 0 | 0 | 1 | NO |
| W30 | 8 | 0.3 | 0 | 0.7 | NO |
| W30NP | 9 | 0.3 | 0 | 0.7 | YES |
| Sample ID | Exp No. | Actual Input Power (kW) | Water Saturation | Nanoparticle’s Concentration (ppm) | Cumulative Transmitted Heat over 55 h (MJ) | Average Transmitted Power (kW) | Transfer Ratio |
|---|---|---|---|---|---|---|---|
| O30W301 | 1 | 4.46 | 0.3 | 0 | 536 | 2.72 | 0.61 ± 0.0116 |
| O30W302 | 2 | 4.42 | 0.3 | 0 | 514 | 2.61 | 0.59 ± 0.0116 |
| O30W303 | 3 | 4.79 | 0.3 | 0 | 575 | 2.92 | 0.61 ± 0.0116 |
| O30W60 | 4 | 5.02 | 0.6 | 0 | 636 | 3.21 | 0.64 ± 0.0116 |
| O30W60NP | 5 | 4.86 | 0.6 | 500 | 653 | 3.30 | 0.68 ± 0.0116 |
| O30 | 6 | 5.02 | 0.0 | 0 | 543 | 2.76 | 0.55 ± 0.0116 |
| DRY | 7 | 5.22 | 0.0 | 0 | 551 | 2.77 | 0.53 ± 0.0116 |
| W30 | 8 | 5.16 | 0.3 | 0 | 595 | 2.99 | 0.58 ± 0.0116 |
| W30NP | 9 | 5.16 | 0.3 | 500 | 651 | 3.30 | 0.64 ± 0.0116 |
| System | Water Saturation | Crude Oil Saturation | Nanoparticle Concentration [ppm] | Alpha [1/cm] |
|---|---|---|---|---|
| Sand with 30% crude oil and no water (either not added or evaporated) | 0 | 0.3 | 0 | 0.007 |
| Sand with 30% crude oil and 30% water | 0.3 | 0.3 | 0 | 0.012 |
| Sand with 30% crude oil and 60% water | 0.6 | 0.3 | 0 | 0.016 |
| Sand with 30% crude oil and no water, but with nanoparticles (O30W60NP in evaporation zone) | 0 | 0.3 | 500 | 0.008 |
| Sand with 30% crude oil, 60% water, and nanoparticles (O30W60NP in non-evaporation zone) | 0.6 | 0.3 | 500 | 0.015 |
| Dry sand | 0 | 0 | 0 | 0.006 |
| Sand with 30% water and no crude oil | 0.3 | 0 | 0 | 0.011 |
| Sand with nanoparticles and no water | 0 | 0 | 500 | 0.006 |
| Sand with nanoparticles and 30% water | 0.3 | 0 | 0 | 0.016 |
| So | Sw | NP | Estimated Alpha [1/cm] | Regression Alpha [1/cm] | Absolute Error [1/cm] |
|---|---|---|---|---|---|
| 0.3 | 0 | 0 | 0.007 | 0.007 | 0.000 |
| 0.3 | 0.3 | 0 | 0.012 | 0.012 | 0.000 |
| 0.3 | 0.6 | 0 | 0.016 | 0.017 | 0.001 |
| 0.3 | 0 | 500 | 0.008 | 0.006 | 0.002 |
| 0.3 | 0.6 | 500 | 0.015 | 0.016 | 0.001 |
| 0 | 0 | 0 | 0.006 | 0.008 | 0.002 |
| 0 | 0.3 | 0 | 0.011 | 0.012 | 0.001 |
| 0 | 0 | 500 | 0.006 | 0.007 | 0.001 |
| 0 | 0.3 | 0 | 0.016 | 0.012 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León, P.A.; Ortíz, A.F.; Gómez-Delgado, J.; Barrera, D.; Tapias, F.; Santos, N.; Mejía-Ospino, E. Numerical Modeling and Multiscale Evaluation of Fe3O4–Graphene Oxide Nanofluids in Electromagnetic Heating for Colombian Heavy Oil Recovery. Energies 2025, 18, 5868. https://doi.org/10.3390/en18225868
León PA, Ortíz AF, Gómez-Delgado J, Barrera D, Tapias F, Santos N, Mejía-Ospino E. Numerical Modeling and Multiscale Evaluation of Fe3O4–Graphene Oxide Nanofluids in Electromagnetic Heating for Colombian Heavy Oil Recovery. Energies. 2025; 18(22):5868. https://doi.org/10.3390/en18225868
Chicago/Turabian StyleLeón, Paola A., Andres F. Ortíz, Jimena Gómez-Delgado, Daniela Barrera, Fabian Tapias, Nicolas Santos, and Enrique Mejía-Ospino. 2025. "Numerical Modeling and Multiscale Evaluation of Fe3O4–Graphene Oxide Nanofluids in Electromagnetic Heating for Colombian Heavy Oil Recovery" Energies 18, no. 22: 5868. https://doi.org/10.3390/en18225868
APA StyleLeón, P. A., Ortíz, A. F., Gómez-Delgado, J., Barrera, D., Tapias, F., Santos, N., & Mejía-Ospino, E. (2025). Numerical Modeling and Multiscale Evaluation of Fe3O4–Graphene Oxide Nanofluids in Electromagnetic Heating for Colombian Heavy Oil Recovery. Energies, 18(22), 5868. https://doi.org/10.3390/en18225868






