Stepwise Single-Axis Tracking of Flat-Plate Solar Collectors: Optimal Rotation Step Size in a Continental Climate
Abstract
1. Introduction
1.1. Tracking Strategies
1.2. State-of-the-Art
1.3. Research Gap and Aim of the Study
2. Materials and Methods
2.1. Simulation Environment
- Solar position calculation—using the NREL Solar Position Algorithm (SPA) implemented in Python to determine solar altitude and azimuth throughout the day [49].
- Tracking strategy application—applying either continuous rotation (aSAT) or discrete stepwise adjustment (rSAT) according to the selected angular step size (ψ = 1–90°).
- Orientation update—modifying the collector surface orientation in the EMS module at each simulation timestep.
- Performance evaluation—EnergyPlus calculated the incident solar radiation on the collector surface, which was then combined with thermal efficiency correlations to determine useful heat output.
2.2. Collectors
2.3. Location and Climatic Conditions
2.4. Flat-Plate Solar Collector Model
2.5. Tracking Strategies and Rotation Step Size
Useful Heat Output Calculation
2.6. Tracking Control
2.7. Model Uncertainty and Limitations
3. Results
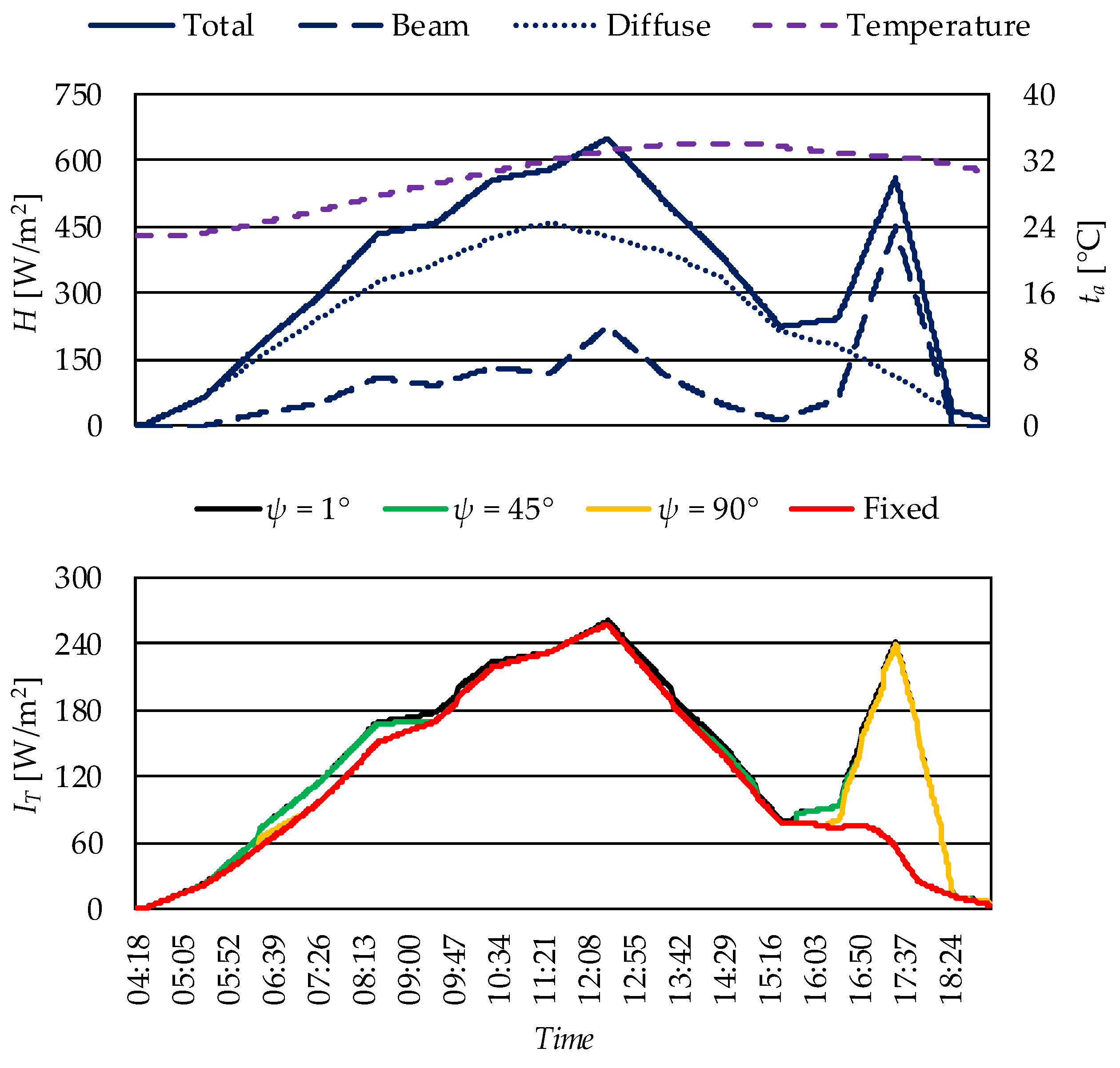
3.1. Incident Solar Irradiance
3.2. Seasonal Thermal Output
3.3. Trade-Off Between Energy Gain and Number of Movements
3.4. Economic Assessment
- ➢
- The actuator ΔCAPEX has the strongest influence on LCOH; doubling its cost (+100%) increases LCOH by only ≈3%, because the investment is small relative to total system cost.
- ➢
- A ±20% change in collector CAPEX shifts LCOH by ±8–9%, while the same variation in OPEX affects it by less than 2%.
- ➢
- Increasing the discount rate from 5% to 7% increases LCOH by about 5%, reflecting lower discounted energy yield.
4. Discussion
Seasonal Limitations
5. Conclusions
- Tracking vs. fixed orientation—The use of tracking increased the incident irradiance by up to 28% and the useful seasonal thermal output by up to 25% relative to the fixed collector. The largest differences occurred during morning and afternoon hours, when fixed systems operated under unfavorable incidence angles.
- Effect of rotation step size (ψ)—For ψ ≤ 15°, the average seasonal performance remained above 90–95% of continuous tracking, while the number of daily movements decreased from 181 (ψ = 1°) to 13–19. At ψ = 45°, the seasonal heat gain was about 12–15% lower than at ψ = 10°, and at ψ = 90°, the benefit over the fixed configuration was reduced to less than 10%.
- Influence of collector type and inlet temperature—The best-performing collector (T2) consistently provided the highest gains, while the weakest (T3) achieved up to 20% lower heat output under identical conditions. Raising the inlet water temperature from 20 °C to 40 °C reduced seasonal useful heat by approximately 30%, regardless of tracking mode.
- Trade-off with number of movements—Continuous tracking requires frequent adjustments (ψ = 1° → 181 daily movements), which is mechanically demanding. Stepwise tracking with ψ = 10–15° offers a practical compromise, with fewer than 20 daily movements and only marginal performance losses compared to continuous tracking.
- Economic performance (LCOH)—While absolute tracking yields the highest energy, its higher mechanical complexity increases costs. Relative tracking with ψ = 10–15° provides the most cost-effective solution, as it retains nearly all of the thermal gain of continuous tracking while avoiding excessive wear.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olabi, A.G. State of the art on renewable and sustainable energy. Energy 2013, 61, 2–5. [Google Scholar] [CrossRef]
- Foley, A.M.; Olabi, A.G. Renewable energy technology developments, trends and policy implications that can underpin the drive for global climate change. Renew. Sustain. Energy Rev. 2017, 68, 1112–1114. [Google Scholar] [CrossRef]
- Sharma, A.K.; Sharma, P.; Gupta, B.; Kumar, A.; Baredar, P. Global trends in solar latent thermal energy storage research (1975–2023). Renew. Sustain. Energy Rev. 2025, 212, 115409. [Google Scholar] [CrossRef]
- Stengler, J.; Bülow, M.; Pitz-Paal, R. Concentrating solar technologies for low-carbon energy. Nat. Rev. Clean Technol. 2025, 1, 719–733. [Google Scholar] [CrossRef]
- Mahalingam, S.; Manap, A.; Floresyona, D.; Rabeya, R.; Afandi, N.; Hasan, Z.; Nugroho, A. Advancements in flexible perovskite solar cells enabling self-powered systems. Renew. Sustain. Energy Rev. 2025, 213, 115488. [Google Scholar] [CrossRef]
- Radek, N.; Konstanty, J.; Pietraszek, J.; Orman, Ł.J.; Szczepaniak, M.; Przestacki, D. The effect of laser beam processing on the properties of WC-Co coatings deposited on steel. Materials 2021, 14, 538. [Google Scholar] [CrossRef]
- Orman, Ł.J.; Radek, N.; Pietraszek, J.; Wojtkowiak, J.; Szczepaniak, M. Laser treatment of surfaces for pool boiling heat transfer enhancement. Materials 2023, 16, 1365. [Google Scholar] [CrossRef]
- Sadeghi, R.; Parenti, M.; Memme, S.; Fossa, M.; Morchio, S. A review and comparative analysis of solar tracking systems. Energies 2025, 18, 2553. [Google Scholar] [CrossRef]
- Kumar, R.; Prasad, K.N.; Paswan, M.K. An SDLSTM-based passive solar tracking system with dual axis position of solar water heater. Therm. Sci. Eng. Prog. 2025, 58, 103220. [Google Scholar] [CrossRef]
- Jamroen, C.; Fongkerd, C.; Krongpha, W.; Komkum, P.; Pirayawaraporn, A.; Chindakham, N. A novel UV sensor-based dual-axis solar tracking system: Implementation and performance analysis. Appl. Energy 2021, 299, 117295. [Google Scholar] [CrossRef]
- Das, M. Exploration of the effect of two-axis PLC solar tracking system on the thermal performance of solar air collector. Case Stud. Therm. Eng. 2021, 28, 101692. [Google Scholar] [CrossRef]
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in solar tracking systems (STS): A review. Renew. Sustain. Energy Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Vaziri Rad, M.A.; Toopshekan, A.; Rahdan, P.; Kasaeian, A.; Mahian, O. A comprehensive study of techno-economic and environmental features of different solar tracking systems for residential photovoltaic installations. Renew. Sustain. Energy Rev. 2020, 129, 109923. [Google Scholar] [CrossRef]
- Saini, P.; Ghasemi, M.; Arpagaus, C.; Bless, F.; Bertsch, S.; Zhang, X. Techno-economic comparative analysis of solar thermal collectors and high-temperature heat pumps for industrial steam generation. Energy Convers. Manag. 2023, 277, 116623. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Prasad, R.K. Application of ANN technique to predict the performance of solar collector systems—A review. Renew. Sustain. Energy Rev. 2018, 84, 75–88. [Google Scholar] [CrossRef]
- Manu, Y.M.; Shashikala, S.V.; Hemchandru, M.K.; Rachitha, P.; Kavya, B.N.; Hongirana, D. Single axis solar tracking system. In Proceedings of the 2nd IEEE International Conference on Advanced Information Technology (ICAIT), Chikkamagaluru, India, 24–27 July 2024. [Google Scholar] [CrossRef]
- Qader, V.S.; Hasan, N.I.; Ali, O.M. An experimental comparison between fixed and single-axis tracking photovoltaic solar panel performance: Zakho city as case study. Al-Rafidain Eng. J. 2023, 28, 272–279. [Google Scholar] [CrossRef]
- Nešović, A.; Lukić, N.; Kowalik, R.; Janaszek, A.; Taranović, D.; Kozłowski, T. Experimental and numerical comparison of glass tube collector with relative single-axis tracking and flat-plate collector without tracking during cloudy-sky days. Sol. Energy 2025, 291, 113412. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Mohanapriya, V.; Manimegalai, V.; Praveenkumar, V.; Sakthivel, P. Implementation of dual axis solar tracking system. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1084, 012112. [Google Scholar] [CrossRef]
- Mamodiya, U.; Tiwari, N. Design and implementation of hardware-implemented dual-axis solar tracking system for enhanced energy efficiency. Eng. Proc. 2023, 59, 122. [Google Scholar] [CrossRef]
- Alami, A.H.; Olabi, A.G.; Mdallal, A.; Rezk, A.; Radwan, A.; Rahman, S.M.A.; Shah, S.K.; Abdelkareem, M.A. Concentrating solar power (CSP) technologies: Status and analysis. Int. J. Thermofluids 2023, 18, 100340. [Google Scholar] [CrossRef]
- Kumba, K.; Upender, P.; Buduma, P.; Sarkar, M.; Simon, S.P.; Gundu, V. Solar tracking systems: Advancements, challenges, and future directions—A review. Energy Rep. 2024, 12, 3566–3583. [Google Scholar] [CrossRef]
- Awasthi, A.; Shukla, A.K.; Murali Manohar, S.R.; Dondariya, C.; Shukla, K.N.; Porwal, D.; Richhariya, G. Review on sun tracking technology in solar PV system. Energy Rep. 2020, 6, 392–405. [Google Scholar] [CrossRef]
- Batayneh, W.; Bataineh, A.; Soliman, I.; Hafees, S.A. Investigation of a single-axis discrete solar tracking system for reduced actuations and maximum energy collection. Autom. Constr. 2019, 98, 102–109. [Google Scholar] [CrossRef]
- Okwu, M.O.; Eruero, O.P.; Abubakar, N.; Edward, B.A.; Oreko, B.U.; Otanocha, O.B.; Orikpete, O.F.; Maware, C.; Ezekiel, K.C.; Ori, C.; et al. Single-axis solar tracking systems: A comprehensive design and performance study. Procedia Comput. Sci. 2025, 253, 2740–2752. [Google Scholar] [CrossRef]
- Barbón, A.; Carreira-Fontao, V.; Bayón, L.; Silva, C.A. Optimal design and cost analysis of single-axis tracking photovoltaic power plants. Renew. Energy 2023, 211, 626–646. [Google Scholar] [CrossRef]
- Ponce-Jara, M.A.; Pazmino, I.; Moreira-Espinoza, Á.; Gunsha-Morales, A.; Rus-Casas, C. Assessment of Single-Axis Solar Tracking System Efficiency in Equatorial Regions: A Case Study of Manta, Ecuador. Energies 2024, 17, 3946. [Google Scholar] [CrossRef]
- Agee, J.T.; Obok Opok, A.; de Lazzer, M. Solar tracker technologies: Market trends and field applications. Adv. Mater. Res. 2007, 18–19, 339–344. [Google Scholar] [CrossRef]
- Abu-Khader, M.; Badran, O.; Abdallah, S. Evaluating multi-axes sun-tracking system at different modes of operation in Jordan. Renew. Sustain. Energy Rev. 2008, 12, 864–873. [Google Scholar] [CrossRef]
- Aghamohammadi, A.; Foulaadvand, M.E. Efficiency comparison between tracking and optimally fixed flat solar collectors. Sci. Rep. 2023, 13, 12712. [Google Scholar] [CrossRef]
- Eiva, U.R.J.; Chowdury, T.A.; Islam, S.S.; Ullah, A.; Tuli, J.N.; Islam, M.T. Comprehensive analysis of fixed tilt and dual-axis tracking photovoltaic systems for enhanced grid integration and energy efficiency. Renew. Energy 2026, 256, 123865. [Google Scholar] [CrossRef]
- Ferdaus, R.A.; Mohammed, M.A.; Rahman, S.; Salehin, S.; Mannan, M.A. Energy efficient hybrid dual axis solar tracking system. J. Renew. Energy 2014, 2014, 629717. [Google Scholar] [CrossRef]
- Fuentes-Morales, R.F.; Diaz-Ponce, A.; Peña-Cruz, M.I.; Rodrigo, P.M.; Valentín-Coronado, L.M.; Martell-Chavez, F.; Pineda-Arellano, C.A. Control algorithms applied to active solar tracking systems: A review. Sol. Energy 2020, 212, 203–219. [Google Scholar] [CrossRef]
- Boukdir, Y.; El Omari, H. Novel high precision low-cost dual axis sun tracker based on three light sensors. Heliyon 2022, 8, e12412. [Google Scholar] [CrossRef]
- Bahrami, A.; Okoye, C.O.; Atikol, U. Technical and economic assessment of fixed, single and dual-axis tracking PV panels in low latitude countries. Renew. Energy 2017, 113, 563–579. [Google Scholar] [CrossRef]
- Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Meiirkhanov, A.; Svanbayev, Y. Optimized single-axis schedule solar tracker in different weather conditions. Energies 2020, 13, 5226. [Google Scholar] [CrossRef]
- Nešović, A.; Lukić, N.; Taranović, D.; Nikolić, N. Theoretical and experimental investigation of the glass tube solar collector with inclined N–S axis and relative E–W single-axis tracking flat absorber. Appl. Therm. Eng. 2024, 236, 121842. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J.; Yang, X. Design and performance analysis of a solar tracking system with a novel single-axis tracking structure to maximize energy collection. Appl. Energy 2020, 264, 114647. [Google Scholar] [CrossRef]
- Nešović, A.; Kowalik, R.; Cvetković, D.; Janaszek, A. Multi-Criteria Decision-Making Method for Simple and Fast Dimensioning and Selection of Glass Tube Collector Type Based on the Iterative Thermal Resistance Calculation Algorithm with Experimental Validation. Appl. Sci. 2024, 14, 6603. [Google Scholar] [CrossRef]
- Kabir, M.H.; Abu Jihad, M.H.; Chowdhury, S. Analysis of Solar Panel Power Investigation Using Fixed Axis, Single Axis, and Dual Axis Solar Tracker. Procedia Comput. Sci. 2025, 252, 708–714. [Google Scholar] [CrossRef]
- Kazem, H.A.; Chaichan, M.T.; Al-Waeli, A.H.A.; Sopian, K. Recent advancements in solar photovoltaic tracking systems: An in-depth review of technologies, performance metrics, and future trends. Sol. Energy 2024, 282, 112946. [Google Scholar] [CrossRef]
- Ali, M.H.; Zakaria, M.; El-Tawab, S. A comprehensive study of recent maximum power point tracking techniques for photovoltaic systems. Sci. Rep. 2025, 15, 14269. [Google Scholar] [CrossRef]
- Kuttybay, N.; Mekhilef, S.; Koshkarbay, N.; Saymbetov, A.; Nurgaliyev, M.; Dosymbetova, G.; Orynbassar, S.; Yershov, E.; Kapparova, A.; Zholamanov, B.; et al. Assessment of solar tracking systems: A comprehensive review. Sustain. Energy Technol. Assess. 2024, 68, 103879. [Google Scholar] [CrossRef]
- Ayadi, O.; Rinchi, B.; Al-Dahidi, S.; Abdalla, M.E.B.; Al-Mahmodi, M. Techno-economic assessment of bifacial photovoltaic systems under desert climatic conditions. Sustainability 2024, 16, 6982. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Z.; Huang, Y.; Ma, Y.; Yang, Z. Design and analysis of a quasi-biaxial solar tracker. Energies 2025, 18, 1554. [Google Scholar] [CrossRef]
- Nešović, A.; Saveljić, I. Influence of rotation step size on incident solar irradiance in flat-plate collectors with single-axis tracking under clear-sky conditions. Precis. Mech. Digit. Fabr. 2025, 2, 83–92. [Google Scholar] [CrossRef]
- EnergyPlus. EnergyPlus Software; 2025. Available online: https://energyplus.net/ (accessed on 27 October 2025).
- NREL. Solar Position Algorithm (SPA); National Renewable Energy Laboratory: Golden, CO, USA, 2003. Available online: https://midcdmz.nrel.gov/spa/ (accessed on 27 October 2025).
- EN 12975-2:2006; Thermal Solar Systems and Components—Solar Collectors—Part 2: Test Methods. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- ISO 9806:2017; Solar Energy—Solar Thermal Collectors—Test Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- Climate-Data.org. Climate: Kragujevac. Available online: https://en.climate-data.org/europe/serbia/kragujevac/kragujevac-4125/ (accessed on 27 October 2025).
- U.S. Department of Energy. EnergyPlus Weather Data (EPW): Kragujevac, Serbia. Available online: https://energyplus.net/weather (accessed on 27 October 2025).
- NASA. Surface Meteorology and Solar Energy (SSE) Data for Renewable Energy; National Aeronautics and Space Administration: Washington, DC, USA, 2020. Available online: https://power.larc.nasa.gov/ (accessed on 27 October 2025).
- U.S. Department of Energy (DOE); National Renewable Energy Laboratory (NREL). EnergyPlus Weather Data (EPW Files and Typical Meteorological Year—TMY3 Datasets). Available online: https://energyplus.net/weather (accessed on 27 October 2025).
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Özden, E.; Kaya, M.N. Comprehensive analysis of key design parameters affecting the efficiency of flat-plate solar thermal collectors. Case Stud. Therm. Eng. 2025, 73, 106458. [Google Scholar] [CrossRef]
- Unar, I.N.; Maitlo, G.; Ahmed, S.; Ali, S.S.; Memon, A.Q.; Kandhro, G.A.; Jatoi, A.S. Performance evaluation of solar flat plate collector using different working fluids through computational fluid dynamics. SN Appl. Sci. 2020, 2, 209. [Google Scholar] [CrossRef]
- Deng, J.; Xu, Y.; Yang, X. A dynamic thermal performance model for flat-plate solar collectors based on the thermal inertia correction of the steady-state test method. Renew. Energy 2015, 76, 679–686. [Google Scholar] [CrossRef]
- Girfoglio, M.; Greco, C.S.; Chiatto, M.; De Luca, L. Modelling of efficiency of synthetic jet actuators. Sens. Actuators A Phys. 2015, 233, 512–521. [Google Scholar] [CrossRef]
- Yang, T.; Liu, W.; Kramer, G.J.; Sun, Q. Seasonal thermal energy storage: A techno-economic literature review. Renew. Sustain. Energy Rev. 2021, 139, 110732. [Google Scholar] [CrossRef]
- Louvet, Y.; Vajen, K. Levelized cost of heat for solar thermal applications in households. Sol. Energy 2025, 285, 113100. [Google Scholar] [CrossRef]















| Tracking Strategy | Advantages | Disadvantages | Typical Applications |
|---|---|---|---|
| (aSAT) | – Nearly continuous alignment with the Sun – High irradiance gain (≈+25–35% vs. fixed) – Mature control algorithms | – Large number of daily movements (≈100–200) – Higher investment and O&M costs – Increased mechanical wear | Large-scale solar thermal fields, medium-sized PV farms |
| (rSAT) | – Stepwise adjustment reduces movements (≈5–15 per day) – Captures most of the gains of aSAT – Lower cost, simpler control – Higher reliability | – Suboptimal alignment between steps – Performance depends strongly on the chosen step size ψ – No standardized design guidelines yet | Small-scale flat-plate collectors, building-integrated systems, rural/off-grid applications |
| (DAT) | – Maximum possible irradiance gain (≈+35–45% vs. fixed) – Nearly perpendicular orientation all day/year – High suitability for concentrating systems | – Most complex and expensive – Requires two actuators and advanced control – Higher structural loads and maintenance | Concentrating solar power (CSP), large PV plants, solar towers |
| Label | Description | η0 [–] | c1 [W/m2 ∙ K] | c2 [W/m2 ∙ K] | Remarks |
|---|---|---|---|---|---|
| T1 | Standard single-glazed, non-selective absorber | 0.74 | 3.6 | 0.015 | Low-cost, representative of entry-level collectors used in domestic systems. |
| T2 | Single-glazed, selective absorber (black-chrome or TiNOX) | 0.77 | 3.2 | 0.010 | Medium-efficiency collector, typical of modern European installations. |
| T3 | Double-glazed, selective absorber, low-iron glass | 0.80 | 2.6 | 0.008 | High-performance design used in research and premium systems. |
| Date | Solar Declination δ [°] | Sunrise Hour Angle ωs [°] | Day Length D [h] | Maximum Solar Altitude hmax [°] |
|---|---|---|---|---|
| 21 June | +23.45 | 113.9 | 15.31 | 69.5 |
| 1 July | +23.00 | 112.7 | 15.22 | 69.0 |
| 10 July | +21.20 | 110.4 | 15.04 | 67.5 |
| 26 July | +18.50 | 106.9 | 14.77 | 65.2 |
| 10 August | +15.20 | 103.3 | 14.45 | 63.0 |
| Collector Type | Optical Efficiency c0 [–] | First-Order Heat Loss c1 [W/(m2∙K)] | Second-Order Heat Loss c2 [W/(m2∙K2)] |
|---|---|---|---|
| T1 (high-performance) | 0.80 | 3.5 | 0.015 |
| T2 (medium-performance) | 0.75 | 4.5 | 0.020 |
| T3 (standard) | 0.72 | 6.0 | 0.030 |
| Scenario | FPSC | ψ [°] | Nψ (–) |
|---|---|---|---|
| S1-1 | SAT | 1 | 181 |
| S1-2 | 2 | 91 | |
| S1-3 | 5 | 37 | |
| S1-4 | 10 | 19 | |
| S1-5 | 15 | 13 | |
| S1-6 | 30 | 7 | |
| S1-7 | 45 | 5 | |
| S1-8 | 90 | 3 | |
| S1-9 | Fixed | - | 1 |
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Rated torque | Ma | 50 | N·m | Nominal torque for azimuth rotation |
| Response time | ta | 1.0 | s·deg−1 | Time to rotate 1° under nominal load |
| Positioning tolerance | δγ | ±0.5 | ° | Angular precision of positioning |
| Maximum angular velocity | ωa, max | 3 | °·s−1 | Maximum speed of the actuator arm |
| Electrical efficiency | ηa | 0.8 | – | Ratio of mechanical to electrical power |
| Standby consumption | P0 | 2 | W | The idle electrical power of the controller |
| Movement power demand | Pm | 15 | W | Average electrical power during motion |
| Rated lifetime (mechanical cycles) | N1 | 5 × 105 | cycles | Expected operational life before service |
| Ambient operating range | Ta, op | –20…+60 | °C | Typical range for outdoor actuator operation |
| Scenario | Equation |
|---|---|
| S1-1 | |
| S1-2 | |
| S1-3 | |
| S1-4 | |
| S1-5 | |
| S1-6 | |
| S1-7 | |
| S1-8 | |
| S1-9 |
| Step Size ψ [°] | Number of Daily Movements | Seasonal Irradiance [kWh·m−2] | Gain vs. Fixed [%] |
|---|---|---|---|
| Fixed | 0 | 1085 | – |
| 45 | 4 | 1126 | +3.8 |
| 30 | 6 | 1145 | +5.5 |
| 20 | 9 | 1168 | +7.6 |
| 15 | 12 | 1179 | +8.7 |
| 10 | 18 | 1190 | +9.7 |
| 5 | 36 | 1197 | +10.3 |
| 1 (continuous) | 181 | 1203 | +10.9 |
| Scenario | Equation | |
|---|---|---|
| S2-1 | S3-1 | |
| S3-2 | ||
| S3-3 | ||
| S2-2 | S3-1 | |
| S3-2 | ||
| S3-3 | ||
| S2-3 | S3-1 | |
| S3-2 | ||
| S3-3 | ||
| ψ [°] | Nψ [–] | Normalized Useful Heat Gain [% of Continuous] |
|---|---|---|
| Fixed | 0 | 88 |
| 45 | 4 | 91 |
| 30 | 6 | 93 |
| 20 | 9 | 95 |
| 15 | 12 | 96 |
| 10 | 18 | 97 |
| 5 | 36 | 98 |
| 1 (continuous) | 181 | 100 |
| Parameter | Symbol | Value | Unit | Source/Note |
|---|---|---|---|---|
| Collector area | Ac | 2.0 | m2 | per module |
| Collector cost | CFPSC | 1800 | PLN/m2 | market average |
| Tracking actuator cost | ΔCAPEX | 600 | PLN per array | includes control electronics |
| Installation and balance of the plant | – | 1000 | PLN/m2 | piping, tank, pumps |
| Annual O&M cost | COPEX | 1% × CAPEX | – | typical maintenance |
| Actuator power demand | Pm | 15 | W | from Table 6 |
| Electricity price | pe | 0.85 | PLN/kWh | EU average |
| Lifetime | n | 20 | years | EN 12975 benchmark |
| Discount rate | r | 5 | % | moderate residential assumption |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalik, R.; Nešović, A. Stepwise Single-Axis Tracking of Flat-Plate Solar Collectors: Optimal Rotation Step Size in a Continental Climate. Energies 2025, 18, 5776. https://doi.org/10.3390/en18215776
Kowalik R, Nešović A. Stepwise Single-Axis Tracking of Flat-Plate Solar Collectors: Optimal Rotation Step Size in a Continental Climate. Energies. 2025; 18(21):5776. https://doi.org/10.3390/en18215776
Chicago/Turabian StyleKowalik, Robert, and Aleksandar Nešović. 2025. "Stepwise Single-Axis Tracking of Flat-Plate Solar Collectors: Optimal Rotation Step Size in a Continental Climate" Energies 18, no. 21: 5776. https://doi.org/10.3390/en18215776
APA StyleKowalik, R., & Nešović, A. (2025). Stepwise Single-Axis Tracking of Flat-Plate Solar Collectors: Optimal Rotation Step Size in a Continental Climate. Energies, 18(21), 5776. https://doi.org/10.3390/en18215776







