Fully Decentralized Sliding Mode Control for Frequency Regulation and Power Sharing in Islanded Microgrids

Abstract

This paper proposes a local sliding mode control (SMC) strategy for frequency regulation and active power sharing in islanded microgrids (MGs). Unlike advanced strategies, either droop-based or droop-free, that rely on inter-inverter communication, the proposed method operates in a fully decentralized manner, using only measurements available at each inverter. In addition, it adopts a minimalist structure that avoids adaptive laws and consensus mechanisms, which simplifies implementation. A discontinuous control law is derived to enforce sliding dynamics on a frequency-based surface, ensuring robust behavior in the face of disturbances, such as clock drifts, sudden load variations, and topological reconfigurations. A formal Lyapunov-based analysis is conducted to establish the stability of the closed-loop system under the proposed control law. The method guarantees that steady-state frequency deviations remain bounded and predictable as a function of the controller parameters. Simulation results demonstrate that the proposed controller achieves rapid frequency convergence, equitable active power sharing, and sustained stability. Owing to its communication-free design, the proposed strategy is particularly well-suited for MGs operating in rural, isolated, or resource-constrained environments. A comparative evaluation against both conventional droop and communication-based droop-free SMC approaches further highlights the method’s strengths in terms of resilience, implementation simplicity, and practical deployability.

1. Introduction

Microgrids (MGs) are self-sufficient energy systems that mainly integrate distributed generation (DG) units, storage components, and loads. When operating in islanded mode, MGs disconnect from the main grid. They must autonomously regulate their internal variables to ensure voltage amplitude/frequency quality, as well as balanced power sharing [1]. Voltage source inverters (VSIs), which constitute the interface layer of DG units, are central to this operation, acting as controllable bridges between energy sources and the islanded grid. From a cyber–physical viewpoint, MGs are regarded as multi-agent systems where each VSI functions as an autonomous agent interacting through electrical couplings such as voltage and frequency [2].

Traditional MG control relies on a hierarchical scheme. Primary control typically applies droop laws to achieve proportional power sharing using only local variables, but it inherently introduces steady-state frequency deviations [3]. Secondary control, often communication-based, compensates for these deviations by coordinating inverters via centralized or distributed algorithms [4,5]. Despite improvements in accuracy and flexibility [6,7], these approaches are vulnerable to communication failures [8,9], and their dependency on digital links limits their applicability in isolated, or degraded infrastructure environments.

To overcome these limitations, some approaches have proposed sparse-communication schemes for frequency restoration and active power sharing [10]. However, such methods still rely on digital channels, and their performance deteriorates in the presence of link failures. Recent advances have aimed at reducing this communication burden, for instance through event-triggered or sampled-data protocols that minimize message exchanges while preserving coordination [11]. Nevertheless, these methods still depend on digital infrastructure and remain vulnerable to packet loss, synchronization errors, or cyberattacks.

As more resilient alternatives, other works have explored fully communication-free control architectures that exploit the physical coupling of the electrical network to enable coordination through purely local interactions [12,13]. In these frameworks, each inverter adjusts its frequency based solely on internal variables, enabling plug-and-play operation and increased robustness in environments where reliable communications cannot be guaranteed. Beyond control-based solutions, other studies have pursued physically grounded strategies to enhance fault resilience without communication. For example, ref. [14] proposes a fault ride-through mechanism based on current limiters that ensures continued system operation under severe conditions, reinforcing the broader shift toward robust, communication-independent architectures across power system domains.

Sliding mode control (SMC) is a robust nonlinear control strategy widely used for its ability to reject matched disturbances and ensure finite-time convergence to a desired manifold [15,16]. Its implementation relies on discontinuous control actions that guide system trajectories onto a predefined sliding surface, providing resilience under model uncertainties and parameter variations. These features make SMC particularly appealing for MG inverter control, where robustness and simplicity are paramount [17].

Most SMC-based approaches for MGs, including [17,18,19,20,21], incorporate communication, consensus dynamics, higher-order sliding modes, or sensor observers that rely on global system information. Moreover, while most existing strategies focus primarily on steady-state performance, they often neglect performance analysis under perturbations. As a result, these methods may struggle to maintain robust operation in the presence of clock mismatches, abrupt load changes, or network reconfigurations.

To the best of the authors’ knowledge, strictly local SMC schemes, where each inverter uses only its own frequency and power measurements, without estimation, synchronization, or messaging, remain largely unexplored in the literature. In response to this gap, this paper proposes a local SMC method for frequency restoration and active power sharing in islanded MGs, entirely free of communication dependencies. The sliding surface is defined solely in terms of the local frequency error, eliminating the need for neighbor information or external synchronization. The proposed control law is embedded within a droop-based hierarchical framework, and its switching strategy operates exclusively on local variables.

This design is particularly suited for resilient MG operation in scenarios where digital communication is impractical, unreliable, or intentionally avoided. A Lyapunov-based analysis is provided to establish theoretical guarantees of closed-loop stability, and simulation results confirm that the system maintains synchronized frequency and balanced power sharing even under disturbances.

Beyond performance and robustness, the communication-free nature of the controller also offers benefits in terms of cybersecurity: avoiding digital links reduces the system’s attack surface. While not the primary focus of this study, related concerns such as attack detection in resource-constrained environments [22] warrant further investigation. Finally, this work openly acknowledges its limitations: the frequency regulation is bounded rather than exact; chattering may occur due to the discontinuous nature of the control law; and the validation is limited to a testbed without hardware-level modeling.

The remainder of this paper is structured as follows. Section 2 presents the MG modeling and Section 3, the local control framework. Section 4 introduces the proposed sliding mode control law. Section 5 develops a formal Lyapunov-based stability analysis. Section 6 reports simulation results on a four-inverter MG. Section 7 discusses system performance and limitations. Finally, Section 8 concludes the paper and outlines directions for future work.

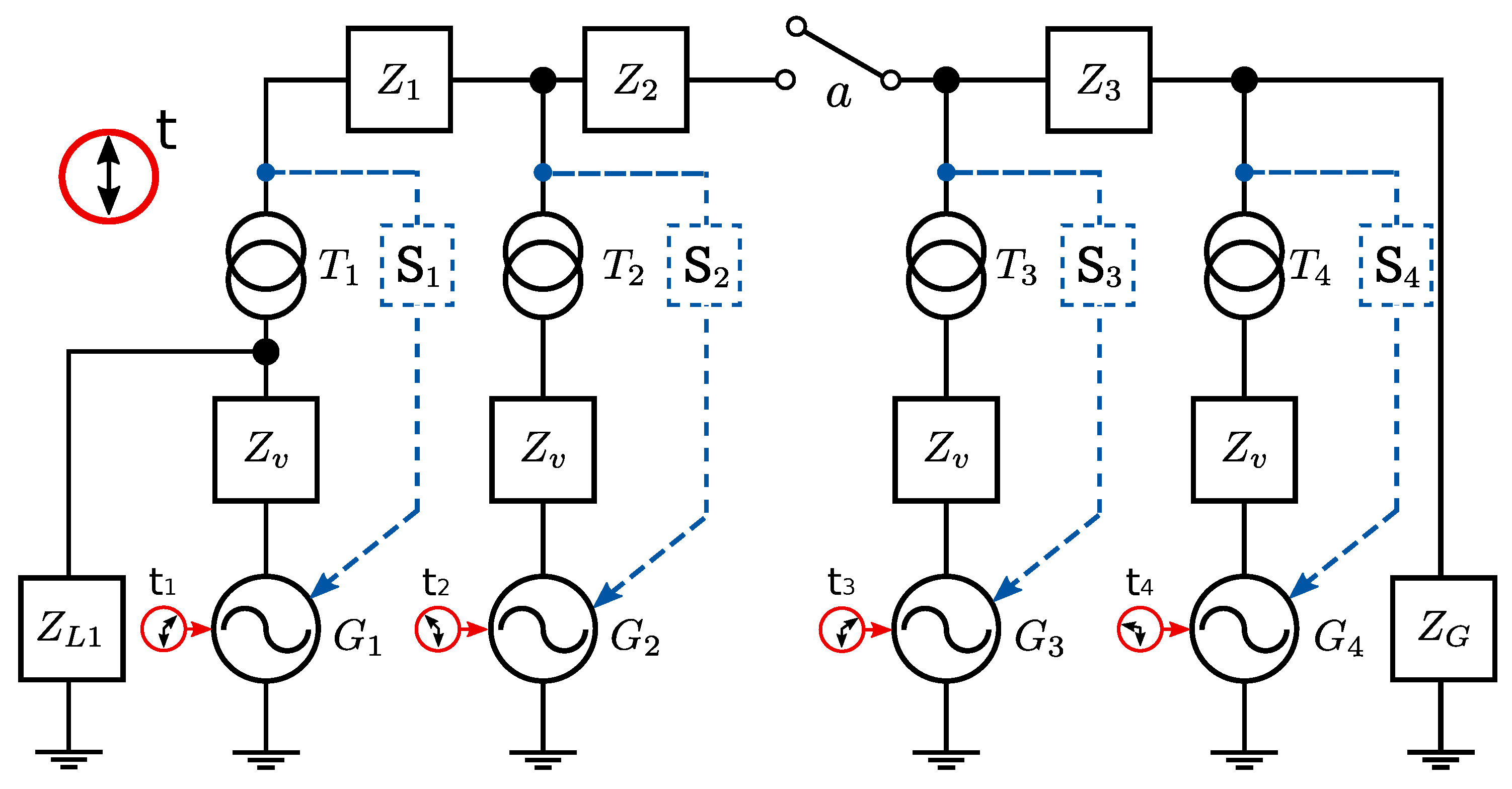
2. MG Electrical Network Model

The electrical structure of the islanded MG is modeled under the assumption of purely local control. Unlike distributed approaches that rely on inter-node communication, the proposed scheme operates without any communication links, and therefore, the dynamic behavior is driven exclusively by local measurements and electrical coupling.

The MG is represented as an undirected graph ${\mathcal{G}}_E=(\mathcal{N},{\mathcal{E}}_E)$, where $\mathcal{N}=\{1,2,\dots ,n\}$ denotes the set of n DG units, and ${\mathcal{E}}_E\subseteq \mathcal{N}\times \mathcal{N}$ is the set of electrical connections among them. Each edge in ${\mathcal{E}}_E$ corresponds to an impedance line characterized by an admittance $y_{ij}=g_{ij}+j{b}_{ij}$, where $g_{ij}$ and $b_{ij}$ denote the conductance and susceptance between each pair of nodes $(i,j)$, respectively.

Under the standard assumptions of power systems modeling [23], namely, uniform voltage magnitudes and small phase angle differences, the active power injected by each node i, $p_i\left(t\right)$, is given by

$$p_i\left(t\right)=v^2\sum _{j=1}^n{g}_{ij}+v^2\sum _{j=1}^n{b}_{ij}\left({\theta }_i\left(t\right)-{\theta }_j\left(t\right)\right),$$

(1)

where v is the common voltage magnitude, and ${\theta }_{i,j}\left(t\right)$ are the voltage phases at nodes $i,j$. The first term accounts for the resistive losses, while the second term represents the power exchange due to phase differences.

Let $\mathbf{p}\left(t\right)={[p_1\left(t\right),\dots ,p_n\left(t\right)]}^{\top }$ be the VSI active powers and $\mathit{\theta }\left(t\right)={[{\theta }_1\left(t\right),\dots ,{\theta }_n\left(t\right)]}^{\top }$, the set of phase angles; the active power injection (1) can be expressed in vector form as

$$\mathbf{p}\left(t\right)=v^{2}G{\mathbf{1}}_n+v^{2}B\mathit{\theta }\left(t\right),$$

(2)

where $G\in {\mathbb{R}}^{n\times n}$ contains the conductance values $g_{ij}$, $B\in {\mathbb{R}}^{n\times n}$ is the susceptance Laplacian matrix of the electrical graph, and ${\mathbf{1}}_n\in {\mathbb{R}}^n$ is the all-ones vector. The Laplacian matrix is defined as

$$B=\left[\begin{array}{cccc}\sum _{j\ne 1}{b}_{1j}& -b_{12}& \cdots & -b_{1n}\\ -b_{21}& \sum _{j\ne 2}{b}_{2j}& \cdots & -b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ -b_{n1}& -b_{n2}& \cdots & \sum _{j\ne n}{b}_{nj}\end{array}\right].$$

(3)

In this work, B is defined under the assumption of a balanced electrical network, where the total susceptance observed at each node is symmetric. Consequently, B is a Laplacian matrix satisfying $B=B^{\top }$, $B⪰0$, and $B·{\mathbf{1}}_n=0$. This structural property simplifies the derivation of stability results. Nonetheless, practical MGs may exhibit topological asymmetries or parameter mismatches that violate this ideal balance.

Taking the time derivative of the power injection (2), and noting that frequency is the time derivative of the phase, $\mathit{\omega }\left(t\right)=\dot{\mathit{\theta }}\left(t\right)$, the dynamic relationship is stated as

$$\dot{\mathbf{p}}\left(t\right)=v^{2}B\mathit{\omega }\left(t\right),$$

(4)

that links the frequency dynamics directly to the rate of change in active power, and serves as the foundation for analyzing the stability of the proposed local sliding mode control law.

3. Local Control Framework

This section revisits the standard droop control paradigm for local frequency regulation in islanded MGs.

3.1. Conventional Droop Control

In islanded MGs, frequency droop control is a widely adopted strategy for decentralized regulation of DG units [3]. The droop method establishes a linear relationship between the frequency deviation and the active power injection at each inverter, enabling autonomous load sharing and frequency regulation based solely on local measurements.

The classical frequency droop control law implemented at each node $i\in \mathcal{N}$ is given by

$${\omega }_i\left(t\right)={\omega }_0-m{p}_i\left(t\right),$$

(5)

where ${\omega }_i\left(t\right)$ is the instantaneous frequency of inverter i, ${\omega }_0$ is the nominal reference frequency, $p_i\left(t\right)$ is its locally measured active power injection (1), and $m_i>0$ is the uniform droop gain applied across all nodes. This scalar coefficient governs the trade-off between dynamic response and steady-state frequency deviation. Although in practice each inverter may have a distinct droop gain $m_i$, this work adopts the homogeneous case $m_i=m$ for all $i\in \mathcal{N}$ to simplify the analysis. The proposed method and its theoretical properties remain applicable to the heterogeneous scenario, which can be addressed through local gain rescaling or adaptive extensions.

Defining the vector of VSI local frequencies $\mathit{\omega }\left(t\right)={[{\omega }_1\left(t\right),\dots ,{\omega }_n\left(t\right)]}^{\top }$, the droop control law (5) can be written as

$$\mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n-m\mathbf{p}\left(t\right).$$

(6)

3.2. Steady-State Requirements for Frequency and Power Sharing

In steady-state conditions, defined as $t\to \infty$, the system is required to satisfy

$$\mathit{\omega }\left(t\right)\to {\omega }_0{\mathbf{1}}_n,$$

(7)

$$\mathbf{p}\left(t\right)\to {\displaystyle \frac{p_T}{n}}{\mathbf{1}}_n,$$

(8)

where $p_T$ is the total active power demanded by the load. These asymptotic conditions ensure frequency synchronization and balanced active power sharing under decentralized and communication-free operation.

3.3. Local Voltage Regulation

Although the main focus of this work is on frequency and active power control, voltage amplitude is assumed to be regulated independently at each node via a conventional voltage droop law. In vector form, this control can be expressed as

$$\mathbf{v}\left(t\right)=v_0{\mathbf{1}}_n-c\mathbf{q}\left(t\right),$$

(9)

where $\mathbf{v}\left(t\right)={[v_1\left(t\right),\dots ,v_n\left(t\right)]}^{\top }$ is the vector of voltage magnitudes, $\mathbf{q}\left(t\right)=[q_1\left(t\right),\dots ,$$q_n{\left(t\right)]}^{\top }$ is the vector of local reactive power injections, $v_0$ is the nominal reference voltage, and $c>0$ is a proportional gain applied identically at all nodes.

4. Sliding Mode-Based Frequency Control

This section introduces an enhancement to conventional droop control through a sliding mode term that enforces finite-time convergence to the nominal frequency.

4.1. Local SMC Law and Sliding Surface

The control objective is to synchronize all local inverter frequencies to a common nominal value ${\omega }_0$, relying solely on local measurements of frequency. To enhance the baseline behavior defined by the conventional droop law (5), a discontinuous sliding term is added. As a result, the dynamic behavior of each ith node is defined by

$${\omega }_i\left(t\right)={\omega }_0-m{p}_i\left(t\right)+k\mathrm{sgn}\left(s_i\left(t\right)\right),$$

(10)

where $k>0$ is the sliding mode gain to enhance robustness, and $s_i\left(t\right)$ is the sliding surface defined as the local frequency error

$$s_i\left(t\right)={\omega }_0-{\omega }_i\left(t\right).$$

(11)

The sign function in (10) applies a maximal corrective action when the error is non-zero and ceases once the system reaches the surface, satisfying $s_i\left(t\right)=0$. This yields the switching behavior

$$\mathrm{sgn}\left(s_i\left(t\right)\right)=\left\{\begin{array}{cc}+1\hfill & \mathrm{if}{s}_i\left(t\right)>0,\hfill \\ 0\hfill & \mathrm{if}{s}_i\left(t\right)=0,\hfill \\ -1\hfill & \mathrm{if}{s}_i\left(t\right)<0.\hfill \end{array}\right.$$

(12)

By aggregating all variables into vector form, the SMC law (10) becomes

$$\mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n-m\mathbf{p}\left(t\right)+k·\mathrm{sgn}\left(\mathbf{S}\left(t\right)\right),$$

(13)

where the vectorial version of the sliding surface in (11) is defined as

$$\mathbf{S}\left(t\right)={\omega }_0{\mathbf{1}}_n-\mathit{\omega }\left(t\right).$$

(14)

Differentiating (14) gives the frequency error dynamics

$$\dot{\mathbf{S}}\left(t\right)=-\dot{\mathit{\omega }}\left(t\right).$$

(15)

This expression clearly shows that the frequency dynamics are directly influenced by the discontinuous control term and do not require neighborhood information or power-sharing calculations, as in droop-free and consensus strategies.

4.2. Sliding Mode Behavior

Once the system trajectories reach the surface $\mathbf{S}\left(t\right)=\mathbf{0}$, the dynamics enter the sliding regime. By enforcing $\dot{\mathbf{S}}\left(t\right)=\mathbf{0}$, the induced motion becomes

$$\dot{\mathit{\omega }}\left(t\right)=\mathbf{0}\Rightarrow \mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n,\forall t\ge t_s,$$

(16)

with $t_s$ being the finite reaching time. Therefore, frequency synchronization is achieved for all nodes.

5. Stability Analysis

The stability of the MG under the proposed sliding mode controller (13) is examined through a Lyapunov-based analysis. Global convergence and asymptotic stability are established by examining the system dynamics in two distinct regions: off the sliding surface and on it.

5.1. Lyapunov-Based Stability Analysis

Consider the Lyapunov candidate function

$$V\left(t\right)={\displaystyle \frac{1}{2}}{\mathbf{S}}^{\top }\left(t\right)\mathbf{S}\left(t\right),$$

(17)

where $\mathbf{S}\left(t\right)={\omega }_0{\mathbf{1}}_n-\mathit{\omega }\left(t\right)$, defined in (14), denotes the vector of frequency errors. This candidate is positive definite for all $\mathbf{S}\left(t\right)\ne \mathbf{0}$ and vanishes only at the equilibrium. Its time derivative, replacing (15), is

$$\dot{V}\left(t\right)={\mathbf{S}}^{\top }\left(t\right)\dot{\mathbf{S}}\left(t\right)=-{\mathbf{S}}^{\top }\left(t\right)\dot{\mathit{\omega }}\left(t\right).$$

(18)

5.1.1. Outside the Sliding Surface

When $\mathbf{S}\left(t\right)\ne \mathbf{0}$, the sign function is locally constant (1 or $-1$), and its derivative is

$${\displaystyle \frac{d}{dt}}\mathrm{sgn}\left(\mathbf{S}\left(t\right)\right)=\mathbf{0},\mathrm{a}.\mathrm{e}.$$

(19)

Under this condition, the dynamics of the frequency (13) become

$$\dot{\mathit{\omega }}\left(t\right)=-m\dot{\mathbf{p}}\left(t\right),$$

(20)

and substituting (4) yields

$$\dot{\mathit{\omega }}\left(t\right)=-m{v}^{2}B\mathit{\omega }\left(t\right).$$

(21)

By substituting (21) into (18) and applying the identity $\mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n-\mathbf{S}\left(t\right)$, the expression becomes

$$\dot{V}\left(t\right)=m{v}^2{\omega }_0{\mathbf{S}}^{\top }\left(t\right)B{\mathbf{1}}_n-m{v}^2{\mathbf{S}}^{\top }\left(t\right)B\mathbf{S}\left(t\right).$$

(22)

Since the power network is balanced, $B⪰0$, then, the susceptance Laplacian satisfies $B{\mathbf{1}}_n=\mathbf{0}$ by construction. Hence, the Lyapunov derivative reduces to

$$\dot{V}\left(t\right)=-m{v}^2{\mathbf{S}}^{\top }\left(t\right)B\mathbf{S}\left(t\right)\le 0,$$

(23)

which confirms that the system exhibits global asymptotic stability outside the sliding surface.

5.1.2. On the Sliding Surface

When $\mathbf{S}\left(t\right)=\mathbf{0}$, the inverter frequencies satisfy $\mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n$, and the system enters the sliding regime. In this regime, the control law becomes discontinuous due to the sign function, which is not uniquely defined at zero. This leads to a set-valued right-hand side in the differential equation, requiring interpretation via the Filippov framework [24,25]. Under this formulation, the control term satisfies

$$\mathrm{sgn}\left(\mathbf{S}\left(t\right)\right)\in {[-1,1]}^n,$$

(24)

and the system dynamics follow the differential inclusion

$$\dot{\mathit{\omega }}\left(t\right)\in \mathcal{F}\left[f\right]\left(\mathit{\omega }\left(t\right)\right):=\overline{\mathrm{co}}\left\{\underset{ϵ\to 0^{\pm }}{lim}f(\mathit{\omega }\left(t\right)+ϵ)\right\},$$

(25)

where $\overline{\mathrm{co}}\{·\}$ denotes the closed convex hull of the limiting vector fields approaching from both sides.

Physically, the Filippov representation avoids discontinuous “jumps” by allowing the trajectories to slide along the manifold $\mathbf{S}\left(t\right)=\mathbf{0}$. This sliding motion corresponds to the desired steady-state regime, where all inverter frequencies synchronize at the nominal value ${\omega }_0$, and the control law adapts within the Filippov set to reject bounded disturbances and model uncertainties. The inverter behavior remains robust and predictable, despite the non-smooth nature of the control input.

To analyze convergence to the sliding surface, consider the Lyapunov function (17). Its time derivative reduces to (23), that is $\dot{V}\left(t\right)=-m{v}^2{\mathbf{S}}^{\top }\left(t\right)B\mathbf{S}\left(t\right)\le 0$, where $m>0$ and $v>0$ are controller gains. Since $B\succ 0$ on the orthogonal subspace ${\mathbf{1}}_n^{\perp }$, it follows that

$$\dot{V}\left(t\right)\le -\alpha {\parallel \mathbf{S}\left(t\right)\parallel }^2,\mathrm{with}\alpha =m{v}^2{\lambda }_{min}\left(B{|}_{{\mathbf{1}}_n^{\perp }}\right)>0,$$

(26)

where ${\lambda }_{min}\left(B{|}_{{\mathbf{1}}_n^{\perp }}\right)$ denotes the smallest non-zero eigenvalue of B restricted to ${\mathbf{1}}_n^{\perp }$. This eigenvalue has a physical interpretation: it quantifies the electrical connectivity among inverters. A larger value implies stronger coupling and faster convergence to the synchronous regime.

From inequality (26), an upper bound on the reaching time can be derived as

$$t_s\le {\displaystyle \frac{V\left(0\right)}{\alpha }}={\displaystyle \frac{{\parallel \mathbf{S}\left(0\right)\parallel }^2}{2\alpha }},$$

(27)

showing that trajectories reach the sliding surface in finite time.

Once the surface is reached, the invariance condition $\dot{\mathbf{S}}\left(t\right)=\mathbf{0}$ implies

$$\dot{V}\left(t\right)=0,V\left(t\right)=\mathrm{const},$$

(28)

confirming that the manifold $\mathbf{S}\left(t\right)=\mathbf{0}$ is invariant for $t\ge t_s$. In this regime, the frequency vector satisfies

$$\mathit{\omega }\left(t\right)={\omega }_0{\mathbf{1}}_n,\forall t\ge t_s,$$

(29)

which guarantees synchronized frequency regulation across all inverters.

In Filippov’s sense, the closed-loop dynamics in sliding mode are governed by the inclusion

$$\dot{\mathit{\omega }}\left(t\right)\in \mathcal{F}\left[-m\dot{\mathbf{p}}\left(t\right)+k\mathrm{sgn}\left(\mathbf{S}\left(t\right)\right)\right]=\mathrm{co}\left\{\underset{ϵ\to 0^{\pm }}{lim}f(\mathit{\omega }\left(t\right)+ϵ)\right\}.$$

(30)

This set-valued formulation ensures well-defined system trajectories even under non-smooth control inputs, and under mild conditions (e.g., transversality and local Lipschitz continuity), guarantees existence and uniqueness of solutions. The result is a robust and stable inverter behavior aligned with the design objectives of the proposed control scheme.

5.2. Steady-State Frequency Under Sliding Mode Control

Assuming that each inverter delivers a constant steady-state power $p_i(\infty )={\displaystyle \frac{P_T}{n}}$, as specified in (8), and that the frequency converges to a common value ${\omega }_i(\infty )={\omega }_{\infty }$ for all $i\in \{1,\dots ,n\}$, substituting these conditions into (10) yields

$${\omega }_{\infty }={\omega }_0-m{\displaystyle \frac{P_T}{n}}+k\mathrm{sgn}({\omega }_0-{\omega }_{\infty }).$$

(31)

The sign function in (31) introduces a piecewise behavior depending on the relation between ${\omega }_{\infty }$ and ${\omega }_0$:

• If ${\omega }_{\infty }<{\omega }_0$, then $\mathrm{sgn}({\omega }_0-{\omega }_{\infty })=1$, and

  $${\omega }_{\infty }={\omega }_0-m{\displaystyle \frac{P_T}{n}}+k.$$

  (32)
• If ${\omega }_{\infty }>{\omega }_0$, then $\mathrm{sgn}({\omega }_0-{\omega }_{\infty })=-1$, and

  $${\omega }_{\infty }={\omega }_0-m{\displaystyle \frac{P_T}{n}}-k.$$

  (33)
• If ${\omega }_{\infty }={\omega }_0$, then $\mathrm{sgn}\left(0\right)\in [-1,1]$, and the condition becomes

  $${\displaystyle \frac{m{P}_T}{n}}=k\xi ,\mathrm{with}\xi \in [-1,1],$$

  (34)

  which implies

  $$\left|{\displaystyle \frac{m{P}_T}{n}}\right|\le k.$$

  (35)

Therefore, the system achieves frequency regulation ${\omega }_{\infty }={\omega }_0$ if and only if condition (35) holds. Otherwise, a bounded steady-state deviation from the nominal frequency will arise, determined by the magnitude of the injected power and the control gain k. Physically, this result reveals the robustness of the control law: as long as the total power demand per inverter remains within a range dictated by ${\displaystyle \frac{k}{m}}$, the system maintains synchronization at the nominal frequency. For higher loads, the control enters a sliding regime with predictable and bounded frequency offsets, still ensuring convergence and consistent operation across all inverters.

5.3. Impact of Chattering on Inverter Operation

The discontinuous term in (10) provides the robustness properties of SMC but also introduces chattering, i.e., high-frequency oscillations of the control action around the sliding surface. In power electronic converters, chattering may degrade power quality, increase switching losses, and cause thermal stress on power semiconductors [26,27].

To mitigate this effect, practical implementations often employ boundary layer approximations [28,29,30] or higher-order sliding modes to smooth the control action. A common boundary layer approximation replaces the discontinuous sign function by a continuous saturation function,

$${\mathrm{sgn}}_{\delta }\left(s_i\right)=\left\{\begin{array}{cc}+1\hfill & \mathrm{if}{s}_i>\delta ,\hfill \\ s_i/\delta \hfill & \mathrm{if}|s_i|\le \delta ,\hfill \\ -1\hfill & \mathrm{if}{s}_i<-\delta ,\hfill \end{array}\right.$$

(36)

where $\delta >0$ defines the layer thickness. Within this layer, the controller behaves as a continuous feedback, limiting the frequency of commutation events.

Under the ideal discontinuous law (10), the control input of inverter i is

$$u_i\left(t\right)=k\mathrm{sgn}\left(s_i\left(t\right)\right).$$

(37)

Because of the discontinuity of $\mathrm{sgn}(·)$, $u_i\left(t\right)$ may switch rapidly when trajectories oscillate near $s_i=0$.

To assess the impact of chattering, a smoothed version of the control input can be introduced as follows:

$$u_i^{\eta }\left(t\right)=k\mathrm{sat}\left({\displaystyle \frac{s_i\left(t\right)}{\eta }}\right),$$

(38)

where

$$\mathrm{sat}\left(x\right)=\left\{\begin{array}{cc}1\hfill & x>1,\hfill \\ x\hfill & \left|x\right|\le 1,\hfill \\ -1\hfill & x<-1,\hfill \end{array}\right.$$

and $\eta >0$ defines the boundary layer thickness. This modification preserves the sliding dynamics for $|s_i|>\eta$ while reducing high-frequency commutation around the surface.

The effective switching frequency induced by chattering can be approximated by the frequency of zero-crossings of $s_i\left(t\right)$. Let $T_c$ be the mean time between consecutive sign changes in $u_i\left(t\right)$, then

$$f_{\mathrm{eff}}={\displaystyle \frac{1}{2T_c}}.$$

(39)

In a PWM-based inverter, the total power dissipated due to switching events is estimated by

$$P_{\mathrm{sw}}=n_s{E}_{\mathrm{sw}}{f}_{\mathrm{eff}},$$

(40)

where $n_s$ is the number of power semiconductors switched per event and $E_{\mathrm{sw}}$ is the energy lost per switching transition. Therefore, reducing $f_{\mathrm{eff}}$ through boundary layers or smoothing techniques is crucial for minimizing switching losses [26,29].

6. Results

This section presents a simulation scenario considering a four-node islanded MG to demonstrate the performance of the proposed strategy.

6.1. Simulation Setup

Figure 1 illustrates the MG structure where four electronically coupled distributed generators $G_{1,2,3,4}$ operate as VSI. Each VSI locally regulates the voltage amplitude and frequency while delivering active and reactive power to supply a common load $Z_G$. Additionally, a local load $Z_{L1}$ is connected to generator $G_1$. $Z_{1,2,3}$ represents the impedances of the transmission line parasitic components, $T_{1,2,3,4}$ models the isolation transformers at the output of each converter, and $S_{1,2,3,4}$ are the local frequency sensors. Times $t_1$ to $t_4$ reflect individual clock drifts across generators. Virtual impedance $Z_v$ is digitally implemented in all VSIs.

The MG components are simulated in MATLAB/Simulink version 2025a, following the modeling approach described in [31]. Electrical dynamics are captured using the SimPowerSystems toolbox, which provides comprehensive libraries for modeling and analyzing power system components. Local control behavior, including the execution of frequency and voltage regulation loops as well as timing effects, is simulated using the TrueTime toolbox [32], enabling co-simulation between power electronics and real-time control kernels. Figure 2 shows the full simulation architecture, which mirrors the physical MG topology presented in Figure 1. Each generator $G_i$ is implemented as a virtual grid-forming converter with embedded control logic executed by a dedicated real-time kernel. Loads, transmission lines, sensors, and transformers are labeled consistently with their experimental counterparts. Supervision blocks continuously monitor variables such as active and reactive power, voltage, and frequency, exporting data to the MATLAB workspace for post-processing. Although the simulation platform supports communication links, this feature is deliberately omitted to preserve the strictly local nature of the proposed control scheme. This setup reflects practical scenarios in rural or isolated MGs, where communication links may be unreliable, expensive, or deliberately omitted.

Each VSI in the simulated scheme of Figure 2 follows the block diagram shown in Figure 3. The control algorithm is executed within a real-time simulation kernel that governs two voltage sources generating sinusoidal signals in the $\alpha \beta$ reference frame. These voltages are synthesized according to the local sliding mode control law. Currents and frequency are measured and fed back into the kernel to compute the frequency correction term.

The most relevant simulation parameters for the MG scenario are listed in

Table 1. Microgrid setup parameters.

Symbol	Description	Value
$v_0$	Grid voltage (rms line to line)	$\sqrt{2}110$ V
${\omega }_0$	Grid frequency (at no load)	$2\pi 60$ rad/s
c	Gains for voltage droop	1 μV/(VAr)
m	Gains for frequency droop	1 mrad/(W · s)
k	Gains for frequency compensation in sliding mode	$2\pi 5$ mrad/(s)
$Z_1$	Transmission line impedance	1.3 m$\mathrm{\Omega }@36.9^{\circ }$
$Z_{2,3}$	Transmission line impedances 2 and 3	1 m$\mathrm{\Omega }@16.7^{\circ }$
$T_{1,2}$	Transformer impedances 1 and 2	0.62 m$\mathrm{\Omega }@37.{01}^{\circ }$
$T_{3,4}$	Transformer impedances 3 and 4	1.31 m$\mathrm{\Omega }@9.{87}^{\circ }$
$Z_G$max	Maximum global load impedance	88 $\mathrm{\Omega }@0^{\circ }$
$Z_G$min	Minimum global load impedance	44 $\mathrm{\Omega }@0^{\circ }$
$Z_{L1}$	Local load impedance 1	88 $\mathrm{\Omega }@0^{\circ }$
$Z_v$	Virtual impedance	3.76 m$\mathrm{\Omega }@{90}^{\circ }$
$d_1$	Clock drift rate in $G_1$	$1.0000$ ppm
$d_2$	Clock drift rate in $G_2$	$1.00001$ ppm
$d_3$	Clock drift rate in $G_3$	$0.9999$ ppm
$d_4$	Clock drift rate in $G_4$	$1.00002$ ppm
h	Sampling period	$0.1$ ms

. When active, clock drifts $d_{1,2,3,4}$ have been deliberately exaggerated to accentuate the impact of asynchrony. The gains m in (6), c in (9), and k in (13), are tuned to ensure smooth and representative behavior across all test cases. For simplicity, identical gain values are assigned to all VSI, although the analysis remains valid even when heterogeneous gains are used.

6.2. Controller Gain Selection and Impact

The parameters c, m, and k govern the dynamic behavior of the droop-based and sliding mode control loops. In this work, these gains are adjusted to balance convergence speed, robustness, and numerical stability in simulation scenarios. Although no formal optimization is applied, their selection follows established engineering principles.

The voltage droop gain c is set to a low value (e.g., 1 μV/VAr) to prioritize voltage stability while minimizing reactive power oscillations. The droop gain m defines the inverse slope of the frequency–power characteristic. Lower values of m improve frequency regulation by reducing steady-state deviation but compromise power-sharing fairness under unbalanced loading. A typical range is 0.5–2 mrad/(W · s); in this paper, a uniform value of $m=1\mathrm{mrad}/(\mathrm{W}·\mathrm{s})$ is used across all inverters for simplicity.

The sliding mode gain k controls the magnitude of the discontinuous switching action. According to (35), k must be sufficiently large to guarantee finite-time convergence and robustness to matched disturbances. However, excessive values of k increase the risk of chattering and associated switching losses. A value of $k=2\pi 5\mathrm{mrad}/\mathrm{s}$ yields satisfactory performance in the tested scenarios.

While gains are chosen uniformly in this study, practical implementations may benefit from heterogeneous tuning based on inverter ratings or local impedance characteristics.

Preliminary sensitivity tests indicate that the system remains stable for parameter variations up to $\pm 30\%$ in both m and k. Increasing k results in faster convergence but amplifies chattering, whereas reducing k diminishes robustness. Similarly, decreasing m improves frequency accuracy but worsens power-sharing precision.

A detailed parametric analysis is outside the scope of this paper. However,

Table 2. Control parameters and observed effects.

Parameter	Effect of Variation
c	Minimal impact unless reactive power is dominant
m	Lower m: better frequency, worse sharing
k	Higher k: faster, more chattering

summarizes the key parameters used and their qualitative impact on system behavior.

6.3. Simulation Results

Figure 4 illustrates the dynamic response of the MG under ideal conditions, where conventional droop control is applied initially, followed sequentially by the activation of the proposed sliding mode controller. The simulation begins at time $t=0$ s with balanced initial conditions, where each inverter regulates its output frequency and active power according to the droop law (6). At time $t=10$ s, the control strategy transitions to the proposed SMC formulation (13). Throughout the entire simulation, voltage and reactive power are regulated via the standard voltage droop mechanism (9). The frequency converges rapidly to its nominal value with negligible steady-state error, significantly reducing the droop-induced deviation, while active power is evenly shared among the inverters.

To evaluate robustness, an MG control experiment employing the proposed SMC strategy is illustrated in Figure 5. The simulation spans 20 s and comprises four distinct phases. From time $t=0$ s, the system initiates operation under clock drift conditions. At $t=5$ s, the global impedance drops to $Z_G=Z_{Gmin}$, increasing the power demand across all inverters. This perturbation is reverted at $t=10$ s, when the impedance returns to its nominal value $Z_G=Z_{Gmax}$. At $t=15$ s, a line fault occurs, fragmenting the electrical network by disconnecting specific links and modifying the grid topology (from a unified structure to isolated pairs: $G_1$–$G_2$ and $G_3$–$G_4$). No communication infrastructure is employed.

To compare control strategies under identical operating conditions, Figure 6 presents two MG experiments lasting 12 s and subjected to the same sequence of disturbances described above. From time $t=2$ s, the system operates under clock drift; at $t=4$ s, a drop in global impedance increases the overall load; at $t=6$ s, the impedance returns to its nominal value; at $t=8$ s, a line fault fragments the electrical network topology; and at $t=10$ s, a communication network failure is introduced in the droop-free SMC implementation. In both experiments, only active power and frequency responses are observed. Figure 6a,c corresponds to the proposed local SMC strategy, while Figure 6b,d depicts the system behavior under the SMC [19] that relies on inter-inverter communication. Despite undergoing the same disturbance sequence, the local SMC maintains stable frequency and balanced power sharing without a communication infrastructure, underscoring its resilience and decentralized nature.

7. Discussion

This section discusses the control performance based on simulation results, emphasizing frequency regulation, robustness, steady-state accuracy, and comparative advantages.

7.1. Active Power Sharing and Frequency Restoration

The proposed local SMC ensures rapid frequency convergence and uniform active power distribution under both ideal and perturbed conditions. In the first experiment (Figure 4), frequency regulation improves markedly after switching from conventional droop to local SMC, converging to a neighborhood of the nominal value, with limited chattering due to the discontinuous nature of the control law. In the second experiment (Figure 5), the controller sustains frequency regulation and power sharing despite perturbations. Although the test case includes only four VSIs, the proposed control law is inherently scalable, as it does not rely on information from neighboring nodes. Nevertheless, in larger networks with heterogeneous line impedances or unbalanced topologies, power-sharing accuracy may deteriorate unless control gains are locally tuned.

7.2. Robustness Under Perturbations

The results in Figure 5 validate the robustness of the proposed method against three realistic sources of disturbances: clock drifts, load changes, and electrical network fragmentation. In all scenarios, the system maintains stable and coordinated operation without inter-node communication. The ability to reject disturbances demonstrates that the sliding mode dynamics remain attractive and invariant, with robustness embedded directly into the local control law. This eliminates dependence on global information and reduces vulnerability to these perturbations. In contrast, the droop-free SMC method becomes unstable after $t=10$ s, when the communication network fails and power sharing among inverters is no longer coordinated.

7.3. Steady-State Accuracy vs. Simplicity

Steady-state values of frequency remain within a small bounded region around the nominal reference, a typical characteristic of discontinuous sliding mode control. This residual oscillation is constrained by the controller gain and can be further reduced with boundary layer techniques. The lack of an integral action in the sliding surface formulation implies a trade-off between frequency restoration accuracy and implementation simplicity. While frequency does not converge exactly to the nominal reference, the deviation remains bounded and predictable. In return, the controller avoids complex filtering, numerical integration, or centralized information exchange, making it highly suitable for deployment in isolated or resource-constrained MGs. This design decision aligns with the goal of achieving robust autonomy at the node level.

The proposed analysis assumes ideal frequency and power measurements, free of noise, delay, or quantization effects. In practice, such imperfections may introduce additional variability in steady-state frequency or interfere with sliding accuracy. Moreover, while the sliding mode law guarantees bounded frequency convergence, it does not enforce exact regulation. This limitation is inherent to the absence of integral action in the surface formulation, and reflects a deliberate design trade-off: by avoiding estimation, filtering, or synchronization layers, the controller preserves structural simplicity and remains entirely communication-free. These characteristics make it well-suited for autonomous operation in constrained environments. Although the control law is inherently scalable, its performance in large, heterogeneous MGs may degrade unless gains are locally adapted.

7.4. Comparison with Communication-Based Approaches

The comparative experiments illustrate the trade-offs among conventional droop, the proposed local SMC, and the communication-based droop-free SMC. While all strategies deliver satisfactory performance under identical disturbances, the local SMC achieves this without requiring synchronization or message exchange. This enhances its resilience to communication failures and makes it a compelling option for islanded or resource-constrained MGs. These observations are summarized in

Table 3. Comparative analysis of droop, local SMC, and droop-free SMC controllers.

Control Method	Advantages	Disadvantages
Conventional Droop Control	Fully decentralized Robust to perturbations Effective for voltage and reactive power regulation	Permanent steady-state frequency deviation Limited dynamic performance Uneven power sharing in presence of perturbations
Local SMC (proposed)	Improved frequency regulation Robust to timing mismatches, load changes, and topology variations No communication required Simple and decentralized implementation	Residual bounded frequency error Chattering due to discontinuous action
Droop-free SMC (with communication)	Precise frequency and power sharing Fast convergence under ideal communication conditions	Vulnerable to communication failure

, which contrasts the advantages and limitations of each approach.

8. Conclusions and Future Work

This work has presented a distributed control strategy for islanded MGs based on sliding mode control, formulated to operate without inter-VSI communication. The proposed method ensures frequency regulation and active power sharing through a discontinuous control law defined locally at each VSI, relying solely on local measurements. These features make this method highly suitable for decentralized, autonomous deployment in resource-constrained environments.

Simulation results demonstrate that the proposed controller effectively rejects both realistic and exaggerated disturbances, including clock mismatches, abrupt load variations, and network fragmentation—while maintaining system stability and ensuring small, bounded steady-state frequency deviations. A comparative evaluation against conventional droop control and a droop-free sliding mode strategy with communication underscores the advantages of the proposed local SMC in terms of modularity, implementation simplicity, and inherent resilience to communication failures.

Future work will address the main limitations of the proposed approach and broaden its applicability. To improve frequency restoration without compromising robustness, the control design can be extended by incorporating integral sliding surfaces based on the accumulated frequency error. This modification aims to eliminate residual steady-state deviations while maintaining locality. In parallel, strategies such as boundary layer approximations, continuous control laws, and hysteresis-based implementations can be studied to mitigate chattering and reduce its impact on switching losses and power quality. Scalability in large, heterogeneous MGs can be addressed through adaptive or data-driven gain tuning methods, which can better accommodate varying network conditions. Furthermore, experimental validation using hardware-in-the-loop testbeds can be pursued to assess practical feasibility under real-time constraints, sensor imperfections, and quantization.