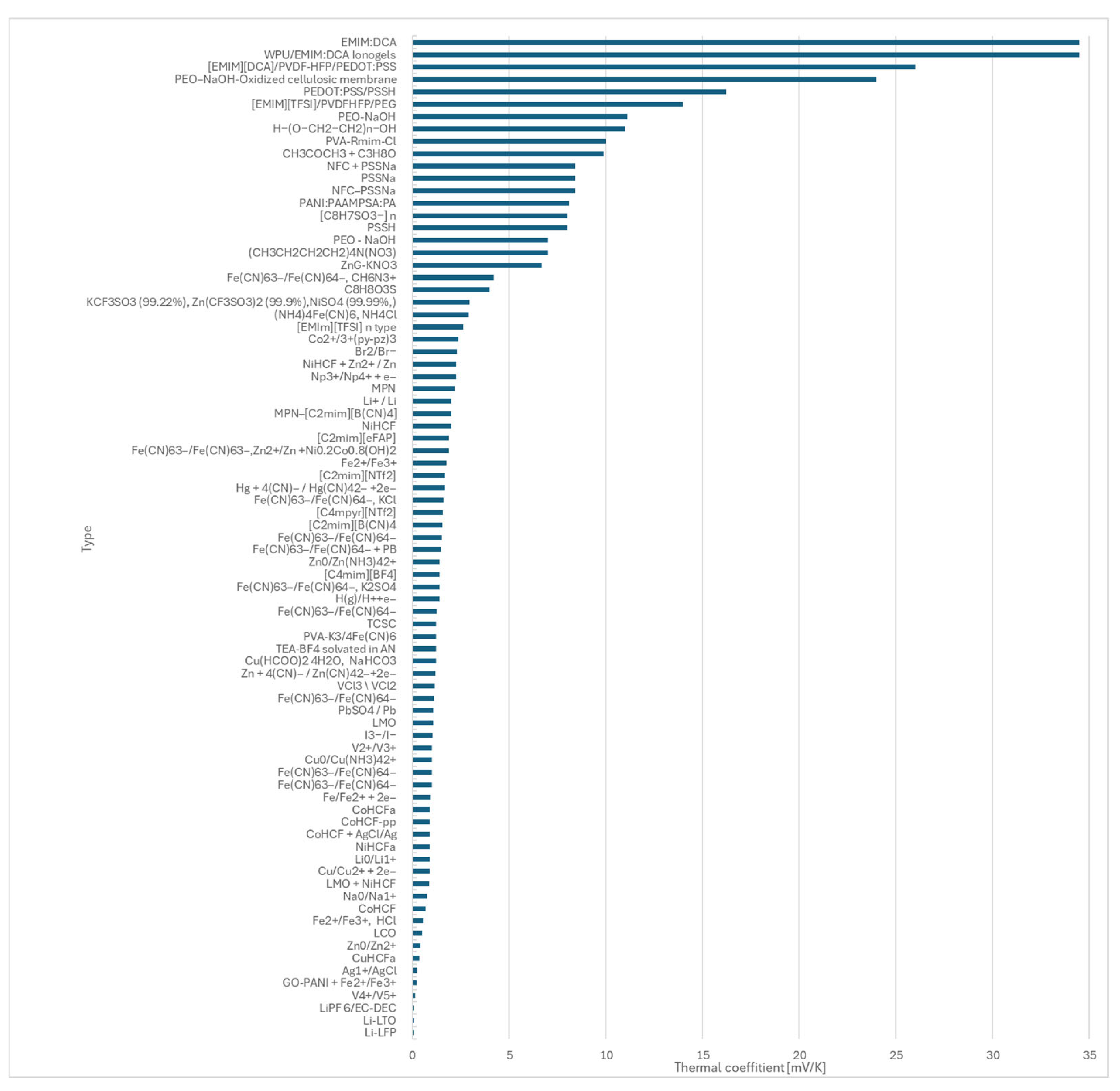
Sensitivity Factors of Thermally Regenerative Electrochemical Cycle Systems Using Fuel Cell’s Waste Heat
Abstract
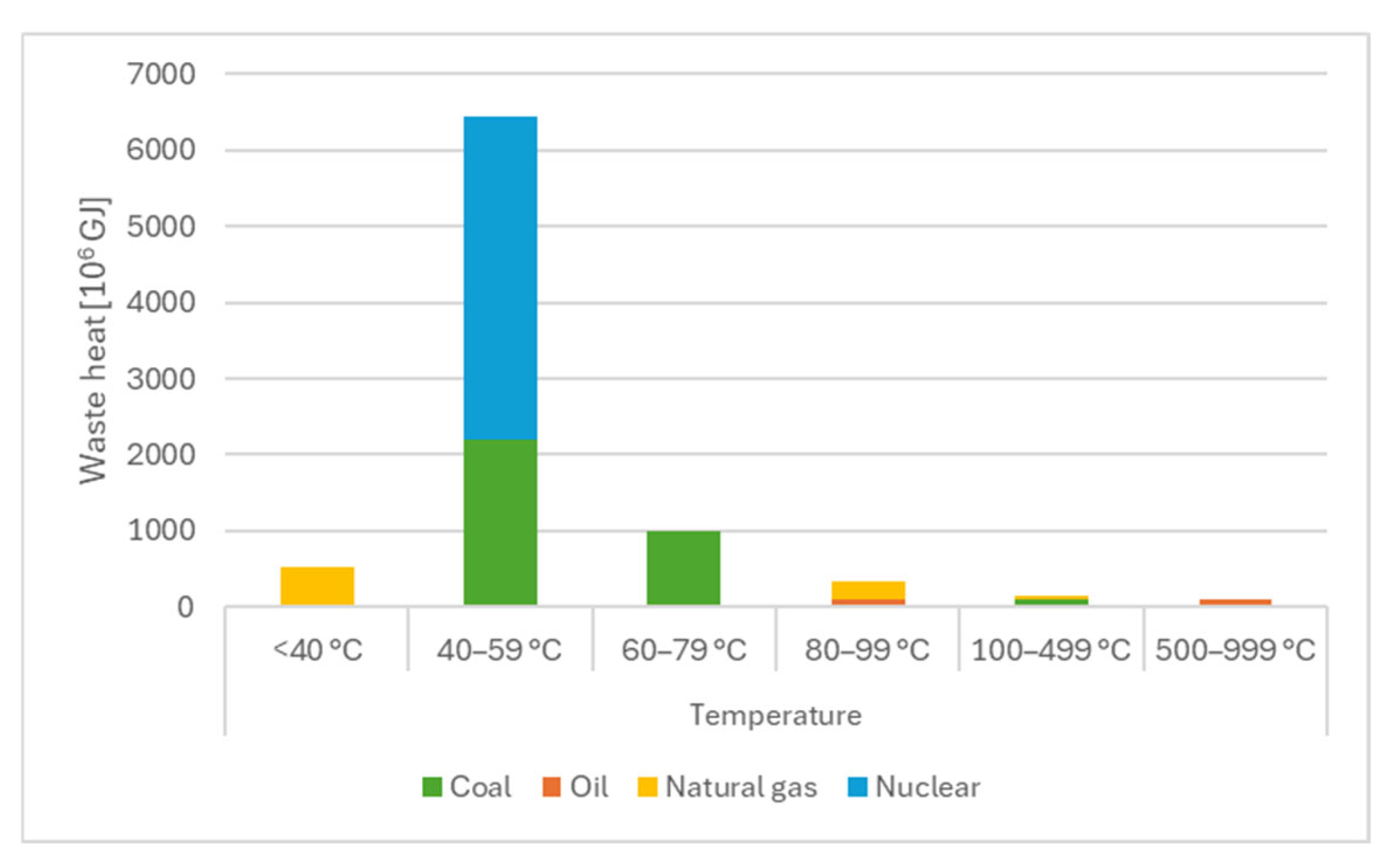
1. Introduction
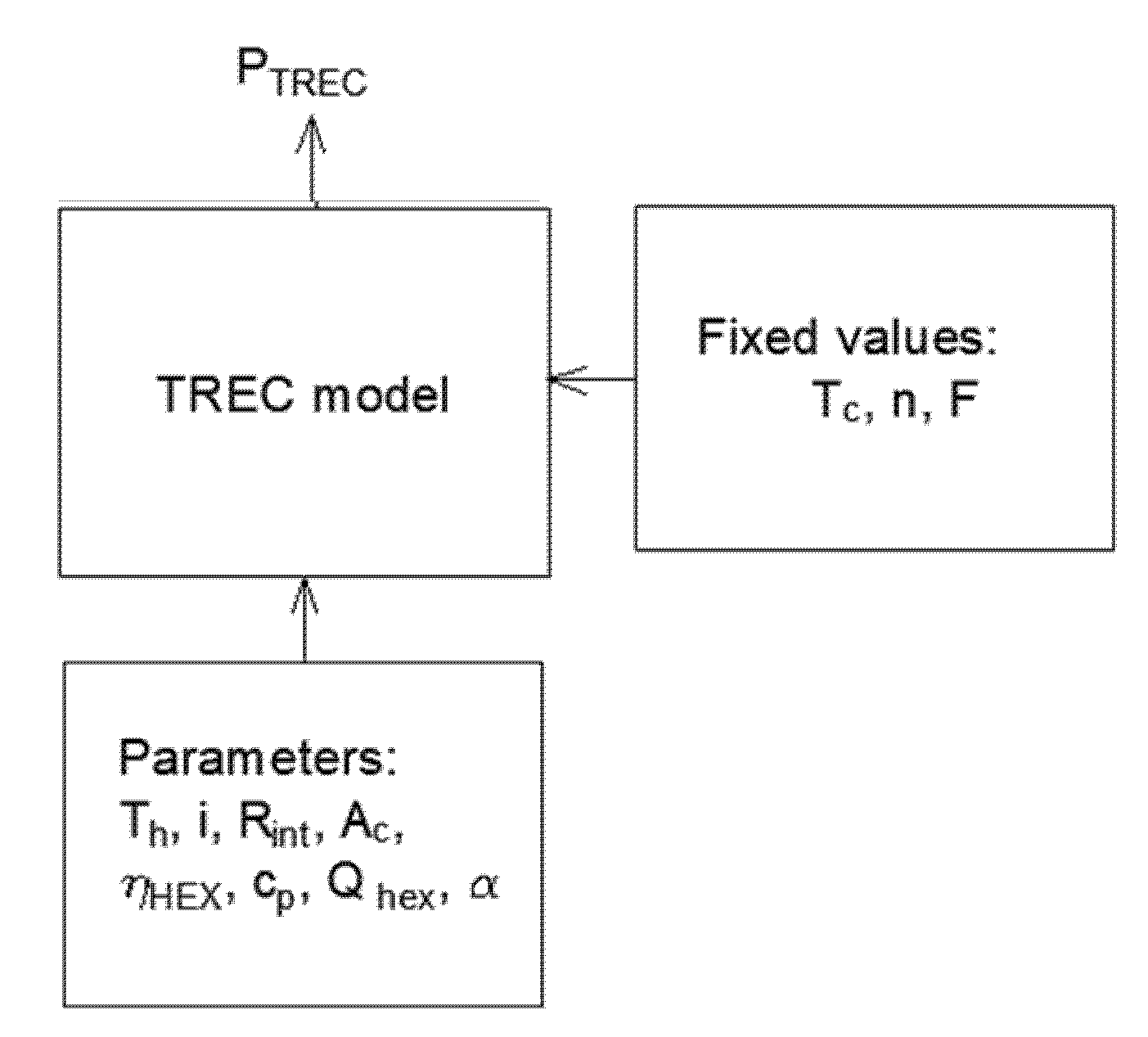
2. Materials and Methods
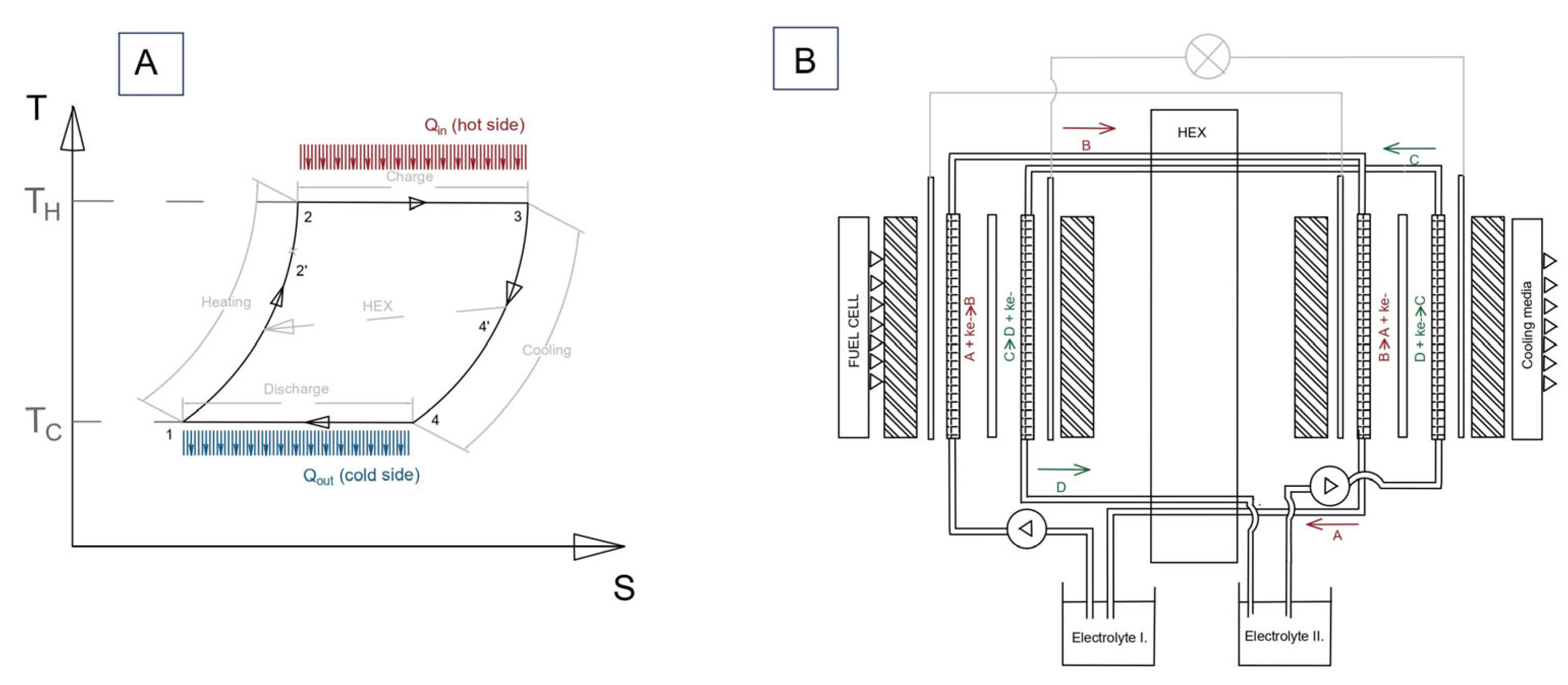
2.1. TREC System Electrochemical Model
2.2. Sensitivity Analysis
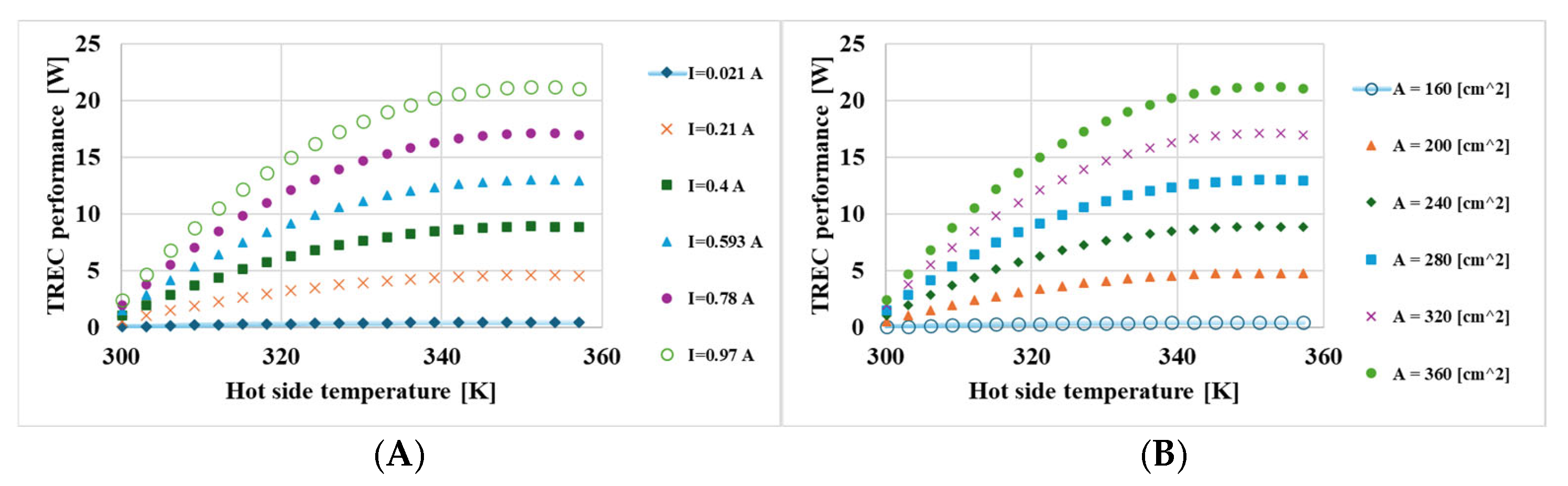
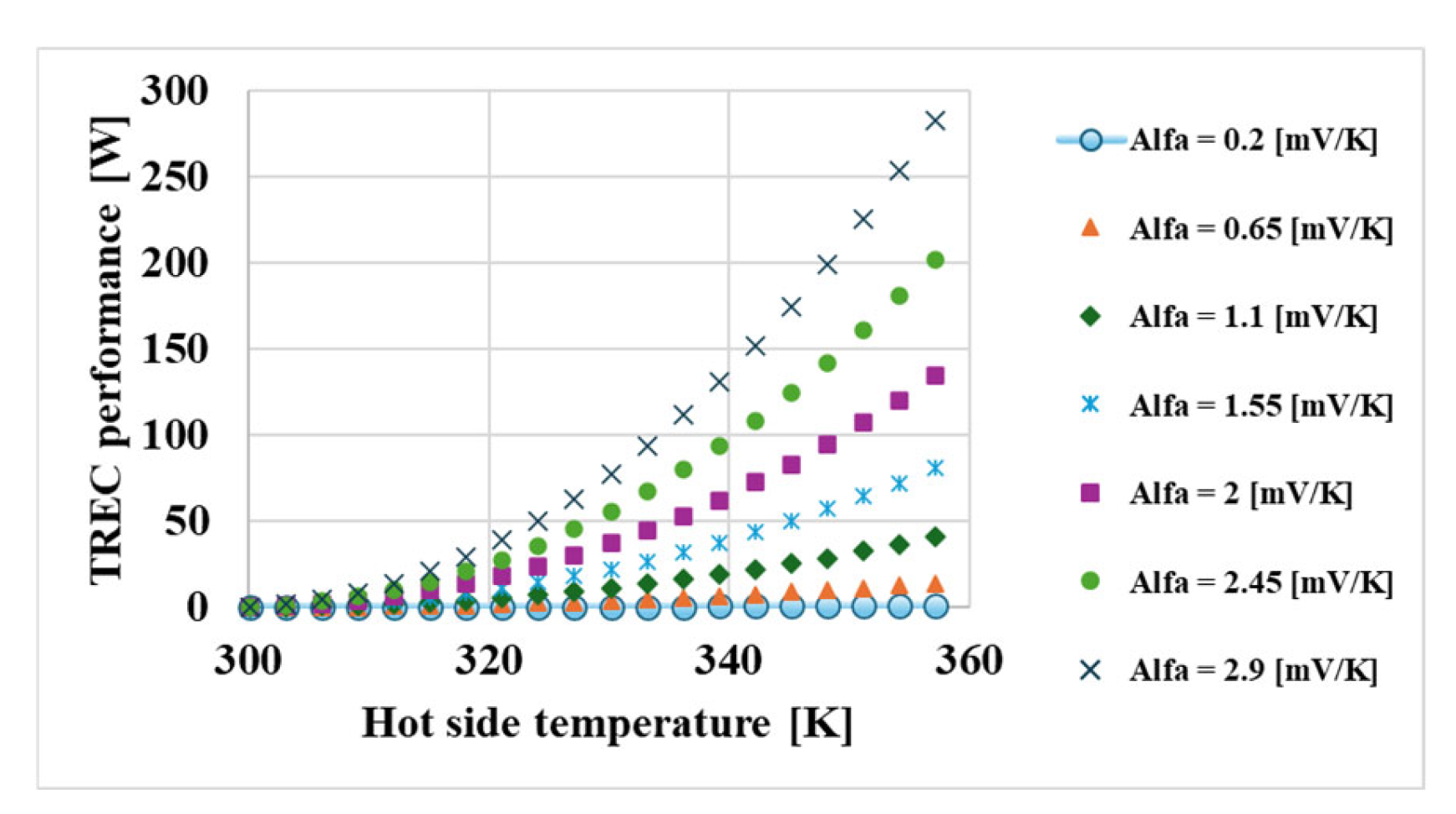
3. Results
4. Discussion
- The thermal coefficient of the redox couples was found to be the most critical factor affecting system performance (γ ≈ 737,800).
- Internal resistance and current density also emerged as highly sensitive parameters, with a considerable influence on performance (γ ≈ 35,035 and γ ≈ 30,287, respectively).
- The hot-side temperature and the size of the active membrane area were identified as sensitive parameters that play a significant role in energy conversion.
- The efficiency of the heat exchanger and the specific heat capacity of the electrolyte have a lesser effect on performance, though they do influence overall system efficiency.
- During the study, literature data for 81 redox couples were reviewed and compared, providing a foundation for future material selection.
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
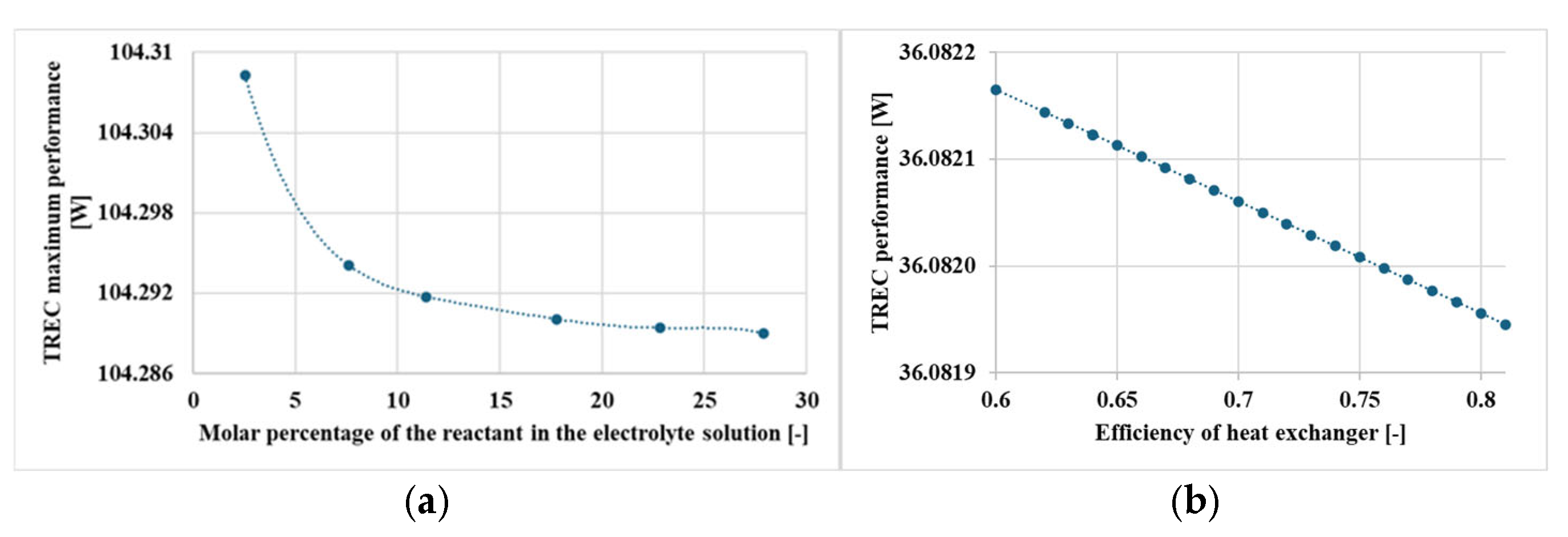
Appendix A.3
| Assumption | Justification | Fixed Value(s) |
|---|---|---|
| Constant specific and molar heat capacity | Variation in the studied temperature range is small | cp = 75.6 J/(mol·K) (test: 58.15–80.77) |
| Free energy fully derived from entropy change | Applied Gibbs–Helmholtz approximation | – |
| Heat transfer only by conduction | Based on aluminum plate conduction | λ = 237 W/mK; thickness = 2 mm; area = 0.16 m2 |
| Neglected pump power | Ion exchange occurs by diffusion, no external driving | Diffusion constant, around 10−9; 10−10 m2/s |
| Constant, symmetric internal resistance | Assumed identical in both cells | Rint = RH = RC = 24.5 Ω (test: 5.14–24.25) |
| Fixed cold-side temperature, fixed humidity | Taken from environment, no external cooling | TC = 297.15 K (24 °C) |
| Hot-side temperature limited by PEM cell | Limited by PEM fuel cell maximum operating temperature | TH = 357.15 K (84 °C); test: 297.15–360.15 K |
| Fixed electrolyte pair | Iodine–KI and ferricyanide–hexacyanoferrate aqueous solutions | 0.1/1 M (I2–KI); 0.375/0.375 M (Fe(CN)63−/Fe(CN)64−) |
| Heat generated by fuel cell is fix and constant | Represents the external heat source | QFC = 50,000 J (test: 23,750–50,000 J) |
References
- Reay, D. Heat Recovery Systems; Library of Congress Cataloging in Publication Data; Spon Press: London, UK, 1979; ISBN 0419114009. [Google Scholar]
- Wilberforce, T.; Muhammad, I. Dynamic modelling and analysis of Organic Rankine Cycle power units for the recovery of waste heat from 110kW Proton Exchange Membrane Fuel cell system. Int. J. Thermofluids 2023, 17, 100280. [Google Scholar] [CrossRef]
- Qian, X.; Shin, J. Thermally regenerative electrochemically cycled flow batteries with pH neutral electrolytes for harvesting low-grade heat. Phys. Chem. Chem. Phys. 2021, 23, 22501–22514. [Google Scholar] [CrossRef]
- Hassan, A.; Corberán, J.; Ramirez, M.; Trebilcock-Kelly, F.; Payá, J. A high-temperature heat pump for compressed heat energy storage applications: Design, modeling, and performance. Energy Rep. 2022, 8, 10833–10848. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Kim, J.; Kim, M.S.; Kim, M.S. Parametric study and performance evaluation of an organic Rankine cycle (ORC) system using low-grade heat at temperatures below 80 °C. Appl. Energy 2017, 189, 55–65. [Google Scholar] [CrossRef]
- Luo, D.; Zhang, H.; Li, Z.; Zhang, P.; Chen, H. Increasing waste heat recovery performance of a hexagonal thermoelectric generator with microchannels. Energy 2025, 334, 137589. [Google Scholar] [CrossRef]
- Ridwan, M.; Gasulla, M.; Reverter, F. Principle and Applications of Thermoelectric Generators: A Review. Sensors 2025, 25, 2484. [Google Scholar] [CrossRef] [PubMed]
- IBISWorld. Total Price of Semiconductor and Electronic Components; Business Environment Profiles; IBISWorld: London, UK, 2025. [Google Scholar]
- Macrotrends. Copper Prices (1959–2025). 2025. Available online: https://www.macrotrends.net/1476/copper-prices-historical-chart-data (accessed on 8 August 2025).
- Hamid, K.; Sajjad, U.; Ahrens, M.U.; Ren, S.; Ganesan, P.; Tolstorebrov, I.; Arshad, A.; Said, Z.; Hafner, A.; Wang, C.-C.; et al. Potential evaluation of integrated high temperature heat pumps: A review of recent advances. Appl. Therm. Eng. 2023, 230, 120720. [Google Scholar] [CrossRef]
- de Bethune, A.; Licht, T.; Swendeman, N. The Temperature Coefficients of Electrode Potentials: The Isothermal and Thermal Coefficients—The Standard Ionic Entropy of Electrochemical Transport of the Hydrogen Ion. J. Electrochem. Soc. 1959, 106, 616–625. [Google Scholar]
- Long, R.; Li, B.; Liu, Z.; Liu, W. Multi-objective optimization of a continuous thermally regenerative electrochemical cycle for waste heat recovery. Energy 2015, 93, 1022–1029. [Google Scholar] [CrossRef]
- Lee, S.; Yang, Y.; Ghasemi, H.; Kraemer, D.; Cheng, G.; Ciu, Y. An electrochemical system for efficiently harvesting low-grade heat energy. Nat. Commun. 2014, 5, 3942. [Google Scholar] [CrossRef]
- Long, R.; Li, B. A hybrid system using a regenerative electrochemical cycle to harvest waste heat from the proton exchange membrane fuel cell. Energy 2015, 93, 2079–2086. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q. Thermally regenerative electrochemical cycle for low-grade heat harnessing. Chem. Phys. Rev. 2021, 2, 021304. [Google Scholar] [CrossRef]
- Gao, C.; Lee, S.; Yang, Y. Thermally regenerative electrochemical cycle for low-grade heat harvesting. ACS Energy Lett 2017, 2, 2326–2334. [Google Scholar] [CrossRef]
- Bleeker, J.; Reichert, S.; Veerman, J.; Vermaas, D. Thermo-electrochemical redox flow cycle for continuous conversion of low-grade waste heat to power. Sci. Rep. 2022, 12, 7993. [Google Scholar] [CrossRef] [PubMed]
- Inoue, D.; Moritomo, Y. Concentration dependence of resistance components in solutions containing dissolved Fe2+/Fe3+. RSC Adv. 2024, 14, 6292–6297. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Harwey, J.; Conclin, M. Use of multi- parameter sensitivity analysis to determine relative importance of factors influencing natural attenuation of mining contaminants. In Proceedings of the Toxic Substances Hydrology Program Meeting, Charleston, SC, USA, 8–12 March 1999. [Google Scholar]
- Correa, J.; Farret, F.; Popov, F.; Simoes, M. Sensitivity Analysis of the Modeling Parameters Used in Simulation of Proton Exchange Membrane Fuel Cells. IEEE Trans. Energy Convers. 2005, 20, 211–218. [Google Scholar] [CrossRef]
- Wang, H.; Kim, S.; Rojas, T.; Zhu, Y.; Li, Y.; Xu, K.; Ngo, A.; Ciu, Y. Correlating Li-Ion Solvation Structures and Electrode PotentialTemperature Coefficients. J. Am. Chem. Soc. 2021, 143, 2264–2271. [Google Scholar] [CrossRef]
- Maldifassi, J.; Russell, J.; Kim, J.; Brightman, E.; Chen, X.; Bae, D. Evaluation of redox pairs for low-grade heat energy harvesting with a thermally regenerative cycle. Energy Adv. 2024, 3, 2877–2886. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Y.; Liu, C.; Mu, K.; Li, K.; Wang, S.; Yang, Y.; Lei, W.; Su, C.; Feng, S. Direct thermal charging cell for converting low-grade heat to electricity. Nat. Commun. 2019, 10, 4151. [Google Scholar] [CrossRef]
- Linford, P.; Xu, L.; Huang, B.; Shao-Horn, Y.; Thompson, C. Multi-cell thermogalvanic systems for harvesting energy from cyclic temperature changes. J. Power Sources 2018, 399, 429–435. [Google Scholar] [CrossRef]
- Quickenden, T.; Mua, Y. A Review of Power Generation in Aqueous Thermogalvanic Cells. J. Electrochem. Soc. 1995, 12, 3985. [Google Scholar] [CrossRef]
- Jiang, J.; Tian, H.; He, X.; Zeng, Q.; Niu, Y.; Zhou, T.; Yang, Y.; Wang, C. A CoHCF system with enhanced energy conversion efficiency for low-grade heat harvesting. J. Mater. Chem. A 2019, 7, 23862–23867. [Google Scholar] [CrossRef]
- Yuan, Z.; Yu, Y.; Li, W.; Wang, C.; Zhong, X.; Sui, X.; Yu, Z.; Han, D.; Shon, H.; Chen, Y. Thermo-osmosis-Coupled Thermally Regenerative Electrochemical. Cycle Effic. Lithium Extr. 2021, 13, 6276–6285. [Google Scholar] [CrossRef]
- Pereira, E.; Andrade, D.; Haas, V.; Watanabe, E.; Cunha, C.; de Sousa, A. Measuring the Self-Efficacy of Health Professionals for Practicing Hand Hygiene and Using Gloves: Development and Validation of an Instrument. Sustainability 2022, 14, 9486. [Google Scholar] [CrossRef]
- Gao, C.; Yin, Y.; Zheng, L.; Liu, Y.; Sim, S.; He, Y.; Zhu, C.; Liu, Z.; Lee, H.; Yuan, Q.; et al. Engineering the Electrochemical Temperature Coefficient for Efficient Low-Grade Heat Harvesting. Adv. Funct. Mater. 2018, 28, 1803129. [Google Scholar] [CrossRef]
- Park, H.; Licon, C.; Sleipness, O. Teaching Sustainability in Planning and Design Education: A Systematic Review of Pedagogical Approaches. Sustainability 2022, 14, 9485. [Google Scholar] [CrossRef]
- Ikeshoji, T. Thermoelectric Conversion by Thin-Layer Thermogalvanic Cells with Soluble Redox Couples. Bull. Chem. Soc. Jpn. 2006, 60, 1505–1514. [Google Scholar] [CrossRef]
- Ikeshoji, T.; Kimura, S.; de Nahui, F.; Yoneya, M. Computer analysis of natural convection in thin-layer thermocells with a soluble redox couple: Part 1. Method and the unsteady problem. J. Electroanal. Chem. Interfacial Electrochem. 1991, 307, 29–45. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, C.; Sim, S.; Kim, M.; Lee, S. Lithium Manganese Oxide in an Aqueous Electrochemical Systemfor Low-Grade Thermal Energy Harvesting. Chem. Mater. 2019, 31, 4379–4384. [Google Scholar] [CrossRef]
- Vassel, S.; Vassel, N. Electrochemical way of converting low-grade heat energy into electricity based on crystalline hydrate melting and crystallization. Int. J. Heat Mass Transf. 2018, 122, 818–822. [Google Scholar] [CrossRef]
- Hornut, J.; Storck, A. Experimental and theoretical analysis of a thermogalvanic undivided flow cell with two aqueous electrolytes at different temperatures. J. Appl. Electrochem. 1991, 21, 1103–1113. [Google Scholar] [CrossRef]
- Reynard, D.; Dennison, C.; Battistel, A.; Girault, H. Efficiency improvement of an all-vanadium redox flow battery by harvesting. J. Power Sources 2018, 390, 30–37. [Google Scholar] [CrossRef]
- Cortesi, A.; Dijoux, L.; Bris, G.; Pénicaud, C. Explaining the Differences between the Environmental Impacts of 44 French Artisanal Cheeses. Sustainability 2022, 14, 9484. [Google Scholar] [CrossRef]
- Chum, H.; Fahlsing, R.; Jayadev, T. Analysys of the Application of Thermogalvanic Cells to the Conversion of Low Grade Heat to Electrochemistry; Solar Energy Research Institute, A Division of Midwest Research Institute: Lakewood, CO, USA, 1980. [Google Scholar]
- Wang, X.; Feng, S. Thermal Capacitive Electrochemical Cycle on Carbon-Based Supercapacitor for Converting Low-grade Heat to Electricity. Front. Mech. Eng. 2017, 3, 20. [Google Scholar] [CrossRef]
- Kundu, A.; Fisher, T. Harnessing the thermogalvanic effect of the ferro/ferricyanide redox couple in a thermally chargeable supercapacitor. Electrochem. Acta 2018, 281, 357–369. [Google Scholar] [CrossRef]
- Chen, D.; Li, Z.; Jiang, J.; Wu, J.; Shu, N.; Zhang, X. Influence of electrolyte ions on rechargeable supercapacitor for high value-added conversion of low-grade waste heat. J. Power Sources 2020, 465, 228263. [Google Scholar] [CrossRef]
- Ikeshoji, T.; Gonçalves, R. Thermogalvanic cells with aqueous redox couples and temperature differences larger than 100 K. J. Appl. Electrochem. 1993, 23, 516–519. [Google Scholar] [CrossRef]
- Burmistrov, I.; Khanna, R.; Gorshkov, N.; Kiselev, N.; Artyukhov, D.; Boychenko, E.; Yudin, A.; Konyukhov, Y.; Kravchenko, M.; Gorokhovsky, A.; et al. Advances in Thermo-Electrochemical (TEC) Cell Performances for Harvesting Low-Grade Heat Energy: A Review. Sustainability 2022, 14, 9483. [Google Scholar] [CrossRef]
- Abraham, J.; Douglas, R.; Pringle, M. High Seebeck coefficient redox ionic liquid electrolytes for thermal energy harvesting. Energy Environ. Sci. 2013, 6, 2639–2645. [Google Scholar] [CrossRef]
- Yang, Y.; Lee, S.; Ghasemi, H.; Loomis, J.; Li, X.; Kraemer, D.; Zheng, G.; Cui, Y.; Chen, G. Charging-free electrochemical system for harvesting low-grade thermal energy. Appl. Phys. Sci. 2014, 111, 17011–17016. [Google Scholar] [CrossRef]
- Quickenden, T.; Vernon, C. Thermogalvanic conversion of heat to electricity. Sol. Energy 1986, 36, 63–72. [Google Scholar] [CrossRef]
- Sun, G.W. A Nickel Hexacyanoferrate Based Thermo-Electrochemical Device For Efficient Heat-to-Electricity Conversion. Master’s Thesis, Department of Mechanical Engineering Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. Available online: https://hdl.handle.net/1721.1/122229 (accessed on 10 August 2025).
- Lazar, M.; Al-Masri, D.; MacFarlane, D.; Pringle, J. Enhanced thermal energy harvesting performance of a cobalt redox couple in ionic liquid–solvent mixtures. Phys. Chem. Chem. Phys. 2016, 18, 1404–1410. [Google Scholar] [CrossRef]
- Kim, K.; Lee, H. Diglyme-Based Thermoelectrochemical Cells Operable at Both Subzero and Elevated Temperatures. Energy Technol. 2019, 7, 1900857. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, S.; Tan, P.; Dai, Y.; Yu, J.; Cheng, R.; Feng, S.; Ni, M. Insights into the thermopower of thermally regenerative electrochemical cycle for low grade heat harvesting. ACS Energy Lett. 2020, 6, 329–336. [Google Scholar] [CrossRef]
- Al-Masri, D.; Dupont, M.; Yunis, R.; MacFarlane, D.; Pringle, J. The electrochemistry and performance of cobalt-based redox couples for thermoelectrochemical cells. Electrochim. Acta 2018, 269, 714–723. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Sherrell, P.; Liu, L.; Wang, Y.; Chen, J. Potentially Wearable Thermo-Electrochemical Cells for Body Heat Harvesting: From Mechanism, Materials, Strategies to Applications. Adv. Sci. 2021, 8, 2100669. [Google Scholar] [CrossRef]
- Hammond, R.; Risen, W. An electrochemical heat engine for direct solar energy conversion. Sol. Energy 1979, 23, 443–449. [Google Scholar] [CrossRef]
- Sun, X.; Chen, H.; Li, Y.; Zeng, D.; Qiu, P.; Zeng, H.; Ji, X.; Chen, L.; Shi, X. Efficient Harvesting Waste Heat by Zn-Ion Battery Under Thermally Regenerative Electrochemical Cycles. Adv. Mater. 2025, 37, 2418482. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhao, D.; Khan, Z.; Puzinas, S.; Jonsson, M.; Berggren, M.; Crispin, X. Ionic Thermoelectric Figure of Merit for Charging of Supercapacitors. Adv. Electron. Mater. 2017, 3, 1700013. [Google Scholar] [CrossRef]
- Duan, J.; Feng, G.; Yu, B.; Li, J.; Chen, M.; Yang, P.; Feng, J.; Liu, K.; Zhou, J. Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest. Nat. Commun. 2018, 9, 5146. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, P.; Zhou, F.; Gao, L.; Sun, D.; Meng, Y.; Wang, X. Zinc-Guided 3D Graphene for Thermally Chargeable Supercapacitors to Harvest Low-Grade Heat. Molecules 2022, 27, 1239. [Google Scholar] [CrossRef]
- Bonetti, M.; Nakamae, S.; Roger, M.; Guenoun, P. Huge Seebeck coefficients in nonaqueous electrolytes. J. Chem. Phys. 2011, 134, 114513. [Google Scholar] [CrossRef]
- Zhao, D.; Fabiano, S.; Berggren, M.; Crispin, X. Ionic thermoelectric gating organic transistors. Nat. Commun. 2017, 8, 14214. [Google Scholar] [CrossRef]
- Kim, S.; Lin, H.; Yu, C. Thermally Chargeable Solid-State Supercapacitor. Adv. Energy Mater. 2016, 6, 1600546. [Google Scholar] [CrossRef]
- Akbar, Z.; Jeon, J.; Jang, S. Intrinsically self-healable, stretchable thermoelectric materials with a large ionic Seebeck effect. Energy Environ. Sci. 2019, 13, 2915–2923. [Google Scholar] [CrossRef]
- Jiao, F.; Naderi, A.; Zhao, D.; Schlueter, J.; Shahi, M.; Sundström, J.; Granberg, H.; Edberg, J.; Ail, U.; Brill, J.; et al. Ionic thermoelectric paper. J. Mater. Chem. A 2017, 5, 16883–16888. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, P. High Seebeck Coefficient Electrochemical Thermocells for EfficientWaste Heat Recovery. ACS Appl. Energy Mater. 2018, 1, 1424–1428. [Google Scholar] [CrossRef]
- Horike, S.; Wei, Q.; Kirihara, K.; Mukaida, M.; Sasaki, T.; Koshiba, Y.; Fukushima, T.; Ishida, K. Outstanding Electrode-Dependent Seebeck Coefficients in Ionic Hydrogels for Thermally Chargeable Supercapacitor near Room Temperature. ACS Appl. Mater. Interfaces 2020, 12, 43674–43683. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Wang, H.; Khan, Z.; Chen, J.; Gabrielsson, R.; Jonsson, M.; Berggren, M.; Crispin, X. Ionic thermoelectric supercapacitors. Energy Environ. Sci. 2016, 9, 1450–1457. [Google Scholar] [CrossRef]
- Zhao, D.; Martinelli, A. Polymer gels with tunable ionic Seebeck coefficient for ultra-sensitive printed thermopiles. Nat. Commun. 2019, 1, 1093. [Google Scholar] [CrossRef]
- Kim, B.; Na, J.; Lim, H.; Kim, Y.; Kim, J.; Kim, E. Robust High Thermoelectric Harvesting Under a SelfHumidifying Bilayer of Metal Organic Framework and. Thermoelectr. Harvest. 2019, 29, 1807549. [Google Scholar] [CrossRef]
- Wang, S.; Li, F.; Easley, A.; Lutkenhaous, J. Real-time insight into the doping mechanism of redox-active organic radical polymers. Nat. Mater. 2019, 18, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Ouyang, J. Ultrahigh Thermoelectric Power Generation from Both Ion Diffusion by Temperature Fluctuation and Hole Accumulation by Temperature Gradient. Adv. Energy Mater. 2020, 10, 2001633. [Google Scholar] [CrossRef]
- Fang, Y.; Cheng, H.; He, H.; Wang, S.; Li, J.; Yue, S.; Zhang, L.; Du, Z.; Ouyang, J. Stretchable and Transparent Ionogels with High Thermoelectric Properties. Adv. Funct. Mater. 2020, 30, 2004699. [Google Scholar] [CrossRef]

| Nomenclature | ||
|---|---|---|
| Symbol | Description | Unit |
| A | Contact area | m2 |
| Ac | Electrode active area | m2 |
| α | Signed sum of thermal coefficients of the cells | V/K |
| BHTH | Activity ratio in hot cell | – |
| BCTC | Activity ratio in cold cell | – |
| Ca | Capacitance | F |
| c | Specific heat | – |
| cp | Molar heat capacity of electrolyte | J/(mol·K) |
| d | Width of the contact areas | m |
| δ | Reaction rate | – |
| f | Objective function | – |
| fN | Objective function (indexed) | – |
| F | Faraday constant | C/mol |
| Gx | Gibbs energy | – |
| Hx | Enthalpy | – |
| i | Current density | A/cm2 |
| I | Current | A |
| k | Loop variable | – |
| λ | Thermal conductivity | W/(m·K) |
| n | Number of electrons transferred | – |
| η | Concentration-dependent viscosity | Pa·s |
| ηX | Efficiency | % |
| ρ | Density of electrolyte | kg/m3 |
| Rx | Inner resistance | Ω |
| Sx | Entropy | – |
| σN | Importance value | – |
| Tx | Hot side temperature | K |
| θ | Fitting parameter | – |
| Ux | (Electrochemical) potential, Voltage | V |
| Vx | Voltage | V |
| Qx | Heat | J |
| ΔQHEX | Heat absorbed in heat exchanger | J |
| γ | Relative sensitivity | – |
| x0N | Observed values | – |
| xPN | Modeled values | – |
| Subscripts and Superscripts | |
|---|---|
| Symbol | Description |
| C | Cold side |
| c | Concentration |
| FC | Fuel cell |
| H | Hot side |
| HEX | Heat exchanger |
| in | Inlet |
| int. | Internal |
| L | Lower |
| N | Parametric index |
| opt. | Optimal |
| OUT | Outlet |
| p | Isobar |
| ref | Reference |
| Res | Resistive |
| TREC | Thermally regenerative electrochemical cycle system |
| V | Volumetric |
| Parameter | Name | Unit | Test Range | Value (If Fixed) |
|---|---|---|---|---|
| Ac | Electrode active area | m2 | 0.016; 0.036 | 0.016 |
| α | Signed sum of thermal coefficients of the cells | V/K | 0.2 ×1 0−3; 3.2 × 10−3 | 1.44 × 10−3 |
| cp | Molar heat capacity of electrolyte | J/(mol K) | 58.15; 80.77 | 75.6 |
| F | Faraday constant | C/mol | 96.485 | 96.485 |
| i | Current density | A/cm2 | 0.0002; 0.006 | 0.0061 |
| λ | Thermal conductivity | W/mK | 237 | 237 |
| n | Number of electrons transferred | - | 2 | 2 |
| QFC | Heat generated by fuel cell | J | 23,750; 50,000 | 50,000 |
| Qin | Inlet heat to the TREC | J | 0; 199,080 | 50,000 |
| RC | Cold cell resistance | Ω | 5.14; 24.25 | 24.5 |
| RH | Hot cell resistance | Ω | 5.14; 24.25 | 24.5 |
| Rint | Inner resistance | Ω | 5.14; 24.25 | 24.5 |
| TC | Cold side temperature | K | 297.15 | 297.15 |
| TH | Hot side temperature | K | 297.15; 360.15 | 357.15 |
| ηHEX | Efficiency of heat exchanger | - | 0.6; 0.8 | 0.7 |
| Dependency | Variable | Sensitivity Factor | Sensitivity Category |
|---|---|---|---|
| Current | Hot side temperature | 1454.7 | Sensitive |
| Resistance of electrodes | 35,035.1 | Highly sensitive | |
| Temperature | Current | 30,287.3 | Highly sensitive |
| Active membrane area | 552.1 | Sensitive | |
| Thermal coefficient | 737,799.5 | Highly sensitive | |
| Molar capacity | 28.5 | Intensive | |
| Efficiency of HEX | 7.64 × 10−8 | Intensive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bereczky, Á.; Lévai, E. Sensitivity Factors of Thermally Regenerative Electrochemical Cycle Systems Using Fuel Cell’s Waste Heat. Energies 2025, 18, 5422. https://doi.org/10.3390/en18205422
Bereczky Á, Lévai E. Sensitivity Factors of Thermally Regenerative Electrochemical Cycle Systems Using Fuel Cell’s Waste Heat. Energies. 2025; 18(20):5422. https://doi.org/10.3390/en18205422
Chicago/Turabian StyleBereczky, Ákos, and Emese Lévai. 2025. "Sensitivity Factors of Thermally Regenerative Electrochemical Cycle Systems Using Fuel Cell’s Waste Heat" Energies 18, no. 20: 5422. https://doi.org/10.3390/en18205422
APA StyleBereczky, Á., & Lévai, E. (2025). Sensitivity Factors of Thermally Regenerative Electrochemical Cycle Systems Using Fuel Cell’s Waste Heat. Energies, 18(20), 5422. https://doi.org/10.3390/en18205422