Multi-Objective Energy Management System in Smart Homes with Inverter-Based Air Conditioner Considering Costs, Peak-Average Ratio, and Battery Discharging Cycles of ESS and EV
Abstract
1. Introduction
- This study examines a multi-objective model using three objective functions for optimizing the energy bill, PAR, and battery discharging cycles of the ESS and EV simultaneously;
- The shiftable appliances, IBACS, ESS, and EV, are scheduled simultaneously, and both ESS and EV trade energy with the main grid to buy and sell energy based on the real-time market pricing model;
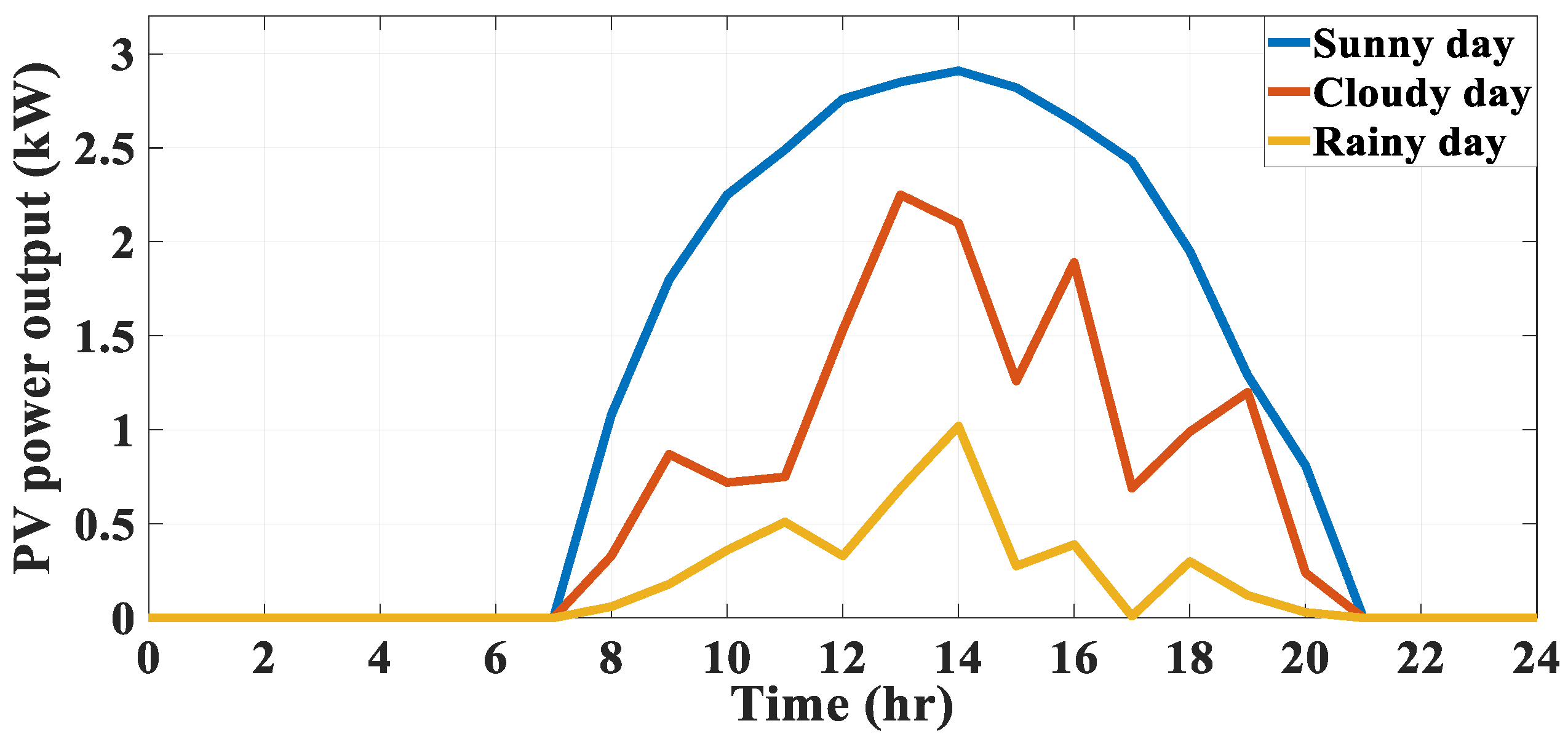
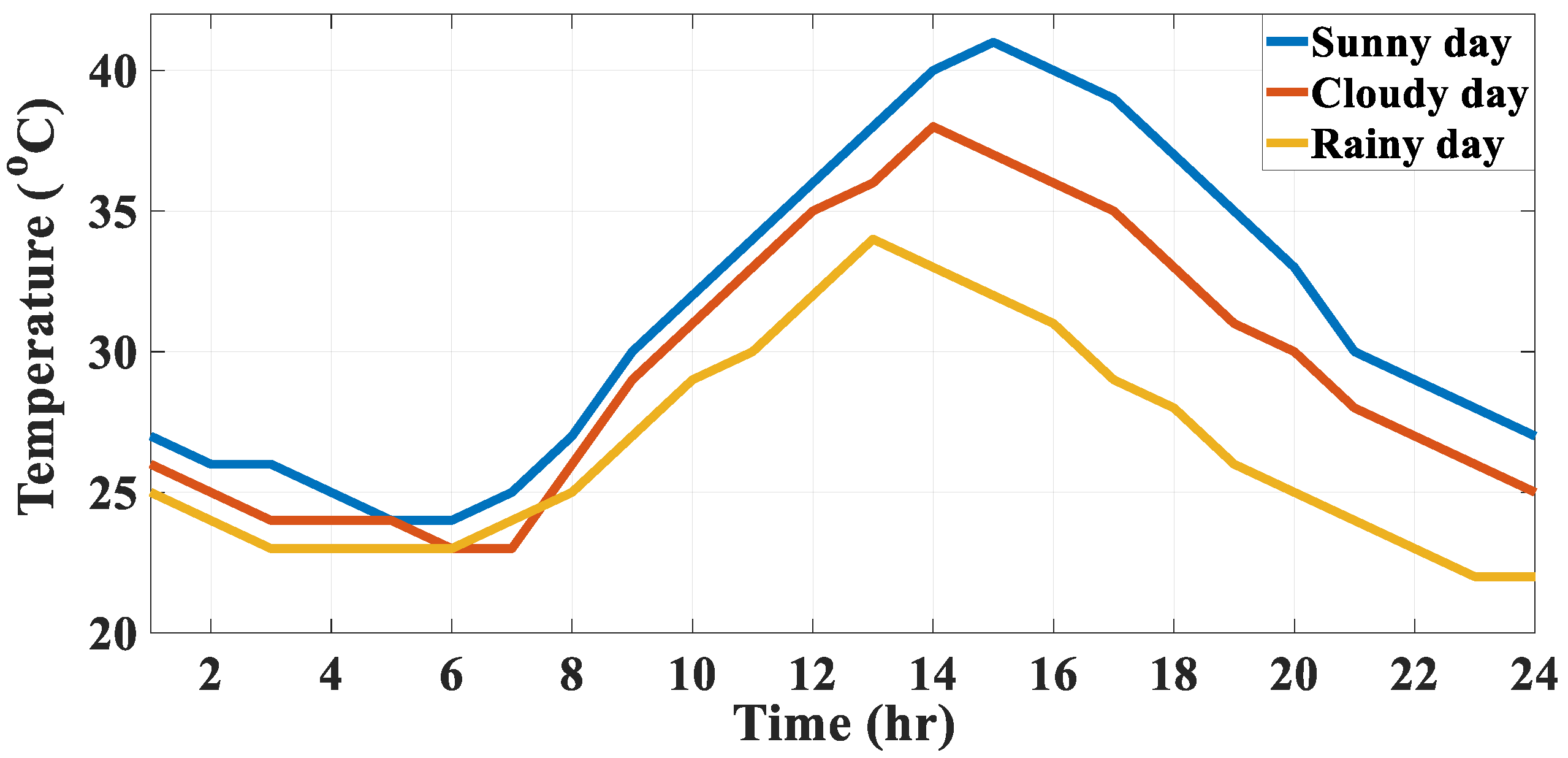
- The proposed SHEMS considers various weather conditions, such as sunny, cloudy, and rainy days;
- An improved multi-objective gray wolf optimizer with a Pareto front is used to solve the proposed multi-objective problem.
2. Problem Formulation
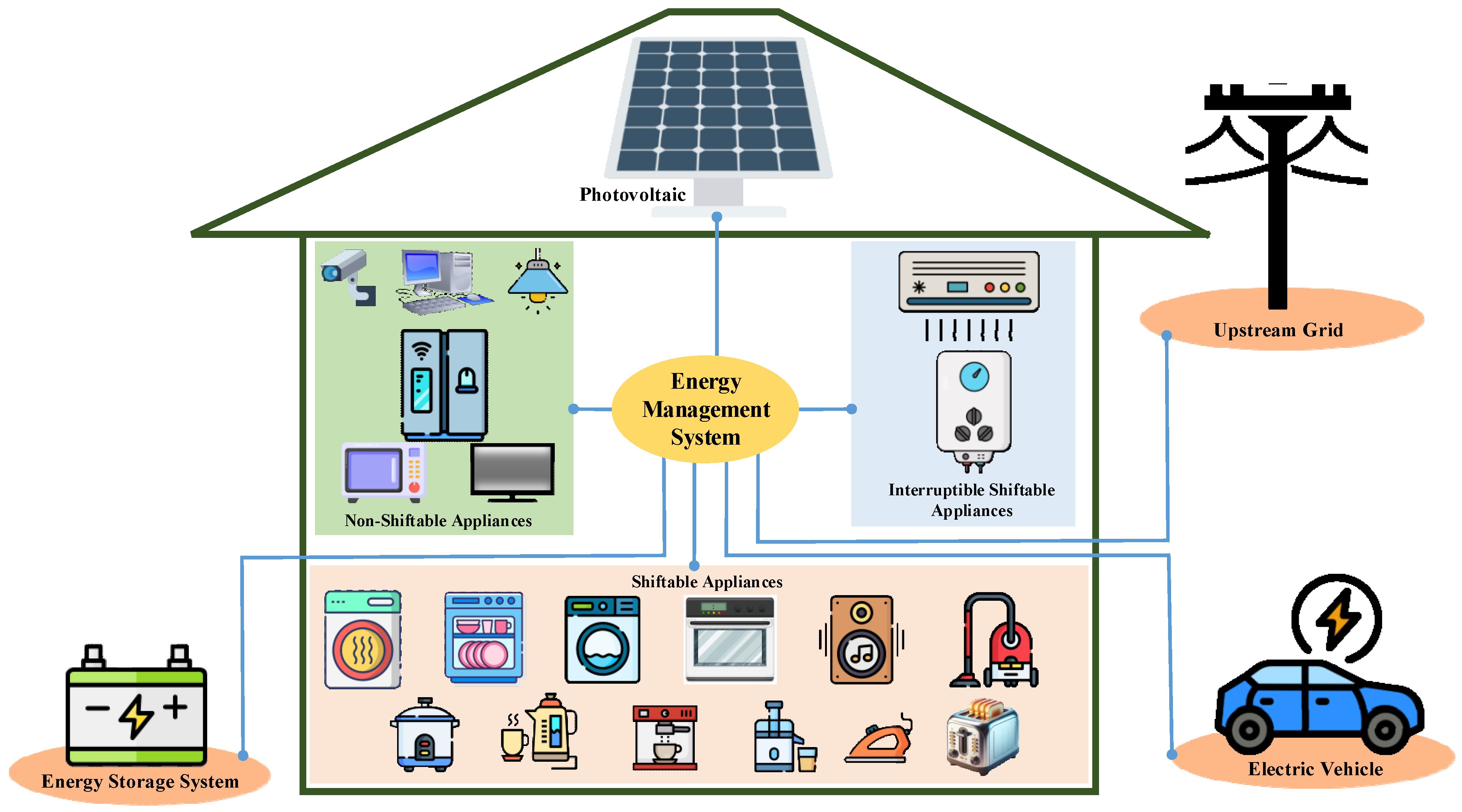
2.1. Load Classification
2.1.1. Non-Shiftable Appliances
2.1.2. Interruptible Appliances
2.1.3. Uninterruptible Appliances
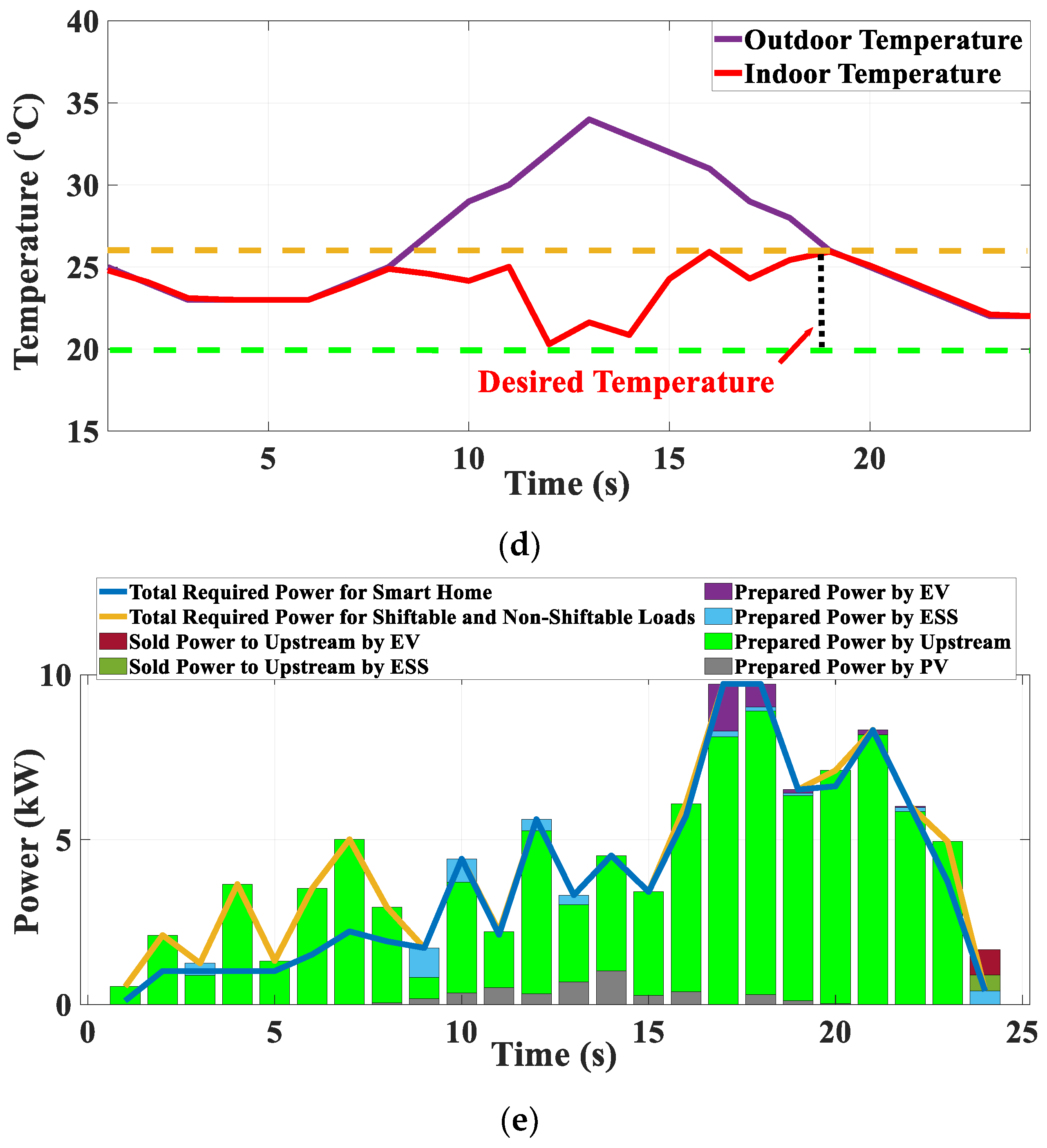
2.1.4. Inverter-Based Air Conditioner System
2.1.5. Total Required Power for Home Appliances
2.2. Rooftop PV System
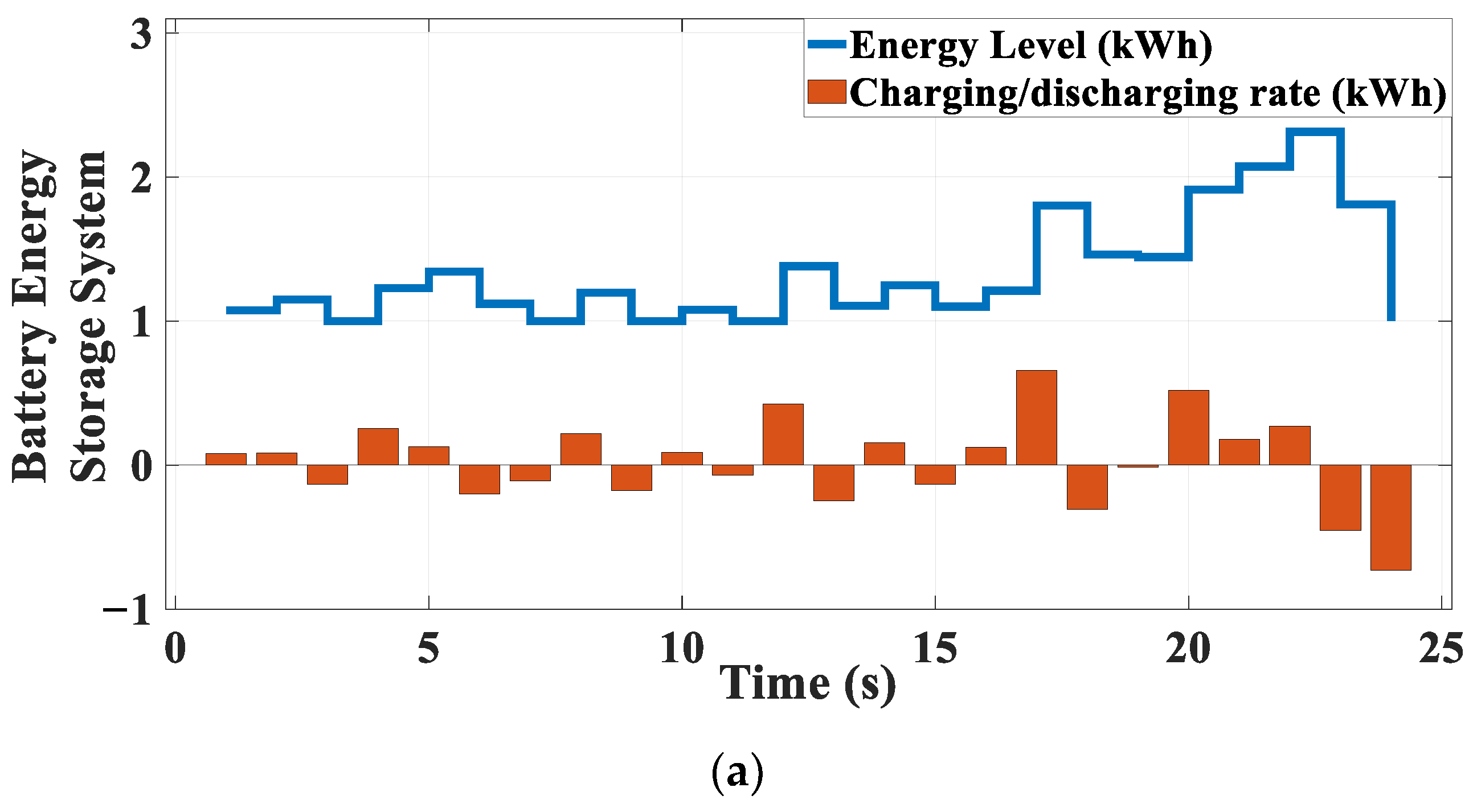
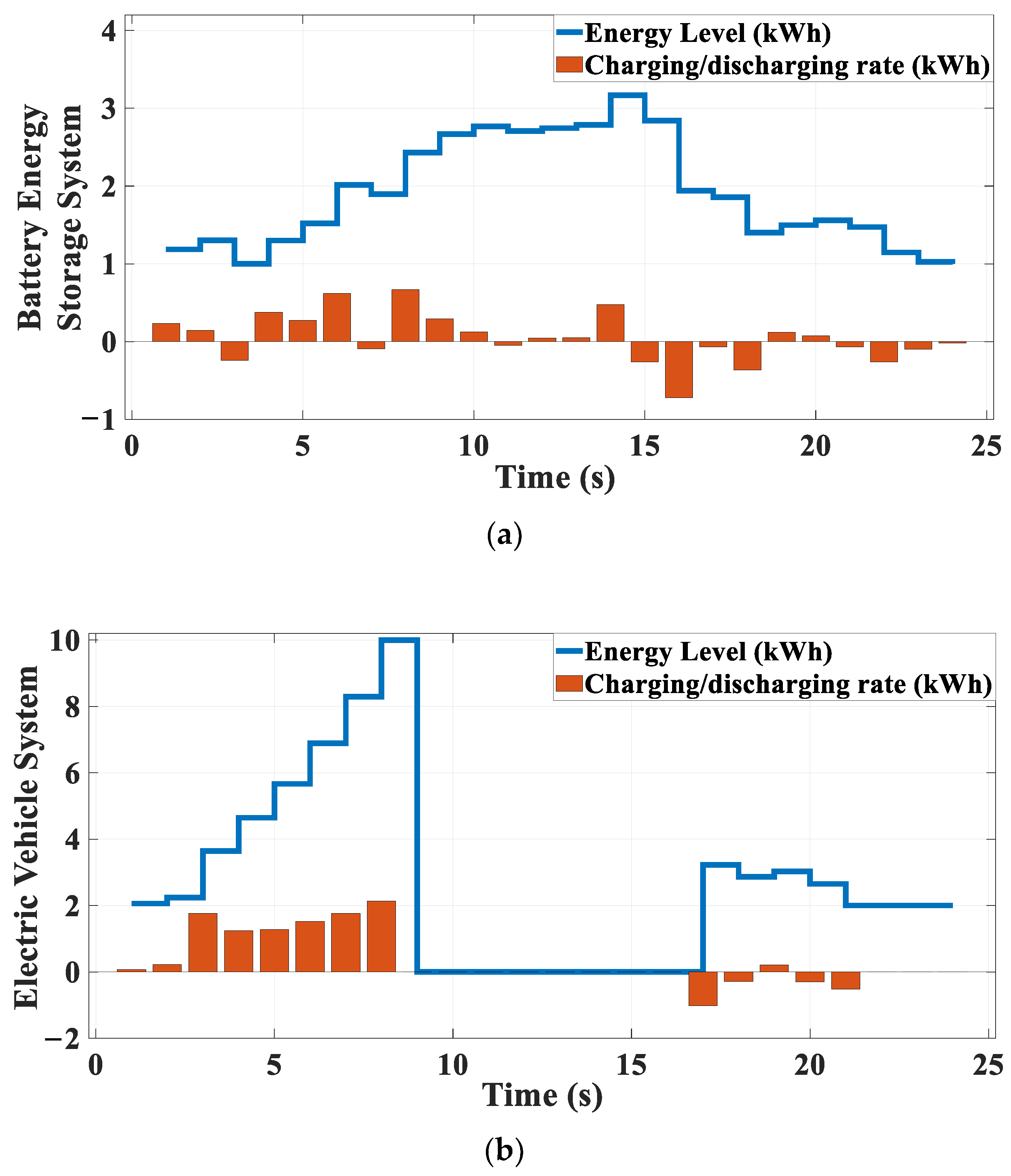
2.3. ESS
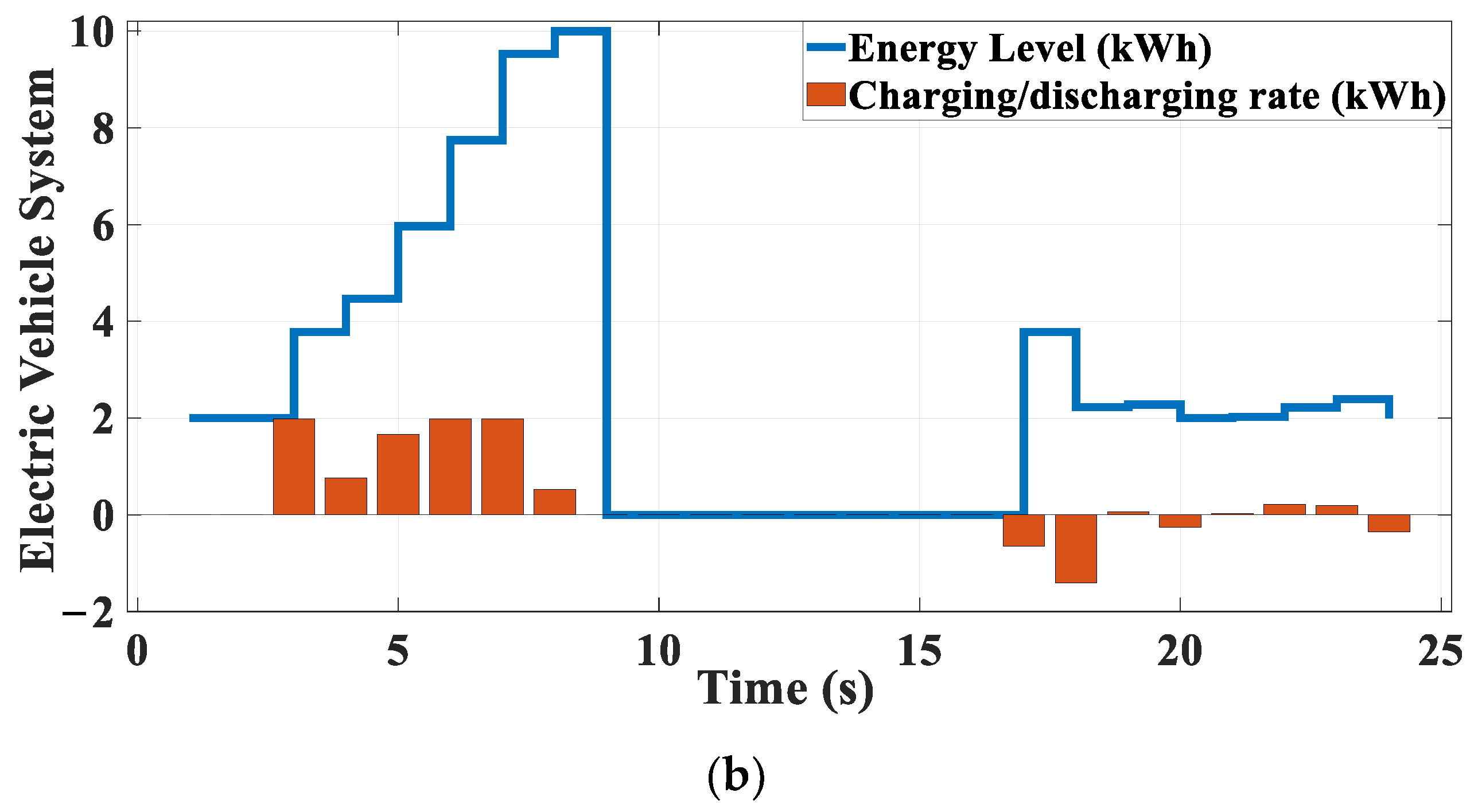
2.4. EV
- and indicate the discharge and charge rates of . It is possible to accumulate or consume just a particular amount of power during a given ;
- and show the minimum and maximum ranges of EV. EV’s power levels must meet and ranges.
2.5. Power Balance Limitations
2.6. Objective Functions
2.6.1. First Objective Function: Total Cost
2.6.2. Second Objective Function: PAR
2.6.3. Third Objective Function: Number of Battery Discharging Cycles of ESS and EV
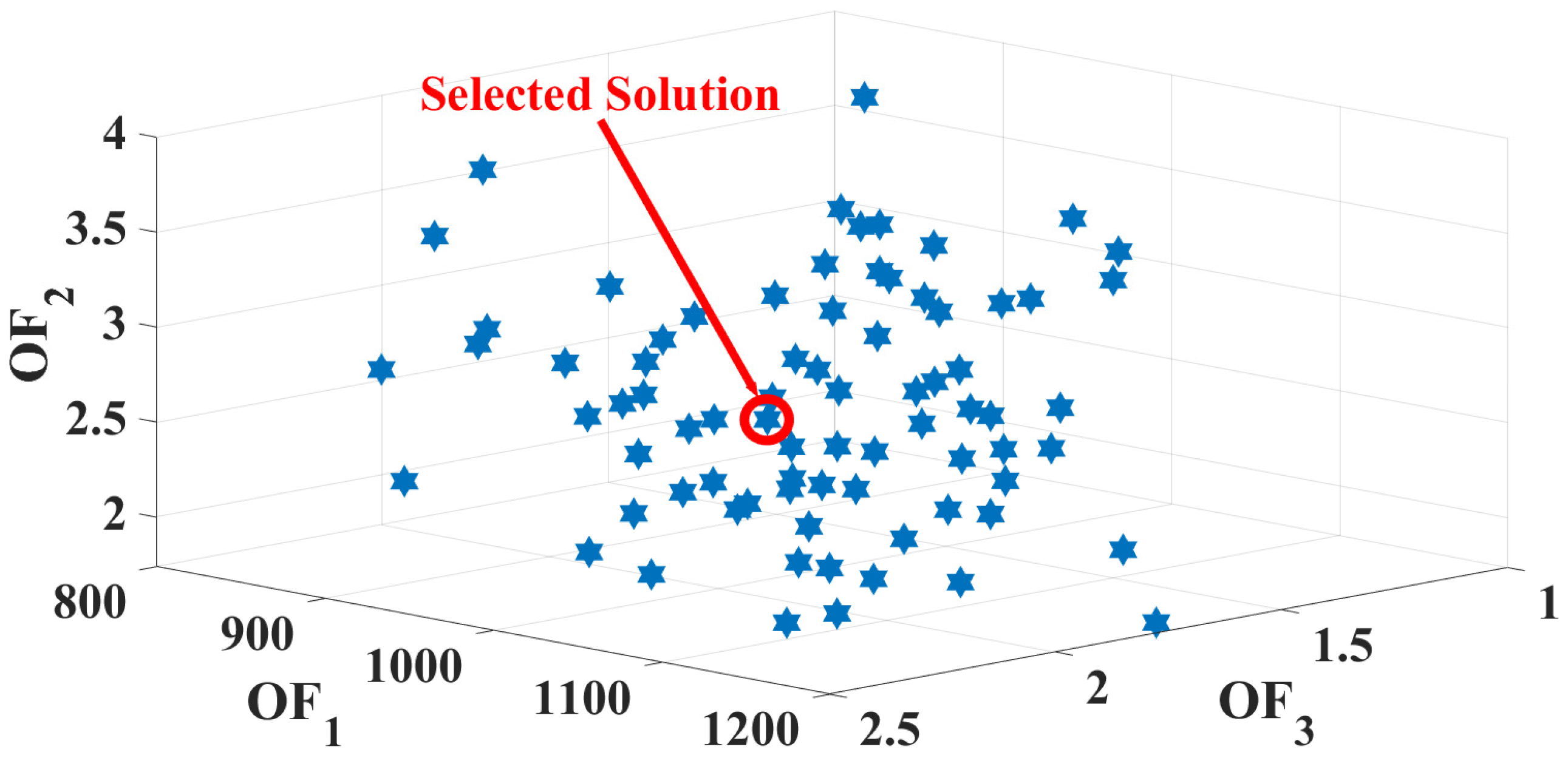
3. Proposed System and Results
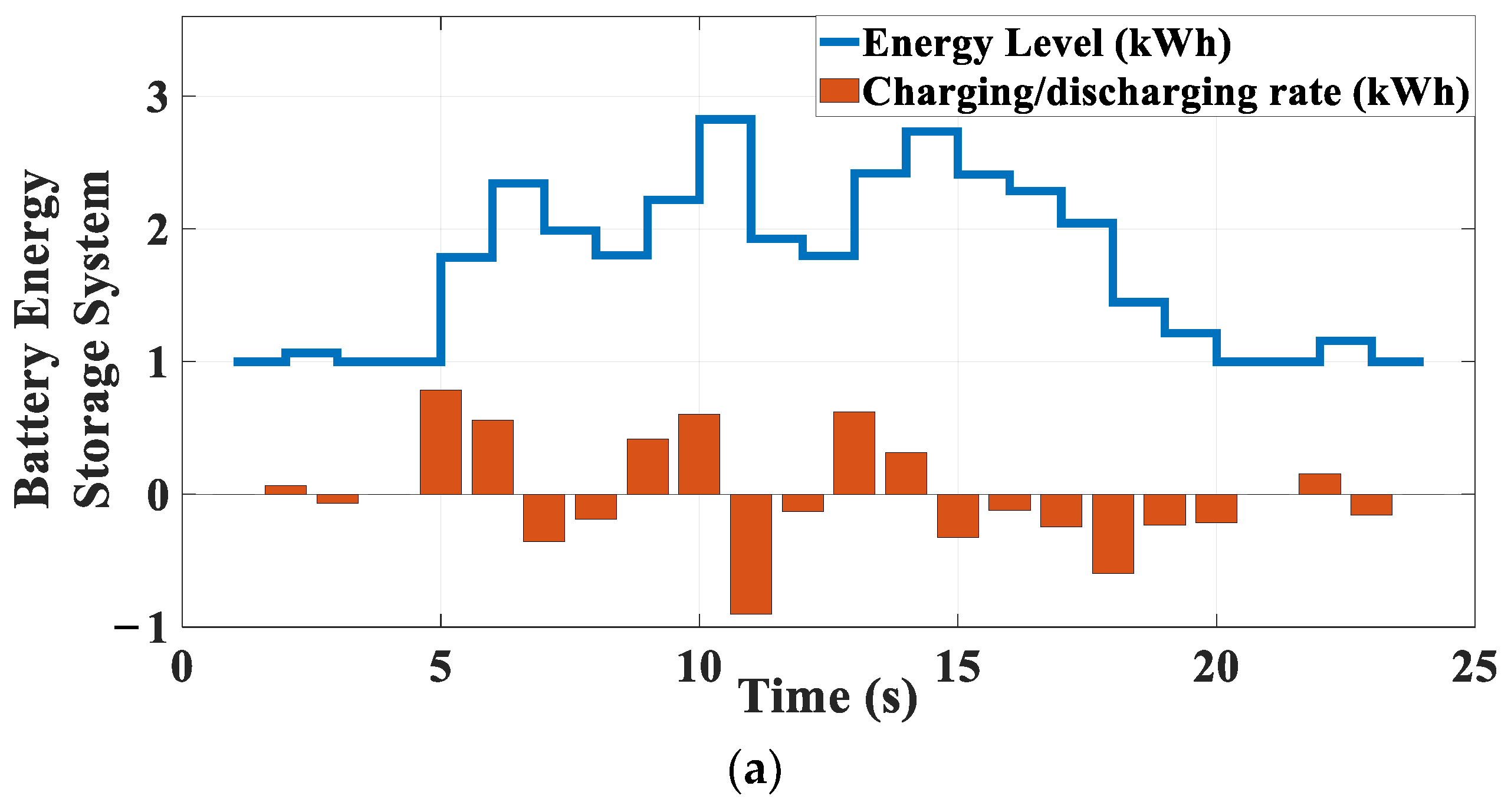
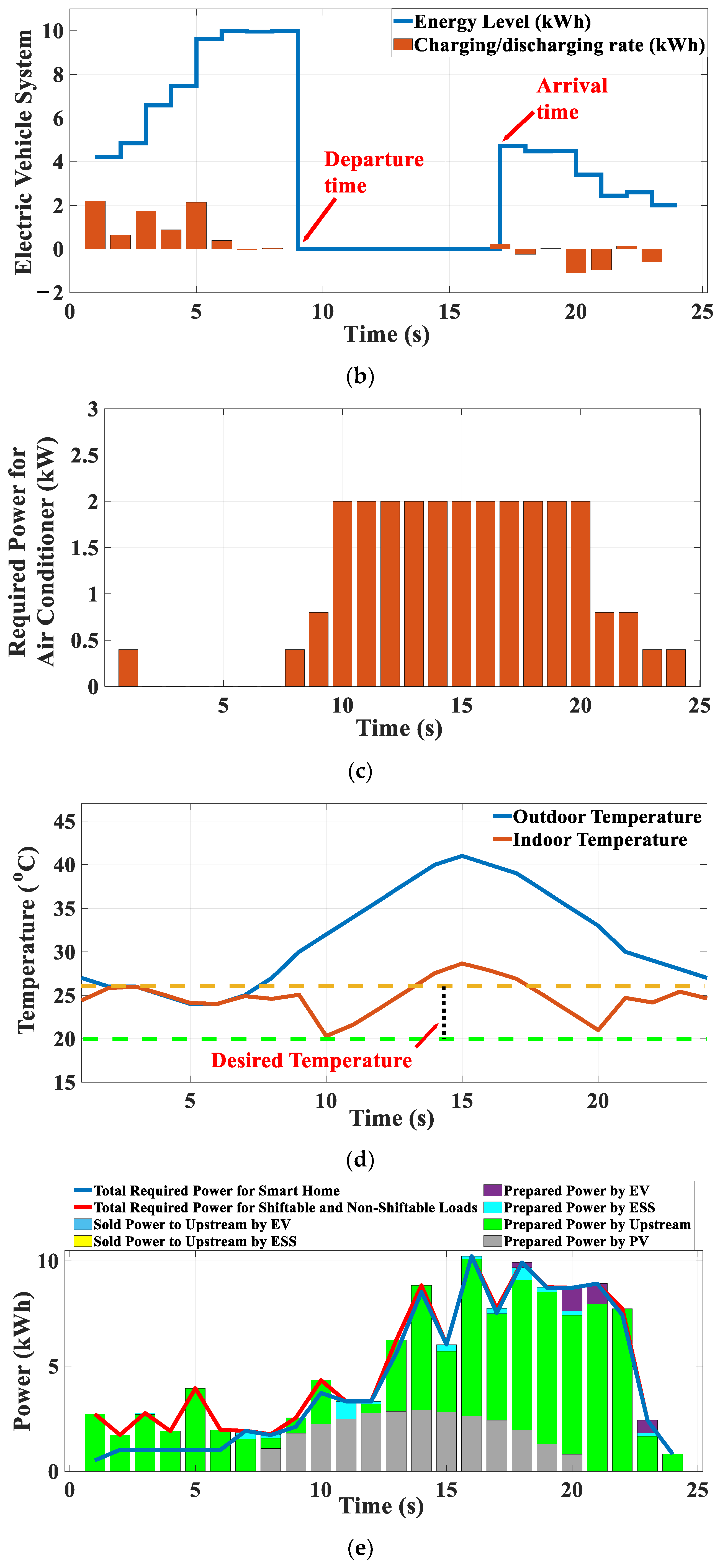
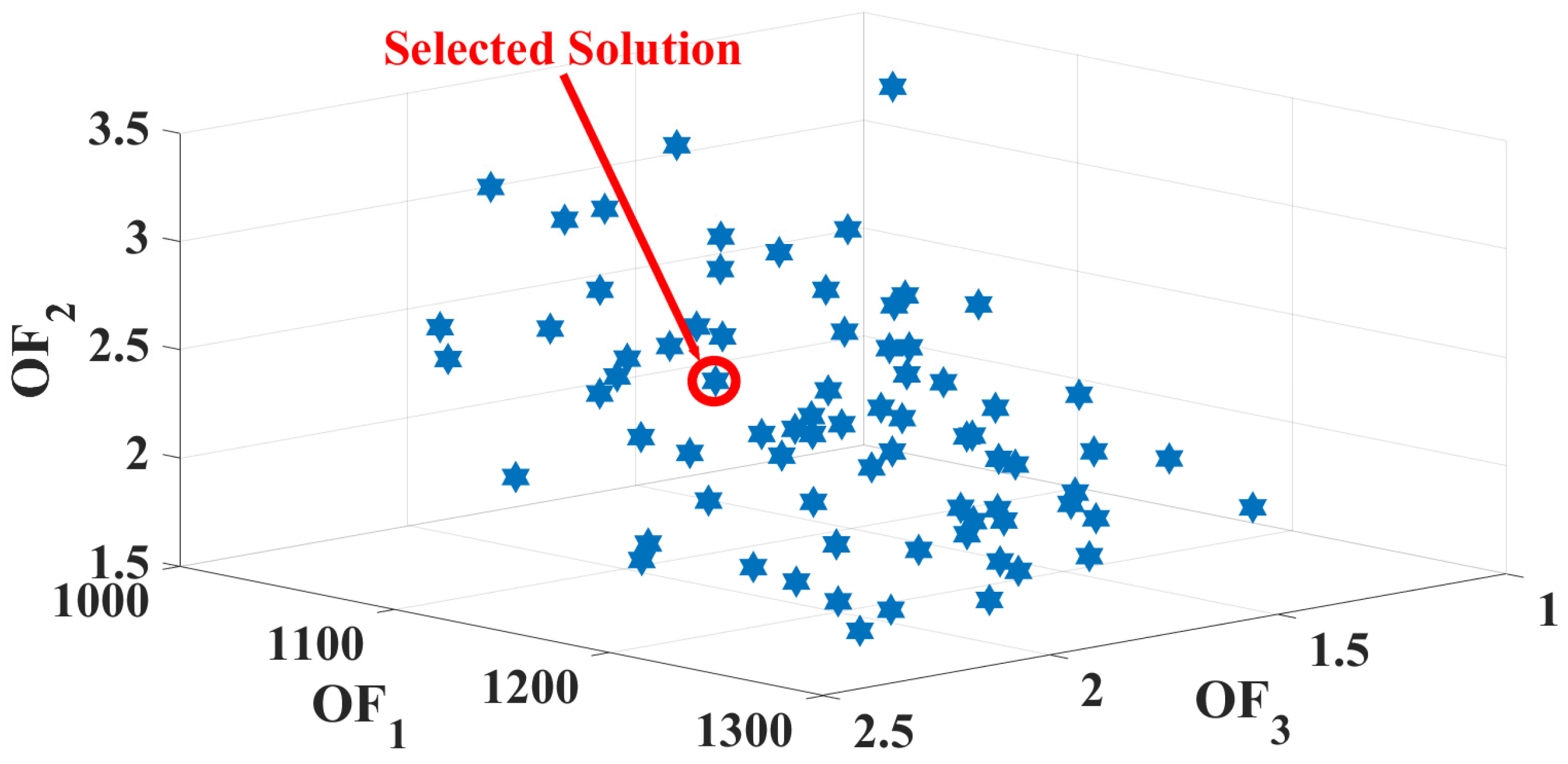
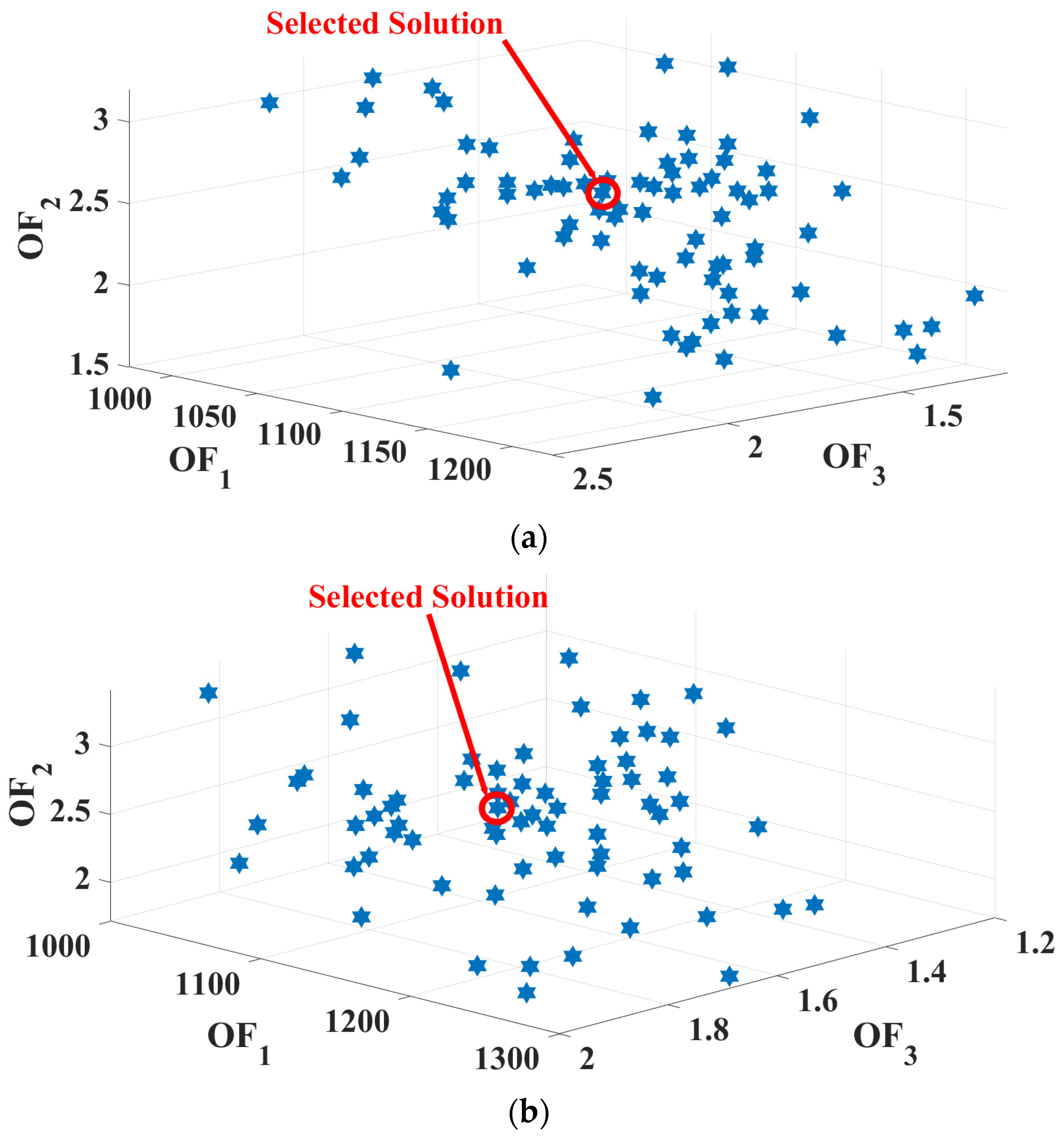
3.1. Scenario 1: SHEMS During a Sunny Day
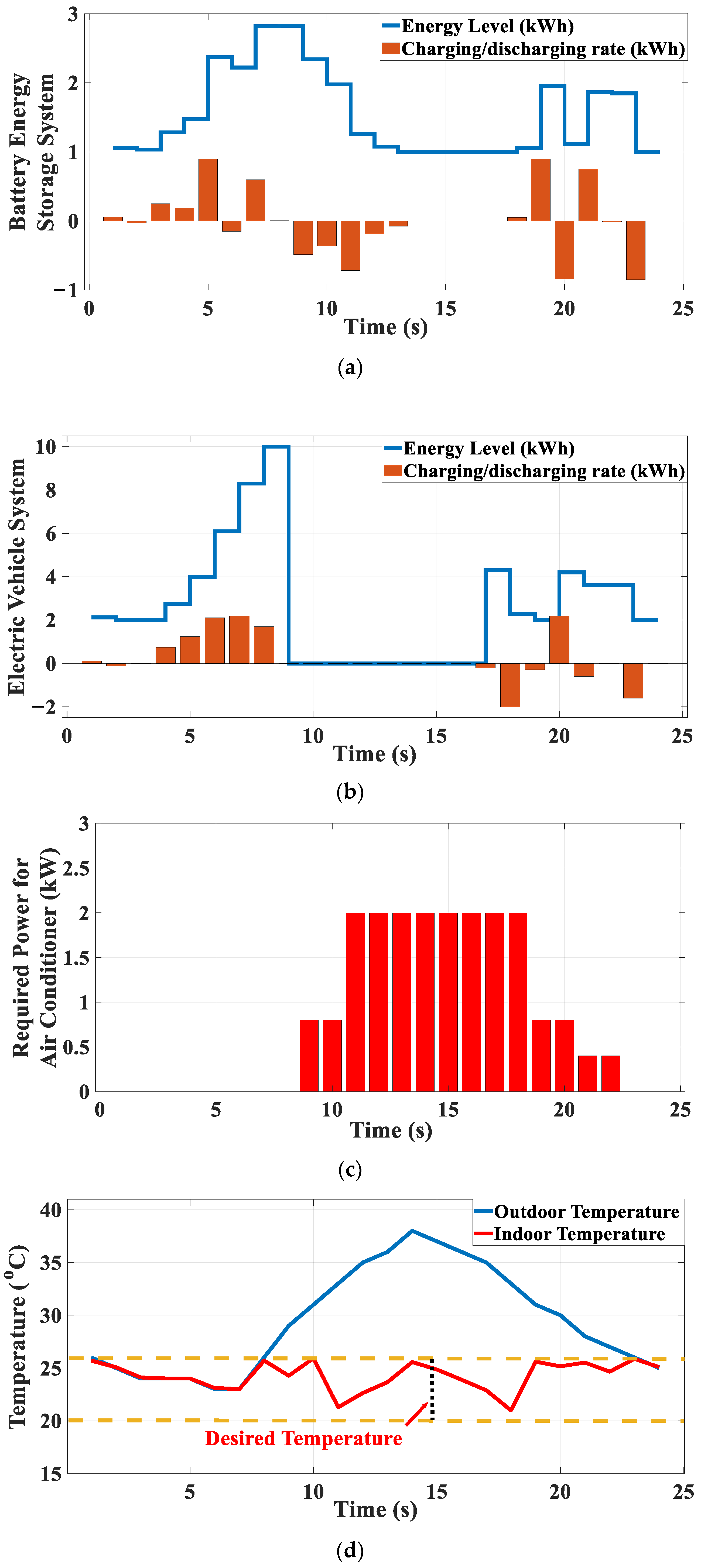
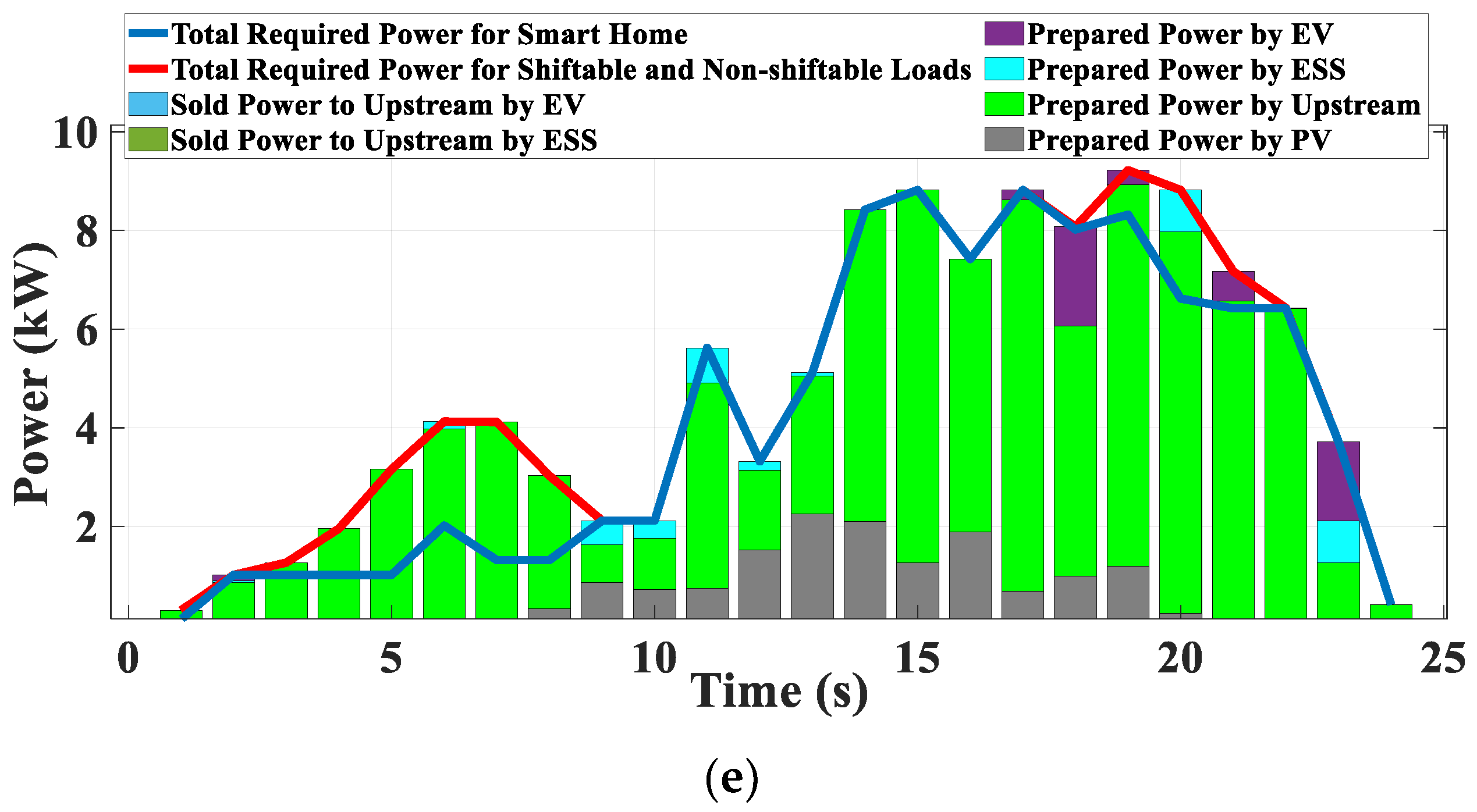
3.2. Scenario 2: SHEMS During a Cloudy Day
3.3. Scenario 3: SHEMS During a Rainy Day
3.4. Scenario 4: Different Efficiencies for ESS and EV
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Purna Prakash, K.; Venkata Pavan Kumar, Y.; Himajyothi, K.; Pradeep Reddy, G. Comprehensive Bibliometric Analysis on Smart Grids: Key Concepts and Research Trends. Electricity 2024, 5, 75–92. [Google Scholar] [CrossRef]
- de Lima, T.D.; Faria, P.; Vale, Z. Optimizing home energy management systems: A mixed integer linear programming model considering battery cycle degradation. Energy Build. 2025, 329, 115251. [Google Scholar] [CrossRef]
- GhasemiGarpachi, M.; Dehghani, M.; Aly, M.; Rodriguez, J. Multi-Objective Improved Differential Evolution Algorithm-Based Smart Home Energy Management System Considering Energy Storage System, Photovoltaic, and Electric Vehicle. IEEE Access 2025, 13, 89946–89966. [Google Scholar] [CrossRef]
- Sheng, H.; Wang, C.; Li, B.; Liang, J.; Yang, M.; Dong, Y. Multi-timescale active distribution network scheduling considering demand response and user comprehensive satisfaction. IEEE Trans. Ind. Appl. 2021, 57, 1995–2005. [Google Scholar] [CrossRef]
- Correia, A.; Ferreira, L.M.; Coimbra, P.; Moura, P.; de Almeida, A.T. Smart thermostats for a campus microgrid: Demand control and improving air quality. Energies 2022, 15, 1359. [Google Scholar] [CrossRef]
- Büyük, M.; Avşar, E.; Inci, M. Overview of smart home concepts through energy management systems, numerical research, and future perspective. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 2024924. [Google Scholar] [CrossRef]
- Hussain, H.M.; Ahmad, A.; Narayanan, A.; Nardelli, P.H.; Yang, Y. Benchmarking of heuristic algorithms for energy router-based packetized energy management in smart homes. IEEE Syst. J. 2022, 17, 2721–2732. [Google Scholar] [CrossRef]
- Han, B.; Zahraoui, Y.; Mubin, M.; Mekhilef, S.; Seyedmahmoudian, M.; Stojcevski, A. Home energy management systems: A review of the concept, architecture, and scheduling strategies. IEEE Access 2023, 11, 19999–20025. [Google Scholar] [CrossRef]
- Malik, A.; Haghdadi, N.; MacGill, I.; Ravishankar, J. Appliance level data analysis of summer demand reduction potential from residential air conditioner control. Appl. Energy 2019, 235, 776–785. [Google Scholar] [CrossRef]
- Ayub, S.; Ayob, S.M.; Tan, C.W.; Ayub, L.; Bukar, A.L. Optimal residence energy management with time and device-based preferences using an enhanced binary grey wolf optimization algorithm. Sustain. Energy Technol. Assess. 2020, 41, 100798. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Zhou, J.Z. Peak shaving operation of hydro-thermal-nuclear plants serving multiple power grids by linear programming. Energy 2017, 135, 210–219. [Google Scholar] [CrossRef]
- Qayyum, F.A.; Naeem, M.; Khwaja, A.S.; Anpalagan, A.; Guan, L.; Venkatesh, B. Appliance scheduling optimization in smart home networks. IEEE Access 2015, 3, 2176–2190. [Google Scholar] [CrossRef]
- Yahia, Z.; Pradhan, A. Optimal load scheduling of household appliances considering consumer preferences: An experimental analysis. Energy 2018, 163, 15–26. [Google Scholar] [CrossRef]
- Öhrlund, I.; Schultzberg, M.; Bartusch, C. Identifying and estimating the effects of a mandatory billing demand charge. Appl. Energy 2019, 237, 885–895. [Google Scholar] [CrossRef]
- Zeeshan, M.; Jamil, M. Adaptive moth flame optimization based load shifting technique for demand side management in smart grid. IETE J. Res. 2022, 68, 778–789. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Jurado, F. Scheduling of smart home appliances for optimal energy management in smart grid using Harris-hawks optimization algorithm. Optim. Eng. 2021, 22, 1625–1652. [Google Scholar] [CrossRef]
- Dinh, H.T.; Yun, J.; Kim, D.M.; Lee, K.H.; Kim, D. A home energy management system with renewable energy and energy storage utilizing main grid and electricity selling. IEEE Access 2020, 8, 49436–49450. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.W.; Xiao, J.W. Peer-to-peer energy sharing among smart energy buildings by distributed transaction. IEEE Trans. Smart Grid 2019, 10, 6491–6501. [Google Scholar] [CrossRef]
- Yelisetti, S.; Saini, V.K.; Kumar, R.; Lamba, R.; Saxena, A. Optimal energy management system for residential buildings considering the time of use price with swarm intelligence algorithms. J. Build. Eng. 2022, 59, 105062. [Google Scholar] [CrossRef]
- Veras, J.M.; Silva, I.R.; Pinheiro, P.R.; Rabêlo, R.A.; Veloso, A.F.; Borges, F.A.; Rodrigues, J.J. A multi-objective demand response optimization model for scheduling loads in a home energy management system. Sensors 2018, 18, 3207. [Google Scholar] [CrossRef]
- Javadi, M.; Nezhad, A.E.; Firouzi, K.; Besanjideh, F.; Gough, M.; Lotfi, M.; Anvari-Moghadam, A.; Catalão, J.P. Optimal operation of home energy management systems in the presence of the inverter-based heating, ventilation and air conditioning system. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Aguilar, J.; Garces-Jimenez, A.; Gallego-Salvador, N.; De Mesa, J.A.; Gomez-Pulido, J.M.; Garcìa-Tejedor, À.J. Autonomic management architecture for multi-HVAC systems in smart buildings. IEEE Access 2019, 7, 123402–123415. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F. Investigation of the demand response potentials of residential air conditioners using grey-box room thermal model. Energy Procedia 2017, 105, 2759–2765. [Google Scholar] [CrossRef]
- Dehghani, M.; Bornapour, S.M.; Sheybani, E. Enhanced Energy Management System in Smart Homes Considering Economic, Technical, and Environmental Aspects: A Novel Modification-Based Grey Wolf Optimizer. Energies 2025, 18, 1071. [Google Scholar] [CrossRef]
- Dehghani, M.; Bornapour, S.M. Smart homes energy management: Optimal multi-objective appliance scheduling model considering electrical energy storage and renewable energy resources. Heliyon 2025, 11, e42417. [Google Scholar] [CrossRef] [PubMed]
- Nezhad, A.E.; Rahimnejad, A.; Gadsden, S.A. Home energy management system for smart buildings with inverter-based air conditioning system. Int. J. Electr. Power Energy Syst. 2021, 133, 107230. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, H.; Wang, Y.; Luo, B.; Fan, L.; Liu, J.; Li, G.h. Multi-objective optimal scheduling of electricity consumption in smart building based on resident classification. J. Build. Eng. 2024, 98, 111085. [Google Scholar] [CrossRef]
- Panah, P.G.; Hooshmand, R.A.; Gholipour, M.; Bornapour, M. Urban microgrid ancillary service provision using plugin electric vehicle and waste-to-energy CHP. J. Energy Storage 2020, 29, 101413. [Google Scholar] [CrossRef]
- Ouria, M.; Correia, A.F.; Moura, P.; Coimbra, P.; de Almeida, A.T. MCDM Optimization-Based Development of a Plus-Energy Microgrid Architecture for University Buildings and Smart Parking. Energies 2025, 18, 3641. [Google Scholar] [CrossRef]
- Amako, E.A.; Arzani, A.; Mahajan, S.M. Heuristic-Based Scheduling of BESS for Multi-Community Large-Scale Active Distribution Network. Electricity 2025, 6, 36. [Google Scholar] [CrossRef]
- Taltavull-Villalonga, V.; Bullich-Massagué, E.; Saldaña-González, A.E.; Sumper, A. Enhancing distribution grid efficiency and congestion management through optimal battery storage and power flow modeling. Electricity 2024, 5, 351–369. [Google Scholar] [CrossRef]
- Li, Y.; Lin, X.; Liu, J. An improved gray wolf optimization algorithm to solve engineering problems. Sustainability 2021, 13, 3208. [Google Scholar] [CrossRef]



| References | Technique | Objective Functions | RER | ESS | Smart EV | IBACS | ||
|---|---|---|---|---|---|---|---|---|
| Cost | PAR | Batteries Discharging Cycles | ||||||
| [12] | Mixed-integer programming | √ | √ | × | √ | × | × | × |
| [15] | Adaptive moth–flame optimization | √ | √ | × | × | × | × | × |
| [16] | Harris hawks optimization algorithm | √ | √ | × | × | × | × | × |
| [17] | Binary particle swarm optimization | √ | √ | × | √ | √ | × | × |
| [19] | Swarm intelligence algorithms | √ | × | × | × | × | × | √ |
| [23] | Genetic, particle swarm, and trust region algorithms | √ | × | × | × | × | × | √ |
| [25] | Improved biogeography-based optimization algorithm | √ | √ | × | √ | √ | × | × |
| [26] | Mixed-integer linear programming | √ | × | × | √ | √ | × | √ |
| This paper | Improved gray wolf optimizer | √ | √ | √ | √ | √ | √ | √ |
| Non-Shiftable Loads | |||||||
| Device | Microwave Oven | Refrigerator | Personal Computers | Lights | Television | Security Cameras | |
| Power Rating (kW) | 1.7 | 0.9 | 0.3 | 0.3 | 0.2 | 0.12 | |
| Start time | 16:00 | 2:00 | 7:00 | 18:00 | 16:00 | 00:00 | |
| Daily Usage (h) | 4 | 22 | 18 | 6 | 8 | 24 | |
| Continuous Shiftable Loads | |||||||
| Device | Cloth Dryer | Dish Washer | Washing Machine | Iron | Vacuum Cleaner | Cooker Oven | Rice Cooker |
| Power Rating (kW) | 2.3 | 1.9 | 1.5 | 1.3 | 1.2 | 0.9 | 0.8 |
| Used Time Slot | 8–22 | 10–23 | 17–21 | 9–20 | 10–18 | 9–20 | 14–22 |
| Daily Usage (h) | 2 | 3 | 2 | 1 | 1 | 3 | 2 |
| Continuous | Interruptible Load | ||||||
| Device | Bread Machine | Electric Kettle | Juicer | Coffee Machine | Music Center | Water Heater | |
| Power Rating (kW) | 0.6 | 0.5 | 0.5 | 0.4 | 0.2 | 2.3 | |
| Used Time Slot | 6–10 | 10–19 | 6–23 | 6–10 | 17–23 | 7–22 | |
| Daily Usage (h) | 1 | 2 | 2 | 1 | 4 | 8 | |
| Parameters | (kWh) | (kWh) | (kWh) | (kW) | (%) |
|---|---|---|---|---|---|
| ESS | 1 | 5 | 1 | 0.9 | 100 |
| EV | 2 | 10 | 2 | 2.2 | 100 |
| (kW) | (°C/kWh) | (°C) | (°C) | (°C) | ||
|---|---|---|---|---|---|---|
| 2.5 | 1 | 0.9 | 5.5 | 20 | 26 | 23 |
| Shiftable Loads | Cloth Dryer | Dish Washer | Washing Machine | Iron | Vacuum Cleaner |
| Used time (h) | 21, 22 | 14–16 | 20, 21 | 13 | 18 |
| Shiftable Loads | Cooker Oven | Rice Cooker | Bread Machine | Electric Kettle | |
| Used time (h) | 18–20 | 15, 16 | 7 | 13, 14 | |
| Shiftable Loads | Juicer | Coffee Machine | Music Center | Water Heater | |
| Used time (h) | 13, 14 | 10 | 20–23 | 14, 16–22 | |
| Shiftable Loads | Cloth Dryer | Dish Washer | Washing Machine | Iron | Vacuum Cleaner |
| Used time (h) | 14, 15 | 21–23 | 19, 20 | 13 | 17 |
| Shiftable Loads | Cooker Oven | Rice Cooker | Bread Machine | Electric Kettle | |
| Used time (h) | 15–17 | 16, 17 | 6 | 13, 14 | |
| Shiftable Loads | Juicer | Coffee Machine | Music Center | Water Heater | |
| Used time (h) | 16, 17 | 6 | 17–20 | 11, 14, 15, 18–22 | |
| Shiftable Loads | Cloth Dryer | Dish Washer | Washing Machine | Iron | Vacuum Cleaner |
| Used time (h) | 20, 21 | 21–23 | 17, 18 | 18 | 14 |
| Shiftable Loads | Cooker Oven | Rice Cooker | Bread Machine | Electric Kettle | |
| Used time (h) | 15–17 | 16, 17 | 8 | 18, 19 | |
| Shiftable Loads | Juicer | Coffee Machine | Music Center | Water Heater | |
| Used time (h) | 6, 7 | 7 | 17–20 | 10, 12, 17–22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghani, M.; Bornapour, S.M.; Ruiz, F.; Rodriguez, J. Multi-Objective Energy Management System in Smart Homes with Inverter-Based Air Conditioner Considering Costs, Peak-Average Ratio, and Battery Discharging Cycles of ESS and EV. Energies 2025, 18, 5298. https://doi.org/10.3390/en18195298
Dehghani M, Bornapour SM, Ruiz F, Rodriguez J. Multi-Objective Energy Management System in Smart Homes with Inverter-Based Air Conditioner Considering Costs, Peak-Average Ratio, and Battery Discharging Cycles of ESS and EV. Energies. 2025; 18(19):5298. https://doi.org/10.3390/en18195298
Chicago/Turabian StyleDehghani, Moslem, Seyyed Mohammad Bornapour, Felipe Ruiz, and Jose Rodriguez. 2025. "Multi-Objective Energy Management System in Smart Homes with Inverter-Based Air Conditioner Considering Costs, Peak-Average Ratio, and Battery Discharging Cycles of ESS and EV" Energies 18, no. 19: 5298. https://doi.org/10.3390/en18195298
APA StyleDehghani, M., Bornapour, S. M., Ruiz, F., & Rodriguez, J. (2025). Multi-Objective Energy Management System in Smart Homes with Inverter-Based Air Conditioner Considering Costs, Peak-Average Ratio, and Battery Discharging Cycles of ESS and EV. Energies, 18(19), 5298. https://doi.org/10.3390/en18195298







