A Review of Cross-Scale State Estimation Techniques for Power Batteries in Electric Vehicles: Evolution from Single-State to Multi-State Cooperative Estimation
Abstract
1. Introduction
2. Battery Modeling
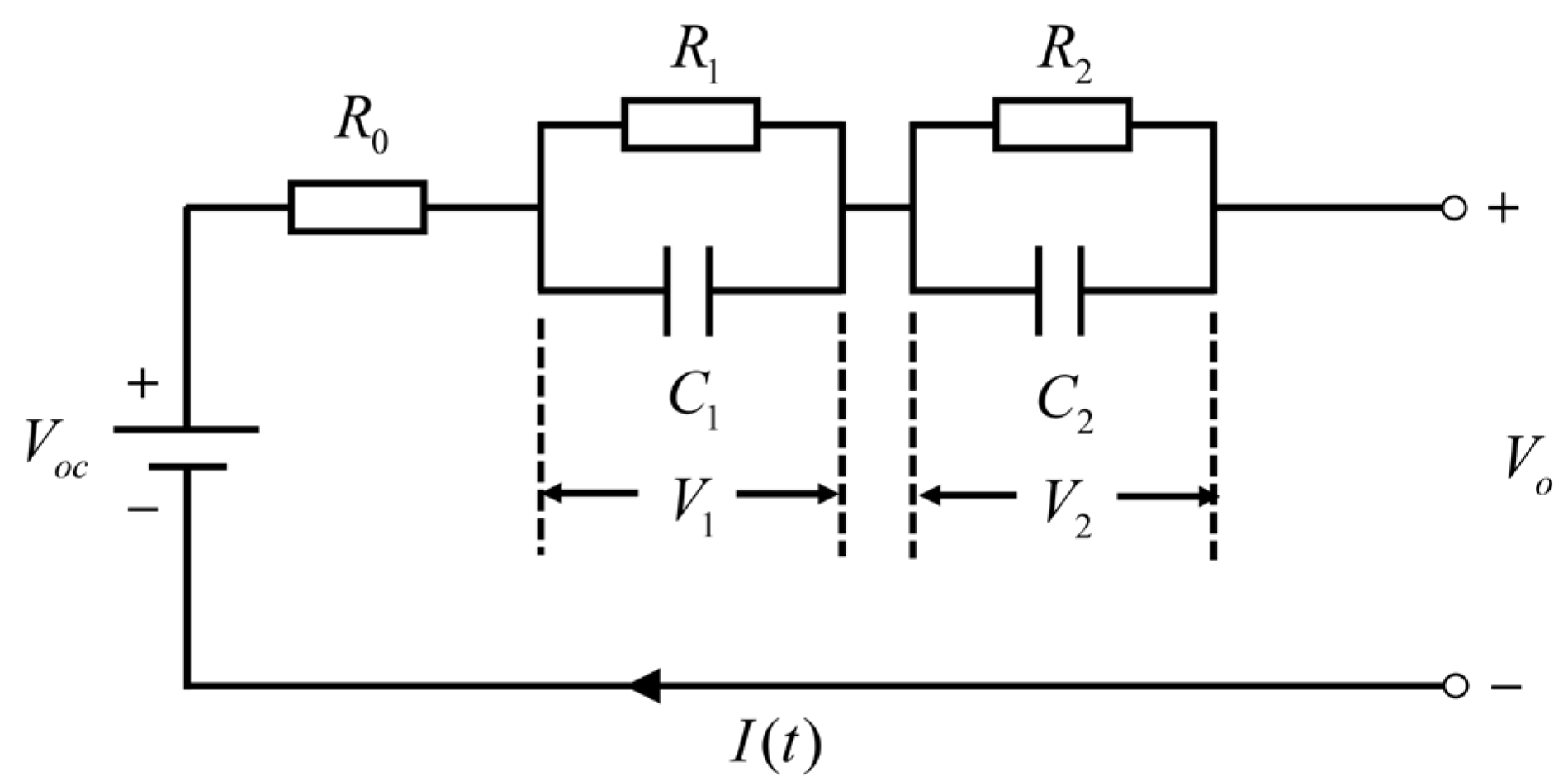
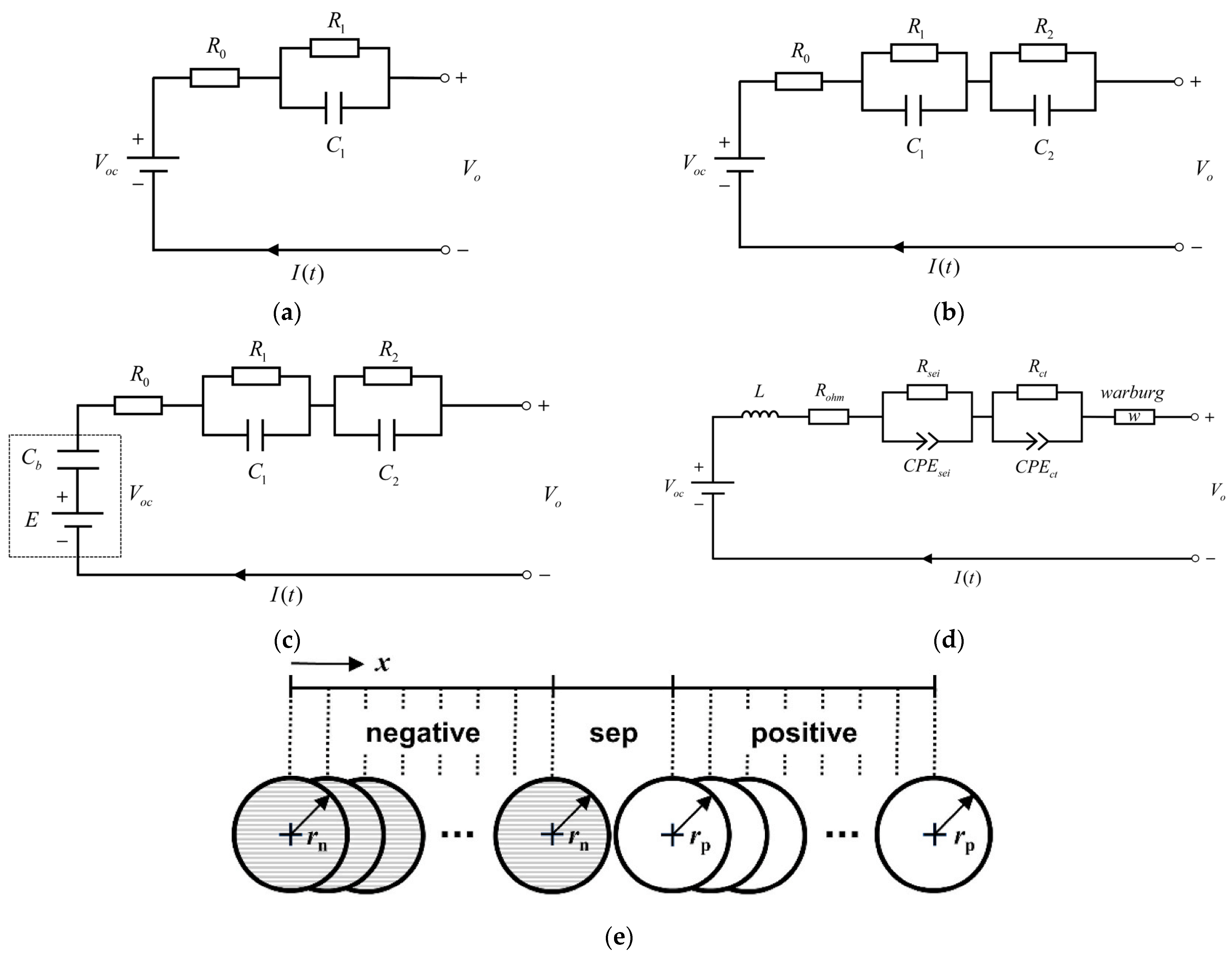
2.1. Equivalent Circuit Model
2.2. Electrochemical Model
2.3. Comparison and Summary of Battery Models
3. State Estimation
3.1. SOC Estimation
3.1.1. Single-State SOC Estimation Using Time-Domain Features
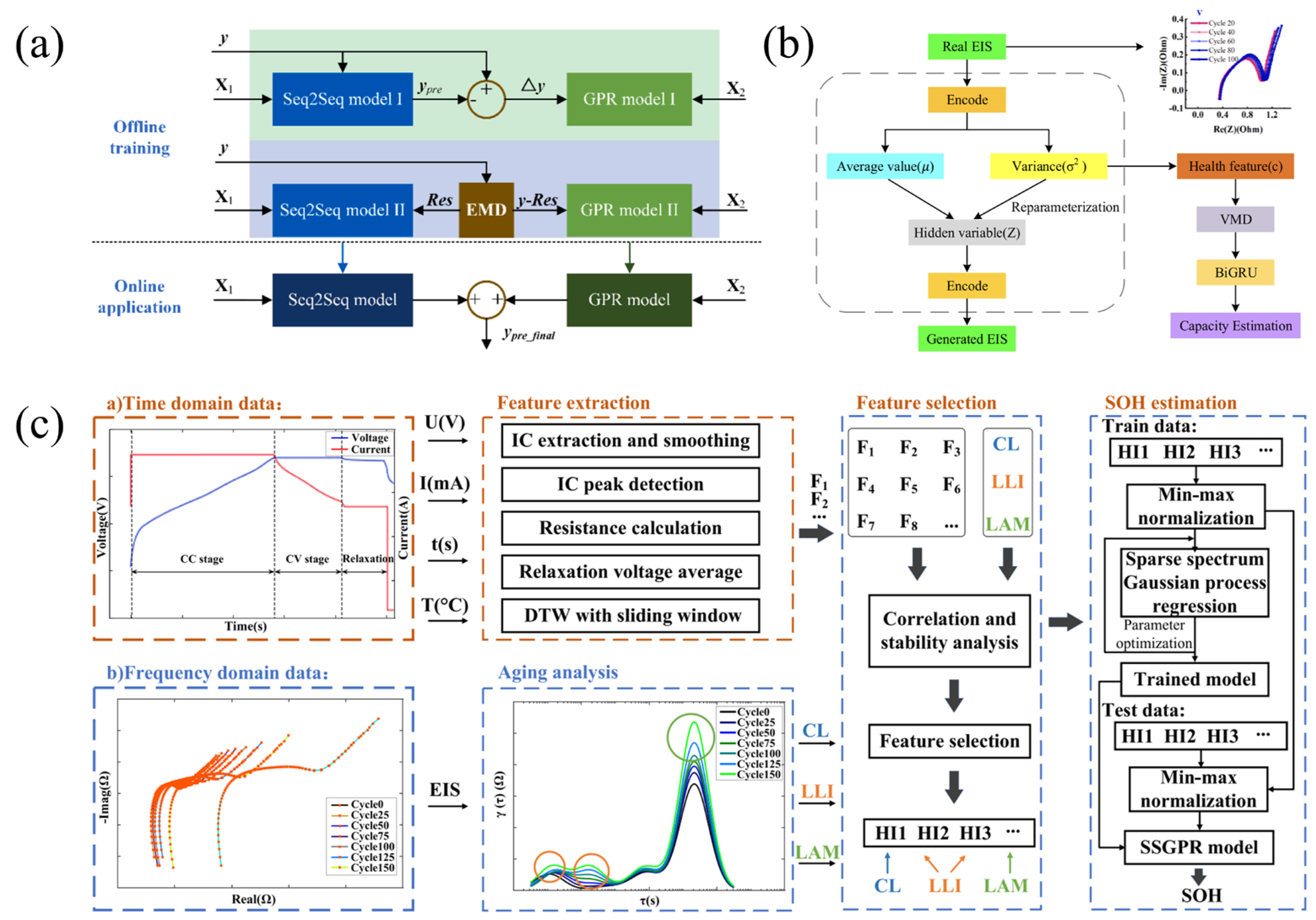
3.1.2. SOC and Multi-State Cooperative Estimation
3.1.3. Comparison and Summary of SOC Estimation
| SOC Estimation Paradigm | Method Example | Core Advantages | Limitations | Future Development Direction |
|---|---|---|---|---|
| Single-state estimation | [39,40,41,43] | High real-time performance | Ignores parameter aging drift | Requires SOH feedback for calibration |
| Multi-state cooperative estimation | [48,49,50,52] | Adapts to model parameter variations induced by aging | Dependent on SOH and model parameter estimation accuracy | Design of online EIS recalibration mechanisms |
3.2. SOH Estimation
3.2.1. Single-State SOH Estimation Using Time-Domain Features
3.2.2. Single-State SOH Estimation Using Frequency-Domain Features
3.2.3. SOH and Multi-State Cooperative Estimation
3.2.4. Comparison and Summary of SOH Estimation
3.3. RUL Prediction
3.3.1. RUL Prediction Using Degradation Empirical Models
3.3.2. Data-Driven RUL Prediction
3.3.3. SOH-RUL Cooperative Prediction
3.3.4. Comparison and Summary of RUL Prediction
3.4. Summary of the Generational Transition
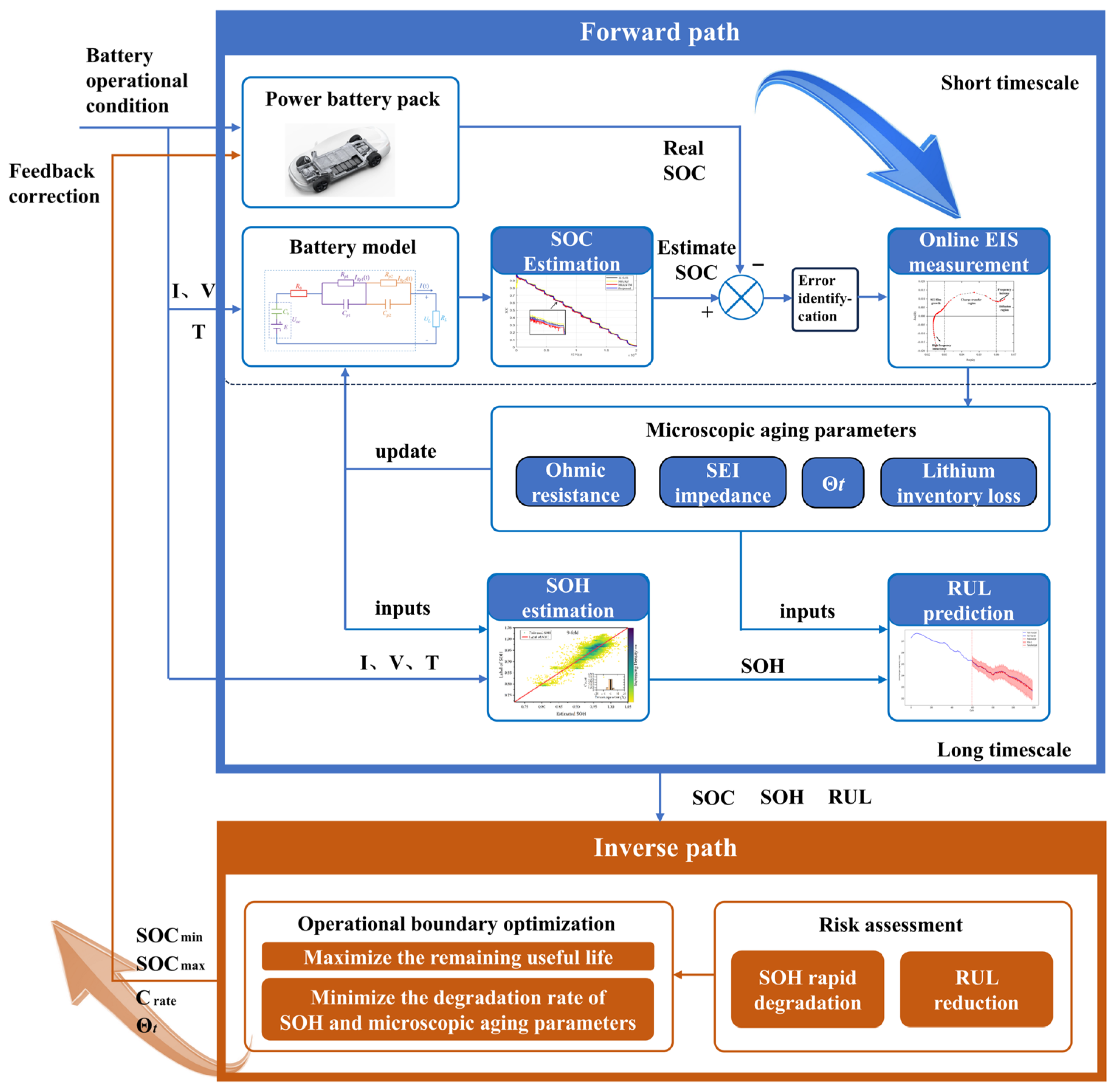
4. Future Evolution: Closed-Loop System for Multi-State Cooperative Estimation
4.1. Development of Multi-State Cooperative Estimation Methods
4.2. Future Evolution of Multi-State Closed-Loop System
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOC | State of Charge |
| SOH | State of Health |
| RUL | Remaining Useful life |
| OCV | Open-Circuit Voltage |
| EIS | Electrochemical Impedance Spectroscopy |
| SEI | Solid Electrolyte Interphase |
| ECM | Equivalent Circuit Model |
| CPE | Constant Phase Element |
| EKF | Extended Kalman Filtering |
| UKF | Unscented Kalman Filtering |
| PF | Particle Filter |
| RBF | Radial Basis Function |
| SVR | Support Vector Regression |
| GPR | Gaussian Process Regression |
| CNN | Convolutional Neural Network |
| LSTM | Long Short Term-Memory |
| GRU | Gated Recurrent Unit |
| PINN | Physics-Informed Neural Network |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
References
- Shen, J.; Zhang, Q.; Tian, S. Impact of the vehicle lightweighting and electrification on the trend of carbon emissions from automotive materials. J. Clean. Prod. 2025, 513, 145677. [Google Scholar] [CrossRef]
- Sharma, I.; Bansal, P.; Dua, R. Breaking down barriers: Emerging issues on the pathway to full-scale electrification of the light-duty vehicle sector. Energy 2025, 326, 136230. [Google Scholar] [CrossRef]
- Amer, M.; Masri, J.; Sajjad, U.; Hamid, K. Electric vehicles: Battery technologies, charging standards, AI communications, challenges, and future directions. Energy Convers. Manag. X 2024, 24, 100751. [Google Scholar] [CrossRef]
- Ockerman, S.; Elfimova, O.; Sapra, H.; Kokjohn, S.; Shumaker, J.; Venkataraman, S. Exploring selective continuous learning for battery state of charge prediction in real-world dynamic charging scenarios. J. Power Sources 2025, 653, 237418. [Google Scholar] [CrossRef]
- Lin, C.; Wu, L.; Tuo, X.; Liu, C.; Zhang, W.; Huang, Z.; Zhang, G. A lightweight two-stage physics-informed neural network for SOH estimation of lithium-ion batteries with different chemistries. J. Energy Chem. 2025, 105, 261–279. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Mao, R.; Li, Y.; Lu, W.; Zhang, J. TPANet: A novel triple parallel attention network approach for remaining useful life prediction of lithium-ion batteries. Energy 2024, 309, 132890. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiong, Y.; Xiao, J.; Yi, T.; Li, C.; Sun, Y. An improved coulomb counting method based on non-destructive charge and discharge differentiation for the SOC estimation of NCM lithium-ion battery. J. Energy Storage 2023, 73, 108917. [Google Scholar] [CrossRef]
- Fahmy, H.M.; Swief, R.A.; Hasanien, H.M.; Alharbi, M.; Maldonado, J.L.; Jurado, F. Hybrid state of charge estimation of lithium-ion battery using the coulomb counting method and an adaptive unscented kalman filter. Energies 2023, 16, 5558. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 2020, 15, 479. [Google Scholar] [CrossRef]
- Ucar, K. Improving electric vehicle state of charge estimation with wavelet transform-integrated 1D-CNN pooling layers. J. Energy Storage 2024, 117, 116202. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, X.; Liu, Z. State of health estimation of power batteries based on multi-feature fusion models using stacking algorithm. Energy 2022, 259, 124851. [Google Scholar] [CrossRef]
- Wang, X.; Dai, K.; Hu, M.; Ni, N. Lithium-ion battery health state and remaining useful life prediction based on hybrid model MFE-GRU-TCA. J. Energy Storage 2024, 95, 112442. [Google Scholar] [CrossRef]
- Cai, N.; Qin, Y.; Chen, X.; Wu, K. Dual time-scale state-coupled co-estimation of state of charge, state of health and remaining useful life for lithium-ion batteries via deep Inter and intra-cycle attention network. J. Energy Storage 2024, 77, 109797. [Google Scholar] [CrossRef]
- Sun, L.; Li, G.; You, F. Combined internal resistance and state-of-charge estimation of lithium-ion battery based on extended state observer. Renew. Sustain. Energy Rev. 2020, 131, 109994. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–308. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Quade, K.; Luder, D.; Gong, J.; Sauer, D.U. Battery degradation diagnosis with field data, impedance-based modeling and artificial intelligence. Energy Storage Mater. 2022, 53, 391–403. [Google Scholar] [CrossRef]
- Xu, J.; Ma, J.; Zhang, K.; Li, J.; Zhao, X.; He, Z.; Wu, X. SOC estimation and internal short circuit fault diagnosis based on DAEKF method for power batteries. J. Energy Storage 2025, 112, 115524. [Google Scholar] [CrossRef]
- Monirul, I.M.; Qiu, L.; Ruby, R.; Ullah, I.; Sharafian, A. Accurate SOC estimation in power lithium-ion batteries using adaptive extended Kalman filter with a high-order electrical equivalent circuit model. Measurement 2025, 249, 117081. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, S.; Yu, C.; Xia, L.; Fernandez, C. Research on SOC estimation for lithium-ion batteries based on improved PNGV equivalence model and AF-UKF algorithm. Int. J. Electrochem. Sci. 2022, 17, 220836. [Google Scholar] [CrossRef]
- Tan, A.H.; Ong, D.S.; Foo, M. Estimation of battery internal resistance using built-in self-scaling method. J. Energy Storage 2023, 59, 106481. [Google Scholar] [CrossRef]
- De Camargo Bortoluzzi, A.; Marujo, D.; de Almeida, A.B.; Jahn, T.G.; de Souza, J.V. An RC model to represent the voltage profile of a second-life lithium-ion battery. In Proceedings of the 2024 Workshop on Communication Networks and Power Systems (WCNPS), Brasilia, Brazil, 12–13 December 2024; pp. 1–7. [Google Scholar]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, H.; Zhang, W.; Li, J.; Chen, X. A modeling method for lithium-ion batteries based on EIS and FFRLS. In Proceedings of the 7th Electronic and Automation Control Conference 2024, Chongqing, China, 15–17 March 2024; pp. 317–321. [Google Scholar]
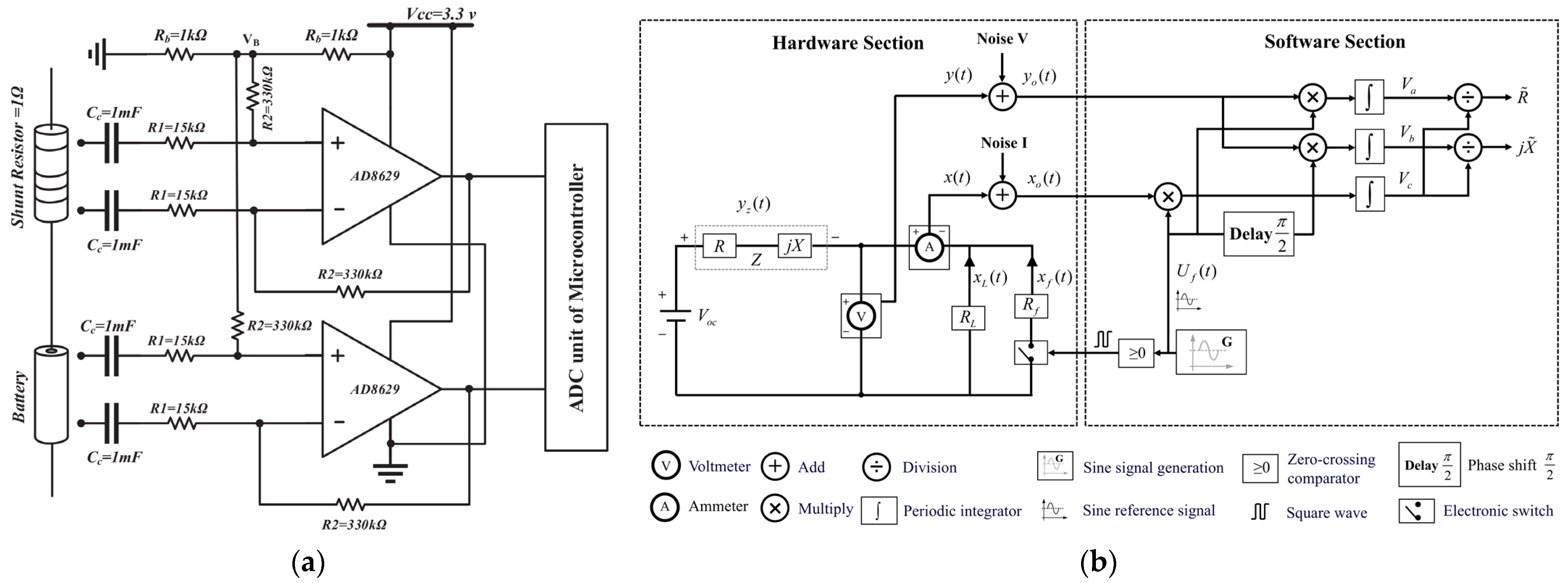
- Abareshi, M.; Sadeghi, E.; Hamzeh, M.; Saif, M.; Alavi, S.M.M. Multi-purpose controllable electrochemical impedance spectroscopy using bidirectional DC–DC converter. J. Energy Storage 2022, 55, 105750. [Google Scholar] [CrossRef]
- Sadeghi, E.; Zand, M.H.; Hamzeh, M.; Saif, M.; Alavi, S.M.M. Controllable electrochemical impedance spectroscopy: From circuit design to control and data analysis. IEEE Trans. Power Electron 2020, 35, 9933–9942. [Google Scholar] [CrossRef]
- Chen, N.; Zhao, X.; Zhou, Y.; Xie, Y.; He, Y.; Yang, C.; Gui, W. Electrochemical impedance spectroscopy online measurement method for lithium-ion batteries based on correlation detection and improved Levenberg-Marquardt algorithm. Measurement 2025, 255, 117995. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, L. A novel composite fractional order battery model with online parameter identification and truncation approximation calculation. Energy 2025, 322, 135561. [Google Scholar] [CrossRef]
- Ai, C.; He, S.; Fan, X. Parameter estimation of fractional-order chaotic power system based on lens imaging learning strategy state transition algorithm. IEEE Access 2023, 11, 13724–13737. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, K.; Zhong, Y.; Yang, D.; Liang, J. Fractional-order modeling and parameter estimation of lithium-ion battery via multi-strategy and mean factor differential evolution. Measurement 2025, 246, 116721. [Google Scholar] [CrossRef]
- Han, S.; Tang, Y.; Rahimian, S.K. A numerically efficient method of solving the full-order pseudo-2-dimensional (P2D) Li-ion cell model. J. Power Sources 2021, 490, 229571. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery state estimation for a single particle model with electrolyte dynamics. IEEE Trans. Control. Syst. Technol. 2016, 25, 453–468. [Google Scholar] [CrossRef]
- Xie, J.; Yu, J.; Liu, L.; Wei, Z.; Dong, Z. Estimating the Charge and Temperature States for Li-Ion Batteries by Coupling Single Particle Kinetics and Electrothermal Effects. IEEE/ASME Trans. Mechatron. 2025, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium-ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Baba, N.; Yoshida, H.; Nagaoka, M.; Okuda, C.; Kawauchi, S. Numerical simulation of thermal behavior of lithium-ion secondary batteries using the enhanced single particle model. J. Power Sources 2014, 252, 214–228. [Google Scholar] [CrossRef]
- Gao, Y.Z.; Wang, J.; Xu, D.H. Nonlinear combination estimation of lithium battery SOC based on equivalent circuit model parameter identification. Veh. Engine 2024, 74–82+89. Available online: https://kns.cnki.net/kcms2/article/abstract?v=of4N6dfUJfwiZVxOyT2zZEXSMH1w0KKX3fV4Mw-3NNm0TVkwlIea8yP_gJn8oEG-XN8smO6BAIV5CYPW5uLUAmQRmXUkxjrJciFNG9j0D5wc0716zX4yRkonE9-mTdSrq0spGRmXHCnkFNq-NIZUji4yk5HV5YQhKL1n0c8t-FUjPDVcgJCIZQ==&uniplatform=NZKPT&language=CHS (accessed on 30 September 2025).
- Lai, X.; Li, Y.F.; Zheng, Y.J. Global estimation of state of charge for lithium-ion batteries based on optimized SOC-OCV curve and EKF. Automot. Eng. 2021, 43, 19–26. [Google Scholar]
- Jeong, Y.M.; Cho, Y.K.; Ahn, J.H.; Ryu, S.H.; Lee, B.K. Enhanced Coulomb counting method with adaptive SOC reset time for estimating OCV. In Proceedings of the IEEE Energy Conversion Congress and Exposition 2014, Pittsburgh, PA, USA, 14–18 September 2014; pp. 1313–1318. [Google Scholar]
- Xia, Y. Comparison and Analysis of SOC Estimation Based on First-Order and Second-Order Thevenin Battery Models Based on EKF. Acad. J. Sci. Technol. 2023, 6, 10–18. [Google Scholar] [CrossRef]
- Zhen, Y.; Xu, Y.H.; Zhang, H.G.; Tong, L. Research on SOC estimation of power battery based on fractional order model multi innovation UKF. Chin. J. Power Sources 2024, 48, 1777–1788. [Google Scholar]
- Chen, N.; Zhao, X.; Chen, J.; Xu, X.; Zhang, P.; Gui, W. Design of a Non-Linear Observer for SOC of Lithium-Ion Battery Based on Neural Network. Energies 2022, 15, 3835. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Ahn, J.; Lee, Y.; Han, B.; Lee, S.; Kim, Y.; Chung, D.; Jeon, J. A highly effective and robust structure-based LSTM with feature-vector tuning framework for high-accuracy SOC estimation in EV. Energy 2025, 32, 136134. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Z. SOC estimation for lithium batteries using a CNN-attention-LSTM model. J. Energy Storage 2025, 130, 117479. [Google Scholar] [CrossRef]
- Tao, J.; Wang, S.; Cao, W.; Fernandez, C.; Blaabjerg, F.; Cheng, L. An innovative multitask learning—Long short-term memory neural network for the online anti-aging state of charge estimation of lithium-ion batteries adaptive to varying temperature and current conditions. Energy 2025, 314, 134272. [Google Scholar] [CrossRef]
- Zhao, Z.; Kou, F.; Pan, Z.; Chen, L.; Luo, X.; Yang, T. High-accuracy state-of-charge fusion estimation of lithium-ion batteries by integrating the Extended Kalman Filter with feature-enhanced Random Forest. J. Energy Storage 2025, 118, 116275. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Y.; Chen, L.; Chen, N.; Wang, H.; Huang, W.; Chen, J. On full-life-cycle SOC estimation for lithium batteries by a variable structure based fractional-order extended state observer. Appl. Energy 2023, 351, 121828. [Google Scholar] [CrossRef]
- Sharma, S.; Panigrahi, B.K. Aging Responsive State of Charge Prediction of Lithium-Ion Battery Using Attention Mechanism Based Convolutional Neural Networks. IEEE Trans. Ind. Appl. 2024, 60, 7342–7355. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, N.; Chen, J.; Liao, J.; Cao, F.; Yang, C. Co-estimation of state of charge and model parameters for lithium-ion batteries based on variational Bayesian under time-varying noise and temperature conditions. J. Energy Storage 2024, 96, 112600. [Google Scholar] [CrossRef]
- Wang, C.; Cui, N.; Cui, Z.; Yuan, H.; Zhang, C. Fusion estimation of lithium-ion battery state of charge and state of health considering the effect of temperature. J. Energy Storage 2022, 53, 105075. [Google Scholar] [CrossRef]
- Bao, Z.; Nie, J.; Lin, H.; Li, Z.; Gao, K.; He, Z.; Gao, M. Dual-Task Learning for Joint State-of-Charge and State-of-Energy Estimation of Lithium-Ion Battery in Electric Vehicle. IEEE Trans. Transp. Electrif. 2025, 11, 558–569. [Google Scholar] [CrossRef]
- Routh, B.; Guha, A.; Mukhopadhyay, S.; Patra, A. Online Co-Estimation of the State-of-Health, State-of-Charge, and Remaining-Useful-Life of Lithium-Ion Batteries Using a Discrete Capacity Loss Model. IEEE Trans. Transp. Electrif. 2025, 11, 6962–6975. [Google Scholar] [CrossRef]
- Chang, C.; Wu, Y.; Jiang, J.; Jiang, Y.; Tian, A.; Li, T.; Gao, Y. Prognostics of the state of health for lithium-ion battery packs in energy storage applications. Energy 2022, 239, 122189. [Google Scholar] [CrossRef]
- Singh, K.; Tjahjowidodo, T.; Boulon, L.; Feroskhan, M. Framework for measurement of battery state-of-health(resistance) integrating overpotential effects and entropy changes using energy equilibrium. Energy 2022, 239, 121942. [Google Scholar] [CrossRef]
- Hou, X.; Guo, X.; Yuan, Y.; Zhao, K.; Tong, L.; Yuan, C.; Teng, L. The state of health prediction of li-ion batteries based on an improved extreme learning machine. J. Energy Storage 2023, 70, 108044. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Gopaluni, R.B.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-Z.; Liang, Z.; Yuan, H.; Yang, L.; Xu, F.; Zhang, Y. Li-ion battery state-of-health estimation based on the combination of statistical and geometric features of the constant-voltage charging stage. J. Energy Storage 2023, 72, 108647. [Google Scholar] [CrossRef]
- Li, F.; Min, Y.; Zhang, Y.; Zhang, Y.; Zuo, H.; Bai, F. State-of-health estimation method for fast-charging lithium-ion batteries based on stacking ensemble sparse Gaussian process regression. Reliab. Eng. Syst. Saf. 2024, 242, 109787. [Google Scholar] [CrossRef]
- Deng, Z.; Xu, L.; Liu, H.; Hu, X.; Duan, Z.; Xu, Y. Prognostics of battery capacity based on charging data and data-driven methods for on-road vehicles. Appl. Energy 2023, 339, 120954. [Google Scholar] [CrossRef]
- Lu, Y.; Guo, D.; Xiong, G.; Wei, Y.; Zhang, J.; Wang, Y.; Ouyang, M. Towards real-world state of health estimation: Part 2, system level method using electric vehicle field data. eTransportation 2024, 22, 100361. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Z.; Liu, P.; Wang, Q.; She, C.; Bauer, P.; Qin, Z. Multistep fast charging-based state of health estimation of lithium-ion batteries. IEEE Trans. Transp. Electrif. 2024, 10, 4640–4652. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Peng, P.; Chen, Z. Health diagnosis for Lithium-ion battery by combining partial incremental capacity and deep belief network during insufficient discharge profile. IEEE Trans. Ind. Electron. 2023, 70, 11242–11250. [Google Scholar] [CrossRef]
- Bilfinger, P.; Rosner, P.; Schreiber, M.; Kröger, T.; Gamra, K.A.; Ank, M.; Wassiliadis, N.; Dietermann, B.; Lienkamp, M. Battery pack diagnostics for electric vehicles: Transfer of differential voltage and incremental capacity analysis from cell to vehicle level. eTransportation 2024, 22, 100356. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Peng, Z.; Liu, D.; Wu, L. A Hybrid Drive Method for Capacity Prediction of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 8, 1000–1012. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A Fast Impedance Calculation-Based Battery State-of-Health Estimation Method. IEEE Trans. Ind. Electron. 2021, 69, 7019–7028. [Google Scholar] [CrossRef]
- Luo, F.; Huang, H.; Ni, L.; Li, T. Rapid prediction of the state of health of retired power batteries based on electrochemical impedance spectroscopy. J. Energy Storage 2021, 41, 102866. [Google Scholar] [CrossRef]
- Xu, Z.; Li, H.; Yazdi, M.; Ouyang, K.; Peng, W. Aging Characteristics and State-of-Health Estimation of Retired Batteries: An Electrochemical Impedance Spectroscopy Perspective. Electronics 2022, 11, 3863. [Google Scholar] [CrossRef]
- Locorotondo, E.; Cultrera, V.; Pugi, L.; Berzi, L.; Pierini, M.; Lutzemberger, G. Development of a battery real-time state of health diagnosis based on fast impedance measurements. J. Energy Storage 2021, 38, 102566. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. Detection of Lithium-Ion Cells Degradation through Deconvolution of Electrochemical Impedance Spectroscopy with Distribution of Relaxation Time. Energy Technol. 2022, 10, 2200547. [Google Scholar] [CrossRef]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. Transfer Learning with Deep Neural Network for Capacity Prediction of Li-ion Batteries Using EIS Measurement. IEEE Trans. Transp. Electrif. 2022, 9, 886–895. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Schaltz, E.; Stroe, D.-I.; Gismero, A.; Yang, B. Degradation mechanism analysis and State-of-Health estimation for lithium-ion batteries based on distribution of relaxation times. J. Energy Storage 2022, 55, 105386. [Google Scholar] [CrossRef]
- Gao, Z.; Jin, Y.; Zhang, Y.; Zhang, Z.; Li, S.; Liu, J.; Wang, H. Static EIS multi-frequency feature points combined with WOA-BP neural network for Li-ion battery SOH estimation. Measurement 2025, 253, 117780. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Y.; Shen, J.; Liu, Y.; Zhang, Y.; Chen, Z.; Wei, F. State of health estimation for lithium-ion batteries based on impedance feature selection and improved support vector regression. Energy 2025, 326, 136135. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, W.; Wang, Y.; Cheng, S.; Wang, J. Estimating battery state of health using impedance spectrum geometric health indicators and recurrent deep sigma point process. J. Energy Storage 2025, 119, 116117. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, B.; Lyu, D.; Wang, L.; Wang, K. Estimation of lithium-ion battery health state using enhanced variational autoencoder and bidirectional gated recurrent unit based on electrochemical impedance spectroscopy. J. Power Sources 2025, 655, 237957. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, F.; Qin, W.; Li, J.; Cheng, X.; Zeng, J. Dynamic internal resistance modeling and thermal characteristics of lithium-ion batteries for electric vehicles by considering state of health. J. Power Sources 2024, 612, 234806. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Chen, N.; Xie, Y.; Wang, H.; Huang, W.; Zhao, X.; Yang, C. State of health estimation of lithium-ion battery aging process based on time-frequency fusion characteristics. J. Power Sources 2024, 596, 234002. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Xu, Y.; Guo, J.; Su, H. A physics-informed hybrid data-driven approach with generative electrode-level features for lithium-ion battery health prognostics. IEEE Trans. Transp. Electrif. 2024, 11, 4857–4871. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. A comparative study of commercial lithium ion battery cycle life in electric vehicle: Capacity loss estimation. J. Power Sources 2014, 268, 658–669. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2016, 9, 1131–1140. [Google Scholar] [CrossRef]
- Shi, H.; Liang, Y.; Wu, B.; Zhang, X.; Wang, Z.; Sun, C. Time-varying nonparametric remaining useful life of systems based on adaptive kernel auxiliary particle filter. IEEE Trans. Instrum. Meas. 2025, 74, 3519414. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Yang, S.; Li, J.; Zhou, F.; Peng, J.; Song, Z. An empirical-informed model for the early degradation trajectory prediction of lithium-ion battery. IEEE Trans. Energy Convers. 2024, 39, 2299–2311. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. A degradation empirical-model-free battery end-of-life prediction framework based on gaussian process regression and Kalman filter. IEEE Trans. Transp. Electrif. 2023, 9, 4898–4908. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, F.; Wang, S.; Meng, J.; Xie, J.; Ling, R.; Yin, H.; Zhang, K.; Chai, Y. Joint nonlinear-drift-driven wiener process-Markov chain degradation switching model for adaptive online predicting lithium-ion battery remaining useful life. Appl. Energy 2023, 341, 121043. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, W.; Zhang, Y.; Zhang, C.; Zhang, C.; Zhang, J. Research on the remaining useful life prediction method for lithium-ion batteries by fusion of feature engineering and deep learning. Appl. Energy 2024, 358, 122325. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, B.; Ahmed, M.; Mao, Z.; Feng, J.; Chen, Z. A hybrid deep learning approach for remaining useful life prediction of lithium-ion batteries based on discharging fragments. Appl. Energy 2024, 358, 122555. [Google Scholar] [CrossRef]
- Yao, X.; Su, K.; Zhang, H.; Zhang, S.; Zhang, H.; Zhang, J. Remaining useful life prediction for lithium-ion batteries in highway electromechanical equipment based on feature-encoded LSTM-CNN network. Energy 2025, 323, 135719. [Google Scholar] [CrossRef]
- Xia, G.; Jia, C.; Shi, Y.; Jia, J.; Pang, X.; Wen, J.; Zeng, J. Remaining useful life prediction of lithium-ion batteries by considering trend filtering segmentation under fuzzy information granulation. Energy 2025, 318, 134810. [Google Scholar] [CrossRef]
- Ni, Y.; Song, K.; Pei, L.; Li, X.; Wang, T.; Zhang, H.; Zhu, C.; Xu, J. State-of-health estimation and knee point identification of lithium-ion battery based on data-driven and mechanism model. Appl. Energy 2025, 385, 125539. [Google Scholar] [CrossRef]
- Chen, H.; Yuan, B.; Lu, Q.; Shah, B.A.; Hu, R.; Wu, H.; Zhou, X.; Han, Q.; Li, S. Extracting health indicators from a single cycle of data based on the aging mechanism to accurately predict the knee point and remaining useful life of spent lithium-ion battery. J. Energy Storage 2025, 132, 117813. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J.; Hu, Y.; Chen, H. A battery prognostics and health management technique based on knee critical interval and linear complexity self-attention transformer in electric vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10216–10230. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Xie, Y.; Zeng, J.; Fernandez, C. Remaining useful life prediction and state of health diagnosis of lithium-ion batteries with multiscale health features based on optimized CatBoost algorithm. Energy 2024, 300, 131575. [Google Scholar] [CrossRef]
- Pang, H.; Chen, K.; Geng, Y.; Wu, L.; Wang, F.; Liu, J. Accurate capacity and remaining useful life prediction of lithium-ion-batteries based on improved particle swarm optimization and particle filter. Energy 2024, 293, 130555. [Google Scholar] [CrossRef]
- Guo, F.; Wu, X.; Liu, L.; Ye, J.; Wang, T.; Fu, L.; Wu, Y. Prediction of remaining useful life and state of health of lithium batteries based on time series feature and Savitzky-Golay filter combined with gated recurrent unit neural network. Energy 2023, 270, 126880. [Google Scholar] [CrossRef]
- Feng, W.; Sun, Z.; Han, Y.; Cai, N.; Zhou, Y. A multi-strategy attention regression network for joint prediction of state of health and remaining useful life of lithium-ion batteries using only charging data. J. Power Sources 2025, 636, 236507. [Google Scholar] [CrossRef]
- Yang, L.; He, M.; Ren, Y.; Gao, B.; Qi, H. Physics-informed neural network for co-estimation of state of health, remaining useful life, and short-term degradation path in lithium-ion batteries. Appl. Energy 2025, 398, 126427. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, B. A multi-time-resolution attention-based interaction network for co-estimation of multiple battery states. Appl. Energy 2025, 381, 125097. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Z.; Zuo, Z.; Wang, Y. Lithium battery charging optimization via multi-stage combined charging strategy in solar-powered vehicles. J. Energy Storage 2024, 83, 110716. [Google Scholar] [CrossRef]
- Du, J.; Zhang, X.; Wang, T.; Song, Z.; Yang, X.; Wang, H.; Ouyang, M.; Wu, X. Battery degradation minimization oriented energy management strategy for plug-in hybrid electric bus with multi-energy storage system. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, K.; Gu, Y.; Wang, J.; Chen, Q. Optimal energy dispatch of grid-connected electric vehicle considering lithium battery electrochemical model. IEEE Trans. Smart Grid 2024, 15, 3000–3015. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, W.; Knapp, M.; Darma, M.S.D.; Mereacre, L.; Su, P.; Hua, W.; Liu-Théato, X.; Dai, H.; Wei, X.; et al. A method to prolong lithium-ion battery life during the full life cycle. Cell Rep. Phys. Sci. 2023, 4. [Google Scholar] [CrossRef]
- Naseri, F.; Gil, S.; Barbu, C.; Cetkin, E.; Yarimca, G.; Jensen, A.; Larsen, P.; Gomes, C. Digital twin of electric vehicle battery systems: Comprehensive review of the use cases, requirements, and platforms. Renew. Sustain. Energy Rev. 2023, 179, 113280. [Google Scholar] [CrossRef]
- Ji, C.; Jin, G.; Zhang, R. Charge process management of lithium-ion batteries based on digital twins: A new way to extend life. J. Process. Control. 2025, 152, 103475. [Google Scholar] [CrossRef]
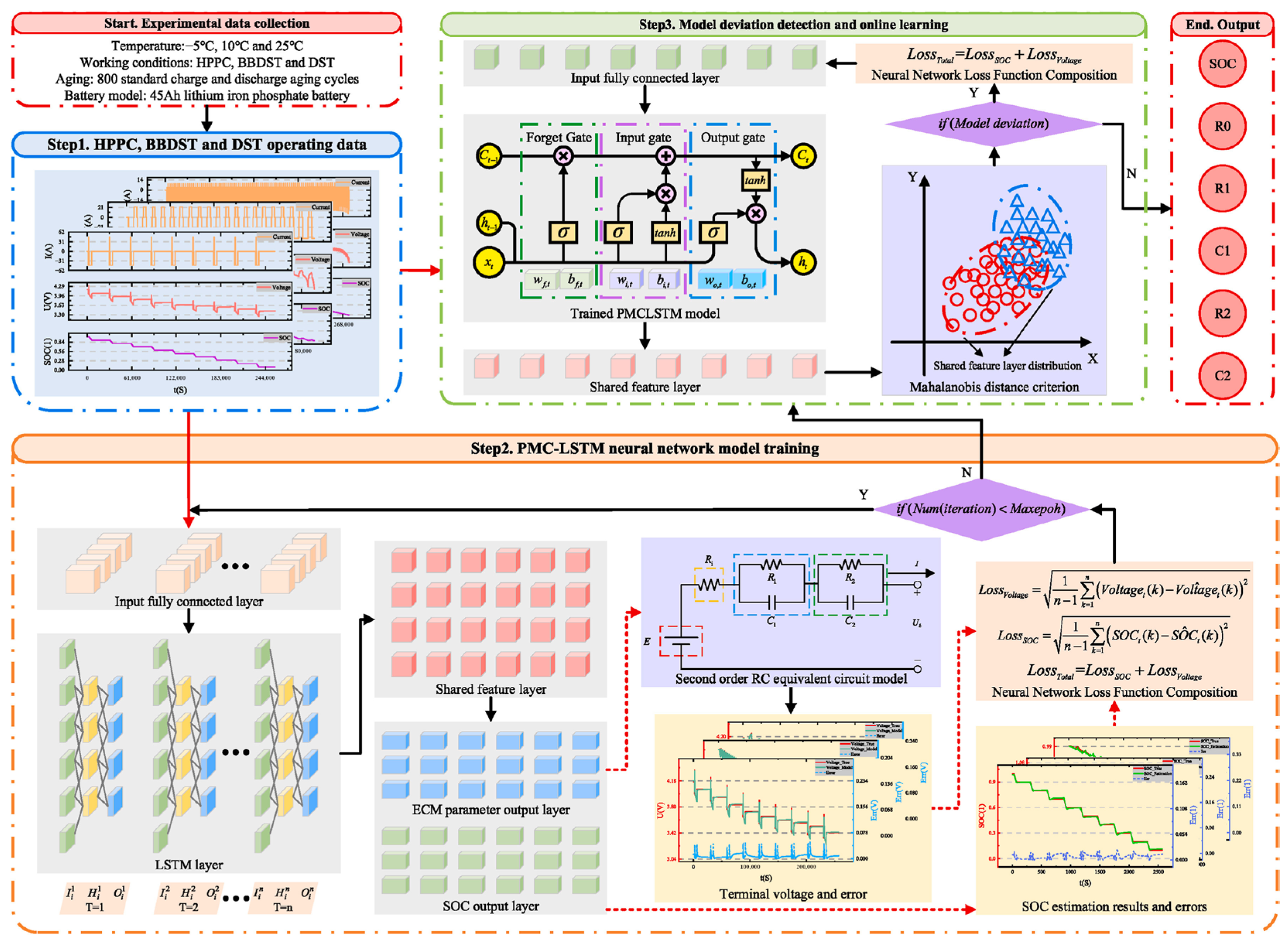
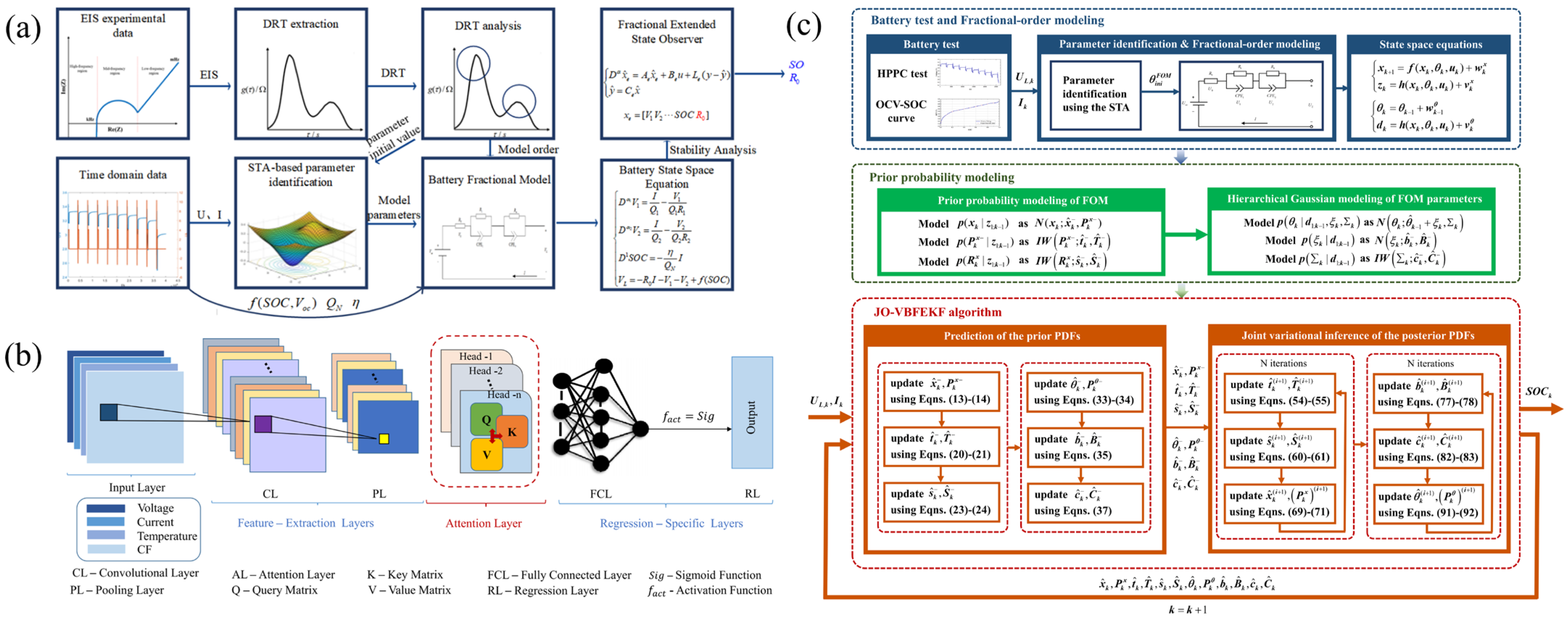
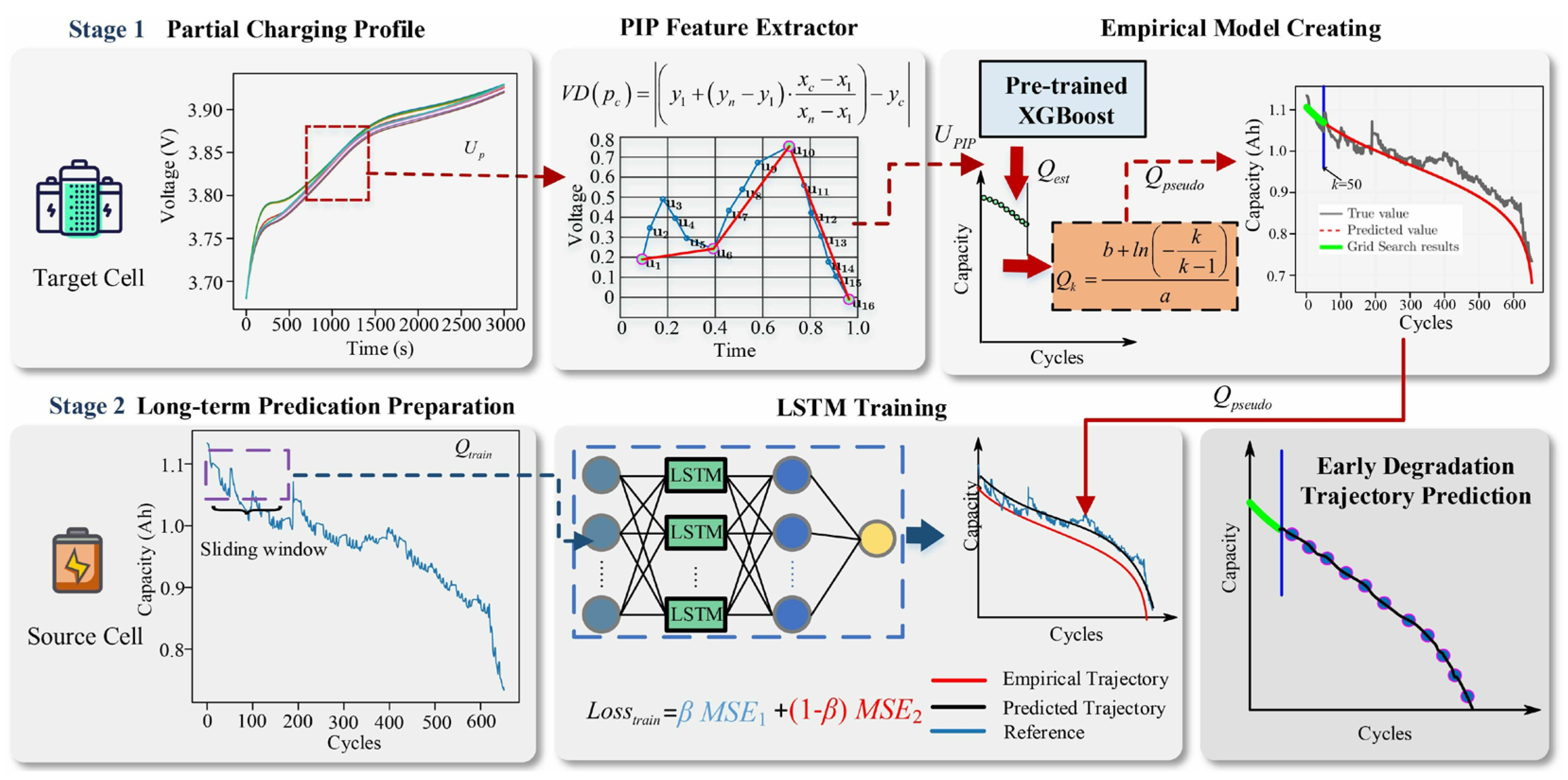
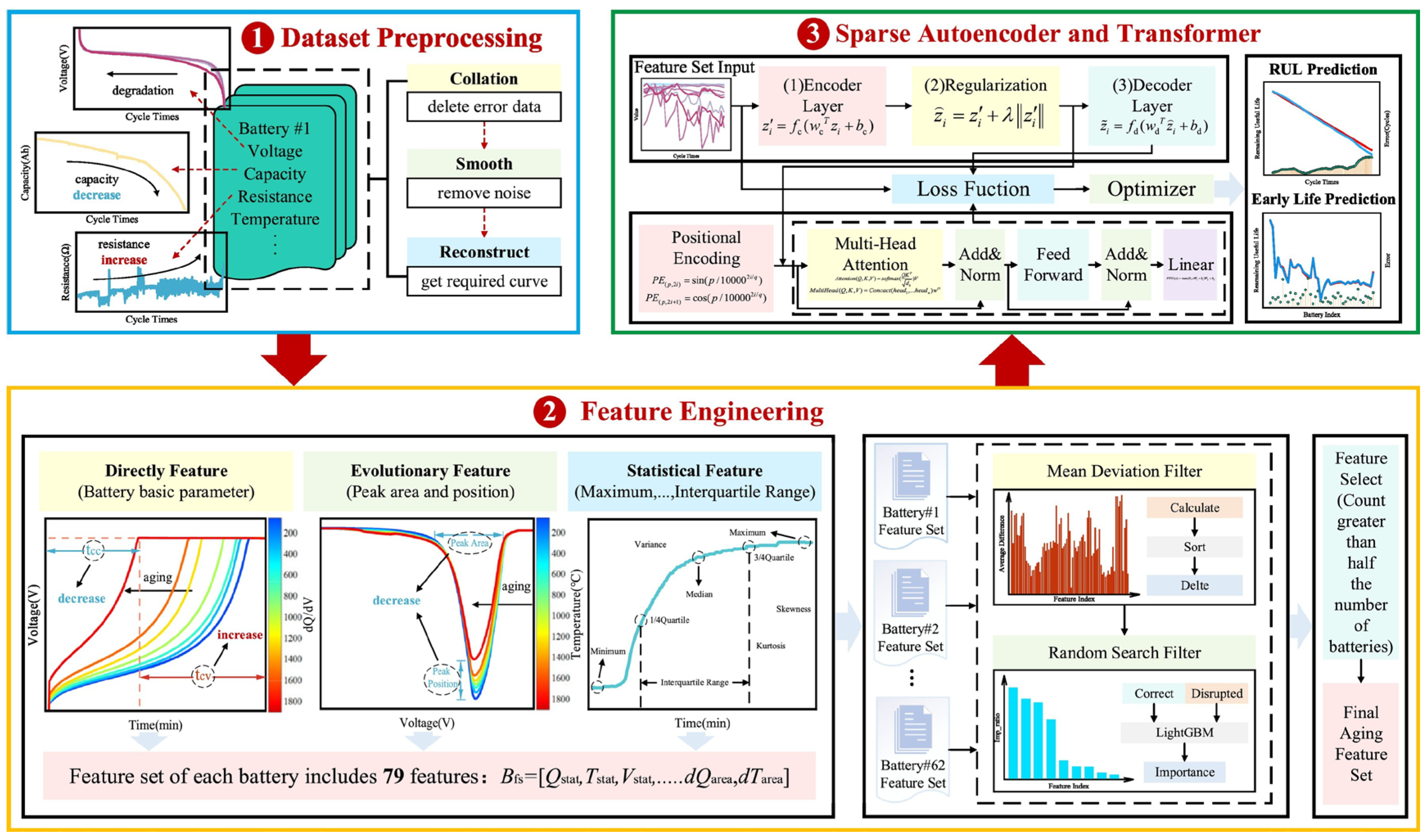
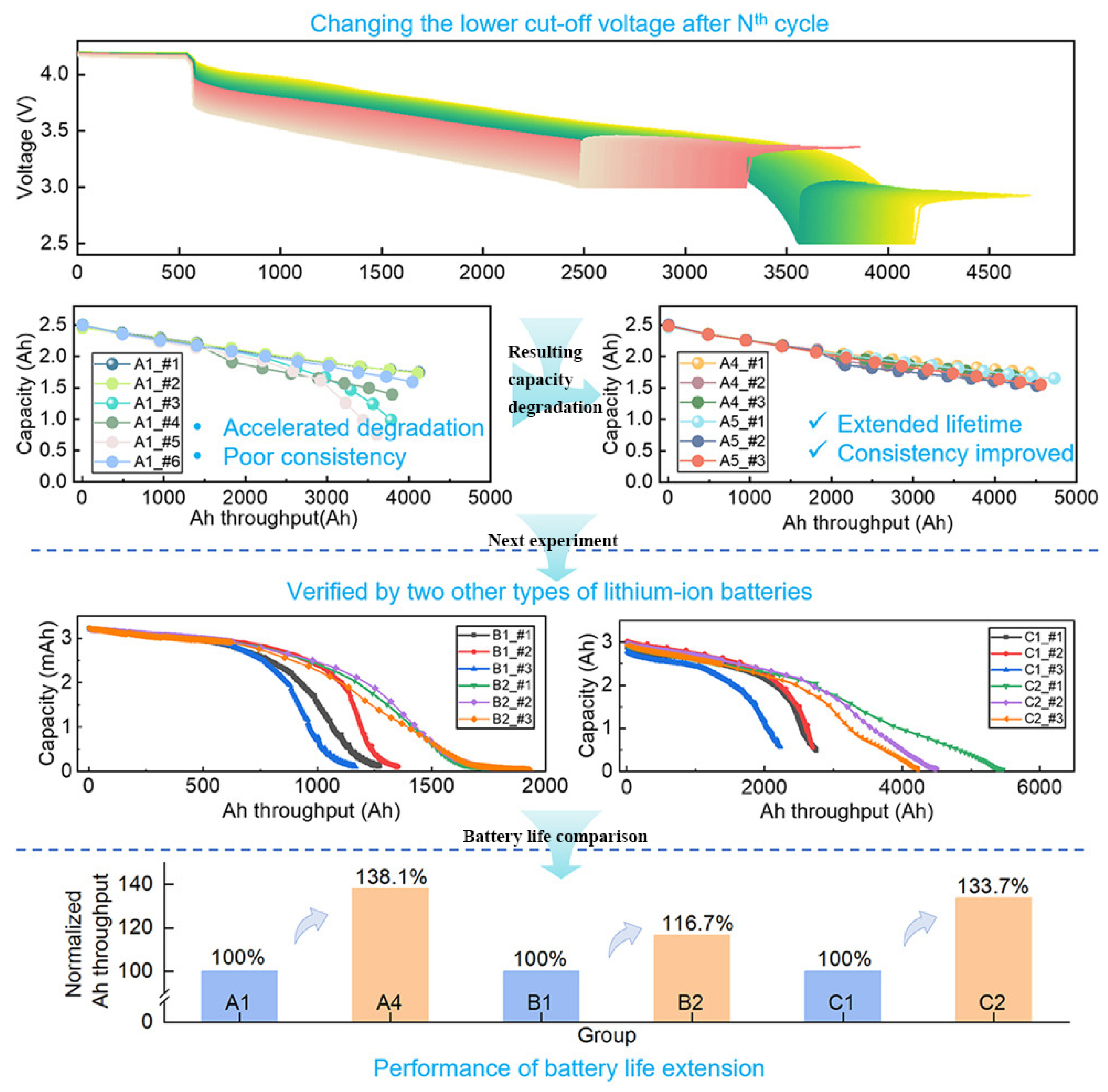
| SOH Estimation Paradigm | Method Example | Core Advantages | Limitations | Future Development Direction |
|---|---|---|---|---|
| Time-domain-based method | [54,55,60,61] | Large data availability with rich aging characteristics | Affected by SOC operating range | High Robustness and Strong Generalization Capability |
| Frequency-domain-based method | [65,66,76,77] | Direct acquisition of electrode-level aging features with intuitive degradation trends | Dependent on accurate online EIS measurements | Driving physics-informed RUL prediction |
| Multi-state cooperative estimation | [78,79,80] | Macro-micro integration | Multi-scale coordination | Bridging SOC and RUL |
| SOH Estimation Paradigm | Method Example | Core Advantages | Challenges | Future Development Direction |
|---|---|---|---|---|
| Empirical Model-Based Methods | [81,82,83,84] | Low computational complexity and high efficiency | Poor adaptability to operational condition variations | Empirical models constrain data-driven models |
| Data-Driven Methods | [87,88,89,90] | Adaptability to complex operating conditions | Requires accurate historical SOH as input | Integration with data generation methods to enhance cross-condition adaptability |
| SOH-RUL Cooperative Estimation | [94,95,96,97] | Suitable for real-time recursive estimation | Requires correction of recursive cumulative errors | Feedback correction of SOH and RUL prediction accuracy |
| State | Generation | Methods | Lab Tests | Datasets |
|---|---|---|---|---|
| SOC | First | Coulomb counting [8], Kalman filtering [40,41] | Capacity test, HPPC test, and OCV-SOC test | New European driving cycle, Federal test procedure [41] |
| Second | Neural networks [44], filtering and neural network hybrid methods [46] | First generation tests under various temperatures and C-rates | DST, BBDST and DST test datasets under different temperature [44,46] | |
| Third | Joint estimation of SOC and battery parameters [48,50] | The EIS test is added to the second-generation tests | RPT and EIS tests datasets [48] FUDS tests datasets [50] | |
| SOH | First | Ampere-hour throughput during the charging process [9] | Capacity test and cycling test | Laboratory cycling test datasets [9] |
| Second | Neural networks [60,77], | Cycling test and real-world electric vehicle data | Real-world commercial electric vehicle data [60,61], EIS datasets [77]. MIT tests datasets [59] | |
| Third | Time-frequency fusion methods [80] Physics-informed neural network [80] | Cycling test, EIS test, and real-world electric vehicle data | NCA and NCM battery datasets with EIS [77] | |
| RUL | First | Empirical models [81], Wiener processes and Markov chain switching models [86] | Cycling test under various temperatures and C-rates | NASA tests datasets [83] |
| Second | Neural networks [6,89], hybrid model [12,88] | Cycling test and random real-world electric vehicle data | CALCE tests datasets [84] MIT tests datasets [87] | |
| Third | Dual time-scale state-coupled co-estimation [13], Physics-informed neural network [98] | Cycling test, EIS test, and random real-world electric vehicle data | NCA and NCM battery datasets with EIS [77] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, N.; Xie, Y.; Cheng, Y.; Wang, H.; Zhou, Y.; Zhao, X.; Chen, J.; Yang, C. A Review of Cross-Scale State Estimation Techniques for Power Batteries in Electric Vehicles: Evolution from Single-State to Multi-State Cooperative Estimation. Energies 2025, 18, 5289. https://doi.org/10.3390/en18195289
Chen N, Xie Y, Cheng Y, Wang H, Zhou Y, Zhao X, Chen J, Yang C. A Review of Cross-Scale State Estimation Techniques for Power Batteries in Electric Vehicles: Evolution from Single-State to Multi-State Cooperative Estimation. Energies. 2025; 18(19):5289. https://doi.org/10.3390/en18195289
Chicago/Turabian StyleChen, Ning, Yihang Xie, Yuanhao Cheng, Huaiqing Wang, Yu Zhou, Xu Zhao, Jiayao Chen, and Chunhua Yang. 2025. "A Review of Cross-Scale State Estimation Techniques for Power Batteries in Electric Vehicles: Evolution from Single-State to Multi-State Cooperative Estimation" Energies 18, no. 19: 5289. https://doi.org/10.3390/en18195289
APA StyleChen, N., Xie, Y., Cheng, Y., Wang, H., Zhou, Y., Zhao, X., Chen, J., & Yang, C. (2025). A Review of Cross-Scale State Estimation Techniques for Power Batteries in Electric Vehicles: Evolution from Single-State to Multi-State Cooperative Estimation. Energies, 18(19), 5289. https://doi.org/10.3390/en18195289