Characteristic Analysis of Boiling Heat Transfer of R32 Refrigerant and Modeling Study of Heat Exchanger
Abstract
1. Introduction
2. Experimental System
3. Results and Discussion
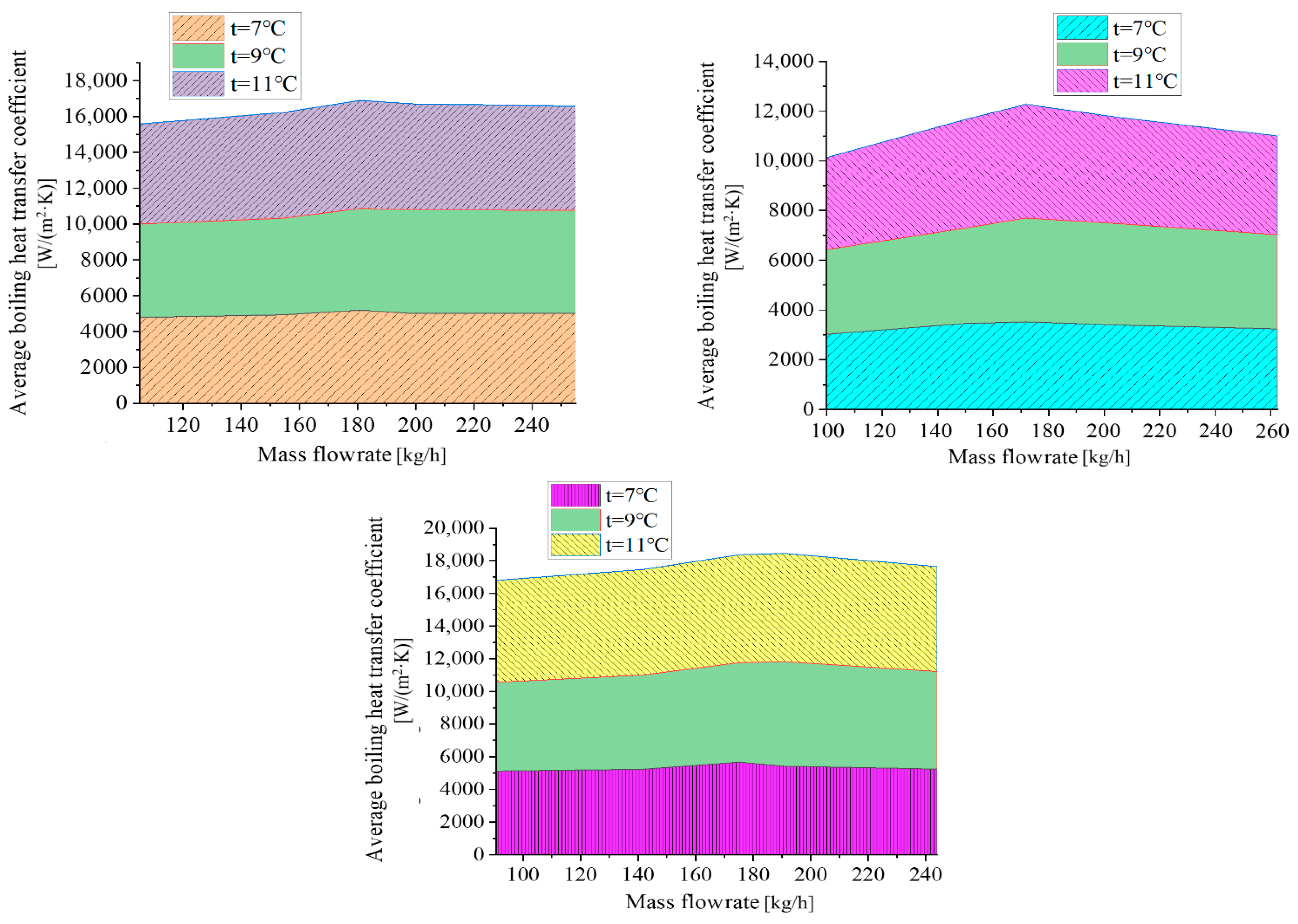
3.1. Effect of Tube Diameter and Mass Flow Rate on Boiling Heat Transfer
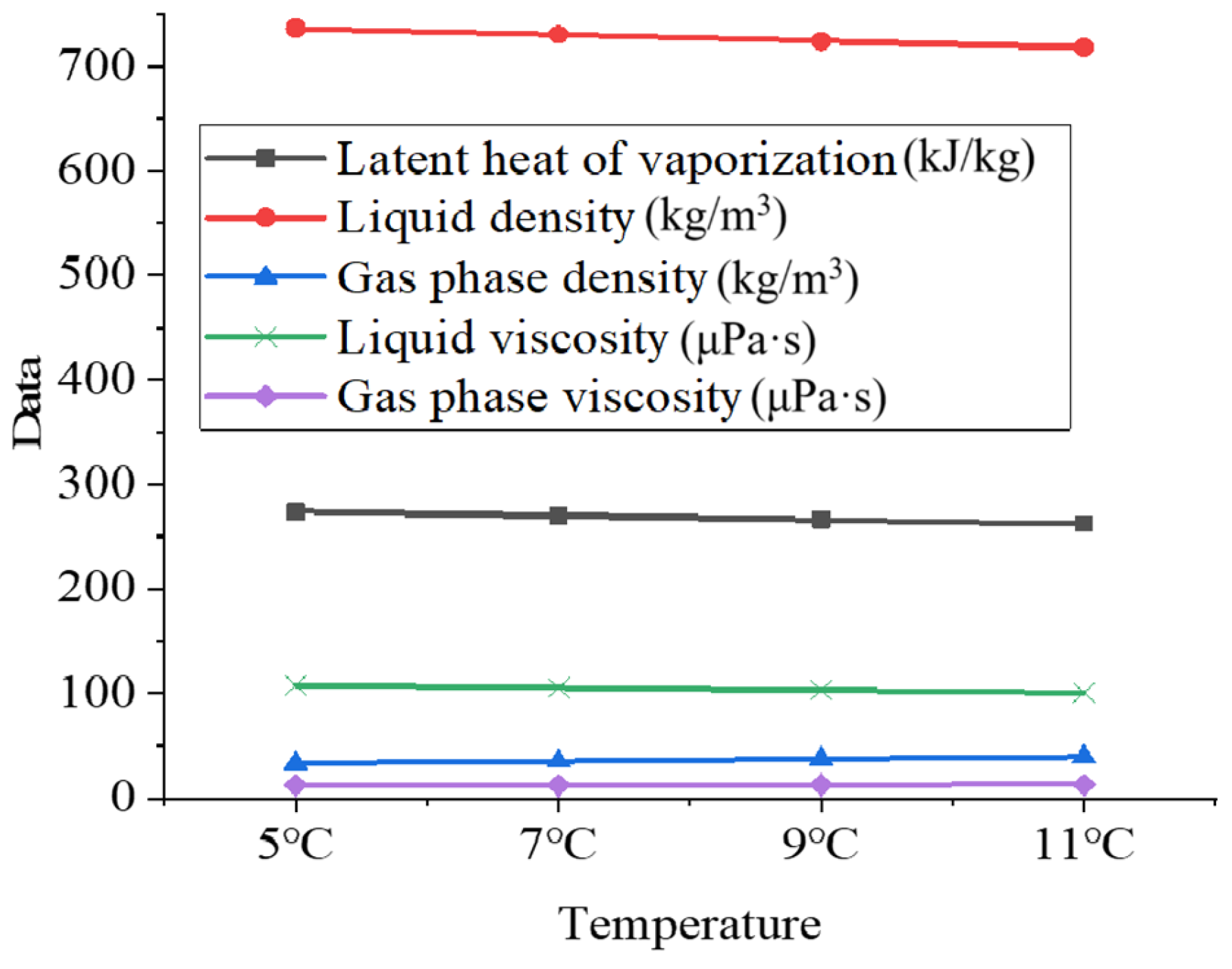
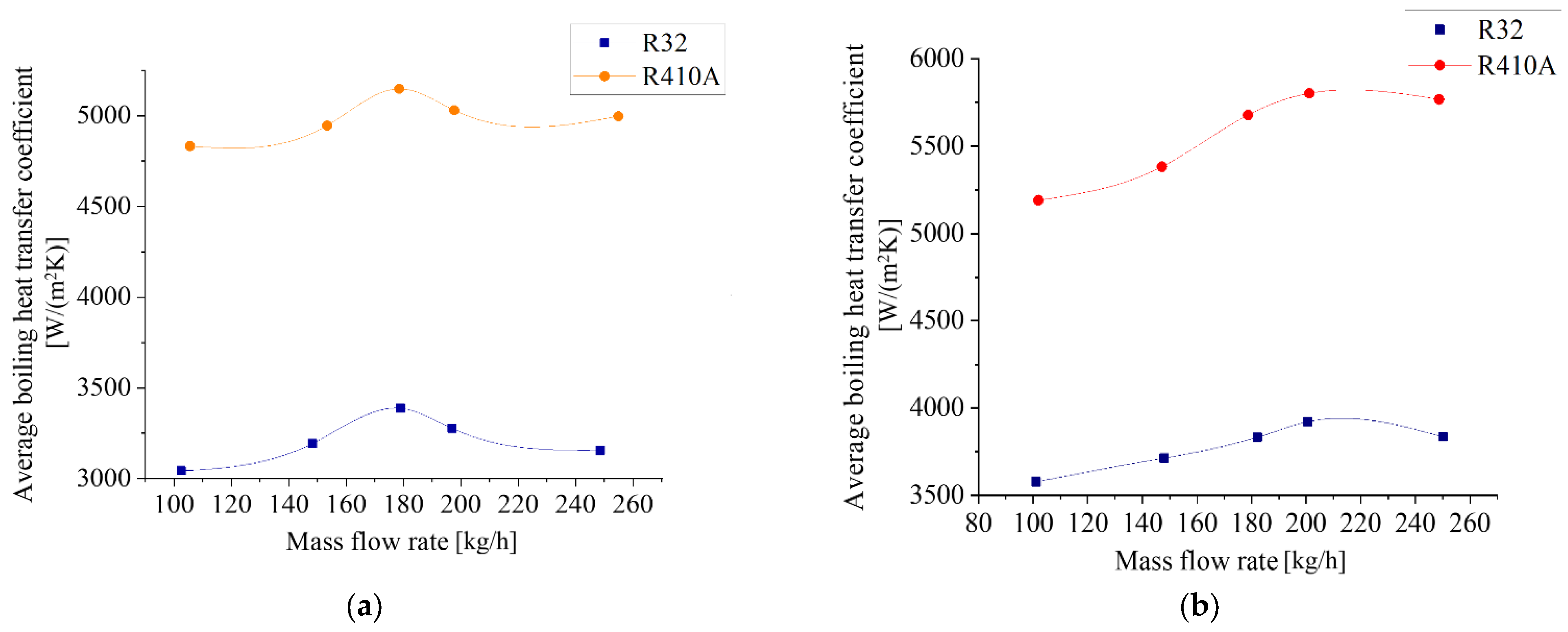
3.2. Effect of Ribbed Tube and Refrigerant Type on Boiling Heat Transfer
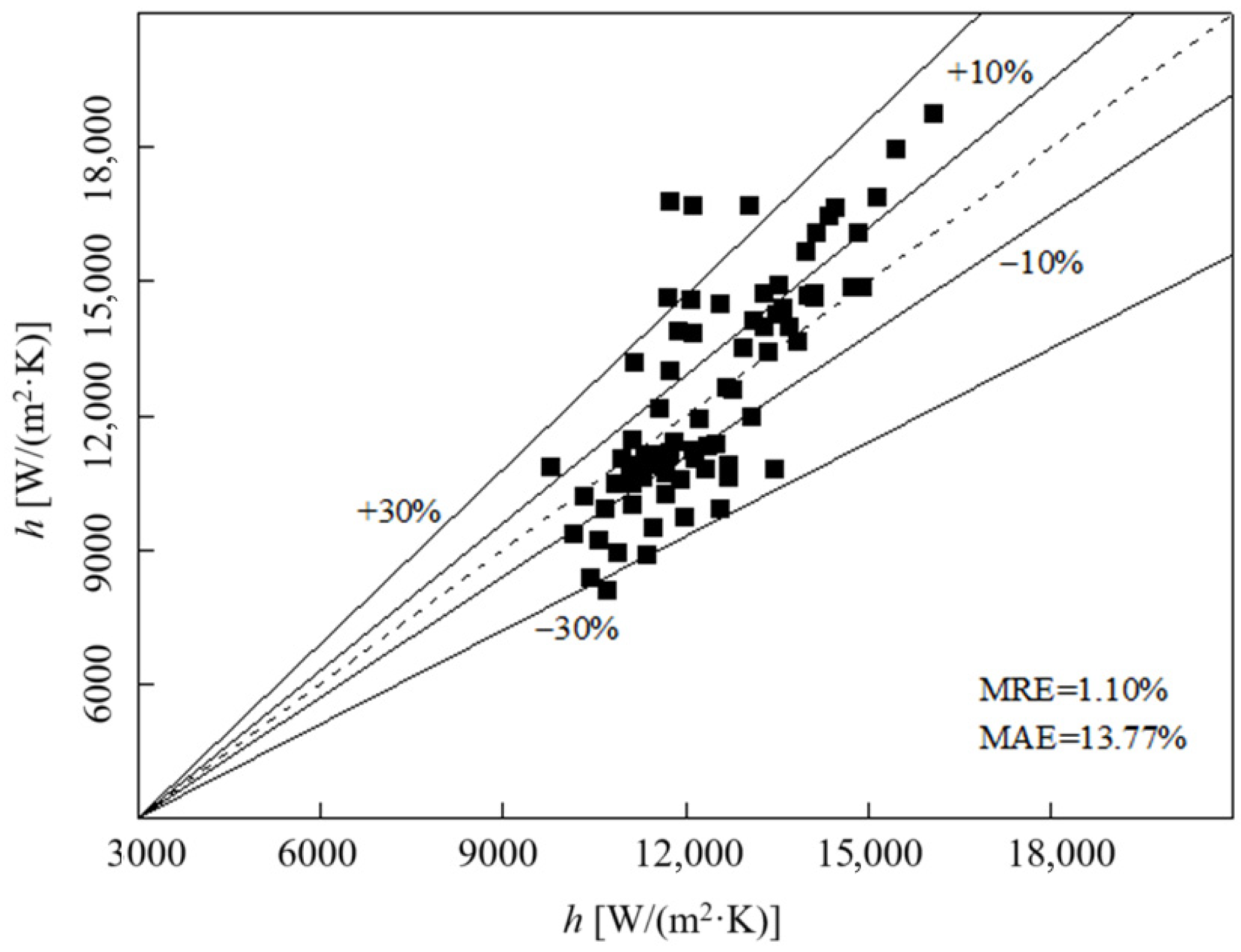
3.3. Research on Modeling of Correlations
4. Conclusions
- (1)
- Observations of the variation in the R32 boiling heat transfer coefficient with mass flow rate across different experimental tubes and saturation temperatures reveal a non-monotonic trend: the average coefficient initially increases and then decreases with rising mass flow rate, irrespective of tube thickness.
- (2)
- Investigations into thermophysical properties such as latent heat, liquid-phase density, gas-phase density, and viscosity at varying saturation temperatures indicate that latent heat, liquid-phase density, and gas-phase viscosity decrease with increasing saturation temperature. Additionally, the effect of flow pattern change may also enhance heat transfer performance.
- (3)
- The average boiling heat transfer coefficients of R32 and R410A refrigerants under different mass flow rates and saturation temperatures are predicted by applying a correlation obtained by experimental statistics. The prediction accuracy is controlled within ±10%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac | Cross-section area, m2 |
| Bo | Boiling number |
| Cp | Specific heat at constant pressure, J/(kg·K) |
| d | Diameter, m |
| Gr | Grashof number |
| h | Heat transfer coefficient, W/(m2·K) |
| L | Tube length, m |
| Pr | Prandtl number |
| q | Mass flow rate, kg/h |
| Q | Heat exchange rate, W |
| Re | Reynolds number |
| T | Temperature, K |
| ΔT | Temperature difference, K |
| u | Velocity, m/s |
| Greek symbols | |
| ρ | Density, kg/m3 |
| λ | Thermal conductivity, W/(mK) |
| Φf | Two-phase friction multiplier |
| μ | Fluid viscosity, Pa·s |
| μwall | Fluid viscosity at wall temperature, Pa·s |
| Subscripts | |
| i | Inlet |
| l | Liquid |
| o | Outlet |
| m | Mean |
| max | Maximum |
| min | Minimum |
| nb | Nucleate boiling |
| r | Refrigerants |
| t | Turbulent |
| w | Water |
References
- Strickland, N.M.; Wimbush, S.C.; Pantoja, A.; Pooke, D.M.; Fee, M.; Chamritskii, V.; Hartwig, Z.; Cheng, J.; Garberg, S.; Sorbom, B. Extended-Performance “SuperCurrent” Cryogen-Free Transport Critical-Current Measurement System. IEEE Trans. Appl. Supercond. 2021, 31, 9000305. [Google Scholar] [CrossRef]
- Oh, S.W.; Denisov, A.O.; Chen, P.; Petta, J.R. Cryogen-free scanning gate microscope for the characterization of Si0.7Ge0.3 quantum devices at milli-Kelvin temperatures. AIP Adv. 2021, 11, 125–130. [Google Scholar] [CrossRef]
- Janta, P.; Pinyo, D.; Yodta, Y.; Vasasiri, P.; Weidenbach, M.; Pursch, M.; Yang, X.G.; Kulsing, C. A multi-location peak parking approach for calculation of second dimensional retention indices for improved volatile compound identification with cryogen-free comprehensive heart-cut two-dimensional gas chromatography. Anal. Methods 2021, 13, 124–132. [Google Scholar] [CrossRef] [PubMed]
- Kryukov, E.; Owczarkowski, M.; Phillipps, D.; Linde, A.J.P.; Burgess, S.; Good, J. A new method to measure the temporal magnetic field instabilities in cryogen-free magnets for magnetic resonance. Solid State Nucl. Magn. Reson. 2021, 113, 101–107. [Google Scholar] [CrossRef]
- Yan, J.; Yao, J.; Shvarts, V.; Du, R.R.; Lin, X. Cryogen-free one hundred microkelvin refrigerator. Rev. Sci. Instrum. 2021, 92, 110–120. [Google Scholar] [CrossRef]
- Chaudhary, S.; Panda, J.J.; Mundlia, S.; Mathimalar, S.; Ahmedof, A.; Raman, K.V. A low noise cryogen-free scanning tunneling microscope–superconducting magnet system with vacuum sample transfer. Rev. Sci. Instrum. 2021, 92, 23–90. [Google Scholar] [CrossRef]
- Tian, J.; Chen, B.; Li, D. Light transmittance dynamics and spectral absorption characteristics during auxiliary cryogen spray cooling in laser dermatology. Lasers Med. Sci. 2022, 37, 2079–2086. [Google Scholar] [CrossRef]
- Li, Y.; Roell, S. Key designs of a short-bore and cryogen-free high temperature superconducting magnet system for 14 T whole-body MRI. Supercond. Sci. Technol. 2021, 34, 125–135. [Google Scholar] [CrossRef]
- Leveratto, A.; Armenio, A.A.; Traverso, A.; De Marzi, G.; Celentano, G.; Malagoli, A. Transport current and magnetization of Bi-2212 wires above liquid Helium temperature for cryogen-free applications. Sci. Rep. 2021, 11, 11660. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Jiang, Y.; Bai, L.; Yang, X.; Zhao, Y. Optimization of a Cryogen-Free Superconducting Prototype Generator with YBCO Field Windings. IEEE Trans. Appl. Supercond. 2021, 31, 5206905. [Google Scholar] [CrossRef]
- Awaji, S.; Badel, A.; Okada, T.; Takahashi, K.; Miyazaki, H.; Hanai, S.; Ioka, S.; Fujita, S.; Muto, S.; Iijima, Y.; et al. Robust REBCO insert coil for upgrade of 25 T cryogen-free superconducting magnet. IEEE Trans. Appl. Supercond. 2021, 31, 4300105. [Google Scholar] [CrossRef]
- Jang, J.Y.; Kim, M.S.; Hwang, Y.J.; Song, S.; Choi, Y.; Choi, Y.S. Development of a Cryogen-Free Compact 3 T Superconducting Magnet for an Electromagnetic Property Measurement System. Appl. Sci. 2021, 11, 3074. [Google Scholar] [CrossRef]
- Wu, W.; Li, D.; Chen, B.; Wang, G. A new mathematical model for accurate quantification of cryogen spray cooling in cutaneous laser surgery using realistic boundary conditions. Lasers Med. Sci. 2021, 36, 1609–1617. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, A.; Kochher, G. Potential of supercritical nitrogen to be used as cryogen for superconducting applications. Mater. Today Proc. 2021, 47, 4345–4349. [Google Scholar] [CrossRef]
- Bahce, E.; Sarigul, E. An investigation of the effects of cryogen application direction on Ti6Al4V alloy milling. J. Adv. Manuf. Eng. 2021, 2, 42–48. [Google Scholar]
- Coe, A.; Li, G.; Andrei, E. Scanning Probe Microscopy Combined with Low Temperature Cryogen-free Operation in an Ultra-High Vacuum High Field Environment. Bull. Am. Phys. Soc. 2022, 56, 96–110. [Google Scholar]
- Majoros, M.; Sumption, M.D.; Parizh, M.; Wan, F.; Rindfleisch, M.A.; Doll, D.; Tomsic, M.; Collings, E.W. Magnetic, mechanical and thermal modeling of superconducting, whole-body, actively shielded, 3 T MRI magnets wound using MgB2 strands for liquid cryogen free operation. IEEE Trans. Appl. Supercond. 2022, 36, 126–130. [Google Scholar] [CrossRef]
- Coe, A.; Li, G.; Andrei, E. Cryogen-free Ultra-High Vacuum Low Temperature High Field Proximal Probe System for the Exploration of Low Dimensional Materials. Bull. Am. Phys. Soc. 2021, 66, 30–50. [Google Scholar]
- Low, D.; Ferguson, G.M.; Jarjour, A.; Schaefer, B.T.; Bachmann, M.D.; Moll, P.J.; Nowack, K.C. Scanning SQUID microscopy in a cryogen-free dilution refrigerator. Rev. Sci. Instrum. 2021, 92, 083704. [Google Scholar] [CrossRef]
- Can, M.; Koluaçik, S.; Bahçe, E.; Gokce, H.; Tecellioglu, F.S. Investigation of thermal damage in bone drilling: Hybrid processing method and pathological evaluation of existing methods. J. Mech. Behav. Biomed. Mater. 2022, 126, 105–130. [Google Scholar] [CrossRef]
- Low, D.; Ferguson, G.M.; Jarjour, A.; Schaefer, B.T.; Nowack, K.C. Design files for a scanning superconducting quantum interference device operated in a cryogen-free dilution refrigerator. Zenodo 2021, 47, 118–120. [Google Scholar]
- Alajlan, A. Crescent-Shaped Hyperpigmentation Following Laser Hair Removal: Case Series of Fifteen Patients. Lasers Surg. Med. 2021, 53, 333–336. [Google Scholar] [CrossRef]
- Chen, J.C. Correlation for boiling heat transfer to saturated fluids in convective flow. Ind. Eng. Chem. Process Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef]
- Choi, K.I.; Pamitran, A.S.; Oh, J.T.; Saito, K. Pressure drop and heat transfer during two-phase flow vaporization of propane in horizontal smooth minichannels. Int. J. Refrig. 2009, 32, 837–845. [Google Scholar] [CrossRef]
- Gungor, K.E.; Winterton, R.H.S. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
- Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat Mass Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
- Pamitran, A.S.; Choi, K.I.; Oh, J.T.; Park, K.W. Two-phase flow heat transfer of propane vaporization in horizontal minichannels. J. Mech. Sci. Technol. 2009, 23, 599–606. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Elsaid, K.; Sayed, E.T.; Abdelkareem, M.A.; Wilberforce, T.; Ramadan, M.; Olabi, A.G. Intensification of heat exchanger performance utilizing nanofluids. Int. J. Thermofluids 2021, 10, 100–117. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Rovira, M.; Duwig, C. Design analysis of the “Schwartz D” based heat exchanger: A numerical study. Int. J. Heat Mass Transf. 2021, 177, 121–141. [Google Scholar] [CrossRef]
- Chupradit, S.; Jalil, A.T.; Enina, Y.; Neganov, D.A.; Alhassan, M.S.; Aravindhan, S.; Davarpanah, A. Use of Organic and Copper-Based Nanoparticles on the Turbulator Installment in a Shell Tube Heat Exchanger: A CFD-Based Simulation Approach by Using Nanofluids. J. Nanomater. 2021, 20, 96–110. [Google Scholar] [CrossRef]
- Cai, W.; Wang, F.; Chen, S.; Chen, C.; Liu, J.; Deng, J.; Kolditz, O.; Shao, H. Analysis of heat extraction performance and long-term sustainability for multiple deep borehole heat exchanger array: A project-based study. Appl. Energy 2021, 289, 116–120. [Google Scholar] [CrossRef]
- Safari, V.; Abolghasemi, H.; Kamkari, B. Experimental and numerical investigations of thermal performance enhancement in a latent heat storage heat exchanger using bifurcated and straight fins. Renew. Energy 2021, 174, 102–121. [Google Scholar] [CrossRef]
- Cooper, M.G. Heat flow rates in saturated nucleate pool boiling-a wide-ranging examination using reduced properties. Adv. Heat Transf. 1984, 16, 157–239. [Google Scholar]
- Chu, W.; Yan, G.; Zhang, H.; Zhao, F.; Wang, Q.; Wang, Q. A review on experimental investigations of refrigerant/oil mixture flow boiling in horizontal channels. Appl. Therm. Eng. 2021, 196, 117270. [Google Scholar] [CrossRef]
- Zhang, W.; Hibiki, T.; Mishima, K. Correlation for flow boiling heat transfer in mini-channels. Int. J. Heat Mass Transf. 2004, 47, 5749–5763. [Google Scholar] [CrossRef]
- Fang, X.; Wu, Q.; Yuan, Y. A general correlation for saturated flow boiling heat transfer in channels of various sizes and flow directions. Int. J. Heat Mass Transf. 2017, 107, 972–981. [Google Scholar] [CrossRef]
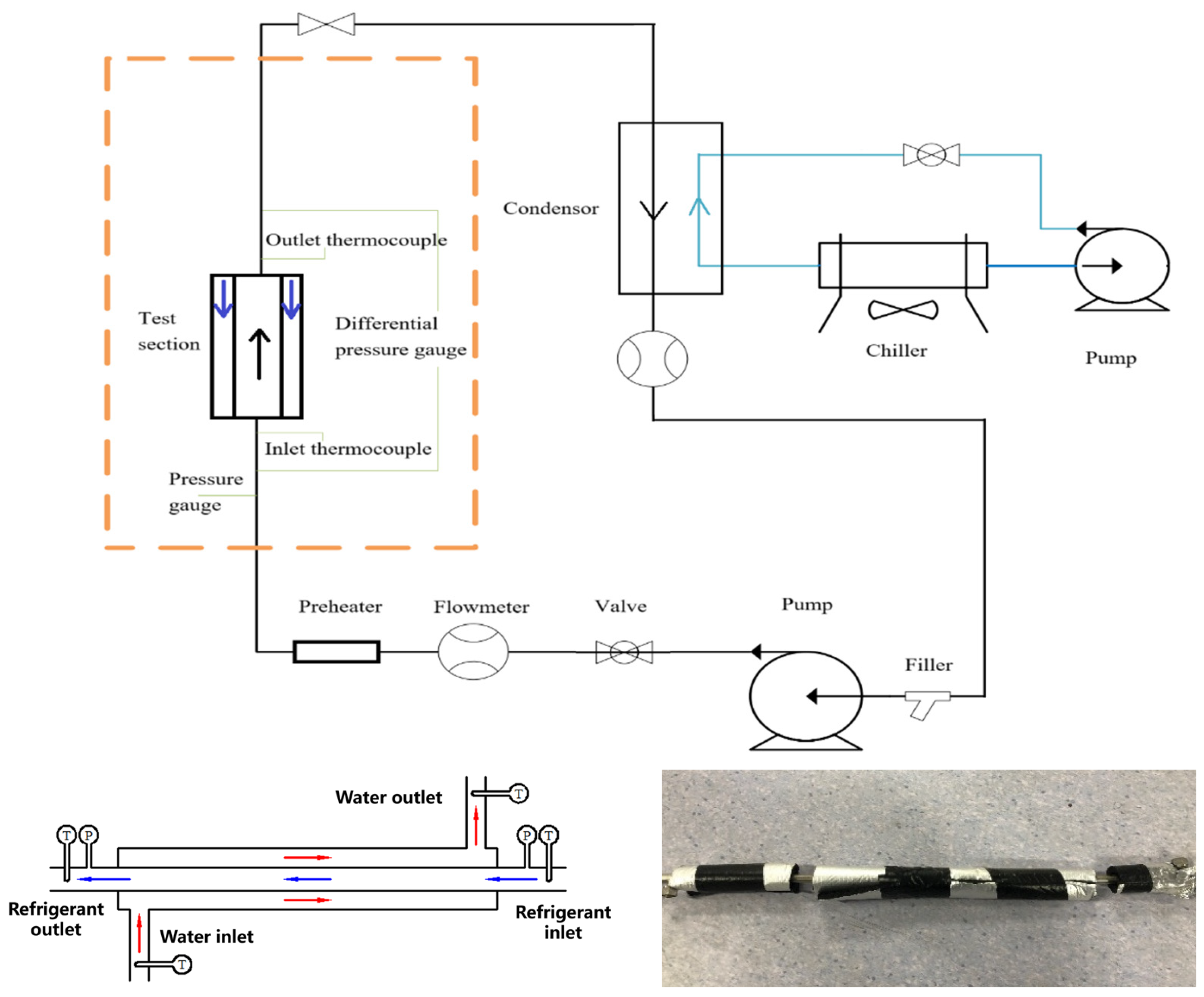


| Type | R22 | R410A | R32 |
|---|---|---|---|
| Boiling point/℃ | −40.8 | −51.5 | −51.7 |
| Critical temperature/℃ | 96 | 72.1 | 78.1 |
| Critical pressure/MPa | 4.99 | 4.93 | 5.81 |
| Flammability | Nonflammable | Nonflammable | Low flammability |
| Toxicity | Nothing | Nothing | Nothing |
| GWP | 1700 | 2100 | 675 |
| ODP | 0.034 | 0 | 0 |
| Molar mass | 86.47 | 72.58 | 52.02 |
| Type | R410A | R32 | Comparison/% |
|---|---|---|---|
| Suction pressure/MPa | 0.998 | 1.018 | +2.0 |
| Exhaust pressure/MPa | 3.385 | 3.472 | +2.6 |
| Pressure difference/MPa | 2.387 | 2.454 | +2.8 |
| Pressure ratio | 3.39 | 3.41 | +0.6 |
| Refrigerating capacity per unit mass (kJ/kg) | 157.41 | 241.04 | +53.1 |
| Inspiratory specific volume | 0.0281 | 0.0389 | +38.4 |
| Refrigerating capacity per unit volume | 5.595 | 6.203 | +10.9 |
| Input power per unit volume | 1822 | 1969 | +8.1 |
| Coefficient of refrigeration | 3.07 | 3.15 | +2.6 |
| Exhaust temperature/°C | 96.4 | 118.4 | +22 |
| Equipment | Type | Range | Accuracy |
|---|---|---|---|
| Flow rates | DMF-1-S3 | 0~400 kg·h−1 | ±0.5% (R) |
| Pressures | Rosemount3051 | 0~6000 kPa | ±0.1% (FS) |
| Thermocouples | T | −200~350 °C | ±0.5 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Zhou, C.; Chu, W.; Luo, Y. Characteristic Analysis of Boiling Heat Transfer of R32 Refrigerant and Modeling Study of Heat Exchanger. Energies 2025, 18, 5258. https://doi.org/10.3390/en18195258
Yu B, Zhou C, Chu W, Luo Y. Characteristic Analysis of Boiling Heat Transfer of R32 Refrigerant and Modeling Study of Heat Exchanger. Energies. 2025; 18(19):5258. https://doi.org/10.3390/en18195258
Chicago/Turabian StyleYu, Bo, Chenjie Zhou, Wenxiao Chu, and Yuye Luo. 2025. "Characteristic Analysis of Boiling Heat Transfer of R32 Refrigerant and Modeling Study of Heat Exchanger" Energies 18, no. 19: 5258. https://doi.org/10.3390/en18195258
APA StyleYu, B., Zhou, C., Chu, W., & Luo, Y. (2025). Characteristic Analysis of Boiling Heat Transfer of R32 Refrigerant and Modeling Study of Heat Exchanger. Energies, 18(19), 5258. https://doi.org/10.3390/en18195258







