Trailing-Edge Noise and Amplitude Modulation Under Yaw-Induced Partial Wake: A Curl–UVLM Analysis with Atmospheric Stability Effects
Abstract
1. Introduction
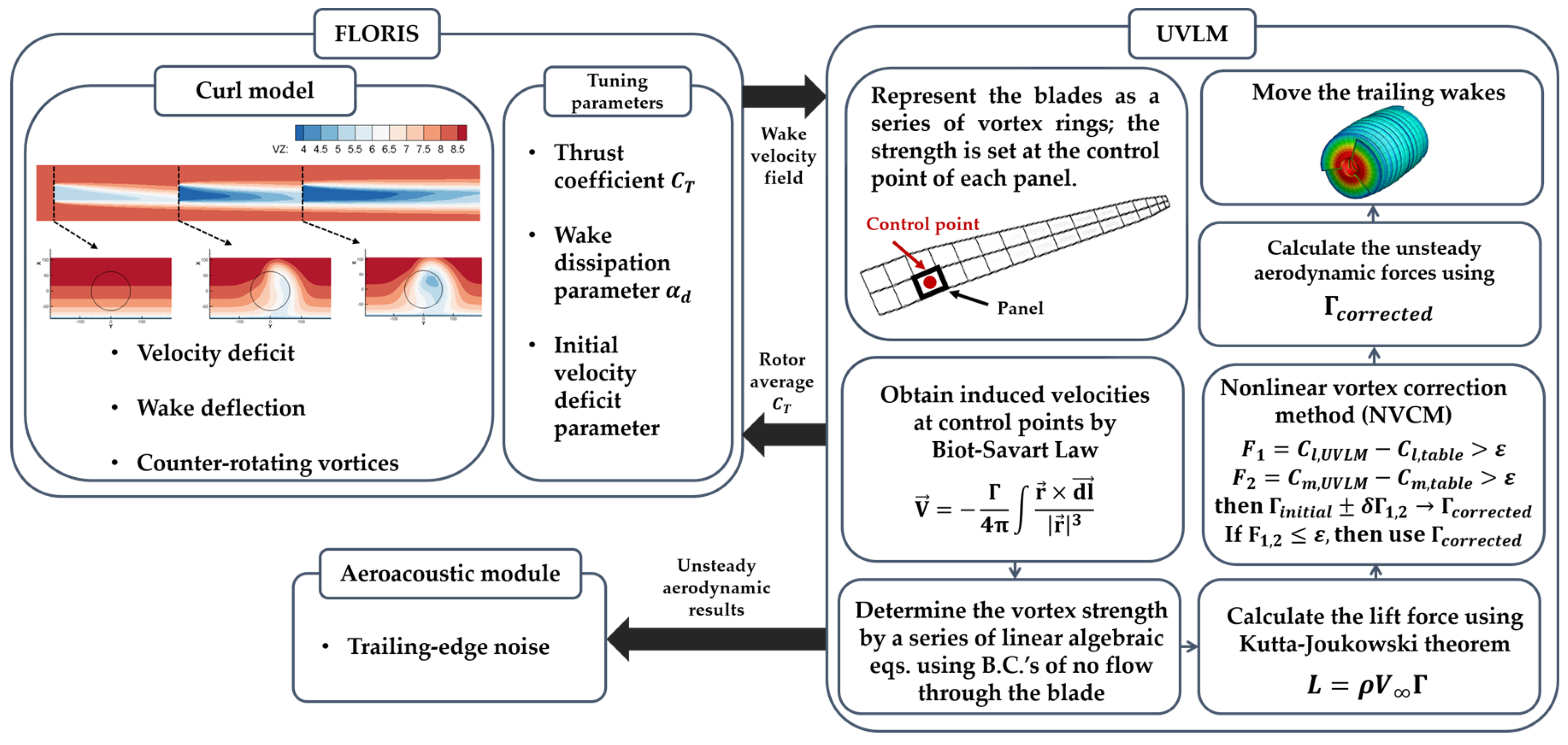
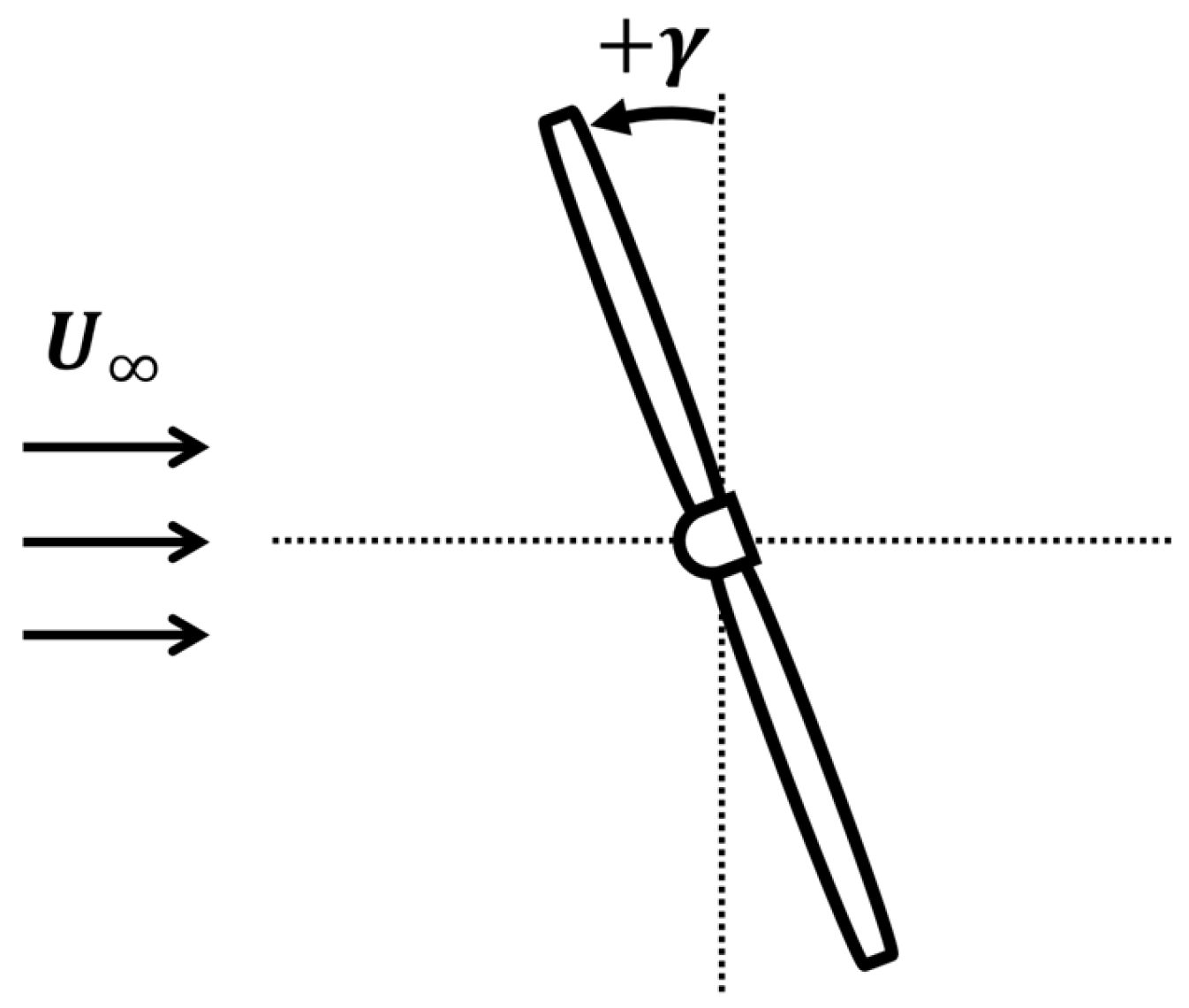
2. Methodology
2.1. Curl Wake Model
2.2. Unsteady Vortex Lattice Method (UVLM)
2.3. Semi-Empirical Formulation for Trailing-Edge Noise
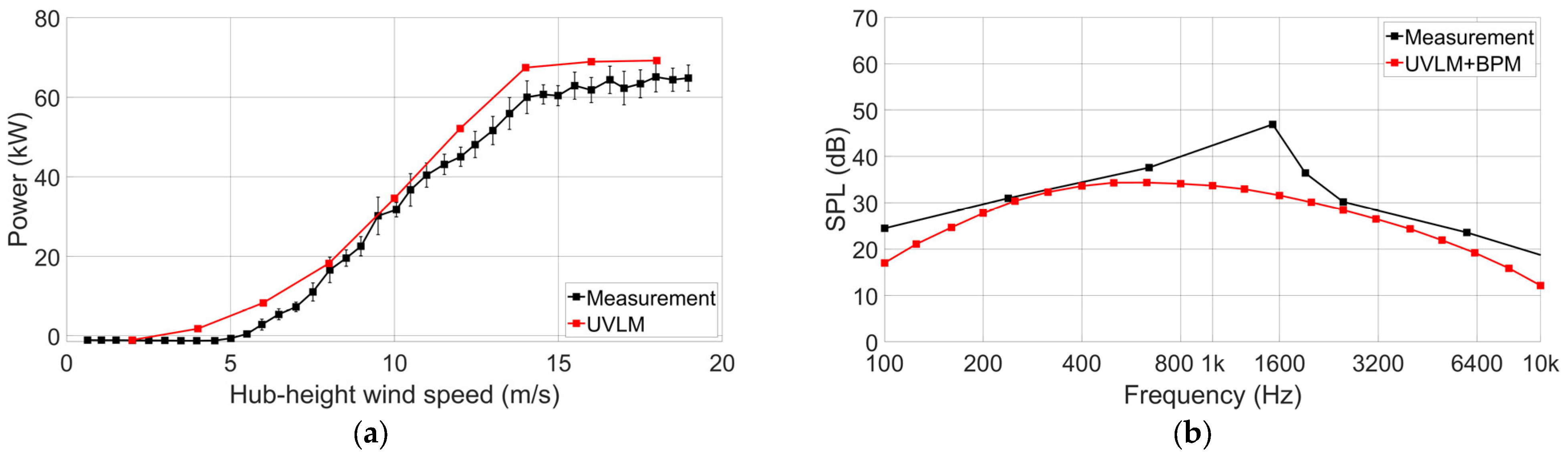
Validation of Trailing-Edge Noise Prediction
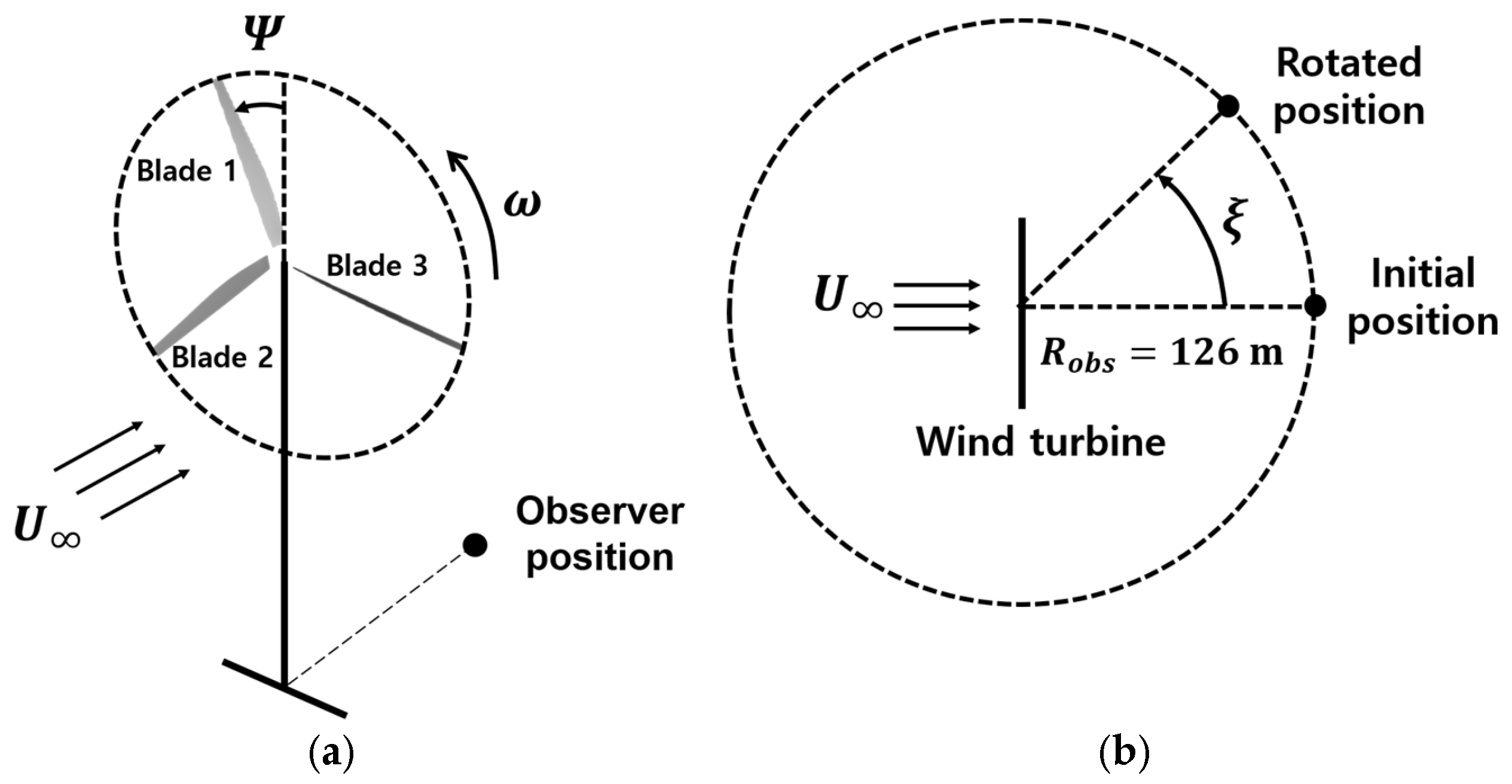
3. Simulation Setup
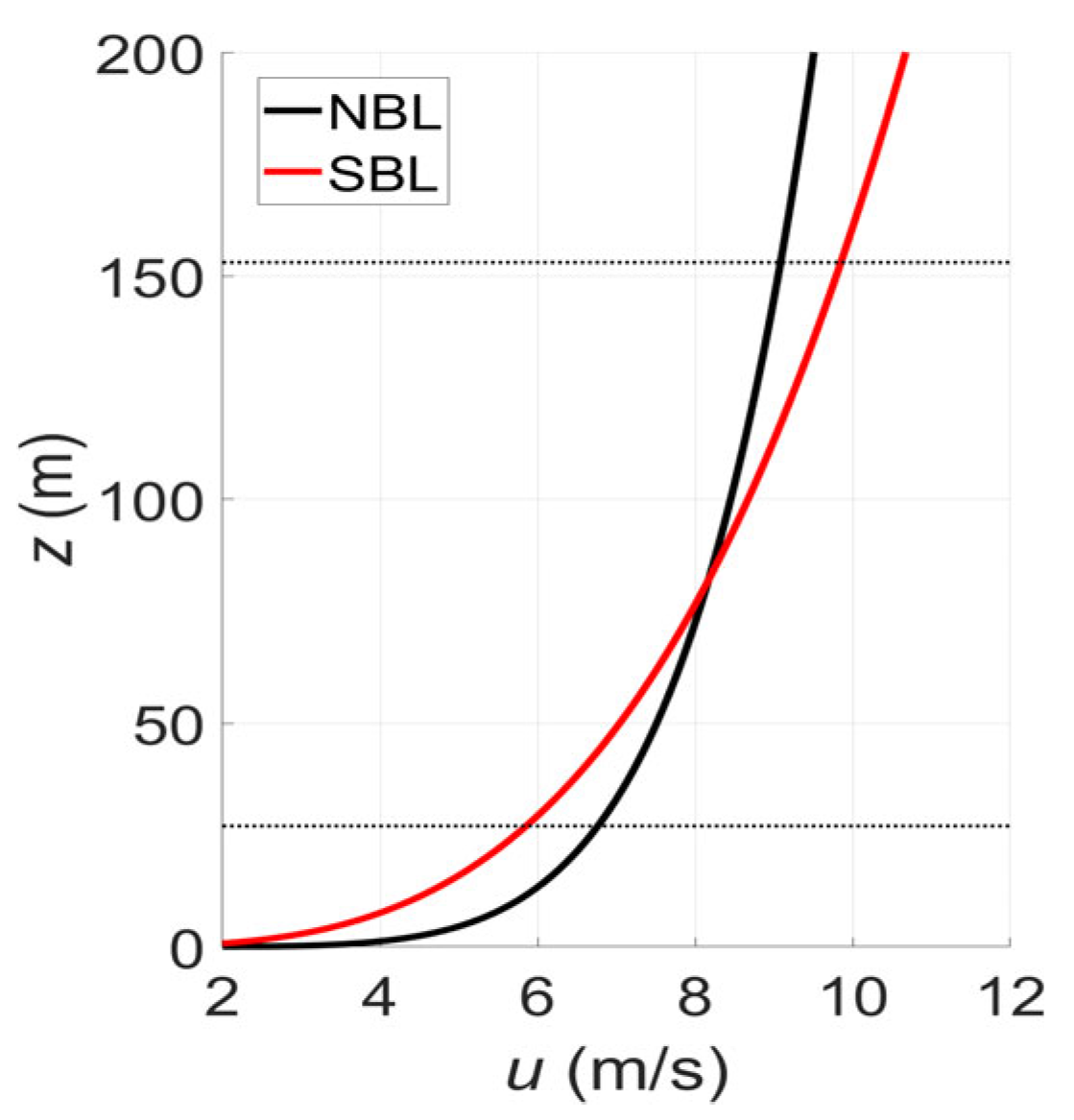
3.1. Atmospheric Boundary Layer
3.2. Wind Turbine Model
3.3. Observer Points for Noise Analysis
4. Results and Discussion
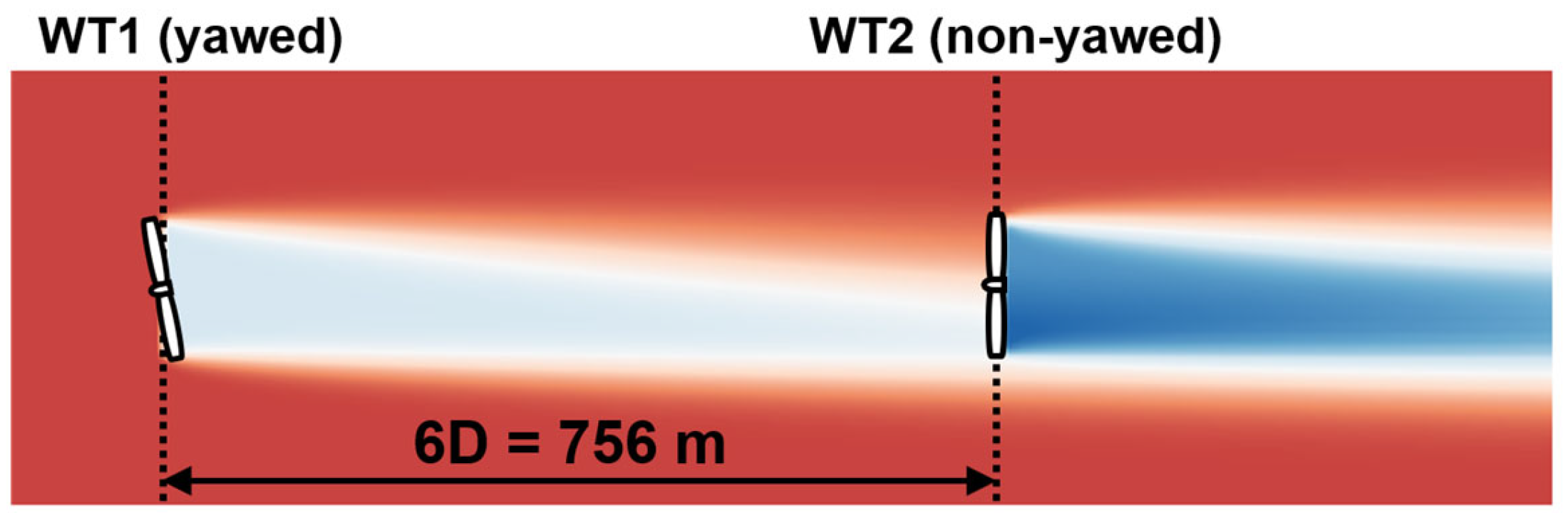
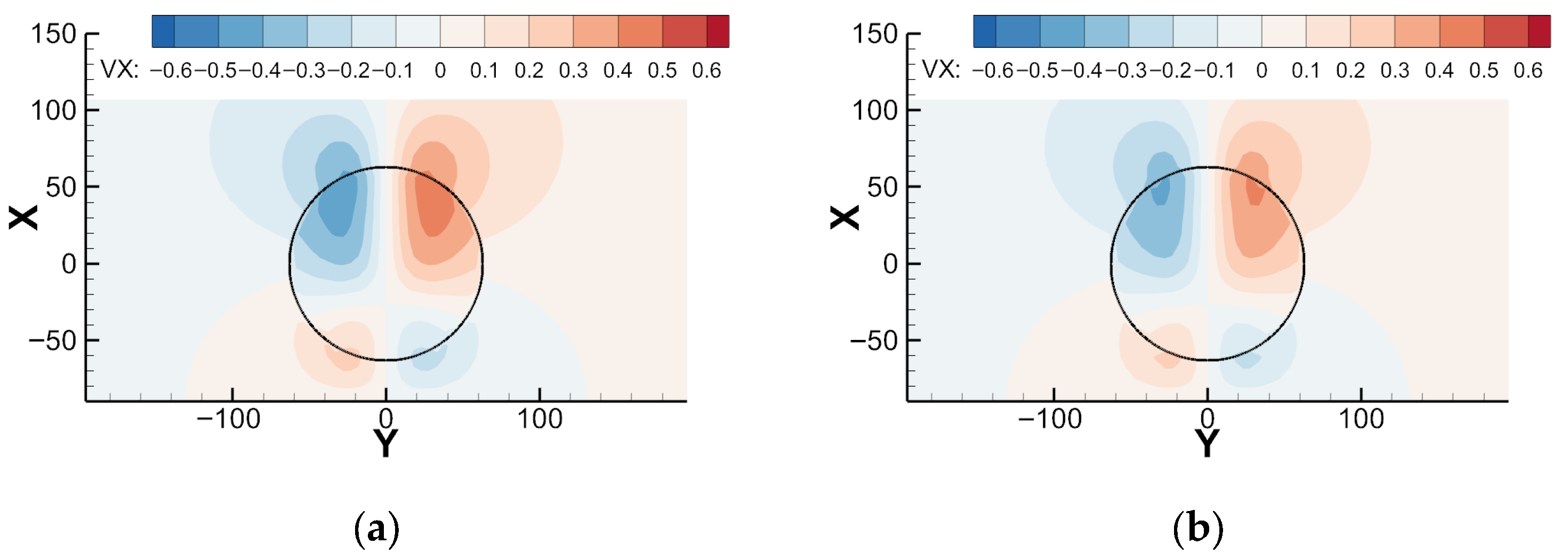
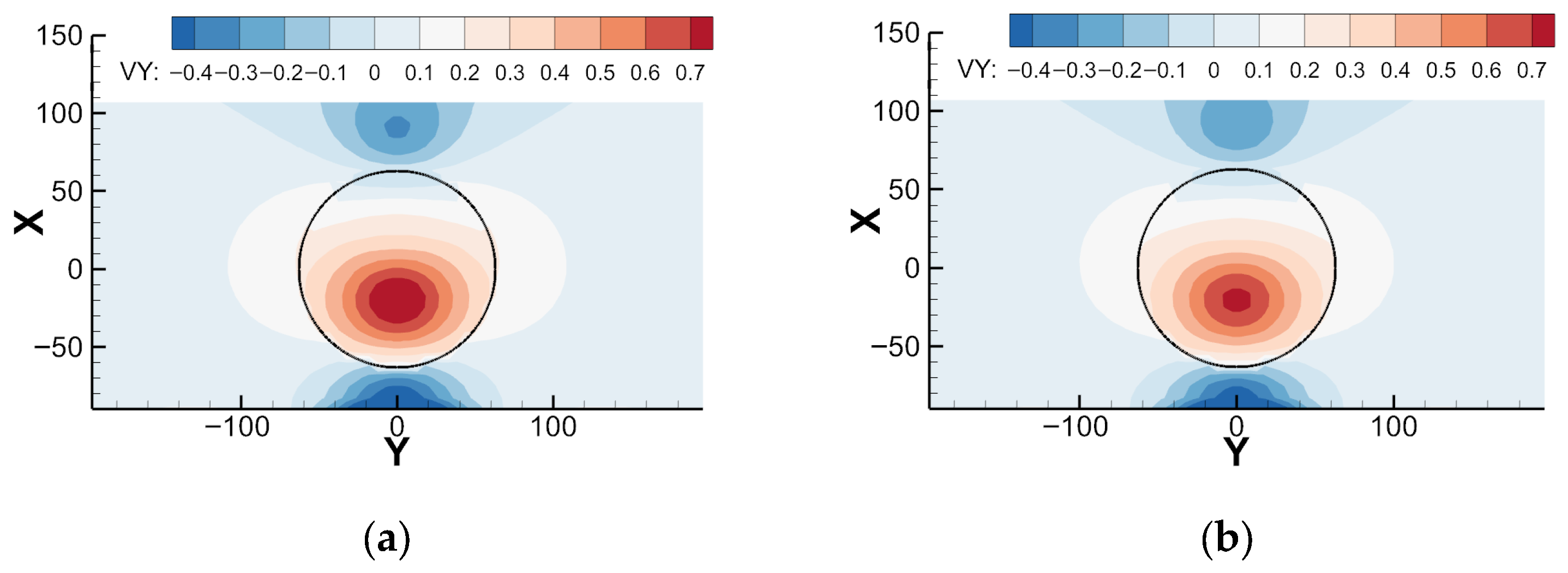
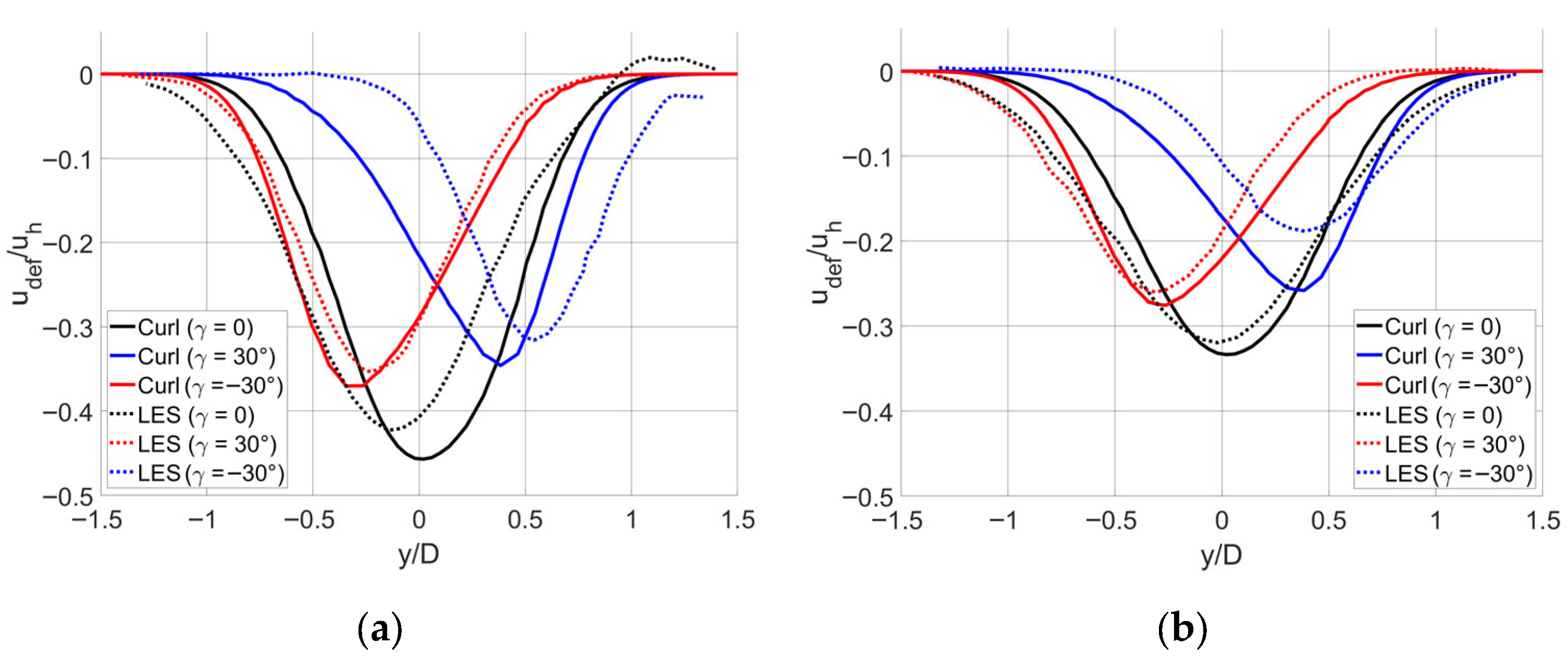
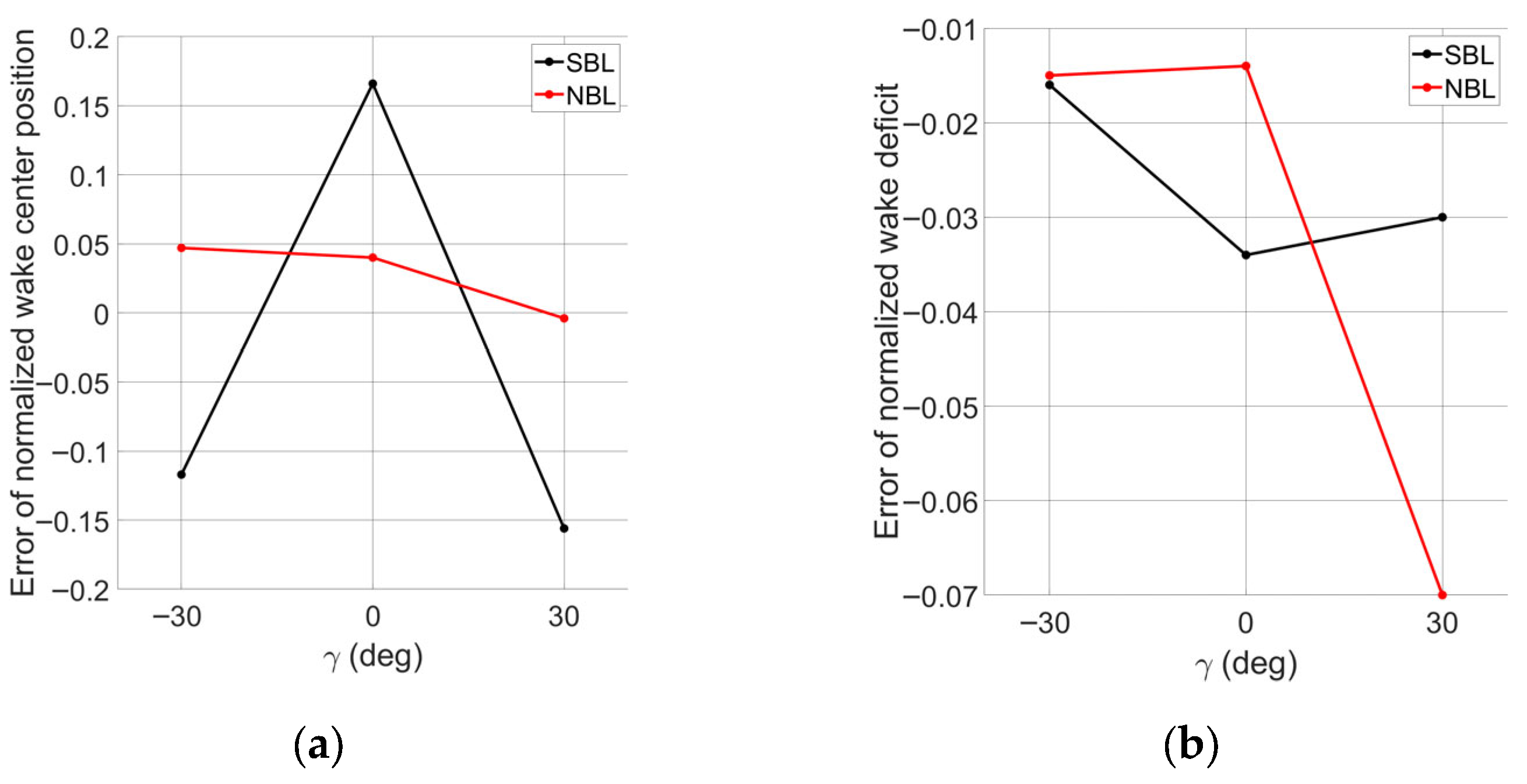
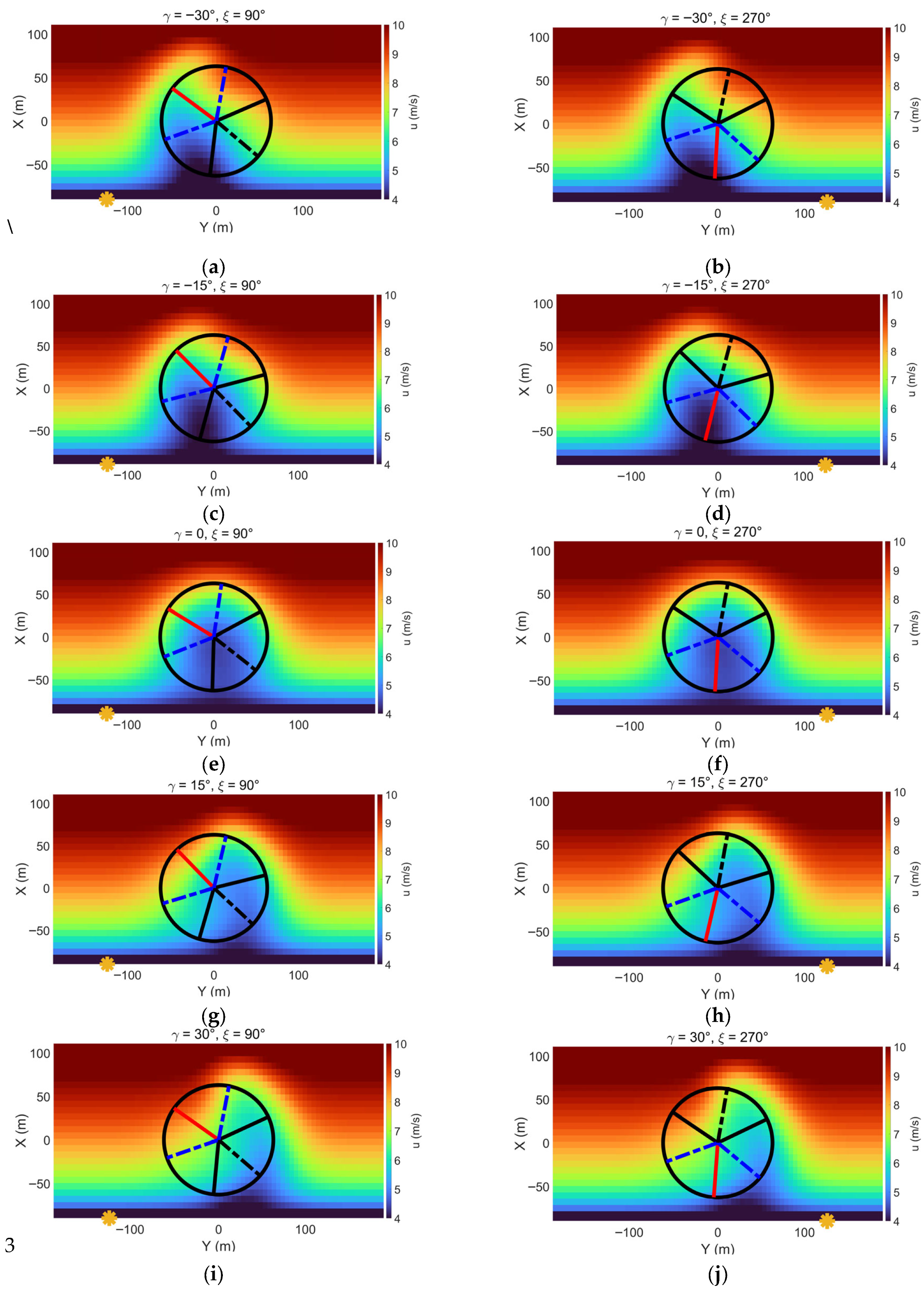
4.1. Wake Prediction with LES-Fitted Curl Model
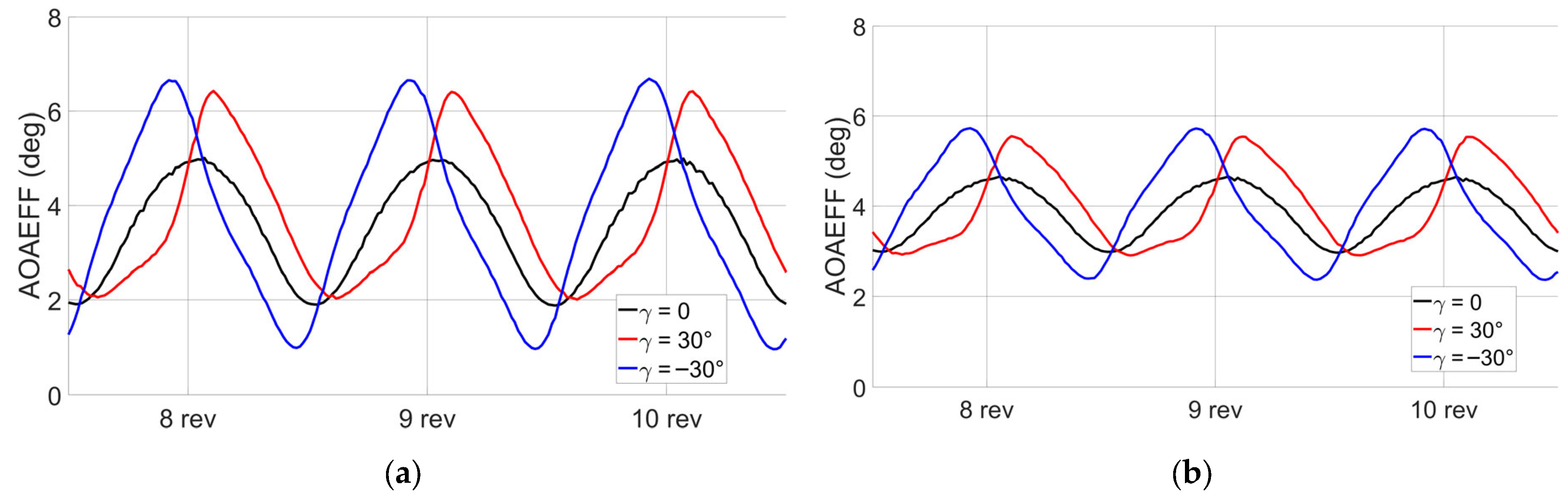
4.2. Average Power and Variation of Effective Angle of Attack
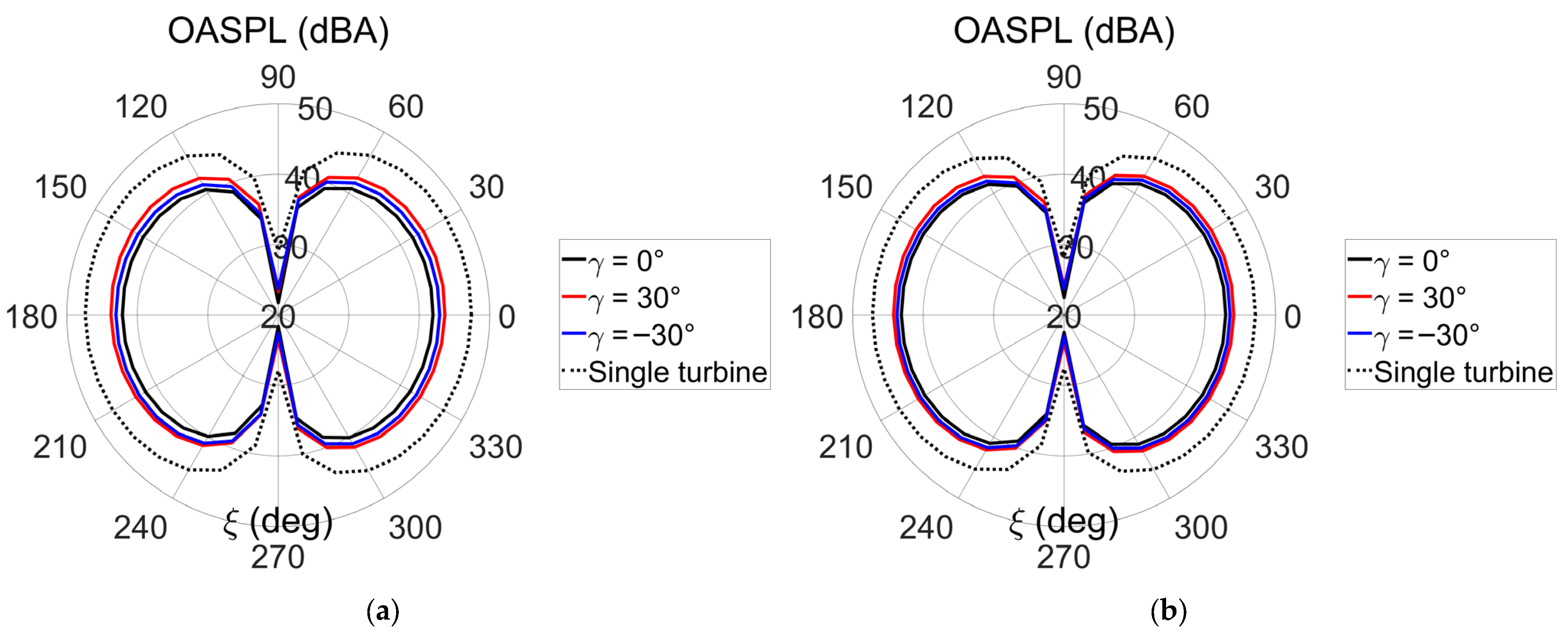
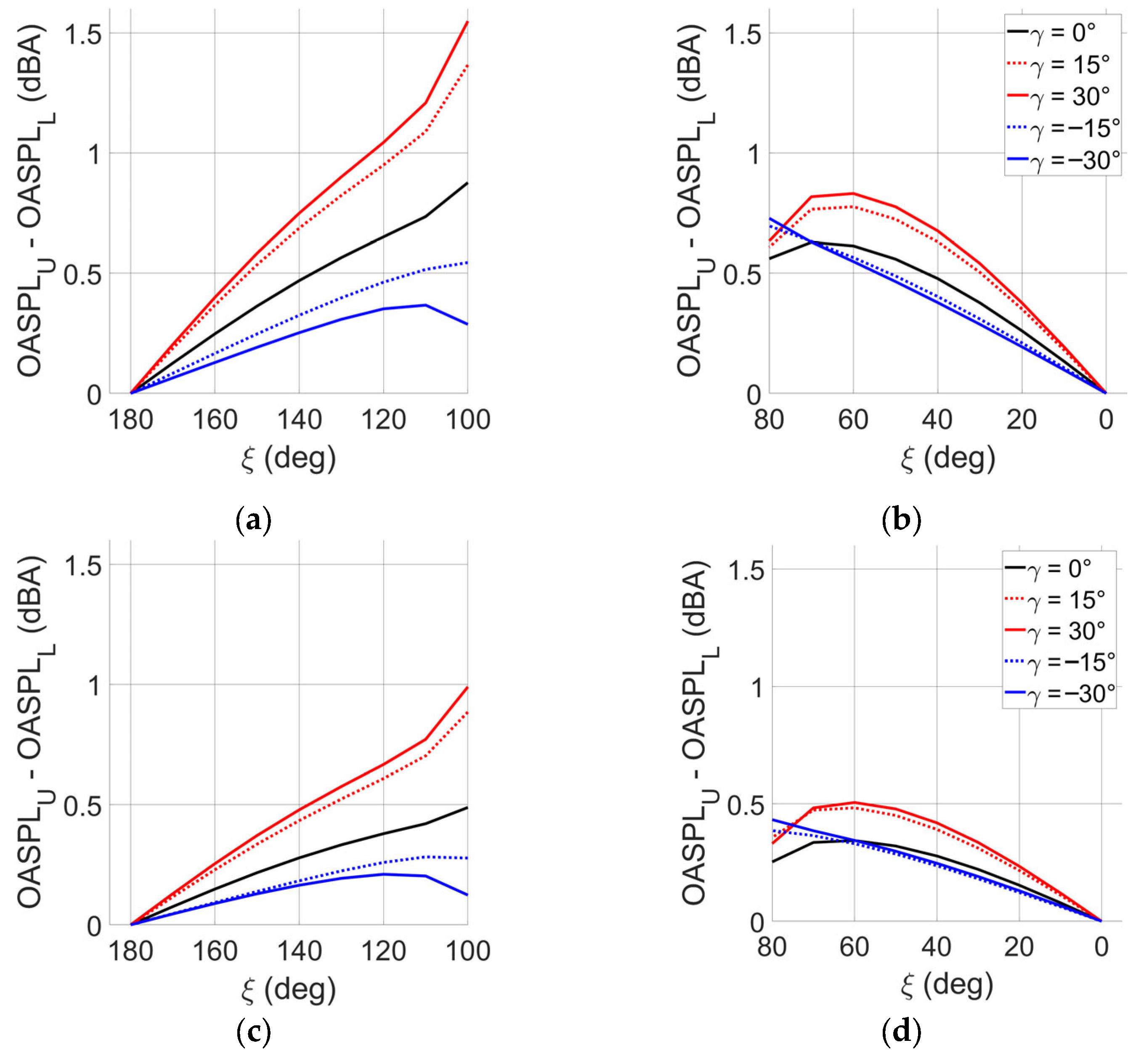
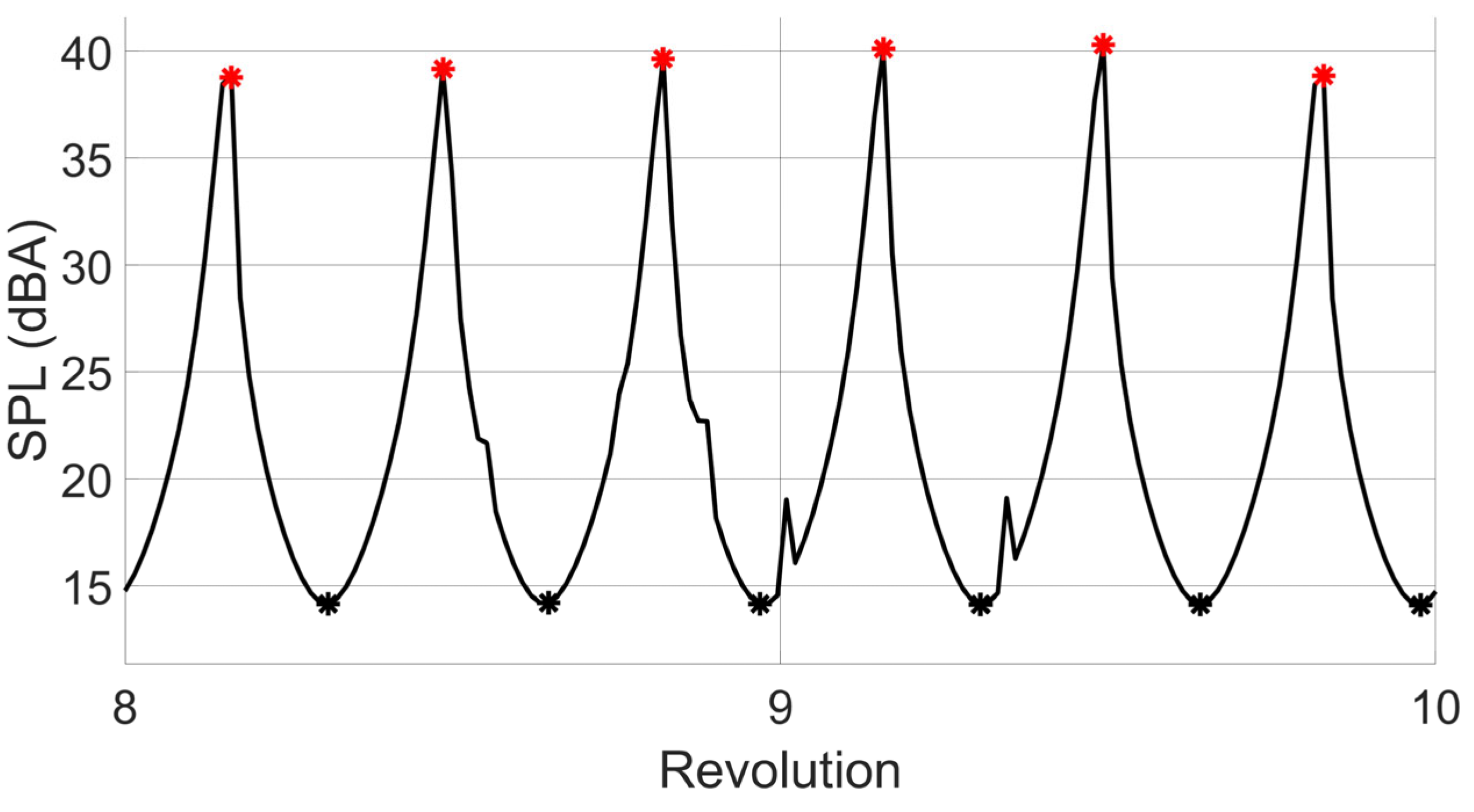
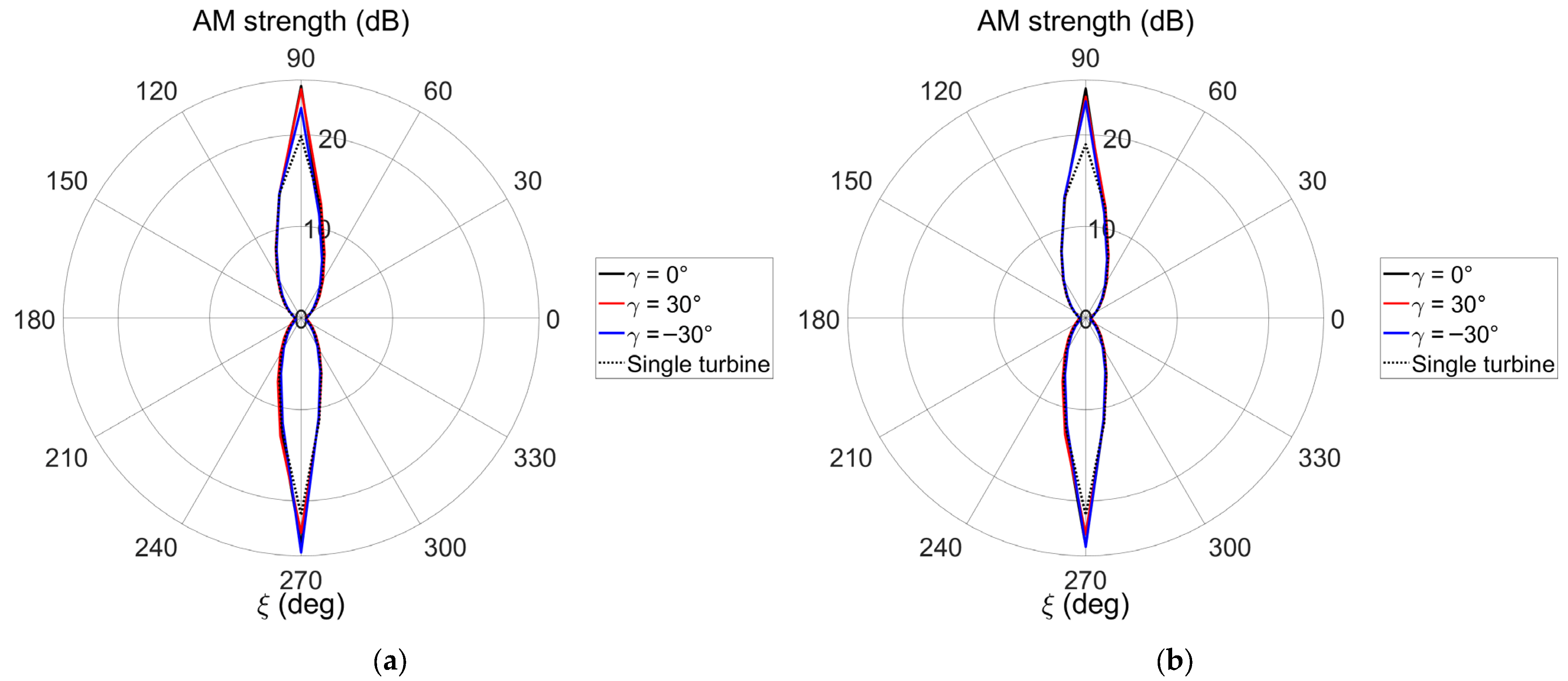
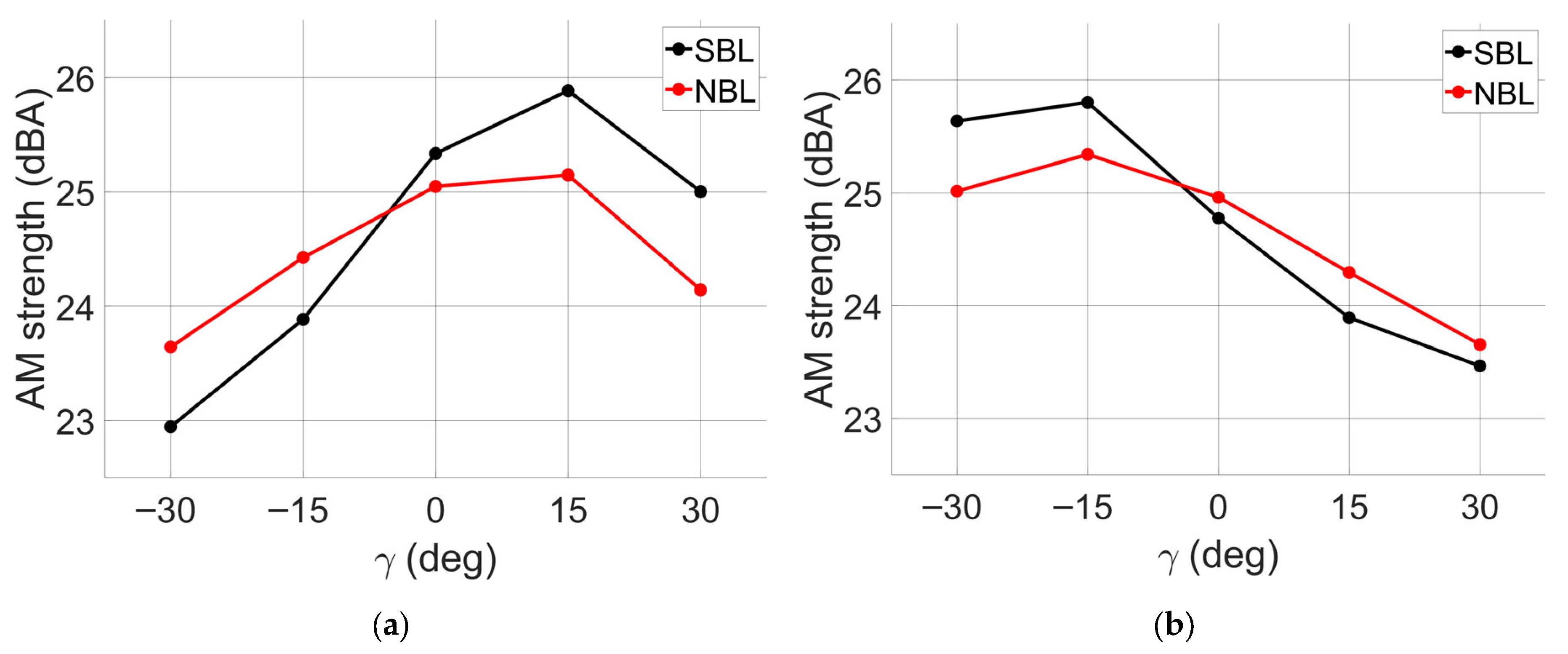
4.3. Overall Sound Pressure Level and Amplitude Modulation of Trailing-Edge Noise
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Amplitude modulation |
| AOAEFF | Effective angle of attack |
| CRV | Counter-rotating vortex |
| D | Rotor diameter |
| High frequency directivity function | |
| Low frequency directivity function | |
| Added turbulence | |
| Amplitude functions | |
| Length of span | |
| LES | Large eddy simulation |
| Freestream Mach number | |
| Mach number of the flow past the trailing edge | |
| NBL | Neutral atmospheric boundary layer |
| OASPL | Overall sound pressure level |
| OASPLU | Overall sound pressure level at the upper semicircle in noise directivity plot |
| OASPLL | Overall sound pressure level at the lower semicircle in noise directivity plot |
| Radial position | |
| Retarded observer distance | |
| Rotor radius | |
| Distance between wind turbine and observing point | |
| SBL | Stable atmospheric boundary layer |
| SPL | Sound pressure level |
| Strouhal number | |
| Ambient turbulent intensity | |
| Streamwise perturbation velocity | |
| Wake deficit | |
| Hub height wind velocity | |
| Upstream turbine hub height freestream velocity | |
| Streamwise velocity components base flow | |
| Spanwise perturbation velocity | |
| Spanwise velocity components base flow | |
| Vertical perturbation velocity | |
| Vertical velocity components base flow | |
| WT | Wind turbine |
| Dissipation scaling parameter | |
| Shear coefficient | |
| Threshold angle of attack | |
| Yaw misalignment angle | |
| Peak of the amplitude function | |
| Vortex strength | |
| Boundary layer displacement thickness | |
| Chordwise angle | |
| Kármán constant | |
| Mixing length | |
| Effective viscosity | |
| Observer position angle | |
| Initial vortex core radius | |
| Spanwise angle | |
| Rotor azimuthal angle | |
| Angular velocity | |
| Subscript | |
| Pressure side component | |
| Suction side component | |
| Angle of attack component | |
References
- Annoni, J.; Gebraad, P.M.O.; Scholbrock, A.K.; Fleming, P.A.; Wingerden, J.-W. van. Analysis of Axial-Induction-Based Wind Plant Control Using an Engineering and a High-Order Wind Plant Model. Wind Energy 2015, 19, 1135–1150. [Google Scholar] [CrossRef]
- Howland, M.F.; Lele, S.K.; Dabiri, J.O. Wind Farm Power Optimization through Wake Steering. Proc. Natl. Acad. Sci. USA 2019, 116, 14495–14500. [Google Scholar] [CrossRef]
- Fleming, P.; Annoni, J.; Shah, J.J.; Wang, L.; Ananthan, S.; Zhang, Z.; Hutchings, K.; Wang, P.; Chen, W.; Chen, L. Field Test of Wake Steering at an Offshore Wind Farm. Wind Energy Sci. 2017, 2, 229–239. [Google Scholar] [CrossRef]
- Fleming, P.; King, J.; Dykes, K.; Simley, E.; Roadman, J.; Scholbrock, A.; Murphy, P.; Lundquist, J.K.; Moriarty, P.; Fleming, K.; et al. Initial Results from a Field Campaign of Wake Steering Applied at a Commercial Wind Farm—Part 1. Wind Energy Sci. 2019, 4, 273–285. [Google Scholar] [CrossRef]
- Fleming, P.; King, J.; Simley, E.; Roadman, J.; Scholbrock, A.; Murphy, P.; Lundquist, J.K.; Moriarty, P.; Fleming, K.; van Dam, J.; et al. Continued Results from a Field Campaign of Wake Steering Applied at a Commercial Wind Farm—Part 2. Wind Energy Sci. 2020, 5, 945–958. [Google Scholar] [CrossRef]
- Wei, D.; Wang, N.; Wan, D.; Strijhak, S. Parametric Study of the Effectiveness of Active Yaw Control Based on Large Eddy Simulation. Ocean Eng. 2023, 271, 113751. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of the Coriolis Force on the Structure and Evolution of Wind Turbine Wakes. Phys. Rev. Fluids 2016, 1, 063701. [Google Scholar] [CrossRef]
- Shibuya, K.; Uchida, T. Wake Asymmetry of Yaw State Wind Turbines Induced by Interference with Wind Towers. Energy 2023, 280, 128091. [Google Scholar] [CrossRef]
- Fleming, P.; Annoni, J.; Churchfield, M.; Martinez-Tossas, L.A.; Gruchalla, K.; Lawson, M.; Moriarty, P. A Simulation Study Demonstrating the Importance of Large-Scale Trailing Vortices in Wake Steering. Wind Energy Sci. 2018, 3, 243–255. [Google Scholar] [CrossRef]
- Thedin, R.; Barter, G.; Jonkman, J.; Mudafort, R.; Bay, C.J.; Shaler, K.; Kreeft, J. Load Assessment of a Wind Farm Considering Negative and Positive Yaw Misalignment for Wake Steering. Wind Energy Sci. 2025, 10, 1033–1053. [Google Scholar] [CrossRef]
- Wei, D.; Wang, N.; Wan, D.; Strijhak, S. Numerical Study on the Asymmetry in Wake Steering of Wind Turbine Under Yawed Conditions. In Proceedings of the 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 5–10 June 2022. [Google Scholar]
- Han, W.; Kim, H.; Son, E.; Lee, S. Assessment of Yaw-Control Effects on Wind Turbine-Wake Interaction: A Coupled Unsteady Vortex Lattice Method and Curled Wake Model Analysis. J. Wind Eng. Ind. Aerodyn. 2023, 242, 105559. [Google Scholar] [CrossRef]
- Oerlemans, S.; Fisher, M.; Maeder, T.; Kögler, K. Reduction of Wind Turbine Noise Using Optimized Airfoils and Trailing-Edge Serrations. AIAA J. 2009, 47, 1470–1481. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.; Choi, W.; Lee, S. Annoyance Caused by Amplitude Modulation of Wind Turbine Noise. Noise Control Eng. J. 2011, 59, 38. [Google Scholar] [CrossRef]
- Hansen, K.L.; Nguyen, P.; Micic, G.; Lechat, B.; Catcheside, P.; Zajamšek, B. Amplitude Modulated Wind Farm Noise Relationship with Annoyance: A Year-Long Field Study. J. Acoust. Soc. Am. J. Acoust. Soc. Am. 2021, 150, 1198–1208. [Google Scholar] [CrossRef]
- Nguyen, P.D.; Hansen, K.L.; Catcheside, P.; Hansen, C.H.; Zajamsek, B. Long-Term Quantification and Characterisation of Wind Farm Noise Amplitude Modulation. Measurement 2021, 182, 109678. [Google Scholar] [CrossRef]
- Blumendeller, E.; Gaßner, L.; Müller, F.J.Y.; Pohl, J.; Hübner, G.; Ritter, J.; Cheng, P.W. Quantification of Amplitude Modulation of Wind Turbine Emissions from Acoustic and Ground Motion Recordings. Acta Acust. 2023, 7, 55. [Google Scholar] [CrossRef]
- Bernardi, C.; Porcacchia, F.; Testa, C.; Palma, P.D.; Leonardi, S.; Cherubini, S. NREL-5MW Wind Turbine Noise Prediction by FWH-LES. Int. J. Turbomach. Propuls. Power 2023, 8, 54. [Google Scholar] [CrossRef]
- Nguyen, P.; Hansen, K.; Lechat, B.; Catcheside, P.; Zajamsek, B.; Hansen, C.H. Benchmark Characterisation and Automated Detection of Wind Farm Noise Amplitude Modulation. Appl. Acoust. 2021, 183, 108286. [Google Scholar] [CrossRef]
- Mascarenhas, D.; Cotté, B.; Doaré, O. Synthesis of Wind Turbine Trailing Edge Noise in Free Field. JASA Express Lett. 2022, 2, 033601. [Google Scholar] [CrossRef]
- Mackowski, L.; Carolus, T.H. Wind Turbine Trailing Edge Noise: Mitigation of Normal Amplitude Modulation by Individual Blade Pitch Control. J. Sound Vib. 2021, 510, 116279. [Google Scholar] [CrossRef]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Dag, K.O.; Moriarty, P. Consistent Modelling of Wind Turbine Noise Propagation from Source to Receiver. J. Acoust. Soc. Am. 2017, 142, 3297–3310. [Google Scholar] [CrossRef]
- Lee, S.; Ayton, L.; Bertagnolio, F.; Moreau, S.; Chong, T.P.; Joseph, P. Turbulent Boundary Layer Trailing-Edge Noise: Theory, Computation, Experiment, and Application. Prog. Aerosp. Sci. 2021, 126, 100737. [Google Scholar] [CrossRef]
- Oerlemans, S. Effect of Wind Shear on Amplitude Modulation of Wind Turbine Noise. Int. J. Aeroacoustics 2015, 14, 715–728. [Google Scholar] [CrossRef]
- Tian, Y.; Cotté, B.; Chaigne, A. Wind Turbine Noise Modeling: Prediction of Amplitude Modulation and Influence of Atmospheric Conditions. In Proceedings of the Forum Acusticum, Kraków, Poland, 7–14 September 2014. [Google Scholar]
- Gebraad, P.M.O.; van Wingerden, J.W. A Control-Oriented Dynamic Model for Wakes in Wind Plants. J. Phys. Conf. Ser. 2014, 524, 012186. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A New Analytical Model for Wind-Turbine Wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- King, J.; Fleming, P.; King, R.; Martínez-Tossas, L.A.; Bay, C.J.; Mudafort, R.; Simley, E. Control-Oriented Model for Secondary Effects of Wake Steering. Wind Energy Sci. 2021, 6, 701–714. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Annoni, J.; Fleming, P.A.; Churchfield, M.J. The Aerodynamics of the Curled Wake: A Simplified Model in View of Flow Control. Wind Energy Sci. 2019, 4, 127–138. [Google Scholar] [CrossRef]
- Bay, C.J.; King, J.; Martìnez-Tossas, L.A.; Mudafort, R.; Hulsman, P.; Kühn, M.; Fleming, P. Toward Flow Control: An Assessment of the Curled Wake Model in the FLORIS Framework. J. Phys. Conf. Ser. 2020, 1618, 022033. [Google Scholar] [CrossRef]
- Blackadar, A. The Vertical Distribution of Wind and Turbulent Exchange in a Neutral Atmosphere. J. Geophys. Res. 1962, 67, 3095–3102. [Google Scholar] [CrossRef]
- Sun, J. Vertical Variations of Mixing Lengths under Neutral and Stable Conditions during CASES-99. J. Appl. Meteorol. Climatol. 2011, 50, 2030–2041. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Effects of Thermal Stability and Incoming Boundary-Layer Flow Characteristics on Wind-Turbine Wakes: A Wind-Tunnel Study. Bound. Layer Meteorol. 2010, 136, 515–533. [Google Scholar] [CrossRef]
- Bartl, J.; Mühle, F.; Schottler, J.; Sætran, L.; Peinke, J.; Adaramola, M.; Hölling, M. Wind Tunnel Experiments on Wind Turbine Wakes in Yaw: Effects of Inflow Turbulence and Shear. Wind Energy Sci. 2018, 3, 329–343. [Google Scholar] [CrossRef]
- Huang, J.; Bou-Zeid, E. Turbulence and Vertical Fluxes in the Stable Atmospheric Boundary Layer. Part I: A Large-Eddy Simulation Study. J. Atmos. Sci. 2013, 70, 1513–1527. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kim, H.; Lee, S.; Lee, S. Numerical Analysis on the Aerodynamics of HAWTs Using Nonlinear Vortex Strength Correction. Curr. Appl. Phys. 2010, 10, S311–S315. [Google Scholar] [CrossRef]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; NASA-RP-1218; NASA Langley Research Center: Hampton, VA, USA, 1989.
- Bortolotti, P.; Branlard, E.; Platt, A.; Moriarty, P.; Sucameli, C.; Bottasso, C.L. Aeroacoustics Noise Model of OpenFAST; NREL/TP-5000-75731; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2020.
- Jacobson, R.; Meadors, M.; Jacobson, E.; Link, H. Power Performance Test Report for the AOC 15/50 Wind Turbine, Test B; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2003. [Google Scholar]
- Moriarty, P.; Migliore, P. Semi-Empirical Aeroacoustic Noise Prediction Code for Wind Turbines; NREL/TP-500-34478; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2003. [CrossRef]
- Dal Monte, A.; De Betta, S.; Raciti Castelli, M.; Benini, E. Proposal for a Coupled Aerodynamic–Structural Wind Turbine Blade Optimization. Compos. Struct. 2017, 159, 144–156. [Google Scholar] [CrossRef]
- IEC 61400-11; Wind Turbines—Part 11: Acoustic Noise Measurement Techniques. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2012.
- Vollmer, L.; Steinfeld, G.; Heinemann, D.; Kühn, M. Estimating the Wake Deflection Downstream of a Wind Turbine in Different Atmospheric Stabilities: An LES Study. Wind Energy Sci. 2016, 1, 129–141. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009.




| Properties | Description |
|---|---|
| Orientation | Downwind |
| Number of blades | 3 |
| Rotor diameter | 15 m |
| Hub height | 25 m |
| Rated wind speed | 12 m/s |
| Cut-in wind speed | 4.9 m/s |
| Cut-out wind speed | 22.3 m/s |
| Blade airfoils | DUxx-A17, NACA64-A17 |
| Parameters | SBL | NBL |
|---|---|---|
| (m/s) | 8.40 | 8.30 |
| TI | 0.04 | 0.083 |
| 0.30 | 0.17 |
| Properties | Description |
|---|---|
| Orientation | Upwind |
| Number of blades | 3 |
| Rotor diameter | 126 m |
| Hub height | 90 m |
| Rated wind speed | 11.4 m/s |
| Blade airfoils | DUxx-A17, NACA64-A17 |
| Wake Model Parameters | SBL | NBL |
|---|---|---|
| 0.02 | 0.02 | |
| Initial wake deficit | 2.10 | 1.70 |
| Mixing length (m) | 9 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Yuk, T.; Yu, K.; Lee, S. Trailing-Edge Noise and Amplitude Modulation Under Yaw-Induced Partial Wake: A Curl–UVLM Analysis with Atmospheric Stability Effects. Energies 2025, 18, 5205. https://doi.org/10.3390/en18195205
Kim H, Yuk T, Yu K, Lee S. Trailing-Edge Noise and Amplitude Modulation Under Yaw-Induced Partial Wake: A Curl–UVLM Analysis with Atmospheric Stability Effects. Energies. 2025; 18(19):5205. https://doi.org/10.3390/en18195205
Chicago/Turabian StyleKim, Homin, Taeseok Yuk, Kukhwan Yu, and Soogab Lee. 2025. "Trailing-Edge Noise and Amplitude Modulation Under Yaw-Induced Partial Wake: A Curl–UVLM Analysis with Atmospheric Stability Effects" Energies 18, no. 19: 5205. https://doi.org/10.3390/en18195205
APA StyleKim, H., Yuk, T., Yu, K., & Lee, S. (2025). Trailing-Edge Noise and Amplitude Modulation Under Yaw-Induced Partial Wake: A Curl–UVLM Analysis with Atmospheric Stability Effects. Energies, 18(19), 5205. https://doi.org/10.3390/en18195205





