GIS-Based Mapping and Development of Biomass-Fueled Integrated Combined Heat and Power Generation in Nigeria
Abstract
1. Introduction
2. Materials and Methods
- Digitization: Data such as road networks and waterlines were digitized and uploaded into the GIS platform.
- DEM analysis: Digital Elevation Model (DEM) analysis was performed on the obtained remotely sensed data to produce the slope, aspect, hill shade, and topographic data.
- Buffer analysis: The Multiple-Ring Buffer analytical tool in the GIS domain was employed to create multiple buffer areas around the roads and waterlines, according to the stipulated criteria.
- Multicriteria Decision (MCD) weighted overlay analysis: The criteria, including forest area, crop areas, settlement, grass lands, waterbodies, barren land, water source distance, accessibility, topography, and aspect, were considered, and the influence weights of the criteria were determined for Nigeria. Meanwhile, criteria including biomass residue area, settlement, accessibility, proximity to waterbody, slope, and aspect were determined for Edo state, Nigeria (see Ukoba et al. [7] for details).
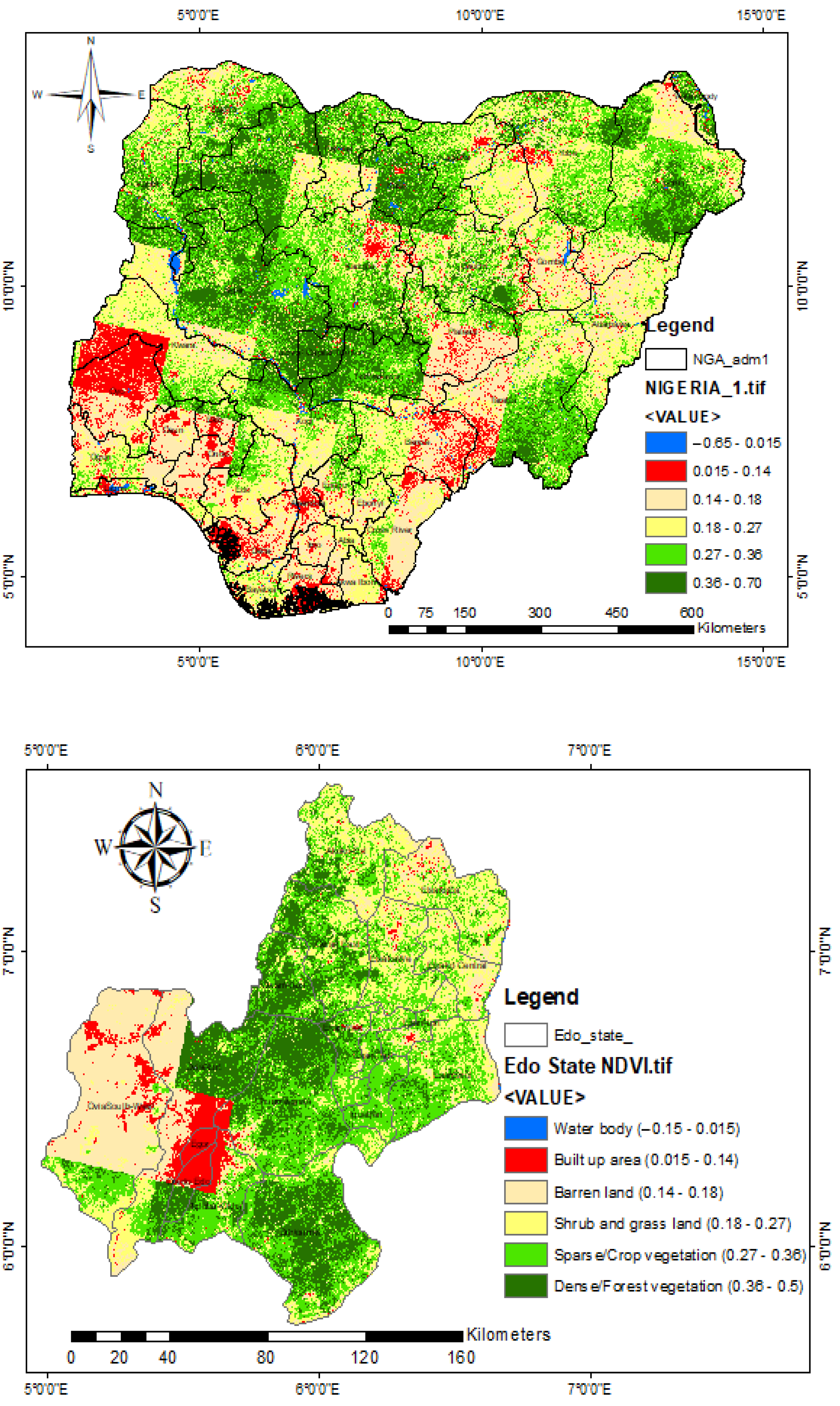
2.1. Normalized Difference Vegetation Index (NDVI) Analysis
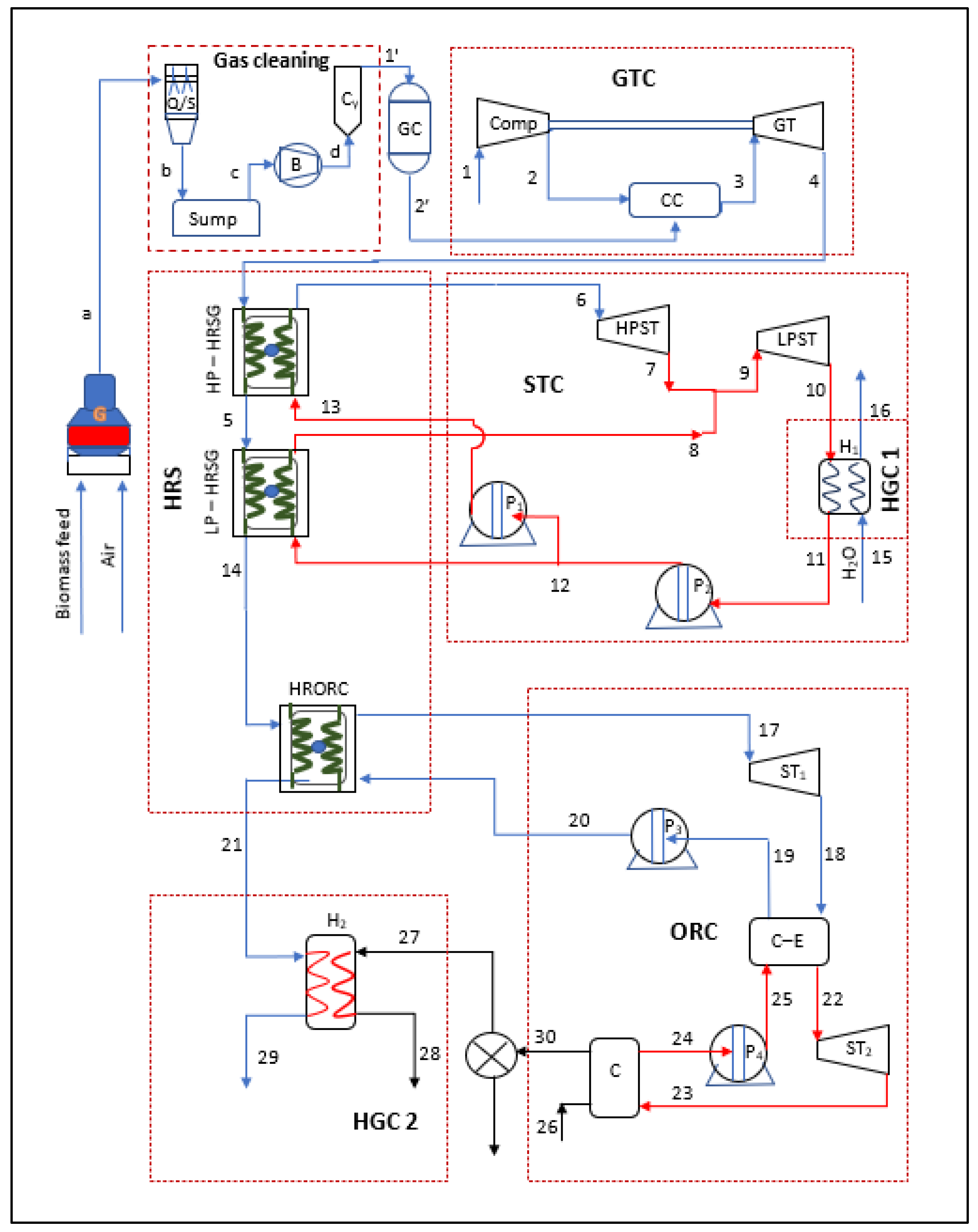
2.2. Analysis of Biomass-Combined Heat and Power Plant (BCHPP)
BCHPP System Description
2.3. Assumptions
- Kinetic and potential energies are negligible;
- No heat loss;
- Steady-state operation;
- Gas behavior is the ideal gas behavior;
- Gasification reaction is at equilibrium;
- Control volume system;
- Complete combustion process.
2.4. Gas Generation (Gasification) Model
2.5. Thermodynamic Analysis of the BCHPP System
2.6. Energy and Exergy Analysis of BCHP Components
2.6.1. Gas Turbine Cycle
2.6.2. Steam Turbine Cycle
2.6.3. Organic Rankine Cycle (ORC)
2.7. BCHP Plant Exergo-Economic Analysis
2.7.1. Equipment/Components Cost
2.7.2. Energy Streams and Material Cost Rate
2.7.3. Biomass Plant System Analysis
Economic Analysis
Environmental Analysis
Sustainability Analysis
| System Component | Symbol | Ref. Year | ||
|---|---|---|---|---|
| Gasifier | 1994 | 368 | ||
| Compressor | 1994 | 368 | ||
| Combustor | 2011 | 468 | ||
| Gas turbine (micro) | 1994 | 368 | ||
| HRSG | 4745 | 1998 | 382 | |
| Steam turbine | 6000 | 1998 | 382 | |
| Heat exchanger | 130 | 2011 | 468 | |
| Pump | 3540 | 1998 | 382 | |
| Evaporator | 130 | 2000 | 394 | |
| Condenser | 1773 | 2000 | 394 |
| Component | Symbol | Cost Rate Balance |
|---|---|---|
| Compressor | ||
| Syngas Storage | ||
| Combustion Chamber | ||
| Gas Turbine | ||
| HP-HRSG | ||
| LP-HRSG | ||
| HP Steam Turbine (HPST) | ||
| LP Steam Turbine (LPST) | ||
| HGC 1 (HXX 1) | ||
| LP-Pump (pump 2) | ||
| HP Pump (pump1) | ||
| HRORCG | ||
| ORC Steam Turbine 1 | ||
| ORC Steam Turbine 2 | ||
| Evaporator–Condenser Unit | ||
| ORC Pump 3 (P-3) | ||
| ORC Pump 4 (P-4) | ||
| ORC Condenser | ||
| HGC 2 |
3. Results and Discussions
| Components | Parameter | Symbols | Values | Units |
|---|---|---|---|---|
| BCHP System | Initial Parameter | |||
| Mass flow of residue | 23.70 | kg/s | ||
| Temperature of biomass | T | 27.00 | °C | |
| Initial pressure of residue | P | 101.33 | kPa | |
| Gasifier temperature | 677.00 | °C | ||
| Design parameter | ||||
| Ambient temperature | T1 | 27.00 | C | |
| Ambient pressure | P1 | 101.33 | kPa | |
| Compressor efficiency | 85.00 | % | ||
| Combustor efficiency | 85.00 | % | ||
| Turbine efficiency | 85.00 | % | ||
| Pump efficiency | 90.00 | % | ||
| Syngas composition (higher heating value (HHV) of syngas) | ||||
| Methane gas | 55.53 | MJ/kg | ||
| Hydrogen gas | 141.80 | MJ/kg | ||
| Carbon (II) oxide | 10.10 | MJ/kg | ||
| Chemical exergy of syngas components | ||||
| Methane gas | 831.70 | kJ/mol | ||
| Hydrogen gas | 236.10 | kJ/mol | ||
| Carbon (II) oxide | 275.10 | kJ/mol | ||
| Carbon (IV) oxide | 19.87 | kJ/mol | ||
| Nitrogen gas | 0.72 | kJ/mol | ||
| Steam | 9.50 | kJ/mol | ||
| GT Cycle | Design condition | |||
| Air inlet temperature | 10.00 | °C | ||
| Pressure ratio | 11.50 | |||
| Temperature ratio | 10.00 | |||
| Syngas temperature | 677.00 | °C | ||
| ST Cycle | Design condition | |||
| HP-HRSG pressure | 15,000 | Kpa | ||
| LP-HRSG pressure | 7500 | Kpa | ||
| HP-Pump mass flow rate | 18 | m/s | ||
| LP-Pump mass flow rate | 51 | m/s | ||
| HP-HRSG efficiency | 85 | % | ||
| LP-HRSG efficiency | 85 | % | ||
| ORC | Design condition | |||
| ORC-HRSG pressure | 1500 | Kpa | ||
| ORC-Condenser pressure | 465 | Kpa | ||
| Parameter | Symbol | Value | Unit | |
|---|---|---|---|---|
| Fuel cost per energy unit | 0.004 | |||
| Engineering/contingency cost | 0.150 | % | ||
| Interest rate | 0.120 | |||
| Operating h/year | N | 8760.000 | h | |
| Maintenance factor | 1.100 | |||
| System lifespan | N | 20.000 | yr | |
| Sources: [23,27,35,39,40] | ||||
| Environmental Data | ||||
| Parameter | Symbol | Value | Unit | Reference |
| Cost of CO2 emission | 3.50000 | [40] | ||
| Cost of CO emission | 0.02086 | [40] | ||
| Cost of NOx emission | 6.85300 | [41] | ||
| Sustainability Data | ||||
| Parameter | Symbol | Value | Unit | |
| Income per capita | 2177.00 | |||
| Energy doubling time | 22.00 | yr | ||
| Energy per capita | 141.00 | |||
| Population doubling time | 25.00 | yr | ||
| Electricity tariff | 0.17 | /kWh | ||
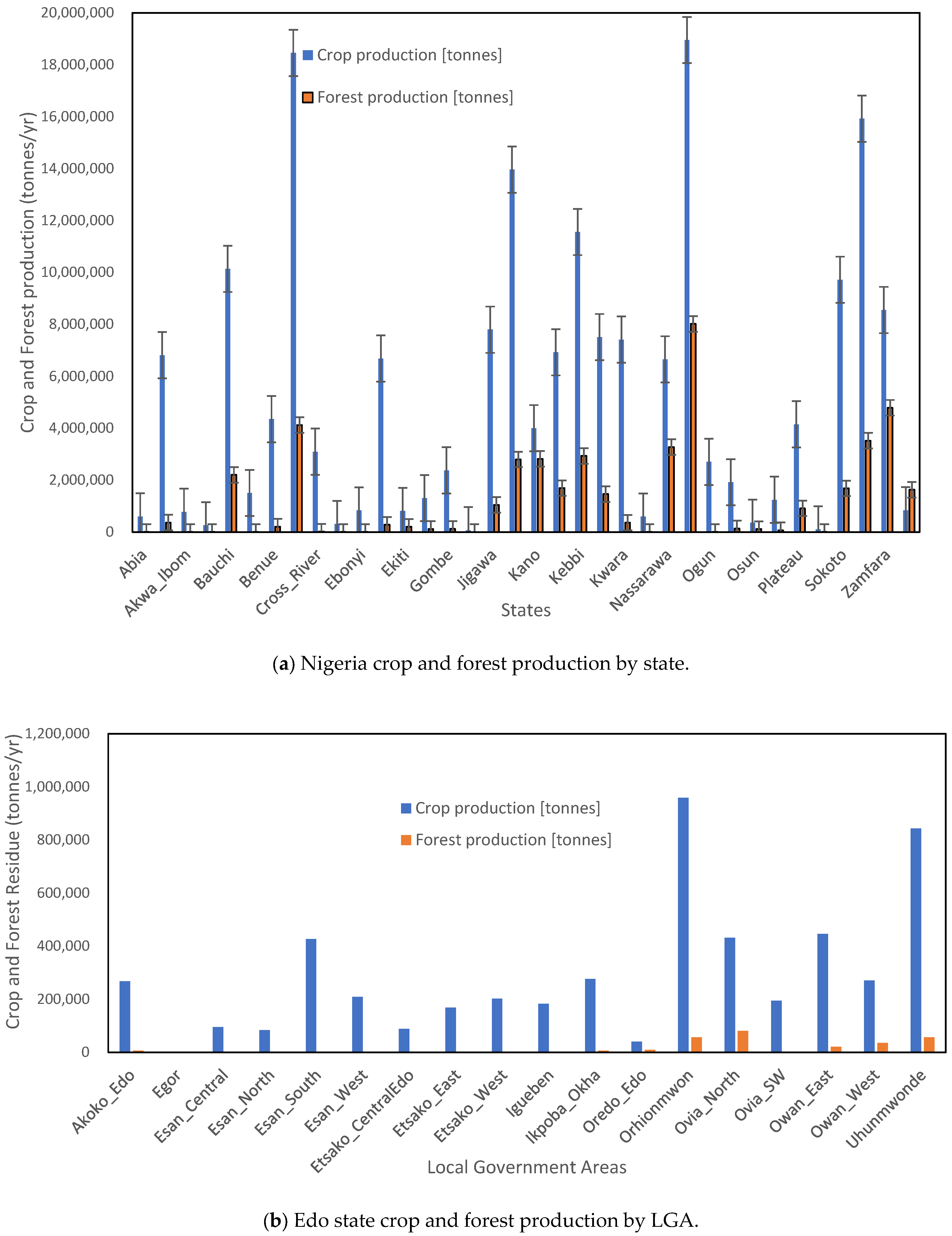
3.1. Result of Crop and Forest Analysis
| Residue | Composition | Ash | MC | ||||
|---|---|---|---|---|---|---|---|
| C | H | O | N | S | |||
| Crop | 40.09 | 7.31 | 42.19 | 1.13 | 0.67 | 8.11 | 8.79 |
| Forest | 48.97 | 5.91 | 44.17 | 0.18 | 0.02 | 0.76 | 2.44 |
| Moisture | 0.00 | 1.22 | 9.98 | 0.00 | 0.00 | ||
| Total | 89.06 | 14.44 | 96.34 | 1.31 | 0.69 | 8.87 | 11.23 |
| Composition of elements (percentage by mass) | |||||||
| Element | Mass (kg) | Percentage (%) | |||||
| Carbon | 89.06 | 44.0 | |||||
| Hydrogen | 14.44 | 7.0 | |||||
| Oxygen | 96.34 | 48.0 | |||||
| Nitrogen | 1.31 | 0.7 | |||||
| Sulfur | 0.69 | 0.3 | |||||
| Molecular formula of biomass residue: | |||||||
| Energy content of biomass (crop and forest) residue and syngas | |||||||
| Parameter | Symbol | Value | Unit | ||||
| Higher heating value of residue | 444.75 | MJ/kg | |||||
| Higher heating value of syngas | 30.47 | MJ/kg | |||||
| Lower heating value of Syngas | 17.15 | MJ/kg | |||||
| Methane gas | 5.20 | % | |||||
| Hydrogen gas | 18.24 | % | |||||
| Carbon (II) oxide | 17.00 | % | |||||
| Carbon (IV) oxide | 12.77 | % | |||||
| Nitrogen gas | 35.36 | % | |||||
| Steam | 11.43 | % | |||||
3.2. Model Validation
| Gasification Constituent Comparison | |||||
| Parameter | Current Model | Literature [46] | Error (%) | Literature [28] | Error (%) |
| Methane gas, | 5.20 | 2.5 | 107.96 | 0.10 | b A.H |
| Hydrogen gas, | 18.24 | 16.0 | 14.00 | 14.48 | 25.97 |
| Carbon (II) oxide, (%) | 17.00 | 19.4 | 12.37 | 21.73 | 21.77 |
| Carbon (IV) oxide, (%) | 12.77 | 12.2 | 4.67 | 8.76 | 45.78 |
| Nitrogen gas, (%) | 35.36 | 49.6 | 28.71 | 49.24 | 28.19 |
| Steam, (%) | 11.43 | N.A | N.A | 5.46 | b A.H |
| System Comparison | |||||
| Parameter | Literature | Current Model | |||
| Energy efficiency (%) | a 63.62; b 60.10; c 62.30; d 82.40 * | 62.94 (GT cycle) 87.16 ** (Integrated plant cycle) | |||
| UCOE (USD/kWh) | a 0.0109; b 0.0100; c 0.0180 | 0.0066 | |||
| Break-even point (years) | a, c 7.5; b 9.0 | 7.5 | |||
| CO2 emission (kg/MWh) | a 141.20 c 148.22; b N.A | 141.73 | |||
| Fuel harmful emission factor (-) | a 0.01853; c 0.00090 b N.A | 0.16340 | |||
| Sustainability index, (-) | a 2.4300; c 2.2500; b N.A | 2.0121 | |||
3.3. Thermodynamic Performance of the BCHP Plant System
3.4. Exergo-Economic, Environmental, and Sustainability Results of the BCHP Plant
| State | Mass Flow Rate, [kg/s] | Pressure [Kpa] | Temperature [k] | Cost Rate of Energy Stream [USD/s] | Unit Cost of Exergy of Stream [USD/MWs] |
|---|---|---|---|---|---|
| 1 | 171.1 | 101.3 | 283.0 | 0.000 | 0.000000 |
| 2 | 171.1 | 1165.0 | 619.4 | 0.000 | 0.000000 |
| 2a | 23.7 | 101.3 | 300.0 | 2.315 | 0.004000 |
| 3 | 194.8 | 1107.0 | 1473.0 | 36.392 | 0.004000 |
| 4 | 194.8 | 114.0 | 1027.0 | 20.916 | 0.004000 |
| 5 | 194.8 | 111.7 | 662.8 | 13.892 | 0.004000 |
| 6 | 18.0 | 14700.0 | 968.8 | 0.601 | 0.001043 |
| 7 | 18.0 | 114.0 | 675.3 | 0.261 | 0.001043 |
| 8 | 51.0 | 7350.0 | 651.7 | 3.335 | 0.002957 |
| 9 | 69.0 | 7350.0 | 657.8 | 6.152 | 0.004000 |
| 10 | 69.0 | 70.0 | 458.5 | 2.488 | 0.004000 |
| 11 | 69.0 | 68.6 | 362.6 | 0.265 | 0.004000 |
| 12a | 18.0 | 7500.0 | 563.7 | 0.489 | 0.001043 |
| 12b | 51.0 | 7500.0 | 563.7 | 1.387 | 0.002957 |
| 13 | 18.0 | 15,000.0 | 790.0 | 0.497 | 0.001043 |
| 14 | 194.8 | 109.5 | 585.0 | 12.724 | 0.004000 |
| 15 | 69.0 | 101.3 | 300.0 | 0.000 | 0.000000 |
| 16 | 69.0 | 99.3 | 445.8 | 0.000 | 0.000000 |
| 17 | 68.0 | 1470.0 | 379.9 | 1.794 | 0.004000 |
| 18 | 68.0 | 465.0 | 344.3 | 1.045 | 0.004000 |
| 19 | 68.0 | 455.7 | 332.7 | 0.38 | 0.004000 |
| 20 | 68.0 | 1500.0 | 333.3 | 0.411 | 0.004000 |
| 21 | 194.8 | 107.3 | 394.2 | 9.875 | 0.004000 |
| 22 | 68.0 | 1470.0 | 379.9 | 1.794 | 0.004000 |
| 23 | 68.0 | 465.0 | 344.3 | 1.045 | 0.004000 |
| 24 | 68.0 | 455.7 | 332.7 | 0.38 | 0.004000 |
| 25 | 68.0 | 1500 | 333.3 | 0.411 | 0.004000 |
| 26 | 69.0 | 101.3 | 300.0 | 0.000 | 0.000000 |
| 27 | 69.0 | 99.3 | 343.5 | 0.000 | 0.000000 |
| 28 | 69.0 | 97.31 | 372.3 | 0.000 | 0.000000 |
| 29 | 194.8 | 105.2 | 347.2 | 9.174 | 0.004000 |
| 30 | 69.0 | 99.3 | 343.5 | 0.000 | 0.000000 |
| Thermo-Economics Results | ||||
| Component | Xk [MUSD] | [USD/s] | [USD/s] | fk [%] |
| Compressor | 11.196460 | 0.052285 | 0.00681 | 88.47171 |
| Combustion Chamber | 0.575298 | 0.002687 | 1.48532 | 0.18054 |
| Gas Turbine | 6.228269 | 0.029085 | 0.38188 | 7.07721 |
| HP-HRSG | 517.200000 | 2.415218 | 12.16984 | 16.55953 |
| LP-HRSG | 165.300000 | 0.771917 | 11.15951 | 6.46961 |
| HP Steam Turbine (HPST) | 44.688300 | 0.208685 | 0.46210 | 31.11061 |
| LP Steam Turbine (LPST) | 68.255810 | 0.318741 | 7.26763 | 4.20149 |
| HGC 1 | 0.000941 | 0.000004 | 0.27603 | 0.00159 |
| LP-Pump (pump 2) | 111.776000 | 0.521971 | 0.00036 | 99.96167 |
| HP Pump (pump1) | 111.776000 | 0.521971 | 0.00080 | 99.84683 |
| HRORCG | 4.627000 | 0.021607 | 2.59572 | 0.82554 |
| ORC Steam Turbine 1 | 58.770000 | 0.274444 | 0.15773 | 63.50367 |
| ORC Steam Turbine 2 | 58.770000 | 0.274444 | 0.15773 | 63.50367 |
| Evaporator–Condenser Unit | 0.184573 | 0.000862 | 0.01742 | 4.71368 |
| ORC Pump 3 (P-3) | 2.004000 | 0.009358 | 0.00866 | 51.94638 |
| ORC Pump 4 (P-4) | 2.004000 | 0.009358 | 0.00203 | 82.16418 |
| ORC Condenser | 0.184573 | 0.000862 | 0.10798 | 0.79192 |
| HGC 2 | 0.022400 | 0.000105 | 4.58823 | 0.00001 |
| Total | 1163.564000 | 5.433604 | 40.84578 | 34.51832 |
| Thermodynamic Characteristics of System Components | ||||
| Component | Heat/Work, /) [MW] | Input Exergy, [MW] | Exergy Destroyed, [MW] | Exergy Efficiency, [%] |
| Compressor | 1673.00 | 1674 | 218.0 | 62 |
| Combustion Chamber | 3340.00 | 11,243 | 2143.0 | 81 |
| Gas Turbine | 3776.00 | 9100 | 93.0 | 98 |
| HP-HRSG | 2853.00 | 5230 | 1660.0 | 57 |
| LP-HRSG | 609.98 | 3470 | 490.0 | 23 |
| HP Steam Turbine (HPST) | 177.13 | 576 | 149.0 | 54 |
| LP Steam Turbine (LPST) | 324.40 | 1540 | 592.0 | 35 |
| HGC 1 | 3367.00 | 622 | 341.0 | 57 |
| LP-Pump (pump 2) | 1143.00 | 66 | 0.6 | 35 |
| HP Pump (pump1) | 2581.00 | 469 | 3.9 | 30 |
| HRORCG | 1799.00 | 3180 | 367.0 | 49 |
| ORC Steam Turbine 1 | 162.24 | 448 | 25.0 | 87 |
| ORC Steam Turbine 2 | 162.24 | 448 | 25.0 | 87 |
| Evaporator–Condenser | 1799.00 | 261 | 30.0 | 48 |
| ORC Pump 3 (P-3) | 8.54 | 95 | 0.8 | 91 |
| ORC Pump 4 (P-4) | 8.54 | 95 | 0.8 | 91 |
| ORC Condenser | 3074.00 | 261 | 170.0 | 46 |
| HGC 2 | 3.41 | 226 | 171.0 | 23 |
| Thermodynamic Characteristics of BCHP Plant Configurations | ||||
| Configuration | Parameter | Symbol | Value | Unit |
| GT_DST_CORC | Net power | 2911.00 | MW | |
| Net heat | 3370.41 | MW | ||
| Thermal Efficiency | 87.16 | % | ||
| Exergy efficiency | 50.30 | % | ||
| Exergy destroyed | 6480.00 | MW | ||
| Flare gas temperature | 74.20 | °C | ||
| Exergo-Economic Result | |||
| Parameter | Symbol | Value | Unit |
| Gasification unit cost | 106.803100 | M USD | |
| Combine BCHP plant equipment cost | 1163.563600 | M USD | |
| Engineering and contingency cost | 174.534500 | M USD | |
| Life cycle cost | 1444.901200 | M USD | |
| Daily energy production cost | 69,864.000000 | MWh/d | |
| Annualized energy production cost | 25,500,360.000000 | MWh/d | |
| Annualized LCC | 193.441600 | M /year | |
| Unit cost of energy | 0.007587 | /kWh | |
| Breakeven point | BEP | 7.500000 | Year |
| Environmental Result | |||
| Amount of CO2 | 31.8338 | kg/s | |
| Specific emission of CO2 | 141.7267 | kg/MWh | |
| Amount of CO | 5.702 × 10−6 | kg/s | |
| Amount of NOx | 2.301 × 10−7 | kg/s | |
| Fuel harmful emission factor | 0.1634 | ||
| Environmental-thermal conversion factor | 0.8641 | ||
| Environmental thermal impact factor | 0.1359 | ||
| Cost of CO2 | 111.4184 | /kg | |
| Cost of CO | 1.189 × 10−7 | USD/kg | |
| Cost of NOx | 1.577 × 10−6 | USD/kg | |
| Sustainability Result | |||
| Sustainability index | 2.0121 | ||
| Energo-environmental sustainability | 5.6206 | ||
| Energo-economic sustainability | 0.6952 | ||
| Sustainability exponent | 3.9073 | ||
3.5. Simulation
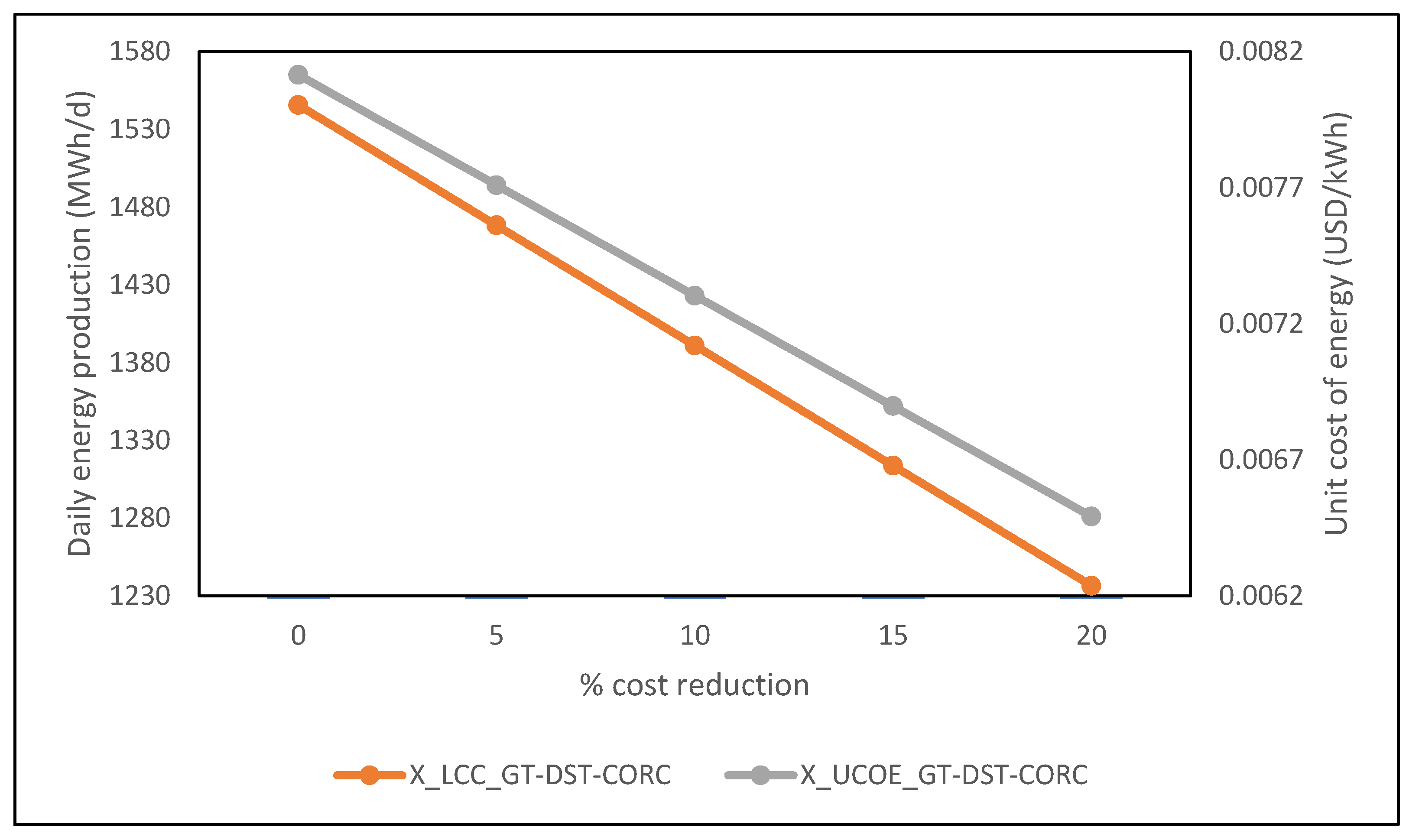
3.5.1. Effect of Equipment Cost
3.5.2. Effect of Interest Rate
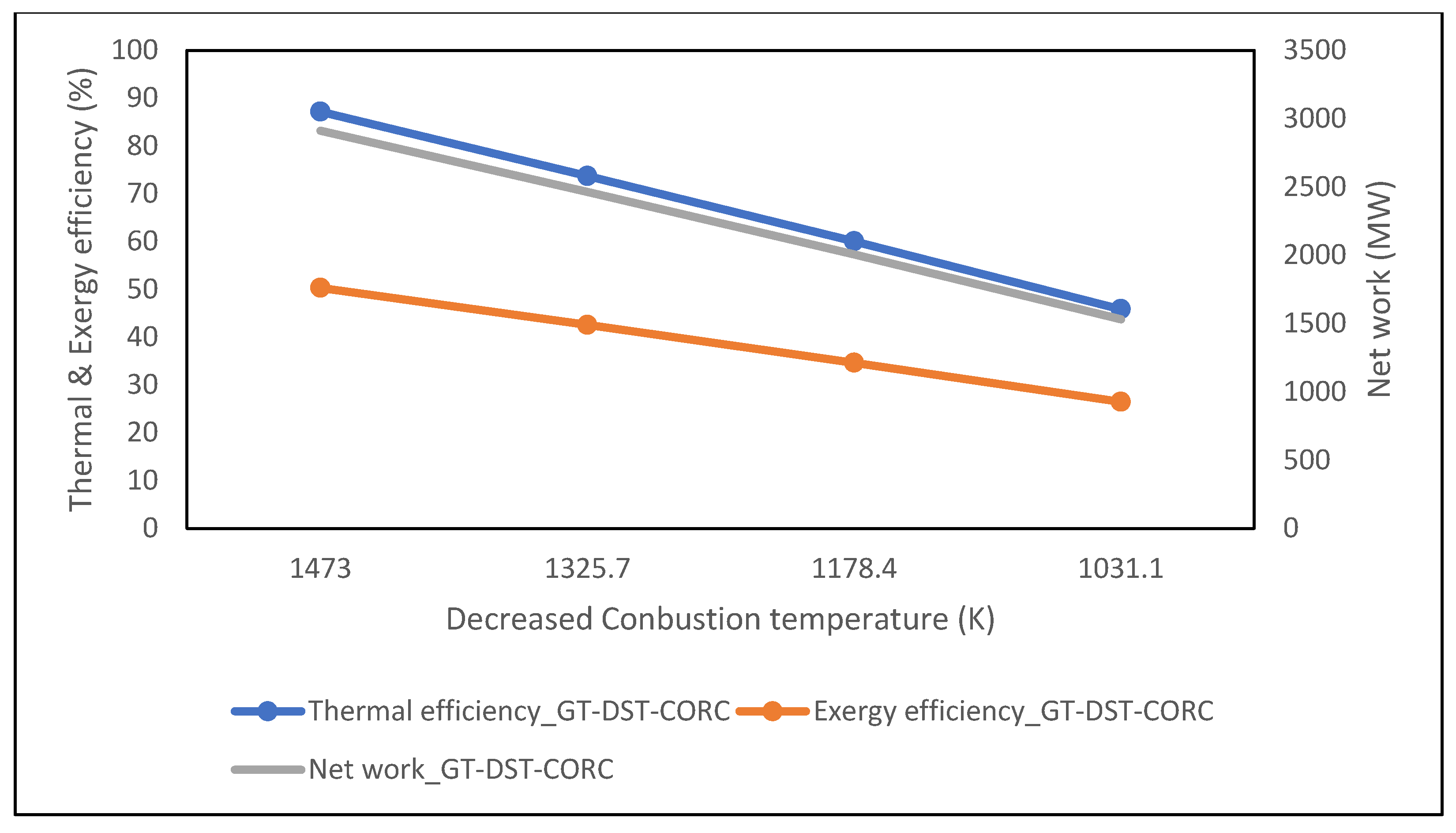
3.5.3. Effect of Combustion Temperature
3.5.4. Effect of Pressure Ratio
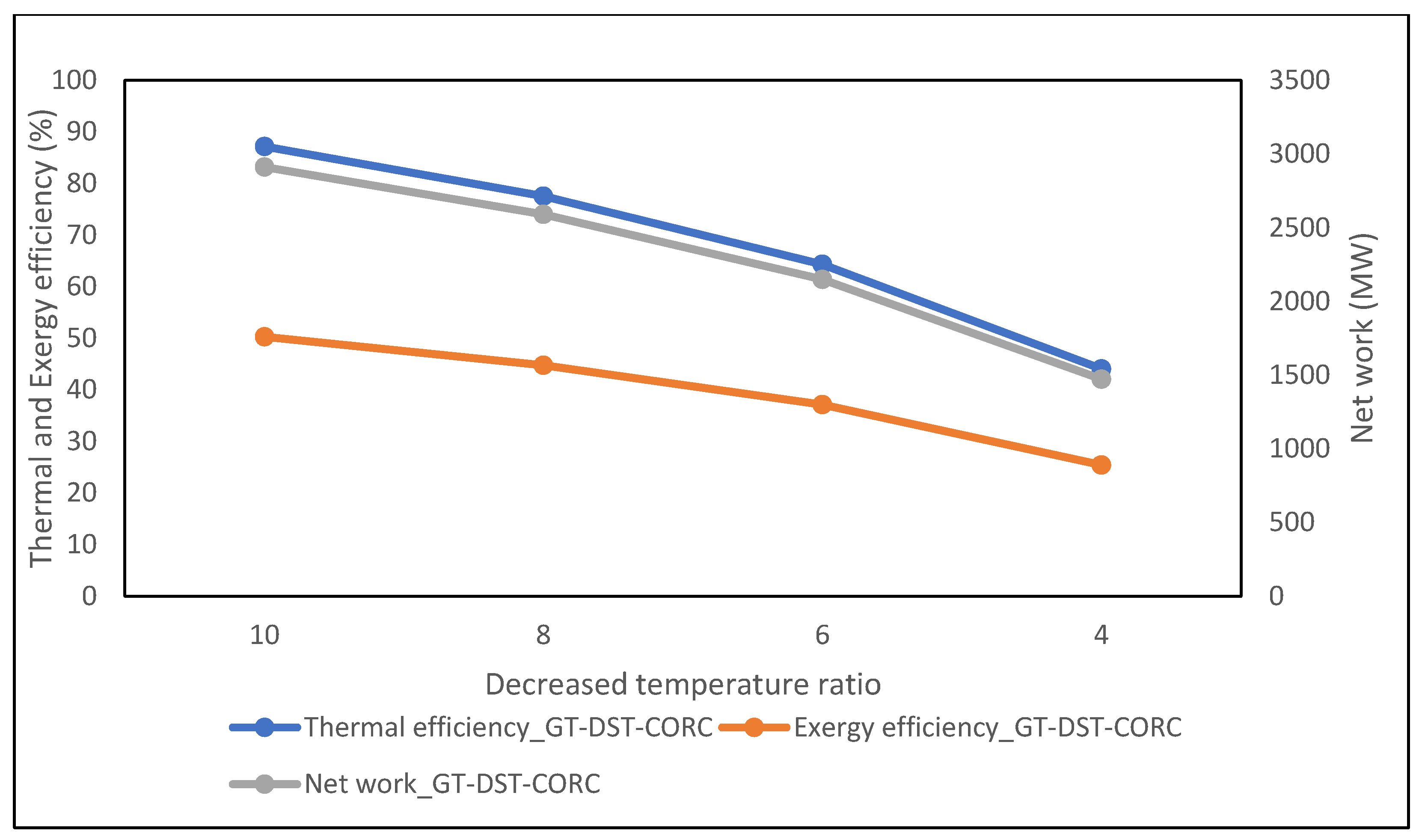
3.5.5. Effect of Temperature Ratio
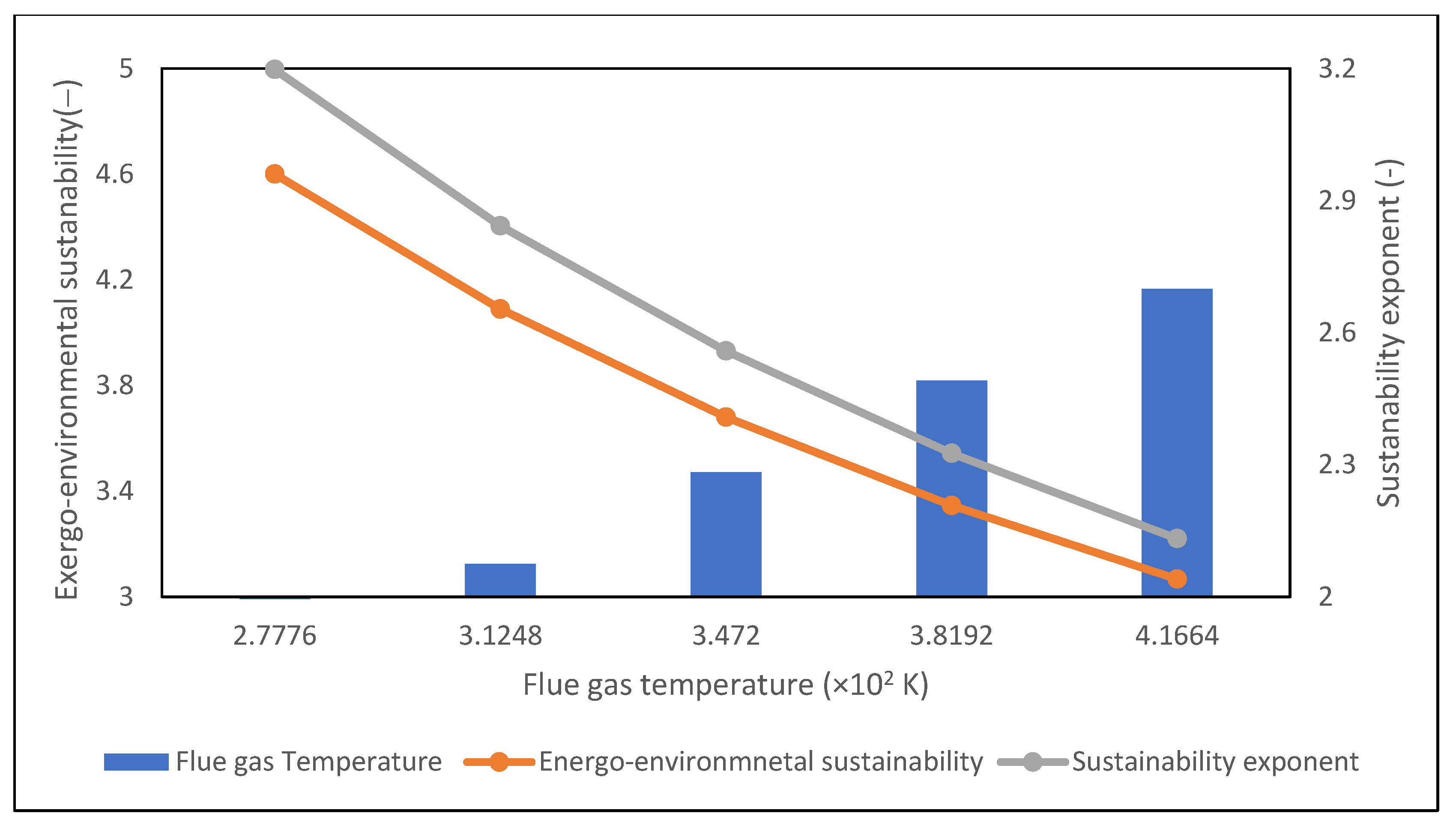
3.5.6. Effect of Flue Gas Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takase, M.; Kipkoech, R.; Essandoh, P.K. A comprehensive review of energy scenario and sustainable energy in Kenya. Fuel Community 2021, 7, 100015. [Google Scholar]
- Owebor, K.; Diemuodeke, E.O.; Briggs, T.A.; Imran, M. Power Situation and renewable energy potentials in Nigeria e A case for integrated multi-generation technology. Renew. Energy 2021, 177, 773–796. [Google Scholar] [CrossRef]
- Pande, C.B.; Moharir, K.N.; Singh, S.K.; Varade, A.M.; Elbeltagi, A.; Khadri, S.; Choudhari, P. Estimation of crop and forest biomass resources in a semi-arid region using satellite data and GIS. J. Saudi Soc. Agric. Sci. 2021, 20, 302–311. [Google Scholar] [CrossRef]
- Ben-iwo, J.; Manovic, V.; Longhurst, P. Biomass resources and biofuels potential for the production of transportation fuels in Nigeria. Renew. Sustain. Energy Rev. 2016, 63, 172–192. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2019. Available online: https://www.iea.org/ (accessed on 17 September 2025).
- Alex-Oke, T.; Bamisile, O.; Cai, D.; Adun, H.; Ukwuoma, C.C.; Tenebe, S.A.; Huang, Q. Renewable energy market in Africa: Opportunities, progress, challenges, and future prospects. Energy Strategy Rev. 2025, 59, 101700. [Google Scholar] [CrossRef]
- Ukoba, M.; Diemuodeke, E.; Briggs, T.; Imran, M.; Ojapah, M.; Owebor, K.; Nwachukwu, C.; Aminu, M.D.; Okedu, K.; Kalam, A.; et al. Optimal sites for agricultural and forest residues energy conversion plant using geographic information system. Heliyon 2023, 9, e19660. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Ukoba, M.O.; Diemuodeke, E.O.; Briggs, T.A.; Imran, M.; Owebor, K.; Nwachukwu, C.O. Geographic information systems (GIS) approach for assessing the biomass energy potential and identification of appropriate biomass conversion technologies in Nigeria. Biomass Bioenergy 2023, 170, 106726. [Google Scholar] [CrossRef]
- Irfan, M.; Zhao, Z.Y.; Ahmad, M.; Mukushimana, M.C. Critical factors influencing wind power industry: A diamond model based study of India. Energy Rep. 2019, 5, 1222–1235. [Google Scholar] [CrossRef]
- Souza, L.L.P.d.; Hamedani, S.R.; Lora, E.E.S.; Palacio, J.C.E.; Comodi, G.; Villarini, M.; Colantoni, A. Theoretical and technical assessment of agroforestry residue potential for electricity generation in Brazil towards 2050. Energy Rep. 2021, 7, 2574–2587. [Google Scholar] [CrossRef]
- Oyedepo, S.O. Energy and sustainable development in Nigeria: The way forward. Energy Sustain. Soc. 2012, 2, 15. [Google Scholar]
- Food and Agricultural Organization of the United Nations (FAO). Energy Conservation in the Mechanical Forest Industries. FAO FORESTRY PAPER 93. 1990. Available online: https://www.fao.org/4/t0269e/t0269e00.htm (accessed on 17 September 2025).
- Oyedepo, S.O.; Dunmade, I.S.; Adekeye, T.; Attabo, A.A.; Olawole, O.C.; Babalola, P.O.; Oyebanji, J.A.; Udo, M.O.; Kilanko, O.; Leramo, R.O. Bioenergy technology development in Nigeria—Pathway to sustainable energy development. Int. J. Environ. Sustain. Dev. 2019, 18, 175–205. [Google Scholar] [CrossRef]
- Kayanta, E.E.; Bello, A.A.; Habon, D.; Elijah, R.I. Availability assessment of groundnut and beans residue using remote sensing and GIS—A case study of Bogoro Local Government Area, Bauchi State, Nigeria. J. Remote Sens. GIS 2018, 7, 249. [Google Scholar]
- Jekayinfa, S.O.; Orisaleye, J.I.; Pecenka, R. An Assessment of Potential Resources for Biomass Energy in Nigeria. Resources 2020, 9, 92. [Google Scholar] [CrossRef]
- Janssen, R.; Ruth, D. Bioenergy for Sustainable Development in Africa; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Ikumapayi, O.M.; Kazeem, R.A.; Ige, E.O.; Ofotoku, D.O.; Adaramola, B.A.; Ting, T.T.; Laseinde, O.T.; Jen, T.; Akinlabi, E.T. Thermo-economic comparative analysis of a simple and cascaded organic Rankine power plants fired by rice husks. Clean. Eng. Technol. 2023, 17, 100692. [Google Scholar] [CrossRef]
- Central Intelligence Agency (CIA). The World Factbook: Nigeria; CIA: Washington, DC, USA, 2012.
- United States Geological Survey (USGS). Science Explorer. Science for a Changing World. 2021. Available online: https://earthexplorer.usgs.gov (accessed on 17 September 2025).
- Saleh, S.; Samad, N.A.F.A. Syngas software for biomass gasification process. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- GS 122-1; FIRED HEATERS TO API 560. B. Standards Group: London, UK, 1996.
- Oko, C.O.C.; Nwachukwu, C.O. Thermo-economic analysis of a waste-to-energy integrated multi-generation power plant. Int. J. Ambient. Energy 2020, 41, 334–347. [Google Scholar] [CrossRef]
- Carcasci, C.; Winchler, L. Thermodynamic analysis of an organic rankine cycle for waste heat recovery from an aeroderivative intercooled gas turbine. Energy Procedia 2016, 101, 862–869. [Google Scholar] [CrossRef]
- Saha, B.; Chakraborty, B.; Pundeer, P. Thermodynamic and thermo economic analysis of organic rankine cycle with multi-objective optimization for working fluid selection with low-temperature waste sources in the Indian industry. In Proceedings of the 5th international seminar on ORC power systems, Athens, Greece, 9–11 September 2019; pp. 5–12. [Google Scholar]
- Darvish, K.; Ehyaei, M.; Atabi, F.; Rosen, M. Selection of optimum working fluid for organic rankine cycles by exergy and exergy-economic analyses. Sustain. Times 2015, 7, 15362–15383. [Google Scholar] [CrossRef]
- Ogorure, O.J.; Oko, C.O.C.; Diemuodeke, E.O.; Owebor, K. Energy, exergy, environmental and economic analysis of an agricultural waste-to-energy integrated multigeneration thermal power plant. Energy Convers. Manag. 2018, 171, 222–240. [Google Scholar] [CrossRef]
- Allesina, G.; Simone, P.; Guidetti, L.; Paolo, T. Modeling of coupling gasification and anaerobic digestion processes for maize bioenergy conversion. Biomass Bioenergy 2015, 81, 444–451. [Google Scholar] [CrossRef]
- Zainal, Z.A.; Ali, R.; Lean, C.H.; Seetharamu, K.N. Prediction of performance of a downdraft gasifier using equilibrium modeling for different biomass materials. Energy Convers. Manag. 2001, 42, 1499–1515. [Google Scholar] [CrossRef]
- McAllister, S.; Chen, J.Y.; Fernandez-Pello, A.C. Fundamentals of Combustion Processes; Mechanical Engineering Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Reed, T.B.; Das, A. Handbook of Biomass Downdraft Gasifier Engine Systems; Biomass Energy Foundation: Normal, IL, USA, 1988. [Google Scholar]
- Basu, P. Chapter 6—Design of biomass gasifiers. In Biomass Gasification and Pyrolysis; Academic Press: Cambridge, MA, USA, 2010; pp. 167–228. [Google Scholar]
- Oko, C.O.C. Engineering Thermodynamics: An Algorithmic Approach, 2nd ed.; University of Port Harcourt Press: Port Harcourt, Nigeria, 2011. [Google Scholar]
- Chitsaz, A.; Mehr, A.S.; Mahmoudi, S.M.S. Exergoeconomic analysis of a trigeneration system driven by a solid oxide fuel cell. Energy Convers. Manag. 2015, 106, 921–931. [Google Scholar] [CrossRef]
- Shokati, N.; Mohammadkhani, F.; Yari, M.; Mahmoudi, S.M.S.; Rosen, M.A. A comparative exergoeconomic analysis of waste heat recovery from a gas turbine-modular helium reactor via organic rankine cycles. Sustainability 2014, 6, 2474–2489. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Ren, J.; Xu, C.; Qian, Z.; Huang, W.; Wang, B. Exergoeconomic analysis and optimization of a biomass integrated gasification combined cycle based on externally fired gas turbine, steam Rankine cycle, organic Rankine cycle, and absorption refrigeration cycle. Entropy 2024, 26, 511. [Google Scholar] [CrossRef] [PubMed]
- Oyedepo, S.O.; Fagbenle, R.O.; Adefila, S.S.; Alam, M.M. Thermoeconomic and thermoenvironomic modeling and analysis of selected gas turbine power plants in Nigeria. Energy Sci. Eng. 2015, 3, 423–442. [Google Scholar] [CrossRef]
- Owebor, K.; Oko, C.O.C.; Diemuodeke, E.O.; Ogorure, O.J. Thermo-environmental and economic analysis of an integrated municipal waste-to-energy solid oxide fuel cell, gas-, steam-, organic fluid- and absorption refrigeration cycle thermal power plants. Appl. Energy 2019, 239, 1385–1401. [Google Scholar] [CrossRef]
- Wygonik, E.; Goodchild, A. Evaluating CO2 emissions, cost, and service quality trade-offs in an urban delivery system case study. IATSS Res. 2011, 35, 7–15. [Google Scholar] [CrossRef]
- Kokalj, F.; Samec, N. Combustion of Municipal Solid Waste for Power Production. In Advances in Internal Combustion Engines and Fuel Technologies; InTech: Vienna, Austria, 2013. [Google Scholar] [CrossRef]
- Chandrappa, R.; Das, D.B. Waste Quantities and Characteristics. In Environmental Science and Engineering; Springer Science and Business Media Deutschland GmbH: Berlin, Germany, 2012; pp. 47–63. [Google Scholar] [CrossRef]
- Owebor, K.; Diemuodeke, O.E.; Briggs, T.A.; Eyenubo, O.J.; Ogorure, O.J.; Ukoba, M.O. Multi-criteria optimisation of integrated power systems for low-environmental impact. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 3459–3476. [Google Scholar] [CrossRef]
- Odukoya, A.; Dincer, I.; Naterer, G.F. Exergy analysis of a gasification-based combined cycle with solid oxide fuel cells for cogeneration. Int. J. Green Energy 2011, 8, 834–856. [Google Scholar] [CrossRef]
- Minutillo, M.; Perna, A.; Jannelli, E.; Cigolotti, V.; Nam, S.W.; Yoon, S.P.; Kwon, B.W. Coupling of Biomass Gasification and SOFC—Gas Turbine Hybrid System for Small Scale Cogeneration Applications. In Energy Procedia; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; pp. 730–737. [Google Scholar] [CrossRef]
- Jack, T.A.; Oko, C.O.C. Exergy and exergoeconomic analysis of a municipal waste-to-energy steam reheat power plant for Port Harcourt city. Int. J. Ambient. Energy 2018, 39, 352–359. [Google Scholar] [CrossRef]
- Haseli, Y.; Dincer, I.; Naterer, G.F. Thermodynamic analysis of a combined gas turbine power system with a solid oxide fuel cell through exergy. Thermochim. Acta 2008, 480, 1–9. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ukoba, M.O.; Diemuodeke, O.E.; Briggs, T.A.; Okedu, K.E.; Ezekwem, C. GIS-Based Mapping and Development of Biomass-Fueled Integrated Combined Heat and Power Generation in Nigeria. Energies 2025, 18, 5207. https://doi.org/10.3390/en18195207
Ukoba MO, Diemuodeke OE, Briggs TA, Okedu KE, Ezekwem C. GIS-Based Mapping and Development of Biomass-Fueled Integrated Combined Heat and Power Generation in Nigeria. Energies. 2025; 18(19):5207. https://doi.org/10.3390/en18195207
Chicago/Turabian StyleUkoba, Michael Ogheneruemu, Ogheneruona Endurance Diemuodeke, Tobinson Alasin Briggs, Kenneth Eloghene Okedu, and Chidozie Ezekwem. 2025. "GIS-Based Mapping and Development of Biomass-Fueled Integrated Combined Heat and Power Generation in Nigeria" Energies 18, no. 19: 5207. https://doi.org/10.3390/en18195207
APA StyleUkoba, M. O., Diemuodeke, O. E., Briggs, T. A., Okedu, K. E., & Ezekwem, C. (2025). GIS-Based Mapping and Development of Biomass-Fueled Integrated Combined Heat and Power Generation in Nigeria. Energies, 18(19), 5207. https://doi.org/10.3390/en18195207









