The Planning of Best Site Selection for Wind Energy in Indonesia: A Synergistic Approach Using Data Envelopment Analysis and Fuzzy Multi-Criteria Decision-Making
Abstract
1. Introduction
2. Literature Review
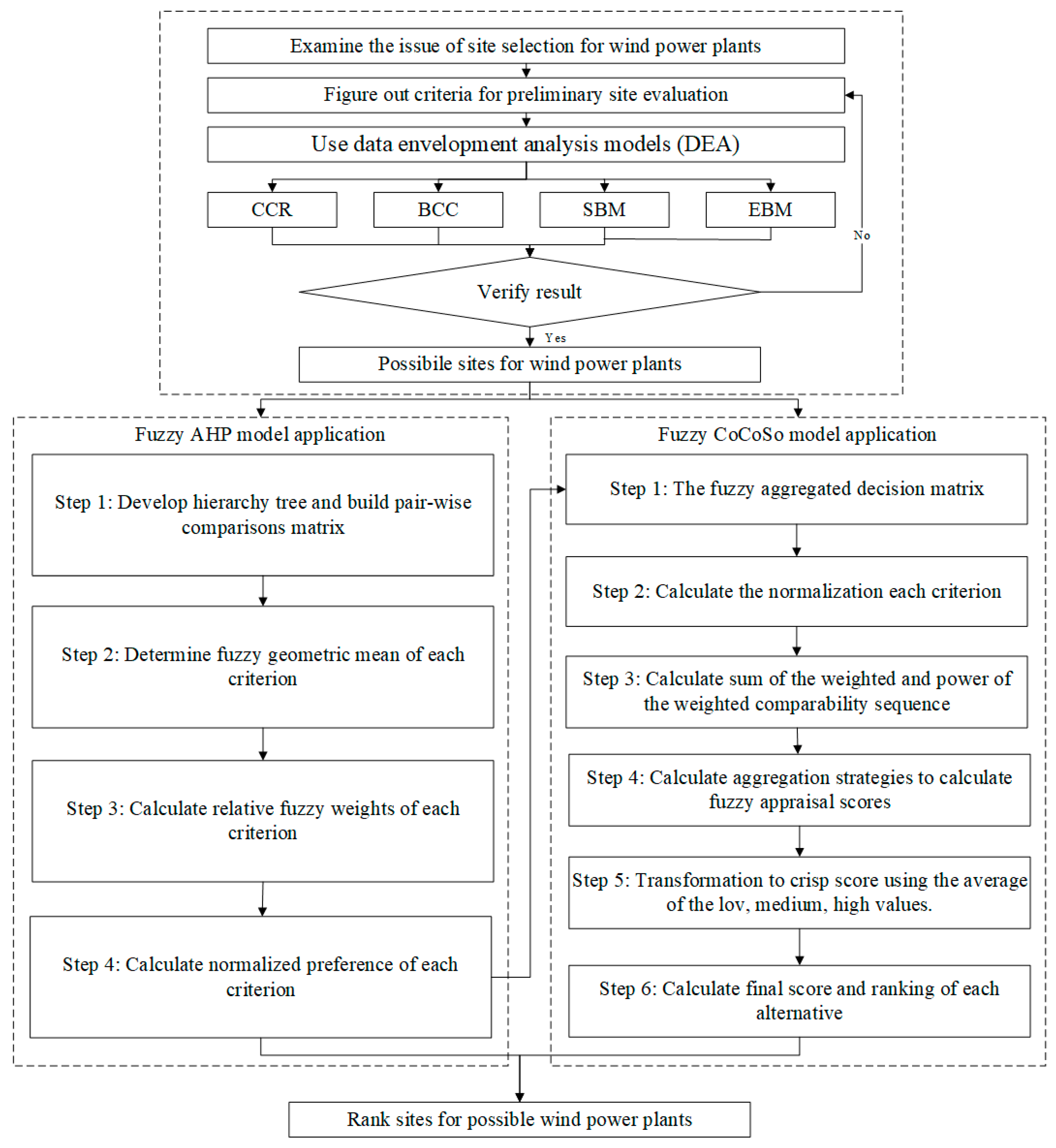
3. Methods
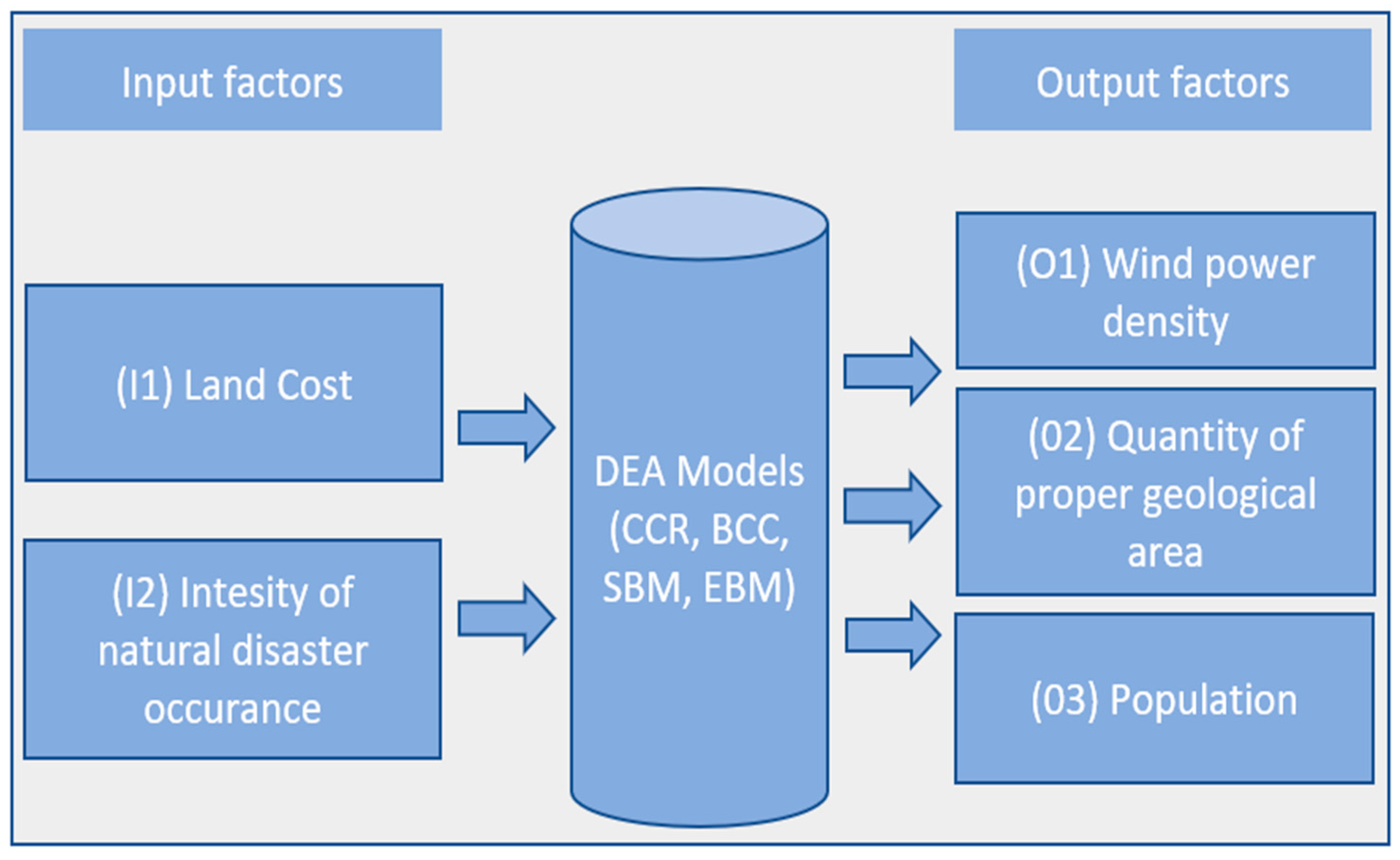
3.1. Data Envelopment Analysis (DEA)
3.1.1. Charnes, Cooper, Rhodes Model (CCR)
3.1.2. Banker, Charnes, and Cooper Model (BCC)
3.1.3. Slack-Based Measure Model (SBM)
3.1.4. Epsilon-Based Measure Model (EBM)
3.2. FAHP
3.3. Fuzzy Combined Compromise Solution Method (F-CoCoSo)
4. A Case Study in Indonesia
4.1. Using DEA Models to Screen Prospective Locations
4.2. Phase II: Ordering the Remaining Locations by Rank
4.2.1. Estimating Fuzzy Weights Using the FAHP Model
4.2.2. Ranking the Location Using the F-CoCoSo Model
5. Discussion
5.1. Methodological Contribution
5.2. Interpretation of Results
5.3. Practical Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Location | DMU | (I1) | (I2) | (O1) | (O2) | (O3) |
|---|---|---|---|---|---|---|
| Aceh | LOC-01 | 4000 | 0.037 | 161 | 540.79 | 5.41 |
| Bali | LOC-02 | 17,000 | 0.015 | 145 | 441.51 | 4.42 |
| Banten | LOC-03 | 16,000 | 0.017 | 209 | 1225.2 | 12.25 |
| Bengkulu | LOC-04 | 6000 | 0.007 | 130 | 206.01 | 2.06 |
| DI Yogyakarta | LOC-05 | 7000 | 0.012 | 196 | 376.19 | 3.76 |
| DKI Jakarta | LOC-06 | 24,000 | 0.009 | 90 | 1068 | 10.68 |
| Gorontalo | LOC-07 | 4000 | 0.005 | 158 | 119.27 | 1.19 |
| Jambi | LOC-08 | 2500 | 0.008 | 76 | 363.11 | 3.63 |
| West Java | LOC-09 | 10,000 | 0.176 | 189 | 4940.5 | 49.41 |
| Central Java | LOC-10 | 7500 | 0.293 | 185 | 3703.2 | 37.03 |
| East Java | LOC-11 | 13,000 | 0.119 | 229 | 4115 | 41.15 |
| West Kalimantan | LOC-12 | 6000 | 0.015 | 70 | 554.14 | 5.54 |
| South Kalimantan | LOC-13 | 8000 | 0.017 | 119 | 418.21 | 4.18 |
| Central Kalimantan | LOC-14 | 6000 | 0.010 | 65 | 274.11 | 2.74 |
| East Kalimantan | LOC-15 | 8000 | 0.013 | 58 | 385.98 | 3.86 |
| Bangka Belitung Islands | LOC-16 | 4000 | 0.013 | 94 | 149.46 | 1.49 |
| Riau Islands | LOC-17 | 8000 | 0.003 | 114 | 217.98 | 2.18 |
| Lampung | LOC-18 | 4000 | 0.014 | 122 | 917.66 | 9.18 |
| Maluku | LOC-19 | 8000 | 0.006 | 225 | 188.17 | 1.88 |
| North Maluku | LOC-20 | 8000 | 0.005 | 78 | 131.93 | 1.32 |
| West Nusa Tenggara | LOC-21 | 8000 | 0.016 | 170 | 547.37 | 5.47 |
| East Nusa Tenggara | LOC-22 | 8000 | 0.014 | 288 | 546.63 | 5.47 |
| Papua | LOC-23 | 10,000 | 0.004 | 131 | 441.86 | 4.42 |
| West Papua | LOC-24 | 12,000 | 0.001 | 100 | 118.33 | 1.18 |
| Riau | LOC-25 | 4000 | 0.008 | 56 | 661.44 | 6.61 |
| West Sulawesi | LOC-26 | 6000 | 0.003 | 99 | 145.86 | 1.46 |
| South Sulawesi | LOC-27 | 8000 | 0.032 | 277 | 922.58 | 9.23 |
| Central Sulawesi | LOC-28 | 6000 | 0.014 | 115 | 306.61 | 3.07 |
| East Sulawesi | LOC-29 | 7000 | 0.006 | 81 | 270.17 | 2.70 |
| North Sulawesi | LOC-30 | 5000 | 0.010 | 158 | 265.95 | 2.66 |
| West Sumatra | LOC-31 | 5000 | 0.032 | 128 | 564.06 | 5.64 |
| South Sumatera | LOC-32 | 6000 | 0.031 | 89 | 865.7 | 8.66 |
| North Sumatera | LOC-33 | 5000 | 0.035 | 143 | 1511.52 | 15.12 |
| Criteria | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 1.0000 | 1.0000 | 1.0000 | 0.7319 | 1.0000 | 1.3663 | 0.8637 | 1.1802 | 1.5930 | 0.8027 | 1.1269 | 1.5397 |
| C12 | 0.7319 | 1.0000 | 1.3663 | 1.0000 | 1.0000 | 1.0000 | 0.5763 | 0.8247 | 1.2221 | 0.6110 | 0.8706 | 1.2699 |
| C13 | 0.6277 | 0.8473 | 1.1578 | 0.8183 | 1.2125 | 1.7351 | 1.0000 | 1.0000 | 1.0000 | 1.3299 | 1.8882 | 2.4403 |
| C21 | 0.6495 | 0.8874 | 1.2457 | 0.7875 | 1.1487 | 1.6367 | 0.4098 | 0.5296 | 0.7519 | 1.0000 | 1.0000 | 1.0000 |
| C22 | 0.6934 | 1.0000 | 1.4422 | 0.5921 | 0.8247 | 1.1895 | 0.5639 | 0.7725 | 1.0760 | 0.6934 | 1.0000 | 1.4422 |
| C23 | 0.9221 | 1.3663 | 1.9031 | 1.0000 | 1.4198 | 1.9082 | 0.5255 | 0.7319 | 1.0845 | 0.8805 | 1.2699 | 1.7351 |
| C24 | 1.0194 | 1.4587 | 1.9316 | 0.4778 | 0.6250 | 0.8874 | 0.8407 | 1.2360 | 1.7021 | 0.9733 | 1.3928 | 1.8801 |
| C25 | 0.9733 | 1.3928 | 1.8801 | 1.0194 | 1.4587 | 1.9316 | 0.7813 | 1.1269 | 1.5819 | 1.2944 | 1.7811 | 2.2521 |
| C31 | 0.5723 | 0.7875 | 1.1055 | 0.8805 | 1.3046 | 1.8523 | 1.2599 | 1.9031 | 2.5487 | 0.9922 | 1.4702 | 2.0317 |
| C32 | 0.6371 | 0.8637 | 1.1895 | 0.7519 | 1.0194 | 1.3868 | 0.4240 | 0.5547 | 0.8091 | 0.4562 | 0.5809 | 0.8091 |
| C33 | 0.3497 | 0.4757 | 0.7376 | 0.7074 | 1.0000 | 1.4137 | 0.3808 | 0.5296 | 0.8091 | 0.4440 | 0.5361 | 0.7180 |
| C34 | 0.5921 | 0.8247 | 1.1895 | 0.5994 | 0.8473 | 1.2125 | 0.6988 | 1.0000 | 1.4310 | 0.6934 | 1.0000 | 1.4422 |
| C41 | 1.0882 | 1.6567 | 2.2894 | 0.6934 | 1.0000 | 1.4422 | 0.4909 | 0.6673 | 0.9367 | 1.0194 | 1.5277 | 2.0784 |
| C42 | 1.2599 | 1.7473 | 2.2188 | 0.9657 | 1.4702 | 2.0873 | 1.0391 | 1.5397 | 2.1596 | 1.0194 | 1.5277 | 2.1504 |
| C43 | 0.3023 | 0.4109 | 0.6250 | 0.6988 | 0.9294 | 1.2457 | 0.3637 | 0.4982 | 0.7376 | 0.3866 | 0.4922 | 0.7180 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| C11 | 0.6934 | 1.0000 | 1.4422 | 0.5255 | 0.7319 | 1.0845 | 0.5177 | 0.6856 | 0.9810 | 0.5319 | 0.7180 | 1.0274 |
| C12 | 0.8407 | 1.2125 | 1.6888 | 0.5240 | 0.7043 | 1.0000 | 1.1269 | 1.5999 | 2.0930 | 0.5177 | 0.6856 | 0.9810 |
| C13 | 0.9294 | 1.2944 | 1.7735 | 0.9221 | 1.3663 | 1.9031 | 0.5875 | 0.8091 | 1.1895 | 0.6322 | 0.8874 | 1.2799 |
| C21 | 0.6934 | 1.0000 | 1.4422 | 0.5763 | 0.7875 | 1.1358 | 0.5319 | 0.7180 | 1.0274 | 0.4440 | 0.5614 | 0.7725 |
| C22 | 1.0000 | 1.0000 | 1.0000 | 0.5399 | 0.7319 | 1.0556 | 0.5763 | 0.7875 | 1.1358 | 0.3971 | 0.5319 | 0.7579 |
| C23 | 0.9474 | 1.3663 | 1.8523 | 1.0000 | 1.0000 | 1.0000 | 0.6988 | 1.0000 | 1.4310 | 0.4630 | 0.6201 | 0.8944 |
| C24 | 0.8805 | 1.2699 | 1.7351 | 0.6988 | 1.0000 | 1.4310 | 1.0000 | 1.0000 | 1.0000 | 0.4700 | 0.6322 | 0.9189 |
| C25 | 1.3195 | 1.8801 | 2.5179 | 1.1181 | 1.6125 | 2.1596 | 1.0882 | 1.5819 | 2.1277 | 1.0000 | 1.0000 | 1.0000 |
| C31 | 0.7319 | 1.0968 | 1.5819 | 0.7665 | 1.1487 | 1.6252 | 0.6673 | 0.8874 | 1.2125 | 0.3637 | 0.4757 | 0.6856 |
| C32 | 0.4562 | 0.5809 | 0.8091 | 0.4562 | 0.5809 | 0.8091 | 0.3866 | 0.4922 | 0.7180 | 0.3166 | 0.4368 | 0.6856 |
| C33 | 0.3839 | 0.4849 | 0.6546 | 0.4098 | 0.5547 | 0.8091 | 1.0676 | 1.4986 | 1.9031 | 0.3515 | 0.4542 | 0.6371 |
| C34 | 0.7813 | 1.1055 | 1.5695 | 0.6988 | 1.0000 | 1.4310 | 0.6934 | 1.0000 | 1.4422 | 0.6371 | 0.8637 | 1.1895 |
| C41 | 0.7024 | 1.0194 | 1.3868 | 0.8637 | 1.2944 | 1.8444 | 0.7519 | 1.0000 | 1.3299 | 0.4630 | 0.6201 | 0.8944 |
| C42 | 1.2030 | 1.7007 | 2.2521 | 1.2944 | 1.8523 | 2.4875 | 1.0391 | 1.5397 | 2.0873 | 1.0882 | 1.5930 | 2.2188 |
| C43 | 0.3971 | 0.4849 | 0.6546 | 0.3866 | 0.5399 | 0.8312 | 0.3866 | 0.4922 | 0.7180 | 0.4409 | 0.5880 | 0.8091 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| C11 | 0.9046 | 1.2699 | 1.7473 | 0.8407 | 1.1578 | 1.5695 | 1.3557 | 2.1020 | 2.8598 | 0.8407 | 1.2125 | 1.6888 |
| C12 | 0.5399 | 0.7665 | 1.1358 | 0.7211 | 0.9810 | 1.3299 | 0.7074 | 1.0000 | 1.4137 | 0.8247 | 1.1802 | 1.6684 |
| C13 | 0.3924 | 0.5255 | 0.7937 | 1.2360 | 1.8029 | 2.3586 | 1.2360 | 1.8882 | 2.6257 | 0.6988 | 1.0000 | 1.4310 |
| C21 | 0.4922 | 0.6802 | 1.0079 | 1.2360 | 1.7215 | 2.1920 | 1.3928 | 1.8654 | 2.2521 | 0.6934 | 1.0000 | 1.4422 |
| C22 | 0.6322 | 0.9117 | 1.3663 | 1.2360 | 1.7215 | 2.1920 | 1.5277 | 2.0621 | 2.6052 | 0.6371 | 0.9046 | 1.2799 |
| C23 | 0.6153 | 0.8706 | 1.3046 | 1.2360 | 1.7215 | 2.1920 | 1.2360 | 1.8029 | 2.4403 | 0.6988 | 1.0000 | 1.4310 |
| C24 | 0.8247 | 1.1269 | 1.4986 | 1.3928 | 2.0317 | 2.5869 | 0.5255 | 0.6673 | 0.9367 | 0.6934 | 1.0000 | 1.4422 |
| C25 | 1.4587 | 2.1020 | 2.7499 | 1.4587 | 2.2894 | 3.1588 | 1.5695 | 2.2015 | 2.8451 | 0.8407 | 1.1578 | 1.5695 |
| C31 | 1.0000 | 1.0000 | 1.0000 | 1.1487 | 1.6438 | 2.1920 | 1.7215 | 2.6693 | 3.5596 | 1.1181 | 1.6125 | 2.0873 |
| C32 | 0.4562 | 0.6084 | 0.8706 | 1.0000 | 1.0000 | 1.0000 | 0.9221 | 1.3663 | 1.9031 | 0.9046 | 1.3299 | 1.8171 |
| C33 | 0.2809 | 0.3746 | 0.5809 | 0.5255 | 0.7319 | 1.0845 | 1.0000 | 1.0000 | 1.0000 | 0.4791 | 0.6201 | 0.8944 |
| C34 | 0.4791 | 0.6201 | 0.8944 | 0.5503 | 0.7519 | 1.1055 | 1.1181 | 1.6125 | 2.0873 | 1.0000 | 1.0000 | 1.0000 |
| C41 | 0.6934 | 1.0000 | 1.4422 | 1.0391 | 1.5397 | 2.0873 | 0.7665 | 1.0968 | 1.5105 | 0.9046 | 1.3557 | 1.8949 |
| C42 | 0.8805 | 1.2699 | 1.7351 | 1.0194 | 1.4587 | 1.9316 | 1.0194 | 1.4986 | 1.9931 | 1.0882 | 1.5819 | 2.1277 |
| C43 | 0.3081 | 0.4222 | 0.6546 | 0.4356 | 0.5809 | 0.8473 | 0.4159 | 0.5654 | 0.8312 | 0.4159 | 0.5399 | 0.7725 |
| Criteria | C41 | C42 | C43 | |||||||||
| C11 | 0.4368 | 0.6036 | 0.9189 | 0.4507 | 0.5723 | 0.7937 | 1.5999 | 2.4336 | 3.3082 | |||
| C12 | 0.6934 | 1.0000 | 1.4422 | 0.4791 | 0.6802 | 1.0355 | 0.8027 | 1.0760 | 1.4310 | |||
| C13 | 1.0676 | 1.4986 | 2.0372 | 0.4630 | 0.6495 | 0.9624 | 1.3557 | 2.0071 | 2.7499 | |||
| C21 | 0.4811 | 0.6546 | 0.9810 | 0.4650 | 0.6546 | 0.9810 | 1.3928 | 2.0317 | 2.5869 | |||
| C22 | 0.7211 | 0.9810 | 1.4236 | 0.4440 | 0.5880 | 0.8312 | 1.5277 | 2.0621 | 2.5179 | |||
| C23 | 0.5422 | 0.7725 | 1.1578 | 0.4020 | 0.5399 | 0.7725 | 1.2030 | 1.8523 | 2.5869 | |||
| C24 | 0.7519 | 1.0000 | 1.3299 | 0.4791 | 0.6495 | 0.9624 | 1.3928 | 2.0317 | 2.5869 | |||
| C25 | 1.1181 | 1.6125 | 2.1596 | 0.4507 | 0.6277 | 0.9189 | 1.2360 | 1.7007 | 2.2679 | |||
| C31 | 0.6934 | 1.0000 | 1.4422 | 0.5763 | 0.7875 | 1.1358 | 1.5277 | 2.3687 | 3.2453 | |||
| C32 | 0.4791 | 0.6495 | 0.9624 | 0.5177 | 0.6856 | 0.9810 | 1.1802 | 1.7215 | 2.2957 | |||
| C33 | 0.6621 | 0.9117 | 1.3046 | 0.5017 | 0.6673 | 0.9810 | 1.2030 | 1.7687 | 2.4042 | |||
| C34 | 0.5277 | 0.7376 | 1.1055 | 0.4700 | 0.6322 | 0.9189 | 1.2944 | 1.8523 | 2.4042 | |||
| C41 | 1.0000 | 1.0000 | 1.0000 | 1.1487 | 1.5695 | 1.9690 | 1.6438 | 2.3687 | 3.1206 | |||
| C42 | 0.5079 | 0.6371 | 0.8706 | 1.0000 | 1.0000 | 1.0000 | 1.3557 | 2.0873 | 2.8374 | |||
| C43 | 0.3204 | 0.4222 | 0.6084 | 0.3524 | 0.4791 | 0.7376 | 1.0000 | 1.0000 | 1.0000 | |||
| Criteria | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aceh | 0.2467 | 0.4333 | 0.6333 | 0.3800 | 0.5800 | 0.7600 | 0.4733 | 0.6733 | 0.8400 | 0.3000 | 0.4800 | 0.6667 |
| DKI Jakarta | 0.2600 | 0.4600 | 0.6533 | 0.2133 | 0.3867 | 0.5800 | 0.3933 | 0.5800 | 0.7533 | 0.2267 | 0.4000 | 0.5933 |
| Gorontalo | 0.1667 | 0.3333 | 0.5267 | 0.2667 | 0.4600 | 0.6600 | 0.4067 | 0.6067 | 0.7800 | 0.5000 | 0.6867 | 0.8400 |
| West Java | 0.3200 | 0.5133 | 0.7000 | 0.3133 | 0.5000 | 0.6867 | 0.2667 | 0.4200 | 0.6000 | 0.3333 | 0.5267 | 0.7133 |
| Central Java | 0.3533 | 0.5533 | 0.7400 | 0.4333 | 0.6333 | 0.8133 | 0.3067 | 0.5000 | 0.6867 | 0.6200 | 0.7933 | 0.9133 |
| Lampung | 0.3667 | 0.5667 | 0.7533 | 0.3933 | 0.5933 | 0.7733 | 0.4200 | 0.6200 | 0.7933 | 0.2733 | 0.4533 | 0.6467 |
| Maluku | 0.2267 | 0.4067 | 0.6067 | 0.2867 | 0.4733 | 0.6667 | 0.3933 | 0.5933 | 0.7733 | 0.5533 | 0.7333 | 0.8733 |
| Papua | 0.2467 | 0.4333 | 0.6267 | 0.4467 | 0.6467 | 0.8267 | 0.5400 | 0.7200 | 0.8600 | 0.3800 | 0.5800 | 0.7600 |
| West Papua | 0.2533 | 0.4333 | 0.6333 | 0.5800 | 0.7600 | 0.9000 | 0.5267 | 0.7133 | 0.8600 | 0.1867 | 0.3400 | 0.5267 |
| Riau | 0.2133 | 0.3667 | 0.5533 | 0.1400 | 0.3067 | 0.5000 | 0.2733 | 0.4467 | 0.6333 | 0.1733 | 0.3267 | 0.5133 |
| North Sumatra | 0.2400 | 0.4133 | 0.6067 | 0.1333 | 0.2933 | 0.4867 | 0.2867 | 0.4667 | 0.6533 | 0.1200 | 0.2533 | 0.4333 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| Aceh | 0.4733 | 0.6667 | 0.8333 | 0.3533 | 0.5533 | 0.7400 | 0.3933 | 0.5933 | 0.7733 | 0.3800 | 0.5800 | 0.7600 |
| DKI Jakarta | 0.2600 | 0.4400 | 0.6267 | 0.3667 | 0.5667 | 0.7533 | 0.2867 | 0.4733 | 0.6667 | 0.2133 | 0.3867 | 0.5800 |
| Gorontalo | 0.4600 | 0.6600 | 0.8267 | 0.2267 | 0.4067 | 0.6067 | 0.4467 | 0.6467 | 0.8267 | 0.2667 | 0.4600 | 0.6600 |
| West Java | 0.1800 | 0.3200 | 0.5000 | 0.2467 | 0.4333 | 0.6267 | 0.5800 | 0.7600 | 0.9000 | 0.3133 | 0.5000 | 0.6867 |
| Central Java | 0.4067 | 0.6067 | 0.7867 | 0.2533 | 0.4333 | 0.6333 | 0.1400 | 0.3067 | 0.5000 | 0.4333 | 0.6333 | 0.8133 |
| Lampung | 0.3800 | 0.5667 | 0.7400 | 0.2133 | 0.3667 | 0.5533 | 0.1333 | 0.2933 | 0.4867 | 0.4733 | 0.6733 | 0.8400 |
| Maluku | 0.5000 | 0.6867 | 0.8400 | 0.2400 | 0.4133 | 0.6067 | 0.4733 | 0.6733 | 0.8467 | 0.3933 | 0.5800 | 0.7533 |
| Papua | 0.4733 | 0.6667 | 0.8267 | 0.4733 | 0.6667 | 0.8333 | 0.4600 | 0.6600 | 0.8400 | 0.4067 | 0.6067 | 0.7800 |
| West Papua | 0.4867 | 0.6733 | 0.8200 | 0.2333 | 0.4200 | 0.6200 | 0.3400 | 0.5400 | 0.7400 | 0.2667 | 0.4200 | 0.6000 |
| Riau | 0.2200 | 0.3800 | 0.5667 | 0.3600 | 0.5467 | 0.7200 | 0.1333 | 0.2867 | 0.4733 | 0.3067 | 0.5000 | 0.6867 |
| North Sumatra | 0.3467 | 0.5400 | 0.7200 | 0.6200 | 0.8000 | 0.9267 | 0.2467 | 0.4333 | 0.6333 | 0.4200 | 0.6200 | 0.7933 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| Aceh | 0.2667 | 0.4200 | 0.6000 | 0.2267 | 0.4000 | 0.5933 | 0.5000 | 0.6867 | 0.8400 | 0.6200 | 0.7933 | 0.9133 |
| DKI Jakarta | 0.3067 | 0.5000 | 0.6867 | 0.5000 | 0.6867 | 0.8400 | 0.4733 | 0.6667 | 0.8267 | 0.2733 | 0.4533 | 0.6467 |
| Gorontalo | 0.4200 | 0.6200 | 0.7933 | 0.3333 | 0.5267 | 0.7133 | 0.4867 | 0.6733 | 0.8200 | 0.5533 | 0.7333 | 0.8733 |
| West Java | 0.3933 | 0.5933 | 0.7733 | 0.6200 | 0.7933 | 0.9133 | 0.2200 | 0.3800 | 0.5667 | 0.3800 | 0.5800 | 0.7600 |
| Central Java | 0.2867 | 0.4733 | 0.6667 | 0.2733 | 0.4533 | 0.6467 | 0.3467 | 0.5400 | 0.7200 | 0.1867 | 0.3400 | 0.5267 |
| Lampung | 0.4467 | 0.6467 | 0.8267 | 0.5533 | 0.7333 | 0.8733 | 0.4733 | 0.6667 | 0.8333 | 0.1733 | 0.3267 | 0.5133 |
| Maluku | 0.5800 | 0.7600 | 0.9000 | 0.3800 | 0.5800 | 0.7600 | 0.2600 | 0.4400 | 0.6267 | 0.1200 | 0.2533 | 0.4333 |
| Papua | 0.1400 | 0.3067 | 0.5000 | 0.1867 | 0.3400 | 0.5267 | 0.4600 | 0.6600 | 0.8267 | 0.2267 | 0.4067 | 0.6067 |
| West Papua | 0.1333 | 0.2933 | 0.4867 | 0.1733 | 0.3267 | 0.5133 | 0.1800 | 0.3200 | 0.5000 | 0.4600 | 0.6533 | 0.8133 |
| Riau | 0.4733 | 0.6733 | 0.8467 | 0.1200 | 0.2533 | 0.4333 | 0.4067 | 0.6067 | 0.7867 | 0.2467 | 0.4333 | 0.6333 |
| North Sumatra | 0.4600 | 0.6600 | 0.8400 | 0.2600 | 0.4400 | 0.6267 | 0.3800 | 0.5667 | 0.7400 | 0.1000 | 0.2200 | 0.3933 |
| Criteria | C41 | C42 | C43 | |||||||||
| Aceh | 0.3133 | 0.5000 | 0.6867 | 0.3800 | 0.5800 | 0.7600 | 0.2267 | 0.4000 | 0.5933 | |||
| DKI Jakarta | 0.4333 | 0.6333 | 0.8133 | 0.1867 | 0.3400 | 0.5267 | 0.5000 | 0.6867 | 0.8400 | |||
| Gorontalo | 0.3933 | 0.5933 | 0.7733 | 0.1733 | 0.3267 | 0.5133 | 0.3333 | 0.5267 | 0.7133 | |||
| West Java | 0.2867 | 0.4733 | 0.6667 | 0.1200 | 0.2533 | 0.4333 | 0.6200 | 0.7933 | 0.9133 | |||
| Central Java | 0.4467 | 0.6467 | 0.8267 | 0.2267 | 0.4067 | 0.6067 | 0.2733 | 0.4533 | 0.6467 | |||
| Lampung | 0.5800 | 0.7600 | 0.9000 | 0.4600 | 0.6533 | 0.8133 | 0.5533 | 0.7333 | 0.8733 | |||
| Maluku | 0.1400 | 0.3067 | 0.5000 | 0.2467 | 0.4333 | 0.6333 | 0.3800 | 0.5800 | 0.7600 | |||
| Papua | 0.3200 | 0.5133 | 0.7000 | 0.1000 | 0.2200 | 0.3933 | 0.1867 | 0.3400 | 0.5267 | |||
| West Papua | 0.3533 | 0.5533 | 0.7400 | 0.2667 | 0.4200 | 0.6000 | 0.1733 | 0.3267 | 0.5133 | |||
| Riau | 0.3667 | 0.5667 | 0.7533 | 0.3067 | 0.5000 | 0.6867 | 0.1200 | 0.2533 | 0.4333 | |||
| North Sumatra | 0.2267 | 0.4067 | 0.6067 | 0.4200 | 0.6200 | 0.7933 | 0.2267 | 0.4067 | 0.6067 | |||
| Criteria | C11 | C12 | C13 | C14 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aceh | 0.1364 | 0.4545 | 0.7955 | 0.3217 | 0.5826 | 0.8174 | 0.0337 | 0.3146 | 0.6517 | 0.3109 | 0.5462 | 0.7731 |
| DKI Jakarta | 0.1591 | 0.5000 | 0.8295 | 0.1043 | 0.3304 | 0.5826 | 0.1798 | 0.4719 | 0.7865 | 0.4034 | 0.6471 | 0.8655 |
| Gorontalo | 0.0000 | 0.2841 | 0.6136 | 0.1739 | 0.4261 | 0.6870 | 0.1348 | 0.4270 | 0.7640 | 0.0924 | 0.2857 | 0.5210 |
| West Java | 0.2614 | 0.5909 | 0.9091 | 0.2348 | 0.4783 | 0.7217 | 0.4382 | 0.7416 | 1.0000 | 0.2521 | 0.4874 | 0.7311 |
| Central Java | 0.3182 | 0.6591 | 0.9773 | 0.3913 | 0.6522 | 0.8870 | 0.2921 | 0.6067 | 0.9326 | 0.0000 | 0.1513 | 0.3697 |
| Lampung | 0.3409 | 0.6818 | 1.0000 | 0.3391 | 0.6000 | 0.8348 | 0.1124 | 0.4045 | 0.7416 | 0.3361 | 0.5798 | 0.8067 |
| Maluku | 0.1023 | 0.4091 | 0.7500 | 0.2000 | 0.4435 | 0.6957 | 0.1461 | 0.4494 | 0.7865 | 0.0504 | 0.2269 | 0.4538 |
| Papua | 0.1364 | 0.4545 | 0.7841 | 0.4087 | 0.6696 | 0.9043 | 0.0000 | 0.2360 | 0.5393 | 0.1933 | 0.4202 | 0.6723 |
| West Papua | 0.1477 | 0.4545 | 0.7955 | 0.5826 | 0.8174 | 1.0000 | 0.0000 | 0.2472 | 0.5618 | 0.4874 | 0.7227 | 0.9160 |
| Riau | 0.0795 | 0.3409 | 0.6591 | 0.0087 | 0.2261 | 0.4783 | 0.3820 | 0.6966 | 0.9888 | 0.5042 | 0.7395 | 0.9328 |
| North Sumatra | 0.1250 | 0.4205 | 0.7500 | 0.0000 | 0.2087 | 0.4609 | 0.3483 | 0.6629 | 0.9663 | 0.6050 | 0.8319 | 1.0000 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| Aceh | 0.4444 | 0.7374 | 0.9899 | 0.2617 | 0.5234 | 0.8037 | 0.1652 | 0.4000 | 0.6609 | 0.1277 | 0.4149 | 0.7340 |
| DKI Jakarta | 0.1212 | 0.3939 | 0.6768 | 0.2430 | 0.5047 | 0.7850 | 0.3043 | 0.5565 | 0.8000 | 0.4149 | 0.7234 | 1.0000 |
| Gorontalo | 0.4242 | 0.7273 | 0.9798 | 0.4486 | 0.7290 | 0.9813 | 0.0957 | 0.3304 | 0.5913 | 0.2872 | 0.6064 | 0.9149 |
| West Java | 0.0000 | 0.2121 | 0.4848 | 0.4206 | 0.6916 | 0.9533 | 0.0000 | 0.1826 | 0.4174 | 0.2447 | 0.5426 | 0.8404 |
| Central Java | 0.3434 | 0.6465 | 0.9192 | 0.4112 | 0.6916 | 0.9439 | 0.5217 | 0.7739 | 0.9913 | 0.0426 | 0.3298 | 0.6489 |
| Lampung | 0.3030 | 0.5859 | 0.8485 | 0.5234 | 0.7850 | 1.0000 | 0.5391 | 0.7913 | 1.0000 | 0.0000 | 0.2660 | 0.5851 |
| Maluku | 0.4848 | 0.7677 | 1.0000 | 0.4486 | 0.7196 | 0.9626 | 0.0696 | 0.2957 | 0.5565 | 0.1383 | 0.4149 | 0.7128 |
| Papua | 0.4444 | 0.7374 | 0.9798 | 0.1308 | 0.3645 | 0.6355 | 0.0783 | 0.3130 | 0.5739 | 0.0957 | 0.3723 | 0.6915 |
| West Papua | 0.4646 | 0.7475 | 0.9697 | 0.4299 | 0.7103 | 0.9720 | 0.2087 | 0.4696 | 0.7304 | 0.3830 | 0.6702 | 0.9149 |
| Riau | 0.0606 | 0.3030 | 0.5859 | 0.2897 | 0.5327 | 0.7944 | 0.5565 | 0.8000 | 1.0000 | 0.2447 | 0.5426 | 0.8511 |
| North Sumatra | 0.2525 | 0.5455 | 0.8182 | 0.0000 | 0.1776 | 0.4299 | 0.3478 | 0.6087 | 0.8522 | 0.0745 | 0.3511 | 0.6702 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| Aceh | 0.1739 | 0.3739 | 0.6087 | 0.1345 | 0.3529 | 0.5966 | 0.4848 | 0.7677 | 1.0000 | 0.6393 | 0.8525 | 1.0000 |
| DKI Jakarta | 0.2261 | 0.4783 | 0.7217 | 0.4790 | 0.7143 | 0.9076 | 0.4444 | 0.7374 | 0.9798 | 0.2131 | 0.4344 | 0.6721 |
| Gorontalo | 0.3739 | 0.6348 | 0.8609 | 0.2689 | 0.5126 | 0.7479 | 0.4646 | 0.7475 | 0.9697 | 0.5574 | 0.7787 | 0.9508 |
| West Java | 0.3391 | 0.6000 | 0.8348 | 0.6303 | 0.8487 | 1.0000 | 0.0606 | 0.3030 | 0.5859 | 0.3443 | 0.5902 | 0.8115 |
| Central Java | 0.2000 | 0.4435 | 0.6957 | 0.1933 | 0.4202 | 0.6639 | 0.2525 | 0.5455 | 0.8182 | 0.1066 | 0.2951 | 0.5246 |
| Lampung | 0.4087 | 0.6696 | 0.9043 | 0.5462 | 0.7731 | 0.9496 | 0.4444 | 0.7374 | 0.9899 | 0.0902 | 0.2787 | 0.5082 |
| Maluku | 0.5826 | 0.8174 | 1.0000 | 0.3277 | 0.5798 | 0.8067 | 0.1212 | 0.3939 | 0.6768 | 0.0246 | 0.1885 | 0.4098 |
| Papua | 0.0087 | 0.2261 | 0.4783 | 0.0840 | 0.2773 | 0.5126 | 0.4242 | 0.7273 | 0.9798 | 0.1557 | 0.3770 | 0.6230 |
| West Papua | 0.0000 | 0.2087 | 0.4609 | 0.0672 | 0.2605 | 0.4958 | 0.0000 | 0.2121 | 0.4848 | 0.4426 | 0.6803 | 0.8770 |
| Riau | 0.4435 | 0.7043 | 0.9304 | 0.0000 | 0.1681 | 0.3950 | 0.3434 | 0.6465 | 0.9192 | 0.1803 | 0.4098 | 0.6557 |
| North Sumatra | 0.4261 | 0.6870 | 0.9217 | 0.1765 | 0.4034 | 0.6387 | 0.3030 | 0.5859 | 0.8485 | 0.0000 | 0.1475 | 0.3607 |
| Criteria | C41 | C42 | C43 | |||||||||
| Aceh | 0.2807 | 0.5263 | 0.7719 | 0.3925 | 0.6729 | 0.9252 | 0.4034 | 0.6471 | 0.8655 | |||
| DKI Jakarta | 0.1140 | 0.3509 | 0.6140 | 0.1215 | 0.3364 | 0.5981 | 0.0924 | 0.2857 | 0.5210 | |||
| Gorontalo | 0.1667 | 0.4035 | 0.6667 | 0.1028 | 0.3178 | 0.5794 | 0.2521 | 0.4874 | 0.7311 | |||
| West Java | 0.3070 | 0.5614 | 0.8070 | 0.0280 | 0.2150 | 0.4673 | 0.0000 | 0.1513 | 0.3697 | |||
| Central Java | 0.0965 | 0.3333 | 0.5965 | 0.1776 | 0.4299 | 0.7103 | 0.3361 | 0.5798 | 0.8067 | |||
| Lampung | 0.0000 | 0.1842 | 0.4211 | 0.5047 | 0.7757 | 1.0000 | 0.0504 | 0.2269 | 0.4538 | |||
| Maluku | 0.5263 | 0.7807 | 1.0000 | 0.2056 | 0.4673 | 0.7477 | 0.1933 | 0.4202 | 0.6723 | |||
| Papua | 0.2632 | 0.5088 | 0.7632 | 0.0000 | 0.1682 | 0.4112 | 0.4874 | 0.7227 | 0.9160 | |||
| West Papua | 0.2105 | 0.4561 | 0.7193 | 0.2336 | 0.4486 | 0.7009 | 0.5042 | 0.7395 | 0.9328 | |||
| Riau | 0.1930 | 0.4386 | 0.7018 | 0.2897 | 0.5607 | 0.8224 | 0.6050 | 0.8319 | 1.0000 | |||
| North Sumatra | 0.3860 | 0.6491 | 0.8860 | 0.4486 | 0.7290 | 0.9720 | 0.3866 | 0.6387 | 0.8655 | |||
| Criteria | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aceh | 0.0049 | 0.0302 | 0.0994 | 0.0106 | 0.0356 | 0.0949 | 0.0013 | 0.0235 | 0.0914 | 0.0101 | 0.0328 | 0.0871 |
| DKI Jakarta | 0.0057 | 0.0332 | 0.1037 | 0.0034 | 0.0202 | 0.0677 | 0.0071 | 0.0352 | 0.1103 | 0.0132 | 0.0388 | 0.0975 |
| Gorontalo | 0.0000 | 0.0189 | 0.0767 | 0.0057 | 0.0261 | 0.0798 | 0.0053 | 0.0319 | 0.1072 | 0.0030 | 0.0171 | 0.0587 |
| West Java | 0.0093 | 0.0392 | 0.1136 | 0.0077 | 0.0292 | 0.0838 | 0.0173 | 0.0553 | 0.1403 | 0.0082 | 0.0292 | 0.0824 |
| Central Java | 0.0114 | 0.0438 | 0.1221 | 0.0129 | 0.0399 | 0.1030 | 0.0115 | 0.0453 | 0.1308 | 0.0000 | 0.0091 | 0.0417 |
| Lampung | 0.0122 | 0.0453 | 0.1250 | 0.0111 | 0.0367 | 0.0969 | 0.0044 | 0.0302 | 0.1040 | 0.0110 | 0.0348 | 0.0909 |
| Maluku | 0.0036 | 0.0272 | 0.0937 | 0.0066 | 0.0271 | 0.0808 | 0.0058 | 0.0335 | 0.1103 | 0.0016 | 0.0136 | 0.0511 |
| Papua | 0.0049 | 0.0302 | 0.0980 | 0.0134 | 0.0409 | 0.1050 | 0.0000 | 0.0176 | 0.0757 | 0.0063 | 0.0252 | 0.0757 |
| West Papua | 0.0053 | 0.0302 | 0.0994 | 0.0191 | 0.0500 | 0.1161 | 0.0000 | 0.0184 | 0.0788 | 0.0159 | 0.0433 | 0.1032 |
| Riau | 0.0028 | 0.0226 | 0.0824 | 0.0003 | 0.0138 | 0.0555 | 0.0150 | 0.0520 | 0.1387 | 0.0164 | 0.0443 | 0.1051 |
| North Sumatra | 0.0045 | 0.0279 | 0.0937 | 0.0000 | 0.0128 | 0.0535 | 0.0137 | 0.0495 | 0.1356 | 0.0197 | 0.0499 | 0.1127 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| Aceh | 0.0152 | 0.0464 | 0.1169 | 0.0096 | 0.0365 | 0.1059 | 0.0061 | 0.0275 | 0.0840 | 0.0065 | 0.0401 | 0.1284 |
| DKI Jakarta | 0.0041 | 0.0248 | 0.0799 | 0.0090 | 0.0352 | 0.1035 | 0.0113 | 0.0383 | 0.1017 | 0.0211 | 0.0699 | 0.1749 |
| Gorontalo | 0.0145 | 0.0458 | 0.1157 | 0.0165 | 0.0509 | 0.1293 | 0.0035 | 0.0227 | 0.0752 | 0.0146 | 0.0586 | 0.1600 |
| West Java | 0.0000 | 0.0134 | 0.0573 | 0.0155 | 0.0483 | 0.1256 | 0.0000 | 0.0126 | 0.0530 | 0.0124 | 0.0524 | 0.1470 |
| Central Java | 0.0117 | 0.0407 | 0.1085 | 0.0152 | 0.0483 | 0.1244 | 0.0193 | 0.0532 | 0.1260 | 0.0022 | 0.0318 | 0.1135 |
| Lampung | 0.0104 | 0.0369 | 0.1002 | 0.0193 | 0.0548 | 0.1318 | 0.0200 | 0.0544 | 0.1271 | 0.0000 | 0.0257 | 0.1023 |
| Maluku | 0.0166 | 0.0484 | 0.1181 | 0.0165 | 0.0502 | 0.1269 | 0.0026 | 0.0203 | 0.0707 | 0.0070 | 0.0401 | 0.1247 |
| Papua | 0.0152 | 0.0464 | 0.1157 | 0.0048 | 0.0254 | 0.0838 | 0.0029 | 0.0215 | 0.0729 | 0.0049 | 0.0360 | 0.1210 |
| West Papua | 0.0159 | 0.0471 | 0.1145 | 0.0158 | 0.0496 | 0.1281 | 0.0077 | 0.0323 | 0.0928 | 0.0195 | 0.0647 | 0.1600 |
| Riau | 0.0021 | 0.0191 | 0.0692 | 0.0107 | 0.0372 | 0.1047 | 0.0206 | 0.0550 | 0.1271 | 0.0124 | 0.0524 | 0.1489 |
| North Sumatra | 0.0086 | 0.0344 | 0.0966 | 0.0000 | 0.0124 | 0.0567 | 0.0129 | 0.0419 | 0.1083 | 0.0038 | 0.0339 | 0.1172 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| Aceh | 0.0071 | 0.0295 | 0.0896 | 0.0037 | 0.0174 | 0.0560 | 0.0122 | 0.0346 | 0.0865 | 0.0210 | 0.0521 | 0.1164 |
| DKI Jakarta | 0.0093 | 0.0378 | 0.1062 | 0.0131 | 0.0352 | 0.0851 | 0.0111 | 0.0332 | 0.0847 | 0.0070 | 0.0266 | 0.0782 |
| Gorontalo | 0.0154 | 0.0501 | 0.1267 | 0.0074 | 0.0253 | 0.0701 | 0.0116 | 0.0337 | 0.0839 | 0.0183 | 0.0476 | 0.1106 |
| West Java | 0.0139 | 0.0474 | 0.1229 | 0.0173 | 0.0419 | 0.0938 | 0.0015 | 0.0137 | 0.0507 | 0.0113 | 0.0361 | 0.0944 |
| Central Java | 0.0082 | 0.0350 | 0.1024 | 0.0053 | 0.0207 | 0.0623 | 0.0063 | 0.0246 | 0.0708 | 0.0035 | 0.0180 | 0.0610 |
| Lampung | 0.0168 | 0.0529 | 0.1331 | 0.0150 | 0.0381 | 0.0890 | 0.0111 | 0.0332 | 0.0856 | 0.0030 | 0.0170 | 0.0591 |
| Maluku | 0.0239 | 0.0645 | 0.1472 | 0.0090 | 0.0286 | 0.0757 | 0.0030 | 0.0178 | 0.0585 | 0.0008 | 0.0115 | 0.0477 |
| Papua | 0.0004 | 0.0179 | 0.0704 | 0.0023 | 0.0137 | 0.0481 | 0.0106 | 0.0328 | 0.0847 | 0.0051 | 0.0230 | 0.0725 |
| West Papua | 0.0000 | 0.0165 | 0.0678 | 0.0018 | 0.0129 | 0.0465 | 0.0000 | 0.0096 | 0.0419 | 0.0145 | 0.0416 | 0.1021 |
| Riau | 0.0182 | 0.0556 | 0.1369 | 0.0000 | 0.0083 | 0.0370 | 0.0086 | 0.0292 | 0.0795 | 0.0059 | 0.0250 | 0.0763 |
| North Sumatra | 0.0175 | 0.0542 | 0.1357 | 0.0048 | 0.0199 | 0.0599 | 0.0076 | 0.0264 | 0.0734 | 0.0000 | 0.0090 | 0.0420 |
| Criteria | C41 | C42 | C43 | |||||||||
| Aceh | 0.0112 | 0.0401 | 0.1089 | 0.0192 | 0.0632 | 0.1588 | 0.0080 | 0.0227 | 0.0594 | |||
| DKI Jakarta | 0.0046 | 0.0267 | 0.0866 | 0.0059 | 0.0316 | 0.1026 | 0.0018 | 0.0100 | 0.0357 | |||
| Gorontalo | 0.0067 | 0.0307 | 0.0940 | 0.0050 | 0.0298 | 0.0994 | 0.0050 | 0.0171 | 0.0501 | |||
| West Java | 0.0123 | 0.0428 | 0.1138 | 0.0014 | 0.0202 | 0.0802 | 0.0000 | 0.0053 | 0.0254 | |||
| Central Java | 0.0039 | 0.0254 | 0.0841 | 0.0087 | 0.0404 | 0.1219 | 0.0067 | 0.0204 | 0.0553 | |||
| Lampung | 0.0000 | 0.0140 | 0.0594 | 0.0247 | 0.0729 | 0.1716 | 0.0010 | 0.0080 | 0.0311 | |||
| Maluku | 0.0210 | 0.0595 | 0.1410 | 0.0100 | 0.0439 | 0.1283 | 0.0038 | 0.0148 | 0.0461 | |||
| Papua | 0.0105 | 0.0388 | 0.1076 | 0.0000 | 0.0158 | 0.0706 | 0.0097 | 0.0254 | 0.0628 | |||
| West Papua | 0.0084 | 0.0347 | 0.1015 | 0.0114 | 0.0421 | 0.1203 | 0.0100 | 0.0260 | 0.0640 | |||
| Riau | 0.0077 | 0.0334 | 0.0990 | 0.0142 | 0.0527 | 0.1411 | 0.0120 | 0.0292 | 0.0686 | |||
| North Sumatra | 0.0154 | 0.0494 | 0.1250 | 0.0219 | 0.0685 | 0.1668 | 0.0077 | 0.0224 | 0.0594 | |||
| Criteria | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aceh | 0.7796 | 0.9490 | 0.9919 | 0.8766 | 0.9675 | 0.9934 | 0.6215 | 0.9173 | 0.9833 | 0.8767 | 0.9644 | 0.9916 |
| DKI Jakarta | 0.7947 | 0.9550 | 0.9934 | 0.7692 | 0.9345 | 0.9824 | 0.7860 | 0.9455 | 0.9906 | 0.9028 | 0.9742 | 0.9953 |
| Gorontalo | 0.0000 | 0.9198 | 0.9827 | 0.8162 | 0.9492 | 0.9877 | 0.7549 | 0.9385 | 0.9895 | 0.7647 | 0.9276 | 0.9790 |
| Jawa Barat | 0.8456 | 0.9657 | 0.9966 | 0.8451 | 0.9559 | 0.9893 | 0.8907 | 0.9779 | 1.0000 | 0.8562 | 0.9578 | 0.9898 |
| Jawa Tengah | 0.8666 | 0.9727 | 0.9992 | 0.8968 | 0.9742 | 0.9961 | 0.8414 | 0.9634 | 0.9973 | 0.0000 | 0.8929 | 0.9681 |
| Lampung | 0.8742 | 0.9749 | 1.0000 | 0.8820 | 0.9692 | 0.9941 | 0.7359 | 0.9347 | 0.9883 | 0.8844 | 0.9678 | 0.9930 |
| Maluku | 0.7520 | 0.9424 | 0.9898 | 0.8295 | 0.9515 | 0.9882 | 0.7635 | 0.9421 | 0.9906 | 0.7142 | 0.9149 | 0.9746 |
| Papua | 0.7796 | 0.9490 | 0.9914 | 0.9013 | 0.9758 | 0.9967 | 0.0062 | 0.8979 | 0.9760 | 0.8310 | 0.9493 | 0.9871 |
| Papua Barat | 0.7874 | 0.9490 | 0.9919 | 0.9392 | 0.9877 | 1.0000 | 0.0000 | 0.9010 | 0.9775 | 0.9222 | 0.9807 | 0.9971 |
| Riau | 0.7288 | 0.9310 | 0.9852 | 0.5764 | 0.9131 | 0.9761 | 0.8737 | 0.9734 | 0.9996 | 0.9257 | 0.9821 | 0.9977 |
| Sumatra Utara | 0.7711 | 0.9441 | 0.9898 | 0.0000 | 0.9086 | 0.9749 | 0.8625 | 0.9698 | 0.9987 | 0.9450 | 0.9890 | 1.0000 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| Aceh | 0.9087 | 0.9810 | 0.9997 | 0.8380 | 0.9558 | 0.9920 | 0.7955 | 0.9389 | 0.9848 | 0.6976 | 0.9186 | 0.9844 |
| DKI Jakarta | 0.7794 | 0.9430 | 0.9867 | 0.8299 | 0.9534 | 0.9911 | 0.8597 | 0.9605 | 0.9918 | 0.8574 | 0.9692 | 1.0000 |
| Gorontalo | 0.9037 | 0.9801 | 0.9993 | 0.8997 | 0.9782 | 0.9993 | 0.7421 | 0.9267 | 0.9807 | 0.8040 | 0.9528 | 0.9955 |
| Jawa Barat | 0.0000 | 0.9070 | 0.9755 | 0.8921 | 0.9746 | 0.9982 | 0.0000 | 0.8896 | 0.9682 | 0.7817 | 0.9427 | 0.9912 |
| Jawa Tengah | 0.8814 | 0.9729 | 0.9971 | 0.8895 | 0.9746 | 0.9979 | 0.9206 | 0.9825 | 0.9997 | 0.5757 | 0.8984 | 0.9783 |
| Lampung | 0.8685 | 0.9669 | 0.9944 | 0.9182 | 0.9832 | 1.0000 | 0.9245 | 0.9840 | 1.0000 | 0.0000 | 0.8800 | 0.9731 |
| Maluku | 0.9181 | 0.9835 | 1.0000 | 0.8997 | 0.9773 | 0.9986 | 0.7126 | 0.9196 | 0.9785 | 0.7075 | 0.9186 | 0.9829 |
| Papua | 0.9087 | 0.9810 | 0.9993 | 0.7649 | 0.9320 | 0.9834 | 0.7234 | 0.9232 | 0.9796 | 0.6634 | 0.9090 | 0.9814 |
| Papua Barat | 0.9135 | 0.9818 | 0.9989 | 0.8947 | 0.9764 | 0.9990 | 0.8194 | 0.9493 | 0.9884 | 0.8455 | 0.9621 | 0.9955 |
| Riau | 0.7182 | 0.9276 | 0.9819 | 0.8494 | 0.9570 | 0.9916 | 0.9282 | 0.9848 | 1.0000 | 0.7817 | 0.9427 | 0.9918 |
| Sumatra Utara | 0.8500 | 0.9625 | 0.9932 | 0.0000 | 0.8863 | 0.9694 | 0.8744 | 0.9664 | 0.9941 | 0.6349 | 0.9039 | 0.9799 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| Aceh | 0.7730 | 0.9253 | 0.9798 | 0.8285 | 0.9499 | 0.9860 | 0.9393 | 0.9881 | 1.0000 | 0.9493 | 0.9903 | 1.0000 |
| DKI Jakarta | 0.8034 | 0.9434 | 0.9867 | 0.9333 | 0.9835 | 0.9973 | 0.9323 | 0.9864 | 0.9995 | 0.8354 | 0.9503 | 0.9871 |
| Gorontalo | 0.8652 | 0.9648 | 0.9939 | 0.8841 | 0.9676 | 0.9921 | 0.9359 | 0.9870 | 0.9992 | 0.9342 | 0.9848 | 0.9983 |
| Jawa Barat | 0.8529 | 0.9605 | 0.9926 | 0.9576 | 0.9919 | 1.0000 | 0.7847 | 0.9476 | 0.9867 | 0.8833 | 0.9683 | 0.9932 |
| Jawa Tengah | 0.7891 | 0.9378 | 0.9852 | 0.8572 | 0.9581 | 0.9888 | 0.8878 | 0.9730 | 0.9950 | 0.7706 | 0.9281 | 0.9791 |
| Lampung | 0.8766 | 0.9688 | 0.9959 | 0.9449 | 0.9874 | 0.9986 | 0.9323 | 0.9864 | 0.9997 | 0.7558 | 0.9249 | 0.9780 |
| Maluku | 0.9236 | 0.9842 | 1.0000 | 0.9007 | 0.9735 | 0.9941 | 0.8332 | 0.9589 | 0.9903 | 0.6497 | 0.9030 | 0.9712 |
| Papua | 0.4974 | 0.8892 | 0.9701 | 0.7928 | 0.9387 | 0.9819 | 0.9285 | 0.9857 | 0.9995 | 0.8054 | 0.9421 | 0.9846 |
| Papua Barat | 0.0000 | 0.8836 | 0.9687 | 0.7763 | 0.9358 | 0.9810 | 0.0000 | 0.9325 | 0.9820 | 0.9095 | 0.9767 | 0.9957 |
| Riau | 0.8872 | 0.9727 | 0.9970 | 0.0000 | 0.9158 | 0.9749 | 0.9117 | 0.9805 | 0.9979 | 0.8193 | 0.9469 | 0.9863 |
| Sumatra Utara | 0.8820 | 0.9708 | 0.9967 | 0.8499 | 0.9562 | 0.9878 | 0.9019 | 0.9762 | 0.9959 | 0.0000 | 0.8896 | 0.9671 |
| Criteria | C41 | C42 | C43 | |||||||||
| Aceh | 0.8359 | 0.9523 | 0.9897 | 0.8517 | 0.9635 | 0.9962 | 0.9396 | 0.9848 | 0.9971 | |||
| DKI Jakarta | 0.7362 | 0.9233 | 0.9807 | 0.6965 | 0.9027 | 0.9752 | 0.8493 | 0.9569 | 0.9872 | |||
| Gorontalo | 0.7767 | 0.9332 | 0.9839 | 0.6768 | 0.8979 | 0.9737 | 0.9098 | 0.9751 | 0.9938 | |||
| Jawa Barat | 0.8466 | 0.9570 | 0.9915 | 0.5416 | 0.8656 | 0.9635 | 0.0000 | 0.9358 | 0.9805 | |||
| Jawa Tengah | 0.7191 | 0.9197 | 0.9796 | 0.7434 | 0.9238 | 0.9834 | 0.9279 | 0.9810 | 0.9958 | |||
| Lampung | 0.0000 | 0.8791 | 0.9660 | 0.8893 | 0.9764 | 1.0000 | 0.8147 | 0.9492 | 0.9845 | |||
| Maluku | 0.9134 | 0.9813 | 1.0000 | 0.7623 | 0.9310 | 0.9859 | 0.8934 | 0.9700 | 0.9922 | |||
| Papua | 0.8284 | 0.9498 | 0.9893 | 0.0000 | 0.8459 | 0.9575 | 0.9519 | 0.9887 | 0.9983 | |||
| Papua Barat | 0.8027 | 0.9420 | 0.9869 | 0.7792 | 0.9275 | 0.9828 | 0.9541 | 0.9895 | 0.9986 | |||
| Riau | 0.7929 | 0.9392 | 0.9860 | 0.8085 | 0.9471 | 0.9905 | 0.9661 | 0.9936 | 1.0000 | |||
| Sumatra Utara | 0.8743 | 0.9676 | 0.9952 | 0.8715 | 0.9707 | 0.9986 | 0.9369 | 0.9844 | 0.9971 | |||
References
- Langer, J.; Quist, J.; Blok, K. Review of Renewable Energy Potentials in Indonesia and Their Contribution to a 100% Renewable Electricity System. Energies 2021, 14, 7033. [Google Scholar] [CrossRef]
- Gualtieri, G. A Comprehensive Review on Wind Resource Extrapolation Models Applied in Wind Energy. Renew. Sustain. Energy Rev. 2019, 102, 215–233. [Google Scholar] [CrossRef]
- Ariani, R.; Hamzani, A.I.; Rahayu, K. Acceleration of Clean Energy Use Based on The 2015 Paris Agreement. J. Energy Eng. Thermodyn. 2022, 2, 1–10. [Google Scholar] [CrossRef]
- Widya Yudha, S.; Tjahjono, B. Stakeholder Mapping and Analysis of the Renewable Energy Industry in Indonesia. Energies 2019, 12, 602. [Google Scholar] [CrossRef]
- Wang, C.-N.; Chung, Y.-C.; Wibowo, F.D.; Dang, T.-T.; Nguyen, N.-A.-T. Site Selection of Solar Power Plants Using Hybrid MCDM Models: A Case Study in Indonesia. Energies 2023, 16, 4042. [Google Scholar] [CrossRef]
- Felix, A.; Hernández-Fontes, J.V.; Lithgow, D.; Mendoza, E.; Posada, G.; Ring, M.; Silva, R. Wave Energy in Tropical Regions: Deployment Challenges, Environmental and Social Perspectives. J. Mar. Sci. Eng. 2019, 7, 219. [Google Scholar] [CrossRef]
- Guild, J. Feed-in-tariffs and the Politics of Renewable Energy in Indonesia and the Philippines. Asia Pac. Policy Stud. 2019, 6, 417–431. [Google Scholar] [CrossRef]
- Umam, M.F.; Selia, S.; Sunaryo, A.F.; Al Asy’ari, M.R. Energy Storage Applications to Address the Challenges of Solar PV and Wind Penetration in Indonesia: A Preliminary Study. Indones. J. Energy 2022, 5, 42–65. [Google Scholar] [CrossRef]
- Fauzy, A.; Yue, C.-D.; Tu, C.-C.; Lin, T.-H. Understanding the Potential of Wind Farm Exploitation in Tropical Island Countries: A Case for Indonesia. Energies 2021, 14, 2652. [Google Scholar] [CrossRef]
- Pristiandaru, D.L.; Pambudi, N.A. Wind Energy in Indonesia. Indones. J. Energy 2019, 2, 65–73. [Google Scholar] [CrossRef]
- Iswadi, A.; Porter, J.S.; Bell, M.C.; Garniati, L.; Harris, R.E.; Priyotomo, G. Establishing an Agenda for Biofouling Research for the Development of the Marine Renewable Energy Industry in Indonesia. J. Mar. Sci. Eng. 2022, 10, 384. [Google Scholar] [CrossRef]
- Situmeang, R.; Mazancová, J.; Roubík, H. Technological, Economic, Social and Environmental Barriers to Adoption of Small-Scale Biogas Plants: Case of Indonesia. Energies 2022, 15, 5105. [Google Scholar] [CrossRef]
- Udin, U. Renewable energy and human resource development: Challenges and opportunities in Indonesia. Int. J. Energy Econ. Policy 2020, 10, 233–237. [Google Scholar] [CrossRef]
- Wang, C.-N.; Huang, Y.-F.; Chai, Y.-C.; Nguyen, V. A Multi-Criteria Decision Making (MCDM) for Renewable Energy Plants Location Selection in Vietnam under a Fuzzy Environment. Appl. Sci. 2018, 8, 2069. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Hai, N.H.; Lan, N.T.K. Spherical Fuzzy Multicriteria Decision-Making Model for Wind Turbine Supplier Selection in a Renewable Energy Project. Energies 2022, 15, 713. [Google Scholar] [CrossRef]
- Rehman, S.; Khan, S. Fuzzy Logic Based Multi-Criteria Wind Turbine Selection Strategy—A Case Study of Qassim, Saudi Arabia. Energies 2016, 9, 872. [Google Scholar] [CrossRef]
- Daneshvar Rouyendegh, B.; Yildizbasi, A.; Arikan, Ü.Z.B. Using Intuitionistic Fuzzy TOPSIS in Site Selection of Wind Power Plants in Turkey. Adv. Fuzzy Syst. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Arı, E.S.; Gencer, C. The Use and Comparison of a Deterministic, a Stochastic, and a Hybrid Multiple-Criteria Decision-Making Method for Site Selection of Wind Power Plants: An Application in Turkey. Wind. Eng. 2020, 44, 60–74. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zheng, L.; Cui, L.; Li, S.; Li, W.; Cai, Y. Site Selection of Wind Farms Using GIS and Multi-Criteria Decision Making Method in Wafangdian, China. Energy 2020, 207, 118222. [Google Scholar] [CrossRef]
- Sadeghi, M.; Karimi, M. Gis-based solar and wind turbine site selection using multi-criteria analysis: Case study Tehran, Iran. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-4/W4, 469–476. [Google Scholar] [CrossRef]
- Qawaqzeh, M.Z.; Miroshnyk, O.; Shchur, T.; Kasner, R.; Idzikowski, A.; Kruszelnicka, W.; Tomporowski, A.; Bałdowska-Witos, P.; Flizikowski, J.; Zawada, M.; et al. Research of Emergency Modes of Wind Power Plants Using Computer Simulation. Energies 2021, 14, 4780. [Google Scholar] [CrossRef]
- Liu, L.R.; Huang, G.H.; Baetz, B.; Turchenek, K. A GIS-Based Decision-Making Support System for Wind Power Plant Site Selection, Case Study for Saskatchewan. J. Environ. Inform. Lett. 2019, 2, 102–110. [Google Scholar] [CrossRef]
- Camargo, L.A.S.; Leonel, L.D.; Rosa, P.S.; Ramos, D.S. Optimal Portfolio Selection of Wind Power Plants Using a Stochastic Risk-Averse Optimization Model, Considering the Wind Complementarity of the Sites and a Budget Constraint. Energy Power Eng. 2020, 12, 459–476. [Google Scholar] [CrossRef]
- Rose, S.; Apt, J. What Can Reanalysis Data Tell Us about Wind Power? Renew. Energy 2015, 83, 963–969. [Google Scholar] [CrossRef]
- Solangi, Y.; Tan, Q.; Khan, M.; Mirjat, N.; Ahmed, I. The Selection of Wind Power Project Location in the Southeastern Corridor of Pakistan: A Factor Analysis, AHP, and Fuzzy-TOPSIS Application. Energies 2018, 11, 1940. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; García-Cascales, M.S.; Lamata, M.T. GIS-Based Onshore Wind Farm Site Selection Using Fuzzy Multi-Criteria Decision Making Methods. Evaluating the Case of Southeastern Spain. Appl. Energy 2016, 171, 86–102. [Google Scholar] [CrossRef]
- Değirmenci, S.; Bingöl, F.; Sofuoglu, S.C. MCDM Analysis of Wind Energy in Turkey: Decision Making Based on Environmental Impact. Environ. Sci. Pollut. Res. 2018, 25, 19753–19766. [Google Scholar] [CrossRef]
- Mohammadzadeh Bina, S.; Jalilinasrabady, S.; Fujii, H.; Farabi-Asl, H. A Comprehensive Approach for Wind Power Plant Potential Assessment, Application to Northwestern Iran. Energy 2018, 164, 344–358. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Odigie, O.; Munda, J.L. A Multi-Criteria GIS Based Model for Wind Farm Site Selection Using Interval Type-2 Fuzzy Analytic Hierarchy Process: The Case Study of Nigeria. Appl. Energy 2018, 228, 1853–1869. [Google Scholar] [CrossRef]
- Güler, E.; Kandemir, S.Y. Evaluation of wind power plant potentials in the marmara region, Turkey via TOPSIS and PROMETHEE methods. In Proceedings of the IEEE 7th Iran Wind Energy Conference (IWEC2021), Shahrood, Iran, 17–18 May 2021; pp. 1–4. [Google Scholar]
- Wu, Y.; Zhang, T.; Xu, C.; Zhang, B.; Li, L.; Ke, Y.; Yan, Y.; Xu, R. Optimal Location Selection for Offshore Wind-PV-Seawater Pumped Storage Power Plant Using a Hybrid MCDM Approach: A Two-Stage Framework. Energy Convers. Manag. 2019, 199, 112066. [Google Scholar] [CrossRef]
- Pambudi, G.; Nananukul, N. Wind Turbine Site Selection in Indonesia, Based on a Hierarchical Dual Data Envelopment Analysis Model. Energy Procedia 2019, 158, 3290–3295. [Google Scholar] [CrossRef]
- Deveci, M.; Ozcan, E.; John, R. Offshore Wind Farms: A Fuzzy Approach to Site Selection in a Black Sea Region. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Mostafaeipour, A.; Sadeghi, S.; Jahangiri, M.; Nematollahi, O.; Rezaeian Sabbagh, A. Investigation of Accurate Location Planning for Wind Farm Establishment: A Case Study. J. Eng. Des. Technol. 2020, 18, 821–845. [Google Scholar] [CrossRef]
- Elhosiny, A.M.; El-Ghareeb, H.; Shabana, B.T.; AbouElfetouh, A. A Hybrid Neutrosophic GIS-MCDM Method Using a Weighted Combination Approach for Selecting Wind Energy Power Plant Locations: A Case Study of Sinai Peninsula, Egypt. Int. J. Fuzzy Log. Intell. Syst. 2021, 21, 12–28. [Google Scholar] [CrossRef]
- Azzioui, A.; Hajji, R.; Ettarid, M.; Bouhamidi, M.H. Towards a Dynamic Multi-Criteria Approach Based on GIS and MCDM for Wind Farm Site-Selection in Morocco. In Proceedings of the 2nd International Conference on Advanced Technologies for Humanity, Rabat, Morocco, 26–27 November 2021; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2020; pp. 92–102. [Google Scholar]
- Saraswat, S.K.; Digalwar, A.K.; Yadav, S.S.; Kumar, G. MCDM and GIS Based Modelling Technique for Assessment of Solar and Wind Farm Locations in India. Renew. Energy 2021, 169, 865–884. [Google Scholar] [CrossRef]
- Feloni, E.; Karandinaki, E. GIS-Based MCDM Approach for Wind Farm Site Selection—A Case Study. J. Energy Power Technol. 2021, 3, 39. [Google Scholar] [CrossRef]
- Asadi, M.; Pourhossein, K. Wind Farm Site Selection Considering Turbulence Intensity. Energy 2021, 236, 121480. [Google Scholar] [CrossRef]
- Sotiropoulou, K.F.; Vavatsikos, A.P. Onshore Wind Farms GIS-Assisted Suitability Analysis Using PROMETHEE II. Energy Policy 2021, 158, 112531. [Google Scholar] [CrossRef]
- Zahid, F.; Tahir, A.; Khan, H.U.; Naeem, M.A. Wind Farms Selection Using Geospatial Technologies and Energy Generation Capacity in Gwadar. Energy Rep. 2021, 7, 5857–5870. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.-T. Location Optimization of Wind Plants Using DEA and Fuzzy Multi-Criteria Decision Making: A Case Study in Vietnam. IEEE Access 2021, 9, 116265–116285. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, K.; Zhao, G. The Influencing Factors and Hierarchical Relationships of Offshore Wind Power Industry in China. Environ. Sci. Pollut. Res. 2021, 28, 52329–52344. [Google Scholar] [CrossRef]
- Nagababu, G.; Puppala, H.; Pritam, K.; Kantipudi, M.P. Two-Stage GIS-MCDM Based Algorithm to Identify Plausible Regions at Micro Level to Install Wind Farms: A Case Study of India. Energy 2022, 248, 123594. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Y.; Huang, N.; Wei, L.; Zhang, Z. Optimal Site Selection Study of Wind-Photovoltaic-Shared Energy Storage Power Stations Based on GIS and Multi-Criteria Decision Making: A Two-Stage Framework. Renew. Energy 2022, 201, 1139–1162. [Google Scholar] [CrossRef]
- Shorabeh, S.N.; Firozjaei, H.K.; Firozjaei, M.K.; Jelokhani-Niaraki, M.; Homaee, M.; Nematollahi, O. The Site Selection of Wind Energy Power Plant Using GIS-Multi-Criteria Evaluation from Economic Perspectives. Renew. Sustain. Energy Rev. 2022, 168, 112778. [Google Scholar] [CrossRef]
- Wu, Y.; Chu, H.; Dong, H.; Xu, C.; Chen, W.; Wu, G. Optimal Site Selection of Rural Wind–Photovoltaic-Storage Station from a Sustainable Development Perspective. Energy Rep. 2022, 8, 8381–8395. [Google Scholar] [CrossRef]
- Ajanaku, B.A.; Strager, M.P.; Collins, A.R. GIS-Based Multi-Criteria Decision Analysis of Utility-Scale Wind Farm Site Suitability in West Virginia. GeoJournal 2022, 87, 3735–3757. [Google Scholar] [CrossRef]
- Kumar, R.; Khetrapal, P.; Badoni, M.; Diwania, S. Evaluating the Relative Operational Performance of Wind Power Plants in Indian Electricity Generation Sector Using Two-Stage Model. Energy Environ. 2022, 33, 1441–1464. [Google Scholar] [CrossRef]
- Konstantinos, I.; Georgios, T.; Garyfalos, A. A Decision Support System Methodology for Selecting Wind Farm Installation Locations Using AHP and TOPSIS: Case Study in Eastern Macedonia and Thrace Region, Greece. Energy Policy 2019, 132, 232–246. [Google Scholar] [CrossRef]
- Li, J.; He, J.; Lu, P.; Ran, X.; Yi, J. Evaluation of Geosites in Changbaishan Global Geopark Based on Fuzzy AHP and TOPSIS. Geoheritage 2025, 17, 43. [Google Scholar] [CrossRef]
- Bychkov, I.V.; Hmelnov, A.E.; Fedorov, R.K.; Fereferov, E.S.; Gachenko, A.S. Research by the Matrosov Institute for System Dynamics in the Field of Geoinformatics: Past, Present, and Future. Geogr. Nat. Resour. 2024, 45, 374–383. [Google Scholar] [CrossRef]
- Xenitidis, K.; Ioannou, K.; Tsantopoulos, G. An Innovative Methodology for the Determination of Wind Farms Installation Location Characteristics Using GIS and Delaunay Triangulation. Energy Sustain. Dev. 2023, 75, 25–39. [Google Scholar] [CrossRef]
- Lu, W.; Qi, S.; Zheng, B.; Zhang, W.; Wang, Z.; Ru, Y.; Zhang, Y.; Ma, L.; Diao, Y.; Fu, L. Optimisation Study of Carbon Dioxide Geological Storage Sites Based on GIS and Machine Learning Algorithms. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 19. [Google Scholar] [CrossRef]
- Xenitidis, K.; Ioannou, K.; Tsantopoulos, G.; Myronidis, D. On the Usage of Artificial Neural Networks for the Determination of Optimal Wind Farms Allocation. Sustainability 2023, 15, 16938. [Google Scholar] [CrossRef]
- Josimović, B.; Srnić, D.; Manić, B.; Knežević, I. Multi-Criteria Evaluation of Spatial Aspects in the Selection of Wind Farm Locations: Integrating the GIS and PROMETHEE Methods. Appl. Sci. 2023, 13, 5332. [Google Scholar] [CrossRef]
- Łaska, G. Wind Energy and Multi-Criteria Analysis in Making Decisions on the Location of Wind Farms. Procedia Eng. 2017, 182, 418–424. [Google Scholar] [CrossRef]
- Villacreses, G.; Gaona, G.; Martínez-Gómez, J.; Jijón, D.J. Wind Farms Suitability Location Using Geographical Information System (GIS), Based on Multi-Criteria Decision Making (MCDM) Methods: The Case of Continental Ecuador. Renew. Energy 2017, 109, 275–286. [Google Scholar] [CrossRef]
- Jun, D.; Tian-tian, F.; Yi-sheng, Y.; Yu, M. Macro-Site Selection of Wind/Solar Hybrid Power Station Based on ELECTRE-II. Renew. Sustain. Energy Rev. 2014, 35, 194–204. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Du, S.; Li, C.; Siu, Y.L.; Rong, Y.; Yang, H. The Impact of Onshore Wind Power Projects on Ecological Corridors and Landscape Connectivity in Shanxi, China. J. Clean. Prod. 2020, 254, 120075. [Google Scholar] [CrossRef]
- Rehman, A.U.; Abidi, M.H.; Umer, U.; Usmani, Y.S. Multi-Criteria Decision-Making Approach for Selecting Wind Energy Power Plant Locations. Sustainability 2019, 11, 6112. [Google Scholar] [CrossRef]
- Ali, Y.; Butt, M.; Sabir, M.; Mumtaz, U.; Salman, A. Selection of Suitable Site in Pakistan for Wind Power Plant Installation Using Analytic Hierarchy Process (AHP). J. Control Decis. 2018, 5, 117–128. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, C.; Jiang, L.; Liao, H. An Integrated Method with PROMETHEE and Conflict Analysis for Qualitative and Quantitative Decision-Making: Case Study of Site Selection for Wind Power Plants. Cogn. Comput. 2020, 12, 100–114. [Google Scholar] [CrossRef]
- Kokologos, D.; Tsitoura, I.; Kouloumpis, V.; Tsoutsos, T. Visual Impact Assessment Method for Wind Parks: A Case Study in Crete. Land. Use Policy 2014, 39, 110–120. [Google Scholar] [CrossRef]
- Sameie, H.; Arvan, M. A Simulation-Based Data Envelopment Analysis (DEA) Model to Evaluate Wind Plants Locations. Decis. Sci. Lett. 2015, 4, 165–180. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T.; Trinh, T.-T.-Q. A Decision Support Model for Measuring Technological Progress and Productivity Growth: The Case of Commercial Banks in Vietnam. Axioms 2021, 10, 131. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Tone, K. A Slacks-Based Measure of Efficiency in Data Envelopment Analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of Feasibility Study of Solar Farms Deployment Using Hybrid AHP-TOPSIS Analysis: Case Study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]

| No | Study | Case Study | Year | Weighted Method |
|---|---|---|---|---|
| 1 | Rose & Apt [24] | US | 2015 | |
| 2 | Sánchez-Lozano et al. [26] | Spain | 2016 | Fuzzy-AHP |
| 3 | Değirmenci et al. [27] | Turkey | 2018 | AHP |
| 4 | Mohammadzadeh Bina et al. [28] | Iran | 2018 | Equal weight |
| 5 | Ayodele et al. [29] | Nigeria | 2018 | Interval type-2 fuzzy AHP |
| 6 | Güler et al. [30] | Turkey | 2018 | |
| 7 | Wang et al. [14] | Vietnam | 2018 | FAHP and FTOPSIS |
| 8 | Solangi et al. [25] | Pakistan | 2018 | AHP and FUZZY |
| 9 | Y. Wu et al. [31] | China | 2019 | Entropy-based fuzzy |
| 10 | Liu et al. [22] | Saskatchewan | 2019 | |
| 11 | Pambudi & Nananukul [32] | Indonesia | 2019 | |
| 12 | Deveci et al. [33] | Turkey | 2020 | Fuzzy method |
| 13 | Xu et al. [19] | China | 2020 | IAHP |
| 14 | Ari & Gencer [18] | Turkey | 2020 | AHP-SMAA |
| 15 | Mostafaeipour et al. [34] | Iran | 2020 | |
| 16 | Elhonsy et al. [35] | Egypt | 2021 | Shannon’s Entropy |
| 17 | Azzioui et al. [36] | Morocco | 2021 | Dynamic AHP |
| 18 | Saraswat et al. [37] | India | 2021 | Fuzzy-AHP |
| 19 | Feloni & Karandinaki [38] | Chania | 2021 | WLC |
| 20 | Asadi & Pourhossein [39] | Iran | 2021 | AHP |
| 21 | Sotiropoulou & Vavatsikos [40] | Greece | 2021 | IDW |
| 22 | Zahid et al. [41] | Pakistan | 2021 | AHP |
| 23 | Wang et al. [42] | Vietnam | 2021 | FAHP, FWASPAS |
| 24 | Xu et al. [43] | China | 2021 | AHP |
| 25 | Nagababu et al. [44] | India | 2022 | Fuzzy-AHP |
| 26 | Gao et al. [45] | Mongolia | 2022 | DEMATEL |
| 27 | Shorabeh et al. [46] | Iran | 2022 | OWA |
| 28 | Y. Wu et al. [47] | China | 2022 | DEMATEL, ANP |
| 29 | Ajanaku et al. [48] | Virginia | 2022 | FAHP |
| 30 | Kumar et al. [49] | India | 2022 | |
| 31 | Ioannou et al. [50] | Greece | 2019 | AHP, TOPIS |
| 32 | Li et al. [51] | China | 2025 | AHP, TOPSIS |
| 33 | Bychkov et al. [52] | 2023 | GIS | |
| 34 | Xenitidis et al. [53] | 2023 | GIS | |
| 35 | Lu et al. [54] | Greece | 2023 | NN |
| 36 | Xenitidis et al. [55] | China | 2023 | NN |
| 37 | Josimović et al. [56] | Serbia | 2023 | GIS, PROMETHE |
| 38 | Laska et al. [57] | Poland | 2017 | PROMETHE |
| No | Authors [Reference] | Wind Power | Geology Condition | Electricity Demand | Distance to Residential Areas | Distance from Roads | Distance to Transmission Line | Costs | Land Use | Land Price | Support Mechanisms | Policies and Laws | Social Impact | Natural Disaster | Wildlife and Habitat | Visual Impact | Ecological Damage |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Villacreses et al. [58] | x | x | x | x | x | x | ||||||||||
| 2 | Mostafaeipour et al. [34] | x | x | x | x | ||||||||||||
| 3 | Jun et al. [59] | x | x | x | x | x | x | x | x | x | |||||||
| 4 | Wang et al. [14] | x | x | x | x | x | x | x | x | ||||||||
| 5 | Ari & Gencer [18] | x | x | x | |||||||||||||
| 6 | Guo et al. [60] | x | x | x | |||||||||||||
| 7 | A.U. Rehman et al. [61] | x | x | x | x | x | x | x | |||||||||
| 8 | Ali et al. [62] | x | x | x | |||||||||||||
| 9 | X. Wu et al. [63] | x | x | x | x | ||||||||||||
| 10 | Pambudi & Nananukul [32] | x | x | x | x | ||||||||||||
| 11 | Kokologos et al. [64] | x | x | x | |||||||||||||
| 12 | Sánchez-Lozano et al. [26] | x | x | x | x | x | x | ||||||||||
| 13 | Ayodele et al. [29] | x | x | x | x | x | |||||||||||
| 14 | Y. Wu et al. [31] | x | x | x | x | ||||||||||||
| This research | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Fuzzy Set | Definition | Fuzzy Scale |
|---|---|---|
| Equal importance | (1, 1, 1) | |
| Weak importance | (1, 2, 3) | |
| Not bad | (2, 3, 4) | |
| Preferable | (3, 4, 5) | |
| Importance | (4, 5, 6) | |
| Fairly important | (5, 6, 7) | |
| Very important | (6, 7, 8) | |
| Absolute | (7, 8, 9) | |
| Perfect | (8, 9, 10) |
| No | Location | DMU | Wind Speed (m/s) |
|---|---|---|---|
| 1 | Aceh | LOC-01 | 4.39 |
| 2 | Bali | LOC-02 | 4.76 |
| 3 | Banten | LOC-03 | 5.77 |
| 4 | Bengkulu | LOC-04 | 4.45 |
| 5 | DI Yogyakarta | LOC-05 | 5.72 |
| 6 | DKI Jakarta | LOC-06 | 3.9 |
| 7 | Gorontalo | LOC-07 | 4.86 |
| 8 | Jambi | LOC-08 | 3.97 |
| 9 | West Java | LOC-09 | 5.34 |
| 10 | Central Java | LOC-10 | 5.23 |
| 11 | East Java | LOC-11 | 5.6 |
| 12 | West Kalimantan | LOC-12 | 4.04 |
| 13 | South Kalimantan | LOC-13 | 4.7 |
| 14 | Central Kalimantan | LOC-14 | 4.12 |
| 15 | East Kalimantan | LOC-15 | 3.67 |
| 16 | Bangka Belitung | LOC-16 | 4.55 |
| 17 | Riau Islands | LOC-17 | 4.55 |
| 18 | Lampung | LOC-18 | 4.48 |
| 19 | Maluku | LOC-19 | 5.92 |
| 20 | North Maluku | LOC-20 | 3.82 |
| 21 | West Nusa Tenggara | LOC-21 | 5.16 |
| 22 | East Nusa Tenggara | LOC-22 | 6.34 |
| 23 | Papua | LOC-23 | 5.22 |
| 24 | West Papua | LOC-24 | 4.07 |
| 25 | Riau | LOC-25 | 3.85 |
| 26 | West Sulawesi | LOC-26 | 3.88 |
| 27 | South Sulawesi | LOC-27 | 5.98 |
| 28 | Central Sulawesi | LOC-28 | 4.23 |
| 29 | East Sulawesi | LOC-29 | 4.04 |
| 30 | North Sulawesi | LOC-30 | 4.82 |
| 31 | West Sumatra | LOC-31 | 4.11 |
| 32 | South Sumatra | LOC-32 | 4.3 |
| 33 | North Sumatra | LOC-33 | 4.33 |
| Factors | Unit | Max | Min | Avg | SD | Factors |
|---|---|---|---|---|---|---|
| (I1) | 1000 IDR/M2 | 24,000 | 2500 | 7909.1 | 5452.30 | (I1) |
| (I2) | Probability score | 0.293 | 0.001 | 0.030 | 0.0818 | (I2) |
| (O1) | W/m2 | 288 | 56 | 137.8 | 65.83 | (O1) |
| (O2) | 1000 Ha | 4941 | 118 | 833.5 | 1441.31 | (O2) |
| (O3) | Million | 49 | 1 | 8.3 | 14.4 | (O3) |
| Factors | Unit | Max | Min | Avg | SD | Factors |
| (I1) | 1000 IDR/M2 | 24,000 | 2500 | 7909.1 | 5452.30 | (I1) |
| (I2) | Probability score | 0.293 | 0.001 | 0.030 | 0.0818 | (I2) |
| No | Location | DMU | CCR-I | BCC-I | SBM-I-C | EBM-I-C |
|---|---|---|---|---|---|---|
| 1 | Aceh | LOC-01 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | Bali | LOC-02 | 0.4262 | 0.4266 | 0.4001 | 0.4261 |
| 3 | Banten | LOC-03 | 0.8715 | 1.0000 | 0.8171 | 0.8715 |
| 4 | Bengkulu | LOC-04 | 0.6829 | 0.7214 | 0.6623 | 0.6829 |
| 5 | DI Yogyakarta | LOC-05 | 0.7440 | 0.7601 | 0.7331 | 0.7412 |
| 6 | DKI Jakarta | LOC-06 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 7 | Gorontalo | LOC-07 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 8 | Jambi | LOC-08 | 0.8953 | 1.0000 | 0.8289 | 0.8810 |
| 9 | West Java | LOC-09 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 10 | Central Java | LOC-10 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 11 | East Java | LOC-11 | 0.9249 | 1.0000 | 0.9215 | 0.9249 |
| 12 | West Kalimantan | LOC-12 | 0.5338 | 0.5770 | 0.4896 | 0.5338 |
| 13 | South Kalimantan | LOC-13 | 0.4570 | 0.4734 | 0.4459 | 0.4570 |
| 14 | Central Kalimantan | LOC-14 | 0.4395 | 0.6283 | 0.4037 | 0.4395 |
| 15 | East Kalimantan | LOC-15 | 0.3956 | 0.4997 | 0.3452 | 0.3956 |
| 16 | Bangka Belitung Islands | LOC-16 | 0.5982 | 0.7067 | 0.4627 | 0.5685 |
| 17 | Riau Islands | LOC-17 | 0.9258 | 1.0000 | 0.8682 | 0.9258 |
| 18 | Lampung | LOC-18 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 19 | Maluku | LOC-19 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 20 | North Maluku | LOC-20 | 0.4652 | 0.7118 | 0.4633 | 0.4652 |
| 21 | West Nusa Tenggara | LOC-21 | 0.6549 | 0.6585 | 0.6370 | 0.6549 |
| 22 | East Nusa Tenggara | LOC-22 | 0.9655 | 1.0000 | 0.9631 | 0.9655 |
| 23 | Papua | LOC-23 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 24 | West Papua | LOC-24 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 25 | Riau | LOC-25 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 26 | West Sulawesi | LOC-26 | 0.8274 | 1.0000 | 0.8010 | 0.8274 |
| 27 | South Sulawesi | LOC-27 | 0.9434 | 1.0000 | 0.7618 | 0.9084 |
| 28 | Central Sulawesi | LOC-28 | 0.5229 | 0.5446 | 0.4941 | 0.5158 |
| 29 | East Sulawesi | LOC-29 | 0.6187 | 0.7530 | 0.5796 | 0.6186 |
| 30 | North Sulawesi | LOC-30 | 0.8276 | 0.8301 | 0.7684 | 0.8124 |
| 31 | West Sumatra | LOC-31 | 0.7009 | 0.7149 | 0.5293 | 0.6819 |
| 32 | South Sumatra | LOC-32 | 0.5423 | 0.6046 | 0.5262 | 0.5422 |
| 33 | North Sumatra | LOC-33 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
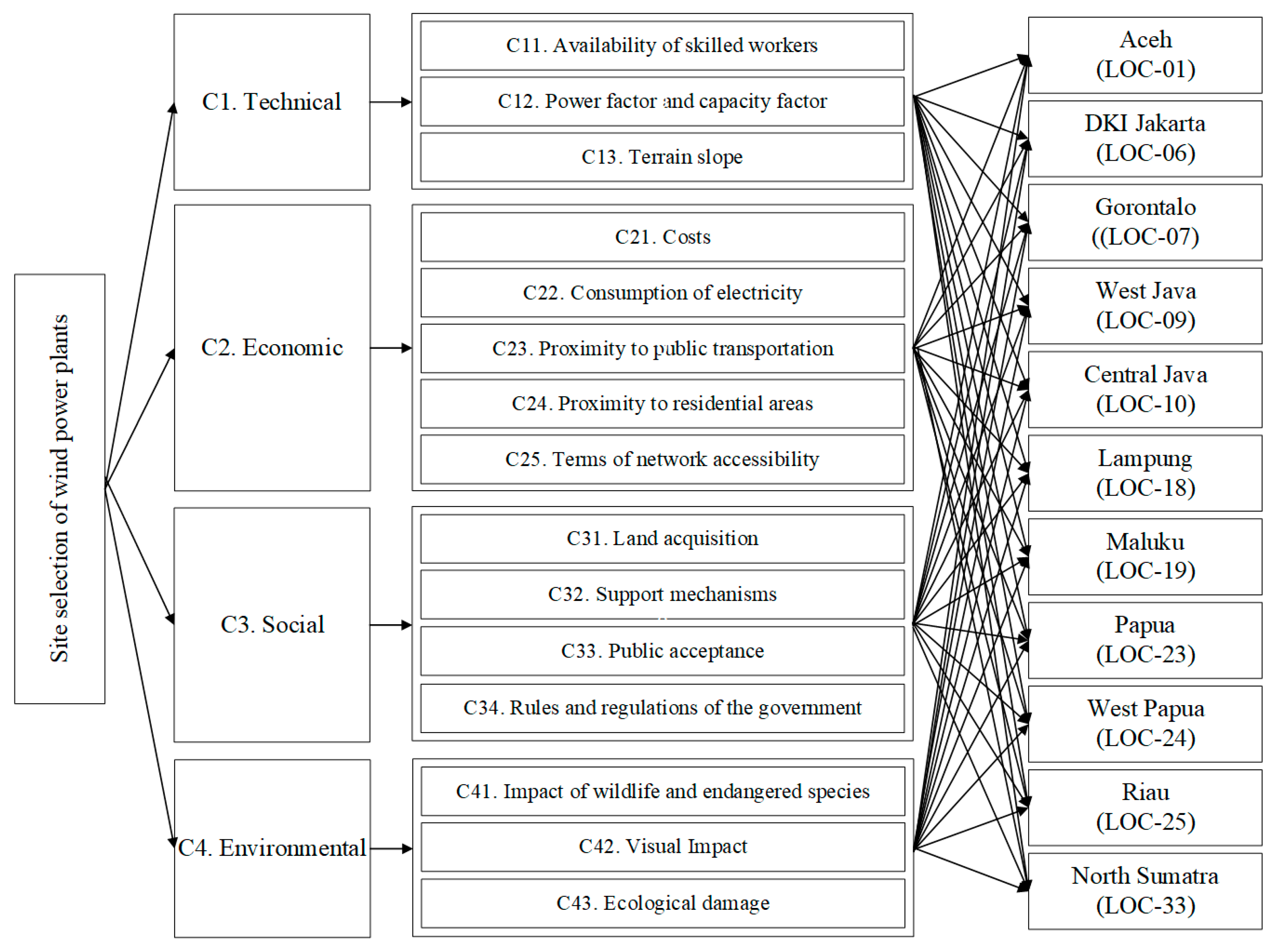
| Main Criteria | Criteria | Definition |
|---|---|---|
| C1. Technical | C11. Availability of skilled workers | Qualified individuals with extensive training and expertise in the wind turbine industry, such as installers, technicians, and other people. |
| C12. Power factor and capacity factor | The capacity factor of a wind turbine is influenced by various factors, such as wind speed, maintenance, downtime, repair downtime, and other related factors. | |
| C13. Terrain slope | The fluctuation of the topography of the Earth’s surface. | |
| C2. Economic | C21. Costs | Expenses associated with the building, operation, and maintenance of a wind power facility. |
| C22. Consumption of electricity | An analysis of the energy use in different regions. | |
| C23. Proximity to public transportation | Quantifying the distance between a proximate road and other potential sites. | |
| C24. Proximity to residential areas | The spatial separation between the population centers (cities or towns) and the numerous prospective locations. | |
| C25. Terms of network accessibility | Proximity to preexisting electrical transmission lines. | |
| C3. Social | C31. Land acquisition | The government has power over the maximum amount of land that can be used for renewable energy projects. |
| C32. Support mechanisms | Political or public dedication to endorse wind projects, such as implementing feed-in tariffs, providing preferential financing, reducing taxes, or offering other forms of subsidies. | |
| C33. Public acceptance | The consensus among social partners, consumer awareness regarding wind power, and its market adoption. | |
| C34. Rules and regulations of the government | The impact of rules and regulations on the development of wind energy systems. | |
| C4. Environmental | C41. Impact on wildlife and endangered species | The impact of wind power facilities on animal habitats and endangered species. |
| C42. Visual impact | The emergence of alterations in the physical environment resulting from the planned construction of a wind farm. | |
| C43. Ecological damage | The environmental impact caused by the development of wind farms includes the erosion of water and soil, as well as the accumulation of building debris. |
| Expert | Work Experience | Education | Skilled Field |
|---|---|---|---|
| Expert 1 | 6 years | Master’s | Geographical Analysis |
| Expert 2 | 4 years | Doctorate | Wind Resource Assessment |
| Expert 3 | 5 years | Doctorate | Environmental Impact |
| Expert 4 | 7 years | Bachelor’s | Engineering and Design |
| Expert 5 | 4 years | Bachelor’s | Regulatory Compliance |
| Expert 6 | 5 years | Master’s | Community Engagement |
| Expert 7 | 9 years | Master’s | Economic Analysis |
| Expert 8 | 8 years | Bachelor’s | Logistics and Accessibility |
| Expert 9 | 4 years | Doctorate | Legal and Land Acquisition |
| Expert 10 | 3 years | Master’s | Sustainability Planning |
| Criteria | Attribute | Fuzzy Geometric Mean | Triangular Fuzzy Weights | Significance Level | ||||
|---|---|---|---|---|---|---|---|---|
| C11 Availability of skilled workers | max | 0.7520 | 1.0278 | 1.4077 | 0.0357 | 0.0664 | 0.1250 | 0.0667 |
| C12 Power factor and capacity factor | max | 0.6922 | 0.9463 | 1.3078 | 0.0328 | 0.0612 | 0.1161 | 0.0617 |
| C13 Terrain slope | min | 0.8299 | 1.1543 | 1.5800 | 0.0394 | 0.0746 | 0.1403 | 0.0747 |
| C21 Costs | min | 0.6875 | 0.9280 | 1.2689 | 0.0326 | 0.0600 | 0.1127 | 0.0603 |
| C22 Consumption of electricity | max | 0.7209 | 0.9746 | 1.3299 | 0.0342 | 0.0630 | 0.1181 | 0.0632 |
| C23 Proximity to public transportation | min | 0.7766 | 1.0804 | 1.4844 | 0.0369 | 0.0698 | 0.1318 | 0.0700 |
| C24 Proximity to residential areas | min | 0.7803 | 1.0641 | 1.4314 | 0.0370 | 0.0688 | 0.1271 | 0.0684 |
| C25 Terms of network accessibility | min | 1.0715 | 1.4941 | 1.9701 | 0.0508 | 0.0966 | 0.1749 | 0.0946 |
| C31 Land acquisition | max | 0.8661 | 1.2218 | 1.6577 | 0.0411 | 0.0790 | 0.1472 | 0.0785 |
| C32 Support mechanisms | max | 0.5772 | 0.7634 | 1.0562 | 0.0274 | 0.0493 | 0.0938 | 0.0501 |
| C33 Public acceptance | max | 0.5283 | 0.6978 | 0.9741 | 0.0251 | 0.0451 | 0.0865 | 0.0460 |
| C34 Rules and regulations of the government | max | 0.6912 | 0.9458 | 1.3106 | 0.0328 | 0.0611 | 0.1164 | 0.0617 |
| C41 Impact on wildlife and endangered species | min | 0.8416 | 1.1786 | 1.5886 | 0.0399 | 0.0762 | 0.1410 | 0.0755 |
| C42 Visual impact | max | 1.0299 | 1.4534 | 1.9326 | 0.0489 | 0.0939 | 0.1716 | 0.0923 |
| C43 Ecological damage | min | 0.4175 | 0.5438 | 0.7725 | 0.0198 | 0.0351 | 0.0686 | 0.0363 |
| Location | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Aceh | 0.0707 | 0.0916 | 0.1302 | 2.8668 | 7.2897 | 17.7998 | 0.7729 | 0.9085 | 0.9985 |
| DKI Jakarta | 0.0698 | 0.0910 | 0.1295 | 2.6430 | 6.8927 | 17.0822 | 0.7628 | 0.9024 | 0.9931 |
| Gorontalo | 0.0660 | 0.0911 | 0.1297 | 2.6269 | 6.9977 | 17.2924 | 0.7206 | 0.9031 | 0.9944 |
| West Java | 0.0565 | 0.0904 | 0.1290 | 2.4084 | 6.7757 | 16.7025 | 0.6171 | 0.8967 | 0.9892 |
| Central Java | 0.0654 | 0.0908 | 0.1295 | 2.5514 | 6.8878 | 17.1855 | 0.7140 | 0.9006 | 0.9933 |
| Lampung | 0.0641 | 0.0917 | 0.1304 | 2.8899 | 7.5368 | 18.0611 | 0.6998 | 0.9091 | 0.9997 |
| Maluku | 0.0688 | 0.0909 | 0.1295 | 2.6713 | 6.9359 | 17.1080 | 0.7514 | 0.9008 | 0.9927 |
| Papua | 0.0585 | 0.0891 | 0.1277 | 2.0406 | 5.9232 | 15.3828 | 0.6395 | 0.8834 | 0.9795 |
| West Papua | 0.0586 | 0.0911 | 0.1296 | 2.6355 | 7.1362 | 17.2868 | 0.6405 | 0.9034 | 0.9941 |
| Riau | 0.0655 | 0.0914 | 0.1300 | 2.7757 | 7.2593 | 17.6507 | 0.7153 | 0.9060 | 0.9969 |
| North Sumatra | 0.0581 | 0.0909 | 0.1296 | 2.5467 | 7.0618 | 17.2781 | 0.6346 | 0.9012 | 0.9937 |
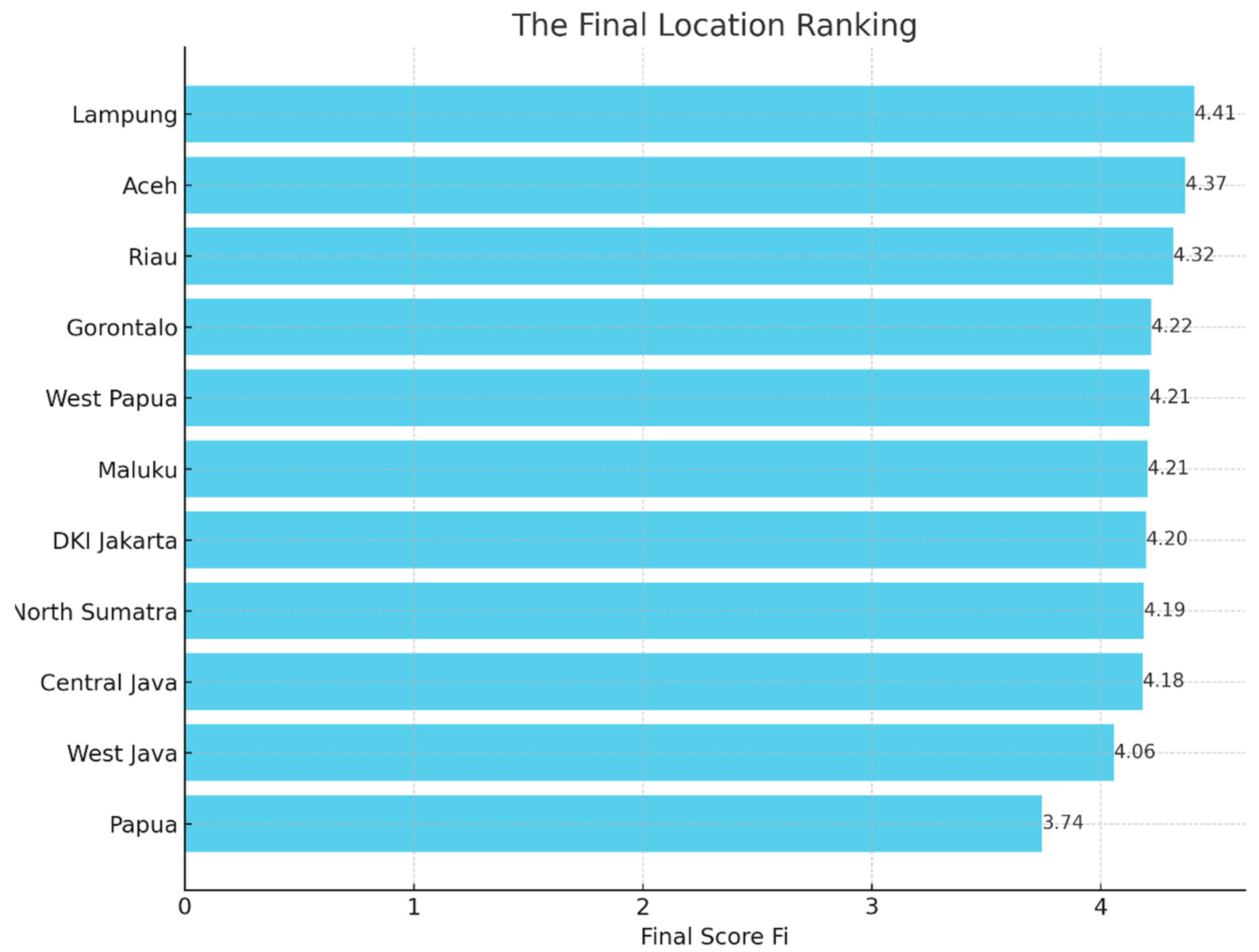
| Location | Final Score Fi | Rank | |||
|---|---|---|---|---|---|
| Aceh | 0.0975 | 9.3187 | 0.8933 | 4.3694 | 2 |
| DKI Jakarta | 0.0968 | 8.8727 | 0.8861 | 4.1981 | 7 |
| Gorontalo | 0.0956 | 8.9723 | 0.8727 | 4.2214 | 4 |
| West Java | 0.0920 | 8.6288 | 0.8343 | 4.0566 | 10 |
| Central Java | 0.0952 | 8.8749 | 0.8693 | 4.1822 | 9 |
| Lampung | 0.0954 | 9.4959 | 0.8695 | 4.4104 | 1 |
| Maluku | 0.0964 | 8.9051 | 0.8816 | 4.2055 | 6 |
| Papua | 0.0918 | 7.7822 | 0.8341 | 3.7442 | 11 |
| West Papua | 0.0931 | 9.0195 | 0.8460 | 4.2119 | 5 |
| Riau | 0.0956 | 9.2286 | 0.8727 | 4.3156 | 3 |
| North Sumatra | 0.0929 | 8.9622 | 0.8432 | 4.1880 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-N.; Chung, Y.-C.; Wibowo, F.D.; Dang, T.-T.; Nguyen, N.-A.-T. The Planning of Best Site Selection for Wind Energy in Indonesia: A Synergistic Approach Using Data Envelopment Analysis and Fuzzy Multi-Criteria Decision-Making. Energies 2025, 18, 4176. https://doi.org/10.3390/en18154176
Wang C-N, Chung Y-C, Wibowo FD, Dang T-T, Nguyen N-A-T. The Planning of Best Site Selection for Wind Energy in Indonesia: A Synergistic Approach Using Data Envelopment Analysis and Fuzzy Multi-Criteria Decision-Making. Energies. 2025; 18(15):4176. https://doi.org/10.3390/en18154176
Chicago/Turabian StyleWang, Chia-Nan, Yu-Chi Chung, Fajar Dwi Wibowo, Thanh-Tuan Dang, and Ngoc-Ai-Thy Nguyen. 2025. "The Planning of Best Site Selection for Wind Energy in Indonesia: A Synergistic Approach Using Data Envelopment Analysis and Fuzzy Multi-Criteria Decision-Making" Energies 18, no. 15: 4176. https://doi.org/10.3390/en18154176
APA StyleWang, C.-N., Chung, Y.-C., Wibowo, F. D., Dang, T.-T., & Nguyen, N.-A.-T. (2025). The Planning of Best Site Selection for Wind Energy in Indonesia: A Synergistic Approach Using Data Envelopment Analysis and Fuzzy Multi-Criteria Decision-Making. Energies, 18(15), 4176. https://doi.org/10.3390/en18154176










