High-Performance Two-Stroke Opposed-Piston Hydrogen Engine: Numerical Study on Injection Strategies, Spark Positioning and Water Injection to Mitigate Pre-Ignition

Abstract

In the pursuit of zero-emission mobility, hydrogen represents a promising fuel for internal combustion engines. However, its low volumetric energy density poses challenges, especially for high-performance applications where compactness and lightweight design are crucial. This study investigates the feasibility of an innovative hydrogen-fueled two-stroke opposed-piston (2S-OP) engine, targeting a specific power of 130 kW/L and an indicated thermal efficiency above 40%. A detailed 3D-CFD analysis is conducted to evaluate mixture formation, combustion behavior, abnormal combustion and water injection as a mitigation strategy. Innovative ring-shaped multi-point injection systems with several designs are tested, demonstrating the impact of injector channels’ orientation on the final mixture distribution. The combustion analysis shows that a dual-spark configuration ensures faster combustion compared to a single-spark system, with a 27.5% reduction in 10% to 90% combustion duration. Pre-ignition is identified as the main limiting factor, strongly linked to mixture stratification and high temperatures. To suppress it, water injection is proposed. A 55% evaporation efficiency of the water mass injected lowers the in-cylinder temperature and delays pre-ignition onset. Overall, the study provides key design guidelines for future high-performance hydrogen-fueled 2S-OP engines.

1. Introduction

Nowadays, the most important theme discussed by the scientific community is represented by climate change and how to reduce it. As reported by the European Environment Agency (EEA) [1], transport was responsible for about a quarter of the EU’s total CO₂ emissions in 2019, of which 71.7% came from road transportation. Among this, a small segment is represented by high-performance vehicles, which face a non-trivial challenge: balancing the need to reduce GHG emissions to comply with regulations while maintaining high levels of performance and driver engagement.

One possible solution could be represented by the substitution of the common carbon fossil fuels with hydrogen (H₂). The choice of hydrogen is due to its interesting characteristics as reported by Verhelst et al. [2]. It has a wide range of flammability (0.1 < φ < 7.1 at 1 atm and 300 K), which enables the use of optimized control strategies at part load to enhance thermal efficiency. Additionally, hydrogen has a high lower heating value (120 MJ/kg) and a laminar flame speed an order of magnitude faster than a gasoline–air mixture, allowing the engine to work at higher revving speeds and with very lean mixtures.

Regarding the knock tendency with hydrogen in Spark-Ignited (SI) engines, it remains a debated issue. The literature reports Research Octane Numbers (RONs) ranging from below 88 up to 130 or even higher under lean conditions [2,3]. When shifting from RON to Methane Number (MN), more suitable for evaluating gaseous fuels, hydrogen is associated with an MN of 0, indicating very low knock resistance compared to methane (MN = 100) [4]. These uncertainties emphasize the need for in-depth analysis of abnormal combustion phenomena when approaching high pressures and temperatures typical of high-performance engines.

Despite its promising characteristics, several drawbacks of hydrogen as a fuel must be carefully addressed. The main one is the low volumetric energy density (70.8 kg/m³ in liquid form and only 0.0824 kg/m³ as a gas) compared to gasoline (about 740 kg/m³) [2,5]. The low density of hydrogen, which can be only partially mitigated through high-pressure storage, indeed represents a major challenge in optimizing vehicle packaging and weight, key factors in high-performance vehicle design. Wallace and Ward [6] found that current technology cannot produce fuel tanks equal in size or weight to gasoline ones while storing the same energy, so higher engine efficiency is needed to close the gap.

In this context, using H₂ in high-performance sports cars requires the design of an engine that combines high specific power with high efficiency. To fully exploit engine performance, stoichiometric mixtures are typically employed at full load, while lean mixtures are preferred at part-load conditions to maximize efficiency, reducing fuel consumption. Thanks to hydrogen’s high flame speed, load control via mixture quality modulation is therefore feasible. Regarding the fuel delivery system, achieving high power density demands a mixture with the highest possible calorific value. For gaseous fuels such as H₂, this can be significantly enhanced by adopting Direct Injection (DI). Eichlseder et al. [7] report that stoichiometric external mixture formation leads to an approximate 30% reduction in indicated mean effective pressure (IMEP), highlighting the need for DI when high specific power is required. Welch et al. [8] show that transitioning from port fuel injection (PFI) to DI improves volumetric efficiency, enhances combustion robustness, reduces backfire and pre-ignition risk, and increases power density. These results are further supported by 3D-CFD simulations conducted by Musy et al. [9], which confirm improvements in both volumetric efficiency and brake power when switching from PFI to DI across different engine speeds and equivalence ratios (EQRs).

Achieving high efficiency, particularly at part load, is also essential for minimizing fuel tank size. Verhelst et al. [10] report increased brake thermal efficiency (BTE) when replacing gasoline with hydrogen under various load, speed and EQR conditions using PFI. The improvement is mainly attributed to the higher flame speed of H₂ compared to gasoline, which results in a more isochoric combustion process, and to its lower density, which reduces pumping losses by enabling greater air displacement. The BTE can be further improved by adopting a DI system, demonstrating that comparable performance with increased efficiency can be achieved using H₂ DI instead of gasoline.

However, targeting high performance also raises concerns about abnormal combustion, particularly due to hydrogen’s wide flammability range and low ignition energy. Pre-ignition and knock are more likely to occur under near-stoichiometric conditions, given the dependence of ignition energy on the EQR. Moreover, the high engine speeds and loads typical of sports cars further promote the occurrence of abnormal combustion [11,12], making it necessary to implement mitigation strategies such as cooled EGR or water injection [13].

Together with an increase in abnormal combustion risk, the adoption of stoichiometric mixtures at full load leads to an adiabatic flame temperature exceeding 1800 K, which results in high production of nitrogen oxides (NOx), the main environmental concern in H₂ engines. Nonetheless, under stoichiometric conditions, NOx emissions are lower than the peak value observed at an EQR of approximately 0.75 [2]. A relevant reduction in NOx production can be achieved by employing a load-based control strategy that switches from lean operation at low load to stoichiometric operation at high load, thereby avoiding the critical operating window with relative air–fuel ratios in the range 0.5 < φ < 1 [14].

Overall, the properties of H₂ make high-performance applications particularly challenging, primarily due to the risk of abnormal combustion and elevated NOx formation. Consequently, the current body of literature on H₂ engines has focused mainly on efficiency improvements and NOx mitigation [15,16], while the achievement of high power density and the associated challenges have received limited attention. In this context, research on high-performance H₂ engines represents an innovative and quite unexplored field of study. Tafel and Martin [17] conducted a study on a four-stroke volume-production engine able to produce 463 kW of power at 7500 rpm, substituting gasoline with H₂ as fuel. The study reveals that to maintain the same level of performance, it is necessary to adopt a DI system combined with a PFI one. Moreover, to avoid pre-ignition occurrence and to limit the NOx production, a lean mixture is used, coupled with water injection as a mitigation strategy. Bao et al. [18] report that an optimized four-stroke DI H₂ engine can achieve a brake mean effective pressure (BMEP) of 17 bar with a BTE equal to 42.1%. Nevertheless, pre-ignition is registered with early injection timing and high engine speeds (>3000 rpm), whereas knock tends to happen with late injection and medium engine speeds (1500 rpm∼2500 rpm). Beyer et al. [19] experimentally evaluated the jet-guided combustion implementation in a H₂ SI single cylinder engine operated in stoichiometric conditions. The study demonstrates the capability of jet-guided strategies for applying stoichiometric H₂ combustion without inducing backfire and knock, achieving high power density. Nevertheless, the adoption of a stoichiometric H₂ combustion leads to an increase in the maximum cylinder pressure gradients towards high engine loads, making it necessary the introduction of dilution effects such as EGR or water injection.

Considering the main advantages and limitations of hydrogen, the classic four-stroke engine architecture may not be ideal, particularly when high power density must be achieved while minimizing the size and weight of the engine. Among alternative designs, the two-stroke opposed-piston (2S-OP) one could be promising, offering several well-documented advantages reported in the literature [20,21,22,23]. The two-stroke cycle ideally doubles the power output for a given engine displacement compared to a four-stroke cycle, enabling high performance with reduced encumbrance and weight. In addition, the OP architecture could result in higher indicated thermal efficiency (ITE) due to reduced heat transfer losses thanks to a more favorable combustion chamber area/volume ratio. The intake manifold design can be optimized for precise control of in-cylinder turbulence through the generation of a swirl motion, a well-organized rotating air vortex aligned with the cylinder axis, which plays a key role in mixture formation and combustion. Furthermore, spark plugs and fuel injectors can be flexibly placed along the cylinder liner, allowing for the design of an optimal combustion and injection system. Finally, the OP architecture’s flat and compact multi-cylinder layout allows a low, central mounting position within the vehicle, helping to lower the car’s center of gravity and reducing packaging issues. Despite the numerous advantages, some drawbacks must be considered when designing a hydrogen-fueled 2S-OP engine. These include the following: the need for custom-made injection and combustion system positioned on the liner surface, with the spark plug acting from peripheral rather than central location; the presence of a mechanical link between the two crankshafts, which complicates the dynamic balance of the engine [24]; the requirement for specially designed piston rings and oil scrapers to minimize the blow-by phenomenon and friction wear; the need for an optimized cooling system due to the high thermal load on the pistons surface due to the absence of a cylinder head; and the risk of pre-ignition due to oil leakage into the combustion chamber [25,26].

These considerations highlight that designing a hydrogen-fueled 2S-OP engine from scratch for high-performance applications is a non-trivial task, requiring significant effort to mitigate the main drawbacks and exploit the advantages of this engine architecture. A common strategy adopted to reduce development time and cost is the use of advanced CAE tools for engine design, structural analyses, and 1D and 3D computational fluid dynamics (CFD) for performance optimization. The reliability of 3D-CFD in accurately reproducing in-cylinder processes is well documented in the literature. Several works have demonstrated its predictive capability in terms of engine performance, mixture formation, combustion evolution and emissions under different operating conditions. For instance, Sfriso et al. [27,28] reproduce experimental performance, flame development and NOx trends in H₂ engines under different operating conditions using the G-Equation (G-EQ) combustion model without case-specific tuning of constants. Aljabri et al. [29] further validate the G-EQ approach under lean and ultra-lean conditions through a calibrated turbulent flame speed (TFS) correlation. Madia et al. [30] compare the ECFM-3Z combustion model with CC-TFC, showing that CC-TFC coupled with Damköhler TFS correlation provides more accurate results with a lower calibration effort at different revving speeds and turbulence levels, including high load operation. In parallel with the combustion analysis, 3D-CFD permits a detailed investigation of the H₂ jet evolution [31], guiding design choices that directly affect the mixing process and, consequently, combustion quality and pollutant formation. As demonstrated by Liu et al. [32], the optimization of piston shape and the number of injector cap holes permits an improvement in mixing quality, an increase in ITE and a reduction in NOx emissions. Finally, Baudone et al. [33] investigate a four-stroke high-performance engine, showing good agreement with experimental data in terms of H₂ jet development, combustion evolution and NOx emissions. For the combustion analysis, the G-EQ combustion model is adopted, with the laminar flame speed (LFS) defined through a look-up table and the TFS derived from the Damköhler correlation. The study demonstrated that this setup can reproduce the experimental data at both 2000 rpm, 4.5 bar IMEP and 6000 rpm, 24 bar IMEP. Collectively, these studies confirm the suitability of 3D-CFD as a robust tool for addressing the key challenges in hydrogen engine development.

The present study builds upon this evidence by employing 3D-CFD simulations to evaluate the feasibility of a virtual prototype of a hydrogen-fueled two-stroke OP engine for sports car applications, targeting a power output of 130 kW/L at 6000 rpm and an ITE of at least 40%. A key constraint is the achievement of a trapping ratio equal to one, in accordance with the requirements of a three-way catalyst-based after-treatment system, avoiding oxygen excess in the exhaust line. As a preliminary step, a 1D engine model was developed to assess whether the target performance could be reached under certain modeling assumptions regarding scavenging efficiency, fuel–air mixing, combustion and encumbrances. The results were promising, and further details on this preliminary study, including model validation, are reported in a previous publication by the authors [34]. Subsequently, a 3D model of the engine was constructed, and peak power operation was simulated using boundary conditions derived from the 1D model. The aim of this step was the validation of the 1D modeling assumptions and the identification of potential critical issues not considered in the 1D framework. Special attention was given to the hydrogen–air mixing process and combustion evolution, testing various injection and spark plug systems for enhanced mixture homogeneity and combustion performance. Subsequently, the risk of pre-ignition under target operating conditions was investigated using detailed chemical kinetics. Pre-ignition was identified as a potential limiting factor in achieving the desired performance, and a sensitivity analysis was conducted on possible mitigation strategies, revealing water injection as an effective solution. Finally, 3D-CFD simulations incorporating water injection were performed to assess its capability in enabling pre-ignition safe operation. This workflow is consistent with the design approach described by Mattarelli et al. [35], which illustrates a possible development process of a two-stroke OP engine from scratch. The 3D-CFD is central to the optimization of scavenging and injection processes, and its outcomes are integrated into 1D modeling to support the definition of a viable prototype.

2. Engine Characteristics and Operation

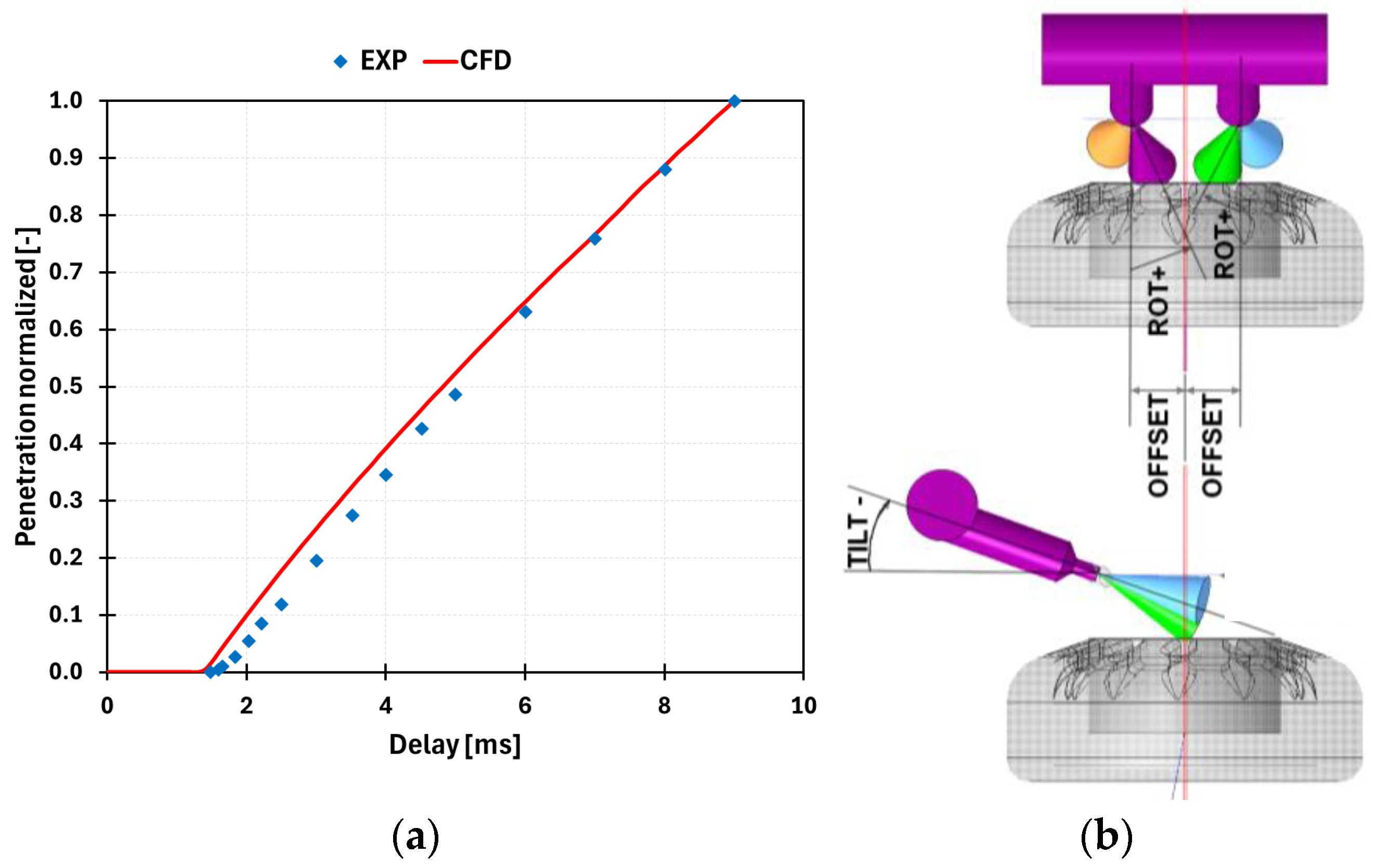
The virtually designed 2S-OP engine is a six-cylinder (twelve-piston) inline engine, whose potential layout is schematically represented in Figure 1a. The displaced volume is 907 cc per cylinder, and the effective compression ratio at the exhaust port closure is 12.5:1. The pistons are connected via their respective connecting rods to two different crankshafts, which are mechanically linked [24]. An offset of 7 CAD is imposed between the crankshafts to delay the closure of the intake ports, located on the intake-side piston, and to optimize the scavenging process. Each of the six cylinders is scavenged through twelve intake ports, which are connected to a common plenum via individual ducts characterized by tilt and swirl angles of 20° and 15°, respectively (see Figure 1b for angle definitions).

The exhaust system consists of a dedicated exhaust manifold for each cylinder, divided into two separate volumes, each of which is connected to four exhaust ports. The intake and exhaust ducts’ shape and orientation, combined with an appropriate exhaust back-pressure and crankshaft offset, have been optimized to guarantee a trapping ratio equal to 1 (defined as the ratio between the in-cylinder fresh air mass trapped and the fresh air mass delivered into the cylinder). Avoiding a short-circuiting of fresh charge in the exhaust manifold is possible, guaranteeing the maximum conversion efficiency of the three-way catalyst and reducing the NOx emissions when the engine is operated at stoichiometry. The main geometrical engine characteristics, derived from a preliminary 1D and 3D optimization study [34], are summarized in

Table 1. Two-stroke OP engine main geometric characteristics referring to a single cylinder.

Displaced Volume	907 cc
Stroke	88 mm
Bore	81 mm
Connecting rod length	175 mm
Compression ratio (EPC volume/minimum volume)	12.5:1
Number of pistons	2
Number of exhaust ports	8
Number of intake ports	12
Exhaust port opening (referring to exhaust piston)	97° aTDC
Exhaust port closure (referring to exhaust piston)	263° aTDC
Scavenge port opening (referring to exhaust piston)	140° aTDC
Scavenge port closure (referring to exhaust piston)	234° aTDC
Offset between the crankshafts	7°
Intake duct tilt angle	20°
Intake duct swirl angle	15°

.

Starting from the preliminary engine geometry, a 3D-CFD model is built, consisting of a single cylinder with two flat pistons moving toward each other. The intake system has been simplified in a toroidal (donut-shaped) volume derived from the more complex intake plenum that supplies all the cylinders, as shown in Figure 1b. To ensure the most homogeneous mixture formation possible, the injection system includes an annular (ring-shaped) injector cap connected to the cylinder via twelve channels, which can be oriented radially, in favor of or contrary to the swirl motion generated by the intake ports, allowing for multi-point direct injection instead of single-point direct injection, as schematized in Figure 2.

The injector ring is supplied by a pintle-type injector, developed by Bosch GmbH for low-pressure direct injection (5–40 bar range) [36,37] and currently applied to a four-stroke single-cylinder prototype high-performance hydrogen engine from Ferrari S.p.A. [38,39]. To minimize the injection duration, the maximum allowable injection pressure of 40 bar is adopted, and the injection duration is modified to match the desired EQR. Various channel geometries and orientations have been tested, as reported in Section 4, with the aim of optimizing the injection phase to achieve a high degree of mixture homogenization. The selected operating condition for the 3D analyses is the most critical one for scavenging, mixing, combustion and knock: maximum revving speed (6000 rpm) at full load. To achieve the performance target, a stoichiometric mixture should be employed while pre-ignition and knock occurrence are avoided. To this end, a direct water injection system is studied using two commercial port fuel injectors to inject water directly into the cylinder through two holes in the cylinder barrel. The port water injectors, each equipped with two nozzles, are positioned below the injector ring and oriented toward the intake ports. The water jets directly face the combustion chamber, thereby improving the vaporization efficiency and cooling effect. The 3D engine model, including the injector ring and water injection system, is shown schematically in Figure 3. The engine operating conditions studied are summarized in

Table 2. Two-stroke OP engine operating conditions.

Simulation Start	45° aTDC
Engine Speed	6000 rpm
Load Condition	Full-load
Average Inlet Pressure	3.32 bar
Average Outlet Pressure	3.17 bar
Lambda	1
Trapping Ratio	1
Number of Injector Ring Channels	12
Fuel Start of Injection (SOI)	157° bTDC
Static Fuel Mass Flow Rate	0.0175 kg/s
Fuel Injection Pressure	40 bar
Number of Water Injectors	2
Water Start of Injection	200° bTDC
Water Injection Duration	88°
Water Mass Injected	55.5 mg
Water Injection Pressure	10 bar
Target Power Output	130 kW/L
Target IMEP	16 bar

.

3. Three-Dimensional CFD Methodology

Three-dimensional CFD simulations are carried out using the commercial software CONVERGE CFD in the 3.0.28 version [40]. The analyzed operating point corresponds to the full-load, peak-power engine condition at 6000 rpm, as it represents the most challenging scenario due to the limited time available for scavenging, injection, mixing and combustion. Furthermore, the high in-cylinder temperature and pressure achieved during the compression stroke and combustion phase make this condition particularly prone to abnormal combustion occurrence. Turbulence is modeled using the Unsteady Reynolds-Averaged Navier–Stokes (URANS) equations coupled with the RNG k-ε turbulence model due to its ability to capture the evolution of strongly rotating vortices such as swirl [41,42]. Time-varying pressure and temperature profiles are imposed as boundary conditions, along with a turbulent intensity fraction of 0.01 and a turbulence length scale of 0.001 m. The thermal boundary layer is modeled using the law of the wall, which avoids the need to explicitly resolve the near-wall conductive sublayer. The heat flux is then estimated using the GRUMO model [43]. The intake-side piston temperature is set to 450 K, the exhaust-side piston to 500 K and the liner to 480 K. Boundary and initial conditions for 3D-CFD simulations are derived from a 1D model of the multi-cylinder version of the engine, validated using data from both preliminary 3D-CFD results and experimental tests conducted under similar operating conditions in a 4-stroke engine. Details of the validation process, along with the 3D model-based optimization of engine geometry and scavenging phase, are reported in a previous work [34]. A variable time-step algorithm is employed, constrained by the maximum convection Courant–Friedrichs–Lewy (CFL) number, set equal to 3 during the injection phase and 1 for the rest of the cycle. Simulations are initialized without imposing any charge motion in the domain. For each configuration, three engine cycles are simulated, with the initial turbulence and flow fields conditions updated from the previous cycle to achieve cyclic convergence in terms of charge motion and trapped mass. To account for the real gas behavior of the injected hydrogen, the Redlich–Kwong–Soave equation of state is used [44]. The high mass diffusivity of the gas is modeled by applying local mixture-average diffusion coefficients computed from a transport properties file [45]. The simulations are carried out using a first-order upwind scheme for the turbulence transport equations, while a second-order spatial discretization scheme is applied to the momentum equation and to the species, energy and passive transport equations. In addition, the turbulent Schmidt number is reduced from 0.78 to 0.5 to improve the capability of the model to capture the high molecular diffusivity of hydrogen, following the results provided by Bifen et al. [46]. A base grid size of 4 mm is used, along with adaptive mesh refinement (AMR) based on velocity, temperature and H₂ concentration. The minimum cell size achieved is 0.25 mm inside the cylinder and injector regions, while in the intake and exhaust regions, the minimum cell size is 0.5 mm. Additionally, a permanent refinement is imposed inside the cylinder to ensure a maximum cell size of 2 mm during the entire simulation time. In the regions of the pintle injector and injector ring, two conical refinements are activated during the injection phase to reduce the cell size from 4 mm to 0.25 mm and 0.125 mm, respectively. The defined mesh setup can reliably reproduce the gas jet shape and penetration, as demonstrated by the validation study in a quiescent vessel reported in [34]. The mesh evolution due to the AMR and fixed refinements during the scavenging phase for water and fuel injection inside the cylinder, the injector ring and the pintle injector is shown in Figure 4. The number of resulting computational cells in the full engine cycle simulation ranges from approximately 300,000 to a peak of 12 million cells during hydrogen injection to capture the interaction between the charge motion and the hydrogen jets in the cylinder as accurately as possible.

The combustion process is simulated using the G-EQ combustion model, with the LFS and flame thickness (LFT) specified through look-up tables generated using the chemistry tool available in the CONVERGE CFD environment. The XJTUNO-2021 chemical mechanism, which is composed of 34 species and 236 reactions, is adopted for this work following the evidence from previous sensitivity studies [47,48]. The TFS is determined using the Damköhler correlation, implemented via a user-defined function (UDF), as shown in Equation (1).

$$s_T=s_L(1+A{\left({\displaystyle \frac{u^{\prime }}{s_L}}\right)}^{{\displaystyle \frac{5}{6}}})$$

(1)

$S_L$ represents the LFS interpolated from the look-up table, while $u^{\prime }$ is the root mean square of the turbulent velocity fluctuations. The empirical coefficient A is set to 3.6 in this study, based on a validation study performed in similar operating conditions on a 4-stroke engine [34]. Ignition is modeled in a simplified manner by introducing an energy source at the spark location. For the evaluation of pre-ignition and knock phenomena in the 3D-CFD environment, the SAGE combustion model is activated only in the unburned zone coupled with the G-EQ model, maintaining the previously described setup and the same chemical mechanism adopted for the evaluation of the LFS [45]. The methodology adopted for the following analyses was demonstrated, as referenced in Section 1, to correctly capture the injection, mixing and combustion phases using H₂ as fuel. A summary of the adopted sub-models is reported in

Table 3. Two-stroke OP engine simulation settings and models.

Simulation type	URANS
Equation of state	Redlich–Kwong–Soave
Maximum convection CFL	1–3
Turbulent Schmidt number	0.5
Base grid size	4 mm
Mesh refinements	AMR + FE
Turbulence model	RNG k-ε
Pressure–velocity coupling	PISO
Wall heat transfer model	GRUMO
Combustion model	G-EQ + SAGE
Chemical mechanism	XJTUNO-2021
Laminar flame speed	Look-up table
Turbulent flame speed correlation	Damköhler

.

3.1. Three-Dimensional CFD Evaluation of EGR Distribution Impact on Laminar Flame Speed

The combination of a highly intense swirl motion, which favors scavenging in the peripheral zone of the cylinder rather than in the central one, along with the constraint of maintaining a trapping ratio equal to 1 (to avoid short-circuiting of fresh charge in the exhaust manifold), can lead to non-negligible residual mass in the cylinder at the end of the scavenging phase influencing both the combustion and the knock tendency of the engine. The effect of having high EGR values is represented by a reduction in the laminar flame speed, as shown in Figure 5, and, consequently, an increase in the combustion duration.

The default setup in CONVERGE CFD software using the G-EQ combustion model allows imposing a fixed EGR value in each cell within a defined region. Given the high stratification of the residual gases inside the cylinder, it is fundamental to consider not only the average EGR value, but also its distribution in the combustion chamber to accurately capture the evolution of the flame. A modification in the model was therefore necessary to consider the impact of EGR stratification on local LFS. Specifically, three passive tracers were defined in the CONVERGE CFD environment to track the mass fractions of oxygen (O₂), nitrogen (N₂) and water (H₂O). Unlike active species, passive tracers allow the calculation of the laminar flame speed using the local EGR value in each cell before the flame front reaches it. In fact, the laminar flame speed is defined based on the unburned values of equivalence ratio, pressure, temperature and residual mass fraction. To verify the reliability of the method, tests were carried out in a simple cubic domain with a pressure of 20 bar, a temperature of 850 K, a homogeneous mixture and an equivalence ratio of 1. The G-EQ combustion model was used, maintaining the same setup described above. Figure 6 shows the differences among three cases: no EGR (green), 20% EGR in each cell calculated through active species (blue), and 20% EGR in each cell with passive tracers (red).

The results obtained from the test case reveal a non-negligible difference in the predicted burn rate using active species instead of calculating EGR through passive tracers. In particular, the use of active species leads to a slower flame front evolution, as shown by the blue line in Figure 6, due to the increase in EGR value within each cell as it is crossed by the flame. This increase in EGR is accompanied by a corresponding reduction in LFS. While this behavior reflects the physical reality of what occurs ahead of the flame front, it does not align with the way LFS values stored in the table are defined, namely, as a function of the unburned values of pressure, temperature, EQR and EGR within each cell in the combustion chamber domain. Conversely, the adoption of passive tracers allows the variables that determine LFS to be frozen during combustion, since passive tracers are not affected by combustion source terms, but are only advected and diffused within the flow.

3.2. Three-Dimensional CFD Water Injection

In the current study, water injection is considered as a knock mitigation strategy. Two key factors are essential for this technology to be effective. The first is the amount of vaporized water. It is crucial that most of the injected water vaporizes rapidly, cooling the charge while avoiding the formation of a liquid film, which would cool the cylinder walls rather than the charge itself. The second factor is the time required to reach a certain level of vaporization percentage. In fact, if the vaporization process is too slow, the water vapor will not have enough time to diffuse and homogenize, thereby failing to effectively lower the charge temperature throughout the cylinder. This leads to high temperature stratification, which may locally nullify the cooling effectiveness. In this context, 3D-CFD proves to be a powerful tool for quickly testing various solutions and verifying, at least virtually, whether the proposed strategies meet the target pre-ignition and knock suppression level. The setup used for the preliminary evaluation was validated against experimental data on the same injector and under similar operating conditions. For the validation process, a cylindrical vessel was modeled. The base mesh size was set to 4 mm, combined with a conical fixed embedding refinement that reduces the cell size around the injector to 1 mm (as in the in-cylinder simulation). The Kelvin–Helmholtz and Rayleigh–Taylor models were used to simulate droplet breakup. The discharge coefficient model was activated, setting the velocity coefficient ($C_v$) equal to the discharge coefficient ($C_d$). The two parameters are defined as shown in Equations (2) and (3), where $v$ is the fluid velocity, ${\rho }_l$ is the liquid density and $P_{inj}$ is the injection pressure. This implies that the orifice is filled by the fluid, since the area coefficient ($C_a$) is equal to 1, as shown in Equation (4). The water injector characteristics are reported in

Table 4. Water injector characteristics and spray vessel initial conditions.

Pressure difference	7.0 bar
Injected mass	74.95 mg
Injection duration	0.0056 s
Temperature	292.15 K
Cv	0.63
Cd	0.63
Spray cone angle	18°
Nozzle N°	2
Nozzle diameter	0.85 mm

, together with the initial conditions adopted for the spray vessel validation.

$$C_v={\displaystyle \frac{v_{real}}{v_{th}}}$$

(2)

$$C_d=\sqrt{{\displaystyle \frac{v^2{\rho }_l}{2P_{inj}}}}$$

(3)

$$C_a={\displaystyle \frac{C_d}{C_v}}$$

(4)

The applied setup allows an accurate reproduction of the spray penetration observed in the experiments, as shown in Figure 7a. Subsequently, the water injectors were implemented in the 2-stroke OP model, setting the start of injection (SOI) at 200 CAD bTDC, the injection duration equal to 88 CAD, and the tilt and spray angles equal to −20° (towards the intake ports) and 60°, respectively, as shown in Figure 7b as the baseline configuration.

3.3. Zero-Dimensional Chemical Kinetics Model

The high power demand typical of sports vehicles requires the use of a stoichiometric hydrogen–air mixture under full-load, peak-power operating conditions. Hydrogen is characterized by a longer ignition delay time, which makes it more resistant to knock compared to gasoline under the same thermodynamic conditions [2]. However, it also leads to higher in-cylinder pressure and temperature during the compression stroke, increasing the risk of pre-ignition and knock phenomena, as reported by Madia et al. [49]. An effective tool for the initial evaluation of engine tendency to abnormal combustion is represented by 0D chemical kinetics simulations that, in the current work, are performed using the commercial tool DARS provided by Siemens PLM (Plano, TX, USA).

The model was built using a Spark Ignition Reactor, which is a variable-volume two-zone homogeneous reactor. The volume variation over time depends on engine speed and geometrical parameters. In this model, the combustion chamber is split into two control volumes: one containing the burned and the other the unburned gases, with the flame front acting as the boundary between them. Each zone maintains a uniform distribution of species and temperature, while pressure is assumed constant across the entire chamber. Prior to ignition, the burned zone remains inactive, while the unburned zone is inactive when combustion is completed. During the combustion process, mass is progressively transferred from the unburned to the burned zone, resulting in a pressure and temperature rise due to both the volume change and the heat released by the consumed fuel. Simultaneously, auto-ignition is modeled by solving chemical kinetics. The rate of fuel mass consumption is governed by a Wiebe function, which defines the fuel burn rate over time and is superimposed by the user. The simulations start at 60 CAD bTDC, after the closure of the exhaust ports and the end of the injection phase, and end at 45 CAD aTDC, covering the most critical crank angle range for abnormal combustion phenomena. The mixture is uniform and stoichiometric, with an EGR value of 18%. The initial pressure and temperature are set to 9.04 bar and 634 K, respectively, consistent with the 3D-CFD simulation values. The XJTUNO-2021 chemical mechanism is used, as in the 3D-CFD analyses. Figure 8 shows the pressure trace evolution of both the 3D and 0D models. The former has been obtained from 3D-CFD. The latter has been obtained through an appropriate tuning of the Wiebe function parameters to match the 3D combustion evolution, without considering chemical kinetics.

4. Results

In the following sections, all the main simulation results are reported and analyzed, starting from mixing analysis, combustion and abnormal combustion onset.

4.1. Mixture Formation Analysis

Charge homogenization could be one of the most critical aspects to face when low-pressure DI of hydrogen is employed and the mixing time available is limited [34,39]. Guaranteeing a correct mixture formation is fundamental for reducing the cycle-to-cycle variability, the NOx production and the onset of abnormal combustion, which is enhanced by local, highly reactive, rich mixtures. The low density of H₂ makes the low-pressure H₂ jets highly affected by the in-cylinder flow motion, such as the organized tumble motion in Spark Ignition (SI)-derived four-stroke engines [39] or the swirl in diesel-derived [50] ones, as well as in the two-stroke OP configuration. The intense rotating swirl vortex results in a circumferential transport of the H₂-rich pockets instead of improving their mixing with the fresh air. One of the aims of this study is to investigate the mixing effectiveness with five possible multi-point injector configurations, realized using a ring-shaped injector cap that allows for easy modification of the jets’ directions without requiring a complete redesign of the hydrogen injector. The goal is to optimize the mixing process and achieve the most homogeneous charge. The characteristics of the injector rings tested are summarized in

Table 5. Injector ring channel diameter, tilt angle and swirl angle.

Injector Ring Case	Diameter	Tilt Angle	Swirl Angle
A	2 mm	−27° to 7.9°	33.6° to 50.6°
B	3 mm	0°	0°
C	3 mm	−30°	0°
D	3 mm	−30°	−15°
E	3 mm	−45°	−15°

, where the tilt and swirl angles for each configuration are reported along with the diameter of the channels. A positive swirl angle indicates that the fuel jets are directed along the swirl motion, while a negative value means they are oriented in the opposite direction. Similarly, a positive tilt angle means the jets are directed toward the exhaust ports, whereas a negative value indicates orientation toward the intake ports.

Case A coincides with the injector ring introduced in the previous work [34], but the results presented here consider the updated and validated methodology for the injection and mixing simulations. The SOI is fixed at 157 CAD bTDC.

The channels’ diameter increases passing from case A, the previous baseline, to the other cases to reduce the pressure rise inside the ring. This prevents a reduction in the pressure difference across the injector, which is responsible for an undesired decrease in the injector flow rate.

Figure 9 shows the probability density function (PDF), the EQR, the temperature, the EGR and the LFS fields for each injector ring tested at the end of the compression stroke, plotted on a section plane normal to the cylinder axis and located at the center of the combustion chamber.

The PDF is an indicator of the level of mixture homogenization, as it highlights the dispersion with respect to the actual average value, represented by the vertical red line (EQR = 1.0). Case E shows a flat distribution, indicating a highly stratified mixture. Better results in terms of charge homogeneity are observed in cases D and B. However, case D still shows non-negligible values around EQR = 2.0, indicating the presence of small rich pockets, as visible from the EQR image. Case B shows a slightly richer average value compared to D, but its extreme values remain closer to the target, despite the presence of both rich and lean pockets. These pockets are smaller overall, although they are in the peripheral zone, where they could still significantly affect flame front formation and evolution due to peripheral ignition. Case A, with channels oriented in favor of both swirl motion and intake ports, shows an extended rich pocket in the top peripheral zone. This might result from injection in the direction of the swirl, which, due to the low density of hydrogen, promotes the rotation of the fuel around the cylinder axis rather than mixing it effectively with the fresh air. This also explains the presence of a very lean pocket in the center of the cylinder. A negative effect on mixture homogeneity of an intense swirl motion is also reported in the literature [50], supporting the importance of a correct combination of ducts’ orientation and swirl intensity to obtain improved charge homogenization. Cases C and E have the same swirl angles as cases B and D, respectively, but differ in the tilt angle. The results highlight the influence of tilt angle on mixture homogeneity, which decreases when the tilt angle reduces. This is well visible when comparing case B to C or case D to E. Moreover, case E, the one with the most negative tilt angle, shows the worst mixture homogenization. Nevertheless, a slightly negative tilt angle is necessary, allowing an advanced injection phasing while avoiding fuel short-circuiting toward the exhaust. It is also important to evaluate the impact of the swirl angle with a fixed tilt angle on mixture formation. Cases C and D, which share the same tilt angle (−30°) but differ in swirl angle (0° for C, −15° for D), show that slightly negative swirl and tilt angles favor a better mixture homogeneity. This result is due to the interaction between the fuel jets and swirl motion. In fact, the collision between them, being highly energetic, favors the spreading of the fuel, ultimately enhancing the mixing process.

Comparing the EQR, temperature and EGR distributions reveals that colder zones are associated with rich pockets and lower EGR content, while hotter zones show lean mixtures with high residual gas concentrations. Cases B and D show the most homogeneous temperature distributions, while case D shows the lowest mean value. The temperature analysis will be resumed in the section on abnormal combustion to evaluate how far the thermal conditions reached are from a pre-ignition and knock-free operation.

The EGR distribution also affects the laminar flame speed and, consequently, the flame front evolution and combustion velocity. Case B features a significant area with EGR lower than 10%, while the rest of the domain is around 18%. Case E shows a similar trend. The other cases exhibit a more homogeneous EGR distribution. The impact of a non-uniform EGR on the combustion process is explored further in the next section, which discusses the sensitivity to spark plug number and position.

Table 6. EQR Standard deviation, maximum and mean temperature values for each injector ring configuration.

Injector Ring Case	EQR STD [-]	Max Temperature	Mean Temperature
A	0.27	2513 K	1240 K
B	0.23	2490 K	1185 K
C	0.29	2488 K	1185 K
D	0.24	2480 K	1173 K
E	0.38	2496 K	1189 K

reports the standard deviation of the PDF and the maximum and mean temperature inside the cylinder at the TDC for each injector ring configuration. Cases B and D show lower standard deviation values, while case E shows the highest.

Considering the mixing, better injector ring configurations among the tested ones are represented by cases D and B, as they show lower EQR standard deviation. Case E is the worst configuration in terms of homogeneity, showing a highly stratified mixture with the highest standard deviation (σ = 0.38). Case A is the worst in terms of temperature value and distribution, with a mean value approximately 60 K higher than the others.

Figure 10a shows the normalized swirl ratio (SR) evolution for each injector ring configuration, along with a green window indicating where the start of combustion (SOC) could occur. The swirl ratio, as reported in Equation (5), is calculated as the ratio of the angular speed of the flow, ${\mathsf{\Omega }}_{flow}$, to the angular speed of the crankshaft, ${\mathsf{\Omega }}_{crankshaft}$, with the direction of the swirl being consistent with the right-hand rule.

$$SR={\displaystyle \frac{{\Omega }_{flow}}{{\Omega }_{crankshaft}}}$$

(5)

The result further confirms the previous analysis, highlighting that maintaining a higher SR does not correspond to a better mixture homogeneity. In fact, case A exhibits a higher SR with respect to cases B and D, but also a higher mixture stratification. The difference in terms of SR between case A and the other two cases is due to the channels’ orientation. Injecting the fuel in favor of swirl motion promotes its acceleration and, consequently, a higher SR. In contrast, case D provokes a deceleration of the swirl vortex, since the fuel is injected contrary to it, with a reduction in the SR. Despite that, the collision between the air swirling column and the fuel jets favors the spread of the fuel inside the fresh air, enhancing the mixing process and leading to a more homogeneous charge. In conclusion, the obtained results show that swirl and tilt angles are strongly linked, and a deeper optimization could be employed to define their best combination to improve mixture homogeneity. From this study, slightly negative swirl (opposite) and tilt angles (upstream of the main air column) appear to be the preferable choice. Before moving on to the combustion phase analysis, it is also important to examine the TKE associated with each injector ring configuration. This parameter is crucial, as it directly affects the combustion process. Figure 10b shows the evolution of the normalized TKE in the final part of the compression stroke, where the start of combustion (SOC) can occur. Case A exhibits the highest TKE, which is attributed to the orientation of the channels. During the injection phase, the fuel jets accelerate the swirl motion, increasing its momentum. As the swirl starts to break down, its energy content is transferred into many smaller vortices, resulting in a high level of TKE. Cases B, D and E show a similar evolution of TKE, which is approximately 25% lower than that of case A at TDC. This difference can be explained by the evolution of the SR. In fact, case A is characterized by a higher SR value that is approximately 30% higher than that of cases D and E and 10% higher than that of cases B and C at the beginning of the cycle. Indeed, as shown in Figure 10a, the SR of case A starts to grow later and breaks down more slowly compared to the other cases, leading to a high level of turbulence at SOC.

In conclusion, case A appears to be the most promising in terms of TKE for promoting a fast combustion process, but it is characterized by a non-optimal mixture homogeneity, with a large rich pocket in the peripheral zone. This can significantly affect combustion stability, making it highly sensitive to the spark plug position. Considering charge homogeneity as the primary requirement, cases B and D emerge as the most promising configurations. They show good mixture homogeneity, lower temperature, with the coldest regions located near the walls, and a sufficient level of residual SR for the following cycles.

4.2. Combustion Analysis: Sensitivity to Spark Plug Number and Position

Considering the results from the mixing analysis, a detailed study on the combustion process is necessary to verify whether the obtained degree of homogenization can guarantee a sufficiently fast and efficient combustion. In fact, the positioning of the spark plug in the combustion chamber periphery, combined with a not perfectly homogeneous mixture, could lead to a very slow combustion initiation, particularly if the spark plug is placed in a region with a very lean mixture. Furthermore, it is noteworthy to underline that the inherently turbulent nature of in-cylinder flow can induce cycle-to-cycle variability in charge stratification. As a result, a highly stratified mixture may contribute to elevated levels of cyclic variability, potentially compromising combustion stability and overall engine performance. To evaluate the EQR distribution impact on engine performance, in this section, the analysis focuses on two critical aspects: the number of spark plugs and their position. The number of spark plugs affects, on one hand, engine design, as it is necessary to ensure sufficient space to fit them between two adjacent cylinders, as shown in Figure 11, and, on the other hand, the combustion evolution and duration, by increasing the total flame front surface area. The spark plug position is closely related to an effective ignition process considering the stratified charge, since placing it in a rich or lean zone can strongly influence the early combustion duration and therefore the overall combustion process, either enabling rapid flame kernel growth or potentially causing misfire.

As a first step, the influence of spark plug position is considered. As schematized in Figure 11, four different spark plug positions were tested for each injector ring configuration. In the base case (yellow star), the spark is in the most convenient position considering the multi-cylinder layout, while in the 90° position (violet star), it is the least convenient position as the second spark plug cannot be placed opposite to the first one due to insufficient space between two adjacent cylinders. The two intermediate cases considered are 45° (blue star) and 60° (green star). The SOC is fixed at TDC for all the analyzed cases. Figure 12a,b present the results in terms of MFB50 and 0–10 combustion duration. The main scope of the analysis is to understand how the combustion evolution is sensitive to spark position when the injector ring configuration is changed. A strong relationship between the local EQR value at the spark location (

Table 7. Average EQRs around spark plug position for each injector ring analyzed.

Case	A	B	C	D	E
Base	1.0	1.0	1.1	0.8	0.5
45°	1.25	1.3	0.85	0.9	0.65
60°	1.3	1.2	0.75	1.05	0.8
90°	1.25	0.8	0.7	1.25	1.3

) and 0–10 combustion duration is noticeable. The very lean mixture pocket near the spark plug in case E leads to misfire with the spark in the base position and to a very delayed combustion with the spark in the 45° position. Such behavior is clearly unacceptable, confirming case E as the worst performing. In all the other cases, the results are similar, without extreme conditions detected. The 0–10 duration is between 7 and 13 CAD, while the combustion phasing is between 20 and 28 CAD aTDC. Cases C and D are characterized by leaner mixture near the spark plug, thus resulting in a longer ignition delay, while in cases A and B, the ignition delay is generally lower. The least variation in terms of ignition delay and combustion phasing with varying spark position is obtained in case B.

Figure 12c shows the 10–90 combustion duration. Cases A, B and D have a constant behavior regardless of the spark plug position, favored by a good level of mixture homogeneity. Cases B and D are faster than case A, despite the latter being characterized by a faster flame kernel growth, as highlighted by the previous analysis on 0–10 combustion duration. The deceleration of the case A flame evolution can be explained by observing its mixture distribution. The presence of a non-negligible lean pocket in the center of the combustion chamber slows down the flame front, increasing the 10–90 combustion duration. This does not happen in cases B and D, where the flame front velocity remains more constant thanks to a more homogeneous mixture distribution. The negative impact of an insufficiently homogeneous charge distribution on 10–90 combustion duration is further highlighted by cases C and E, which are the cases with a higher EQR standard deviation value, where the 10–90 combustion duration is strongly dependent on spark plug position. The Energy Conversion Efficiency (ECE) is shown in Figure 12d. The ECE is defined as the ratio between the maximum cumulative heat release, indicated as ${CHR}_{max}$, obtained by integrating the Apparent Heat Release Rate (AHRR), and the chemical energy that can be theoretically released by the fuel, as reported in Equation (6).

$${\eta }_{EC}={\displaystyle \frac{{CHR}_{max}}{m_{f}LHV}}$$

(6)

$LHV$ represents the hydrogen lower heating value, while $m_f$ is the fuel mass injected. Cases A, B, C and D are characterized by high and constant values of ECE, around 75%, regardless of spark plug position. This confirms both the stability of the combustion and the ability to achieve nearly complete combustion in a short time, particularly for cases B and D. Case E, on the other hand, shows a maximum ECE below 50%, highlighting slow combustion and strong sensitivity to spark plug location.

Finally, Figure 13 shows the IMEP values as a function of MFB50 for each injector ring and spark plug position tested. Case B exhibits an IMEP of approximately 15.8 bar and an MFB50 of about 22 CAD, regardless of the spark plug position. A similarly stable behavior is observed for case D, with IMEP values ranging from 14 to 15.3 bar and MFB50 between 25 and 28 CAD. For cases A and C, the IMEP variation is comparable to that of case D, whereas the MFB50 variation is roughly doubled. Case E clearly delivers unacceptable results in terms of both IMEP and MFB50, highlighting the occurrence of incomplete combustion due to a highly inhomogeneous charge. In conclusion, cases B and D demonstrate a faster and more stable combustion process, along with higher ECE values for all spark plug positions tested, compared to the other injector ring cases.

Nevertheless, with SOC fixed at TDC and a single spark plug, cases B and D reach maximum IMEP values of 15.8 bar and 15.3 bar, respectively, when the spark plug is at the 90° position. These values do not meet the minimum performance requirement of IMEP being fixed at 16 bar. A first possible approach for improving combustion performance is to advance the SOC. To assess this, a SOC sweep was carried out for cases B and D with the spark plug positioned at 90° to verify whether the IMEP target could be achieved. Figure 14 shows the IMEP as a function of MFB50 for cases B and D, comparing the new simulations, performed with SOC advanced by 2 and 5 CAD bTDC. The results show that, for case B, the performance requested of at least 16 bar of IMEP is overcome by advancing the SOC by 2 CAD, achieving an IMEP value of 16.3 bar with an MFB50 around 20 CAD aTDC. For case D to overcome the lower limit of 16 bar of IMEP, it is necessary to advance the SOC further, but the target performance can be achieved with almost the same combustion phasing of around 21.5 CAD aTDC in both cases.

A second possible solution for accelerating the combustion process is represented by the introduction of a second spark plug placed opposite to the first one. In this way, the total flame front is effectively doubled, which brings advantages not only in terms of combustion duration but also in terms of combustion stability. At the beginning, the dual spark plug system is tested only on cases B and E, as they represent the best and worst scenarios from the single spark plug position analysis. Among the possible configurations, the 90° case is excluded due to the space between adjacent cylinders being insufficient to fit two spark plugs. Therefore, the 60° configuration is considered as the limiting case. The SOC is fixed at TDC. Figure 15 shows the IMEP as a function of MFB50 for cases B and E with single (SS) and dual (DS) spark plug systems. Passing from an SS to a DS system, maintaining the SOC at TDC, the MFB50 decreases thanks to the presence of the second flame front that accelerates the combustion process. The result is an improvement in the IMEP. For case B, the IMEP passes from 15.8 to 17.3 bar, whereas for case E, it passes from 11.5 to 14 bar. Despite the strong improvement in the performance with the DS system, case E is confirmed to be unfeasible due to strongly delayed combustion and far-from-target engine performance.

Despite the promising results obtained in terms of IMEP for case B, it is important to consider that an excessively fast combustion produces a rapid increase in in-cylinder pressure and temperature, enhancing the risk of knock. For this reason, an MFB50 target of 20 CAD is fixed, since it can be considered a good compromise between performance and knock risk. After the target MFB50 is fixed, a final evaluation of combustion performance is carried out, testing the DS system in the 60° position in each injector ring configuration, with the aim of defining the best compromise in terms of mixture homogeneity, combustion performance and knock tendency. The SOC is adjusted to match the MFB50 target, accepting a deviation within ±0.5 CAD, as shown in Figure 16a. The results reported in Figure 16b reveal similar 0–10 and 10–90 combustion durations for cases A, B, C and D of approximately 5 and 20 CAD, respectively, while those for case E remained significantly slower than the others. Figure 16c shows the IMEP as a function of MFB50. All the cases are well aligned in terms of MFB50, but only cases B and D present an IMEP value higher than the target one of 16 bar. Among them, case D is the best with an IMEP of about 16.5 bar. Case B has a slightly lower IMEP due to slightly delayed combustion phasing. Finally, the ECE is shown in Figure 16d. All the cases present an ECE value higher than 70%, with the highest (approximately equal to 76%) obtained in case D. Considering all the results, case D appears to be the most promising configuration, guaranteeing a good level of charge homogenization, the lowest in-cylinder average temperature and a good combustion performance.

The sensitivity of DS positioning with a fixed spark timing was also evaluated to further assess the performance of case D. Although detailed results are omitted for conciseness, the findings indicate a stable behavior, with combustion duration remaining nearly constant (between 19 and 20 CAD) and an energy conversion efficiency of about 76%. Under fixed spark timing, the MFB50 variation stays below 2 CAD, leading to a maximum IMEP reduction of only 0.5 bar as the spark position changes. The optimal performance is achieved with the DS 60° configuration, which was the reference case previously considered.

A final comparison between the best SS (90°) and DS (60° × 2) system positions for injector ring case D is shown in Figure 17. For both systems, the MFB50 is fixed at 20 CAD, obtained by setting the SOC to 3.5 CAD bTDC for the SS case and 4 CAD aTDC for the DS case. Figure 17a shows the IMEP that met the target of 16 bar in both cases. The DS case exhibits a faster combustion, with both 0–10 and 10–90 combustion durations being shorter, especially the latter, which is reduced by 7 CAD, as reported in Figure 17b. Furthermore, the advanced SOC of the SS case results in a more rapid rise in in-cylinder pressure during the early combustion phase (illustrated in Figure 17c), thereby increasing the risk of knock. Conversely, the DS case presents a lower pressure rise rate that, coupled with reduced end-gas volume (due to the higher flame area), could be effective in reducing the knock risk. In conclusion, although similar performance can be achieved using an SS instead of a DS system in case D, the DS configuration is preferable. It enables faster combustion completion (27.5% faster), resulting in a lower peak of pressure and in a limited exposure of unburned mixture to critical thermodynamic conditions, thus reducing the risk of knock.

4.3. Zero-Dimensional Pre-Ignition and Knock Analysis

In this section, the analysis focuses on understanding whether the conditions of in-cylinder pressure, temperature, mixture homogeneity and EGR level, obtained from previous analyses, can trigger pre-ignition or knock. An initial evaluation of potential abnormal combustion was carried out using a 0D chemical kinetics tool. A baseline case is created for the 0D model, imposing initial temperature and pressure corresponding to the in-cylinder ones at 100 CAD bTDC (considered as the effective compression stroke start). A stoichiometric and fully homogeneous air–fuel mixture is imposed, with an EGR value of 18%. The SOC is fixed at TDC. Figure 18a shows the difference between the baseline cases with and without the activation of the chemical kinetics. Pre-ignition occurs around 10 CAD bTDC, highlighting the necessity to identify a mitigation strategy to avoid it. A reduction in in-cylinder temperature at the end of the compression stroke is the objective to be pursued. To evaluate the temperature reduction that is necessary to complete the combustion of pre-ignition and knock, a sensitivity analysis on initial temperature is conducted. Starting from the baseline temperature of 634 K, a sweep of it is performed until a pre-ignition- and knock-free condition is met. The temperature sweep is performed by fixing the cylinder’s trapped mass, slightly adjusting the initial pressure. The results, shown in terms of temperature evolution, are summarized in Figure 18b.

A complete combustion without the occurrence of pre-ignition is obtained by reducing the initial temperature by 140 K with respect to the baseline, leading to a 230 K temperature reduction at TDC. However, a knock-free condition can also be considered if auto-ignition occurs at a certain MFB threshold. Following the study from Corrigan et al. [51], the threshold is fixed to MFB70 (for the sake of post-processing), and the results of the temperature sweep are summarized in Figure 19. To achieve knock-free operation, the temperature at TDC must be reduced by nearly 200 K compared to the current level, which corresponds to a reduction of more than 120 K at the start of the compression stroke. This represents a highly challenging objective to meet.

To obtain the relevant in-cylinder temperature reduction requested at TDC, different strategies can be adopted. A possibility is represented by a (strong) reduction in the compression ratio, which unfortunately leads to a drop in the engine performance and efficiency. A second option is the use of a mitigation strategy such as cooled EGR or water injection, which permits maintaining a high level of performance and efficiency. It is important to underline that the 0D simulations do not account for mixture inhomogeneity, which can even worsen the current scenario, advancing the auto-ignition.

4.4. Three-Dimensional CFD Pre-Ignition and Knock Analysis

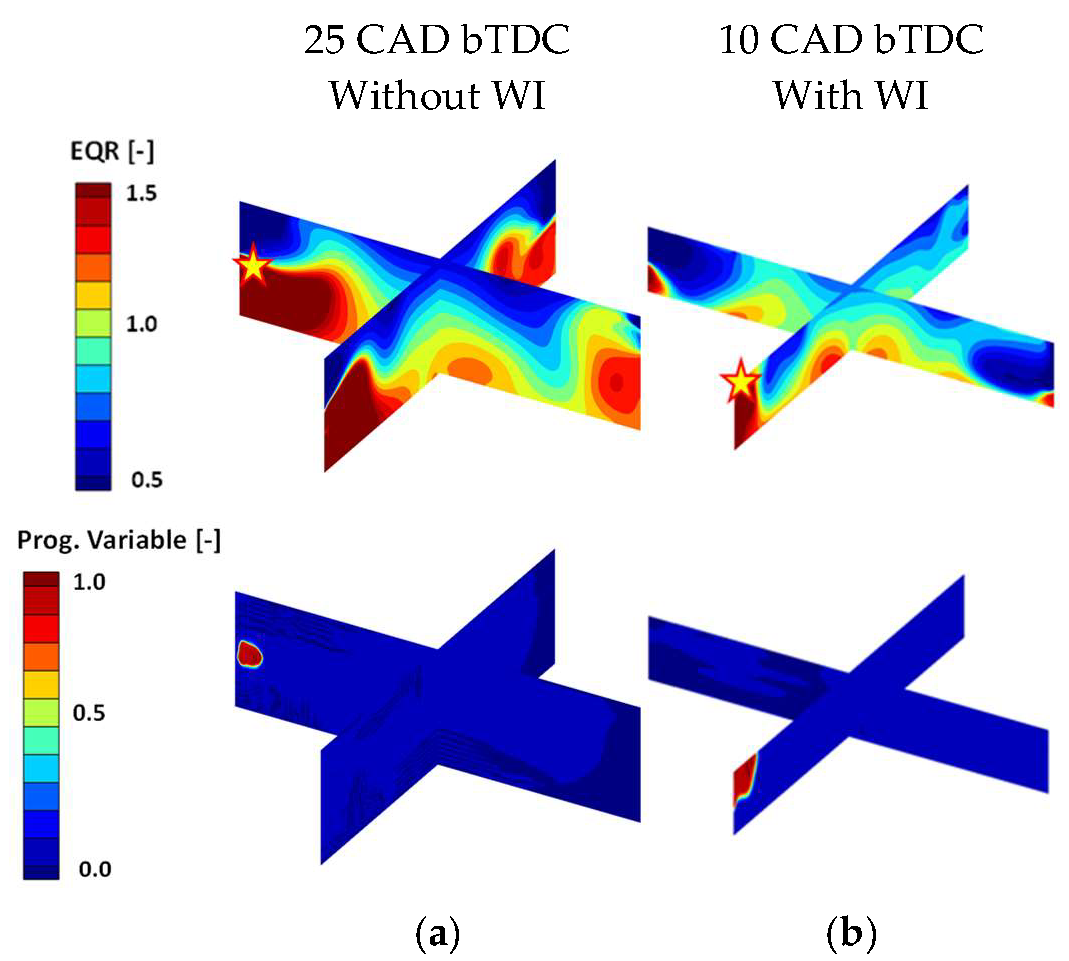
Considering the results from the 0D simulations, more detailed analyses using 3D-CFD are performed to verify whether the previous results are overoptimistic or not. Possible critical zones are represented by rich pockets, as well as by very hot zones, especially near the in-cylinder walls. For this reason, due to the impossibility of capturing these phenomena using a 0D tool, two new simulations are carried out in the 3D-CFD environment using the G-EQ combustion model coupled to chemical kinetics in the unburned region (SAGE). The simulations are run on injector ring case D, due to the good quality of mixture homogenization and temperature distribution compared to the other cases, from 100 CAD bTDC to 45 CAD aTDC, starting with an initial pressure and average temperature of 9.04 bar and 634 K, respectively. The SOC is fixed at 4 CAD aTDC. To validate the 0D results, the first simulation is performed assuming a perfectly stoichiometric and homogeneous mixture, as in 0D. In contrast, the second simulation mapped the fluid flow field, turbulence, temperature, mixture distribution, and EGR using values from the previous 3D simulation without detailed chemistry. Figure 20a,b show the evolution of pressure and temperature in both the 0D and 3D environments. The 3D No-Knock case represents the pressure trace evolution obtained using DS without activating knock modeling. The two homogeneous cases, from 3D (“3D-HOM”) and 0D (“0D Baseline”), exhibit similar behavior, demonstrating that the 0D tool can accurately predict the timing of auto-ignition under simplified conditions. However, the comparison between the 0D and 3D stratified (“3D”) cases highlights a significant advance of about 20 CAD in the pre-ignition onset only due to the transition from a homogeneous to a stratified mixture, EGR and temperature. For a more detailed investigation of the pre-ignition locations, Figure 20c–e show the EQR, temperature and progress variable evolution, respectively. The first pre-ignition event occurs around 30 CAD aTDC and reveals that the triggering condition is the combination of a rich pocket and a temperature above 750 K. Indeed, considering temperature alone is not sufficient; in fact, there are in-cylinder zones with even higher temperatures where the mixture does not ignite. This suggests that a higher temperature is required for the auto-ignition of a leaner mixture. The second pre-ignition event, on the other hand, shows two ignition points characterized by a lean mixture and temperatures exceeding 2200 K, confirming that pre-ignition can also occur in lean zones if very high temperature is reached.

In conclusion, both mixture homogenization and temperature distribution are fundamental and must be optimized as much as possible. A good level of mixture homogeneity, by avoiding the formation of rich pockets, could allow for higher in-cylinder temperature without triggering pre-ignition. Conversely, lower in-cylinder temperature makes it possible to tolerate a more inhomogeneous mixture distribution without pre-ignition. Another important result shown in the images is that the ignition points are located very close to the cylinder walls. Therefore, optimizing the cooling of these surfaces is also crucial to avoid abnormal combustion phenomena. Considering the difficulty in achieving a perfect mixture homogenization, a possible solution to prevent pre-ignition and knock phenomena could be represented by the use of water injection. This approach permits a reduction in in-cylinder temperature, allowing for a more stratified mixture. However, if the temperature reduction obtained through water injection is still insufficient to suppress abnormal combustion, the final countermeasure may consist in lowering the compression ratio, albeit at the expense of engine performance and efficiency.

4.5. Three-Dimensional CFD Preliminary Study on Water Injection

The previous section highlighted that the target performance cannot be achieved due to the onset of pre-ignition, resulting from the combined effect of high in-cylinder temperature along with a stratified mixture distribution. Consequently, the development of an effective mitigation strategy becomes mandatory. Although there is still room for optimization of the injection strategy, the CFD results indicate that a certain degree of mixture inhomogeneity is expected and should therefore be accepted. For this reason, the effectiveness of water injection (WI) in reducing in-cylinder gas temperature during the compression stroke has been numerically assessed.

As is well established in the literature, WI can enhance volumetric efficiency and mitigate knock occurrence by cooling the charge and acting as a diluent [13,52]. To maximize this cooling effect while avoiding the need for excessively high water quantities, WI efficiency, defined as the fraction of the injected water that successfully vaporizes inside the cylinder, becomes a critical parameter. This aspect is particularly relevant when employing port water injection (PWI) instead of direct water injection (DWI), since the formation of wall films significantly reduces effectiveness by preventing the liquid from directly contributing to charge cooling. A potential technical solution for implementing WI in the 2S-OP engine is investigated to assess the achievable cooling level and its effectiveness in suppressing pre-ignition without resorting to compression ratio reduction. Exploiting the OP architecture, water can be injected directly into the cylinder during the first half of the compression stroke through holes in the cylinder barrel, using a low-pressure system specifically designed for PWI. Since the injectors are not exposed to hot combustion gases, no costly redesign is required to withstand high thermal loads. This configuration combines the simplicity and cost-effectiveness of PWI with the high efficiency typically associated with DWI. The start of injection is set at 200 CAD bTDC, with an injection duration of 90 CAD, allowing the injection of almost 55 mg of water at an injection pressure of 10 bar. The injectors are orientated with a tilt angle of −20° (towards the intake ports) and a spray angle of 60°, enabling injection against the upward air flow and thus enhancing the evaporation rate. Figure 21 shows the in-cylinder mass evolution of the liquid water injected. Although the water SOI occurs 200 CAD bTDC, the liquid starts to evaporate around 125 CAD bTDC, as indicated by the increase in the vapor mass (green line) and the decrease in the liquid water mass (yellow line). The red line exhibits the film mass evolution that reduces the cooling capability of the water injected, as explained previously. Furthermore, despite the presence of the vertical air column due to the orientation of the intake ducts, the liquid spray does not reach the exhaust manifold; i.e., water short-circuit is avoided. Thus, the only limit to cooling efficiency is represented by the liquid film formation on the cylinder walls. At TDC, the mass of water evaporated is around 32 mg, which corresponds to 58% of the total water mass injected, while the masses of the liquid film and the water still in liquid form are around 21 mg and 2.5 mg, respectively, corresponding to 38% and 4% of the total water mass injected.

From this analysis, two possible critical aspects are highlighted. The first is the relevant amount of the water film obtained at TDC, subtracting the useful water from cooling the charge. As shown in Figure 22, the water droplets’ motion is strongly influenced by the swirling air column from the intake ports. The droplets are transported around the combustion chamber, leading to a relevant concentration of them on the liner at TDC, opposite to the port water injectors, due to the high water jet penetration. The rest of the film mass is located on the intake piston surface due to the orientation of the port water injectors. The second critical aspect is represented by the delay in the vaporization process that starts close to the beginning of the compression stroke, limiting both the amount of vapor generated, and thus the cooling effect on the charge, and the temperature homogenization, reducing the capability of eliminating the hot critical zone inside the combustion chamber.

Figure 23a shows the temperature evolution from water SOI to TDC with (green) and without (red) WI. The difference in in-cylinder temperature between the two cases remains almost zero until 100 CAD bTDC, when the liquid water starts to evaporate. Despite the delay, the in-cylinder average temperature at TDC of the case with WI is approximately 85 K lower than that of the cases without WI. This temperature reduction is almost 100 K lower than the one expected from the 0D study. To further assess the effectiveness of WI, a full 3D simulation including detailed chemistry is performed, and the results are reported in Figure 23b. The introduction of WI delays the pre-ignition onset of the stratified case (red line) by 15 CAD, while the homogeneous one (yellow line) is still the one with the most delayed pre-ignition. In other words, the negative effect of the mixture stratification overcomes the beneficial one of WI. This result clearly highlights the importance of the mixture homogeneity in avoiding abnormal combustion phenomena and the necessity to improve the cooling effect to enhance both the vaporization efficiency and temperature homogenization, maintaining this level of charge stratification.

In Figure 24, the EQR field at pre-ignition onset is reported, comparing the cases with and without WI. As previously described, without WI, auto-ignition starts around 25 CAD bTDC from a rich and relatively cold pocket. Thanks to the introduction of WI, the temperature has been significantly reduced, delaying the pre-ignition onset by 15 CAD. The trigger, as in the case without WI, is from a rich–cold zone rather than from a hot–stoichiometric or lean one, confirming that cooling the charge alone is not sufficient. To avoid auto-ignition, it is fundamental to improve the mixture homogeneity, mainly avoiding the formation of rich pockets.

The results obtained by introducing WI have revealed that a further optimization of the mitigation strategy is necessary to achieve the in-cylinder temperature reduction required to avoid the pre-ignition onset. In particular, the critical aspects that influence the efficiency of WI are the injector orientation and position, the total water mass injected and the water SOI angle with respect to the TDC. All these parameters are strictly linked, and the best compromise must be identified to increase the cooling effectiveness. The developed CFD model allows this optimization to be performed, and that will be the object of the next works.

5. Conclusions

This paper describes critical aspects that must be considered in the design of a H₂-fueled 2S-OP engine for high-performance vehicles. In particular, the analysis focuses on a stoichiometric full-load, peak-power operating point at 6000 rpm, one of the most challenging conditions in terms of mixture formation and combustion completeness due to the high engine speed. Moreover, this operating point is also critical with respect to abnormal combustion, since the high load leads to severe in-cylinder temperature and pressure when coupled to a stoichiometric mixture. The power output target was set at 130 kW/L (corresponding to 16 bar of IMEP) and an ITE above 40%.

A complete analysis of the engine model was carried out using detailed 3D-CFD and chemical kinetics simulations. The main findings can be summarized as follows:

• The best mixture homogeneity was obtained by orienting the injector channels slightly against the in-cylinder swirl motion and towards the intake ports (swirl angle −15°, tilt angle −30°). On the contrary, combining radial channels with a highly negative tilt angle (−45°) worsened both the EQR and temperature distribution. Overall, the mixture formation remains critical, and a certain degree of inhomogeneity must be accepted.
• The combustion analyses have shown that, without a sufficient mixture homogeneity, the risk of misfire and high cycle-to-cycle variability becomes significant. While an SS system could still achieve the performance target, a DS system is preferable. With adequate mixture homogeneity, the DS configuration makes the spark plug location almost negligible, ensuring rapid combustion completion despite the high EGR fraction. It reduces the pressure and the temperature rise rate during the early combustion phase due to a delayed SOC for a fixed combustion phasing, thereby mitigating knock tendency.
• Due to the high in-cylinder pressure and temperature, the engine is prone to pre-ignition, which was found to be strongly influenced by mixture stratification. In particular, the triggering zones were characterized either by rich–cold pockets instead of lean–hot ones, highlighting the importance of improving the mixture homogeneity while simultaneously reducing the in-cylinder temperature. Pre-ignition onset represents the main limiting factor preventing achievement of the performance target, making the adoption of mitigation strategies essential.
• The WI analysis yielded promising results, with a sufficiently high degree of water vaporization and a significant reduction in in-cylinder temperature, leading to a delay in the pre-ignition onset. Nevertheless, the temperature at TDC remained too high to avoid pre-ignition. Therefore, further optimization of the WI parameters, namely SOI, injector orientation and injection duration, is required to fully assess the effectiveness of WI as a mitigation strategy.

In conclusion, achieving high specific power output and efficiency with a 2S-OP architecture fueled with hydrogen involves critical challenges that only detailed 3D-CFD analyses can effectively reveal. Among these, mixture formation stands out as the most crucial process to optimize, since ensuring a highly homogeneous mixture is essential for achieving knock-free operation at high loads. This study demonstrates the value of detailed numerical simulations in identifying and resolving such challenges, paving the way for innovative and disruptive technical solutions while reducing the time and costs associated with prototype development and testing. Future work will focus on the detailed optimization of hydrogen injection and PWI to define the maximum performance achievable with this distinctive engine architecture, while operating within the prescribed technical constraints.