A Decoupled Two-Stage Optimization Framework for the Multi-Objective Coordination of Charging Efficiency and Battery Health
Abstract
1. Introduction
2. Battery Characteristic Testing and Model Parameter Identification
3. Two–Step Optimization Based on Adaptive SOC Staging
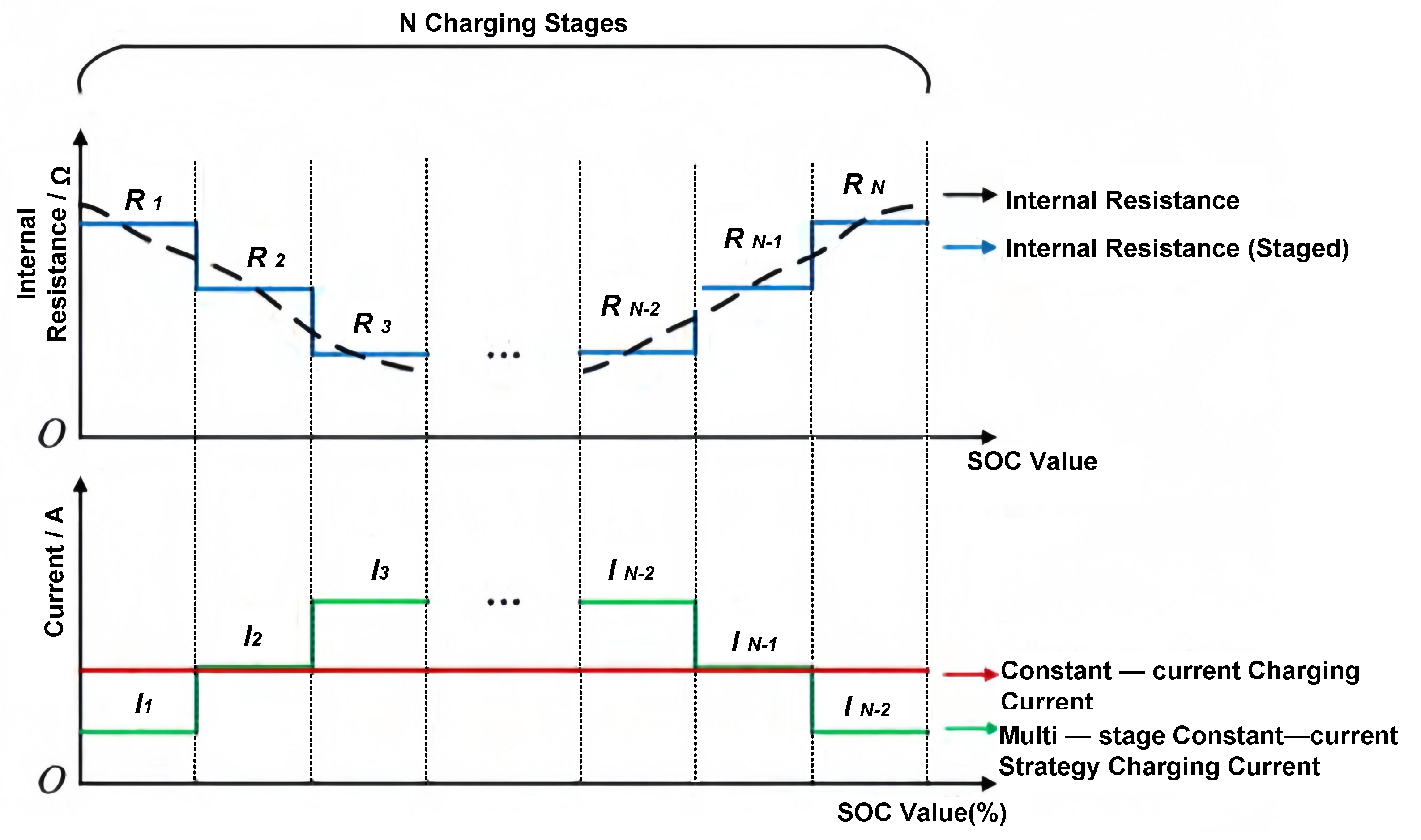
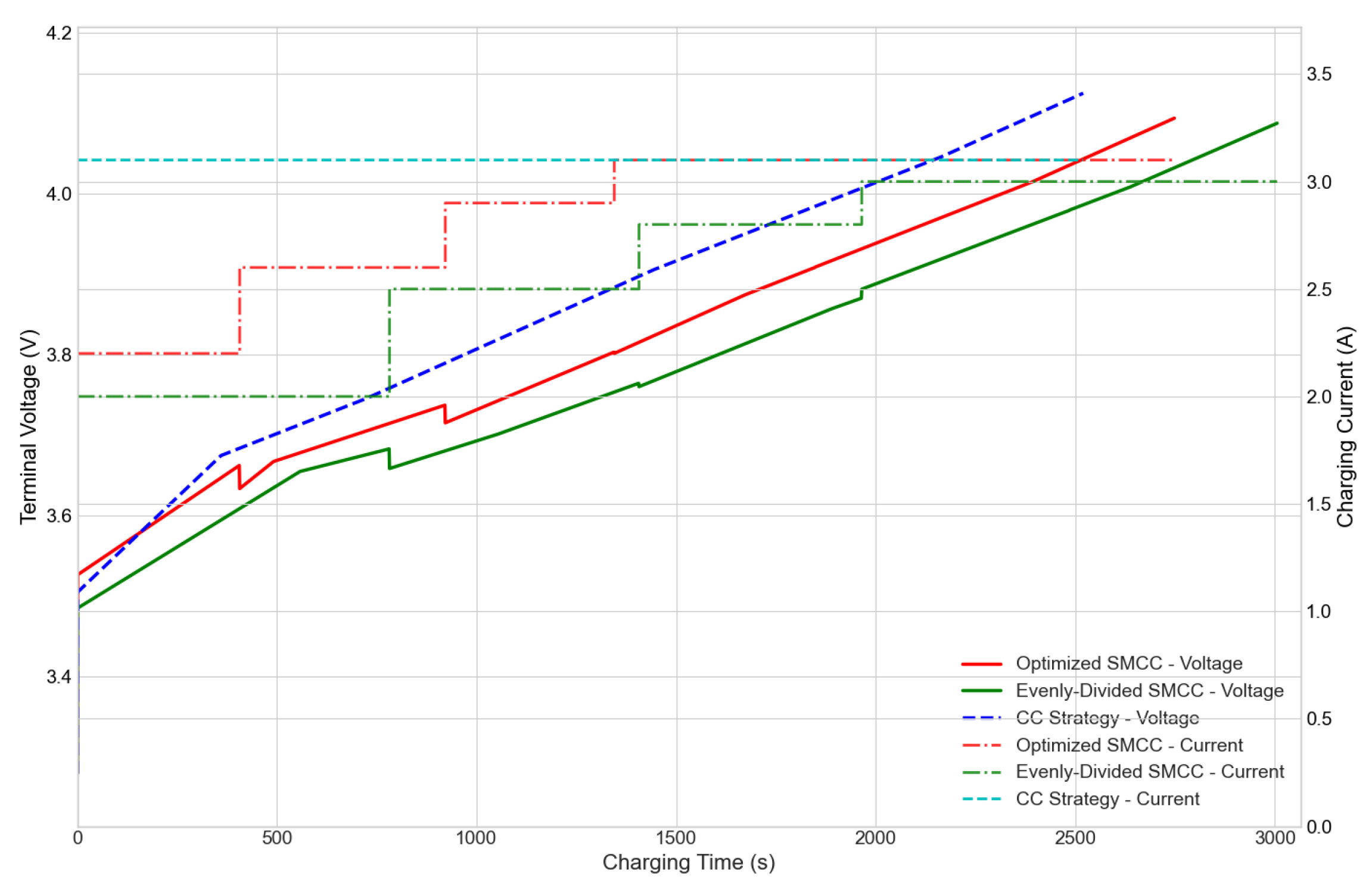
3.1. Improved SMCC Strategy
3.2. Charging Strategy Optimization Model
3.3. Two–Phase Optimization Charging Strategy
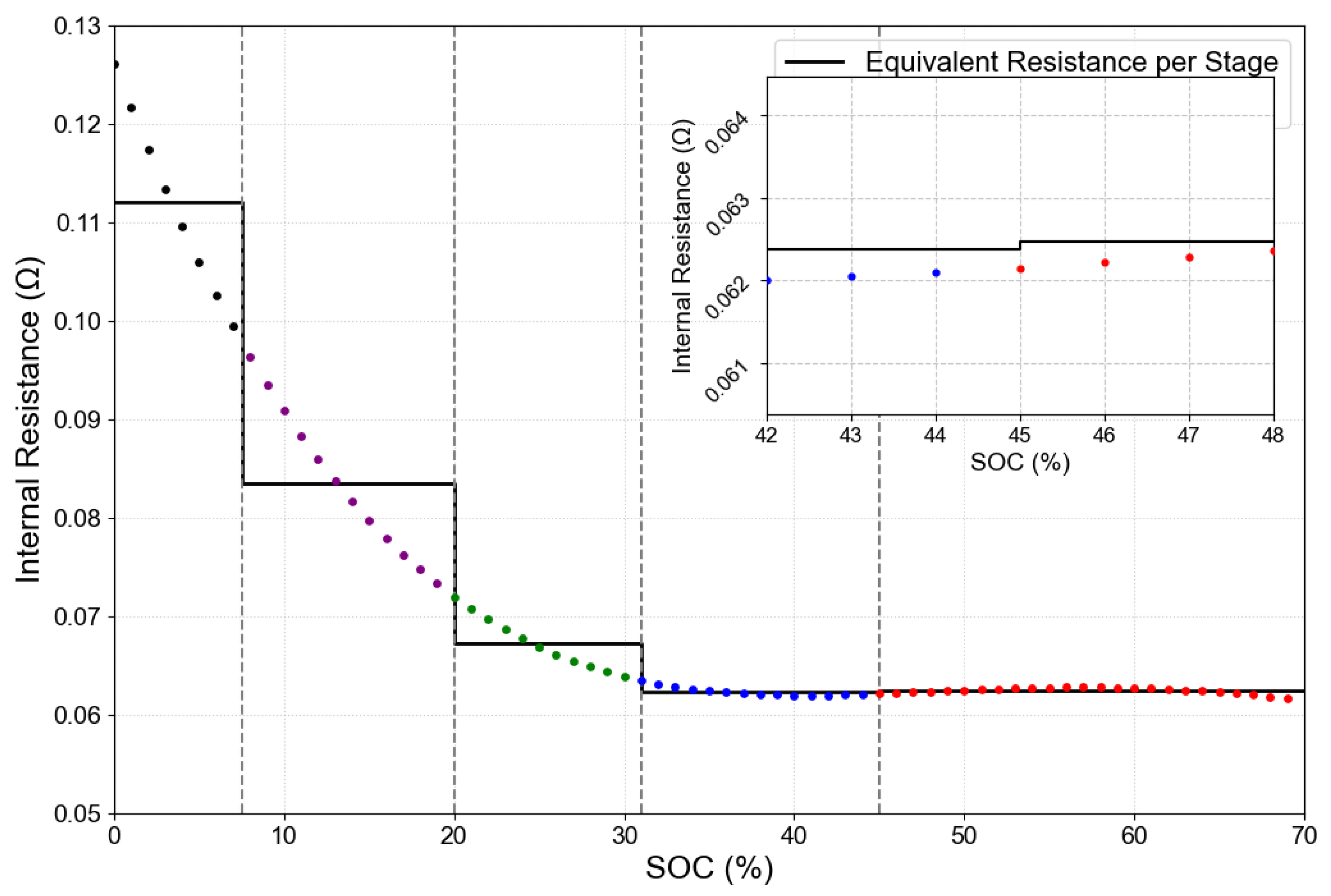
3.3.1. Step 1: SOC Staging Optimization Based on the Clustering Algorithm
3.3.2. Step 2: Tiered Current Multi-Objective Optimization Solution
- (1)
- Construction of the Initial Sample Library
- (2)
- WNN Modeling
- (3)
- Enhanced MOPSO for Multi–Objective Pareto Front Exploration
- Logistic Chaotic Initialization
| Algorithm 1 Multi-Strategy Enhanced MOPSO–Part 1: Initialization. |
|
- 2.
- Adaptive t–Distribution Mutation
- 3.
- Velocity Clamping
| Algorithm 2 Multi-Strategy Enhanced MOPSO–Part 2: Main Iteration Loop. |
|
- 4.
- Crowding Distance–Based Tournament Leader Selection
| Algorithm 3 Multi–Strategy Enhanced MOPSO–Part 3: Sub-procedures. |
|
- (4)
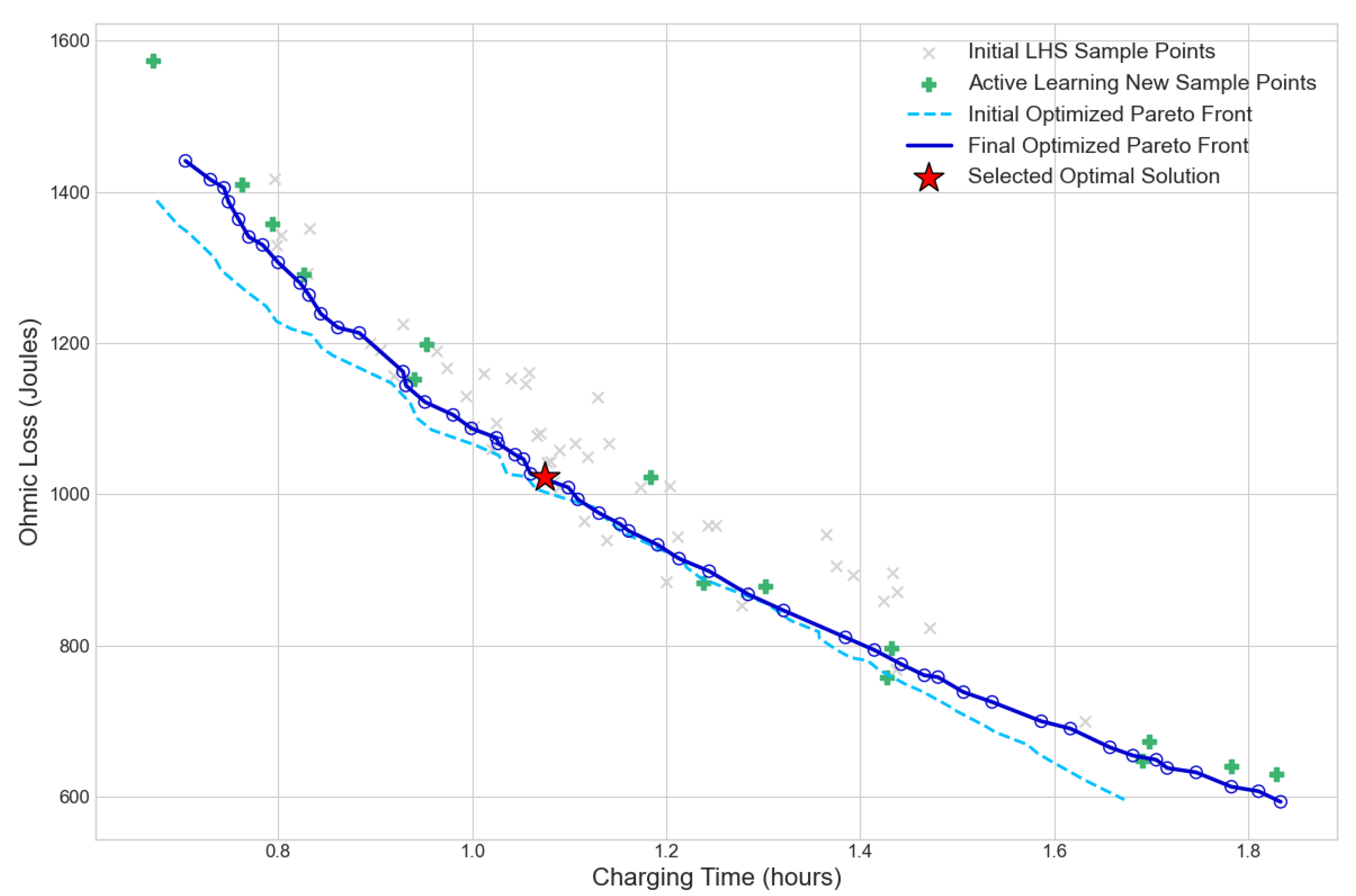
- Closed–Loop Optimization Mechanism Based on Active Learning
4. Results and Discussion
4.1. Analysis and Discussion of Optimization Results
Clustering-Based Multi–Phase Optimization Results
4.2. Comparative Experimental Analysis
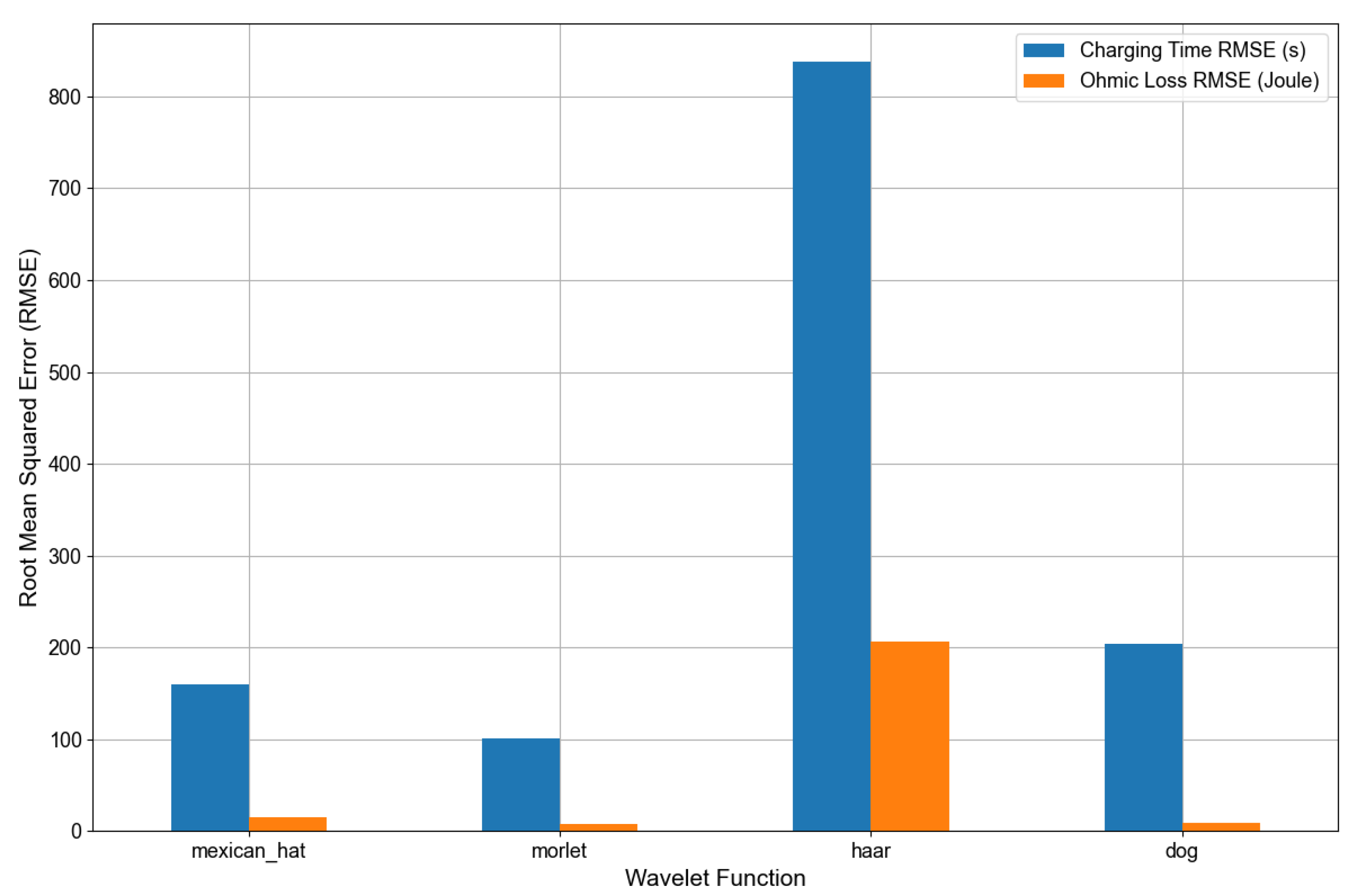
4.2.1. Analysis of Experimental Results for Wavelet Basis Function Selection
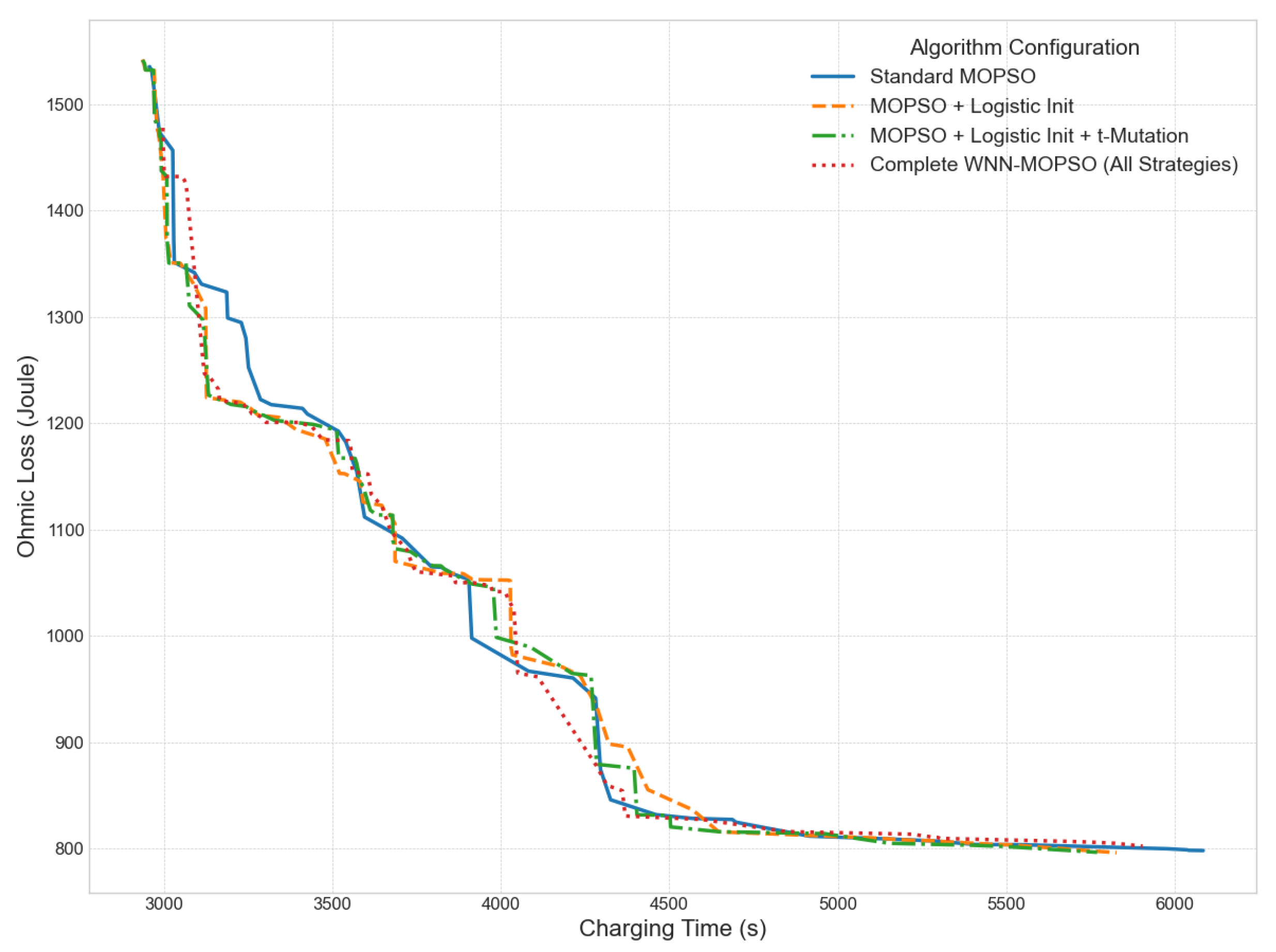
4.2.2. Ablation Study Verification for the Performance Enhancement of the WNN–MOPSO Algorithm Driven by Multi–Strategy Synergy
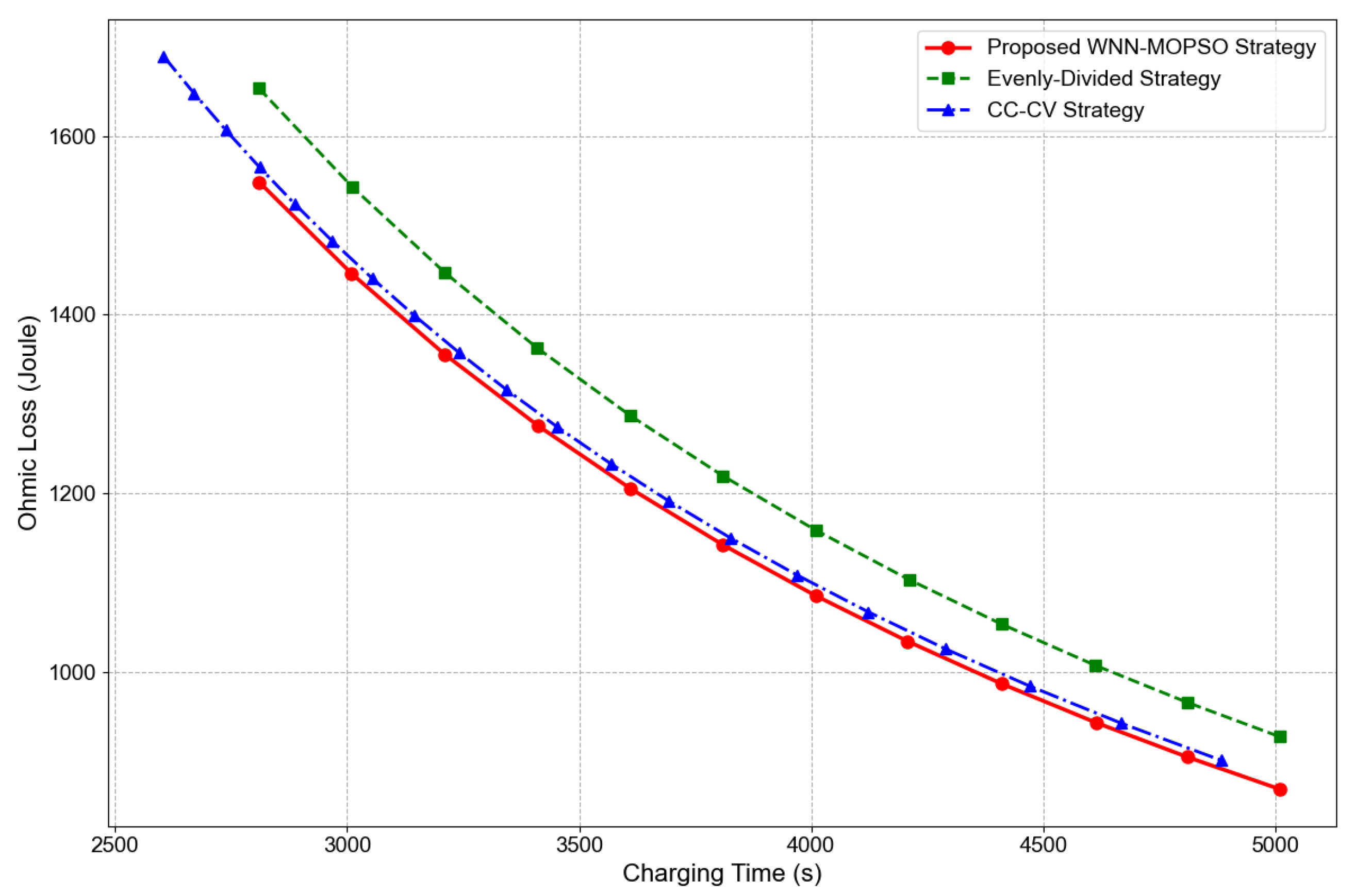
4.2.3. Performance Comparison of Three Charging Strategies
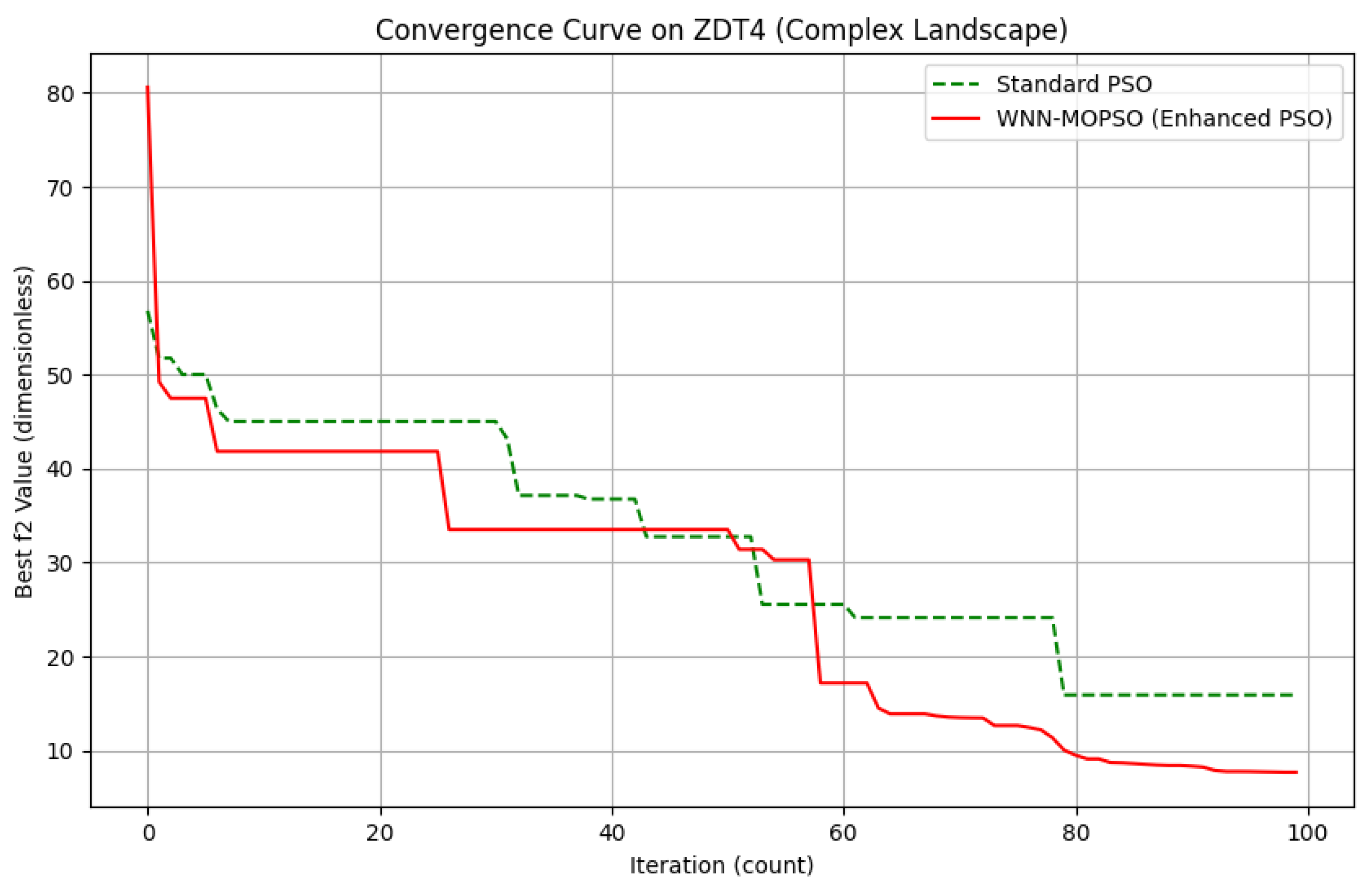
4.2.4. Convergence Performance Comparison of Different Optimization Algorithms
4.2.5. Comparison of Pareto Fronts for Three Strategies
4.3. Experimental Validation
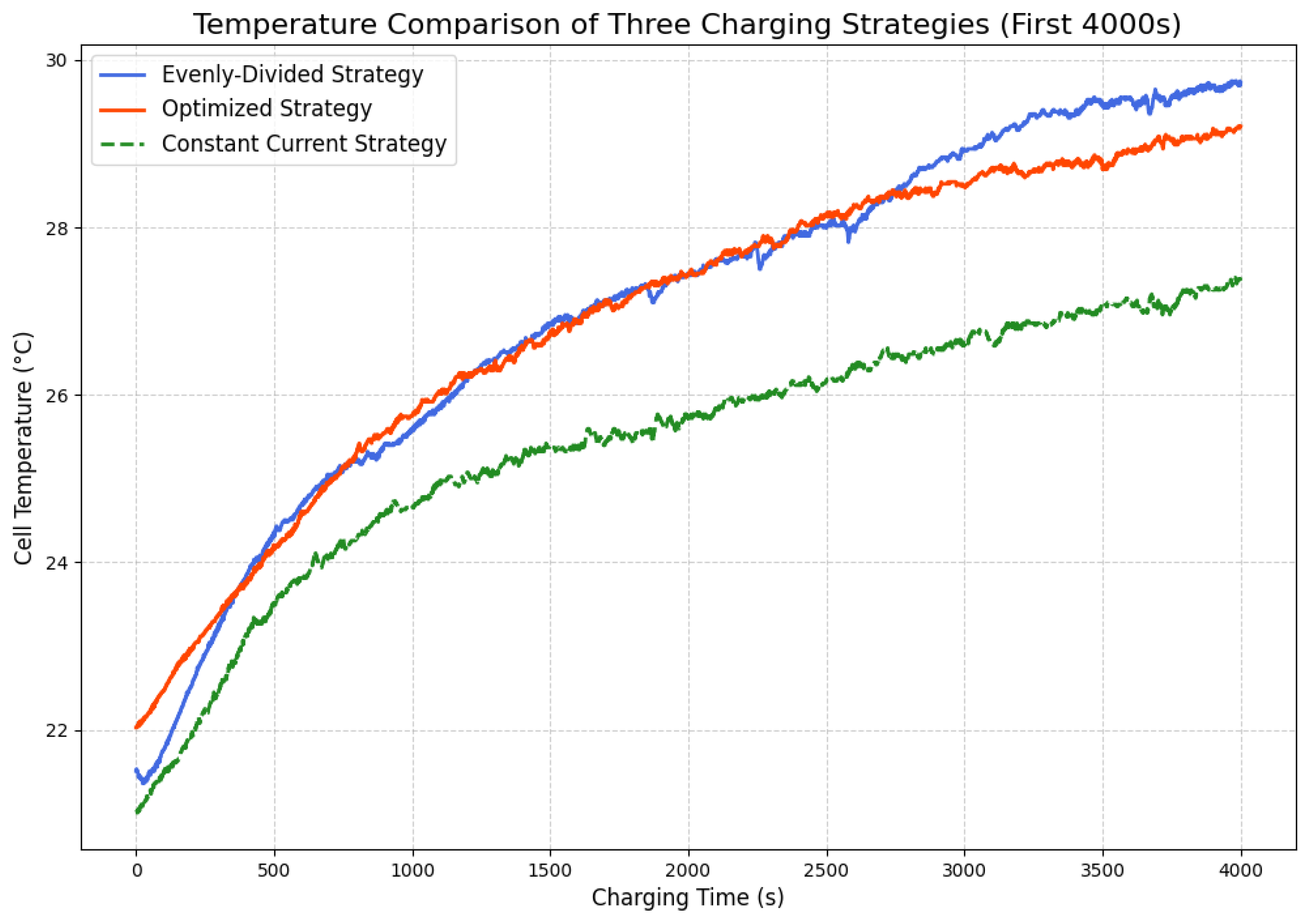
4.3.1. Thermal Stability Analysis
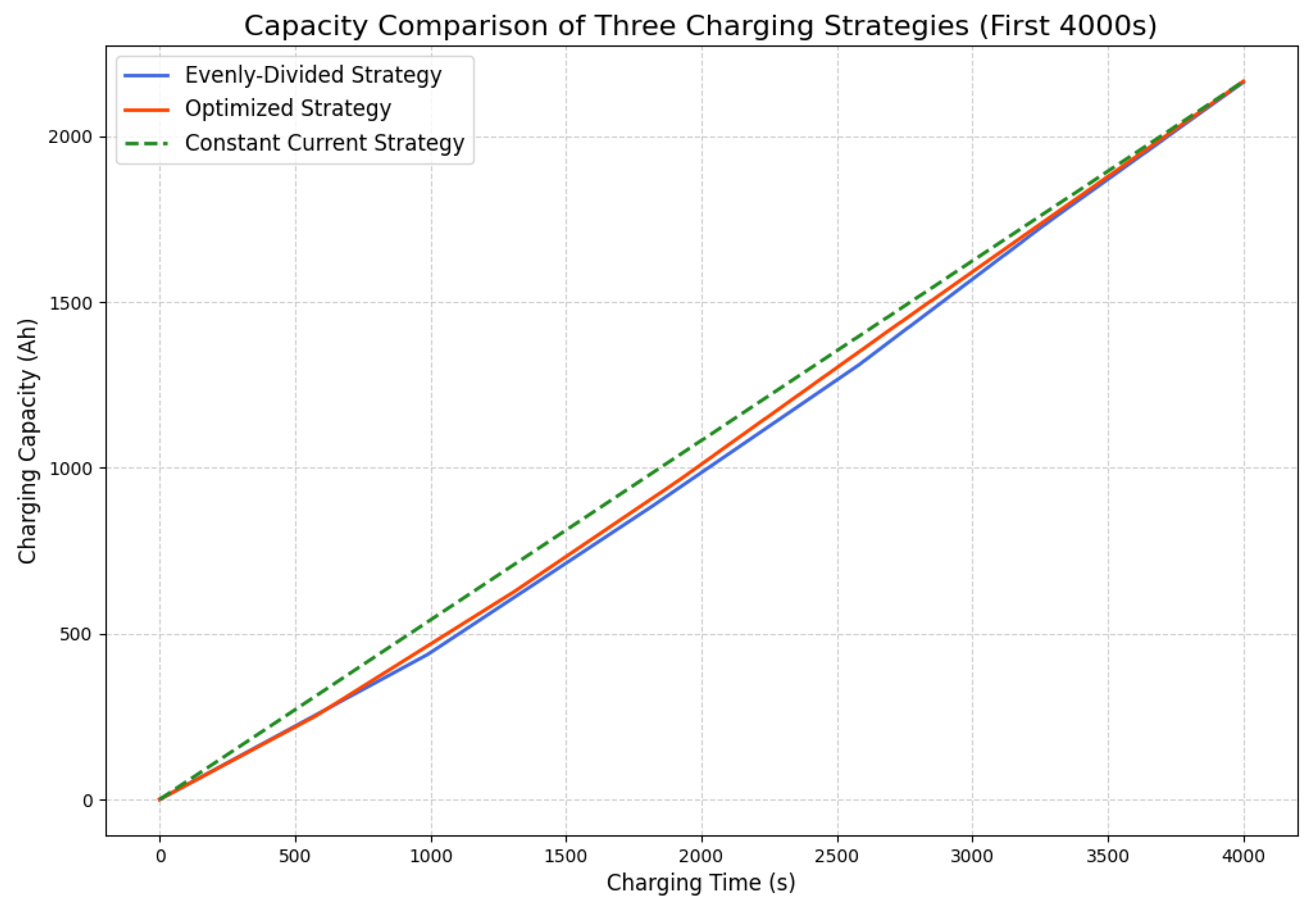
4.3.2. Charging Performance Analysis
5. Conclusions
- The SOC staging technique utilizes an enhanced canopy–bisecting K–means clustering algorithm to adaptively partition the charging process. This segmentation is predicated on the "U–shaped" distribution characteristic of the internal resistance against the SOC curve. This solution decreases the internal resistance SSE by 53.6% compared to the five–phase equal–division method. It utilizes tight phases in the low SOC region to precisely capture the dynamic properties of internal resistance, while implementing wide phases in the high–SOC region to streamline the charging control method. This method markedly improves the flexibility of the battery’s internal condition.
- A WNN approximation model was developed with the Mexican hat wavelet as its activation function, exhibiting enhanced predictive accuracy. Its RMSE for ohmic loss is 790% lower than that of the Haar wavelet. Moreover, its charging time prediction inaccuracy is 38.5% smaller than that of the DOG wavelet. This model can effectively replace practical experiments in modeling the nonlinear relationships of the charging process. The MOPSO method incorporates numerous essential tactics, such as Logistic chaotic initialization, adaptive t-distribution mutation, and crowding–degree–based tournament leader selection. This technique reduces the IGD metric by 97.6% on the ZDT2 test function, demonstrating enhanced convergence and variety of the solution set, hence facilitating a swift search for optimal solutions.
- The active learning strategy functions inside a cycle of optimization, sampling, and retraining. In this procedure, high–potential solutions are chosen from the Pareto front. The samples are utilized to calibrate the physical model and rectify the prediction bias of the WNN. This technique exhibits significant efficiency: the IGD between the Pareto front and the genuine optimal boundary can be decreased by 87.6% after merely five repetitions. This outcome clearly demonstrates the efficacy of the iterative optimization method. The notable enhancement verifies that the co–evolutionary mechanism of modeling and optimization can efficiently and consistently augment the optimization capacity for intricate battery systems.
- The experimentally observed lower charging temperature corroborates the reduced theoretical ohmic losses revealed in earlier simulations. This not only directly confirms the proposed strategy’s significant suppression of peak charging temperature but also experimentally validates its core capability to enhance battery thermal stability. Furthermore, the reduction in peak temperature during charging can slow the rates of internal side reactions and degradation of electrode active materials, effectively delaying battery aging and providing critical technical support for extending cycle life.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CC | Constant Current |
| CV | Constant Voltage |
| MCC | Multistage Constant Current |
| VMCC | Voltage-based Multistage Constant Current |
| SMCC | State-of-Charge-based Multistage Constant Current |
| MOP | Multi-Objective Problem |
| PSO | Particle Swarm Optimization |
| WNN | Wavelet Neural Network |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| HPPC | Hybrid Pulse Power Characterization |
| IGD | Inverted Generational Distance |
| DM | Diversity Metric |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| SSE | Sum of Squared Errors |
| RMSE | Root Mean Square Error |
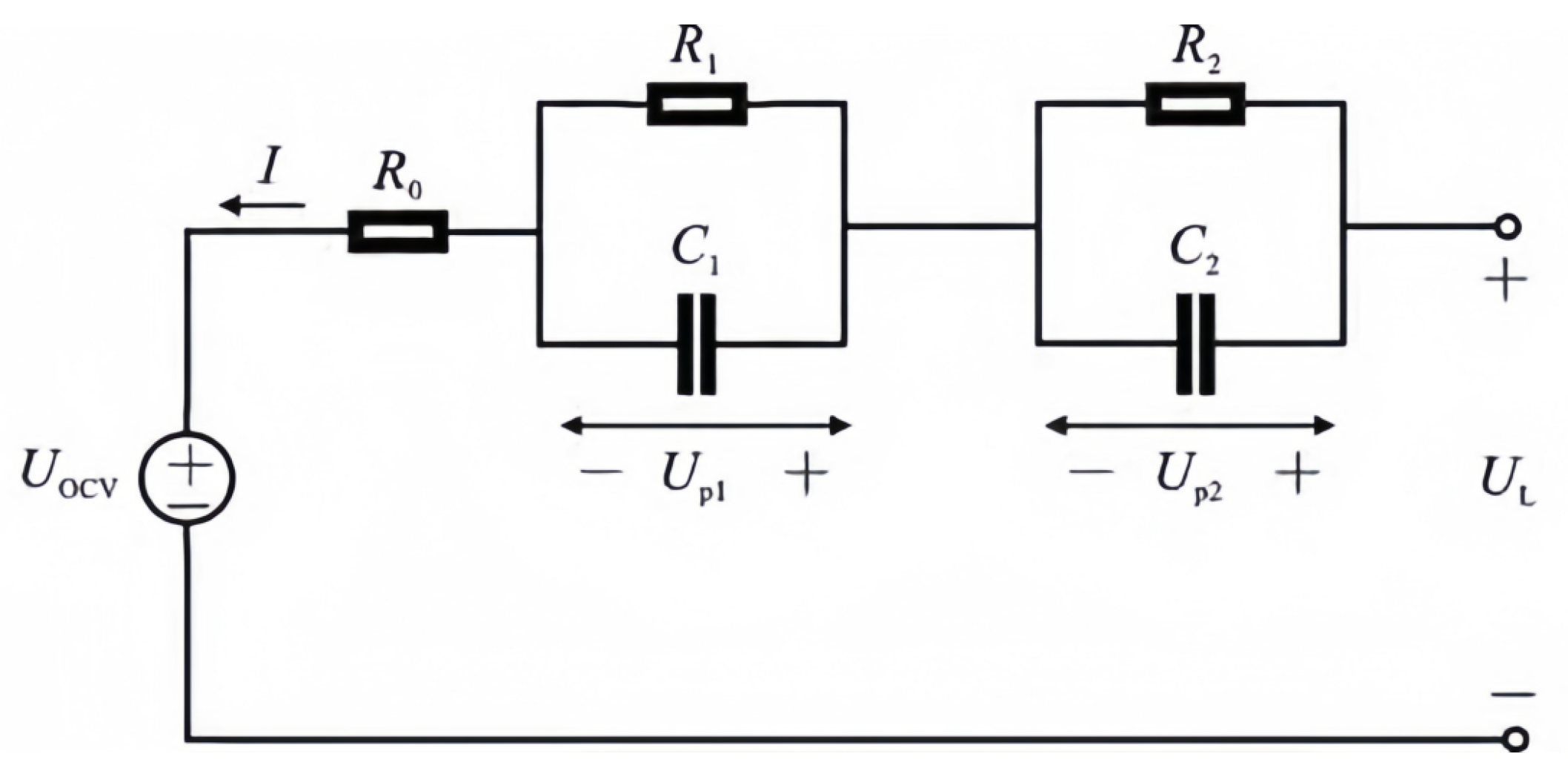
Appendix A. Electrochemical Model (ECM) Construction
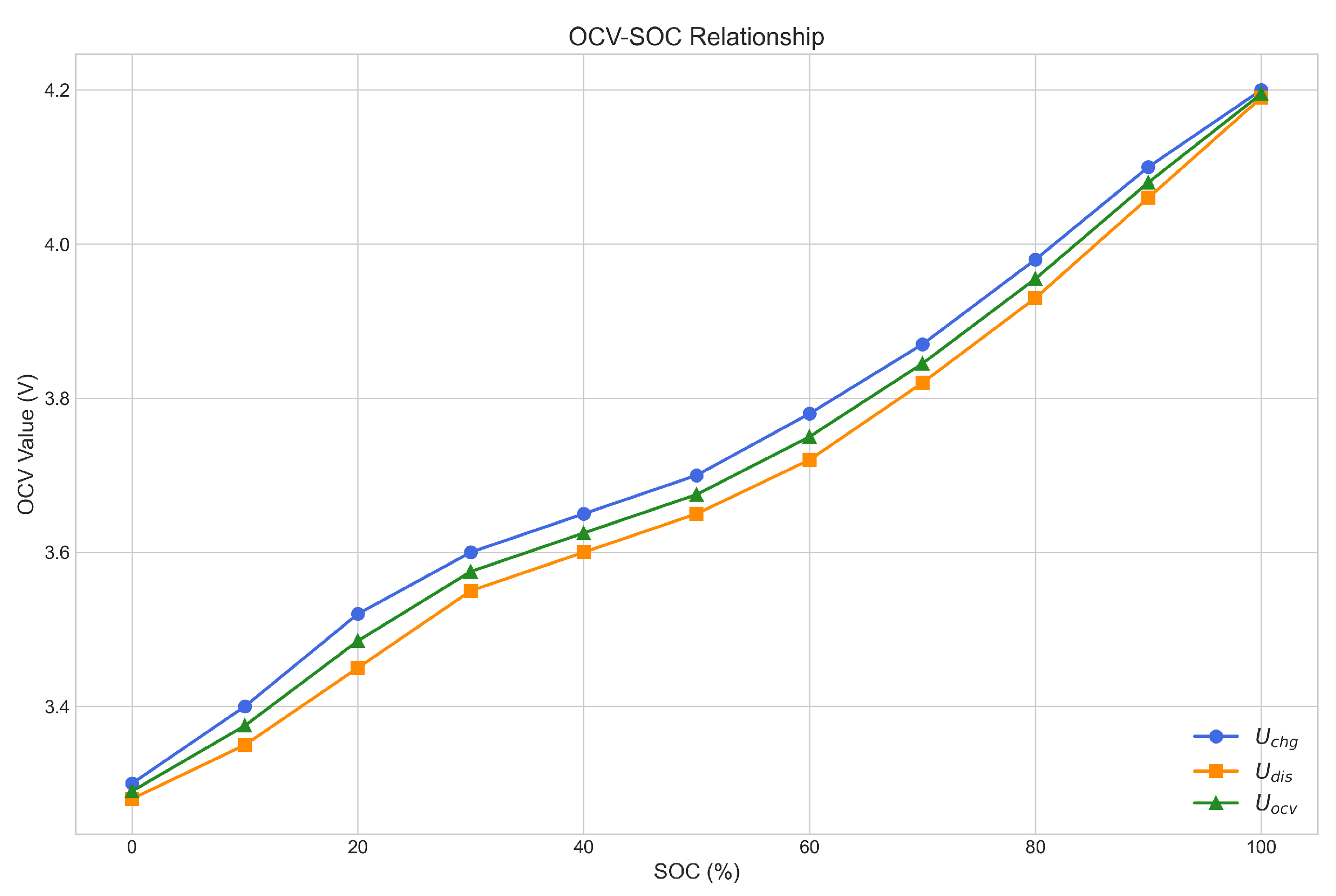
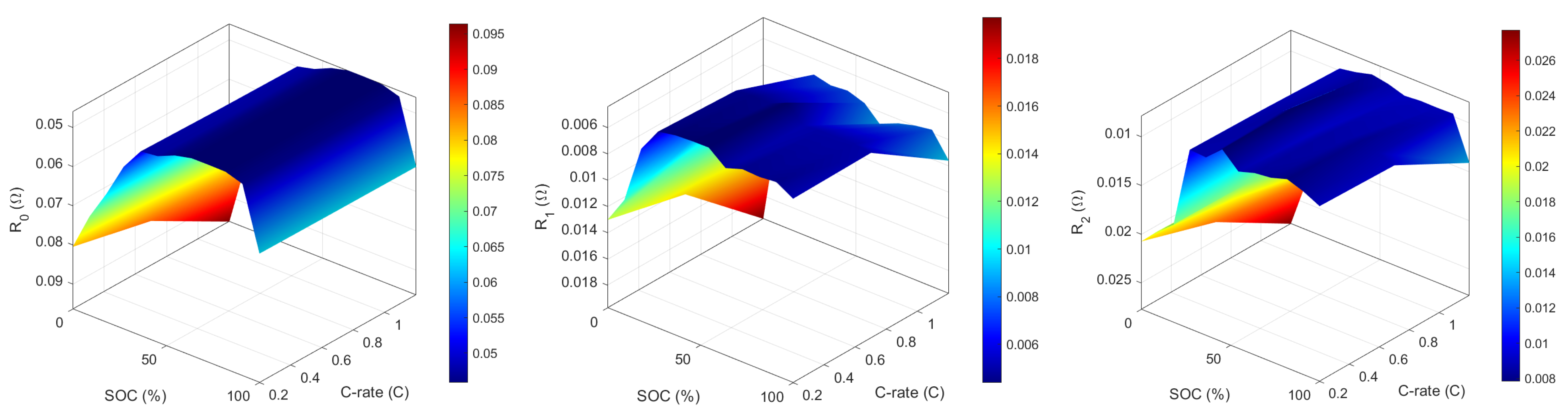
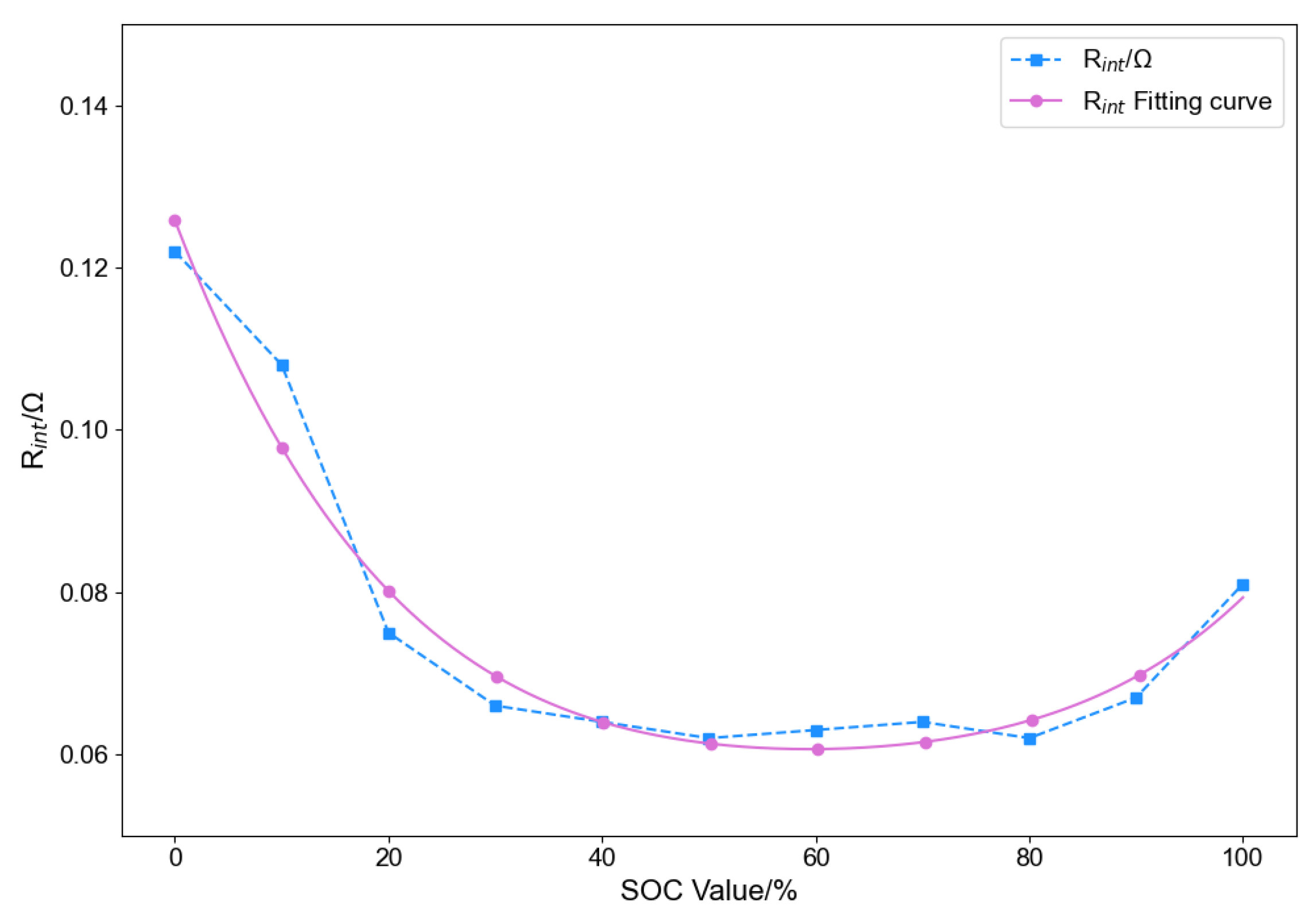
Appendix B. Battery Characterization Tests and Parameter Acquisition

References
- Bondarde, M.P.; Wadekar, P.H.; Some, S. Synthesis of sulfur-doped carbon nanoparticle for the improvement of supercapacitive performance. J. Energy Storage 2020, 32, 101783. [Google Scholar] [CrossRef]
- Kumar, K.; Pareek, K. Fast charging of lithium-ion battery using multistage charging and optimization with Grey relational analysis. J. Energy Storage 2023, 68, 107704. [Google Scholar] [CrossRef]
- Dong, H.; Huang, W.; Zhao, Y. Low complexity state-of-charge estimation for lithium-ion battery pack considering cell inconsistency. J. Power Sources 2021, 515, 230599. [Google Scholar] [CrossRef]
- Vott, C.; Chen, X.; Shen, W.; Kapoor, A. New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation. J. Power Sources 2015, 273, 413–422. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Gao, Y.; Zhang, W. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- Sungur, B.; Kaleli, A. State of charge estimation for lithium-ion batteries using optimized model based on optimal HPPC conditions created using Taguchi method and multi-objective optimization. Appl. Sci. 2024, 14, 9245. [Google Scholar] [CrossRef]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z.; et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef]
- Ahn, J.H.; Lee, B.K. High-efficiency adaptive-current charging strategy for electric vehicles considering variation of internal resistance of lithium-ion batteries. IEEE Trans. Power Electron. 2019, 34, 3041–3052. [Google Scholar] [CrossRef]
- Lin, X.W.; Li, Y.B.; Wu, W.T.; Zhou, Z.F.; Chen, B. Advances on two-phase heat transfer for lithium-ion battery thermal management. Renew. Sustain. Energy Rev. 2024, 189, 114052. [Google Scholar] [CrossRef]
- Nouri, A.; Lachheb, A.; El Amraoui, L. Optimizing efficiency of Vehicle-to-Grid system with intelligent management and ANN-PSO algorithm for battery electric vehicles. Electr. Power Syst. Res. 2024, 226, 109936. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Wang, S.; Zhang, Z. Multi-objective optimization of electric vehicle charging and discharging in a V2G network using a hybrid Harris Hawks and Particle Swarm Optimization algorithm. Energy 2023, 282, 128221. [Google Scholar] [CrossRef]
- Yang, R.; Lu, J.; Sun, Z.; Huang, W. Multi-objective optimization of parking charging strategy for extended-range hybrid electric vehicle based on MOMSA. World Electr. Veh. J. 2025, 16, 203. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI. PPSN 2000. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1917, pp. 849–858. [Google Scholar] [CrossRef]
- Li, K.; Zhang, H.; Xie, Y.; Fu, C. Study on self-adaptive multistage constant current charging based on electro-thermal-aging coupling model. J. Northeast. Univ. Nat. Sci. 2019, 40, 1323–1329. [Google Scholar] [CrossRef]
- Lei, H.; Hu, X.; Zhao, J.; Deng, D.; Wang, R. Research progress and prospects of public transportation charging station layout methods. World Electr. Veh. J. 2024, 15, 63. [Google Scholar] [CrossRef]
- Aghili Mehrizi, A.; Yeganehdoust, F.; Madikere Raghunatha Reddy, A.K.; Farhad, S. Challenges and issues facing ultrafast-charging lithium-ion batteries. Batteries 2025, 11, 209. [Google Scholar] [CrossRef]
- Duan, S.; Xia, K.; Zhu, W. Multi-stage optimization charging strategy for lithium-ion batteries considering diverse application scenarios. Energy Storage Sci. Technol. 2025, 14, 779–788. [Google Scholar] [CrossRef]
- Tobias, A.V.; Wahab, A. Autonomous ‘self-driving’ laboratories: A review of technology and policy implications. R. Soc. Open Sci. 2025, 12, 250646. [Google Scholar] [CrossRef]
- Cheng, F.; Liu, H. Charging strategies optimization for lithium-ion battery: Heterogeneous ensemble surrogate model-assisted advanced multi-objective optimization algorithm. Energy Convers. Manag. 2025, 342, 120170. [Google Scholar] [CrossRef]
- Acikkapi, M.S.; Ozkaynak, F. A method to determine the most suitable initial conditions of chaotic map in statistical randomness applications. IEEE Access 2021, 9, 1482–1494. [Google Scholar] [CrossRef]
- Yang, X.; Liu, J.; Liu, Y.; Xu, P.; Yu, L.; Zhu, L.; Chen, H.; Deng, W. A novel adaptive sparrow search algorithm based on chaotic mapping and t-distribution mutation. Appl. Sci. 2021, 11, 11192. [Google Scholar] [CrossRef]
- Chen, W.; Wu, H.; Gao, H.; Li, Y. A Two-Layer Optimization Strategy for Battery Energy Storage Systems to Achieve Primary Frequency Regulation. Energies 2023, 16, 2811. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, T.-W.; Hsu, S.-H.; Jiang, J.-A. Taguchi-based PSO for searching an optimal four-stage charge pattern of Li-ion batteries. J. Energy Storage 2019, 23, 444–453. [Google Scholar] [CrossRef]
- Zhao, J.; Song, C.; Li, G. Fast-Charging Strategies for Lithium-Ion Batteries: Advances and Perspectives. ChemPlusChem 2022, 87, e202200155. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Ouyang, M.; Li, X.; Lu, L.; Li, J.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]





| Battery Parameter | Value | Battery Parameter | Value |
|---|---|---|---|
| Nominal Capacity /(A·h) | 3.25 | Charging Cut–off Voltage/V | 4.2 |
| Maximum Charging Current/A | 1 C | Discharging Cut–off Voltage/V | 2.5 |
| Standard Charging Current/A | 0.5 C |
| Number of Neurons | RMSE of Charging Time (s) | RMSE of Ohmic Loss (J) | Training Time (ms/Epoch) |
|---|---|---|---|
| 10 | 158.4 | 45.2 | 3.1 |
| 15 | 146.8 | 41.7 | 4.5 |
| 20 | 142.3 | 38.5 | 5.2 |
| 25 | 143.1 | 39.8 | 6.6 |
| Phase | Internal Resistance () | Range Width (%) | ||
|---|---|---|---|---|
| Equal Div. | Optimized | Equal Div. | Optimized | |
| 1 | 0.1025 | 0.1120 | 14 | 8 |
| 2 | 0.0722 | 0.0836 | 14 | 12 |
| 3 | 0.0629 | 0.0673 | 14 | 11 |
| 4 | 0.0624 | 0.0624 | 14 | 14 |
| 5 | 0.0625 | 0.0625 | 14 | 25 |
| Total SSE | ||||
| Equal Division | 0.0028 | |||
| Optimization | 0.0013 | |||
| Parameter Name | Algorithm Name | Value |
|---|---|---|
| Population Size | PSO/MOPSO/MOPSO Improved | 100 |
| Total Number of Iterations | PSO/MOPSO/MOPSO Improved | 250 |
| Archive Size | MOPSO/MOPSO Improved | 100 |
| Inertia Weight w | MOPSO/MOPSO Improved | 0.5 |
| Learning Factors | MOPSO/MOPSO Improved | 1.5, 1.5 |
| Neighborhood Size k | MOPSO Improved | 5 |
| Velocity Limiting Factor | MOPSO Improved | 0.2 |
| Mutation Operator | MOPSO Improved | Polynomial Mutation |
| Test Function | Metric | PSO | MOPSO | Improved MOPSO |
|---|---|---|---|---|
| Mean (Std. Dev.) | Mean (Std. Dev.) | Mean (Std. Dev.) | ||
| IGD | 0.367295 (0.070451) | 0.429102 (0.290745) | 0.010145 (0.001940) | |
| ZDT2 | DM | 5.054480 (0.532240) | 1.412817 (0.000815) | 1.413160 (0.001817) |
| SP | 0.475596 (0.078511) | 0.010616 (0.003143) | 0.009268 (0.002339) | |
| IGD | 6.006661 (2.264237) | 7.338512 (3.618626) | 7.338512 (3.618626) | |
| ZDT4 | DM | 151.445495 (27.401011) | 2.895908 (3.190638) | 1.445408 (2.217614) |
| SP | 18.963343 (4.462454) | 0.401359 (0.453505) | 0.260423 (0.564899) | |
| IGD | 0.237902 (0.031811) | 0.046466 (0.000353) | 0.046515 (0.000389) | |
| ZDT6 | DM | 8.532387 (0.382996) | 2.402346 (1.310316) | 2.853585 (1.749217) |
| SP | 0.362554 (0.099496) | 0.120608 (0.130768) | 0.139851 (0.146945) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, X.; Shi, L.; Chen, X.; Lei, X. A Decoupled Two-Stage Optimization Framework for the Multi-Objective Coordination of Charging Efficiency and Battery Health. Energies 2025, 18, 5180. https://doi.org/10.3390/en18195180
Yi X, Shi L, Chen X, Lei X. A Decoupled Two-Stage Optimization Framework for the Multi-Objective Coordination of Charging Efficiency and Battery Health. Energies. 2025; 18(19):5180. https://doi.org/10.3390/en18195180
Chicago/Turabian StyleYi, Xin, Lingxia Shi, Xiaoyang Chen, and Xu Lei. 2025. "A Decoupled Two-Stage Optimization Framework for the Multi-Objective Coordination of Charging Efficiency and Battery Health" Energies 18, no. 19: 5180. https://doi.org/10.3390/en18195180
APA StyleYi, X., Shi, L., Chen, X., & Lei, X. (2025). A Decoupled Two-Stage Optimization Framework for the Multi-Objective Coordination of Charging Efficiency and Battery Health. Energies, 18(19), 5180. https://doi.org/10.3390/en18195180






