Sub-Module Capacitor Voltage Ripple Suppression in MMDTC-Based PET Using Three-Port Active Bridge
Abstract
1. Introduction
- (1)
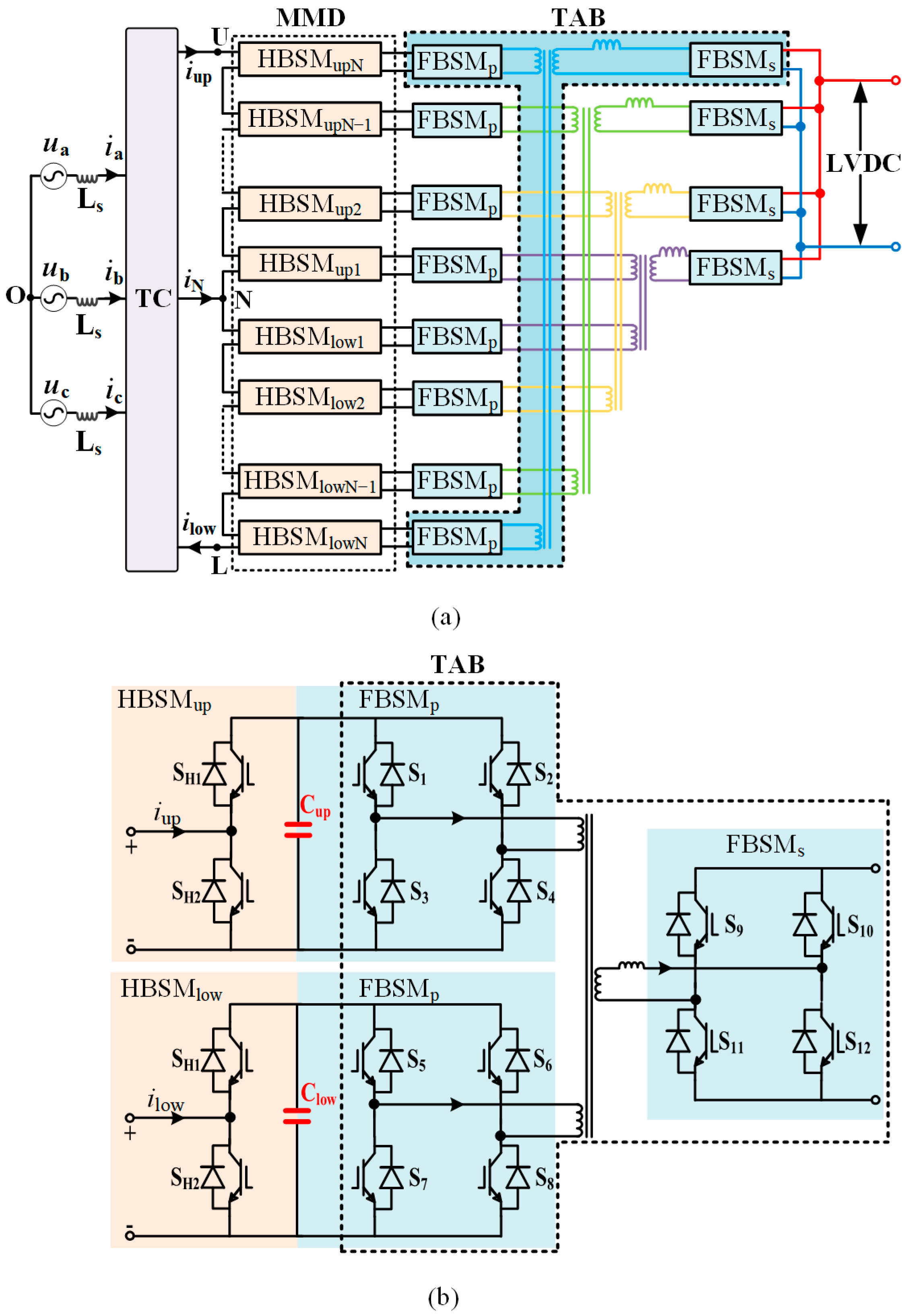
- Novel TAB-based topology for MMDTC-PET: A TAB-based MMDTC-PET structure is proposed where the two input terminals of each TAB are connected to corresponding sub-modules in the upper and lower arms, respectively. This configuration enables direct power coupling between paired sub-modules while maintaining isolation from the LVDC bus.
- (2)
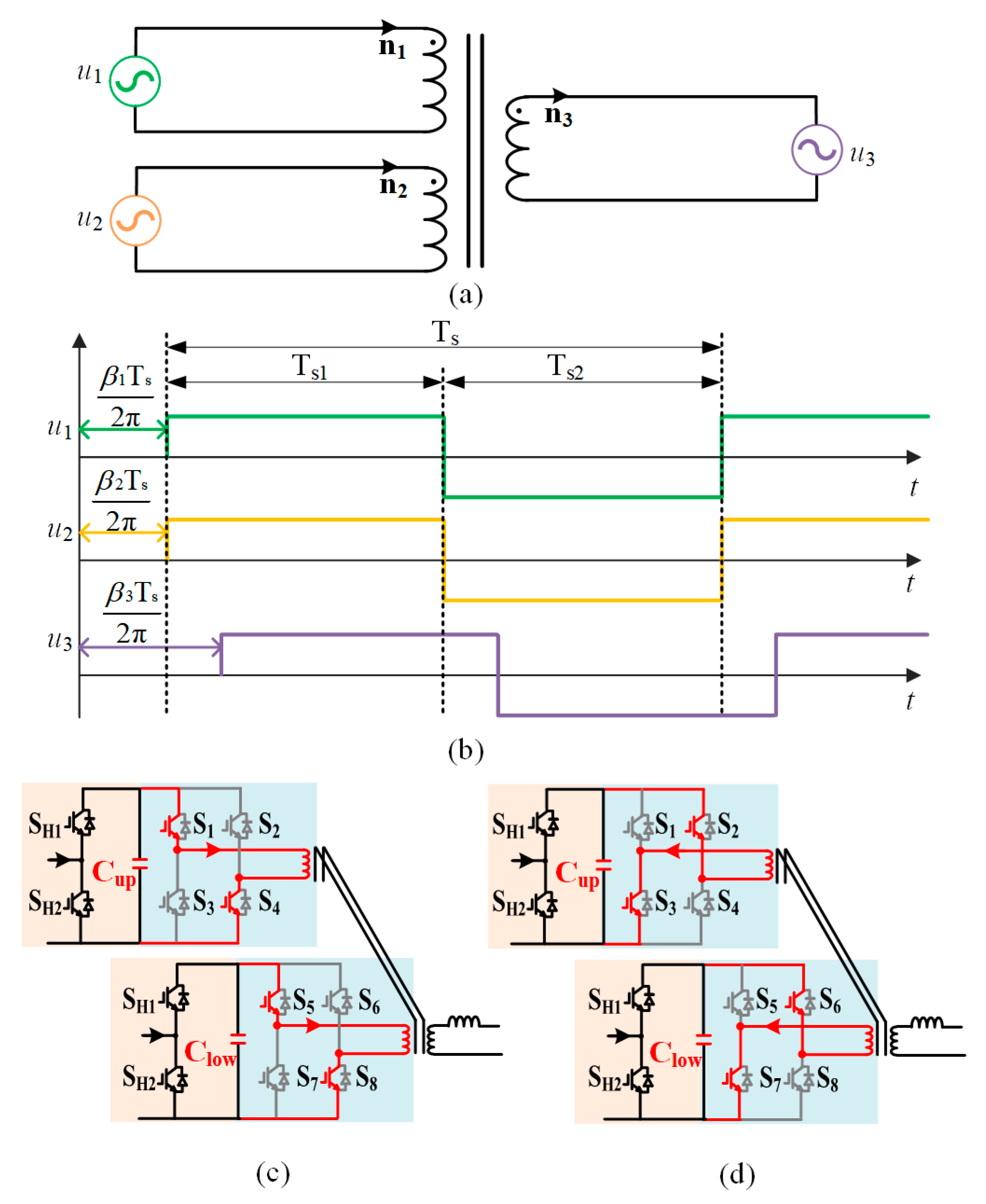
- Switched-capacitor principle implementation: By employing identical phase-shift modulation for the two input-side full bridges of TAB, the sub-module capacitors in upper and lower arms naturally form a switched-capacitor configuration under high-frequency switching states to suppress the capacitor voltage ripple.
- (3)
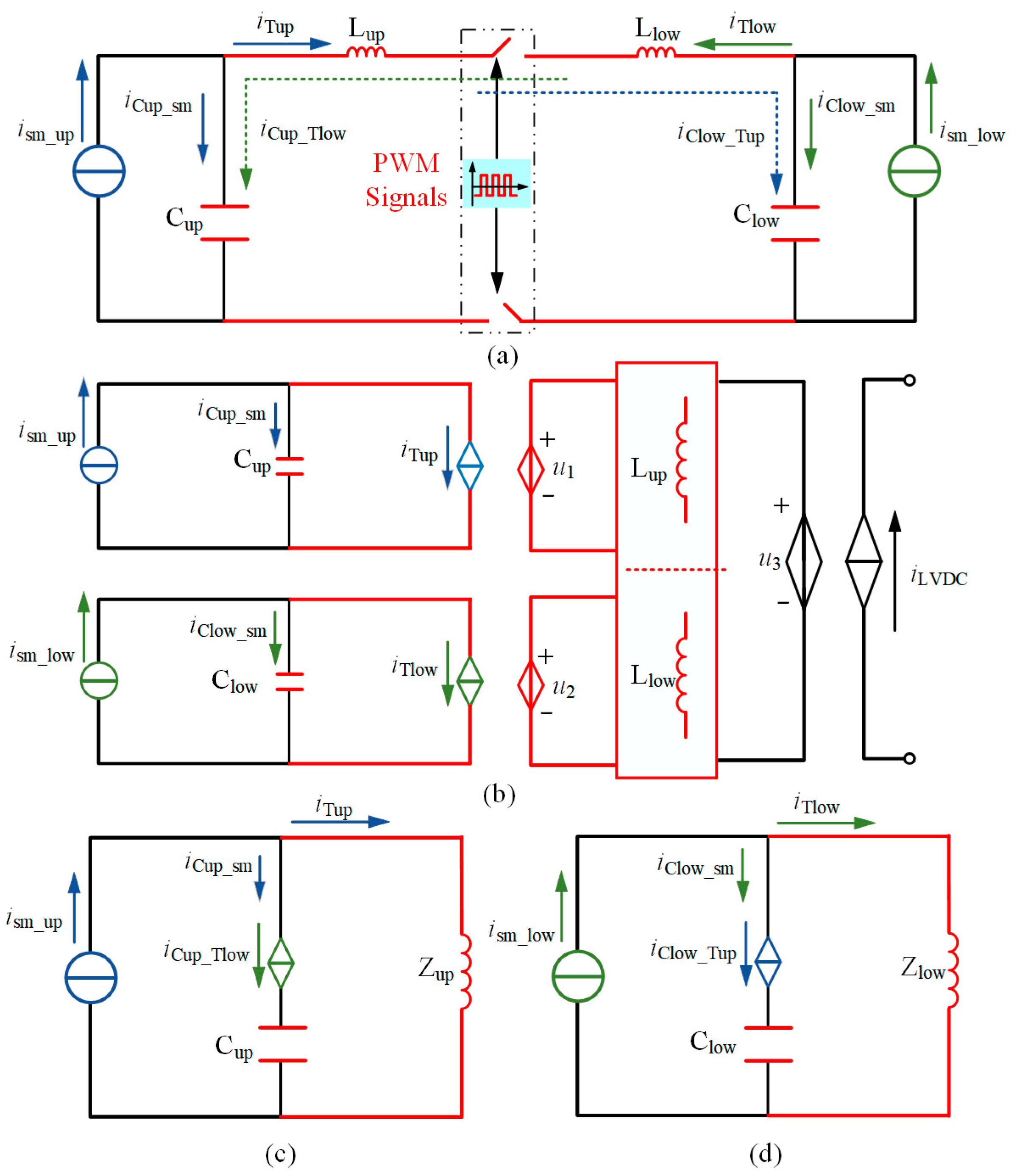
- Inherent ripple power cancelation mechanism: The proposed scheme leverages the characteristic that AC power components in upper and lower arms have equal amplitudes but opposite phases. These components are automatically transferred through the low-impedance switched-capacitor path to the secondary side where they cancel out, achieving ripple suppression without active control intervention.
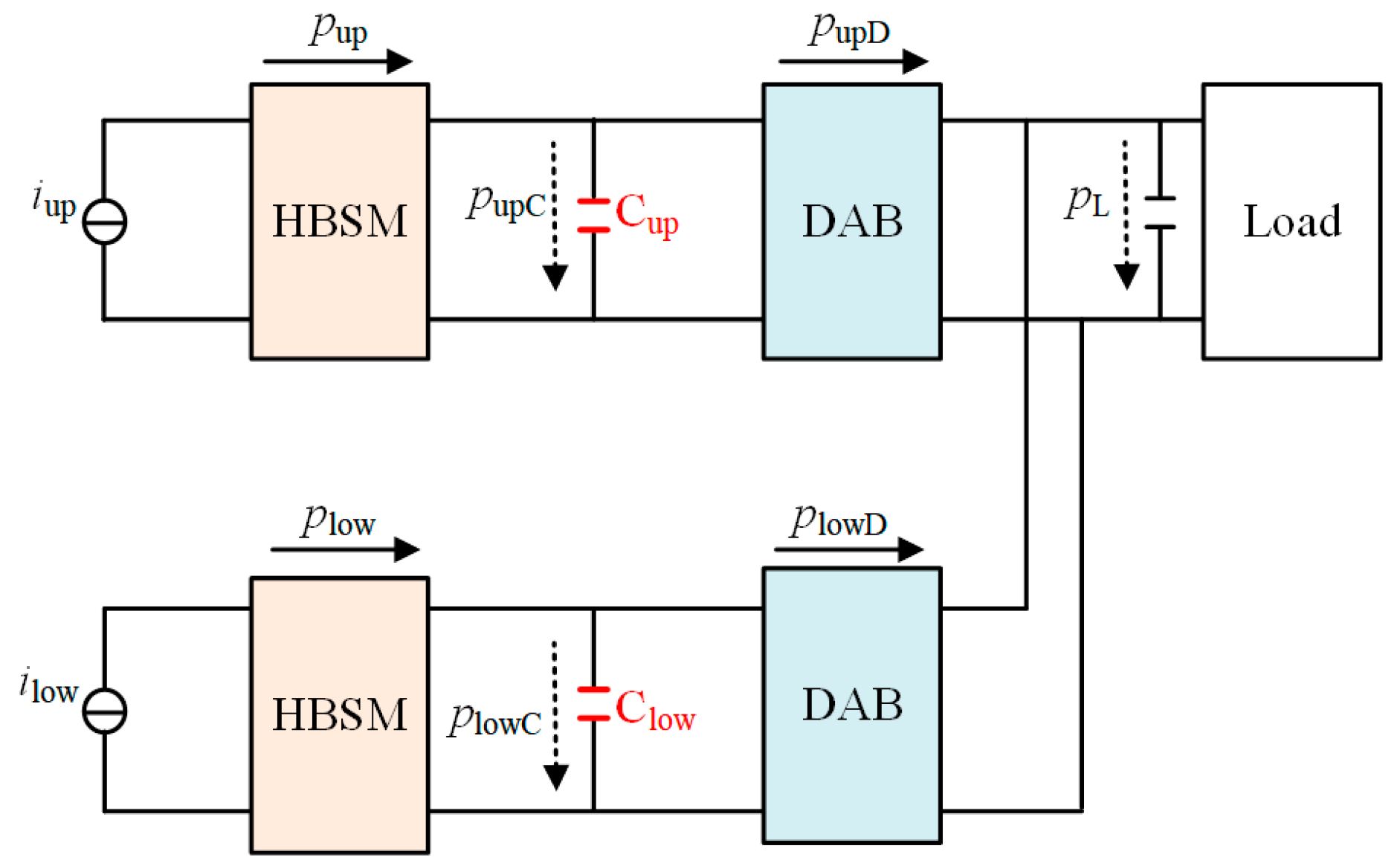
2. DAB-Based MMDTC-PET
2.1. Topology Structure
2.2. Working Principle
2.3. The Generation Mechanism of Voltage Ripple Across Capacitor
3. The Proposed TAB-Based MMDTC-PET
3.1. Topology Structure
3.2. Analysis of the Voltage Ripple Suppression Principle
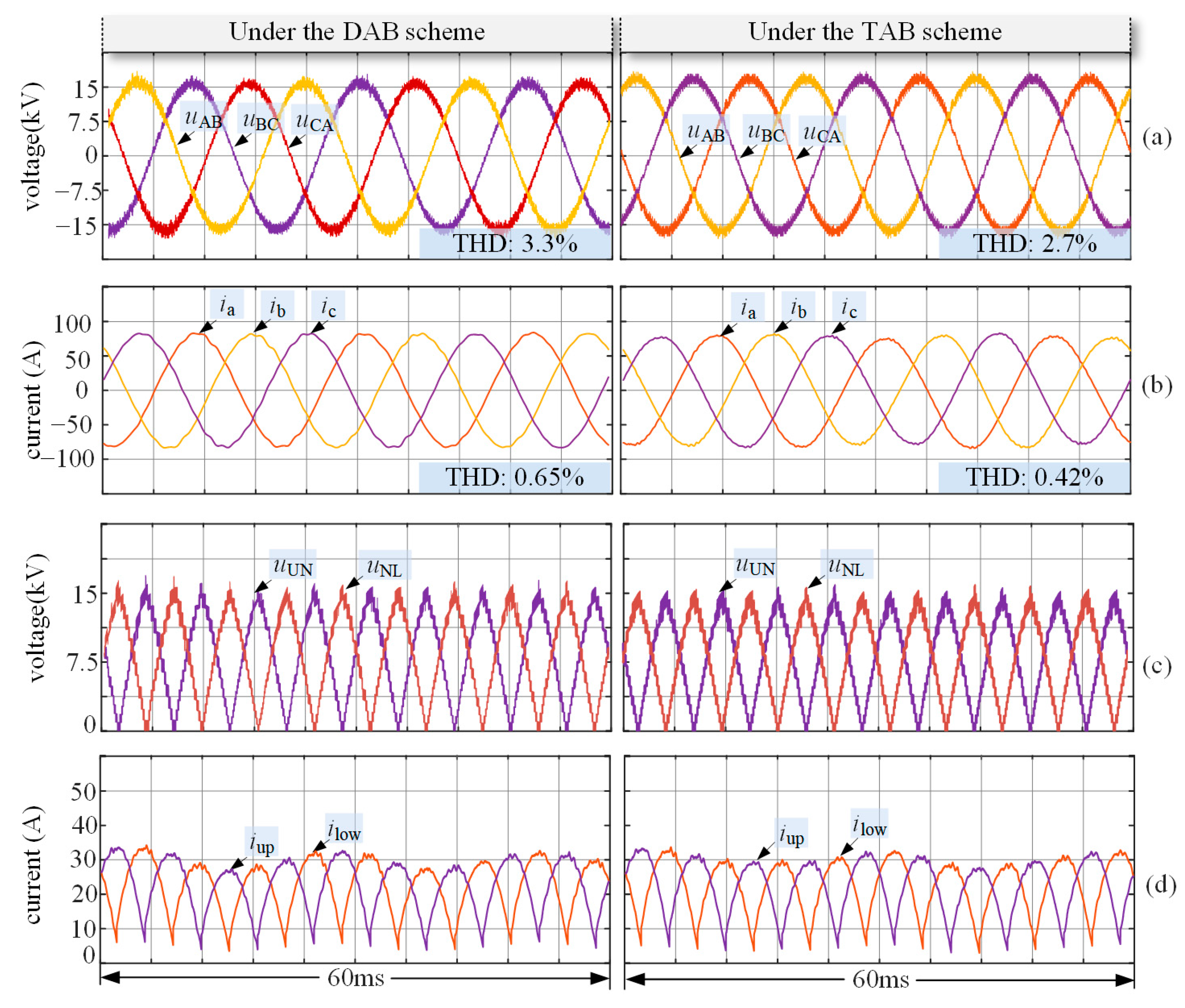
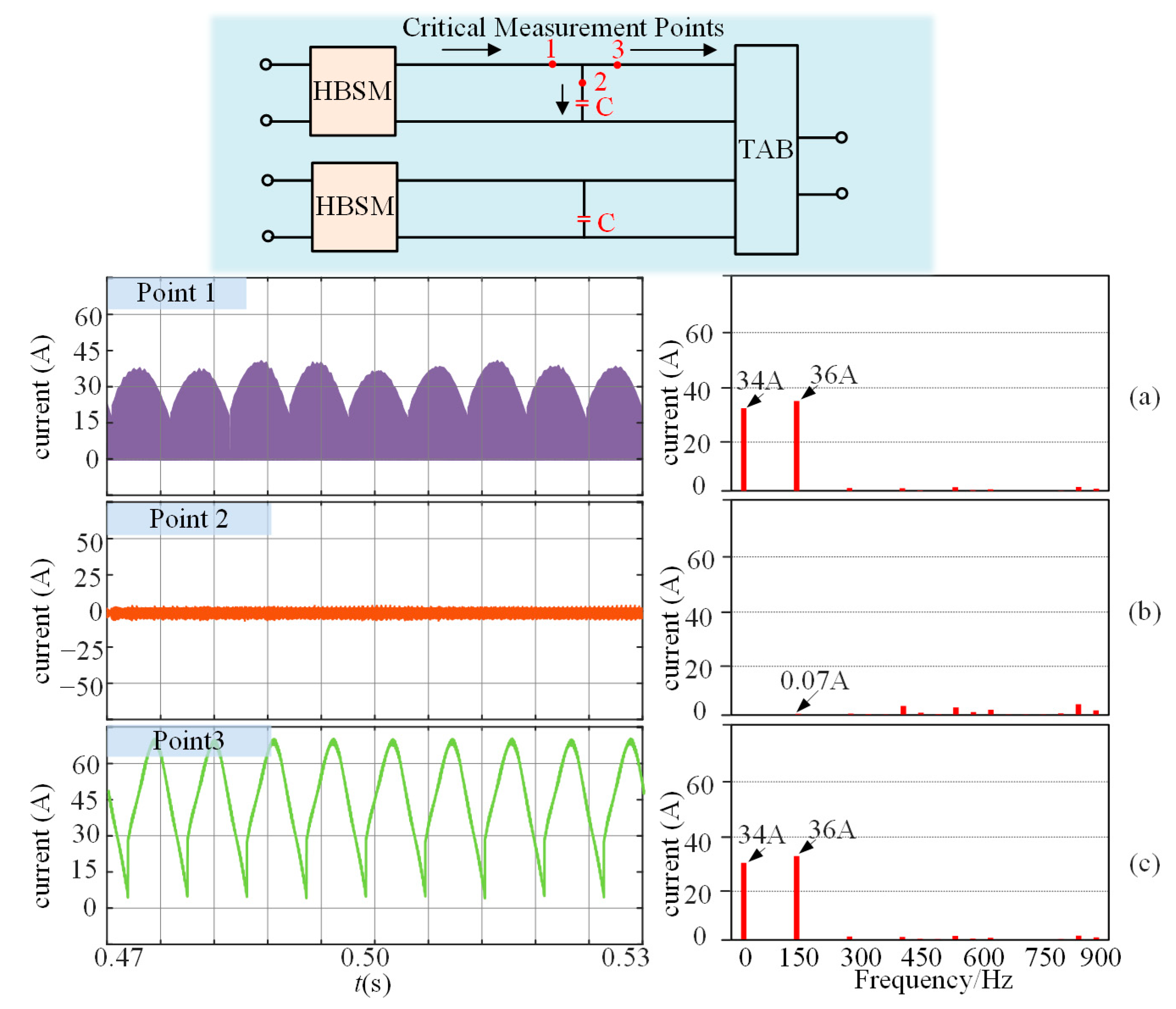
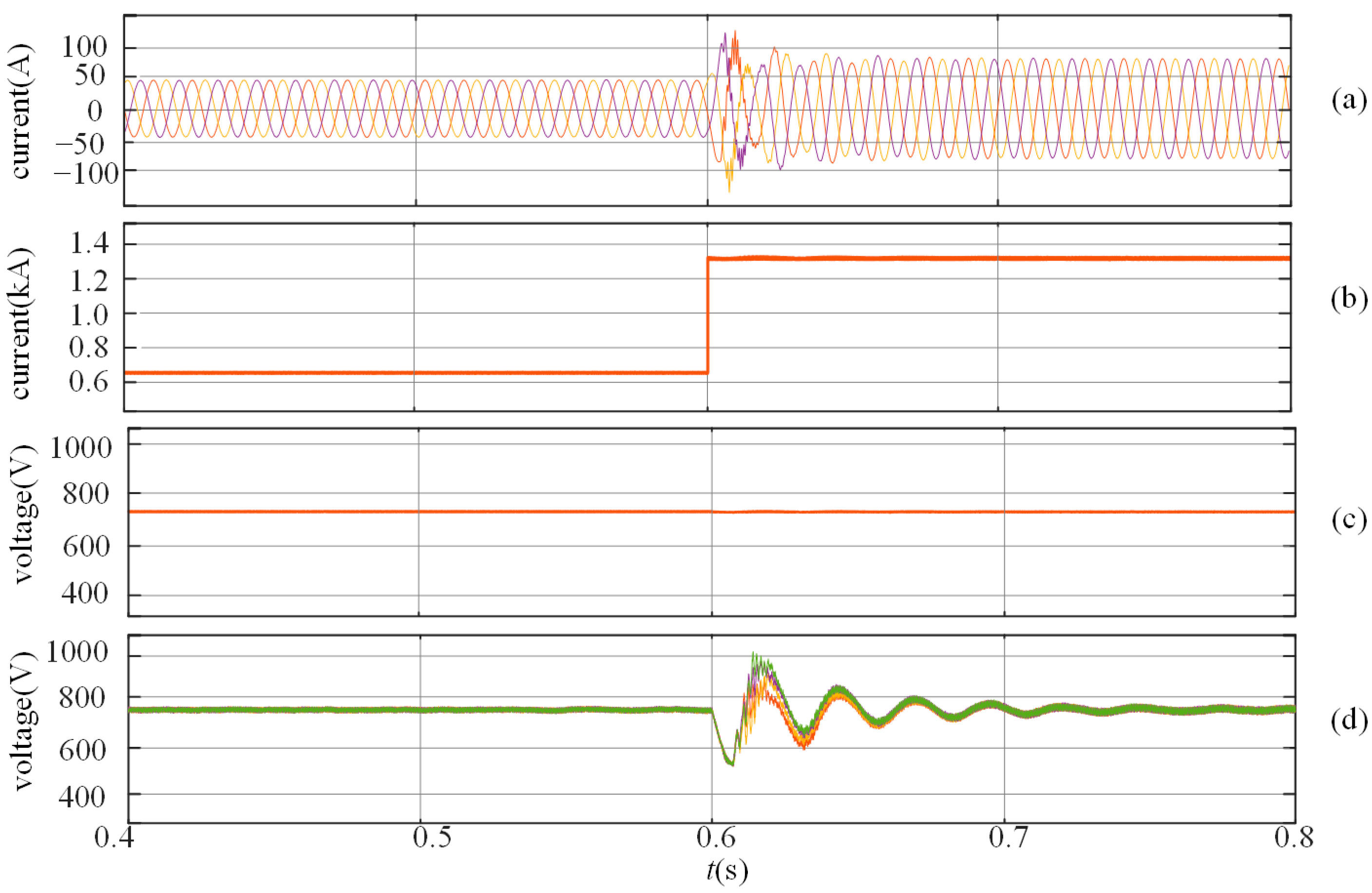
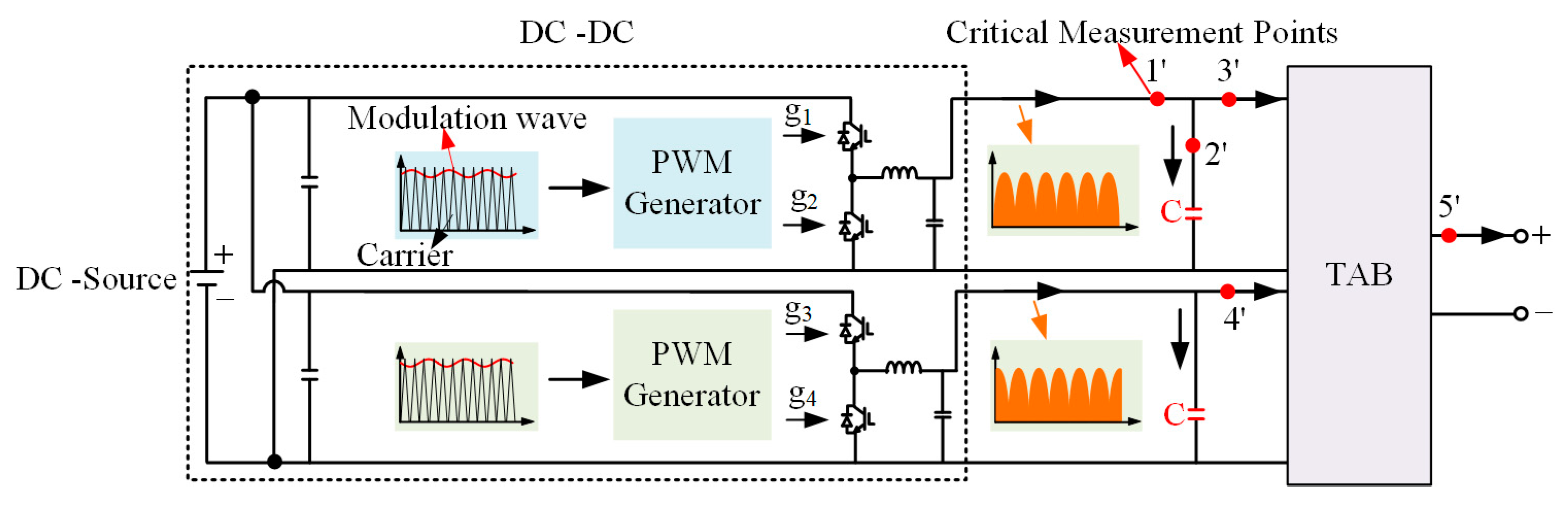
4. Simulation and Experimental Validation
4.1. Simulation Results
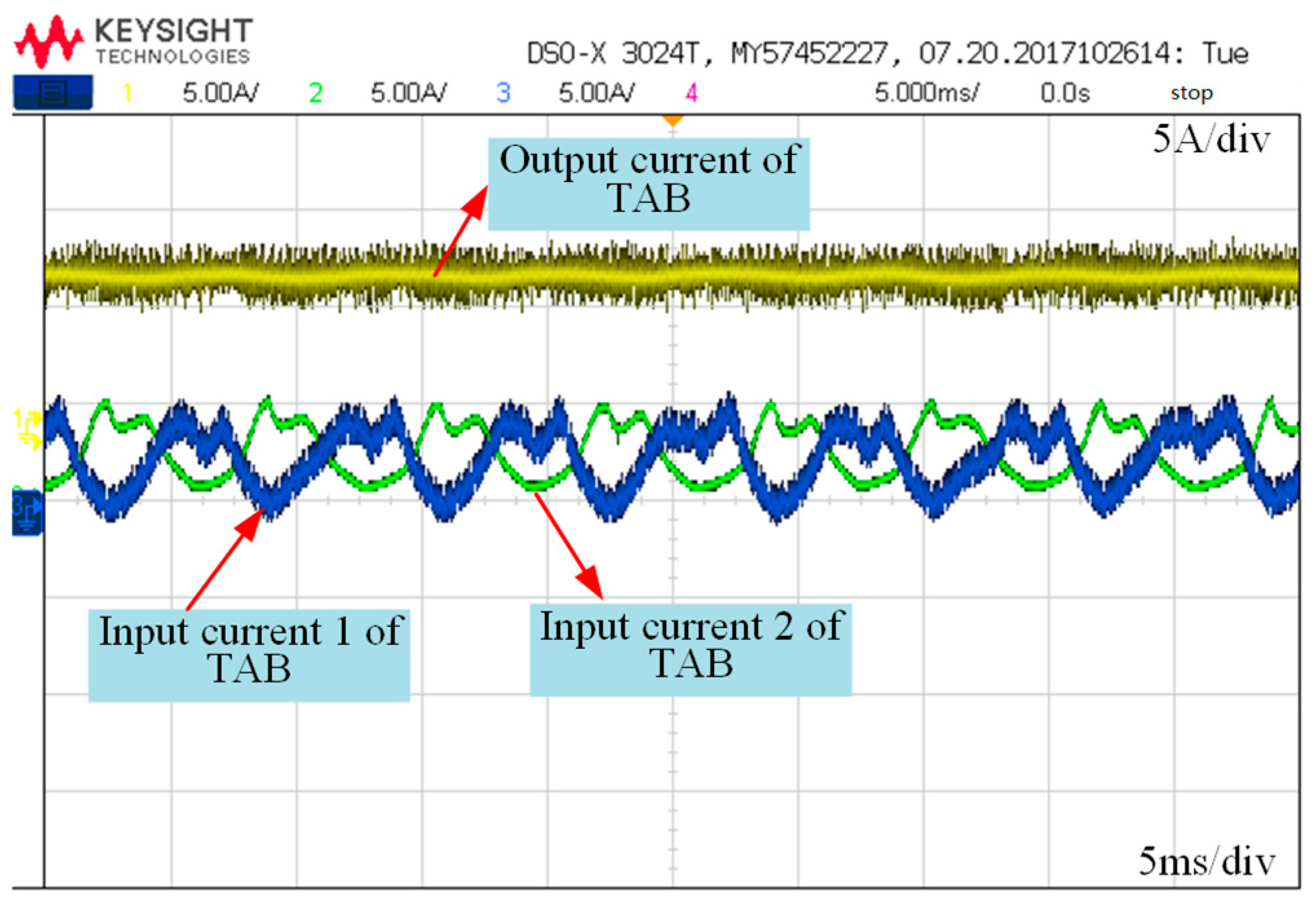
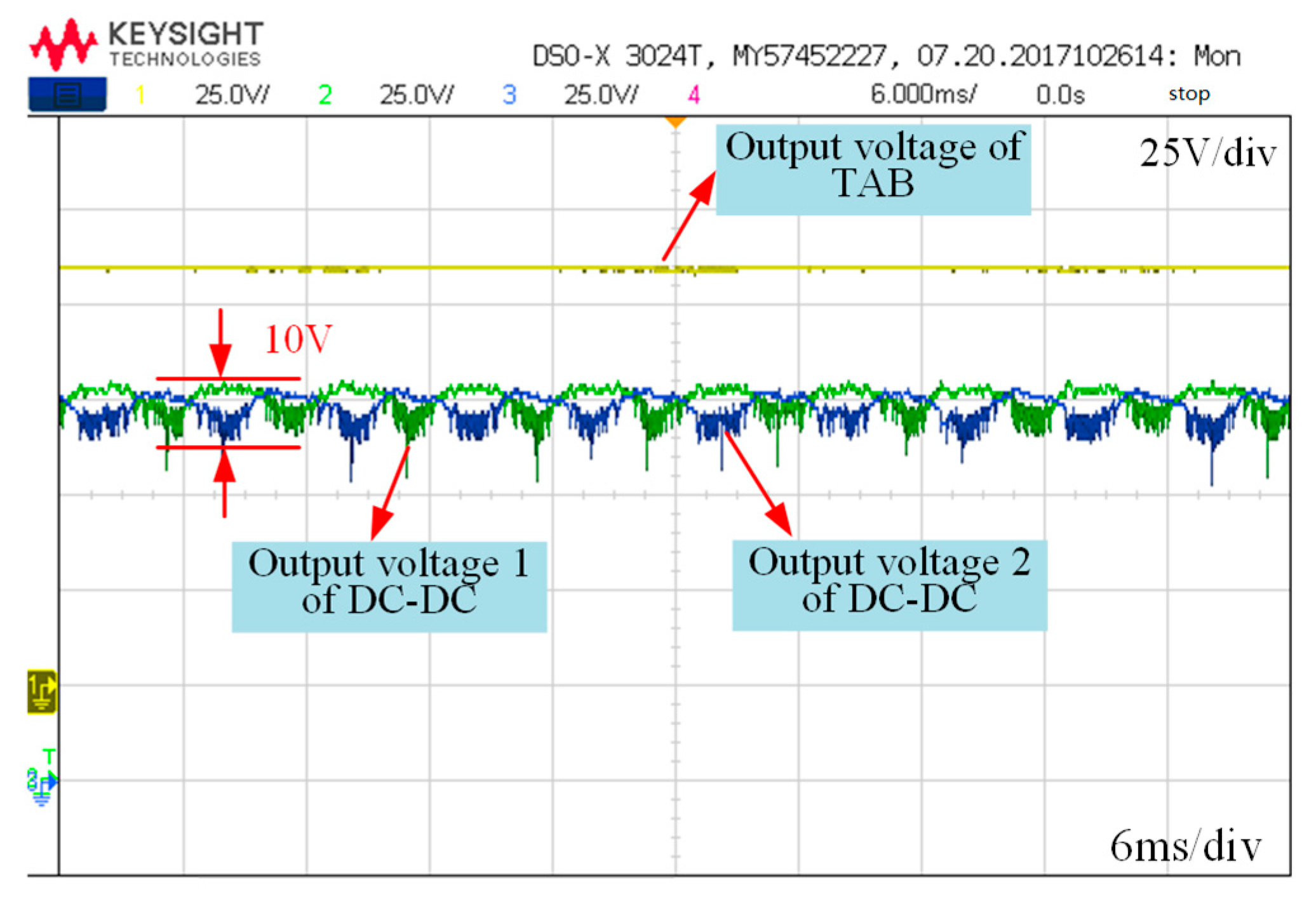
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- She, X.; Huang, A.Q.; Burgos, R. Review of Solid-State Transformer technologies and their application in power distribution systems. IEEE J. Em. Sel. Top. P. 2013, 1, 186–198. [Google Scholar] [CrossRef]
- Sun, X.; Teng, J.; Qi, L.; Pan, Y.; Bu, Z.; Zhang, M. Research on triple-port MMC-Based PET scheme based on high frequency links interconnection of horizontal sub-modules. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020. [Google Scholar]
- Li, F.; Li, Q.; Zhang, J.; Kou, J.; Ye, J.; Song, W. Detection and diagnosis of data integrity attacks in solar farms based on multilayer long short-term memory network. IEEE Trans. Power Electron. 2021, 36, 2495–2498. [Google Scholar] [CrossRef]
- Huber, J.E.; Kolar, J.W. Solid-State Transformers: On the origins and evolution of key concepts. IEEE Ind. Electron. M. 2016, 10, 19–28. [Google Scholar] [CrossRef]
- Dannier, A.; Rizzo, R. An overview of power electronic transformer: Control strategies and topologies. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012. [Google Scholar]
- Moghaddam, I.N.; Chowdhury, B.; Doostan, M. Optimal sizing and operation of battery energy storage systems connected to wind farms participating in electricity markets. IEEE T. Sustain. Energ. 2019, 1, 1184–1193. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power balance of cascaded H-Bridge multilevel converters for large-scale photovoltaic integration. IEEE Trans. Power Electron. 2016, 31, 292–303. [Google Scholar] [CrossRef]
- Heinemann, L. An actively cooled high power, high frequency transformer with high insulation capability. In Proceedings of the Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.02CH37335), Dallas, TX, USA, 10–14 March 2002. [Google Scholar]
- Briz, F.; Lopez, M.; Rodriguez, A.; Arias, M. Modular power electronic transformers: Modular multilevel converter versus cascaded H-Bridge solutions. IEEE Ind. Electron. M. 2016, 10, 6–19. [Google Scholar] [CrossRef]
- Guillod, T.; Krismer, F.; Färber, R.; Franck, C.M.; Kolar, W. Protection of MV/LV solid-state transformers in the distribution grid. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Zhang, G.; Chen, J.; Zhang, B.; Zhang, Y. A critical topology review of power electronic transformers: In view of efficiency. Chin. J. Electr. Eng. 2018, 4, 90–95. [Google Scholar] [CrossRef]
- Niu, D.; Gao, F.; Xu, T.; Ma, Z. Thyristor-based T-type converter with modular multilevel DC-link. IEEE Trans. Power Electron. 2022, 37, 6792–6806. [Google Scholar] [CrossRef]
- Liu, S.; Niu, D.; Zhang, L.; Lin, J.; Fang, J.; Li, Z. Low-Capacitance operation and its hierarchical control for STATCOM based on T-Type converter with MMDTC. IEEE Trans. Power Electron. 2025, 40, 1153–1167. [Google Scholar] [CrossRef]
- Wang, R.; Wang, F.; Boroyevich, D.; Ning, P. A high power density single phase PWM rectifier with active ripple energy storage. IEEE Trans. Power Electron. 2011, 26, 1430–1443. [Google Scholar] [CrossRef]
- Li, H.; Zhang, K.; Zhao, H.; Fan, S.; Xiong, J. Active power decoupling for high-power single-phase PWM rectifiers. IEEE Trans. Power Electron. 2013, 28, 1308–1319. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, J.; Gao, F.; Gao, S.; Rogers, D.J.; Zhu, X. Integrated high- and low-frequency current ripple suppressions in a single-phase onboard charger for EVs. IEEE Trans. Power Electron. 2021, 36, 1717–1729. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, X.; Mao, W.; Zhao, T.; Wang, F.; Dai, Z. An optimized third harmonic injection method for reducing dc-link voltage fluctuation and alleviating power imbalance of three-phase cascaded H-Bridge photovoltaic inverter. IEEE Trans. Ind. Electron. 2020, 67, 2488–2498. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Z.; Zhang, H.; Zhao, C.; Gao, F.; Luo, L.; Luan, K.; Wang, P.; Li, Y. High-frequency-link current stress optimization of cascaded H-Bridge-Based solid-state transformer with third-order harmonic voltage injection. IEEE J. Em. Sel. Top. P. 2021, 9, 1027–1038. [Google Scholar] [CrossRef]
- Isobe, T.; Barrera-Cardenas, R.A.; He, Z.; Zou, Y.; Terazono, K.; Tadano, H. Control of three-phase solid-state transformer with phase-separated configuration for minimized energy storage capacitors. IEEE J. Em. Sel. Top. P. 2020, 8, 3014–3028. [Google Scholar] [CrossRef]
- Liu, C.; Lai, J.-S. Low frequency current ripple reduction technique with active control in a fuel cell power system with inverter load. IEEE Trans. Power Electron. 2007, 22, 1429–1436. [Google Scholar] [CrossRef]
- Yin, X.; Luo, D.; Li, Z.; Su, Z. A method for secondary ripple voltage suppression in bidirectional isolated DC-DC converter. Trans. Electrotech. Soc. 2018, 33, 1356–1363. [Google Scholar]
- Wang, D.; Nahid-Mobarakeh, B.; Emadi, A. Second harmonic current reduction for a Battery-Driven grid interface with three-phase dual active bridge DC–DC converter. IEEE Trans. Ind. Electron. 2019, 66, 9056–9064. [Google Scholar] [CrossRef]
- Li, X.; Cheng, L.; He, L.; Zhu, Z.; Yang, Y.; Wang, C. Capacitor voltage ripple minimization of a modular three-phase AC/DC power electronics transformer with four-winding power channel. IEEE Access. 2020, 8, 119594–119608. [Google Scholar] [CrossRef]
- Pan, Y.; Teng, J.; Yang, C.; Bu, Z.; Wang, B.; Li, X.; Sun, X. Capacitance minimization and constraint of CHB power electronic transformer based on switching synchronization hybrid phase-shift modulation method of high frequency link. IEEE Trans. Power Electron. 2023, 38, 6224–6242. [Google Scholar] [CrossRef]
- Wang, Z.; Teng, J.; Zhang, M.; Bu, Z.; Lin, X.; Qi, L.; Zhao, W.; Li, X.; Sun, X. Common-Mode voltage suppression strategy for CHB-Based motor drive based on topology and modulation optimization. IEEE Trans. Power Electron. 2025, 40, 1697–1716. [Google Scholar] [CrossRef]
- Teng, J.; Sun, X.; Pan, Y.; Liu, X.; Zhang, Y.; Zhao, W.; Li, X. An inductive-filtering strategy of submodule ripple-power in triple-port MMC-Based SST applied to hybrid medium and low voltage AC/DC interface. IEEE Trans. Power Electron. 2022, 37, 8015–8032. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, G.; Li, W.; Zhao, G.; Deng, Z. A three-phase integrated power electronic transformer with the capability of DC fault clearance. CSEE J. Power Energy Syst. 2021, 7, 785–796. [Google Scholar]
- Ma, Y.; Xiao, J.; Lin, H.; Wang, Z. A novel battery integration method of modular multilevel converter with battery energy storage system for capacitor voltage ripple reduction. IEEE Trans. Ind. Electron. 2021, 68, 12250–12261. [Google Scholar] [CrossRef]
- Pan, Y.; Teng, J.; Bu, Z.; Wang, J.; Yang, C.; Li, X.; Sun, X. A cascaded modular isolated back-to-back solid state transformer scheme for AC/DC/AC interconnection with improved performance and simple control. IEEE Trans. Power Electron. 2023, 38, 11050–11068. [Google Scholar] [CrossRef]
- Bu, Z.; Teng, J.; Sun, X.; Pan, Y.; Pan, Y. Low-frequency voltage ripples decoupling with switched-capacitor conversion for an MMC-Based SST. IEEE Trans. Ind. Electron. 2022, 69, 11293–11303. [Google Scholar] [CrossRef]
- Sun, X.; Teng, J.; Bu, Z.; Pan, Y.; Zhao, W.; Li, X. Research on triple-port SST Scheme based on the natural elimination of MMC submodule voltage fluctuation and imbalance. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3697–3710. [Google Scholar] [CrossRef]
- Mueller, J.A.; Kimball, J.W. Model-based determination of closed-loop input impedance for dual active bridge converters. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar]








| Variable | Symbol | Value |
|---|---|---|
| Rated grid phase voltage | Vg | 10 kV |
| AC filtering inductor | Ls | 2 mH |
| Rated active power | Prated | 1 MW |
| Fundamental frequency | f | 50 Hz |
| Number of SMs per arm | N | 20 |
| Voltage of submodule capacitor | uc | 750 V |
| Submodule capacitor | C | 0.5 mF |
| Carrier frequency | fc | 10 kHz |
| LVDC bus voltage | uLVDC | 750 V |
| DAB Transformer Turn Ratio | n1:n2 | 1:1 |
| TAB Transformer Turn Ratio | n1:n2:n3 | 1:1:1 |
| DAB additional inductor | L | 25 μH |
| TAB additional inductor | L | 25 μH |
| Switching frequency | fs | 40 kHz |
| (a) | ||||||||||
| Model | Capacitance | Cost Per | Normal Voltage | |||||||
| ALF80(1)122FP500 | 1.2 mF | $19.84 | 500 V | |||||||
| (b) | ||||||||||
| Type | Double DABs | Single TAB | ||||||||
| Capacitance required | 4.8 mF | 0.5 mF | ||||||||
| Total Number of capacitors | 18 (Two in series and nine in parallel) | 2 (Two in series) | ||||||||
| Total cost | $317.44 | $39.68 | ||||||||
| (c) | ||||||||||
| Model | Normal Voltage | Cost Per | Rated Current | Switching Frequency | ||||||
| APTGL90H120T3G (IGBT) | 1200 V | $112.8 | 110 A | 20–50 kHz | ||||||
| FF50R12RT4HOSA1(IGBT) | 1200 V | $60.7 | 50 A | 20–50 kHz | ||||||
| (d) | ||||||||||
| Type | Double DABs | Single TAB | ||||||||
| Total Number of IGBTs | 16(FF50R12RT4HOSA1) | 8(FF50R12RT4HOSA1) + 4(APTGL90H120T3G) | ||||||||
| Total cost | $971.2 | $936.8 | ||||||||
| Variable | Symbol | Value |
|---|---|---|
| Rated active power | Prated | 500 W |
| Input voltage of DC-source | U1 | 105 V |
| Output voltage of TAB | U2 | 100 V |
| Load | R | 20 Ω |
| PWM carrier frequency | fc | 10 kHz |
| Switching frequency | fs | 10 kHz |
| Submodule capacitor | C | 470 μF |
| TAB additional inductor | L | 167 μH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, X.; Niu, D.; Yan, Q.; Wang, D.; Li, Z.; Zhang, L. Sub-Module Capacitor Voltage Ripple Suppression in MMDTC-Based PET Using Three-Port Active Bridge. Energies 2025, 18, 5178. https://doi.org/10.3390/en18195178
Cui X, Niu D, Yan Q, Wang D, Li Z, Zhang L. Sub-Module Capacitor Voltage Ripple Suppression in MMDTC-Based PET Using Three-Port Active Bridge. Energies. 2025; 18(19):5178. https://doi.org/10.3390/en18195178
Chicago/Turabian StyleCui, Xiangzheng, Decun Niu, Qizhong Yan, Dong Wang, Zhenwei Li, and Lei Zhang. 2025. "Sub-Module Capacitor Voltage Ripple Suppression in MMDTC-Based PET Using Three-Port Active Bridge" Energies 18, no. 19: 5178. https://doi.org/10.3390/en18195178
APA StyleCui, X., Niu, D., Yan, Q., Wang, D., Li, Z., & Zhang, L. (2025). Sub-Module Capacitor Voltage Ripple Suppression in MMDTC-Based PET Using Three-Port Active Bridge. Energies, 18(19), 5178. https://doi.org/10.3390/en18195178







