Analysis of Electromechanical Swings of a Turbogenerator Based on a Fractional-Order Circuit Model
Abstract
1. Introduction
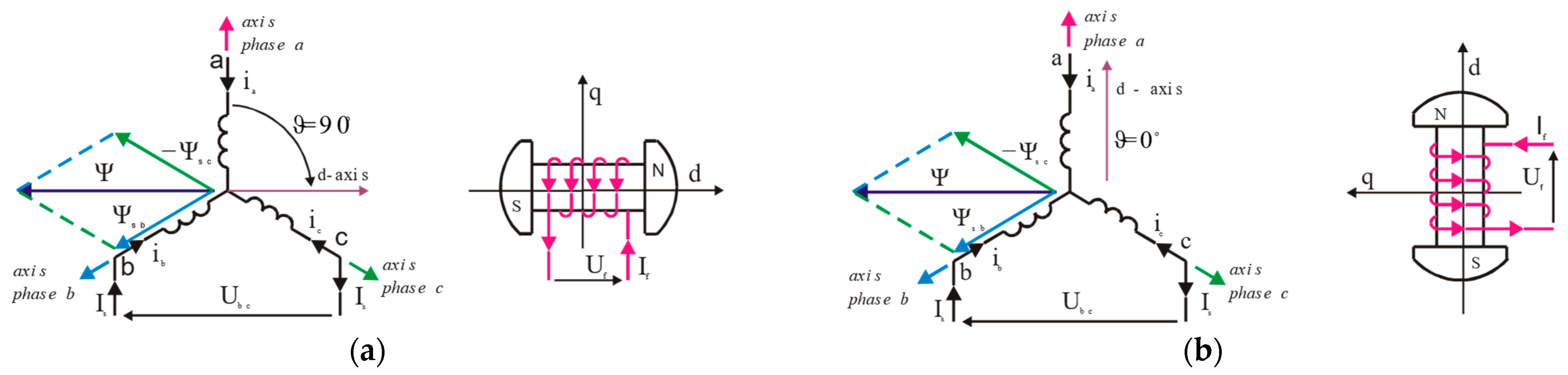
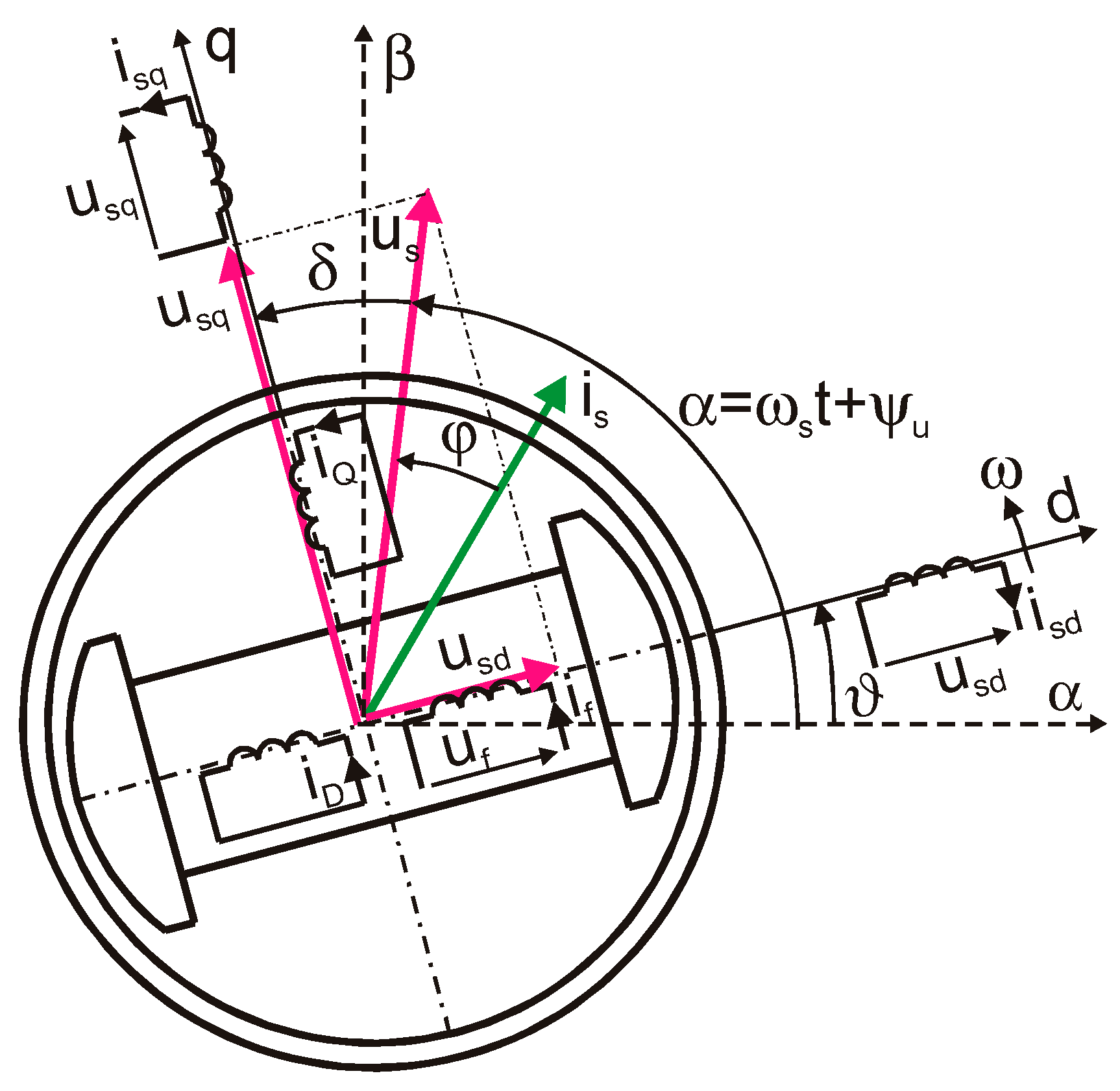
2. Mathematical Model of a Synchronous Machine
3. Identification of Equivalent Circuit Parameters
4. Analysis of Electromechanical Swings of a Turbogenerator Under Small Disturbances Around the Equilibrium Point
4.1. Linearization of Differential Equations
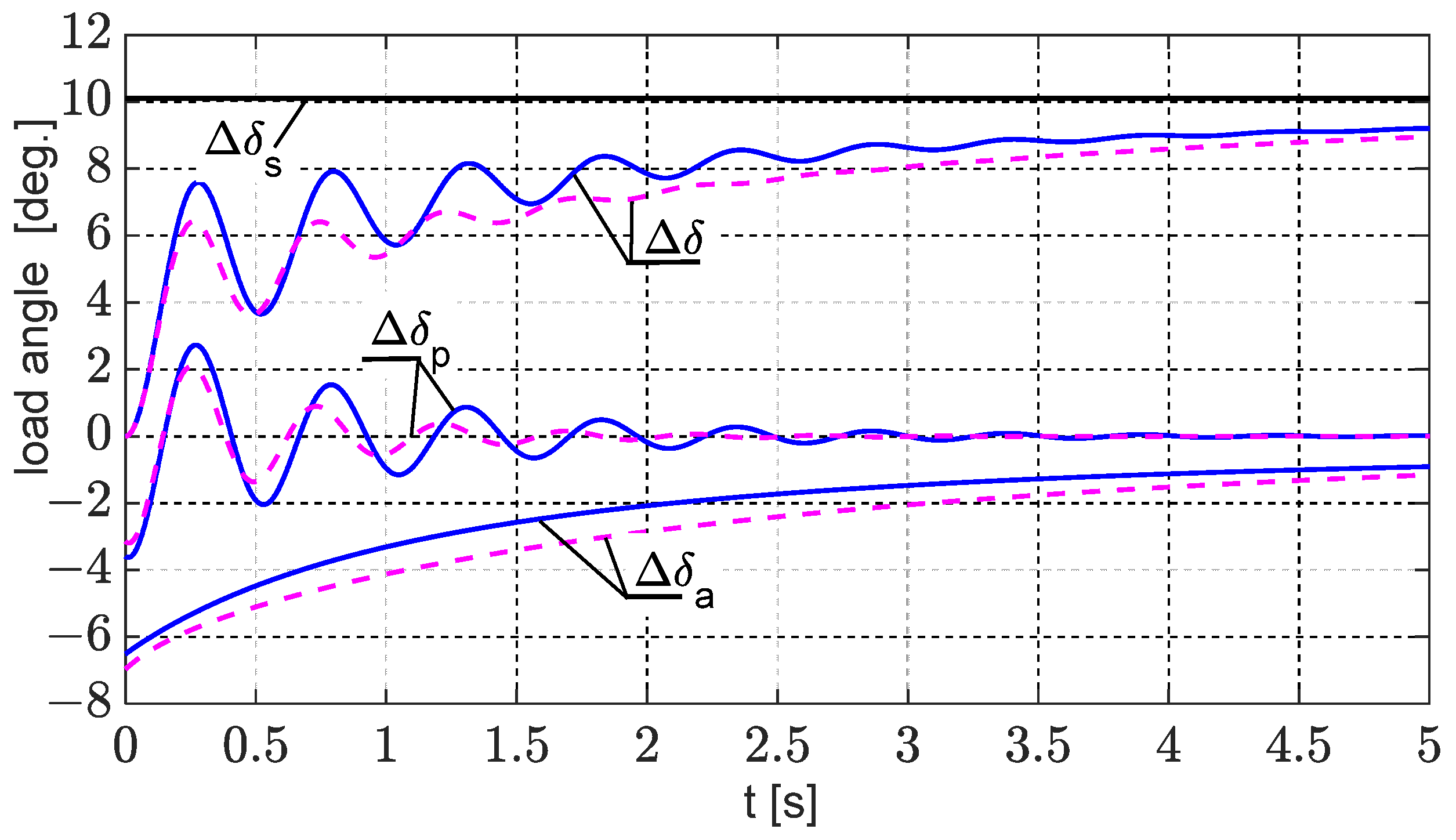
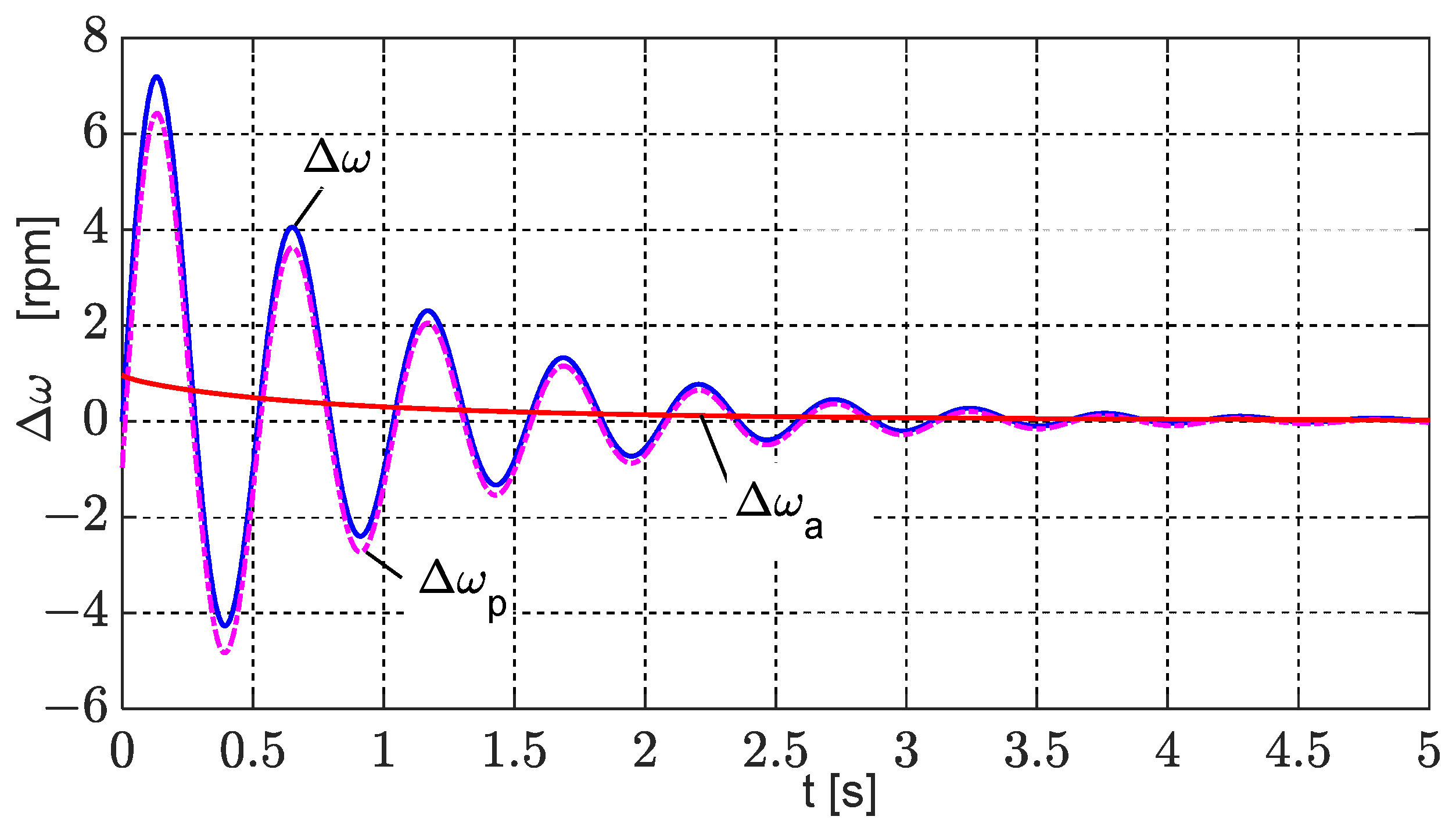
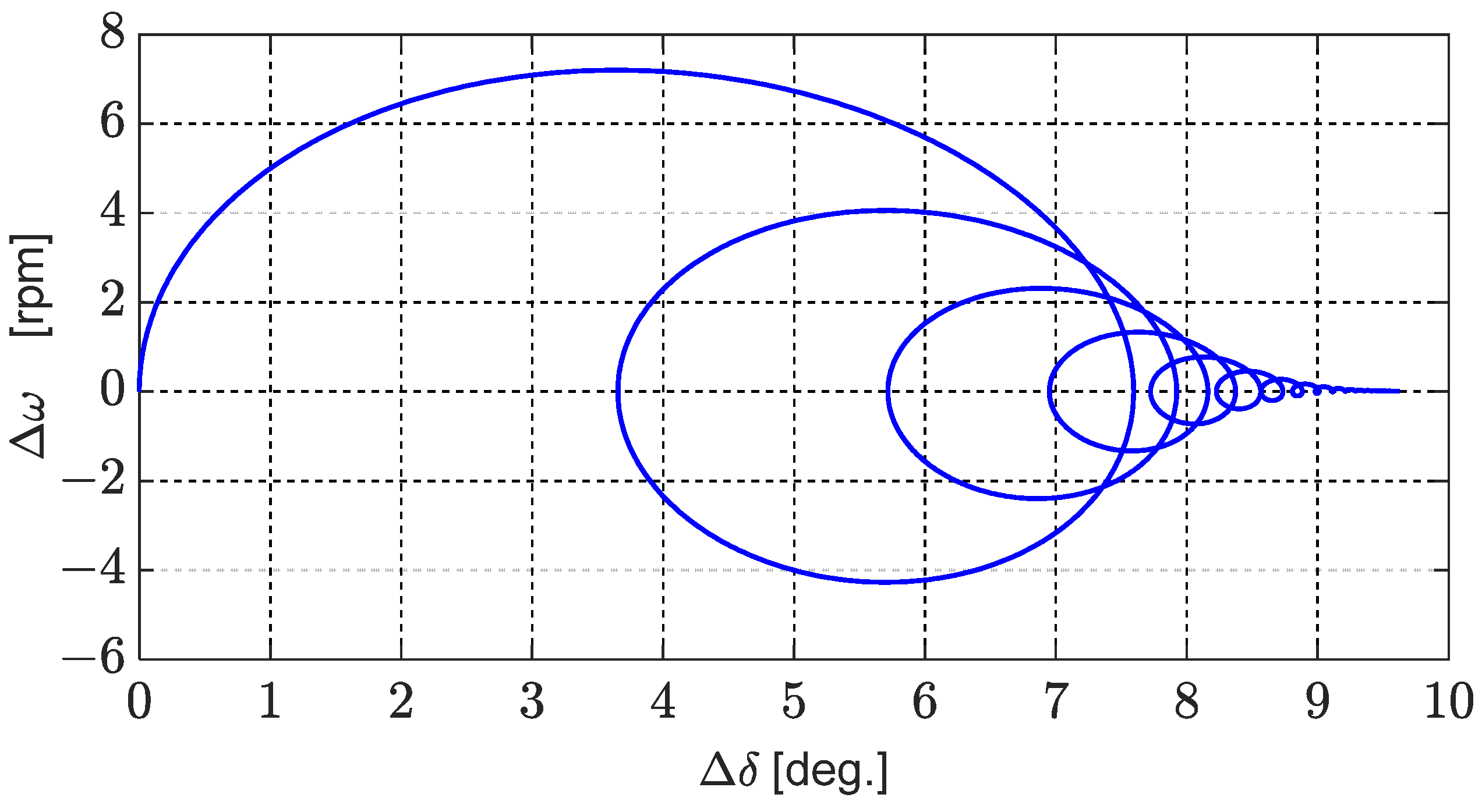
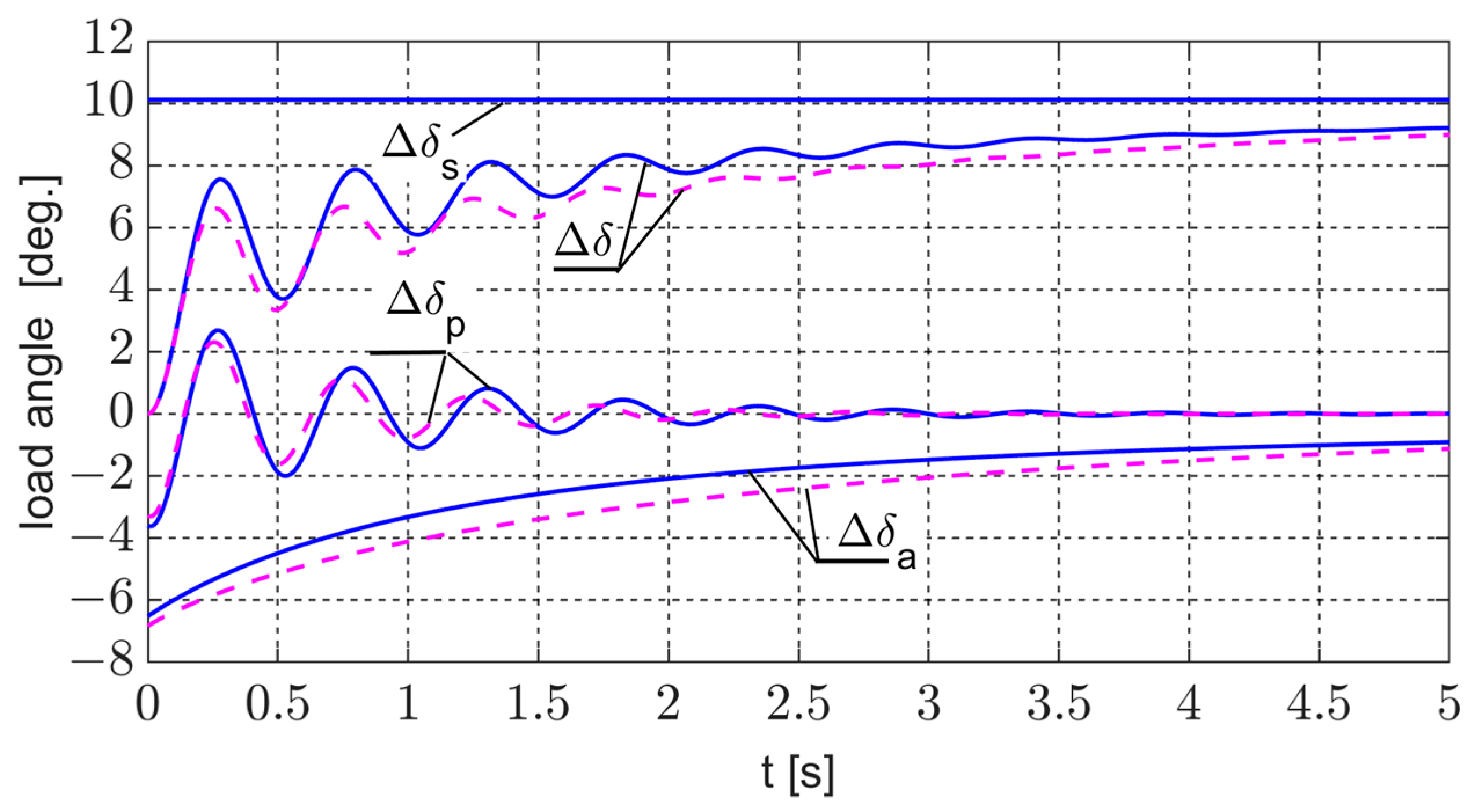
4.2. Calculation of Transients
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| SSFR | Standstill Frequency Response |
Appendix A
Appendix B
Appendix B.1
Appendix B.2
References
- Paszek, S. Selected Methods for Assessment and Improvement of Power System Angular Stability; Silesian University of Technology Publishing House: Gliwice, Poland, 2012. [Google Scholar]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Muechling, H. Handbook of Mathematics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lindfield, G.; Penny, J. Numerical Method. Using Matlab; Academic Press, Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Machowski, J.; Białek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Kutt, F.; Sienkiewicz, Ł.; Racewicz, S.; Michna, M.; Ryndzionek, R. Development of an emulation platform for synchronous machine power generation system using a nonlinear functional level model. Arch. Electr. Eng. 2024, 73, 281–297. [Google Scholar] [CrossRef]
- Luo, S.; Jian, Y.; Gao, Q. Synchronous generator modeling and semi-physical simulation. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kamwa, I.; Viarouge, P.; Le-Huy, H.; Dickinson, J. A Frequency-Domain Maximum Likelihood Estimation of Synchronous Machine High-Order Models Using SSFR Test Data. IEEE Trans. Energy Convers. 1992, 7, 525–536. [Google Scholar] [CrossRef]
- IEEE Std 1110™-2019; IEEE Guide for Synchronous Generator Modeling Practices and Parameter Verification with Applications in Power System Stability Analyses. The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 2020. [CrossRef]
- Wang, Q.Y.; Wang, S. Steady State Accuracy of Second-Order Generator Dynamic Models in Generator Parameter Validation Testing. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Jalloul, A.; Trigeassou, J.K.; Jelassi, K.; Melchior, P. Fractional Order of Rotor Skin Effect in Induction Machines. In Nonlinear Dynamic; Springer: Berlin/Heidelberg, Germany, 2013; pp. 801–813. [Google Scholar] [CrossRef]
- Nadolski, R.; Staszak, J. Analysis of the Field Current after Three-Phase Sudden Short-Circuit of Turbogenerator using Equivalent Circuit. In Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 1995; Volume 78, pp. 399–406. [Google Scholar]
- Xia, P.; Liang, Z. A Parameter Identification Method for Fractional Order Inductance of Iron Core Reactor. In Proceedings of the 2016 1st International Conference on Information Technology, Information Systems and Electrical Engineering, Yogyakarta, Indonesia, 23–24 August 2016; pp. 31–36. [Google Scholar] [CrossRef]
- Nadolski, R.; Staszak, J.; Harbaoui, L. Consideration of Solid Rotor Damping Circuit in Natural Hunting of Turbogenerator. Arch. Electr. Eng. 1998, XLVII, 235–245. [Google Scholar]
- Jalloul, A.; Trigeassou, J.K.; Jelassi, K.; Melchior, P. Non Integer Identification of Rotor Skin Effect in Induction Machines. Int. J. Electr. Comput. Eng. 2013, 3, 344–358. Available online: https://ijece.iaescore.com/index.php/IJECE/article/view/5458/4993 (accessed on 15 August 2025). [CrossRef]
- Racewicz, S.; Kutt, F.; Michna, M.; Sienkiewicz, Ł. Comparative Study of Integer and Non-Integer Order Models of Synchronous Generator. Energies 2020, 13, 4416. [Google Scholar] [CrossRef]
- Staszak, J. Solid-Rotor Induction Motor Modeling Based on Circuit Model Utilizing Fractional-Order Derivatives. Energies 2022, 15, 6371. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.Q.; Atherton, D.P. Linear Feedback Control. In Analysis and Design with Matlab; Society for Industrial Applied Mathematics: Philadelphia, PA, USA, 2007. [Google Scholar]
- Spałek, D. Synchronous Generator Model with Fractional Order Voltage Regulator PIbDa. Acta Energetica 2015, 2, 78–84. [Google Scholar] [CrossRef]
- Tzounas, G.; Dassios, I.; Murad, M.A.A.; Milano, F. Theory and Implementation of Fractional Order Controllers for Power System Applications. IEEE Trans. Power Syst. 2020, 35, 4622–4631. [Google Scholar] [CrossRef]
- Hammami, R.; Bazine, I.; Jelassi, K. Parametric Identification of Fractional Park’s Model: Modal Approach. In Proceedings of the 7th International Conference on Modelling, Identification and Control (ICMIC), Sousse, Tunisia, 18–20 December 2015. [Google Scholar] [CrossRef]
- Minnich, S.H.; Chari, M.V.K.; Berkery, J.F. Operational Inductances of Turbine-Generators by the Finite-Element Method. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 20–27. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Analysis of Electrical Machinery and Drives System, 2nd ed.; IEEE Press, John Willey & Sons: Piscataway, NJ, USA, 2002. [Google Scholar]
- Paszek, W. Transient of AC Electrical Machines; WNT: Warszawa, Poland, 1986. [Google Scholar]
- Bastos, J.P.A.; Sadowski, N. Electromagnetic Modeling by Finite Element Method; Marcel Dekker: New York, NY, USA, 2003. [Google Scholar]
- Meeker, D. Finite Element Method Magnetics. User Manual, Version 4.2, 2015. Available online: https://www.femm.info/Archives/doc/manual42.pdf (accessed on 15 August 2025).
- Optimization Toolbox. User’s Guide Matlab; The MathWorks, Inc.: Natick, MA, USA, 2010. [Google Scholar]
- Babau, R.; Boldea, I.; Miller, T.J.E.; Muntean, N. Complete Parameter Identification of Large Induction Machines from No-Load Acceleration-Deceleration Test. IEEE Trans. 2007, 54, 1962–1972. [Google Scholar] [CrossRef]
- Lipo, T.A. Analysis of Synchronous Machines; CRC Press, Taylor & Francis Group: Boca Raton, FA, USA; London, UK; New York, NY, USA, 2012. [Google Scholar]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V.P. Design of Rotating Electrical Machines; John Wiley & Sons Ltd.: Chichester, UK, 2014. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Control; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rogosin, S.; Giraldi, F.; Mainardi, F. On the Laplace Transforms of Derivatives of Special Functions with Respect to Parameters. Mathematics 2025, 13, 1980. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Function with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1992. [Google Scholar]
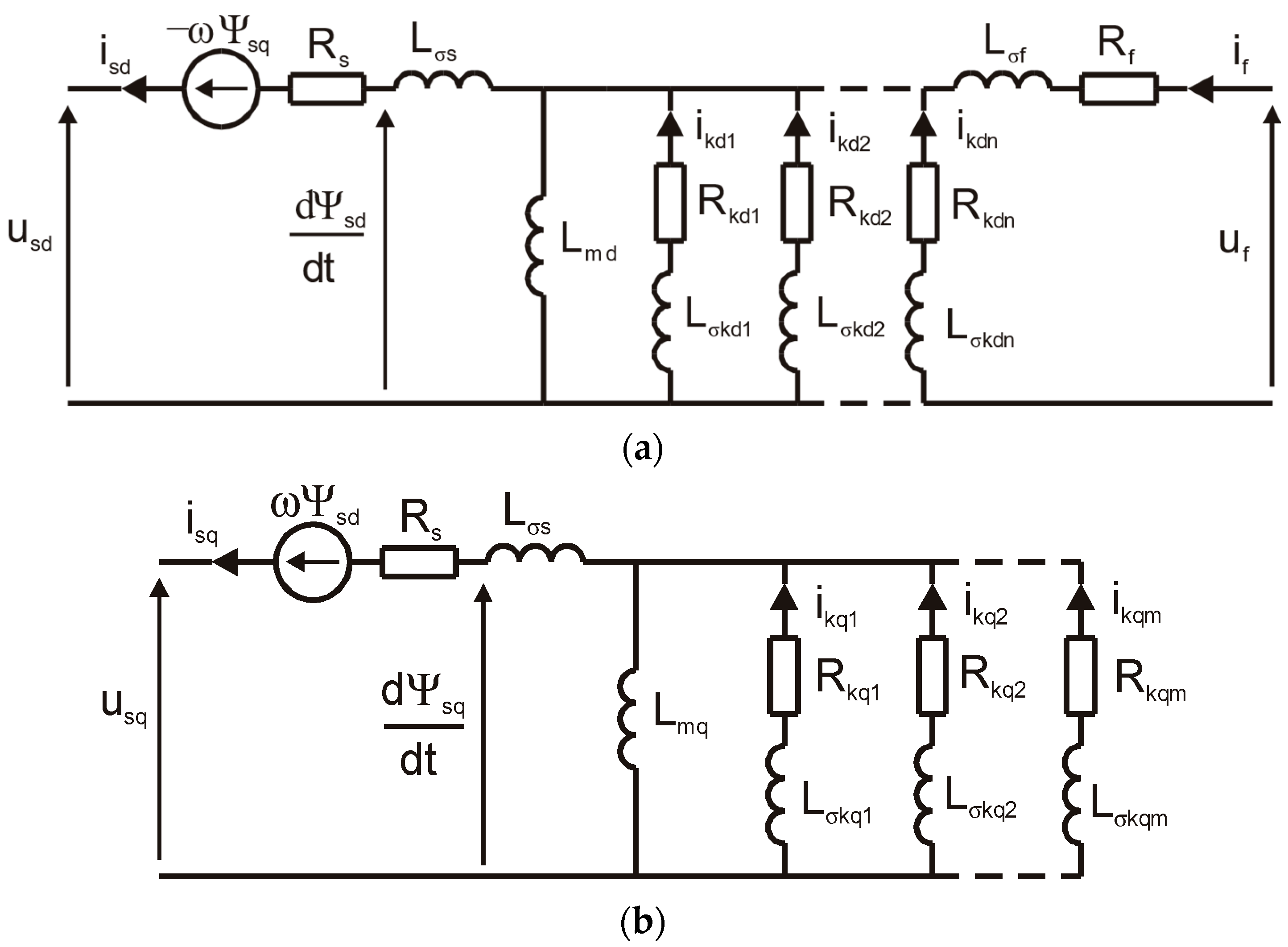
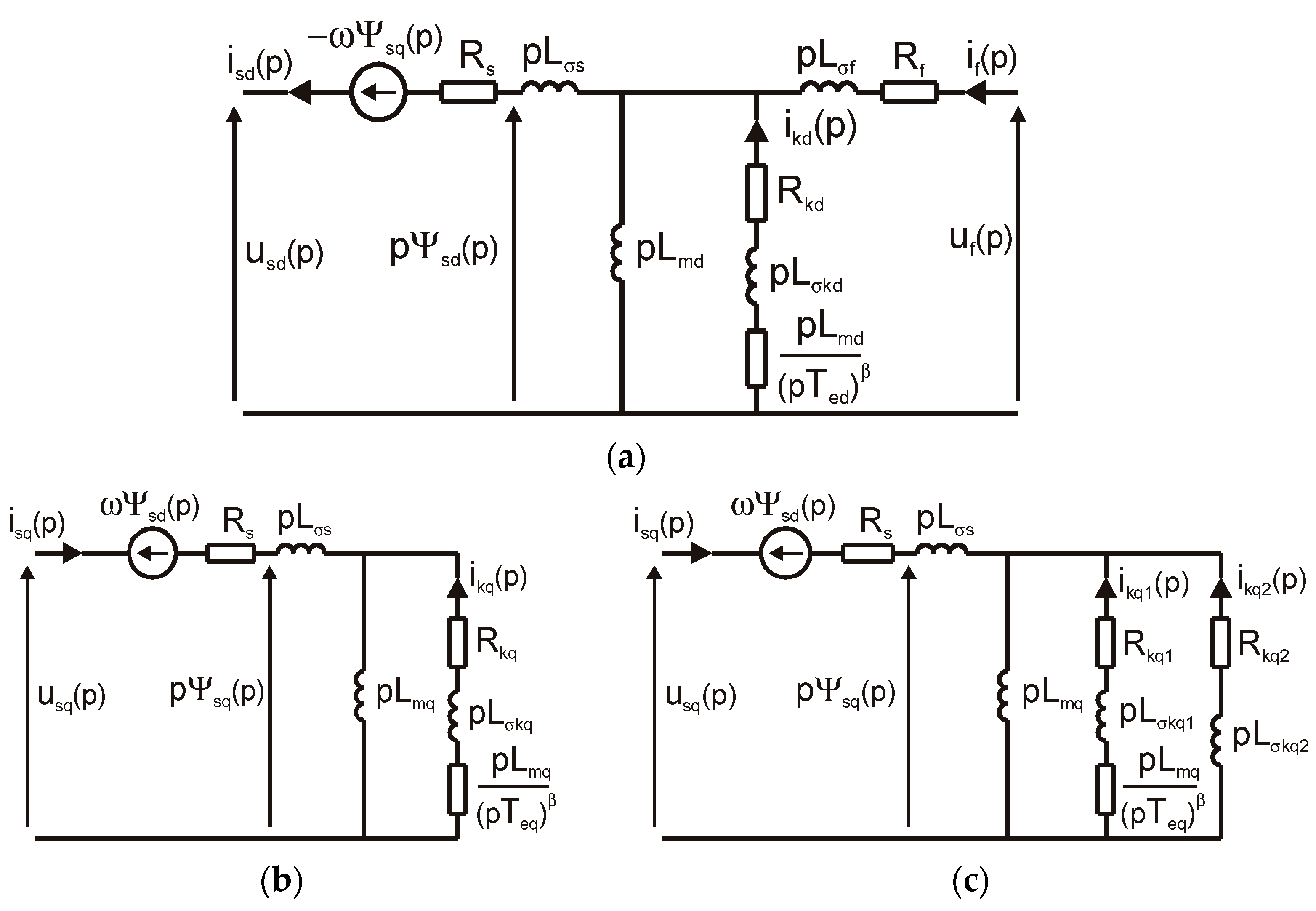
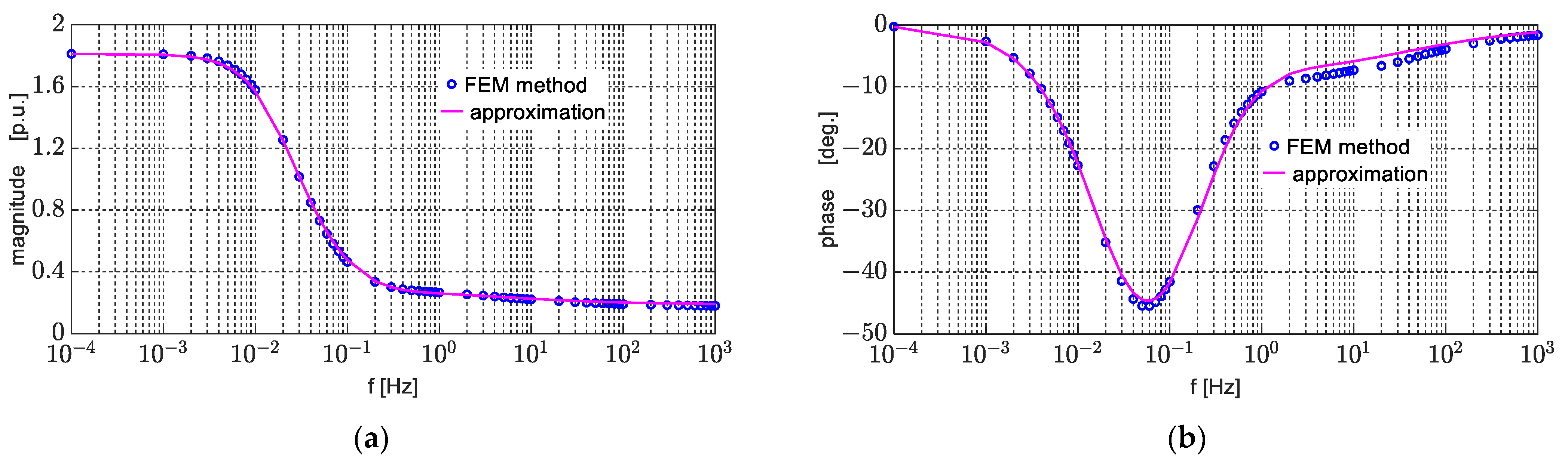
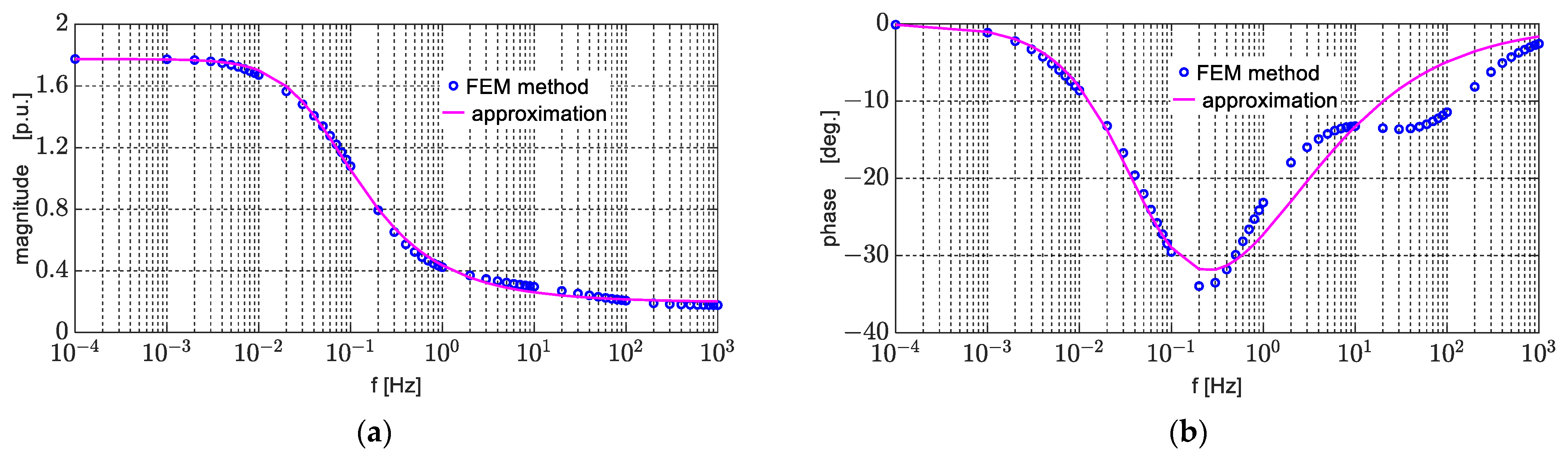
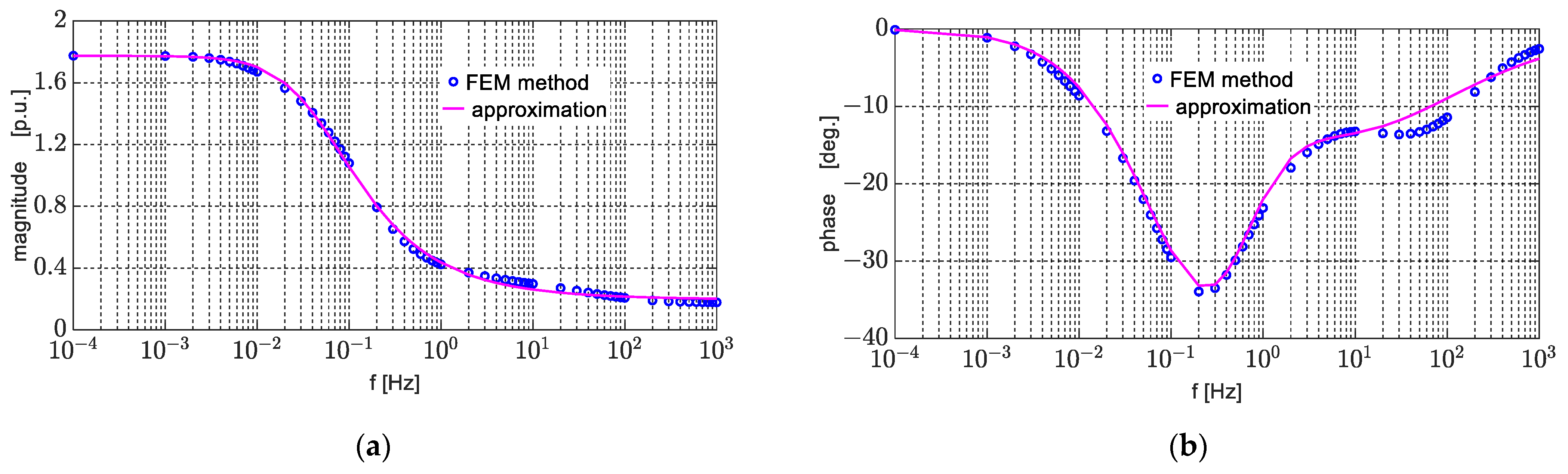
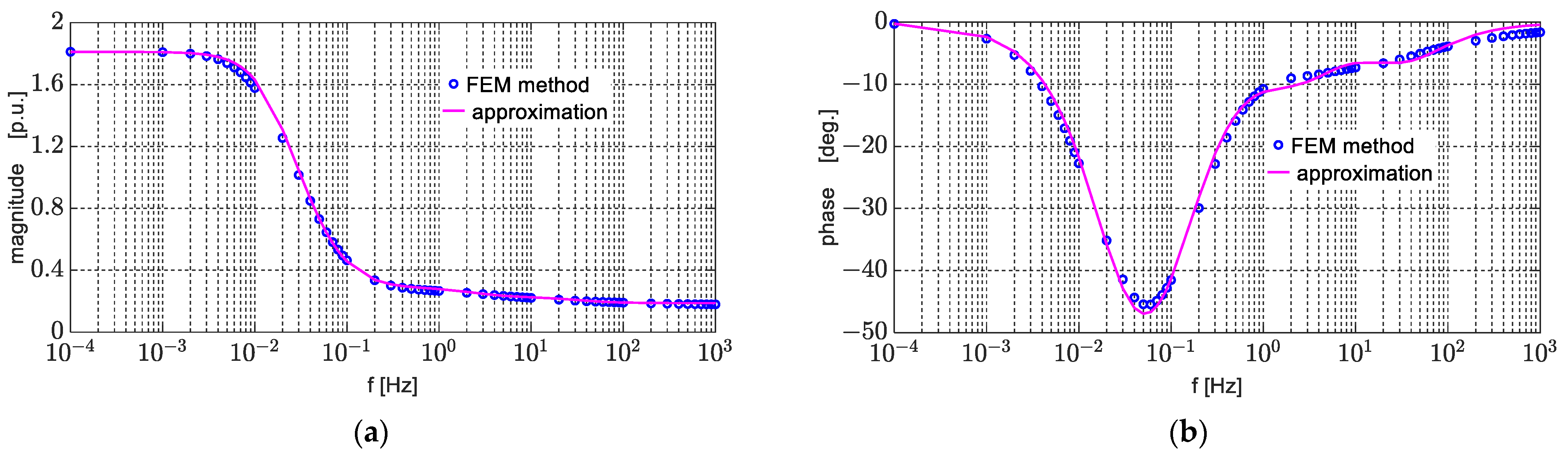
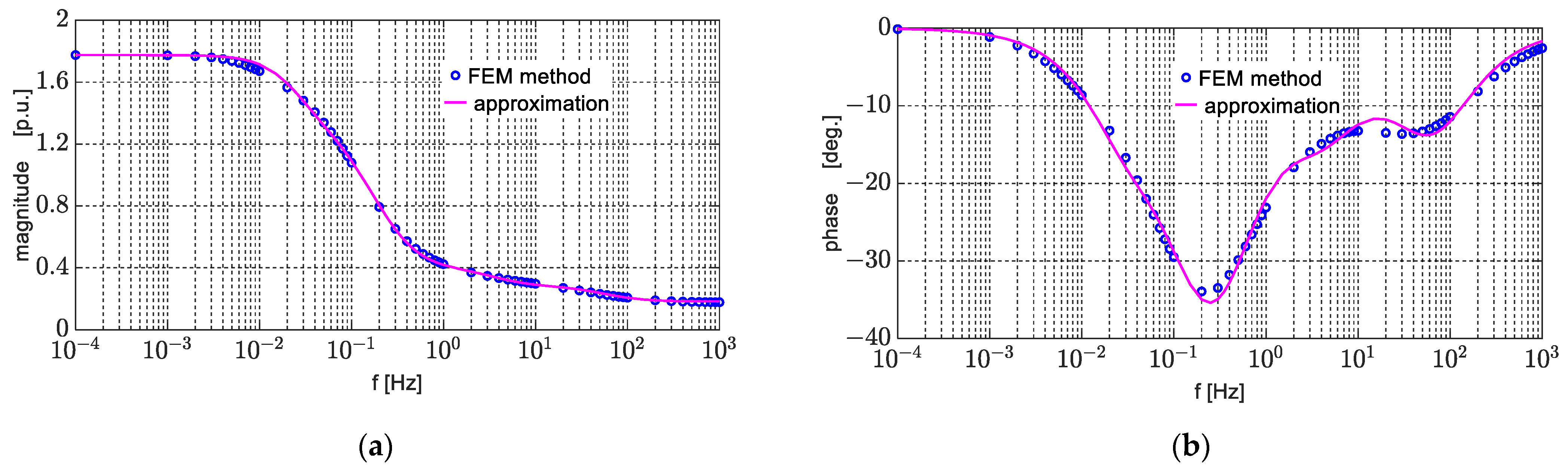
| Parameter | d-Axis Figure 2a | Parameter | q-Axis | |
|---|---|---|---|---|
| Figure 2b | Figure 2c | |||
| Lsd [p.u.] | 1.812 | Lsq [p.u.] | 1.775 | 1.775 |
| Lσs [p.u.] | 0.186 | Lσs [p.u.] | 0.186 | 0.186 |
| Rkd [p.u.] | 0.001083 | Rkq [p.u.] | 0.001457 | |
| Lσkd [p.u.] | 0.000012 | Lσkq [p.u.] | 0.01029 | |
| Lσf [p.u.] | 0.1197 | Teq [s] | 5.952 | 0.97 |
| Rf [p.u.] | 0.00128 | Rkq1 [p.u.] | 0.001593 | |
| Ted [s] | 11.708 | Lσkq1 [p.u.] | 0.000011 | |
| α | 0.5 | Rkq2 [p.u.] | 0.00735 | |
| εm [%] | 1.53 | Lσkq2 [p.u.] | 0.4722 | |
| εφ [%] | 6.32 | α | 0.5 | 0.5 |
| R2m | 0.9998 | εm [%] | 2.98 | 3.2 |
| R2φ | 0.9958 | εφ [%] | 21.69 | 8.31 |
| R2m | 0.9987 | 0.9985 | ||
| R2φ | 0.8901 | 0.9839 | ||
| Parameter | d-Axis | Parameter | q-Axis |
|---|---|---|---|
| Figure 1a | Figure 1b | ||
| Lsd [p.u.] | 1.812 | Lsq [p.u.] | 1.775 |
| Lσs [p.u.] | 0.186 | Lσs [p.u.] | 0.186 |
| Td1 [p.u.] | 386.560 | Tq1 [p.u.] | 1362.9 |
| Td2 [p.u.] | 18.047 | Tq2 [p.u.] | 109.288 |
| Td3 [p.u.] | 1.301 | Tq3 [p.u.] | 10.3458 |
| Td01 [p.u.] | 2450.7 | Tq4 [p.u.] | 0.6357 |
| Td02 [p.u.] | 22.872 | Tq01 [p.u.] | 1912.3 |
| Td03 [p.u.] | 1.565 | Tq02 [p.u.] | 352.0454 |
| εm [%] | 2.85 | Tq03 [p.u.] | 14.5075 |
| εφ [%] | 6.51 | Tq04 [p.u.] | 0.9744 |
| R2m | 0.9992 | εm [%] | 1.87 |
| R2φ | 0.9955 | εφ [%] | 5.49 |
| R2m | 0.9995 | ||
| R2φ | 0.9930 |
| i | Fractional-Order Model | Lumped-Parameter Model |
|---|---|---|
| Figure 2c | Figure 1 | |
| qi | qi | |
| 1 | −1.1904∙100 | −1.5723∙100 |
| 2 | −5.3160∙10−1 | −7.6868∙10−1 |
| 3 | −1.2412∙10−1 | −9.3459∙10−2 |
| 4 | −6.5951∙10−4 | −5.3735∙10−2 |
| 5 | −9.9400∙10−2 + j1.2725∙10−1 | −6.4067∙10−3 |
| 6 | −9.9400∙10−2 − j1.2725∙10−1 | −1.4487∙10−3 |
| 7 | −1.9889∙10−2 + j4.550∙10−2 | −6.2823∙10−4 |
| 8 | −1.9889∙10−2 − j4.550∙10−2 | −4.6353∙10−3 + j4.0803∙10−2 |
| 9 | −8.2872∙10−3 + j9.3595∙10−2 | −4.6353∙10−3 − j4.0803∙10−2 |
| 10 | −8.2872∙10−3 − j9.3595∙10−2 | |
| 11 | 1.3273∙10−1 + 1.4535∙10−1 | |
| 12 | 1.3273∙10−1 + 1.4535∙10−1 |
| Parameter | Fractional-Order Model | Lumped-Parameter Model (Figure 1) | |
|---|---|---|---|
| One Circuit in the q-Axis (Figure 2b) | Two Circuits in the q-Axis (Figure 2c) | ||
| αh [p.u.] | −0.00565 | −0.0035094 | −0.0046353 |
| ωh [p.u.] | 0.04168 | 0.038585 | 0.040803 |
| Th [s] | 0.563 | 0.907 | 0.687 |
| fh [Hz] | 2.08 | 1.93 | 2.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staszak, J. Analysis of Electromechanical Swings of a Turbogenerator Based on a Fractional-Order Circuit Model. Energies 2025, 18, 5170. https://doi.org/10.3390/en18195170
Staszak J. Analysis of Electromechanical Swings of a Turbogenerator Based on a Fractional-Order Circuit Model. Energies. 2025; 18(19):5170. https://doi.org/10.3390/en18195170
Chicago/Turabian StyleStaszak, Jan. 2025. "Analysis of Electromechanical Swings of a Turbogenerator Based on a Fractional-Order Circuit Model" Energies 18, no. 19: 5170. https://doi.org/10.3390/en18195170
APA StyleStaszak, J. (2025). Analysis of Electromechanical Swings of a Turbogenerator Based on a Fractional-Order Circuit Model. Energies, 18(19), 5170. https://doi.org/10.3390/en18195170






