Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines
Abstract
1. Introduction
| Reference | Proposed Architecture | Application | Comparison & Accuracy |
|---|---|---|---|
| [44] | Phase Current Characteristics (PCCs) + Back Propagation Neural Network (BP NN) | Temperature rise of the generator bearing fault | High accuracy, strong reliability, and good applicability. |
| [45] | Kernel Principal Component Analysis (KPCA) + Support Vector Machine (SVM) | Rotor unbalance | Kernel Principal Component Analysis combined with Support Vector Machine achieves higher recognition accuracy compared to Support Vector Machine and Principal Component Analysis-Support Vector Machine. |
| [46] | Principal Component Analysis (PCA)—Hierarchical K-Nearest Neighbours (HKNN) + Euclidean Distance | Rotor unbalance, rotor misalignment | Reduces algorithm complexity while improving analysis accuracy. |
| [47] | Empirical Mode Decomposition (EMD) + Fuzzy K-Means Clustering (FK) + Convolutional Neural Network (CNN) | Wind turbine generator bearing fault | Enhances the signal-to-noise ratio, expanding the fault diagnosis capability. |
| [48] | Hilbert-Huang Transform (HHT) + Support Vector Machine (SVM) + Empirical Frequency Decomposition (EFD) + Particle Swarm Optimization (PSO) | Synchronous motor fault diagnosis using vibration acceleration data | Particle Swarm Optimisation achieves 95.83% accuracy, outperforming Genetic Algorithm (87.5% accuracy). Optimisation time: 2.091 s, evolution cycles: 30 iterations. |
| [49] | Principal Component Analysis (PCA) + Support Vector Machine (SVM) | Rotor bending, rotor unbalance | Average fault recognition rate: 94.5%. |
| [50] | Wavelet Transform (WT) + Dempster-Shafer Theory (D-S) | Wind Turbine Generator bearing fault | Enhances the signal-to-noise ratio and broadens the scope of fault detection. |
- Which key TM and CPD tools can be applied for fault diagnosis in wind turbines?
- Which combinations of TM and CPD tools are most effective for detecting different types of faults?
2. Materials and Methods
2.1. Literature Search Strategy
- “Trend Monitoring” OR “Change Point Detection” AND “Wind Turbines
- “Structural Health Monitoring” OR “Condition Monitoring” AND “Wind Turbine”
2.2. Inclusion and Exclusion Criteria
2.2.1. Inclusion Criteria
- Peer-reviewed journal articles and conference papers.
- Studies published within the last 15 years (2010–2025).
- Research focuses on TM and CPD methods for wind turbine fault detection.
- Studies discussing the integration of TM-CPD for predictive maintenance.
2.2.2. Exclusion Criteria
- Non-English publications.
- Studies focusing on unrelated condition monitoring techniques.
- Patents, books, and non-peer-reviewed materials (unless significant to the field).
2.3. Study Selection
2.4. Analysis of Selected Articles
3. The Evolution of Fault Diagnosis: From Traditional Methods to TM-CPD Integration
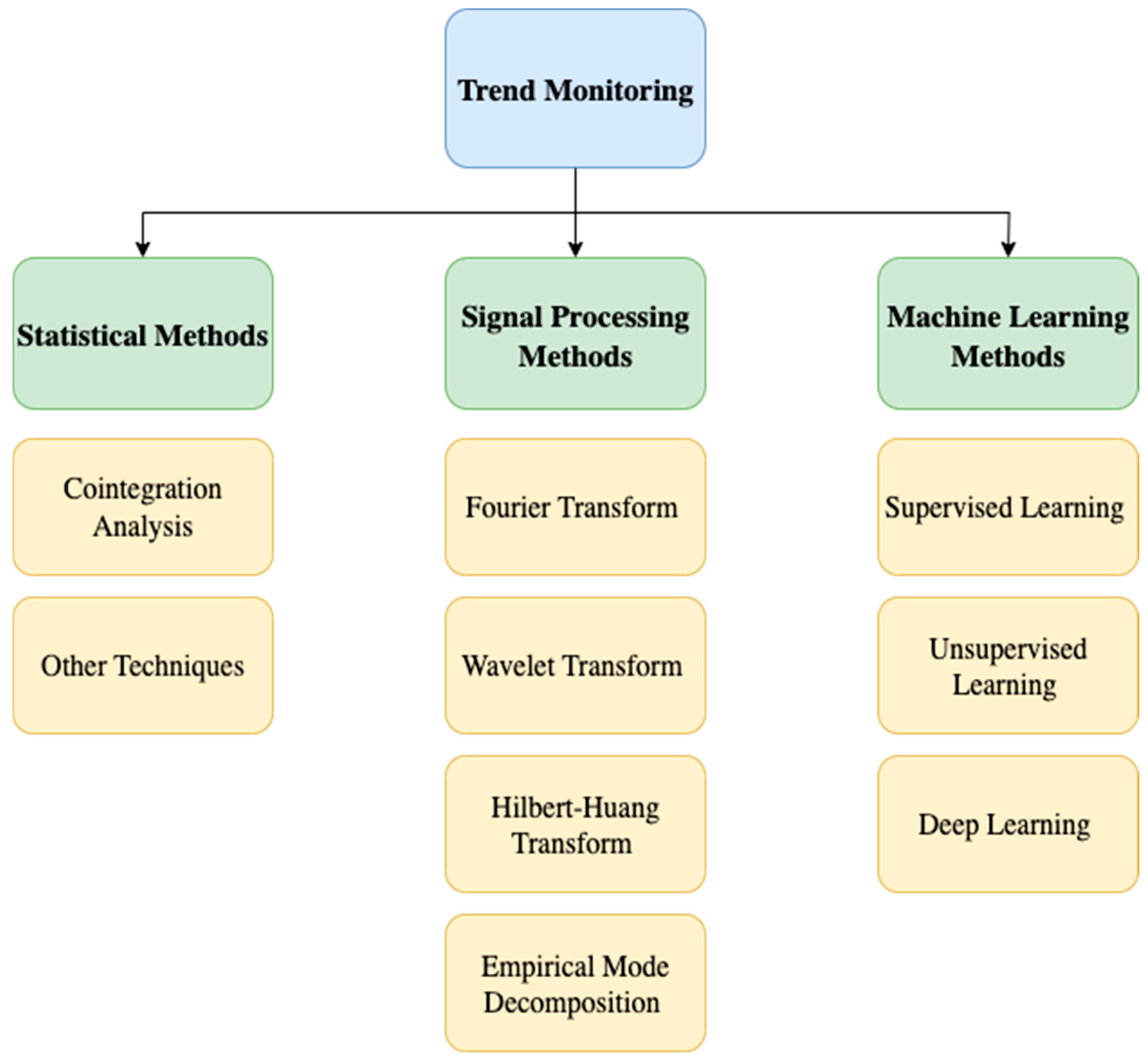
3.1. Trend Monitoring: The Art of Reading the Future
3.1.1. Machine Learning Methods
3.1.2. Signal Processing
- Fast Fourier Transform (FFT);
- Wavelet Transform (WT);
- Hilbert-Huang Transform (HHT);
- Empirical Mode Decomposition (EMD).
Fast-Fourier Transform (FFT)
- is the DFT coefficient at frequency index .
- is the time-domain signal sampled at .
- is the total number of samples.
- is the imaginary unit .
- represents the complex exponential basis function, capturing periodicities in the signal.
- is the time-frequency representation of .
- is the window function (e.g., Hamming, Gaussian) that segments the signal.
- represents the time shift of the window.
- represents the frequency bin.
Wavelet Transform
- is the wavelet coefficient, representing how much the signal correlates with a wavelet at a given scale and position.
- is the original signal (e.g., vibration signals from a wind turbine).
- is the mother wavelet, a predefined function localised in time and frequency.
- is the scale factor, controlling the frequency resolution of the wavelet.
- is the translation factor, determining the time localisation of the wavelet.
- ∗ represents the complex conjugate of the wavelet function.
- is the wavelet coefficient, representing how much the signal correlates with the wavelet at scale and position .
- is the discrete signal, typically sampled from the original continuous-time signal .
- is the discrete wavelet function, given by Equation (8):
- controls the scale (frequency resolution).
- controls the translation (time shift).
- is the mother wavelet.
Hilbert-Huang Transform (HHT)
- (a)
- Empirical Mode Decomposition (EMD)—This step decomposes the signal into a set of Intrinsic Mode Functions (IMFs).
- (b)
- Hilbert Spectral Analysis (HSA)—Each IMF is then analysed to compute its instantaneous amplitude and frequency, producing a detailed time-frequency representation.
Empirical Mode Decomposition (EMD)
- (a)
- The number of extrema and zero-crossings should be equal or differ by no more than one.
- (b)
- The mean value of the envelope defined by the local maxima and minima must be zero.
- (a)
- Identify all local maxima and minima.
- (b)
- Generate the upper and lower envelopes by applying cubic spline interpolation.
- (c)
- Compute the mean envelope using Equation (9):
- (d)
- Extract the detail component:
- (e)
- Repeat the process on until the signal is fully decomposed into IMFs.
Hilbert Transform
Hilbert Spectral Analysis (HHT)
3.1.3. Statistical Methods
Cointegration Analysis
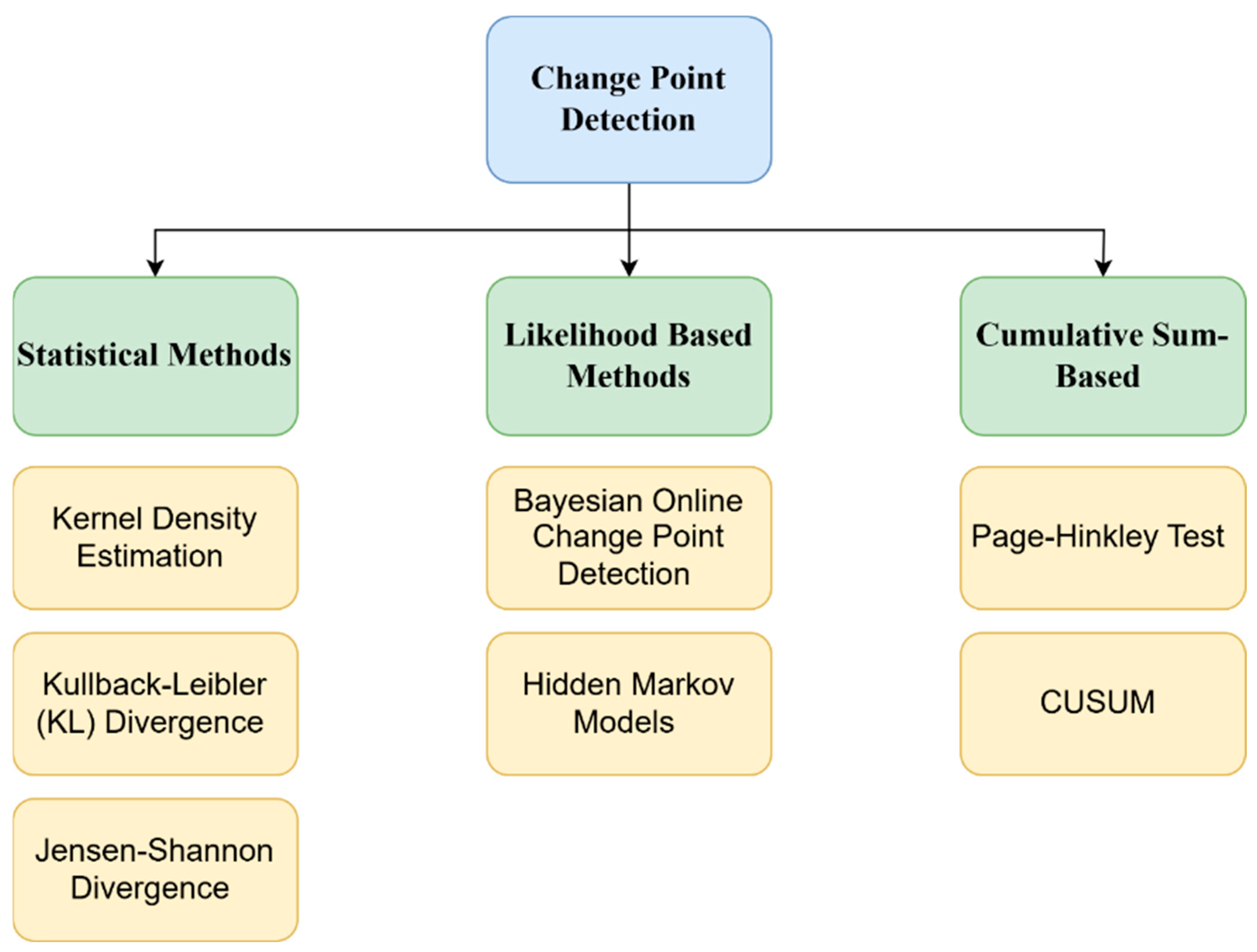
3.2. Overview of CPD and Its Methods
- (1)
- Kernel Density Estimation (KDE);
- (2)
- Kullback–Leibler (KL) Divergence;
- (3)
- Jensen-Shannon Divergence (JSD);
- (4)
- Bayesian Online Change Point Detection (BOCPD);
- (5)
- CUSUM.
3.2.1. Kernel Density Estimation (KDE)
- (a)
- is the estimated probability density function (PDF) at point .
- (b)
- is the number of data points.
- (c)
- is the bandwidth (smoothing parameter) that controls the smoothness of the density estimate.
- (d)
- Small : KDE captures more details but may lead to overfitting (high variance).
- (e)
- Large : KDE becomes smoother, but essential features might be lost (high bias).
- (f)
- Optimal : Often selected using Silverman’s rule of thumb:
- (g)
- is the kernel function, which determines the shape of the contribution of each data point.
- (h)
- is the standard deviation of the data.
3.2.2. KL Divergence
- (a)
- represents the actual probability distribution of the signal (e.g., normal operating condition).
- (b)
- represents the approximate or reference distribution (e.g., a distribution under a faulty condition).
- (c)
- The logarithm is typically base 2 (bits) or natural log (nats).
3.2.3. Jensen-Shannon Divergence (JSD)
- is the Kullback–Leibler divergence.
- is the mixture distribution and can be written as in Equation (25):
3.2.4. Bayesian Online Change Point Detection (BOCPD)
- Step 1: Compute the Run-Length Probability
- is the run length at time .
- is the observed data (e.g., vibration amplitude, temperature).
- is the transition probability, typically modelled as a hazard function .
- is the likelihood of the new data given the current run length.
- Step 2: Define the Hazard Function
- A constant hazard function (e.g., ) assumes a fixed probability of change at each time step.
- A time-varying hazard function adapts based on external conditions (e.g., increasing failure rate over time in wind turbines).
- Step 3: Compute the Predictive Distribution
- Step 4: Update the Evidence
3.2.5. CUSUM
- (a)
- Standard CUSUM (One-Sided)
- (1)
- Upper CUSUM : Detects an increase in mean.
- (2)
- Lower CUSUM : Detects a decrease in mean.
- are the upper and lower cumulative sums at time .
- is the observed value at time (e.g., vibration level, temperature).
- is the baseline mean value under normal conditions.
- is the drift threshold, which defines the minimum shift in mean that should be detected (typically , where is the desired detectable shift).
- The max (0, …) ensures the cumulative sum resets when the deviation is within normal limits.
- (b)
- Stopping Criterion (Threshold )
4. The Need for Integration of TM and CPD
4.1. Why Are Change Point Detection (CPD) or Trend Monitoring Alone Not Enough?
4.1.1. Limitations of Trend Monitoring (TM)
4.1.2. Limitations of Change Point Detection (CPD)
4.2. How Does Combining TM & CPD Improve Fault Detection?
4.3. Selecting the Optimal TM-CPD Combination for Wind Turbine Fault Detection
4.3.1. Trade-Offs in TM-CPD Methods
4.3.2. Type of Fault (Sudden or Gradual)
4.3.3. Data Availability (Real-Time vs. Historical Data)
4.3.4. Sensitivity & Accuracy (Balancing False Alarms and Missed Faults)
4.4. Best TM-CPD Combinations in Real-World Wind Turbine Monitoring
5. Case Study: Applying Findings on Wind Turbine Blade Failure
- (a)
- Mass imbalance fault (at 1.3 m/s wind speed):
- Only one imbalance defect was applied, and data were collected under 1.3 m/s wind speed conditions.
- The defect alters the inertial distribution, producing periodic vibrations characteristic of rotor asymmetry.
- Simulated by attaching a 5 g mass at 18 cm from the blade root of one blade.
- (b)
- Blade crack fault (at 4.5 m/s wind speed):
- Simulated by introducing a crack on the blade body, representing foreign object damage during operation.
- While the dataset does not provide explicit numerical dimensions (depth or length), the crack fault reflects a realistic degradation mode that weakens stiffness and alters vibration responses.
- One crack defect was applied, and data were collected under 4.5 m/s wind speed conditions.
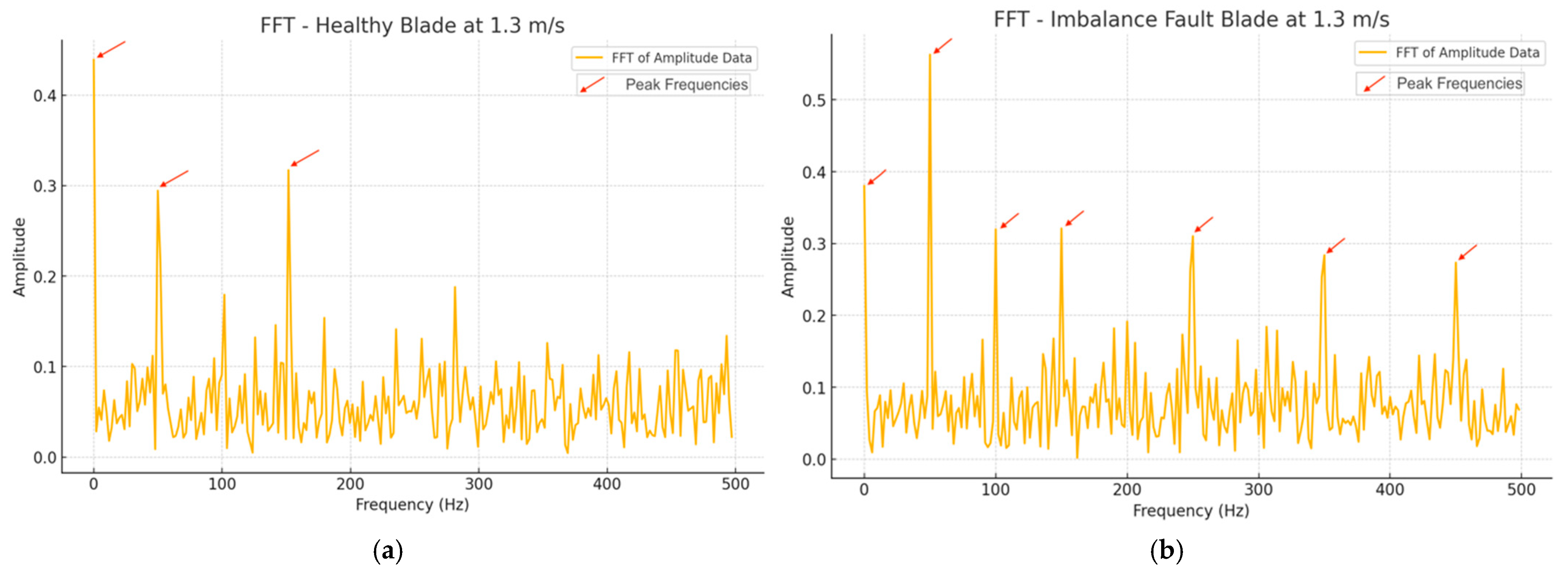
5.1. FFT-Based Detection of Blade Imbalance Fault at (1.3 m/s)
- In Figure 10a, the dominant frequency peaks primarily appear at 0 Hz, 50 Hz, and 150 Hz, indicating that the wind turbine is operating normally without disturbances. These frequencies correspond to the fundamental vibration frequencies of the turbine, confirming smooth and defect-free operation. As shown in the figure, the frequency plot exhibits a relatively simple and stable distribution, with most of the energy concentrated near the central vibration frequency.
- Blade imbalance disrupts the smooth operation of the turbine, generating vibrations at higher frequencies. In the FFT spectrum of the imbalance fault, frequency peaks appear at 0 Hz, 50 Hz, 100 Hz, 150 Hz, 250 Hz, 350 Hz, and 450 Hz. These additional peaks at higher frequencies represent elevated harmonic frequencies, reflecting the resonant effects caused by the imbalance.
- The FFT plot for the imbalance fault appears more complex, with an increased number of distinct peaks, indicating that the fault has introduced irregularities into the vibration patterns. Such complexity typically reflects stronger resonant frequencies or harmonics, caused by the uneven mass distribution on the blade.
5.2. KL Divergence-Based Detection of Blade Imbalance Fault at 1.3 m/s
- KL Divergence measures how much one probability distribution differs from another. In this case, it quantifies the difference between the frequency distributions of the healthy condition and the imbalance fault condition.
- The KL Divergence between the frequency distributions of the healthy blade and the imbalance fault blade at a blade speed of 1.3 m/s is 0.3942.
- A KLD value of 0.3942 indicates a significant deviation in the vibration signal’s frequency content between the healthy and faulty states. As the KLD increases, the distributions become more distinct.
- This KLD value confirms that the imbalance fault introduces measurable changes in the vibration pattern, demonstrating that the fault can be reliably detected using FFT combined with KL Divergence.
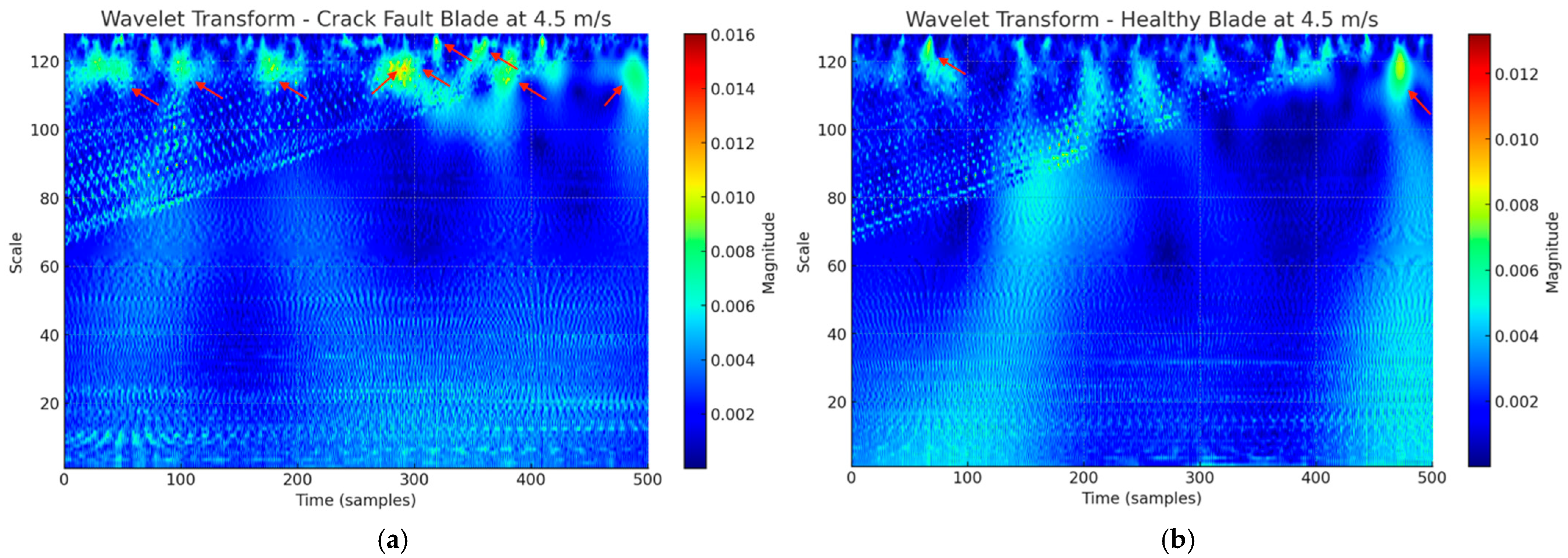
5.3. WT-Based Detection of Blade Crack Fault at 4.5 m/s
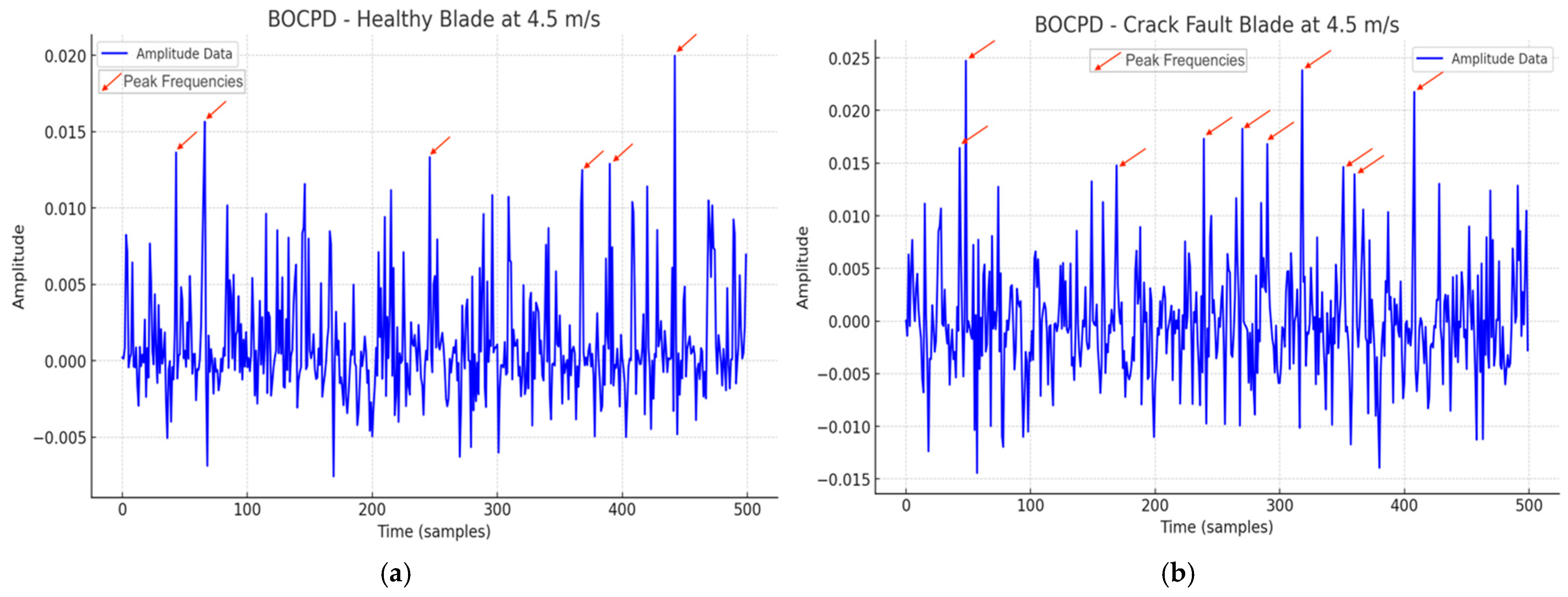
5.4. BOCPD-Based Detection of Blade Crack Fault at (4.5 m/s)
6. Conclusions
7. Future Research Directions for TM-CPD in Wind Turbine Monitoring
- Exploration of Novel TM–CPD Combinations: Beyond the combinations demonstrated in this review (e.g., FFT–KLD for imbalance detection, WT–BOCPD for crack detection), other TM–CPD pairings merit systematic evaluation. Comparative studies across diverse fault modes and operating conditions could establish best-practice frameworks for different turbine subsystems (e.g., gearbox, generator, blades).
- AI-Enhanced Hybrid Algorithms: Future work should embed TM–CPD approaches within advanced machine learning (ML) and deep learning architectures. Hybrid models could combine feature extraction from TM with adaptive thresholds from CPD, potentially incorporating reinforcement learning to continuously improve fault detection and reduce false alarms.
- Real-Time and Edge Computing Solutions: Current TM–CPD implementations often face computational bottlenecks. Leveraging edge computing and lightweight algorithm design would enable real-time monitoring directly on turbine controllers, reducing latency and supporting immediate fault response.
- Integration with Digital Twins: Digital twin models of wind turbines can serve as virtual testbeds for validating TM–CPD methods under controlled conditions. Combining physical models with real-time SCADA data through digital twins would allow TM–CPD systems to adapt dynamically to evolving operating states and predict degradation trends.
- Towards Predictive Maintenance: While current TM–CPD methods are largely diagnostic, future research should extend their application toward predictive frameworks. Integrating time-to-failure estimation, probabilistic forecasting, and remaining useful life (RUL) modelling with TM–CPD could shift monitoring from reactive to proactive strategies, enhancing turbine resilience and reducing maintenance costs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TM | Trend Monitoring |
| CPD | Change Point Detection |
| GW | Gigawatt |
| FFT | Fast Fourier Transform |
| WT | Wavelet Transform |
| HHT | Hilbert-Huang Transform |
| HSA | Hilbert Spectral Analysis |
| KLD | Kullback–Leibler Divergence |
| BOCPD | Bayesian Online Change Point Detection |
| CUSUM | Cumulative Sum Control Chart |
| PRISMA | Preferred Reporting Items for Systematic Review and Meta Analysis |
| ML | Machine Learning |
| KNN | K-Nearest Neighbor |
| RF | Random Forest |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| SCADA | Supervisory Control And Data Acquisition |
| MLP | Multi-Layer Perceptron |
| PNN | Probabilistic Neural Network |
| RBFNN | Radial Basis Function Neural Network |
| BP | Back Propagation |
| DT | Decision Tree |
| HMM | Hidden Markov Model |
| CA | Classification Algorithms |
| BPNN | Back Propagation Neural Network |
| EML | Extreme Machine Learning |
| SOM | Self-Organizing Map |
| ART | Adaptive Resonance Theory |
| CNN | Convolutional Neural Network |
| DBN | Deep Belief Network |
| SAE | Stacked Autoencoder |
| RNN | Recurrent Neural Network |
| TL | Transfer Learning |
| EMD | Empirical Mode Decomposition |
| DFT | Discrete Fourier Transform |
| FT | Fourier Transform |
| IDFT | Inverse Discrete Fourier Transform |
| STFT | Short-Time Fourier Transform |
| DWT | Discrete Wavelet Transform |
| NDT | Non-Destructive Testing |
| IMFs | Intrinsic Mode Functions |
| KDE | Kernel Density Estimation |
| JSD | Jensen-Shannon Divergence |
| Probability Density Function | |
| SHM | Structural Health Monitoring |
| KPCA | Kernel Principal Component Analysis |
| ADF | Augmented Dickey–Fuller |
References
- Satymov, R.; Bogdanov, D.; Breyer, C. Techno-Economics of Offshore Wind Power in Global Resolution. Appl. Energy 2025, 393, 125980. [Google Scholar] [CrossRef]
- Zhang, Y.; Ravishanker, N.; Zou, J. Structural Break Detection in Financial Durations. Appl. Stoch. Models Bus. Ind. 2018, 34, 992–1006. [Google Scholar] [CrossRef]
- Guo, S.; Guo, W.; Abolhassani, A.; Kalamdani, R.; Puchala, S.; Januszczak, A.; Jalluri, C. Manufacturing Process Monitoring with Nonparametric Change-Point Detection in Automotive Industry. J. Manuf. Sci. Eng. Trans. ASME 2019, 141, 1–47. [Google Scholar] [CrossRef]
- Wang, C.S.H.; Xie, Y.M. Structural Change and Monitoring Tests. In Handbook of Financial Econometrics and Statistics; Springer: New York, NY, USA, 2015; pp. 873–902. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, J.; Wang, X.L.; Lund, R.; Lu, Q.Q. A Review and Comparison of Changepoint Detection Techniques for Climate Data. J. Appl. Meteorol. Clim. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Lee, T.-S. Change-Point Problems: Bibliography and Review. J. Stat. Theory Pr. 2010, 4, 643–662. [Google Scholar] [CrossRef]
- Lin, Y.; Kruger, U.; Gu, F.; Ball, A.; Chen, Q. Monitoring Nonstationary and Dynamic Trends for Practical Process Fault Diagnosis. Control Eng. Pr. 2019, 84, 139–158. [Google Scholar] [CrossRef]
- Antoniadis, A.; Gijbels, I. Detecting Abrupt Changes by Wavelet Methods. J. Nonparametr. Stat. 2002, 14, 7–29. [Google Scholar] [CrossRef]
- van den Burg, G.J.J.; Williams, C.K.I. An Evaluation of Change Point Detection Algorithms. arXiv 2020, arXiv:2003.06222. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Li, W.; Yang, Y.; Hong, Y. An Integrated Statistical Approach to Identify the Nonlinear Trend of Runoff in the Hotan River and Its Relation with Climatic Factors. Stoch. Environ. Res. Risk Assess. 2011, 25, 223–233. [Google Scholar] [CrossRef]
- Schleicher, C.; Barillas, F.; Beaudry, P.; Karnizova, L.; Kim, C.-S. Structural Time Series Models with Common Trends and Common Cycles. Comput. Econ. Financ. 2003, 108. Available online: https://ideas.repec.org/p/sce/scecf3/108.html (accessed on 12 August 2025).
- Lin, Y.; Kruger, U.; Chen, Q. Monitoring Nonstationary Dynamic Systems Using Cointegration and Common-Trends Analysis. Ind. Eng. Chem. Res. 2017, 56, 8895–8905. [Google Scholar] [CrossRef]
- Simon, J.; Moll, J.; Krozer, V. Trend Decomposition for Temperature Compensation in a Radar-Based Structural Health Monitoring System of Wind Turbine Blades. Sensors 2024, 24, 800. [Google Scholar] [CrossRef]
- Sun, T.; Yu, G.; Gao, M.; Zhao, L.; Bai, C.; Yang, W. Fault Diagnosis Methods Based on Machine Learning and Its Applications for Wind Turbines: A Review. IEEE Access 2021, 9, 147481–147511. [Google Scholar] [CrossRef]
- Rezamand, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.K.; Saif, M. A New Hybrid Fault Detection Method for Wind Turbine Blades Using Recursive PCA and Wavelet-Based PDF. IEEE Sens. J. 2020, 20, 2023–2033. [Google Scholar] [CrossRef]
- Avalos-Almazan, G.; Aguayo-Tapia, S.; Rangel-Magdaleno, J.; Paternina, M.R.A. Bearing Fault Detection in Induction Motors Using the ROCOF and K-Nearest Neighbors Algorithm. In Proceedings of the 2023 IEEE 14th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives, SDEMPED 2023, Chania, Greece, 28–31 August 2023; pp. 192–197. [Google Scholar] [CrossRef]
- Jiang, L.; Cui, J.; Wang, J. A DPCA-Based Online Fault Indicator for Gear Faults Using Three-Direction Vibration Signals. J. Vibroengineering 2018, 20, 1340–1354. [Google Scholar] [CrossRef]
- Moreno, S.R.; Coelho, L.D.S.; Ayala, H.V.H.; Mariani, V.C. Wind Turbines Anomaly Detection Based on Power Curves and Ensemble Learning. IET Renew. Power Gener. 2020, 14, 4086–4093. [Google Scholar] [CrossRef]
- Li, Q.; Li, M.; Fu, C.; Wang, J. Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine. Electronics 2024, 13, 3621. [Google Scholar] [CrossRef]
- Jin, X.; Xu, Z.; Qiao, W. Condition Monitoring of Wind Turbine Generators Using SCADA Data Analysis. IEEE Trans. Sustain. Energy 2021, 12, 202–210. [Google Scholar] [CrossRef]
- Fang, Y.; Rasel, M.A.K.; Richmond, P.C. A Stylized Trend Analysis Approach for Process Monitoring and Fault Diagnosis. Process Saf. Prog. 2018, 37, 411–418. [Google Scholar] [CrossRef]
- Lei, X.; Chen, Z.; Li, H.; Wei, S. A Change-Point Detection Method for Detecting and Locating the Abrupt Changes in Distributions of Damage-Sensitive Features of SHM Data, with Application to Structural Condition Assessment. Struct. Health Monit. 2022, 22, 1161–1179. [Google Scholar] [CrossRef]
- Reese, S.; Li, Y. Testing for Structural Breaks in the Presence of Data Perturbations: Impacts and Wavelet Based Improvements. J. Stat. Comput. Simul. 2013, 85, 3468–3479. [Google Scholar] [CrossRef]
- Marsick, A.; André, H.; Khelf, I.; Leclère, Q.; Antoni, J. Benefits of Mann–Kendall Trend Analysis for Vibration-Based Condition Monitoring. Mech. Syst. Signal Process. 2024, 216, 111486. [Google Scholar] [CrossRef]
- Pan, Y.; Zheng, Z. Bayesian Online Change Point Detection Method for Process Monitoring. In Proceedings of the 32nd Chinese Control and Decision Conference, CCDC 2020, Hefei, China, 22–24 August 2020; pp. 3389–3393. [Google Scholar] [CrossRef]
- Tochev, E.; Rengasamy, D.; Pfifer, H.; Ratchev, S. System Condition Monitoring through Bayesian Change Point Detection Using Pump Vibrations. IEEE Int. Conf. Autom. Sci. Eng. 2020, 2020, 667–672. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, J.; Wang, K. Bayesian Online Change Detection of Multimode Processes with Application to Wind Turbines. IEEE Trans. Instrum. Meas. 2024, 73, 2527011. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Wang, C.-B.; Ma, Z.-G.; Chen, W.; Ni, Y.-Q.; Wang, C.-F.; Yan, B.-G.; Guan, P.-X. Bayesian Dynamic Linear Model Framework for Structural Health Monitoring Data Forecasting and Missing Data Imputation during Typhoon Events. Struct. Health Monit. 2022, 21, 2933–2950. [Google Scholar] [CrossRef]
- Dao, P.B. A CUSUM-Based Approach for Condition Monitoring and Fault Diagnosis of Wind Turbines. Energies 2021, 14, 3236. [Google Scholar] [CrossRef]
- Turner, P. Power Properties of the CUSUM and CUSUMSQ Tests for Parameter Instability. Appl. Econ. Lett. 2010, 17, 1049–1053. [Google Scholar] [CrossRef]
- Lei, X.; Chen, Z.; Li, H.; Wei, S. Detecting and Testing Multiple Change Points in Distributions of Damage-Sensitive Feature Data for Data-Driven Structural Condition Assessment: A Distributional Time Series Change-Point Analytic Approach. Mech. Syst. Signal Process. 2023, 196, 110344. [Google Scholar] [CrossRef]
- Niu, Y.S.; Hao, N.; Zhang, H. Multiple Change-Point Detection: A Selective Overview. Stat. Sci. 2016, 31, 611–623. [Google Scholar] [CrossRef]
- Polunchenko, A.S.; Tartakovsky, A.G. State-of-the-Art in Sequential Change-Point Detection. Methodol. Comput. Appl. Probab. 2012, 14, 649–684. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A Survey of Methods for Time Series Change Point Detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef]
- Zhang, Z.; Doganaksoy, N. Change Point Detection and Issue Localization Based on Fleet-Wide Fault Data. J. Qual. Technol. 2022, 54, 453–465. [Google Scholar] [CrossRef]
- Letzgus, S. Change-Point Detection in Wind Turbine SCADA Data for Robust Condition Monitoring with Normal Behaviour Models. Wind Energy Sci. 2020, 5, 1375–1397. [Google Scholar] [CrossRef]
- Dao, P.B. Condition Monitoring and Fault Diagnosis of Wind Turbines Based on Structural Break Detection in SCADA Data. Renew. Energy 2022, 185, 641–654. [Google Scholar] [CrossRef]
- Bilendo, F.; Lu, N.; Badihi, H.; Meyer, A.; Cali, U.; Cambron, P. Multitarget Normal Behavior Model Based on Heterogeneous Stacked Regressions and Change-Point Detection for Wind Turbine Condition Monitoring. IEEE Trans. Ind. Inf. 2024, 20, 5171–5181. [Google Scholar] [CrossRef]
- Latiffianti, E.; Sheng, S.; Ding, Y. Wind Turbine Gearbox Failure Detection Through Cumulative Sum of Multivariate Time Series Data. Front. Energy Res. 2022, 10, 904622. [Google Scholar] [CrossRef]
- Dao, P.B. On Wilcoxon Rank Sum Test for Condition Monitoring and Fault Detection of Wind Turbines. Appl. Energy 2022, 318, 119209. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Lamb Wave Based Structural Damage Detection Using Stationarity Tests. Materials 2021, 14, 6823. [Google Scholar] [CrossRef]
- Dao, P.B.; Barszcz, T.; Staszewski, W.J. Anomaly Detection of Wind Turbines Based on Stationarity Analysis of SCADA Data. Renew. Energy 2024, 232, 121076. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057. [Google Scholar] [CrossRef]
- Guo, P.; Fu, J.; Yang, X. Condition Monitoring and Fault Diagnosis Ofwind Turbines Gearbox Bearing Temperature Based on Kolmogorov-Smirnov Test and Convolutional Neural Network Model. Energies 2018, 11, 2248. [Google Scholar] [CrossRef]
- Yin, Z.; Hou, J. Recent Advances on SVM Based Fault Diagnosis and Process Monitoring in Complicated Industrial Processes. Neurocomputing 2016, 174, 643–650. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Sheng, D.; Chen, J.; Yu, Z. Fault Diagnosis Method of Peak-Load-Regulation Steam Turbine Based on Improved PCA-HKNN Artificial Neural Network. Proc. Inst. Mech. Eng. O J. Risk Reliab. 2021, 235, 1026–1040. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, M.; Huang, X. Bearing Fault Diagnosis Based on Speed Signal and CNN Model. Energy Rep. 2022, 8, 904–913. [Google Scholar] [CrossRef]
- Wang, Y.S.; Ma, Q.H.; Zhu, Q.; Liu, X.T.; Zhao, L.H. An Intelligent Approach for Engine Fault Diagnosis Based on Hilbert-Huang Transform and Support Vector Machine. Appl. Acoust. 2014, 75, 1–9. [Google Scholar] [CrossRef]
- Li, P.; Li, X.; Jiang, L.; Cao, Y. Fault Diagnosis of Asynchronous Motor Based on KPCA and PSOSVM. Zhendong Ceshi Zhenduan/J. Vib. Meas. Diagn. 2014, 34, 616–620. [Google Scholar]
- Hoang, D.T.; Kang, H.J. A Motor Current Signal-Based Bearing Fault Diagnosis Using Deep Learning and Information Fusion. IEEE Trans. Instrum. Meas. 2020, 69, 3325–3333. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Tobias, A.M.; Pinar Pérez, J.M.; Papaelias, M. Condition Monitoring of Wind Turbines: Techniques and Methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Purarjomandlangrudi, A.; Nourbakhsh, G.; Esmalifalak, M.; Tan, A. Fault Detection in Wind Turbine: A Systematic Literature Review. Wind Eng. 2013, 37, 535–547. [Google Scholar] [CrossRef]
- Schubel, P.J.; Crossley, R.J.; Boateng, E.K.G.; Hutchinson, J.R. Review of Structural Health and Cure Monitoring Techniques for Large Wind Turbine Blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Kusiak, A.; Zhang, Z.; Verma, A. Prediction, Operations, and Condition Monitoring in Wind Energy. Energy 2013, 60, 1–12. [Google Scholar] [CrossRef]
- Bindi, C.; Zappalá, D.; Crabtree, C.J.; Tavner, P. Survey of Commercially Available SCADA Data Analysis Tools for Wind Turbine Health Monitoring; Durham University: Durham, UK, 2014. [Google Scholar]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Kaewniam, P.; Cao, M.; Alkayem, N.F.; Li, D.; Manoach, E. Recent Advances in Damage Detection of Wind Turbine Blades: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2022, 167, 112737. [Google Scholar] [CrossRef]
- Welte, T.M.; Wang, K. Models for Lifetime Estimation: An Overview with Focus on Applications to Wind Turbines. Adv. Manuf. 2014, 2, 79–87. [Google Scholar] [CrossRef]
- Crabtree, C.J.; Zappalá, D.; Tavner, P.J. Survey of Commercially Available Condition Monitoring Systems for Wind Turbines; Durham University: Durham, UK, 2014. [Google Scholar]
- Wang, K.S.; Sharma, V.S.; Zhang, Z.Y. SCADA Data Based Condition Monitoring of Wind Turbines. Adv. Manuf. 2014, 2, 61–69. [Google Scholar] [CrossRef]
- Antoniadou, I.; Manson, G.; Staszewski, W.J.; Barszcz, T.; Worden, K. A Time–Frequency Analysis Approach for Condition Monitoring of a Wind Turbine Gearbox under Varying Load Conditions. Mech. Syst. Signal Process. 2015, 64–65, 188–216. [Google Scholar] [CrossRef]
- Wymore, M.L.; Van Dam, J.E.; Ceylan, H.; Qiao, D. A Survey of Health Monitoring Systems for Wind Turbines. Renew. Sustain. Energy Rev. 2015, 52, 976–990. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis—Part II: Signals and Signal Processing Methods. IEEE Trans. Ind. Electron. 2015, 62, 6546–6557. [Google Scholar] [CrossRef]
- Kandukuri, S.T.; Klausen, A.; Karimi, H.R.; Robbersmyr, K.G. A Review of Diagnostics and Prognostics of Low-Speed Machinery towards Wind Turbine Farm-Level Health Management. Renew. Sustain. Energy Rev. 2016, 53, 697–708. [Google Scholar] [CrossRef]
- De Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A Review of Wind Turbine Bearing Condition Monitoring: State of the Art and Challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Yang, W.; Peng, Z.; Wei, K.; Tian, W. Structural Health Monitoring of Composite Wind Turbine Blades: Challenges, Issues and Potential Solutions. IET Renew. Power Gener. 2017, 11, 411–416. [Google Scholar] [CrossRef]
- Uma Maheswari, R.; Umamaheswari, R. Trends in Non-Stationary Signal Processing Techniques Applied to Vibration Analysis of Wind Turbine Drive Train—A Contemporary Survey. Mech. Syst. Signal Process. 2017, 85, 296–311. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA Data for Wind Turbine Condition Monitoring—A Review. IET Renew. Power Gener. 2017, 11, 382–394. [Google Scholar] [CrossRef]
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A Survey of Artificial Neural Network in Wind Energy Systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox Condition Monitoring in Wind Turbines: A Review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Abid, K.; Mouchaweh, M.S.; Cornez, L. Fault Prognostics for the Predictive Maintenance of Wind Turbines: State of the Art. Commun. Comput. Inf. Sci. 2019, 967, 113–125. [Google Scholar] [CrossRef]
- Leite, G.d.N.P.; Araújo, A.M.; Rosas, P.A.C. Prognostic Techniques Applied to Maintenance of Wind Turbines: A Concise and Specific Review. Renew. Sustain. Energy Rev. 2018, 81, 1917–1925. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef]
- Moeini, R.; Entezami, M.; Ratkovac, M.; Tricoli, P.; Hemida, H.; Hoeffer, R.; Baniotopoulos, C. Perspectives on Condition Monitoring Techniques of Wind Turbines. Wind Eng. 2019, 43, 539–555. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, D. A Survey of Condition Monitoring and Fault Diagnosis toward Integrated O&M for Wind Turbines. Energies 2019, 12, 2801. [Google Scholar] [CrossRef]
- Leahy, K.; Gallagher, C.; O’Donovan, P.; O’Sullivan, D.T.J. Issues with Data Quality for Wind Turbine Condition Monitoring and Reliability Analyses. Energies 2019, 12, 201. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S. Reliability Improvement of Wind Turbine Power Generation Using Model-Based Fault Detection and Fault Tolerant Control: A Review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A Review of Failure Modes, Condition Monitoring and Fault Diagnosis Methods for Large-Scale Wind Turbine Bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Papaelias, M. An Overview of Wind Turbine Maintenance Management. In Non-Destructive Testing and Condition Monitoring Techniques for Renewable Energy Industrial Assets; Butterworth-Heinemann: Oxford, UK, 2020; pp. 31–47. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Hassan, A.A.; Phong Ba, D. Bridging Data and Diagnostics: A Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines; Center for Open Science: Washington, DC, USA, 2025. [Google Scholar] [CrossRef]
- Kabir, M.J.; Oo, A.M.T.; Rabbani, M. A Brief Review on Offshore Wind Turbine Fault Detection and Recent Development in Condition Monitoring Based Maintenance System. In Proceedings of the 2015 Australasian Universities Power Engineering Conference: Challenges for Future Grids, AUPEC 2015, Wollongong, NSW, Australia, 27–30 September 2015. [Google Scholar] [CrossRef]
- Tong, C. Advanced Materials Enable Renewable Wind Energy Capture and Generation. In Introduction to Materials for Advanced Energy Systems; Springer: Cham, Switzerland, 2019; pp. 379–444. [Google Scholar] [CrossRef]
- Altaf, S.; Ahmad, S. Machine Health Monitoring and Fault Diagnosis Techniques Review in Industrial Power-Line Network. In Modeling and Simulation in Engineering—Selected Problems; IntechOpen: London, UK, 2020. [Google Scholar]
- Liu, H.; Wang, Y.Z.; Zeng, T.; Wang, H.F.; Chan, S.C.; Ran, L. Wind Turbine Generator Failure Analysis and Fault Diagnosis: A Review. IET Renew. Power Gener. 2024, 18, 3127–3148. [Google Scholar] [CrossRef]
- Hou, J.; Lu, X.; Zhong, Y.; He, W.; Zhao, D.; Zhou, F. A Comprehensive Review of Mechanical Fault Diagnosis Methods Based on Convolutional Neural Network. J. Vibroengineering 2024, 26, 44–65. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, Y.; Tan, F.; Wang, X.; Zhang, Y.; Liao, J.; Yang, F.; Guo, Z. Research on an Intelligent Diagnosis Method of Mechanical Faults for Small Sample Data Sets. Sci. Rep. 2022, 12, 21996. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, X.; Sun, W. Intelligent Fault Warning Method for Wind Turbine Gear Transmission System Driven by Digital Twin and Multi-Source Data Fusion. Appl. Sci. 2025, 15, 8655. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O.; López-Meraz, R.A. Fault Detection of Wind Turbine Induction Generators through Current Signals and Various Signal Processing Techniques. Appl. Sci. 2020, 10, 7389. [Google Scholar] [CrossRef]
- Chen, B.; Matthews, P.C.; Tavner, P.J. Wind Turbine Pitch Faults Prognosis Using A-Priori Knowledge-Based ANFIS. Expert. Syst. Appl. 2013, 40, 6863–6876. [Google Scholar] [CrossRef]
- Kumar, R.R.; Andriollo, M.; Cirrincione, G.; Cirrincione, M.; Tortella, A. A Comprehensive Review of Conventional and Intelligence-Based Approaches for the Fault Diagnosis and Condition Monitoring of Induction Motors. Energies 2022, 15, 8938. [Google Scholar] [CrossRef]
- Ahn, J.; Kim, D.; Song, M.; Min, J.; Hwang, J.; Kwon, J.; Kim, H.J. ℓ1 Trend Filtering-Based Change Point Detection for Pumping Line Balance of Deposition Equipment. IEEE Trans. Semicond. Manuf. 2022, 35, 137–145. [Google Scholar] [CrossRef]
- Soleymani, A.; Scott, K.A. Arctic Marginal Ice Zone Interannual Variability and Change Point Detection Using Two Definitions (1983–2022). Environ. Res. Lett. 2023, 18, 124002. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of Trend Detection Methods and Their Application to Detect Temperature Changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Bai, J. Estimating Cross-Section Common Stochastic Trends in Nonstationary Panel Data. J. Econ. 2004, 122, 137–183. [Google Scholar] [CrossRef]
- Hu, Z.; Duan, L.X.; Zhang, L. Bin Application of Improved KNNC Method in Fault Pattern Recognition of Rolling Bearings. Zhendong Chongji/J. Vib. Shock. 2013, 32, 84–87. [Google Scholar]
- Cabrera, D.; Sancho, F.; Sánchez, R.V.; Zurita, G.; Cerrada, M.; Li, C.; Vásquez, R.E. Fault Diagnosis of Spur Gearbox Based on Random Forest and Wavelet Packet Decomposition. Front. Mech. Eng. 2015, 10, 277–286. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Dao, P.B. On Cointegration Analysis for Condition Monitoring and Fault Detection of Wind Turbines Using SCADA Data. Energies 2023, 16, 2352. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, D.; Junsheng, C. A Roller Bearing Fault Diagnosis Method Based on EMD Energy Entropy and ANN. J. Sound. Vib. 2006, 294, 269–277. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Vibration-Based Fault Diagnosis of a Rotor Bearing System Using Artificial Neural Network and Support Vector Machine. Int. J. Model. Identif. Control 2012, 15, 185–198. [Google Scholar] [CrossRef]
- Samanta, B.; Al-Balushi, K.R.; Al-Araimi, S.A. Artificial Neural Networks and Genetic Algorithm for Bearing Fault Detection. Soft Comput. 2006, 10, 264–271. [Google Scholar] [CrossRef]
- Qian, P.; Tian, X.; Kanfoud, J.; Lee, J.L.Y.; Gan, T.H. A Novel Condition Monitoring Method of Wind Turbines Based on Long Short-Term Memory Neural Network. Energies 2019, 12, 3411. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Y.; Ding, Z. The Application of Heterogeneous Information Fusion in Misalignment Fault Diagnosis of Wind Turbines. Energies 2018, 11, 1655. [Google Scholar] [CrossRef]
- Gao, Q.W.; Liu, W.Y.; Tang, B.P.; Li, G.J. A Novel Wind Turbine Fault Diagnosis Method Based on Intergral Extension Load Mean Decomposition Multiscale Entropy and Least Squares Support Vector Machine. Renew. Energy 2018, 116, 169–175. [Google Scholar] [CrossRef]
- Ponnuswamy, B.; Columbus, C.; Lakshmi, S.R.; Chithambaram, J. Wind Turbine Fault Modeling and Classification Using Cuckoo-Optimized Modular Neural Networks. Rev. Roum. DES Sci. Tech. —Série Électrotechnique et Énergétique 2023, 68, 369–374. [Google Scholar] [CrossRef]
- Vamsi, I.; Sabareesh, G.R.; Penumakala, P.K. Comparison of Condition Monitoring Techniques in Assessing Fault Severity for a Wind Turbine Gearbox under Non-Stationary Loading. Mech. Syst. Signal Process. 2019, 124, 1–20. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. A Data Driven Approach for Condition Monitoring of Wind Turbine Blade Using Vibration Signals through Best-First Tree Algorithm and Functional Trees Algorithm: A Comparative Study. ISA Trans. 2017, 67, 160–172. [Google Scholar] [CrossRef]
- Herp, J.; Ramezani, M.H.; Bach-Andersen, M.; Pedersen, N.L.; Nadimi, E.S. Bayesian State Prediction of Wind Turbine Bearing Failure. Renew. Energy 2018, 116, 164–172. [Google Scholar] [CrossRef]
- Zhong, J.H.; Zhang, J.; Liang, J.; Wang, H. Multi-Fault Rapid Diagnosis for Wind Turbine Gearbox Using Sparse Bayesian Extreme Learning Machine. IEEE Access 2019, 7, 773–781. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, Z.; Jiang, Y.; Zhu, J. Wind Turbine Health State Monitoring Based on a Bayesian Data-Driven Approach. Renew. Energy 2018, 125, 172–181. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Wang, R. Fuzzy Scalar Quantisation Based on Hidden Markov Model and Application in Fault Diagnosis of Wind Turbine. J. Eng. 2017, 2017, 2685–2689. [Google Scholar] [CrossRef]
- Shin, S.H.; Kim, S.R.; Seo, Y.H. Development of a Fault Monitoring Technique for Wind Turbines Using a Hidden Markov Model. Sensors 2018, 18, 1790. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Makis, V.; Zuo, H.; Cai, J. Optimal Bayesian Control Policy for Gear Shaft Fault Detection Using Hidden Semi-Markov Model. Comput. Ind. Eng. 2018, 119, 21–35. [Google Scholar] [CrossRef]
- Qin, X.; Li, Q.; Dong, X.; Lv, S. The Fault Diagnosis of Rolling Bearing Based on Ensemble Empirical Mode Decomposition and Random Forest. Shock. Vib. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Gan, H.; Jiao, B. Fault Diagnosis of Wind Turbine’s Gearbox Based on Improved GA Random Forest Classifier. DEStech Trans. Eng. Technol. Res. 2018, 206–210. [Google Scholar] [CrossRef]
- Wu, B.; Li, X. Fault Diagnosis Method Based on Kernel Fuzzy C-Means Clustering with Gravitational Search Algorithm. In Proceedings of the Proceedings of 2018 IEEE 7th Data Driven Control and Learning Systems Conference, DDCLS 2018, Enshi, China, 25–27 May 2018. [Google Scholar]
- Zhang, J.; Jiang, N.; Li, H.; Li, N. Online Health Assessment of Wind Turbine Based on Operational Condition Recognition. Trans. Inst. Meas. Control 2019, 41, 2970–2981. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Cheng, M. Application of Multi-Class Fuzzy Support Vector Machine Classifier for Fault Diagnosis of Wind Turbine. Fuzzy Sets Syst. 2016, 297, 128–140. [Google Scholar] [CrossRef]
- Han, S.; Li, J.; Liu, Y. Tabu Search Algorithm Optimized ANN Model for Wind Power Prediction with NWP. Energy Procedia 2011, 12, 733–740. [Google Scholar] [CrossRef]
- Qian, P.; Zhang, D.; Tian, X.; Si, Y.; Li, L. A Novel Wind Turbine Condition Monitoring Method Based on Cloud Computing. Renew. Energy 2019, 135, 390–398. [Google Scholar] [CrossRef]
- Wang, X.B.; Yang, Z.X.; Wong, P.K.; Deng, C. Novel Paralleled Extreme Learning Machine Networks for Fault Diagnosis of Wind Turbine Drivetrain. Memet. Comput. 2019, 11, 127–142. [Google Scholar] [CrossRef]
- Pashazadeh, V.; Salmasi, F.R.; Araabi, B.N. Data Driven Sensor and Actuator Fault Detection and Isolation in Wind Turbine Using Classifier Fusion. Renew. Energy 2018, 116, 99–106. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. A Study of Various Blade Fault Conditions on a Wind Turbine Using Vibration Signals through Histogram Features. J. Eng. Sci. Technol. 2018, 13, 102–121. [Google Scholar]
- Fadda, M.L.; Moussaoui, A. Hybrid SOM–PCA Method for Modeling Bearing Faults Detection and Diagnosis. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 268. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Li, L.; Liu, C. Wind Turbines Abnormality Detection through Analysis of Wind Farm Power Curves. Measurement 2016, 93, 178–188. [Google Scholar] [CrossRef]
- Ben Ali, J.; Saidi, L.; Harrath, S.; Bechhoefer, E.; Benbouzid, M. Online Automatic Diagnosis of Wind Turbine Bearings Progressive Degradations under Real Experimental Conditions Based on Unsupervised Machine Learning. Appl. Acoust. 2018, 132, 167–181. [Google Scholar] [CrossRef]
- Wan, X.J.; Liu, L.; Xu, Z.; Xu, Z. Gearbox Fault Diagnosis Based on Selective Integrated Soft Competitive Learning Fuzzy Adaptive Resonance Theory. J. Comput. Inf. Sci. Eng. 2019, 19, 011008. [Google Scholar] [CrossRef]
- Monteiro, R.P.; Cerrada, M.; Cabrera, D.R.; Sánchez, R.V.; Bastos-Filho, C.J.A. Using a Support Vector Machine Based Decision Stage to Improve the Fault Diagnosis on Gearboxes. Comput. Intell. Neurosci. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Grezmak, J.; Wang, P.; Sun, C.; Gao, R.X. Explainable Convolutional Neural Network for Gearbox Fault Diagnosis. Procedia CIRP 2019, 80, 476–481. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep Learning and Its Applications to Machine Health Monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Helbing, G.; Ritter, M. Deep Learning for Fault Detection in Wind Turbines. Renew. Sustain. Energy Rev. 2018, 98, 189–198. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, X.; Zou, J. The Optimized Deep Belief Networks with Improved Logistic Sigmoid Units and Their Application in Fault Diagnosis for Planetary Gearboxes of Wind Turbines. IEEE Trans. Ind. Electron. 2019, 66, 3814–3824. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Wang, Y. An Intelligent Diagnosis Scheme Based on Generative Adversarial Learning Deep Neural Networks and Its Application to Planetary Gearbox Fault Pattern Recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Yu, J. A Selective Deep Stacked Denoising Autoencoders Ensemble with Negative Correlation Learning for Gearbox Fault Diagnosis. Comput. Ind. 2019, 108, 62–72. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Deep Learning-Based Intelligent Fault Diagnosis Methods toward Rotating Machinery. IEEE Access 2020, 8, 9335–9346. [Google Scholar] [CrossRef]
- Dong, S.; He, K.; Tang, B. The Fault Diagnosis Method of Rolling Bearing under Variable Working Conditions Based on Deep Transfer Learning. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–13. [Google Scholar] [CrossRef]
- Mi, J.; Chu, M.; Hou, Y.; Jin, J.; Huang, W.; Xiang, T.; Wu, D. A Fault Diagnosis Method for Rolling Bearing Based on Deep Adversarial Transfer Learning With Transferability Measurement. IEEE Sens. J. 2024, 24, 984–994. [Google Scholar] [CrossRef]
- Li, D.; Cai, Z.; Qin, B.; Deng, L. Signal Frequency Domain Analysis and Sensor Fault Diagnosis Based on Artificial Intelligence. Comput. Commun. 2020, 160, 71–80. [Google Scholar] [CrossRef]
- Ogaili, A.A.F.; Hamzah, M.N.; Jaber, A.A. Enhanced Fault Detection of Wind Turbine Using EXtreme Gradient Boosting Technique Based on Nonstationary Vibration Analysis. J. Fail. Anal. Prev. 2024, 24, 877–895. [Google Scholar] [CrossRef]
- Ismail, A.; Saidi, L.; Sayadi, M. Wind Turbine Power Converter Fault Diagnosis Using DC-Link Voltage Time–Frequency Analysis. Wind Eng. 2019, 43, 329–343. [Google Scholar] [CrossRef]
- Zappalá, D.; Tavner, P.J.; Crabtree, C.J.; Sheng, S. Side-Band Algorithm for Automatic Wind Turbine Gearbox Fault Detection and Diagnosis. IET Renew. Power Gener. 2014, 8, 380–389. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, P.; Sheng, S.; Twomey, J.M. A Two-Stage Diagnosis Framework for Wind Turbine Gearbox Condition Monitoring. Int. J. Progn. Health Manag. 2013, 4, 21–31. [Google Scholar] [CrossRef]
- Igarashi, T.; Hamada, H. Studies on the Vibration and Sound of Defective Rolling Bearings: First Report: Vibration of Ball Bearings with One Defect. Bull. JSME 1982, 25, 994–1001. [Google Scholar] [CrossRef]
- Igarashi, T.; Yabe, S. Studies on the Vibration and Sound of Defective Rolling Bearings: Second Report: Sound of Ball Bearings with One Defect. Bull. JSME 1983, 26, 1791–1798. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A Review on Machinery Diagnostics and Prognostics Implementing Condition-Based Maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Du, Y.; Wang, X. Research on Fault Detection of High Voltage Inverter Based on STFT. In Proceedings of the 2010 Chinese Control and Decision Conference, CCDC 2010, Xuzhou, China, 26–28 May 2010. [Google Scholar]
- Avdaković, S.; Muftić Dedović, M.; Sadiković, E.; Duran, E.; Šiljak, A. Fault Diagnostics in Wind Turbines Utilizing Advanced Signal Processing Techniques—A Literature Review. Lect. Notes Netw. Syst. 2024, 1143, 731–748. [Google Scholar] [CrossRef]
- Janeliukstis, R. Continuous Wavelet Transform-Based Method for Enhancing Estimation of Wind Turbine Blade Natural Frequencies and Damping for Machine Learning Purposes. Measurement 2021, 172, 108897. [Google Scholar] [CrossRef]
- Heydari, A.; Garcia, D.A.; Fekih, A.; Keynia, F.; Tjernberg, L.B.; De Santoli, L. A Hybrid Intelligent Model for the Condition Monitoring and Diagnostics of Wind Turbines Gearbox. IEEE Access 2021, 9, 89878–89890. [Google Scholar] [CrossRef]
- Li, Q.; Hu, W.; Peng, E.; Liang, S.Y. Multichannel Signals Reconstruction Based on Tunable Q-Factor Wavelet Transform-Morphological Component Analysis and Sparse Bayesian Iteration for Rotating Machines. Entropy 2018, 20, 263. [Google Scholar] [CrossRef]
- Peng, Z.K.; Chu, F.L.; Tse, P.W. Singularity Analysis of the Vibration Signals by Means of Wavelet Modulus Maximal Method. Mech. Syst. Signal Process. 2007, 21, 780–794. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind Turbine Condition Monitoring: Technical and Commercial Challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Yen, N.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A 1996, 454, 903–995. [Google Scholar] [CrossRef]
- Qian, H.; Dongxiang, J.; Liangyou, H. Application of Hilbert-Huang Transform Method on Fault Diagnosis for Wind Turbine Rotor. Key Eng. Mater. 2009, 413–414, 159–166. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. Hilbert-Huang Transform and Its Applications; World Scientific Publishing Company: Singapore, 2005. [Google Scholar]
- Huang, N.E.; Shen, S.S.P. Hilbert-Huang Transform and Its Applications, 2nd ed.; World Scientific Publishing Company: Singapore, 2014; Volume 16. [Google Scholar]
- Kažys, R.; Tumšys, O.; Pagodinas, D. Ultrasonic Detection of Defects in Strongly Attenuating Structures Using the Hilbert-Huang Transform. NDT E Int. 2008, 41, 457–466. [Google Scholar] [CrossRef]
- Li, Q.F.; Wang, Y.; Xi, L.Y. Research on Ultrasonic Testing of Coarse-Grain Materials with Hilbert-Huang Transform. Adv. Mater. Res. 2013, 820, 97–101. [Google Scholar] [CrossRef]
- Liu, B.; Huang, P.; Hou, D.; Chen, X.; Zhang, G. Application of Hilbert-Huang Transform for Defect Recognition in Pulsed Eddy Current Testing. Nondestruct. Test. Eval. 2015, 30, 233–251. [Google Scholar] [CrossRef]
- Huang, S.; Wang, S. The Electromagnetic Ultrasonic Guided Wave Testing. In New Technologies in Electromagnetic Non-Destructive Testing; Springer: Singapore, 2016. [Google Scholar]
- Al Ahmar, E.; Choqueuse, V.; Benbouzid, M.E.H.; Amirat, Y.; El Assad, J.; Karam, R.; Farah, S. Advanced Signal Processing Techniques for Fault Detection and Diagnosis in a Wind Turbine Induction Generator Drive Train: A Comparative Study. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, ECCE 2010—Proceedings, Atlanta, GA, USA, 12–16 September 2010; pp. 3576–3581. [Google Scholar] [CrossRef]
- Lu, D.; Qiao, W.; Gong, X.; Qu, L. Current-Based Fault Detection for Wind Turbine Systems via Hilbert-Huang Transform. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Wang, Y.; Ma, X.; Qian, P. Wind Turbine Fault Detection and Identification Through PCA-Based Optimal Variable Selection. IEEE Trans. Sustain. Energy 2018, 9, 1627–1635. [Google Scholar] [CrossRef]
- Sedghi, S.; Dastfan, A.; Ahmadyfard, A. Fault Detection of a Seven Level Modular Multilevel Inverter via Voltage Histogram and Neural Network. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia: “Green World with Power Electronics”, ICPE 2011-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011. [Google Scholar]
- Tan, Y.; Zhang, H.; Zhou, Y. Fault Detection Method for Permanent Magnet Synchronous Generator Wind Energy Converters Using Correlation Features among Three-Phase Currents. J. Mod. Power Syst. Clean Energy 2020, 8, 168–178. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, L.; Zhang, Y.; Yin, Z. Research on AC Arc Fault Characteristics Based on the Difference between Adjacent Current Cycle. In Proceedings of the 2019 Prognostics and System Health Management Conference, PHM-Qingdao 2019, Qingdao, China, 25–27 October 2019. [Google Scholar]
- Chen, W.; Bazzi, A.M. Logic-Based Methods for Intelligent Fault Diagnosis and Recovery in Power Electronics. IEEE Trans. Power Electron. 2017, 32, 5573–5589. [Google Scholar] [CrossRef]
- Baghli, M.; Delpha, C.; Diallo, D.; Hallouche, A.; Mba, D.; Wang, T. Three-Level NPC Inverter Incipient Fault Detection and Classification Using Output Current Statistical Analysis. Energies 2019, 12, 1372. [Google Scholar] [CrossRef]
- Yuan, Y.; Chai, Y.; Qu, J.; Yang, Z.; Xu, S. Circuit Fault Diagnosis Method of Wind Power Converter with VMD-SVM. In Proceedings of the Chinese Control Conference, CCC, Chengdu, China, 27–29 July 2016; Volume 2016. [Google Scholar]
- Huang, Z.; Wang, Z.; Yao, X.; Zhang, H. Multi-Switches Fault Diagnosis Based on Small Low-Frequency Data for Voltage-Source Inverters of PMSM Drives. IEEE Trans. Power Electron. 2019, 34, 6845–6857. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Zhang, H. A Diagnosis Algorithm for Multiple Open-Circuited Faults of Microgrid Inverters Based on Main Fault Component Analysis. IEEE Trans. Energy Convers. 2018, 33, 925–937. [Google Scholar] [CrossRef]
- Zhang, X.X. Fault Diagnosis for PWM Inverter Based on LMD. In Proceedings of the Proceedings—2019 4th International Conference on Mechanical, Control and Computer Engineering, ICMCCE 2019, Hohhot, China, 24–26 October 2019. [Google Scholar]
- Zivot, E.; Wang, J. Modeling Financial Time Series with S-PLUS®, 2nd ed.; Springer: New York, NY, USA, 2006; ISBN 0387279652. [Google Scholar]
- Engle, R.F.; Granger, C.W.J. Co-Integration and Error Correction: Representation, Estimation, and Testing. Appl. Econom. 2015, 39, 107–135. [Google Scholar] [CrossRef]
- Johansen, S. Statistical Analysis of Cointegration Vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Cross, E.J.; Worden, K.; Chen, Q. Cointegration: A Novel Approach for the Removal of Environmental Trends in Structural Health Monitoring Data. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2712–2732. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Cointegration Approach for Temperature Effect Compensation in Lamb-Wave-Based Damage Detection. Smart Mater. Struct. 2013, 22, 095002. [Google Scholar] [CrossRef]
- Tabrizi, A.A.; Al-Bugharbee, H.; Trendafilova, I.; Garibaldi, L. A Cointegration-Based Monitoring Method for Rolling Bearings Working in Time-Varying Operational Conditions. Meccanica 2017, 52, 1201–1217. [Google Scholar] [CrossRef]
- Salvetti, M.; Sbarufatti, C.; Cross, E.; Corbetta, M.; Worden, K.; Giglio, M. On the Performance of a Cointegration-Based Approach for Novelty Detection in Realistic Fatigue Crack Growth Scenarios. Mech. Syst. Signal Process. 2019, 123, 84–101. [Google Scholar] [CrossRef]
- He, H.; Wang, W.; Zhang, X. Frequency Modification of Continuous Beam Bridge Based on Co-Integration Analysis Considering the Effect of Temperature and Humidity. Struct. Health Monit. 2019, 18, 376–389. [Google Scholar] [CrossRef]
- Sousa Tomé, E.; Pimentel, M.; Figueiras, J. Damage Detection under Environmental and Operational Effects Using Cointegration Analysis—Application to Experimental Data from a Cable-Stayed Bridge. Mech. Syst. Signal Process. 2020, 135, 106386. [Google Scholar] [CrossRef]
- Turrisi, S.; Cigada, A.; Zappa, E. A Cointegration-Based Approach for Automatic Anomalies Detection in Large-Scale Structures. Mech. Syst. Signal Process. 2022, 166, 108483. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Cointegration and How It Works for Structural Health Monitoring. Measurement 2023, 209, 112503. [Google Scholar] [CrossRef]
- Dao, P.B. Lamb Wave-Based Structural Damage Detection: A Time Series Approach Using Cointegration. Materials 2023, 16, 6894. [Google Scholar] [CrossRef] [PubMed]
- Długosz, J.; Dao, P.B.; Staszewski, W.J.; Uhl, T. Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images. Sensors 2024, 24, 1980. [Google Scholar] [CrossRef] [PubMed]
- Dao, P.B.; Staszewski, W.J.; Barszcz, T.; Uhl, T. Condition Monitoring and Fault Detection in Wind Turbines Based on Cointegration Analysis of SCADA Data. Renew. Energy 2018, 116, 107–122. [Google Scholar] [CrossRef]
- Dao, P. Condition Monitoring of Wind Turbines Based on Cointegration Analysis of Gearbox and Generator Temperature Data. Diagnostyka 2018, 19, 63–71. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J.; Uhl, T. Operational Condition Monitoring of Wind Turbines Using Cointegration Method. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Cham, Switzerland, 2018; Volume 9, pp. 223–233. [Google Scholar]
- Sun, X.; Xue, D.; Li, R.; Li, X.; Cui, L.; Zhang, X.; Wu, W. Research on Condition Monitoring of Key Components in Wind Turbine Based on Cointegration Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2019, 575, 012015. [Google Scholar]
- Zhang, B.; Zhang, C.; Duan, H.; Ma, Y.; Li, J.; Cui, L. Realization of Condition Monitoring of Gear Box of Wind Turbine Based on Cointegration Analysis. In Advances in Asset Management and Condition Monitoring. Smart Innovation, Systems and Technologies; Springer: Cham, Switzerland, 2020; Volume 166, pp. 281–291. [Google Scholar]
- Qadri, B.A.; Ulriksen, M.D.; Damkilde, L.; Tcherniak, D. Cointegration for Detecting Structural Blade Damage in an Operating Wind Turbine: An Experimental Study. In Dynamics of Civil Structures; Conference Proceedings of the Society for Experimental Mechanics Series; Taylor & Francis Group: Abingdon, UK, 2020; pp. 173–180. [Google Scholar] [CrossRef]
- Xu, M.; Li, J.; Wang, S.; Yang, N.; Hao, H. Damage Detection of Wind Turbine Blades by Bayesian Multivariate Cointegration. Ocean. Eng. 2022, 258, 111603. [Google Scholar] [CrossRef]
- Knes, P.; Dao, P.B. Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach. Energies 2024, 17, 5055. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. A Hierarchical Modeling Strategy for Condition Monitoring and Fault Diagnosis of Wind Turbine Using SCADA Data. Measurement 2024, 227, 114325. [Google Scholar] [CrossRef]
- Kuai, H.; Civera, M.; Coletta, G.; Chiaia, B.; Surace, C. Cointegration Strategy for Damage Assessment of Offshore Platforms Subject to Wind and Wave Forces. Ocean Eng. 2024, 304, 117692. [Google Scholar] [CrossRef]
- Zolna, K.; Dao, P.B.; Staszewski, W.J.; Barszcz, T. Nonlinear Cointegration Approach for Condition Monitoring of Wind Turbines. Math. Probl. Eng. 2015, 2015, 978156. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Tan, L.S.L. Analytic Natural Gradient Updates for Cholesky Factor in Gaussian Variational Approximation. J. R. Stat. Soc. Ser. B Stat. Methodol. 2025, 87, 930–956. [Google Scholar] [CrossRef]
- Seichepine, N.; Essid, S.; Févotte, C.; Cappé, O. Piecewise Constant Nonnegative Matrix Factorization. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing—Proceedings, Florence, Italy, 4–9 May 2014; pp. 6721–6725. [Google Scholar] [CrossRef]
- Desobry, F.; Davy, M.; Doncarli, C. An Online Kernel Change Detection Algorithm. IEEE Trans. Signal Process. 2005, 53, 2961–2974. [Google Scholar] [CrossRef]
- Angelosante, D.; Giannakis, G.B. Group Lassoing Change-Points in Piecewise-Constant AR Processes. EURASIP J. Adv. Signal Process. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Harchaoui, Z.; Vallet, F.; Lung-Yut-Fong, A.; Cappé, O. A Regularized Kernel-Based Approach to Unsupervised Audio Segmentation. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing—Proceedings, Taipei, Taiwan, 19–24 April 2009; pp. 1665–1668. [Google Scholar] [CrossRef]
- Koo, B.; Seo, M.H. Structural-Break Models under Mis-Specification: Implications for Forecasting. J. Econ. 2013, 188, 166–181. [Google Scholar] [CrossRef]
- Frick, K.; Munk, A.; Sieling, H. Multiscale Change Point Inference. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 495–580. [Google Scholar] [CrossRef]
- Yiu, A.; Fong, E.; Holmes, C.; Rousseau, J. Semiparametric Posterior Corrections. J. R. Stat. Soc. Ser. B Stat. Methodol. 2025, 87, 1025–1054. [Google Scholar] [CrossRef]
- Lavielle, M.; Teyssière, G. Adaptive Detection of Multiple Change-Points in Asset Price Volatility. In Long Memory in Economics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 129–156. ISBN 354022394X. [Google Scholar]
- Chen, J.; Gupta, A.K. Parametric Statistical Change Point Analysis: With Applications to Genetics, Medicine, and Finance; Birkhäuser: Boston, MA, USA, 2014; pp. 1–273. [Google Scholar] [CrossRef]
- Franzke, C. Multi-Scale Analysis of Teleconnection Indices: Climate Noise and Nonlinear Trend Analysis. Nonlinear Process. Geophys. 2009, 16, 65–76. [Google Scholar] [CrossRef]
- Lung-Yut-Fong, A.; Lévy-Leduc, C.; Cappé, O. Distributed Detection/Localization of Change-Points in High-Dimensional Network Traffic Data. Stat. Comput. 2012, 22, 485–496. [Google Scholar] [CrossRef]
- Lévy-Leduc, C.; Roueff, F. Detection and Localization of Change-Points in High-Dimensional Network Traffic Data. Ann. Appl. Stat. 2009, 3, 637–662. [Google Scholar] [CrossRef]
- Maleki, S.; Bingham, C.; Zhang, Y. Development and Realisation of Changepoint Analysis for the Detection of Emerging Faults on Industrial Systems. IEEE Trans. Ind. Inf. 2016, 12, 1180–1187. [Google Scholar] [CrossRef]
- Rimkus, M.; Kokoszka, P.; Prabakar, K.; Wang, H. Toward Statistical Real-Time Power Fault Detection. Commun. Stat. Case Stud. Data Anal. Appl. 2023, 9, 196–217. [Google Scholar] [CrossRef]
- Garramiola, F.; Poza, J.; Madina, P.; Del Olmo, J.; Ugalde, G. A Hybrid Sensor Fault Diagnosis for Maintenance in Railway Traction Drives. Sensors 2020, 20, 962. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Wang, K.S. Wind Turbine Fault Detection Based on SCADA Data Analysis Using ANN. Adv. Manuf. 2014, 2, 70–78. [Google Scholar] [CrossRef]
- Liu, W. Intelligent Fault Diagnosis of Wind Turbines Using Multi-Dimensional Kernel Domain Spectrum Technique. Measurement 2019, 133, 303–309. [Google Scholar] [CrossRef]
- Saravanan, V.; Siehien, P.; Yoo, S.; Van Dam, H.; Flynn, T.; Kelly, C.; Ibrahim, K.Z. An Evaluation of Real-Time Adaptive Sampling Change Point Detection Algorithm Using KCUSUM. arXiv 2024, arXiv:2402.10291. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, X. Kullback-Leibler Divergence Based Wind Turbine Fault Feature Extraction. In Proceedings of the ICAC 2018—2018 24th IEEE International Conference on Automation and Computing: Improving Productivity through Automation and Computing, Newcastle Upon Tyne, UK, 6–7 September 2018. [Google Scholar]
- Ji, S.; Zhang, Z.; Ying, S.; Wang, L.; Zhao, X.; Gao, Y. Kullback-Leibler Divergence Metric Learning. IEEE Trans. Cybern. 2022, 52, 2047–2058. [Google Scholar] [CrossRef]
- Jaramillo, F.; Gutiérrez, J.M.; Orchard, M.; Guarini, M.; Astroza, R. A Bayesian Approach for Fatigue Damage Diagnosis and Prognosis of Wind Turbine Blades. Mech. Syst. Signal Process. 2022, 174, 109067. [Google Scholar] [CrossRef]
- Tsaknaki, I.-Y.; Lillo, F.; Mazzarisi, P. Bayesian Autoregressive Online Change-Point Detection with Time-Varying Parameters. Commun. Nonlinear Sci. Numer. Simul. 2024, 142, 108500. [Google Scholar] [CrossRef]
- Li, X.; Li, P.; Jiang, L.; Cao, Y. Fault Diagnosis Method of Asynchronous Motor Based on Heterogeneous Information Feature Fusion. Yi Qi Yi Biao Xue Bao/Chin. J. Sci. Instrum. 2013, 34, 227–233. [Google Scholar]
- Zhang, J.; Sun, H.; Sun, Z.; Dong, W.; Dong, Y. Fault Diagnosis of Wind Turbine Power Converter Considering Wavelet Transform, Feature Analysis, Judgment and BP Neural Network. IEEE Access 2019, 7, 179799–179809. [Google Scholar] [CrossRef]
- Heibati, R.; Alipour-Sarabi, R.; Mohammad, S.; Bathaee, T. A Survey on the Most Practical Signal Processing Methods in Conditional Monitoring in Wind Turbines. Sci. Iran. 2023, in press. [Google Scholar] [CrossRef]
- Maurya, M.R.; Rengaswamy, R.; Venkatasubramanian, V. Fault Diagnosis Using Dynamic Trend Analysis: A Review and Recent Developments. Eng. Appl. Artif. Intell. 2007, 20, 133–146. [Google Scholar] [CrossRef]
- Alexandrov, T.; Bianconcini, S.; Dagum, E.B.; Maass, P.; McElroy, T.S. A Review of Some Modern Approaches to the Problem of Trend Extraction. Econ. Rev. 2012, 31, 593–624. [Google Scholar] [CrossRef]
- Ma, B.; Zhao, Y.; Zhang, Y.; Jiang, Q.L.; Hou, X.Q. Machinery Early Fault Detection Based on Dirichlet Process Mixture Model. IEEE Access 2019, 7, 89226–89233. [Google Scholar] [CrossRef]
- Feng, X.; Lin, S.; Liu, W.; Liang, W.; Liu, M. Distributionally Robust Optimal Dispatch of Offshore Wind Farm Cluster Connected by VSC-MTDC Considering Wind Speed Correlation. CSEE J. Power Energy Syst. 2023, 9, 1021–1035. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K.; Qian, X.; Gendeel, M. Robust Fault-Detection Based on Residual K–L Divergence for Wind Turbines. IET Renew. Power Gener. 2019, 13, 2400–2408. [Google Scholar] [CrossRef]
- Philippe, W.P.J.; Zhang, S.; Eftekharnejad, S.; Ghosh, P.K.; Varshney, P.K. Mixed Copula-Based Uncertainty Modeling of Hourly Wind Farm Production for Power System Operational Planning Studies. IEEE Access 2020, 8, 138569–138583. [Google Scholar] [CrossRef]
- Wang, M.; Shi, Z.; Luo, W.; Sui, Y.; Wu, D. Distributionally Robust Optimal Scheduling of Integrated Energy Systems Including Hydrogen Fuel Cells Considering Uncertainties. Energy Rep. 2023, 10, 1575–1588. [Google Scholar] [CrossRef]
- Avendaño-Valencia, L.D.; Abdallah, I.; Chatzi, E. Virtual Fatigue Diagnostics of Wake-Affected Wind Turbine via Gaussian Process Regression. Renew. Energy 2021, 170, 539–561. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, X. A Hybrid LSTM-KLD Approach to Condition Monitoring of Operational Wind Turbines. Renew. Energy 2022, 181, 554–566. [Google Scholar] [CrossRef]
- Teixeira, R.; O’Connor, A.; Nogal, M. Probabilistic Sensitivity Analysis of Offshore Wind Turbines Using a Transformed Kullback-Leibler Divergence. Struct. Saf. 2019, 81, 101860. [Google Scholar] [CrossRef]
- Wanjiku, R.N.; Nderu, L.; Kimwele, M. Dynamic Fine-Tuning Layer Selection Using Kullback–Leibler Divergence. Eng. Rep. 2023, 5, e12595. [Google Scholar] [CrossRef]
- Asperti, A.; Trentin, M. Balancing Reconstruction Error and Kullback-Leibler Divergence in Variational Autoencoders. IEEE Access 2020, 8, 199440–199448. [Google Scholar] [CrossRef]
- Van Erven, T.; Harrëmos, P. Rényi Divergence and Kullback-Leibler Divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z.; Chen, G.; Pedrycz, W.; Liu, L.; Aggarwal, M. Generalized TODIM Method Based on Symmetric Intuitionistic Fuzzy Jensen–Shannon Divergence. Expert. Syst. Appl. 2024, 237, 121554. [Google Scholar] [CrossRef]
- Osán, T.M.; Bussandri, D.G.; Lamberti, P.W. Quantum Metrics Based upon Classical Jensen–Shannon Divergence. Phys. A Stat. Mech. Its Appl. 2022, 594, 127001. [Google Scholar] [CrossRef]
- Virosztek, D. The Metric Property of the Quantum Jensen-Shannon Divergence. Adv. Math. 2021, 380, 107595. [Google Scholar] [CrossRef]
- Nielsen, F. On a Generalization of the Jensen-Shannon Divergence and the Jensen-Shannon Centroid. Entropy 2020, 22, 221. [Google Scholar] [CrossRef] [PubMed]
- Erdman, C.; Emerson, J.W. Bcp: An R Package for Performing a Bayesian Analysis of Change Point Problems. J. Stat. Softw. 2008, 23, 1–13. [Google Scholar] [CrossRef]
- Xu, Q.; Lu, S.; Zhai, Z.; Jiang, C. Adaptive Fault Detection in Wind Turbine via RF and CUSUM. IET Renew. Power Gener. 2020, 14, 1789–1796. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M.R. An Improved Process Monitoring by Mixed Multivariate Memory Control Charts: An Application in Wind Turbine Field. Comput. Ind. Eng. 2020, 142, 106343. [Google Scholar] [CrossRef]
- Gálvez-Carrillo, M.; Kinnaert, M. Sensor Fault Detection and Isolation in Doubly-Fed Induction Generators Accounting for Parameter Variations. Renew. Energy 2011, 36, 1447–1457. [Google Scholar] [CrossRef]
- Chesterman, X.; Verstraeten, T.; Daems, P.J.; Perez Sanjines, F.; Nowé, A.; Helsen, J. The Detection of Generator Bearing Failures on Wind Turbines Using Machine Learning Based Anomaly Detection. J. Phys. Conf. Ser. 2022, 2265, 032066. [Google Scholar] [CrossRef]
- Shaheen, B.W.; Hanieh, A.A.; Németh, I. Fault Detection of a Wind Turbine’s Gearbox, Based on Power Curve Modeling and an on-Line Statistical Change Detection Algorithm. Acta Polytech. Hung. 2021, 18, 175–196. [Google Scholar] [CrossRef]
- Liu, F.; Gao, S.; Tian, Z.; Liu, D. A New Time-Frequency Analysis Method Based on Single Mode Function Decomposition for Offshore Wind Turbines. Mar. Struct. 2020, 72, 102782. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, T.; Chu, F. Meshing Frequency Modulation Assisted Empirical Wavelet Transform for Fault Diagnosis of Wind Turbine Planetary Ring Gear. Renew. Energy 2019, 132, 1373–1388. [Google Scholar] [CrossRef]
- Strömbergsson, D.; Marklund, P.; Berglund, K.; Larsson, P.E. Bearing Monitoring in the Wind Turbine Drivetrain: A Comparative Study of the FFT and Wavelet Transforms. Wind Energy 2020, 23, 1381–1393. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, J.; Qin, M.; Feng, J.; Li, M. Modulation Signal Detection of Wind Turbine’s Vibration Based on Feature Extraction of the Energy Spectrum. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2014, 34, 166–171. [Google Scholar] [CrossRef]
- Murph, A.C.; Storlie, C.B.; Wilson, P.M.; Williams, J.P.; Hannig, J. Bayes Watch: Bayesian Change-Point Detection for Process Monitoring with Fault Detection. arXiv 2023, arXiv:2310.02940. [Google Scholar] [CrossRef]
- Ogaili, A.A.F.; Abdulhady Jaber, A.; Hamzah, M.N. Wind Turbine Blades Fault Diagnosis Based on Vibration Dataset Analysis. Data Brief 2023, 49, 109414. [Google Scholar] [CrossRef] [PubMed]
- Ali, W.; El-Thalji, I.; Giljarhus, K.E.T.; Delimitis, A. Developing Predictive Maintenance Framework for Wind Turbine Blade Erosion: State of the Art and Concept Analysis. In Proceedings of the 2024 IEEE International Conference on Industrial Engineering and Engineering Management, Bangkok, Thailand, 15–18 December 2024; pp. 69–73. [Google Scholar] [CrossRef]
- Hızal, Ç.; Turan, G.; Aktaş, E.; Ceylan, H. A Mode Shape Assembly Algorithm by Using Two Stage Bayesian Fast Fourier Transform Approach. Mech. Syst. Signal Process. 2019, 134, 106328. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, S.; Jing, X.; Peng, Y.; Wu, H.; Kwok, N. Damage Detection Techniques for Wind Turbine Blades: A Review. Mech. Syst. Signal Process. 2020, 141, 106445. [Google Scholar] [CrossRef]
- Sharma, V. A Review on Vibration-Based Fault Diagnosis Techniques for Wind Turbine Gearboxes Operating Under Nonstationary Conditions. J. Inst. Eng. (India) Ser. C 2021, 102, 507–523. [Google Scholar] [CrossRef]
- Miao, Q.; Makis, V. Condition Monitoring and Classification of Rotating Machinery Using Wavelets and Hidden Markov Models. Mech. Syst. Signal Process. 2007, 21, 840–855. [Google Scholar] [CrossRef]
- Qian, P.; Ma, X.; Zhang, D. Estimating Health Condition of the Wind Turbine Drivetrain System. Energies 2017, 10, 1583. [Google Scholar] [CrossRef]
- Qin, S.; Wang, K.; Ma, X.; Wang, W.; Li, M. Ensemble Learning-Based Wind Turbine Fault Prediction Method with Adaptive Feature Selection. Commun. Comput. Inf. Sci. 2017, 728, 572–582. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Fan, Y.; Shangguan, L.; Yang, Y. A Review of Research on Wind Turbine Bearings’ Failure Analysis and Fault Diagnosis. Lubricants 2022, 11, 14. [Google Scholar] [CrossRef]
- Lan, J.; Chen, N.; Li, H.; Wang, X. A Review of Fault Diagnosis and Prediction Methods for Wind Turbine Pitch Systems. Int. J. Green Energy 2024, 21, 1613–1640. [Google Scholar] [CrossRef]
- Yang, C.; Qian, Z.; Pei, Y.; Wei, L. A Data-Driven Approach for Condition Monitoring of Wind Turbine Pitch Systems. Energies 2018, 11, 2142. [Google Scholar] [CrossRef]
- Nalisa Hanim Binti Shahrulhisham, N.; Hen Chong, K.; Yaw, C.T.; Koh, S.P. Application of Machine Learning Technique Using Support Vector Machine in Wind Turbine Fault Diagnosis. J. Phys. Conf. Ser. 2022, 2319, 12017. [Google Scholar] [CrossRef]
- Abouhnik, A.; Albarbar, A. Wind Turbine Blades Condition Assessment Based on Vibration Measurements and the Level of an Empirically Decomposed Feature. Energy Convers. Manag. 2012, 64, 606–613. [Google Scholar] [CrossRef]
- Song, C.; Zhang, N.; Shao, J.; Wang, Y.; Liu, X.; Jiang, C. Diagnosis of Wind Turbine Yaw System Based on Self-Attention–Long Short-Term Memory (LSTM). Electronics 2025, 14, 617. [Google Scholar] [CrossRef]
- Chou, J.S.; Tu, W.T. Failure Analysis and Risk Management of a Collapsed Large Wind Turbine Tower. Eng. Fail. Anal. 2011, 18, 295–313. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, R.; Li, J.; Jia, Z.; Yang, T.; Tao, T.; Guo, X.; Yang, Y.; Liu, S. Preliminary Test for 3D Surface Strain Measurement in the Tower and Foundation of Offshore Wind Turbines Using DOFS. Sensors 2023, 23, 6734. [Google Scholar] [CrossRef]
- Zhao, Q.; Yuan, Y.; Sun, W.; Fan, X.; Fan, P.; Ma, Z. Reliability Analysis of Wind Turbine Blades Based on Non-Gaussian Wind Load Impact Competition Failure Model. Measurement 2020, 164, 107950. [Google Scholar] [CrossRef]


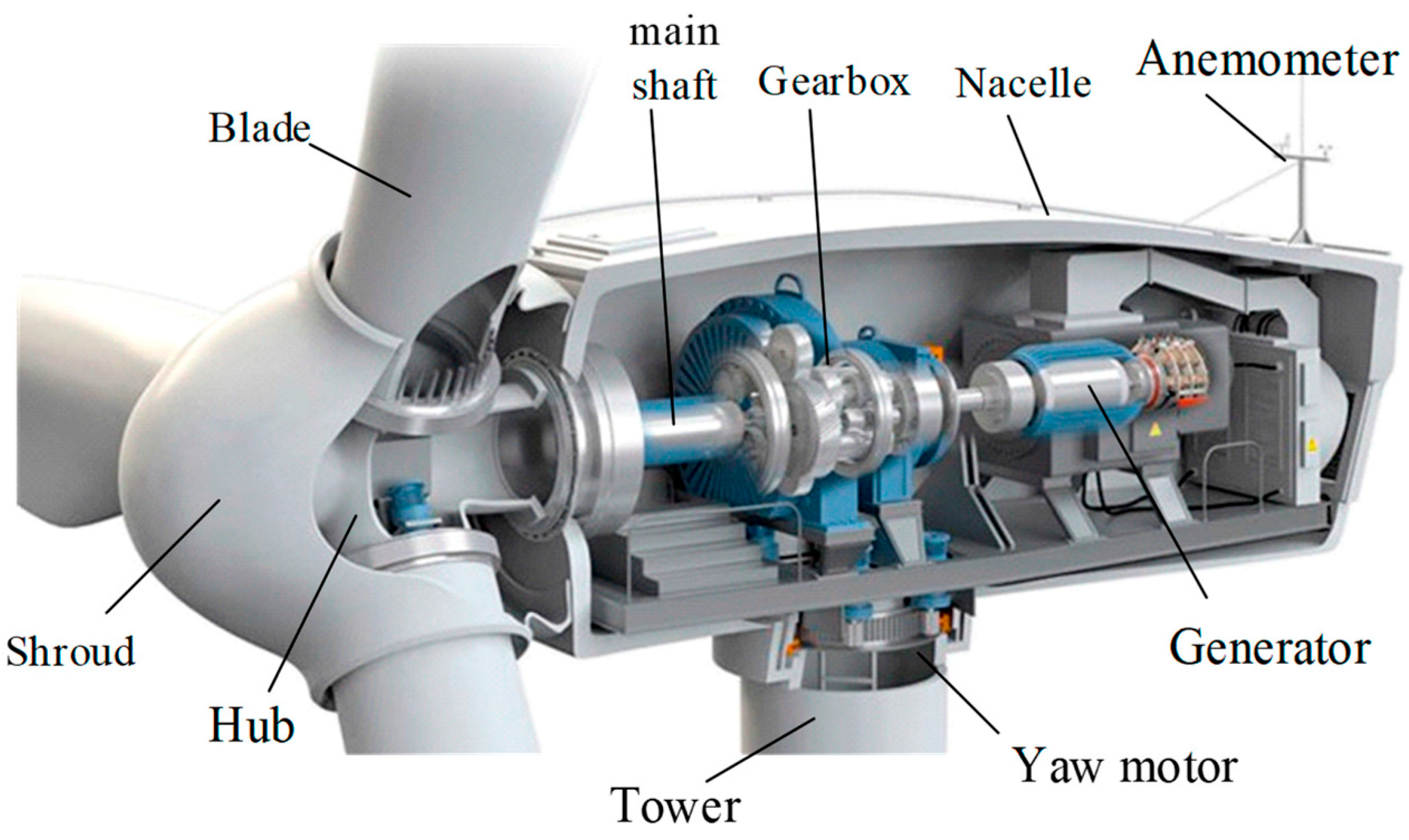

| Sr. No. | Author(s), Year | Brief Description | Focus Category | Ref. No. |
|---|---|---|---|---|
| 1 | García Márquez et al., 2012 | A survey of diagnosis methods as well as signal processing algorithms for the condition monitoring of wind turbines, but only up to signal-based methods, and without a thorough literature survey that would cover the full potential and limitations of the present techniques | Trend Monitoring | [51] |
| 2 | Purarjomandlangrudi et al., 2013 | A systematic but relatively brief literature review on signal-based diagnosis techniques used in wind turbine condition monitoring | Trend Monitoring | [52] |
| 3 | Schubel et al., 2013 | A relatively brief review of damage diagnosis techniques, specifically for structural health and cure monitoring in wind turbine blades | Trend Monitoring | [53] |
| 4 | Kusiak et al., 2013 | Survey of the wide range of issues involved in existing methodologies and techniques of wind speed forecast, system control, and the condition monitoring of wind turbines, whose primary drawback lies in being constrained to some signal-based techniques and lacking in providing an exhaustive literature survey on the specific subject of the condition monitoring of turbines | Trend Monitoring | [54] |
| 5 | Bindi et al., 2014 | A review of commercially available supervisory control and data acquisition (SCADA) systems and related analysis software for SCADA-based condition monitoring and optimisation of the performance of wind turbines, but without a systematic review of the literature beyond the commercially available SCADA-based systems themselves | Trend Monitoring | [55] |
| 6 | Tchakoua et al., 2014 | A discussion of the diagnosis techniques and maintenance tactics of the wind turbine, but the debate only involves the signal-based techniques, without adequate discussion of the failure processes of the different wind turbine parts | Trend Monitoring | [56] |
| 7 | Kaewniam et al., 2022 | A review of the literature on diagnosis procedures, covering various signal processing techniques, sensor technologies, and NDT approaches used for WTB damage identification and monitoring. | Trend Monitoring | [57] |
| 8 | Welte and Wang, 2014 | A brief account of methods and schemes of prognosis and life prediction of the parts of a wind turbine, which is relatively short, whose general, non-specialised-for-wind-turbines text is essential | Change Point Detection | [58] |
| 9 | Crabtree et al., 2014 | A survey of commercially available condition monitoring systems for wind turbines, but it misses a comprehensive review of literature beyond the commercial condition monitoring systems alone | Trend Monitoring | [59] |
| 10 | Wang et al., 2014 | A survey of SCADA-related condition monitoring methods in wind turbines, and the introduction of an intelligent system for the fault diagnosis and prognosis of wind turbines based on SCADA data, but confined to SCADA-related methods only, hence not providing an exhaustive review | Trend Monitoring | [60] |
| 11 | Antoniadou et al., 2015 | A short list of some of the relevant signal processing and machine learning methods applied in structural and condition monitoring of wind turbines, with some examples of application, but by no means an exhaustive survey | Trend Monitoring | [61] |
| 12 | Wymore et al., 2015 | A component-by-component analysis of a few diagnosis methods employed in the structural and condition monitoring of the key parts of a wind turbine, but covering only some of the signal-based methods | Trend Monitoring | [62] |
| 13 | Qiao and Lu, 2015 | A relatively broad literature review in two parts: (1) failure modes and characteristics of essential parts/subsystems of the main wind turbine, and (2) diagnosis/prognosis technologies and necessary signal processing technologies used in the condition monitoring of the wind turbine, but mainly a summary of the popular signal-based diagnosis technologies, while the model-based technologies or non-destructive condition monitoring technologies are very concisely summarised | Trend Monitoring | [63] |
| 14 | Kandukuri et al., 2016 | A review of diagnosis/prognosis techniques, which is mainly limited to some signal-based methods, and, in particular,, the condition monitoring of low-speed bearings and planetary gearboxes in wind turbines | Trend Monitoring | [64] |
| 15 | Azevedo et al., 2016 | A review of diagnosis/prognosis techniques taking into consideration the technical, economic, and operational challenges, but that applies only to specific signal-based techniques, and namely, the condition monitoring of bearings in wind turbines | Trend Monitoring | [65] |
| 16 | Yang et al., 2017 | A review of structural health monitoring techniques, which does not yet constitute a comprehensive review, is limited to some signal-based methods for wind turbine blades | Trend Monitoring | [66] |
| 17 | Uma Maheswari and Umamaheswari, 2017 | A review of drivetrain condition monitoring in wind turbines, however, is limited to the vibration monitoring technique, including non-stationary signal processing algorithms, and specifically for drivetrain components | Trend Monitoring | [67] |
| 18 | Tautz-Weinert and Watson, 2017 | A review of diagnosis techniques for wind turbine condition monitoring, however, is limited to SCADA-based techniques only | [68] | |
| 19 | Marugán et al., 2018 | A survey of the applications of artificial neural networks (ANNs) in wind energy systems for forecasting, design optimisation, fault diagnosis, and optimal control, but not a review of the literature further than the ANNs techniques and the condition monitoring in general | Trend Monitoring | [69] |
| 20 | Salameh et al., 2018 | A review of diagnosis techniques for wind turbine condition monitoring, but it is restricted to some signal-based methods, and specifically, the condition monitoring of gearboxes in wind turbines | Trend Monitoring | [70] |
| 21 | Abid et al., 2018 | A literature survey of prognosis methods applied to wind turbines, as well as an introduction to various prognosis stages, such as construction of health indicators, detection of degradation, and estimation of remaining useful life (RUL), but not the failure modes of various wind turbine parts, nor some crucial parts like rotor blades | Change Point Detection | [71] |
| 22 | Leite et al., 2018 | A review of prognosis techniques and RUL estimation methods for the critical components of wind turbines, but it does not address the failure modes of different wind turbine components | Trend Monitoring | [72] |
| 23 | Wei et al., 2019 | A review of the diagnosis and signal processing techniques of wind turbine condition monitoring, but only till some signal-related methods, that are, the condition monitoring of the gears, rotors, and bearings of the wind turbine | Trend Monitoring | [73] |
| 24 | Moeini et al., 2019 | A review of diagnosis techniques for wind turbine condition monitoring, but it only includes some signal-based methods, and the majority of non-destructive condition monitoring technologies are simply missing | Trend Monitoring | [74] |
| 25 | Zhang and Lu, 2019 | A review of the diagnosis technologies of wind turbine condition monitoring in three aspects of energy flow, information flow, and integrated O&M system, but no complete review, including some signal-based technologies without mentioning non-destructive technologies of condition monitoring | Trend Monitoring | [75] |
| 26 | Leahy et al., 2019 | A data quality problem survey for the aid of SCADA-based condition monitoring of wind turbines, while limiting the discussion of data quality problems, SCADA-based methods only | Trend Monitoring | [76] |
| 27 | Habibi et al., 2019 | A tutorial-style review on diagnosis techniques and fault-tolerant control methods used in wind turbines, which is limited to model-based techniques only | Change Point Detection | [77] |
| 28 | Liu and Zhang, 2020 | A survey of the failure modes and diagnosis methods of the bearings of wind turbines; however, the survey was only up to some signal-based techniques and particularly for the bearings (main bearings, gearbox bearings, generator bearings, blade bearings, and yaw bearings) | Trend Monitoring | [78] |
| 29 | Márquez F and, Papaelias M, 2020 | A survey of non-destructive condition monitoring technologies for the diagnosis of wind turbine blades, but the primary area of review, as its remit indicates, is the non-destructive technologies, and, in particular,, the wind turbine blades | Trend Monitoring | [79] |
| 30 | The current study | This study demonstrates how integrating tools from Trend Monitoring and Change Point Detection can improve condition monitoring and early fault detection of wind turbines | Trend Monitoring + Change Point Detection |
| Fault Diagnosis Technique | Description | Limitations of the Traditional Approach | Ref. No. |
|---|---|---|---|
| Model-Based | Uses mathematical models to simulate wind turbine behaviour and detect deviations indicating faults. | Highly complex models require significant computational power, making real-time applications particularly challenging. | [77] |
| Signal-Based | Analyses real-time signals (vibration, temperature, electromagnetic) and compares them with healthy reference signals. | Sensitive to sensor placement and noise, making it prone to false positives. | [89] |
| Knowledge-Based | Leverages historical failure data and machine learning classifiers to detect anomalies in turbine performance. | Requires extensive labelled failure data for training; lacks adaptability to unseen faults. | [90] |
| Methods | Input Data | Advantages | Disadvantages | Monitoring Components | Articles |
|---|---|---|---|---|---|
| Support Vector Machine (SVM) | Vibration signal, SCADA | Higher diagnostic accuracy with fewer samples. | Kernel function selection is critical, as it may converge to a local minimum. | Bearings, Gears, Blades | [104,105,106] |
| Decision Tree (DT) | Vibration signal, generator current signal | Good global optimisation and generalisation capabilities. | Easily overfits; cannot build active networks. | Gears, Generation system | [107,108] |
| Bayesian Methods (Bayes) | Vibration signal, SCADA | Deepens fault understanding; needs minimal data processing. | Sensitive to error categories; relies on hypothetical models. | Gearbox, Blades, Bearings | [109,110,111] |
| Hidden Markov Model (HMM) | Vibration signal | Fast fault diagnosis with low computational complexity. | Cannot fully utilise historical data; ambiguous topology in diagnosis. | Bearings | [112,113,114] |
| Random Forest (RF) | Vibration signal | Robust and not sensitive to outliers. | Complex training; high computational cost. | Bearings, Gearbox | [115,116] |
| Classification Algorithms (CA) | Vibration signal, SCADA | Handles massive data efficiently. | Requires predefined categories; relies on cluster selection. | Bearings, Gearbox | [117,118] |
| Back Propagation Neural Network (BPNN) | Vibration signal | Self-learning with fault tolerance. | Slow convergence speed; may overfit. | Gearbox, Transmission chain, Generator fault | [119,120] |
| Extreme Learning Machine (ELM) | Vibration signal, SCADA | Fast learning speed and adapts to new situations. | Limited learning due to a single hidden layer. | Gearbox, Transmission chain | [121,122] |
| Radial Basis Function Neural Network (RBFNN) | Vibration signal | Strong nonlinear fitting and fast convergence. | Performance depends on data quality and sample selection. | Blades, Actuators | [123,124] |
| Self-Organising Map (SOM) | Vibration signal, SCADA | Visualisation support with simple implementation. | High training cost. | Bearings, Gearbox | [125,126] |
| Adaptive Resonance Theory (ART) | Vibration signal | Learn new problems without prior data. | Losing information may occur. | Bearings, Gearbox | [127,128] |
| Convolutional Neural Network (CNN) | Vibration signal | Simplifies network complexity and avoids overfitting. | Requires large datasets, high computational cost, and fixed input length. | Bearings, Gearbox | [129,130] |
| Deep Belief Network (DBN) | Vibration signal, SCADA | Versatile, handles nonlinear high-dimensional data. | Handles only one-dimensional data; long computation time. | Gearbox | [131,132,133] |
| Stacked Autoencoder (SAE) | Vibration signal | No need for large datasets; overcomes gradient diffusion. | Long training time; risk of overfitting. | Bearings, Gearbox | [134,135] |
| Recurrent Neural Network (RNN) | Vibration signal | Diagnoses slow-developing faults and solves gradient disappearance. | No clear rules for selecting hidden neurons. | Bearings, Gearbox | [103,136] |
| Transfer Learning (TL) | Vibration signal, SCADA | High diagnostic accuracy under variable conditions; adaptive to new faults. | Negative transfer learning may occur. | Bearings, Gearbox | [137,138] |
| Feature | Trend Monitoring (TM) | Change Point Detection (CPD) | Integrated TM + CPD Approach |
|---|---|---|---|
| Detects What Changed? | Yes. TM methods analyse frequency shifts, amplitude changes, and transient fluctuations in wind turbine signals. | No. CPD does not describe what changed, only that a change has occurred. | Best of both. TM identifies what kind of fault is occurring, and CPD validates the significance of the change. |
| Detects When It Happened? | No. TM identifies trends over time but lacks precise timing accuracy. | Yes. CPD pinpoints the exact moment of change. | TM detects the nature of change, and CPD determines the exact time of occurrence. |
| Distinguishes Fault from Normal Variations? | No. TM methods may incorrectly interpret minor operational fluctuations as faults, resulting in false positives. | Yes. CPD applies statistical thresholds to confirm whether a change is significant. | TM identifies trends, while CPD quantifies whether the change is a genuine fault or just normal variation. |
| Useful for Real-Time Monitoring? | Not always. Some TM methods (e.g., FFT) require post-processing, which makes them less ideal for real-time fault detection. | Yes. CPD methods, such as BOCPD and CUSUM, operate in real-time, making them suitable for continuous condition monitoring. | TM identifies potential faults, and CPD confirms them in real-time, enabling faster maintenance response. |
| Works for Both Sudden and Gradual Faults? | No. TM works well for sudden changes (e.g., FFT, WT) but struggles with gradual deterioration. | Yes. CPD methods, such as CUSUM, can track slowly developing faults over time. | TM detects changes, and CPD helps differentiate sudden failures from progressive degradation. |
| Helps in Fault Classification? | Yes. TM methods, such as the Wavelet Transform and HHT, help distinguish between blade damage, gear misalignment, and bearing faults. | No. CPD only detects when a fault occurs, without explaining its nature. | TM provides fault classification, while CPD adds statistical validation, improving diagnostic accuracy. |
| Reduces False Alarms? | No. TM alone can misinterpret external environmental changes (such as wind variations and temperature fluctuations) as faults. | Yes. CPD ensures only statistically significant changes are flagged. | TM identifies anomalies, and CPD filters out false alarms, making fault detection more reliable. |
| Helps Predict Future Failures? | No. TM detects ongoing changes but does not forecast when failure might happen. | Yes. CPD (CUSUM, BOCPD) tracks fault progression and helps predict failures before they become critical. | TM provides trending insights, and CPD enables predictive maintenance, preventing unexpected failures. |
| Method | Category | Computational Cost | Real-Time Efficiency | Accuracy | Best Used For |
|---|---|---|---|---|---|
| Fast Fourier Transform (FFT) | TM—Frequency Analysis | Low | High | Moderate | Detecting frequency shifts in wind turbine vibrations. |
| Wavelet Transform (WT) | TM—Time-Frequency Analysis | High | Moderate | High | Identifying transient faults and multi-frequency changes. |
| Hilbert-Huang Transform (HHT) | TM—Instantaneous Frequency Analysis | High | Low | High | Tracking nonlinear and real-time frequency variations. |
| Empirical Mode Decomposition (EMD) | TM—Signal Decomposition | High | Moderate | High | Decomposing complex signals into intrinsic mode functions for analysing non-stationary faults. |
| Adaptive Filtering Denoising (AFD) | TM—Signal Smoothing | Low | High | Moderate | Preprocessing and noise reduction before fault detection. |
| Kernel Density Estimation (KDE) | CPD—Statistical Distribution | High | Low | High | Detecting statistical shifts in vibration distributions. |
| Kullback–Leibler Divergence (KL Divergence) | CPD—Statistical Divergence | High | Low | High | Measuring how much two distributions differ for fault detection. |
| Jensen-Shannon Divergence (JSD) | CPD—Statistical Divergence | Moderate | Moderate | High | Capturing statistical changes in turbine operation over time. |
| Bayesian Online Change Point Detection (BOCPD) | CPD—Bayesian Real-Time Detection | High | High | High | Detecting real-time change points for sudden faults. |
| Cumulative Sum (CUSUM) | CPD—Cumulative Sum-Based Detection | Low | High | Moderate | Tracking gradual long-term changes in turbine components. |
| Condition | Best TM Methods | Best CPD Methods | Why This Works? |
|---|---|---|---|
| Sudden Faults (e.g., gearbox misalignment, blade cracks) | WT, HHT | BOCPD, KL Divergence | Detects transient changes; CPD confirms real-time faults. |
| Gradual Faults (e.g., bearing wear, rotor imbalance) | EMD, AFD | CUSUM, JSD | Tracks long-term degradation; CPD identifies cumulative trends. |
| Real-Time Monitoring | FFT, HHT | BOCPD, CUSUM | Fast processing; CPD validates immediate and gradual faults. |
| Historical Fault Analysis | WT, EMD | KL Divergence, JSD | Monitors frequency evolution; CPD quantifies statistical shifts. |
| High Sensitivity | WT, HHT | KL Divergence, JSD | Captures subtle changes; CPD enhances statistical robustness. |
| Low False Alarms | AFD, FFT | BOCPD, CUSUM | Reduces noise and unnecessary alerts; CPD filters meaningful trends. |
| Computational Efficiency | FFT, AFD | BOCPD, CUSUM | Lightweight processing with effective real-time detection. |
| Harsh Environments | WT, EMD | BOCPD, JSD | Adapts to noise; CPD dynamically updates fault probabilities. |
| Easy Interpretation | FFT, CUSUM | CUSUM, BOCPD | Simple analysis; CPD adds statistical validation. |
| Fault Type | Best TM Method | Best CPD Method | Why This TM Method? | Why This CPD Method? | Detection Sensitivity | Components | References |
|---|---|---|---|---|---|---|---|
| Blade Crack Fault | WT | BOCPD | WT captures the frequency spikes. | BOCPD confirms abrupt changes in vibration trends. | High, may generate false positives in noisy conditions. | Blade Crack | [15,25,26,27,151,221,223,249,250,252] |
| Blade Imbalance Fault | FFT | KLD | FFT isolates imbalance-specific frequency components. | KLD detects statistical shifts in frequency distributions. | Moderate, effective for cyclic imbalance patterns. | Blade Imbalance | [218,219,234,236,250,253] |
| Blade Erosion Fault | WT | BOCPD | WT captures the irregularities in the frequency. | BOCPD finds the abrupt changes. | High, may generate false positives in noisy conditions. | Blade Erosion | [15,26,27,151,223,252,254] |
| Blade Twist Fault | FFT | CUSUM | FFT isolates twist-specific frequency components. | CUSUM detects the cumulative deviations. | Moderate to high, in detecting twist pattern. | Blade Twist | [29,66,124,192,255,256] |
| Gearbox Failure | WT | BOCPD | WT isolates gearbox-specific vibrations while filtering noise. | BOCPD detects abrupt shifts in vibration, confirming wear or misalignment. | High, effective gearbox-specific frequency bands. | Gearbox | [97,107,129,143,247,250,257,258] |
| Electrical Malfunction | FFT | KLD | FFT identifies abnormal distortions & electrical signals. | KLD tracks shift in power signal distributions. | High, useful for early-stage electrical failures. | Generator | [218,234,250] |
| Rotor Misalignment | EMD | JSD | EMD separates rotor-specific vibration components. | JSD detects minor statistical deviations in signal behaviour. | Moderate, well-suited for progressive rotor misalignment. | Rotor | [100,115,154,239,259] |
| Bearing Failure | AFD | CUSUM | AFD isolates bearing frequency bands. | CUSUM tracks cumulative deviations. | High, effective for early bearing wear detection. | Bearing | [29,243,260,261] |
| Torque Fluctuations | HHT | KL Divergence | HHT identifies fluctuations in torque components. | KLD quantifies statistical differences in power variations. | High, helpful in detecting generator load inconsistency. | Main Shaft | [155,157,218] |
| Pitch System Failure | FFT | BOCPD | FFT detects irregularities in pitch actuator signals. | BOCPD confirms sudden variations in pitch response time. | High, crucial for maintaining optimal aerodynamic efficiency. | Pitch System | [27,111,221,250,262,263] |
| Loose Bolts or Structural Instability | WT | CUSUM | WT captures transient, impact-like frequency signals. | CUSUM tracks cumulative shifts in vibrational consistency. | High, crucial for detecting progressive structural looseness. | Loose Bolts | [8,15,29,243,250] |
| Yaw System Malfunction | EMD | KL Divergence | EMD separates yaw-specific signal variations. | KL D identifies statistical deviations in yaw data. | Moderate, effective for detecting yaw misalignment over time. | Yaw System | [115,154,218,264,265,266] |
| Tower Foundation Instability | WT | JSD | WT captures long-term shifts in ground vibrations. | JSD detects evolving statistical variations. | High, useful for monitoring structural health. | Tower | [97,241,267,268] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Hassan, A.; Dao, P.B. Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines. Energies 2025, 18, 5166. https://doi.org/10.3390/en18195166
Al Hassan A, Dao PB. Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines. Energies. 2025; 18(19):5166. https://doi.org/10.3390/en18195166
Chicago/Turabian StyleAl Hassan, Abu, and Phong Ba Dao. 2025. "Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines" Energies 18, no. 19: 5166. https://doi.org/10.3390/en18195166
APA StyleAl Hassan, A., & Dao, P. B. (2025). Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines. Energies, 18(19), 5166. https://doi.org/10.3390/en18195166







